Hierarchical Wavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions
Abstract
:1. Introduction
2. Fundamental Theories
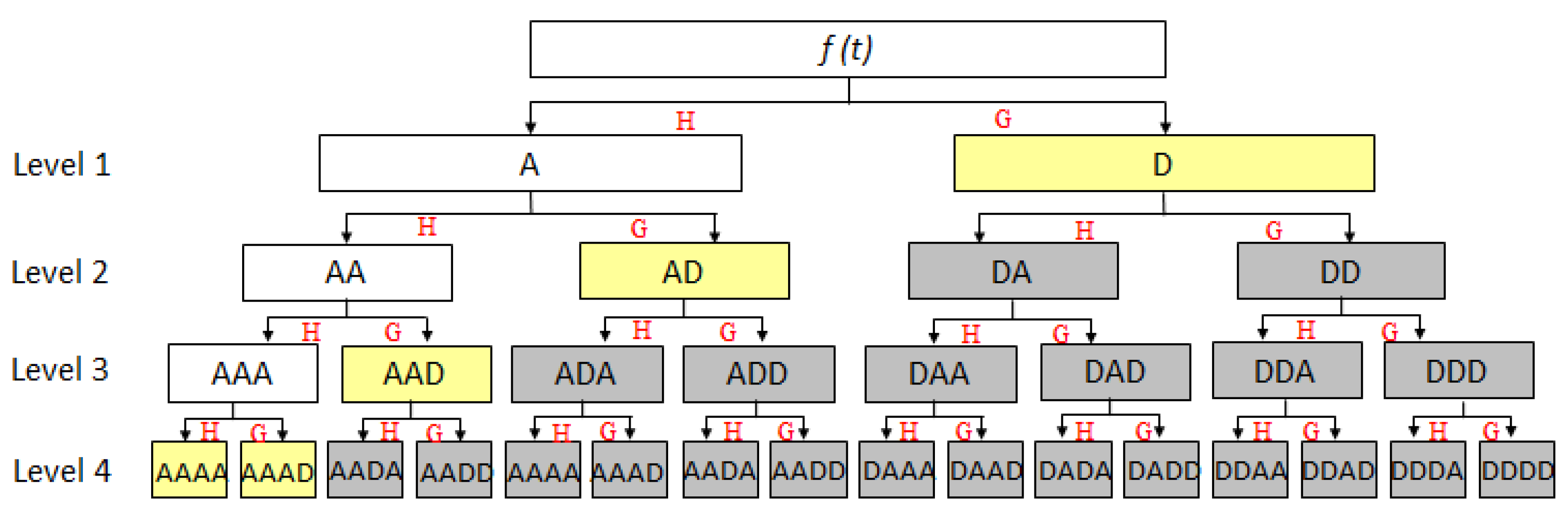
2.1. Wavelet Packet Transform (WPT)
2.2. Nonlinear Principal Component Analysis
3. Damage Identification Paradigm
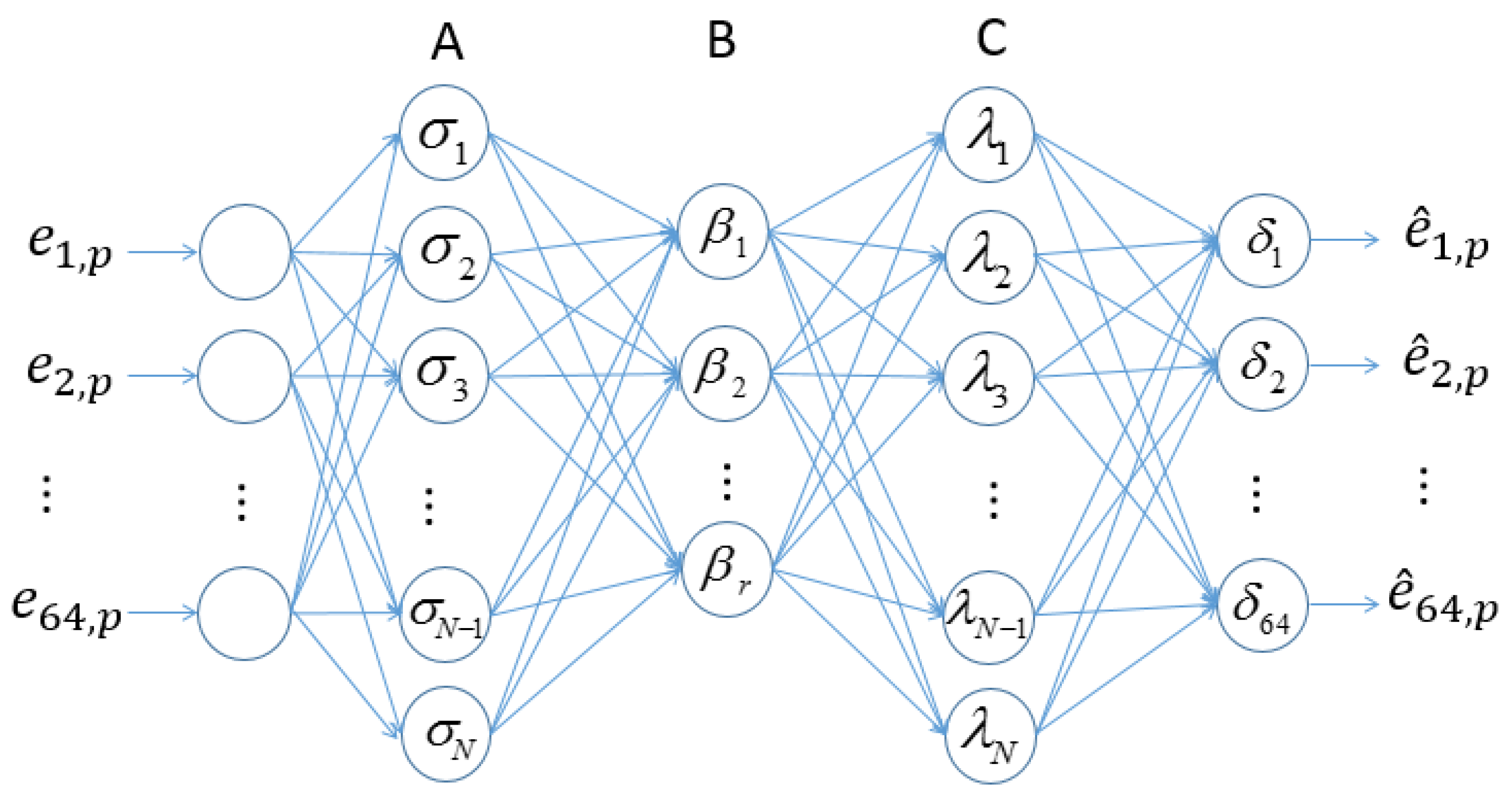
3.1. Formation of Damage Features Using AANNs
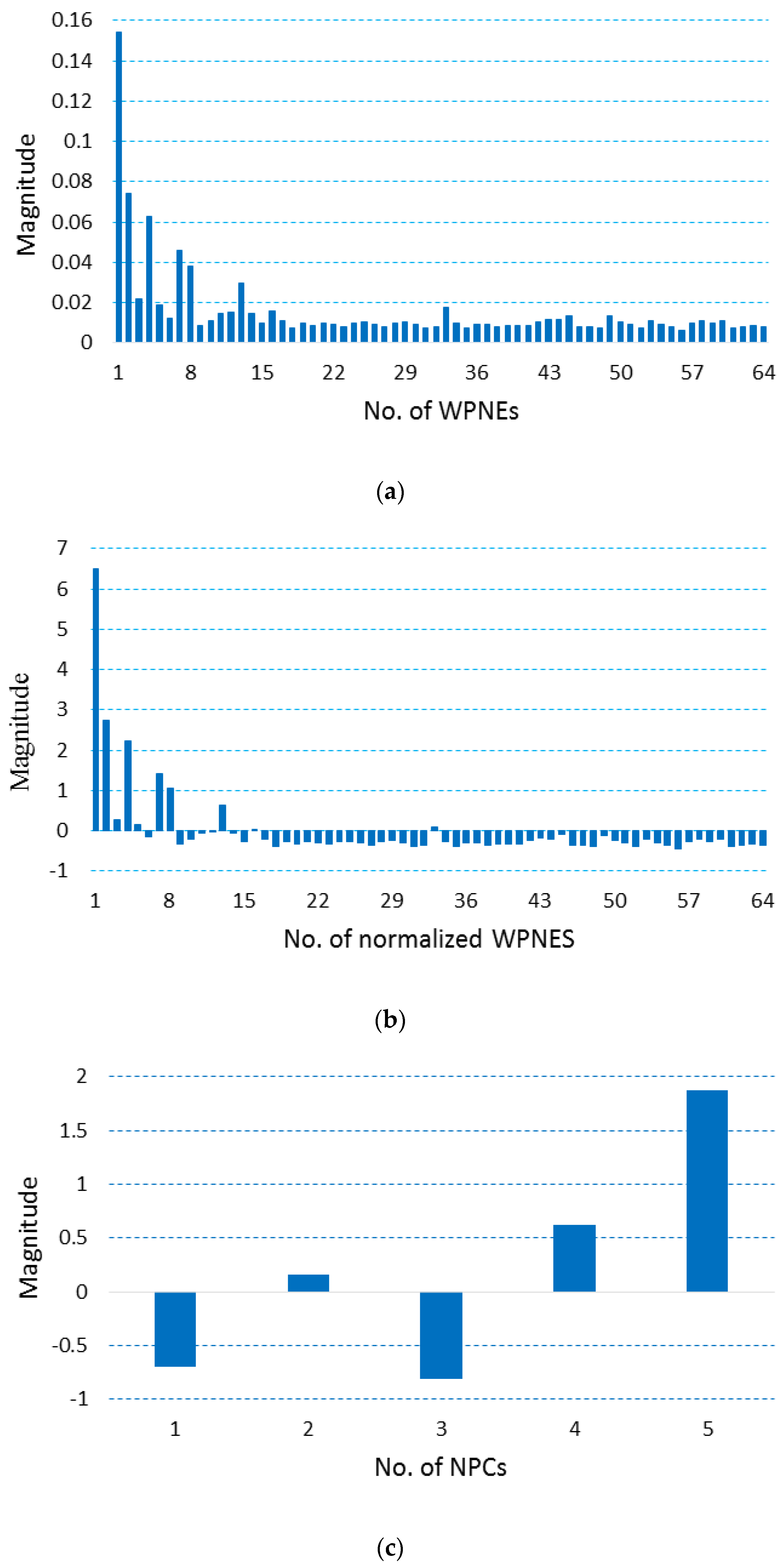
3.1.1. Wavelet Packet Node Energies (WPNEs)
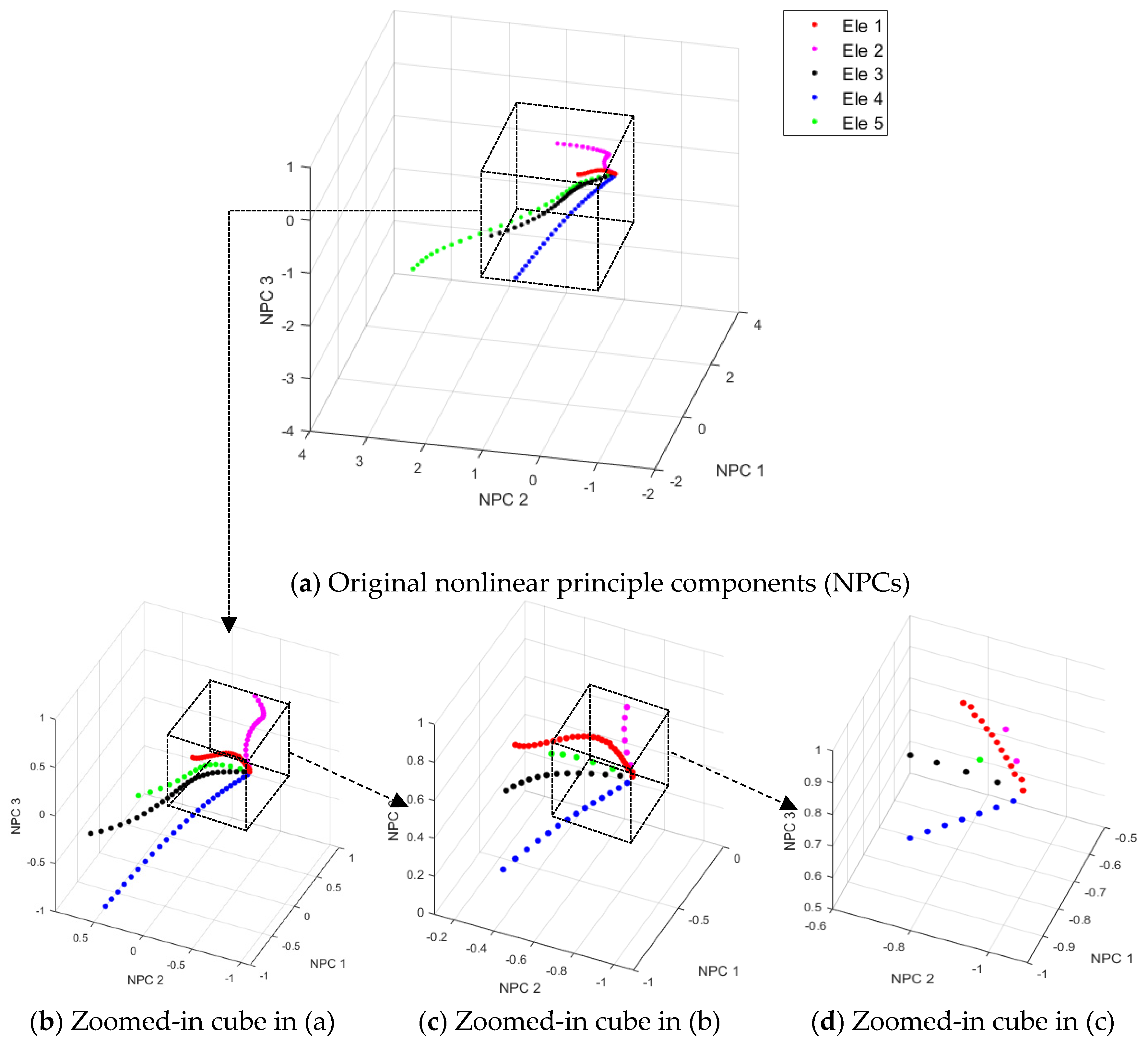
3.1.2. Damage Feature Extraction
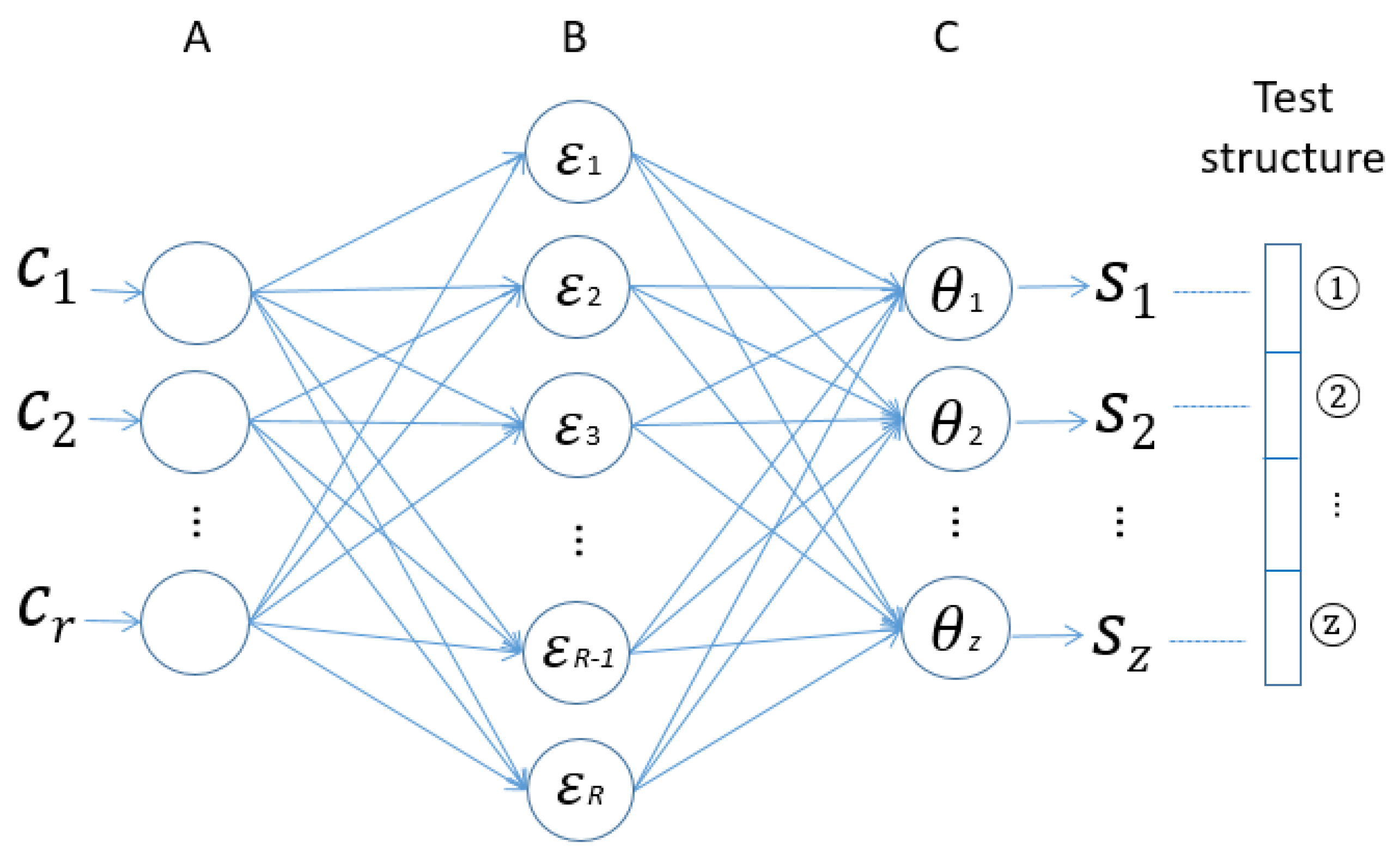
3.2. Damage Pattern Recognition
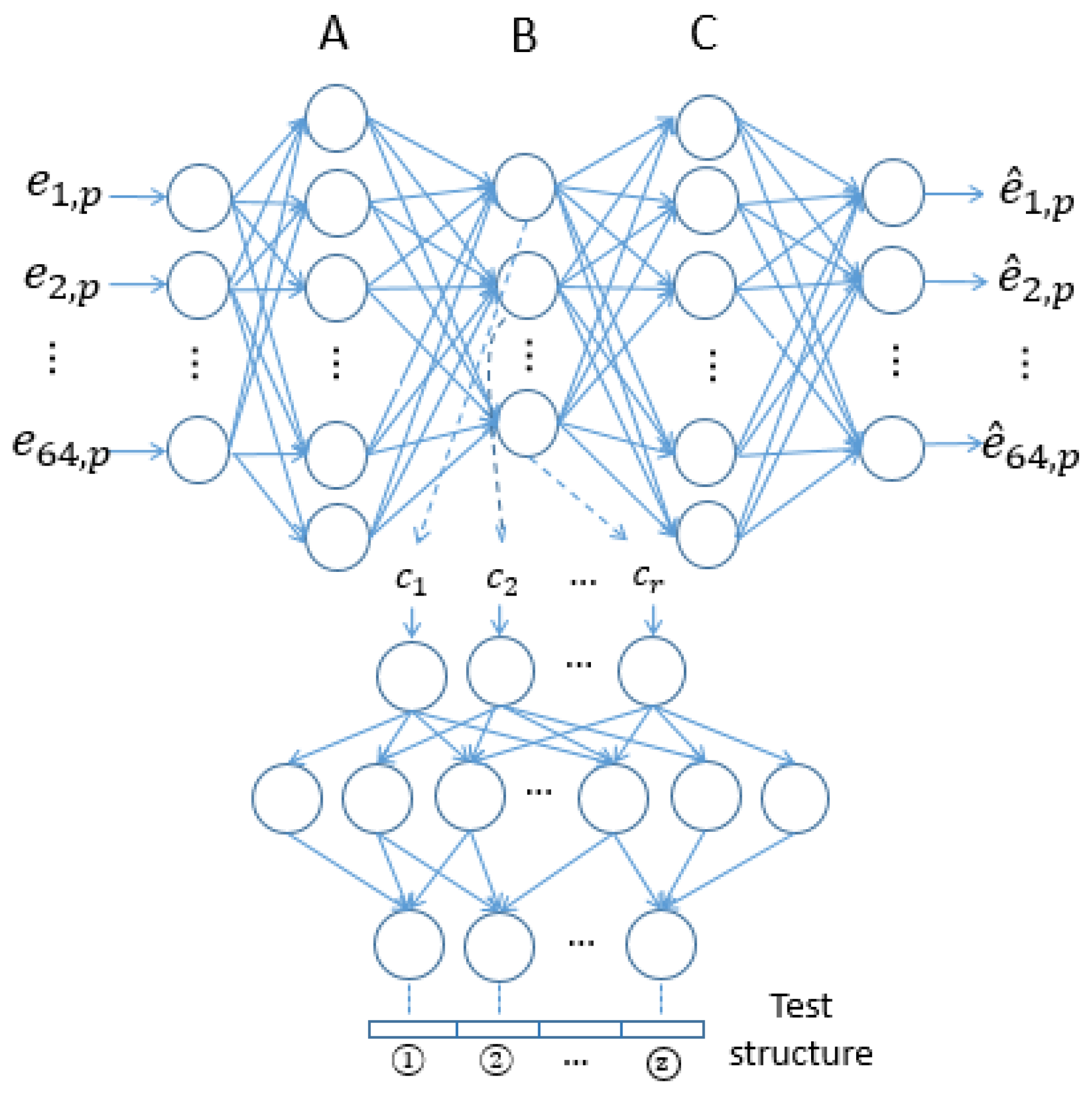
3.3. Hierarchical Neural Network Model
- (i)
- WPNEs are much more sensitive to damage than WPT coefficients, natural frequencies, and mode shapes.
- (ii)
- AANNs acting as a smart NLPCA tool can extract damage features from WPNEs. Such extracted damage features have lower dimensionality than WPNEs while preserving enough damage information.
- (iii)
- LMNNs can capture the underlying relations between damage features and damage states, on which they can recognize structural damage patterns.
- (iv)
- The special structure of the hierarchical neural network model requires a small set of training samples of damaged cases to produce accurate prediction results of damage identification with great noise robustness.
- (v)
- The hierarchical neural network model is easily implemented in a computational language, e.g., Matlab, to create an automatic program of intelligent damage assessment.
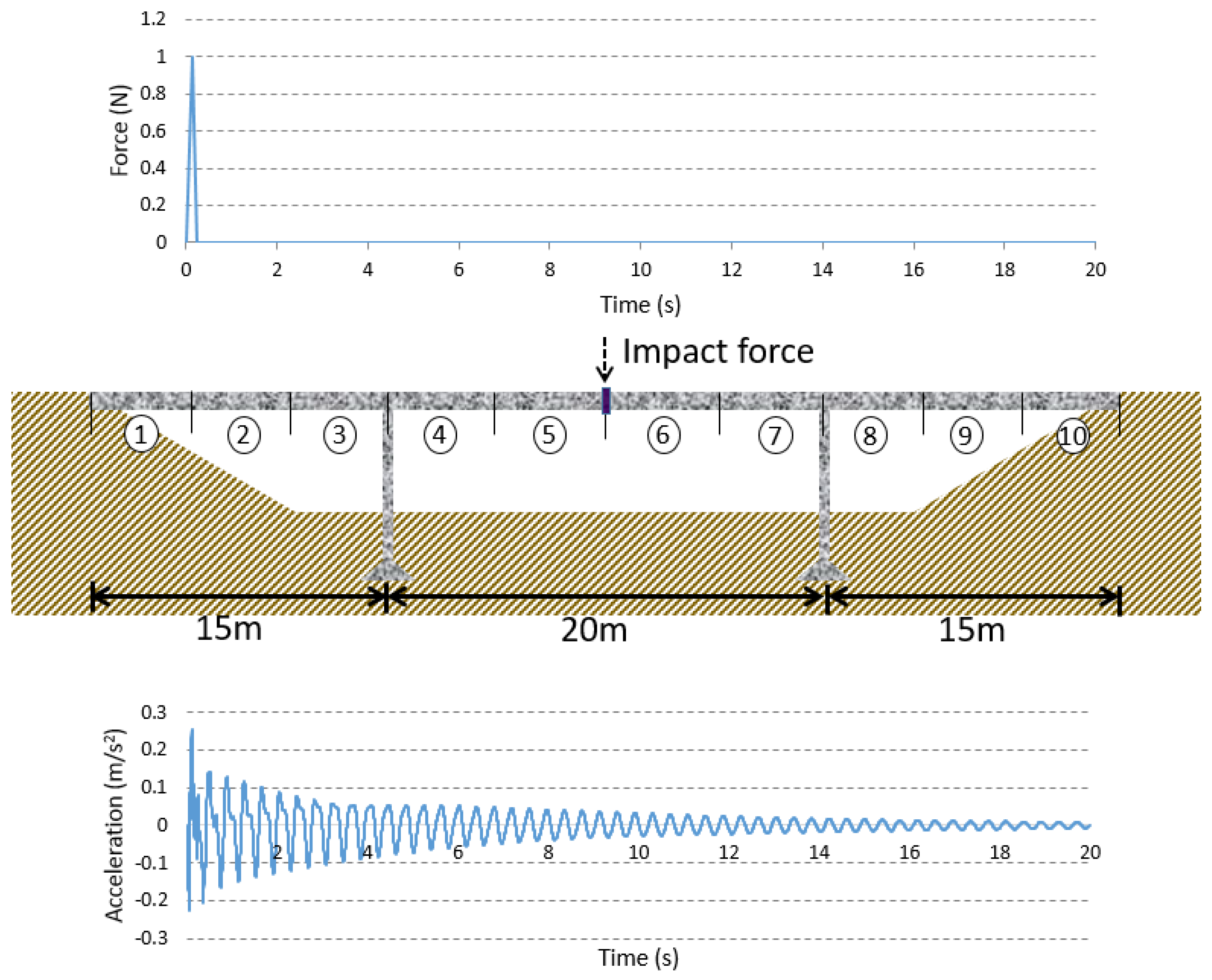
4. Numerical Verification
4.1. Damage Cases
4.2. Damage Feature Extraction
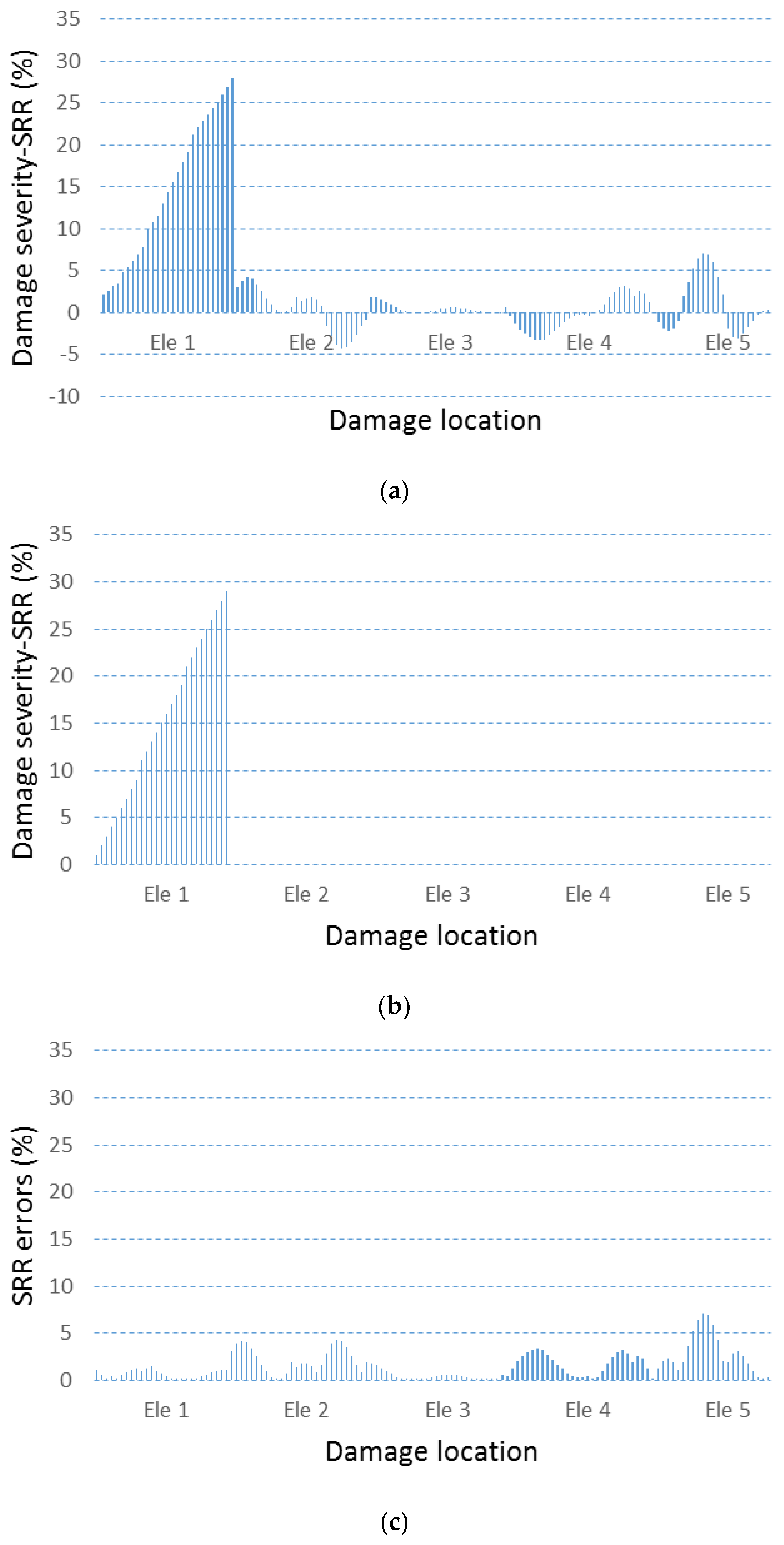
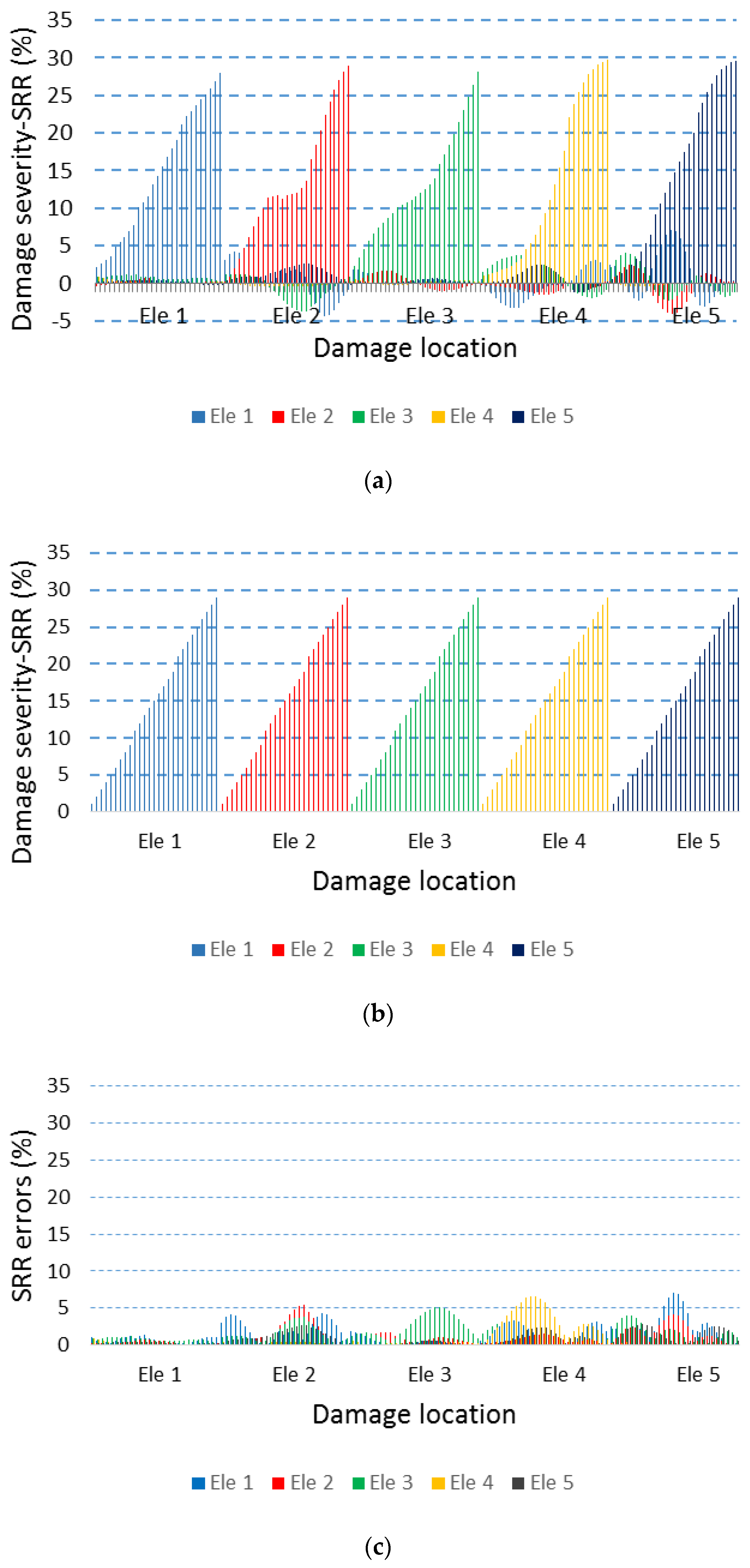
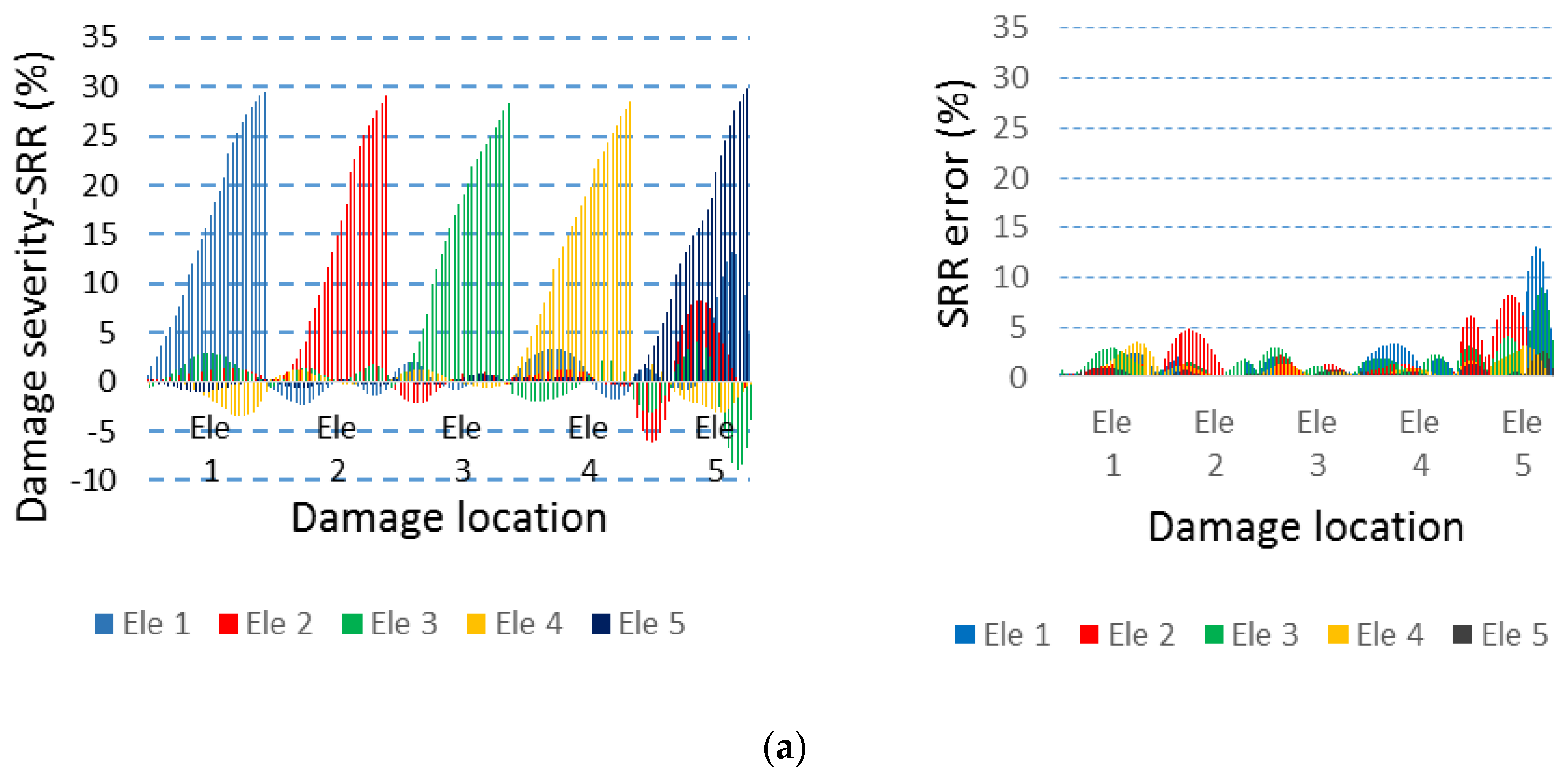
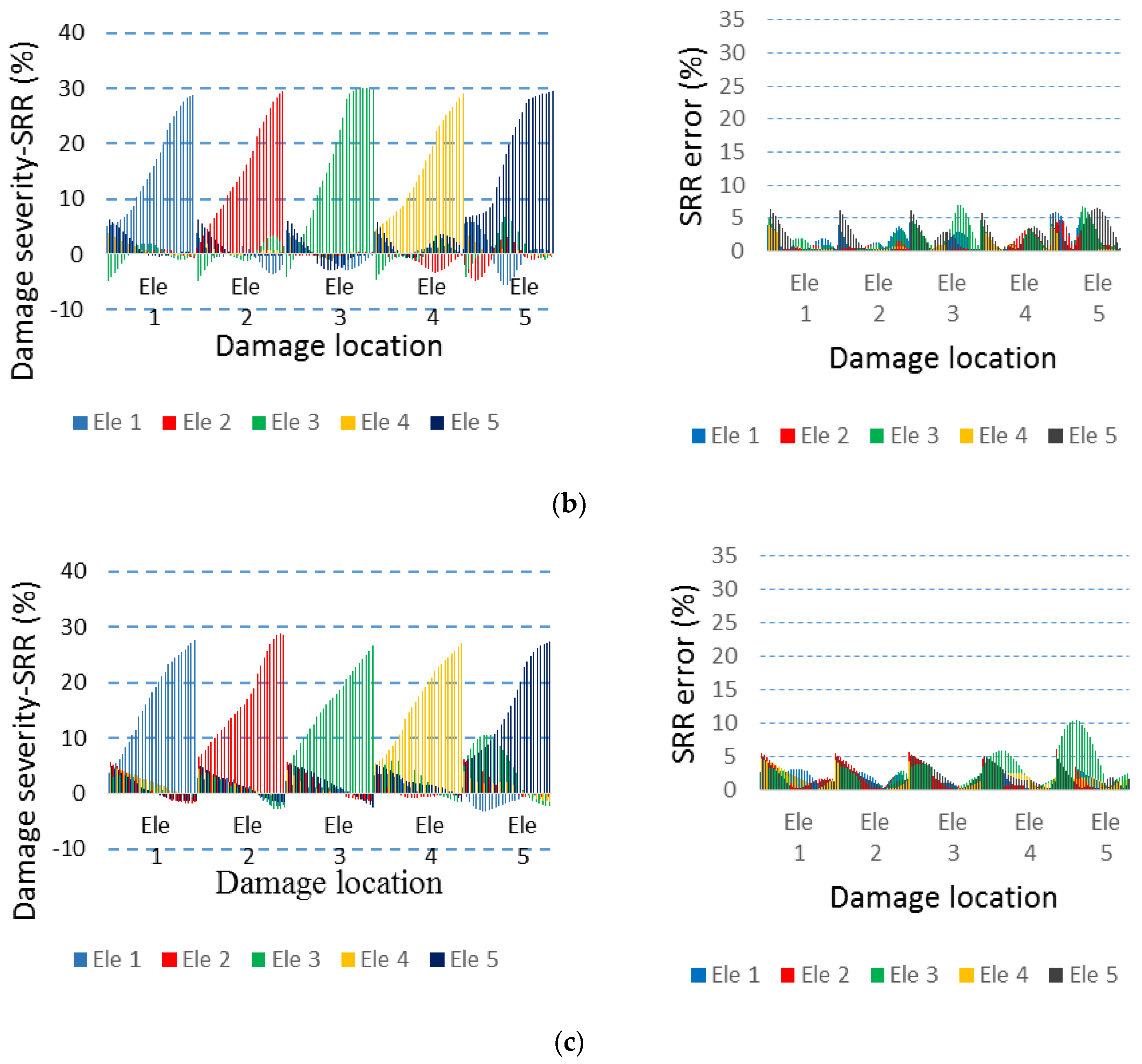
4.3. Damage Pattern Recognition
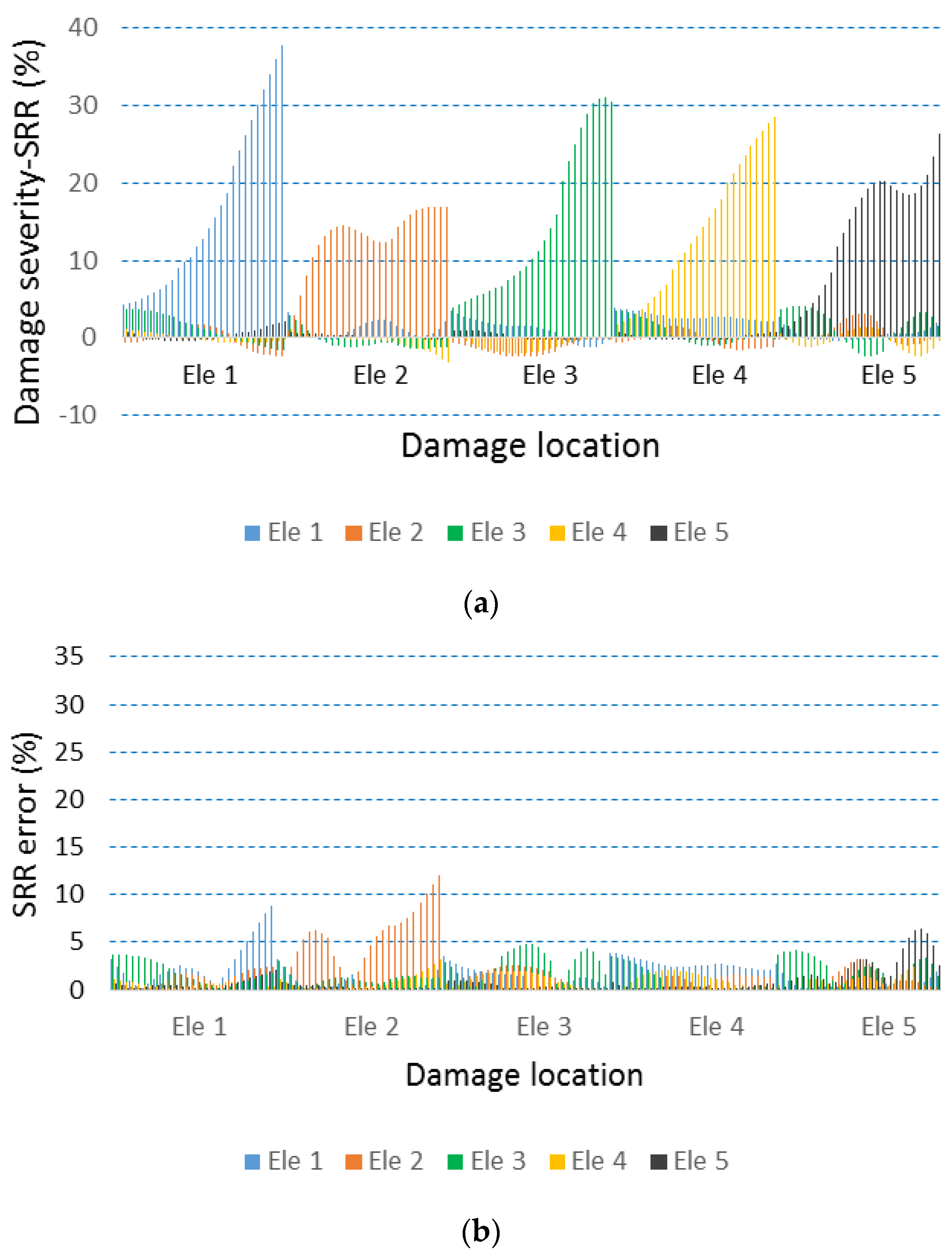
4.4. Robustness Against Noise
5. Comparison with Traditional Methods
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sohn, H.; Farrar, C.R.; Hemez, F.M. A Review of Structural Health Monitoring Literature: 1996–2001; LA-13976-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003. [Google Scholar]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Ou, J.P.; Li, H. Structural health monitoring in mainland China: Review and future trends. Struct. Health Monit. 2010, 9, 219–231. [Google Scholar]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 310–314. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Proc. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Yan, G.; Duan, Z.; Ou, J.P. Review on structural damage detection based on vibration data. Earthq. Eng. Eng. Vib. 2007, 27, 95–103. [Google Scholar]
- Fan, W.; Qiao, P.Z. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2010, 9, 83–111. [Google Scholar]
- Su, Z.Q.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]
- Zumpano, G.; Meo, M. A new damage detection technique based on wave propagation for rails. Int. J. Solids Struct. 2006, 43, 1023–1046. [Google Scholar] [CrossRef]
- Ostachowicz, W. Damage detection of structures using spectral finite element method. Comput. Struct. 2008, 86, 454–462. [Google Scholar] [CrossRef]
- Vakil-Baghmisheh, M.T.; Peimani, M.; Sadeghi, M.H. Crack detection in beam-like structures using genetic algorithms. Appl. Soft Comput. 2008, 8, 1150–1160. [Google Scholar] [CrossRef]
- Lam, H.F.; Yuen, K.V.; Beck, J.L. Structural health monitoring via measured Ritz vectors utilizing artificial neural networks. Comput. Aided Civ. Infrastruct. Eng. 2006, 21, 232–241. [Google Scholar] [CrossRef]
- Ding, Z.C.; Cao, M.S.; Jia, H.L.; Pan, L.X.; Xu, H. Structural dynamics-guided hierarchical neural-networks scheme for locating and quantifying damage in beam-type structures. J. Vibroeng. 2014, 16, 3595–3608. [Google Scholar]
- Mehrjoo, M.; Khaji, N. Ghafory-Ashtiany, Application of genetic algorithm in crack detection of beam-like structures using a new cracked Euler–Bernoulli beam element. Appl. Soft Comput. 2013, 13, 867–880. [Google Scholar] [CrossRef]
- Beena, P.; Ganguli, R. Structural damage detection using fuzzy cognitive maps and Hebbian learning. Appl. Soft Comput. 2011, 11, 1014–1020. [Google Scholar] [CrossRef]
- Cao, M.S.; Qiao, P.Z.; Ren, Q.W. Improved hybrid wavelet neural network methodology for time-varying behavior prediction of engineering structures. Neural Comput. Appl. 2009, 18, 821–832. [Google Scholar] [CrossRef]
- Hossain, M.S.; Ong, Z.C.; Ismail, Z.; Noroozi, S.; Khoo, S.Y. Artificial neural networks for vibration based inverse parametric identifications: A review. Appl. Soft Comput. 2017, 52, 203–219. [Google Scholar] [CrossRef]
- Hakim, S.J.S.; Razak, H.A. Modal parameters based structural damage detection using artificial neural networks—A review. Smart Struct. Syst. 2014, 14, 159–189. [Google Scholar] [CrossRef]
- Worden, K.; Burrows, A.P. Optimal sensor placement for fault detection. Eng. Struct. 2001, 23, 885–901. [Google Scholar] [CrossRef]
- Worden, K.; Ball, A.D.; Tomlinson, G.R. Fault location in structures using neural networks. In Proceedings of the 75th Meeting of the AGARD Structures and Materials Panel on Smart Structures for Aircraft and Spacecraft, Lindau, Germany, 5–7 October 1992; pp. 1–9. [Google Scholar]
- Ni, Y.Q.; Wang, B.S.; Ko, J.M. Constructing input vectors to neural networks for structural damage identification. Smart Mater. Struct. 2002, 11, 825–833. [Google Scholar] [CrossRef]
- Zubaydi, A.; Haddara, M.R.; Swamidas, A.S.J. Damage identification in a ship’s structure using neural networks. Ocean Eng. 2002, 29, 1187–1200. [Google Scholar] [CrossRef]
- Sahoo, B.; Maity, D. Damage assessment of structures using hybrid neuro-genetic algorithm. Appl. Soft Comput. 2007, 7, 89–104. [Google Scholar] [CrossRef]
- Hakim, S.J.S.; Razak, H.A. Frequency response function-based structural damage identification using artificial neural networks—A review. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 1750–1764. [Google Scholar] [CrossRef]
- Cao, M.S.; Qiao, P.Z. Integrated wavelet transform and its application to vibration mode shapes for the damage detection of beam-type structures. Smart Mater. Struct. 2008, 17, 6777–6790. [Google Scholar] [CrossRef]
- Hou, Z.K.; Noori, M.N.; Amand, R.S. Wavelet-based approach for structural damage detection. J. Eng. Mech. 2000, 126, 677–683. [Google Scholar] [CrossRef]
- Taha, M.M.R. Wavelet transform for structural health monitoring: A compendium of uses and features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Cao, M.S.; Cheng, L.; Su, Z.Q. A multi-scale pseudo-force model in wavelet domain for identification of damage in structural components. Mech. Syst. Signal Proc. 2012, 28, 638–659. [Google Scholar] [CrossRef]
- Yen, G.G.; Lin, K.C. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar] [CrossRef]
- Han, J.G.; Ren, W.X.; Sun, Z.S. Wavelet packet based damage identification of beam structures. Int. J. Solids Struct. 2005, 42, 6610–6627. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q.; Tian, Y.J. Statistical damage classification method based on wavelet packet analysis. Struct. Eng. Mech. 2013, 46, 459–486. [Google Scholar] [CrossRef]
- Jiang, X.; Mahadevan, S.; Adeli, H. Bayesian wavelet packet denoising for structural system identification. Struct. Control Health Monit. 2007, 14, 333–356. [Google Scholar] [CrossRef]
- Ravanfar, S.A.; Razak, H.A.; Ismail, Z. A hybrid wavelet based–approach and genetic algorithm to detect damage in beam-like structures without baseline data. Exp. Mech. 2016, 56, 1–16. [Google Scholar] [CrossRef]
- Chiariotti, P.; Martarelli, M.; Revel, G.M. Delamination detection by Multi-Level Wavelet Processing of Continuous Scanning Laser Doppler Vibrometry data. Opt. Lasers Eng. 2017. [Google Scholar] [CrossRef]
- Asgarian, B.; Aghaeidoost, V.; Shokrgozar, H.R. Damage detection of jacket type offshore platforms using rate of signal energy using wavelet packet transform. Mar. Struct. 2016, 45, 1–21. [Google Scholar] [CrossRef]
- Yam, L.H.; Yan, Y.J.; Jiang, J.S. Vibration-based damage detection for composite structures using wavelet transform and neural network identification. Compos. Struct. 2003, 60, 403–412. [Google Scholar] [CrossRef]
- Zhu, F.; Deng, Z.; Zhang, J. An integrated approach for structural damage identification using wavelet neuro-fuzzy model. Expert Syst. Appl. 2013, 40, 7415–7427. [Google Scholar] [CrossRef]
- Diao, Y.S.; Li, H.J.; Wang, Y. A two-step structural damage detection approach based on wavelet packet analysis and neural network. In Proceedings of the IEEE International Conference on Machine Learning and Cybernetics, 13–16 August 2006; pp. 3128–3133. [Google Scholar]
- Taha, M.M.R. A neural-wavelet technique for damage identification in the ASCE benchmark structure using phase II experimental data. Adv. Civ. Eng. 2010, 2010, 1–13. [Google Scholar] [CrossRef]
- Yan, G.R.; Duan, Z.D.; Ou, J.P. Structural damage detection by wavelet transform and probabilistic neural network. Smart Struct Mater. 2005, 5765, 892–900. [Google Scholar]
- Evagorou, D.; Kyprianou, A.; Lewin, P.L. Feature extraction of partial discharge signals using the wavelet packet transform and classification with a probabilistic neural network. IET Sci. Meas. Technol. 2010, 4, 177–192. [Google Scholar] [CrossRef]
- Torres-Arredondo, M.A.; Buethe, I.; Tibaduiza, D.A. Damage detection and classification in pipework using acousto-ultrasonics and non-linear data-driven modelling. J. Civ. Struct. Health Monit. 2013, 3, 297–306. [Google Scholar] [CrossRef]
- Sahin, M.; Shenoi, R.A. Quantification and localization of damage in beam-like structures by using artificial neural networks with experimental validation. Eng. Struct. 2003, 25, 1785–1802. [Google Scholar] [CrossRef]
- Jeyasehar, C.A.; Sumangala, K. Nondestructive evaluation of prestressed concrete beams using an artificial neural network (ANN) approach. Struct. Health Monit. 2006, 5, 313–323. [Google Scholar] [CrossRef]
- Chakraverty, S.; Gupta, P.; Sharma, S. Neural network-based simulation for response identification of two-storey shear building subject to earthquake motion. Neural Comput. Appl. 2010, 19, 367–375. [Google Scholar] [CrossRef]
- Law, S.S.; Li, X.Y.; Zhu, X.Q. Structural damage detection from wavelet packet sensitivity. Eng. Struct. 2005, 27, 1339–1348. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R.Q. Wavelet Packet Transform-Theory and Applications for Manufacturing; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kruger, U.; Zhang, J.; Xie, L. Developments and applications of nonlinear principal component analysis—A review. Lect. Notes Comput. Sci. Eng. 2008, 58, 1–43. [Google Scholar]
- Cao, M.S.; Pan, L.X.; Gao, Y.F. Neural network ensemble-based parameter sensitivity analysis in civil engineering systems. Neural Comput. Appl. 2015, 26, 1–8. [Google Scholar] [CrossRef]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AICHE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Sun, Z.; Chang, C.C. Structural damage assessment based on wavelet packet transform. J. Struct. Eng. 2002, 128, 1354–1361. [Google Scholar] [CrossRef]
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef] [PubMed]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical damage classification under changing environmental and operational conditions. J. Intell. Mater. Syst. Struct. 2002, 13, 561–574. [Google Scholar] [CrossRef]
- Suratgar, A.A.; Tavakoli, M.B.; Hoseinabadi, A. Modified Levenberg-Marquardt method for neural networks training. World Acad. Sci. Eng. Technol. 2005, 6, 46–48. [Google Scholar]
- Maeck, J.; Peeters, B.; Deroeck, G. Damage identification on the Z24 bridge using vibration monitoring. Smart Mater. Struct. 2001, 10, 512–517. [Google Scholar] [CrossRef]
- Reynders, E.; Wursten, G.; Roeck, G.D. Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification. Struct. Health Monit. 2013, 13, 82–93. [Google Scholar] [CrossRef]
- Spiridonakos, M.D.; Chatzi, E.N.; Sudret, B. Polynomial chaos expansion models for the monitoring of structures under operational variability. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2016, 2. [Google Scholar] [CrossRef]
- Sun, Y. Combined neural network and PCA for complicated damage detection of bridge. In Proceedings of the International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; pp. 524–528. [Google Scholar]
| Properties | Values |
|---|---|
| Mass density | |
| Young’s modulus | |
| Cross-sectional area | |
| Moment of inertial | |
| Damping ratio |
| Case Number | Damaged Element | SRR (%) |
|---|---|---|
| 1–30 | 1 | 1, 2, …, 30 |
| 31–60 | 2 | 1, 2, …, 30 |
| 61–90 | 3 | 1, 2, …, 30 |
| 91–120 | 4 | 1, 2, …, 30 |
| 121–150 | 5 | 1, 2, …, 30 |
| Element | Training Set | Testing Set |
|---|---|---|
| SRR (%) | SRR (%) | |
| 1 | 10 | 1, 2, …, 9 |
| 20 | 11, 12, …, 19 | |
| 30 | 21, 22, …, 29 | |
| 2 | 10 | 1, 2, …, 9 |
| 20 | 11, 12, …, 19 | |
| 30 | 21, 22, …, 29 | |
| 3 | 10 | 1, 2, …, 9 |
| 20 | 11, 12, …, 19 | |
| 30 | 21, 22, …, 29 | |
| 4 | 10 | 1, 2, …, 9 |
| 20 | 11, 12,…, 19 | |
| 30 | 21, 22, …, 29 | |
| 5 | 10 | 1, 2, …, 9 |
| 20 | 11, 12, …, 19 | |
| 30 | 21, 22, …, 29 |
| Noise | SNR (dB) | |||
| 10 | 20 | 30 | ||
| MSE | 4.892 | 4.94 | 7.138 | 3.309 |
| Maximum error | 13.1 | 7.048 | 10.462 | 7.044 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.-S.; Ding, Y.-J.; Ren, W.-X.; Wang, Q.; Ragulskis, M.; Ding, Z.-C. Hierarchical Wavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions. Appl. Sci. 2017, 7, 391. https://doi.org/10.3390/app7040391
Cao M-S, Ding Y-J, Ren W-X, Wang Q, Ragulskis M, Ding Z-C. Hierarchical Wavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions. Applied Sciences. 2017; 7(4):391. https://doi.org/10.3390/app7040391
Chicago/Turabian StyleCao, Mao-Sen, Yu-Juan Ding, Wei-Xin Ren, Quan Wang, Minvydas Ragulskis, and Zhi-Chun Ding. 2017. "Hierarchical Wavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions" Applied Sciences 7, no. 4: 391. https://doi.org/10.3390/app7040391
APA StyleCao, M.-S., Ding, Y.-J., Ren, W.-X., Wang, Q., Ragulskis, M., & Ding, Z.-C. (2017). Hierarchical Wavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions. Applied Sciences, 7(4), 391. https://doi.org/10.3390/app7040391








