Simplified Swarm Optimization-Based Function Module Detection in Protein–Protein Interaction Networks
Abstract
:1. Introduction
- We investigate PPI datasets and existing function module detection methods and select four typical species of protein-protein interaction data from the DIP database for the experiment. A specific data crawler is developed to extract data features from these datasets.
- The proposed PPIN function module detection is described from a few aspects: system model, feature selection, mathematical description, model optimization, etc. The proposed solution implements an SSO algorithm for clustering proteins with similar function and imports biological gene ontology knowledge for further identification.
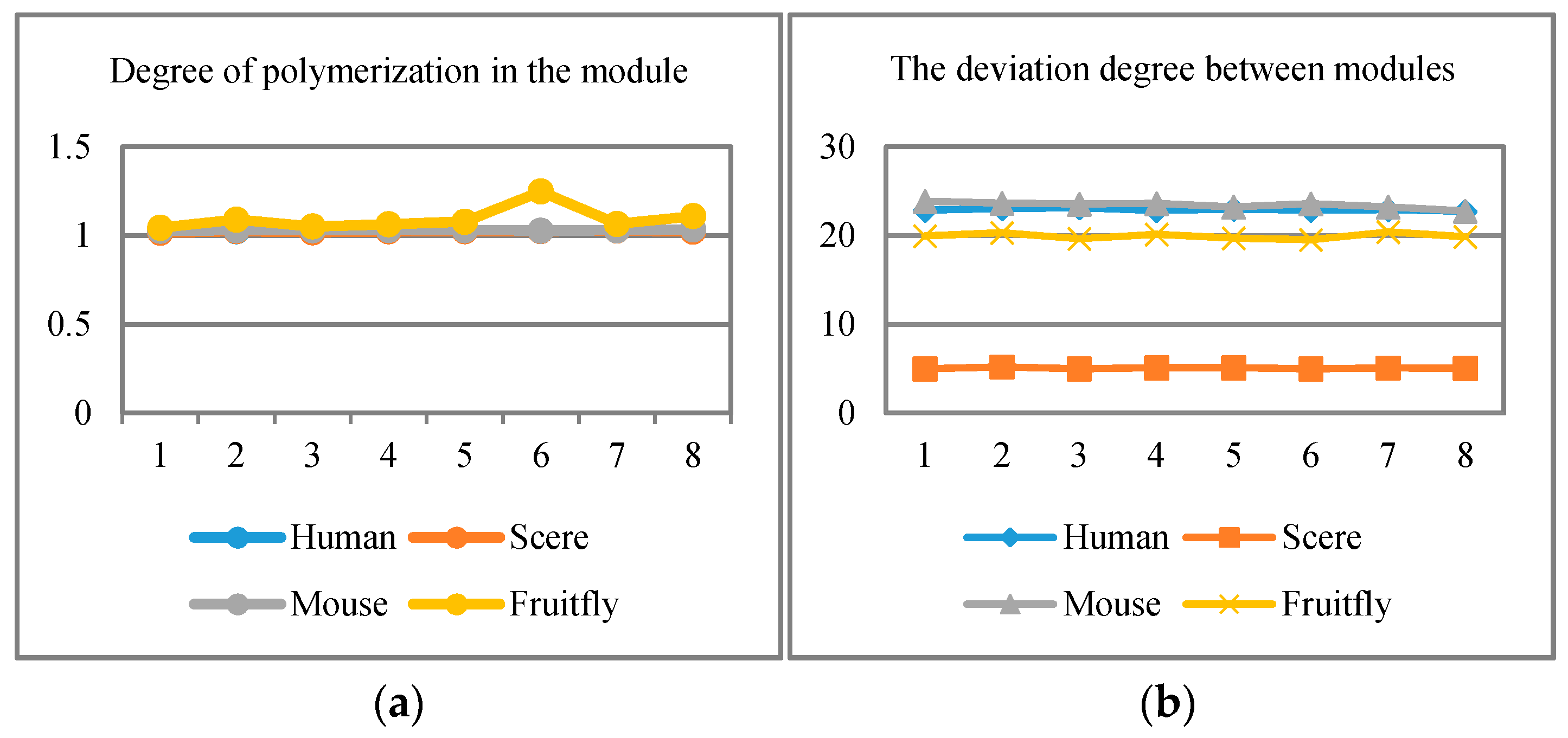
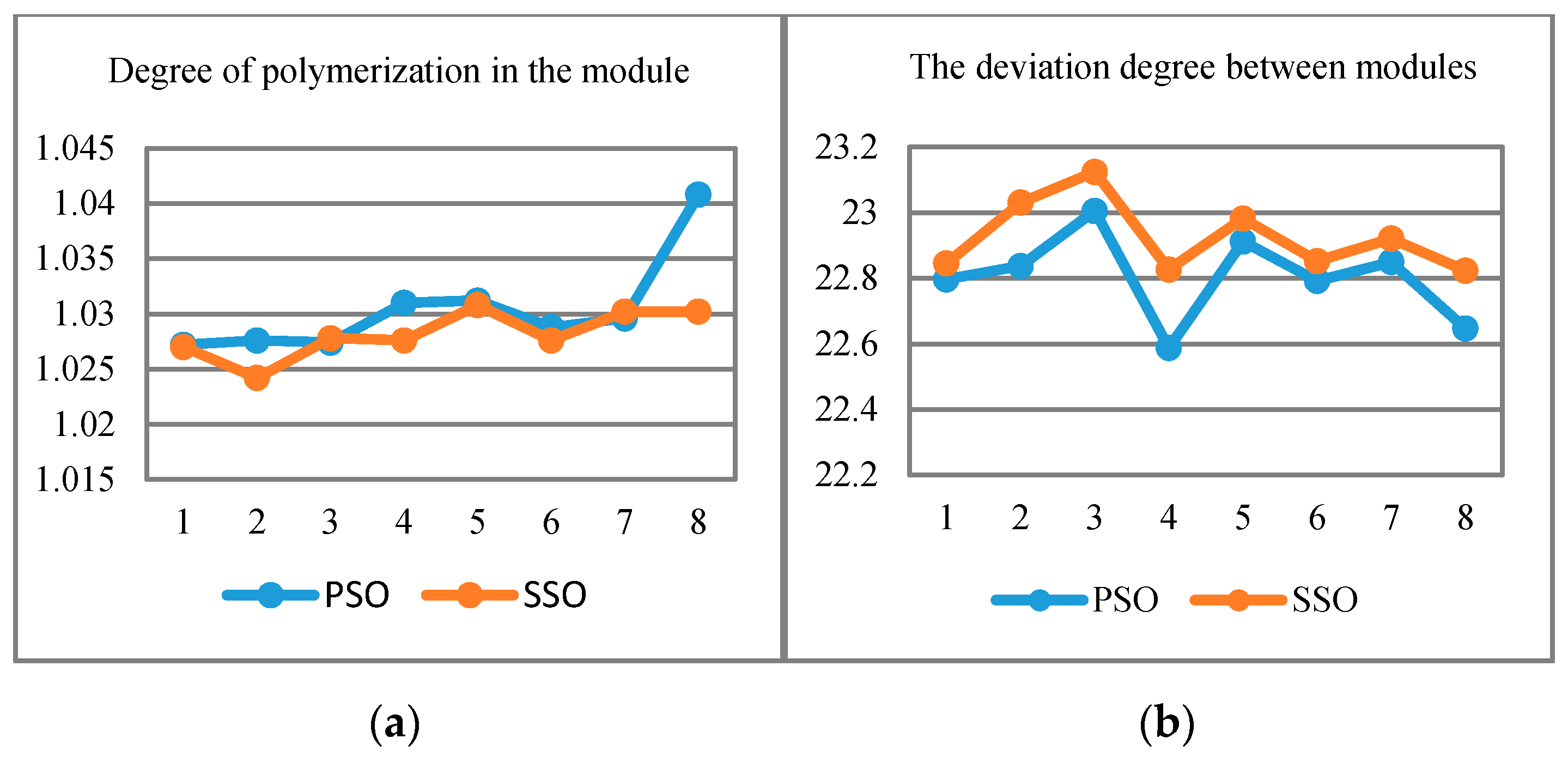
- Experiments are conducted to validate feasibility and efficiency of the proposed approaches. The evaluation of “degree of polymerization” and “similarity between classes” further proves the precision improvement and correctness of our proposed solution.
2. Related Works
2.1. Protein–Protein Interaction Datasets
2.2. Existing Works
2.3. Clustering Evaluation
2.4. Discussion
3. Simplified Swarm Optimization-Based Detection
3.1. Interaction Model
3.2. Feature Extraction
- Noise Filter. Noise data refers to the existence of errors, redundant data, or abnormal data in crawled data. For example, in interaction.xml-based crawled data, the tag field “DIP-nnE” may be empty or not found. Therefore, eliminating noise and redundant data is the first step before the experiment.
- Feature Selection. Feature selection is performed through the manual respection of protein xml data. For example, in the main part of the XML file, the tag names “interactorList” and “interactionList” indicate the interaction relationship among protein nodes. Therefore, feature data are selected through the manual inspection of protein data.
- Feature Extraction and Reformat. After the feature selection, related data (e.g., protein id and interactor id) are extracted, reformatted, and stored in the structured database.
3.3. Mathematics Model
3.3.1. Model Establishment
3.3.2. Parameter Setting
3.4. Model Optimization
3.4.1. Module Planning Based on Function Information
3.4.2. Module Planning Based on Topology
4. Experiments
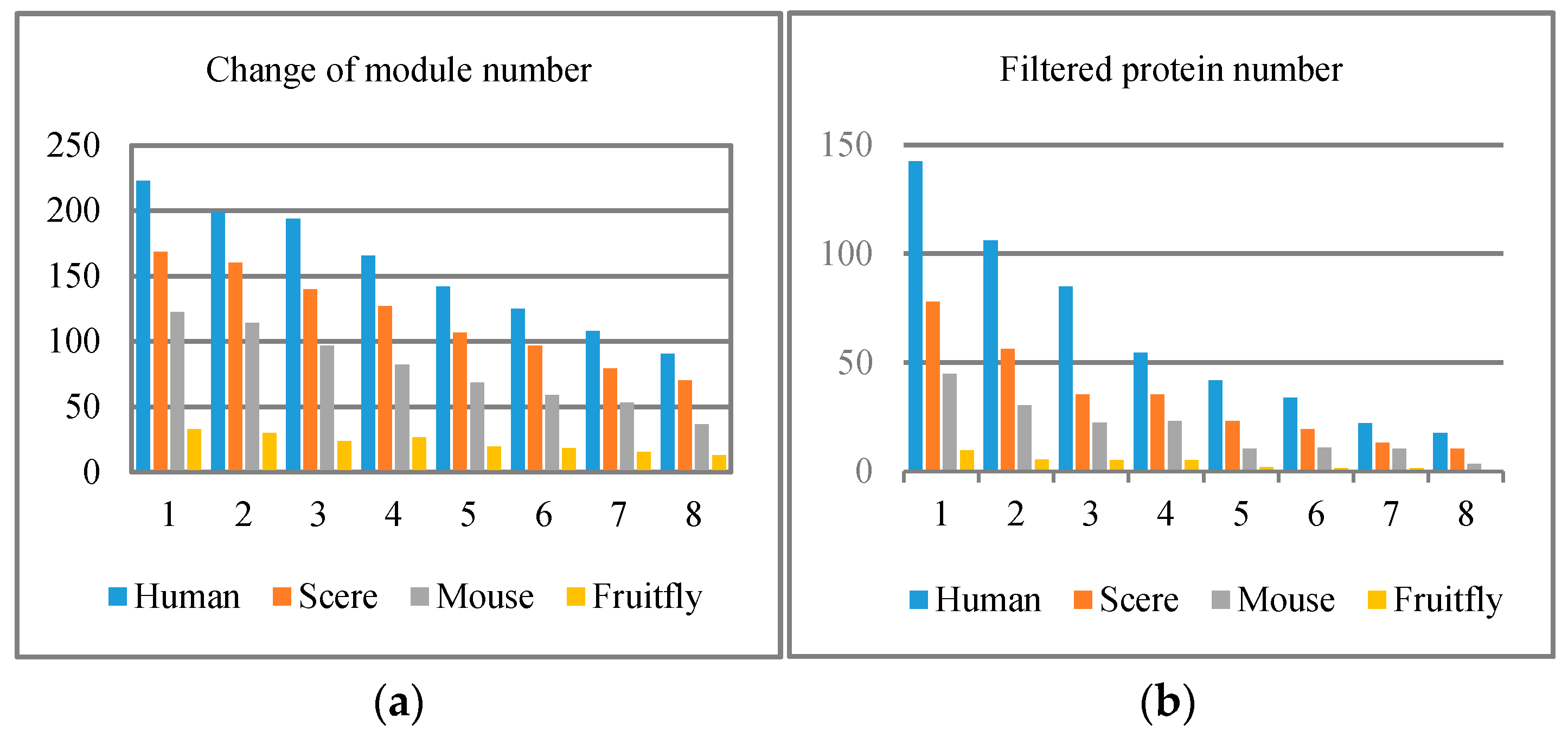
4.1. Dataset Description
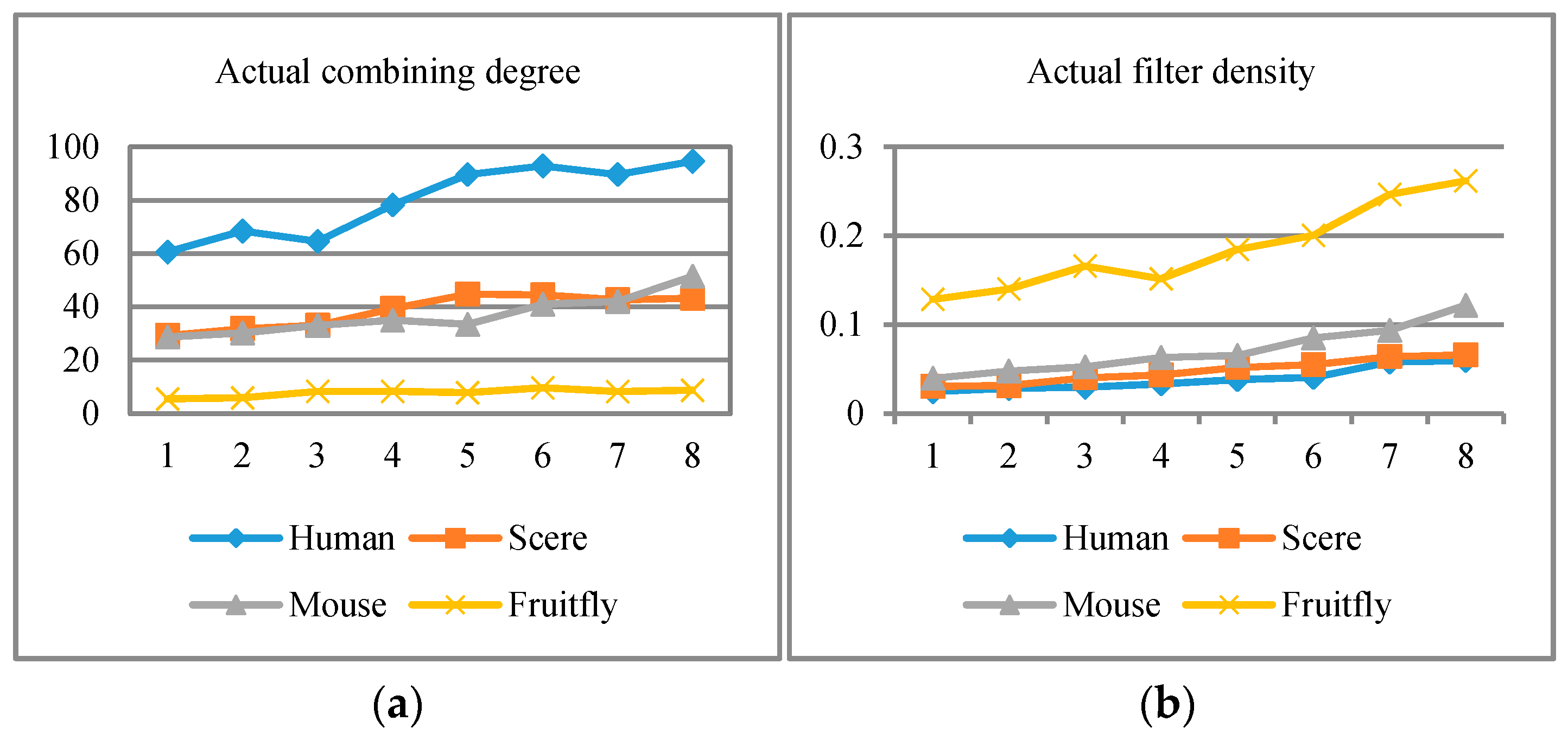
4.2. Evaluations
4.2.1. Complexity and Running Times
4.2.2. Results Analysis via Threshold Setting
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, B.; Guan, J. From function to interaction: A new paradigm for accurately predicting protein complexes based on protein-to-protein interaction networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 616–627. [Google Scholar] [PubMed]
- Islam, M.F.; Hoque, M.M.; Banik, R.S.; Roy, S.; Sumi, S.S.; Hassan, F.M.N.; Tomal, M.T.S.; Ullah, A.; Rahman, K.M.T. Comparative analysis of differential network modularity in tissue specific normal and cancer protein interaction networks. J. Clin. Bioinform. 2013, 3, 19. [Google Scholar] [CrossRef] [PubMed]
- Ahn, Y.Y.; Bagrow, J.P.; Lehmann, S. Link communities reveal multiscale complexity in networks. Nature 2010, 435, 761–764. [Google Scholar] [CrossRef] [PubMed]
- Kachroo, A.H.; Laurent, J.M.; Yellman, C.M.; Meyer, A.G.; Wilke, C.O.; Marcotte, E.M. Systematic humanization of yeast genes reveals conserved functions and genetic modularity. Science 2015, 348, 921–925. [Google Scholar] [CrossRef] [PubMed]
- Tanay, A.; Sharan, R.; Kupiec, M.; Shamir, R. Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proc. Natl. Acad. Sci. USA 2004, 101, 2981–2986. [Google Scholar] [CrossRef] [PubMed]
- Szklarczyk, D.; Franceschini, A.; Wyder, S.; Forslund, K.; Heller, D.; Huerta-Cepas, J.; Simonovic, M.; Roth, A.; Santos, A.; Tsafou, K.P.; et al. Protein–protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015, 39, D561–D568. [Google Scholar]
- Ding, Y.; Tang, J.; Guo, F. Identification of Protein–Protein Interactions via a Novel Matrix-Based Sequence Representation Model with Amino Acid Contact Information. Int. J. Mol. Sci. 2016, 17, 1623. [Google Scholar] [CrossRef] [PubMed]
- Szklarczyk, D.; Franceschini, A.; Kuhn, M.; Simonovic, M.; Roth, A.; Minguez, P.; Doerks, T.; Stark, M.; Muller, J.; Bork, P.; et al. The STRING database in 2011: Functional interaction networks of proteins, globally integrated and scored. Nucleic Acids Res. 2011, 1093, D561–D568. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Li, X.; Zhang, Z.; Song, J. Identifying Coevolution between Amino Acid Residues in Protein Families: Advances in the Improvement and Evaluation of Correlated Mutation Algorithms. Curr. Bioinform. 2013, 8, 148–160. [Google Scholar] [CrossRef]
- Li, H.; Chang, Y.; Yang, L.; Bahar, I. The Gaussian network model database for biomolecular structural dynamics. Nucleic Acids Res. 2016, 44, D415–D422. [Google Scholar] [CrossRef] [PubMed]
- Blohm, P.; Frishman, G.; Smialowski, P. A database of non-interacting proteins derived by literature mining, manual annotation and protein structure analysis. Nucleic Acids Res. 2014, 42, D396–D400. [Google Scholar] [CrossRef] [PubMed]
- Orchard, S.; Ammari, M.; Aranda, B.; Breuza, L.; Briganti, L.; Broackes-Carter, F.; Nancy, H.; Campbell, G.C.; Chen, C.; del-Toro, N. The MIntAct project—IntAct as a common curation platform for 11 molecular interaction databases. Nucleic Acids Res. 2014, 1093, D358–D363. [Google Scholar] [CrossRef] [PubMed]
- Motono, C.; Nakata, J.; Koike, R. A comprehensive database of predicted structures of all human proteins. Nucleic Acids Res. 2011, 39, D487–D493. [Google Scholar] [CrossRef] [PubMed]
- Licata, L.; Briganti, L.; Peluso, D. MINT, the molecular interaction database: 2012 update. Nucleic Acids Res. 2012, 40, D857–D861. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.Z.; Jiao, L.; Yang, C.C.; Lv, J.W.; Zhang, A.D. MAE-FMD: Multi-agent evolutionary method for functional module detection in protein-protein interaction networks. BMC Bioinform. 2014, 15, 325. [Google Scholar] [CrossRef] [PubMed]
- Ester, B.M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density Based algorithm for discovering clusters in large spatial databases with Noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013. [Google Scholar]
- Newman, M.E. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Hartuv, E.; Shamir, R. A clustering algorithm based on graph connectivity. Inf. Proc. Lett. 2000, 76, 175–181. [Google Scholar] [CrossRef]
- Rujirapipat, S.; Mcgarry, K.; Nelson, D. Bioinformatic Analysis Using Complex Networks and Clustering Proteins Linked with Alzheimer’s Disease. In Advances in Computational Intelligence Systems; Springer: Cham, Germany, 2017; pp. 219–230. [Google Scholar]
- Ruan, P.; Hayashida, M.; Maruyama, O.; Akutsu, T. Prediction of heterotrimeric protein complexes by two-phase learning using neighboring kernels. BMC Bioinform. 2014, 15, S6. [Google Scholar] [CrossRef] [PubMed]
- Lei, X.J. The Information Flow Clustering Model and Algorithm Based on the Artificial Bee Colony Mechanism of PPI Network. Chin. J. Comput. 2012, 35, 134–145. [Google Scholar] [CrossRef]
- Dorigo, M. Ant Colony Optimization; MIT Press/Bradford Books: Cambridge, MA, USA, 2004. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Ji, J.Z.; Liu, Z.J. Ant colony optimization with multi-agent evolution for detecting functional modules in protein-protein interaction networks. In Proceedings of the 3rd International Conference on Information Computing and Applications, Chengdu, China, 14–16 September 2012; pp. 445–453. [Google Scholar]
- Rodriguez-Soca, Y.; Munteanu, C.R.; Dorado, J.; Pazos, A.; Prado-Prado, F.J.; González-Díaz, H. A web server for prediction of unique targets in trypanosome proteome by using electrostatic parameters of protein-protein interactions. J. Proteome Res. 2010, 9, 1182–1190. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Soca, Y.; Munteanu, C.R.; Dorado, J.; Rabuñal, J.; Pazos, A.; González-Díaz, H. A web-server predicting complex biopolymer targets in plasmodium with entropy measures of protein–protein interactions. Polymer 2010, 51, 264–273. [Google Scholar] [CrossRef]
- Ji, J.; Liu, Z.; Zhang, A.; Jiao, L.; Liu, C. Improve ant colony optimization for detecting functional modules in protein-protein interaction networks. In Proceedings of the 3rd International Conference on Information Computing and Applications, Chengdu, China, 14–16 September 2012; pp. 404–413. [Google Scholar]
- Debby, D.W.; Ran, W.; Hong, Y. Fast prediction of protein-protein interaction sites based on Extreme Learning Machines. Neurocomputing 2014, 128, 258–266. [Google Scholar]
- Schlicker, A.; Albrecht, M. FunSimMat: A comprehensive functional similarity database. Nucleic Acids Res. 2008, 36, D434–D439. [Google Scholar] [CrossRef] [PubMed]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
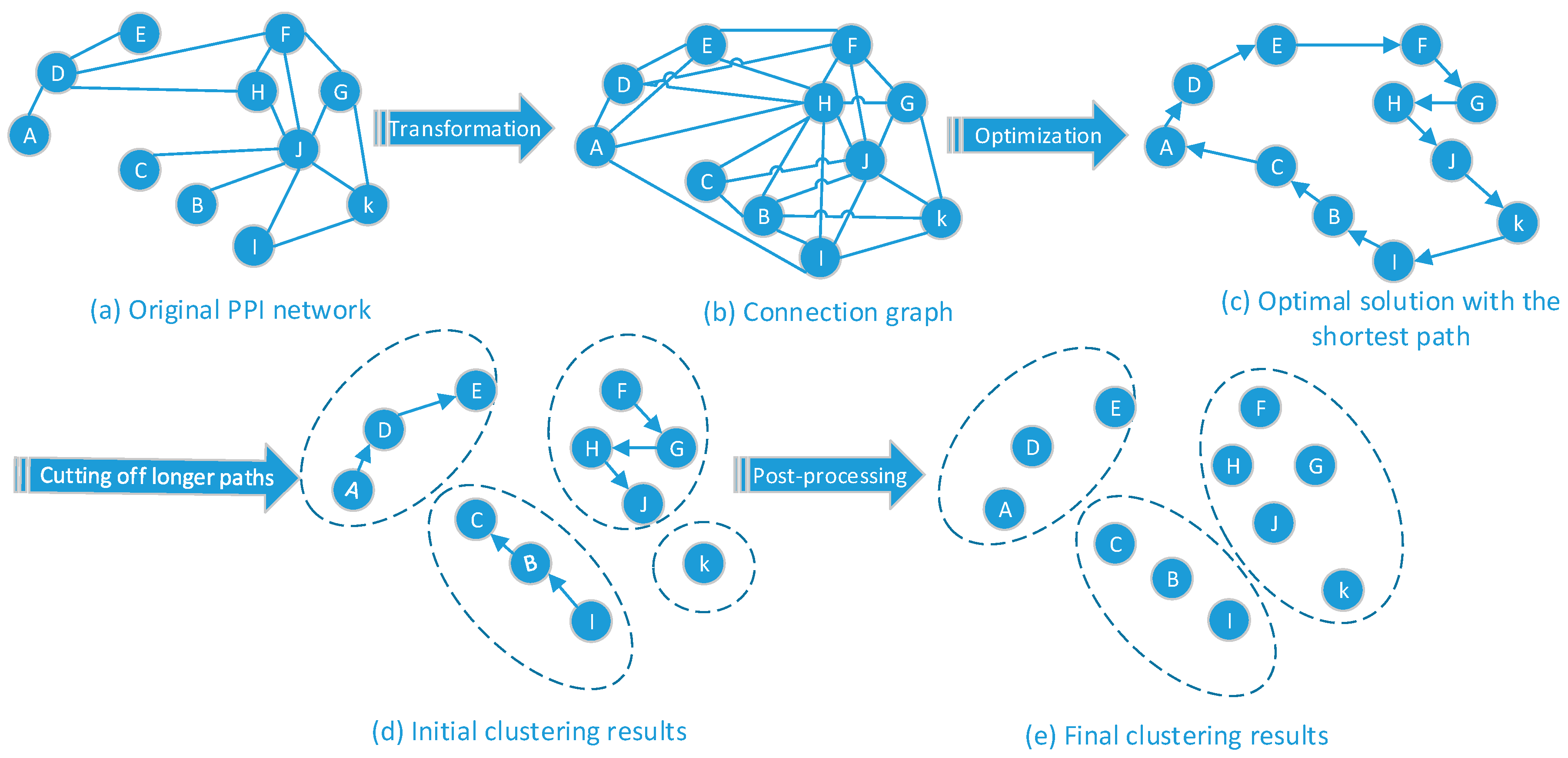
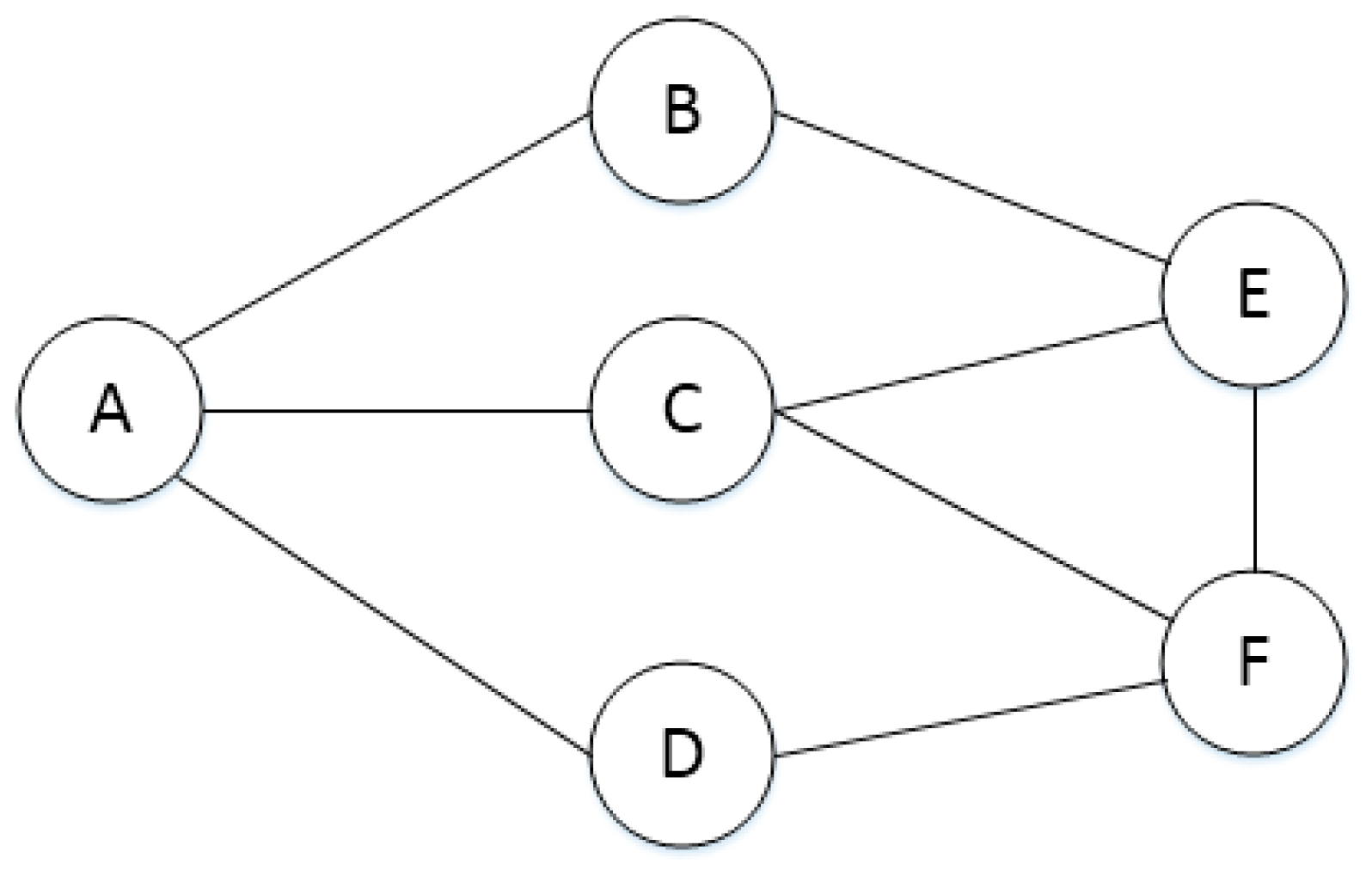
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 0 | 1 | 0 |
| C | 1 | 0 | 0 | 0 | 1 | 1 |
| D | 1 | 0 | 0 | 0 | 0 | 1 |
| E | 0 | 1 | 1 | 0 | 0 | 1 |
| F | 0 | 0 | 1 | 1 | 1 | 0 |
| Parameter Setting | PSO | SSO |
|---|---|---|
| MAX_GEN | 500 | 500 |
| Number of Particle | 100 | 100 |
| Maximum Fitness | 1.0 | 1.0 |
| Cw, Cp, Cg | - | 0.1, 0.55, 0.8 |
| Weight | 0.9–0.4·t/MAX_GEN | - |
| c1, c2 2 | 2.0, t/MAX_GEN | - |
| Species | Before Matching | After Matching | ||
|---|---|---|---|---|
| Interaction | Interactor | GO Annotation | Interactor & GO Annotation | |
| Human | 8412 | 4823 | 20,201 | 3394 |
| Scere | 24,668 | 2340 | 4680 | 2325 |
| Mouse | 2498 | 2259 | 1480 | 1447 |
| Fruitfly | 680 | 607 | 3299 | 269 |
| Category | SSO | PSO | ||||||
|---|---|---|---|---|---|---|---|---|
| Threshold | Fruitfly | Mouse | Scere | Human | Fruitfly | Mouse | Scere | Human |
| 0.05 | 4.4 | 71.2 | 171.6 | 731.6 | 5.4 | 148.6 | 205.6 | 710.2 |
| 0.055 | 4 | 69.4 | 150.4 | 501.4 | 5 | 167.4 | 217.8 | 650 |
| 0.06 | 4 | 75.6 | 181.6 | 451.8 | 5 | 163.2 | 217.8 | 637.8 |
| 0.065 | 4 | 73.6 | 150.8 | 407.6 | 5 | 168 | 203.8 | 683.8 |
| 0.07 | 4 | 107.4 | 153 | 418.8 | 5 | 146 | 204.8 | 629.6 |
| 0.075 | 4 | 78 | 150.8 | 375.6 | 5 | 168 | 204.4 | 758.2 |
| 0.08 | 4 | 74.6 | 167.2 | 395.2 | 5 | 166.4 | 206 | 751.2 |
| 0.085 | 4 | 76.4 | 158.8 | 402 | 5 | 167.2 | 205 | 771.2 |
| Category | SSO | PSO | ||||||
|---|---|---|---|---|---|---|---|---|
| Threshold | Fruitfly | Mouse | Scere | Human | Fruitfly | Mouse | Scere | Human |
| 0.05 | 33 | 122.4 | 168.6 | 223 | 25.8 | 94.8 | 174.2 | 223.4 |
| 0.055 | 30 | 114 | 160 | 198.8 | 27 | 92.2 | 163.8 | 202.8 |
| 0.06 | 23.6 | 96.6 | 139.8 | 193.6 | 22.6 | 82.6 | 139.8 | 187.4 |
| 0.065 | 26.8 | 82.2 | 127 | 165.4 | 18 | 72.4 | 129.6 | 161.2 |
| 0.07 | 19.8 | 68.8 | 106.6 | 142 | 16.2 | 66 | 110.8 | 147 |
| 0.075 | 18.4 | 59 | 96.8 | 125 | 14.4 | 60.8 | 101.8 | 126 |
| 0.08 | 15.6 | 53.2 | 79.4 | 108 | 15.4 | 46.4 | 79.2 | 109 |
| 0.085 | 13.2 | 36.8 | 70.2 | 90.4 | 11.6 | 41.8 | 74.6 | 96.8 |
| Category | SSO | PSO | ||||||
|---|---|---|---|---|---|---|---|---|
| Threshold | Fruitfly | Mouse | Scere | Human | Fruitfly | Mouse | Scere | Human |
| 0.05 | 9.8 | 45 | 77.8 | 142.4 | 10 | 280.2 | 342.4 | 706 |
| 0.055 | 5.6 | 30.4 | 56.2 | 106 | 9 | 172.6 | 205.2 | 432.8 |
| 0.06 | 5.2 | 22.4 | 35.4 | 84.8 | 6 | 95 | 102 | 270 |
| 0.065 | 5.2 | 23.2 | 35.4 | 54.6 | 4.4 | 56 | 64 | 234.4 |
| 0.07 | 2 | 10.4 | 23.2 | 42 | 3.4 | 45.6 | 35.8 | 157 |
| 0.075 | 1.6 | 11 | 19.4 | 33.8 | 4.4 | 17.8 | 33.8 | 100.8 |
| 0.08 | 1.4 | 10.4 | 13.2 | 22.2 | 1.4 | 12 | 18 | 70.2 |
| 0.085 | 0.8 | 3.6 | 10.4 | 17.8 | 1.4 | 6.4 | 13.8 | 48.2 |
| Category | SSO | PSO | ||||||
|---|---|---|---|---|---|---|---|---|
| Threshold | Fruitfly | Mouse | Scere | Human | Fruitfly | Mouse | Scere | Human |
| 0.05 | 1.0448 | 1.028 | 1.016 | 1.027 | 1.0842 | 1.0288 | 1.0178 | 1.0272 |
| 0.055 | 1.0906 | 1.0298 | 1.0256 | 1.0242 | 1.0688 | 1.0278 | 1.0172 | 1.0276 |
| 0.06 | 1.0516 | 1.0296 | 1.0182 | 1.0278 | 1.0666 | 1.0334 | 1.0248 | 1.0274 |
| 0.065 | 1.0634 | 1.0326 | 1.0236 | 1.0276 | 1.071 | 1.031 | 1.025 | 1.031 |
| 0.07 | 1.0778 | 1.0306 | 1.0246 | 1.0308 | 1.0852 | 1.0356 | 1.0238 | 1.0312 |
| 0.075 | 1.2486 | 1.0274 | 1.025 | 1.0276 | 1.093 | 1.0296 | 1.0254 | 1.0288 |
| 0.08 | 1.0658 | 1.03 | 1.029 | 1.0302 | 1.098 | 1.0334 | 1.0244 | 1.0296 |
| 0.085 | 1.1094 | 1.0342 | 1.022 | 1.0302 | 1.105 | 1.0362 | 1.0282 | 1.0408 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wu, L.; Ye, S.; Chen, R. Simplified Swarm Optimization-Based Function Module Detection in Protein–Protein Interaction Networks. Appl. Sci. 2017, 7, 412. https://doi.org/10.3390/app7040412
Zheng X, Wu L, Ye S, Chen R. Simplified Swarm Optimization-Based Function Module Detection in Protein–Protein Interaction Networks. Applied Sciences. 2017; 7(4):412. https://doi.org/10.3390/app7040412
Chicago/Turabian StyleZheng, Xianghan, Lingting Wu, Shaozhen Ye, and Riqing Chen. 2017. "Simplified Swarm Optimization-Based Function Module Detection in Protein–Protein Interaction Networks" Applied Sciences 7, no. 4: 412. https://doi.org/10.3390/app7040412
APA StyleZheng, X., Wu, L., Ye, S., & Chen, R. (2017). Simplified Swarm Optimization-Based Function Module Detection in Protein–Protein Interaction Networks. Applied Sciences, 7(4), 412. https://doi.org/10.3390/app7040412





