Audio Time Stretching Using Fuzzy Classification of Spectral Bins
Abstract
:1. Introduction
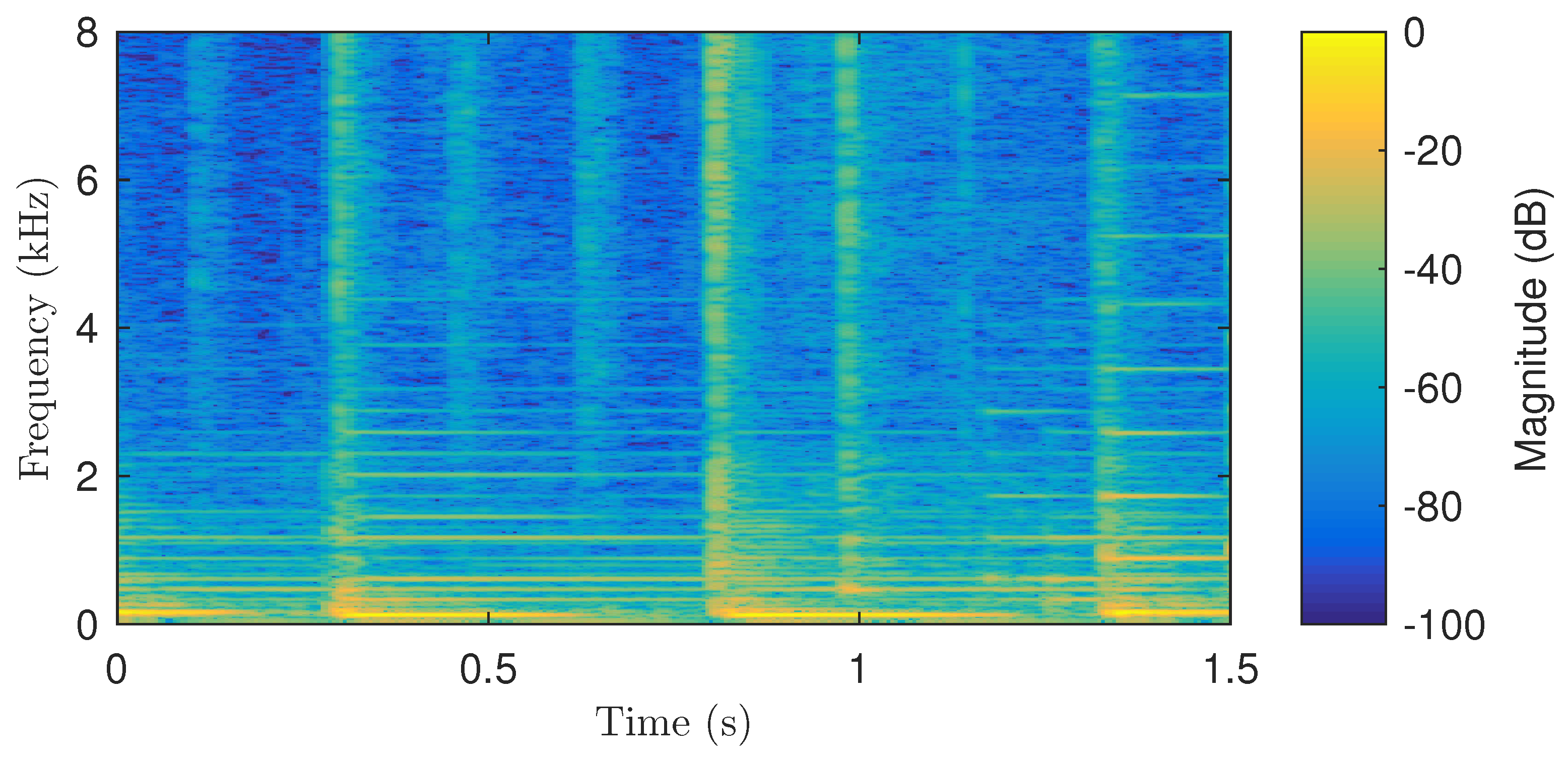
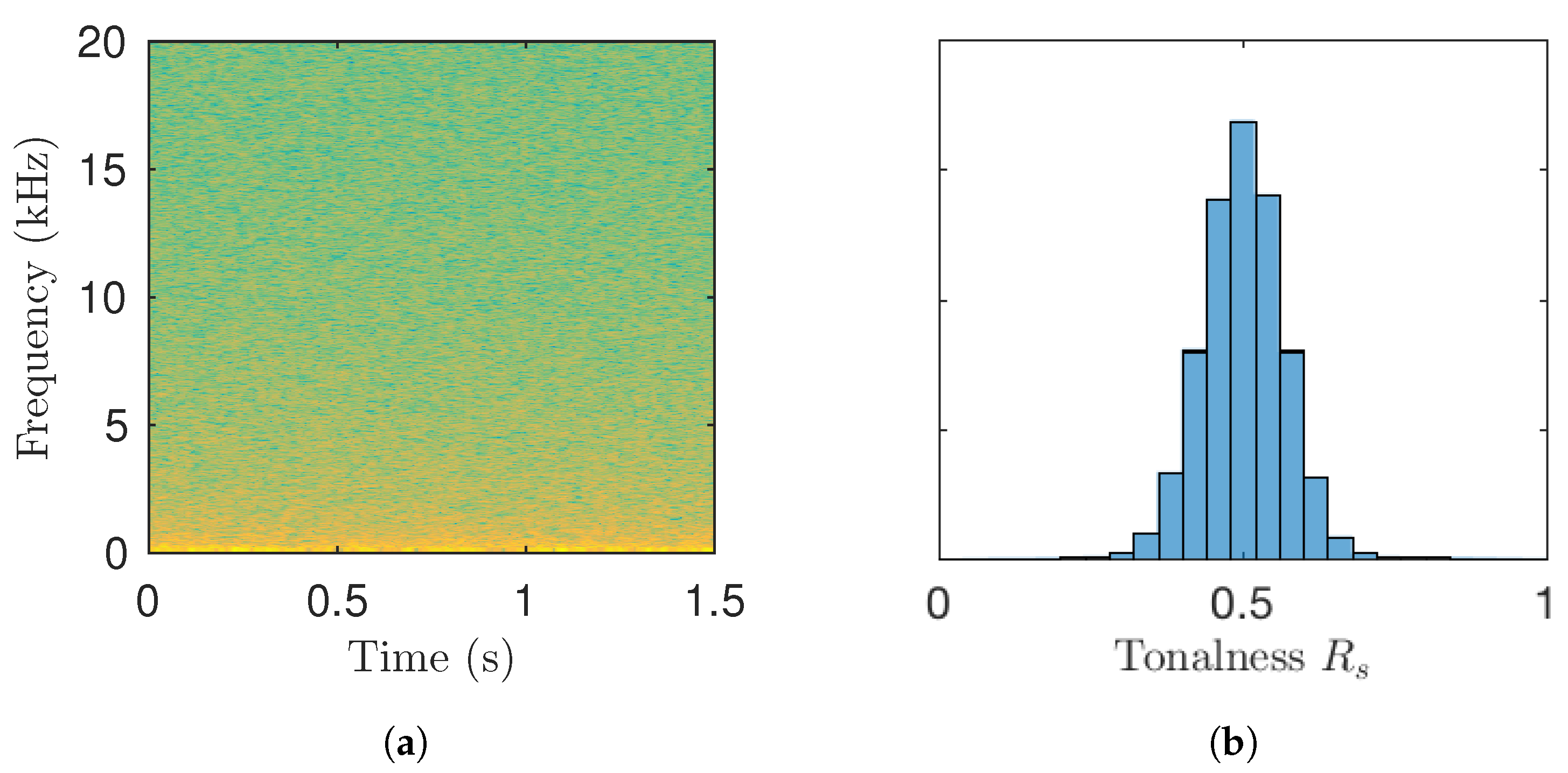
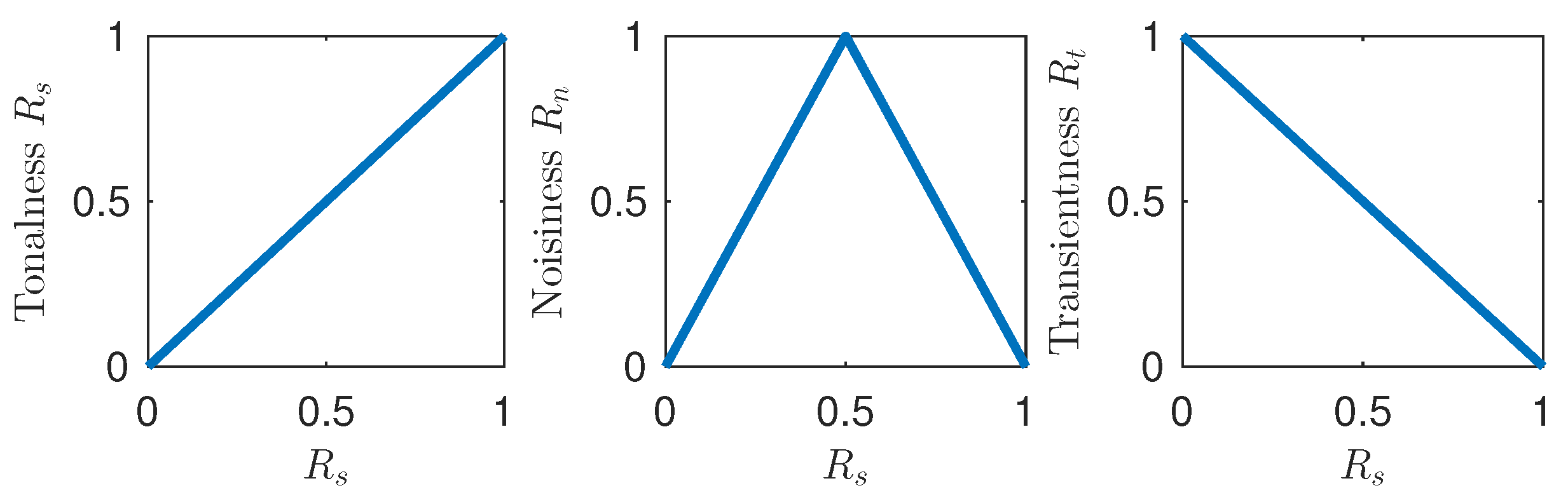
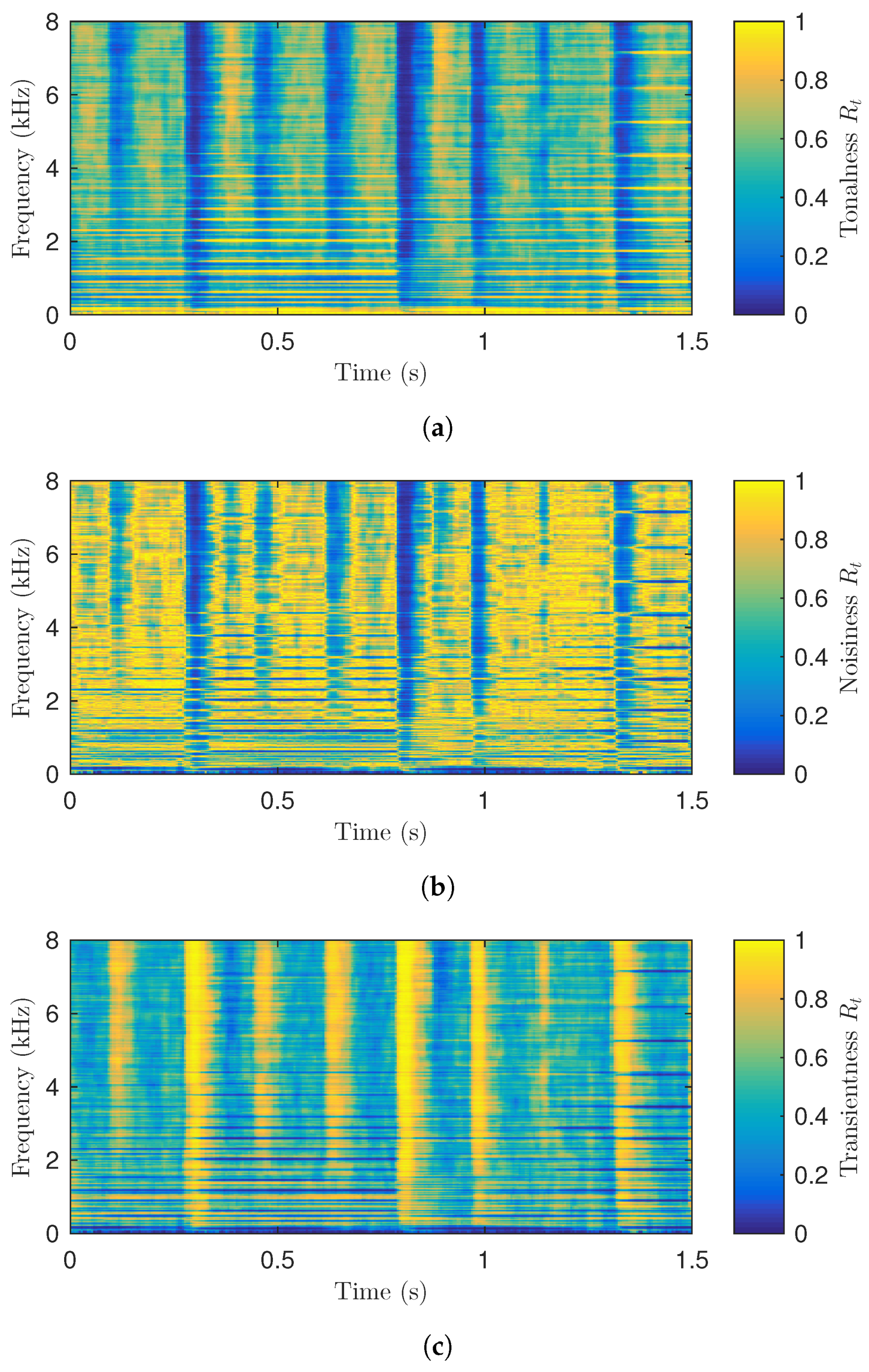
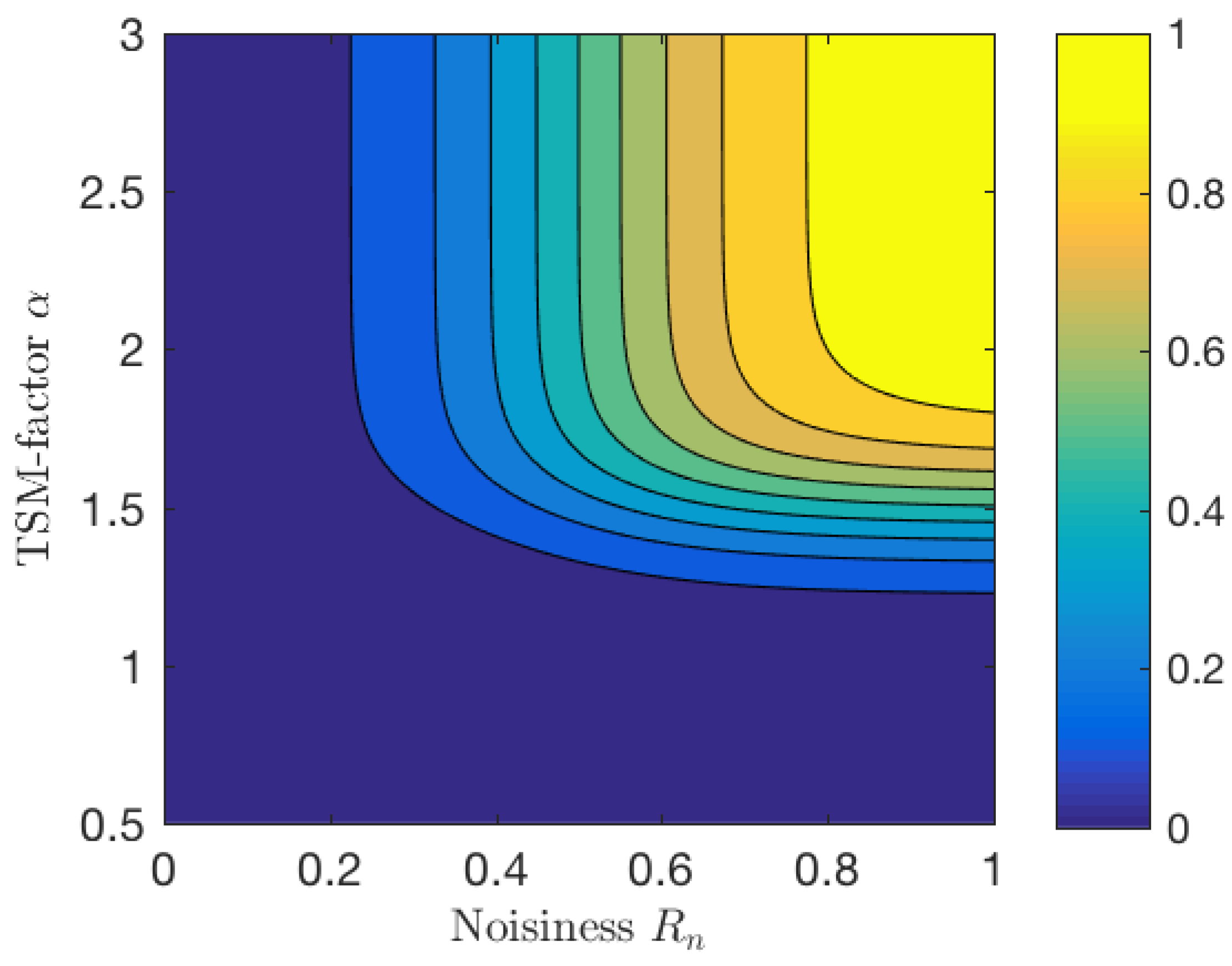
2. Fuzzy Classification of Bins in the Spectrogram
3. Novel Time-Scale Modification Technique
3.1. Proposed Phase Propagation
3.2. Transient Detection and Preservation
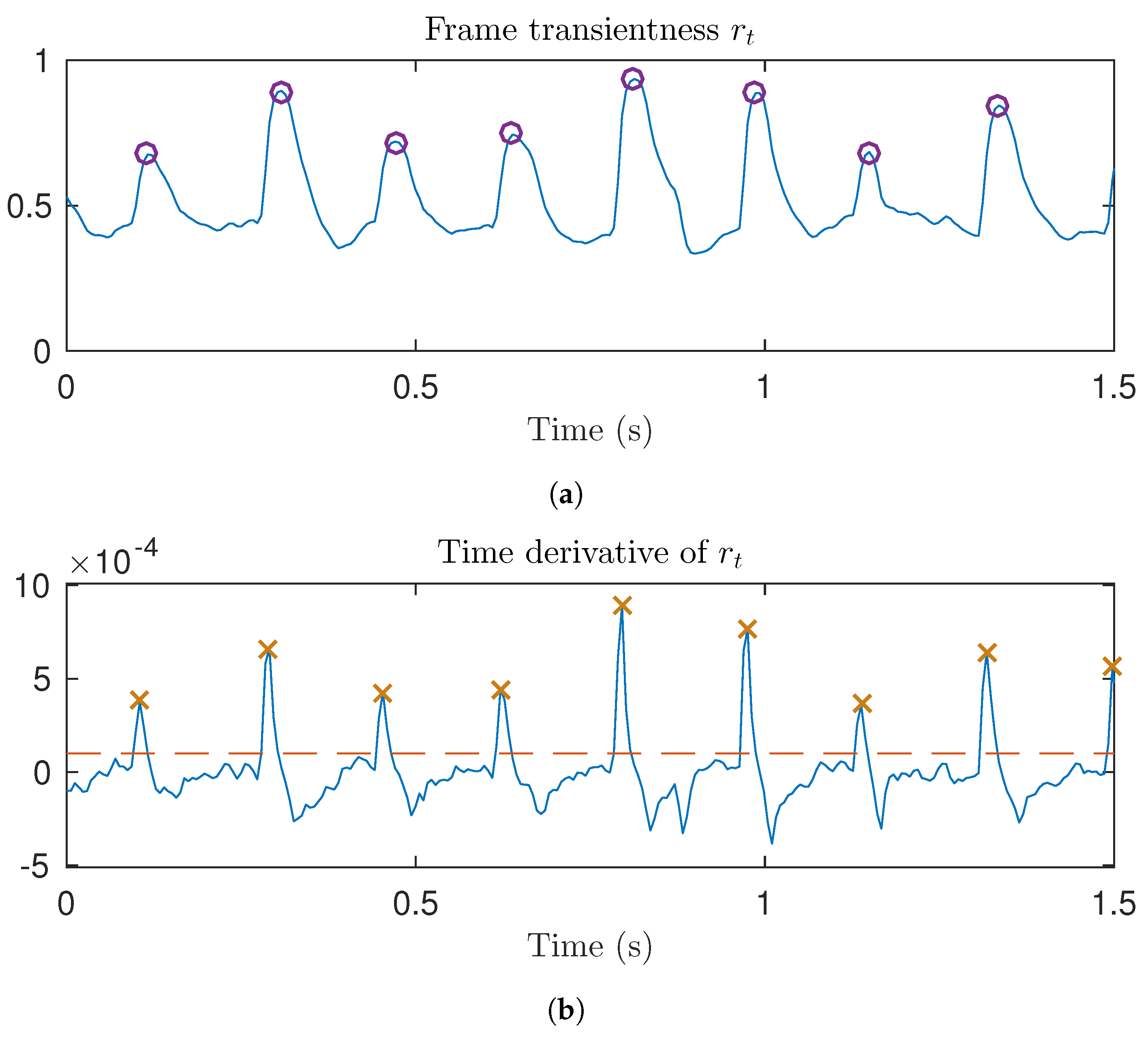
3.2.1. Detection
3.2.2. Transient Preservation
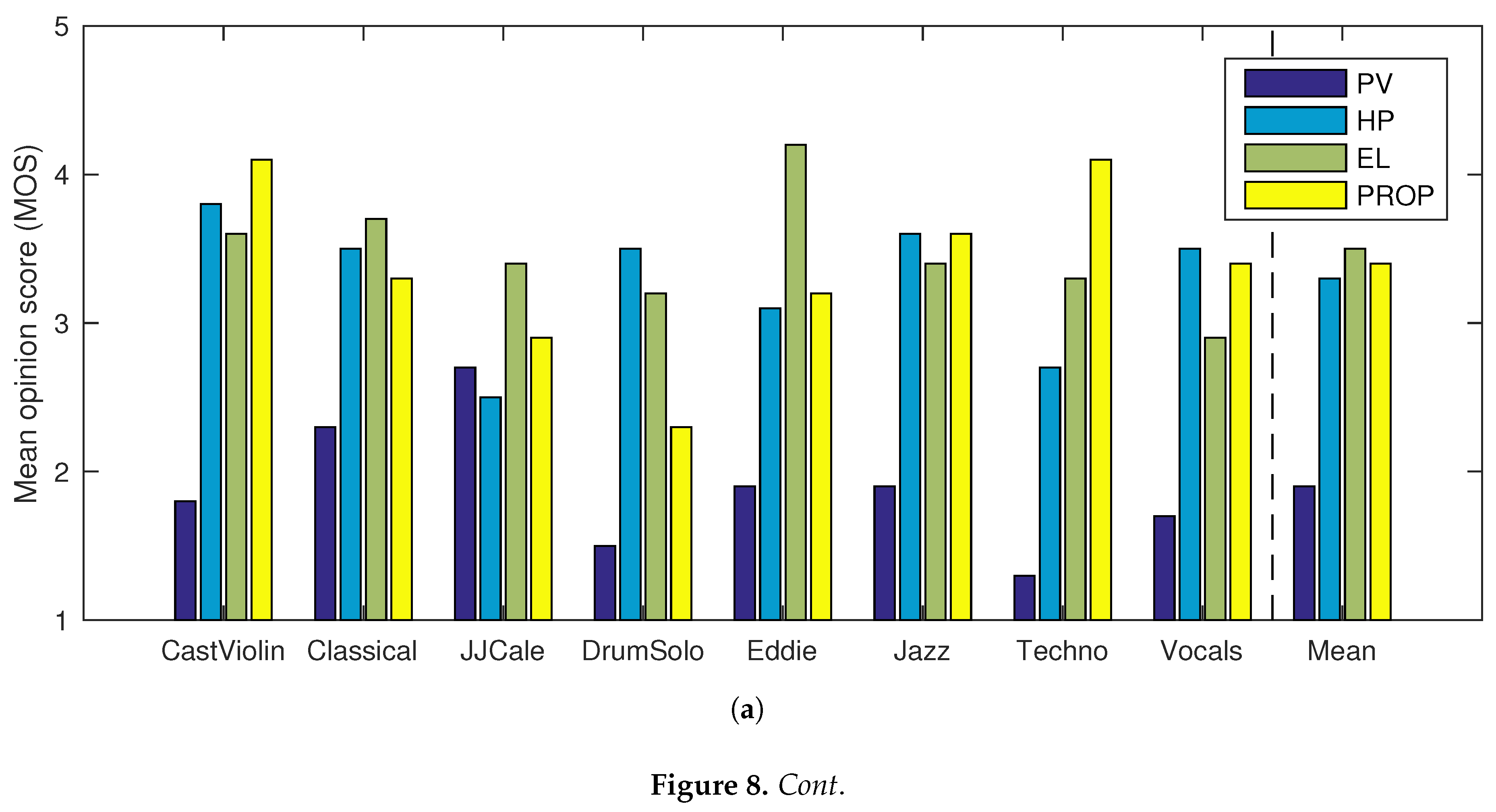
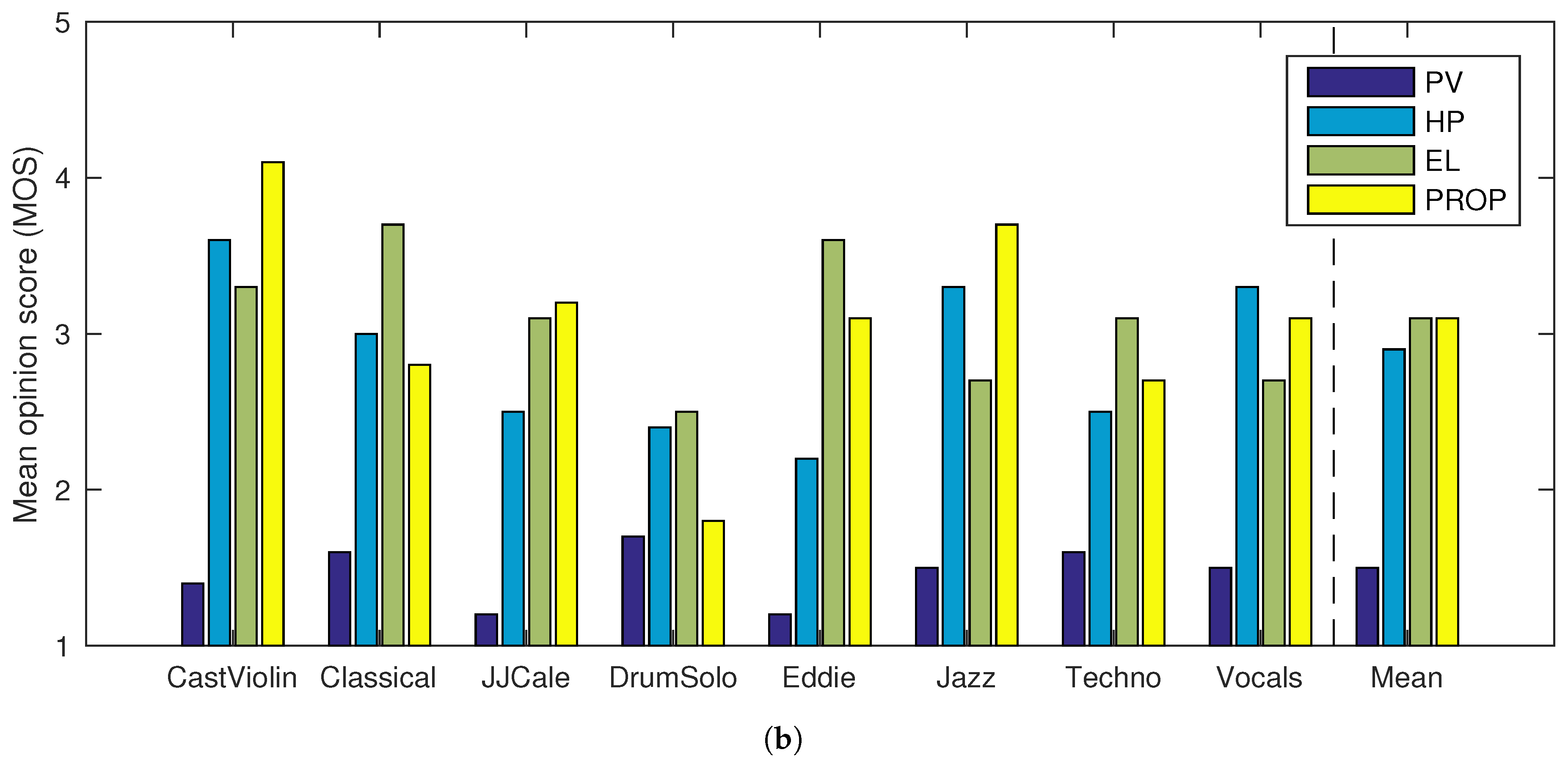
4. Evaluation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moulines, E.; Laroche, J. Non-parametric techniques for pitch-scale and time-scale modification of speech. Speech Commun. 1995, 16, 175–205. [Google Scholar] [CrossRef]
- Barry, D.; Dorran, D.; Coyle, E. Time and pitch scale modification: A real-time framework and tutorial. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Espoo, Finland, 1–4 September 2008; pp. 103–110. [Google Scholar]
- Driedger, J.; Müller, M. A review of time-scale modification of music signals. Appl. Sci. 2016, 6, 57. [Google Scholar] [CrossRef]
- Amir, A.; Ponceleon, D.; Blanchard, B.; Petkovic, D.; Srinivasan, S.; Cohen, G. Using audio time scale modification for video browsing. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences (HICSS), Maui, HI, USA, 4–7 January 2000. [Google Scholar]
- Cliff, D. Hang the DJ: Automatic sequencing and seamless mixing of dance-music tracks. In Technical Report; Hewlett-Packard Laboratories: Bristol, UK, 2000; Volume 104. [Google Scholar]
- Donnellan, O.; Jung, E.; Coyle, E. Speech-adaptive time-scale modification for computer assisted language-learning. In Proceedings of the Third IEEE International Conference on Advanced Learning Technologies, Athens, Greece, 9–11 July 2003; pp. 165–169. [Google Scholar]
- Dutilleux, P.; De Poli, G.; von dem Knesebeck, A.; Zölzer, U. Time-segment processing (chapter 6). In DAFX: Digital Audio Effects, Second Edition; Zölzer, U., Ed.; Wiley: Chichester, UK, 2011; pp. 185–217. [Google Scholar]
- Moinet, A.; Dutoit, T.; Latour, P. Audio time-scaling for slow motion sports videos. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Maynooth, Ireland, 2–5 September 2013; pp. 314–320. [Google Scholar]
- Haghparast, A.; Penttinen, H.; Välimäki, V. Real-time pitch-shifting of musical signals by a time-varying factor using normalized filtered correlation time-scale modification (NFC-TSM). In Proceedings of the International Conference on Digital Audio Effects (DAFx), Bordeaux, France, 10–15 September 2007; pp. 7–13. [Google Scholar]
- Santacruz, J.; Tardón, L.; Barbancho, I.; Barbancho, A. Spectral envelope transformation in singing voice for advanced pitch shifting. Appl. Sci. 2016, 6, 368. [Google Scholar] [CrossRef]
- Verma, T.S.; Meng, T.H. An analysis/synthesis tool for transient signals that allows a flexible sines+transients+noise model for audio. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 30 March–4 April 1998; pp. 3573–3576. [Google Scholar]
- Levine, S.N.; Smith, J.O., III. A sines+transients+noise audio representation for data compression and time/pitch scale modifications. In Proceedings of the Audio Engineering Society 105th Convention, San Francisco, CA, USA, 26–29 September 1998. [Google Scholar]
- Verma, T.S.; Meng, T.H. Time scale modification using a sines+transients+noise signal model. In Proceedings of the Digital Audio Effects Workshop (DAFx), Barcelona, Spain, 19–21 November 1998. [Google Scholar]
- Verma, T.S.; Meng, T.H. Extending spectral modeling synthesis with transient modeling synthesis. Comput. Music J. 2000, 24, 47–59. [Google Scholar] [CrossRef]
- Roucos, S.; Wilgus, A. High quality time-scale modification for speech. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Tampa, FL, USA, 26–29 April 1985; Volume 10, pp. 493–496. [Google Scholar]
- Verhelst, W.; Roelands, M. An overlap-add technique based on waveform similarity (WSOLA) for high quality time-scale modification of speech. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Minneapolis, MN, USA, 27–30 April 1993; pp. 554–557. [Google Scholar]
- Moulines, E.; Charpentier, F. Pitch-synchronous waveform processing techniques for text-to-speech synthesis using diphones. Speech Commun. 1990, 9, 453–467. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.D.; Kim, H.S. Variable time-scale modification of speech using transient information. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Münich, Germany, 21–24 April 1997; Volume 2, pp. 1319–1322. [Google Scholar]
- Wong, P.H.; Au, O.C.; Wong, J.W.; Lau, W.H. On improving the intelligibility of synchronized over-lap-and-add (SOLA) at low TSM factor. In Proceedings of the IEEE Region 10 Annual Conference on Speech and Image Technologies for Computing and Telecommunications (TENCON), Brisbane, Australia, 2–4 December 1997; Volume 2, pp. 487–490. [Google Scholar]
- Portnoff, M. Time-scale modification of speech based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 374–390. [Google Scholar] [CrossRef]
- Laroche, J.; Dolson, M. Improved phase vocoder time-scale modification of audio. IEEE Trans. Speech Audio Process. 1999, 7, 323–332. [Google Scholar] [CrossRef]
- Laroche, J.; Dolson, M. Phase-vocoder: About this phasiness business. In Proceedings of the IEEE ASSP Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19–22 October 1997. [Google Scholar]
- Röbel, A. A new approach to transient processing in the phase vocoder. In Proceedings of the 6th International Conference on Digital Audio Effects (DAFx), London, UK, 8–11 September 2003; pp. 344–349. [Google Scholar]
- Bonada, J. Automatic technique in frequency domain for near-lossless time-scale modification of audio. In Proceedings of the International Computer Music Conference (ICMC), Berlin, Germany, 27 August–1 September 2000; pp. 396–399. [Google Scholar]
- Duxbury, C.; Davies, M.; Sandler, M.B. Improved time-scaling of musical audio using phase locking at transients. In Proceedings of the Audio Engineering Society 112th Convention, München, Germany, 10–13 May 2002. [Google Scholar]
- Röbel, A. A shape-invariant phase vocoder for speech transformation. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Graz, Austria, 6–10 September 2010; pp. 298–305. [Google Scholar]
- Zivanovic, M.; Röbel, A.; Rodet, X. Adaptive threshold determination for spectral peak classification. Comput. Music J. 2008, 32, 57–67. [Google Scholar] [CrossRef]
- Driedger, J.; Müller, M.; Ewert, S. Improving time-scale modification of music signals using harmonic-percussive separation. IEEE Signal Process. Lett. 2014, 21, 105–109. [Google Scholar] [CrossRef]
- Fitzgerald, D. Harmonic/percussive separation using median filtering. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Graz, Austria, 6–10 September 2010; pp. 217–220. [Google Scholar]
- Zadeh, L.A. Making computers think like people. IEEE Spectr. 1984, 21, 26–32. [Google Scholar] [CrossRef]
- Del Amo, A.; Montero, J.; Cutello, V. On the principles of fuzzy classification. In Proceedings of the 18th International Conference of the North American Fuzzy Information Processing Society, New York, NY, USA, 10–12 June 1999; pp. 675–679. [Google Scholar]
- Kraft, S.; Lerch, A.; Zölzer, U. The tonalness spectrum: Feature-based estimation of tonal components. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Maynooth, Ireland, 2–5 September 2013; pp. 17–24. [Google Scholar]
- Ono, N.; Miyamoto, K.; Le Roux, J.; Kameoka, H.; Sagayama, S. Separation of a monaural audio signal into harmonic/percussive components by complementary diffusion on spectrogram. In Proceedings of the European Signal Processing Conference (EUSIPCO), Lausanne, Switzerland, 25–29 August 2008; pp. 1–4. [Google Scholar]
- Nagel, F.; Walther, A. A novel transient handling scheme for time stretching algorithms. In Proceedings of the Audio Engineering Society 127th Convention, New York, NY, USA, 9–12 October 2009. [Google Scholar]
- Jillings, N.; Moffat, D.; De Man, B.; Reiss, J.D. Web Audio Evaluation Tool: A browser-based listening test environment. In Proceedings of the 12th Sound and Music Computing Conference, Maynooth, Ireland, 26 July–1 August 2015; pp. 147–152. [Google Scholar]
- Zplane Development. Élastique Time Stretching & Pitch Shifting SDKs. Available online: http://www.zplane.de/index.php?page=description-elastique (accessed on 20 October 2017).
- Driedger, J.; Müller, M. TSM toolbox: MATLAB implementations of time-scale modification algorithms. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Erlangen, Germany, 1–5 September 2014; pp. 249–256. [Google Scholar]

| Name | Description |
|---|---|
| CastViolin | Solo violin and castanets, from [37] |
| Classical | Excerpt from Bólero, performed by the London Symphony Orchestra |
| JJCale | Excerpt from Cocaine, performed by J.J. Cale |
| DrumSolo | Solo performed on a drum set, from [37] |
| Eddie | Excerpt from Early in the Morning, performed by Eddie Rabbit |
| Jazz | Excerpt from I Can See Clearly, performed by the Holly Cole Trio |
| Techno | Excerpt from Return to Balojax, performed by Deviant Species and Scorb |
| Vocals | Excerpt from Tom’s Diner, performed by Suzanne Vega |
| PV | HP | EL | PROP | PV | HP | EL | PROP | |
|---|---|---|---|---|---|---|---|---|
| CastViolin | 1.8 | 3.8 | 3.6 | 4.1 | 1.4 | 3.6 | 3.3 | 4.1 |
| Classical | 2.3 | 3.5 | 3.7 | 3.3 | 1.6 | 3.0 | 3.7 | 2.8 |
| JJCale | 2.7 | 2.5 | 3.4 | 2.9 | 1.2 | 2.5 | 3.1 | 3.2 |
| DrumSolo | 1.5 | 3.5 | 3.2 | 2.3 | 1.7 | 2.4 | 2.5 | 1.8 |
| Eddie | 1.9 | 3.1 | 4.2 | 3.2 | 1.2 | 2.2 | 3.6 | 3.1 |
| Jazz | 1.9 | 3.6 | 3.4 | 3.6 | 1.5 | 3.3 | 2.7 | 3.7 |
| Techno | 1.3 | 2.7 | 3.3 | 4.1 | 1.6 | 2.5 | 3.1 | 2.7 |
| Vocals | 1.7 | 3.5 | 2.9 | 3.4 | 1.5 | 3.3 | 2.7 | 3.1 |
| Mean | 1.9 | 3.3 | 3.5 | 3.4 | 1.5 | 2.9 | 3.1 | 3.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damskägg, E.-P.; Välimäki, V. Audio Time Stretching Using Fuzzy Classification of Spectral Bins. Appl. Sci. 2017, 7, 1293. https://doi.org/10.3390/app7121293
Damskägg E-P, Välimäki V. Audio Time Stretching Using Fuzzy Classification of Spectral Bins. Applied Sciences. 2017; 7(12):1293. https://doi.org/10.3390/app7121293
Chicago/Turabian StyleDamskägg, Eero-Pekka, and Vesa Välimäki. 2017. "Audio Time Stretching Using Fuzzy Classification of Spectral Bins" Applied Sciences 7, no. 12: 1293. https://doi.org/10.3390/app7121293
APA StyleDamskägg, E.-P., & Välimäki, V. (2017). Audio Time Stretching Using Fuzzy Classification of Spectral Bins. Applied Sciences, 7(12), 1293. https://doi.org/10.3390/app7121293







