Micro-Focusing of Broadband High-Order Harmonic Radiation by a Double Toroidal Mirror
Abstract
1. Introduction
2. Experimental Setup
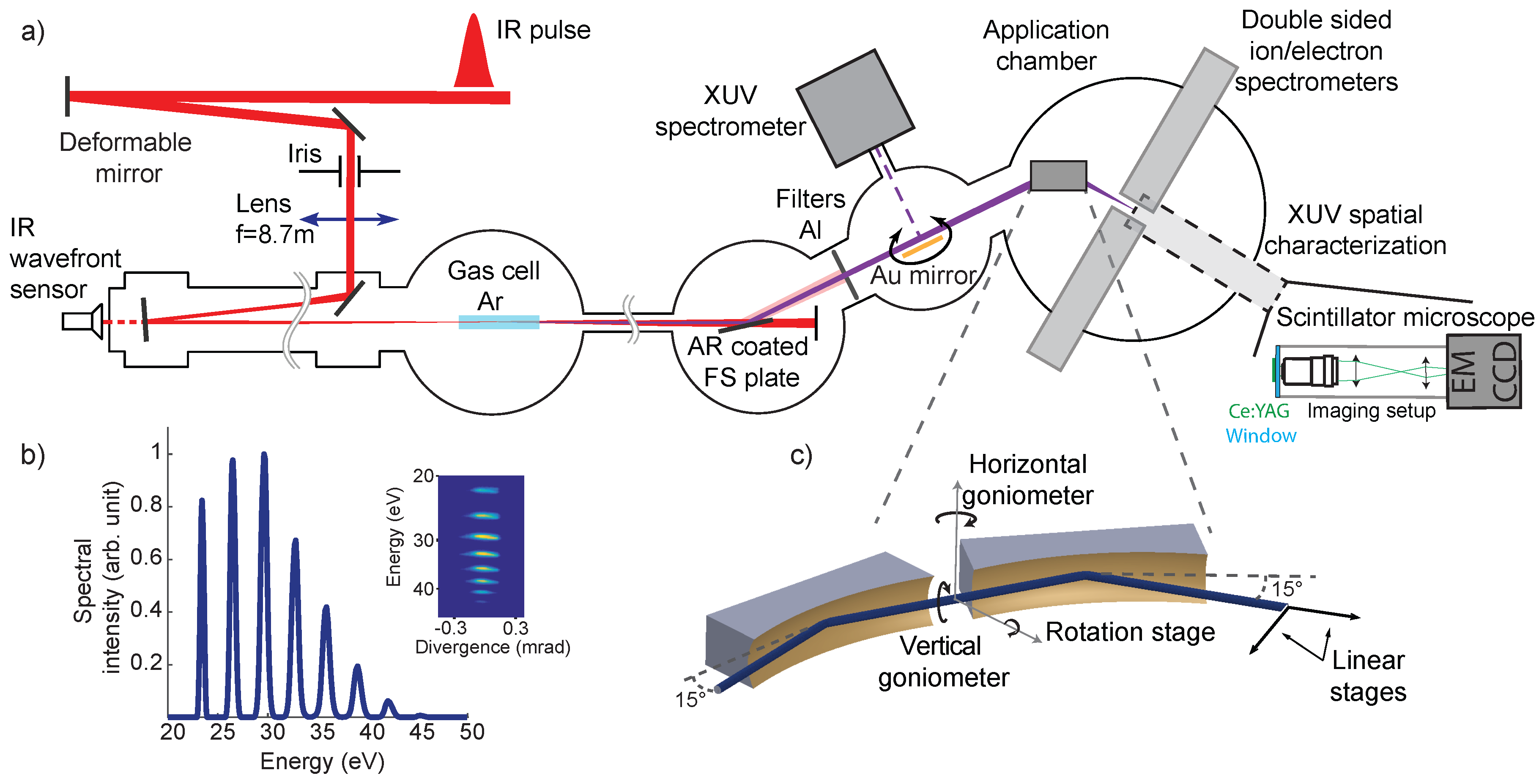
2.1. Beamline
2.2. Micro-Focusing
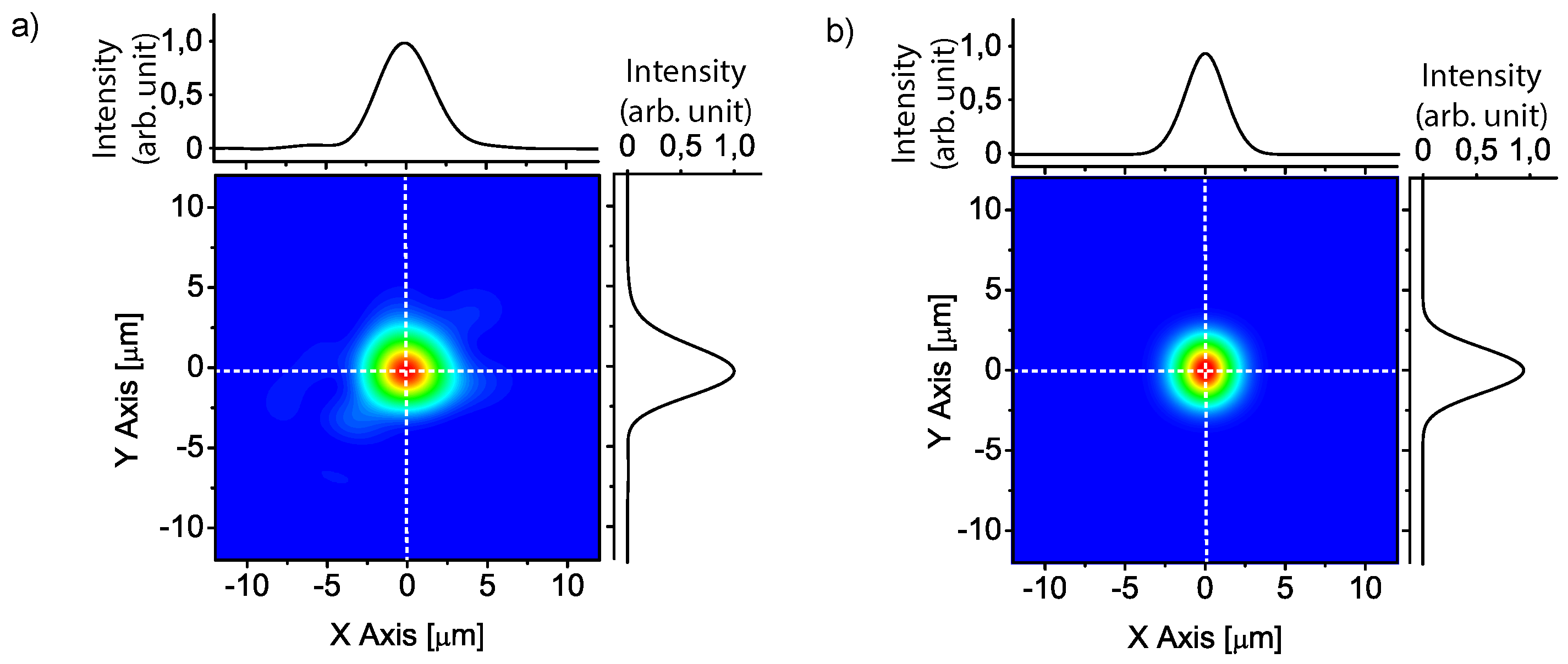
2.3. Direct Focus Measurements
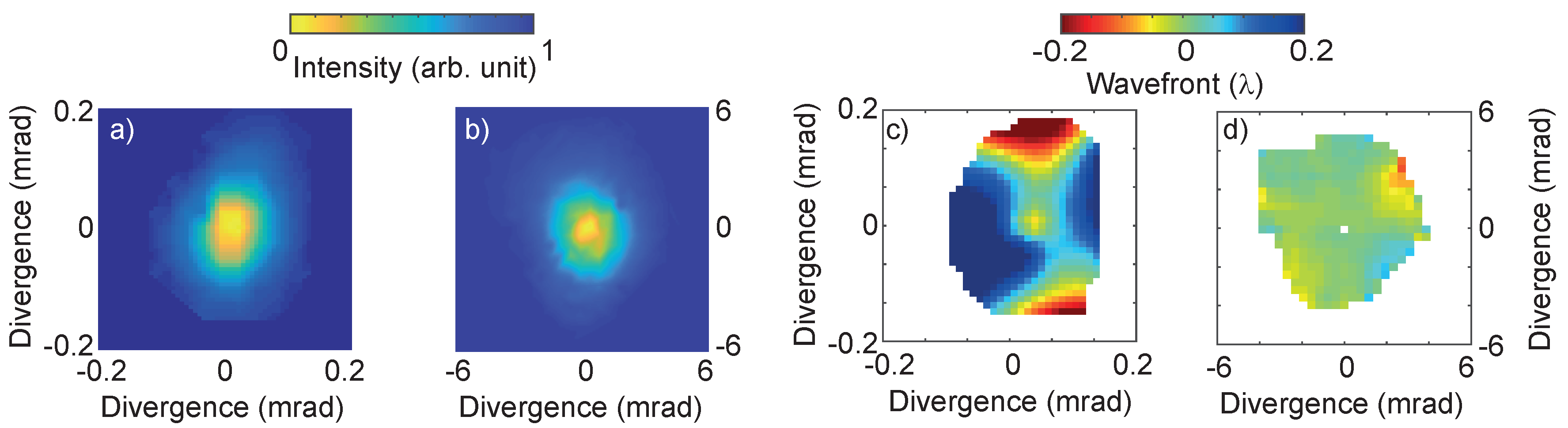
3. Wavefront Measurements and Optimization of the Focal Spot Size
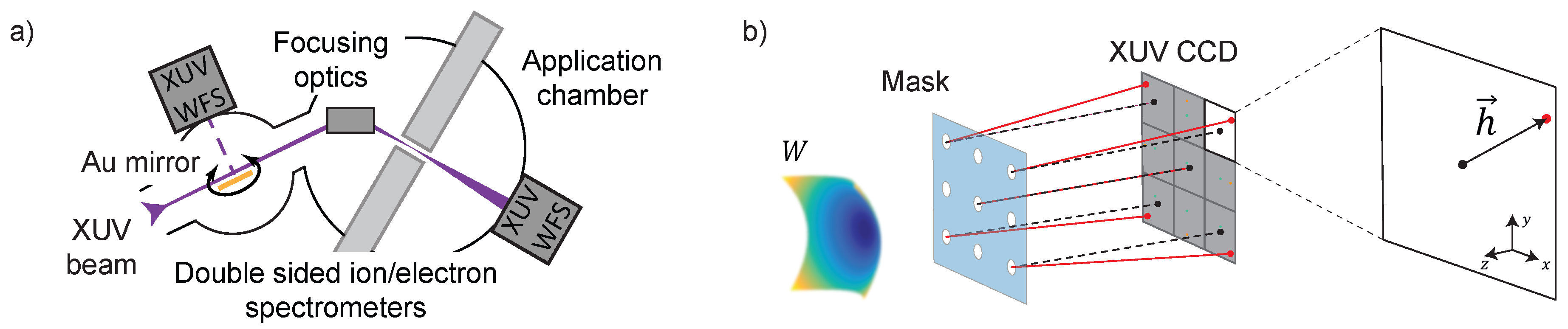
3.1. Hartmann Wavefront Sensor
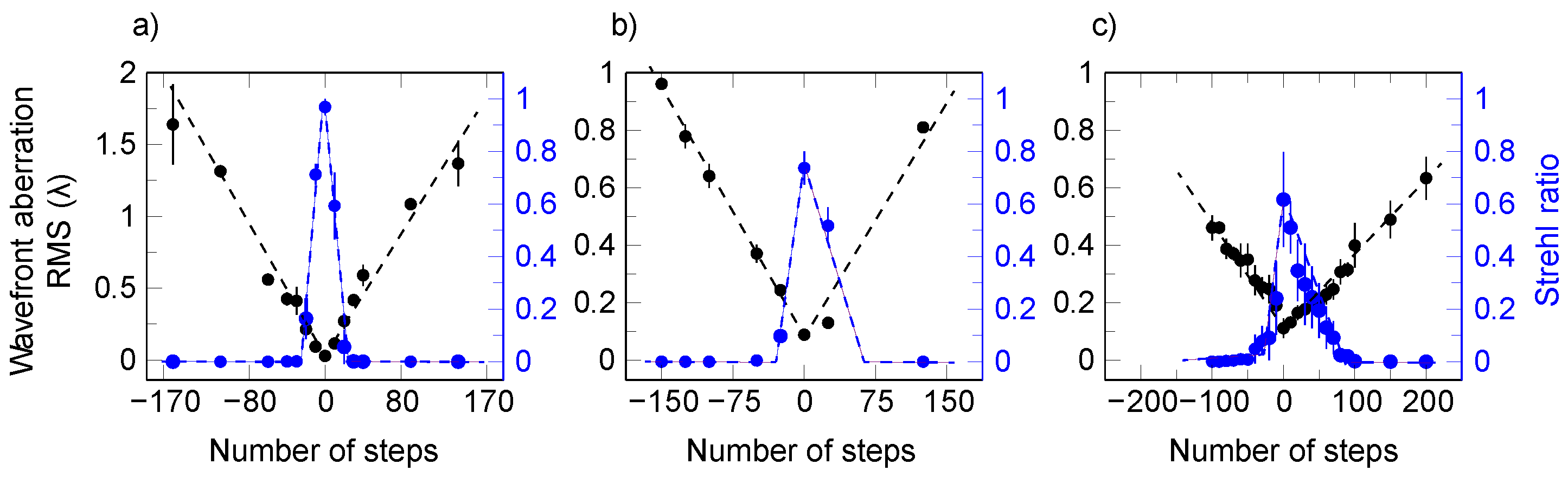
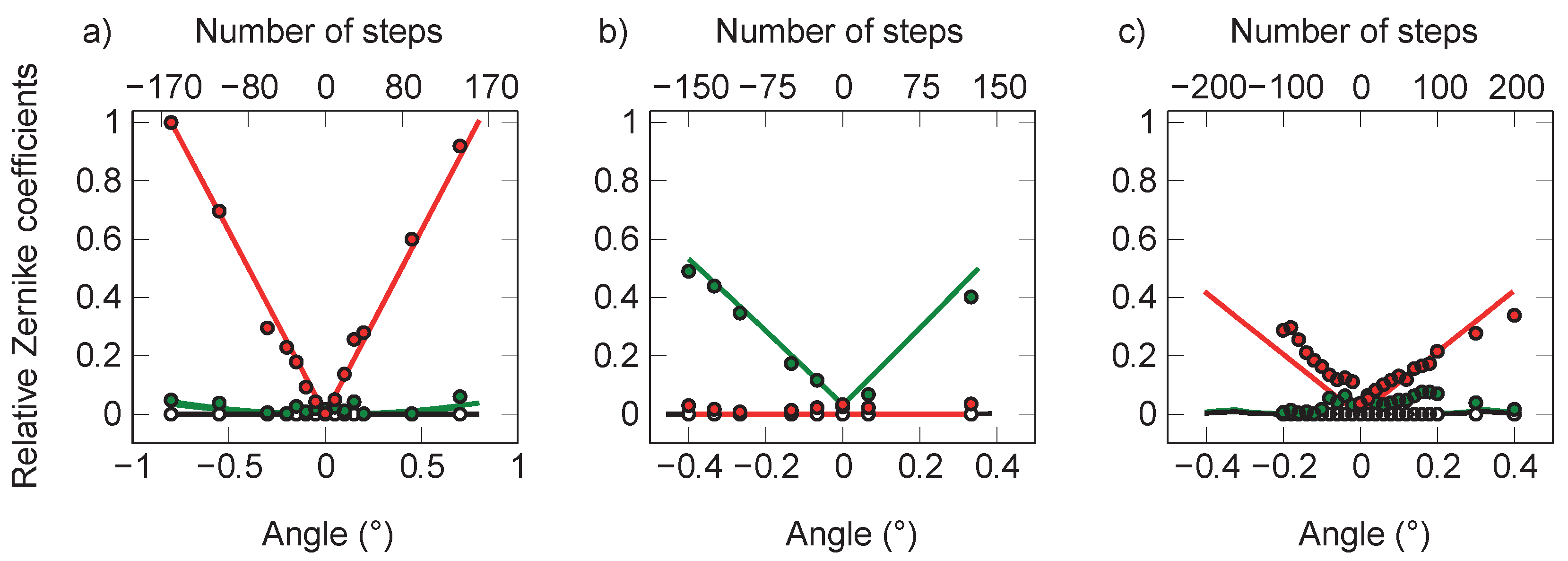
3.2. Alignment of the Focusing Optics
3.3. Size of the Focal Spot
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McPherson, A.; Gibson, G.; Jara, H.; Johann, U.; Luk, T.S.; McIntyre, I.A.; Boyer, K.; Rhodes, C.K. Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. J. Opt. Soc. Am. B 1987, 4, 595. [Google Scholar] [CrossRef]
- Ferray, M.; L’Huillier, A.; Li, X.F.; Lompre, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B At. Mol. Opt. Phys. 1988, 21, L31–L35. [Google Scholar] [CrossRef]
- Ishii, N.; Kaneshima, K.; Kitano, K.; Kanai, T.; Watanabe, S.; Itatani, J. Carrier-envelope phase-dependent high harmonic generation in the water window using few-cycle infrared pulses. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ren, X.; Yin, Y.; Cheng, Y.; Cunningham, E.; Wu, Y.; Chang, Z. Polarization gating of high harmonic generation in the water window. Appl. Phys. Lett. 2016, 108. [Google Scholar] [CrossRef]
- Tzallas, P.; Charalambidis, D.; Papadogiannis, N.A.; Witte, K.; Tsakiris, G.D. Direct observation of attosecond light bunching. Nature 2003, 426, 267–271. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, P.; Skantzakis, E.; Nikolopoulos, L.A.A.; Tsakiris, G.D.; Charalambidis, D. Extreme-ultraviolet pump–probe studies of one-femtosecond-scale electron dynamics. Nat. Phys. 2011, 7, 781–784. [Google Scholar] [CrossRef]
- Nabekawa, Y.; Hasegawa, H.; Takahashi, E.J.; Midorikawa, K. Production of Doubly Charged Helium Ions by Two-Photon Absorption of an Intense Sub-10-fs Soft X-Ray Pulse at 42 eV Photon Energy. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Manschwetus, B.; Rading, L.; Campi, F.; Maclot, S.; Coudert-Alteirac, H.; Lahl, J.; Wikmark, H.; Rudawski, P.; Heyl, C.M.; Farkas, B.; et al. Two-photon double ionization of neon using an intense attosecond pulse train. Phys. Rev. A 2016, 93, 1–5. [Google Scholar] [CrossRef]
- Hergott, J.F.; Kovacev, M.; Merdji, H.; Hubert, C.; Mairesse, Y.; Jean, E.; Breger, P.; Agostini, P.; Carré, B.; Salières, P. Extreme-ultraviolet high-order harmonic pulses in the microjoule range. Phys. Rev. A 2002, 66. [Google Scholar] [CrossRef]
- Takahashi, E.; Nabekawa, Y.; Otsuka, T.; Obara, M.; Midorikawa, K. Generation of highly coherent submicrojoule soft x rays by high-order harmonics. Phys. Rev. A 2002, 66. [Google Scholar] [CrossRef]
- Midorikawa, K.; Nabekawa, Y.; Suda, A. XUV multiphoton processes with intense high-order harmonics. Progress Quantum Electron. 2008, 32, 43–88. [Google Scholar] [CrossRef]
- Rudawski, P.; Heyl, C.M.; Brizuela, F.; Schwenke, J.; Persson, A.; Mansten, E.; Rakowski, R.; Rading, L.; Campi, F.; Kim, B.; et al. A high-flux high-order harmonic source. Rev. Sci. Instrum. 2013, 84. [Google Scholar] [CrossRef] [PubMed]
- Kühn, S.; Dumergue, M.; Kahaly, S.; Mondal, S.; Füle, M.; Csizmadia, T.; Farkas, B.; Major, B.; Várallyay, Z.; Cormier, E.; et al. The ELI-ALPS facility: The next generation of attosecond sources. J. Phys. B At. Mol. Opt. Phys. 2017, 50. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ren, X.; Yin, Y.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.; Wu, Y.; et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Valentin, C.; Douillet, D.; Kazamias, S.; Lefrou, T.; Grillon, G.; Augé, F.; Mullot, G.; Balcou, P.; Mercère, P.; Zeitoun, P. Imaging and quality assessment of high-harmonic focal spots. Opt. Lett. 2003, 28, 1049–1051. [Google Scholar] [CrossRef] [PubMed]
- Morlens, A.S.; López-Martens, R.; Boyko, O.; Zeitoun, P.; Balcou, P.; Varjú, K.; Gustafsson, E.; Remetter, T.; L’Huillier, A.; Kazamias, S.; et al. Design and characterization of extreme-ultraviolet broadband mirrors for attosecond science. Opt. Lett. 2006, 31, 1558–1560. [Google Scholar] [CrossRef] [PubMed]
- Ménesguen, Y.; De Rossi, S.; Meltchakov, E.; Delmotte, F. Aperiodic multilayer mirrors for efficient broadband reflection in the extreme ultraviolet. Appl. Phys. A Mater. Sci. Process. 2010, 98, 305–309. [Google Scholar] [CrossRef]
- Wieland, M.; Wilheim, T.; Spielmann, C.; Kleinberg, U. Zone-plate interferometry at 13 nm wavelength. Appl. Phys. B Lasers Opt. 2003, 76, 885–889. [Google Scholar] [CrossRef]
- Poletto, L.; Frassetto, F.; Calegari, F.; Trabattoni, A.; Nisoli, M. Micro-focusing of attosecond pulses by grazing-incidence toroidal mirrors. Opt. Express 2013, 21, 13040–13051. [Google Scholar] [CrossRef] [PubMed]
- Suda, A.; Mashiko, H.; Midorikawa, K. Focusing intense high-order harmonics to a micron spot size. Springer Ser. Chem. Phys. 2007, 85, 183–198. [Google Scholar]
- Bourassin-Bouchet, C.; Mang, M.M.; Delmotte, F.; Chavel, P.; de Rossi, S. How to focus an attosecond pulse. Opt. Express 2013, 21, 2506–2520. [Google Scholar] [CrossRef] [PubMed]
- Underwood, J.H. Imaging properties and aberrations of spherical optics and nonspherical optics. In Experimental Methods in the Physical Sciences; Academic Press: Cambridge, MA, USA, 1998; Volume 31. [Google Scholar]
- Frassetto, F.; Anumula, S.; Calegari, F.; Trabattoni, A.; Nisoli, M.; Poletto, L. Microfocusing beamline for XUV-XUV pump-probe experiments using HH generation. In Proceedings of the Society of Photo-Optical Instrumentation Engineers SPIE 9208, San Diego, CA, USA, 5 September 2014. [Google Scholar]
- Wolter, H. Spiegelsysteme streifenden Einfalls als abbildende Optiken für Röntgenstrahlen. Ann. Phys. 1952, 445, 94–114. [Google Scholar] [CrossRef]
- Gaetz, T.J.; Jerius, D.; Edgar, R.J.; Van Speybroeck, L.P.; Schwartz, D.A.; Markevitch, M.L.; Taylor, S.C.; Schulz, N.S. Orbital verification of the CXO high-resolution mirror assembly alignment and vignetting. In Proceedings of the Society of Photo-Optical Instrumentation Engineers SPIE 4012, Munich, Germany, 18 July 2000. [Google Scholar]
- Mildner, D.F.R.; Gubarev, M.V. Wolter optics for neutron focusing. Nucl. Instrum. Meth. A 2011, 634, 7–11. [Google Scholar] [CrossRef][Green Version]
- Khaykovich, B.; Gubarev, M.V.; Bagdasarova, Y.; Ramsey, B.D.; Moncton, D.E. From x-ray telescopes to neutron scattering: Using axisymmetric mirrors to focus a neutron beam. Nucl. Instrum. Meth. A 2011, 631, 98–104. [Google Scholar] [CrossRef]
- Bennett, G.R. Advanced laser-backlit grazing-incidence x-ray imaging systems for inertial confinement fusion research. I. Design. Appl. Opt. 2001, 40, 4570–4587. [Google Scholar] [CrossRef] [PubMed]
- Ellis, R.J.; Trebes, J.E.; Phillion, D.W.; Kilkenny, J.D.; Glendinning, S.G.; Wiedwald, J.D.; Levesque, R.A. Four-frame gated Wolter x-ray microscope. Rev. Sci. Instrum. 1990, 61, 2759–2761. [Google Scholar] [CrossRef]
- Le Déroff, L.; Salières, P.; Carré, B. Beam-quality measurement of a focused high-order harmonic beam. Opt. Lett. 1998, 23, 1544–1546. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.G.; Park, J.J.; Sung, J.H.; Nam, C.H. Wave-front phase measurements of high-order harmonic beams by use of point-diffraction interferometry. Opt. Lett. 2003, 28, 480–482. [Google Scholar] [CrossRef] [PubMed]
- Frumker, E.; Paulus, G.G.; Niikura, H.; Villeneuve, D.M.; Corkum, P.B. Frequency-resolved high-harmonic wavefront characterization. Opt. Lett. 2009, 34, 3026–3028. [Google Scholar] [CrossRef] [PubMed]
- Austin, D.R.; Witting, T.; Arrell, C.A.; Frank, F.; Wyatt, A.S.; Marangos, J.P.; Tisch, J.W.G.; Walmsley, I.A. Lateral shearing interferometry of high-harmonic wavefronts. Opt. Lett. 2011, 36, 1746–1748. [Google Scholar] [CrossRef] [PubMed]
- Mercère, P.; Zeitoun, P.; Idir, M.; Le Pape, S.; Douillet, D.; Levecq, X.; Dovillaire, G.; Bucourt, S.; Goldberg, K.A.; Naulleau, P.P.; et al. Hartmann wave-front measurement at 134 nm with λ_EUV/120 accuracy. Opt. Lett. 2003, 28, 1534–1536. [Google Scholar] [CrossRef] [PubMed]
- Le Pape, S.; Zeitoun, P.; Idir, M.; Dhez, P.; Rocca, J.J.; François, M. Electromagnetic-Field Distribution Measurements in the Soft X-Ray Range: Full Characterization of a Soft X-Ray Laser Beam. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Moszyński, M.; Ludziejewski, T.; Wolski, D.; Klamra, W.; Norlin, L. Properties of the YAG:Ce scintillator. Nucl. Instrum. Meth. A 1994, 345, 461–467. [Google Scholar] [CrossRef]
- Jaeglé, P.; Sebban, S.; Carillon, A.; Jamelot, G.; Klisnick, A.; Zeitoun, P.; Rus, B.; Nantel, M.; Albert, F.; Ros, D. Ultraviolet luminescence of CsI and CsCl excited by soft x-ray laser. J. Appl. Phys. 1997, 81, 2406–2409. [Google Scholar] [CrossRef]
- Hauri, C.P.; Biegert, J.; Keller, U.; Schaefer, B.; Mann, K.; Marowski, G. Validity of wave-front reconstruction and propagation of ultrabroadband pulses measured with a Hartmann-Shack sensor. Opt. Lett. 2005, 30, 1563–1565. [Google Scholar] [CrossRef] [PubMed]
- Southwell, W. Wave-front estimation from wave-front slope measurements. J. Opt. Soc. Am. 1980, 70, 998–1006. [Google Scholar] [CrossRef]
- Lakshminarayanan, V.; Fleck, A. Zernike polynomials: A guide. J. Mod. Opt. 2011, 58, 545–561. [Google Scholar] [CrossRef]
- Chériaux, G.; Rousseau, J.P.; Ferré, S.; Notebaert, L.; Pittman, M.; Chambaret, J.P. Caractérisation et contrôle de la répartition d’énergie et du front d’onde d’impulsions femtosecondes. In Systèmes Femtosecondes; Number 1 in Intégrations Des Savoirs Et Savoir-Faire; Publications de l’Université de Saint-Étienne: Saint-Étienne, France, 2001; pp. 141–156. [Google Scholar]
- Mahajan, V.N. Strehl ratio for primary aberrations in terms of their aberration variance. J. Opt. Soc. Am. 1983, 73, 860–861. [Google Scholar] [CrossRef]
- Harvey, J.E.; Irvin, R.G.; Pfisterer, R.N. Modeling physical optics phenomena by complex ray tracing. Opt. Eng. 2015, 54. [Google Scholar] [CrossRef]
| Tangential | Sagittal | |||
|---|---|---|---|---|
| [mm] | [mm] | [mm] | [mm] | |
| First mirror | 2050 | 265.3 | 137.2 | 265.0 |
| Second mirror | 4213 | 545.2 | 281.8 | 544.4 |
| Combined | Focal length = 164.2 mm | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coudert-Alteirac, H.; Dacasa, H.; Campi, F.; Kueny, E.; Farkas, B.; Brunner, F.; Maclot, S.; Manschwetus, B.; Wikmark, H.; Lahl, J.; et al. Micro-Focusing of Broadband High-Order Harmonic Radiation by a Double Toroidal Mirror. Appl. Sci. 2017, 7, 1159. https://doi.org/10.3390/app7111159
Coudert-Alteirac H, Dacasa H, Campi F, Kueny E, Farkas B, Brunner F, Maclot S, Manschwetus B, Wikmark H, Lahl J, et al. Micro-Focusing of Broadband High-Order Harmonic Radiation by a Double Toroidal Mirror. Applied Sciences. 2017; 7(11):1159. https://doi.org/10.3390/app7111159
Chicago/Turabian StyleCoudert-Alteirac, Hélène, Hugo Dacasa, Filippo Campi, Emma Kueny, Balázs Farkas, Fabian Brunner, Sylvain Maclot, Bastian Manschwetus, Hampus Wikmark, Jan Lahl, and et al. 2017. "Micro-Focusing of Broadband High-Order Harmonic Radiation by a Double Toroidal Mirror" Applied Sciences 7, no. 11: 1159. https://doi.org/10.3390/app7111159
APA StyleCoudert-Alteirac, H., Dacasa, H., Campi, F., Kueny, E., Farkas, B., Brunner, F., Maclot, S., Manschwetus, B., Wikmark, H., Lahl, J., Rading, L., Peschel, J., Major, B., Varjú, K., Dovillaire, G., Zeitoun, P., Johnsson, P., L’Huillier, A., & Rudawski, P. (2017). Micro-Focusing of Broadband High-Order Harmonic Radiation by a Double Toroidal Mirror. Applied Sciences, 7(11), 1159. https://doi.org/10.3390/app7111159







