The Stability of New Single-Layer Combined Lattice Shell Based on Aluminum Alloy Honeycomb Panels
Abstract
1. Introduction
2. Experimental Study on Stability of NSCLS
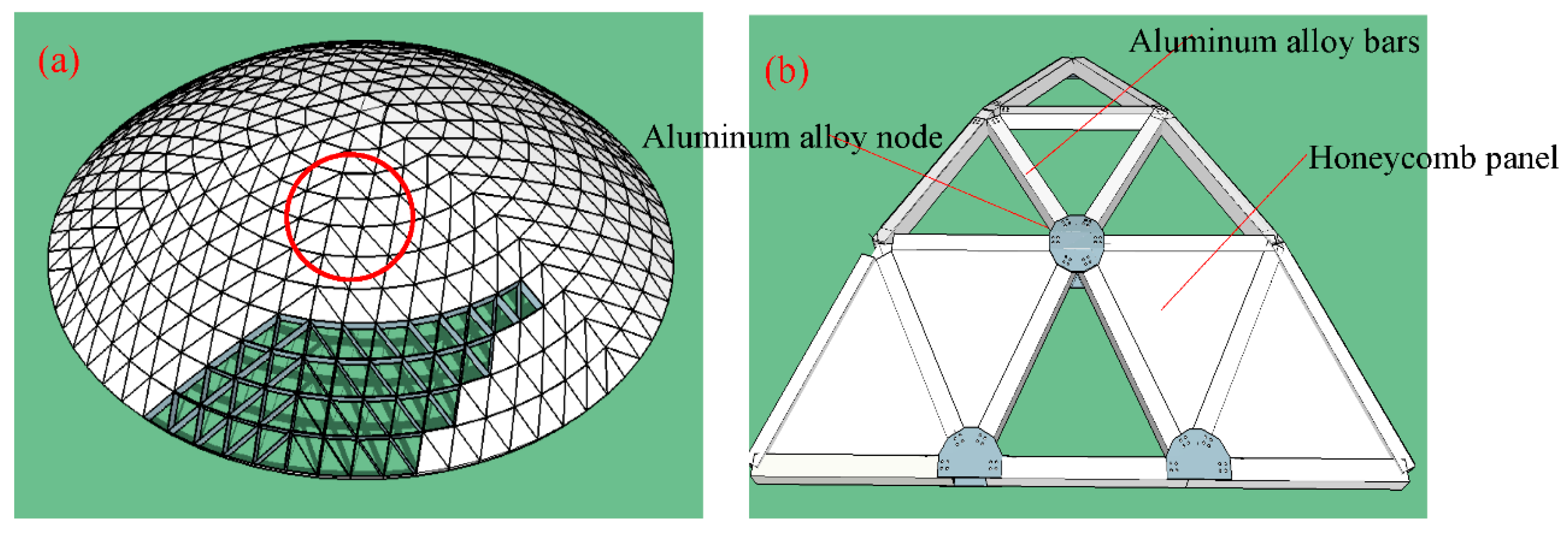
2.1. The Design and Fabrication of the Test Model
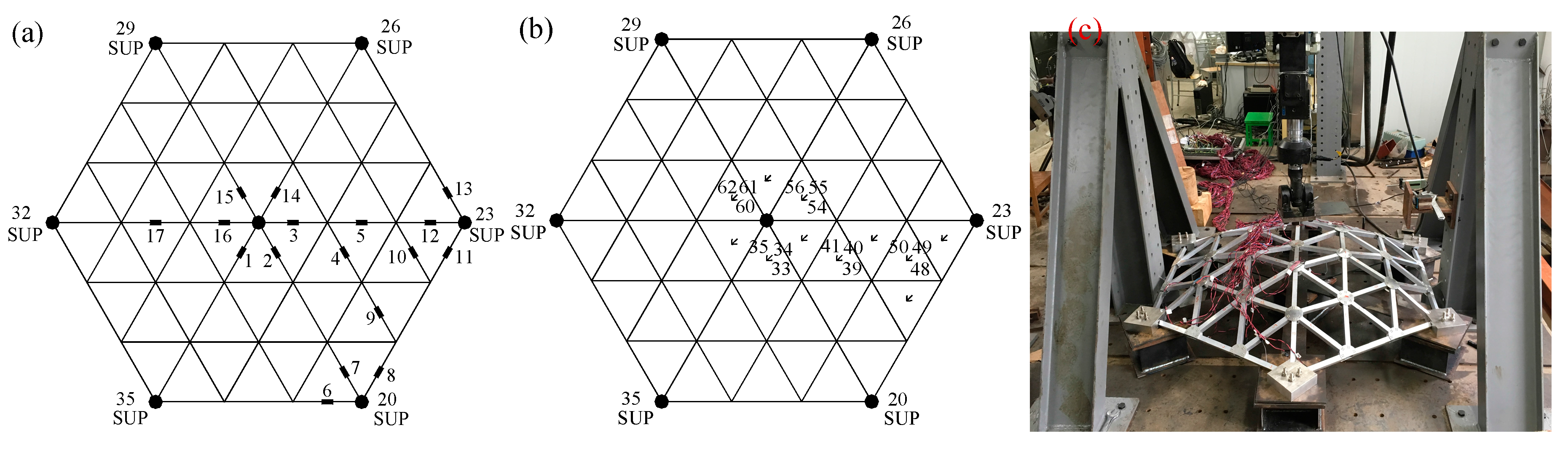
2.2. Loading and Testing Methods
2.3. Results and Discussion
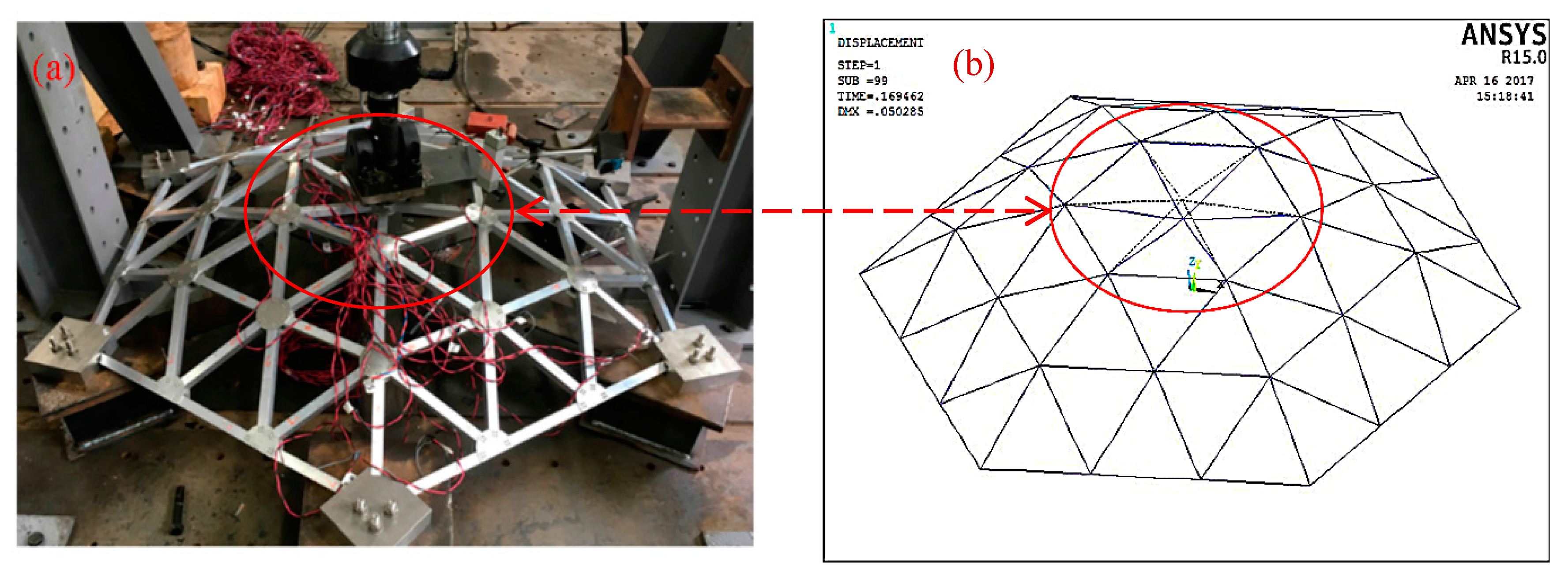
2.3.1. Failure Patterns of the Test Models
Failure Pattern of the Lattice Shell Model with No Aluminum Alloy Plate
The Failure Mode of the Combined Lattice Shell Model
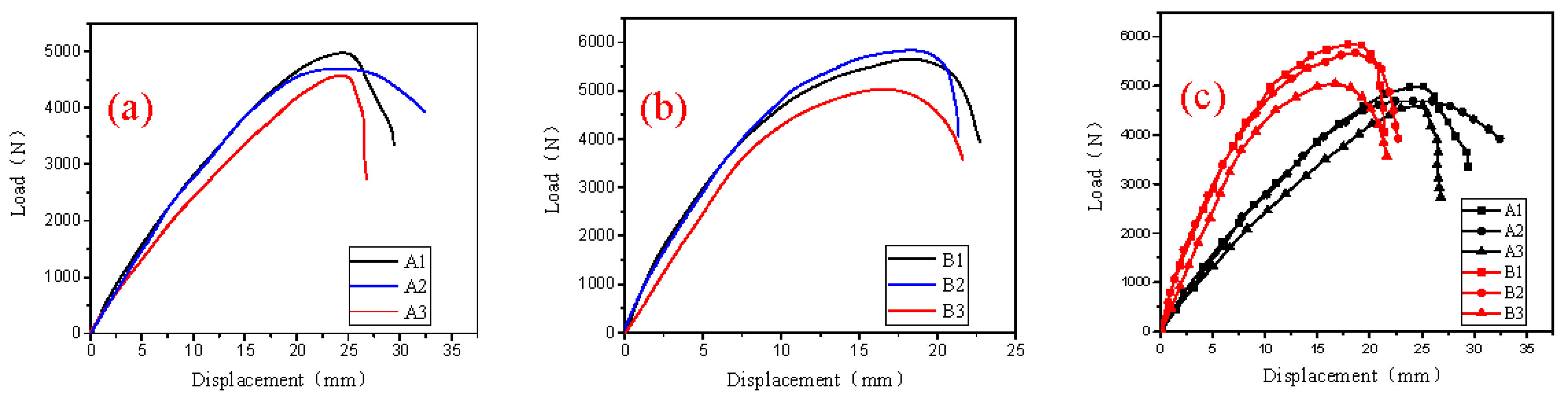
2.3.2. Load-Displacement Curve of the Test Model
3. Analysis of the Nonlinear Stability of NSCLS to Defects
3.1. Basic Assumptions
3.2. Analytical Methods
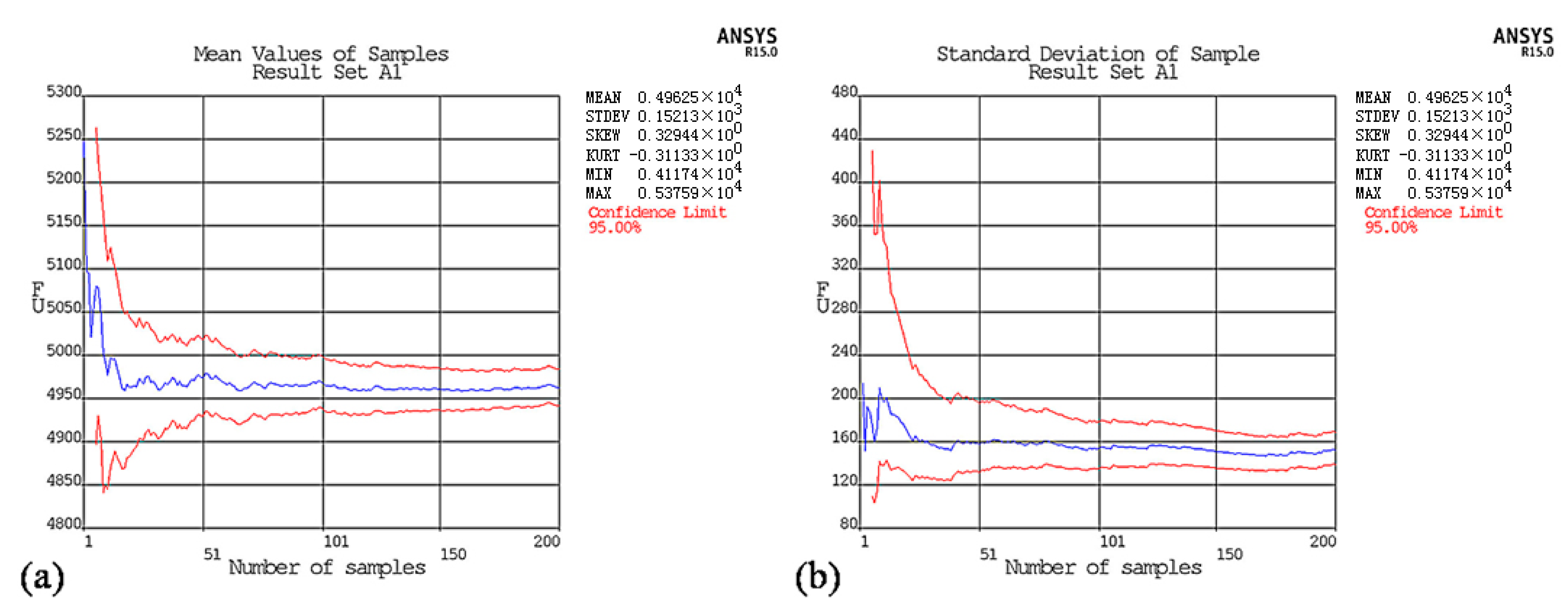
3.3. Experimental Verification of Random Defect Mode Method
3.3.1. Results for Model A1, the Defect-Free Lattice Shell Model with No Aluminum Plate
3.3.2. Analysis of the Combined Lattice Shell with Defects (Model B2)
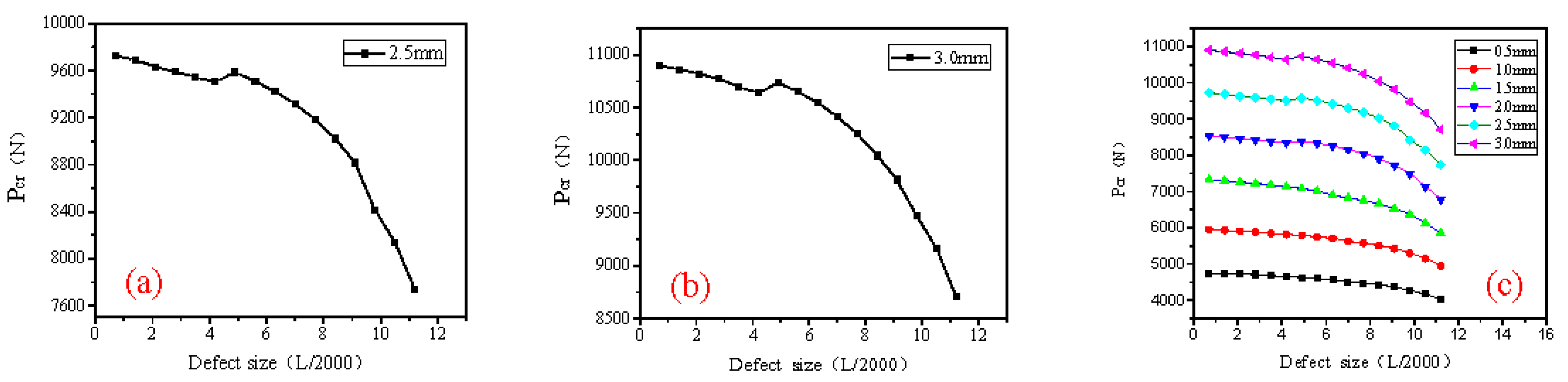
4. The Stability of NSCLS for Different Defect Sizes
5. Conclusions
- (1)
- By precision processing six models using a CNC machine and accounting for the initial geometric defects in the aluminum alloy lattice shell models, the authors performed a stability comparison. The results show that the overall stiffness and stable bearing capacity of the lattice shell are remarkably improved due to the aluminum alloy reinforcing plate. Regardless of whether there are geometric defects, the steady bearing capacity of the new combined lattice shells is approximately 16% higher than that of a lattice shell with the same span and no reinforcing plate. The magnitude of the increase for the lattice shell model with no defects is higher than that of the model with defects.
- (2)
- The NSCLS is a defect-sensitive structure. The influence of geometric defects on its stable bearing capacity is very obvious. The results of comparing the lattice shell models show that the sensitivities of the two types of structures are different. The bearing capacity of the defective model with no plate is approximately 7% lower than that of the model without defects. In the combined lattice shell model, the bearing capacity of the model with defects is 12% lower than that of the model without defects.
- (3)
- The finite element analysis results of applying the random defect mode method show that the theoretical failure patterns of the experimental models are basically consistent with those that were measured in the tests. The average difference between the theoretical stable bearing capacity and the experimental value is 5.7%. The theoretical load-displacement curves are also very close to the ones that were obtained in the tests. This indicates that the random defect mode method with a truncated Gaussian distribution is reasonable and reliable. It has sufficient accuracy. It can be used in structural analysis and design in practical engineering.
- (4)
- As the lowest-order buckling mode is unable to characterize the most unfavorable distribution of defects in the new structure, the critical load obtained using the uniform defect mode is frequently not the smallest critical load. Therefore, the existing specification of defect sizes can no longer be applicable. By calculating and analyzing nearly 20,000 NSCLS, we find that after the initial geometric defect value of the combined lattice shell reaches 3/1000 of the shell’s span, the stable bearing capacity decreases sharply. We recommend that the values be used as the maximum defect size for the combined lattice shell. The studies in this paper provide a theoretical basis for future design specifications for new composite lattice shell structures.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ma, Y.X.; Zheng, Y.D.; Meng, H.Y.; Song, W.H.; Yao, X.F.; Lv, H.X. Heterogeneous PVA hydrogels with micro-cells of both positive and negative Poisson’s ratios. J. Mech. Behav. Biomed. Mater. 2013, 23, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Dirks, J.-H.; Dürr, V. Biomechanics of the stick insect antenna: Damping properties and structural correlates of the cuticle. J. Mech. Behav. Biomed. Mater. 2011, 4, 2031–2042. [Google Scholar] [CrossRef] [PubMed]
- Koester, K.J.; Barth, H.D.; Ritchie, R.O. Effect of aging on the transverse toughness of human cortical bone: Evaluation by R-curves. J. Mech. Behav. Biomed. Mater. 2011, 4, 1504–1513. [Google Scholar] [CrossRef] [PubMed]
- Donius, A.E.; Liu, A.; Berglund, L.A.; Ulrike, G.K. Wegst Superior mechanical performance of highly porous, anisotropic nanocellulose–montmorillonite aerogels prepared by freeze casting. J. Mech. Behav. Biomed. Mater. 2014, 37, 88–99. [Google Scholar] [CrossRef] [PubMed]
- Tuo, W.Y.; Chen, J.X.; Wu, Z.S.; Xie, J.; Wang, Y. Characteristics of the tensile mechanical properties of fresh and dry forewings of beetles. Mater. Sci. Eng. C 2016, 65, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.X.; Zu, Q.; Wu, G.; Xie, J. Review of beetle forewing structure and biomimetic applications in China(II). Mater. Sci. Eng. C 2015, 50, 620–633. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.X.; Gu, C.; Guo, S.; Wan, C.; Wang, X.; Xie, J.; Hu, X. Integrated honeycomb technology motivated by the structure of beetle forewings. Mater. Sci. Eng. C 2012, 32, 1813–1817. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liu, C.; Chen, J.X.; Tao, Y.; Gu, Y. The influence mechanism of processing holes on the flexural properties of biomimetic integrated honeycomb plates. Mater. Sci. Eng. C 2016, 69, 798–803. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.X.; He, C.L.; Gu, C.L.; Liu, J.X.; Mi, C.W.; Guo, J.S. Compressive and flexural properties biomimetic integrated honeycomb plates. Mater. Des. 2014, 64, 214–220. [Google Scholar] [CrossRef]
- Chen, J.X.; Tuo, W.Y.; Zhang, X.M.; He, C.L.; Xie, J.; Liu, C. Compressive failure modes and parameter optimization of the trabecular structure of biomimetic fully integrated honeycomb plates. Mater. Sci. Eng. C 2016, 69, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Bourada, M.; Tounsi, A.; Houari, M.S.A.; Adda Bedia, E.A. A new four-variable refined plate theory for thermal buckling analysis of functionally graded sandwich plates. J. Sand. Struct. Mater. 2011, 14, 5–33. [Google Scholar] [CrossRef]
- Zyniszewski, S.S.; Smith, B.H.; Hajjar, J.F.; Arwade, S.R.; Schafer, B.W. Local buckling strength of steel foam sandwich panels. Thin-Walled Struct. 2012, 59, 11–19. [Google Scholar] [CrossRef]
- Katunin, A. Vibration-based spatial damage identification in honeycomb-core sandwich composite structures using wavelet analysis. J. Compos. Struct. 2014, 118, 385–391. [Google Scholar] [CrossRef]
- Zhao, C.Q.; Ma, J. Assembled Honeycombed Sheet Light Empty Stomach Building and Roof Structure System. Patent Application No. 200810100745.X, 21 April 2010. [Google Scholar]
- Zhao, C.Q.; Ma, J.; Tao, J. Experimental study on load capacity of new fabricated honeycomb panel open-web roof structures. J. Southeast Univ. (Nat. Sci. Ed.) 2014, 44, 626–630. [Google Scholar]
- Zhao, C.Q.; Zheng, W.D.; Ma, J.; Zhao, Y.J. Lateral compressive buckling performance of aluminum honeycomb panels for long-span hollow core roofs. Materials 2016, 9, 444. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.Q.; Zheng, W.D.; Ma, J.; Zhao, Y.J. Shear strength of different bolt connectors on large span aluminium alloy honeycomb sandwich structure. Appl. Sci. 2017, 7, 450. [Google Scholar] [CrossRef]
- Liu, H.B.; Ding, Y.Z.; Chen, Z.H. Static stability behavior of aluminum alloy single-layer spherical latticed shell structure with Temcor joints. Thin-Walled Struct. 2017, 46, 82–89. [Google Scholar] [CrossRef]
- Sugizaki, K.; Kohmura, S.; Hangai, Y. Experimental study on structural behaviour of an aluminum single-layer lattice shell. Trans. AIJ 1996, 61, 113–122. [Google Scholar] [CrossRef]
- Hiyama, Y.; Takashima, H.; Iijima, T. Experiments and analyses of unit single-layer reticular domes using aluminum ball joints for the connections. Trans. AIJ 1999, 64, 33–40. [Google Scholar] [CrossRef][Green Version]
- Guo, H.N.; Xiong, Z.; Luo, Y.F. Block tearing and local buckling of aluminum alloy gusset joint plates. KSCE J. Civ. Eng. 2016, 20, 820–831. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Wang, X.D. Structural design and analysis of aluminum dome for Caofeidian coal storage. Key Eng. Mater. 2016, 710, 396–401. [Google Scholar] [CrossRef]
- Gui, G.Q.; Wang, Y.E. Nonlinear stability analysis of single-layer aluminum alloy reticulated spherical shells. Eng. Mech. 2006, 23, 32–35. [Google Scholar]
- Attard, M.M.; Hunt, G.W. Sandwich Column Buckling: A Hyperelastic Formulation. J. Solids Struct. 2008, 45, 5540–5555. [Google Scholar] [CrossRef]
- Boudjemai, A.; Amri, R.; Mankour, A.; Salem, H.; Bouanane, M.H.; Boutchicha, D. Modal analysis and testing of hexagonal honeycomb plates used for satellite structural design. Mater. Des. 2012, 35, 266–275. [Google Scholar] [CrossRef]
- Ravishankar, B.; Sankar, B.V.; Haftka, R.T. Homogenization of integrated thermal protection system with rigid insulation bars. In Proceedings of the 51st AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Orlando, FL, USA, 12–15 April 2010; American Institute of Aeronautics and Astronautics: Boston, MA, USA, 2010. [Google Scholar]
- Standardization Administration of China JGJ7-2010. Technical Specification for Spatial Lattice Structures; Standard Press of China: Beijing, China, 2010. [Google Scholar]



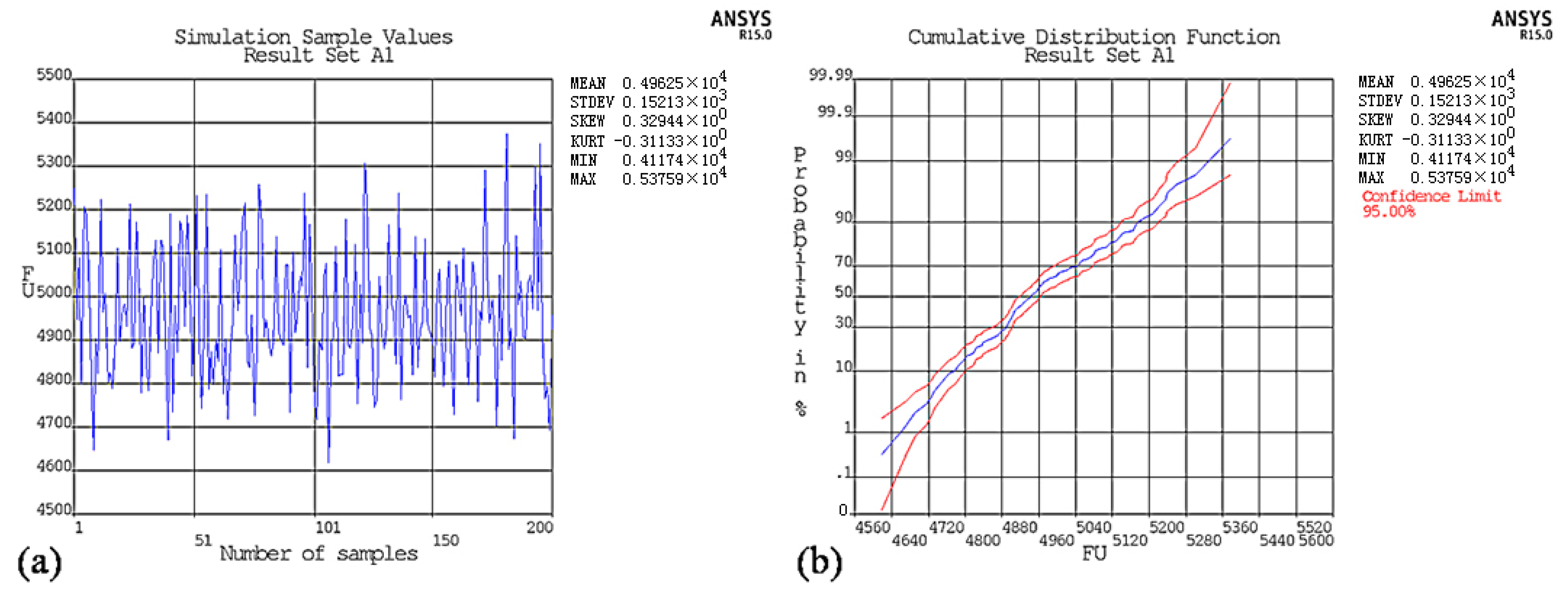

| Pe/N | Dmax/mm | Cd | Pmax/N | Pmin/N | Pμ/N | Pσ/N | Pcr |
|---|---|---|---|---|---|---|---|
| 4879 | 1.4 | 0.423 | 5376 | 4617 | 4962 | 152 | 4506 |
| Pe/N | Dmax/mm | Cd | Pmax/N | Pmin/N | Pμ/N | Pσ/N | Pcr |
|---|---|---|---|---|---|---|---|
| 5058 | 1.4 | 0.423 | 6210 | 3787 | 5256 | 220 | 4596 |
| Model Configuration | Lattice Shell with No Plate | Combined Lattice Shell | ||||
|---|---|---|---|---|---|---|
| Experimental Value (N) | Simulated Value (N) | Error (%) | Experimental Value (N) | Simulated Value (N) | Error (%) | |
| Without defects | 4879 | 4506 | 7.6 | 5761 | 5947 | 3.2 |
| 4601 | 2.1 | 5556 | 6.6 | |||
| With defects | 4652 | 4305 | 7.5 | 4958 | 4596 | 7.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Zhao, Y.; Ma, J. The Stability of New Single-Layer Combined Lattice Shell Based on Aluminum Alloy Honeycomb Panels. Appl. Sci. 2017, 7, 1150. https://doi.org/10.3390/app7111150
Zhao C, Zhao Y, Ma J. The Stability of New Single-Layer Combined Lattice Shell Based on Aluminum Alloy Honeycomb Panels. Applied Sciences. 2017; 7(11):1150. https://doi.org/10.3390/app7111150
Chicago/Turabian StyleZhao, Caiqi, Yangjian Zhao, and Jun Ma. 2017. "The Stability of New Single-Layer Combined Lattice Shell Based on Aluminum Alloy Honeycomb Panels" Applied Sciences 7, no. 11: 1150. https://doi.org/10.3390/app7111150
APA StyleZhao, C., Zhao, Y., & Ma, J. (2017). The Stability of New Single-Layer Combined Lattice Shell Based on Aluminum Alloy Honeycomb Panels. Applied Sciences, 7(11), 1150. https://doi.org/10.3390/app7111150





