On the Seismic Design of Structures with Tilting Located within a Seismic Region
Abstract
:1. Introduction
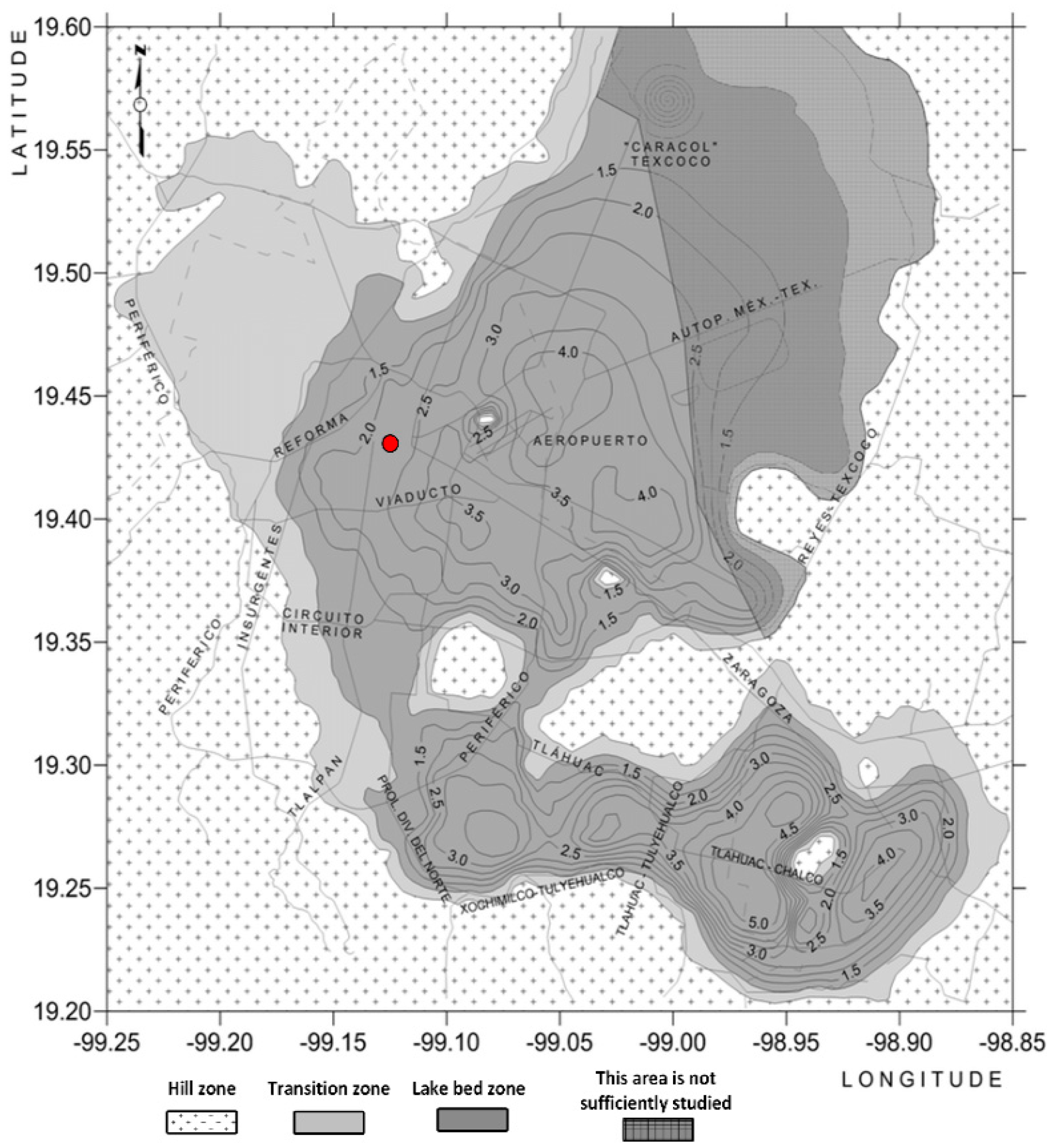
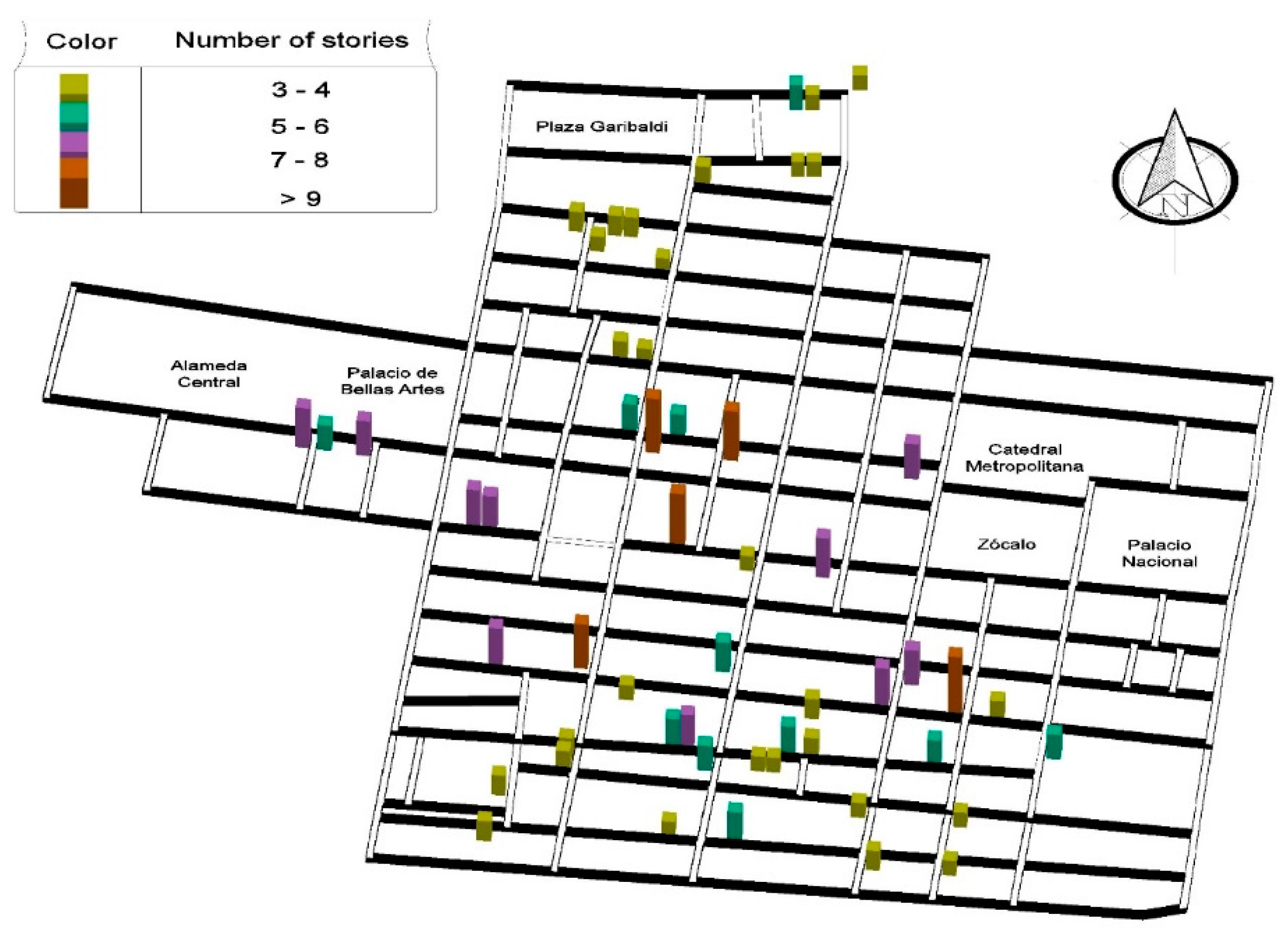
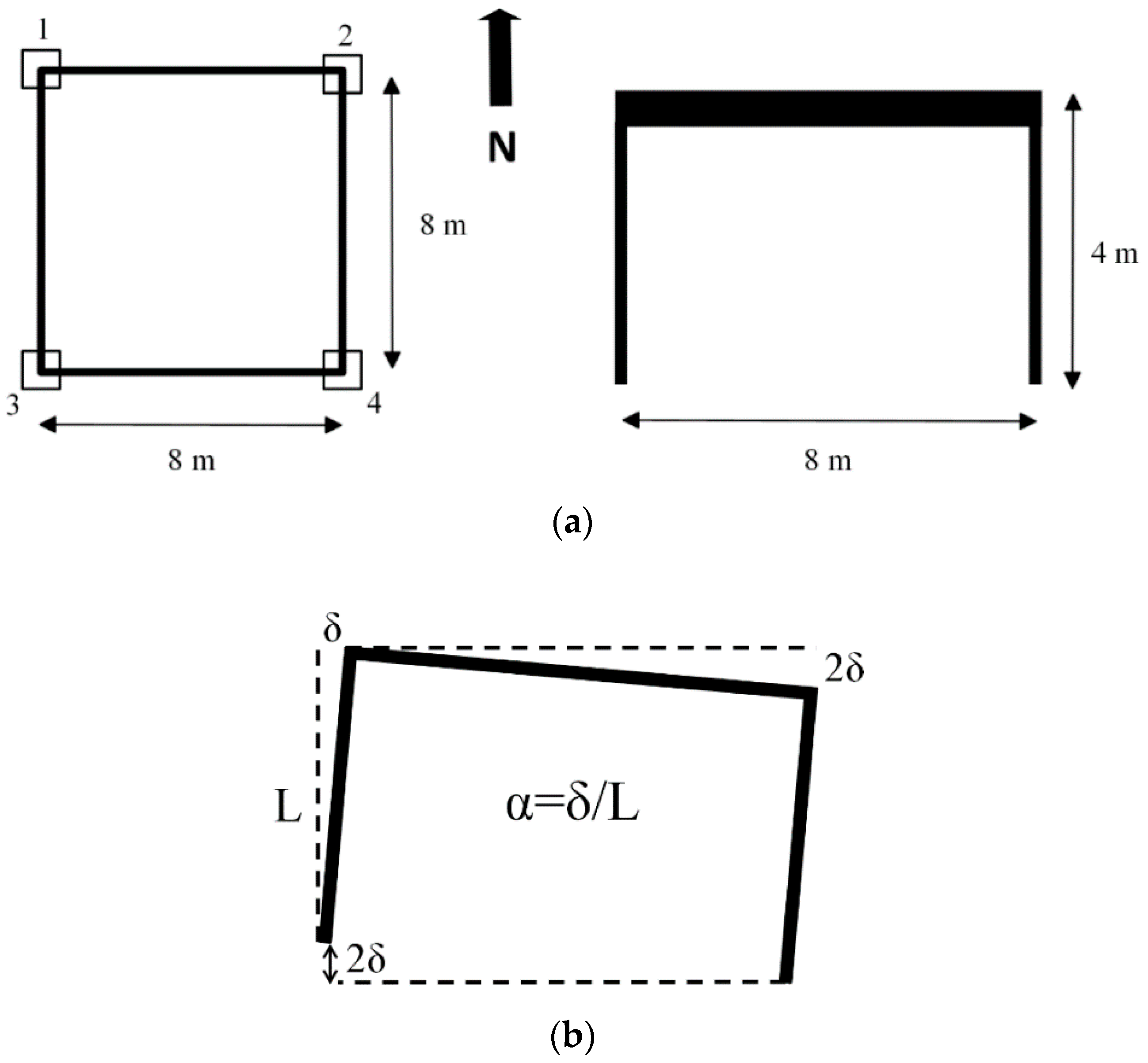
Buildings with Asymmetric Yielding Produced by Tilting in Mexico City
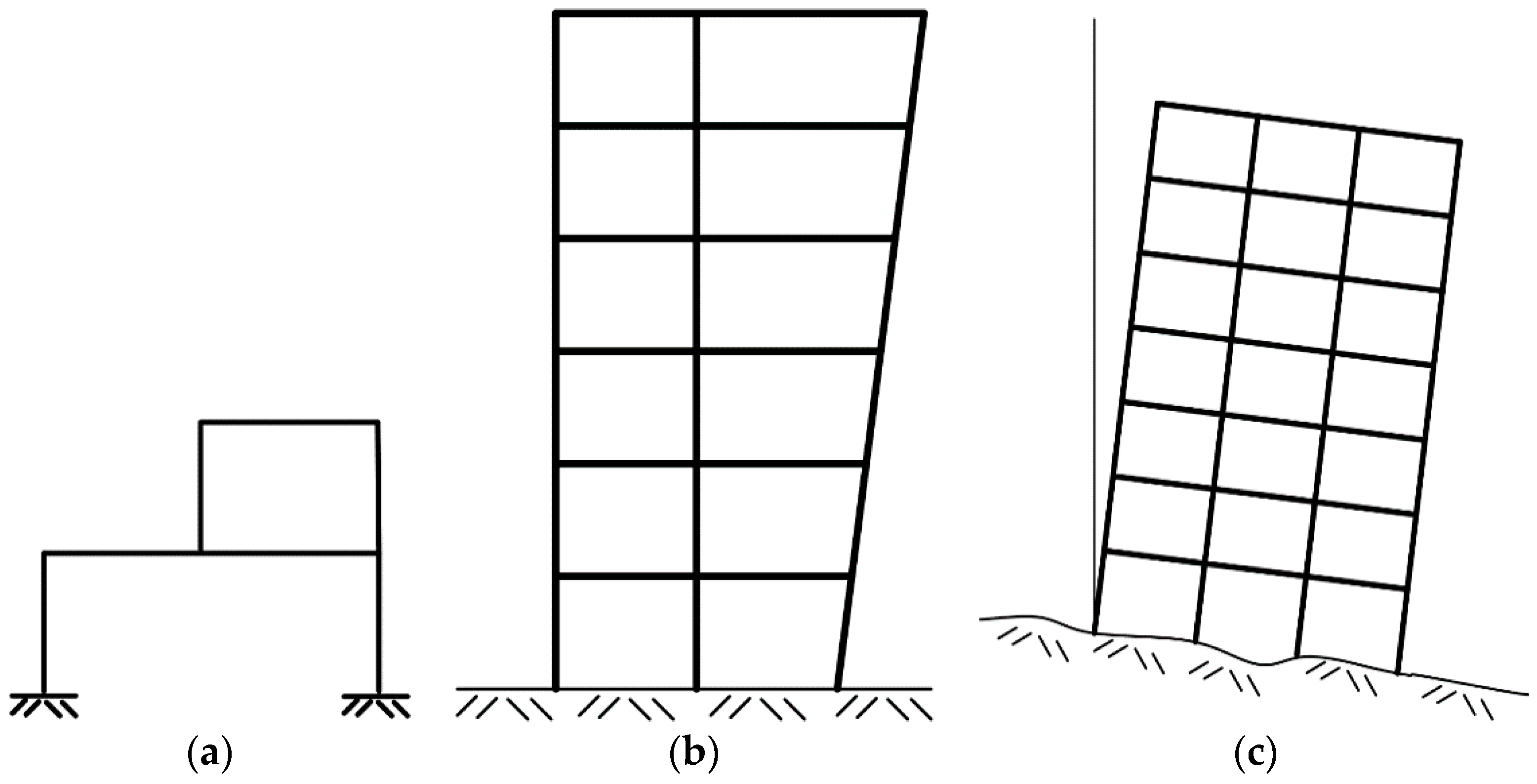
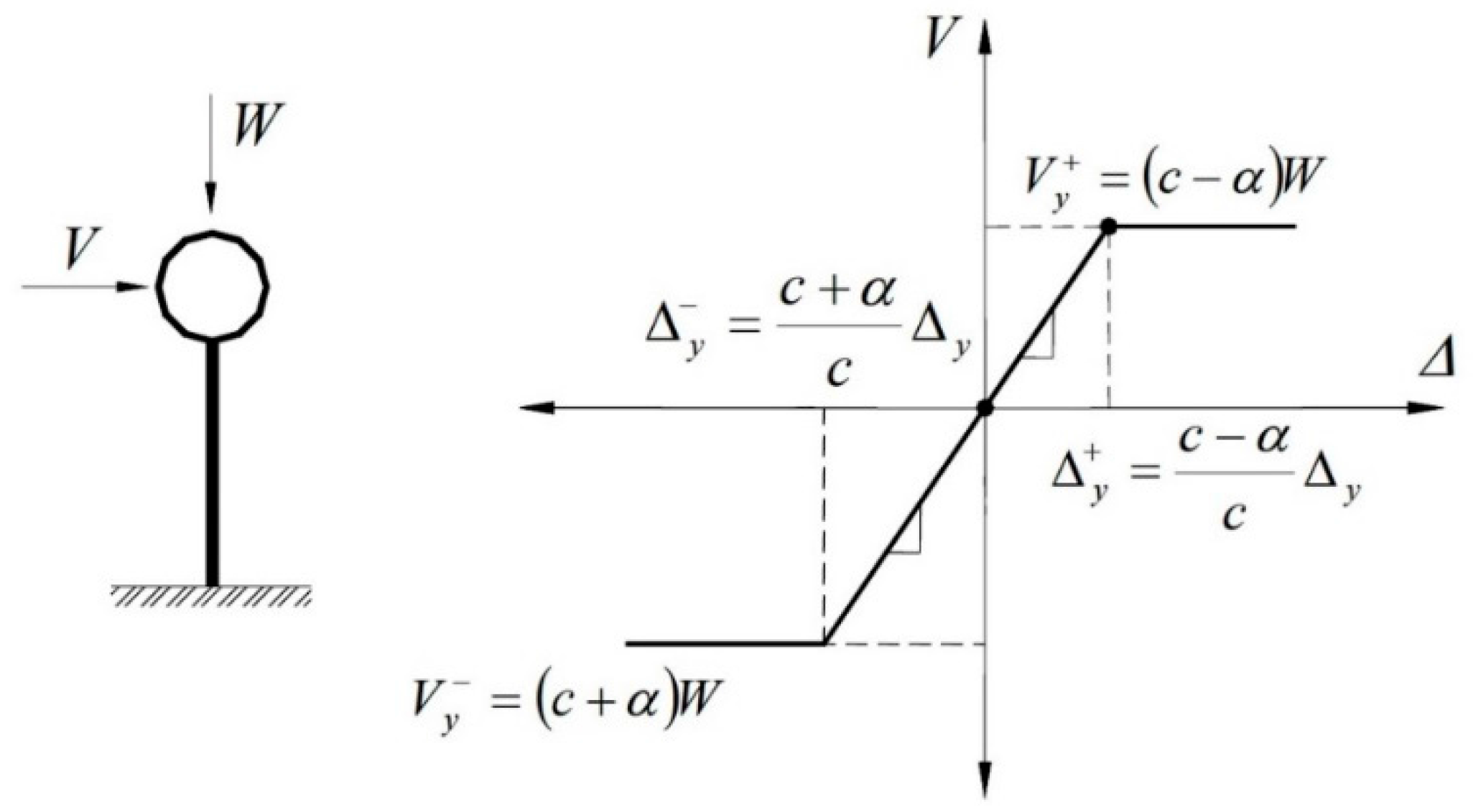
2. Simplified Structural Models
3. General Methodology
3.1. Evaluation of the Structural Reliability
3.2. Steps to Follow for the Proposed Methodology
- (1)
- Firstly, several nonlinear time history analyses are carried out for simplified structural systems with different characteristics of base shear coefficient (c), asymmetric level (α), and vibration period (T1). This is performed with the aim of obtaining the EDP as a function of seismic intensity. The maximum ductility demand of the systems (µ) is taken here as the EDP of interest. In order to calculate the maximum ductility demand of the systems, it is necessary to estimate first the ductility demand in both E-W and N-S directions (µx, µy) considering the simultaneous action of both horizontal components of the seismic ground motions; µx and µy are calculated by taking the maximum horizontal displacement of the center of mass of the structural systems in each direction (dX, dY) divided by their yield displacement, dy, which in turn is estimated by a nonlinear static analysis). Finally, the maximum ductility demand is defined in this study as the maximum of the ductility values estimated in each horizontal direction, as indicated in Equation (2).
- (2)
- Next, the median (D) and standard deviation (σlnD) of the ductility demand logarithms are calculated.
- (3)
- Fragility curves for several values of the maximum ductility demand are obtained using Equation (3):where all the variables were defined before, and Φ represents the Gaussian cumulative distribution function.
- (4)
- Ductility demand hazard curves (DDHC, Equation (1)) are obtained for symmetric yielding systems, and alternatively, for systems with different levels of asymmetric yielding.
- (5)
- Considering the ductility demand hazard curves corresponding to a wide variety of systems with different characteristics, ductility uniform exceedance rate spectra (µ-UERS) are obtained for several mean annual rate of exceedance values. To explicitly display the increment in the expected ductility demand of asymmetric yielding systems with respect to symmetric systems, ratios of µ-UERS corresponding to asymmetric yielding systems with respect to symmetric ones are calculated.
- (6)
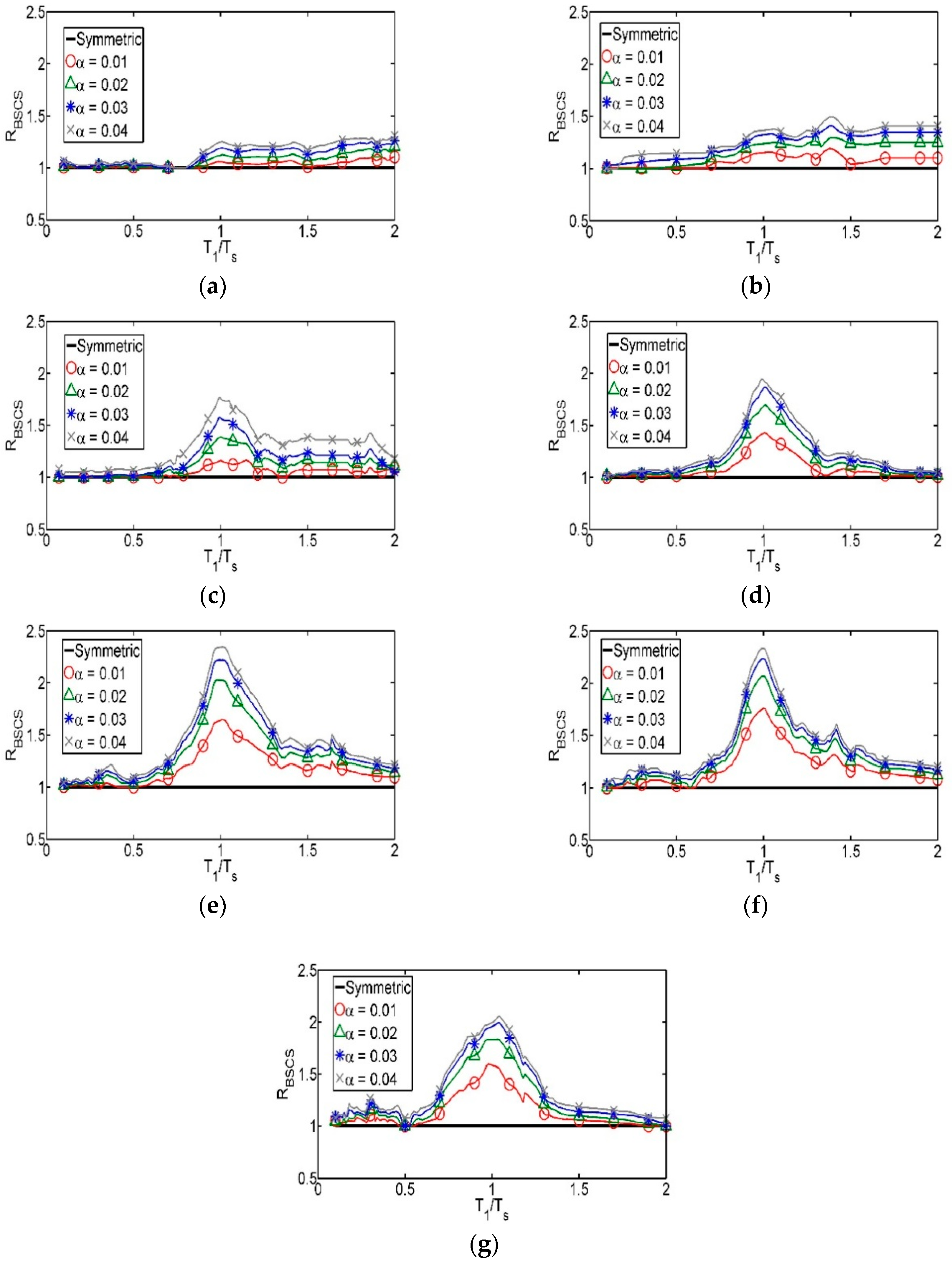
- The next step is to obtain base shear coefficient spectra (BSCS) for symmetric as well as for asymmetric yielding systems employing a linear interpolation process. This procedure consists in selecting a value of the ductility demand and the associated values of T1 and c, corresponding to a given µ-UERS. The process is repeated several times in order to obtain a data set T1 vs c for each value of the ductility demand considered. More details about this process can be found in [22]. Ratios between BSCS of systems with different levels of asymmetric yielding with respect to symmetric systems, RBSCS, are calculated with the objective of quantifying the additional lateral strength requirement of systems with asymmetric yielding to achieve a seismic performance equivalent to their symmetric counterparts. These ratios can be expressed as:
- (7)
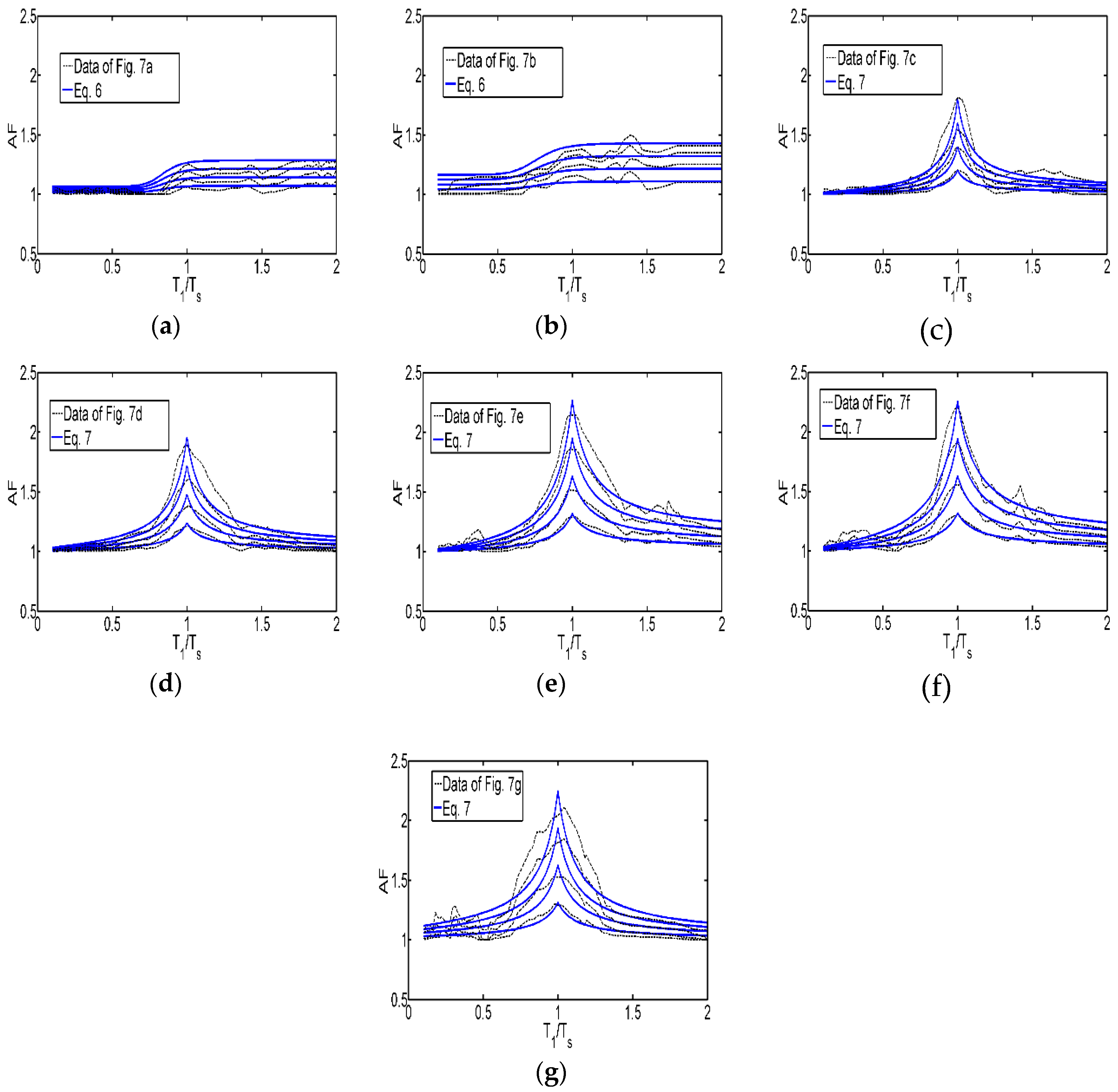
- A simplified mathematical expression is fitted to the ratios of the base shear coefficient spectra obtained in step 6. The proposed expression is a function of the asymmetry level (α) of the structural system, the ratio between the fundamental vibration period of the system and the dominant period of the soil, and the maximum ductility demand of the system.
- (8)
- Steps (1) to (7) are repeated for the seismic zones of interest (having different soil dominant periods, from firm ground to very soft soil). The resulting mathematical expressions for each zone will be compared between them to evaluate the influence of the dominant period of the soil on the strength amplification factors. Hence, general rules for the seismic region under study can be proposed.
4. Seismic Zones Analyzed
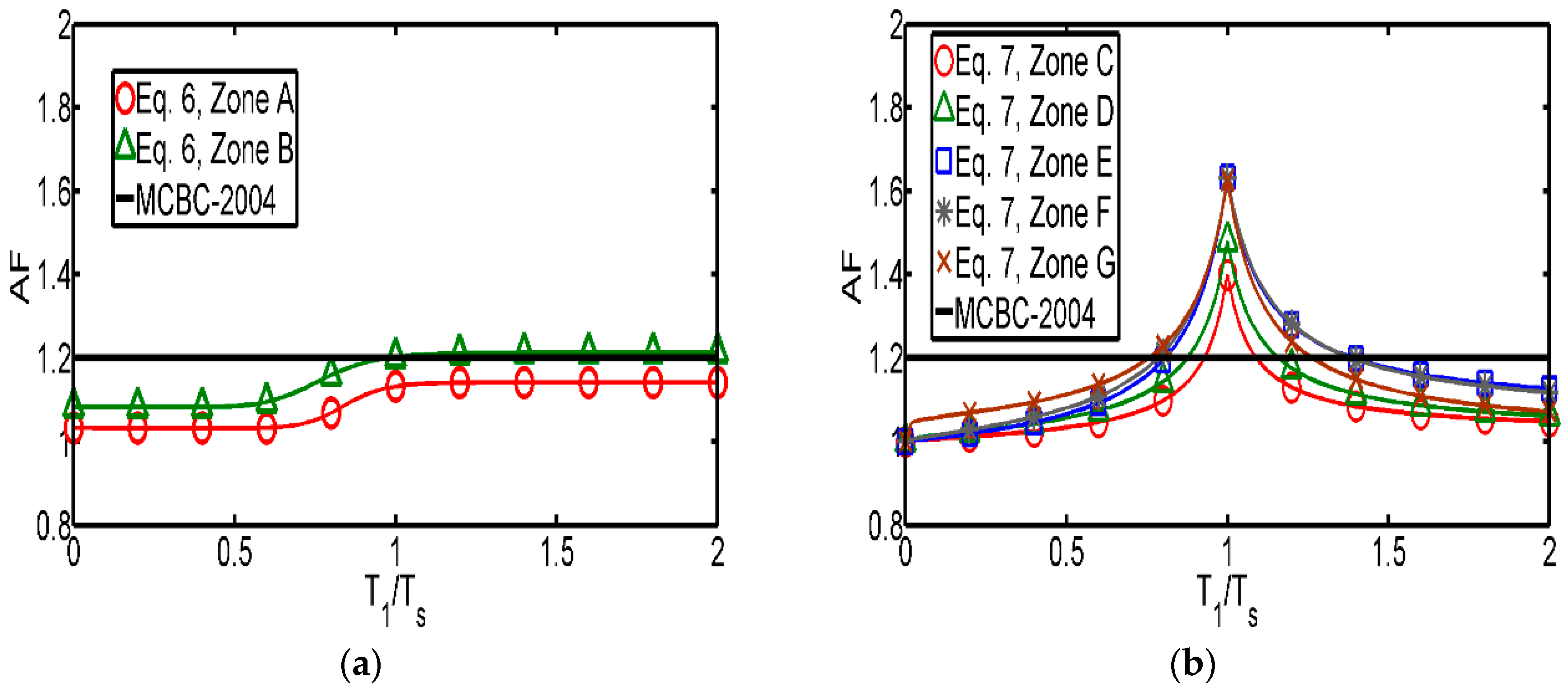
5. Mathematical Expressions of Strength Amplification Factors Corresponding to the Seismic Region of Interest
Comparison of the Proposed Mathematical Expressions with that Recommended in the Current Mexico City Building Code
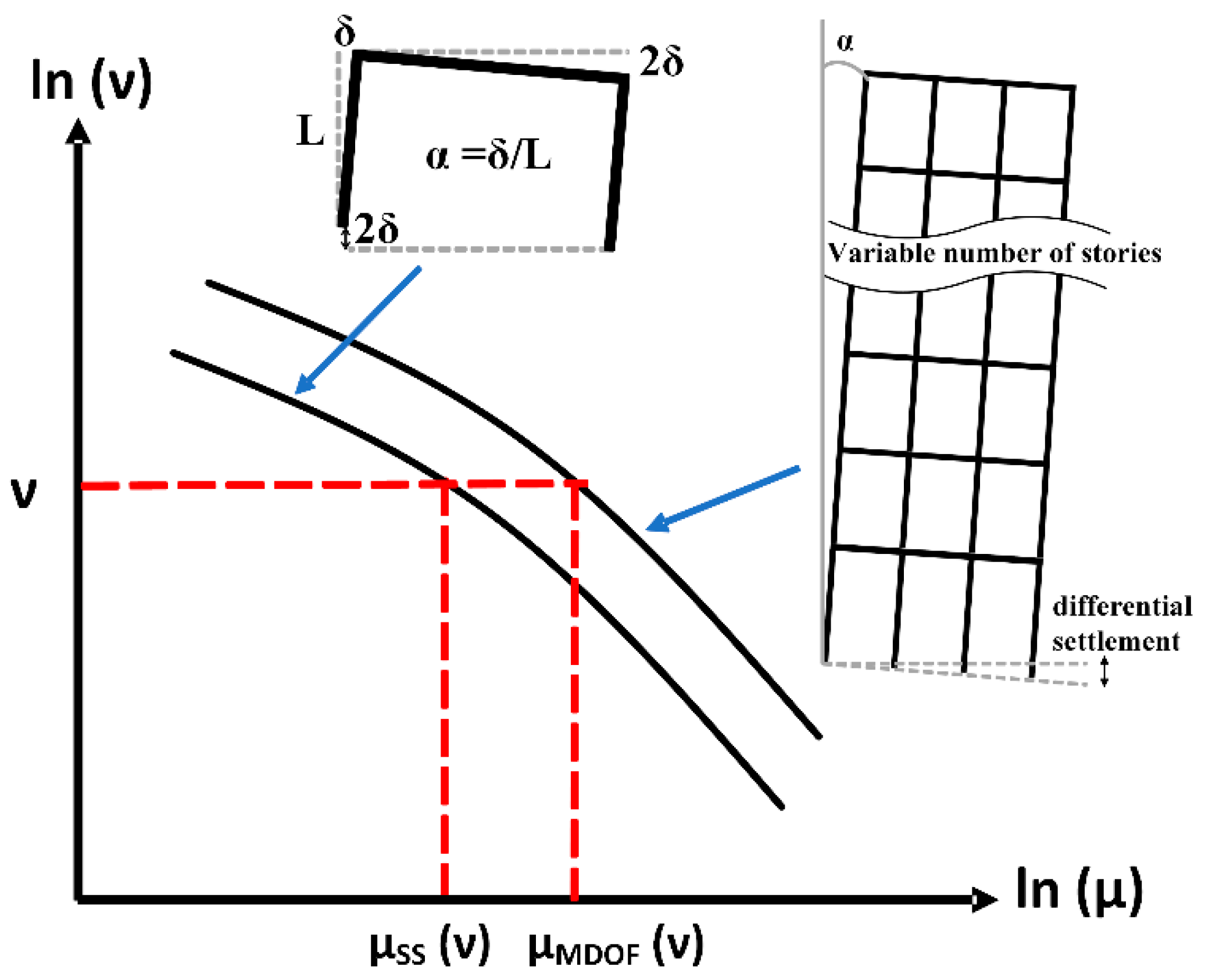
6. Ductility Transformation Factors between Simplified and MDOF Systems
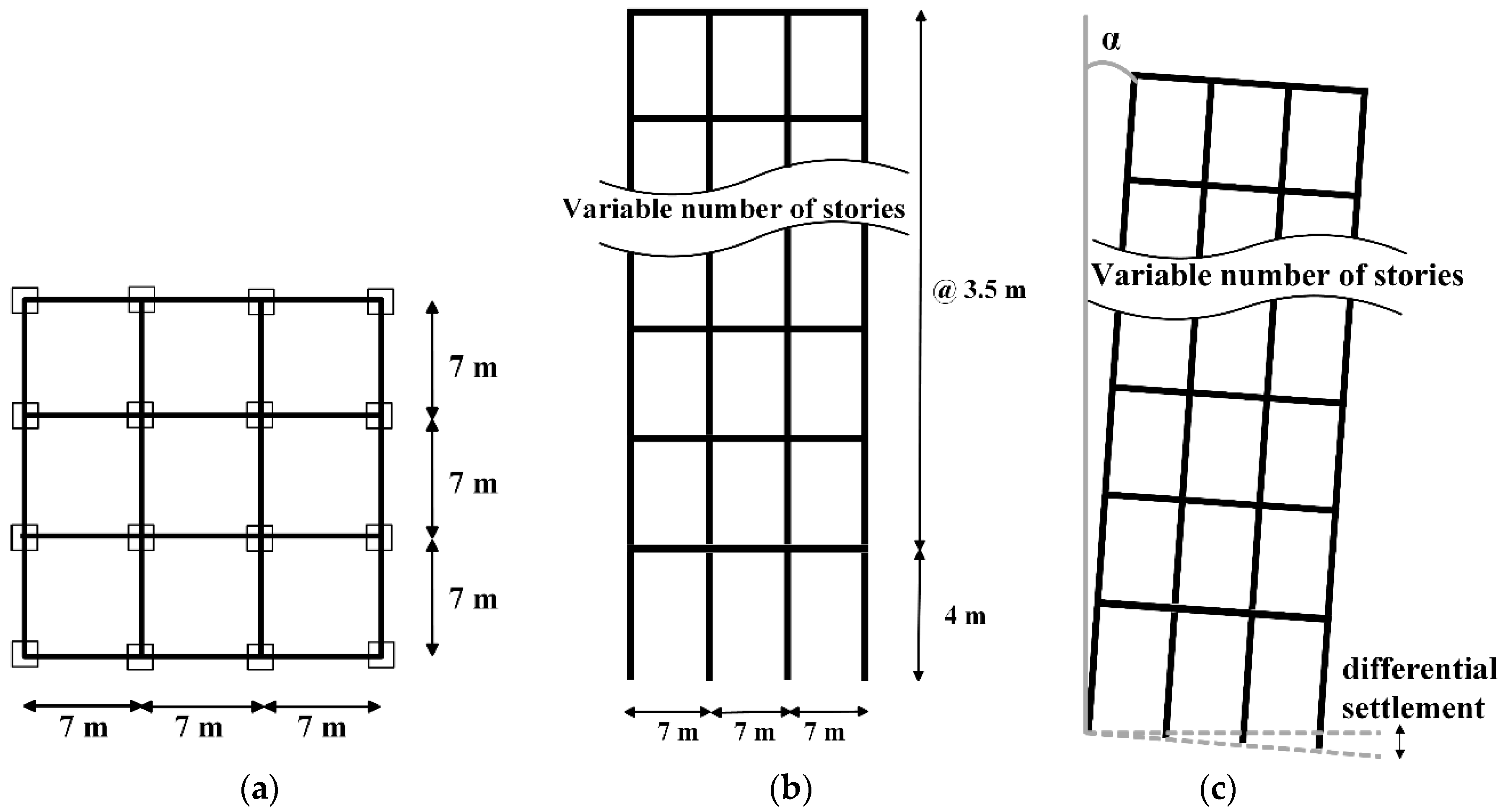
6.1. Characteristics of the Buildings Analyzed
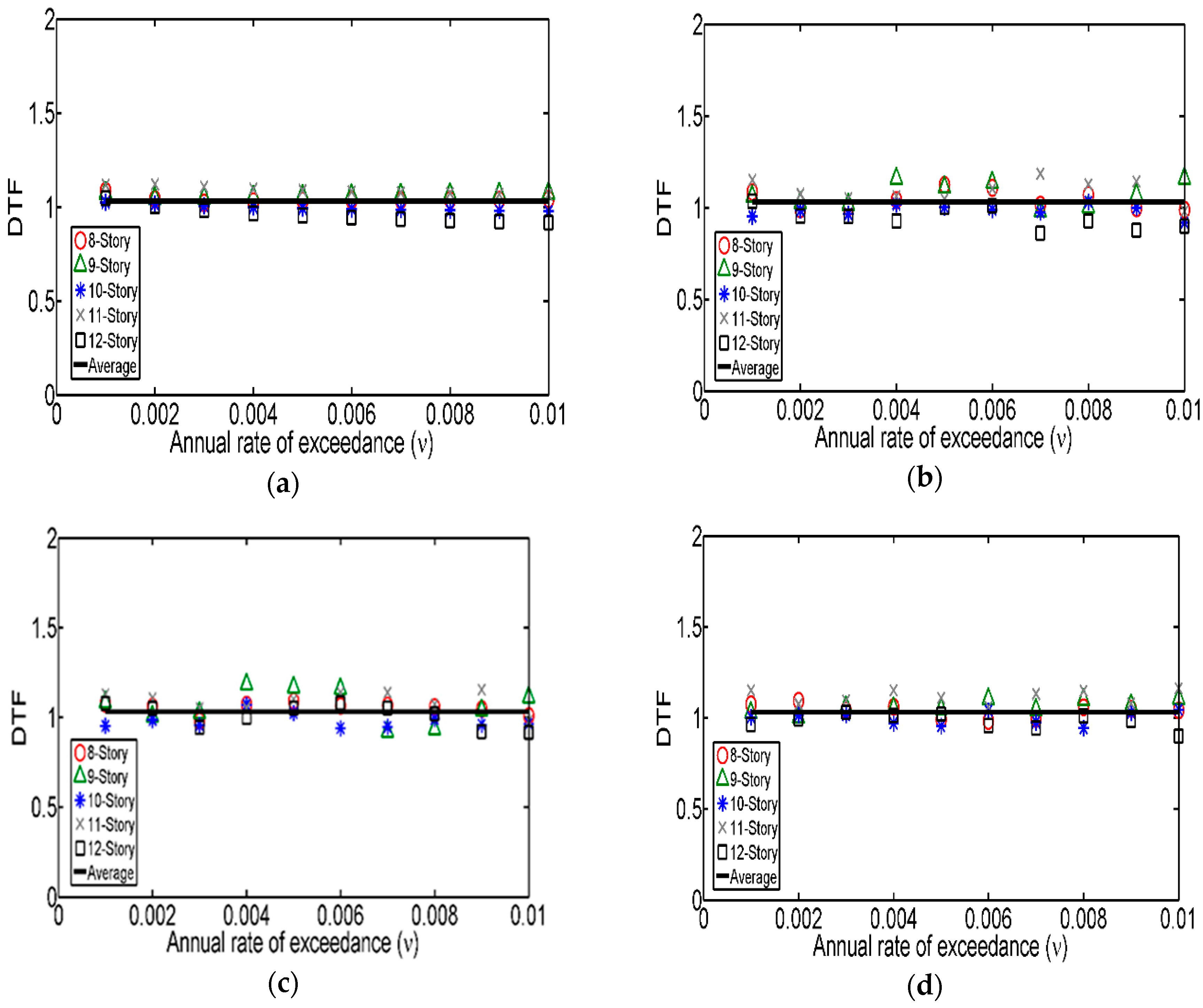
6.2. Ductility Transformation Factors (DTF)
7. Conclusions
- Results indicate that the additional lateral strength requirement of structures with asymmetric yielding is higher for those with fundamental vibration periods close to the dominant period of the soil where they are located; this requirement is even higher for structures located on soft soils.
- Simplified mathematical expressions were proposed for the estimation of strength amplification factors for structures with asymmetric yielding, considering different soil conditions. The expressions correspond to the valley of Mexico and depend on factors such as the ductility of the structure, the level of asymmetric yielding, and the ratio between the fundamental vibration period of the structure and that of the dominant period of the soil.
- The proposed mathematical expressions are more conservative than that recommended in the current Mexico City Building Code (MCBC-2004) for intermediate and soft soils, especially for structures whose vibration period is close to the dominant period of the soil where they are located. Although the expression proposed in the MCBC-2004 leads to conservative results for firm ground, results indicate that the effect of asymmetric yielding is much more detrimental on intermediate and soft soils than on firm ground. The expressions developed in this study have been approved by the Technical Committee for Seismic Design of the MCBC, and will be incorporated in the new version of the Mexico City Building Code.
- It was verified that the value of the expected ductility demand of asymmetric yielding MDOF systems, associated with a given return period, is almost equal to that corresponding to their equivalent simplified systems. The implication of this is that the use of simplified structural systems to estimate strength amplification factors for MDOF structures with asymmetric yielding is appropriate.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ellingwood, B.; MacGregor, J.G.; Galambos, T.V.; Cornell, C.A. Probability Based Load Criteria: Load Factors and Load Combinations. ASCE J. Struct. Div. 1982, 108, 978–997. [Google Scholar]
- Rosenblueth, E.; Esteva, L. Reliability basis for some Mexican codes. ACI Publ. SP-31 1972, 31, 1–41. [Google Scholar]
- Mexico City Building Code (MCBC). Complementary Technical Norms for Earthquake Resistant Design; MCBC: Mexico City, Mexico, 2004. [Google Scholar]
- National Research Council of Canada. National Building Code of Canada (NBCC); National Research Council of Canada: Ottawa, ON, Canada, 2005.
- FEMA. Next-Generation Performance-Based Seismic Design Guidelines, Prepared by the Applied Technology Council for the Federal Emergency Management Agency; Report No. FEMA 445; FEMA: Washington, DC, USA, 2006.
- FEMA. Next-Generation Methodology for Seismic Performance Assessment of Buildings, Prepared by the Applied Technology Council for the Federal Emergency Management Agency; Report No. FEMA P-58; FEMA: Washington, DC, USA, 2012.
- Rosenblueth, E. Seismic design requirements in a Mexican 1976 code. Earthq. Eng. Struct. Dyn. 1979, 7, 49–61. [Google Scholar] [CrossRef]
- Zhai, C.; Xie, L. The modification of strength reduction factors for MDOF effect. Adv. Struct. Eng. 2006, 9, 477–490. [Google Scholar] [CrossRef]
- Ruiz-García, J.; Miranda, E. Probabilistic estimation of maximum inelastic displacement demands for performance-based design. Earthq. Eng. Struct. Dyn. 2007, 36, 1235–1254. [Google Scholar] [CrossRef]
- Newmark, N.M.; Hall, W.J. Earthquake Spectra and Design; EERI Monograph Series; Earthquake Engineering: Oakland, CA, USA, 1982. [Google Scholar]
- Wu, J.P.; Hanson, R.D. Inelastic response spectra with high damping. J. Struct. Div. (ASCE) 1989, 115, 1412–1431. [Google Scholar] [CrossRef]
- Ramirez, O.M.; Constantinou, M.C.; Kircher, C.A.; Whittaker, A.S.; Johnson, M.W.; Gomez, J.D.; Chrysostomou, C.Z. Development and Evaluation of Simplified Procedures for Analysis and Design of Buildings with Passive Energy Dissipation Systems; Report No. MCEER-00-0010; Multidisciplinary Center for Earthquake Engineering Research (MCEER): New York, NY, USA, 2000. [Google Scholar]
- Arroyo-Espinoza, D.; Terán-Gilmore, A. Strength reduction factors for ductile structures with passive energy dissipating devices. J. Earthq. Eng. 2003, 7, 297–325. [Google Scholar] [CrossRef]
- Cameron, W.; Green, R. Damping correction factors for horizontal ground-motion response spectra. Bull. Seismol. Soc. Am. 2007, 97, 934–960. [Google Scholar] [CrossRef]
- Castillo, T.; Ruiz, S.E. Reduction factors for seismic design spectra for structures with viscous energy dampers. J. Earthq. Eng. 2014, 18, 323–349. [Google Scholar] [CrossRef]
- Ruiz, S.E.; Rosenblueth, E.; Diederich, R. The Mexico Earthquake of September 19, 1985—Seismic response of asymmetrically yielding structures. Earthq. Spectra 1989, 5, 103–111. [Google Scholar] [CrossRef]
- Ruiz, S.E. Influence of intensity of motion on the seismic response of structures with asymmetric force-deformation curves. Earthq. Eng. Struct. Dyn. 1991, 20, 1–9. [Google Scholar] [CrossRef]
- Terán-Gilmore, A.; Juarez, H.; Frausto, M. On the dynamic response of regular structures exhibiting tilt. Earthq. Eng. Struct. Dyn. 2000, 29, 1343–1374. [Google Scholar] [CrossRef]
- Moon, K.S. Comparative evaluation of structural systems for tilted tall buildings. Int. J. High-Rise Build. 2014, 3, 89–98. [Google Scholar]
- Carpinteri, A.; Invernizzi, S.; Lacidogna, G. In situ damage assessment and nonlinear modelling of an historical masonry tower. Eng. Struct. 2005, 27, 387–395. [Google Scholar] [CrossRef]
- Terán-Gilmore, A.; Arroyo-Espinoza, D. Planteamiento de factores de amplificación de resistencia para estructuras con asimetría en fluencia (Approach about resistance amplification factors for structures with asymmetric yielding). Revista de Ingeniería Sísmica 2005, 72, 81–106. [Google Scholar]
- Valenzuela-Beltrán, F.; Ruiz, S.E.; Reyes-Salazar, A.; Bojórquez, E. Reliability-based strength amplification factors for structures with asymmetric yielding. J. Earthq. Eng. 2016. [Google Scholar] [CrossRef]
- Avilés, J.; Pérez-Rocha, L.E. Regional subsidence of Mexico City and its effects on seismic response. Soil Dyn. Earthq. Eng. 2010, 30, 981–989. [Google Scholar] [CrossRef]
- Rosenblueth, E. Code specification of safety and serviceability. Conference Preprints Reports. In Proceedings of the International Conference on Planning and Design of Tall Buildings, Bethlehem, PA, USA, 21–26 August 1972; pp. 23–51. [Google Scholar]
- Cornell, C.A. A probability-based structural code. ACI J. 1969, 66, 974–985. [Google Scholar]
- Hao, G.; Liang, X.; Zhang, S. The new approximate calculation method for the first order reliability. Appl. Math. 2013, 4, 505–509. [Google Scholar] [CrossRef]
- Gaxiola-Camacho, J.R.; Azizsoltani, H.; Villegas-Mercado, F.J.; Haldar, A. A novel reliability technique for implementation of Performance-Based Seismic Design of structures. Eng. Struct. 2017, 142, 137–147. [Google Scholar] [CrossRef]
- Galambos, T.V.; Ravindra, M.K. Tentative Load and Resistance Factor Design Criteria for Steel Buildings; Research Report 18; Structural Division, Washington University: St. Louis, MO, USA, 1973. [Google Scholar]
- Basha, B.; Babu, G.L. Reliability-based load and resistance factor design approach for external seismic stability of reinforced soil walls. Soil Dyn. Earthq. Eng. 2014, 60, 8–21. [Google Scholar] [CrossRef]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. The probabilistic basis for the 2000 SAC/FEMA steel moment frame guidelines. J. Struct. Eng. 2000, 128, 526–533. [Google Scholar] [CrossRef]
- Montiel, M.A.; Ruiz, S.E. Influence of structural capacity uncertainty on seismic reliability of building structures under narrow-band motions. Earthq. Eng. Struct. Dyn. 2007, 36, 1915–1934. [Google Scholar] [CrossRef]
- Baker, J.; Gupta, A. Bayesian treatment of induced seismicity in probabilistic seismic hazard analysis. Bull. Seismol. Soc. Am. 2016, 106, 860–870. [Google Scholar] [CrossRef]
- Bradley, B.; Burks, L.; Baker, J. Ground motion selection for simulation-based seismic hazard and structural reliability assessment. Earthq. Eng. Struct. Dyn. 2015, 44, 2321–2340. [Google Scholar] [CrossRef]
- Sfahani, M.G.; Guan, H.; Loo, Y. Seismic reliability and risk assessment of structures based on fragility analysis—A review. Adv. Struct. Eng. 2015, 18, 1653–1669. [Google Scholar] [CrossRef]
- Frangopol, D.M. Structural optimization using reliability concepts. J. Struct. Eng. 1985, 111, 2288–2301. [Google Scholar] [CrossRef]
- Esteva, L. Design general. In Design of Earthquake Resistant Structures; Rosenblueth, E., Ed.; Pentech Press: London, UK, 1980; Chapter 3. [Google Scholar]
- Kang, Z.; Luo, Y. Reliability-based structural optimization with probability and convex set hybrid models. Struct. Multidiscip. Optim. 2010, 42, 89–102. [Google Scholar] [CrossRef]
- Miller, M.; Baker, J. Ground-motion intensity and damage map selection for probabilistic infrastructure network risk assessment using optimization. Earthq. Eng. Struct. Dyn. 2015, 44, 1139–1156. [Google Scholar] [CrossRef]
- Cornell, C.A. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar]
- Esteva, L. Bases para la Formulación de Decisiones de Diseño Sísmico (Basis for the Formulation of Seismic Design Decisions. Ph.D. Thesis, Facultad de Ingeniería, Universidad Nacional Autónoma de México, Mexico City, Mexico, 1968. [Google Scholar]
- Cornell, C.A.; Krawinkler, H. Progress and challenges in seismic performance assessment. PEER Center News 2000, 3, 1–3. [Google Scholar]
- Shome, N.; Cornell, C.A. Probabilistic Seismic Demand Analysis of Nonlinear Structures; Report No. RMS-35; Department of Civil and Environmental Engineering, Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Baker, J.W.; Cornell, C.A. Spectral shape, epsilon and record selection. Earthq. Eng. Struct. Dyn. 2006, 35, 1077–1095. [Google Scholar] [CrossRef]
- Jalayer, F.; Beck, J.L.; Porter, K.A. Effects of ground motion uncertainty on predicting the response of an existing RC frame structure. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Bojórquez, E.; Iervolino, I.; Reyes-Salazar, A.; Ruiz, S.E. Comparing vector-valued intensity measures for fragility analysis of steel frames for the case of narrow-band ground motions. Eng. Struct. 2012, 45, 472–480. [Google Scholar] [CrossRef]
- Brown, P.C.; Lowes, L.N. Fragility Functions for Modern Reinforced-Concrete Beam-Column Joints. Earthq. Spectra 2007, 23, 263–289. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 740–757. [Google Scholar] [CrossRef]
- Bojórquez, J.; Ruiz, S.E.; Bojórquez, E.; Reyes-Salazar, A. Probabilistic seismic response transformation factors between SDOF and MDOF systems using Artificial Neural Networks. J. Vibroeng. 2016, 18, 2248–2262. [Google Scholar] [CrossRef]
- Bojórquez, E.; Bojórquez, J.; Ruiz, S.E.; Reyes-Salazar, A.; Velázquez-Dimas, J. Response transformation factors for deterministic-based and reliability-based seismic design. Struct. Eng. Mech. 2013, 46, 755–773. [Google Scholar] [CrossRef]
- Computers and Structures Inc.; ETABS. Analysis and Design of Buildings Software; Computers and Structures Inc.: Berkeley, CA, USA, 2016. [Google Scholar]
- Uniform Building Code. Structural Engineering Design Provisions Vol. 2. In Proceedings of the International Conference of Building Officials, Whittier, CA, USA, May 1994; Available online: http://digitalassets.lib.berkeley.edu/ubc/UBC_1994_v1.pdf (accessed on 22 August 2017).
- Carr, A.J. 3D RUAUMOKO: Inelastic Three-Dimensional Dynamic Analysis Program; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2007. [Google Scholar]

| Zone | Range of Period (s) | Average Dominant Period, Ts (s) |
|---|---|---|
| A | Ts ≤ 0.5 | 0.62 |
| B | 0.5 < Ts ≤ 1.0 | 0.96 |
| C | 1.0 < Ts ≤ 1.5 | 1.41 |
| D | 1.5 < Ts ≤ 2.0 | 1.98 |
| E | 2.0 < Ts ≤ 2.5 | 2.55 |
| F | 2.5 < Ts ≤ 3.0 | 3.03 |
| G | 3.0 < Ts ≤ 4.0 | 3.61 |
| Zone | Dominant Period (s) | a | b | c | d |
|---|---|---|---|---|---|
| A | Ts ≤ 0.5 | (3.5µ − 1.5) α | 13.4 | 0.1 | 1.6α + 1 |
| B | 0.5 < Ts ≤ 1.0 | (4.8µ − 3) α | 8.8 | 0.1 | 4.1α + 1 |
| C | 1.0 < Ts ≤ 1.5 | (1.5µ − 1.4) α | 0.7 | 0.08 | 1 |
| D | 1.5 < Ts ≤ 2.0 | (2µ − 1.6) α | 0.5 | 0.1 | 1 |
| E | 2.0 < Ts ≤ 2.5 | (1.5µ + 0.8) α | 0.9 | 0.12 | 1 |
| F | 2.5 < Ts ≤ 3.0 | (1.5µ + 1.1) α | 0.7 | 0.13 | 1 |
| G | 3.0 < Ts ≤ 4.0 | (1.9µ − 0.05) α | 0.1 | 0.12 | 1 |
| Building | T1 | Vb | W | c | dy | du |
|---|---|---|---|---|---|---|
| (s) | (Ton) | (Ton) | (m) | (m) | ||
| 8-story | 1.2 | 1332.45 | 3807 | 0.35 | 0.168 | 0.63 |
| 9-story | 1.22 | 1498.2 | 4540 | 0.33 | 0.181 | 0.65 |
| 10-story | 1.33 | 1563.02 | 5042 | 0.31 | 0.195 | 0.69 |
| 11-story | 1.4 | 1721.1 | 5737 | 0.3 | 0.223 | 0.74 |
| 12-story | 1.48 | 1772.68 | 6331 | 0.28 | 0.246 | 0.78 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valenzuela-Beltrán, F.; Ruiz, S.E.; Reyes-Salazar, A.; Gaxiola-Camacho, J.R. On the Seismic Design of Structures with Tilting Located within a Seismic Region. Appl. Sci. 2017, 7, 1146. https://doi.org/10.3390/app7111146
Valenzuela-Beltrán F, Ruiz SE, Reyes-Salazar A, Gaxiola-Camacho JR. On the Seismic Design of Structures with Tilting Located within a Seismic Region. Applied Sciences. 2017; 7(11):1146. https://doi.org/10.3390/app7111146
Chicago/Turabian StyleValenzuela-Beltrán, Federico, Sonia E. Ruiz, Alfredo Reyes-Salazar, and J. Ramón Gaxiola-Camacho. 2017. "On the Seismic Design of Structures with Tilting Located within a Seismic Region" Applied Sciences 7, no. 11: 1146. https://doi.org/10.3390/app7111146
APA StyleValenzuela-Beltrán, F., Ruiz, S. E., Reyes-Salazar, A., & Gaxiola-Camacho, J. R. (2017). On the Seismic Design of Structures with Tilting Located within a Seismic Region. Applied Sciences, 7(11), 1146. https://doi.org/10.3390/app7111146







