3D Suspended Polymeric Microfluidics (SPMF3) with Flow Orthogonal to Bending (FOB) for Fluid Analysis through Kinematic Viscosity
Abstract
:1. Introduction
2. Materials and Methods
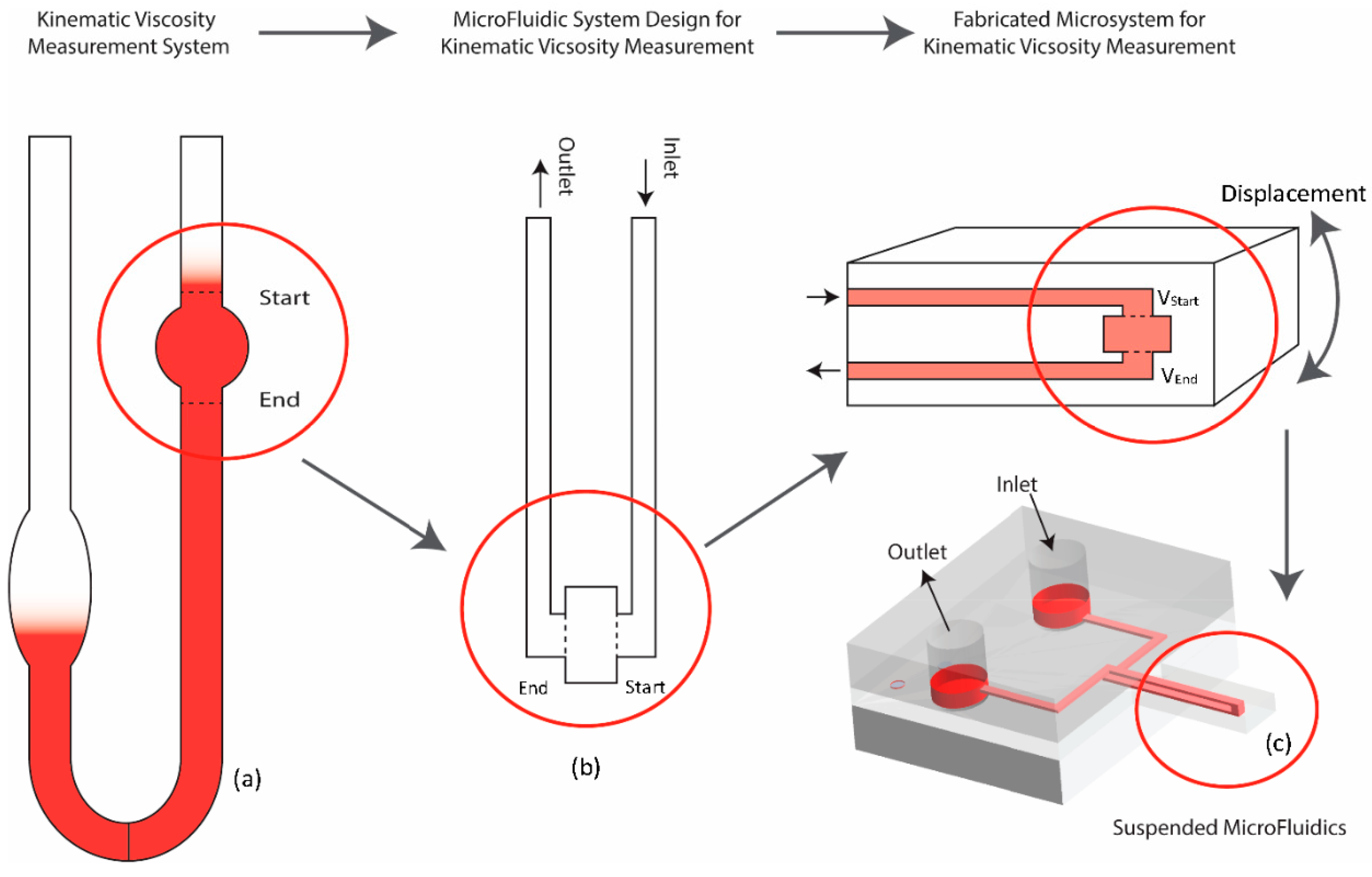
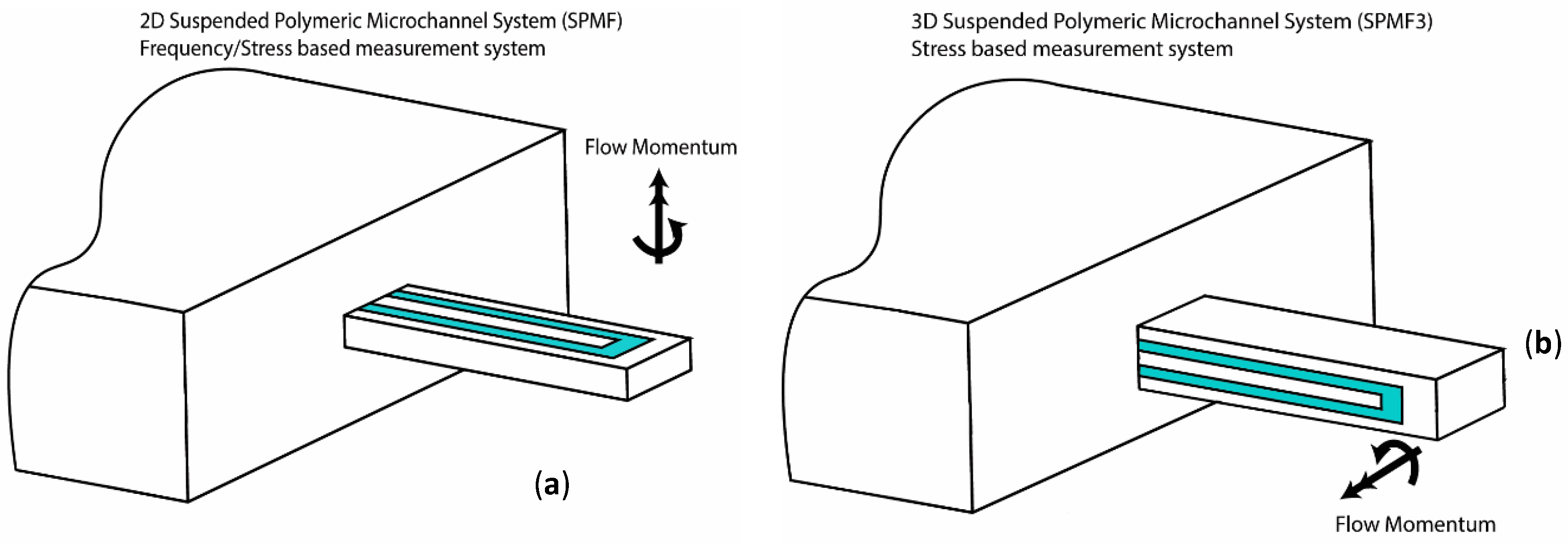
2.1. 3D Suspended Polymeric Microfluidics
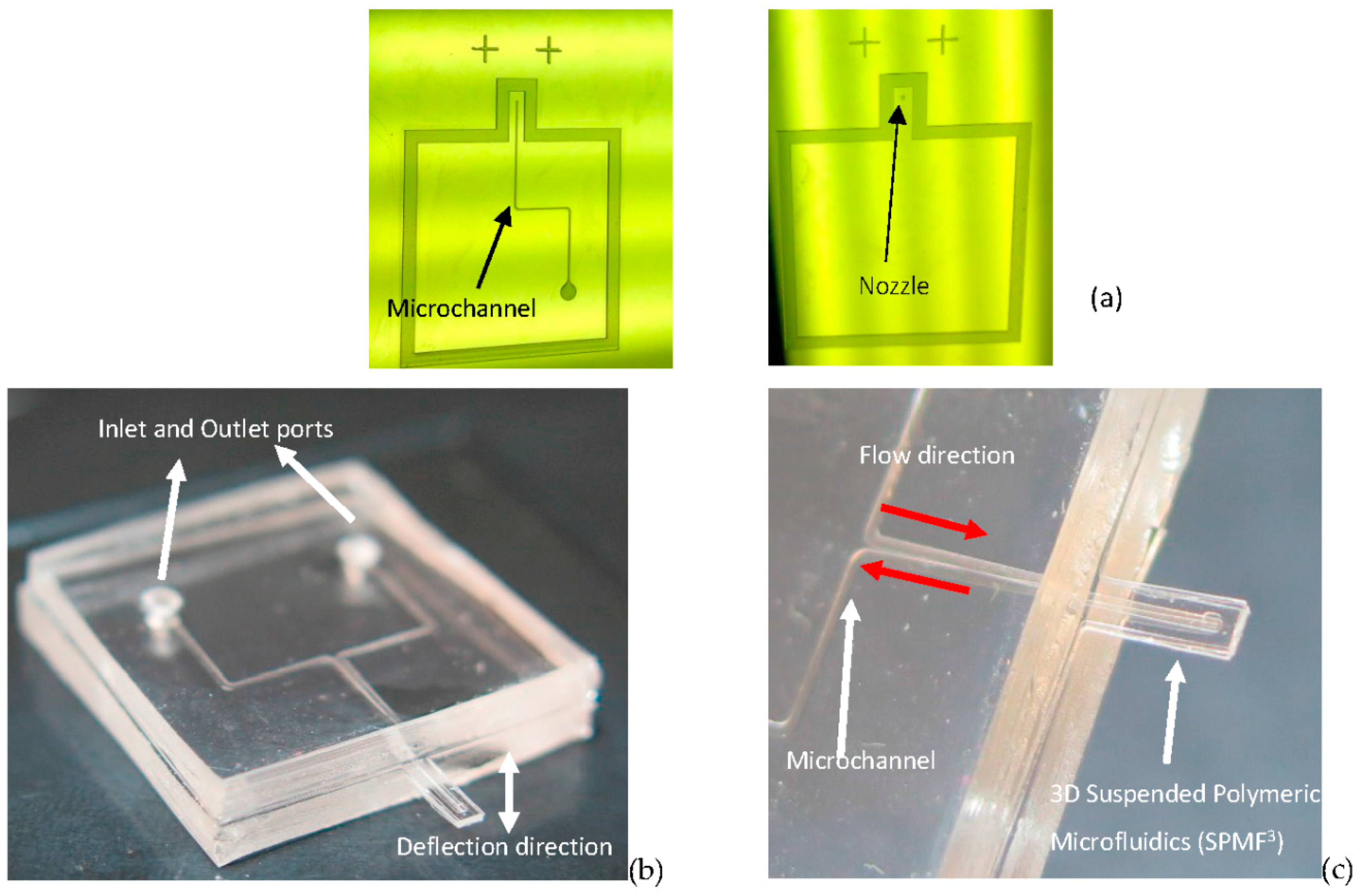
2.2. Fabrication of the Device
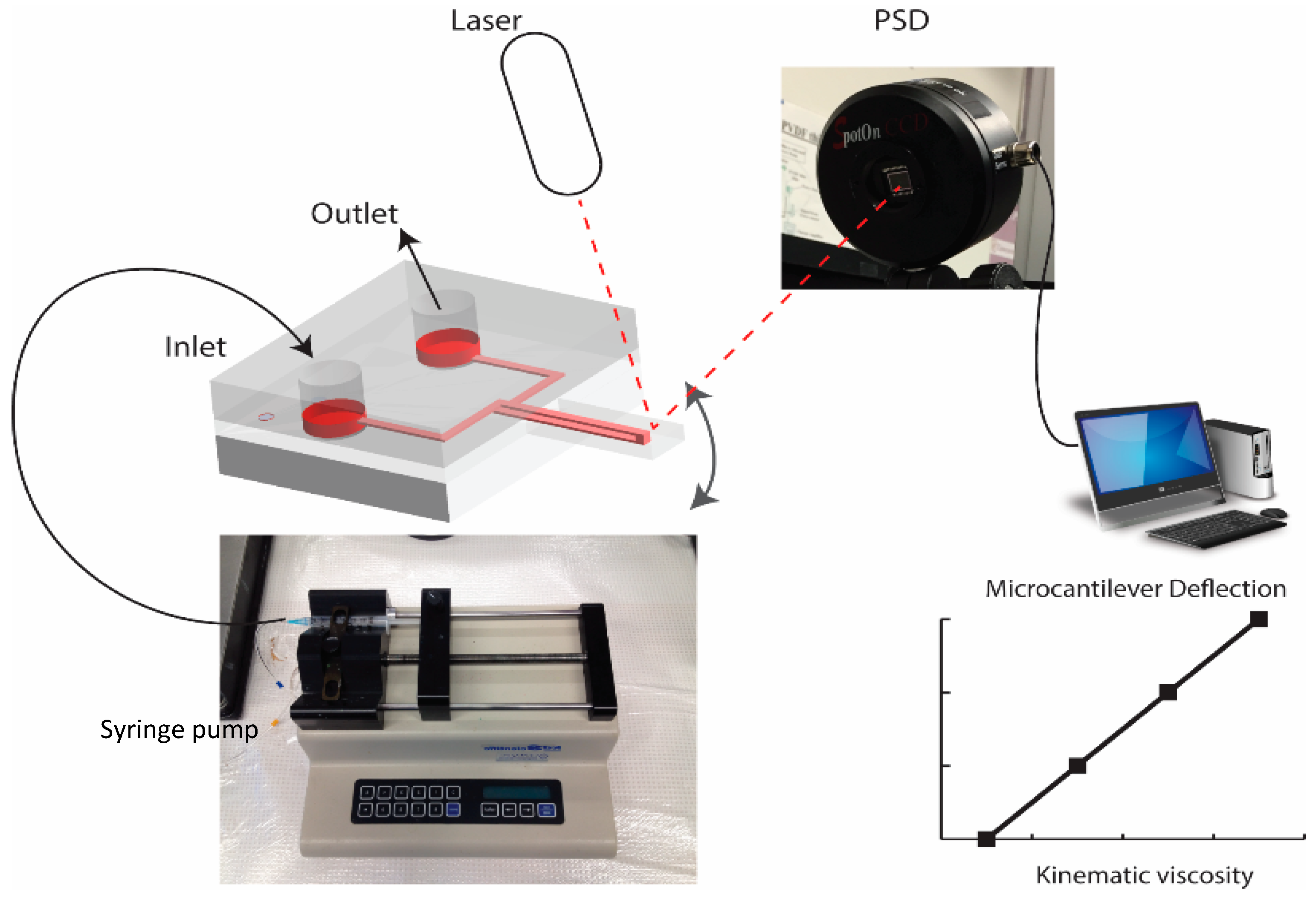
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trope, G.E.; Lowe, G.D.; McArdle, B.M.; Douglas, J.T.; Forbes, C.D.; Prentice, C.M.; Foulds, W.S. Abnormal blood viscosity and haemostasis in long-standing retinal vein occlusion. Br. J. Ophthalmol. 1983, 63, 137–142. [Google Scholar] [CrossRef]
- Cho, Y.; Kensey, K. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Hartnett, J.; Lee, W. Non-Newtonian viscosity measurements in the intermediate shear rate range with the falling-ball viscometer. J. Non-Newton. Fluid Mech. 1984, 15, 61–74. [Google Scholar] [CrossRef]
- Sader, J.E. frequency response of cantilever bemas immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Muramatsu, H.; Tamiya, E.; Karube, I. Computation of equivalent circuit parameters of quartz crystals in contact with liquids and study of liquid properties. Anal. Chem. 1988, 60, 2142–2146. [Google Scholar] [CrossRef]
- Angelescu, D.; Chen, H.; Jundt, J.; Berthet, H.; Mercier, B.; Marty, F. Highly integrated microfluidic sensors. In Proceedings of the SPIE, San Diego, CA, USA, 10–14 August 2008. [Google Scholar]
- Jakoby, B.; Scherer, M.; Buskies, M.; Eisenschmid, H. An automotive engine oil viscosity sensor. IEEE Sens. J. 2003, 3, 562–568. [Google Scholar] [CrossRef]
- Matsiev, L. Application of flexural mechanical resonators to high throughput liquid characterization. In Proceedings of the 2000 IEEE Ultrasonics Symposium, San Juan, Puerto Rico, 22–25 October 2000. [Google Scholar]
- Wang, S. Engine oil condition sensor: Method for establishing correlation with total acid number. Sens. Actuators B Chem. 2002, 86, 122–126. [Google Scholar] [CrossRef]
- Goubaidoulline, I.; Reuber, J.; Merz, F.; Johannsmann, D. Simultaneous determination of density and viscosity of liquids based on quartz crystal resonators covered with nanoporous alumina. J. Appl. Phys. 2005, 98, 014305. [Google Scholar] [CrossRef]
- Herrmann, F.; Hahn, D.; Buttgenback, S. Separate determination of liquid density and viscosity with sagittally corrugated Love-mode sensors. Sens. Actuators A Phys. 1999, 78, 99–107. [Google Scholar] [CrossRef]
- Durdag, K. Solid state acoustic wave sensors for real-time in-line measurement of oil viscosity. Sens. Rev. 2008, 28, 68–73. [Google Scholar] [CrossRef]
- Martin, B. Viscosity and density sensing with ultrasonic plate waves. Sens. Actuators A Phys. 1990, 22, 704–708. [Google Scholar] [CrossRef]
- Wenzel, S.; Martin, B.; White, R. Generalized Lamb-wave multisensory. In Proceedings of the IEEE Ultrasonics Symposium, Chicago, IL, USA, 2–5 October 1988. [Google Scholar]
- Wolf, S.; Tauber, R. Silicon Processing for the VLSI Era; Lattice Press: Sunset Beach, CA, USA, 1986. [Google Scholar]
- Puchades, I.; Fuller, L.F. A Thermally Actuated Microelectromechanical (MEMS) Device for Measuring Viscosity. J. Microelectromech. Syst. 2011, 20, 601–609. [Google Scholar] [CrossRef]
- Boss, C.; Meurville, E.; Sallese, J.-M.; Ryser, P. A viscosity-dependent affinity sensor for continuous monitoring of glucose in biological fluids. Biosens. Bioelectron. 2011, 30, 223–228. [Google Scholar] [CrossRef] [PubMed]
- Muramatsu, H.; Kimura, K.; Ataka, T. A quartz crystal viscosity sensor for monitoring coagulation reaction and its application to a multichannel coagulation detector. Biosens. Bioelectron. 1991, 6, 353–358. [Google Scholar] [CrossRef]
- Shih, W.; Li, X.; Gu, H.; Shih, W.; Aksay, I.A. Simultaneous liquid viscosity and density determination with piezoelectric unimorph cantilevers. J. Appl. Phys. 2001, 89, 1497. [Google Scholar] [CrossRef]
- Naik, T.; Longmire, E.; Mantell, S. Dynamic response of a cantilever in liquid near a solid wall. Sens. Actuators 2003, 102, 240–245. [Google Scholar] [CrossRef]
- Rezazadeh, G.; Ghanbari, M.; Mirzaee, I. Simultaneous Measurement of Fluids viscosity and density using a microbeam. In Proceedings of the International Conference on Perspective Technologies and Methods in MEMS Design, Lviv-Polyana, Ukraine, 22–24 April 2009. [Google Scholar]
- Huang, X.; Li, S.; Schultz, J.; Wang, Q.; Lin, Q. Mems sensor for continuous monitoring of glucose in Subcutaneous Tissue. In Proceedings of the IEEE 22nd International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009. [Google Scholar]
- Belmiloud, N.; Dufour, I.; Nicu, L.; Colin, A.; Pistre, J. Vibrating Microcantilever used as a viscometer and microrheometer. In Proceedings of the IEEE Sensors, Daegu, Korea, 22–25 October 2006. [Google Scholar]
- Harrison, C.; Fornari, A.; Hua, C.; Ryu, S.; Goodwin, A.R.; Hsu, K.; Marty, F.; Mercier, B. A microfluidic MEMS sensor for the measurement of density and viscosity at high pressure. In Proceedings of the SPIE, San Jose, CA, USA, 29 January–1 February 2007; Volume 6465, p. 64650U. [Google Scholar]
- Reichel, E.; Riesch, C.; Keplinger, F.; Jakoby, B.; Microelectronics, I.; Kepler, J. Remote electromagnetic excitation of miniaturized in-plane plate resonators for sensing applications. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008. [Google Scholar]
- Ronaldson, K.A.; Fitt, A.D.; Goodwin, A.R.H.; Wakeham, W.A. Transversely Oscillating MEMS Viscometer: The “Spider”. Int. J. Thermophys. 2006, 27, 1677–1695. [Google Scholar] [CrossRef]
- Agoston, A.; Keplinger, F.; Jakoby, B. Evaluation of a Vibrating Micromachined Cantilever Sensor for Measuring the Viscosity of Complex Organic Liquids. Sens. Actuators A 2005, 123, 82–86. [Google Scholar] [CrossRef]
- Galambos, P.; Forster, F. An optical micro-fluidic viscometer. In Proceedings of the Micro-Electro-Mechanical Systems (MEMS), ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 15–20 November 1998. [Google Scholar]
- Andrews, M.; Harris, P. Damping and gas viscosity measurements using a microstructure. Sens. Actuators A Phys. 1995, 49, 103–108. [Google Scholar] [CrossRef]
- Lara, M.M.; Atkinson, C. Theoretical model on the interaction of a vibrating beam and the surrounding viscous fluid with applications to density and viscosity sensors. In Proceedings of the IEEE Sensors, Vienna, Austria, 24–27 October 2004. [Google Scholar]
- Zeng, H.; Zhao, Y. On-Chip Blood Viscometer towards Point-of-Care Hematological Diagnosis. In Proceedings of the IEEE 22nd International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009. [Google Scholar]
- Dinsdale, A.; Moore, F. Viscosity and Its Measurement; Chapman and Hall: London, UK, 1962. [Google Scholar]
- Viswanath, D.S.; Ghosh, T.K.; Prasad, D.H.L.; Dutt, N.K.; Rani, K.Y. Viscosity of Liquids, Theory, Estimation, Experiment, and Data; Springer: Berlin, Germany, 2007. [Google Scholar]
- Sadabadi, H. Nano-integrated Polymeric Suspended Microfluidic Platform for Ultra-Sensitive Bio-Molecular Recognition. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2013. [Google Scholar]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
- Sadabadi, H.; Packirisamy, M. Nano-integrated Polymeric Suspended Microfluidic (SPMF) Platform for Ultra-Sensitive Bio-Molecular Recognition of Bovine Growth Hormones. Sci. Rep. 2017, 7, 10969. [Google Scholar] [CrossRef] [PubMed]
- Beaulieua, L.; Godin, M.; Laroche, O.; Tabard-Cossa, V.; Grutter, P. A complete analysis of the laser beam deflection systems used in cantilever-based systems. Ultramicroscopy 2007, 107, 422–430. [Google Scholar] [CrossRef] [PubMed]
- Vliet, T.V.; Walstra, P. Relationship between viscosity and fat content of milk and cream. Texture Stud. 1980, 11, 65–68. [Google Scholar] [CrossRef]
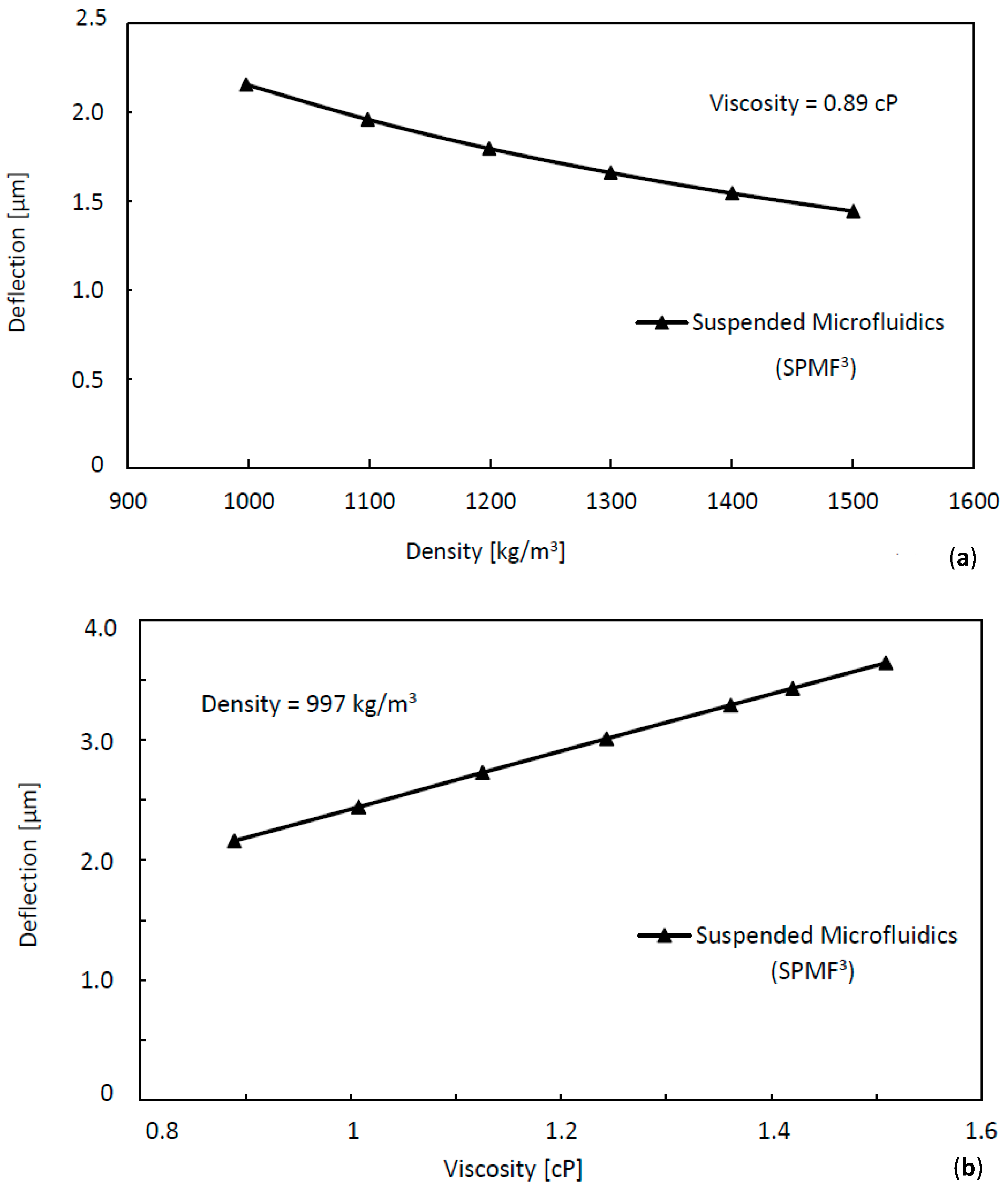
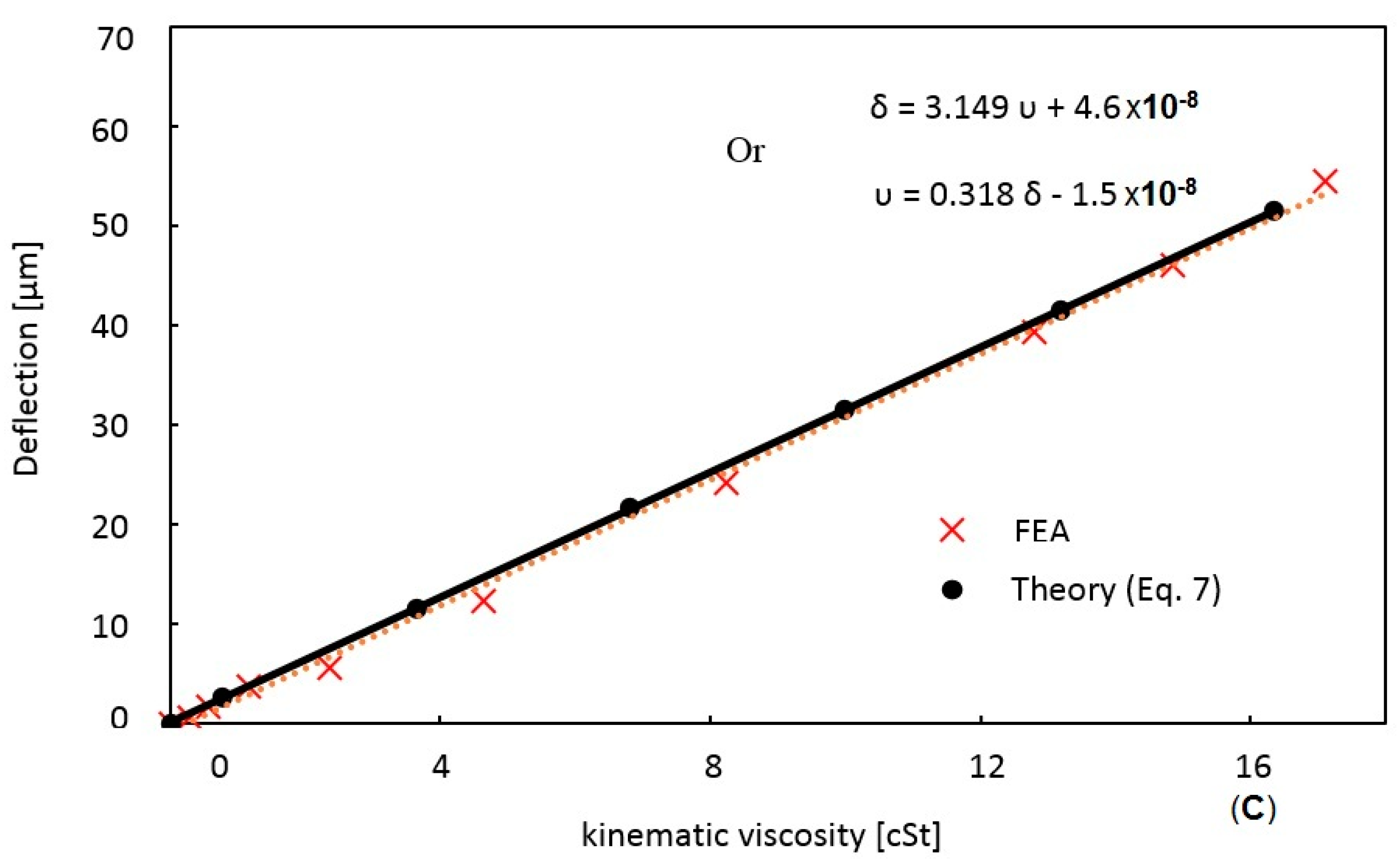
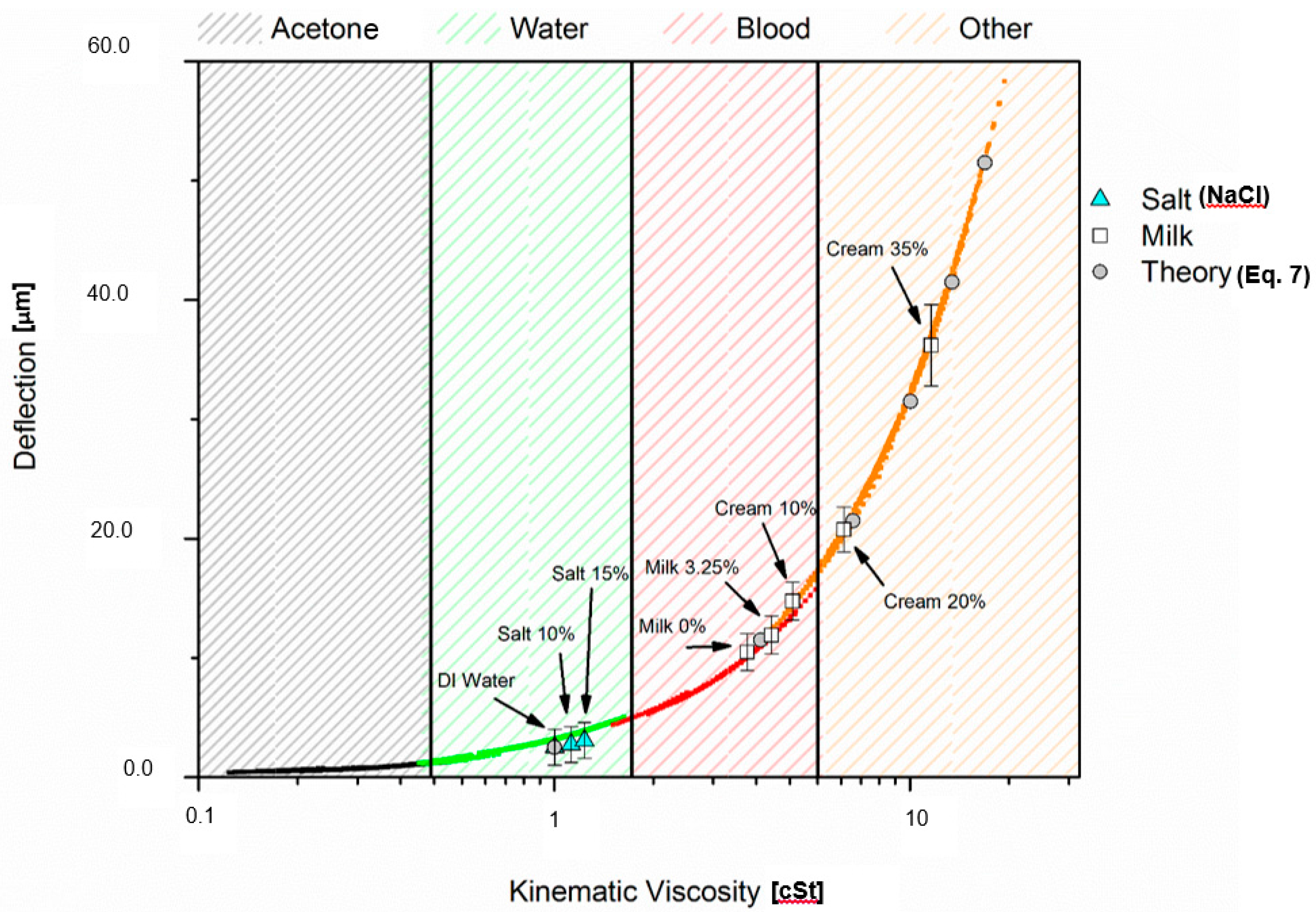
| Fluid | Concentration | Density (kg/m3) | Dynamic Viscosity (cP) | Kinematic Viscosity (cSt) | Tip Deflection (μm) |
|---|---|---|---|---|---|
| Water-Salt wt % | 0% | 999 | 1.002 | 1.00 | 2.51 |
| 10% | 1070 | 1.193 | 1.11 | 2.75 | |
| 15% | 1110 | 1.350 | 1.21 | 3.08 | |
| Milk-Fat wt % | 0% | 1033 | 3.594 | 3.48 | 10.48 |
| 3.25% | 1030 | 4.192 | 4.07 | 11.90 | |
| 10% | 1025 | 4.797 | 4.68 | 14.85 | |
| 20% | 1012 | 6.598 | 6.52 | 20.80 | |
| 35% | 994 | 11.391 | 11.46 | 36.21 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzban, M.; Packirisamy, M.; Dargahi, J. 3D Suspended Polymeric Microfluidics (SPMF3) with Flow Orthogonal to Bending (FOB) for Fluid Analysis through Kinematic Viscosity. Appl. Sci. 2017, 7, 1048. https://doi.org/10.3390/app7101048
Marzban M, Packirisamy M, Dargahi J. 3D Suspended Polymeric Microfluidics (SPMF3) with Flow Orthogonal to Bending (FOB) for Fluid Analysis through Kinematic Viscosity. Applied Sciences. 2017; 7(10):1048. https://doi.org/10.3390/app7101048
Chicago/Turabian StyleMarzban, Mostapha, Muthukumaran Packirisamy, and Javad Dargahi. 2017. "3D Suspended Polymeric Microfluidics (SPMF3) with Flow Orthogonal to Bending (FOB) for Fluid Analysis through Kinematic Viscosity" Applied Sciences 7, no. 10: 1048. https://doi.org/10.3390/app7101048
APA StyleMarzban, M., Packirisamy, M., & Dargahi, J. (2017). 3D Suspended Polymeric Microfluidics (SPMF3) with Flow Orthogonal to Bending (FOB) for Fluid Analysis through Kinematic Viscosity. Applied Sciences, 7(10), 1048. https://doi.org/10.3390/app7101048






