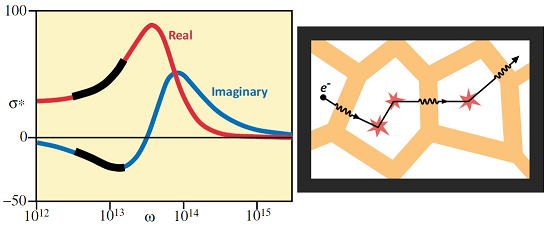
Dynamics of Carrier Transport in Nanoscale Materials: Origin of Non-Drude Behavior in the Terahertz Frequency Range
Abstract
:1. Introduction
2. Dynamics of Free Carriers in Nanomaterials
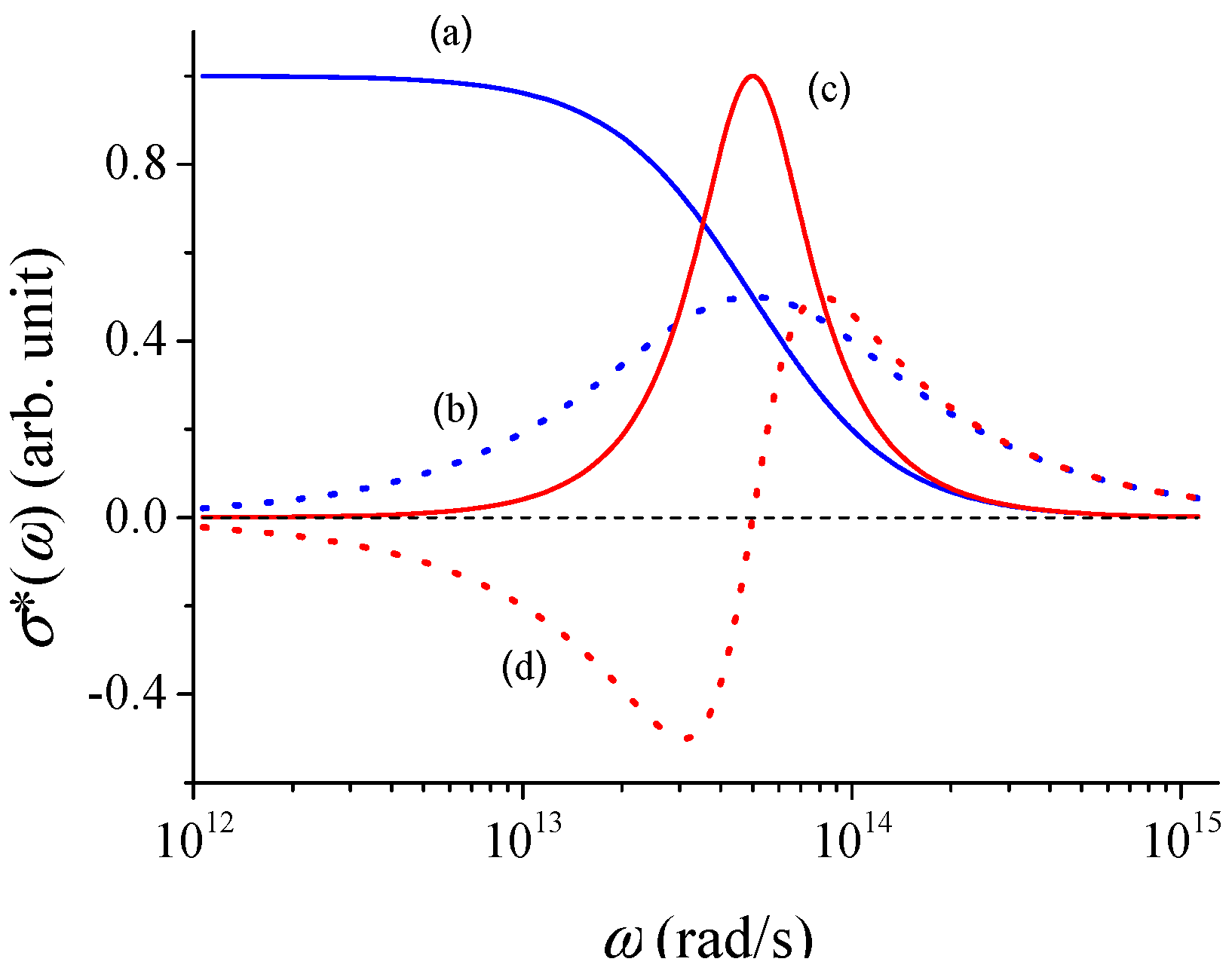
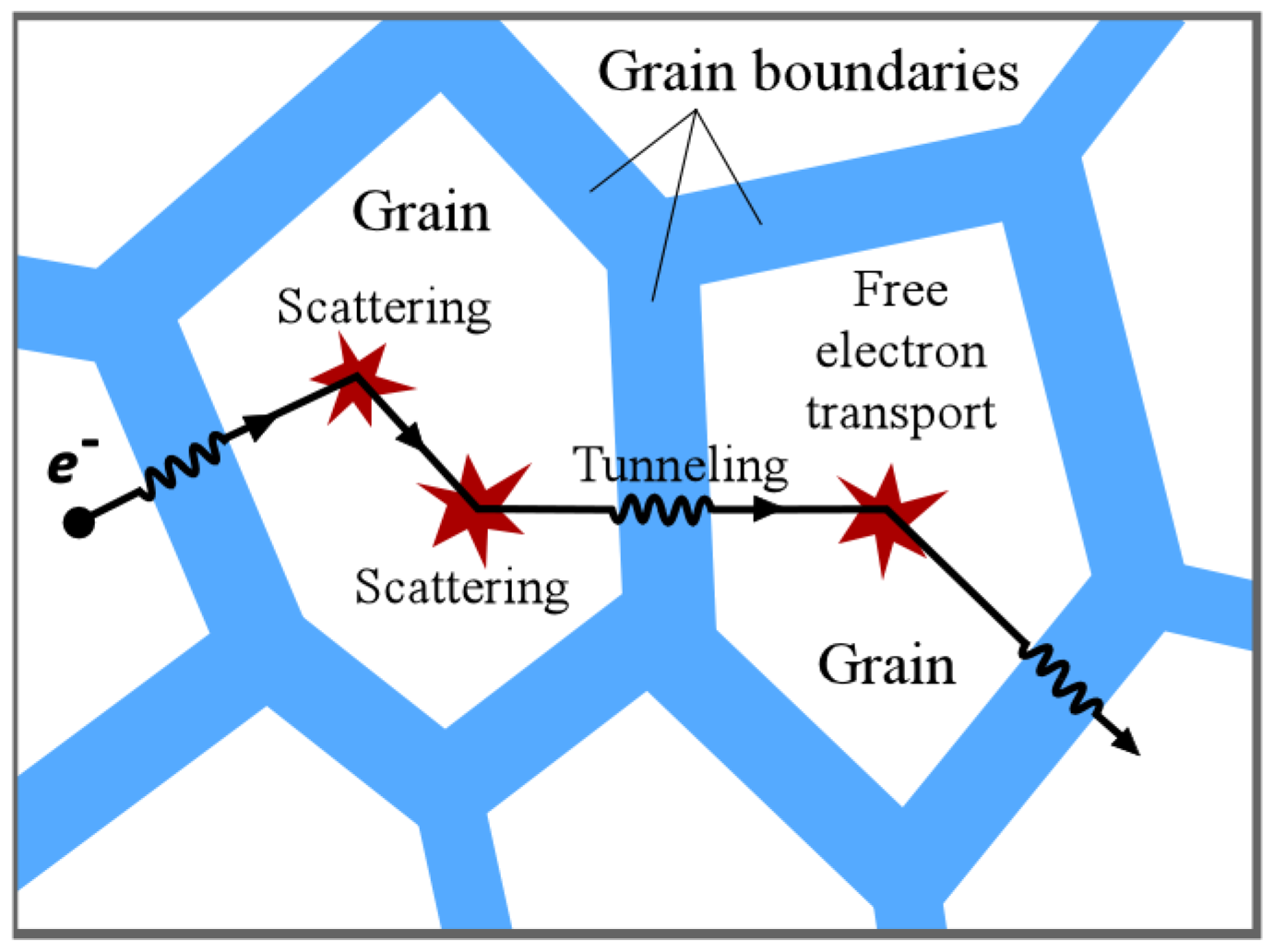
3. Typical Examples of THz Conductivity in Nanomaterials
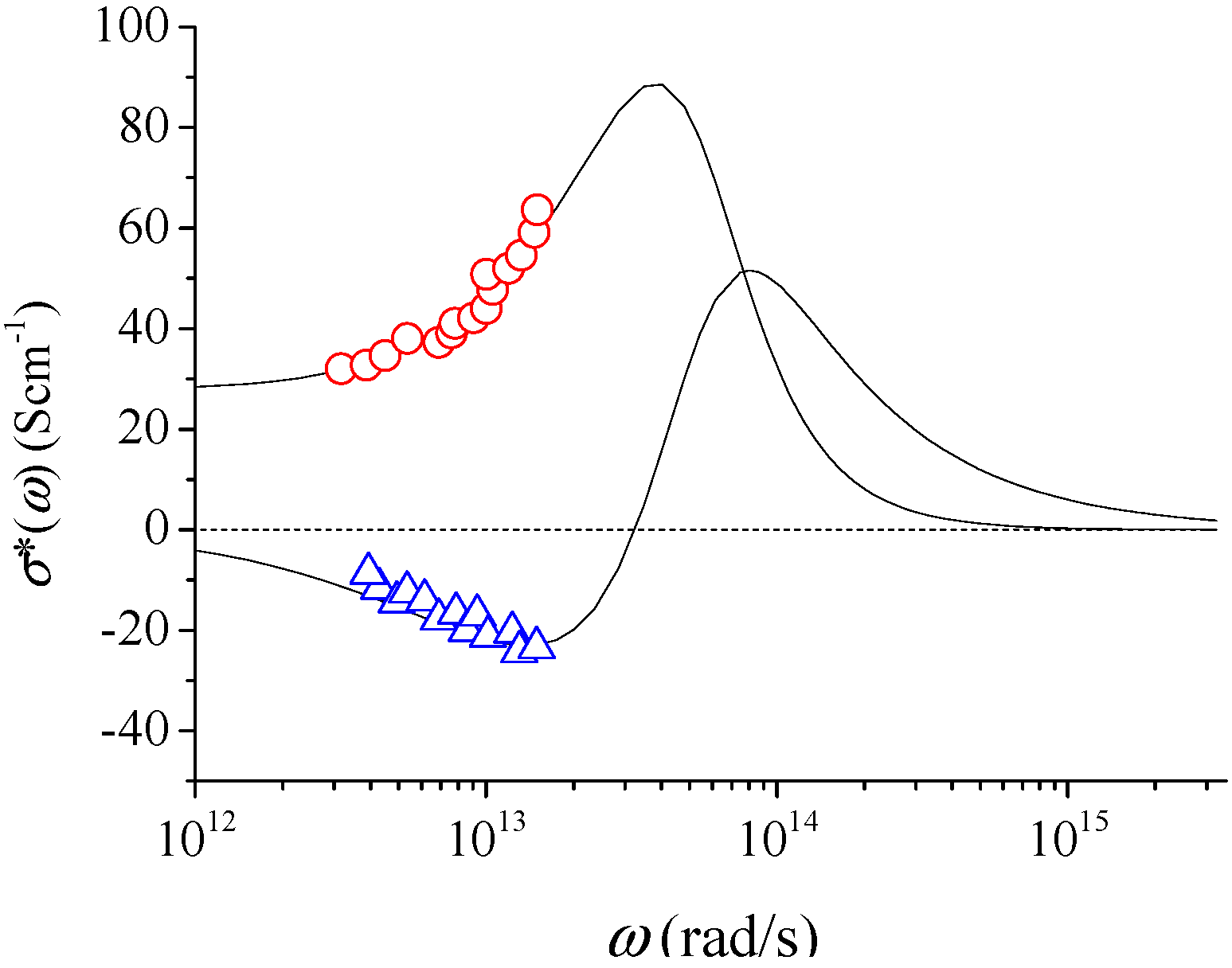
| Quantity | Si | Ge2Sb2Te5 | ZnO | SnO2 | Au | Cryst-ZnO |
|---|---|---|---|---|---|---|
| f | 0.83 | 0.996 | 0.94 | 0.97 | 0.999 | 1 |
| m* | 0.3 | 0.3 | 0.3 | 0.3 | 1 | 0.24 |
| n (cm−3) | 5.3 × 1018 | 1.5 × 1020 | 7.0 × 1019 | 1.0 × 1020 | 1.0 × 1022 | 4.5 × 1017 |
| τ (s) | 2.0 × 10−14 | 2.4 × 10−14 | 4.0 × 10−14 | 5.0 × 10−14 | 3.0 × 10−14 | 2.7 × 10−14 |
| nt (cm−3) | 2.0 × 1019 | 2.0 × 1019 | 1.6 × 1018 | 1.6 × 1018 | 1.5 × 1021 | - |
| τt (s) | 4.0 × 10−13 | 2.0 × 10−11 | 2.0 × 10−14 | 9.0 × 10−13 | 3.0 × 10−12 | - |
| ε∞ | - | 320 | 14 | 15 | 1 | - |
| σeff(0) (S cm−1) | 28.0 | 15.4 | 4.0 | 11.4 | 55,000 | 142 |
| σdc (S cm−1) | 1–10 | 20 | 4 | 0.6 | - | 46 |
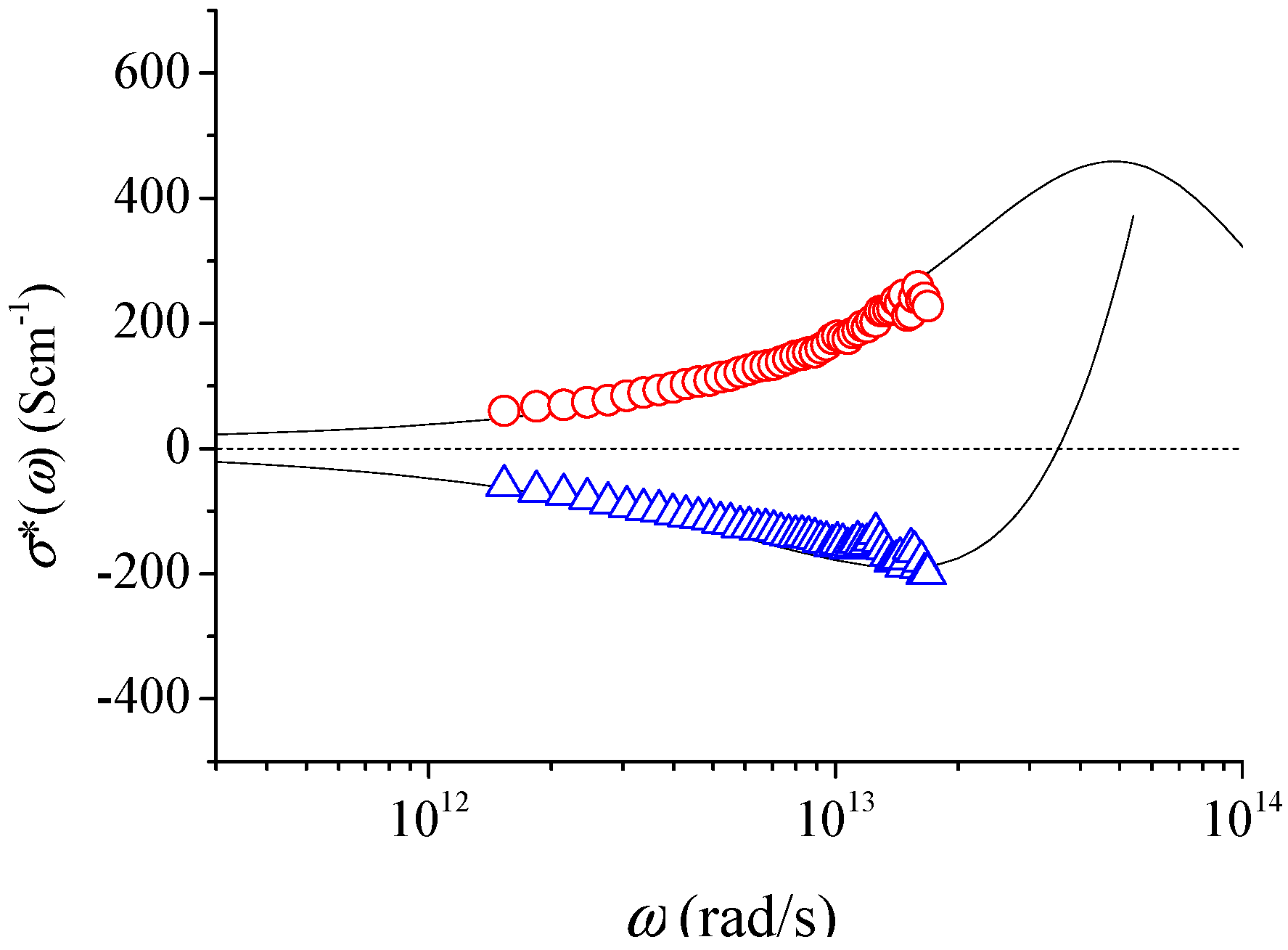
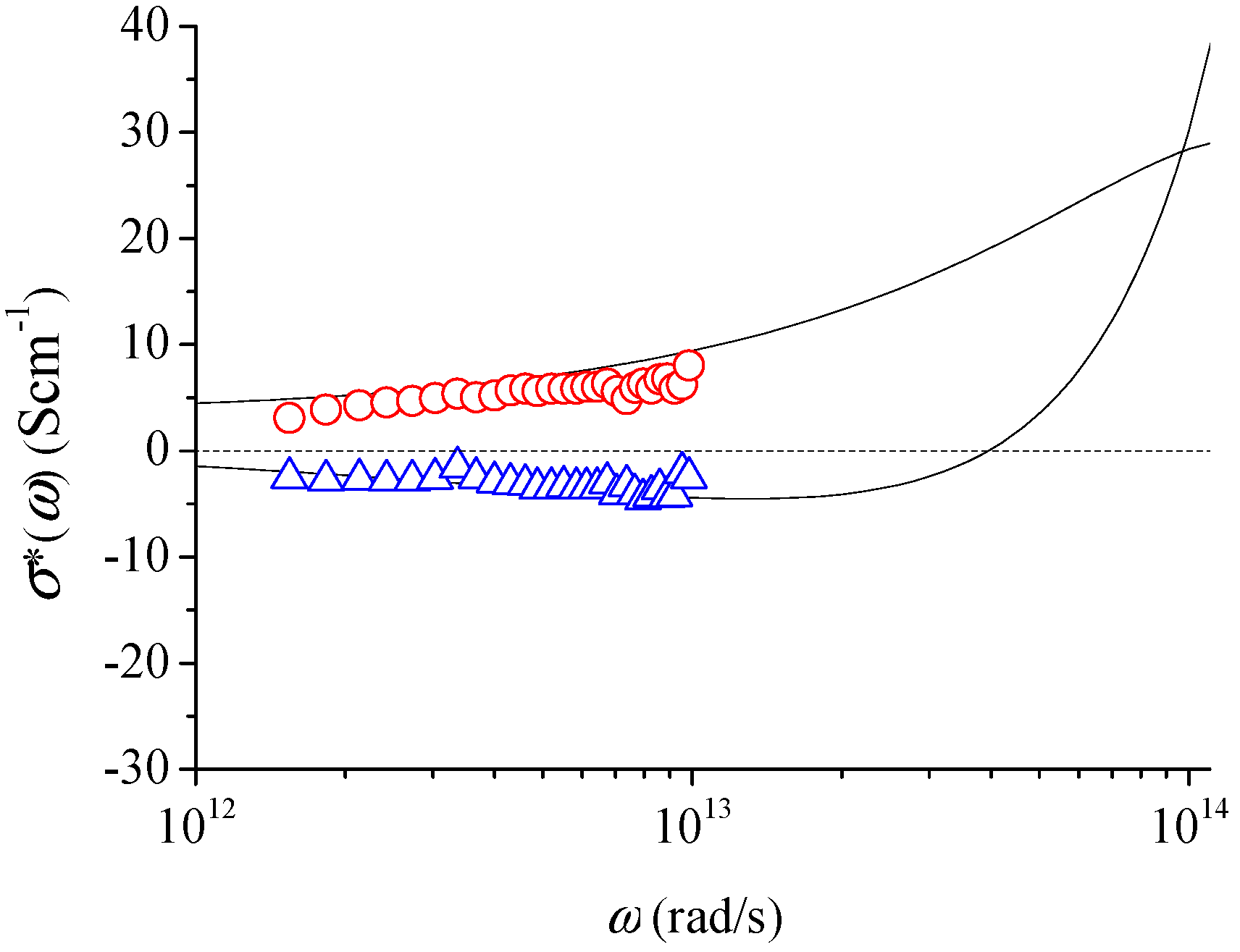
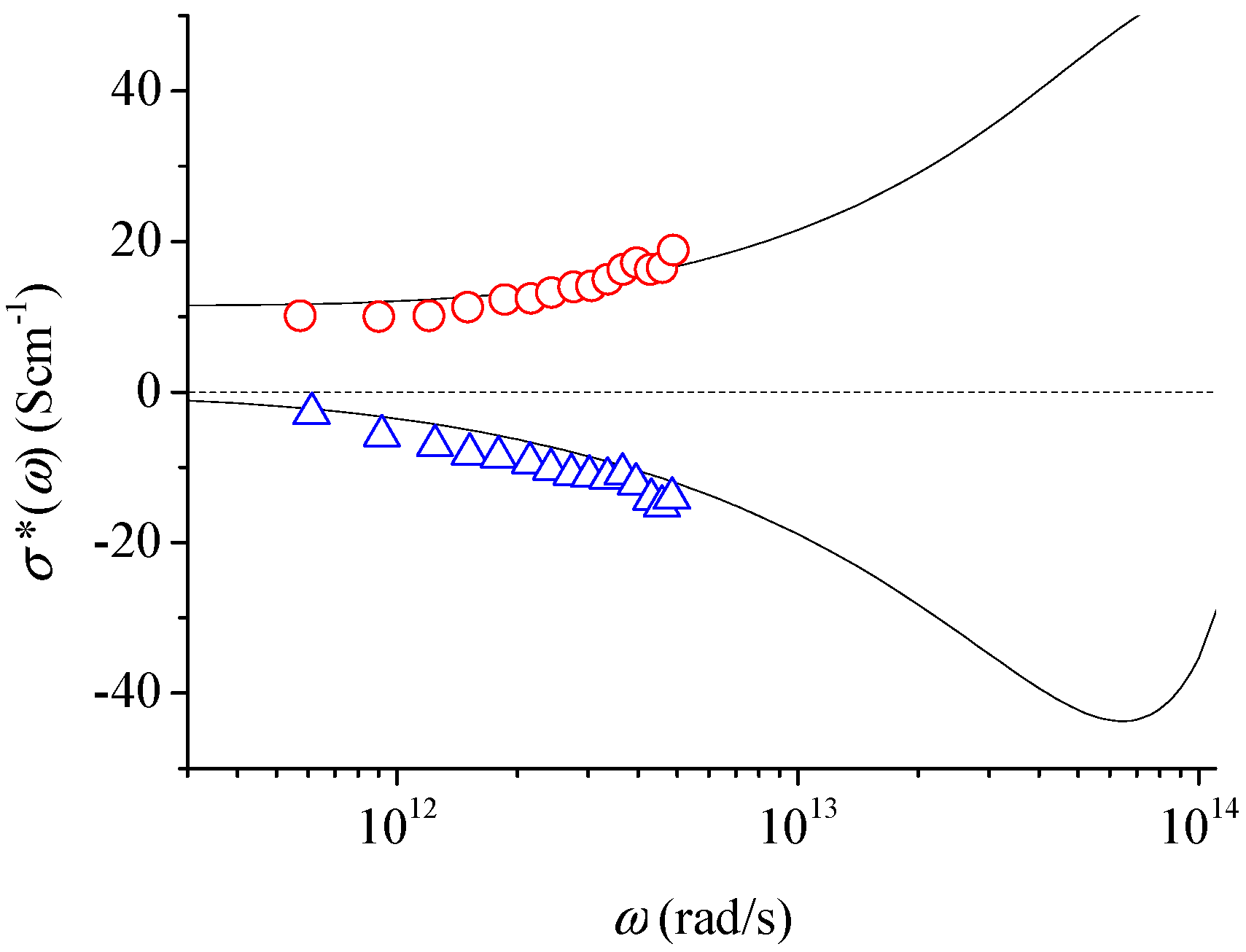
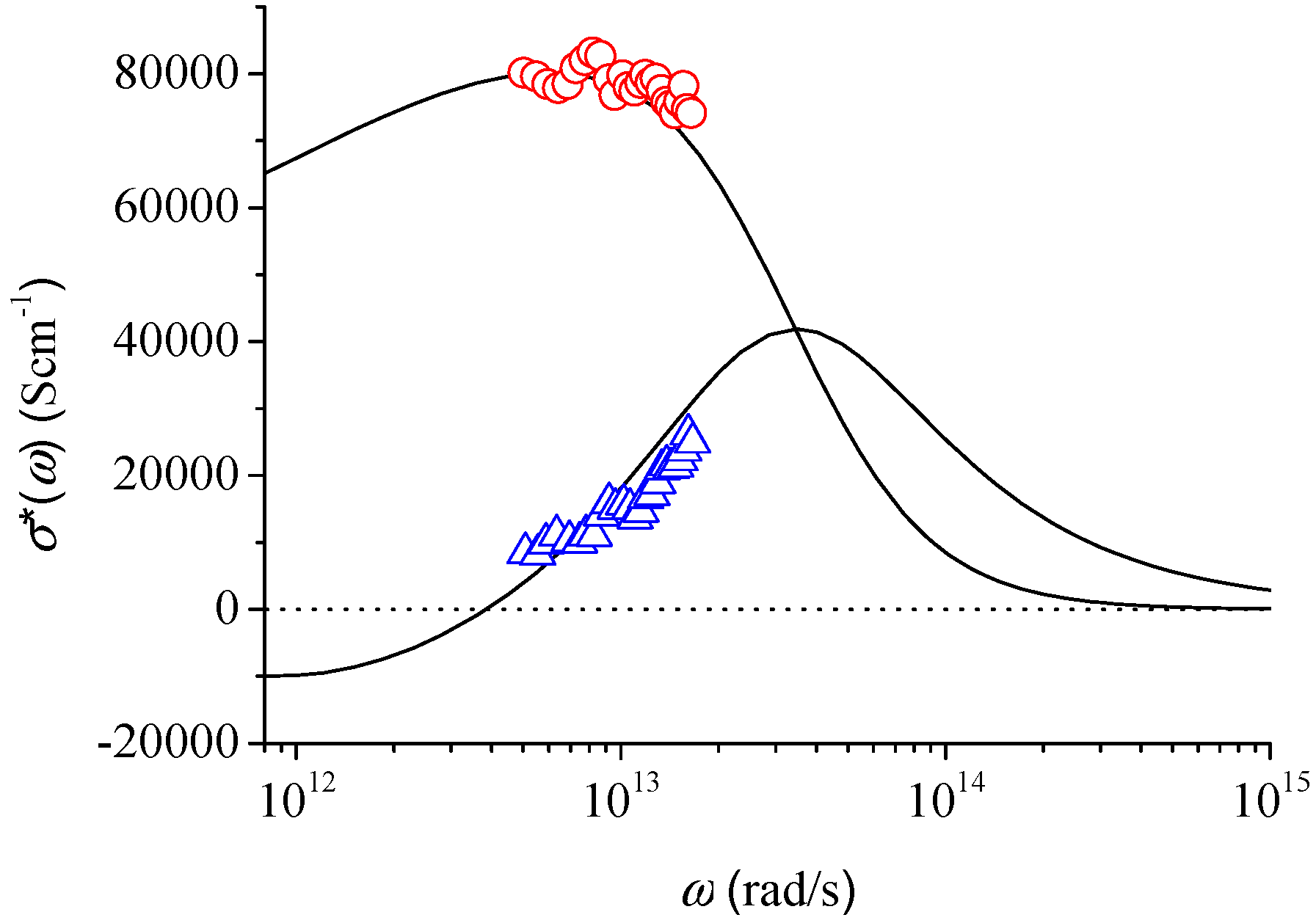
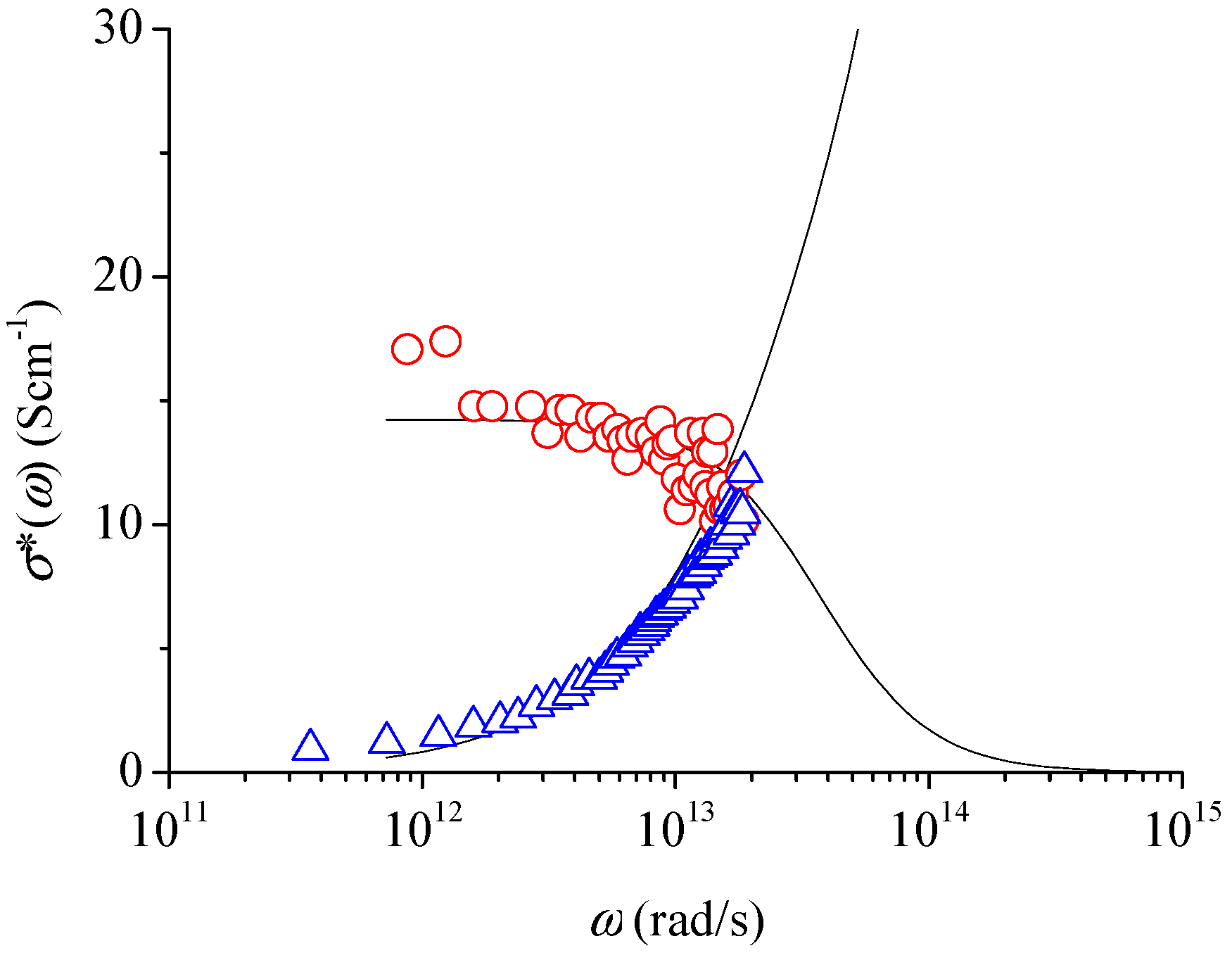
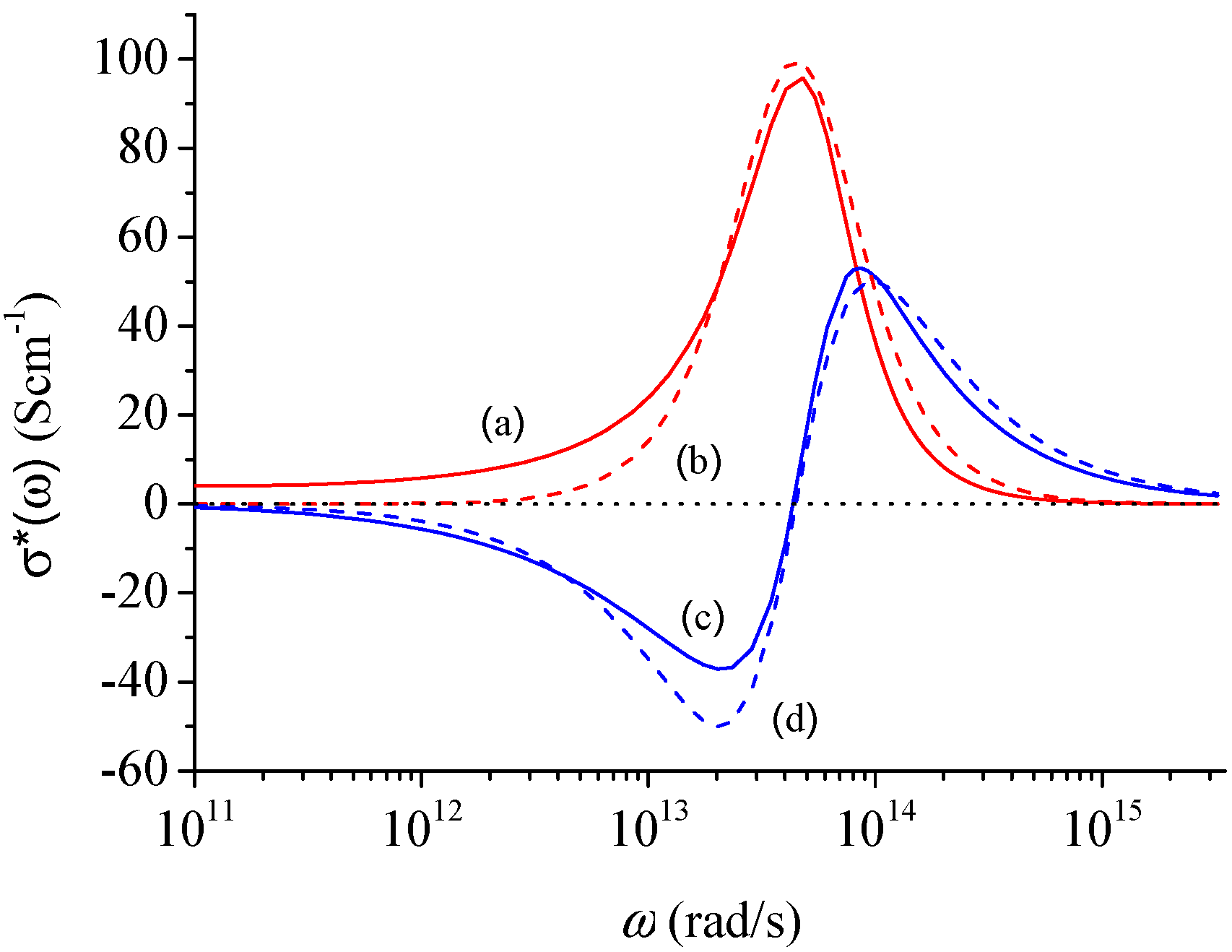
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lloyd-Hughes, J.; Jeon, T.-I. A review of the terahertz conductivity of bulk and nano-materials. J. Infrared Milli Terahertz Waves 2012, 33, 871–927. [Google Scholar] [CrossRef]
- Shimakawa, K. Electrical properties of nanocrystalline media: Optical conductivity and non-Drude behavior in the terahertz frequency range. Can. J. Phys. 2014, 92, 1–4. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Thoman, A.; Kern, A.; Helm, H.; Walther, M. Nanostructured gold films as broadband terahertz antireflection. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Lovrincic, R.; Pucci, A. Infrared optical properties of chrorium nanoscale films with a phase transition. Phys. Rev. B 2009, 80. [Google Scholar] [CrossRef]
- Takano, K.; Shibuya, K.; Akiyama, K.; Nagashima, T.; Miyamaru, F.; Hangyo, M. A metal-to-insulator transition in cut-wire-grid metamaterials in the terahertz region. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Nienhuys, H.-K.; Sundstrom, V. Influence of plasmons on terahertz conductivity measurements. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Cooke, D.G.; MacDounald, A.N.; Hryciw, A.; Wang, J.; Li, L.; Meldrum, A.; Hegmann, F.A. Transient terahertz conductivity in photoexcited nanocrystal films. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Cooke, D.G.; MacDonald, A.N.; Hryciw, A.; Meldrum, A.; Wang, J.; Frank, Q.L.; Hegmann, F.A. Ultrafast terahertz conductivity of photoexcited nanocrystalline silicon. J. Mater. Sci. Mater. Electron. 2007, 18, 447–452. [Google Scholar] [CrossRef]
- Ahn, H.; Ku, Y.-P.; Wang, Y.-C.; Chuang, C.-H. Terahertz spectroscopic study of vertically aligned InN nanorods. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Fekete, L.; Kuzel, P.; Nemec, H.; Kadlec, F.; Dejneka, A.; Stuchlick, J.; Fejfar, A. Ultrafast carrier dynamics in microcrystalline silicon probed by time-resolved terahertz spectroscopy. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Nemec, H.; Kuzel, P.; Sandstrom, V. Far-infrared response of free charge carrier localized in semiconductor nanoparticles. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Kadlec, F.; Kadlec, C.; Kuzel, P. Contrast in terahertz conductivity of phase-change materials. Solid. State Commun. 2012, 152, 852–855. [Google Scholar] [CrossRef]
- Shimakawa, K.; Wagner, T.; Frumar, M.; Kadlec, F.; Kadlec, C.; Kasap, S. Terahertz and direct current losses and the origin of non-Drude terahertz conductivity in the crystalline states of phase change materials. J. Appl. Phys. 2013, 114. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Tang, S.H.; Zhang, X.; Sow, C.H. Composition-dependent ultra-high photoconductivity in ternary CdSxSe1−x nanobelts as measured by optical pump-terahertz probe spectroscopy. Nano Res. 2013, 6, 808–821. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Tang, S.H.; Sow, C.H.; Zhang, X. Composition-dependent electron transport in CdSxSe1−x nanobelts: A THz spectroscopy study. Opt. Lett. 2014, 39, 567–570. [Google Scholar] [CrossRef] [PubMed]
- Turner, G.M.; Beard, M.; Schmuttenmaer, C.A. Conductivity of ZnO nanowires, nanoparticles, and thin films using time-resolved THz spectroscopy. J. Phys. Chem. B 2006, 110, 25229–25239. [Google Scholar]
- Qazilbash, M.M.; Brehm, M.; Chae, B.-G.; Ho, P.-C.; Andreev, G.O.; Kim, B.-J.; Yun, S.J.; Baratsky, A.V.; Maple, M.B.; Kleilmann, F.; et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 2007, 318, 1750–1753. [Google Scholar] [CrossRef] [PubMed]
- Coker, T.I.; Titova, I.V.; Foumax, S.; Bandulet, H.-C.; Brassard, D.; Kieffer, Q.L.; El Khakani, M.A.; Hegmann, F.A. Teahertz conductivity of the metal-insulator transition in a nanogranular VO2 films. Appl. Phys. Lett. 2010, 97. [Google Scholar] [CrossRef]
- Parkinson, P.; Lloyd-Hughes, J.; Gao, Q.; Tan, H.H.; Jagadish, C.; Johnston, M.B.; Herz, L.M. Transient terahertz conductivity of GaAs nanowires. Nano Lett. 2007, 7, 2162–2165. [Google Scholar] [CrossRef]
- Smith, N.V. Classical generalization of the Drude Formula for the optical conductivity. Phys. Rev. B 2001, 64. [Google Scholar] [CrossRef]
- Shimakawa, K.; Itoh, T.; Naito, H.; Kasap, S. The origin of non-Drude terahertz conductivity in nanomaterials. Appl. Phys. Lett. 2012, 100. doi:10.1063/1.3697404. Erratum, 2012, 100. [Google Scholar] [CrossRef]
- Dyre, J.C.; Schroder, T.W. Universality of ac conduction in disordered solids. Rev. Mod. Phys. 2000, 72, 873–894. [Google Scholar] [CrossRef]
- Shimakawa, K.; Ganjoo, A. AC photoconductivity of hydrogenated amorphous silicon: Influence of long-range potential fluctuations. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Kasap, S.; Capper, P.; Kouighia, C.; Ruda, H. (Eds.) Electrical Conduction in Metals and Semiconductors. In The Springer Handbook of Electronic and Photonic Materials; Springer: Heidelberg, Germany, 2007; pp. 19–44.
- Bruggeman, D.A.G. Berechnung verschiedener physikalisher konstanten substanzen I. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef] [PubMed]
- Skoromets, V.; Nemec, H.; Kopec, K.; Kuzel, P.; Peters, K.; Fattakhova-Rohlfing, D.; Vetushka, A.; Muller, M.; Ganzerova, K.; Fejfar, A. Conductivity mechanisms in Sb-doped SnO2 nanoparticles assebmblies: DC and Terahertz regime. J. Phys. Chem. C 2015, 119, 19485–19495. [Google Scholar]
- Walther, M.; Cooke, D.G.; Sherstan, C.; Hajar, M.; Freeman, M.R.; Hegmann, F.C. Terahertz conductivity of thin gold films at the metal-insulator percolation transition. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Zhang, X.H.; Guo, H.G.; Yong, A.M.; Ye, J.D.; Tan, S.T. Terahertz dielectric response and optical conductivity of n-type single crystal ZnO epilayers grown by metalorganic chemical vapor deposition. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Zhang, W.; Azad, A.K.; Grischkowsky, D. Terahertz studies of carrier dynamics and dielectric response of n-type freestanding epitaxial GaN. Appl. Phys. Lett. 2003, 82, 2841–2843. [Google Scholar] [CrossRef]
- Ponseca, C.S.; Nemec, H.; Wallentin, J.; Auttu, N.; Beech, J.P.; Iqbal, A.; Borgstrom, M.; Pistol, M.-E.; Samurlson, L.; Yartsev, A. Bulk-like transverse electron mobility in an array of heavily n-doped InP nanowires probed by terahertz spectroscopy. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Nemec, H.; Zajac, V.; Kuzel, P.; Maly, P.; Gutsch, S.; Hiller, D.; Zachrias, M. Charge transport in silicon nanocrystal superlattices in the terahertz regime. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- Willis, K.J.; Hagness, S.C.; Knezevic, I. Terahertz conductivity of doped silicon calculated using the ensemble Monte Carlo/finite-difference time-domain simulation technique. Appl. Phys. Lett. 2010, 96. [Google Scholar] [CrossRef]
- Yang, C.-S.; Lin, M.-H.; Chang, C.-H.; Yu, P.; Shieh, J.-M.; Shen, C.-H.; Wada, O.; Pan, C.-L. Non-Drude behavior in Indium-Tin-Oxide Nanowhisker and thin films investigated by transmission and reflection THz time-domain spectroscopy. IEEE JQE 2013, 49, 677–690. [Google Scholar] [CrossRef]
- Slepyan, G.Y.; Maksimenko, S.A.; Lakhatakia, A.; Yevtushenko, O.; Gusakov, A.V. Electrodynamics of carbon nanotubes: Dynamic conductivity, impedance boundary conditions, and surface wave propagation. Phys. Rev. B 1999, 60, 17136–17149. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimakawa, K.; Kasap, S. Dynamics of Carrier Transport in Nanoscale Materials: Origin of Non-Drude Behavior in the Terahertz Frequency Range. Appl. Sci. 2016, 6, 50. https://doi.org/10.3390/app6020050
Shimakawa K, Kasap S. Dynamics of Carrier Transport in Nanoscale Materials: Origin of Non-Drude Behavior in the Terahertz Frequency Range. Applied Sciences. 2016; 6(2):50. https://doi.org/10.3390/app6020050
Chicago/Turabian StyleShimakawa, Koichi, and Safa Kasap. 2016. "Dynamics of Carrier Transport in Nanoscale Materials: Origin of Non-Drude Behavior in the Terahertz Frequency Range" Applied Sciences 6, no. 2: 50. https://doi.org/10.3390/app6020050
APA StyleShimakawa, K., & Kasap, S. (2016). Dynamics of Carrier Transport in Nanoscale Materials: Origin of Non-Drude Behavior in the Terahertz Frequency Range. Applied Sciences, 6(2), 50. https://doi.org/10.3390/app6020050