A Near-Hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics
Abstract
:1. Introduction
2. The Attitude Control Problem Statement of the Prototype Ducted Fan MAV
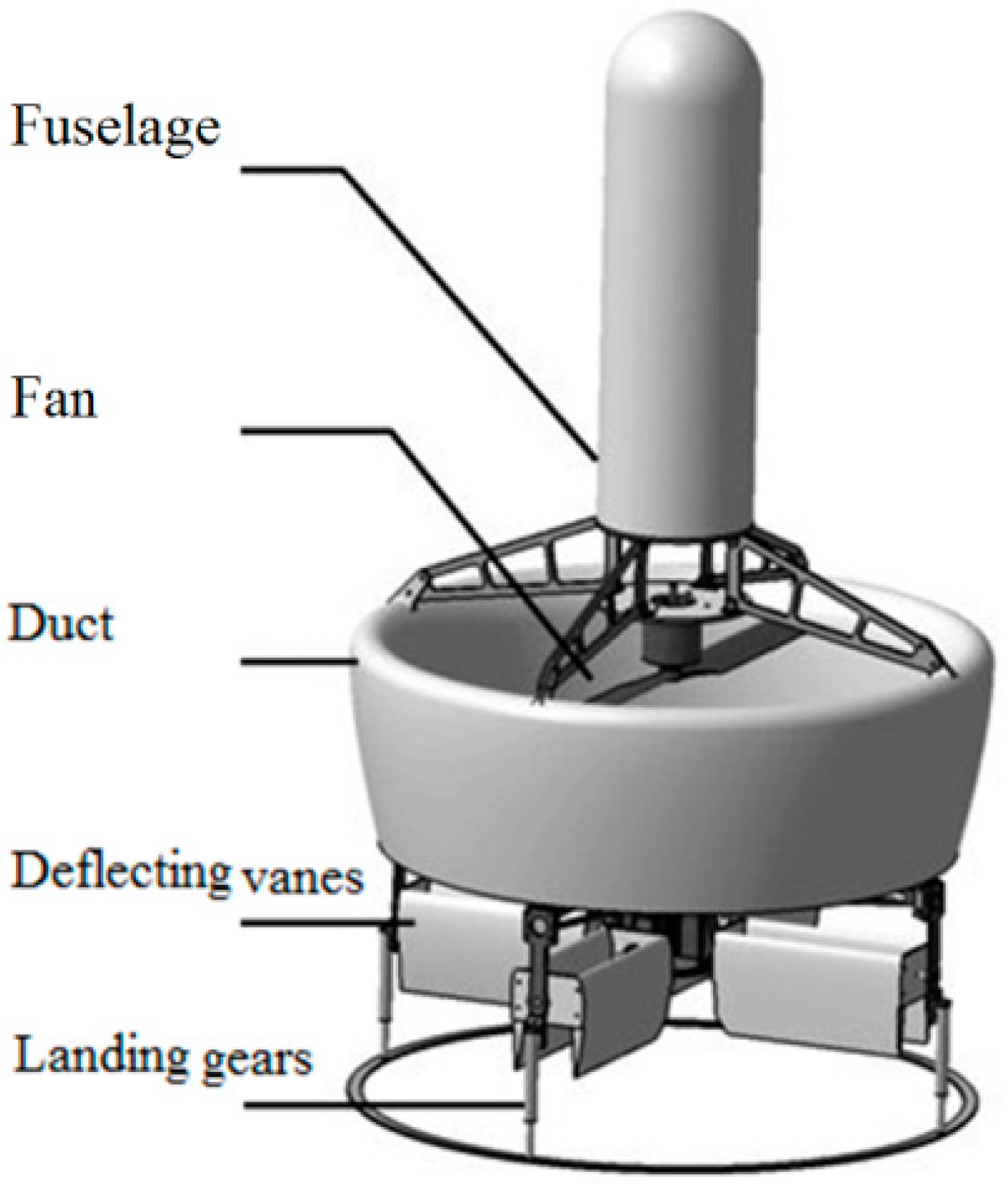
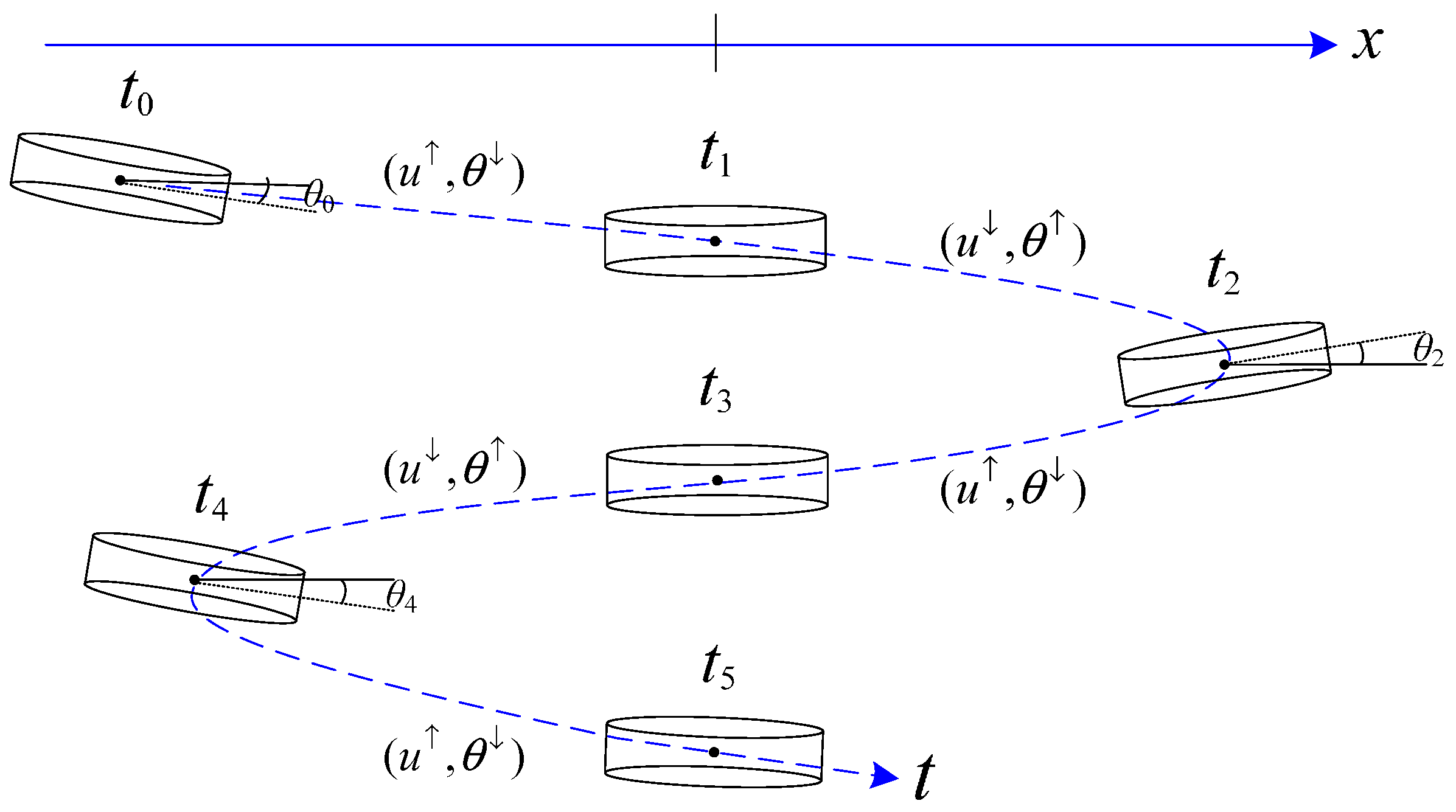
3. The Adaptive Attitude Control Strategy of the MAV with Actuator Dynamics
3.1. The Online Parameter Estimation Method for the MAV
3.2. The Adaptive Gain Scheduling Algorithm
4. Numerical and Experimental Tests
4.1. Numerical Simulation
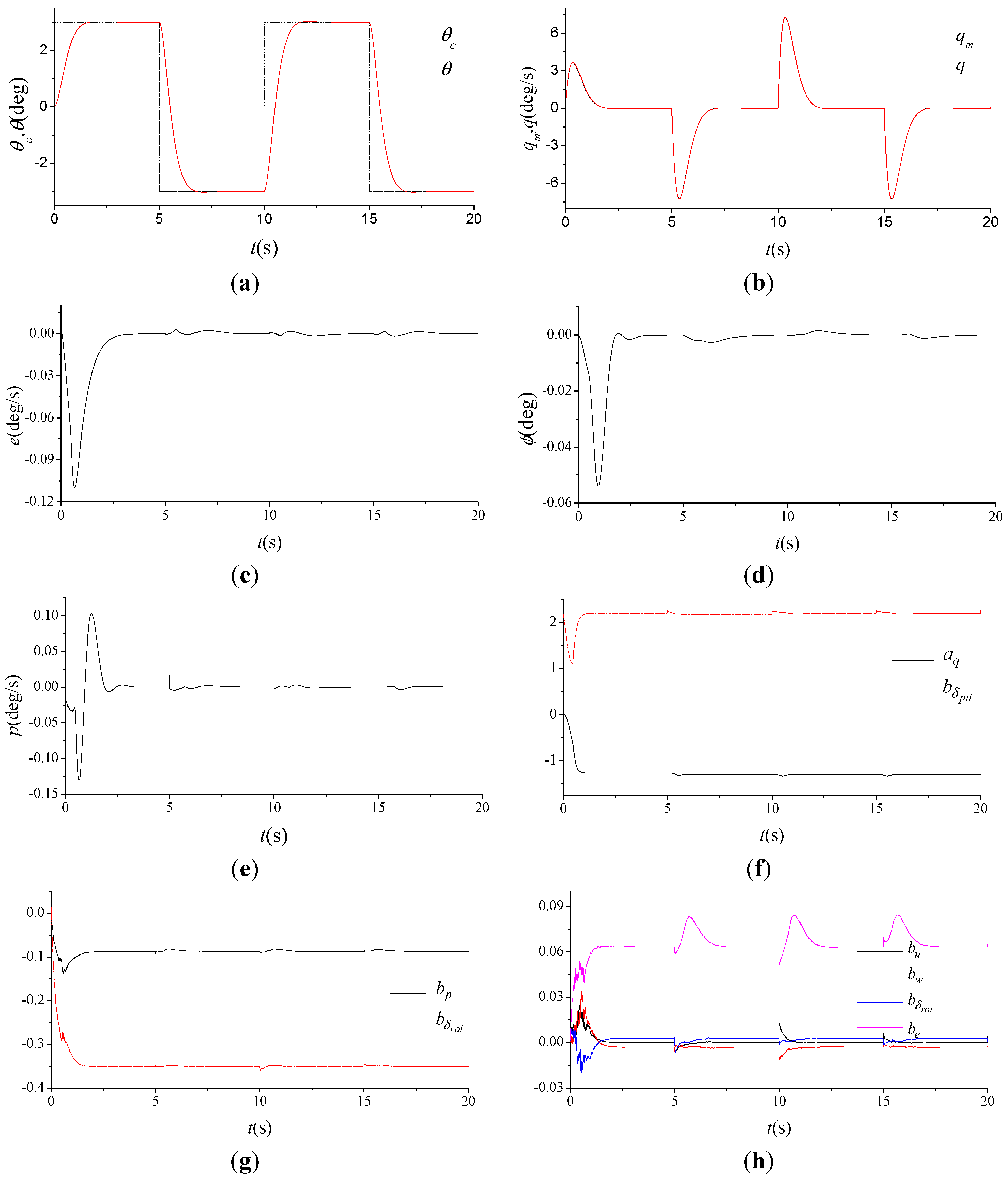
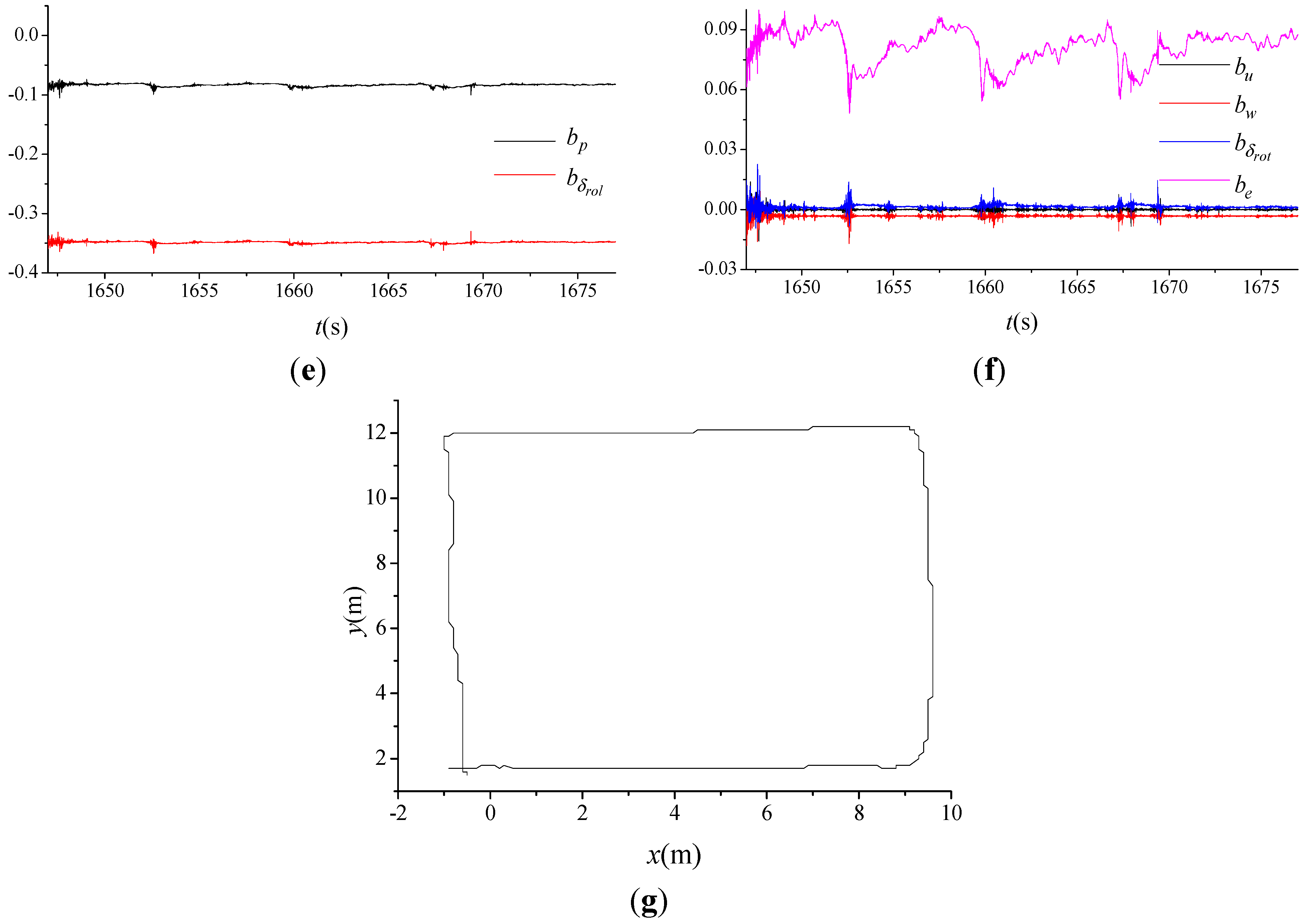
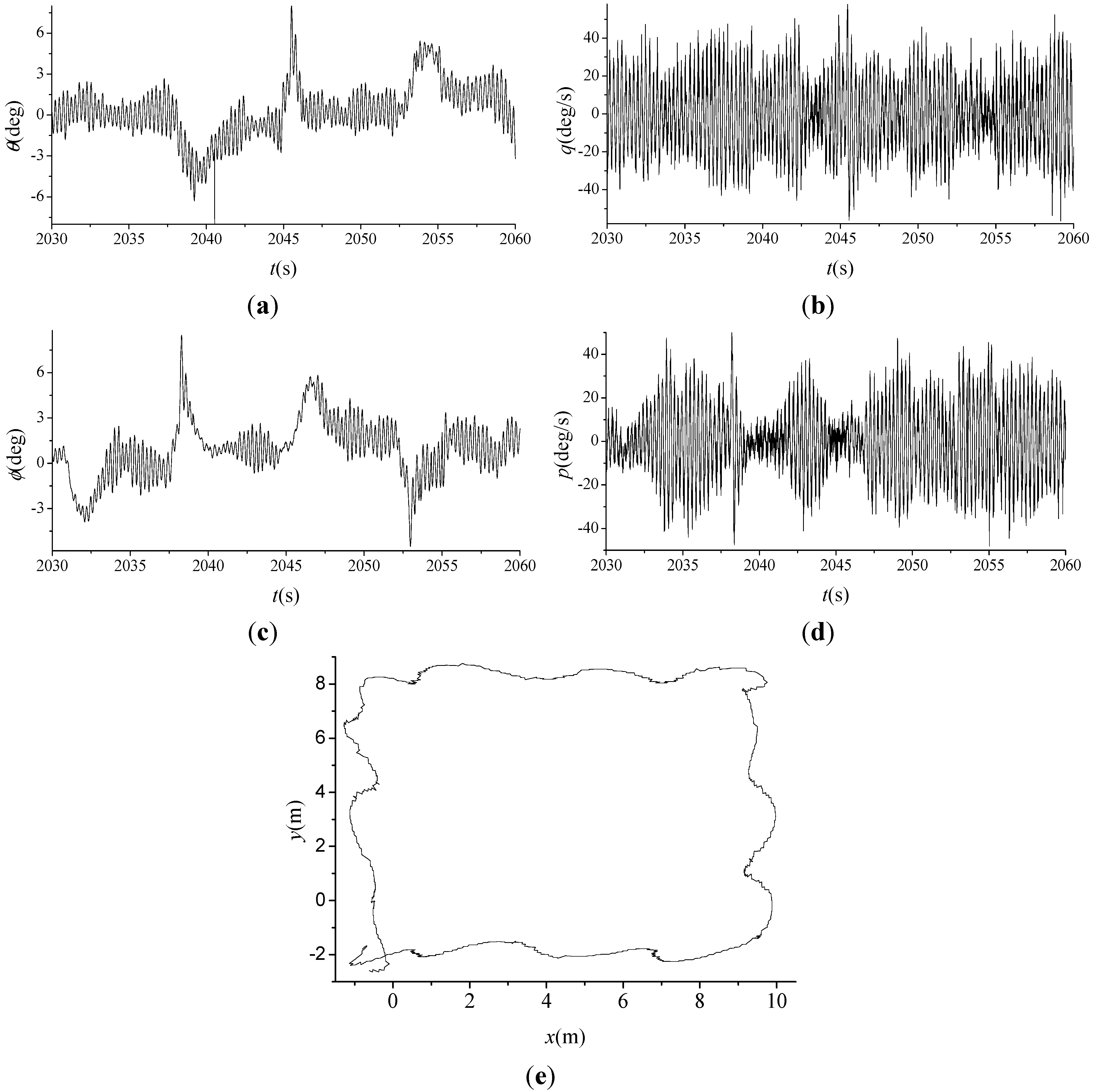
4.2. Near-hover Flight Tests

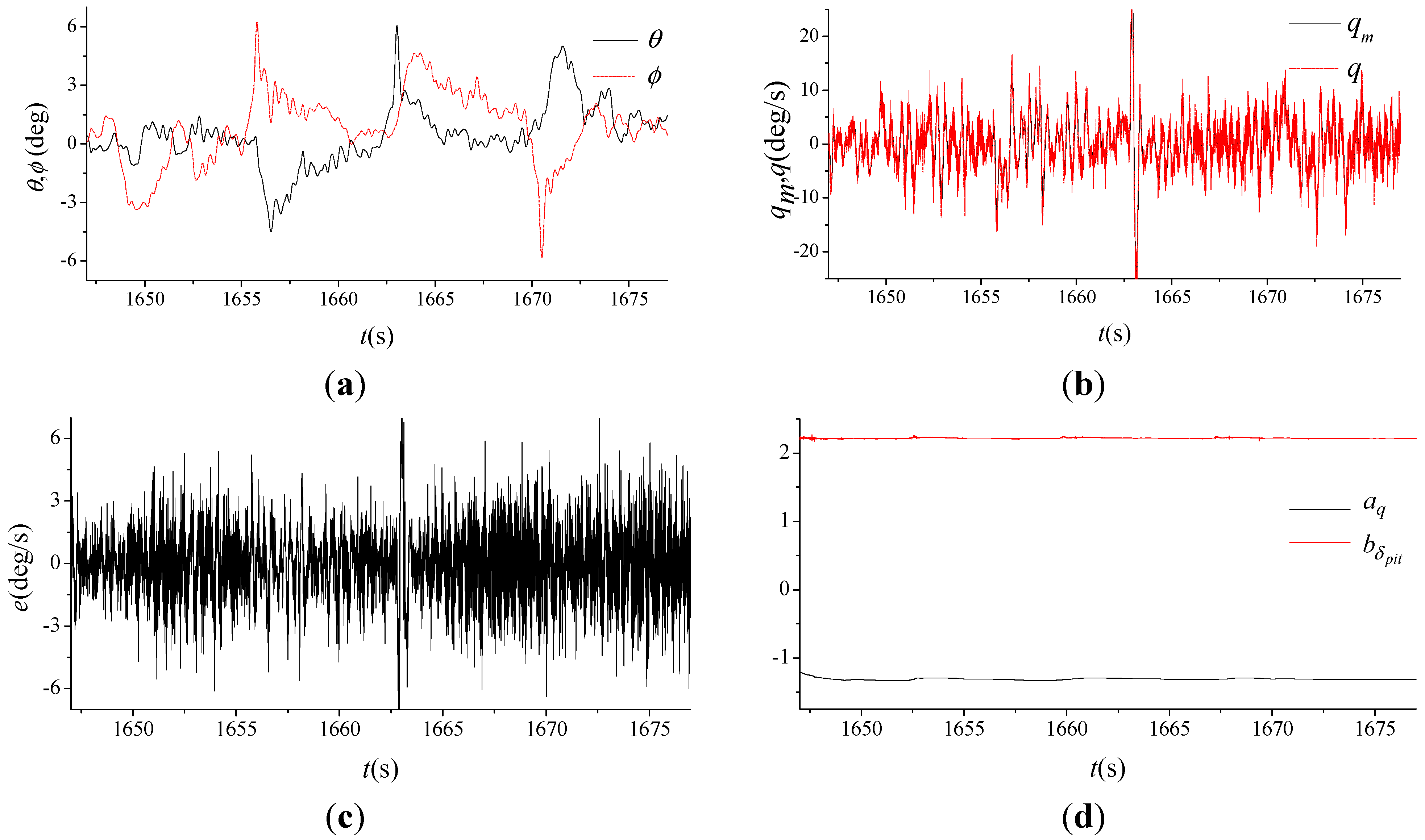
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| identification parameters | |
| desired model parameters | |
| system matrix and control matrix | |
| tracking error | |
| attitude tracking error | |
| unknown equivalent trim error vector | |
| nonlinear kinematic function | |
| actuator transfer function | |
| filter transfer functions | |
| proportional and differential coefficients | |
| predetermined feedback gain | |
| identification parameter vector | |
| aerodynamic parameters | |
| linearized roll, pitch and yaw rates, deg/s | |
| roll, pitch and yaw rates, deg/s | |
| identification model output | |
| filtered state and input vector | |
| time constants of , and , respectively | |
| input vector and its linearized version | |
| trim input vector and its estimate error | |
| nominal trim input vector | |
| linearized forward, lateral and vertical velocities, m/s | |
| forward, lateral and vertical velocities, m/s | |
| Lyapunov function candidate | |
| state vector and its linearized version | |
| nominal trim state vector | |
| optional positive number | |
| identification parameter errors | |
| identification parameter error vector | |
| equivalent input disturbance | |
| movements of the left, right, front and back servo motors, respectively, deg | |
| linearized manipulated input signals of pitch axis, roll axis, yaw axis and rotational speed of the ducted fan, respectively, deg | |
| manipulated input signals of pitch axis, roll axis, yaw axis and rotational speed of the ducted fan, respectively, deg | |
| input signal of actuator | |
| attitude control signal | |
| optional component part of learning laws | |
| optional positive definite diagonal matrix | |
| diagonal elements of | |
| unknown aerodynamic parameter set | |
| trim state vector and its estimate error | |
| optional positive number | |
| linearized pitch, roll and yaw angles, deg | |
| pitch, roll and yaw angles, deg | |
| pitch command, deg | |
| diagonal elements of | |
| element of | |
| infinite-norm | |
| outputs of in response to ,, respectively | |
| outputs of in response to ,, respectively |
References
- Walsh, D.; Cycon, J.P. The Sikorsky Cypher UAV: A multi-purpose platform with demonstrated mission flexibility. In Annual Forum Proceedings-American Helicopter Society; American Helicopter Society: Washington, DC, USA, 1998; Volume 54, pp. 1410–1418. [Google Scholar]
- Lipera, L.; Colbourne, J.; Tischler, M.; Mansur, M.; Rotkowitz, M.; Patangui, P. The micro craft istar micro-air vehicle: Control system design and testing. In Annual Forum Proceedings-American Helicopter Society; AHS International: Washington, DC, USA, 2001; Volume 57, pp. 1–11. [Google Scholar]
- Pflimlin, J.M.; Soueres, P.; Hamel, T. Hovering flight stabilization in wind gusts for a ducted fan UAV. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC’04), Paradise Island, Bahamas, 14–17 December 2004; pp. 3491–3496.
- Martin, P.; Boxwell, D. Design, analysis and experiments on a 10-inch ducted rotor VTOL UAV. In American Helicopter Society (AHS) International Specialists Meeting on Unmanned Rotorcraft: Design, Control and Testing; American Helicopter Society: Phoenix, AZ, USA, 2005; pp. 18–20. [Google Scholar]
- Pereira, J.; Chopra, I.; Gessow, A. Effects of shroud design variables on hover performance of a shrouded rotor for micro air vehicle applications. In Proceedings of the AHS International Specialists’ Meeting on Unmanned Rotorcraft, Phoenix, AZ, USA, 18–20 January 2005.
- Salluce, D.N. Comprehensive System Identification of Ducted Fan UAVs. In Doctoral Dissertation; California Polytechnic State University: San Luis Obispo, CA, USA, 2004. [Google Scholar]
- Ko, A.; Ohanian, O.J.; Gelhausen, P. Ducted fan UAV modeling and simulation in preliminary design. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit (No. 2007–6375), Keystone, CO, USA, 20 August 2007.
- Johnson, E.N.; Turbe, M.A. Modeling, control, and flight testing of a small ducted fan aircraft. J. Guid. Control Dyn. 2006, 29, 769–779. [Google Scholar] [CrossRef]
- Metni, N.; Pflimlin, J.M.; Hamel, T.; Soueres, P. Attitude and gyro bias estimation for a VTOL UAV. Control Eng. Pract. 2006, 14, 1511–1520. [Google Scholar]
- Peddle, I.K.; Jones, T.; Treurnicht, J. Practical near hover flight control of a ducted fan (SLADe). Control Eng. Pract. 2009, 17, 48–58. [Google Scholar] [CrossRef]
- Sheng, S.; Mian, A.A.; Zhao, C.; Jiang, B. Autonomous take-off and landing control for a prototype unmanned helicopter. Control Eng. Pract. 2010, 18, 1053–1059. [Google Scholar] [CrossRef]
- Naldi, R.; Gentili, L.; Marconi, L.; Sala, A. Design and experimental validation of a nonlinear control law for a ducted-fan miniature aerial vehicle. Control Eng. Pract. 2010, 18, 747–760. [Google Scholar] [CrossRef]
- Pflimlin, J.M.; Soueres, P.; Hamel, T. Position control of a ducted fan VTOL UAV in crosswind. Int. J. Control 2007, 80, 666–683. [Google Scholar] [CrossRef]
- Pflimlin, J.M.; Binetti, P.; Soueres, P.; Hamel, T.; Trouchet, D. Modeling and attitude control analysis of a ducted-fan micro aerial vehicle. Control Eng. Pract. 2010, 18, 209–218. [Google Scholar] [CrossRef]
- Hess, R.A.; Ussery, T.M. Sliding mode techniques applied to the control of a micro-air vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Austin, TX, USA, 12 August 2003; pp. 11–14.
- Hess, R.A.; Bakhtiari-Nejad, M. Sliding Mode Control of a Nonlinear Model of an Unmanned Aerisl Vehicle. J. Guid. Control Dyn. 2008, 31, 1163–1165. [Google Scholar] [CrossRef]
- Spaulding, C.M.; Mansur, M.H.; Tischler, M.B.; Hess, R.A.; Franklin, J.A. Nonlinear inversion control for a ducted fan UAV. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit (No. 2005–6231), San Francisco, CA, USA, 17 August 2005.
- Chwa, D.; Choi, J.Y.; Seo, J.H. Compensation of actuator dynamics in nonlinear missile control. IEEE Trans. Control Syst. Technol. 2004, 12, 620–626. [Google Scholar] [CrossRef]
- Manouchehri, A.; Hajkarami, H.; Ahmadi, M.A.S. Hovering control of a ducted fan VTOL Unmanned Aerial Vehicle (UAV) based on PID control. In Proceedings of the 2011 International Conference on Electrical and Control Engineering (ICECE), Yichang, China, 16–18 September 2011; pp. 5962–5965.
- Duan, H.; Sun, C. Pendulum-like oscillation controller for micro aerial vehicle with ducted fan based on LQR and PSO. Sci. China Technol. Sci. 2013, 56, 423–429. [Google Scholar] [CrossRef]
- Cai, G.; Chen, B.M.; Dong, X.; Lee, T.H. Design and implementation of a robust and nonlinear flight control system for an unmanned helicopter. Mechatronics 2011, 21, 803–820. [Google Scholar] [CrossRef]
- Avanzini, G.; Ciniglio, U.; Matteis, G.D. Full-envelope robust control of a shrouded-fan unmanned vehicle. J. Guid. Control Dyn. 2006, 29, 435–443. [Google Scholar]
- Aruneshwaran, R.; Suresh, S.; Wang, J.; Venugopalan, T.K. Neural adaptive flight controller for ducted-fan UAV performing nonlinear maneuver. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Singapore, 16–19 April 2013; pp. 51–56.
- Lee, W.; Bang, H. Control of ducted fan UAV by fuzzy gain scheduler. In Proceedings of the International Conference on Control, Automation and Systems, ICCAS’07, Seoul, Korea, 17–20 October 2007; pp. 812–816.
- Omar, Z. Intelligent Control of a ducted-fan VTOL UAV with conventional control surfaces. In Doctoral Dissertation; RMIT University: Melbourne, Australia, 2010. [Google Scholar]
- Hua, M.D.; Hamel, T.; Morin, P.; Samson, C. Control of a class of thrust-propelled underactuated vehicles and application to a VTOL drone. In Proceedings of the IEEE International Conference on Robotics and Automation, 2009. ICRA’09, Kobe, Japan, 12–17 May 2009; pp. 972–978.
- Zhang, N. Ducted fan unmanned aircraft flight dynamics analysis and control study. In Dissertation; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2011. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, S.; Sun, C. A Near-Hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics. Appl. Sci. 2015, 5, 666-681. https://doi.org/10.3390/app5040666
Sheng S, Sun C. A Near-Hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics. Applied Sciences. 2015; 5(4):666-681. https://doi.org/10.3390/app5040666
Chicago/Turabian StyleSheng, Shouzhao, and Chenwu Sun. 2015. "A Near-Hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics" Applied Sciences 5, no. 4: 666-681. https://doi.org/10.3390/app5040666
APA StyleSheng, S., & Sun, C. (2015). A Near-Hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics. Applied Sciences, 5(4), 666-681. https://doi.org/10.3390/app5040666





