Laser-Driven Very High Energy Electron/Photon Beam Radiation Therapy in Conjunction with a Robotic System
Abstract
:1. Introduction
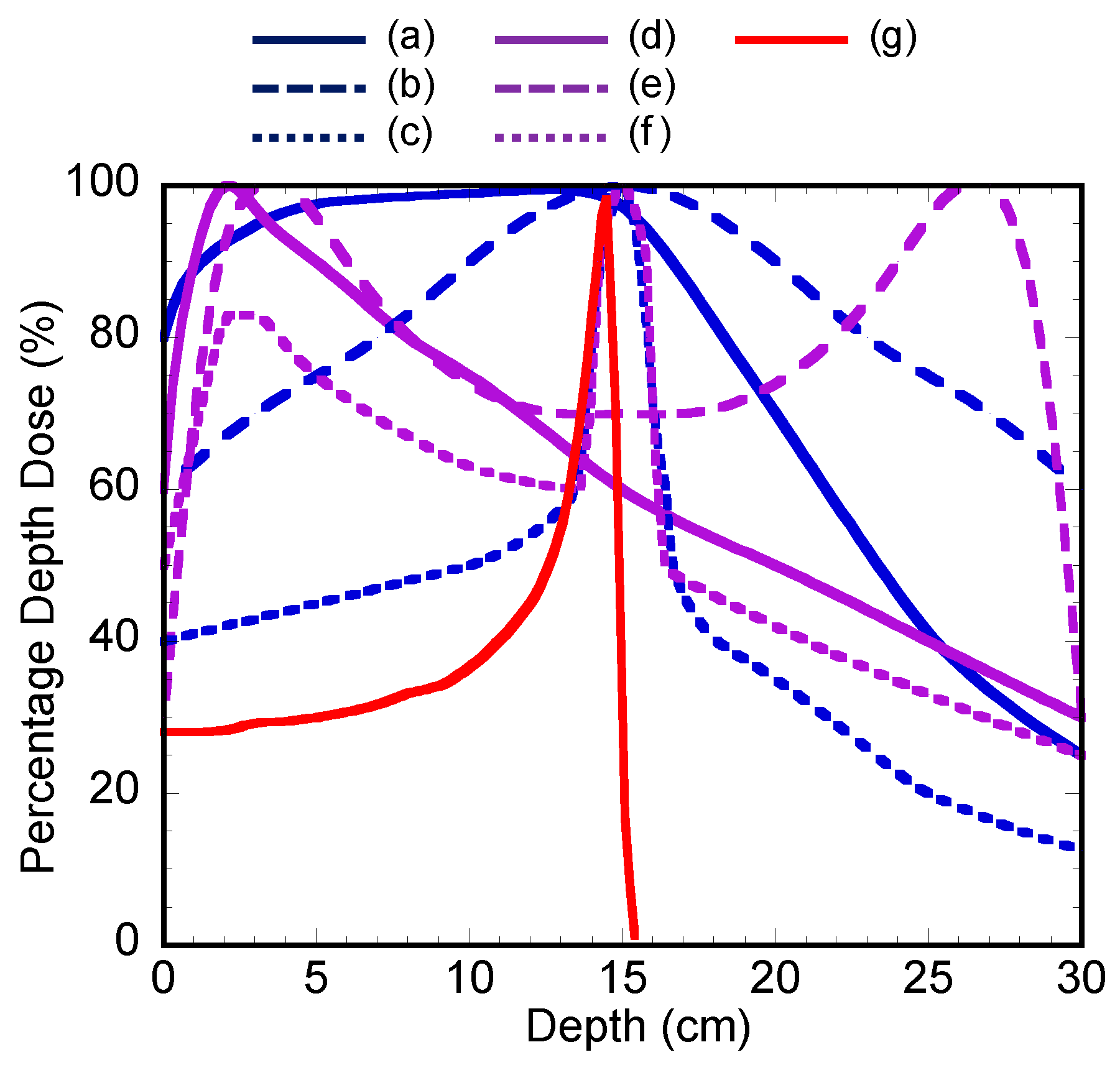
2. Laser-Driven Very-High-Energy Electron/Photon Beam Radiation Therapy System
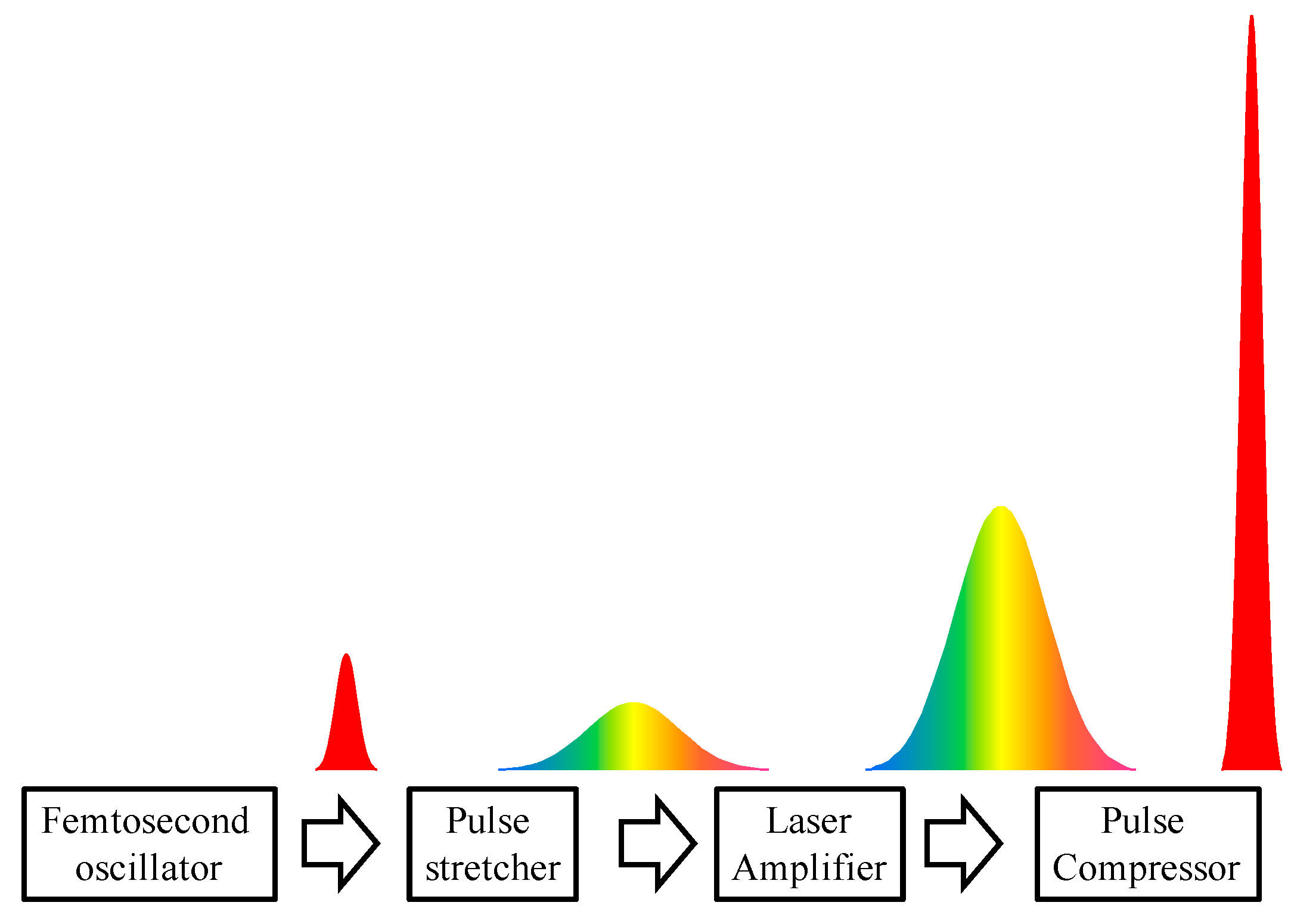
2.1. Drive Laser System
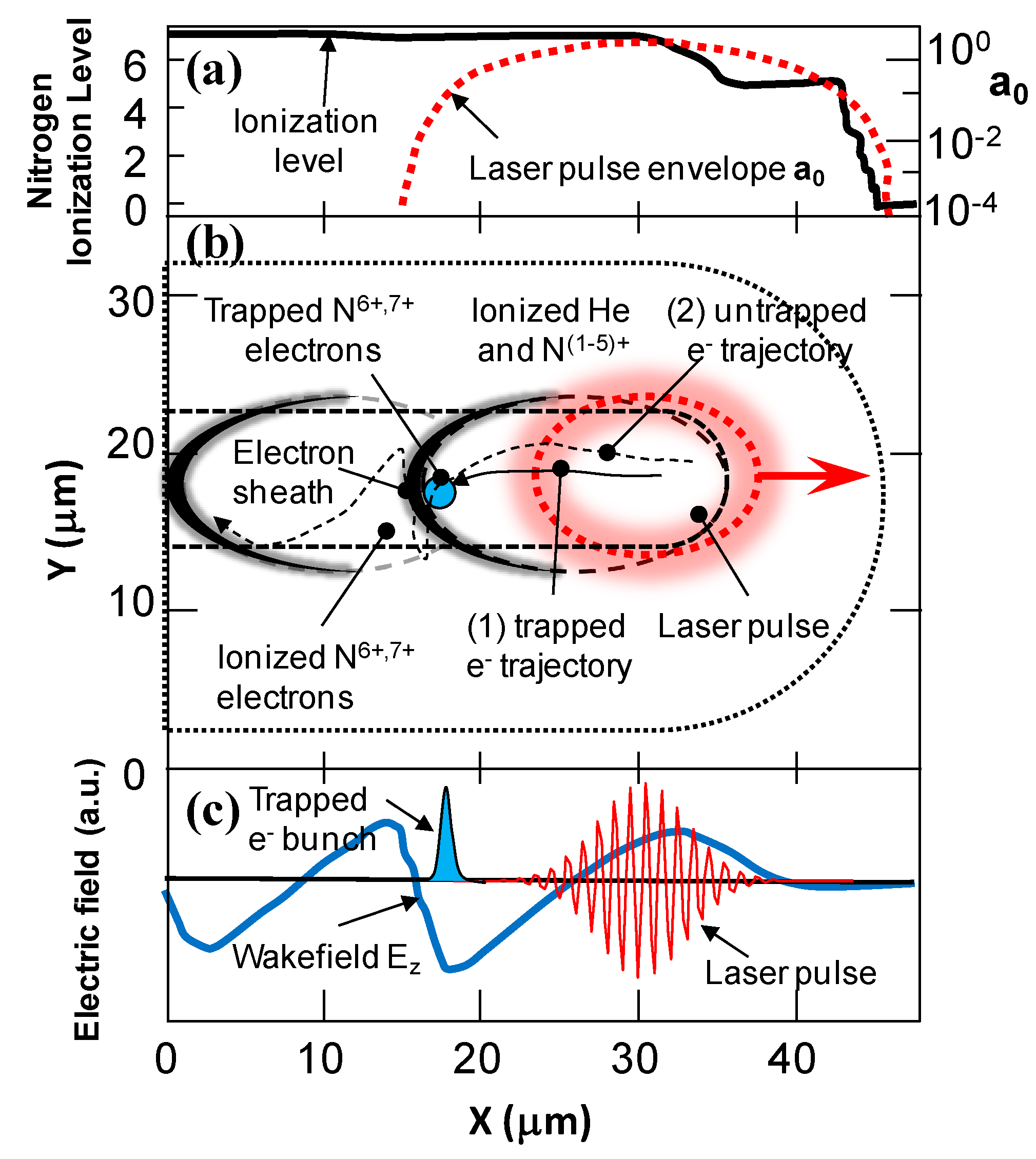
2.2. Design of Laser Plasma Accelerators for VHE Electron Beams
| Parameters | Symbols |
|---|---|
| Speed of light in vacuum | c |
| Laser wavelength | λL |
| Laser angular frequency | ωL |
| Laser intensity | IL |
| Laser spot radius | rL |
| Laser pulse duration | τL |
| Laser peak power | PL |
| Laser pulse energy | UL |
| Normalized vector potential | a0 |
| Normalized matched spot radius | Rm |
| Critical power for relativistic self-focusing | Pc |
| Electron charge | e |
| Electron mass | me |
| Classical electron radius | re |
| Plasma electron density | ne |
| Plasma electron frequency | ωp |
| Plasma wave number | kp |
| Critical plasma density | nc |
| Group velocity | vg |
| Normalized group velocity | βg |
| Relativistic factor related to the group velocity | γg, γg0 |
| Correction factor of the group velocity | κself |
| Bubble radius | RB |
| Accelerating electric field with beam loading | EZ |
| Accelerating electric field without beam loading | EM |
| Non- relativistic wave-breaking field | E0 |
| Reduction factor of the accelerating field | α |
| Maximum energy gain | Wmax |
| Design electron beam energy | Eb |
| Normalized maximum energy gain | ∆γmax |
| Dephasing length | Ldp |
| Accelerator length | Lacc |
| Pump depletion length | Lpd |
| Electron beam charge | Qb |
| Root mean square electron beam radius | σb |
| Beam loading efficiency | ηb |
| Case | A | B | C | D | E |
|---|---|---|---|---|---|
| Electron beam energy [MeV] | 50 | 100 | 150 | 200 | 250 |
| Laser wavelength [μm] | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| Laser energy per pulse [mJ] | 33 | 63 | 92 | 121 | 149 |
| Peak power [TW] | 1.7 | 3.2 | 4.6 | 6.0 | 7.5 |
| Pulse duration [fs] | 20 | 20 | 20 | 20 | 20 |
| Matched spot radius [μm] | 3.6 | 5.0 | 6.0 | 6.9 | 7.6 |
| Plasma density [1019 cm−3] | 2.3 | 1.2 | 0.8 | 0.6 | 0.5 |
| Accelerator length [mm] | 0.2 | 0.5 | 0.9 | 1.4 | 1.9 |
| Charge per bunch [pC] | 10 | 10 | 10 | 10 | 10 |
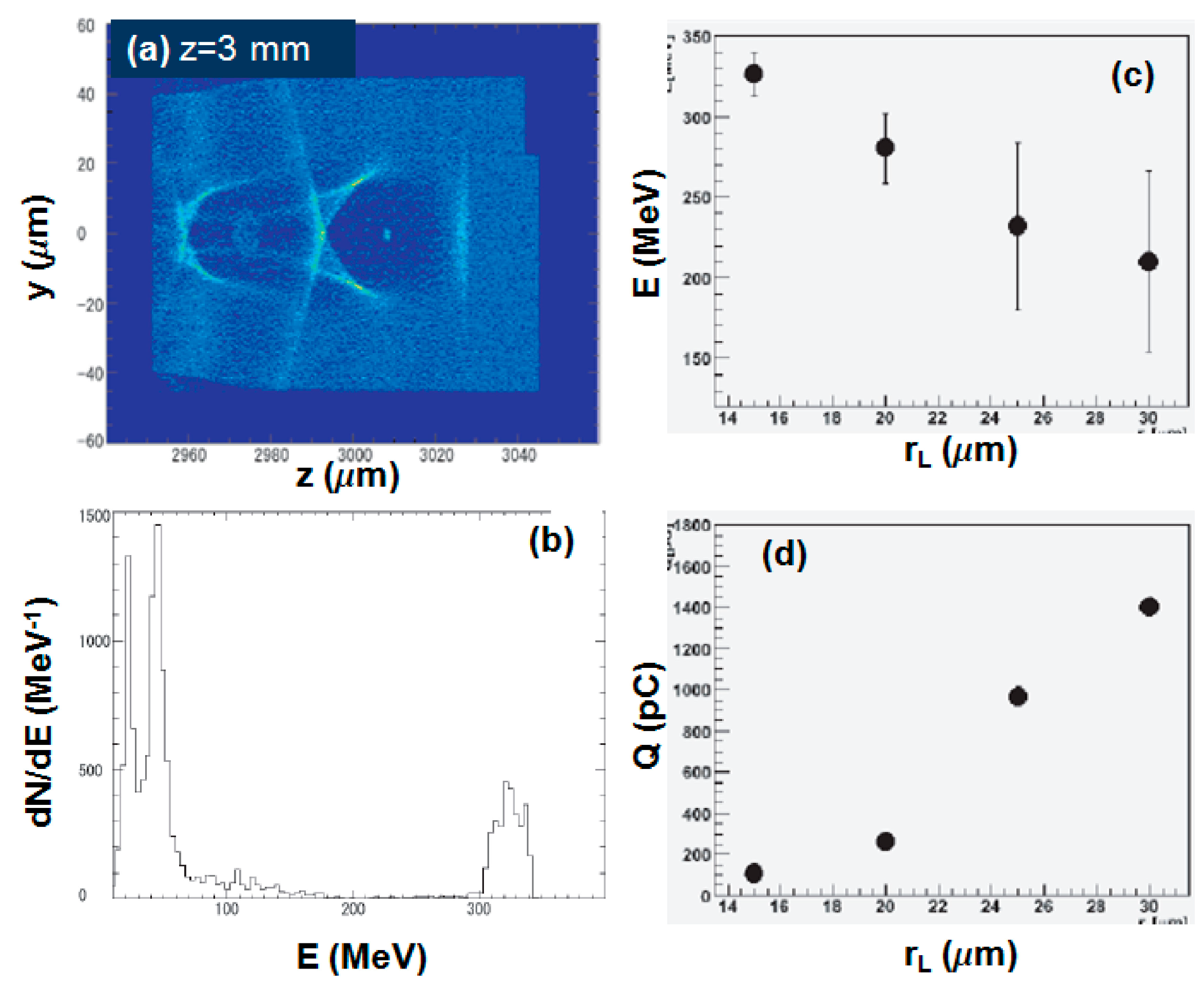
2.3. Simulations on Laser Plasma Accelerators
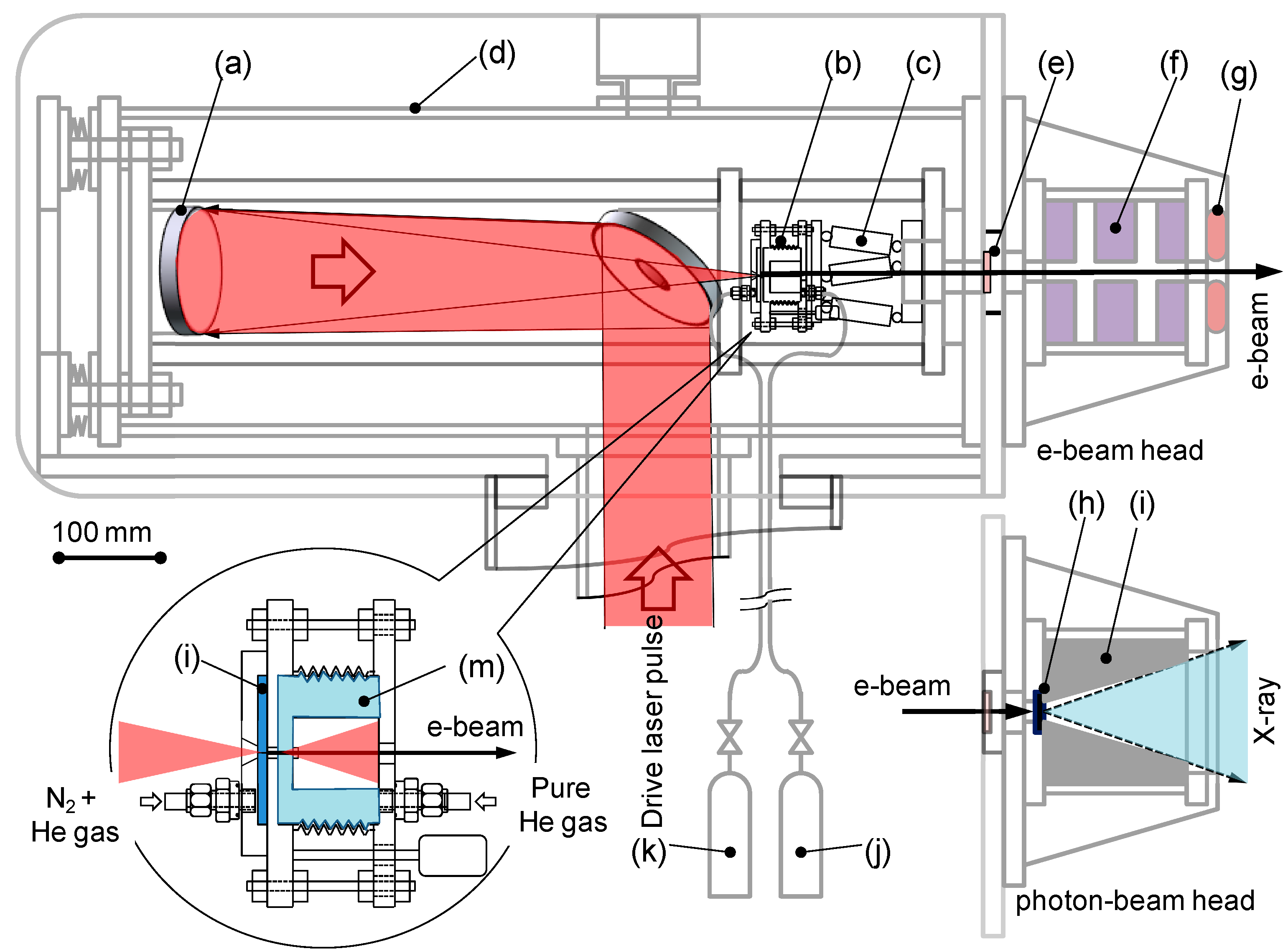
2.4. An Embodiment of Laser-Driven VHE Electron- and Photon-Beam Sources
2.5. Laser Beam Stabilizing System
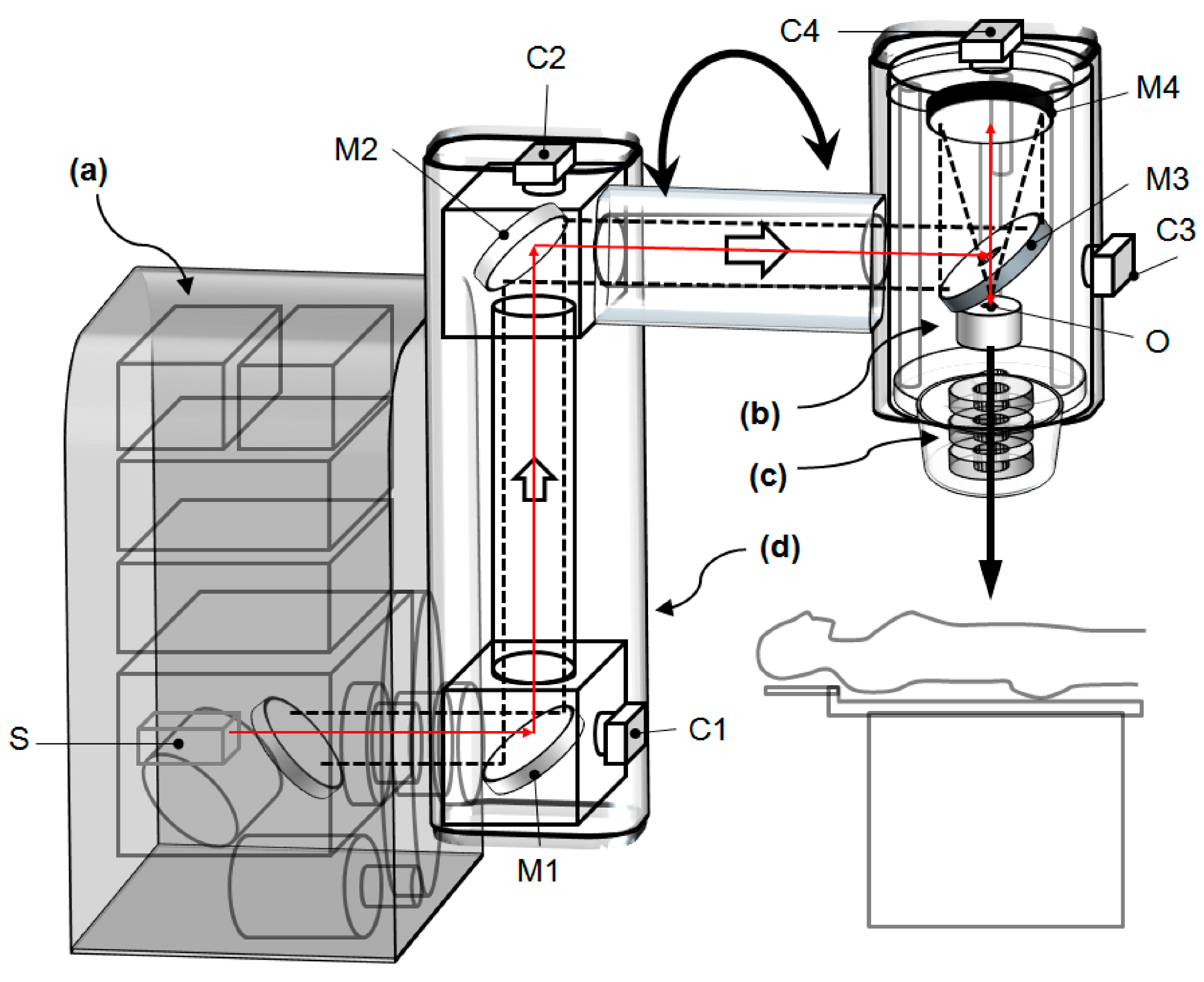
3. Conceptual Design of Laser In-Frame Robotic Gantry
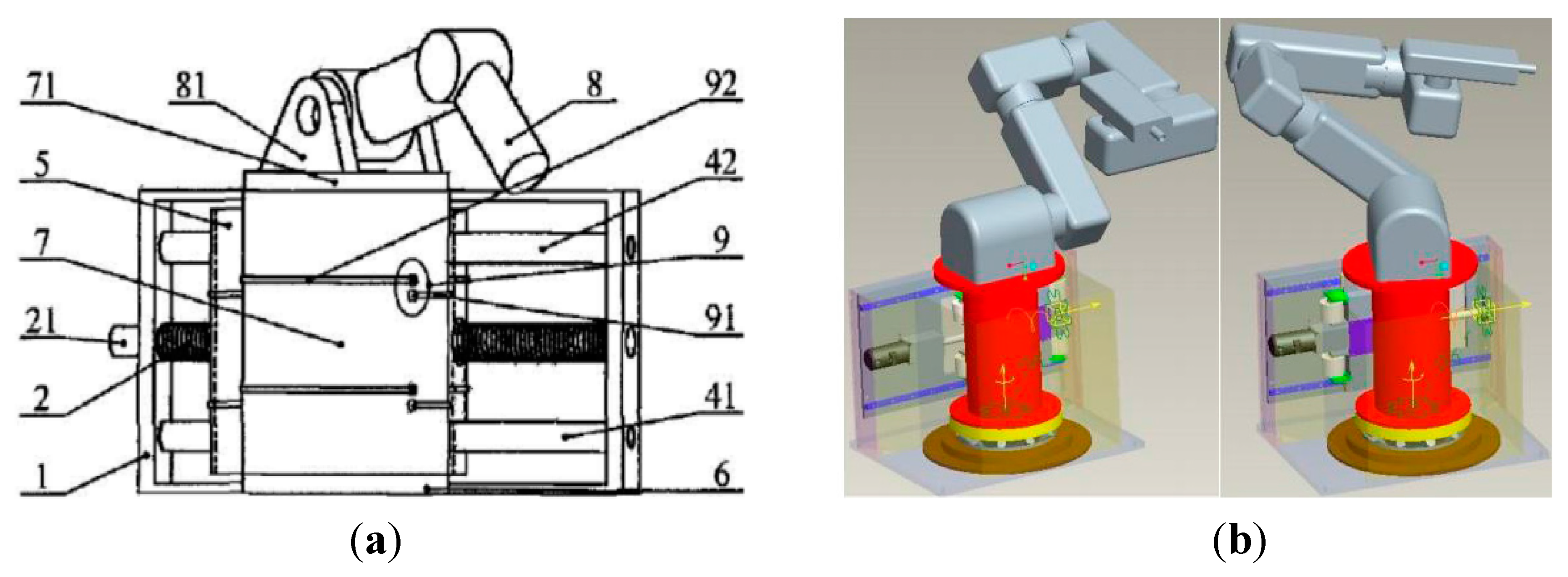
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Cancer Institute at the National Institutes of Health. Radiation Therapy for Cancer. Available online: http://www.cancer.gov/cancertopics/factsheet/Therapy/radiation (accessed on 25 September 2013).
- Whittum, D.H. Microwave Electron Linacs for Oncology. In Reviews of Accelerator Science and Technology; Chao, A.W., Chou, W., Eds.; World Scientific: Singapore, 2009; Volume 2, pp. 63–92. [Google Scholar]
- Kwoh, Y.S.; Hou, J.; Jonckheere, E.A.; Hayall, S. A robot with improved absolute positioning accuracy for CT guided stereotactic brain surgery. IEEE Trans. Biomed. Eng. 1988, 35, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Coste-Manière, È.; Olender, D.; Kilby, W.; Schulz, R.A. Robotic whole body stereotactic radiosurgery: Clinical advantages of the CyberKnife integrated system. Int. J. Med. Robot. Compt. Assist. Surg. 2005, 1, 28–39. [Google Scholar]
- Adler, J.R., Jr.; Chang, S.D.; Murphy, M.J.; Doty, J.; Geis, P.; Hancock, S.L. The Cyberknife: A frameless robotic system for radiosurgery. Stereotact. Funct. Neurosurg. 1997, 69, 124–198. [Google Scholar] [CrossRef]
- Dieterich, S.; Gibbs, I.C. The Cyber Knife in Clinical Use: Current Roles, Future Expectations. In IMRT, IGRT, SBRT; Meyer, J.L., Ed.; Karger: Basel, Switzerland, 2011; Volume 43, pp. 181–194. [Google Scholar]
- Murray, L.J.; Robinson, M.H. Radiotherapy: Technical aspects. Medicine 2010, 39, 698–704. [Google Scholar] [CrossRef]
- DesRosiers, C.; Moskvin, V.; Bielajew, A.F.; Papiez, L. 150–250 MeV electron beams in radiation therapy. Phy. Med. Biol. 2000, 45, 1781–1805. [Google Scholar] [CrossRef]
- Yeboah, C.; Sandison, G.A. Optimized treatment planning for prostate cancer comparing IMPT, VHEET and 15 MV IMXT. Phys. Med. Biol. 2002, 47, 2247–2261. [Google Scholar] [CrossRef] [PubMed]
- Loo, B.W.; Maxim, P.G.; Dolgashev, V.A. Pluridirectional very high electron energy radiation therapy systems and processes. U.S. Patent 13/765,017, 12 February 2013. [Google Scholar]
- Subiel, A.; Moskvin, V.; Welsh, G.H.; Cipiccia, S.; Reboredo, G.D.; Evans, P.; Partridge, M.; DesRosiers, C.; Anania, M.P.; Cianchi, A.; et al. Dosimetry of Very High Energy Electrons (VHEE) for radiotherapy applications. Phys. Med. Biol. 2014, 59. [Google Scholar] [CrossRef]
- Moskvin, V.; Subiel, A.; Desrosiers, C.; Wiggins, M.; Maryanski, M.; Mendonca, M.; Boyd, M.; Sorensen, A.; Cipiccia, S.; Issac, R.; et al. Characterization of the Very High Energy Electrons, 150–250 MeV (VHEE) Beam Generated by ALPHA-X Laser Wakefield Accelerator Beam Line for Utilization in Monte Carlo Simulation for Biomedical Experiment Planning. Med. Phys. 2012, 39. [Google Scholar] [CrossRef]
- Friesel, D.L.; Antaya, T.A. Medical Cyclotrons. In Reviews of Accelerator Science and Technology; Chao, A.W., Chou, W., Eds.; World Scientific: Singapore, 2009; Volume 2. [Google Scholar]
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267–270. [Google Scholar] [CrossRef]
- Leemans, W.P.; Nagler, B.; Gonsalves, A.J.; Toth, C.; Nakamura, K.; Geddes, C.G.R.; Esarey, E.; Schroeder, C.B.; Hooker, S.M. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Clayton, C.E.; Ralph, J.E.; Albert, F.; Fonseca, R.A.; Glenzer, S.H.; Joshi, C.; Lu, W.; Marsh, K.A.; Martins, S.F.; Mori, W.B.; et al. Self-guided laser wakefield acceleration beyond 1 Gev using ionization-induced injection. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, M.; Wang, W.; Wang, C.; Liu, J.; Deng, A.; Xu, J.; Xia, C.; Li, W.; Zhang, H.; et al. Laser wakefield acceleration of electron beams beyond 1 GeV from an ablative capillary discharge waveguide. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Wang, X.; Zgadzaj, R.; Fazel, N.; Li, Z.; Yi, S.A.; Zhang, X.; Henderson, W.; Chang, Y.Y.; Korzekwa, R.; Tsai, H.E.; et al. Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef]
- Kim, H.T.; Pae, K.H.; Cha, H.J.; Kim, I.J.; Yu, T.J.; Sung, J.H.; Lee, S.K.; Jeong, T.M.; Lee, J. Enhancement of electron energy to the multi-GeV regime by a dual-stage laser-wakefield accelerator pumped by petawatt laser pulses. Phys. Rev. Lett. 2013, 111. [Google Scholar] [CrossRef] [PubMed]
- Kameshima, T.; Hong, W.; Sugiyama, K.; Wen, X.; Wu, Y.; Tang, C.; Zhu, Q.; Gu, Y.; Zhang, B.; Peng, H.; et al. 0.56 GeV laser electron acceleration in ablative-capillary-discharge plasma channel. Appl. Phys. Exp. 2008, 1. [Google Scholar] [CrossRef]
- Karsch, S.; Osterhoff, J.; Popp, A.; Rowlands-Rees, T.P.; Major, Z.; Fuchs, M.; Marx, B.; Hörlein, R.; Schmid, K.; Veisz, L.; et al. GeV-scale electron acceleration in a gas-filled capillary discharge waveguide. New J. Phys. 2007, 9, 415–425. [Google Scholar] [CrossRef]
- Lundh, O.; Lim, J.; Rechatin, C.; Ammoura, L.; Ben-Ismail, A.; Davoine, X.; Gallot, G.; Goddet, J.P.; Lefebvre, E.; Malka, V.; et al. Few femtosecond, few kiloampere electron bunch produced by a laser-plasma accelerator. Nat. Phys. 2011, 7, 219–222. [Google Scholar] [CrossRef]
- Hafz, N.A.M.; Jeong, T.M.; Choi, I.W.; Lee, S.K.; Pae, K.H.; Kulagin, V.V.; Sung, J.H.; Yu, T.J.; Hong, K.H.; Hosokai, T.; et al. Stable generation of GeV-class electron beams from self-guided laser-plasma channels. Nat. Photon. 2008, 2, 571–577. [Google Scholar] [CrossRef]
- Liu, J.S.; Xia, C.Q.; Wang, W.T.; Lu, H.Y.; Wang, C.; Deng, A.H.; Li, W.T.; Zhang, H.; Liang, X.Y.; Leng, Y.X.; et al. All-optical cascaded laser wakefield accelerator using ionization-induced injection. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef]
- Pollock, B.B.; Clayton, C.E.; Ralph, J.E.; Albert, F.; Davidson, A.; Divol, L.; Filip, C.; Glenzer, S.H.; Herpoldt, K.; Lu, W.; et al. Demonstration of a narrow energy spread, similar to ~0.5 GeV electron beam from a two-stage laser wakefield accelerator. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Pak, A.; Marsh, K.A.; Martins, S.F.; Lu, W.; Mori, W.B.; Joshi, C. Injection and trapping of tunnel-ionized electrons into laser-produced wakes. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- McGuffey, C.; Thomas, A.G.R.; Schumaker, W.; Matsuoka, T.; Chvykov, V.; Dollar, F.J.; Kalintchenko, G.; Yanovsky, V.; Maksimchuk, A.; Krushelnick, K.; et al. Ionization induced trapping in a laser wakefield accelerator. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Liu, J.; Wang, W.; Lu, H.; Cheng, W.; Deng, A.; Li, W.; Zhang, H.; Liang, X.; Leng, Y.; et al. Effects of self-focusing on tunnel-ionization-induced injection in a laser wakefield accelerator. Phys. Plasmas 2011, 18. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Comm. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Mourou, G.; Brocklesby, B.; Tajima, T.; Limpert, J. The future is fiber accelerators. Nat. Photonics 2013, 7, 258–261. [Google Scholar] [CrossRef]
- Nakajima, K. Conceptual designs of a laser plasma accelerator-based EUV-FEL and an all-optical Gamma-beam source. High Power Laser Sci. Eng. 2014, 2. [Google Scholar] [CrossRef]
- Kostyukov, I.; Pukhov, A.; Kiselev, S. Phenomenological theory of laser-plasma interaction in “bubble” regime. Phys. Plasmas 2004, 11, 5256–5264. [Google Scholar] [CrossRef]
- Kalmykov, S.; Yi, A.; Khudik, V.; Shvets, G. Electron self-injection and trapping into an evolving plasma bubble. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Nieter, C.; Cary, J.R. VORPAL: An versatile plasma simulation code. J. Comput. Phys. 2004, 196, 448–473. [Google Scholar] [CrossRef]
- Lim, J.K.; Frigola, P.; Travish, G.; Rosenzweig, J.B.; Anderson, S.G.; Brown, W.J.; Jacob, J.S.; Robbins, C.L.; Tremaine, A.M. Adjustable, short focal length permanent-magnet quadrupole based electron beam final focus system. Phys. Rev. ST Accel. Beams 2005, 8. [Google Scholar] [CrossRef]
- Association for Nuclear Technology in Medicine. Particle beam therapy facilities in Japan. Available online: http://www.antm.or.jp/05_treatment/04.html (accessed on 28 November 2014). (In Japanese)
- Yasui, K. Current status and problems of particle beam therapy in advanced medical services for cancer. Available online: http://dl.ndl.go.jp/view/download/digidepo_8392376_po_075504.pdf (accessed on 28 November 2014). (In Japanese)
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakajima, K.; Yuan, J.; Chen, L.; Sheng, Z. Laser-Driven Very High Energy Electron/Photon Beam Radiation Therapy in Conjunction with a Robotic System. Appl. Sci. 2015, 5, 1-20. https://doi.org/10.3390/app5010001
Nakajima K, Yuan J, Chen L, Sheng Z. Laser-Driven Very High Energy Electron/Photon Beam Radiation Therapy in Conjunction with a Robotic System. Applied Sciences. 2015; 5(1):1-20. https://doi.org/10.3390/app5010001
Chicago/Turabian StyleNakajima, Kazuhisa, Jianjun Yuan, Liming Chen, and Zhengming Sheng. 2015. "Laser-Driven Very High Energy Electron/Photon Beam Radiation Therapy in Conjunction with a Robotic System" Applied Sciences 5, no. 1: 1-20. https://doi.org/10.3390/app5010001





