Effect of Different Infill Types on the Cyclic Behavior of Steel Plate Shear Walls

Abstract

The steel plate shear wall (SPSW) is a prevalent lateral load-resisting system in high-rise steel buildings. Comprising a boundary frame and an infill plate, its performance is the focus of this study. This work aims to investigate the effects of different infill plate types of identical weight and boundary frame characteristics on the seismic behavior of SPSWs. A numerical method is proposed to enable a comprehensive comparison of the seismic behavior of different SPSW types of equal weight. The model is validated using previously published numerical and experimental works. The study examines unstiffened (USPSW), stiffened (SSPSW), and corrugated steel plate shear walls (CSPSW). The effects of boundary frame stiffness were studied, with key performance metrics, such as load-carrying capacity, stiffness, and energy dissipation capacity, analyzed in detail. It is found that SSPSWs exhibit superior seismic behavior compared to USPSWs and CSPSWs. The load-carrying capacity of SSPSWs is approximately 14% and 24% higher than that of USPSWs and CSPSWs, respectively. USPSWs demonstrate greater sensitivity to boundary frame stiffness than CSPSWs.

1. Introduction

The steel plate shear wall, comprising a boundary frame and infill panel as shown in Figure 1a, is a prevalent lateral load-resisting system in modern high-rise steel buildings. This structural system is favored by designers due to its numerous advantages, including a high strength-to-weight ratio, efficient constructability, and the capacity to reduce overall seismic demands on the foundational structure. Fundamentally, the the steel plate shear wall (SPSW)provides exceptional lateral strength, significant initial stiffness (often denoted as K1), and reliable shear performance, making it a robust choice for regions prone to seismic activity or high wind loads [1,2].

SPSWs can be systematically classified based on the configuration and treatment of the infill plate. The primary categories include unstiffened steel plate shear walls (USPSWs), which utilize thin plates that buckle elastically but develop significant post-buckling strength; stiffened steel plate shear walls (SSPSWs), which employ welded stiffeners to delay or prevent buckling and enhance performance; composite steel plate shear walls, which integrate concrete to improve buckling resistance and damping characteristics [3]; and corrugated steel plate shear walls (CSPSWs), which use profiled plates to geometrically increase out-of-plane stiffness, Figure 1b. The CSPSWs can be further subdivided according to the orientation of the corrugations: horizontally corrugated steel plate shear walls (HCSPSWs) and vertically corrugated steel plate shear walls (VCSPSWs). The distinct geometries and configurations of USPSWs, SSPSWs, HCSPSWs, and VCSPSWs are depicted in Figure 2, highlighting the physical differences that underlie their behavioral mechanics.

The design and analysis of these systems are guided by established principles. For unstiffened walls, the AISC Design Guide 20 [4] provides a fundamental equation for estimating the ultimate shear strength of the infill panel, which is driven by the formation of a diagonal tension field. This capacity is given by Equation (1):

$$V_{m,PW}=0.5f_y{t}_w{L}_{CF}\mathrm{s}\mathrm{i}\mathrm{n} 2\alpha$$

(1)

where $V_{m,PW}$ is the maximum load-carrying capacity of the plate, $f_y$ is the yield strength of the steel material, $t_w$ is the thickness of the wall panel, $L_{CF}$ is the clear distance between column flanges, and $\alpha$ is the angle of inclination of the tension field from the vertical direction, typically taken as 40°. This equation encapsulates the post-buckling strength mechanism that defines USPSW behavior. In contrast, for corrugated steel plate shear walls with deep corrugations, the buckling behavior is markedly different. The corrugations significantly increase the shear buckling stress, often allowing it to reach the material’s shear yield stress before instability occurs. Consequently, the lateral strength can be conservatively estimated using a yield-based approach. According to principles adapted from design manuals for bridges with corrugated webs, the shear capacity can be expressed by Equation (2):

$$V_{m,CW}={\tau }_{cr}{t}_w{L}_{CF}$$

(2)

where $V_{m,CW}$ is the maximum load-carrying capacity of the corrugated panel, and ${\tau }_{cr}$ is the critical shear stress, which for deeply corrugated panels can be taken as equal to the shear yielding stress ${\tau }_y$. The shear yielding stress is derived from the Von Mises yield criterion, as shown in Equation (3):

$${\tau }_y=f_y/\sqrt{3}$$

(3)

Here, $f_y$ is the uniaxial yield strength, $t_w$ is the thickness of the panel, and $L_{CF}$ remains the clear distance between column flanges. This formulation highlights a strength mechanism based more on material yield within a stiffened geometry rather than on post-buckling tension field action.

The behavioral dichotomy between USPSWs and CSPSWs is profound. A USPSW, characterized by a high height-to-thickness ratio (λ often exceeding 150), typically reaches its elastic shear buckling limit under a relatively low level of lateral displacement. However, its most significant attribute is the substantial post-buckling load-carrying capacity it maintains. This capacity is attributed entirely to the phenomenon of the tension field [5,6,7]. After initial buckling, the plate cannot support additional compressive stresses but can continue to resist load through a diagonal tensile membrane stress field that forms between the boundary elements. This tension field acts as a series of plastic hinges, dissipating substantial amounts of input seismic energy through stable cyclic yielding. The formation of this field is accompanied by pronounced out-of-plane deformations of the thin plate, which are a signature characteristic of USPSW response.

Conversely, the CSPSW presents an alternative strategy. The geometric corrugations act as integral ribs, providing substantial out-of-plane flexural rigidity. This makes CSPSWs an attractive choice to circumvent the complex on-site construction processes associated with welding numerous discrete stiffeners or casting concrete. The corrugation induces an anisotropic stiffness property known as the “Accordion Effect” [8,9]. This effect means the stiffness and strength are significantly greater in the direction parallel to the corrugation ribs than in the direction perpendicular to them. This anisotropy directly informs performance: a VCSPSW possesses enhanced axial stiffness, making it more effective at resisting vertical and global bending loads, while a HCSPSW offers superior in-plane shear stiffness and strength, making it more efficient for lateral load resistance.

The evolution of SPSW research reflects a continuous pursuit of improved performance. A substantial body of work has been dedicated to understanding and enhancing the seismic behavior, load-carrying capacity, and energy dissipation of these systems [5,10,11,12,13,14,15,16,17,18,19,20]. Early foundational research on USPSWs established the tension field theory and demonstrated that thin plates could provide excellent seismic performance through substantial ductility and energy dissipation, even after buckling [11]. Experimental studies, such as those on single-span, three-story specimens, further quantified the influence of parameters like infill plate thickness on the global hysteretic response [5]. Large-scale cyclic tests on multi-story USPSWs confirmed their capability to sustain high story drifts, up to 4%, while maintaining stable energy dissipation [13].

Recognizing the limitations of USPSWs, such as large out-of-plane deformations and pinched hysteretic loops, research expanded into SSPSWs. The addition of stiffeners, either horizontally, vertically, or diagonally, delays the onset of buckling, increases the elastic shear strength, and can lead to fuller, more stable hysteresis loops [15,18].

This enhancement, however, comes at the cost of increased fabrication complexity and material.

Parallel research avenues explored infill plate connectivity. The integrity of the connection between the infill plate and the boundary frame is critical for force transfer and the development of the tension field. Numerical studies have shown that partially connected plates, such as those with only 80% of their perimeter welded, suffer significant reductions in load-carrying capacity, stiffness, ductility, and energy dissipation compared to fully connected systems [21]. This work underscores the importance of connection design but primarily considers intentional, predefined connection patterns rather than the progressive, unpredictable separation that may occur due to weld cracking from fatigue, overloading, or imperfections.

The exploration of CSPSWs represents a convergence of ideas from plate girder bridge design and building structures. The favorable performance of corrugated webs in girders, particularly their high shear buckling strength, prompted their investigation for SPSWs. Studies on corrugated plates in coupling beams showed improved rotational capacity [22], while analytical work developed equivalent plate models for corrugated structures [23]. Research into the shear buckling behavior of trapezoidal and sinusoidal profiles provided foundational understanding [24,25,26]. As focus shifted to building applications, experimental and numerical studies on CSPSWs reported promising results, including significant improvements in energy dissipation capacity, ductility ratio, and initial stiffness compared to USPSWs [9,27,28,29]. Parametric studies further revealed the influence of corrugation geometry, such as the number of folds and the sinusoidal versus trapezoidal shape, on lateral strength.

Despite the extensive body of literature, critical gaps persist, which this paper aims to address. First, while numerous studies compare the behavior of one SPSW type to another, these comparisons are often not conducted on an equitable basis of constant material weight. A fair comparison of structural efficiency must account for the amount of material used. A stiffened or corrugated wall may outperform a plain wall of the same thickness, but it also uses more steel. This study provides a fundamentally different perspective on SPSW infill performance by decoupling geometric efficiency from material quantity. By enforcing identical steel weight and boundary conditions across all models, the work exposes the true mechanical role of infill geometry in governing stress redistribution, buckling mode formation, and cyclic energy dissipation. The results demonstrate unequivocally that superior seismic performance can be achieved through geometric optimization of the infill plate rather than increased steel content, directly challenging a prevailing implicit assumption in the existing literature. These findings establish clear, design-relevant criteria for developing materially efficient and high-performance SPSW systems.

To bridge these gaps, the study objective is to perform a rigorous, normalized comparative study of the seismic behavior of SPSWs with different infill types, namely, USPSW, SSPSW, and CSPSW (in both horizontal and vertical orientations), where all systems are designed to have precisely the same weight per unit area. This ensures that observed performance differences are attributable to the efficiency of the structural form, not simply to the quantity of material. To achieve these objectives, this paper employs advanced nonlinear finite element analysis. Detailed models of SPSWs are developed using the ABAQUS software v 6.14, incorporating both material and geometric nonlinearities to accurately capture cyclic inelastic behavior, buckling, and post-buckling response. The modeling approach is first rigorously validated against independent experimental and numerical results from the literature to ensure its predictive reliability. A comprehensive parametric study is then conducted, examining the effects of infill type and boundary frame stiffness (comparing “strong” frames designed per capacity principles to “weaker” frames). The systems are subjected to a quasi-static cyclic loading protocol. The response is evaluated through a detailed analysis of hysteretic curves, backbone envelopes, energy dissipation capacity, stiffness degradation, and failure modes. By integrating these analyses, this work provides new insights into the material-efficient design of SPSWs and a critical assessment of their vulnerability to connection failure, contributing to both the optimization of new designs and the reliable assessment of existing structures.

2. Finite Element Modeling

The investigation of nonlinear behaviors in unstiffened (USPSW), stiffened (SSPSW), and corrugated (CSPSW) steel plate shear walls necessitates the implementation of accurate finite element analysis. To this end, both the boundary frame and the infill panel were discretized using four-node, quadrilateral shell elements with reduced integration, designated as S4R in the ABAQUS element library. This element selection was made specifically to mitigate the shear locking phenomenon [30,31]. Shear locking is an undesired numerical artifact where an element exhibits artificially high shear stiffness under bending deformation, leading to an overly stiff structural response and underestimated deflections. This issue predominantly affects fully integrated, first-order (linear) solid elements subjected to bending. It is effectively circumvented by employing elements with higher-order shape functions, such as quadratic elements, or by using reduced-integration schemes. Consequently, the S4R shell element, which combines a general shell formulation with a reduced integration hourglass control, was adopted for all components to ensure an accurate representation of both bending and membrane actions without spurious stiffness [31]. In the ABAQUS numerical model, the infill plate is merged with the boundary frame to simulate a fully welded connection. This modeling approach ensures full compatibility of displacements and forces at the plate–frame interface and accurately represents the behavior of a continuous welded joint. The following sections detail the critical aspects of the structural modeling process: the mechanical properties of the materials, the applied boundary conditions, the prescribed cyclic loading history, and the incorporation of initial geometric imperfections.

2.1. Mechanical Properties of Steel Materials

For the parametric analyses, distinct material properties were assigned to the boundary frame and the infill panel to reflect common design practices. The steel for the boundary frame was assigned a yield strength (Fy) of 345 MPa, while the infill panel material was assigned a yield strength of 235 MPa. Both materials shared common elastic properties: an elastic modulus (E) of 206,000 MPa and a Poisson’s ratio (ν) of 0.3. To model the post-yield material behavior, a linear isotropic hardening rule was implemented with a tangent hardening modulus (Eh) defined as E/100. As previously noted, all structural members were modeled using the four-node, reduced-integration S4R shell element. The analysis explicitly accounted for both material and geometric nonlinearities. Material nonlinearity is essential because the system response becomes nonlinear and irreversible once the material stress exceeds the yield point. Furthermore, the constitutive response under cyclic loading differs significantly from that under monotonic loading due to phenomena such as the Bauschinger effect, necessitating a nonlinear material model [32]. Geometric nonlinearity is equally critical due to substantial changes in the system’s geometry during loading. These changes include large out-of-plane deformations, the formation and reversal of diagonal tension fields, potential snap-through behavior in corrugated panels, and instances of zero or negative tangent stiffness. To capture this complex inelastic cyclic response within the parametric study’s scope, an isotropic hardening model was employed [31].

2.2. Modal Analysis and Initial Defect

The infill materials and configurations examined in this study were selected to represent practical SPSW solutions that can be fabricated using conventional steel plates and standard welding procedures. To isolate the intrinsic effect of infill geometry from material quantity, all models were designed with identical steel weight. The numerical models correspond to a representative story-level SPSW with boundary frame proportions consistent with typical mid-rise steel buildings, and fully welded infill-to-frame connections were assumed in accordance with common seismic design practice. Initial geometric imperfections were explicitly incorporated into the models based on the first buckling mode shapes obtained from linear eigenvalue analysis, allowing the effects of fabrication tolerances and initial out-of-plane deviations on buckling behavior and cyclic response to be realistically captured.

Initial geometric imperfections, out-of-plane deviations from the ideal geometry resulting from fabrication, storage, or erection, must be accounted for in cyclic analysis due to their influence on buckling behavior and ultimate strength. For consistency with prior studies on thin USPSWs, the initial imperfection magnitude was defined as 1/1000 of the plate length [33]. Recognizing the greater out-of-plane stiffness of CSPSWs, this study adopted a larger imperfection magnitude of 1/750 of the panel height [34]. The imperfection pattern was applied using the ABAQUS “Imperfection” command. This method first performs an eigenvalue buckling analysis to determine the fundamental buckling mode shape, which is then scaled by the specified amplitude factor to create a realistic initial imperfection in the infill plate geometry.

2.3. Boundary Conditions and History Loading

Nonlinear cyclic analyses were performed on the defined groups of thin USPSW, CSPSW, and SSPSW models. Lateral displacement was applied as a prescribed history at a control point on the exterior column flange within the top-right panel zone. The displacement-controlled cyclic loading protocol follows the general form of commonly used seismic qualification procedures, with increasing drift levels and repeated cycles to capture degradation and energy dissipation. The displacement protocol was applied incrementally to achieve target story drift ratios of 0.25%, 0.5%, 1%, 1.5%, 2%, 2.5%, 3%, and 4%, with each drift amplitude cycled twice, as illustrated in Figure 3. A fixed boundary condition was imposed at the base of the columns, restraining all nodes in this region against translation and rotation in all six degrees of freedom. To simulate the stabilizing effect of the floor diaphragm, out-of-plane displacements were constrained for all nodes along the beam centerlines and at all beam-column connection nodes, thereby preventing global out-of-plane buckling of the frame.

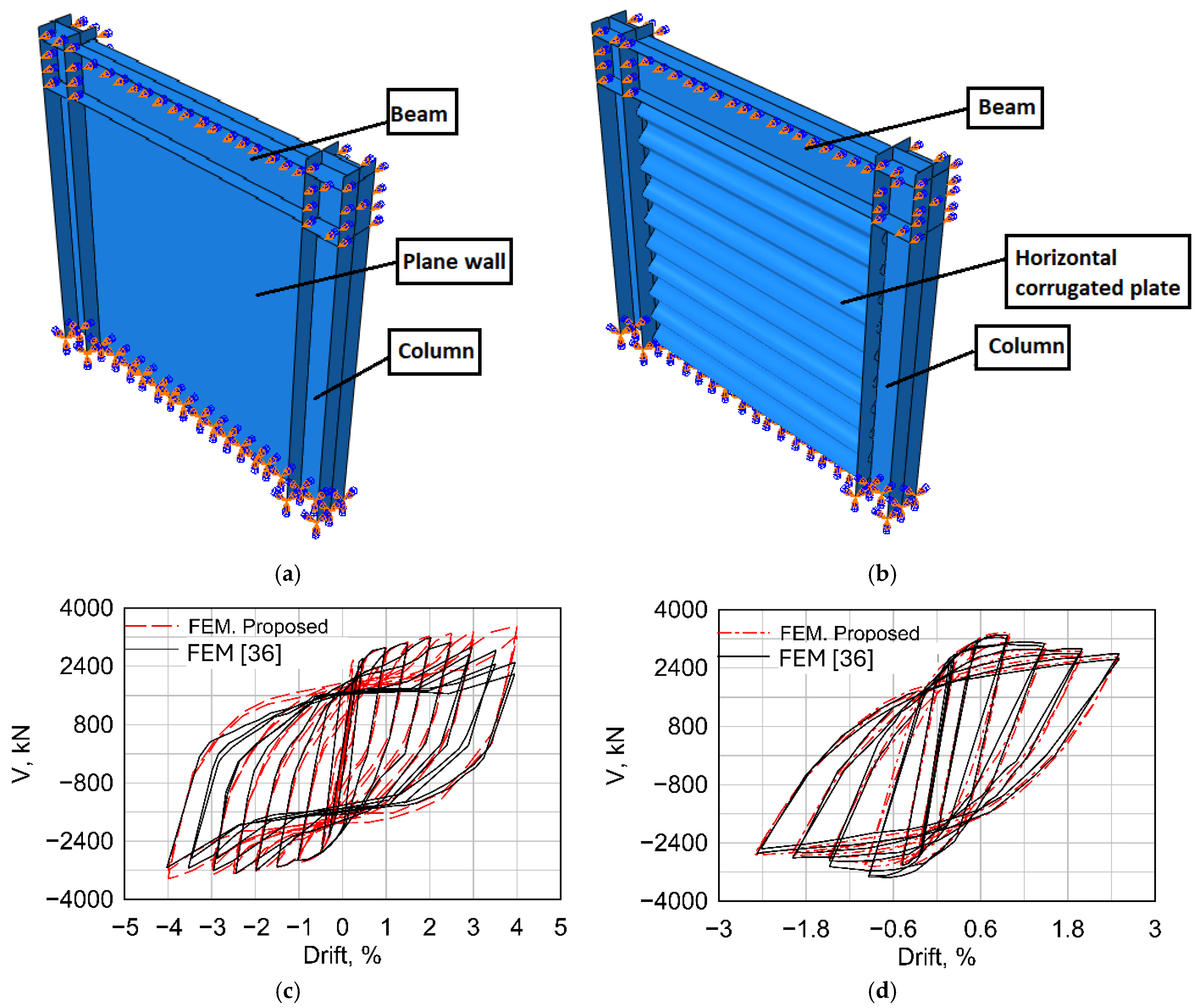
3. Model Validation

To verify the accuracy of the numerical simulation, previously published quasi-static test results were used [35,36]. Finite element models were created, and the hysteretic curves were compared to the experimental results.

3.1. Experimental Validation

For validation, this study utilized experimental results from a quasi-static cyclic test on a three-story, single-bay USPSW specimen designated SC4T [35]. The infill plates had dimensions of 1000 mm in height, 1500 mm in width, and a thickness of 5 mm. The internal beams were H200 × 200 × 16 × 16 sections, while the top beam and columns were H400 × 200 × 16 × 16 and H250 × 250 × 20 × 20 sections, respectively. The detailed specimen geometry is presented in Figure 4a.

The material for both the infill panels and boundary elements was steel grade SM490, with a yield stress (Fy) of 330 MPa. To accurately simulate cyclic inelastic behavior, Chaboche adopted a combined nonlinear isotropic/kinematic hardening constitutive model [37,38]. The material constitutive model and the validation of local and global buckling behavior of the infill plate are defined following [33]. This model is essential for predicting cyclic deformation, as it captures both the expansion of the yield surface (isotropic hardening) and its translation in stress space (nonlinear kinematic hardening). The model formulation, originally summarized by Chaboche et al. [37,38], requires the calibration of two isotropic hardening parameters (Q∞ and b) and eight kinematic hardening parameters (C1, γ1, C2, γ2, C3, γ3, C4, γ4), representing four back-stress components. The isotropic parameters Q∞ (the maximum change in yield surface size) and b (its saturation rate) are determined from stabilized cyclic stress–strain data, where Q∞ is derived from the difference between cyclic and monotonic curves, and b is fitted to the peak stress evolution per cycle. The kinematic parameters, defining the hardening modulus (C) and its decay rate with plastic strain (γ), are calibrated from hysteresis loops obtained via strain-controlled uniaxial cyclic tests [39]. The specific calibrated parameters used are listed in

Table 1. Hardening parameters of materials (ABAQUS).

Parameter	Value, N/mm2	Parameter	Value
Q∞	21	b	1.2
C1	7993	γ1	175
C2	6773	γ2	116
C3	2854	γ3	34
C4	1450	γ4	29

Where C is the kinematic hardening modulus, γ is the rate at which hardening modulus decreases with the plastic strain, Q∞ is the maximum change in the size of the yield surface, and b is the rate at which the initial yield stress changes with the plastic strain.

. The boundary frame and infill panel were modeled with S4R shell elements. The model’s base was fixed, and an initial geometric imperfection of 1/1000 of the plate height was introduced. The cyclic loading protocol, applied via a reference point at the mid-span of the top beam until ultimate failure, is depicted in Figure 3.

3.1.1. Load-Carrying Capacity

The deformed shape of the present finite element model for the sample SC4T is found in Figure 4b. In addition, the load-displacement curves for the experiment test can be seen in Figure 4c [35]. The previous finite element modeling shows differences in the maximum lateral capacities of about 7% and 9% in the positive and negative direction and some differences in hysteretic behavior. However, the present numerical simulation shows hysteretic behavior similar to the experimental results, with a difference in the load-carrying capacity of 4%. The reason for the bigger difference between previous simulations and experimental results was the absence of a cyclic hardening parameter in the definition of the material. It can be concluded that the current numerical simulation technique can be used to predict the nonlinear behavior of SPSWs.

3.1.2. Failure Mode

Figure 4d shows good agreement between the FEM deformed shape with Von Mises stress distribution and those observed in the experimental tests. Local buckling and tension-field action of the steel plates developed in all stories, resulting in plastic deformation distributed along the height of the specimens. After yielding of all steel plates, plastic hinges formed at the beam ends and at the column base due to the moment–frame action. The fracture of the welded connections occurred at the column base or at the beam–column connections. Although local fractures developed in the steel plates, the internal forces were redistributed to the adjacent plates; therefore, these local fractures had no significant effect on the overall strength or deformation capacity of the system.

3.2. Numerical Validation

Another validation for this modeling technique was performed by using a previously published numerical study [36]. In that study, eight USPSW models with a single bay and one floor were studied [36]. The models SC-PW and SC-HSW were selected for the validation of the current FEM. The FEMs’ geometry and configurations are shown in Figure 5a,b. The wall dimensions were 3000 × 3000 × 5 mm, the length of the corrugation wave was 300 mm, and the amplitude was 60 mm. The boundary column’s section was HW400 × 400 × 13 × 21 mm, and the top beam’s section was HM500 × 300 × 11 × 15 mm. The material of the infill panel had a yield strength of 235 MPa, while the boundary frame material had a yield strength of 345 MPa, with an elastic modulus E = 2.06 GPa, a Poisson’s ratio ν = 0.3, and hardening modulus Eh = 1/100E. A similar technique was adopted in previous works [33,40]. For SC-PW, the present FEM had an initial stiffness greater than the previous FEA by about 3% and a higher load-carrying capacity by about 4.4%, as shown in Figure 5c. For SC-HSW, the present simulation had less initial stiffness than the previous simulation by about 0.7% and less load-carrying capacity by about 3.7%, as shown in Figure 5d. The current finite element modeling results have good agreement with the previously published works.

4. Problem Description

Two distinct groups of thin steel plate shear wall systems, unstiffened (USPSW), stiffened (SSPSW), and corrugated (CSPSW), were modeled using the ABAQUS finite element software v 6.14. The first group represents systems with a strong boundary frame, denoted by the prefix ‘S’, while the second group represents systems with a weak boundary frame, denoted by the prefix ‘W’. This parametric study investigates the influence of three primary variables: panel type, corrugation direction, and the stiffness of the boundary elements. The panel type variable includes plane (P), stiffened with horizontal stiffeners (HS), and sinusoidal corrugated panels. For corrugated panels, the direction of sinusoidal corrugation is considered either horizontal (H) or vertical (V). It is noted that for stiffened panels, this study is limited to the configuration with horizontal stiffeners.

For the strong boundary frame case, the beam and column sections were designed following capacity design principles outlined in AISC Design Guide 20 [41,42]. The beam section used was HM500 × 300 × 11 × 15 (analogous to W21 × 68), and the column section was HW400 × 400 × 13 × 21 (analogous to W14 × 132). The models in this category are designated as follows:

• SPt5 and SPt6.75 represent strong-frame plane walls with plate thicknesses of 5 mm and 6.75 mm, respectively.
• SHt5 and SVt5 represent strong-frame walls with horizontal and vertical sinusoidal corrugations, respectively.
• SPt5-HS represents the strong-frame stiffened wall with horizontal stiffeners.
  The models SPt6.75, SHt5, SVt5, and SPt5-HS were designed to possess the same weight per unit area, enabling a direct comparison of structural efficiency.

In the weak boundary frame case, the flexural stiffness of the boundary elements was intentionally reduced by approximately 40% compared to the strong case. The corresponding beam section was HM400 × 300 × 10 × 16 (equivalent to W16 × 67), and the column section was HW350 × 350 × 12 × 19 (equivalent to W14 × 90). All wall panels in this group maintained a height of 3000 mm, a span of 3000 mm, and a base thickness of 5 mm. The weak-case models are designated as follows:

• WPt5 represents the weak-frame plane wall.
• WHt5 and WVt5 represent weak-frame walls with horizontal and vertical corrugations, respectively.
• WPt5-HS represents the weak-frame stiffened wall with horizontal stiffeners.

All models in the set {WHt5, WVt5, WPt5-HS} were also designed to have an identical weight per unit area. The cross-section of the horizontal stiffeners used in models SPt5-HS and WPt5-HS is shown in Figure 1c, with a stiffener height of 120 mm, a flange width of 60 mm, and a thickness of 5 mm. The geometry of the strong and weak-case models is presented in Figure 6.

All wall models share common global dimensions: a width of 3000 mm, a height of 3000 mm, and thus an aspect ratio of 1.0. For corrugated panels, the sinusoidal profile has a wavelength of 300 mm and an amplitude of 60 mm, as depicted in Figure 1b. The HCSPSW and VCSPSW models use identical corrugation geometry, differing only in orientation. The weight equivalency between the stiffened wall and the corrugated wall was achieved by sizing the stiffeners to account for the additional material in the corrugated panel’s fold length, the developed length of the sheet before profiling. The complete matrix of the parametric case study is summarized in

Table 2. Parametric case study.

Group #	Notation	Wall Type	Thickness (mm)	Parameter
S *	SPt6.75	Plane	6.75	Infill type
	SPt5	Plane	5
	SHt5	H-Corrugated
	SVt5	V-Corrugated
	SPt5-HS	Plane
W **	WHt5	H-Corrugated		Boundary Stiffness
	WVt5	V-Corrugated
	WPt5	Plane
	WPt5-HS	Plane

* Strong boundary frame with HW400 × 400 × 13 × 21 for columns and HM 500 × 300 × 11 × 15 for beams. ** Weak boundary frame HW 350 × 350 × 12 × 19 for columns and HM 400 × 300 × 10 × 16 for beams.

, and Figure 7 shows the geometries of the FE models.

5. Results and Discussion

5.1. Effect of Panel Type and Direction of Corrugation

The seismic influence of panel type and corrugation direction is assessed by comparing the results of models SPt5, SHt5, SVt5, SPt5-HS, and SPt6.75. For an equitable comparison of structural efficiency, the models SHt5, SVt5, SPt5-HS, and SPt6.75 were designed to possess identical weight. Nonlinear cyclic analyses were performed on all five models, and their hysteretic responses were recorded.

The load-drift hysteretic curves for the strong-frame walls (SPt5, SHt5, SVt5, SPt5-HS, SPt6.75) are presented in Figure 8, with drift ratio (%) on the x-axis and lateral load capacity (kN) on the y-axis. These curves demonstrate a clear and significant influence of panel configuration on cyclic behavior. Figure 8a reveals that the horizontally corrugated wall (SHt5) sustains a higher load capacity than the plain wall (SPt5) during the initial loading phases, up to approximately ±1.5% drift. However, upon reaching its peak strength, SHt5 experiences plastic buckling, leading to a more rapid degradation of its load-carrying capacity compared to SPt5. The plain wall maintains its strength through stable post-buckling tension field action. Figure 8a also illustrates the characteristic reduction in reloading stiffness, a consequence of cumulative plastic deformation from cyclic loading reversals.

As shown in Figure 8b, both the stiffened wall (SPt5-HS) and the plain wall (SPt5) rely on tension field action for their post-buckling strength. However, the addition of stiffeners results in significantly plumper hysteresis loops and enhanced system stiffness for SPt5-HS. Figure 8c highlights the impact of corrugation orientation. For identical geometries and boundary conditions, the horizontally corrugated panel (SHt5) exhibits greater initial load capacity than the vertically corrugated panel (SVt5), attributable to the “accordion effect” where horizontal ribs directly resist shear deformation. After SHt5 yields and undergoes plastic buckling, its capacity converges with that of SVt5. Collectively, Figure 8a,d,e indicate that corrugated walls exhibit fundamentally different strength development mechanisms compared to plain or stiffened walls of equivalent weight. The direct comparison in Figure 8d between the equal-weight SHt5 and SPt5-HS models shows the superior seismic performance of the stiffened system. SHt5′s capacity degrades rapidly after peaking at around ±1% drift due to plastic buckling, whereas SPt5-HS continues to gain strength via the tension field. Similarly, Figure 8e compares SHt5 with a thicker plain wall of the same mass (SPt6.75). While SHt5′s strength decays post-peak, SPt6.75 demonstrates a stable, increasing load capacity up to the maximum applied drift of ±4%.

To quantify these observations, backbone curves were derived from the hysteretic loops by extracting the peak load from the first cycle at each drift amplitude in both push and pull directions, as illustrated in Figure 9 [36]. These envelopes allow for the evaluation of key parameters: initial stiffness (K1 at 0.25% drift), secondary stiffness (K2 at 0.5% drift), yield point (determined via the equivalent energy method), and maximum load capacity (Vm). The yield point (Δy, Vy) marks the onset of significant local buckling and plasticity, while the maximum point (Δm, Vm) defines the peak strength.

Quantitative data from Figure 9 and

Table 3. Cyclic results of SPSWS, stiffened SPSW and COSPSW.

Model	Direction	K1 (kN/mm)	K2 (kN/mm)	Δy (mm)	Vy (kN)	Δm (mm)	Vm (kN)
SPt5	push −	300.8	152.13	16.3	2479.5	130	3267.17
	pull +	299.9	158.1	16.3	2855.2	130	3203.4
SPt6.75	push −	369.7	186.88	16.3	2433	130	3511.95
	pull +	369.25	196.16	16.3	3521.3	130	3507.93
SHt5	push −	275.49	174.4	16.3	2823.95	32.5	2984.27
	pull +	275.492	175.57	16.3	2823	32.5	3225.2
SVt5	push −	271.83	175.85	8.1	2208.7	32.5	3042.45
	pull +	271.93	173.8	16.3	2812.1	32.5	3093.0
SPt5-HS	push −	303.17	166.18	8.1	2472.1	130	4016.8
	pull +	302	162.6	8.1	2463.2	130	3989.5

Where K_i is the initial stiffness, K₂ is the second cyclic stiffness, Δ_y represents yield displacement, V_y represents yield force, Δ_m represents displacement at maximum lateral capacity, and V_m represents maximum lateral strength capacity.

show that, at 0.5% drift in the push direction, the K2 stiffness of SHt5, SVt5, SPt5-HS, and SPt6.75 exceeds that of the baseline SPt5 by 14.6%, 15.6%, 9%, and 22.8%, respectively.

At the maximum drift of 4%, the plain wall SPt5 attains a load capacity similar to the peak values of SHt5 and SVt5, which those walls reached at only ±1% drift. More significantly, at 4% drift, SPt5-HS and SPt6.75 surpass SPt5′s capacity by approximately 23% and 7.5%, respectively. SPt5-HS shows the greatest strength enhancement. Therefore, for identical material weight, a horizontally stiffened wall demonstrates superior seismic behavior compared to a horizontally corrugated wall.

5.2. Effect of Boundary Frame Stiffness

This section investigates the influence of boundary element stiffness on the seismic behavior of USPSWs, SSPSWs, and CSPSWs. The hysteretic responses of the corrugated, unstiffened, and stiffened walls with weak boundary frames are compared to their strong-frame counterparts in Figure 10a–d. As designed, systems with weak boundary elements exhibit approximately 40% lower initial frame stiffness. Consequently, these models demonstrate the same fundamental cyclic behavioral patterns but with consistently reduced lateral strength and initial stiffness. The analysis reveals that USPSWs and SSPSWs display greater sensitivity to weakened boundary conditions. Furthermore, the detrimental effect on lateral strength is more pronounced for horizontally corrugated systems (SHt5 vs. WHt5) than for vertically corrugated ones (SVt5 vs. WVt5).

Backbone curves were derived from the hysteretic loops in both loading directions, as presented in Figure 11 Key performance metrics, including initial stiffness (K1), secondary stiffness (K2), yield point, and maximum load, were extracted from these envelopes and are summarized in

Table 4. Cyclic results of SPSWS, COSPSW and stiffened SPSW with different Frames.

Model	Direction	Ki (kN/mm)	K2 (kN/mm)	Δy (mm)	Vy (kN)	Δm (mm)	Vm (kN)
SPt5	push −	300.8	152.1	16.3	2479.5	130	3267.1
	pull +	299.9	158.08	16.3	2855.2	130	3203.3
WPt5	push −	287.05	127.5	8.1	2326.8	130	2673.05
	pull +	286.30	126.3	8.1	2332.2	130	2686.04
SHt5	push −	275.49	174.4	16.3	2823.95	32.5	2984.27
	pull +	275.49	175.57	16.3	2823	32.5	3225.2
WHt5	push −	258.34	161.697	8.1	2099	16.25	2627.59
	pull +	258.36	163	16.3	2626.4	32.5	2788.6
SVt5	push −	271.83	175.85	8.1	2208.7	32.5	3042.45
	pull +	271.93	173.8	16.3	2812.1	32.5	3093.04
WVt5	push −	256.09	163.8	16.3	2648.8	32.5	2697.0
	pull +	256.19	162.5	16.3	2625.6	32.5	2735.0
SPt5-HS	push −	303.1	166.18	8.1	2472.1	130	4016.79
	pull +	302	162.6	8.1	2463.2	130	3989.5
WPt5-HS	push −	289.29	152.7	16.3	2480	130	3383.4
	pull +	288.2	157.0	16.3	2701	130	3429.17

Where K_i is the initial stiffness, K₂ is the second cyclic stiffness, Δ_y represents yield displacement, V_y represents yield force, Δ_m represents displacement at maximum lateral capacity, and V_m represents maximum lateral strength capacity.

, following the methodology established previously. Quantitatively, Figure 11 and Table 4 show that the 40% reduction in boundary frame stiffness resulted in a degradation of the K2 stiffness (at 0.5% drift) by approximately 16% for the weak plane wall (WPt5), and by about 7% and 8% for the weak corrugated walls (WHt5, WVt5) and stiffened wall (WPt5-HS), respectively. This indicates that USPSWs experienced the greatest stiffness reduction, while CSPSWs were the least affected. At the maximum examined drift of 4%, the reduction in boundary stiffness caused a decline in ultimate load-carrying capacity of about 18% for WPt5, 12% for WHt5, 11% for WVt5, and 16% for WPt5-HS. These results demonstrate that the reduction in boundary member stiffness has a more substantial impact on the system’s ultimate load capacity than on its initial stiffness. In summary, plane and stiffened steel plate walls are more susceptible to the effects of a weaker boundary frame. The relative insensitivity of the VCSPSW can be attributed to its vertical corrugations, which act as integral vertical ribs that engage more directly with and help resist frame action.

5.3. Properties Degradation and Energy Dissipation Capacity

Lateral strength degradation is a critical metric that reflects cumulative damage mechanisms such as plastic buckling, significant out-of-plane deformations, and local failures in the infill panel and boundary columns under repeated cyclic displacement. In this study, the strength degradation is quantified using the coefficient (η), defined as the ratio of the load-carrying capacity in the second cycle to that in the first cycle at an identical drift ratio. Figure 12a presents the strength degradation coefficient (η) for the strong-frame models. For most systems, η remains between 0.85 and 1.0. The notable exception occurs for the plain walls (SPt5 and SPt6.75) at the second cycle, where η drops to approximately 0.8. This pronounced degradation is attributed to the initial yielding and buckling of the plain infill panel, which immediately reduces its resistance. The CSPSW systems (SHt5, SVt5) exhibit higher η values than the USPSWs. This occurs because the efficient, diagonal tension field that forms and reverses in a plain panel causes significant cyclic strength loss. Although a tension field develops in corrugated panels, its effectiveness is diminished by the pre-existing geometric profile of the sheet, leading to less severe cyclic degradation. Cyclic stiffness degradation, another key performance indicator, is represented by the stiffness parameter Ki. This value is calculated according to the method by [43] using Equation (4):

$$Ki={\sum }_{i=1}^n{P}_j^i/{\sum }_{i=1}^n{∆}_j^i$$

(4)

where $P_j^i$ is the peak load-carrying capacity in each cycle and ${∆}_j^i$ is the peak displacement for each cycle drift. The stiffness degradation for all systems is plotted in Figure 12b, showing a steady decline with increasing drift. The thicker plain wall (SPt6.75) possesses the highest initial stiffness, but it degrades below the SSPSW level after approximately ±1% drift. The baseline thin plain wall (SPt5) consistently exhibits the lowest cyclic stiffness.

Energy dissipation capacity, measured by the cumulative area enclosed within the hysteretic loops, directly reflects the seismic performance of a lateral system. Figure 13a shows the accumulated energy dissipation over 12 cycles for the strong-frame models. Compared to the baseline SPt5, the energy dissipation of SPt6.75, SHt5, SVt5, and SPt5-HS is higher by 14%, 29%, 32%, and 50%, respectively. The VCSPSW (SVt5) dissipates slightly more energy than the HCSPSW (SHt5). SPt5-HS demonstrates the greatest enhancement, while SPt6.75 shows the least. Figure 13b presents the energy dissipation for the weak-frame models. The trend persists, with SSPSWs and CSPSWs outperforming USPSWs. Reducing the boundary frame stiffness by 40% decreases the energy dissipation capacity of WPt5, WHt5, WVt5, and WPt5-HS by 18%, 15%, 12%, and 12%, respectively. This confirms that the energy dissipation of USPSWs is more sensitive to boundary frame stiffness than that of CSPSWs. Furthermore, VCSPSWs are less sensitive to frame stiffness reduction than HCSPSWs.

5.4. Comparison Between Systems Mechanisms

In general, corrugated steel plate shear walls (SHt5 and SVt5) exhibit lateral load-resisting mechanisms fundamentally different from those of plain SPSWs (SPt5 and SPt5-HS), with direct implications for seismic design. Plain SPSWs develop a stable diagonal post-buckling tension field, producing fuller hysteresis loops with limited pinching, gradual stiffness degradation, and sustained energy dissipation at large drift demands—attributes favorable for ductility-based seismic design. In contrast, deeply corrugated infill plates mobilize shear resistance at small drifts, followed by inelastic shear buckling and progressive corrugation straightening, which result in pronounced pinching, accelerated stiffness loss, and reduced energy dissipation at higher drift levels. Accordingly, while corrugated SPSWs can effectively enhance initial stiffness and strength, their post-peak degradation must be explicitly accounted for when targeting higher performance levels in performance-based seismic design.

5.5. Comparison Between Systems Failure Modes

Figure 14 shows the different failure modes for the systems. The development and evolution of elastic and plastic stresses throughout the cyclic loading process, as well as their maximum magnitudes and associated locations, are shown in Figure 15. The gray color denotes areas of plastic deformation in the plate and the frame. The corrugated plate exhibited initial yielding at 8.5 s. No distinct tension-field strips were observed at 8.75, 10.38 s. Local plate failure occurred at 17 s, corresponding to a drift ratio of 1%, at which point the load-carrying capacity began to degrade. It can be seen that the different details can change the deformed shape and failure mode of the models. Due to the cyclic loading process, two-way tension strips appear, and obvious out-of-plane deformation occurs. For plane SPSW, i.e., SPt5, WPt5, and SPt6.75, clear two-way tension strips occur, and local buckling occurs at the top and bottom of boundary columns. For CSPSW with a horizontally corrugated sheet, i.e., SHt5 and WHt5, no clear tension field strips form, and local buckling occurs at the bottom of the columns. The maximum deformations occur at the vertical centerline. The maximum out-of-plane shear buckling for SVt5 and WVt5 occurs at the horizontal centerline. Using a vertical corrugated steel plate lessens the impact of shear deformation on the boundary columns. For SPt5-HS and WPt5-HS, local failure occurs at the bottom and top of the columns. The out-of-plane deformation was effectively restrained by stiffeners.

6. Conclusions

This paper presented a comprehensive numerical investigation into the cyclic behavior of steel plate shear walls through nonlinear finite element analysis. The study examined the effects of infill panel type, corrugation direction, and boundary frame stiffness on key performance metrics: initial stiffness, load-carrying capacity, and energy dissipation. The principal findings are summarized as follows:

• Accurate finite element models were developed and validated against published experimental and numerical benchmarks, achieving a predictive error within 4%. The analysis revealed that a HCSPSW exhibits 15% and 11% higher stiffness at 0.5% drift in the push and pull directions, respectively, and dissipates 29% more energy than an unstiffened wall (USPSW). The HCSPSW also showed approximately 4.3% greater load capacity than a vertically corrugated wall (VCSPSW) in the pull direction, while the VCSPSW itself demonstrated 32% higher energy dissipation than the USPSW.
• At 0.5% drift, a stiffened wall (SSPSW) with U120 stiffeners showed 9.2% greater stiffness than a USPSW. The SSPSW achieved 23% and 24.5% higher lateral strength than the USPSW and 34.6% and 23.7% higher strength than the HCSPSW in the push and pull directions, respectively. Its energy dissipation exceeded that of the USPSW by about 50%. The USPSW was found to be more sensitive to reductions in boundary frame stiffness than CSPSWs, and the VCSPSW was less sensitive to weaker frames than the HCSPSW.
• For equivalent infill weight per unit area, the SSPSW configuration demonstrated superior overall seismic performance, with a load-carrying capacity approximately 14% and 24% higher than the USPSW and CSPSW, respectively. Therefore, the SSPSW system is recommended over USPSW and CSPSW systems to enhance the seismic resilience of buildings.
• For practical engineering application, a performance-based selection guideline is proposed: USPSWs may be suitable for low drift demands (up to 0.5%), CSPSWs for medium drifts (0.5–1%), and SSPSWs for high cyclic drift levels where maximum strength and energy dissipation are critical.

7. Limitations and Future Work

This study is based on a limited number of SPSW configurations and is intended to identify behavioral trends rather than provide direct design recommendations. Future research should include systematic parametric and numerical studies to examine the influence of key variables, along with experimental validation under different scales and dynamic loading conditions to support performance-based seismic design. The main directions for future work are as follows:

• The effects of loading rate, strain-rate sensitivity, and seismic spectral characteristics are not addressed herein. Future studies incorporating dynamic loading conditions, such as shake-table testing or nonlinear time-history analyses under recorded ground motions, are recommended to extend the applicability of the findings to realistic seismic responses.
• Future studies will consider more advanced constitutive models, such as combined isotropic–kinematic hardening formulations, to improve the accuracy of cyclic response simulation.
• A comprehensive parametric study considering different wavelengths and amplitudes of sinusoidal corrugation will be conducted. Since the performance of corrugated plates is highly sensitive to these geometric parameters.