A Synchronous Data Approach to Analyze Cloud-Induced Effects on Photovoltaic Plants Using Ramp Detection Algorithms

Featured Application

Distributed Power Systems Monitoring.

Abstract

The proliferation of photovoltaic energy in the electricity grid presents a significant challenge in terms of management, control, and optimization, especially due to its dependence on weather behavior and cloud passing. Even if there are a great number of articles centered on study cloud passing effects, such as voltage flickers, voltage fluctuations, or ramping events, the approaches are quite heterogeneous and lack a broader perspective. A key factor might be the limiting data sets, as wide power generation data sets often omit meteorological data and vice versa. This study uses an advanced monitoring system based on phasor measurement units (PMUs), developed by the authors. The monitoring system is installed at a photovoltaic plant and generates high-quality synchronous irradiance and power data, enabling the joint analysis of irradiance transients, solar power ramp rates, and voltage fluctuations. Therefore, the results of this article present a detailed analysis of the production parameters of photovoltaic plants, focusing on the effects of passing clouds on the photovoltaic plant’s power, current, and voltage. To that end, compression algorithms such as the Swinging Door Algorithm (SDA), commonly used to detect ramp events, were employed. It was found that SDA produces a similar ramp rate output with power and irradiance data, suggesting that both data sets may be complementary. In addition, voltage fluctuations attributable to passing clouds were analyzed.

1. Introduction

Renewable energies, especially photovoltaic (PV) energy, have gained substantial significance in recent decades. The installed capacity of PV plants has increased steadily, now standing at nearly ten times the capacity recorded a decade ago, from just 38,396 MW in 2014 to 452,116 MW in 2024 [1]. Spain, where this study was conducted, ranked seventh worldwide in terms of installed PV energy capacity [2].

Nevertheless, PV energy poses some challenges that must be overcome. Recently, there has been concern that, in electrical systems with significant solar energy integration, the variability of energy generation associated with weather conditions could compromise grid stability [3,4]. Among the effects studied in the literature are voltage flickers [5,6], ramping events [7,8,9] and power fluctuation or voltage fluctuation [6,10]. These phenomena are difficult to predict, as they are often caused by passing clouds.

Furthermore, although these cloud passage effects have a common origin, the approaches to studying them are quite heterogeneous and lack a global vision [11]. There are works focused on modeling and forecasting cloud movement [7,12,13,14] that fail to transfer these advances into power ramp event detection. This includes state-of-art modeling techniques such as those based on sky-imager ramp forecasting [7,13,14].

On the other hand, there are other studies that analyze the impact of such events on power generation and their detection, particularly when they are critical to grid stability [15,16], but which ignore their meteorological origin. These studies focusing on potential applications, such as operational forecasting or grid stability assessment would also benefit from incorporating meteorological data. Some articles that jointly address cloud movement and power ramps were found [7,17], but they are in the minority and base their results on models and simulations.

This discrepancy in the literature is likely due to the absence of data sets that simultaneously record solar irradiance and generation measurements using the same transmission rate. Without synchronous measurements, it becomes difficult to accurately capture the dynamic relationship between irradiance fluctuations and power output, particularly under rapidly changing atmospheric conditions [17,18]. Asynchronous sampling introduces temporal mismatches that mask short-term variability and system response dynamics. High-frequency, synchronized irradiance–power measurements are therefore essential to improve forecasting models and facilitate PV integration into the electrical grid. This study introduces a novel application of a monitoring system based on Phasor Measurement Units (PMUs) to record power and solar irradiance in PV plants with high temporal resolution and synchronized data. This monitoring system, developed by the authors and described in detail in a previous article [19], enables the unified analysis of all recorded parameters, and the precise study of their strong interrelation. Additionally, it addresses the issue of the high sampling rate required to detect ramp events [17,18].

Therefore, the main goal of this work is to expand the existing literature by jointly analyzing the effects of cloud movement on a PV plant using four key parameters. Specifically, this study addresses SPRR, SPRE and voltage fluctuations. To this end, a compression algorithm was employed. This algorithm generates sequences of ramps that, when applied to power data, are used to compute the Solar Power Ramp Rate (SPRR). By selecting only the most pronounced ramp segments, Solar Power Ramp Events (SPRE) can be identified. This method is widely applied in the analysis of ramp rates [7,12,13,15,20]. In the methodology (Section 3), ramp detection methods are introduced and compared in order to select one of them for the one of them for the presentation of the results. Finally, since voltage measurements are synchronized with irradiance, Section 4 studies the relationship between SPRE and voltage fluctuations.

To sum up, this article introduces a novel methodology for the joint analysis of PV energy production parameters. The approach combines meteorological data (solar irradiance) with electrical power data (real power, voltage, and current) with the aim of filling a gap in the literature and bringing together different aspects of the same phenomenon. With that purpose, a self-developed monitoring system based on PMU devices and a compression algorithm was employed to detect and identify ramp events. Such integration would substantially enhance applications like online monitoring, operational forecasting, and grid stability assessment.

The rest of the article continues as follow: Section 2 presents compression algorithms. Section 3 describes the specific characteristics of the monitoring system and used data. Section 4 presents the experimental results and, finally, the conclusions of this work are detailed in Section 5.

2. Ramps Detection Methods

The literature presents multiple ramp detection methods and different iterations of those methods that focus on both PV and wind energy. For example, the Gharaie et al. work [21] divides ramp detection methods into conventional and emerging techniques, although those emerging techniques are enhancements of the conventional methods. Therefore, in the present section, only conventional ramp methods are discussed, and later Section 2.2 discusses some improvements to those algorithms’ output. Concerning alternative methods used in wind energy that do not return upward or downward ramps, such as the wavelet transform [22,23], they were excluded from consideration in this study. They were considered incompatible with the implementation of the proposed methodology. Nonetheless, they may offer valuable insights for future or complementary research.

The methods discussed in this work were initially conceived as compression algorithms to reduce the volume occupied by time series in databases. They extract and cluster data trends, highlighting only those data points that mark the beginning and end of a trend. This behavior aligns with that required to identify the start and end of a ramp in different measurements: In particular, three compression algorithms are discussed.

• L1-sw Algorithm. This algorithm was first presented in [24] for wind power ramp detection. It is widely discussed in the literature but suffers from high computational cost and limited performance [15,24]
• Deadband Algorithm. It is implemented in EVSystem’s framework as the “GE Historian algorithm” [25] and in Weatherford’s CygNet software as the ‘CygNet Swinging Door’ [26]. In both implementations, the algorithm compresses time series data. It was first applied to solar ramp detection in [27].
• Swinging Door Algorithm (SDA). It is the most cited algorithm for ramp detection in PV [7,12,15,16], although it was first proposed in [28] as a compression algorithm. Notably, Siemens’ WinCC software uses it for data compression [29].

Both Deadband algorithm and SDA have very similar results [27] and similar computational performance, outperforming other methods [21]. Since there exists an available open-source implementation [30], this work focuses exclusively on the SDA.

The SDA method reduces data points by drawing straight lines between start/end points, saving only significant changes within a set tolerance threshold $ϵ$. It opens an error band around the last saved point and only saves a new point if it falls outside the band, then recalculates a new error band from the new point, capturing data efficiently without storing every single reading. This mechanism is illustrated in Figure 1 with an example. A time series formed by the points A, B, C, D, and E is evaluated. In step 1, point A is recorded as the starting reference. To evaluate B, the segments $B(A+ϵ)$ and $B(A-ϵ)$ are checked. If $\alpha +\beta >{180}^{\circ }$, then the point is stored. Otherwise, the point is discarded. In the Figure 1 example, B is discarded. Therefore, for the next step, the $\alpha$ and $\beta$ angles computed in step 1 are still considered, along with the new ${\alpha }^{\prime }$ and ${\beta }^{\prime }$ calculated in step 2 using the same method. From each pair ($\alpha$, ${\alpha }^{\prime }$, and $\beta$, ${\beta }^{\prime }$), the greater value is retained. In the example (step 2), ${\alpha }^{\prime }>\alpha$ whereas ${\beta }^{\prime }<\beta$, so ${\alpha }^{\prime }$ is chosen and $\beta$ is maintained. In step 2, C is discarded as well as $({\alpha }^{\prime }+\beta )<180$. Finally, repeating the process in step 3, the sum of the angles ${\alpha }^{″}$ and ${\beta }^{″}$ reaches ${180}^{\circ }$ hence, point D is stored.

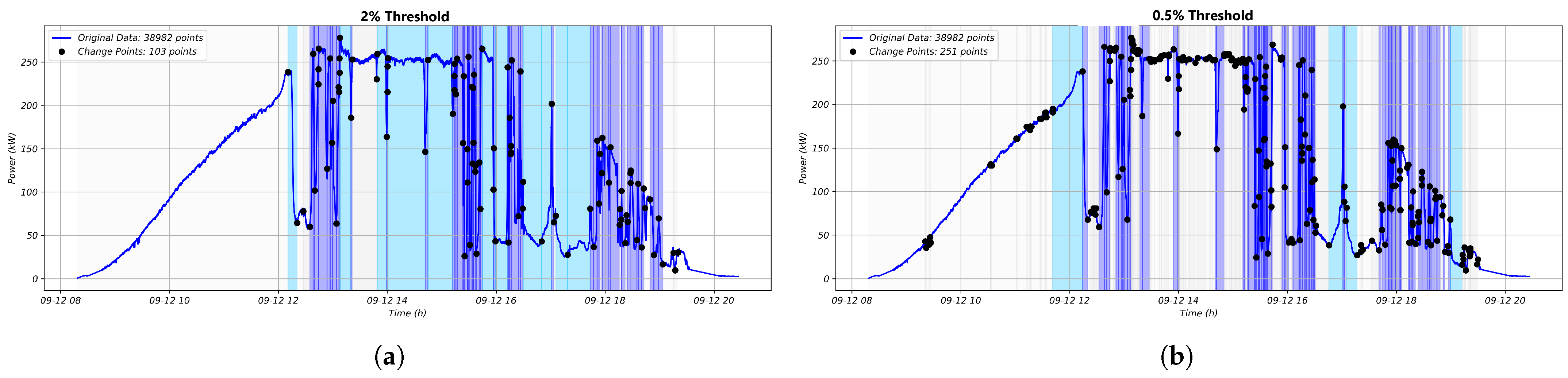
2.1. Threshold Selection

The algorithms presented in Section 2 rely on a user-defined threshold $ϵ$ that defines the accuracy of ramp detection. However, no universally accepted method exists for determining the optimal value of this parameter, as it strongly depends on factors specific to each PV plant, including its location, panel type, and solar panel inclination [16]. Moreover, it varies according to the specific application and the targeted goal.

In applications where the objective is to detect significant SPRE in accordance with regulations, the threshold must be adjusted accordingly. However, no universally accepted standard exists; instead, each country is progressively developing its own [31,32]. In Europe, for example, the European Network of Transmission System Operators for Electricity (ENTSO-E) leaves it up to each Transmission System Operator (TSO) to decide [33]. Some TSOs choose absolute values such as 2 MW/min in Hawaii [34], 30 MW/min in Ireland [34] or 100 kW/s in Denmark [35], while others are based on installed capacity, such as in China [36] and Puerto Rico [34] where the limit corresponds to 10%/min of the electricity generation. This approach aligns more closely with those reported in the literature, which often involve defining a threshold $ϵ$ relative to the percentage of production [15,16]. In [15] a small value of $ϵ$ is selected in order to subsequently optimize the algorithm by adding ramps and removing non-critical ones. Meanwhile, ref. [16] proposed using the natural variability index (NVI) described in [9,37] for automatic threshold calibration.

Conversely, when the objective is to detect any ramping event or to compute the SPRR or irradiance ramp rate, greater flexibility is allowed in defining the threshold. In [38], values of 1% and 10% of the PV plant output power are selected for the two proposed examples. In [7], a 10%/min of output power is selected, and an equivalent irradiance threshold is subsequently determined using a modeled PV plant.

The main goal of this work is to analyze the behavior of the parameters detected in the PV plant under conditions with and without passing clouds. Therefore, the selection of the threshold is left to discretion. In Section 4.3.1 several thresholds are tested using sample days, and the most suitable threshold is selected. Based on those results, in Section 4.3.3 SPREs are calculated according to the definitions given in Section 2.2.

2.2. Modified SDA

Several enhancements to SDA have been proposed in the literature, such as those introduced in [15,16]. In both cases, the objective is to detect SPRE exclusively caused by passing clouds. Therefore, the enhancements involve merging redundant segments and excluding those unrelated to cloud passage by analyzing ramps detected by the SDA.

On the one hand, regarding ramp merging, the SDA detects changes in slope; therefore, consecutive ramps with the same direction, either upward or downward, are concatenated to calculate the actual ramp rate. An example is shown in Figure 2. The segments with a green background are ascending segments, whereas those with a red background are descending segments. In the Figure 2a, a series of consecutive ascending ramps with varying slopes is detected, although they constitute segments of a single ramp. Figure 2b shows the ramps after aggregation, distinctly highlighting the targeted ramp events. This improvement, previously documented only for SDA, may be similarly applied to other compression algorithms, e.g., the Deadband algorithm.

On the other hand, the classification of events and the extraction of significant ramps are necessary for detecting SPRE; however, they are undesirable when analyzing SDA behavior or comparing parameters on days with and without passing clouds, as they may result in loss of information. Therefore, in this work, both the complete set of ramp-rate output and significant SPRE are shown. Since there is no unified or standard definition for significant SPREs in the literature, two SPRE definitions from [16] were used. These values were selected as 10% of the PV plant production, as they also correspond to the limits set in [34,36] standards, as seen in Section 2.2.

Definition 1.

Solar power variation is greater than 10% of the installed capacity of the PV plant.

Definition 2.

Solar power variation is greater than 10% of the installed capacity of the PV plant within a time span of one hour or less.

3. Data Set

A previously developed framework by the authors was employed, enabling high-quality, synchronized acquisition of production and meteorological measurements [19,39,40]. The monitoring framework relies on PMUs, which are commonly deployed in distribution networks and are increasingly used in other contexts due to their high reporting rates—up to 10 measurements per second—and precise time synchronization via GPS, achieving timing offsets below 30 ns for 95% of the time [41]. This characteristic renders PMUs highly suitable for monitoring distribution networks, distributed energy resources (DERs), or any entities requiring precise scrutiny, including PV systems. Their integration in PV plants exhibits an upward trajectory [42,43,44].

The distinctive novelty of this framework lies in its capability to simultaneously record synchronized measurement data from PMUs, PMU-like data from data acquisition (DAQ) devices, as well as meteorological data. Incorporating meteorological data into the same PMU dataframe ensures that recorded parameters remain perpetually synchronized and facilitates their joint analysis, as demonstrated in the results section (Section 4). Other viable approaches exist if they ensure perfectly synchronized parameters. For instance, employing solely PMU devices with analog inputs for pyranometers at each node is feasible but entails substantial costs.

The data used in this study was recorded at a PV plant of 4 MW located in Cordoba, southern Spain, belonging to the company Solar del Valle S.L. The panels are tilted at 30º, facing south. The PV plant contains four transformer centers (TC). A compactRIO-9054 (cRIO) that works as a PMU was installed in one of the TCs, while the remaining TCs were equipped with compactDAQ-9185 (cDAQ), which are National Instruments (NI) devices. They collectively acquire production data from the entire PV plant, along with irradiance data from a grid of pyranometers. As mentioned, the proposed framework is readily adaptable to incorporate diverse meteorological data relevant to PV plant analysis, and it currently includes irradiance as a first implementation. A total of 20 pyranometers were deployed in a grid covering half of the PV plant, aligned with the predominant direction of cloud movement. These measurements are introduced through analog input modules in the nearest cDAQ devices, namely those located in TC1 and TC2. Figure 3b shows the location of these devices in the PV plant.

Device synchronization is critical to ensure that measurements from multiple devices are time-aligned, enabling them to be analyzed coherently. The equipment is synchronized with each other using the Time Sensitive Networking (TSN) protocol, which provides nanosecond-level precision across all nodes [45]. The PMU will collect all measurements and assign timestamps based on its GPS-synchronized clock, ensuring precise temporal alignment with data from other locations within the PV plant.

The measurements collected are sent in accordance with the IEEE C37.118.2 standard for synchrophasors [46] up to a Phasor Data Concentrator (PDC). This application collects all data packets transmitted by the PMU, verifies the integrity of the packets, and transmits the validated data to a database. In this case, a Time Series Data Base (TSDB) management system was used, specifically designed for the storage of sequential temporal data. Given this management interface, users can efficiently access stored data, both production and irradiance data. Figure 3a shows the data flow indicating the software used, openPDC as PDC and InfluxDB as TSDB manager.

The merits of this framework, along with a detailed technical description, are presented in [19]. The system records the waveform and analyzes the parameters determined from it, as reflected in the following equations with an aggregation time of 1 s. The four parameters to be measured correspond to phase 2 of TC1. At that point, 13 inverters are aggregated, producing a total of approximately 1 MW, or 322 kW per phase. The results are expected to be representative of the entire plant, as the four TCs share a common coupling point and employ comparable panels and inverters. Specifically, parameters are measured at the point where the TC is connected to the electrical grid.

• Power. Correspond to the average of the instantaneous power (P). It is calculated based on the instantaneous values of current and voltage as shown in Equation (1)

  $$P={\displaystyle \frac{1}{N}}\sum _{k=1}^N{p}_k=v_k{i}_k$$

  (1)

  where $v_k$, $i_k$ and $p_k$ refers to the instantaneous voltage, current and power correspondingly, and N is the number of samples in one second.
• Current. It corresponds to the RMS values according to Equation (2)

  $$I_{RMS}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{k=1}^N{i}_k^2}$$

  (2)
• Voltage. As well as the current, it corresponds to an RMS value according to Equation (3)

  $$V_{RMS}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{k=1}^N{v}_k^2}$$

  (3)
• Irradiance. Irradiance correspond to the Global Horizontal Irradiance (GHI), read every 100 ms and aggregated every second.

For the present analysis, within the registered period, only 67 completely clear-sky days were found, as most days exhibited some type of cloud-passing event. To maintain balanced classes, an equal number of days with passing clouds were selected. Once again, days with a higher number of events were chosen, while days with a single cloud-passing event were excluded, as these could exhibit mixed behavior and yield inconclusive results. While a larger dataset spanning more days would be of interest, this data is considered sufficient to demonstrate the proposed methodology using field data. Moreover, analyzing a larger dataset would incur significant computational costs. The classification was done manually, and data is presented in chronological order. Data are expressed in per unit (p.u.) values for consistency and comparability throughout most of the analysis. The values used to normalize the analyzed parameters of the original parameters were 322 kW (real power), 1230 A (current), 1300 ${\mathrm{W}/\mathrm{m}}^2$ (GHI) and 230 V (voltage).

4. Experimental Results

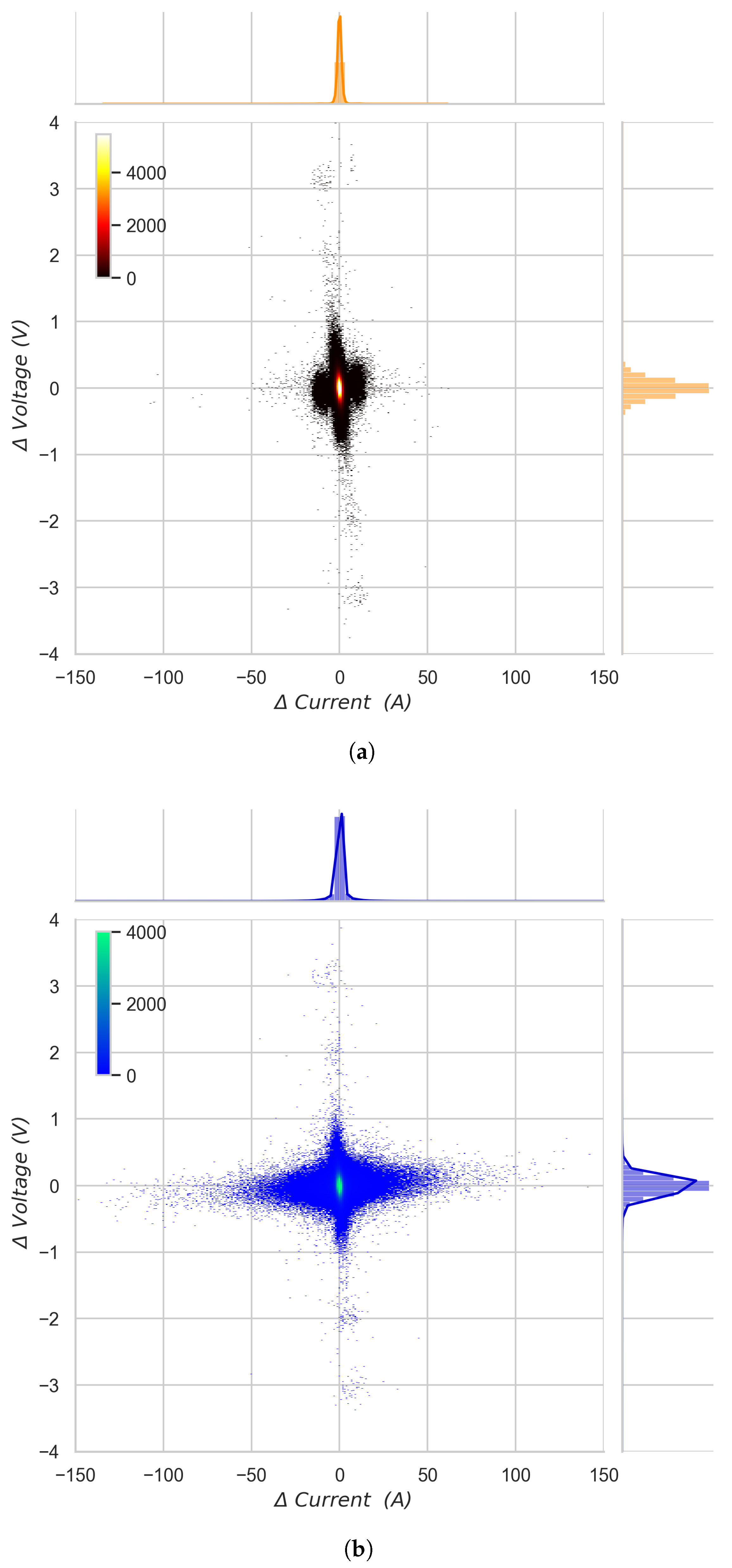
4.1. Analysis of the Initial Dataset

Figure 4 shows heat maps with the raw data. The X-axis represents the 67 selected days, whereas the Y-axis represents the 24 h of the day. Although night-time hours are included here, they will be removed for subsequent analysis as they do not provide information on production [20]. The graph clearly shows low night-time power and current values (shown in purple), with the current remaining constant at approximately 20–30 A. This value represents a residual current, magnified by measurement error due to its deviation from the rated current of the current sensors. The figure shows the difference between days with and without passing clouds for power, current, and GHI, whereas voltage exhibits no similarly evident distinction between the two conditions. Even so, the voltage profile reveals a midday increase in magnitude on both clear-sky days and days with passing clouds. The current and power heat maps for clear-sky days show three days with lower values, due to an inverter malfunction during those days.

The correlation among these parameters was analyzed using the Pearson Correlation Coefficient (PCC). Figure 5 shows the correlation matrix. It is observed that three of the measurements exhibit similar behavior, particularly power and current. The weaker correlation between voltage and other variables indicates a shared behavioral trend, while also suggesting that additional factors, independent of the PV plant energy production, influence grid voltage.

This correlation becomes evident when the measurements are normalized. For example, Figure 6 presents the normalized parameters analyzed for a clear-sky day and a day with passing clouds. As expected, power, current, and GHI behave very similarly throughout the day on both days. Meanwhile, voltage fluctuations arise not only from rapid changes in daily generation due to passing clouds but also from external grid-related factors, as indicated by the variability observed even on clear-sky days, as depicted in the example day in Figure 4. This figure indicates that voltage usually reaches its maximum daily value at midday, which coincides with the peak of PV production. It then decreases as production declines, reaching its minimum value typically during night-time. These patterns overlap with the transient effects, among others, produced by cloud passages observed on the days shown in the example days in Figure 6a.

Figure 7 shows the voltage values measured at the point of common coupling of the PV plant, compared to the values of the current produced and injected into the electrical grid. Despite voltage fluctuations, a linear relationship of direct proportionality between voltage and production was observed. This trend was characterized through linear regression. The result is shown in Figure 7a, together with the distribution of voltage and current values represented for the 134 days. Data recorded throughout the day is shown in green, while data recorded at night was discarded and shown in grey together with daily data. It can be observed that during daytime periods, the voltage distribution shifts upward, with the mean voltage being 1.32 V higher and the median 0.87 V higher than when night-time data are included. This indicates a greater occurrence of elevated voltage values during the day. Moreover, for a given current level, the voltage varies within a constant range of approximately 10 V, suggesting that while PV plant output power increases voltage, additional grid-related factors contribute to its fluctuation. Although specific voltage values at a grid point cannot be predicted a priori, an existing study of local plants using inverter data revealed comparable trends consistent with these findings [47]. As expected, at no point do the measurements exceeded the limits specified by the European standard EN 50160 for voltage characteristics of electricity supplied by public distribution networks [33], neither those imposed by the Spanish regulation [48]. The standards limits are set at a $\pm 10\%$ of 230 V (207 V–253 V), and a limit of 7% (214 V, 246 V), respectively.

Figure 7b presents the I–V data for the daytime period, distinguishing between clear-sky days (orange) and days with passing clouds (blue). In both cases, a positive correlation and slope were observed, consistent with previous findings reported in [47,49] using inverter data, although the coefficient of determination $r^2$ was slightly higher for days with clouds passing. The recorded data revealed the lowest voltage values (outliers) on clear days without passing clouds, as indicated by the orange points below the regression line. Nevertheless, all values remained within the standard limits. For voltage distribution, both the mean and median were higher on clear-sky days, by 0.68 V and 0.74 V, respectively, compared to days with passing clouds.

4.2. Data–Gradient Correlation Analysis

The gradient at each point was determined as the rate of change of the variable per unit time, obtained by subtracting each value from that measured at the preceding instant. Figure 8 shows two heat maps with the gradient values obtained, separated by clear-sky days (Figure 8a) and days with passing clouds (Figure 8b). The color scale represents the number of data points at each value. The graph’s axes were cropped to enhance readability. On the X-axis, three outliers were observed on days with passing clouds, corresponding to changes of −334.091 A, −259.21 A and −157.98 A. On the Y-axis, each graph displays between ten and twenty-five outliers, including a voltage drop to 0 V on one clear-sky day, producing deviations of +233.3 V and −233.3 V. All outliers align with the prominent cross-shaped pattern.

Figure 8 displays all voltage variations, regardless of magnitude, as the gradient calculation method applies no filtering. Therefore, most fluctuations reflect minor variations likely attributable to noise and measurement error, present on both days with and without cloud passing. When voltage and current variations are correlated, days with passing clouds exhibit voltage fluctuations of less than 1 V corresponding to larger changes in current. The cross-shaped distribution suggests a weak correlation between current and voltage fluctuations.

Nevertheless, a clear distinction emerges between days with and without cloud passing. Days with passing clouds show a greater number of high current variations exceeding 50 A compared to clear-sky days. These high current changes generally correspond to voltage fluctuations between 0 and 0.5 V rather than the largest voltage deviations. Notably, these fluctuations occur between consecutive samples taken at one-second intervals, which may explain why voltage fluctuations caused by sudden drops in generation are either less pronounced or develop more gradually, with their magnitude spread across successive samples.

In this section, fluctuation values were calculated by subtracting each measurement from the preceding one. However, this approach does not reflect the actual PV plant behavior, as it fails to account for the accumulation of consistent trends over time. When the variation maintains the same direction across successive points, the enhanced SDA method aggregates these changes, yielding the total magnitude variation over the period. Consequently, the next section aims to calculate a ramp rate that more accurately characterizes the observed cloud-induced effects using the enhanced SDA method. Section 4.3 focuses on SPRR, irradiance fluctuations and SPRE, while Section 4.4 focuses on voltage fluctuations induced by cloud passing.

4.3. Algorithm-Based Detection and Evaluation of Power, Current, and Irradiance Ramps

4.3.1. Evaluation of the SDA Threshold Effect on GHI, Current and Power

As explained in Section 2.1, the SDA output depends heavily on a threshold $ϵ$. Figure 9 shows how the number of ramps detected for each parameter varies on days with and without cloud passing, depending on the chosen threshold. In all three cases, the threshold values $ϵ$ are defined as percentages of the nominal magnitudes. Under ideal conditions, clear-sky days should yield two detected ramps, one increasing and one decreasing, whereas days with passing clouds should yield an indeterminate but larger number of ramps. However, as actual measured data, it contains inherent noise requiring filtering, derived from inverter dynamics and dependent on inverter aggregation and plant size. It nevertheless must comply with Total Harmonic Distortion (THD) limiting standards, such as IEC TR 61000-3-6:2008 [50].

The graph indicates that low values of $ϵ$ (e.g., 0.5%) can detect minor current fluctuations in the PV plant caused by the combined output of multiple inverters, regardless of cloud movement, which leads to a substantial number of non-significant ramps on clear-sky days. This means that with a (0.5%) threshold, noise is not being correctly filtered. Once noise is adequately filtered, varying thresholds may alter results but not conclusions, as this study compares parameters relatively. Higher thresholds capture large, long-duration ramps, while lower ones yield more and shorter events. This behavior remains consistent across all parameters regardless of threshold. Consequently, a threshold of $ϵ=2\%$ was selected, as it effectively filters electromagnetic noise and reliably identifies clear-sky conditions while maximizing event detection.

Figure 10 shows the results obtained when applying the chosen threshold of 2% to two example days, a clear-sky day (Figure 10b) and a day with passing clouds (Figure 10a). Ascending slopes are indicated in green color and descending ramps in red. Under clear-sky conditions, two ramps are accurately identified, whereas cloudy conditions yield 104 detected ramps for the represented day.

4.3.2. GHI, Current, and Power Comparison

Figure 11 compares the key features (duration, ramp rate, and magnitude) of the segments detected using the improved SDA algorithm. This comparison is possible because the measurements are synchronized to the nanosecond and collected using comparable methods, enabling accurate evaluation of their duration and magnitude. The three parameters have a similar number of ramps: 11,917 for power, 12,195 for current, and 11,519 for GHI.

The power and current exhibit nearly identical behavior. In contrast, GHI ramps are both faster and last longer. Half of the GHI ramps last under 31 s, whereas the median duration for power ramps is approximately 71 s. In magnitude, the average GHI ramp corresponds to 20.89% of the GHI (about 272 ${\mathrm{W}/\mathrm{m}}^2$), compared to 16.8% (54.09 kW) for power. Moreover, GHI displays higher ramp-rate values than the power parameter.

The results are partially attributable to the data origin. The GHI parameter, measured at a single location, exhibits sharper variations than current and power, which represent the aggregate output of all inverters connected to a TC. The selected threshold also influences the detected ramp sizes; it is assumed that an appropriate value was predetermined. Higher thresholds capture only large, long-duration ramps, whereas lower thresholds produce more smaller and shorter ramps.

4.3.3. SPRR and SPRE

As discussed in Section 2, certain applications aim to identify only significant SPREs. The process begins with the previously computed SPRR, followed by an evaluation of which events satisfy the significance criteria defined in Section 2.1. However, as is common in the literature [15,16], the outcome depends on the initially detected ramps. Figure 12 illustrates how the number of detected ramps varies with different thresholds. In contrast to the other figures in this article, Figure 12 was generated using 35 days per class, owing to current computational constraints. A lower threshold yields many non-significant ramps, while the number of true SPREs remains relatively stable. Nevertheless, the accuracy in locating the start and end points of SPRE can change, as demonstrated in Figure 13, which compares ramp detection for two thresholds: the one selected in the previous section (Figure 13a) and a lower one (Figure 13b). Ramps satisfying Definition 1 are shown in light blue, and those satisfying Definition 2 in purple. The results vary depending on the selected threshold $ϵ$, underscoring the importance of adapting this parameter to SPRE detection criteria from the outset and aligning it with applicable regulations at each site.

4.4. Analysis of Voltage Fluctuations Induced by Cloud Passage

Since the voltage demonstrates divergent behavior in the early results (Section 4), it is addressed separately in this section.

Since the voltage was measured at the point of common coupling, it was influenced not only by the PV plant’s production but also by other electrical grid phenomena. Therefore, it has been analyzed through four representative cases shown in Figure 14. Tests 1 and 2 correspond to two-hour periods with cloud passing, Test 3 represents a full day with cloud passing, and Test 4 corresponds to a clear-sky day. Only data recorded during periods of PV plant output power were included in all tests.

The relationship between voltage and the other parameters was first studied. To this end, the PCC was recalculated using only the data from each individual test. The resulting values are presented in

Table 1. Pearson Correlation Coefficient for every test data.

PCC	Power	Current	GHI
Voltage Test 1	0.88	0.88	0.88
Voltage Test 2	0.78	0.77	0.72
Voltage Test 3	0.71	0.7	0.68
Voltage Test 4	0.52	0.5	0.51

. As shown, stronger correlations were observed during rapid transitions induced by passing clouds (Tests 1 and 2), whereas in Test 4, where such fluctuations were absent, the correlation was lower but remained positive. This outcome is consistent with the general trend described in Section 4.1, where an increase in the PV plant output power corresponds to an increase in voltage. In Test 3, which comprises an entire day affected by cloud passing, an intermediate correlation value was obtained, as the data set includes periods with both cloudy and clear-sky conditions. During clear-sky periods, when PV production remains more stable, the influence of factors unrelated to the PV plant on voltage becomes more apparent.

The influence of power fluctuations on voltage fluctuations, themselves induced by passing clouds, is presented for the four tests in Figure 14. Figure 15 shows the detected SPREs (following the color scheme in Figure 13) together with the voltage. For the voltage, the same SDA was applied to detect sudden changes. The threshold was manually determined based on the test presenting the highest PCC (Test 1), resulting in a selected value of $ϵ$ = 0.5 V. In Tests 1 and 2, the voltage was observed to detect both the events identified in the power signal and additional events occurring exclusively in the voltage. Test 3 illustrates more clearly that, during midday, voltage variations are influenced by power drops, whereas at the beginning and end of the day, voltage fluctuations appear to arise from independent events. Ultimately, in Test 4, despite the absence of detectable SPRE, numerous voltage fluctuations were recorded, presumably originating from other sources within the electrical grid.

Finally, Figure 16 compares the key features (duration, ramp rate, and magnitude) of the segments detected using the improved SDA algorithm on clear-sky days versus on days with passing clouds. The number of ramps was slightly higher on days with passing clouds (16,519) compared to clear-sky days (15,127). The magnitude of ramps between both types of days is similar, as previously intuited when studying the gradient in Figure 8, where the X-axis doesn’t have any visible differences, in contrast with the Y-axis. However, the histogram indicates some variation in distribution. This reflects that fluctuations in PV production at the analyzed plant as a result of cloud passage have an effect on voltage variations at the point of common coupling, slightly increasing the fluctuating behavior of the voltage compared to that recorded on days without cloud cover.

5. Conclusions

The integration of ramp detection with high-quality synchronous PMU data introduces a novel and state-of-the-art methodology for the analysis of cloud-induced effects in PV plants. The synchronism among parameters enables meaningful comparisons and a comprehensive view of cloud effects, while the ramp detection method allows for a clear and structured analysis. Future research could extend these results by applying alternative ramp detection methods, such as those mentioned in Section 2.

This study compares the ramp rate of solar power with irradiance transients and found that both exhibit remarkably similar behavior, as expected, though this relationship had not previously been demonstrated on-field due to the absence of synchronous measurements. The median ramp duration was more than one minute for power (71 s) and just over half of a minute for irradiance (31 s), highlighting the rapid nature of these phenomena. Such detailed analysis would not have been possible with data from power inverters alone; the use of PMU data synchronized to the millisecond with irradiance measurements guarantees both the robustness and validity of these results.

With regard to voltage, its fluctuations depend on both meteorological and grid-related factors, which are typically analyzed independently due to the uncommon availability of synchronized voltage and irradiance data. By examining four example scenarios, the influence of cloud movement on voltage variability was observed. A modest rise in both the number and magnitude of fluctuations (approximately 1.15–4.6 V) was observed on days with passing clouds, although the statistical significance remains uncertain. Considerable grid voltage variability occurs irrespective of weather conditions, indicating that the majority of voltage fluctuations are not directly attributable to the PV plant’s operation or its response to cloud passing at this site and penetration level. Future research incorporating grid-side data would provide valuable insights into the origin of fluctuations.

For future research, it would be valuable to further investigate the cloud-induced effects identified in this study. In particular, the relationships between SPRE and cloud movement, and among voltage fluctuations and SPRE, merit deeper analysis. It would also be interesting to study the influence of cloud cover on other parameters that also affect PV production, such as changes in the temperature of the module cells, and their effect on production and, consequently, on voltage fluctuations. Bringing together the different cloud-induced PV transients with their main cause is a necessary step to ensure grid stability in distribution grids with high PV penetration. This comprehensive understanding not only supports the development of control and stability strategies and enhances forecasting capabilities but also broadens the existing knowledge base within this field.