Evaluation of Displacement Demands for Existing RC Buildings Using Spectral Reduction Based on Equivalent Viscous Damping

Abstract

This study investigates the relationship between spectral reduction and structural demand using different equivalent viscous damping approaches for existing reinforced concrete (RC) buildings. In that regard, 20 existing reinforced concrete buildings ranging from three to seven stories were selected. Equivalent viscous damping ratios were obtained based on the building period and ductility values using Applied Technology Council (ATC) 40 and Priestley et al. approaches. Subsequently, the corresponding spectral reduction factors were computed using various spectral reduction models existing in the literature. These reduction factors were then applied to design spectra defined for different soil classes in Turkish Building Earthquake Code (TBEC) 2018 to estimate the inelastic spectral demands. Finally, a comparison was conducted in terms of the obtained spectral reduction coefficients and spectral demands, highlighting the influence of different damping models on expected structural response.

1. Introduction

Nonlinear static procedures (NSPs) provide a simplified and sufficiently accurate method for evaluating the seismic performance of structures. In the literature, nonlinear static analysis (pushover analysis) is widely used to study the seismic behavior of structures. Panyakapo [1] mentions that pushover analysis procedures have been improved to estimate more accurate displacement demands. Guettala et al. [2] mentioned these developed methods as cyclic pushover [1,3,4,5], displacement-based pushover [6], energy-based pushover [7,8], and adaptive pushover [9,10,11]. In this study, monotonic static pushover analysis has been preferred. On the other hand, NSPs consider the deformation of energy associated with lateral forces applied on the capacity curve and do not fully account for hysteretic energy dissipation mechanisms associated with the cyclic nature of earthquake ground motions [12,13]. Spectral scaling procedures are applied to the elastic response spectrum to incorporate hysteretic energy, damping, and inelastic effects, effectively transforming the spectrum into a demand curve compatible with NSPs [14].

Recent research has extensively focused on spectrum-scaling methods for various damping ratios. In the literature, terms such as damping modification factor, damping reduction factor, and spectral scaling are commonly used to refer to techniques that derive higher-damping spectra from the conventional 5% damped elastic spectrum. These studies typically compare the damping modification factors obtained from selected horizontal and vertical components of ground motion records against those proposed by existing analytical formulations and seismic design codes. Several investigations have examined the influence of source characteristics (e.g., magnitude, depth), source-to-site distance, and site conditions on reduction factors [15,16,17,18,19,20,21,22,23]. In addition, vertical spectral reduction has been explored in several studies [24,25,26,27,28,29]. Studies on damping reduction are primarily performed on single-degree-of-freedom (SDOF) systems with a specific period range, although SDOF systems are practically employed in several studies [30,31,32]. In contrast, there are some studies [12,14,33] that investigated spectrum reduction factors for MDOF systems. Similarly, Landi et al. [34] examined the equivalent damping ratios for MDOF systems. This research employed real existing buildings modeled as multi-degree of freedom (MDOF) systems. Using the periods and ductility values of existing buildings for the displacement demands obtained according to the code-specified spectrum and evaluated.

Spectral scaling methods in the literature are generally categorized into two main groups: damping-based approaches and ductility/ lateral-strength-based approaches, depending on the primary parameter governing the reduction in the elastic spectral ordinates. Damping-based methods represent decreasing demand, with an equivalent viscous damping ratio (ξ_eq) that represents inelastic (hysteretic) energy loss. In these methods, the spectral reduction factor is an explicit function of ξ_eq. In contrast, methods based on ductility/ lateral-strength-based express the spectral reduction factor in terms of the displacement ductility ratio (μ) or lateral resistance ratio (R). The fundamental assumption is that the structure’s non-elastic energy dissipation capacity is related to how far beyond the yield limit it can deform or how much additional strength it possesses.

Equivalent viscous damping ratios represent the combined effect of damping and hysteretic energy dissipation. Spectral reduction factors (expression may change as SR, RF, or B in the literature) are then derived based on these; that is, the spectral reduction factors are applied to the elastic response spectra (commonly given for 5% viscous damping) to adjust for different equivalent viscous damping values in the structures and reduce spectral ordinates (acceleration, displacement, or velocity). These coefficients are calculated depending on the damping ratio, building period, hysteretic behavior, soil conditions, and sometimes ground-motion characteristics.

Several studies in the literature describe SR only as a function of ξ_eq [35,36,37,38]. There are also studies in the literature [37,39,40,41,42,43] that define the spectral reduction (SR) coefficient as a function of both the ξ_eq and period (T) [44].

This study considers a comparative evaluation of damping-based approaches found in the literature. For this purpose, the equivalent viscous damping ratios of 20 existing reinforced concrete buildings were calculated using the ATC-40 [45] and Priestley [38] methods. Subsequently, reduction factors for the buildings were determined based on spectral reduction factor approaches reported in the literature [37,38,39,42,46]. These reduction factors were then applied to scale the TBEC-2018 [47] regulation spectra, and the seismic demand values were obtained based on the building periods and compared.

2. Methods

In this study, nonlinear analytical models of 20 existing reinforced concrete buildings were developed in accordance with the assessment criteria defined for existing structures in TEC-2007 [48], TBEC-2018 [47], and Eurocode 8 Part 3 (EC8/3) [49]. Following the nonlinear analyses, the ductility capacities of the buildings were determined using the corresponding capacity curves. Ductility values were subsequently substituted into the ATC-40 [45] and Priestley [38] formulations available in the literature to compute equivalent viscous damping ratios for each building.

Thereafter, the resulting ductility values were also inserted into the spectral reduction factor expressions reported in the literature, and the corresponding reduction factors were calculated for each case. Subsequently, the obtained reduction factors were applied to the displacement respond spectra defined in TBEC-2018 for different soil classes (ZC and ZD). Using these reduced spectra, the displacement demands corresponding to the fundamental period of each building were determined. Figure 1 presents the methodological workflow of the study.

In other words, once the ductility value of a given building was obtained in the X-direction according to TEC-2007, two equivalent damping ratios were calculated using the ATC-40 and Priestley approaches. These two damping ratios were then considered separately in the computation of six different spectral reduction factors. For the same building, 12 reduction factors were calculated for each soil class by using the corner period values associated with the ZC and ZD soil classifications.

The resulting reduction factors were then applied to the corresponding displacement response spectra defined by TBEC-2018 to derive the reduced displacement spectra. This yielded a total of 24 displacement demand values corresponding to the periods of the building. This approach enabled the comparison of the variations in displacement demand arising solely from methodological differences, although the buildings had identical period and damping characteristics.

2.1. Nonlinear Building Models

The damping-based spectral reduction factors (SR) are formulated as a function of structural ductility. For this reason, establishing the relationship between lateral load-carrying capacity and displacement is essential in determining SR values. In this study, ductility ratios were obtained from bidirectional capacity curves derived through nonlinear pushover analyses. Based on the calculated ductility, the corresponding equivalent viscous damping ratios and, subsequently, the spectral reduction factors were evaluated.

It is well recognized that the adopted code provisions for modeling existing buildings significantly influence the predicted structural performance. One of the primary parameters affected by these provisions is the period of the structure, which depends on the effective stiffness definitions specified in seismic design codes. Seismic codes define different approaches to account for stiffness degradation in structural members. In TEC-2007, the effective stiffness coefficients are defined as a function of the axial load ratio, ranging from 0.40 to 0.80 for columns, while a constant value of 0.40 is specified for beams. In TBEC-2018, constant effective stiffness factors are recommended, with values of 0.70, 0.50, and 0.35 for columns, walls, and beams, respectively. In EC8/3, the effective member stiffness is calculated using formulations that depend on the yield moment (M_y), yield rotation (θ_y), and shear span (L_s). Unlike the other seismic codes, Eurocode adopts a member-based stiffness approach, in which stiffness is evaluated separately at both ends of the member based on sectional yielding properties. The mean value of the two end stiffnesses is then taken as the effective stiffness, expressed as the ratio of effective to gross stiffness (EI_eff/EI₉). Calculations indicated that the stiffness coefficients derived using the EC8/3 approach were significantly lower than those obtained from other seismic code provisions. This pronounced reduction in member stiffness leads to an increase in the fundamental periods of the buildings. Cirak Karakas et al. [50] demonstrated that the building periods obtained using EC8/3 are generally larger than those calculated according to Turkish seismic codes. Consistent with these findings, the results of the present study also indicate a systematic increase in the fundamental periods when the EC8/3 approach is adopted.

Another critical aspect in the seismic performance assessment of existing buildings is the calculation of plastic rotation capacities corresponding to sectional damage states, as prescribed by the relevant codes. In brief, the Turkish seismic codes define the rotation capacities for concrete and steel members primarily based on the strain limits of materials. However, it is noteworthy that the bounds of strain limits differ between the two codes. In contrast, EC8/3 determines these capacities using empirical formulations expressed in terms of chord rotation. The differences in approaches adopted by the seismic codes lead to distinct damage limit states for the same structural member. Consequently, under the same conditions, the assumed code directly influences the predicted building displacement capacity. The assumptions regarding these calculations are described in detail within the respective code provisions.

In this study, the ductility and period values obtained for the buildings were used to calculate the equivalent viscous damping ratios. As emphasized in the previous sections, the seismic code assumptions adopted in the nonlinear static pushover analyses are expected to cause significant variations in both period and ductility capacity of the structures. To conduct this comparison, a total of 20 reinforced concrete residential buildings located in Denizli, Türkiye, were selected. The buildings consist of 3 to 7 stories, representing typical low- to mid-rise building stock. Half of the buildings were originally designed in accordance with the Turkish Earthquake Code of 1975 [51]. The other half were designed according to the Turkish Earthquake Code of 1998 and subsequent regulations [52]. In this study, the buildings designed according to TEC-1975 are referred to as old buildings (BOs), while others are referred to as new buildings (BNs).

Structural models were modeled in SAP2000 [53] based on the original structural drawings, and Figure 2 shows a 3-story and 5-story old building as a sample. The story heights of the buildings considered in the study generally range between 2.4 m and 3.6 m. While the story heights are uniform across all floors in some buildings, they vary in others. Several buildings were observed to have larger story heights on the lower floors compared to the upper stories. Detailed information for the properties of buildings can be provided by the authors upon request.

Based on the data derived from the original structural projects, the concrete com-pressive strength and reinforcing steel yield strength were taken as 16 MPa and 220 MPa for the old buildings, respectively. For the new buildings, the concrete strength was equal to or greater than 20 MPa, and the steel yield strength was 420 MPa. Structural models of buildings were subjected to dead loads provided by structural design projects, and live loads were taken as 0.2 t/m² for rooms, 0.35 t/m² for staircases, and 0.5 t/m² for balconies, in accordance with the load regulations currently applied in Türkiye.

Nonlinear numerical models were developed for each building considered in this study, in accordance with the provisions of three different seismic design codes: TEC-2007, TBEC-2018, and Eurocode 8 Part 3. Strength and deformation capacities of structural members were determined by moment–curvature analyses depending on modified Kent–Park model [54], and plastic hinges were attained to [55] critical regions of the members to represent nonlinear behavior of buildings. During the analyses, P-Δ effects were also considered. Additionally, the shear behavior and acceptance limits of members were reduced for shear-deficient elements, as structural performance is related to member damage limits, as emphasized by Palanci et al. [56].

The plastic hinge formation determined by pushover analysis corresponding to the first occurrence of the three damage limits (IO, LS, and CP) is presented in Figure 3, Figure 4 and Figure 5 for the five-story old building. These figures also show the capacity curves together with the displacement values at which the damage limits first occur.

The results obtained for the building highlight how the strength and deformation relationships differ when the same building is evaluated under different code provisions. The influence of code-specific stiffness coefficients on the periods is clearly reflected in the capacity curves. Accordingly, the periods obtained according to the Turkish codes are relatively similar, whereas those derived using EC8 differ significantly. As expected, the stiffness of capacity curves derived based on the EC8/3 provisions, which yield the lowest effective stiffness, are clearly lower than that obtained from the other seismic codes. When comparing the obtained displacement capacities, it is noteworthy that the displacement capacity for TBEC-2018 is considerably lower. In contrast, the largest displacement capacity was obtained for TEC-2007. It can also be observed that the yield displacement determined by EC8/3 is significantly larger compared to the other codes. Although the ultimate displacement value derived from EC8/3 is relatively high, the corresponding yielding displacements are also larger. TEC-2007 provided higher ductility values compared to other seismic codes.

The base shear and roof displacement (i.e., capacity curves) of the buildings were obtained from static pushover analyses for both directions of buildings. Consequently, 40 capacity curves were obtained for each seismic code, yielding a total of 120 curves (see Figure 6). To provide a clear view, the capacity curves were averaged according to construction year and seismic code and plotted in Figure 7. The average periods of the old buildings for TEC-2007, TBEC-2018, and EC8/3 were calculated as 0.62 s, 0.59 s, and 1.19 s, respectively, while those of the new buildings were 0.70 s, 0.67 s, and 1.10 s. The corresponding average ductility values were 5.66, 2.80, and 1.90 for the old buildings, and 5.59, 2.52, and 2.18 for the new buildings.

2.2. Equivalent Viscous Damping Ratios

In nonlinear static procedures (NSPs), spectral scaling is employed to modify the demand spectrum, accounting for the increased damping or energy dissipation capacity of the structure, thereby providing a more realistic estimation of the performance point derived from the intersection of capacity and demand spectra. Spectral scaling methods are generally classified into two main categories: damping-based methods and ductility/lateral strength (R-μ-T)-based methods. For the first category, the spectral accelerations and displacements are scaled using the spectral reduction factor (SR or B) given in Equation (1) in Monteiro et al.’s [12] and Casarotti et al.’s [14] articles (see Figure 8a). In contrast, for the second category, the spectral acceleration values are reduced according to Equation (2) (see Figure 8b).

$$\begin{gathered} S_{a,damp}=B.S_{a,el5\%} \\ {S}_{d,damp}=B.S_{d,el5\%} \\ {S}_{d,damp}={\displaystyle \frac{S_{a,damp}}{{\omega }^2}} \end{gathered}$$

(1)

$$\begin{gathered} S_{a,duct}={\displaystyle \frac{S_{a,el5\%}}{R}} \\ {S}_{d,duct}={\displaystyle \frac{\mu }{R}}{S}_{a,el5\%}=C.S_{d,el5\%} \end{gathered}$$

(2)

In earthquake engineering, the method of equivalent viscous damping was recommended by Jacobsen [57] and Rosenblueth and Herrera [58]. The most notable aspect of the equivalent viscous damping (EVD) approach is that it accounts for the influence of different hysteretic characteristics on energy dissipation and, consequently, on inelastic displacement demands. In contrast, most building codes disregard this effect and generally adopt the equal displacement rule, irrespective of the hysteretic properties of the structure [59].

In seismic analysis, the equivalent viscous damping is used to approximate the energy dissipation of inelastic structures within a linear elastic framework. This approach allows for a more realistic estimation of seismic demands by representing hysteretic energy dissipation through an effective damping ratio.

In the study, bilinear capacity curves obtained for different code provisions were used to determine the displacements corresponding to yielding and ultimate states, from which the ductility ratios of the buildings were calculated. The equivalent viscous damping ratios (ξ_eq) were then calculated based on these ductility levels using two damping-based approaches adopted from the literature.

The first approach employed in this study is the ATC-40 [45] method. As in Equation (3), the method correlates the damping ratio with the ductility demand of structural members, considering the number of yielding cycles and hysteretic energy dissipation. Typically, the damping ratio increases with the ductility demand, reflecting the enhanced energy dissipation of highly inelastic members.

In Equation (3), the factor “K” is an adjustment parameter introduced to approximately represent the changes in the hysteretic behavior of the structure between the initial and subsequent loading cycles. This factor depends on the structural characteristics of the building, the quality of the structural system, and the duration properties of the ground motion. The ATC-40 [45] proposes three structural behavior types for the application of this coefficient. In this study, considering that older buildings generally possess lower material strengths and inadequate detailing, “K” recommended for Type C behavior was adopted for the analyses of existing buildings. Conversely, for newer buildings with adequate material quality and detailing, “K” corresponding to Type B behavior was used.

$${\xi }_{eq-ATC40}={\xi }_0+K{\displaystyle \frac{2}{\pi }}\left[{\displaystyle \frac{\left(1-\alpha \right)\left(\mu -1\right)}{\mu -\alpha \mu +\alpha {\mu }^2}}\right]$$

(3)

Another approach used in the equivalent viscous damping calculations is the method proposed by Priestley et al. [38]. In this approach, the equivalent viscous damping is computed from the ratio of hysteretic energy dissipated during cyclic loading to the maximum elastic strain energy. This method accounts for member-specific properties, such as axial load level, section geometry, and reinforcement detailing, providing a more refined estimate of damping for both columns and beams. Priestley’s method is often preferred when more accurate evaluation of nonlinear response is required, particularly in performance-based seismic design and assessment studies.

In Equation (4), the coefficient “C” is an empirical parameter that represents the hysteretic energy dissipation capacity of the structure and therefore varies depending on the type and detailing of the structural system. The hysteretic behavior of reinforced concrete members under cyclic loading can be modeled using Takeda-based hysteresis rules, and the selection of “C” may be aligned with the assumed hysteretic response characteristics. In this study, the Takeda-Thin model, which corresponds to C = 0.444, was adopted to reflect the relatively limited energy dissipation capacity of the considered structures.

$${\xi }_{eq-Priestley}={\xi }_0+C\left({\displaystyle \frac{\mu -1}{\pi \mu }}\right)$$

(4)

2.3. Spectral Reduction Factors

Using the equivalent damping ratios (ξ_eq) obtained for the buildings, spectral reduction factors were calculated based on existing method equations reported in the literature. In this study, the methods available in the literature were directly adopted without any modification. Results from two equivalent viscous damping methods were used to calculate the reduction coefficient compared to expanding the dataset.

For calculations, the buildings were assumed to be situated on ZC and ZD soils according to TBEC-2018, and the corner periods of the response spectrum were applied accordingly. The building periods used in the calculations were derived from the structural periods determined in accordance with TEC-2007, TBEC-2018, and EC8/3. The spectral reduction factors used in the study are explained below:

(a)

Newmark and Hall [39] expression:

In this method, the spectral reduction factors are determined based on the corner periods T_b and T_c, T_d which separate the constant acceleration, constant velocity, and constant displacement regions of the response spectrum. In the equation, ξ_eq denotes the equivalent viscous damping ratio, which accounts for the combined contributions of inherent material damping and additional energy dissipation associated with inelastic deformation.

$$B_{N-H}=\left\{\begin{array}{c}{B}_{N-H,a}={\displaystyle \frac{3.21-0.68\mathrm{l}\mathrm{n} \left(100{\xi }_{eq}\right)}{2.12}} T_b\le T<T_c\\ B_{N-H,v}={\displaystyle \frac{2.31-0.41\mathrm{l}\mathrm{n} \left(100{\xi }_{eq}\right)}{1.65}}{ T}_c\le T<T_d\\ B_{N-H,d}={\displaystyle \frac{1.82-0.27\mathrm{l}\mathrm{n} \left(100{\xi }_{eq}\right)}{1.39}} T\ge T_d\end{array}\right.$$

(5)

(b)

Eurocode 8 [46] expression:

In this method, the reduction factor is determined based on the building period and the corner period of the response spectrum. Here, ξ_eq represents the equivalent viscous damping ratio. The reduction factor “η” is limited to a minimum value of 0.55.

$$\begin{gathered} B_{EC8}=\left\{\begin{array}{c}1-(1-\eta ){\displaystyle \frac{T}{T_b}} 0\le T<T_b\\ \eta T\ge T_b\end{array}\right. \\ \eta =\sqrt{{\displaystyle \frac{10}{5+100{\xi }_{eq}}}}\ge 0.55 \end{gathered}$$

(6)

(c)

Ramirez et al. [37] expression:

The damping coefficients B_short and B_long account for the effect of structural damping on the short- and long-period regions of the response spectrum, respectively, enabling appropriate scaling of the spectral demands for different damping levels. “B” coefficients are determined based on the damping ratio, following the approach proposed by Ramirez. In the equation, T_b and T_c represent to the corner periods for the constant acceleration and velocity spectral regions.

$$1/B_{Ram}=\left\{\begin{array}{c}1-(B_{short}-1) {\displaystyle \frac{T}{T_b}} 0\le T<T_b\\ B_{short}-(B_{short}-B_{long}){\displaystyle \frac{(T-T_b)}{(T_c-T_b)}}{ T}_b\le T<T_c\\ B_{long} T\ge T_c\end{array}\right.$$

(7)

(d)

Lin and Chang [42] expression:

This method is based on an approach that depends on the building period (T) and the equivalent viscous damping ratio (ξ_eq).

$$\begin{gathered} B_{Lin-Chang}=1-{\displaystyle \frac{\alpha T^{0.3}}{{\left(T+1\right)}^{0.65}}} \\ \alpha =1.303+0.436\mathrm{l}\mathrm{n} ({\xi }_{eq}) \end{gathered}$$

(8)

(e)

Priestley [38] expression:

This method was developed for far-field ground motions and calculates the reduction factor based on the equivalent viscous damping (ξ_eq) of the structure.

$$B_{Priestley}={\left({\displaystyle \frac{0.07}{0.02+{\xi }_{eq}}}\right)}^{0.5}$$

(9)

(f)

Combined Eurocode 8 and Ramirez et al.:

A combined approach based on Eurocode 8 and Ramirez is proposed to provide a simplified formulation that captures the overall period-dependent trend of the reduction factor (RF). In this approach, EC8 is used for the short-period range, where it generally yields lower RF values, while the Ramirez formulation is applied to the long-period range, where it provides higher RF estimates [14]. In the equation, T_dd represents the new corner period, obtained based on the values derived from Ramirez et al. and EC8, and its calculation is presented below.

$$B_{Comb EC8-Ram}=\left\{\begin{array}{c}{B}_{EC8} 0\le T<T_{dd}=T_d{\displaystyle \frac{B_{Ram}}{B_{EC8}}}\\ B_{Ram} T\ge T_{dd}\end{array}\right.$$

(10)

2.4. Seismic Demand Calculation

According to TBEC-2018, soil types are classified into six categories (from ZA to ZF) based on shear wave velocity, standard penetration test (SPT), or undrained shear strength for cohesive soils. Class C corresponds to very dense or compact soil or soft rock (360 < Vs ≤ 760 m/s), and Class D corresponds to medium-dense soil (180 < Vs ≤ 360 m/s). These soil classes are used to define site factors that modify spectral accelerations in seismic design, reflecting the influence of local ground conditions on structural response. In this study, seismic demands were determined using the design spectra, with a 5% damping ratio specified for ZC and ZD soil classes in TBEC-2018.

Each spectrum was reduced using the spectral reduction factors obtained for the respective building, and demand values corresponding to the periods of the buildings were obtained. This approach enabled a consistent comparison of the influence of spectral reduction factors, both for a given spectrum and across different soil classifications.

The acceleration and displacement spectra obtained for ZC and ZD soil classes are presented in Figure 9. In the figure, the blue lines represent the ZC soil class, while the red lines correspond to the ZD soil class.

3. Evaluation of Results

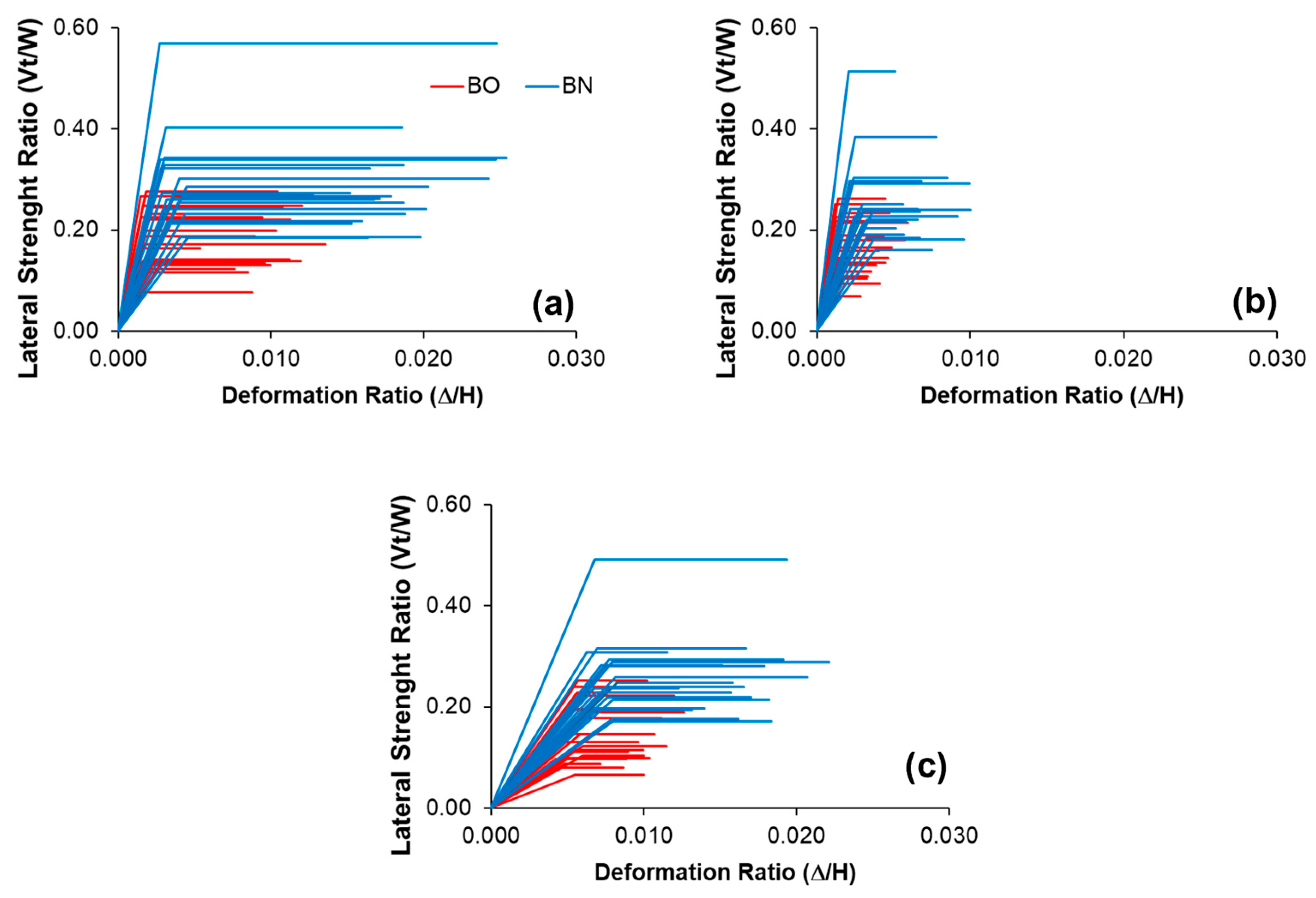
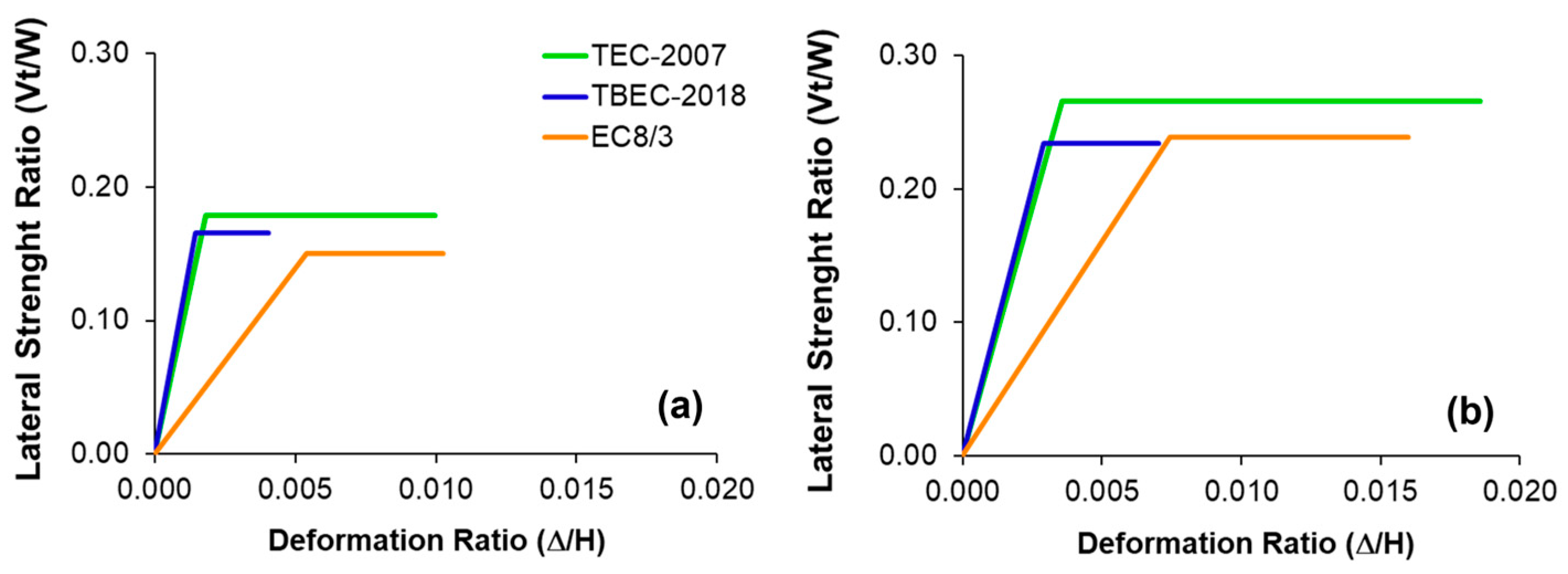
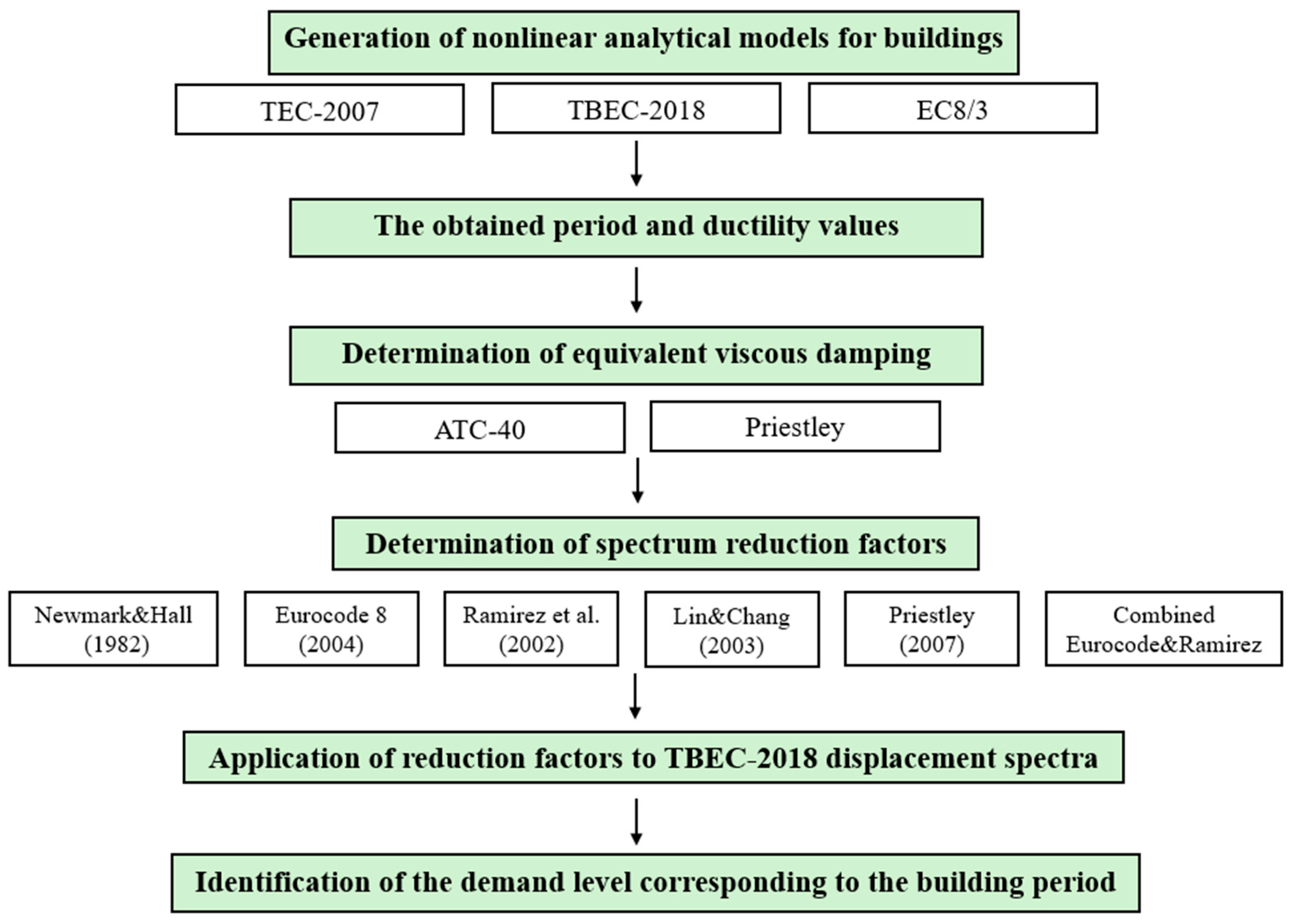
3.1. Equivalent Viscous Damping Ratios

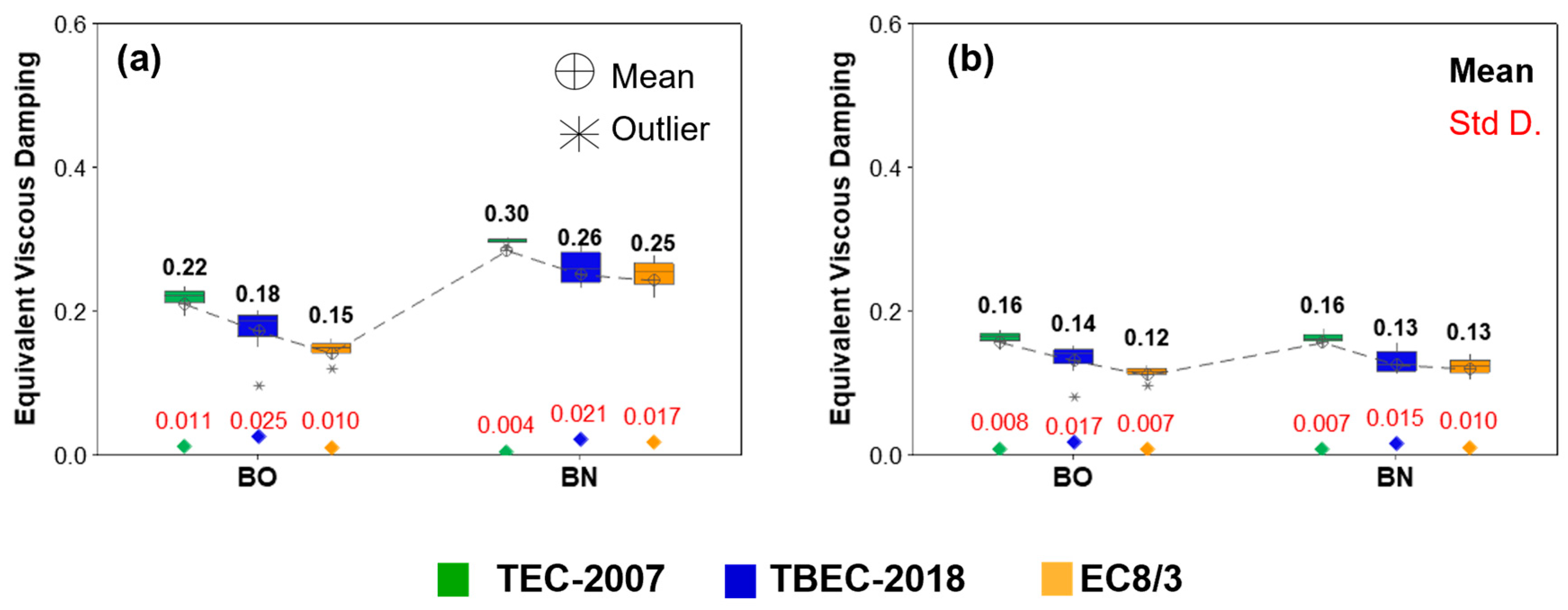
For each building, the equivalent viscous damping ratios were estimated using the ATC-40 and Priestley approaches, resulting in values ranging from approximately 8% to 30%. According to the ATC-40 approaches, the equivalent viscous damping ratios of the old buildings varied between 10% and 24%, while those of the new buildings were between 22% and 30%. In contrast, equivalent viscous damping ratios of the Priestley approach were between 8% and 17% for the old buildings and between 11% and 18% for the new buildings.

The distribution around the median value of the equivalent viscous damping ratios with respect to the building’s construction year and seismic code is presented in Figure 10. In the plots, the green, blue, and orange colors correspond to the TEC-2007, TBEC-2018, and EC8 regulations, respectively. The mean value of each distribution is highlighted in bold, while the standard deviation of each dataset is indicated in red.

The results show that equivalent viscous damping ratios obtained using the ATC-40 method differ between old and new buildings. This difference is governed not only by variations in ductility but also by the use of the building type-dependent K coefficient inherent in the ATC-40 formulation. This amplification effect is most pronounced for newer buildings, demonstrating that the ATC-40 formulation is more sensitive to structural classification than to ductility alone. In contrast, damping ratios calculated using the Priestley method are unaffected by building age.

The ductility values specified in the codes also influenced the damping ratios. Ductility values determined from TEC-2007 are higher than the others, corresponding to the highest damping ratios. For new buildings, the average ductility values obtained for TBEC-2018 and EC8/3 are similar, which has also affected the damping ratios.

Furthermore, it was observed that the average damping values computed according to ATC-40 are higher than those obtained from the Priestley approach. When the ratios of the mean damping values obtained using the ATC-40 approach to those obtained using the Priestley method are examined, it is observed that the ATC-40 approach results in approximately 30% higher damping for older buildings and about 93% higher damping for newer buildings. For both damping approaches, the equivalent damping ratios decrease as the average ductility values decrease.

Overall, these findings indicate that the choice of damping formulation has a direct and non-negligible impact on subsequent spectral reduction and displacement demand calculations.

3.2. Spectral Reduction Factors

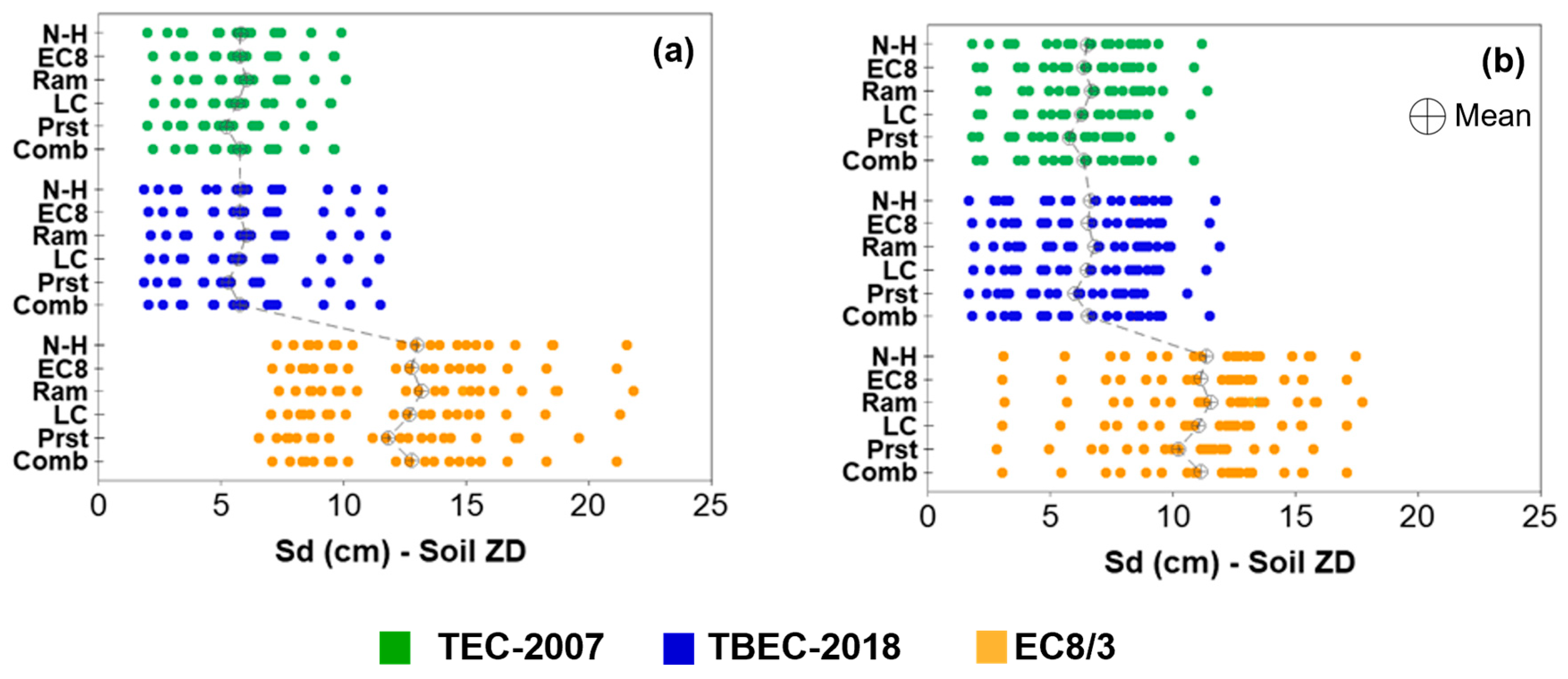
In this section, the displacement demands corresponding to the building periods are examined, considering the effects of the adopted seismic code, soil classification, equivalent viscous damping ratio, and spectral reduction approach.

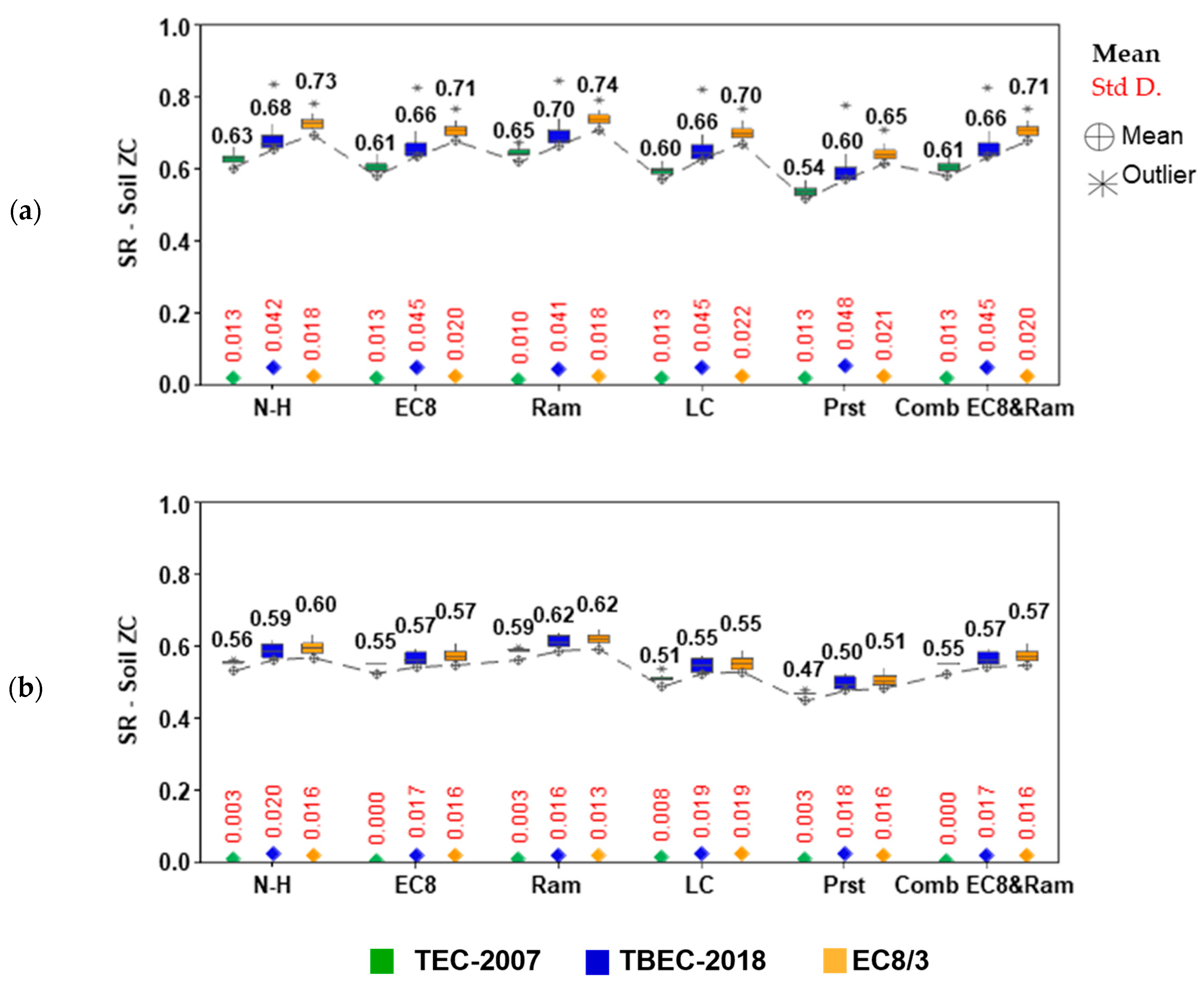
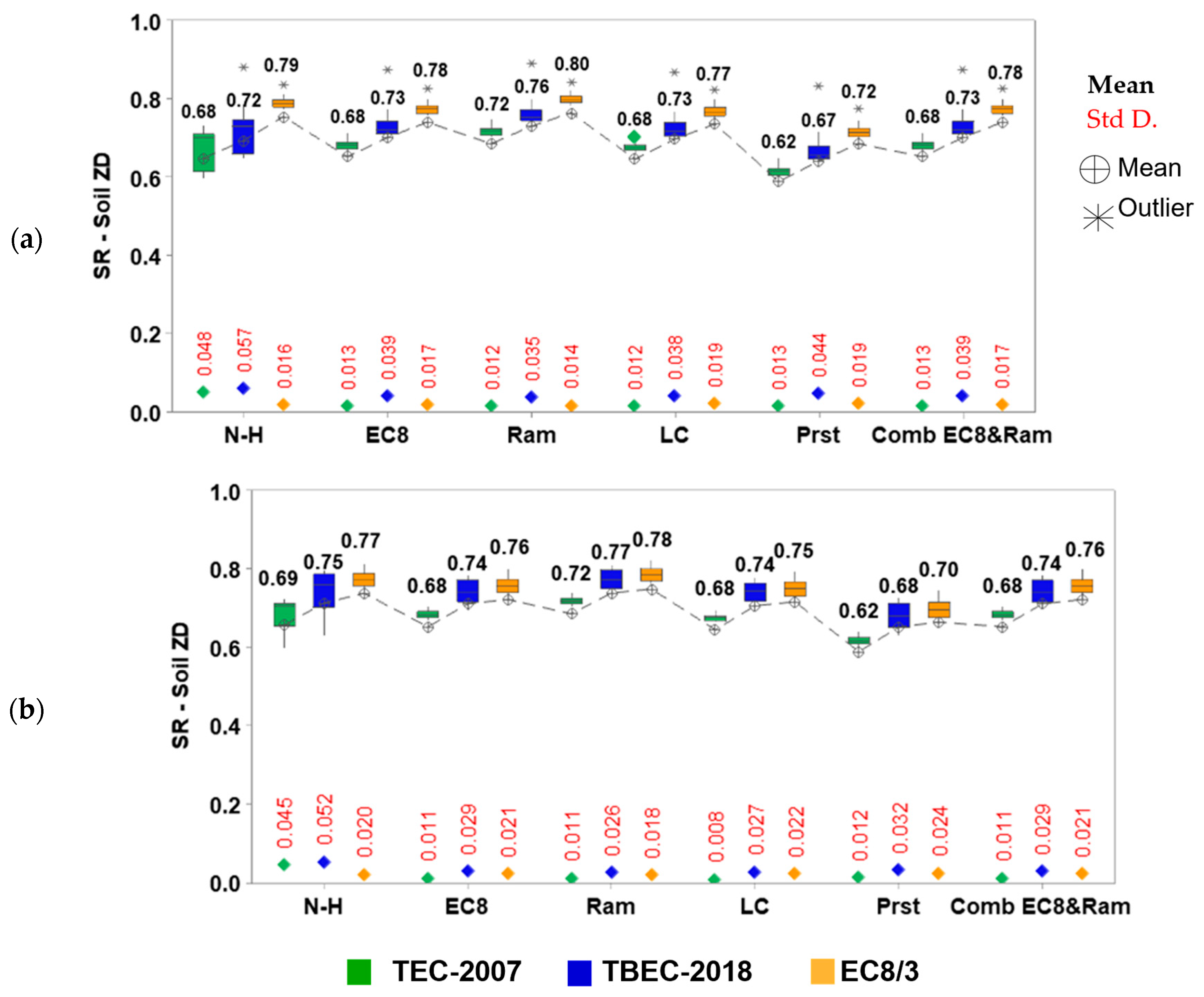
Figure 11 presents the spectral reduction factors (SR) for ZC soils, calculated using the equivalent viscous damping ratios obtained from the ATC-40 method, for both old (on the left) and new (on the right) buildings. Similarly, Figure 12 shows the results obtained using the Priestley method. The design codes are represented by different colors, with the mean values indicated in bold above the distributions, while the standard deviations are shown in red below the distributions. 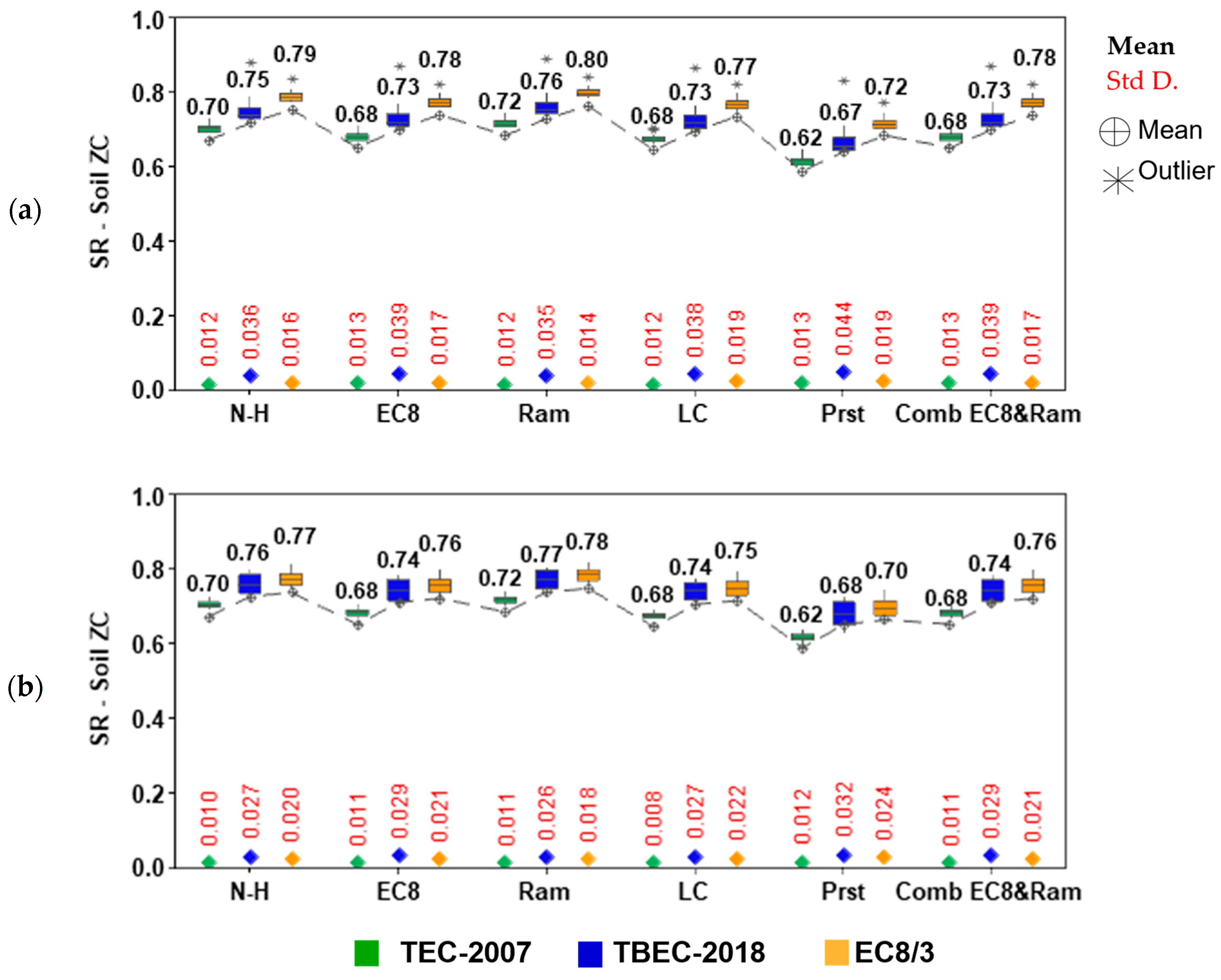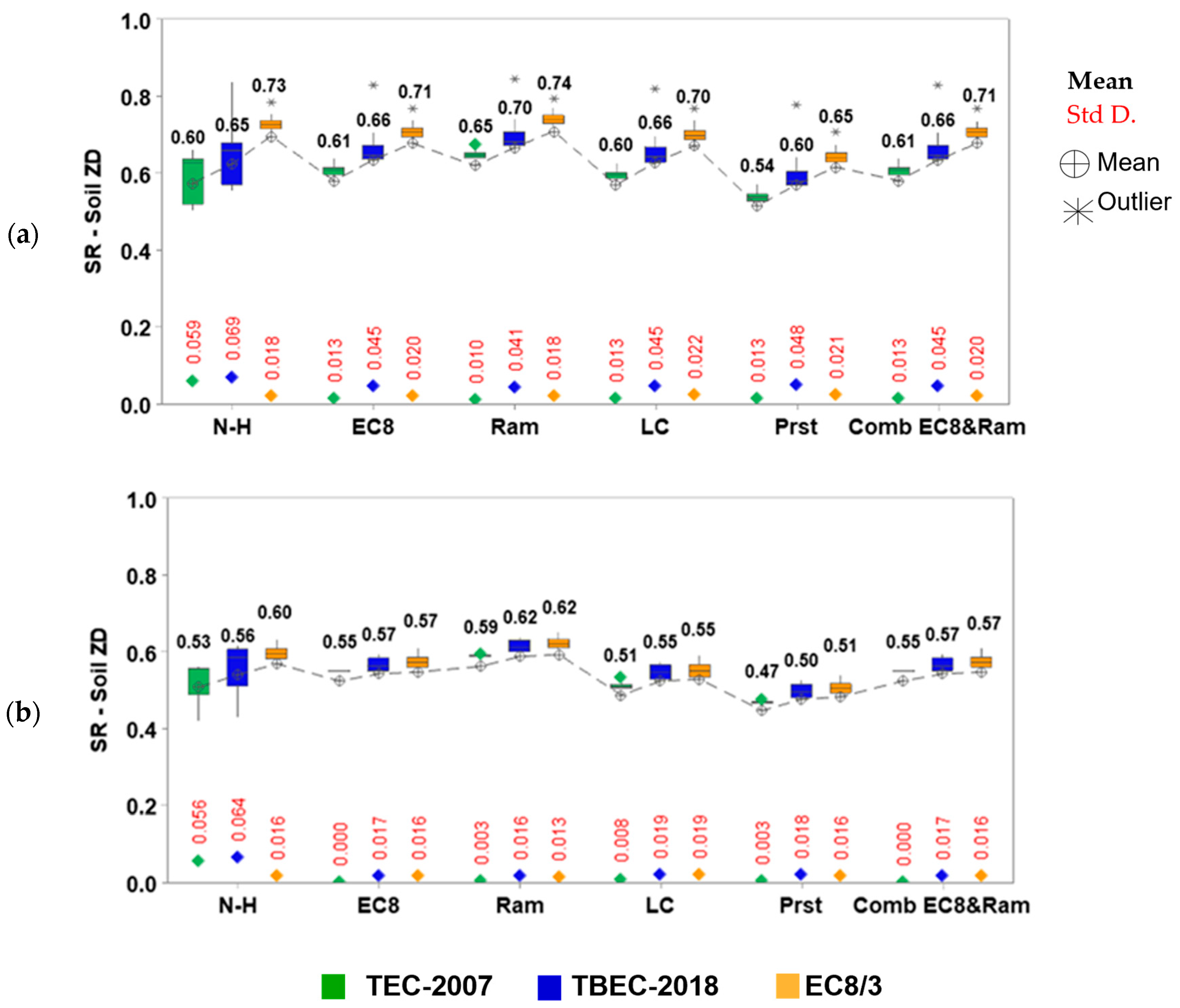Figure 13 and Figure 14 illustrate the distribution of the spectral reduction factors obtained for ZD soils.

Structures with higher damping ratios generally exhibit lower spectral reduction factors. While period effects slightly reduce the reduction factors as the building period increases, this influence is minor compared to that of the damping ratio.

Since ATC-40 provides higher equivalent damping ratios than the Priestley method, the corresponding reduction factors from ATC-40 are smaller. This difference is more pronounced for newer buildings, reflecting the sensitivity of the reduction factors to both damping and construction year. Mean of Priestley damping values are approximately 10% larger than those obtained from ATC-40 approach for older buildings across all seismic codes, soil types, and methods. For newer buildings, this difference is approximately 30%.

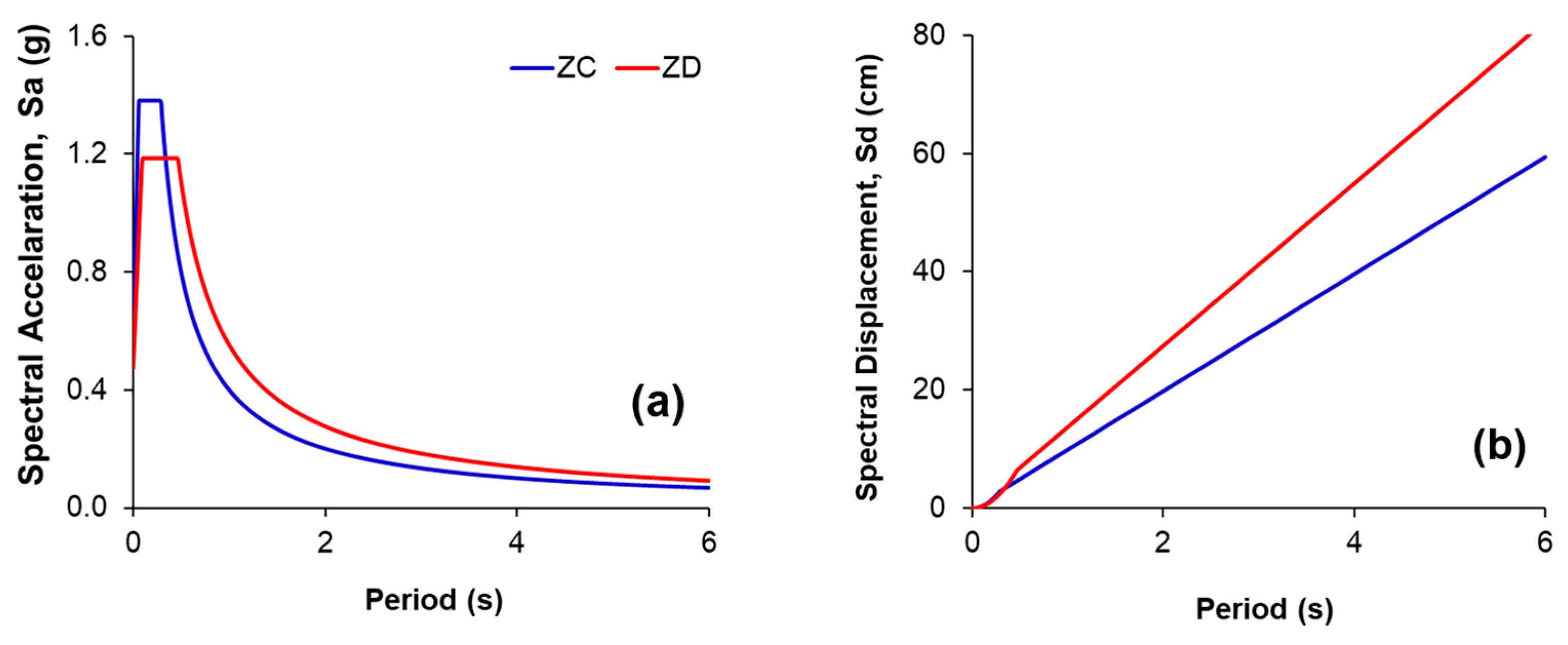
Soil conditions also affect the reduction factors. It can be seen in Figure 9 that as the soil condition deteriorates, the corner periods increase, and the spectrum generally becomes broader. This leads to variations in the spectral reduction formulations that are defined with respect to these corner periods. In the present study, this effect was particularly evident for the Newmark–Hall approach. When the spectral reduction factors were compared for ATC-40, regardless of the construction year, it was observed that the values for soil class ZD were lower than those for ZC for the Newmark method. Specifically, for ZC soils, the reduction factors were found to be approximately 6% higher for TEC-2007 and TBEC-2018. All periods obtained from EC8/3 fall within the constant-velocity region in both spectra. Consequently, the spectral reduction coefficients for both soil classes are identical. In contrast, for the Priestley method, the reduction factors for ZC soils were, on average, 4% higher than those for ZD. When Figure 13 and Figure 14 are examined, the scatter of the distributions obtained for the TEC-2007 and TBEC-2018 regulations is larger on ZD soils. This is due to the larger corner periods.

Across the six evaluated spectral reduction methods, the Ramirez approach consistently produces the highest reduction factors, indicating a more conservative estimate of displacement demands, while the Priestley method gives the lowest values. Meanly, for the same period, the displacement demand obtained using the Ramirez approach is highest. Consequently, performance assessments based on Ramirez are likely to predict more critical performance levels for the same building capacity. The mean reduction coefficients obtained for the methods were evaluated by dividing the mean values of Priestley, and the results were compared. For old buildings, the average reduction coefficient obtained for the Ramirez results using ATC-40 damping was determined to be 17% greater than that of Priestley, regardless of the code. Values obtained for the Priestley damping were 14% greater. For new buildings, these values were 24% and 14%, respectively.

The SR equations vary because they are derived from different earthquake databases, resulting in differences among the formulations. In this study, although the average values are similar, it is observed that the variations differ. These differences naturally arise from the characteristics of the buildings and the methods applied. Additionally, the results are affected by using different equivalent viscous damping approaches, diverse code provisions, and the properties of each building.

The relationship between damping ratios and the ductility values of the codes is evident from the average values. TEC-2007, which has the highest damping ratios, yields the lowest SR factors. A similar trend can be observed for the other codes as well. However, for new buildings, since the ductility values for TBEC-2018 and EC8/3 are closer, the obtained values for these buildings are also quite similar.

The distribution of reduction factors shows greater scatter for TEC-2007 and TBEC-2018 on ZD soils, which is attributed to the larger corner periods in these soil classes. These observations highlight that both the choice of damping model and soil characteristics significantly influence spectral reduction, and hence seismic performance evaluation.

3.3. Spectral Demand

Figure 15, Figure 16, Figure 17 and Figure 18 below illustrate the distribution of displacement values obtained for each method with respect to their median values. Consistent with the previous sections, the seismic codes are represented using the same colors: green indicates TEC-2007, blue indicates TBEC-2018, and orange indicates EC8/3. The mean value corresponding to each method is represented by a dashed line.

It is known that the SR coefficients obtained according to the codes follow an increasing order of TEC-2007, TBEC-2018, and EC8/3. Accordingly, a similar ranking can be expected for the resulting displacements. Period differences arising from the definitions in the codes have a noticeable effect on the displacements. Examination of the results shows that EC8/3 displacement demands are higher for both soil classes and building age groups. This is mainly due to the effective stiffness coefficients defined in EC8/3, which lead to longer periods and, consequently, larger spectral displacement demands.

The average displacement values obtained using the Priestley method are greater than those obtained with ATC-40. When comparing the results for new and old buildings, it is seen that, according to the ATC-40 method, old buildings have higher displacement demands. In contrast, this is not always the case for the Priestley method.

Comparing across soil classes, ZD soils consistently produce higher displacement demands than ZC. The ratio of the displacement demands obtained for ZD to ZC across all spectrum reduction (SR) methods were examined and comparatively evaluated. For older buildings, the demand for ZD is approximately 27–34% higher than for ZC under TEC-2007 and 25–31% higher under TBEC-2018 when using ATC-40. For newer buildings, ZD soil demands are generally 28–35% higher than ZC, depending on the code and damping method. Similar trends are observed with both old and new buildings, with EC8/3 periods showing nearly 39% higher demands for ZD soils.

For ZC soils, the Priestley method consistently produces the lowest displacement demands, while the Ramirez method yields the highest, regardless of building year or code. To highlight these differences, displacement demands from other methods were normalized with respect to the Priestley results (

Table 1. Ratios of displacement demands from SR methods relative to the Priestley method (old buildings).

		ZC Soil					ZD Soil
		N-H	EC8	Ram	LC	Comb EC8&Ram	N-H	EC8	Ram	LC	Comb EC8&Ram
ATC-40	TEC-2007	1.17	1.13	1.20	1.10	1.13	1.11	1.13	1.20	1.10	1.13
	TBEC-2018	1.15	1.11	1.17	1.10	1.11	1.09	1.11	1.17	1.10	1.11
	EC8/3	1.13	1.10	1.15	1.09	1.10	1.13	1.10	1.15	1.09	1.10
Priestley	TEC-2007	1.14	1.11	1.16	1.10	1.11	1.10	1.11	1.16	1.10	1.11
	TBEC-2018	1.12	1.09	1.14	1.09	1.09	1.08	1.09	1.14	1.09	1.09
	EC8/3	1.10	1.08	1.12	1.07	1.08	1.10	1.08	1.12	1.07	1.08

and

Table 2. Ratios of displacement demands from SR methods relative to the Priestley method (new buildings).

		ZC Soil					ZD Soil
		N-H	EC8	Ram	LC	Comb EC8&Ram	N-H	EC8	Ram	LC	Comb EC8&Ram
ATC-40	TEC-2007	1.19	1.17	1.26	1.09	1.17	1.13	1.17	1.26	1.09	1.17
	TBEC-2018	1.18	1.14	1.24	1.10	1.14	1.13	1.14	1.24	1.10	1.14
	EC8/3	1.18	1.13	1.23	1.10	1.13	1.18	1.13	1.23	1.10	1.13
Priestley	TEC-2007	1.14	1.11	1.16	1.10	1.11	1.11	1.11	1.16	1.10	1.11
	TBEC-2018	1.12	1.09	1.13	1.08	1.09	1.09	1.09	1.13	1.08	1.09
	EC8/3	1.11	1.09	1.13	1.08	1.09	1.11	1.09	1.13	1.08	1.09

). When building periods were determined according to Turkish codes, ATC-40 damping led to average displacement demands 10–20% higher than Priestley for older buildings, and slightly lower differences for newer buildings. For EC8/3 periods, other methods gave 9–15% higher than the Priestley method. When equivalent damping was computed using the Priestley approach, these differences were further reduced, indicating that the choice of damping model has a significant effect on the estimated demands, especially for newer buildings with shorter periods. Overall, these results confirm that both the method for calculating spectral reduction and the choice of damping model substantially influence the predicted displacement demands, with the Ramirez method providing the most conservative estimates and Priestley the least.

For ZD soil and older buildings using ATC-40 damping, TEC-2007 periods result in demands roughly 10–20% higher than Priestley, TBEC-2018 periods 9–17% higher, and EC8/3 periods 9–15% higher. Using Priestley damping, these differences are slightly smaller. For newer buildings, ATC-40-based differences increase, reaching 26% for TEC-2007, while using Priestley damping, the differences remain moderate. These results confirm that both the choice of spectral reduction method and soil class have a substantial effect on predicted displacement demands. The Ramirez method consistently provides conservative estimates, while Priestley yields the lowest demands, and soil class differences can amplify displacements by up to 40%.

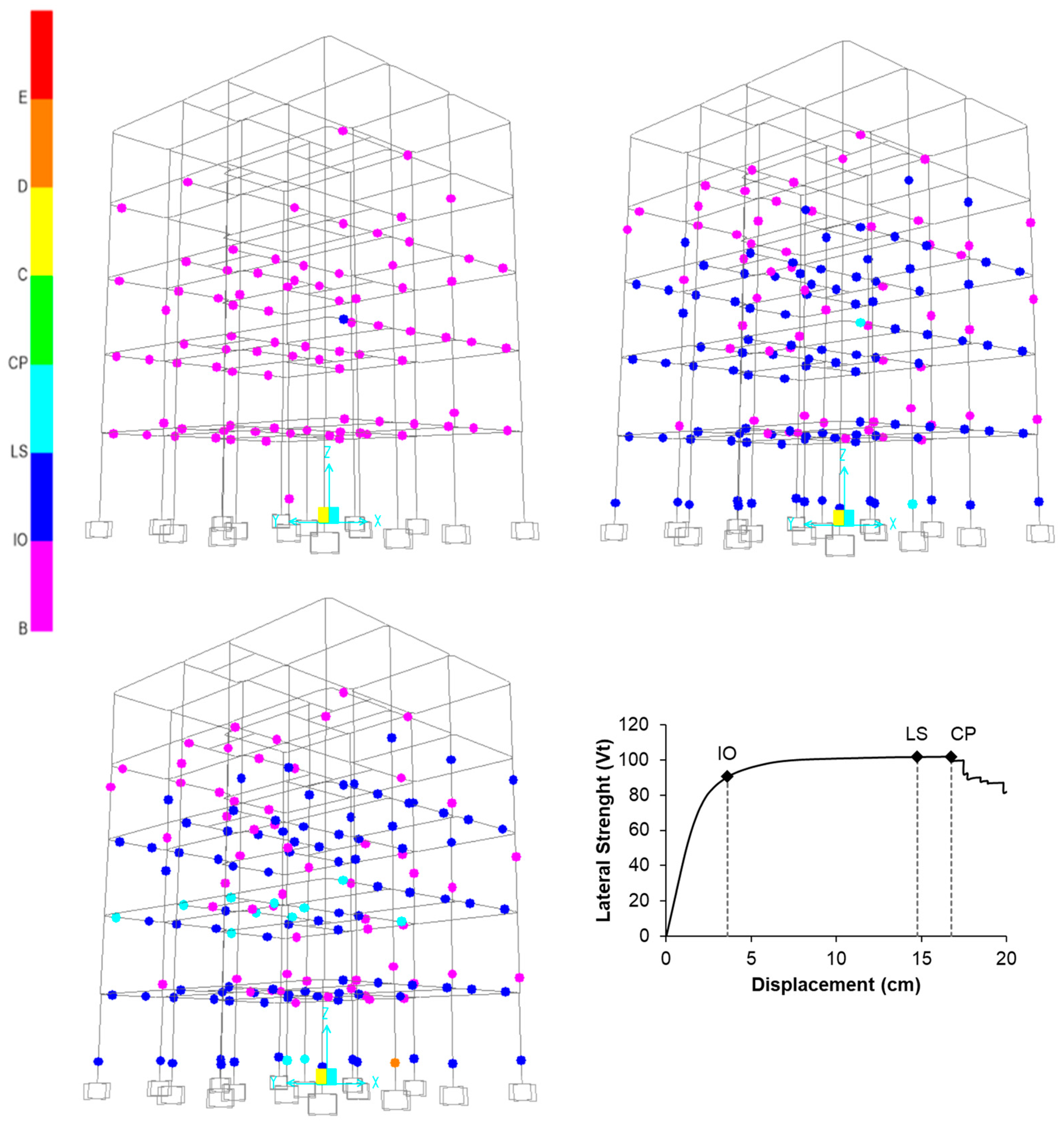
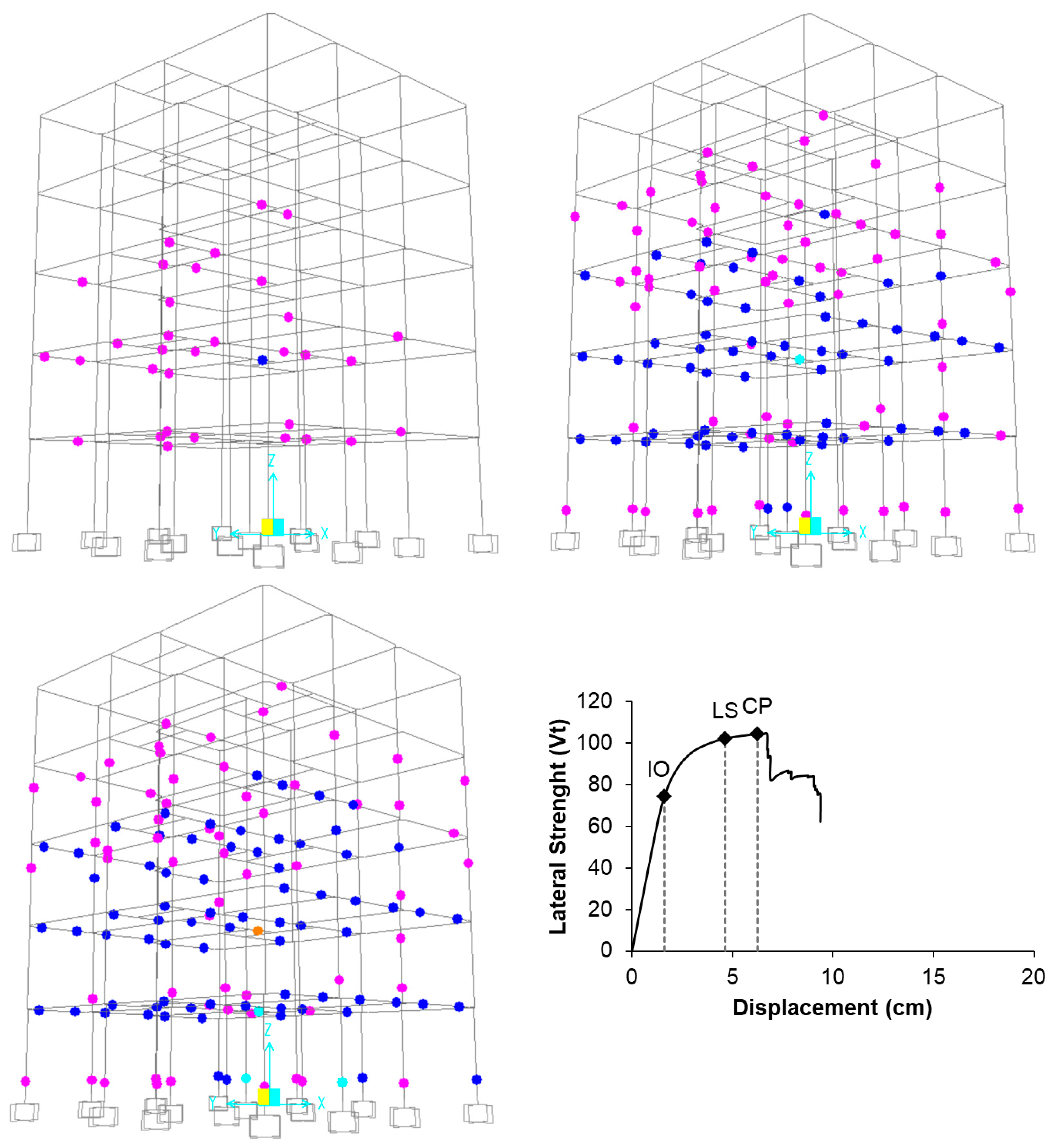
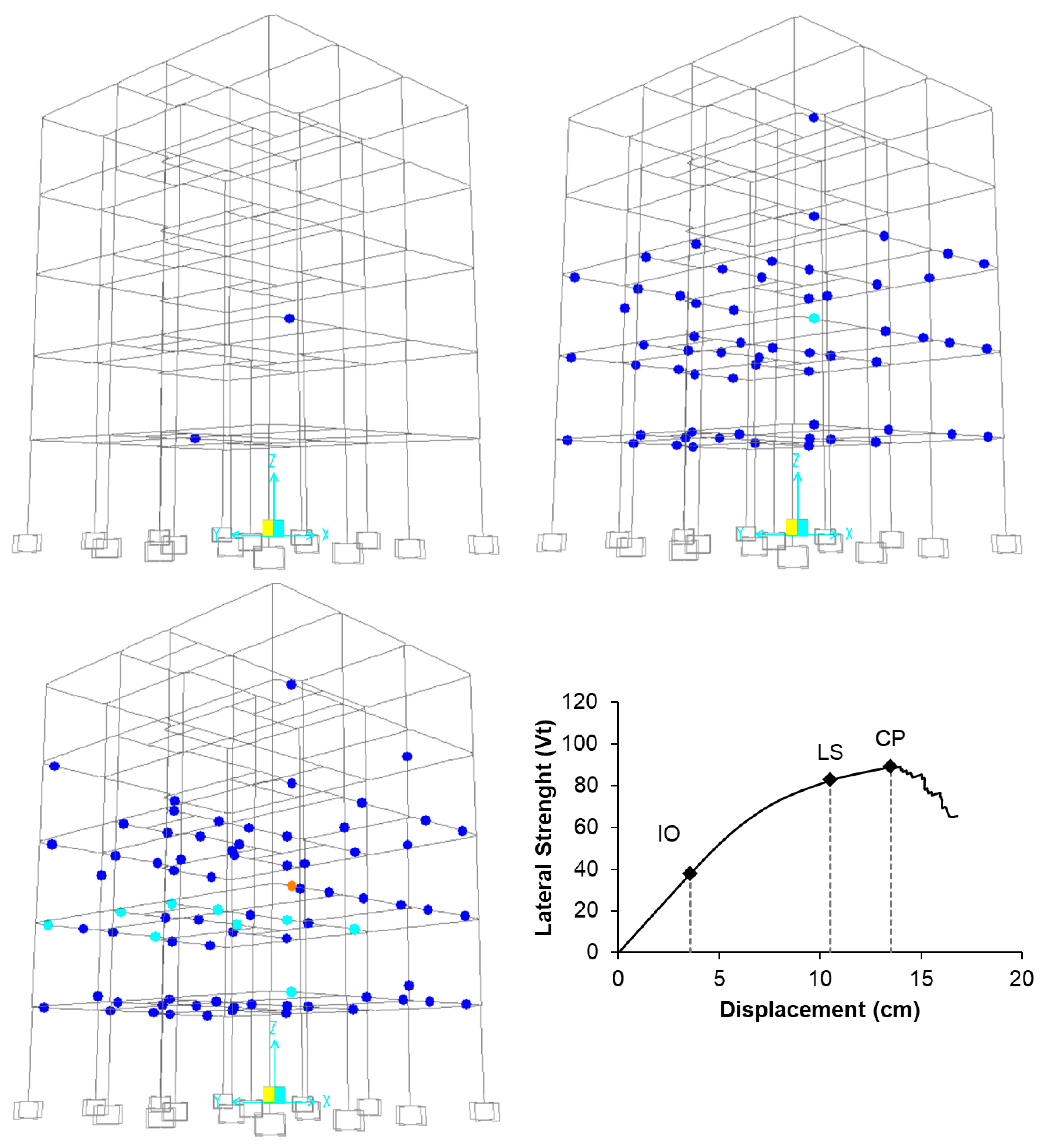
In this study, building performance levels (Immediate Occupancy—IO, Life Safety—LS, and Collapse Prevention—CP) were determined based on the obtained member damage limits. In the Turkish seismic codes, performance limits of buildings are defined in terms of the number of member damages for each direction. In contrast, EC8/3 does not provide such definitions; therefore, certain assumptions were made to establish performance limits under EC8/3. Accordingly, the CP level was adopted following the approach in the Turkish codes, the IO level was assumed equal to the yield displacement obtained from bilinearization, and the LS level was defined as 75% of the collapse, similar with the damage limit definitions. Using demand values obtained from different SR methods, the performance levels for each building direction were evaluated. The numerical distributions of these performance levels with respect to codes, SR methods, and soil types are presented in

Table 3. Performance state of BOs based on SR methods according to TEC-2007.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	0	0	0	0	2	0	1	0	0	0	0	0
	IO	20	20	20	20	18	20	19	20	20	20	20	20
	LS	0	0	0	0	0	0	0	0	0	0	0	0
	CP	0	0	0	0	0	0	0	0	0	0	0	0
Priestley	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	20	20	20	20	20	20	20	20	20	20	20	20
	LS	0	0	0	0	0	0	0	0	0	0	0	0
	CP	0	0	0	0	0	0	0	0	0	0	0	0

,

Table 4. Performance state of BNs based on SR methods according to TEC-2007.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	9	9	5	11	14	9	1	1	1	1	3	1
	IO	11	11	15	9	6	11	19	19	19	19	17	19
	LS	0	0	0	0	0	0	0	0	0	0	0	0
	CP	0	0	0	0	0	0	0	0	0	0	0	0
Priestley	Y	1	1	1	1	4	1	1	1	1	1	1	1
	IO	19	19	19	19	16	19	19	19	19	19	19	19
	LS	0	0	0	0	0	0	0	0	0	0	0	0
	CP	0	0	0	0	0	0	0	0	0	0	0	0

,

Table 5. Performance state of BOs based on SR methods according to TBEC-2018.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	11	12	11	12	14	12	6	3	3	4	7	3
	LS	2	1	2	2	3	1	1	4	3	3	2	4
	CP	7	7	7	6	3	7	13	13	14	13	11	13
Priestley	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	8	8	7	8	12	8	2	1	1	2	3	1
	LS	4	4	5	4	1	4	4	3	3	2	4	3
	CP	8	8	8	8	7	8	14	16	16	16	13	16

,

Table 6. Performance state of BNs based on SR methods according to TBEC-2018.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	0	0	0	0	3	0	2	0	0	0	0	0
	IO	20	20	20	20	17	20	13	15	13	15	19	15
	LS	0	0	0	0	0	0	4	4	5	4	0	4
	CP	0	0	0	0	0	0	1	1	2	1	1	1
Priestley	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	14	15	14	16	19	15	6	6	6	6	7	6
	LS	5	4	5	3	0	4	6	6	4	6	9	6
	CP	1	1	1	1	1	1	8	8	10	8	4	8

,

Table 7. Performance state of BOs based on SR methods according to EC8/3.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	9	9	7	9	15	9	0	0	0	0	0	0
	LS	10	10	11	10	4	10	4	9	4	9	13	9
	CP	1	1	2	1	1	1	16	11	16	11	7	11
Priestley	Y	0	0	0	0	0	0	0	0	0	0	0	0
	IO	3	4	1	4	9	4	0	0	0	0	0	0
	LS	14	13	15	13	10	13	1	1	1	2	7	1
	CP	3	3	4	3	1	3	19	19	19	18	13	19

and

Table 8. Performance state of BNs based on SR methods according to EC8/3.

		ZC Soil						ZD Soil
		N-H	EC8	Ram	LC	Prst	Comb EC8&Ram	N-H	EC8	Ram	LC	Prst	Comb EC8&Ram
ATC-40	Y	20	20	19	20	20	20	4	6	1	7	13	6
	IO	0	0	1	0	0	0	15	13	18	12	7	13
	LS	0	0	0	0	0	0	1	1	1	1	0	1
	CP	0	0	0	0	0	0	0	0	0	0	0	0
Priestley	Y	6	8	6	9	14	8	0	0	0	0	0	0
	IO	13	12	13	11	6	12	16	16	16	16	16	16
	LS	1	0	1	0	0	0	3	3	3	3	4	3
	CP	0	0	0	0	0	0	1	1	1	1	0	1

.

The obtained performance limits are influenced by the characteristics of the buildings and the provisions of the codes. Accordingly, the highest displacement capacities belong to TEC-2007 buildings, while the lowest capacities correspond to TBEC-2018 buildings. Although the displacement values obtained for the methods are similar, building performance varies depending on the capacity. The results largely confirm that buildings reach collapse according to the Ramirez method. As expected, the number of damages at higher damage states (LS and CP) is observed for ZD. Additionally, the number of buildings reaching collapse is lower for new buildings since these buildings are more ductile. The use of different damping ratios also affects building performance. The results indicate that building performance varies depending on the applied reduction factor method and damping method.

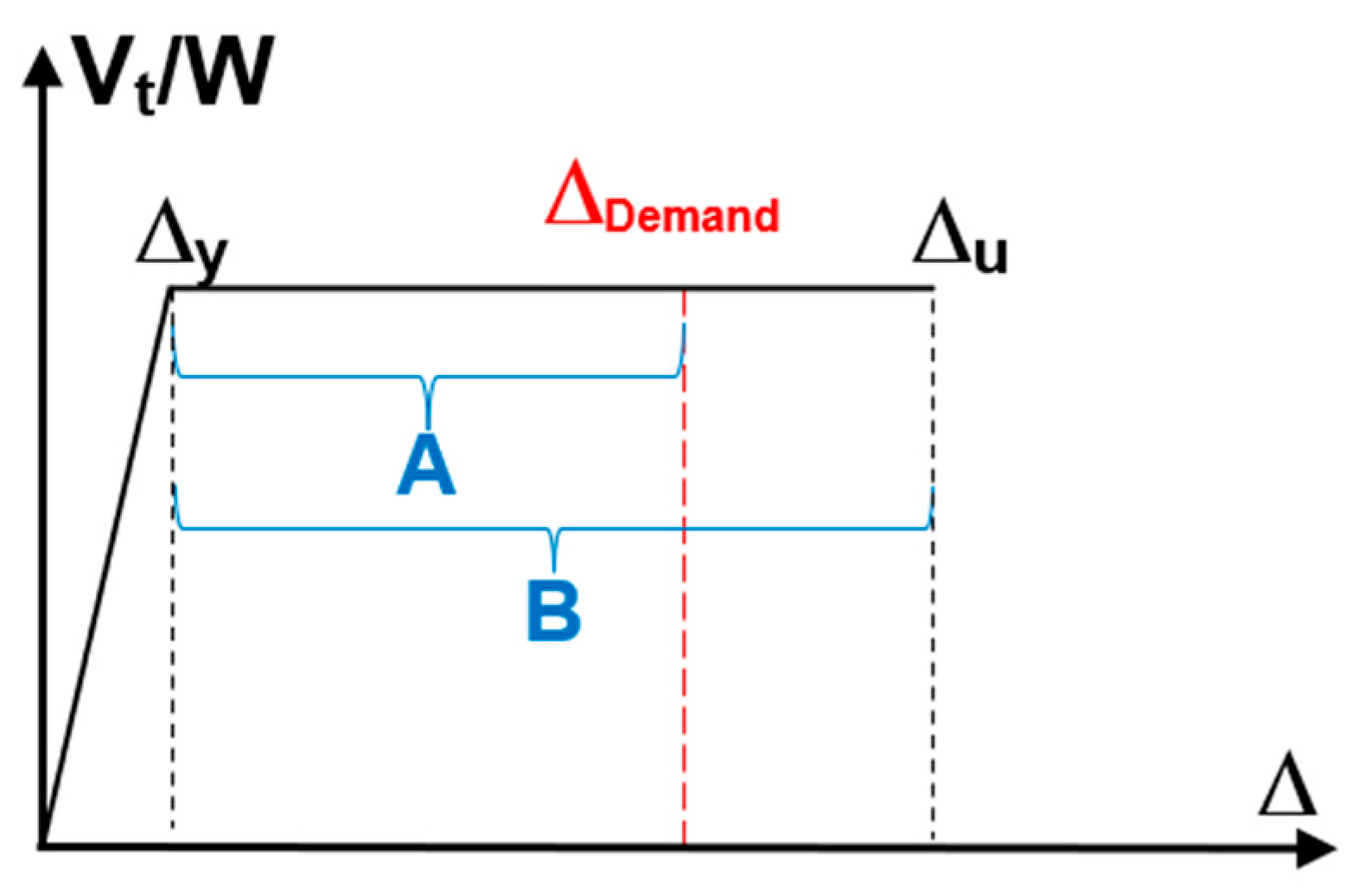
To investigate the influence of different spectral reduction factors on structural performance, the plastic ductility capacities (sketched as “B” in Figure 19) of the buildings were obtained from the capacity curves. Subsequently, plastic ductility demands (sketched as “A” in Figure 19) were calculated by subtracting the yield displacement of the structure from the displacement demands. The ratio of the plastic ductility demand to the plastic ductility capacity was then evaluated, as shown in Figure 19 (Pl_Ratio= A/B). If this ratio is equal to or greater than 1.0, the building is considered to be at the collapse performance level; otherwise, the collapse limit state is not exceeded.

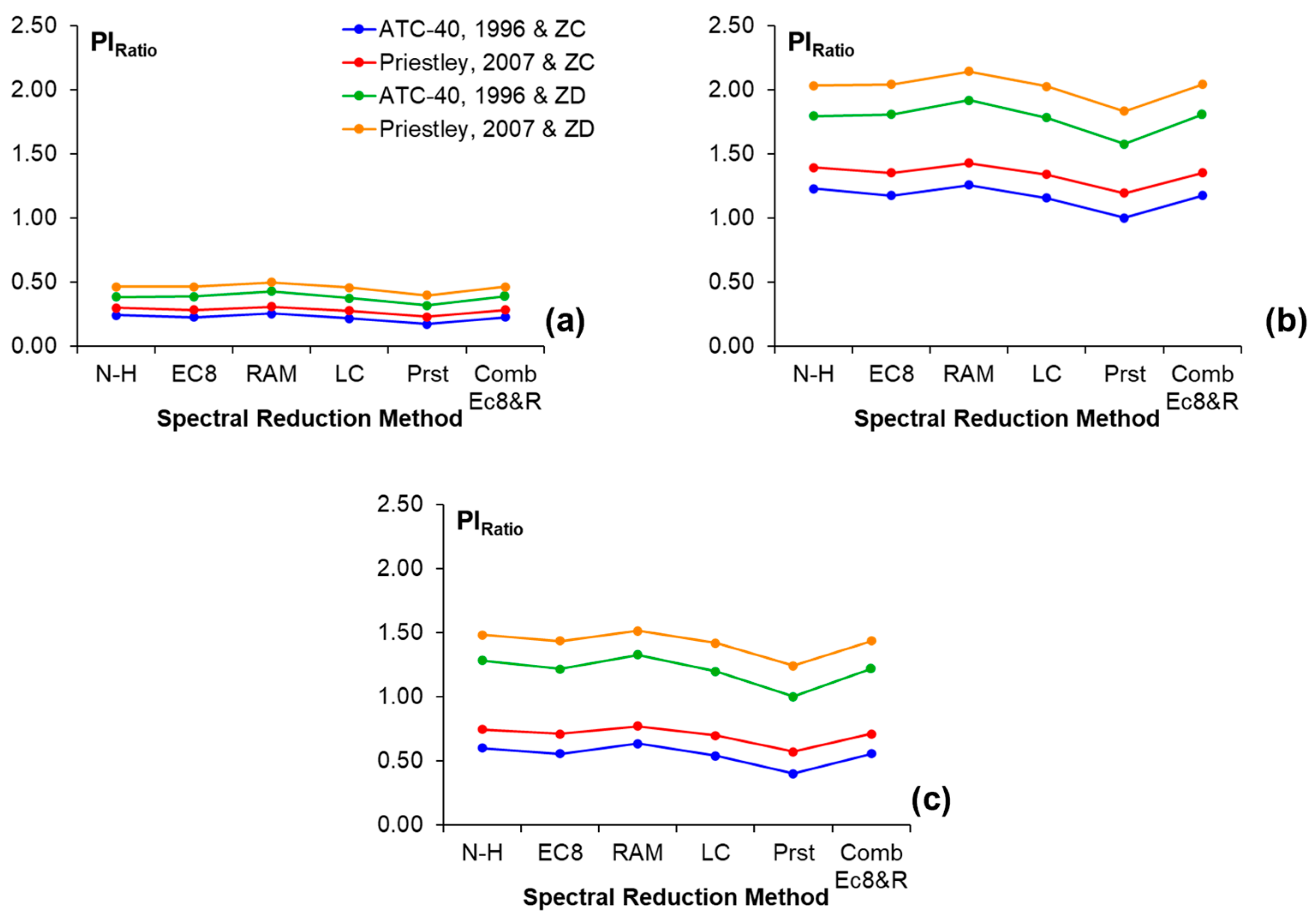
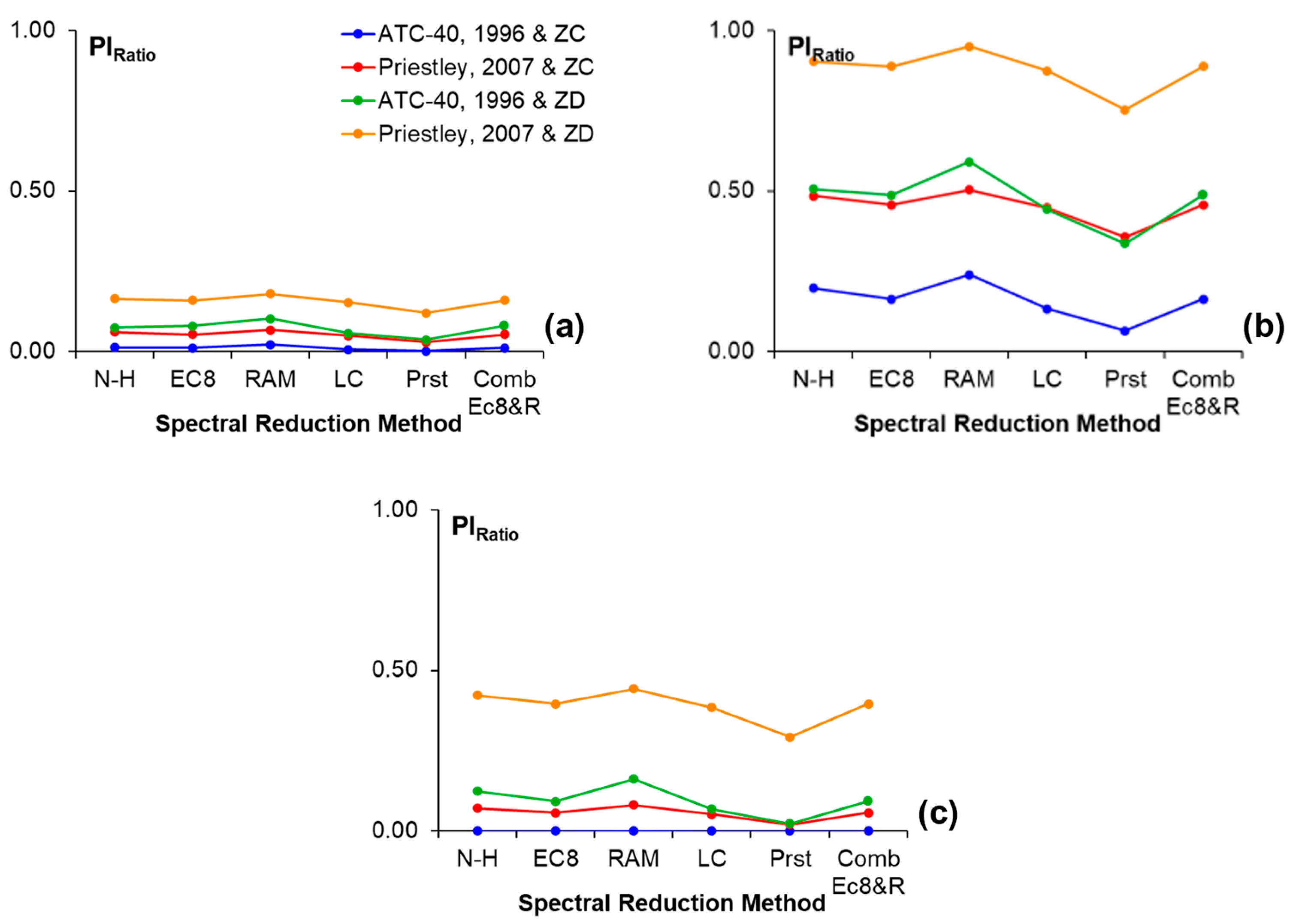
Average Pl_Ratio values are shown in Figure 20 and Figure 21, according to equivalent viscous damping, soil type, and codes. The evaluation of these values shows that the Ramirez method consistently produces the highest ratios, whereas the Priestley method yields the lowest.

According to Figure 20 and Figure 21, Pl_Ratio appears to be more critical when equivalent damping ratio was obtained according to the Priestley method. This situation is more apparent in older buildings, owing to insufficient ductility and strength capacities. Therefore, the plastic ductility ratios obtained for these buildings are higher than those of newer buildings. As can be seen from the capacity curves presented in Figure 7, the highest displacement capacities were obtained from TEC-2007. For this reason, the Pl_Ratio of buildings determined according to TEC-2007 is less than one. In contrast, the displacement capacities obtained for TBEC-2018 buildings are considerably smaller, and hence the ratios calculated for TBEC-2018 are larger than the others. The displacement demands obtained for both seismic codes are similar; however, the displacement capacities determined according to the codes differ significantly. Therefore, remarkable differences are observed between the plastic capacity ratios [50]. Although the displacement demands obtained for EC8/3 are higher, due to the approaches adopted in the code, the yielding displacement occurs at a larger deformation level. Therefore, the resulting Pl_Ratio values are not affected by the demand values; the plastic demand capacity decreases, and Pl_Ratio does not reach very large values.

As clearly observed in Figure 9, the displacement values corresponding to the same period are larger for ZD soil types than for ZC soils. Therefore, the demand displacements obtained for ZD soils increase. In contrast, the capacities obtained for the buildings remain constant. As a result, the Pl_Ratio for ZD soils is higher.

4. Conclusions

This study evaluated the seismic displacement demand and plastic demand–capacity ratios of 20 existing reinforced concrete buildings designed under different seismic codes by applying multiple spectrum reduction and damping estimation approaches. Unlike most previous studies based on idealized or SDOF, the analyses were performed on real buildings. Structural properties such as building period and the ductility values of these buildings were determined in accordance with these codes and demand values corresponding to different spectrum reduction factors were compared. This constitutes the primary contribution of the study and enables a direct assessment of how code provisions and methodological choices influence seismic performance evaluation in practice.

The results demonstrate that seismic demand estimates are governed by three interacting mechanisms: code-dependent period definitions, equivalent viscous damping formulations, and spectrum reduction method formulations. Differences between old and new buildings arise primarily through their ductility-dependent damping estimates rather than age alone. Newer buildings exhibit higher plastic ductility capacities due to their strength and deformation capacity, which directly increases equivalent damping and alters spectral reduction factors.

Both the ductility values and structural periods significantly influence damping ratios, SR factors, and resulting displacement demands. TEC-2007 buildings, having higher ductility and damping ratios, correspond to lower SR factors, while TBEC-2018 and EC8/3 exhibit closer values for new buildings due to similar ductility assumptions. The SR coefficients follow an increasing order of TEC-2007, TBEC-2018, and EC8/3, which is reflected in the displacement demands.

For older buildings, the SR values obtained using Priestley damping are approximately 11% higher than those based on ATC-40 damping across all seismic codes for both soil classes. In contrast, this difference increases to approximately 30% for newer buildings.

The SR coefficients are also governed by the corner periods of the response spectra and the period limits defined in the reduction formulations. The Newmark–Hall method highlights spectrum differences, yielding SR values approximately 6% higher for ZC soils, whereas this trend is not consistently observed in the other methods. Similar variations occur at different periods due to changes in effective structural stiffness. Thus, EC8/3 shows no noticeable soil-dependent variation in SR values.

The ATC-40 approach yields systematically higher equivalent damping ratios than the Priestley method, particularly for newer buildings, due to the coefficient distinguishing structural characteristics. ATC-40 method, the equivalent viscous damping ratios obtained for new and old buildings were found to be approximately 93% and 30% higher, respectively. However, these large differences in damping ratios do not translate proportionally into displacement demands, indicating a nonlinear sensitivity between damping, spectral reduction, and displacement response. In contrast, the Priestley approach produces lower and more stable damping values, resulting in consistently more spectral reduction factors and displacement demands.

Across all codes, soil classes, and building ages, the Ramirez method produces the largest displacement demands and plastic demand–capacity ratios, while the Priestley method yields the lowest. This confirms that the Ramirez approach is the most conservative in displacement-based performance assessment. Differences among methods persist even when identical damping ratios are used, highlighting that the mathematical formulation of the spectrum reduction method itself is a critical source of variability.

For the Ramirez method, the displacement values obtained using ATC-40 damping ratios are approximately 17% and 24% higher for old and new buildings, respectively. When Priestley damping is adopted, this difference is reduced to about 14% for both building years, indicating that the sensitivity of the building type classification of ATC-40 damping.

Code-dependent period definitions significantly affect demand estimates. EC8/3 produces longer effective periods due to lower stiffness assumptions; however, because these periods generally exceed the corner period of the spectrum, the resulting displacement demands are less sensitive to soil class. In contrast, Turkish codes exhibit stronger soil-dependent variations, particularly for ZD soils, where displacement and plastic ratios increase consistently due to larger spectral ordinates, while structural capacities remain unchanged. The use of different spectral conditions results in an average difference of approximately 30% in displacement demands.

Overall, the findings demonstrate that building age influences seismic response indirectly through ductility-controlled damping and capacity definitions rather than as an independent parameter. The study clearly shows that the choice of damping estimation model and spectrum reduction approach can alter displacement demands and performance classification, even for the same building. Therefore, these methodological choices are not interchangeable and should be treated as a critical component of seismic performance assessment frameworks.