A Stress-Relief Concept and Its Energy-Dissipating Support for High-Stress Soft-Rock Tunnels

Abstract

When tunnels pass through high-stress, weak, and fractured rock layers, conventional rigid supports often struggle to resist the significant loosening pressure and deformation pressure from the surrounding rock, leading to various large deformation disasters. To address the limitations of support control in high in situ stress soft-rock tunnels, this study proposed a stress-relief concept for the surrounding rock based on the convergence–confinement method. An analytical elastoplastic model and a parameter selection approach for support design were developed accordingly. Guided by the mechanical behavior of tunnel supports under this concept, a novel circumferential yielding element with friction reduction and energy-dissipation capabilities was designed and validated through laboratory tests. Unlike previous reinforced or yielding support approaches, the proposed method provides a synchronized reduction in support resistance with surrounding-rock stress release, offering a fundamentally different and more adaptive deformation-control mechanism for high-stress soft-rock tunnels. Field applications were conducted in the asymmetric large-deformation section of the Qiaojia Tunnel, where full-face monitoring determined the design parameters of the energy-dissipating support (EDS) system. Field test data show that, compared with conventional rigid supports, the proposed system can effectively control asymmetric deformation, reducing the surrounding rock pressure difference between the left and right tunnel shoulders from 0.84 MPa to 0.23 MPa, highlighting its advantages for stabilizing high-stress soft-rock tunnels. The results provide a practical framework for designing adaptive support systems that combine controlled yielding and energy dissipation.

1. Introduction

With the rapid development of transportation infrastructure in western China and mountainous regions, a large number of deep-buried and extra-long tunnels have been constructed. Under conditions of high in situ stress, soft-rock, and fractured fault zones, tunnel excavation has often been affected by poor self-stability of surrounding rock, pronounced structural stress, and softening or swelling of the rock mass upon water exposure [1,2]. Typical cases include the Taba Yi Tunnel, Gaoligongshan Tunnel, Wuqiaoling Tunnel, Lianchengshan Tunnel, and Yangjiaping Tunnel [3], all of which have frequently experienced various types of geological hazards due to weak rock strata. Taking the Yangjiaping Tunnel as an example, influenced by the Qianfoshan oblique thrust fault zone and other structural factors, the surrounding rock stress was readjusted after excavation. Combined with severe rock weathering, poor interlayer cohesion, and water-induced softening and disintegration, the maximum deformation of the initial support reached 1052 mm, and the proportion of tunnel sections experiencing large deformation disasters reached 70.5%. Such disasters not only threaten structural safety but also significantly hinder construction progress and increase project costs [4]. Although traditional support systems have been widely applied, they often fail to cope with large deformations of the surrounding rock, resulting in a vicious cycle of “reinforcement–failure–re-reinforcement”.

Extensive studies have been carried out by researchers worldwide on the control of large deformations in tunnels. The convergence–confinement method [5] has provided an important theoretical framework for analyzing the interaction between surrounding rock and support, leading to the development of several control theories and methods, including reinforced support, key-zone bearing, stress compensation, and yielding control.

The concept of reinforced support [6,7] enhances the bearing capacity by increasing the thickness and stiffness of the support or by applying multi-layer primary linings. However, this approach inevitably leads to a substantial increase in construction cost, and under extremely high in situ stress conditions, it often fails to achieve satisfactory support performance.

The key-zone or key-layer bearing theories, such as the loosening zone support theory [8], key-zone control theory [9], and the New Austrian Method full-section reinforcement theory [10], are based on reinforcing the loosening or plastic zones of the surrounding rock so that the rock mass and the support structure jointly form a load-bearing system. This approach helps to reduce the structural load and control rock loosening deformation. Nevertheless, the current detection technologies cannot accurately determine the extent of the loosening zone, and the detection process remains complicated and time-consuming.

The rock stress compensation theory [11] analyzes changes in the stress state of the surrounding rock after excavation. By restoring the stress of the surrounding rock to its initial or elastic state, large deformations can be effectively controlled. However, its construction process is complex, technically demanding, and costly, and the resulting effectiveness is often disproportionate to the investment.

The yielding control theory allows for greater deformation of the surrounding rock to fully release the accumulated energy and expand the plastic zone, enabling deeper rock layers to participate in the load-bearing system. Representative theories include the energy release theory [12], yielding support theory [13,14], and active-yielding support theory [15,16]. Although existing yielding supports can release part of the accumulated energy, their mechanical response remains unclear, and they often fail to provide sufficient bearing capacity during the early stages of deformation. Therefore, the mechanism of large deformation in high in situ stress soft-rock tunnels is still not fully understood, and adaptable, practical control technologies are still lacking.

To address these issues, this study proposed a stress-relief control concept consistent with the stress release behavior of the surrounding rock. Based on this concept, a friction-reducing and energy-dissipating support structure with a “rigid–relief–rigid” mechanical characteristic was developed. Relying on field monitoring data, an on-site application study was conducted to verify the engineering applicability of the proposed support system in asymmetric large-deformation tunnel sections. The results provide a feasible technical approach and practical reference for tunnel construction under similar complex geological conditions.

Accordingly, the objective of this study is to establish and validate a stress-relief–based deformation-control framework through analytical modeling, element development, parameter determination, and field evaluation of the proposed energy-dissipating support (EDS) system.

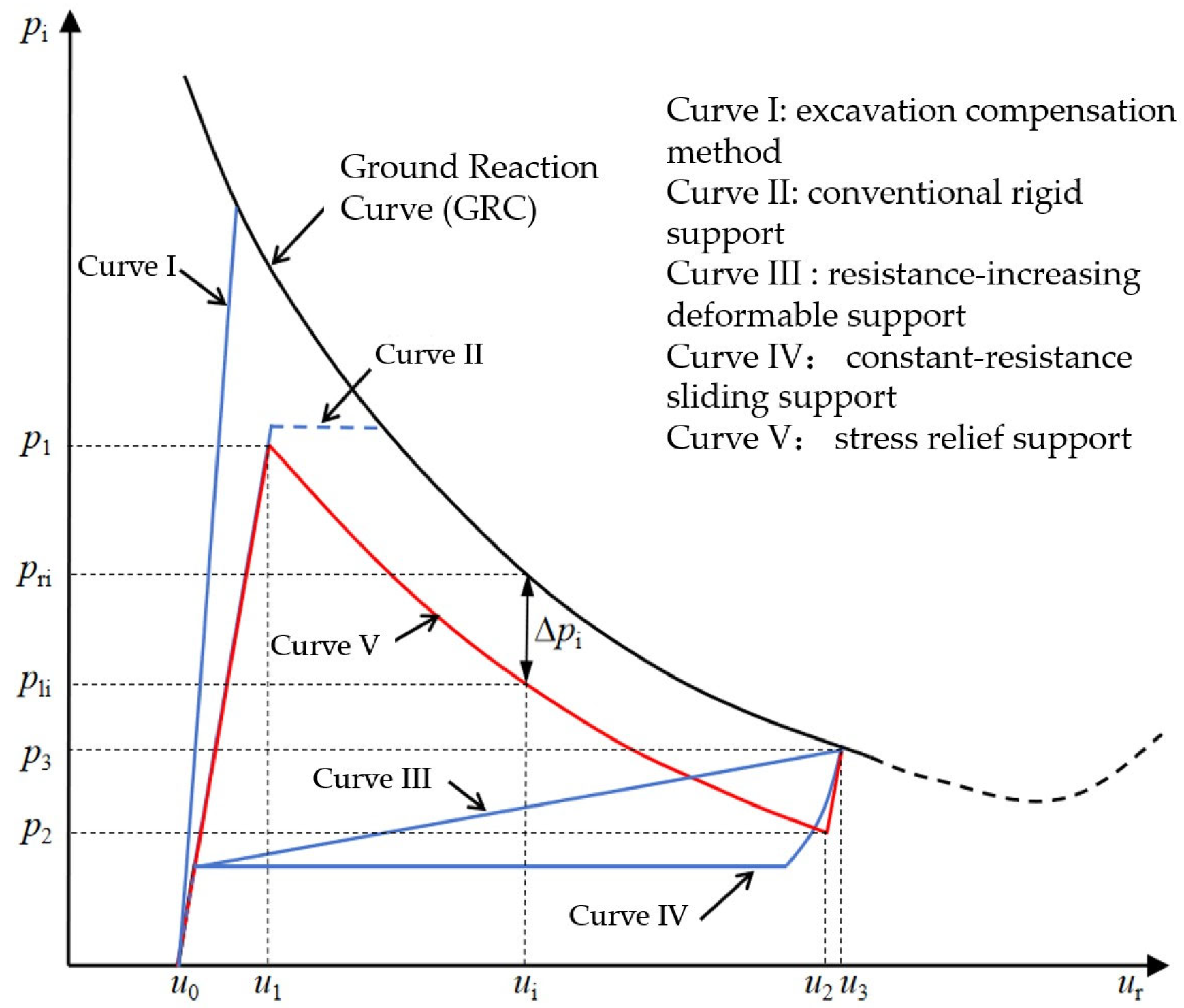
2. Stress-Relief Concept for Surrounding Rock in High In Situ Stress Tunnels

2.1. Fundamentals of the Stress-Relief Control Concept

The traditional convergence–confinement method mainly focuses on the intersection point between the characteristic curves of the surrounding rock and the support under a stable state, while neglecting the mechanical evolution process from excavation to stabilization. For high in situ stress tunnels with large deformation, this limitation often results in a significant deviation between the actual support pressure and the virtual support pressure, leading to early-stage rapid deformation, intensified rock disturbance, and even support failure or collapse.

To overcome this deficiency, a new control concept—stress-relief control— was proposed by integrating the existing convergence–confinement method with the yielding philosophy of tunnel support. The core idea of the stress-relief control concept is to gradually and dynamically release the surrounding rock pressure through a decreasing support resistance corresponding to the progressive deformation of the tunnel. After installation, the support initially provides a relatively high resistance to reduce the difference between the virtual and actual support pressures at the tunnel boundary. As the deformation of the surrounding rock increases and the stress is gradually released, the support resistance decreases correspondingly until deformation reaches a stable state.

Throughout the entire deformation process, the virtual support pressure required for stability and the actual support resistance decrease synchronously. As a result, the disturbance of the surrounding rock is effectively controlled, and the radial unbalanced force of the rock mass remains at a low level. Consequently, the development of the plastic zone and the deformation rate of the surrounding rock stay within a safe and controllable range.

Figure 1 illustrates the schematic comparison of the convergence–confinement relationships for different methods, including the excavation compensation method, rigid support, constant-resistance sliding support, resistance-increasing deformable support, and the stress-relief method proposed in this study.

In Figure 1, u₀ represents the radial pre-deformation of the surrounding rock at the time of support installation. Curve I corresponds to the excavation compensation method [11], and Curve II represents the conventional rigid support. Both belong to the traditional resistive-type support system. The former relies on prestressed anchors to provide high initial resistance, which effectively suppresses plastic failure but is limited by complex construction procedures and high costs. The latter depends on shotcrete and steel arches to provide stiffness, allowing rapid initial stabilization of the surrounding rock. However, under high in situ stress conditions, such rigid supports are prone to brittle failure, making post-failure deformation control difficult.

Curves III and IV represent the characteristic curves of increasing-resistance deformable support [17] and constant-resistance deformable support [18], respectively, both of which fall under the category of yielding support. In increasing-resistance deformable support, a segment of the rigid primary lining is typically replaced with an adaptive element capable of gradually increasing stiffness. However, during the early deformation stage of the surrounding rock, the support resistance provided by both increasing-resistance and constant-resistance deformable supports is significantly lower than the required virtual support pressure for rock mass stability. This insufficiency can lead to excessively rapid deformation and an accelerated expansion of the plastic zone, making arch formation difficult and compromising overall tunnel stability.

Curve V represents the stress-relief support proposed in this study, which combines the advantages of both resistance and yielding. It exhibits a “rigid–relief–rigid” three-stage mechanical characteristic:

• A high initial stiffness stage, suppressing rapid loosening of the surrounding rock;
• A moderate stress-relief stage, guiding gradual energy release and controlling the deformation rate;
• A final re-stiffening stage, promoting deformation convergence and providing structural redundancy.

Figure 2 illustrates the support theory of the stress-relief method based on the Mohr–Coulomb criterion. In the figure, the in situ stress of the stratum at infinity is denoted as p₀. After tunnel excavation, the radial and tangential stresses at the tunnel wall are 0 and 2p₀, respectively. Before stress redistribution, the radial stresses at the elastic and plastic boundaries of the surrounding rock are represented by σ_rp and σ_θp, respectively.

After tunnel support installation, an initial compensatory pressure p_i1, comparable to that provided by rigid support, is applied to the tunnel wall. This reduces the circumferential stress concentration in the surrounding rock and prevents the deeper rock mass from prematurely entering the plastic state, thereby creating favorable conditions for gradual stress release in the surrounding rock.

At the end of the rigid stage, the stress in the surrounding rock still exceeds the failure envelope, causing the rock to continue developing plastically to release internal stress. The core mechanism of the stress-relief method lies in the synchronous reduction in support resistance with the progressive release of surrounding rock stress. Throughout both the elastic and plastic stages, the radial unbalanced force acting on the surrounding rock remains at a very low level. The slow stress release of the shallow rock also mitigates disturbance to the deeper surrounding rock, which defines the stress-relief stage.

Because the plastic stress–strain field of the surrounding rock exhibits a significant time-dependent effect, deformation and failure develop gradually from shallow to deep layers. The radial support pressure of the deep rock is jointly provided by the shallow rock and the support structure. The stress-relief method effectively prevents shallow surrounding rock from entering the plastic state too rapidly or from insufficient support resistance, thereby avoiding the possibility of deeper rock rapidly yielding and disturbing even deeper zones. Compared with other support methods, the stress-relief support can more effectively reduce the disturbance depth of the surrounding rock and enhance the overall safety and stability of the support process.

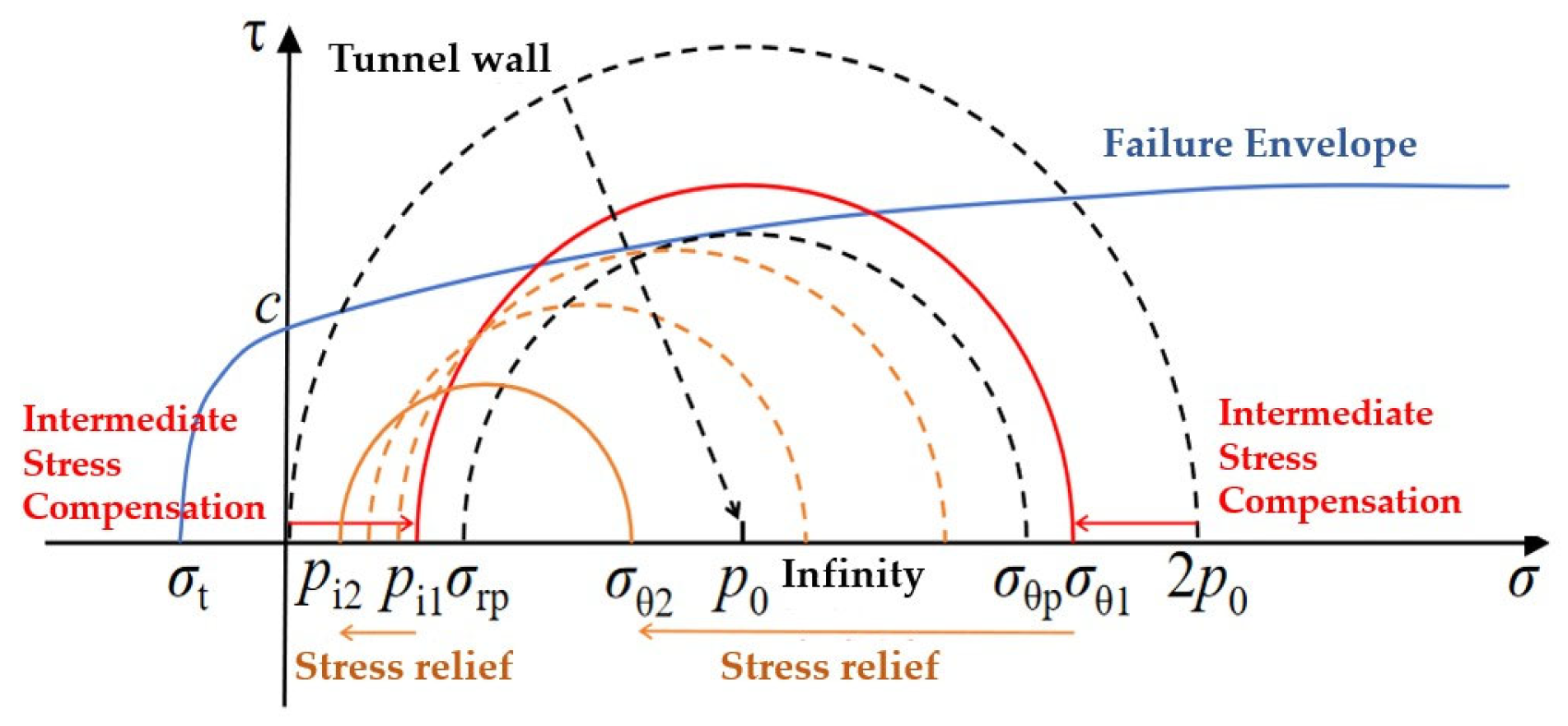
2.2. Elastoplastic Solution of the Surrounding Rock–Support System Under the Stress-Relief Control Concept

To facilitate the theoretical derivation, the mechanical behavior of the stress-relief element was simplified using the following assumptions: in its three stages—rigid–relief–rigid—the first and third stages were regarded as infinitely rigid, with axial stiffness equivalent to that of conventional rigid supports; the second stage represents the stress-relief phase, during which the bearing capacity gradually decreases from F_θmax to F_θmin as the compressive deformation increases, while the element length reduces from h₀ to h₁.

The force–displacement relationship of the stress-relief phase can be approximately modeled using a trigonometric function, as illustrated in Figure 3. It was assumed that the horizontal thrust F_N and the inclined rod length l remain constant throughout the compression process of the stress-relief element. Both ends of the inclined rods are hinged, and no horizontal friction acts on the ground. As the vertical compression displacement increases, both the inclination angle α and the remaining height h of the stress-relief element decrease continuously, leading to a corresponding reduction in the axial bearing capacity F_θ. This mechanism simulates the stress-relief stage, in which the support resistance gradually decreases with increasing deformation, reflecting the progressive energy release of the surrounding rock.

To facilitate the theoretical analysis, it was assumed that both the surrounding rock and the lining exhibit axisymmetric geometry, and the surrounding rock pressure acts as hydrostatic pressure. Therefore, the support resistance is equal in magnitude to the surrounding rock pressure and is denoted as p_i. The relationship between the axial force of the lining and the surrounding rock pressure can be expressed as follows:

$$F_{\mathsf{\theta }}=p_{\mathrm{i}}Rz,$$

(1)

where z is the longitudinal calculation length along the tunnel axis (taken as 1 m), and R is the tunnel radius.

It was assumed that the initial support is installed when the radial deformation of the surrounding rock reaches u₀. At the end of the first (“rigid”) stage of the initial support structure with stress-relief elements, the radial displacement and radial support pressure of the tunnel are as follows:

$$\{\begin{array}{c}{u}_1=u_0\\ p_1={\displaystyle \frac{F_{\theta max}}{Rz}}\end{array}.$$

(2)

According to the geometrical relationship of compressive deformation (as shown in Figure 3), during the stress-relief stage, the relationship between the axial bearing capacity F_θ of the stress-relief element and the constant horizontal thrust F_N can be expressed as follows:

$$F_{\theta }=F_N{\displaystyle \frac{2h}{\sqrt{4l^2-h^2}}}.$$

(3)

The total circumferential compression of all stress-relief elements installed around the tunnel can be expressed as follows:

$$u_{\theta }=n\left(h_0-h\right),$$

(4)

where u_θ is the circumferential compression length, and n is the number of stress-relief elements installed around the full ring. The relationship between the radial convergence deformation u_r of the circular tunnel and the circumferential compression deformation u_θ can be approximately written as follows:

$$u_r={\displaystyle \frac{u_{\theta }}{2\pi }}.$$

(5)

Since the circumferential deformation of the steel-arch–concrete lining under rock pressure is negligible compared to that of the energy-dissipating structure, the lining outside the stress-relief elements can be assumed to behave as an infinitely rigid material. By combining Equations (2)–(5), the relationship between surrounding rock pressure and radial deformation for the stress-relief support structure can be expressed as follows:

$$p_i={\displaystyle \frac{2F_N}{Rz}}{\left[4{\left({\displaystyle \frac{ln}{n{h}_0-2\pi u_r}}\right)}^2-1\right]}^{-{\displaystyle \frac{1}{2}}}.$$

(6)

Considering that the stress-relief support is installed when the surrounding rock deformation reaches u₀, u_r in Equation (6) can be replaced by (u_r−u₀) for use in the convergence–confinement analysis. Thus, the radial displacement and support pressure at the end of the second (“relief”) stage of the initial support structure incorporating stress-relief elements are as follows:

$$\{\begin{array}{c}{u}_2=u_0+{\displaystyle \frac{n\left(h_0-h_1\right)}{2\pi }}\\ p_2={\displaystyle \frac{2F_N}{Rz}}{\left[4{\left({\displaystyle \frac{ln}{n{h}_1}}\right)}^2-1\right]}^{-{\displaystyle \frac{1}{2}}}\end{array},$$

(7)

Assuming that the surrounding rock follows an ideal elastoplastic constitutive model and that the dilatancy of the plastic zone is negligible, the relationship between the support pressure p_i at the tunnel wall and the radial displacement u_r under hydrostatic pressure can be expressed as follows:

$$p_i=\left(p_0+c\mathit{cot}\phi \right)\left(1-\mathit{sin}\phi \right){\left({\displaystyle \frac{IR}{u_r}}\right)}^{{\displaystyle \frac{N_{\phi }-1}{2}}}-c\mathit{cot}\phi ,$$

(8)

where

$$I={\displaystyle \frac{1}{2G}}\left(p_0\mathit{sin}\phi +c\mathit{cos}\phi \right)$$

(9)

is the displacement coefficient, which can be used to construct the ground reaction curve (GRC) of the surrounding rock for the convergence–confinement method under the stress-relief support concept.

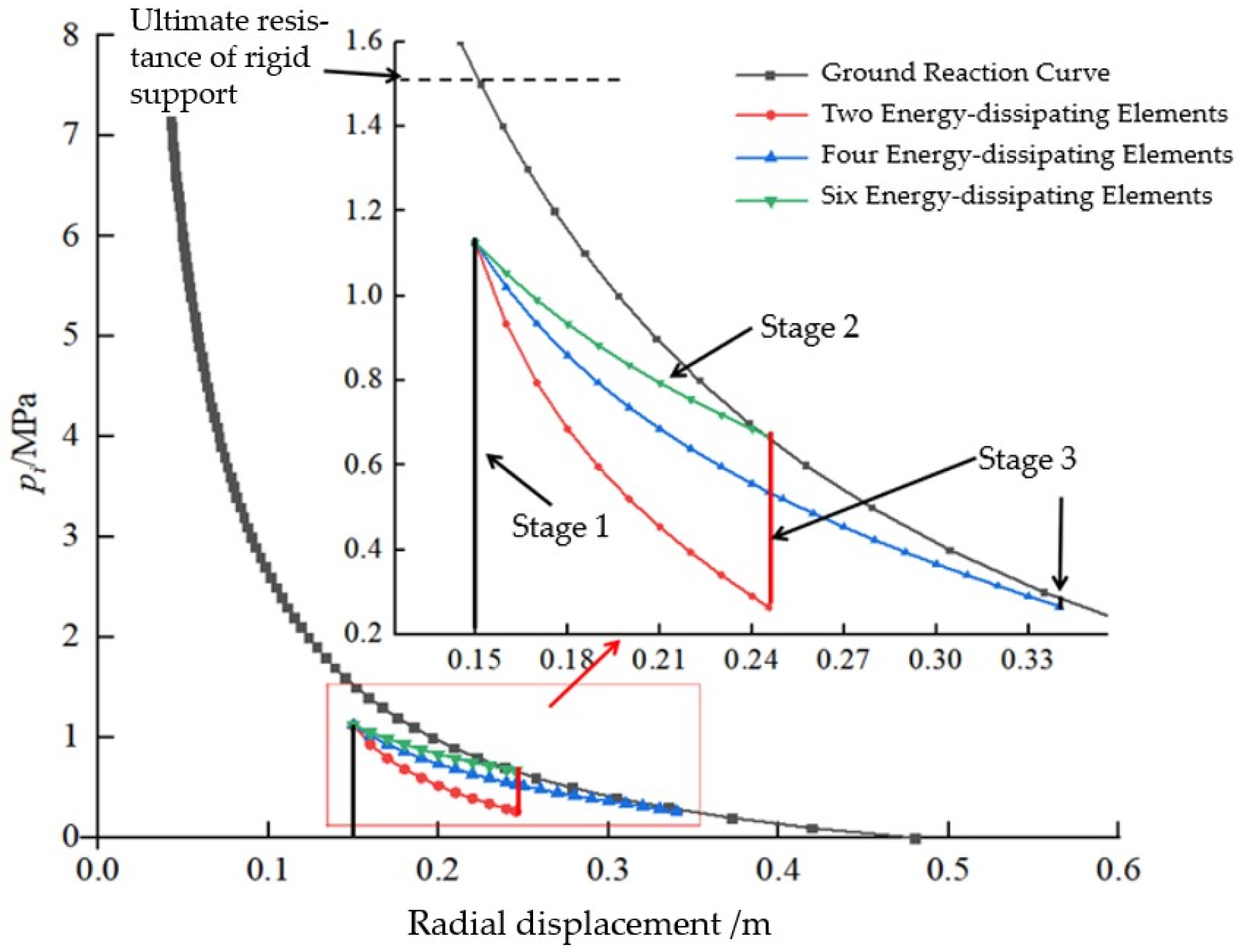
2.3. Influence of Stress-Relief Support Parameters on Tunnel Control Performance

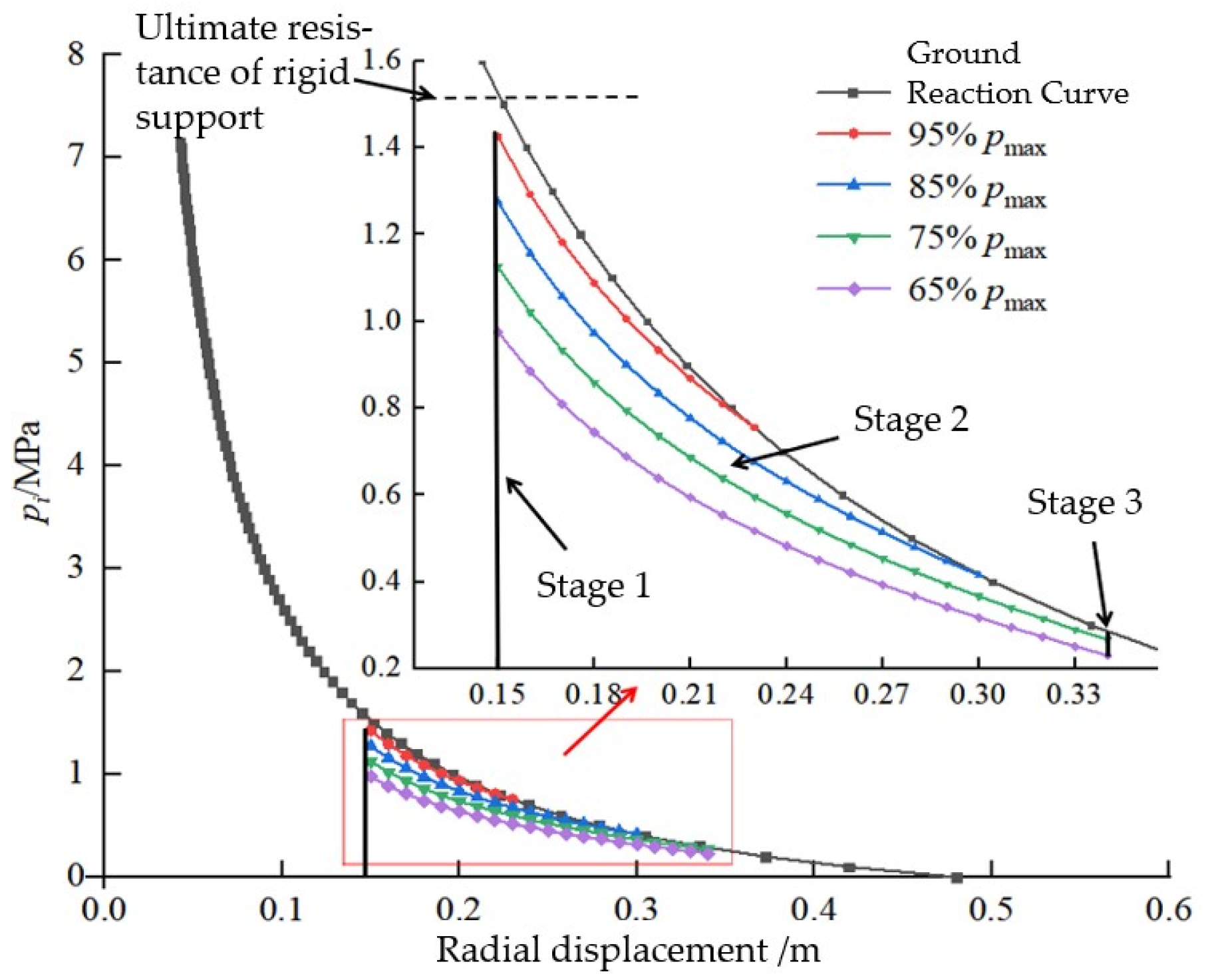
2.3.1. Influence of Peak Resistance on Support Performance

This subsection aims to investigate how the peak support resistance of the stress-relief support system affects its overall performance and deformation-control capability.

The peak resistance at the end of the rigid stage of the stress-relief support is determined by the constant horizontal resistance of the stress-relief element. In the convergence–confinement method, the closer the coordinate point corresponding to the initial peak resistance of the stress-relief support is to the GRC, the lower the radial unbalanced force of the surrounding rock and the slower its deformation rate.

In this analysis, the tunnel radius was set to R = 6 m, and the in situ stress was p₀ = 15 MPa. The surrounding rock was classified as Grade IV, representing relatively weak lithology. Its mechanical parameters are listed in

Table 1. Physical and mechanical parameters of the surrounding rock.

Rock Grade	Unit Weight (kN/m3)	Deformation Modulus (GPa)	Poisson’s Ratio	Cohesion (MPa)
Grade IV Rock	20	1.5	0.35	0.4

. The number of stress-relief elements arranged circumferentially was n = 4, with an initial height h₀ = 0.5 m, a height at ultimate compression h₁ = 0.2 m, and an inclined rod length l = 0.3 m.

The peak resistance of the first (“rigid”) stage of the stress-relief support was set to 95%, 85%, 75%, and 65% of the ultimate bearing capacity of the rigid support (p_max = 1.5 MPa). Substituting these parameters into Equations (6) and (8) yields the convergence–confinement curves of the stress-relief support, as shown in Figure 4.

As shown in Figure 4, when the peak resistance at the end of the first stage of the stress-relief support is 95% and 85% of the ultimate bearing capacity of the rigid support, the two characteristic curves intersect in the second stage. At the intersection, the deformations are 0.23 m and 0.30 m, and the corresponding support resistances are 0.75 MPa and 0.40 MPa, respectively. The deformations of the stress-relief support at these points correspond to 42.1% and 78.9% of the ultimate deformation. Excessively high peak resistance restricts the normal performance of the stress-relief support in friction reduction, stress relief, and energy dissipation.

When the peak resistance of the stress-relief support is reduced to 75% and 65% of the ultimate bearing capacity of the rigid support, the characteristic curves intersect in the third stage, where the energy-dissipating structure is completely compressed. In this case, the radial deformation of the tunnel is 0.34 m, and the support resistance is 0.31 MPa.

The support safety factor, defined as the ratio of the ultimate support resistance to the support resistance at stabilization, increases with decreasing peak resistance, reaching values of 2.00, 3.75, 4.84, and 4.84, respectively. This indicates a trend of increasing and then stabilizing the safety factor. Appropriately reducing the peak resistance of the stress-relief support facilitates the release of surrounding rock pressure. However, an excessively low peak resistance may result in a large radial unbalanced force during the deformation convergence process, causing increased disturbance to the surrounding rock and expansion of the plastic zone radius.

In practical applications, the peak bearing capacity of the stress-relief elements should be matched with the axial force of the primary support at their installation location during the critical construction step. Generally, the peak capacity of the elements should not exceed the maximum primary support axial force that may occur at that location, in order to prevent structural crushing. At the same time, it should be set slightly lower than the primary support axial force corresponding to the construction step in which the axial force at that location first reaches a high level, ensuring that the elements can promptly enter their flexible compression stage.

2.3.2. Influence of the Number of Stress-Relief Elements on Support Performance

This subsection aims to examine how the number of stress-relief units influences the overall support performance and deformation-control effectiveness.

The number of stress-relief elements determines the maximum allowable deformation of the stress-relief support. In this analysis, the tunnel radius was set to R = 6 m, and the in situ stress was p₀ = 15 MPa. The mechanical parameters of the surrounding rock are the same as those listed in Table 1. The peak resistance of the first stage of the stress-relief support was set to 75% of the ultimate bearing capacity of the rigid support, while the number of energy-dissipating elements was set to 2, 4, and 6, respectively. The resulting convergence–confinement curves are shown in Figure 5.

As shown in Figure 5, the number of stress-relief elements does not affect the peak resistance of the first stage of the stress-relief support. As the number of elements increases, the support characteristic curve becomes closer to the GRC under the same radial displacement, and the decay of support resistance becomes slower.

When two stress-relief elements were installed, the support characteristic curve gradually deviated from the GRC with increasing radial displacement, and the resistance provided during deformation decayed rapidly. In this case, the stabilization of deformation primarily depended on the third (“rigid”) stage.

When six energy-dissipating structures were installed, although the allowable deformation of the stress-relief support increased, the support resistance decreased too slowly with deformation. As a result, the GRC and the support characteristic curve intersected during the second stage, indicating that the stress-relief capacity was not fully utilized. The radial displacement and support resistance at stabilization were similar to those obtained when two elements were installed, and stabilization occurred during the third stage.

In fact, as the number of stress-relief elements continues to increase, the support characteristic curve of the stress-relief support approaches that of a constant-resistance yielding support, where the second segment of the curve tends to become horizontal. Therefore, the number of stress-relief elements should be selected based on the in situ stress conditions and mechanical properties of the surrounding rock to avoid excessively rapid or excessively slow stress release.

In summary, a lower peak resistance of the stress-relief support corresponds to a larger deformation at the intersection point of the GRC and support curve, and a higher radial unbalanced stress at the tunnel wall before stabilization. Conversely, a greater number of stress-relief elements leads to a slower decay of support resistance under the same deformation increment.

In practical engineering applications, the design parameters of the stress-relief support should consider both construction cost and structural safety.

For tunnels with favorable surrounding rock and insignificant rheological behavior, a support system with lower peak resistance and fewer stress-relief elements can be adopted to reduce cost and achieve low-carbon, sustainable construction.

For tunnels with poor-quality surrounding rock, rapid daily deformation rates, or significant rheological effects, a support system with higher peak resistance and more stress-relief elements should be selected to reduce the radial unbalanced force and decrease the deformation rate. However, the number of stress-relief elements should not be excessive, as premature intersection of the GRC and support curve would hinder the proper performance of the stress-relief mechanism.

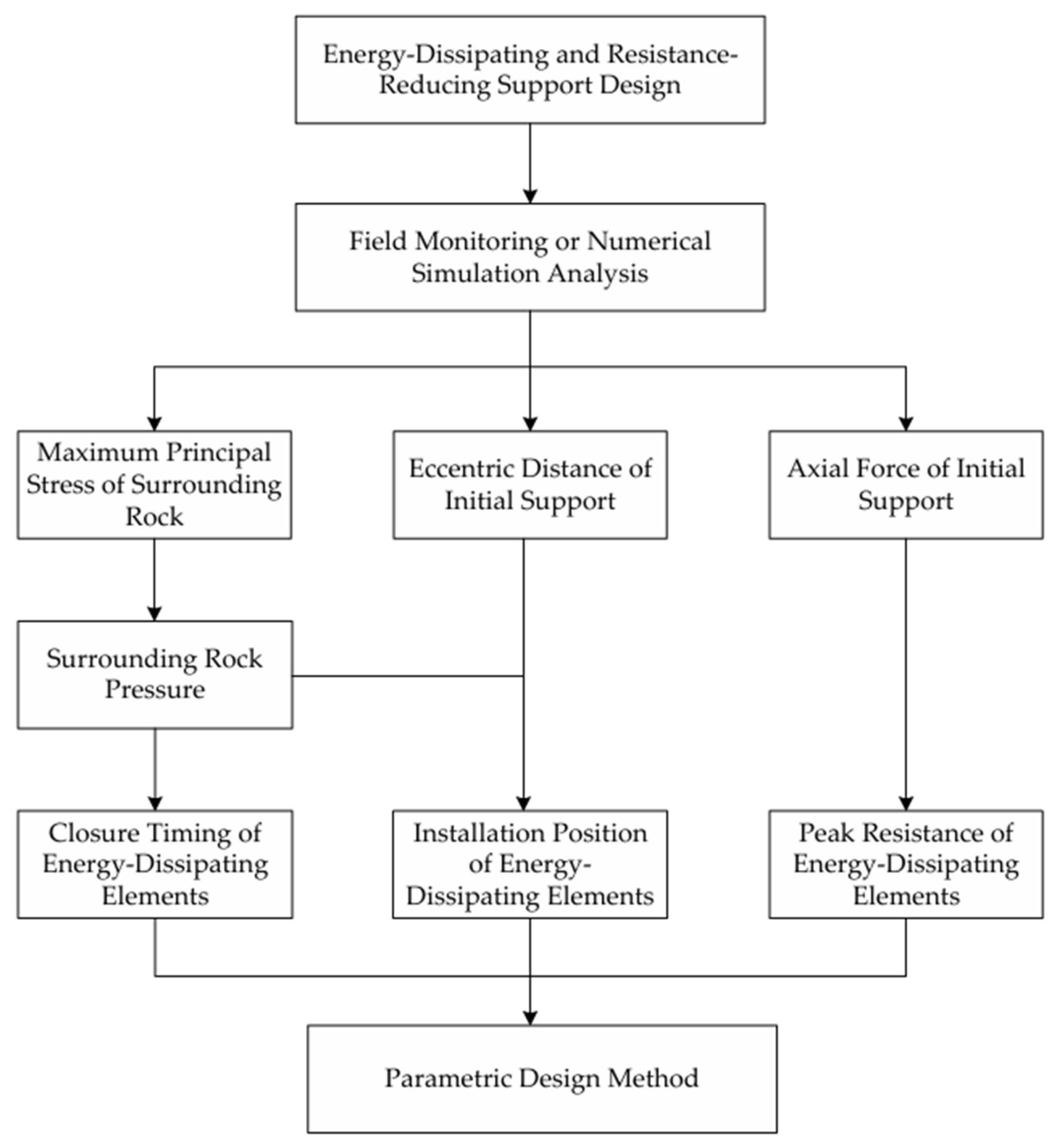
2.4. Parameter Design Method for Stress-Relief Support Structures

Based on the analysis presented in Section 2.3, the parameter design method for stress-relief support systems can be summarized as follows, as illustrated in Figure 6:

• For tunnels under different in situ stress conditions, obtain the surrounding rock stress field and the internal force distribution of the primary support through numerical simulation or field monitoring.
• Extract the maximum principal stress at the interface between the surrounding rock and the primary support as the surrounding rock pressure. Identify zones with relatively low pressure and determine feasible installation locations for the stress-relief elements by also considering construction convenience.
• Extract the axial force and bending moment of the primary support to determine how the eccentricity evolves with staged excavation. Based on the requirement that the installation location of the stress-relief element should remain under compressive stress across the entire section, verify the safety of the selected installation location derived from the surrounding rock stress field.
• Determine the closure timing of the stress-relief elements according to the evolution of surrounding rock pressure after each excavation step. To ensure sufficient stress release, the elements should generally be closed when the surrounding rock pressure stabilizes following the support installation of the subsequent excavation step.
• Extract the primary support axial force at the installation location under different in situ stress conditions and analyze its variation during staged excavation. Based on these data, determine the appropriate range for the peak bearing capacity of the stress-relief elements.

In summary, this section proposes and systematically elaborates the stress-relief control concept for high in situ stress and large-deformation tunnels. By addressing the limitations of the classical convergence–confinement method, a three-stage support strategy—“rigid–relief–rigid”—was developed. The mechanical model and convergence–confinement calculation approach for stress-relief support were established, followed by a parameterized design method for stress-relief elements. These developments provide both a theoretical basis and practical guidance for support design in high-stress tunnel engineering.

3. Design of the Friction-Reducing and Energy-Dissipating Support Structure

In Section 2, a stress-relief control concept was proposed. To apply this concept to practical engineering, it is necessary to design a support unit with a “rigid–relief–rigid” mechanical behavior, featuring a clear mechanical principle and a simple structure.

Based on a review of existing yielding support structures, a friction-reducing and energy-dissipating structural unit is proposed, as shown in Figure 7. This unit is based on the steel plate/curved steel plate limited-resistance energy-dissipating structure proposed by Qiu Wenge [19], but uses an S-shaped steel plate as the support to prevent lateral instability of the steel plate, which could lead to a sudden reduction in the stiffness of the friction-reducing and energy-dissipating structure.

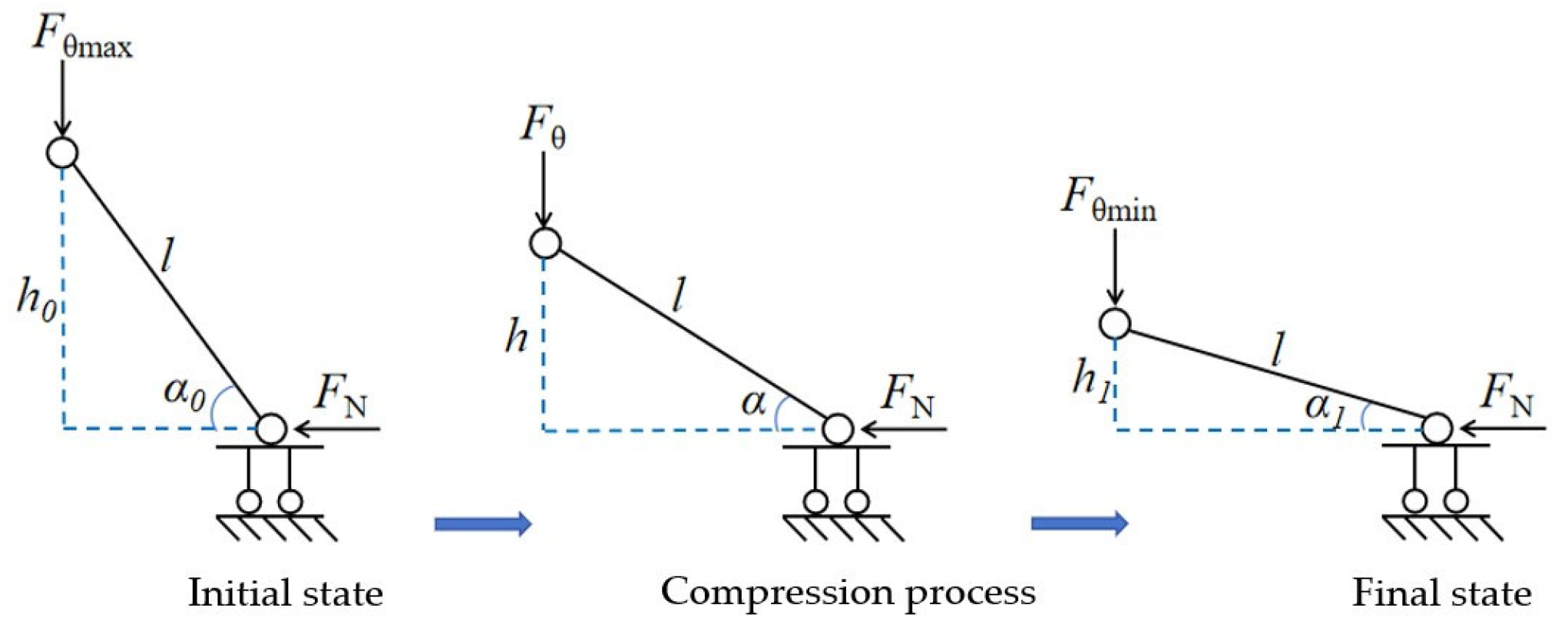
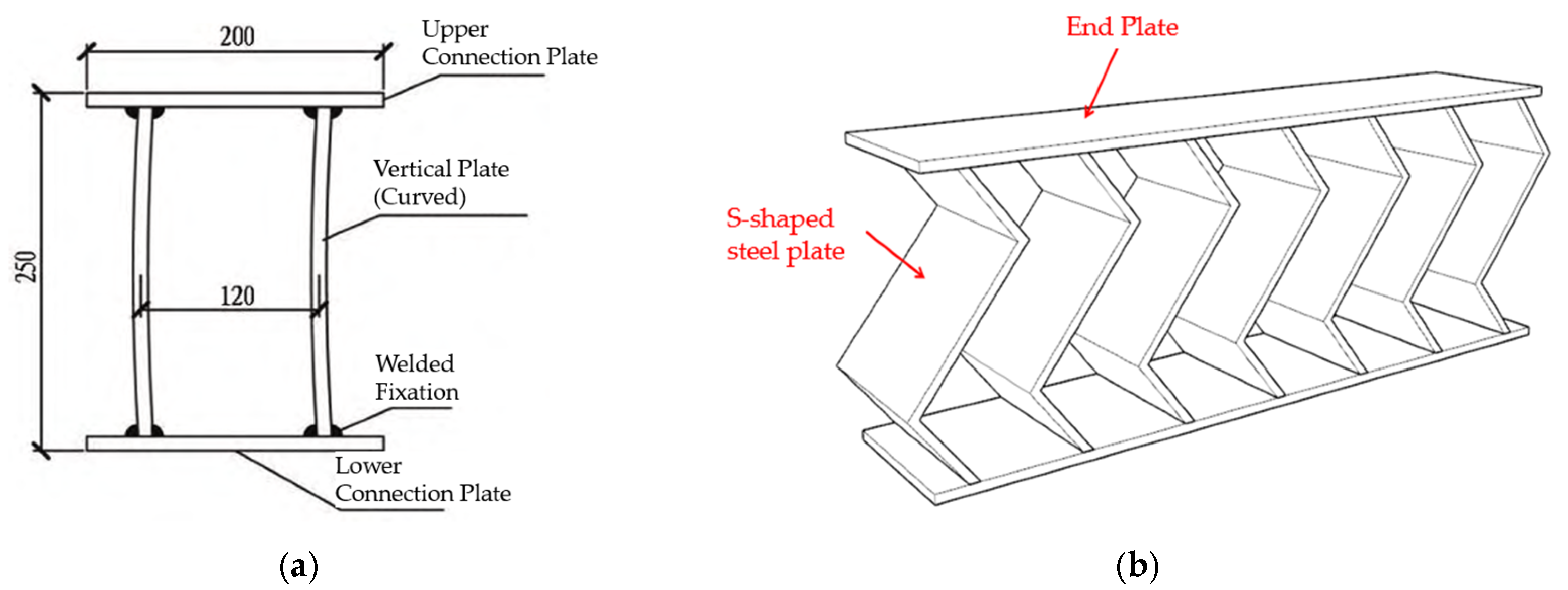
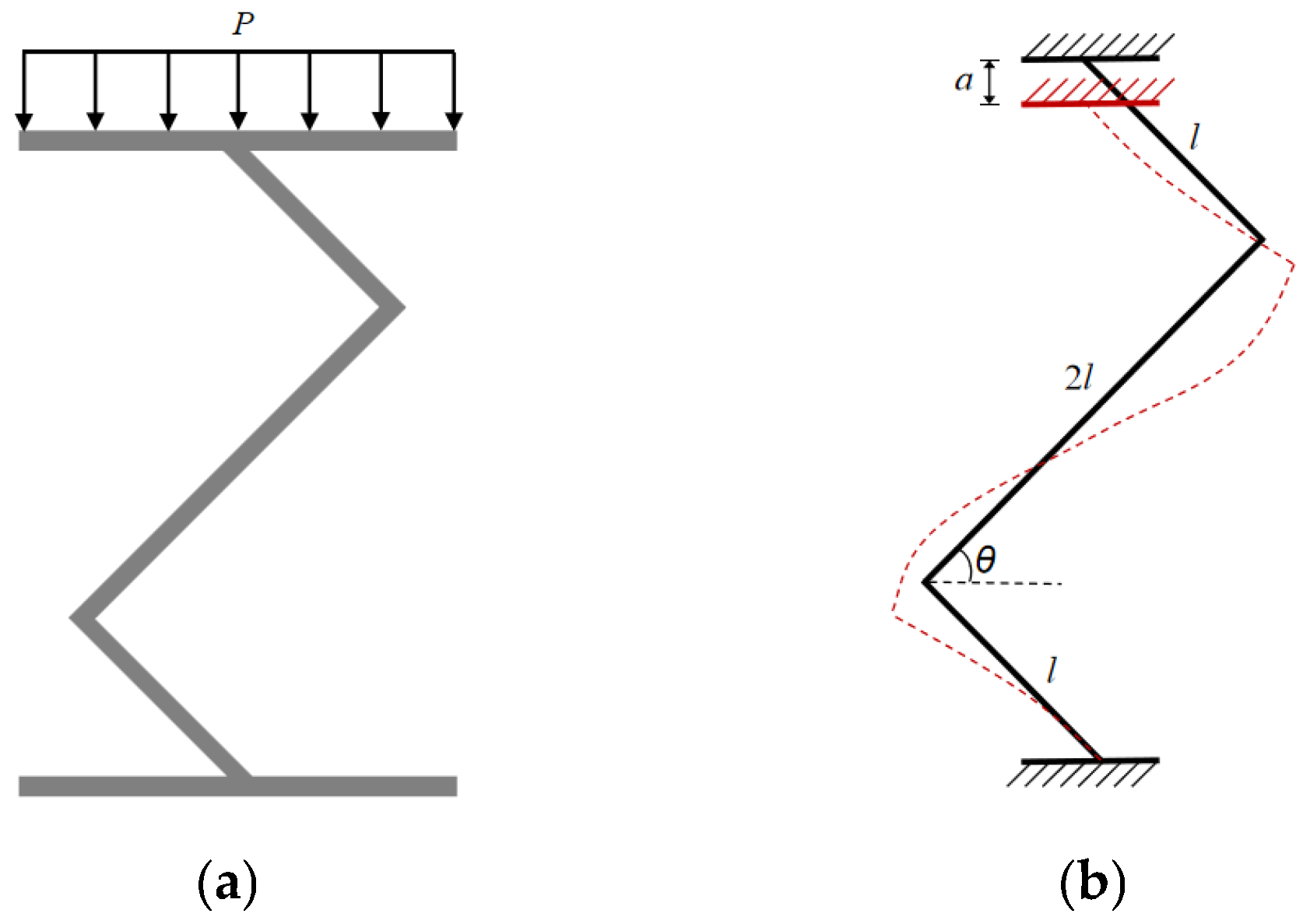
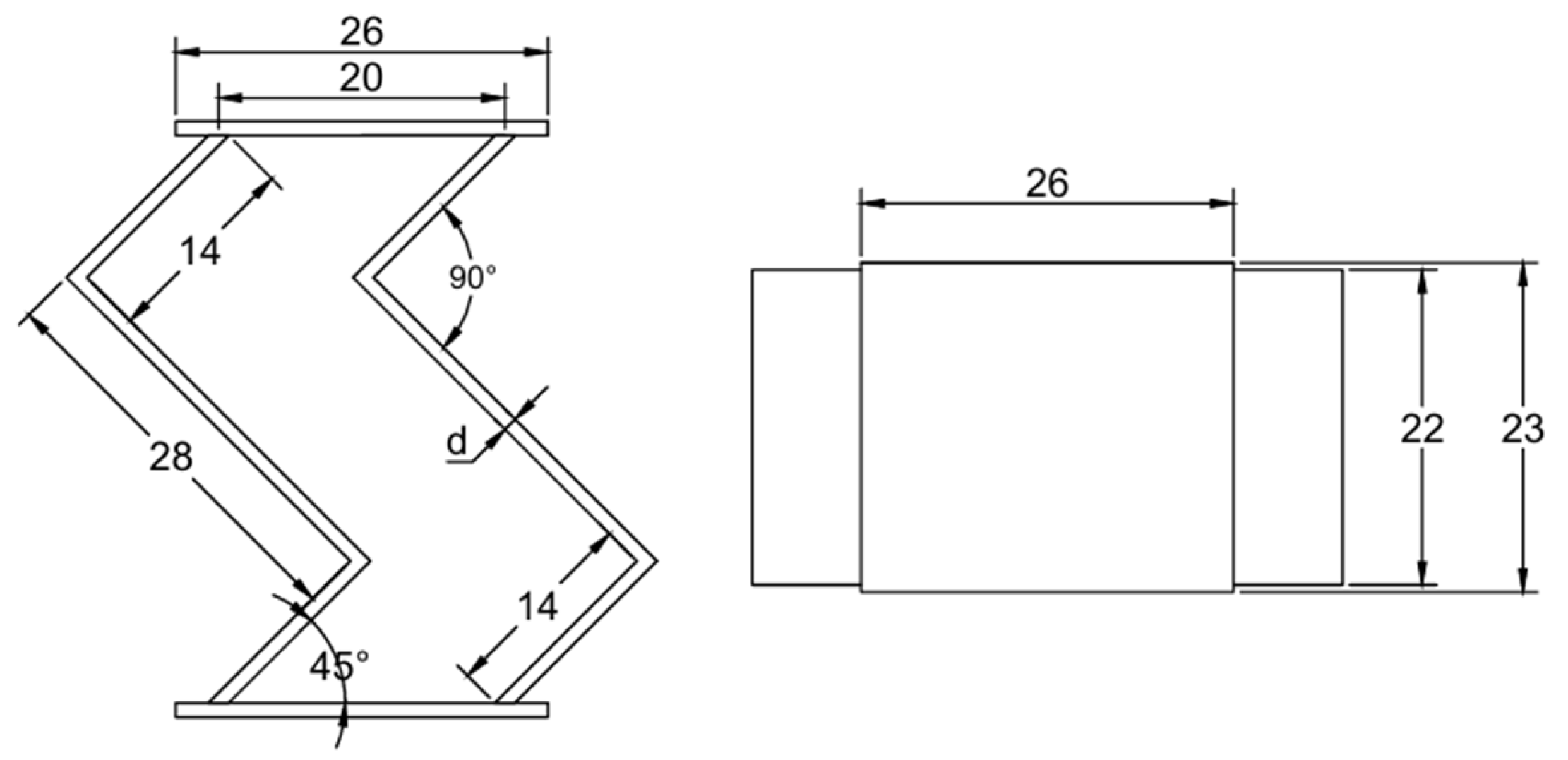
3.1. Mechanical Model and Calculation of the Friction-Reducing and Energy-Dissipating Element

The friction-reducing and energy-dissipating element employs an S-shaped steel plate as the core component. The element is fixed at both the top and bottom ends, forming a simple structure that allows for the establishment of a mechanical model using classical structural mechanics.

Let the thickness, width, and height of the steel plate be t, b, and h, respectively, with an initial bending angle of 2θ. The element is subjected to a vertical compressive load P, corresponding to a vertical displacement a. The S-shaped steel plate and the end plates are abstracted as a fixed–fixed structure, which produces only vertical displacement under vertical loading. The mechanical model is illustrated in Figure 8.

As the compressive deformation increases, plastic hinges form at the locations of maximum bending moment on the S-shaped steel plate. Assuming the steel follows an ideal elastoplastic constitutive law, the structure in the pre-yield stage can be analyzed using the force method, expressed as follows:

$${\delta }_{ij}{X}_j+{∆}_{ic}={∆}_i,$$

(10)

where δij is the displacement at the point of action of Xi along its direction, caused by a unit load Xj = 1 acting alone; Δic is the displacement at the point of action of Xi due to known support displacement; Δi is the displacement at the point of action of Xi in the original structure.

By solving for the redundant reaction forces and substituting the results, the axial bearing capacity of the element can be obtained as

$$F_{\theta s}={\displaystyle \frac{12EIk}{7n^2{l}^3}}\times a,$$

(11)

where F_θS is the axial bearing capacity per unit length of the friction-reducing and energy-dissipating element during the elastic stage; k is the number of S-shaped steel plates per meter of the stress-relief support; E is the elastic modulus of steel; I is the moment of inertia; and a is the vertical displacement at the support.

When the edge section stress of the steel plate reaches the yield strength σs, plastic hinges begin to form, and the maximum elastic displacement of the steel plate is

$$a_{smax}={\displaystyle \frac{7n{l}^2{\sigma }_s{W}_p}{9EI}},$$

(12)

where W_p is the section modulus at full plastic yield. After the formation of plastic hinges, internal forces are redistributed, and the vertical bearing capacity gradually decreases, which can be expressed as follows:

$$F_{\theta p}{\displaystyle \frac{2{\sigma }_{\mathrm{s}}{W}_{\mathrm{p}}k}{n^{,}{l}^{,}}}.$$

(13)

It can thus be seen that the S-shaped steel plate exhibits a “rigid–relief–rigid” mechanical behavior during compression:

• In the elastic stage, the element provides a large bearing capacity.
• In the plastic (stress relief) stage, the bearing capacity decreases gradually as the bending angle reduces, allowing progressive stress relief and energy dissipation.
• Upon ultimate compression, the stiffness increases again, and the mechanical response approaches that of a rigid support system.

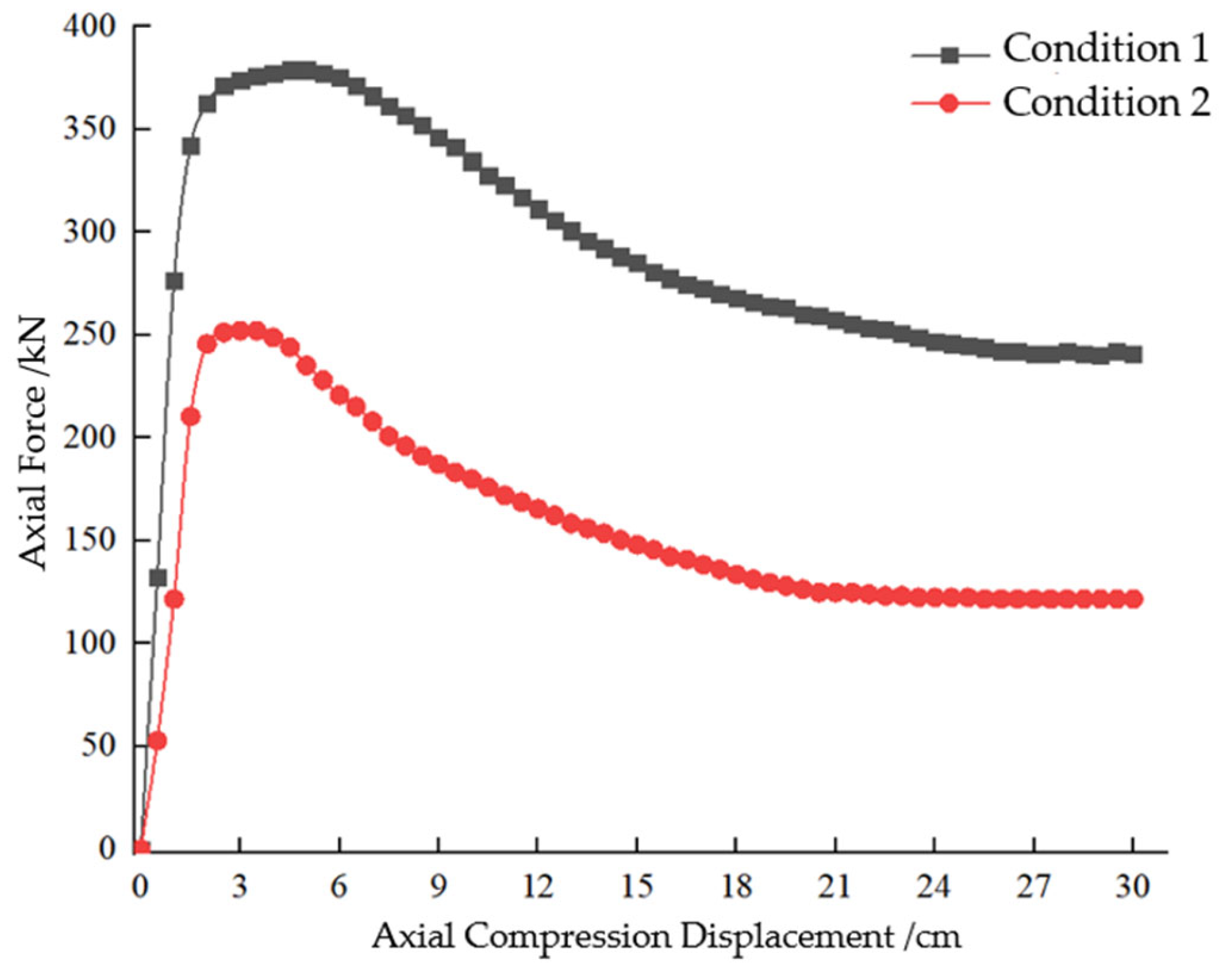
3.2. Laboratory Compression Test Analysis of the Friction-Reducing and Energy-Dissipating Element

To verify the mechanical performance of the stress-relief elements and assess the deviation between theoretical calculations and actual behavior, axial compression tests were conducted using a 600 kN microcomputer-controlled electronic universal testing machine, as shown in Figure 9. The technical specifications of the loading system are listed in

Table 2. Technical specifications of the loading system.

Item	Specification
Model	Hualong WAW-600
Maximum static test load	600 kN
Load measurement range	4–100% FS
Load accuracy	<±1%
Maximum piston speed	100 mm/min
Maximum piston displacement	600 mm

.

The main geometric parameters of the stress-relief element are shown in Figure 10.

Two loading conditions were designed for the compression tests, with one specimen tested under each condition. Except for the steel plate thickness, all other parameters of the stress-relief elements were kept identical. The detailed test parameters are listed in

Table 3. Test parameters for the axial compression experiments.

Test ID	Steel Plate Material	Plate Thickness d (cm)	Compression Stroke (cm)	Loading Rate (cm/min)
Condition 1	Q235	1.0	30	0.2
Condition 2	Q235	0.8	30	0.2

.

During the uniaxial compression test, a preload of 0.1 kN was first applied, followed by displacement-controlled loading at a rate of 0.2 cm/min. Loading was terminated when the displacement reached 30 cm. The force–displacement curves obtained under the two test conditions are shown in Figure 11. Both curves exhibit a smooth overall trend, where the bearing capacity increases rapidly in the initial stage, followed by a stress-relief phase due to the development of plastic hinges, and finally approaches a stable resistance similar to constant-resistance support. This behavior clearly demonstrates the three-stage “rigid–relief–rigid” characteristic of the element.

During compression, the peak bearing capacities appeared at axial displacements of 6 cm and 3 cm for Conditions 1 and 2, respectively. The peak axial bearing capacity of Condition 2 was approximately 65.9% of that of Condition 1. According to the theoretical Equation (10), the calculated ratio was 64%, with an error of only about 3%, indicating that the theoretical formula provides an accurate prediction of the peak bearing capacity of the friction-reducing and energy-dissipating element.

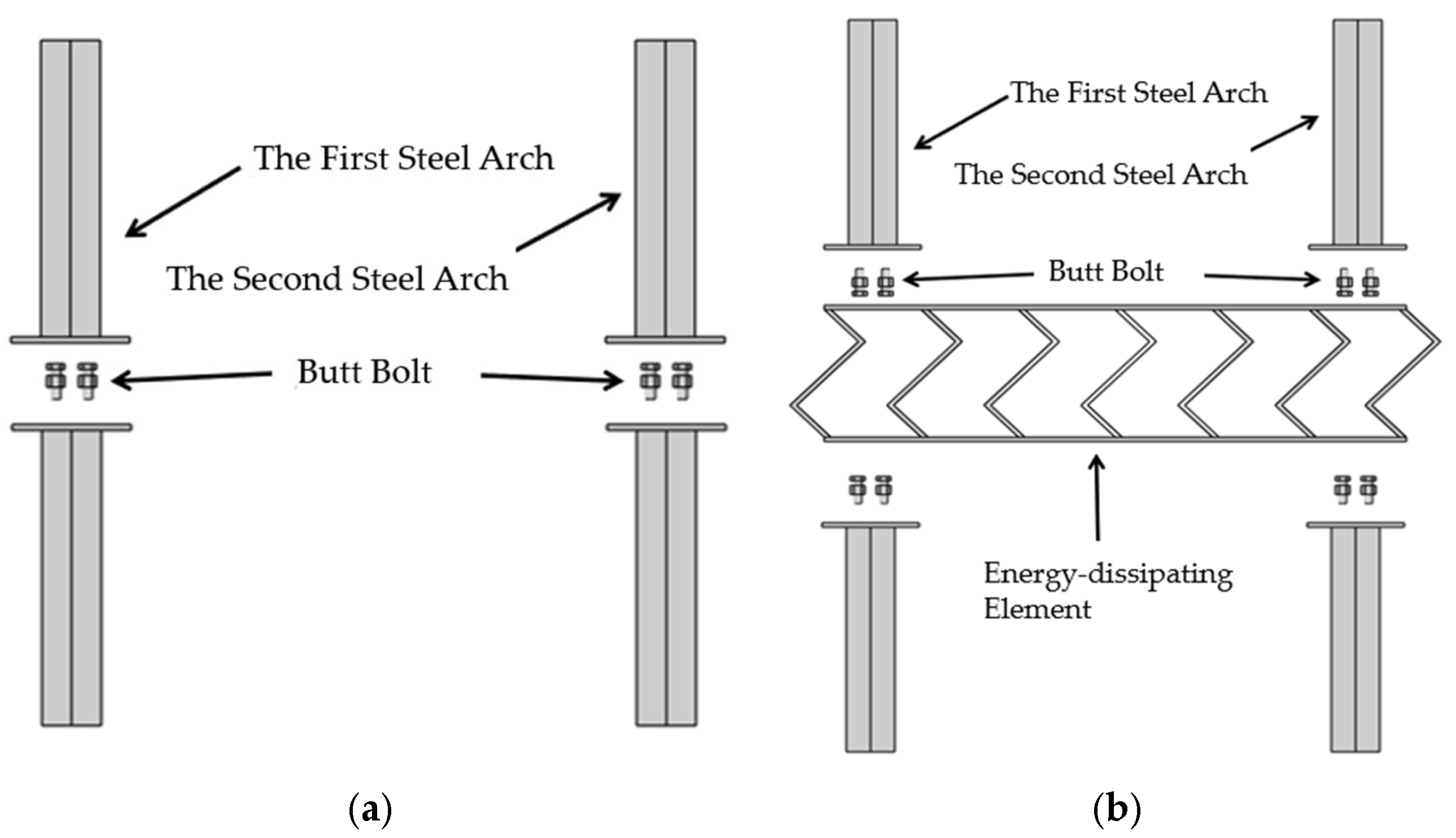
3.3. Installation Procedure of the Friction-Reducing and Energy-Dissipating Element

Mountain tunnels in China are generally constructed using the New Austrian Tunneling Method (NATM), adopting a bench excavation and composite support system consisting of primary support and secondary lining. Based on the construction procedure, the installation sequence of the friction-reducing and energy-dissipating element was designed accordingly.

The friction-reducing and energy-dissipating element is installed together with the steel arch. In the conventional rigid primary support, the connection sequence of the steel arch is I-beam–connection plate–bolted joint–connection plate–I-beam. In the optimized design, one connection plate section is replaced by the friction-reducing and energy-dissipating element, forming the sequence I-beam–connection plate–bolted joint–energy-dissipating element–bolted joint–connection plate–I-beam, as shown in Figure 12.

The installation of the friction-reducing and energy-dissipating element can be divided into the following three steps:

• The friction-reducing and energy-dissipating elements are prefabricated in a steel processing plant and transported to the tunnel face together with the steel arches. During on-site assembly, each element is bolted between two arch segments to form an integrated primary support frame.
• After assembly, the primary shotcrete layer is applied. The gaps between the S-shaped steel plates are temporarily covered with wooden boards or geotextile to prevent inadvertent filling. The protection is removed after shotcreting to allow subsequent observation of the deformation behavior of the element.
• For the next construction cycle, the newly installed elements are welded to the ends of the previously installed ones to improve longitudinal stiffness and prevent uneven axial compression. Once the elements reach stable deformation or the designed deformation limit, the remaining gaps between the S-shaped plates are filled with shotcrete to complete the integrated support structure.

In summary, compared with conventional support systems, this support structure exhibits a distinctive “initial stiffness followed by stress relief” mechanical behavior, consistent with the stress-relief concept proposed in this study. Its mechanical principle is clear, and the structure is simple, allowing the installation of the friction-reducing and energy-dissipating elements to be integrated into existing construction procedures without additional steps, thus demonstrating significant practical engineering value.

4. Application of Energy-Dissipating Support in Asymmetrically Stressed Tunnels with Large Deformation

This section presents the engineering application of the energy-dissipating support system in the Qiaojia Tunnel along the Ludian–Qiaojia Expressway in Yunnan Province, China. The study focused on an asymmetrically stressed large-deformation section in the left tunnel bore near the exit, where the proposed support system was implemented for deformation control. By comparing the mechanical responses and support performance between the energy-dissipating support section and the conventional rigid support section, the interaction mechanism between the surrounding rock and the support structure was analyzed, thereby verifying the advantages of the proposed system in tunnel engineering.

4.1. Engineering Overview of Qiaojia Tunnel

The Qiaojia Tunnel of the Ludian–Qiaojia Expressway is located in Qiaojia County, Yunnan Province, where both the entrance and exit portals are situated on steep cliff slopes. The regional geomorphology of the tunnel area is strongly influenced by lithology and tectonic structures. The entrance portal lies on a riverbank slope incised by the Qiaomaidi River, while the exit portal is positioned on a valley slope eroded by the Jinsha River. The tunnel alignment passes through a high-mountain region characterized by structural denudation and karstic erosion slopes. The terrain in the site area is highly undulating, with elevations ranging from 1069 m to 2782 m and a relative relief of approximately 1713 m, representing a typical high-mountain landscape shaped by structural erosion and dissolution.

The asymmetrically stressed large-deformation zone in the left tunnel bore extends from chainage ZK67 + 070 to ZK66 + 950, with a total length of about 130 m. The classification of the surrounding rock along this section, based on chainage divisions, is summarized in

Table 4. Basic quality index (BQ) or corrected value [BQ] and classification of surrounding rock.

Chainage Range	Length (m)	Rock Class	[BQ]	${\mathit{K}}_{\mathbf{v}}$	${\mathit{V}}_{\mathbf{p}}$	${\mathit{R}}_{\mathbf{c}}$	${\mathit{K}}_1$	${\mathit{K}}_2$	${\mathit{K}}_3$	BQ
ZK67 + 170~ZK67 + 020	150	Ⅴ1	242	0.45	2900	33.00	0.5	0.2	0	312
ZK67 + 020~ZK66 + 850	170	Ⅴ1	227	0.45	2900	21.40	0.3	0.2	0	277
ZK66 + 850~ZK66 + 650	200	Ⅳ3	262	0.55	3000	21.40	0.2	0.2	0	309

.

After excavation and a period of primary support, a series of large-deformation failures occurred, including cracking and spalling of the shotcrete, bending of steel ribs, and uplift of the invert. The final crown settlement reached 22.9 cm, the horizontal convergence at the arch waist was 24.3 cm, and the vertical settlement of the right shoulder reached 30.1 cm, all exceeding the maximum design allowance.

To mitigate these issues, several reinforcement measures were successively implemented, including increasing the reserved deformation space, thickening the primary lining and steel ribs, and reducing the spacing between ribs. However, despite these reinforcements, the large-deformation problem of the surrounding rock persisted, and local cracking and spalling continued to occur. Consequently, the energy-dissipating support system was introduced in this asymmetrically stressed, large-deformation section to fully release the surrounding rock pressure and adjust the uneven stress and deformation distribution within the primary support.

4.2. Design Parameters and Installation of Energy-Dissipating Support

Before the installation of the energy-dissipating support, it is essential to analyze and determine the placement of the elements, their peak load capacity, and element height based on the tunnel deformation characteristics, surrounding rock pressures, and support stress conditions. This targeted design enables controlled release of surrounding rock pressure, thereby mitigating the effects of asymmetric rock stress on the internal forces and deformation of the initial support. Consequently, long-term monitoring of the rigid support sections is required, with the monitoring point layout illustrated in Figure 13.

Surrounding rock pressure at each point is measured using earth pressure cells, installed between the back of the steel arch and two adjacent steel arches, to monitor the average pressure behind the initial support. Internal forces of the initial support are monitored using rebar strain gauges, welded at the junctions of the inner and outer flanges and the web of the steel arch, enabling measurement of axial force, bending moment, and eccentricity, from which relevant internal force parameters of the initial support can be calculated. The models of the monitoring instruments are listed in

Table 5. Models of monitoring instruments.

No.	Measured Item	Instrument	Specification	Monitoring Frequency
1	Steel arch stress	Wire-type surface strain gauge	2000 με	1 time/day
2	Contact pressure between the surrounding rock and the initial support	Earth pressure cell	1.2 MPa	1 time/day
3	Foundation bearing capacity below the arch foot	Earth pressure cell	3 MPa	1 time/day

.

Based on the monitoring results, the peak surrounding rock pressure distribution, the peak axial force distribution of the initial support, and the envelope of the initial support eccentricity were plotted, as shown in Figure 14.

As shown in Figure 14a, the surrounding rock pressure around the tunnel section exhibited a pronounced asymmetric distribution, with the maximum peak pressure located near the right arch shoulder. Geological observations at the tunnel face revealed a stratified rock mass inclined approximately 15° to the horizontal plane. Under excavation disturbance, rock blocks loosened and detached along the vertical bedding near the right arch shoulder, resulting in significant loosening pressure acting on the primary support in this area.

As illustrated in Figure 14b, the axial force of the primary support was relatively high at the tunnel crown and right arch shoulder but lower near the left arch shoulder and both arch feet. To prevent premature compression failure of the energy-dissipating elements during the early stage of support loading, these elements should not be installed at locations with high initial axial forces.

Figure 14c presents the eccentricity envelope of the primary support in the rigid-support section. Large fluctuations and alternating positive–negative eccentricities were observed at the tunnel crown. The negative eccentricity at the left arch shoulder and the positive eccentricity at the left arch waist were both significant, indicating that installing energy-dissipating elements in these areas could induce unilateral compression and asymmetric instability.

Based on the above analysis, the energy-dissipating elements in the test section were installed unilaterally near the right arch waist, where eccentricity was relatively small and close to the high-pressure concentration zone at the right arch shoulder. This configuration effectively released the axial force transmitted through the primary support. To avoid interference from the upper-step foot-locking bolts, the installation position was set 90 cm above the right arch foot of the upper step.

According to the internal force monitoring results of the primary support, the average axial force at the right arch waist reached 856.7 kN three days after the installation of the initial support. Subsequently, the internal force fluctuated between 746.7 kN and 1407.5 kN. Based on these data, the bearing capacity of the energy-dissipating element was designed accordingly. The total element height was set to 40 cm, with an allowable compression stroke of 20 cm and a width of 23 cm. The initial angle of the S-shaped steel plates was 90°, the plate thickness was 1 cm, and the spacing between the two plates was 20 cm.

As described in Section 3.1, the peak bearing capacity per meter of the energy-dissipating element is 956.5 kN, while the minimum capacity within the compression stroke is 650.6 kN, which satisfies the design requirements for surrounding rock stress relief.

After determining these design parameters, construction and installation of the energy-dissipating support were carried out according to the procedure described in Section 3.3. The field installation results are shown in Figure 15.

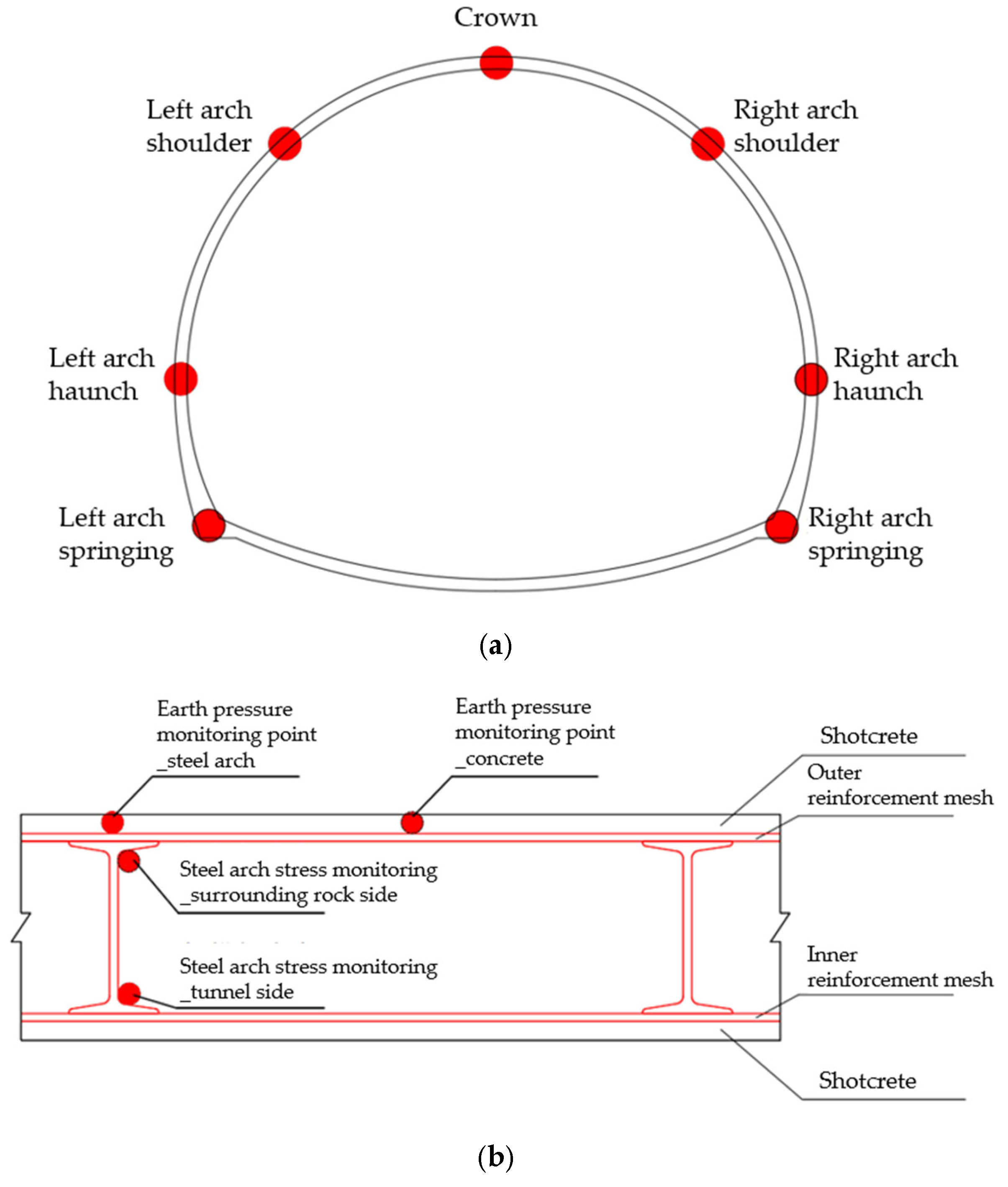
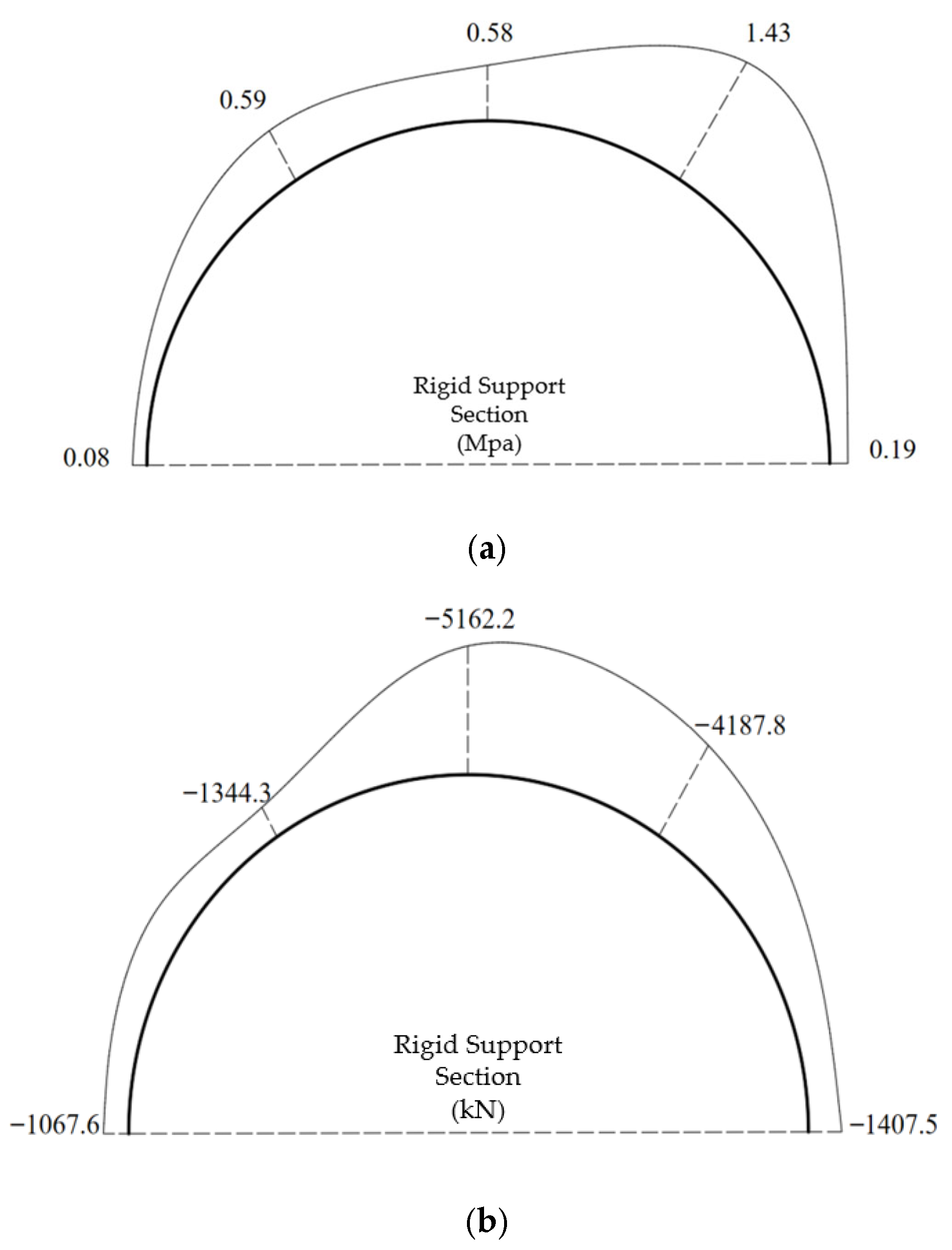
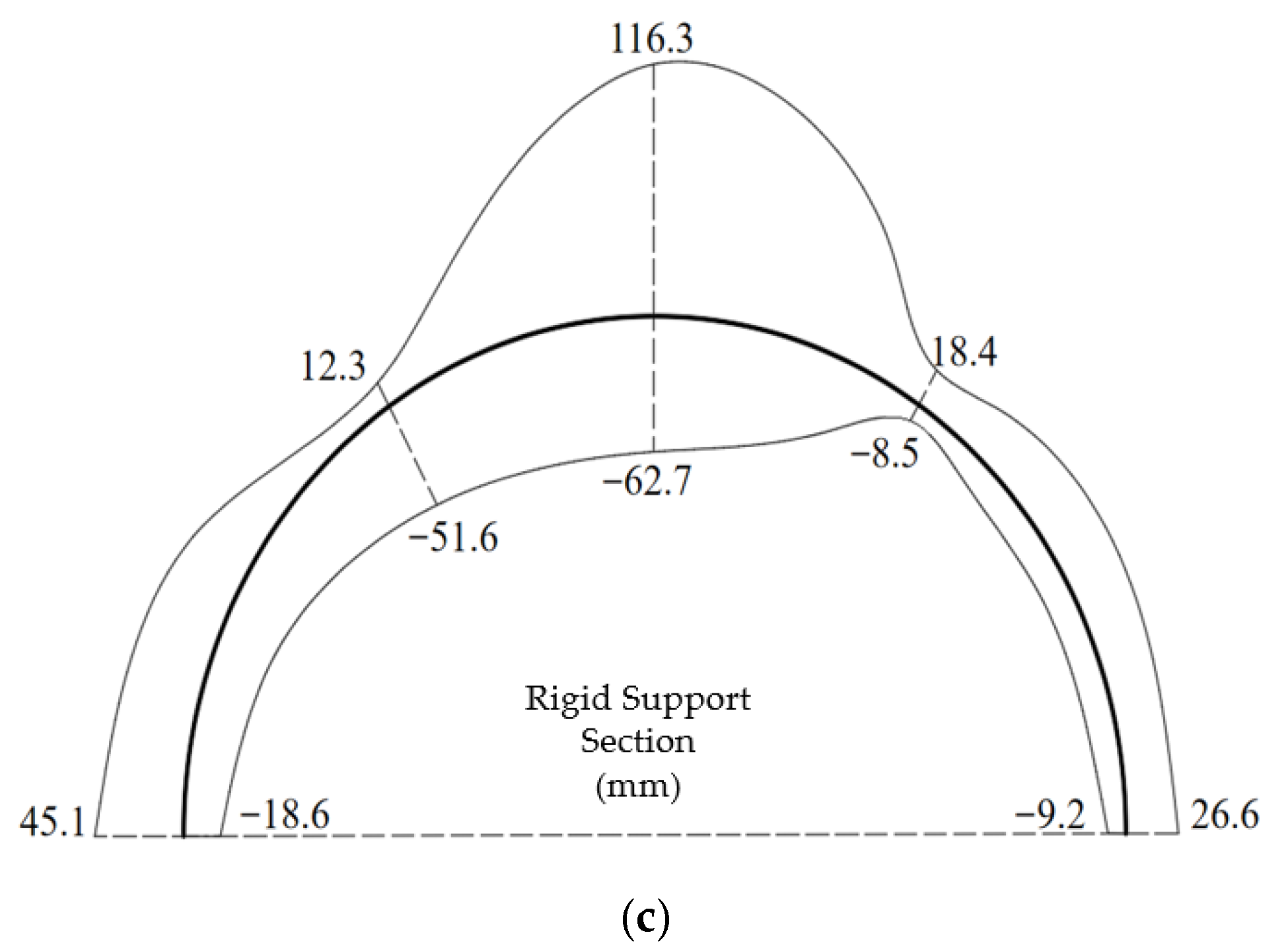
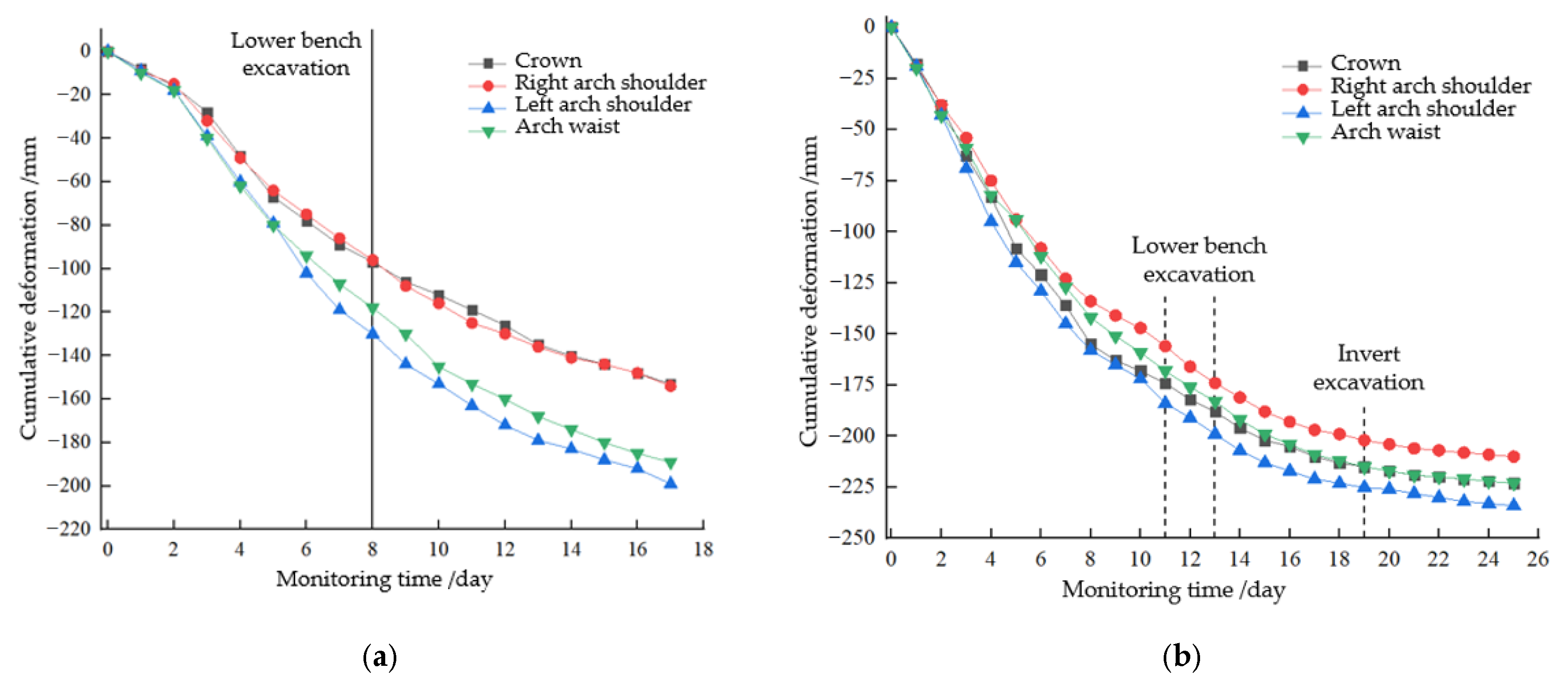
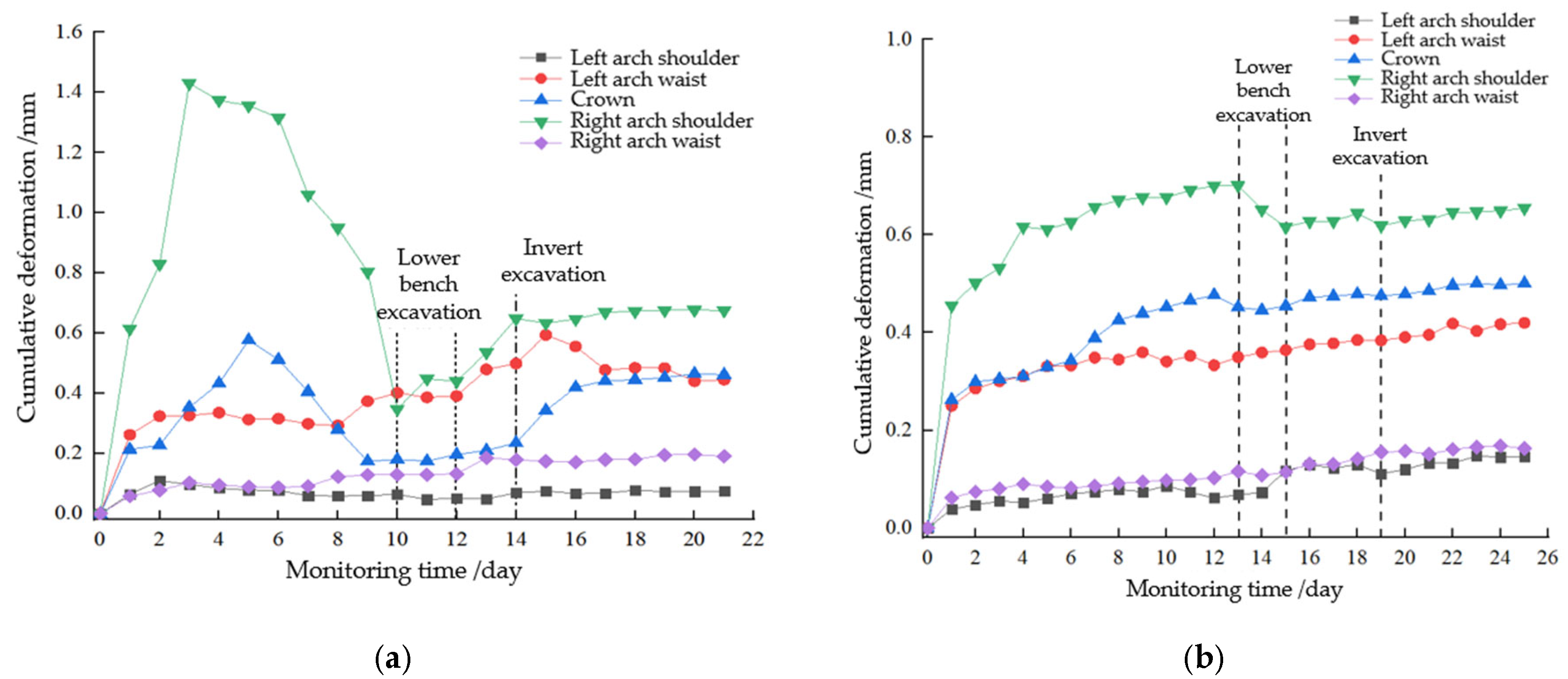
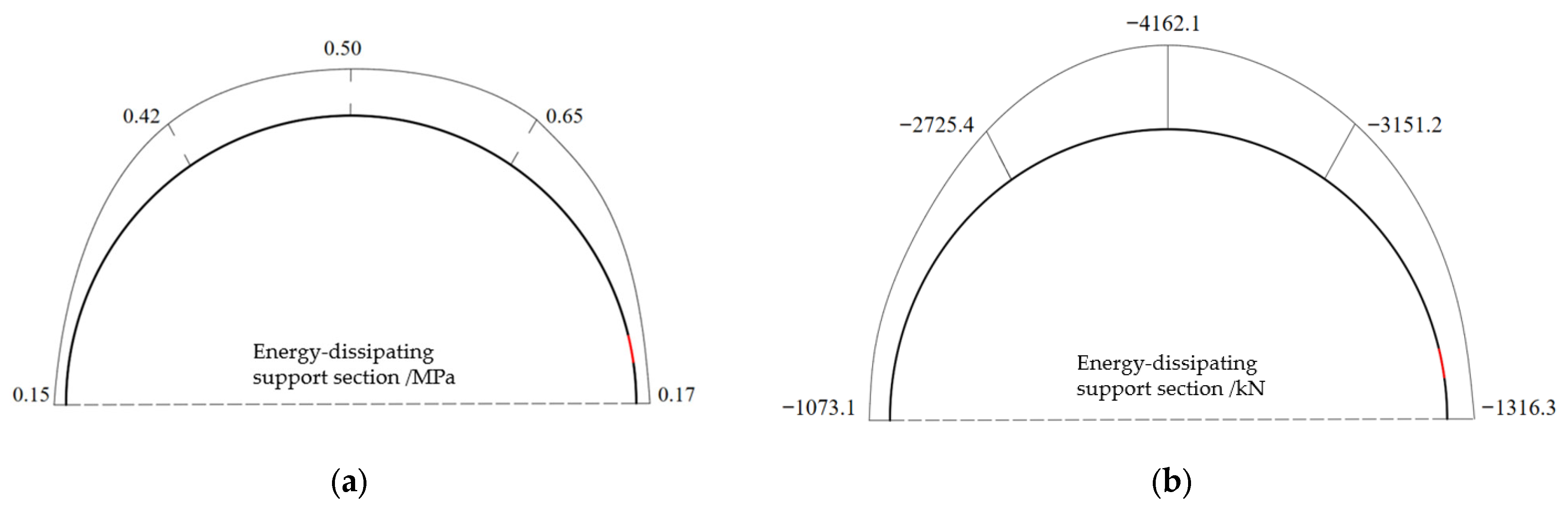
4.3. Analysis of the Control Effect of Energy-Dissipating Support

A comparison of the apparent support performance between the energy-dissipating support section and the rigid-support section is shown in Figure 16. The sprayed concrete surface in the energy-dissipating support section appeared smoother, and the energy-dissipating elements exhibited uniform longitudinal compression along the tunnel, with no indication of initial support failure. In contrast, cracking and spalling of the shotcrete were clearly observed in the rigid-support section.

Reflective markers were installed in the energy-dissipating support section to monitor crown settlement and peripheral convergence. The cumulative deformation curves of the surrounding rock under rigid support and energy-dissipating support are shown in Figure 17.

As illustrated in Figure 17, under the energy-dissipating support system, the final deformations of the tunnel crown, left arch shoulder, right arch shoulder, and horizontal convergence were 22.3 cm, 21.0 cm, 23.4 cm, and 22.2 cm, respectively. Compared with the rigid-support tunnel, the overall deformation magnitude was slightly larger; however, the differential deformation between the left and right arch shoulders was significantly reduced. The gradual compression of the energy-dissipating element near the right arch waist provided greater deformation capacity and improved the adaptability of the surrounding rock, resulting in a more uniform expansion of the plastic zone and mitigation of stress concentration at the right arch shoulder.

Overall, following alternate excavation and lower-bench support, the deformation rate of the tunnel supported by the energy-dissipating system was substantially slower than that of the rigid-support section, and the stabilization time of tunnel deformation was notably shorter.

The comparison of the surrounding rock pressure monitoring curves under rigid support and energy-dissipating support is shown in Figure 18. It can be observed that the temporal variation trends of the surrounding rock pressure differ significantly between the two support types. After the installation of the energy-dissipating support, the surrounding rock pressure near the right arch shoulder increased rapidly due to the influence of asymmetric ground stress, and the pressure at both arch shoulders rose sharply in the early stage. As the “stress-relief” function of the energy-dissipating elements gradually took effect, the surrounding rock obtained sufficient deformation space, allowing the internal stress to be dynamically released, and the subsequent growth rate of pressure became markedly slower.

In contrast, under rigid support, the limited deformation capacity prevented the timely release of accumulated energy within the surrounding rock. Consequently, the stress at the right arch shoulder increased rapidly, causing cracking and failure of the primary lining. Local loosening and void formation in the surrounding rock led to a rapid pressure drop in this area. Following the installation of the lower bench support, part of the stored energy was released, and the shallow rock mass was re-compacted against the support, resulting in a rebound of pressure. The surrounding rock pressure finally stabilized only after the invert was closed.

Throughout the full monitoring period under energy-dissipating support, the peak surrounding rock pressures at the tunnel crown, left arch shoulder, and right arch shoulder were 0.46 MPa, 0.42 MPa, and 0.78 MPa, respectively—representing reductions of 20.2%, 29.2%, and 45.4% compared with the corresponding peaks under rigid support. Furthermore, the peak pressure difference between the left and right arch shoulders under energy-dissipating support was 0.32 MPa, which is 59.2% lower than that of the rigid-support section.

These results demonstrate that the energy-dissipating support, through localized, gradual, and dynamic compression deformation of its elements, effectively released and redistributed the surrounding rock pressure. Compared with the rigid support, which undergoes a “stiff resistance–crushing release” process, the energy-dissipating support exhibited a “stiff–buffered–stiff” mechanical behavior that better conforms to the stress and deformation characteristics of asymmetrically stressed tunnels with large deformation.

By combining the surrounding rock pressure distribution and the axial force distribution characteristics of the energy-dissipating support section, the overall control effects of the energy-dissipating support can be further summarized, as illustrated in Figure 19.

From Figure 19, several key findings can be observed. First, through the gradual compression of the energy-dissipating elements, the high stress originally concentrated near the right arch shoulder was progressively transferred to the deeper and peripheral rock mass. This stress-relief mechanism effectively reduced the degree of stress concentration, expanded the plastic zone, and enhanced the load-bearing capacity of the surrounding rock. Meanwhile, the relatively high initial support resistance prevented excessive deformation and potential instability of the rock mass.

Second, the energy-dissipating support plays a significant role in reducing the stress acting on the support structure and improving the internal force distribution. Conventional rigid support systems often encounter difficulties in accommodating excessive localized pressure caused by weak surrounding rock or asymmetric stress, which may lead to local damage or overall instability of the structure. In contrast, the energy-dissipating support, characterized by its distinctive “stiff–buffered–stiff” mechanical behavior, undergoes gradual compression under the action of surrounding rock pressure, thereby absorbing and dissipating part of the released energy and effectively reducing the stress burden on the support structure.

Third, after the unilateral installation of the energy-dissipating elements, dynamic redistribution of the internal forces occurred within the support system. The axial force at the left arch shoulder, which was initially small and underutilized, increased, while the axial forces at the tunnel crown and right arch shoulder decreased, resulting in a more uniform distribution of internal forces across the section. When the energy-dissipating elements were covered with sprayed concrete, and the support system re-entered the “rigid” phase, although the overall deformation was relatively large, the internal forces remained moderate, allowing the structure to maintain its load-bearing function effectively.

More importantly, because the energy-dissipating elements had absorbed and released a substantial amount of energy during the early stage of deformation, the surrounding rock pressure was effectively alleviated, and the stress state of the support structure became more stable. This improved stability is particularly beneficial for mitigating the long-term rheological behavior of the surrounding rock.

5. Discussion and Conclusions

5.1. Discussion

This study focuses on large deformation in high in situ stress soft surrounding rock and proposes a stress-relief control concept based on the full-process evolution characteristics of the convergence–constraint method. After excavation, the surrounding rock exhibits time-dependent stress evolution. Conventional rigid support, due to its high initial stiffness, suppresses necessary shallow deformation and delays the release of deep-seated energy, leading to sudden stress concentration and structural cracking when disturbed. Existing yielding-support designs mainly consider the stabilized state and insufficiently account for the mechanical response during the excavation–stabilization process. In high-stress tunnels, inadequate early-stage stiffness can rapidly increase radial imbalance forces.

In contrast, the energy-dissipating support system effectively matches the time-dependent behavior of the surrounding rock. It first provides adequate resistance to control rapid deformation, then gradually releases strain energy through plastic compression of the S-shaped steel plates, producing a smoother stress path and reducing asymmetric stress concentration. Once the energy release is completed, the element closes and regains high stiffness, ensuring long-term stability. This “rigid–relief–rigid” response actively regulates stress redistribution, lowers peak stress, and mitigates asymmetric deformation more effectively than rigid support.

It should be noted that the system was applied in a gently inclined, asymmetrically stressed tunnel, where rapid stress release caused early closure of the elements. Monitoring ended before secondary lining installation, so long-term rheological effects were not captured. Furthermore, the case study involved a single geological condition, and broader applicability under varied geological settings requires further investigation.

5.2. Conclusions

Building on the proposed stress-relief concept, this study integrates theoretical modeling, component testing, and field application. The key findings are as follows:

• A stress-relief support system with a “rigid–relief–rigid” variable-stiffness response is proposed. It provides high initial stiffness to restrain early loosening, then reduces resistance with deformation to maintain low radial imbalance force, and finally re-stiffens to promote rapid stabilization.
• A three-stage mechanical model is established based on the stress-relief mechanism and the convergence–constraint curve. By representing the relief stage with trigonometric functions, analytical solutions for all stages and a corresponding parameter-determination method are derived.
• A friction-reducing energy-dissipating element utilizing plastic bending of S-shaped steel plates is developed. Structural analysis and uniaxial compression tests verify both the theoretical model and the characteristic “rigid–relief–rigid’’ response.
• Field application in the Qiaojia Tunnel shows significant improvement in deformation control. Crown settlement (22.3 cm) and shoulder differential deformation (2.4 cm) meet design limits. Compared with rigid support, peak surrounding-rock pressures decreased by 20.2–45.4%, and the left–right shoulder pressure difference was reduced by 59.2%, effectively mitigating asymmetric deformation.