Development and Evaluation of Frequency Sensitivity Models in Ultrasonic Fatigue Testing of Ferritic-Pearlitic Steels

Abstract

The increased test frequency inherent in Ultrasonic Fatigue Testing (UFT) is commonly observed to result in an increased fatigue resistance for ferritic, low-carbon steels. In this investigation, the fatigue response of S275J2 ferritic structural steel is evaluated at both 20 kHz and 50 Hz. At the ultrasonic frequency, an increase in the fatigue limit of 136 MPa and an increase in the finite life region of 150 MPa was observed, alongside a reduction in the slope of the S-N curve. By combining the S275J2 results with additional data from the literature, generalised versions of previously proposed frequency sensitivity models are produced by evaluating the model coefficients as a function of different combinations of the material properties. Additionally, a new frequency sensitivity model was proposed by evaluating the empirical change in the S-N curve coefficients as a function of these material properties. For all of the models, it was found that the best correlation was against the ferrite content divided by the tensile strength. The generalised forms of these models were rearranged to produce correction factors, which allow the conventional frequency fatigue response to be estimated based on the UFT test. The most reliable correction method was found to be using the empirical change in the S-N curve exponent.

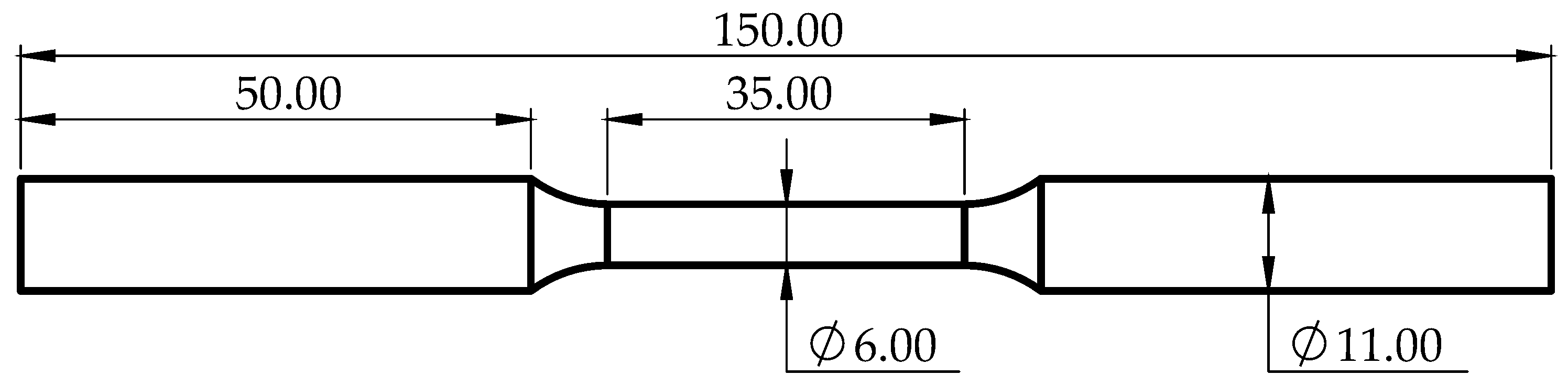
1. Introduction

Steel materials are traditionally believed to exhibit a fatigue limit at around ${10}^7$ cycles, beyond which any cyclic plastic deformation can be considered to be negligible, and an infinite fatigue life expected. In recent years, however, it has been observed that this traditional value of the fatigue limit is inaccurate, and that fatigue failure can still occur even after billions of cycles, in what is known as the very high cycle fatigue (VHCF) regime [1].

Acquiring reliable test data in this VHCF regime using conventional fatigue testing methods, which operate at frequencies of 10–100 Hz, is both time-consuming and expensive, however, thereby necessitating the use of accelerated testing methods to efficiently produce VHCF data. For this purpose, Ultrasonic Fatigue Testing (UFT) is typically employed. UFT makes use of a piezoelectric actuator to produce a controlled vibration at high frequencies, which is then amplified using an acoustic horn and used to excite the longitudinal resonant frequency of a test specimen [2]. This allows a cyclic load to be imparted in a specimen at a frequency of 20 kHz, therefore enabling fatigue tests to be carried out up to 1000 times faster than using conventional fatigue testing (CFT) methods.

However, the use of such high test frequencies introduces several challenges. The increased loading rate and shortened test duration of UFT can significantly affect the fatigue response [3], in a phenomenon referred to as the frequency effect. This effect is particularly pronounced for heavily ferritic steels, for which the fatigue lives obtained through UFT are typically much longer than those observed at conventional frequencies. For example, Klusák et al. [4] found that the fatigue life at an equivalent stress amplitude was extended by two decades when tested at ultrasonic frequencies, while Bach et al. [5] observed an increase in the fatigue limit of 58% for a C15E steel under UFT. Similar observations are reported for a variety of high ferrite-content steels throughout the literature [6,7,8,9].

This difference in fatigue behaviour is typically attributed to the Seeger Effect within the body-centred-cubic (BCC) $\alpha$-ferrite regions of the steel [10]. As described by Mughrabi et al. [10], slip mechanisms in BCC materials are inherently temperature sensitive, and the transitional temperature is a function of strain rate. Thus, the energy required to cause dislocation motion in BCC metals increases with strain rate, leading to a higher effective yield strength and correspondingly a higher fatigue strength in UFT [10]. In addition, the increased strain rate can potentially cause the deformation glide mechanisms to transition from the athermal regime to the thermally-activated regime, changing the crack initiation mechanisms from intragranular slip band formation at conventional frequencies to intergranular cracking at ultrasonic frequencies [11,12]. Until the effect of the test frequency on the fatigue behaviour for ferritic steels can be fully quantified, the usability of UFT to produce VHCF data that is applicable to conventional frequency applications remains limited.

Bach et al. [5] proposed a frequency sensitivity parameter, m, based on the Hart strain rate sensitivity equation [13]. Parameter m is evaluated by comparing the stress amplitude of specimens that lasted for an equivalent number of cycles to failure at each test frequency, thereby providing a method to quantify the frequency sensitivity of a material based on the finite life fatigue region. The definition of this proposed parameter is given in Equation (1), where ${\sigma }_{\mathrm{a}}$ is the stress amplitude and f is the test frequency [14]. The subscripts C and U are used to denote the values from Conventional and Ultrasonic frequency testing, respectively:

$$m={\displaystyle \frac{ln\left({\sigma }_{\mathrm{a},\mathrm{U}}\right)-ln\left({\sigma }_{\mathrm{a},\mathrm{C}}\right)}{ln\left(f_{\mathrm{U}}\right)-ln\left(f_{\mathrm{C}}\right)}},$$

(1)

where m was evaluated for C15E, C45E and C60E ferritic-pearlitic carbon steels. It was observed that the frequency sensitivity appears to correlate strongly with the ferrite volume % [5]. Notably, this model has only been used as a comparative measure of the frequency sensitivity, and has not been applied to predict the frequency sensitivity for a given steel.

Guennec et al. [12] produced a model, based on the Arrhenius relation, which predicts the fatigue limit of ferritic-pearlitic carbon steels based purely on the test frequency and ferrite content, as shown below:

$${\sigma }_{\mathrm{fl}}={\sigma }_{\mathrm{Y}}{10}^{{\lambda }_{\alpha }}{\left(\%Fe\right)}^{K_{\alpha }}exp\left({\displaystyle \frac{{10}^{{\lambda }_{\beta }}{(\%Fe)}^{K_{\beta }}}{T_{\mathrm{o}}ln\left(\frac{f_{\mathrm{o}}}{f}\right)}}\right),$$

(2)

where ${\sigma }_{\mathrm{fl}}$ is the fatigue limit, ${\sigma }_{\mathrm{Y}}$ is the quasistatic yield strength of the material, $\%Fe$ is the ferrite volume content of the material, $T_{\mathrm{o}}$ is room temperature ($T_{\mathrm{o}}$ = 293 K), $f_{\mathrm{o}}$ is the frequency corresponding to the vibratory factor (taken as $f_{\mathrm{o}}=2·{10}^9$ ${\mathrm{s}}^{-1}$ [12]), and ${\lambda }_{\alpha }$, $K_{\alpha }$, ${\lambda }_{\beta }$ and $K_{\beta }$ are all empirically obtained constants. A generalised form of the model (2) was created by fitting it against a range of carbon steels from the literature. This generalised model was able to estimate the fatigue limit of a given steel at a specified test frequency, with an error of less than 10% in most cases.

In a previous investigation by the authors [8,9,15], the average difference between the finite-life region S-N curves at conventional and ultrasonic frequencies was used to evaluate the frequency sensitivity for S275JR, S355JR, and Q355B grade structural steels. This average difference was also subtracted from the UFT S-N curve to act as a correction factor, which worked well for the S355JR, but not for the Q355B due to the observed change in the slope of the S-N curve.

Therefore, the aims of the current investigation are as follows. Firstly, S-N curves at both conventional and ultrasonic frequencies will be produced for the structural steel grade S275J2, to evaluate the influence of the test frequency on the fatigue resistance for this material. This data, combined with the previous literature results, will then be used to develop generalised frequency sensitivity models, which will also be applied as correction factors to the UFT data.

2. Experimental Analysis of S275J2 Steel

2.1. Material Characterisation

The material evaluated in the current investigation was S275J2 structural steel, as defined by the standard EN 10025-2 [16]. S275 is a low-carbon ferritic-pearlitic steel grade that is commonly used throughout the industry due to its low cost, good formability, and high ductility. The J2 subgrade denotes an impact toughness of >27 J at −20 °C, thereby making it useful for industrial applications in cold operating environments.

All test specimens were manufactured from a 1 m × 1 m × 15 mm S275J2 steel plate. The chemical composition of the steel plate, provided in

Table 1. Chemical composition of the S275J2 steel (wt%), obtained from optical emission spectroscopy.

Material	C	Si	Mn	S	P	Cr	Ni	Cu	Al	N	Fe
S275J2	0.17	0.18	0.92	0.009	0.013	0.08	0.05	0.03	0.036	0.004	Bal.

, was evaluated using Optical Emission Spectroscopy. Yield strength, ${\sigma }_{\mathrm{Y}}$, tensile strength ${\sigma }_{\mathrm{UTS}}$, and elastic modulus, E, were determined through quasistatic tensile tests in an Instron 8801 servo-hydraulic testing machine (Instron, Norwood, MA, USA), according to the procedures in ASTM A370 [17]. A diagram of the specimen used for the tensile tests is presented in Figure 1. Material hardness was evaluated using a 500 g indenter, following the ASTM E384 standard [18]. The volume fraction of the $\alpha$-ferrite phase, %Fe, was evaluated using a systematic manual point count procedure according to ASTM E562 [19], and the average ferrite grain size was evaluated using the machine learning image classification software Ilastik v.1.4.0. A representative micrograph of the S275J2 steel used for micrography is presented in Figure 2, showing the heavily layered bands of $\alpha$-ferrite and pearlite. A table of the corresponding material properties obtained from these tests is given in

Table 2. Key material properties evaluated for S275J2 steel.

Material	Yield Strength, ${\mathit{\sigma }}_{\mathbf{Y}}$ (MPa)	Tensile Strength, ${\mathit{\sigma }}_{\mathbf{UTS}}$ (MPa)	Elastic Modulus, E (GPa)	Vickers Hardness (HV 0.5)	$\mathit{\alpha }$-Ferrite Vol. Fraction, %Fe	Ave. Ferrite Grain Diameter (μm)
S275J2	303	469	211	131	75	10.1

.

2.2. Fatigue Test Procedure

UFT tests were carried out in a Shimadzu USF-2000A ultrasonic fatigue testing machine (Shimadzu, Kyoto, Japan) at a frequency of 20 kHz, following the procedures specified in WES-1112 [20]. Hourglass specimens with a gauge diameter of 3 mm were used for the test, with a shoulder length of 7 mm to achieve the desired resonant frequency of 20 kHz. The surface of the gauge section was mechanically polished to Ra < 0.2 $\mathsf{\mu }$m. Each end of the UFT specimen was screwed into an acoustic horn, and the mean stress in the loading stack was continually adjusted to 0 N between load pulses to avoid any mean stress effects. To determine the failure point of a specimen, the USF-2000A’s crack detection feature was used, which terminates the test if the specimen’s resonant frequency drops below 19.5 kHz. To enable inspection of the fracture surface, the two parts of the specimen could then be completely separated by applying a tensile force of 1 kN. To counteract the heat generation from internal plasticity dissipation in UFT, compressed air cooling and intermittent loading were applied. The specimen’s surface temperature was monitored using an IR spot sensor with a diameter of 1 mm and a sampling rate of 20 ms, which automatically stopped the test if the temperature exceeded 30 °C.

It is important to ensure that the risk volume—the volume of the material which is experiencing at least 90% of the peak stress—is kept consistent between all test frequencies in order to avoid the influence of any size effects [21]. As such, specialised fatigue test specimens were produced for use at conventional frequencies, with a gauge section matching that of the UFT specimens. The geometry of both the UFT and conventional frequency specimens is detailed in Figure 3.

Conventional frequency fatigue tests were carried out at 50 Hz in an Instron E3000 ElectroPuls testing machine, following BS ISO 1099 [22]. All tests were carried out under stress-controlled axial loading with zero mean stress, in environmental conditions and at room temperature. The fatigue failure point was taken when the specimen fractured into two separate pieces. This does result in a discrepancy in where the failure point is defined between the tests at the two frequencies; however, this is considered negligible as very little fatigue life remains once the crack is large enough to trigger the automatic fracture detection in the UFT machine [20]. The fatigue test set-ups at both 50 Hz and 20 kHz are shown in Figure 4.

3. Results

3.1. S275J2 Fatigue Testing Results

The fatigue results for the S275J2 at both test frequencies are presented in Figure 4. A large difference in fatigue resistance was observed between the two test frequencies, as would be expected for a ferritic steel. Notably, all of the fatigue results obtained at 20 kHz, including the UFT fatigue limit, are at stress amplitudes that are higher than the quasi-static yield strength of 303 MPa. It is proposed that this is due to the increased strength of S275J2 steel at the elevated strain rate of the 20 kHz test frequency. For similar structural steels, the yield strength at strain rates corresponding to UFT tests can be up to 150 MPa higher than the quasistatic yield strength [23,24]. The influence of strain rate on the material strength—and the corresponding influence this has on the fatigue resistance—will be investigated further in a future investigation.

By fitting a power law trendline to the two frequencies, it can also be seen that there was a reduction in the slope of the S-N curve at 20 kHz. Assuming the power law S-N curve for a given material is given by Equation (3), where ${\sigma }_{\mathrm{a}}$ is the stress amplitude and N is the number of cycles to failure, then the corresponding values for coefficient a and exponent b for S275J2 at each test frequency are given in

Table 3. S-N curve parameters obtained for S275J2 at conventional and ultrasonic frequencies.

Test Frequency	a	b
50 Hz	521.58	−0.064
20 kHz	495.95	−0.021

:

$${\sigma }_{\mathrm{a}}=a{N}^b.$$

(3)

To quantify the difference in fatigue resistance between the two test frequencies, two different approaches were used. Firstly, the % increase in fatigue limit when testing at ultrasonic frequencies, defined as $D_{\lim }$, can be used. For the S275J2, the CFT fatigue limit was 189 MPa, and the UFT fatigue limit was 325 MPa. This therefore corresponds to an increase in fatigue limit of 136 MPa at ultrasonic frequencies, or a % increase of $D_{\lim }$= 72% over the conventional frequency fatigue limit.

Secondly, the difference in the fatigue resistance within the finite life region can be used. At an equivalent number of cycles to failure, the difference in survivable stress amplitude between the ultrasonic and conventional frequency S-N curves was determined. This comparison was applied across the entire finite-life region of the S-N curve, using the longest-lived specimen at 50 Hz as the upper bound and the shortest-lived specimen at 20 kHz as the lower bound to avoid bias from extrapolated data beyond these limits. These limits are shown in Figure 5. Using this procedure, the average difference between the curves within these limits was evaluated to be 150 MPa. Defining $D_{\mathrm{fin}}$ as the average % increase in survivable stress amplitude at an equivalent number of cycles when tested at ultrasonic frequencies corresponds to a value of $D_{\mathrm{fin}}$ = 67% for the S275J2 steel.

3.2. Fractography Analysis

All of the S275J2 test specimens failed from surface fracture initiation, regardless of the test frequency or the number of cycles to failure. Scanning electron microscopy (SEM) images of the UFT specimens, taken using a Hitachi S3700-N machine, are presented in Figure 6. No clear defects or inclusions were observable at the initiation site. This is consistent with other high-ferrite steels tested in the literature, where surface failures are observed, even within the VHCF regime [5,12,25,26].

3.3. Comparison to S275JR

In Figure 7, the S275J2 results are compared against the results obtained for the S275JR subgrade from a previous investigation by the authors [8,9]. As expected, S275JR exhibits a similar response to the S275J2, with an equivalent increase in the fatigue limit of 130 MPa at ultrasonic frequencies, but a greater increase in the survivable stress amplitude in the finite life region of 172 MPa. The most notable distinction between the response of the two subgrades is that S275JR does not appear to show the reduction in the slope of the S-N curve that is observed for S275J2. This mirrors the observations made by the authors in a previous investigation for Q355B and S355JR grade steels [9,15]. As the S275JR and S355JR were both tested with a larger cylindrical specimen geometry at conventional frequencies, it is therefore proposed that this difference is due to the influence of the inconsistent specimen size on the fatigue results, highlighting the importance of keeping the specimen geometry consistent across the test frequencies.

4. Generalised Frequency Sensitivity Model Development

A method was sought to estimate the difference between the CFT and UFT fatigue response for a given ferritic-pearlitic steel, without requiring a full set of test data to be produced at both frequencies. To accomplish this, a generalised model must be developed which can evaluate the difference between the fatigue response at conventional and ultrasonic frequencies of a steel, based only on its material properties.

To achieve this, a new frequency sensitivity model was developed, based on using the difference in the S-N curve parameters at conventional and ultrasonic frequencies as a measure of the frequency sensitivity. By examining how the parameters a and b shift at ultrasonic frequencies across a range of ferritic-pearlitic steels reported in the literature, an empirical relationship between these changes and the steels’ material properties can be established.

In addition to this original approach, an updated and generalised form of the strain rate sensitivity model proposed by Bach et al. [5] will also be developed. Updated versions of the frequency sensitivity parameter, m, will be proposed and fitted to the material properties of the literature steels, resulting in generalized versions of the model.

4.1. Selection of Literature Data

A number of additional test results for ferritic-pearlitic steels from the literature were considered in addition to the S275J2 results produced in this investigation. The literature results selected for comparison were for ferritic-pearlitic steels, which were tested at room temperature, and had a direct comparison between ultrasonic frequencies (20 kHz) and conventional frequencies (1–200 Hz). Important values such as the material strength, ferrite content, and fatigue limit at each frequency were extracted from the papers. The full list of papers and corresponding properties is detailed in

Table 4. Details of steels taken from the literature.

Material	${\mathit{\sigma }}_{\mathbf{Y}}$ (MPa)	${\mathit{\sigma }}_{\mathbf{UTS}}$ (MPa)	%Fe	Ferrite Grain Size (μm)	Hardness (HV)	CFT Fatigue Limit (MPa)	UFT Fatigue Limit (MPa)	Source
S275JR	314	469	82	14.3	146	210 (15 Hz)	340 (20 kHz)	[8]
S355JR	388	513	76	6.4	167	240 (20 Hz)	370 (20 kHz)	[15]
Q355B	424	560	79	10.4	174	—	—	[15]
C15E	—	—	94.56	8.6	—	190 (110 Hz)	290 (20 kHz)	[5]
C45E	—	—	49.97	6.2	—	225 (110 Hz)	310 (20 kHz)	[5]
C60E	—	—	10.28	3.7	—	315 (110 Hz)	370 (20 kHz)	[5]
S15C	274	441	83.1	15.5	161	192 (20 Hz)	248 (20 kHz)	[26]
S38C	374	603	50	—	—	250 (10 Hz)	370 (19.8 kHz)	[7]
S45C	343	620	47	11	—	219 (30 Hz)	303 (20 kHz)	[12]
Q345	395	550	70	—	180	230 (158 Hz)	340 (20 kHz)	[27]
S355J0	359	507	76 *	3.7	—	225 (10 Hz)	340 (20 kHz)	[4]
S355J2	382	554	76 *	3.7	—	270 (10 Hz)	346 (20 kHz)	[4]
Wheel Steel A	656	959	13.6	—	287	441 (150 Hz)	415 (20 kHz)	[28]
Wheel Steel B	647	965	9.2	—	288	434 (150 Hz)	403 (20 kHz)	[28]
Wheel Steel C	625	959	8.7	—	286	432 (150 Hz)	409 (20 kHz)	[28]
Wheel Steel D	620	946	9.6	—	276	431 (150 Hz)	401 (20 kHz)	[28]
XC70	513	927	14.5 *	—	305	360 (30 Hz)	350 (20 kHz)	[29]
0.13%C steel	210	370	85.5 *	—	123	170 (10 Hz)	209 (20 kHz)	[6]

* ferrite content not provided—therefore estimated from %C using the lever rule.

.

It is important to note that there is significant variability in the test procedures between the investigations. The test frequencies, especially at conventional frequencies, were not consistent, which may lead to inaccuracies when comparing them against each other. The number of cycles used for a run-out specimen also varied between the investigations, which will influence the point at which fatigue limit values are identified. Additionally, the specimen geometries varied between the different investigations, and in most cases, it was not kept consistent at both test frequencies, likely leading to size effects being present. The number of tested specimens in each investigation is also inconsistent, sometimes being as low as 3 for Nonaka et al. [7], which may lead to inaccurate S-N curves. The S355J0 and S355J2 [4] investigations also used liquid cooling instead of air cooling, which has sometimes been reported to cause a reduction in fatigue resistance from factors such as cavitation erosion in Trško et al. [30]. The 0.13%C specimens investigated by Tsutsumi et al. [6] had drilled holes to act as artificial initiation sites, which will reduce the number of cycles spent in the crack initiation phase.

It can therefore be seen that there is a large amount of variance in the test procedures throughout the literature, leading to large uncertainties when comparing results against each other. This highlights the need to develop a more prescriptive and widespread standard for UFT to ensure better consistency in future investigations. Until then, any observed trends between investigations can only be considered to be approximate.

For each of the literature steels, $D_{\lim }$ and $D_{\mathrm{fin}}$ were evaluated using the procedure described in Section 3. Plots of the corresponding $D_{\lim }$ and $D_{\mathrm{fin}}$ values for each of the steels are presented in Figure 8 and Figure 9, respectively.

For both approaches, a general increase in the frequency sensitivity with ferrite content can be seen; however, there is significant scatter in the results, especially beyond 70% ferrite volume %, where the increase in fatigue strength at ultrasonic frequencies ranges from 20–80%. Additionally, the moderate ferrite content materials (S45C, C45E) are well within the region of scatter of the high ferrite content materials and do not appear to be notably less sensitive to the test frequency, despite this being previously reported by Bach et al. [5]. It is therefore difficult to identify a direct correlation between ferrite content and the frequency sensitivity using this approach alone.

Another factor that must be considered is the change in the gradient of the S-N curves at ultrasonic frequencies. Most of the literature steels exhibited a reduction in the slope of the S-N curve at ultrasonic frequencies, with the only exceptions being the C15E [5] and the Wheel Steels tested by Li et al. [28], which showed an increase in the gradient. The severity of this gradient reduction varied between materials, with it being very small for the C45E, S38C, S355JR and S275JR steels, and being very large for S45C, S355J0, 0.13%C, and Q355B steels.

4.2. Evaluation of the Change in S-N Curve Parameters

Taking an S-N curve in the form of Equation (3), then the ratio of the survivable stress amplitude at low and high stress amplitudes at an equivalent number of cycles to failure, N, can be defined using Equation (4), where the C and U subscripts denote the conventional and ultrasonic frequency fatigue values, respectively. The change in the fatigue response at ultrasonic frequencies can therefore be defined by the two parameters: the change in the coefficient, $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$, which represents the change in intercept when plotted on a log-log graph, and the change in the exponent, $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$, which represents the change in the gradient when plotted on a log-log graph:

$${\displaystyle \frac{{\sigma }_{\mathrm{a},\mathrm{C}}}{{\sigma }_{\mathrm{a},\mathrm{U}}}}={\displaystyle \frac{a_{\mathrm{C}}}{a_{\mathrm{U}}}}{N}^{\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)}.$$

(4)

To produce a generalised model, $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ were therefore evaluated for all of the materials in Table 4, and the corresponding values were plotted against different combinations of the material properties.

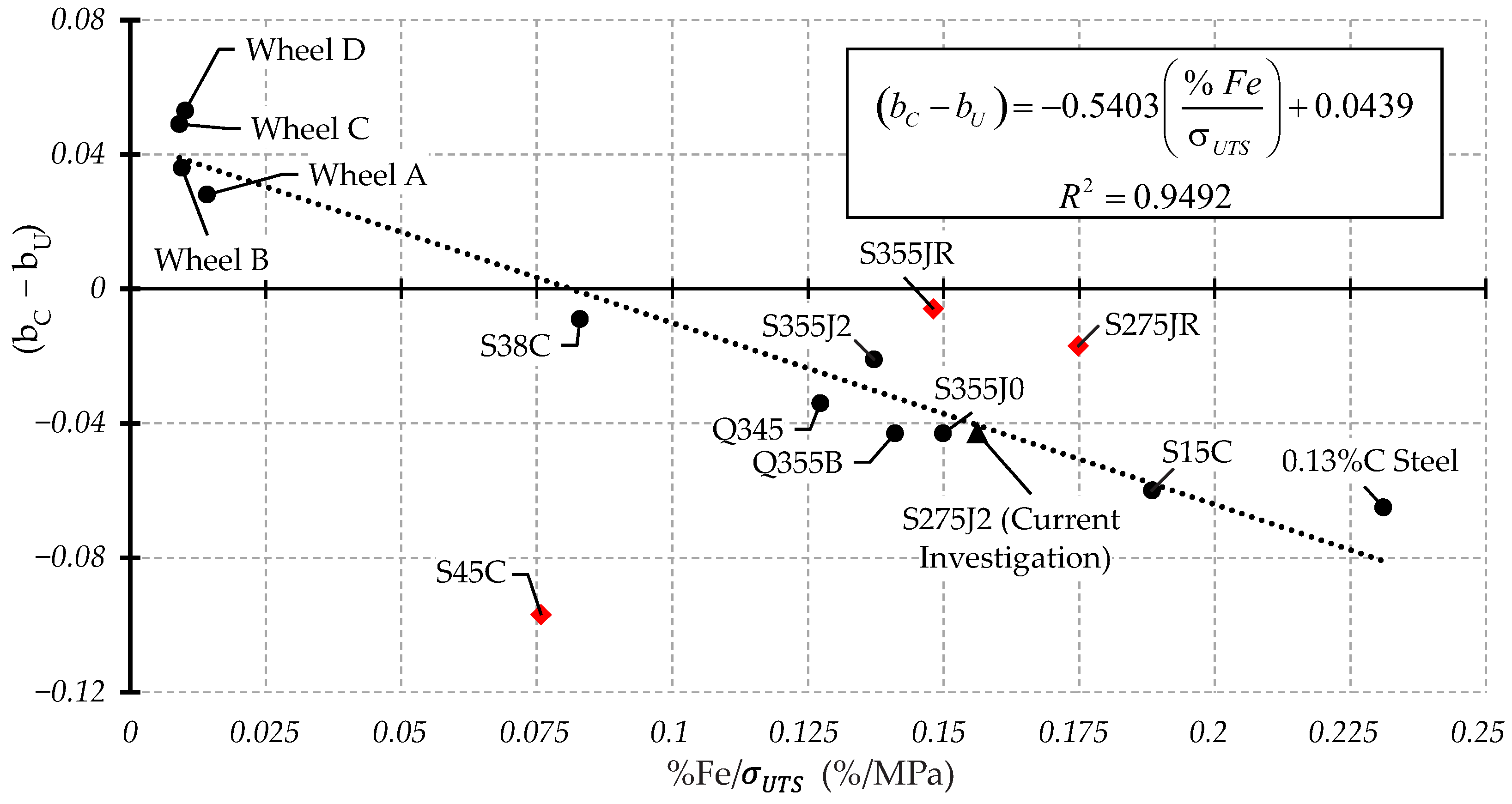
The material properties considered for comparison were the hardness, ferrite content, grain size, and strength, as well as combinations of these. Out of these options, it was found that the closest trends were against %Fe/${\sigma }_{\mathrm{UTS}}$. The resultant scatter plots of $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ against %Fe/${\sigma }_{\mathrm{UTS}}$ are presented in Figure 10 and Figure 11, respectively. A linear correlation was observed for both $\left(a_C/a_U\right)$ and $\left(b_C-b_U\right)$, using a least-squares regression in Microsoft Excel, with a coefficient of determination of $R^2$ = 0.8613 and $R^2$ = 0.9492 respectively. Some outliers can be seen, however.

The S275JR and S355JR previously investigated by the authors also appear to be outliers, with a lower $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and a higher $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ when compared to similar steels. It is proposed that this is indicative of specimen size influences when comparing across test frequencies, as these materials were both tested with larger cylindrical specimens at conventional frequencies. The equivalent steel grades tested by the authors with consistent geometries across the test frequencies (Q355B and S275J2) lie much closer to the other literature data and the corresponding trendlines.

Existing size effect models for UFT testing are typically predicated upon the size of an internal defect from which a crack originates [31], and as such are not applicable to the materials in the current investigation, where UFT failures almost exclusively continue to originate from the specimen surface. As such, it is recommended for future work to carry out additional testing to robustly quantify and compare the influence of the size effect for ferritic steels under both CFT and UFT. As it stands, the S275JR and S355JR have been excluded when evaluating the trendline. Additionally, the S45C steel tested by Guennec et al. [12] has a much higher $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and a lower $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ than similar steels, as a result of the particularly steep gradient observed in the conventional frequency results. As such, the S45C was also excluded when evaluating the trendline. A table showing additional error metrics for the resultant $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ trendlines is provided in

Table 5. Error metrics for $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ trendlines against %Fe/${\sigma }_{\mathrm{UTS}}$.

Parameter	${\mathit{R}}^2$	Standard Deviation	Mean Absolute Standardised Residual	Maximum Absolute Standardised Residual	95% Confidence Interval of Standardised Residuals
$\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$	0.861	0.153	0.775	1.841	(−1.739, 1.266)
$\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$	0.949	0.00971	0.464	1.644	(−1.605, 1.057)

.

4.3. Bach Frequency Sensitivity Model

The frequency sensitivity model proposed by Bach et al. [5] was provided in Equation (1) as it was presented in the original work; however, some modifications can be made to this model to enhance its accuracy. The model was based on Hart’s definition of a strain rate sensitivity parameter, m, for a linear load relaxation test, as provided in Equation (5) according to [13], where ${\sigma }_{\mathrm{true}}$ is the true stress and $\dot{\epsilon }$ is the strain rate:

$$m={\displaystyle \frac{\mathrm{d}ln\left({\sigma }_{\mathrm{true}}\right)}{\mathrm{d}ln\left(\dot{\epsilon }\right)}}.$$

(5)

To convert this to a cyclic load case, Bach et al. replaced ${\sigma }_{\mathrm{true}}$ with stress amplitude, ${\sigma }_{\mathrm{a}}$, and replaced $\dot{\epsilon }$ with the test frequency, f, to obtain Equation (1) according to [5]. The relationship between strain rate and test frequency is not linear for a sinusoidal load, however, as the strain rate also varies with the amplitude of the loading. Deriving the root mean square strain rate, ${\dot{\epsilon }}_{\mathrm{RMS}}$, in terms of the test frequency, f, yields Equation (6), which can then be substituted for $\dot{\epsilon }$ in Equation (5) to obtain an updated form of the Bach frequency sensitivity model:

$${\dot{\epsilon }}_{\mathrm{RMS}}=\sqrt{2}\pi f{\displaystyle \frac{{\sigma }_{\mathrm{a}}}{E}}.$$

(6)

This is provided in Equation (7), where the updated frequency sensitivity parameter is denoted by $m^{\prime }$:

$$m^{\prime }={\displaystyle \frac{ln\left({\sigma }_{\mathrm{a},\mathrm{U}}\right)-ln\left({\sigma }_{\mathrm{a},\mathrm{C}}\right)}{ln\left({\sigma }_{\mathrm{a},\mathrm{U}}·f_{\mathrm{U}}\right)-ln\left({\sigma }_{\mathrm{a},\mathrm{C}}·f_{\mathrm{C}}\right)}}.$$

(7)

Additionally, m is not an inherent material parameter, as the observed m value will vary depending on the CFT frequency, $f_{\mathrm{C}}$, used to evaluate it. This can be demonstrated by applying the Bach model to the results produced at different CFT test frequencies for a single material by Guennec et al. [26]. Figure 12 shows m evaluated for the same S15C steel using the results from three different conventional frequencies. This trend is also observed when plotting $m^{\prime }$.

As can be seen in Figure 12, the relationships between the frequency sensitivity parameters and $f_{\mathrm{C}}$ both follow a logarithmic trend. This logarithmic trend can therefore be used to correct m or $m^{\prime }$ to an arbitrary frequency of $f_{\mathrm{C}}$ = 20 Hz, provided that the ultrasonic frequency is kept constant at 20 kHz. Assuming the slope of this trendline is consistent between similar materials, this would allow better comparison of the frequency sensitivity between results that were produced at different test frequencies. The corresponding correction for $m^{\prime }$ is given in Equation (8), where ${m^{\prime }}_{\mathrm{fC}}$ is the frequency sensitivity parameter evaluated at the conventional frequency $f_{\mathrm{C}}$, and ${m^{\prime }}_{20}$ is the frequency sensitivity parameter corrected to 20 Hz. Assuming that this trend is consistent between the literature materials, ${m^{\prime }}_{20}$ can therefore be used to more accurately compare the frequency sensitivity of steels which were tested at different conventional frequencies:

$${m^{\prime }}_{20}={m^{\prime }}_{\mathrm{fC}}+0.0038ln\left({\displaystyle \frac{20}{f_{\mathrm{C}}}}\right).$$

(8)

The frequency sensitivity parameters m, $m^{\prime }$, and ${m^{\prime }}_{20}$ were evaluated for all of the literature steels. Parameters m, $m^{\prime }$ and ${m^{\prime }}_{20}$ were evaluated for up to 5 pairs of data points for each material, with the average values for each being presented in Figure 13. A negative m value represents a material in which a reduction in the fatigue resistance was observed at ultrasonic frequencies. It is worth noting that, as these frequency sensitivity parameters are evaluated using pairs of data points at an equivalent number of cycles to failure at each frequency [5], the resultant values are highly dependent on which specimens happened to last an equivalent number of cycles before failure. As such, evaluating m, $m^{\prime }$, and ${m^{\prime }}_{20}$ is particularly sensitive to the scatter in fatigue results. For some of the literature steels, there were no pairs of data points that were sufficiently close to each other, and thus the frequency sensitivity parameters could not be ascertained.

From Figure 13, it can be seen that m, $m^{\prime }$, and ${m^{\prime }}_{20}$ all yield similar values for each of the steels, with the overall trends being the same for all three versions of the model. In all cases, the $m^{\prime }$ and ${m^{\prime }}_{20}$ values were slightly lower than the original m values; however, with the biggest difference seen for the materials with the highest frequency sensitivity. As a result, this results in a small improvement in scatter over the original m model. A general increase in all of the frequency sensitivity parameters with ferrite content can be seen, with a large amount of scatter still present between 70 and 85% ferrite. In contrast to the approach using the empirical change in the S-N curve parameters, the S275JR, S355JR, and S45C results do not appear to be significant outliers. Following this, generalised versions of the Bach model were produced based on both the $m^{\prime }$ and ${m^{\prime }}_{20}$ parameters. 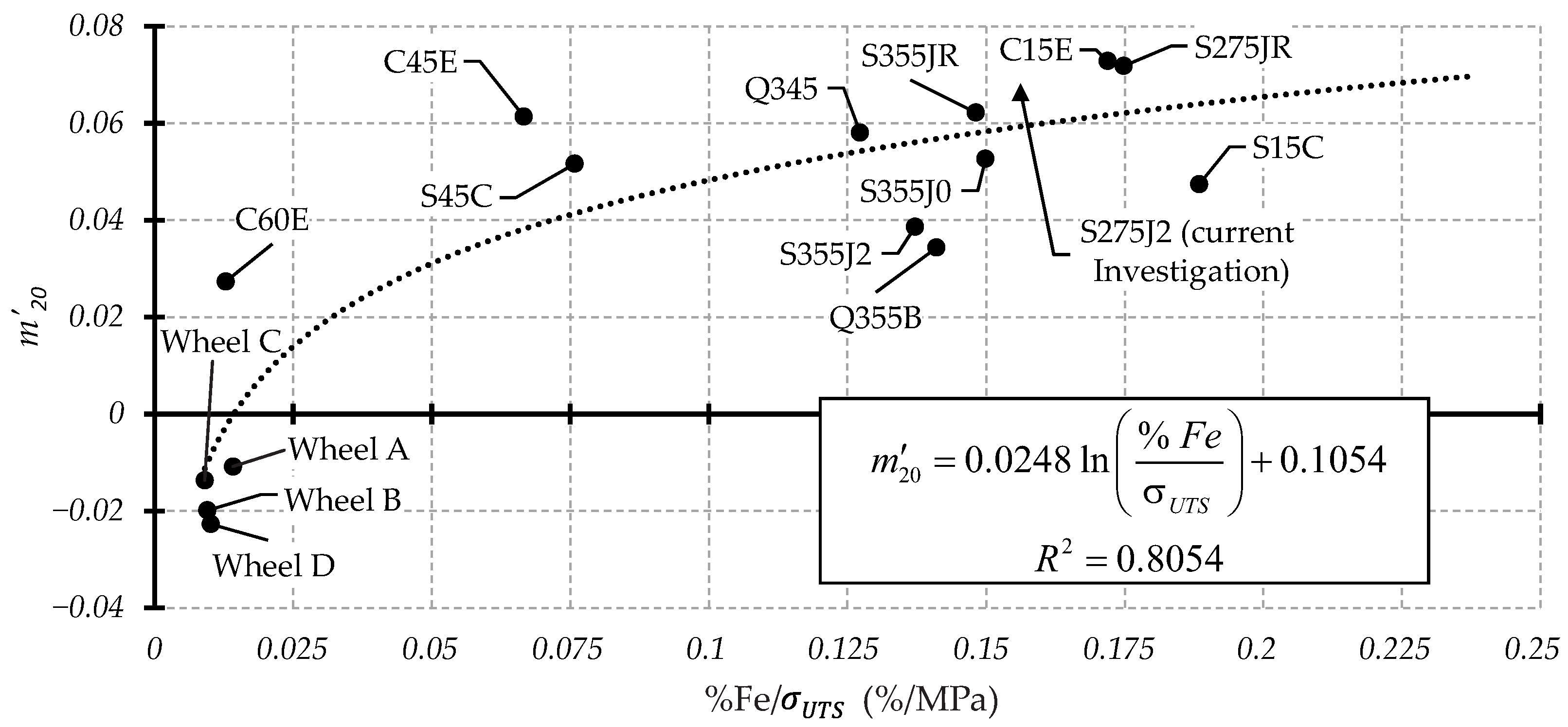Parameters $m^{\prime }$ and ${m^{\prime }}_{20}$ were evaluated as a function of the material properties, following the same procedure outlined for $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ in Section 4.2. It was again found that the best trends were against %Fe/${\sigma }_{\mathrm{UTS}}$, as shown in Figure 14 and Figure 15 for $m^{\prime }$ and ${m^{\prime }}_{20}$ respectively. Logarithmic trendlines were fitted to the experimental data using a least-squares regression in Microsoft Excel. Notably, the ${m^{\prime }}_{20}$ version of the model exhibits an improved correlation coefficient in comparison to the $m^{\prime }$ version, with $R^2$ values of 0.8054 and 0.7467 for the two versions, respectively. This shows that the test frequency used to carry out the CFT tests does have a tangible influence on the measured frequency sensitivity, contributing to the scatter observed between the results. As such, it is clear that for a generalised frequency sensitivity model to be sufficiently robust, it must take into account any variations in the CFT test frequency. Additional error metrics for the $m^{\prime }$ and ${m^{\prime }}_{20}$ trendlines are presented in

Table 6. Error metrics for $m^{\prime }$ and ${m^{\prime }}_{20}$ trendlines against %Fe/${\sigma }_{\mathrm{UTS}}$.

Parameter	${\mathit{R}}^2$	Standard Deviation	Mean Absolute Standardised Residual	Maximum Absolute Standardised Residual	95% Confidence Interval of Standardised Residuals
$m^{\prime }$	0.747	0.0121	0.554	1.981	(−1.918, 0.759)
${m^{\prime }}_{20}$	0.805	0.0112	0.546	2.012	(−1.877, 0.902)

.

5. Application of Models as UFT Correction Factors

With generalised versions of the frequency sensitivity models now produced, it was desired to evaluate whether they could be suitably used to correct the UFT S-N curves to match the CFT test data, which would enable the accelerated evaluation of fatigue data for lower frequency applications.

To use the empirical change in the S-N curve as a correction factor, $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ can be evaluated for a given steel using the relation in Figure 10, then applied to the coefficients of the UFT S-N curve to evaluate the equivalent CFT curve. For comparison, the $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ correction and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ correction were each applied separately to the UFT S-N curve, as well as applying both corrections together.

To apply the modified Bach model as a correction factor, Equation (7) can be rearranged to give the low frequency stress amplitude ${\sigma }_{\mathrm{a},\mathrm{C}}$, in terms of the high frequency stress amplitude, ${\sigma }_{\mathrm{a},\mathrm{U}}$ and the frequency sensitivity parameter, $m^{\prime }$, as presented in Equation (9). Hence, by evaluating the $m^{\prime }$ value for a given steel using the relation in Figure 14, the UFT stress amplitude can be converted into an equivalent CFT stress amplitude:

$${\sigma }_{\mathrm{a},\mathrm{C}}={\sigma }_{\mathrm{a},\mathrm{U}}{\left({\displaystyle \frac{f_{\mathrm{U}}}{f_{\mathrm{C}}}}\right)}^{{\displaystyle \frac{m^{\prime }}{m^{\prime }-1}}}.$$

(9)

For additional comparison, the generalised frequency sensitivity model previously proposed by Guennec et al. [12] was also applied as a correction factor by combining Equation (2) for both the UFT and CFT test frequencies, to evaluate the ratio of the corresponding fatigue limits. This yields the relationship in Equation (10):

$${\displaystyle \frac{{\sigma }_{\mathrm{fl},\mathrm{U}}}{{\sigma }_{\mathrm{fl},\mathrm{C}}}}=exp\left({\displaystyle \frac{{10}^{2.6318}{\left(\%Fe\right)}^{0.5095}}{T_0}}\left({\displaystyle \frac{1}{ln\left(\frac{f_0}{f_{\mathrm{U}}}\right)}}-{\displaystyle \frac{1}{ln\left(\frac{f_0}{f_{\mathrm{C}}}\right)}}\right)\right).$$

(10)

The corrected UFT curves produced using each of these methods are compared against the actual CFT data for the S275J2 steel in Figure 16. For comparison, the corrected UFT curves are also evaluated for the Q355B from the previous investigation by the authors [15], in Figure 17.

The corrections from the Bach and Guennec models all provide a similar response, as they both shift the ultrasonic S-N curve directly downwards with no correction made to the gradient. As previously discussed in Section 4.1, however, a reduction in the S-N curve gradient is commonly observed for ferritic steels tested in UFT. Neither the Generalised Bach nor Guennec models consider this change in gradient, resulting in the corresponding corrected UFT curves not being aligned with the CFT test results. This highlights the inaccuracies of using these models directly as correction factors and the necessity of including a gradient correction. For the empirical change in the S-N curve approach, it can immediately be seen that applying only the intercept correction, $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$, provided an inaccurate result, as in many cases the intercept of the S-N curve was actually higher in the CFT tests than in the UFT tests. Therefore, applying the intercept correction alone inaccurately predicted a greater fatigue resistance at the lower test frequencies. Note, however, that $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ has previously been successfully applied as a correction factor for 34CrNiMo6 and 42CrMo4 alloy steels by Teixeira et al. [32], and thus this approach may still be viable for other classes of steel.

From all of the evaluated correction factors, it was found that either applying only the empirical gradient correction, $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$, or both the $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ and $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ corrections together provide the best estimations of the CFT S-N curves. Both of these approaches captured the change in gradient for the S275J2 and Q355B steels, as well as approximately aligning with the stress amplitude range of the CFT data.

In Figure 18, the number of cycles to failure evaluated from the corrected UFT S-N curves is compared to the corresponding value from the CFT S-N curve at an equivalent stress amplitude, in order to evaluate the accuracy of the corrected curves. For both of the steels, it can be seen that applying $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ and $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$ together provided a non-conservative estimate of the CFT curve. For the S275J2, the number of cycles to failure from the corrected curve was overestimated by a factor of 20, which would be unusable for design applications. For the Q355B steel, the number of cycles to failure was overestimated by 2–10 times. Applying only $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ provides conservative estimates of the CFT S-N curves, with the number of cycles to failure being underestimated for both of the steels. For the S275J2, the corrected S-N curve was within a factor of 1.3 of the CFT curve along the full finite life region. For the Q355B, however, the corrected UFT S-N curve underestimated the CFT curve by approximately one decade, diverging further at low numbers of cycles to failure.

Out of the models applied in the current investigation, it can therefore be seen that the UFT S-N curve corrected using $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ provided the best estimate of the CFT data: approximating the slope of the CFT S-N curve and providing conservative estimates of the conventional frequency fatigue life for both materials. However, there is still significant variability in how much the corrected curve undercuts the conventional frequency data, with the Q355B CFT results in particular being underestimated by approximately one decade. The further the $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ value for a given steel strays from the empirical trendline in Figure 11, the greater the difference between the corrected UFT and CFT results will be.

The key to improving the accuracy of this approach would therefore be to improve the correlation between $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ and the material parameters in Figure 11, by further identifying and evaluating the causes of the scatter. Due to the reliance on the disparate literature data to build the generalised versions of these models, however, it is currently difficult to determine how much of the scatter in the correlation is due to stochastic fatigue effects, due to the influence of additional material factors, or due to the variance in the test parameters between the different investigations. To achieve this goal, it would therefore be necessary to test a wide range of ferritic steels with equivalent specimen geometries under a consistent set of test conditions. From this data, a more accurate correlation for $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ could be determined, leading to the production of a more consistently reliable correction factor.

6. Conclusions

In this investigation, the conventional and ultrasonic frequency fatigue response of S275J2 steel was evaluated, to determine the influence of the test frequency on the fatigue response. Additionally, a new frequency sensitivity model based on the change in S-N curve parameters was proposed, alongside updated versions of Bach’s frequency sensitivity model. Generalised versions of these models were produced by empirically fitting the model parameters against %Fe/${\sigma }_{\mathrm{UTS}}$. Finally, the generalised forms of these models—alongside the generalised model previously proposed by Guennec et al. [12]—were applied as correction factors to allow the conventional frequency fatigue response to be estimated based on the UFT S-N curve.

The key findings are as follows:

• S275J2 was found to exhibit an increase in the fatigue limit of 130 MPa, and an average increase in the finite life stress amplitude of 172 MPa when tested at 20 kHz. A reduction in the slope of the S-N curve was also observed at ultrasonic frequencies.
• A number of inconsistencies were identified between the test parameters used to evaluate the frequency sensitivity of ferritic-pearlitic steels in the literature investigations. These inconsistencies may be contributing to the scatter in the generalised models. This highlights the need to develop a more prescriptive UFT test method to improve the comparability of results.
• The proposed updates to Bach’s frequency sensitivity model resulted in a slightly reduced scatter when evaluated across a variety of ferritic-pearlitic steels. This reduced scatter resulted in an improvement of the $R^2$ from 0.747 to 0.805 when developing generalised versions of the model.
• When applied as correction factors to the UFT S-N curves, the Generalised Bach and Guennec models did not account for the change in the gradient in the S-N curve. This led to a poor alignment of the corrected UFT S-N curve to the CFT data.
• Applying the empirical change in the exponent, $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$, and the change in gradient of the S-N curve, $\left(a_{\mathrm{C}}/a_{\mathrm{U}}\right)$, together as a correction factor resulted in the number of cycles to failure at conventional frequencies being overestimated by up to a factor of 20.
• Applying solely $\left(b_{\mathrm{C}}-b_{\mathrm{U}}\right)$ provided the best UFT correction factor, as it matched the gradient of the CFT SN curve and underestimated the number of cycles to failure for both of the evaluated steels. Using this method, the conventional frequency fatigue life of S275J2 was underestimated by a factor of 1.3, whereas for Q355B it was underestimated by a factor of 10. This variability in the accuracy of the corrected UFT curve represents a limitation of this approach as it currently stands. To improve the accuracy of the model, further testing of a variety of ferritic-pearlitic steels under consistent test conditions is necessary.