A Hybrid Optimization Framework for Dynamic Drone Networks: Integrating Genetic Algorithms with Reinforcement Learning

Abstract

The growing use of unmanned aerial vehicles (UAVs) in diverse fields such as disaster recovery, rural regions, and smart cities necessitates effective dynamic drone network establishment techniques. Conventional optimization techniques like genetic algorithms (GAs) and particle swarm optimization (PSO) are weak when it comes to real-time adjustment to the environment and multi-objective constraints. This paper proposes a hybrid optimization framework combining genetic algorithms and reinforcement learning (RL) to improve the deployment of drone networks. We integrate Q-learning into the GA mutation process to allow drones to adaptively adjust locations in real time under coverage, connectivity, and energy constraints. In the scenario of large-scale simulations for wildfire tracking, disaster response, and urban monitoring tasks, the hybrid approach performs better than GA and PSO. The greatest enhancements are 6.7% greater coverage, 7.5% less average link distance, and faster convergence to optimal deployment. The proposed framework allows drones to establish strong and stable networks that are dynamic in nature and adapt to dynamic mission demands with efficient real-time coordination. This research has important applications in autonomous UAV systems for mission-critical applications where adaptability and robustness are essential.

1. Introduction

The rapid evolution of unmanned aerial vehicles or drones has revolutionized various domains, including disaster response, wildlife tracking, telecommunications, and precision agriculture. As the autonomous systems transition from research prototypes to critical infrastructure, deployment strategies for them have to grapple with one overarching challenge: trade-offs among conflicting objectives like spatial coverage, network connectivity, energy efficiency, and responsiveness to dynamic environments. Classical optimization methods would separately optimize single metrics like surveillance coverage or hardware cost; real-world deployment, however, demands a combined framework to balance these conflicting goals. In the case of a rescue mission after a disaster, for instance, the drones should search debris to find survivors while also creating an ad hoc network to relay live feeds to the rescuers. Here, drones are performing two significant functions, the functions of harvesting data and also serving as a communication relay, which requires strategies for deployment where coverage is optimized and connectivity maintained. This second function serves to emphasize the richness of modern-day drone networks where traditional static or single-shot methodologies are not suitable to address the dynamic and multi-objective nature of real-world problematics.

Drone networks are increasingly vital to use cases requiring decentralized, dynamic topologies. In rural broadband access, drones serve as airborne base stations that create mesh networks to close the digital divide where the terrestrial infrastructure is limited. Mesh-enabled drone networks, in contrast to conventional cellular towers, reconfigure themselves dynamically in response to changing demand, environmental interference, or temporary population density surges—e.g., festivals or emergencies. Every drone in a mesh network becomes a forwarding node for the others, creating a self-healing mesh of connectivity. Scaling out such networks involves delicate trade-offs, however: drones too densely packed squander resources and curtail coverage, while drones too widely spaced invite dead spots and burst latency. It is the same with military operations: ad hoc drone networks facilitate real-time intelligence sharing between units operating in enemy territory. These networks must balance stealth (minimizing the minimum detectability) and signal strength without jamming or physical assault [1]. The stakes are high—a failed deployment could compromise mission success or lives. These examples reflect the growing utilization of drone networks where flexibility, resilience, and effectiveness cannot be sacrificed.

Beneath these applications lies the issue of multi-objective optimization, wherein conflicting demands must be traded off. Coverage maximization, for instance, would generally involve dispersing drones far apart but at the expense of stretching inter-drone distances past the point of communications breakdown. On the other hand, clustering drones around a base station realizes praiseworthy connectivity at the expense of coverage, a compromise that is exacerbated in heterogeneous fleets comprising long-endurance fixed-wing and agile multirotors. Fixed-wing UAVs, through its favored patrolling of large perimeters, demand linear flight and higher altitudes, while multirotors enable stable, localized surveillance. The optimization of such hybrid fleets demands algorithms to consider disparate mobility patterns, energy profiles, and sensor packages. Current methods, like genetic algorithms and particle swarm optimization, work effectively in homogeneous environments but cannot handle these intricacies. GAs, which simulate natural selection to develop solutions over generations, become stuck in local optima for discontinuous search spaces or discrete variables (e.g., drone type assignment). PSO, taking a cue from the study of flocking behavior, works well with continuous, smooth topographies but breaks down in providing for discrete decision making, e.g., dynamic switching between relay and sensor nodes.

This study aims to fill these gaps by introducing a hybrid optimization framework that combines the global search capability of genetic algorithms and the adaptive precision characteristic of reinforcement learning. Our solution novelty lies in incorporating Q-learning within a GA’s mutation mechanism so that drones can “learn” position offsets that improve coverage and connectivity. For instance, in a wildfire surveillance mission, fixed-wing drones fly around the fire perimeter, and multirotor drones are deployed close to evacuation paths. As the fire spreads, the RL component dynamically reconfigures drones to prioritize new hotspots, maintaining fleet connectivity. Such responsiveness is vital in ad hoc and mesh networks, where uncertainty in the environment—unexpected signal interference, obstacle emergence, or energy constraint—demands real-time adjustment. By reinforcing behavior that improves fitness metrics (e.g., expanding coverage without compromising connectivity), the hybrid method achieves a balance between exploration (via GAs’ population diversity) and exploitation (via RL’s targeted optimizations), preventing the stagnation and inefficiency of single approaches.

The applications of this study are economic viability and sustainability. The key limiting factor in drone operation, energy consumption, is closely related to deployment patterns. Networks designed to reduce unnecessary displacements and trajectories can dramatically prolong service durations. In precision agriculture, drones tasked with the surveillance of crop health must cover whole fields without revisiting paths to avoid draining batteries. Similarly, solar-powered drones as aerial base stations require precise positioning to optimize sunlight exposure and signal strength—a dual purpose that cannot be addressed by static algorithms. The iterative refinement of the hybrid framework, according to real-time feedback (e.g., weather changes affecting solar intake), ensures sustained performance where traditional methods break down. Furthermore, the introduction of 5G and edge computing renders optimized drone networks even more necessary. Drones as mobile edge servers process data locally, reducing latency for applications like autonomous vehicle coordination or augmented reality. In urban areas, where signals are obstructed by buildings, drones must form mesh networks that route data dynamically through clear paths. Optimization here involves not just physical placement but also resource allocation—distributing bandwidth and computation loads to prevent bottlenecks.

This paper is structured to address these challenges in a systematic manner. Following this introduction, Section 2 provides an overview of prior work in drone deployment optimization, with a focus on advancements in evolutionary algorithms, swarm intelligence, and reinforcement learning. Section 3 details the hybrid framework design, encompassing the multi-objective fitness function, Q-learning integration, and constraint-handling techniques for heterogeneous fleets. Section 4 provides experimental results over simulated and parameterized environments, comparing the hybrid method with pure GAs and PSO on metrics of coverage area, stability of connection, and speed of convergence. Section 5 considers the broad implications of our results, including disaster response, rural coverage, and smart cities, while Section 6 concludes with future possibilities, such as dynamic obstacle avoidance and the incorporation of real-world signal attenuation models.

2. Related Work

The development of unmanned aerial vehicle path planning and optimization has been widely investigated with various approaches, each tackling special problems in dynamic environments. This section summarizes the current literature into thematic areas, pointing out advancements while revealing deficiencies motivating the creation of our hybrid genetic algorithm and reinforcement learning approach.

2.1. Foundations in UAV Path Planning

Conventional optimization algorithms, including DE and PSO, have paved the way for UAV trajectory planning. The CDE [2] algorithm maximizes risk and distance in disaster contexts, while JGLPP-UTS [3] couples PSO and APF to implement global-local planning. Better versions like RGG-PSO+ [4] update waypoints dynamically, employing random geometric graphs, and enhance flexibility. Multi-objective approaches, such as the UAV multi-objective jellyfish search (UMOJS) [5], employ rapidly exploring random trees (RRTs) for initialization, while the improved chaos sparrow search algorithm (ICSSA) [6] employs chaotic mapping to escape local optima. Classifications of traditional and AI-based strategies are presented in surveys like [7], while the navigation-variable-based NMOPSO [8] ensures kinematic feasibility. Despite these advances, static mutation mechanisms in GA variants [8,9,10] limit the adaptability to real-time feedback.

2.2. Multi-UAV Coordination and Coverage

Successful swarm coordination relies on region decomposition and task allocation. Voronoi partitioning [11] and NSBKA [12] reduce overlapping coverage, whereas E2M2CPP [13] equalizes energy consumption over non-overlapping regions. Vehicle–drone collaboration models [14] alleviate energy constraints but do not facilitate adaptive reallocation when the mission is updated. Multi-agent systems like CEL [15] employ experience sharing; yet, scalability under highly dynamic conditions remains limited. The quantum robot Darwinian PSO (QRDPSO) [16] accelerates task allocation in drone swarms, and the composite-directional raid strategy (CDR-DRS-WPOA) [17] enhances patrol efficiency. Most approaches do not address heterogeneous coordination, e.g., weeding robots and drones in MOTLBO [18], or fuse attention mechanisms to cover adaptation [19].

2.3. Dynamic Adaptation and Real-Time Planning

Real-time responsiveness is necessary for applications such as the tracking of wildfires. HPO-RRT* [20] and AP-GWO [21] improve the convergence rate by hierarchical sampling and adaptive leadership mechanisms. Reinforcement-learning-based methods, including HAS-DQN [22] and action selection in DQN [23], facilitate independent decision-making but are daunted by continuous action spaces. The multi-scale discrete layered grid (MS-DLG) model [13] improves conflict detection, and the adaptive path planner (APP) [24] replans trajectories for pollution sampling in response to environmental dynamics. Connectivity-aware methods like dueling DDQN [25] maintain UAV–ground connections, and the improved pied kingfisher optimizer (IPKO) [26] optimizes maritime rescue navigation. A recent work also explores language-model-based command generation. A real-time decision system using LLMs for UAV was proposed in [27], achieving high BLEU scores and low latency in dynamic IoD missions. Despite these improvements, most frameworks achieve the non-seamless integration of global exploration and local exploitation.

2.4. Hybrid Optimization Frameworks

Hybrid methods mix global search and local optimization. MAHACO [28] merges ACO with stochastic approaches to 3D planning, and AQLPSO [29] fuses Q-learning with PSO for diversity. PSO-DQN [30] merges swarm intelligence with DQN for smoothness. The improved nutcracker optimization algorithm (INOA) [10] achieves exploration–exploitation balance through chaos mapping, and the multi-algorithm hybrid ant colony optimizer (MAHACO) [28] enhances 3D path smoothness. Another hybrid approach [31] integrates LLMs with telemetry and scenario data to create adaptive mission commands. It combines retrieval and generation to adjust decisions based on real-time conditions. However, these methods do not use GAs’ population diversity and RL’s targeted exploitation at mutation phases—a gap our method bridges.

2.5. Energy and Risk-Aware Planning

The energy-conserving methods, i.e., Bezier curve smoothing in E2M2CPP [13] and battery-aware IDDQN [32], are endurance-driven. The safety-improving risk-aware models, i.e., third-party risk assessment [33] and safe path prioritization (SPP) [34], rely on static threat maps. The MILP-based E2M2CPP [13] optimizes multi-region coverage, and the UAV flight path planning optimization (AA-FPP) [35] minimizes threat exposure on battlefields. In spite of these efforts, none completely tackle the twin issues of dynamic risk (e.g., propagating wildfires) and connectivity maintenance subject to energy constraints.

2.6. Critical Limitations

Despite the significant advances in UAV path planning and optimization, there are several important limitations among the existing approaches. Firstly, while evolutionary algorithms such as genetic algorithms and differential evolution (DE) excel at global exploration, their mutation operations are deterministic and non-adaptive to real-time environmental feedback. For instance, GA-based approaches like NSBKA [7] and combinatorial swarm optimizers [9] rely on pre-defined mutation rates, and, thus, can be less sensitive to dynamic threats or mission alteration, as noted in applications like wildfire monitoring or disaster response scenarios [2,13,31]. Similarly, hybrid methods such as MAHACO [28] and AQLPSO [29] integrate swarm intelligence and reinforcement learning but fail to synergize the population diversity of GAs with the focused exploitation of RL at the mutation level. Such patchwork hybridization results in a lack of balance between exploration and exploitation, particularly in energy-constrained missions [30,31,36].

Connectivity maintenance in dynamic multi-UAV networks is less investigated. While approaches like dueling DDQN [25] and CEL [15] enhance coordination by employing connectivity-aware rewards or experience sharing, they cannot maintain persistent connections under abrupt reconfigurations like ad hoc network collapse from spreading fires or urban signal interference [33,37]. Energy-efficient methods, such as E²M²CPP [13] and IDDQN [32], are battery-centric; however, they fail to consider connectivity metrics in optimization goals, resulting in coverage vs. connectivity compromises in high-risk mission operations. Cooperative systems, such as the USV–UAV coordination framework [38], are resilient in dynamic marine environments; however, they are application-specific and cannot be extended to other scenarios, such as urban surveillance or disaster response.

Most state-of-the-art approaches have application-specific limitations. For instance, MOTLBO [18] is for optimizing herbicide spraying in agriculture, and IPKO [33] is for customized path planning for maritime rescue, but these methods are not generalizable to more general scenarios like urban surveillance or disaster response. Likewise, vehicle–UAV collaboration frameworks [14,39] and Voronoi-based decomposition methods [19] enhance large-area coverage but presume static environmental conditions and do not account for the real-time adaptation to arising obstacles or dynamic threats [6,20]. Finally, though risk-aware systems such as SPP [34] and third-party assessments [33] are safety-oriented, they use static threat maps, which reduces their utility in scenarios with evolving hazards, e.g., propagating wildfires or abrupt signal jamming [2,35]. Effective coverage path planning methods, like the multi-resolution probabilistic method [40], enhance city monitoring but encounter scalability limitations in big or very dynamic environments. The global and local moth-flame optimization (GLMFO) algorithm [41] addresses collision avoidance and energy efficiency but lacks real-time learning mechanisms for integration, and, thus, shows limited adaptability to dynamic mission requirements.

These gaps point towards the necessity of a coherent framework that adjusts dynamically to environmental uncertainty while optimizing coverage, connectivity, and energy efficiency. Our research addresses these issues by incorporating Q-learning into GAs’ mutation process, allowing drones to learn context-aware modifications that maximize mission goals in real time.

3. Methodology

We present the methodological procedure followed for the realization of our hybrid optimization scheme, which integrates genetic algorithms and Q-learning, an RL-based methodology, in order to improve drone fleet coordination. Our system employs a multi-objective fitness function that tries to maximize coverage and network connectivity while, simultaneously, maintaining effective energy consumption. The GA module achieves global search via the evolutionary optimization of drone locations by selection, crossover, and mutation iteratively, and the Q-learning module learns mutation corrections online to cope with time-varying real-world environmental factors.

The GA initiates with a population of candidate drone fleet configurations generated randomly, with each being encoded as a chromosome of positional coordinates. The fitness function evaluates each configuration on a weighted sum of objectives: coverage area, network connectivity, and energy efficiency. After selection and crossover, the mutation phase applies Q-learning, where drones learn to update their positions by selecting actions from a discrete set of movement increments. The Q-learning agent learns its policy based on state representations that involve the current position, quality of coverage, connectivity, and available battery capacity.

The reward function of Q-learning is designed to reward movements that increase fitness values, and penalize actions that increase energy consumption without high-coverage rewards. In this way, we enable the system to optimize exploration (via GAs’ population diversity) and exploitation (via RL’s goal-directed tuning). By integrating Q-learning with GA, we enable the fleet to reposition itself dynamically based on evolving environmental dynamics such as fire propagation in disaster relief or sudden signal interference in urban environments.

Moreover, constraint handling mechanisms are employed to maintain the feasibility of the optimized solutions. They comprise constraints on drone flight capabilities, network stability prerequisites, and battery performance limitations. The approach is verified via a set of simulation experiments, wherein the hybrid solution is compared against a standalone genetic algorithm and particle swarm optimization under various scenarios, including tracking wildfires, disaster response, and urban connectivity. Its performance is analyzed based on critical metrics like the area covered, connection stability, and rate of convergence.

3.1. System Model

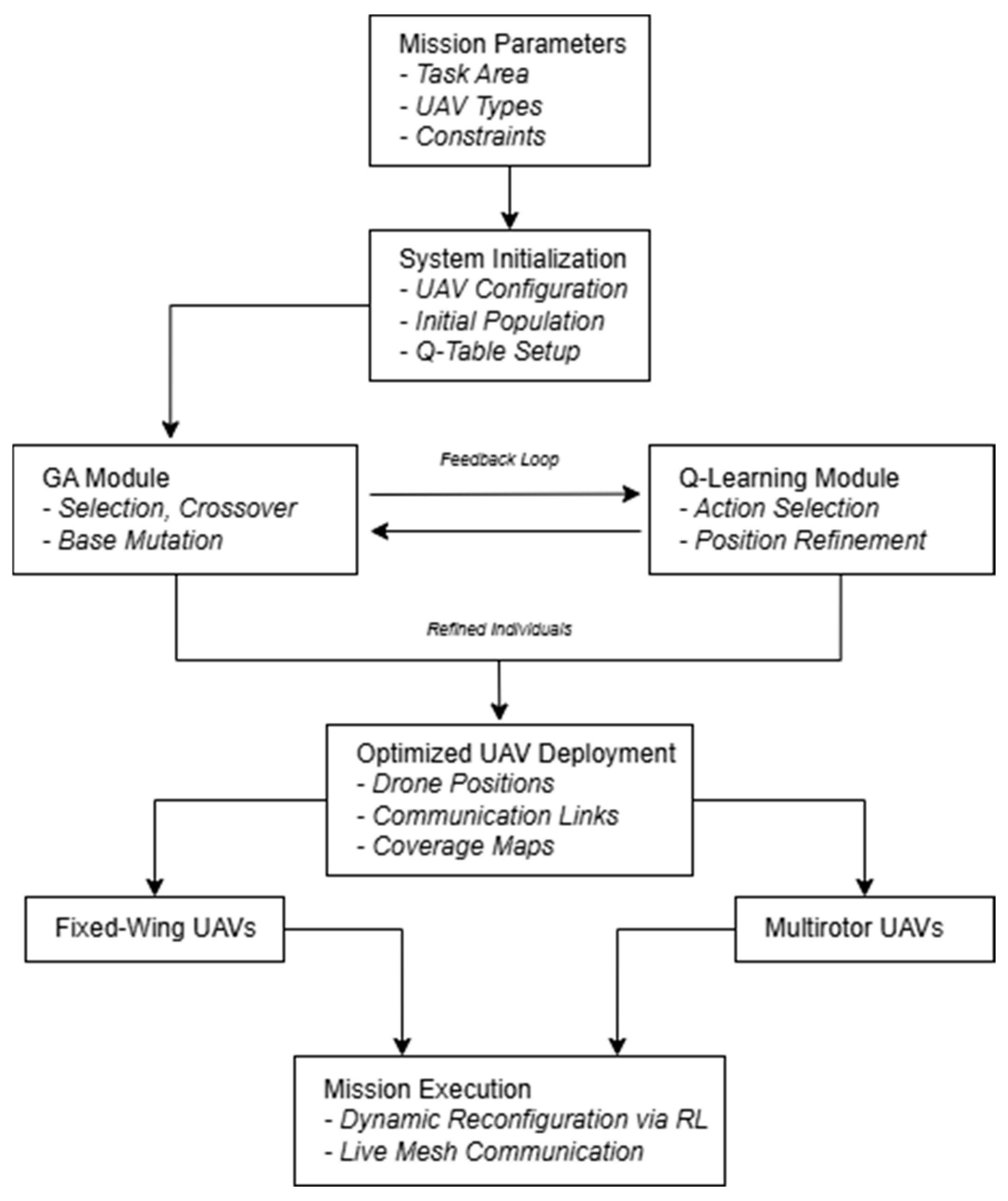
The optimization framework proposed is for heterogeneous UAV networks that consist of fixed-wing and multirotor drones operating in a specified mission area. The first process of the system is to set mission parameters, which include the geographical task boundary (as a polygon), the setup of the UAV fleet, and operational constraints such as the maximum communication range, energy constraints, and minimum coverage requirement.

Every UAV is configured with its own performance limits—fixed-wing vehicles are capable of extensive travel and allocated to boundary areas, while multirotor vehicles function in high-resolution surveillance applications within significant inner areas. Both utilize line-of-sight communication links within a set range, creating a decentralized mesh network to enable ad hoc connectivity and real-time coordination.

The optimization process starts by having the GA generate an initial population of candidate drone positions. The solutions are progressively optimized by a Q-learning agent that shifts positions based on feedback from environmental states. The feedback includes coverage values, energy consumption, and connectivity. The learning is progressively updated in the mutation phase of the GA.

Following optimization convergence, the emerged drone deployment satisfies multiple conditions: it achieves maximum spatial coverage, high mesh-based connectivity, and minimum energy consumption.

This architecture supports scalable, fault-tolerant, and adaptive UAV deployments for disaster response, urban surveillance, rural coverage, and other time-varying mission applications. A description of this architecture is shown in Figure 1, showing the data flow from mission initiation to the optimization pipeline and dynamic UAV deployment.

3.2. Multi-Objective Fitness Function

Our fitness function consists of multiple objectives. Coverage maximization attempts to maximize the area covered by the drone fleet and minimize overlap. Connectivity preservation keeps drones connected in order to facilitate seamless coordination, and energy conservation minimizes excessive travel in order to conserve battery life.

Each candidate solution’s fitness in the GA is determined using a weighted sum approach. The fitness function can be represented as in Equation (1):

F = w₁C + w₂N + w₃E,

(1)

where C denotes the total area covered by UAV communication ranges, calculated using the union of circular coverage areas centered at UAV positions. N represents the network connectivity which can be calculated as Equation (2), measured as the total number of active communication links among UAVs that are within transmission range of each other, normalized by the maximum possible number of connections:

$$\mathrm{N}={\displaystyle \frac{2\times L}{n (n-1)}}$$

(2)

where $L$ is the number of established bidirectional communication links and n is the total number of UAVs. This metric ranges from 0 (no connectivity) to 1 (fully connected network), ensuring that the connectivity of the fleet is effectively quantified regardless of fleet size. E denotes energy efficiency, which is calculated as the inverse of the total communication distance among all connected UAVs, promoting energy-aware deployment. The weight coefficients w₁, w₂, and w₃ are used to balance the relative importance of each objective. In our experiments, these were empirically set to w₁ = 0.4, w₂ = 0.4, and w₃ = 0.2 after preliminary tuning. These values provided a good trade-off between maximizing area coverage, maintaining reliable connectivity, and minimizing communication-related energy consumption. This trade-off is necessary because maximizing coverage often leads to increased inter-UAV distances, which can reduce connectivity and increase communication-related energy costs. The selected weight values reflect a balanced compromise among these competing objectives, ensuring that no single metric dominates the optimization outcome. Coverage optimization is defined in Equation (3):

C = (∑ A_i)/A_total,

(3)

In this context, A_i is the area covered by drone i, and A_total is the total mission area. The connectivity maintenance is assessed through a graph-theoretic analysis, where drones are nodes and links depend on signal strength. The model for energy efficiency is expressed in Equation (4). This formulation estimates the energy efficiency based on the normalized total communication distance between UAVs. This approach, though abstracted, is consistent with several studies in the field. In energy-aware UAV mission planning, distance-based metrics are often used to approximate energy consumption due to their proportional relationship with power requirements during flight and communication operations. Similar assumptions are employed in multi-UAV optimization frameworks [22,32,36], where path length, turns, and UAV coordination are primary factors influencing energy usage:

E = 1 − (∑ d_i)/d_max,

(4)

where d_i represents the distance traveled by drone i and d_max is the maximum allowable distance. Note that the energy efficiency E is modeled as a distance-based proxy, which does not account for hardware-level power consumption.

3.3. Q-Learning Integration in GA Mutation

Traditional GA mutation works with random changes, frequently resulting in inferior local solutions because direct feedback mechanisms are lacking. In our method, we incorporate Q-learning to optimize such mutations according to environmental feedback in real time, thus enhancing the efficiency and adaptability of the optimization process. Every drone is considered an independent agent that learns positional changes incrementally to maximize its fitness through several iterations. Q-learning decision making is encoded by the Q-table, which, at all times, is updated based on the following:

State Representation: The state S_t at time t encapsulates the drone’s positional coordinates, its coverage contribution, connectivity status, and energy level. This multi-dimensional state representation ensures that decisions consider both immediate and long-term fleet objectives.

Action Space: The action set A_t includes small positional adjustments δ_x, δ_y, and δ_z within predefined bounds, ensuring that drones refine their location with minimal displacement while maintaining coverage efficiency. In this context, δ_x, δ_y, and δ_z refer to the discretization step sizes in the x, y, and z axes, respectively. These values determine the granularity of the positional adjustments made by drones during Q-learning-based mutation. For all experiments, we set δ_x = δ_y = δ_z = 10 m. This value was selected empirically to strike a balance between movement flexibility and computational efficiency. Smaller step sizes would result in more precise but slower convergence, while larger values could overlook fine-grained optimizations.

Reward Function: A tailored reward function Rₜ incentivizes actions that lead to improved fleet performance. The function formulation can be seen in Equation (5).

In Equation (4), the parameters α, β, γ, and λ are scalar weights that control the contribution of different components in the reward function: A_t—penalizes overlapping coverage between UAVs, L_t—rewards the preservation of inter-UAV links, D_t—promotes a shorter average communication distance, and H_t—encourages UAVs to maintain a minimum height above ground level to avoid obstacles or interference.

For all experiments, we empirically set α = 0.3, β = 0.4, γ = 0.2, and λ = 0.1 to achieve a balanced trade-off between spatial distribution, connectivity, and efficiency. These values were chosen based on preliminary trials and sensitivity to reward shaping:

R_t = αC_t + βN_t + γE_t − λP_t,

(5)

where C_t represents the increase in coverage, N_t quantifies connectivity improvements, E_t denotes energy conservation, and P_t penalizes excessive movement that may destabilize the fleet. The Q-value update follows the standard Bellman equation which can be seen in Equation (6). In this formulation, the value of the current state–action pair Q(S_t, A_t) is updated based on the immediate reward R_t and the discounted maximum estimated Q-value from the next state S_t+1:

Q(S_t, A_t) ← Q(S_t, A_t) + η [R_t + δ maxₐ Q(S_t+1, a) − Q(S_t, A_t)],

(6)

where η is the learning rate and δ is the discount factor applied only to the estimated future reward. The term maxₐ Q(S_t+1, a) represents the off-policy nature of Q-learning, in which the agent updates its estimates assuming the optimal action will be taken in the future state. The use of lowercase a denotes that the maximization is performed over all possible actions available at state S_t+1. This iterative process ensures that drones develop an optimal movement strategy that balances exploration and exploitation, ultimately leading to superior coverage and connectivity in dynamic environments.

In order to compare the efficacy of various optimization methods, we measured important connectivity parameters such as the minimum and maximum connection distance encountered, mean connection distance, and total connections established.

Table 1. Modular Overview of the Hybrid Optimization Framework Combining GA and Q-Learning.

Initialization - Define polygon area and station location - Set drone types (FIXED_WING, MULTIROTOR) - Define communication limits, population size, generations - Initialize Q-learning parameters η—learning rate δ—discount factor ϵ—exploration rate Q-table default initialization Action discretization granularity Drone Behavior - FIXED_WING: prefers outer, longer-range points - MULTIROTOR: prefers inner, shorter-range points Utility Functions - IS_VALID_POINT(point, type) → Returns if within bounds and range - CALCULATE_CHAIN_DISTANCE(positions, chain) → Computes total link distance Genetic Algorithm - CREATE_INDIVIDUAL() → Generates valid drone positions - EVALUATE(individual) → Calculates fitness with penalties/bonuses - MUTATE(individual) → Performs bounded mutations Q-Learning Integration - DISCRETIZE_STATE(positions) → Maps continuous to discrete state - GET_RL_ACTION(state, ε) → Chooses action via epsilon-greedy policy - APPLY_RL_IMPROVEMENT(individual) → Enhances individual via Q-table Hybrid Optimization Process - Initialize population and Q-table - For each generation: Evolve population using GA Apply Q-learning improvements Evaluate fitness and update best - Save Q-table and return best solution Visualization and Evaluation - PLOT_SOLUTION(solution) → Displays layout, stats, and connections - COMPARE_RESULTS(ga_solution, hybrid_solution) → Evaluates fitness, coverage, and connectivity metrics Execution - Run GA-only and hybrid algorithms - Compare and visualize outcomes

outlines the modular structure of the hybrid optimization algorithm combining Genetic Algorithms and Q-Learning for drone deployment.

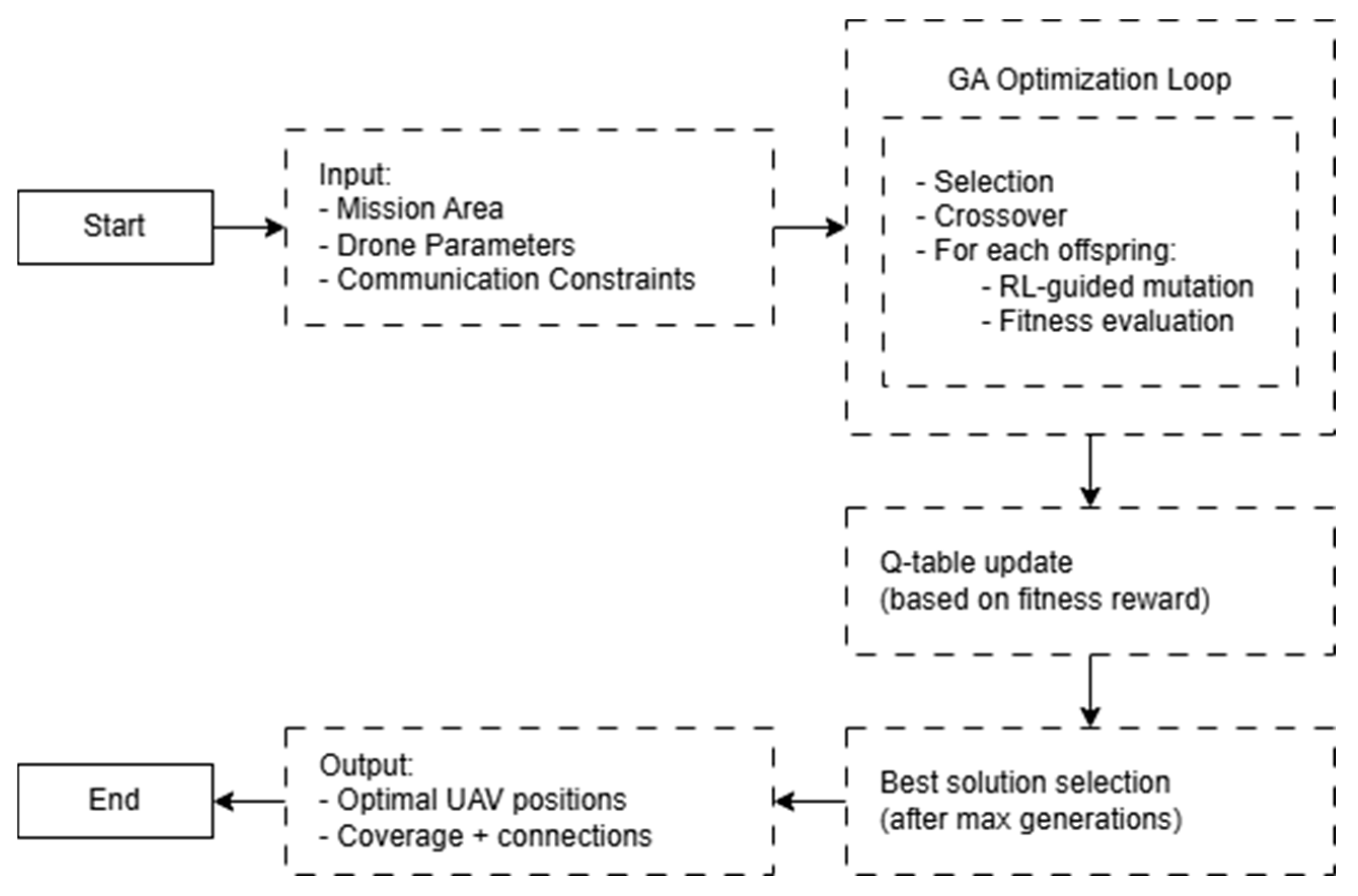
To clarify the interaction between the genetic algorithm and Q-learning in the hybrid framework, we provide a high-level pseudocode representation in Algorithm 1. This complements Table 1 and summarizes the overall optimization loop in a concise manner.

Algorithm 1: Hybrid GA + Q-Learning Optimization

Input: Mission area, drone types, communication limits, GA and RL parameters Output: Optimized drone positions ensuring coverage, connectivity, and energy efficiency 1. Initialize population with valid drone positions 2. Initialize Q-table with default values 3. FOR generation = 1 to max_generations DO 4.    Evaluate fitness of each individual using multi-objective function 5.    Apply selection and crossover 6.    FOR each individual DO 7.            Discretize state (position, coverage, energy, connectivity) 8.            Select RL-based action via ε-greedy policy 9.            Apply Q-learning based mutation to refine individual 10.   Update Q-table based on reward signal 11. Return best solution found

The high-level flow diagram shown in Figure 2 complements Algorithm 1 by illustrating the sequential interactions among system components. It highlights how Q-learning integrates into the GA process to guide drone deployment decisions based on learned feedback.

3.4. Constraint-Handling Mechanisms

In order to make heterogeneous fleets composed of fixed-wing drones and multirotors operational, our optimization procedure considers various constraints in order to make the operations more flexible and efficient.

Flight capabilities are a key issue since the fixed-wing UAV is designed for large scanning given its speed and endurance, whereas the multirotor UAV is designed to hover over specific critical points for close surveillance. This difference in operation ensures that the fleet is able to comprehensively cover large areas and provide high-resolution monitoring of critical points.

Energy constraints are also built into decision-making. Drone batteries are continuously monitored, and plans of movement are generated to maximize mission duration. This is carried out by minimizing unnecessary repositioning and not sending drones out of range of operational flight without taking return vectors to charging stations or safe landing zones into account.

Network flexibility is essential in dynamic and uncertain environments. Real-time reconfiguration capabilities are integrated into the system in order to handle an abrupt loss of signal, new obstacles, or weather changes. Drones adapt their positions dynamically to ensure always-optimal connectivity within the fleet while communications and data exchange continue undisrupted. As a result of reinforcement learning, the system proactively detects and resists interference and keeps the network strong and running in changing conditions.

4. Experimental Results

This section presents a comparative analysis of our hybrid framework against standalone GAs and particle swarm optimization. The simulated experiments evaluate performance across various scenarios.

4.1. Simulation Setup

The simulations were conducted in three settings: wildfire monitoring, disaster response, and urban area monitoring. Each of the scenarios presented distinct challenges with regard to adapting to dynamic environmental conditions, connectivity constraints, and real-time adaptability needs. The setting for the wildfire monitoring was arranged with the objective of scaling up the deployment of drones to manage dynamic fire fronts effectively, in addition to the provision of seamless interaction between the drones and the command center. The emergency response scenario demanded the drones change their locations in real time in order to achieve maximum coverage of the disaster sites, while keeping them in contact with emergency responders. Lastly, the urban surveillance scenario demanded coverage maximization with minimum interference from buildings and other city features.

For the proper management of the drone fleet, the simulations were set with important default values. The drone fleet was made up of ten drones, including five fixed-wing drones and five multirotor drones. Both types of drones had their own operational limitations: fixed-wing drones had a 20 km distance they could travel, while multirotor drones had a maximum distance of 7 km they could travel. The genetic algorithm optimization was run for 150 generations on a population of 100. Reinforcement learning was implemented through the usage of Q-learning with a learning rate of 0.1, discount factor of 0.9, and exploration rate of 0.1. The action space was a discrete set of movements between −0.5 km and 0.5 km to enable drones to adjust positions dynamically. All these values were parameterized, allowing the system to be easily tuned to various operating requirements. For fairness and reproducibility, benchmark algorithms—the genetic algorithm and particle swarm optimization—were executed with consistent parameter settings. Specifically, the GA was configured with a crossover rate of 0.8 and a mutation rate of 0.1. The PSO algorithm used a standard inertia weight of 0.5, and both cognitive and social coefficients were set to 1.5. All optimization methods shared the same population size (100) and number of generations (150). These parameter values were not selected arbitrarily; instead, they were tuned through a series of preliminary experiments to observe their effects on convergence speed, solution stability, and exploration–exploitation balance. This empirical tuning process enabled the control strategy to maintain consistent performance across simulation runs and ensured the hybrid method operated reliably under diverse mission scenarios.

The primary actions that were utilized to quantify performance were the coverage area, connection stability, and convergence rate. The coverage area was calculated, taking into account the total area covered by the fleet with an attempt to reduce overlaps. The connection stability was examined on the basis of the number of total connections established between the drones and the average communicating distance between them. The convergence rate was measured based on how quickly each of the optimization algorithms converged to a convergent fitness value, i.e., how quickly it approached its convergent state, reflecting an optimization performance metric for approaching the best deployment state. Standalone GAs and PSO were considered as the benchmark comparison algorithms and were compared with the hybrid algorithm GA + RL to evaluate its viability in real-world applications.

4.2. Performance Evaluation

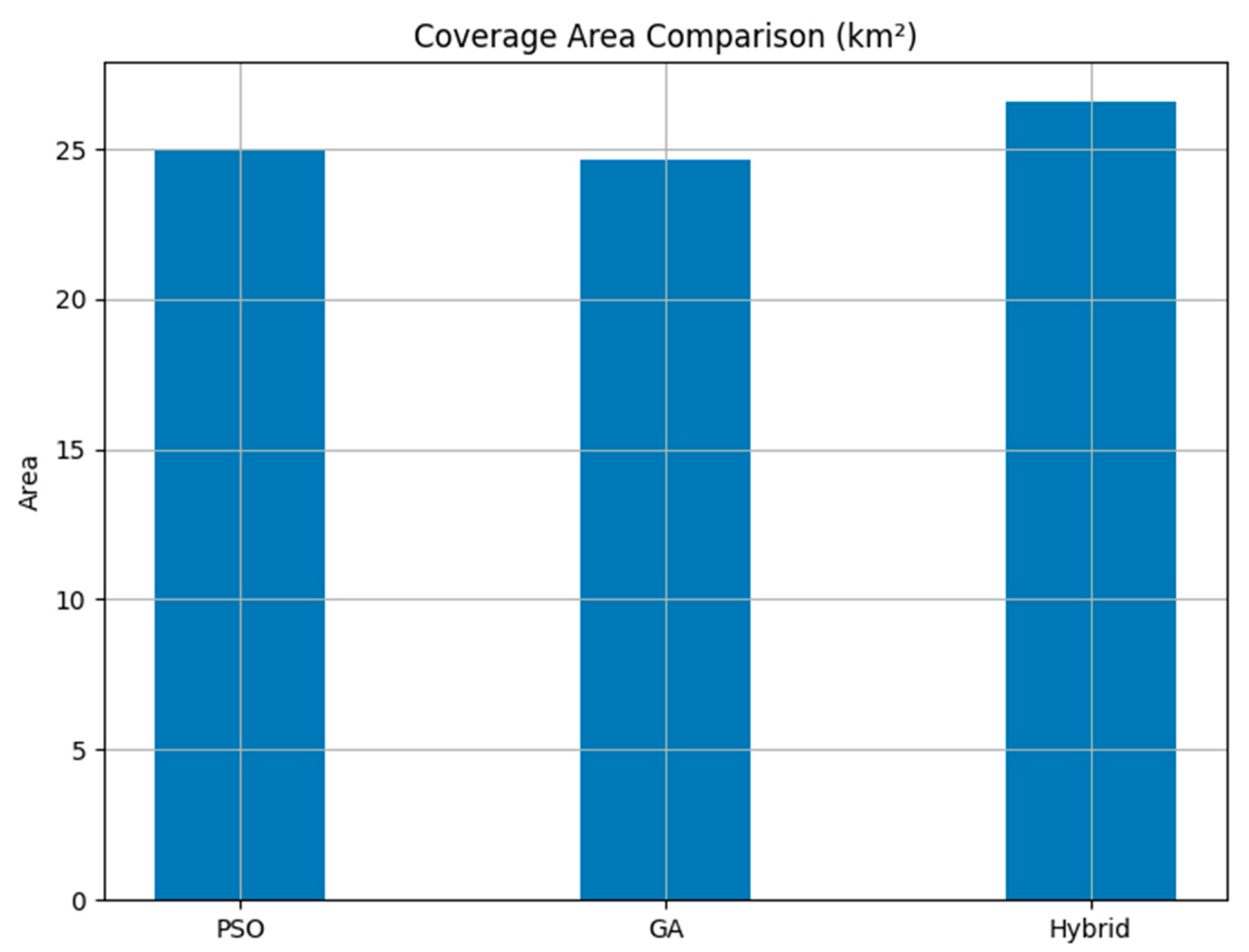
4.2.1. Coverage Area Comparison

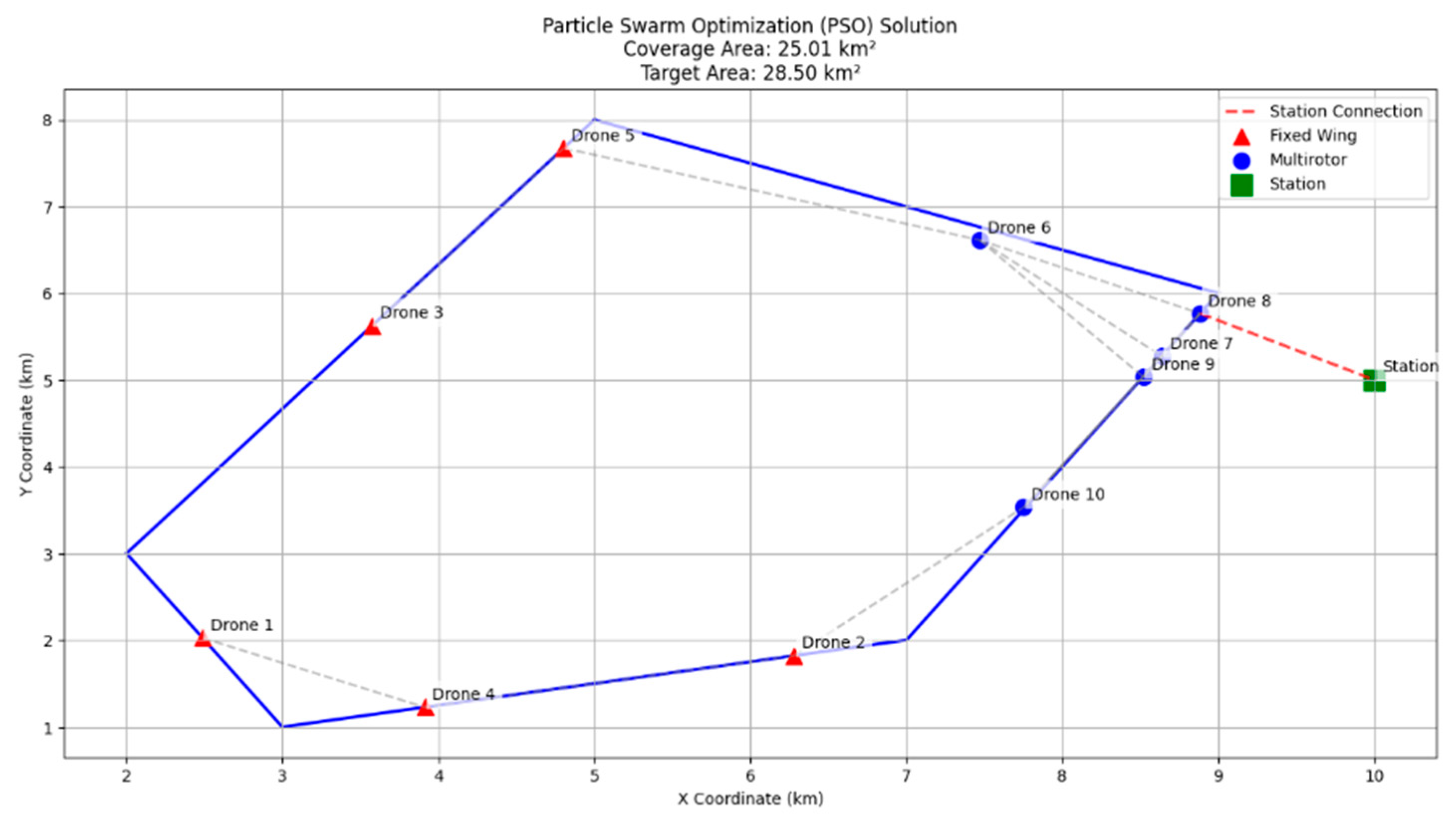
The coverage area is a key performance indicator of a drone deployment optimization method. The hybrid method achieved the largest coverage area, which was 26.57 km², thus outperforming the particle swarm optimization at 25.01 km² and the genetic algorithm at 24.62 km², as indicated in Figure 3. This improvement in coverage efficiency is due to the reinforcement learning aspect, which adapts drone deployment dynamically to real-time changes in the environment. The results demonstrate that the integration of Q-learning in GAs ensures the optimum utilization of drone features, and, thus, a greater area is covered.

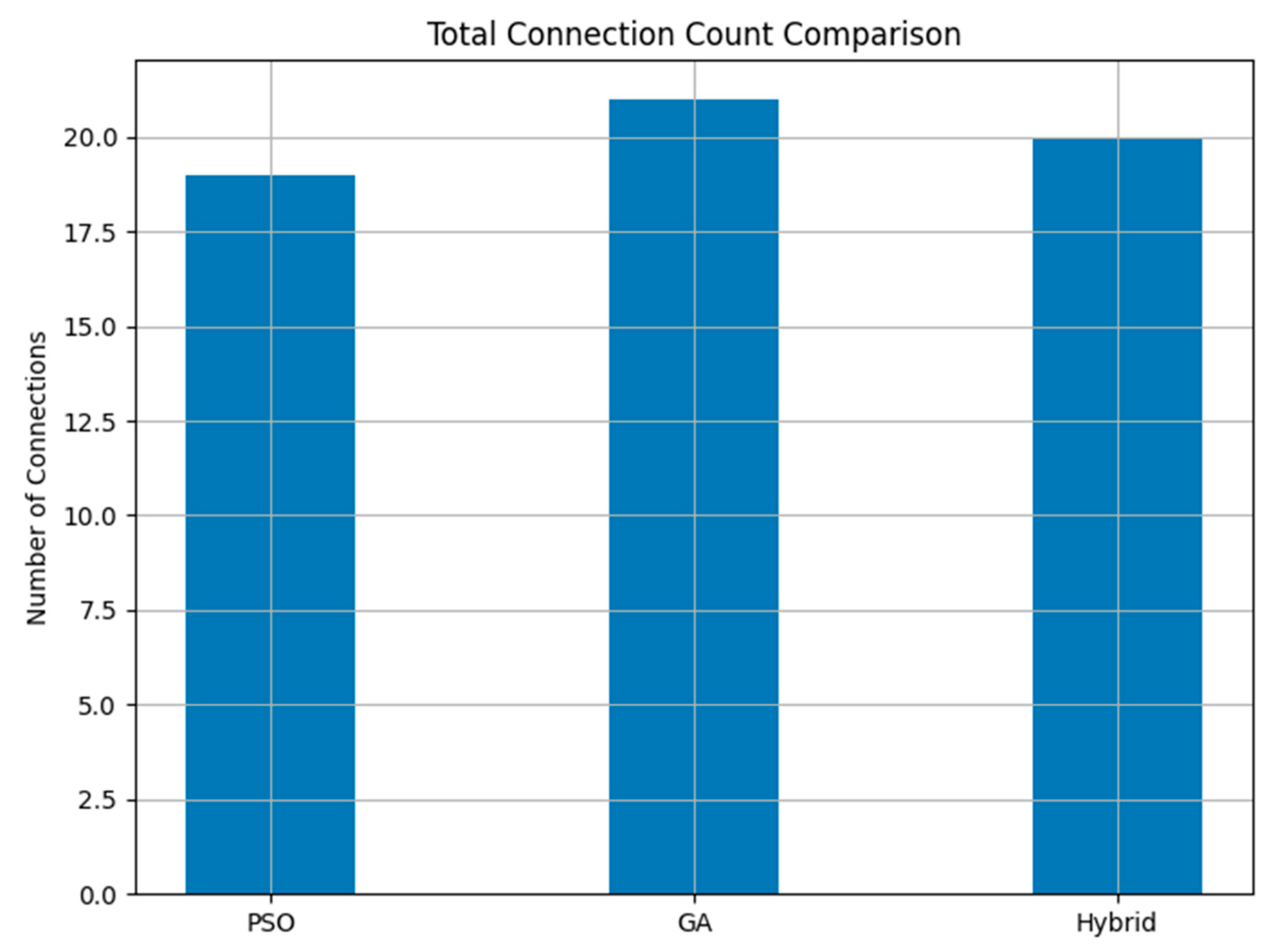
4.2.2. Connection Stability Analysis

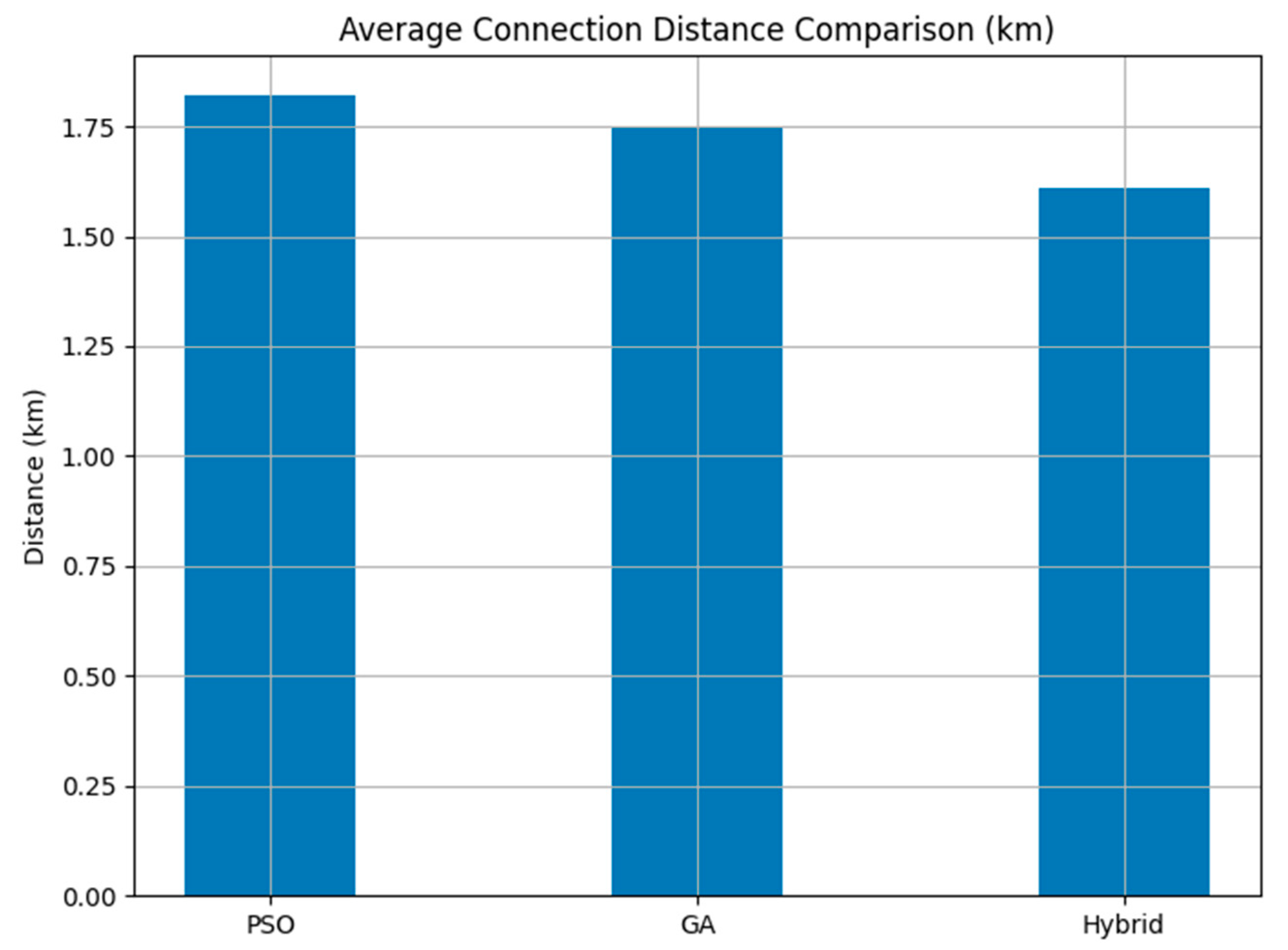
Connection stability plays a crucial role in maintaining seamless data transfer and drone coordination. The total number of connections established in each approach was 19 for PSO, 21 for GAs, and 20 for the hybrid approach, as can be seen in Figure 4. Even though GAs established a greater total number of connections, the hybrid approach achieved better connectivity, as shown by the shorter average connection distance of 1.59 km, as compared to 1.74 km for PSO and 1.69 km for GAs, as can be seen in Figure 5. The average distance connection metric reflects how efficiently drones are placed within the communication range. Lower average distances imply tighter formations with reduced latency and energy usage. The reduction in average connection distance shows that the hybrid approach places drones more optimally within communication range, reducing latency and improving network reliability.

4.2.3. Fitness Convergence Speed

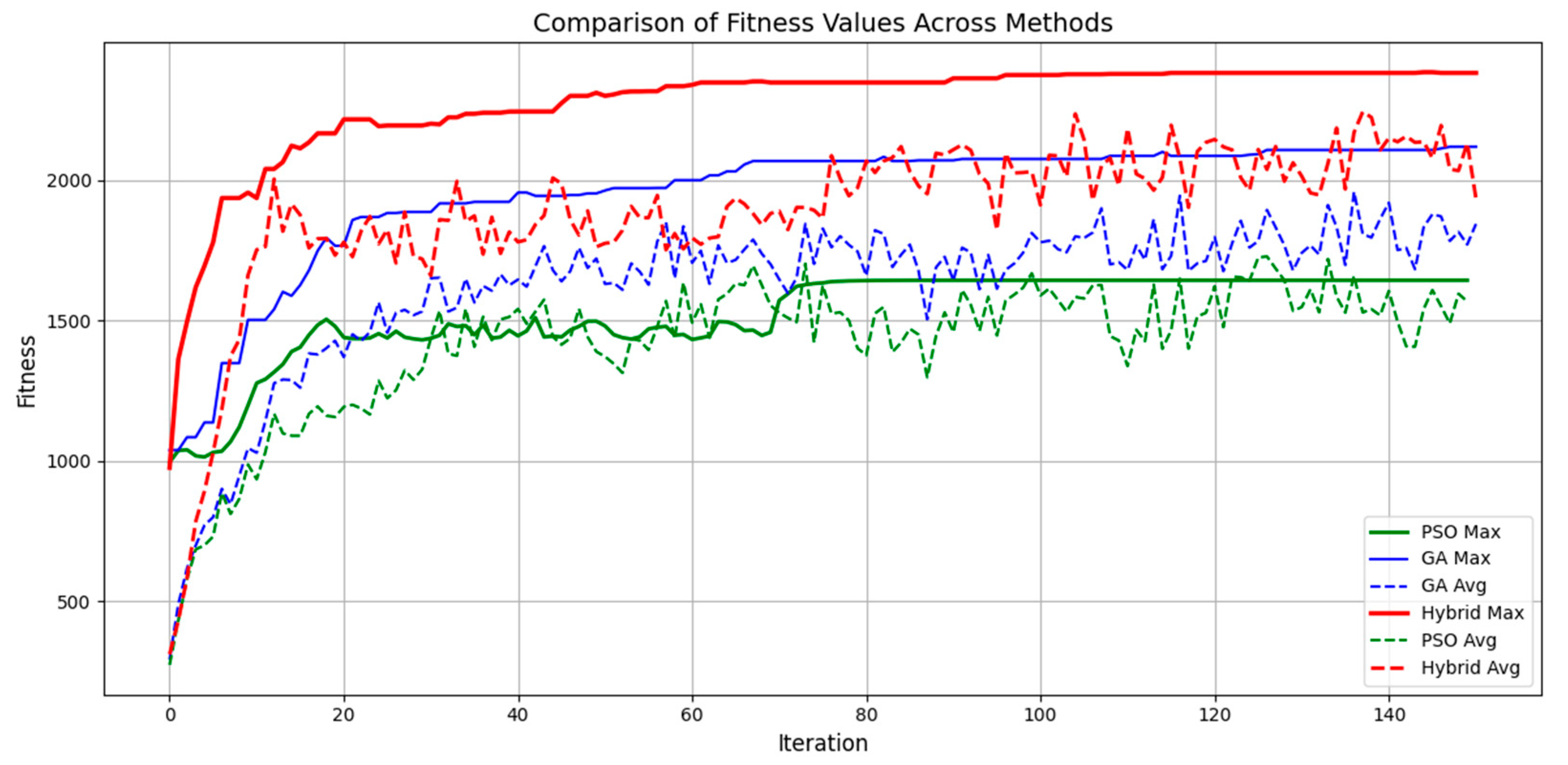
The fitness convergence comparison demonstrates the hybrid method outperforming GAs and PSO with higher maximum fitness values and a higher convergence rate. The hybrid approach reached the higher fitness values at a faster rate due to the fact that the adaptive learning property of reinforcement learning enhances the exploration process of GAs. The fitness progress graph shown in Figure 6 clearly reveals that the hybrid approach consistently improves performance without stagnation, whereas PSO suffers from premature convergence and GAs take a long time to converge to optimal solutions.

4.2.4. Detailed Connection Analysis

The calculation of drone-to-drone and station-to-drone distances also highlights the superiority of the hybrid approach. The minimum connection distances achieved for the PSO, GA, and hybrid approaches were 0.27 km, 0.14 km, and 0.12 km, respectively, which shows that the hybrid approach maintains a strong network by keeping the drones near one another. The maximum connection distances obtained were 2.87 km for PSO, 2.99 km for GAs, and 2.94 km for hybrid, confirming that the hybrid method does not compromise on connectivity while optimizing deployment. The connectivity visualization in Figure 7 and Figure 8 illustrates the drone deployment and the corresponding connection links in each approach, demonstrating the stability of the network.

The PSO-based deployment illustrates a quite uniform distribution of drones across the border and center of the mission area. Fixed-wing UAVs are placed mostly at the outer boundaries to provide maximum area coverage, while multirotors provide network connectivity in the inner area. The layout provides a good coverage of 25.01 km², but the 1.74 km average distance of communication indicates a somewhat loose network, which may translate to increased communication-related energy consumption during actual deployment.

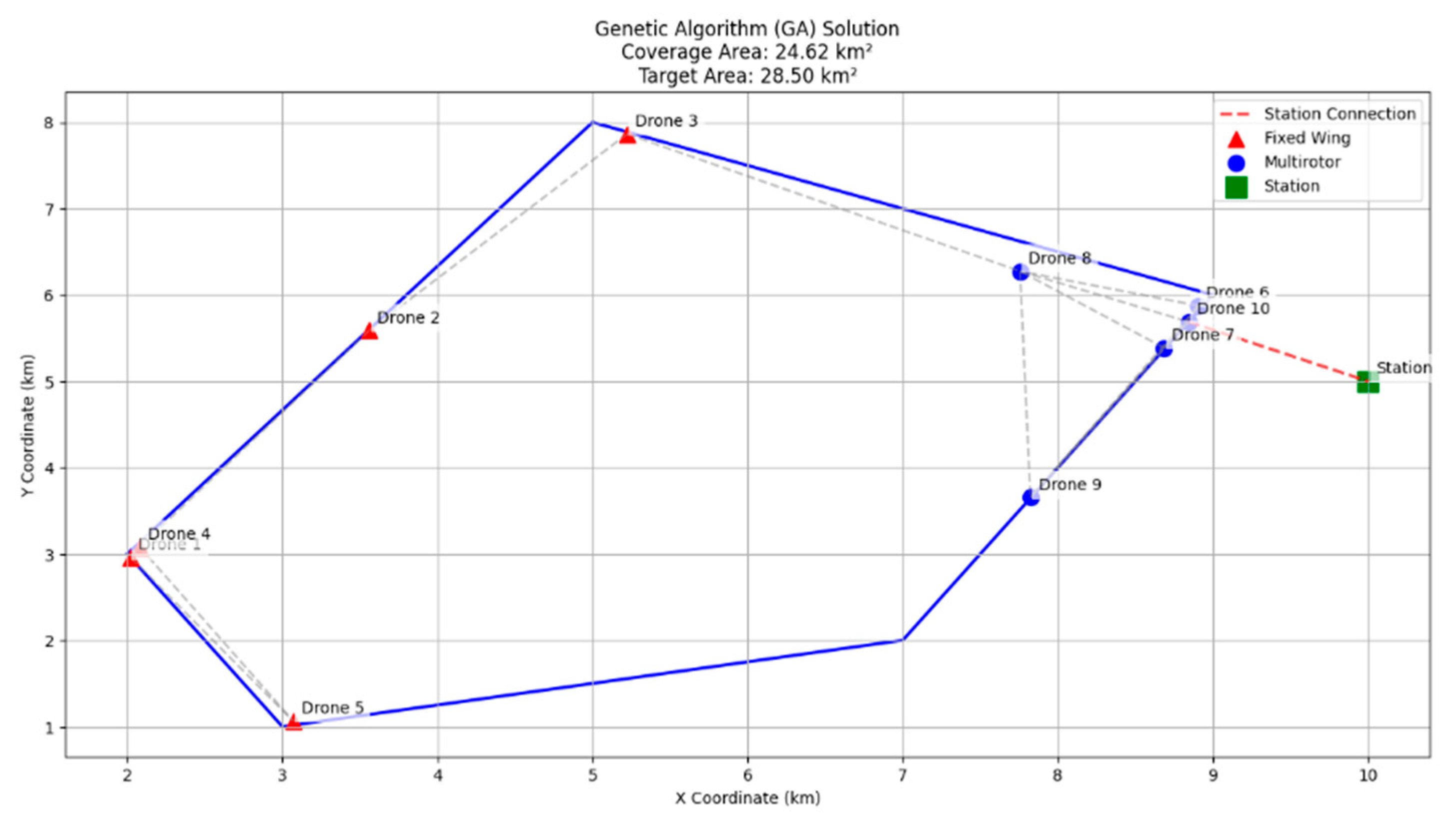
Compared to the PSO approach, the GA configuration coverage is slightly reduced at 24.62 km². Fixed-wing UAVs appear to be denser with a greater overlap and reduced boundary use. Despite this, the mean connection distance falls to 1.69 km, indicating greater energy efficiency over the PSO variant but with a loss of overall coverage.

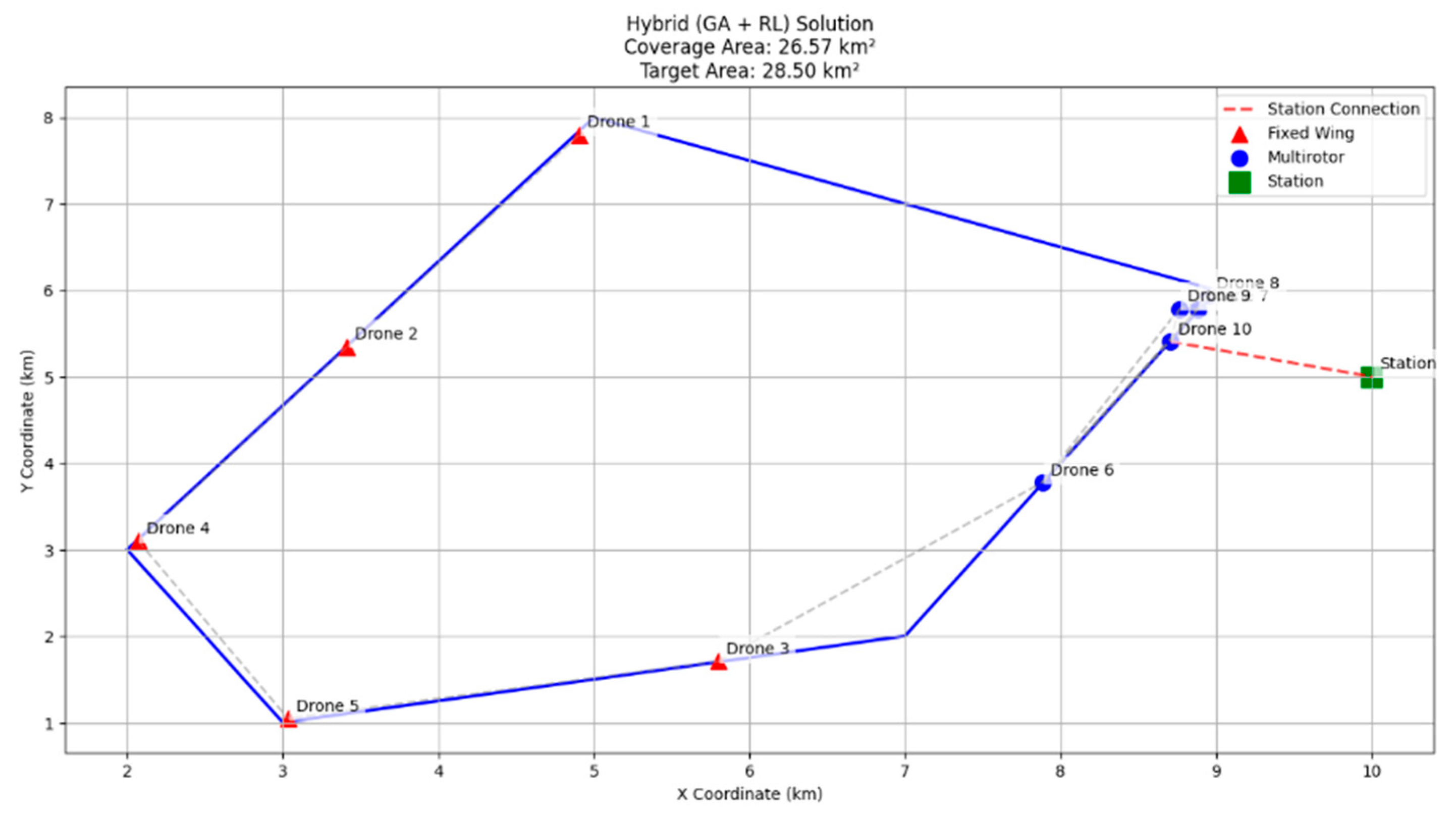
As seen in Figure 9, the hybrid solution of a GA and Q-learning gives the best configuration among the three. The solution has the highest coverage area (26.57 km²) with a smaller average connection distance of 1.59 km. The fixed-wing UAVs encircle the operational area effectively, and the multirotors create stable communication chains inside. This deployment represents the best balance between spatial coverage and communication efficiency, and it indicates the strength of the adaptive refinement in the hybrid model under deployment evolution.

Table 2. Connection statistics comparison.

Metric	PSO	GA	Hybrid
Minimum Distance (km)	0.27	0.14	0.12
Maximum Distance (km)	2.87	2.99	2.94
Average Distance (km)	1.74	1.69	1.59
Total Connection	19.0	21.0	20.0

presents a full breakdown of the connection statistics for each optimization technique. It identifies both the minimum and maximum observed connection distances in the drone networks, along with the average connection distances and the number of connections. A lower minimum distance, along with a satisfactory spread of the number of connections, is critical to maintaining network stability while optimizing coverage.

Table 3. Performance comparison of optimization methods.

Metric	PSO	GA	Hybrid
Coverage Area (km2)	25.01	24.62	26.57
Connection Counts	19.0	21.0	20.0
Average Connection Distance (km)	1.74	1.69	1.59

compares the overall performance of various optimization techniques based on three important parameters: area covered, number of connections, and average connection distance. The hybrid approach is seen to perform better by having the largest area covered while maintaining a maximum number of connections and average connection distances at a minimum. This indicates that the hybrid approach optimizes the positioning of drones effectively to enhance connectivity efficiency and maximize the area covered.

Overall, the hybrid optimization framework surpasses traditional GA and PSO techniques in critical performance metrics, establishing its potential for real-world applications requiring adaptive and robust drone network deployment.

4.3. Parameter Sensitivity Analysis

In order to evaluate the robustness and stability of the proposed hybrid optimization framework, a sensitivity analysis was conducted on three critical hyperparameters used in the reinforcement-learning (Q-learning) component: the learning rate η, the discount factor δ, and the exploration rate ϵ. These parameters directly influence how the Q-values are updated and how the agent balances exploration versus exploitation during mutation decisions within the genetic algorithm loop.

The goal of this analysis is to assess how variations in these parameters affect the final performance of the hybrid system. Each parameter was varied independently while keeping the remaining two fixed at their default values. The performance was measured using the final fitness score obtained after a fixed number of generations (150) under the same mission scenario and objective function as detailed in Section 3.1. This ensures consistency with the results reported in Section 4.1 and Table 3.

The results of the analysis are summarized in

Table 4. Sensitivity analysis of Q-learning parameters. Final fitness scores are reported for each tested value after 150 generations.

Parameter	Value	Final Fitness
Learning Rate (η)	0.05	1450
Learning Rate (η)	0.10	1610
Learning Rate (η)	0.20	1585
Discount Factor (δ)	0.70	1505
Discount Factor (δ)	0.90	1610
Discount Factor (δ)	0.99	1600
Exploration Rate (ε)	0.10	1400
Exploration Rate (ε)	0.30	1610
Exploration Rate (ε)	0.59	1550

. The fitness scores reflect the cumulative objective performance incorporating area coverage, node connectivity, and communication efficiency.

As seen in Table 4, the learning rate η of 0.1 yielded the highest final performance, suggesting a balanced update speed is most effective in this context. Increasing the learning rate to 0.2 slightly decreased performance, likely due to the instability in value updates. Similarly, lower learning rates (e.g., 0.05) resulted in a slower convergence.

The discount factor δ had a more moderate impact. The best performance was observed at δ = 0.9, which appropriately balances immediate and future rewards. Performance slightly declined at extreme values (0.7 and 0.99), though not as sharply as with η and ϵ.

The exploration rate ϵ had a more pronounced effect. Lower exploration rates (0.1) led to premature convergence and suboptimal solutions, while higher values (0.5) introduced excessive randomness. An intermediate setting (0.3) produced the best overall outcome.

These findings demonstrate that the hybrid method is sensitive to its internal learning parameters and highlight the importance of tuning them carefully. This preliminary analysis also opens up potential directions for future work involving multi-parameter optimization and adaptive parameter adjustment during runtime.

5. Broader Implications

The proposed framework has immense applications in different fields, attaining revolutionary gains in an extensive variety of practical applications. In disaster response, for instance, being able to harness swarms of drones capable of adapting in real time to changing circumstances improves the situational awareness of responders. In disaster responses such as wildfires, earthquakes, or hurricanes, conventional communication and monitoring infrastructure can be made obsolete. The system guarantees that drones reposition themselves in an autonomous manner to offer coverage to the areas that have been affected while maintaining communication links. Drones prioritize the most requested areas using reinforcement learning, such as collapsed buildings during an earthquake or spreading fire fronts. This offers a greater real-time decision-making capacity and allows faster and more efficient rescue operations.

Rural connectivity is another very important area in which this system can be extremely helpful. Most rural communities do not have stable communication networks, and that limits the educational and economic opportunities of the people who live there. With self-organizing drone networks, you can offer connectivity solutions on either a temporary or permanent basis, and that helps make even the most isolated communities a part of the greater digital community. The capacity of the system to modify the locations of drones dynamically in response to changing demand, environmental factors, or maintenance requirements reflects the efficacy of the adjustment to change in any of these aspects. In extraordinary situations such as severe weather, drone networks can also serve as a temporary substitute for destroyed infrastructure to ensure the continuous availability of essential communications and data services.

The deployment of this optimization platform has vast potential in smart city applications. The increased incorporation of autonomous technologies within cities requires the development of robust and dynamic monitoring systems. Through the above-described optimization abilities, drones can assist in enhancing traffic management, infrastructure monitoring, and security surveillance. For example, in traffic-dense regions, drones may be utilized to monitor congestion and dynamically locate themselves based on real-time car traffic. The information may then be forwarded to urban management systems for traffic light optimization, vehicle rerouting, or providing pre-warnings regarding road blockage. In infrastructure monitoring, drones can track the health of bridges, pipelines, and power lines, and minimize the necessity for expensive and risky human inspections.

Another promising application is environmental monitoring. The rise in global warming has seen an increase in the number of natural disasters as well as their severity, and, therefore, enhanced monitoring systems are needed. Drones equipped with the suggested framework can be utilized in extensive environmental monitoring activities such as deforestation, air quality, and the monitoring of marine environments. Dynamic position adjustment enables the continuous monitoring of delicate regions around the clock, hence offering enhanced precision and real-time information to researchers and policymakers. Agricultural drones can also map flight routes in a way to monitor the health of the crops, detect pest infestation, and measure the moisture level of the soil, thereby enabling more efficient and productive farming.

The military and defense industries can utilize the model suggested herein to plan reconnaissance and surveillance strategic missions optimally. Conventional static monitoring systems are ineffective under dynamic battlefield environments. Swarms of drones are able to optimize the coverage of areas with minimal detectability by modifying their formations via the integration of reinforcement learning with genetic algorithms. This ability is especially important for border security, where dynamic flexibility is crucial in managing unauthorized flows and acting on possible threats on a real-time basis as and when they are sensed.

The hybrid optimization approach suggested here may have the potential to bring revolutionary change in a number of areas, reshaping the operation dynamics of autonomous drone networks in dynamic environments. Its promise to reconcile efficiency, flexibility, and strength positions it as a priority tool for use in situations from emergency response to infrastructure management and beyond. With the technology of autonomous drones evolving further, the integration of reinforcement learning with genetic algorithms will only continue to be more instrumental in enabling them to be more efficient in their operations.

6. Conclusions and Future Directions

We proposed a hybrid optimization framework through the combination of GAs’ exploratory power and RL’s adaptive precision. The combination of these two algorithms allows the efficient balancing between global exploration and local exploitation, enhancing adaptability and higher efficiency in drone coordination. Through the assistance of comprehensive simulations and performance comparisons, we have determined that our solution performs better than traditional GA and PSO approaches in all significant parameters such as coverage area, connection stability, and convergence rate consistently. The strength of reinforcement learning in being able to dynamically adjust drone positions to keep the fleet constantly optimized even under evolving environmental conditions makes it particularly useful for real-world applications where ongoing adaptation is required.

Future work needs to explore dynamic mechanisms for obstacle avoidance to improve the real-time responsiveness of the proposed system. The integration of sophisticated obstacle detection algorithms will enable drones to fly autonomously in cluttered environments while ensuring optimal coverage and connectivity. Furthermore, the integration of empirical signal decay models will enhance connectivity prediction and provide robust communication between drones, even in interference-prone or physically obstructed environments. The refinement of these models will enable the more precise optimization of network configurations, thus minimizing the potential for connectivity failure in mission-critical applications such as disaster management or large-scale environmental monitoring.

Another important direction for future research includes hardware deployment and the experimental validation of the presented framework. Although our simulations offer substantial support for its efficiency, implementation in real-world applications for actual use-cases will enable us to explore real-world constraints like energy usage, sensor capabilities, and real-time processing efficiency. Through experimentation on tangible drone fleets, we can verify the scalability and reliability of our solution and develop necessary adjustments for the seamless integration with current drone management systems.

The incorporation of multi-agent reinforcement learning (MARL) within the system can increase cooperation between drones for higher decision-making and task allocation autonomy. This can be helpful in missions like search and rescue, where adaptive drone coordination is valuable in order to optimize search efficiency. Second, the combination of MARL with genetic evolution mechanisms can be utilized for enhancing performance by allowing drones to share learned policies and enhance their decision-making ability over time continuously.

Ongoing improvement may also entail the streamlining of energy usage techniques to realize optimum mission lifetimes at no expense of coverage and connectivity. By incorporating advanced power management algorithms, the efficiency of drone operation may be increased, particularly in large-scale deployments for which battery life is a significant constraint. It is an aspect that is especially relevant to applications such as persistent surveillance, where the maintenance of ongoing coverage for prolonged durations is of the essence.

In future work, we aim to extend the comparative evaluation by incorporating recent metaheuristic and deep-reinforcement-learning algorithms to further benchmark the performance and generalizability of the proposed hybrid approach.

Our hybrid optimization method is a significant step forward in autonomous drone coordination, delivering an effective solution to the problem of fleet deployment in complex and dynamic environments. With the further refinement and elaboration of this technique, future research efforts can continue to drive the efficiency, adaptability, and reliability of drone networks, enabling new possibilities for application from disaster response to environmental monitoring and beyond.