Abstract
Hailstorms, exacerbated by global warming, inflict escalating economic losses on infrastructure, yet existing research overlooks wind–hail synergy in impact dynamics. This study employs a wind-tunnel-integrated hail impact simulator to analyze how wind speed, hail diameter, and velocity collectively influence impact behavior. Key results reveal that higher wind speeds shorten the impact duration, accelerate peak force attainment, and amplify peak forces by up to 18.9% compared to windless conditions. Smaller hailstones exhibit reduced wind sensitivity, while combined increases in wind speed and hail diameter/velocity proportionally elevate peak forces. Momentum transfer from wind-driven fragmented hail clusters enhances force generation, demonstrating wind’s critical role in damage potential. A multivariate regression model predicting peak impact loads is proposed, offering actionable insights for wind–hail-resistant structural design.
1. Introduction
Hailstorms are highly destructive natural disasters, often accompanied by strong winds and torrential rainfall, causing severe damage to crops and surface-level structures [1,2,3,4]. Data indicate that hailstorms inflict substantial economic losses on transportation systems and building structures worldwide [5,6]. Furthermore, under the influence of global warming, the annual economic losses attributed to wind–hail disasters are projected to escalate [7,8]. The impact of hail on building envelopes has garnered significant attention from property owners and stakeholders, presenting unique challenges for both construction materials and agricultural resilience. Despite the high frequency of hail events and their associated damage, the synergistic effects of strong winds on hail impact performance remain poorly understood. Current research predominantly isolates hail impacts from wind interactions, neglecting critical aerodynamic influences such as wind-driven hail acceleration, fragmentation dynamics, and momentum transfer. This knowledge gap underscores the imperative to investigate hail impact behavior under combined wind–hail conditions, which is essential for advancing disaster-resistant design standards and mitigation strategies.
Cui Q et al. [9] conducted a comparative analysis of three simulation methods for modeling hail impacts at medium velocities (10–50 m/s). Their findings demonstrated that the Arbitrary Lagrange–Euler (ALE) method coupled with the MAT155 material model exhibited superior performance in predicting contact force distributions during medium-velocity impacts. Tippmann et al. [10] developed a strain-rate-sensitive ice material model incorporating scatter-defined compressive strength data for hailstones. This model accurately replicated the failure progression observed in impact experiments, particularly the initiation and propagation of longitudinal cracks, and elucidated the evolving relationship between these cracks and peak impact forces. Macdonald J R et al. [11] employed a hybrid experimental–numerical approach to detect and evaluate the impact characteristics of hailstones with varying diameters on structural components. Sadighi et al. [12] utilized numerical simulations to investigate the evolution of delamination damage in carbon fiber laminates subjected to repeated hail impacts. Their results revealed that cumulative damage from multiple impacts significantly reduced the load-bearing capacity and increased the likelihood of structural failure. Donaldson J et al. [13] conducted experimental studies on fully bonded single-layer roof system models using a negative-pressure vacuum chamber. Their work established a correlation between hail-induced adhesive failure and the wind resistance degradation of roof systems. Chen et al. [14] quantitatively analyzed the structural response and wind–hail debris penetration resistance of composite structural insulated panels (SIPs) under hail impacts. They further developed fragility curves for SIPs against wind-driven hail impacts using LS-DYNA R7.0 software, providing a predictive framework for a vulnerability assessment. Liu et al. [15] conducted a comparative study on the dynamic responses of membrane structures subjected to hail impacts, incorporating factors such as hailstone diameter, displacement, velocity, and acceleration. Their research combined experimental tests and numerical simulations to evaluate the mechanical behavior of these structures under varying impact conditions. Song Z [16] experimentally analyzed the influence of impact location and velocity on the failure mechanisms of composite panels, investigating damage propagation and force transfer during hailstone collisions. The study highlighted how localized stress concentrations and interfacial delamination govern the structural integrity of composite materials under repetitive impacts. Uz M E [17] developed an experimental methodology to determine the dent resistance of steel roof panels and predict dent depth. This approach integrated critical parameters, including hailstone size, impact velocity, panel type, and roof strength, to assess the failure risk of roofing systems under wind-driven hail scenarios. Additionally, natural hailstones exhibit complex layered structures. Kim et al. [18,19] compared the impact effects of homogeneous and parallel-layered hailstones, demonstrating that the hailstone microstructure significantly influences the impact force characteristics and target damage. Layered hailstones exhibited delayed fragmentation due to interlayer bonding, resulting in higher peak impact forces compared to their homogeneous counterparts [20]. These findings underscore the necessity of accounting for microstructural heterogeneity in hail impact modeling for accurate risk assessments.
In summary, current research on structural wind–hail disasters, both domestically and internationally, predominantly focuses on the isolated impact of hailstones on structures while neglecting the synergistic effects of wind on hail impact dynamics [21]. However, wind speed is a critical parameter that cannot be overlooked in assessing the losses caused by wind–hail disasters [22,23,24,25]. Furthermore, existing studies primarily investigate high-velocity hail impacts, with limited attention to low- and medium-velocity hailstones. This gap underscores the practical significance of exploring such scenarios.
To fill this important knowledge gap, this study is the first to experimentally investigate the aerodynamic modulation of hail impact dynamics by wind speed, which greatly improves the validity compared to traditional vertical impact tests. This work establishes, for the first time, a quantitative framework for wind-speed-dependent hail impact forces, effectively reducing the gap between idealized laboratory conditions and real-world meteorological scenarios. This study leverages a self-developed integrated hail impact simulation device to conduct wind tunnel experiments under varying wind speeds. The experiments systematically examine the correlations among wind speed, hailstone diameter, hail velocity, and peak impact forces. Based on the experimental results, a predictive model for peak hail impact loads is proposed, tailored for wind–hail-disaster-resistant structural design. This model provides actionable insights for enhancing structural resilience against combined wind–hail hazards, offering a valuable reference for engineering applications.
2. Experimental Overview
2.1. Coupled Wind–Hail Experimental System
This study is conducted in the smooth-flow-suction-type, single-test-section, low-speed wind tunnel at the Wind Engineering Research Center of Hunan University of Science and Technology. The test section dimensions are 21.0 m (length) × 4.0 m (width) × 3.0 m (height). The wind tunnel is equipped with a circular turntable adjustable over a rotation range of 0–360°, and exhibits exceptional flow field performance, characterized by flow velocity non-uniformity below 1% and turbulence intensity below 0.5%. The maximum achievable wind speed within the tunnel is 30 m/s, approximating the wind speed of a Category 1 typhoon.
Currently, most hail impact experiments employ pneumatic launchers [26,27]. To simulate coupled wind–hail scenarios, this study develops a self-designed vertical hail impact testing apparatus tailored for wind tunnel experiments. The system comprises two main components: a hail launching device and a data acquisition system in Figure 1. As can be seen in Figure 1, the experiment is carried out in the turntable of the wind tunnel test section, and the hail launching system consists of a control system and a hail launcher, in which the hail launcher utilizes a customized pneumatic pumping system as the dynamic loading mechanism for the impact test, and different hail launching speeds can be achieved by adjusting the air pressure in the pneumatic chamber in the hail launcher through the control system. Velocities can be measured from the hail launcher’s built-in infrared laser velocimeter and an external synchronized high-speed camera, which can also be used to detect the integrity of the hail launched by the hail launcher. This platform enables the simulation of hail impacts with different diameters and velocities under controlled wind speeds. Additionally, a hail protection net is installed at the downstream end of the wind tunnel test section to prevent fragmented hail particles from entering the fan and damaging its blades.

Figure 1.
Wind–hail coupling test platform.
The data acquisition system comprises wind speed measurement devices and impact force measurement devices. A three-dimensional pulsating anemometer (TFI) is selected to measure and monitor wind speed at a height of 50 cm above the target panel during the experiments. The impact force measurement setup consists of a custom-designed force measurement bracket and a force-measuring balance. The bracket, with a height of 50 cm, is positioned at the center of the wind tunnel turntable. A customized bracket is connected to the force-measuring balance and is securely mounted on it, as shown in Figure 2. The DELTA six-component, high-frequency, force-measuring balance (manufactured by DMS International Co., Ltd., headquartered in Hong Kong, China.) is employed in this study. This device integrates force sensors, a rigid cross frame, and a base. Data acquisition is performed at a sampling frequency of 1500 Hz, which adequately meets the requirements for capturing data under low-to-medium-velocity impacts. During the impact process, the friction between the hailstones and the panel is negligible, with only normal pressure acting on the panel. Consequently, the force-measuring balance is used to measure the normal impact force (Z-axis) under vertical impacts. The bracket is installed at a height of 50 cm, and the target panel is a flat steel plate with dimensions of 50 cm × 50 cm × 5 mm.

Figure 2.
The force measurement system consists of two parts: (a) force-measuring balance and (b) custom-designed force measurement bracket.
2.2. Parameters and Fabrication of Simulated Hail
According to the available data, approximately 70% of hailstones during hailstorms have diameters smaller than 4 cm [28]. In this study, simulated hailstones with diameters of 2.4 cm, 2.8 cm, and 3.2 cm were selected based on the Chinese National Standard GB/T 27957-2011 (Grade of Hail) [29]. During the fabrication process, the partial surface melting of the hailstones was intentionally induced to facilitate demolding, resulting in a slight reduction in their actual mass compared to theoretical values. The theoretical mass of the simulated hail was calculated using sphere mass Formula (1). The actual mass was weighed by precision electronic scales. The measured parameters of the simulated hailstones are summarized in Table 1.

Table 1.
Related parameters of hail with different sizes.
In the equation, : the density of the hailstone, taken as = 0.9 × 103 kg/m3; : the circular ratio; and : the radius of the hailstone (unit: m).
In this study, simulated hailstones were fabricated using aluminum molds. Each hailstone mold consisted of two aluminum alloy hemispherical shells. A small hole was drilled on the top surface of the mold to facilitate water injection and the internal positioning of the hailstone core. The interface between the two hemispherical molds was sealed with silicone sealant and secured via bolted fastening. However, due to technical limitations in replicating natural hailstones in laboratory settings, pure water ice was employed as a substitute for the hailstone material [30,31]. Pure water was injected into the aluminum molds using a syringe, followed by freezing in a −23 °C refrigeration chamber for over 24 h [32,33] to ensure complete solidification. During demolding, the volume expansion effect of ice [34] was accounted for: after removal from the mold, the hailstones were allowed to rest at room temperature until partial surface melting occurred, enabling natural demolding. This step also alleviated the internal stresses caused by volumetric expansion, preventing additional cracks in the hailstones. The demolded hailstones were resealed and stored in the −23 °C refrigeration chamber until testing. The physical mold is illustrated in Figure 3.

Figure 3.
The force measurement system consists of two parts: (a) hail-making mold interior and (b) hail-making mold shell.
2.3. Determination of Experimental Parameters
In nature, the relationship between the terminal velocity and size of freely falling hailstones is relatively consistent [35,36]. Statistical analyses indicate that hailstones are predominantly spherical in shape [37]. Therefore, in this study, hailstones are assumed to be spherical for analytical purposes. When hailstones are modeled as spheres, the theoretical terminal velocity is calculated as follows:
In the equation, : the terminal velocity of the hailstone (unit: m/s); : gravitational acceleration, taken as = 9.8 m/s2; : the density of the hailstone, taken as = 0.9 × 103 kg/m3; : air density at a standard temperature (20 °C), taken as = 1.205 kg/m3; : the diameter of the hailstone (unit: m); and : dimensionless drag coefficient. For smooth spherical hailstones, the empirical relationship = 0.41D0.185 applies when 0.5 cm ≤ < 5 cm, where is the hailstone diameter in centimeters.
The custom bracket was rigidly attached to the force balance and securely mounted on the balance while performing the experiment to prevent severe wind vibration from affecting the results. The ambient temperature was 20 degrees.
Table 2 shows the theoretical terminal velocities of three different sizes of hailstones calculated according to Equation (2), and the actual mass of the hailstones.

Table 2.
Determination of the theoretical velocity of hailstones.
This study conducted a comparative investigation based on the theoretical terminal velocity of hailstones, utilizing three different hailstone diameters (d = 2.4, 2.8, 3.2 cm), four wind speeds (Vw = 0, 5, 9, 11 m/s), and varying launch velocities of hailstone particles. The systematic analysis focused on the impact behavior of hailstones under different wind speeds and particle parameters. The specific experimental conditions are summarized in Table 3.

Table 3.
Experimental conditions.
3. Experimental Analysis and Results
3.1. Investigating the Influence of Wind Speed on Hail Impact Force Dynamics
In this experiment, with wind speed as the variable, 3.2 cm diameter hailstone particles were selected as test objects to investigate the time–history curve of the impact force during vertical impacts (90° angle of attack) on a metal force-measuring panel at a velocity of 26 m/s. The experimental results are shown in Figure 4.
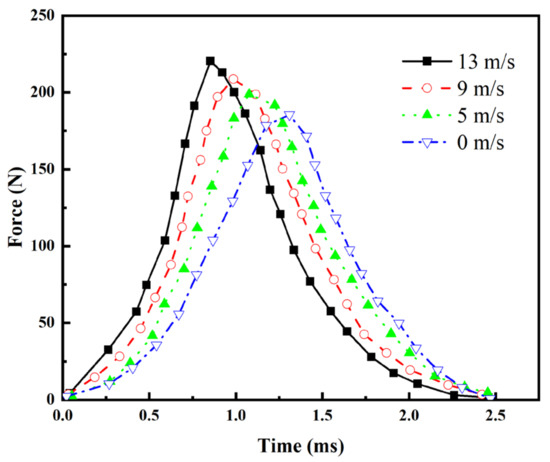
Figure 4.
Time-course curves of hailstone impact forces under different wind speeds.
As shown in Figure 4, during the impact tests, although the total duration of hailstone impacts showed no significant variation with changing wind speeds, the time required to reach the peak impact force decreased progressively as the wind speed increased, while the peak impact force magnitude rose substantially. At a wind speed of 13 m/s, the peak impact force of the hailstones reached its maximum value, exhibiting an increase of approximately 18.9% compared to the windless condition (0 m/s). The reason for this phenomenon was hypothesized to be based on the theory of hydrodynamics: when wind interacts with spherical hailstones, the resulting aerodynamic forces arise from the superposition of pressure and tangential shear stresses acting on the hailstone interface. These forces can be decomposed into streamwise (axial) and transverse (normal) components relative to the incoming direction. The transverse component consists of lift and downward pressure and is determined by the pressure gradient around the surface of the hailstones. For vertically descending hailstones, downforce is greater than lift due to asymmetric flow separation and unfavorable pressure gradients in the windward hemisphere. This downward net lateral force amplifies the vertical impact force through momentum transfer. These findings demonstrate that wind speed is an indispensable parameter for evaluating the damage potential of hailstorms. Hailstones driven by strong winds exhibit significantly enhanced destructive capacity. Ignoring wind effects and considering only hail impacts in isolation would lead to an overestimation of structural impact resistance, thereby compromising the accuracy of risk assessments for wind–hail disasters.
3.2. Study on the Effects of Wind Speed on Hail Impact Force Variation Patterns Across Different Diameters
To further investigate the coupling mechanisms between wind speed and hailstones of varying diameters, this study analyzed the time–history curves of impact forces for three hailstone diameters (2.4 cm, 2.8 cm, and 3.2 cm) at a constant launch velocity of 23 m/s under different wind speeds, as illustrated in Figure 5. As shown in Figure 5, the impact force–time curves for all hailstone diameters exhibit a pulsed shape, with short impact durations concentrated between 0 s and 0.0025 s. Due to the limited variation in hailstone diameters, the influence of wind speed on impact duration was negligible at 0 m/s. However, with increasing wind speeds, smaller diameter hailstones reached peak forces earlier and exhibited shorter interaction times. This indicates that wind exerts distinct effects on hailstones of different sizes.
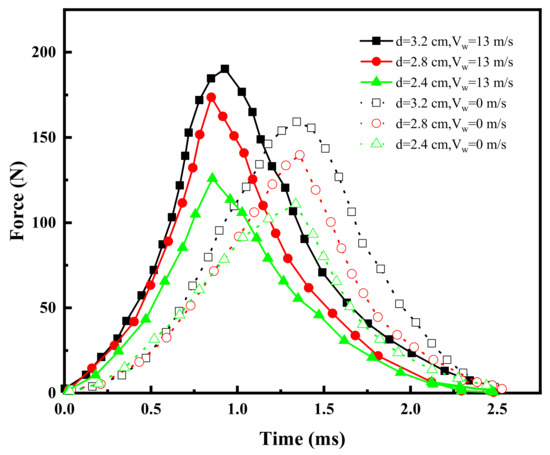
Figure 5.
Impact force–time-course curves under simultaneous variations in wind speed and hailstone diameter.
Peak hail impact is the value of the maximum impact force produced instantaneously by hail when it strikes the surface of an object. As shown in Table 4, the peak impacts of 2.4 cm, 2.8 cm, and 3.2 cm hailstones were 110.9 N, 139.7 N, and 159.2 N at a wind speed of 0 m/s, respectively. Under a wind speed of 13.5 m/s, these values increased to 126.0 N, 173.6 N, and 190.3 N, corresponding to a minimum increase of over 10% in structural panel impact forces. These results demonstrate a clear positive correlation between peak impact forces and both wind speed and hailstone diameter.

Table 4.
The effect of wind speed on the peak impact force of hailstones.
Figure 6 shows the comparative curves of the impact forces for hailstones with varying diameters at a constant velocity of 23 m/s under different wind speeds. As depicted in Figure 6, the peak impact forces exhibit a positive correlation with wind speed, increasing as wind speed rises. Notably, larger hailstones demonstrate more pronounced increases in peak impact forces.
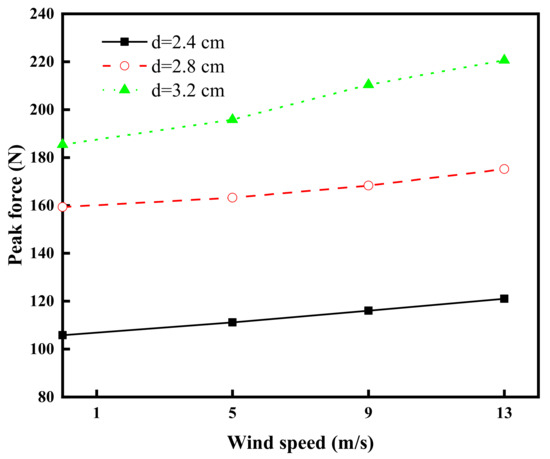
Figure 6.
Peak force curves for different hail diameters.
Furthermore, significant gaps between the peak force curves of different hailstone diameters indicate that particle size markedly influences impact forces, with larger hailstones generating greater impact forces. Additionally, the effect of wind speed on impact forces varies with hailstone diameter: larger hailstones are more significantly influenced by wind speed, as evidenced by steeper slopes in their peak force curves and more substantial increases in peak forces.
3.3. Formatting of Mathematical Components
To further investigate the coupling mechanisms between wind speed and hailstone velocity, this study selected 3.2 cm hailstones as the test subject and analyzed the patterns of the variation in the impact forces under two wind speeds ( = 0 m/s, = 13 m/s) and varying hail velocities, as shown in Figure 7 and Figure 8.
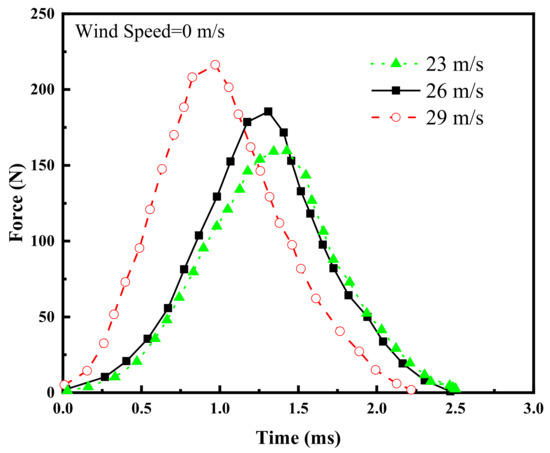
Figure 7.
Time-course curves of hail impacts with different velocities at a 0 m/s wind speed.
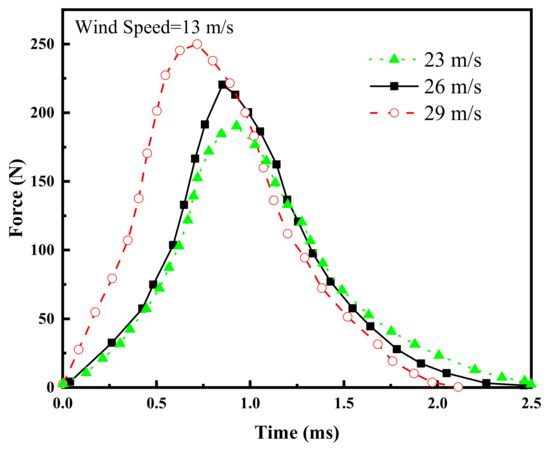
Figure 8.
Time-course curves of hail impacts with different velocities at a 13 m/s wind speed.
From the figures, it is evident that hail velocity significantly influences the impact duration: higher hail velocities result in shorter impact durations, faster attainment of peak impact forces, and greater peak force magnitudes. The effect of wind speed on hail impact forces is primarily reflected in the peak impact force. As illustrated, higher wind speeds lead to larger peak impact forces, with increases exceeding 15% in magnitude. These results unequivocally demonstrate that wind speed is a critical factor influencing hail impact forces and cannot be overlooked in structural risk assessments.
3.4. Factors Influencing the Damage Potential of Hailstorms
In the assessment of hail-induced damage potential, the maximum impact force is a primary indicator, which is correlated with the maximum impact kinetic energy of hailstones. The kinetic energy of a hailstone depends on its velocity and mass [38]. The formula for calculating hailstone kinetic energy can be expressed as:
In the equation, : kinetic energy of hail (unit: ); : mass of the hailstone (unit: ); and : velocity of the hailstone (unit: ).
Figure 9 presents the relationship between the maximum impact force and the kinetic energy of hailstones under wind speeds of 0 m/s and 13 m/s. Linear regression analysis of the experimental data revealed a strong linear correlation between the maximum impact force and kinetic energy across different wind speeds, with good agreement. The results demonstrate that higher wind speeds lead to greater maximum impact forces.
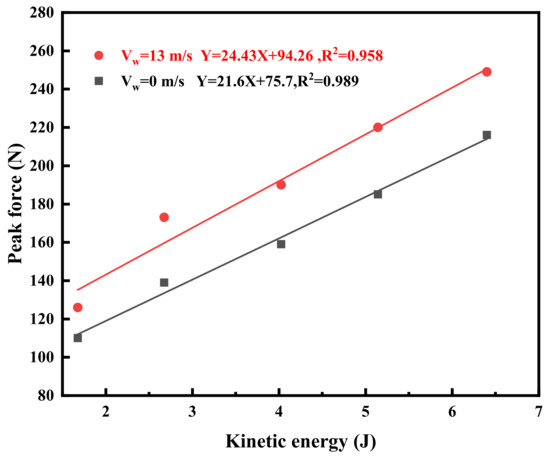
Figure 9.
Peak impact force against kinetic energy of hail.
According to the momentum theorem, the maximum impact force is related to the momentum transfer capacity of the hailstone prior to complete fragmentation. During impact, a portion of the hailstone’s momentum is converted into the impact force, while the remainder is transferred to the momentum of the fragmented cluster particles. Under strong winds, the momentum of these cluster fragments is further converted into additional impact force, thereby enhancing momentum transfer in the impact direction and generating higher impact forces. Consequently, the inclusion of wind significantly amplifies the impact forces during hail collisions.
These findings highlight that wind speed is a critical factor in assessing hail-induced damage potential. Higher wind speeds correlate with stronger destructive capacity, underscoring the necessity of incorporating wind effects into hail risk evaluation frameworks for structural and agricultural applications.
4. Multivariate Regression Analysis of Hail Impact Forces
In engineering practice, multiple linear regression is commonly employed to explore the relationships between dependent variables and multiple independent variables [39]. This is because when actual phenomena occur, the observed results are usually influenced by multiple interacting determinants. Multivariate regression analysis, which incorporates an optimal combination of independent variables to predict or estimate dependent variables, demonstrates superior predictive accuracy and empirical validity compared to univariate approaches that rely on a single predictor. This multivariate approach not only mitigates confounding effects but also aligns more closely with the complex causal architectures inherent in nature.
In this study, to numerically calculate and predict the impact forces of hailstones on structures for engineering design reference, hail impact simulations under varying wind speeds were conducted in a wind tunnel laboratory using a self-developed integrated hail impact simulation device. A systematic comparative analysis was performed to investigate the interrelationships among wind speed, hailstone diameter, hail velocity, and hail impact force. Based on the experimental results, a peak hail impact load prediction model applicable to diverse conditions was proposed, offering significant implications for structural design to combat wind–hail disasters.
To perform the multivariate regression analysis, the experimental data were processed using SPSS 27.0 software. Through iterative trial and error, the regression model was hypothesized as follows:
In the equation, : peak load of hail impact on the structure (unit: N); : wind speed (unit: m/s); : diameter of the hailstone (unit: m); and : velocity of the hailstone (unit: m/s).
The results of the multivariate regression analysis model are presented in Table 5:

Table 5.
Determination of regression coefficient (dependent variable: force/N).
As shown in Table 5, hail diameter, hail velocity, and wind speed all had statistically significant effects on the peak hail impact force. Based on the magnitudes of the standardized coefficient beta, velocity exerted the strongest influence on peak displacement, followed by hailstone diameter, with wind speed demonstrating the weakest effect.
The estimated coefficients of the model were k1 = 2.321, k2 = 6375.502, k3 = 9.487, and k4 = −262.402. Based on the significance levels of each coefficient, all coefficients exhibited p ≤ 0.001 < 0.05, indicating statistically significant effects on hail impact forces. Furthermore, the overall model validity was confirmed through an F-test, leading to the establishment of the linear regression equation as follows:
In the equation, : peak load of hail impact on the structure (unit: N); : wind speed (unit: m/s); d: diameter of the hailstone (unit: m); and : velocity of the hailstone (unit: m/s).
The following F-test [40] was conducted to evaluate the regression equation. Original hypothesis (H0): k1 = k2 = k3 = 0 (F-test original hypothesis: all parameters in the model are zero). Alternative hypothesis (H1): At least one of k1, k2, and k3 is non-zero (F-test alternative hypothesis: not all parameters in the model are zero). If the original hypothesis holds, the independent variables have no significant effect on the dependent variable. Conversely, if the original hypothesis is rejected, the independent variables significantly influence the dependent variable, indicating a statistically significant linear relationship between the variables. The test results are summarized in Table 6.

Table 6.
F-test.
Based on the results of the F-test (p ≤ 0.001 < 0.05), the regression equation is statistically significant overall, demonstrating a linear relationship between hail impact force and the variables of wind speed, hail diameter, and hail velocity.
To validate the robustness and reliability of the model, a residual analysis was performed on the regression equation (Table 7), where the residual ei (defined as with denoting the observed impact force and the predicted value) quantifies the deviation between observed and predicted values.

Table 7.
Residual analysis of variables.
As shown in Figure 10 and Figure 11, the mean and standardized residuals are both zero, and the residuals are uncorrelated with each independent variable (weighted residuals = 0). The histogram of standardized residuals approximates an inverted bell-shaped curve with near symmetry, indicating that the residual distribution largely conforms to normality. Additionally, the standardized residual P-P plot demonstrates that the observed residuals closely follow the diagonal line, with deviations oscillating around expected values, confirming a strong linear relationship between observed and theoretical residuals. These diagnostic results validate the assumptions required for multiple linear regression modeling.
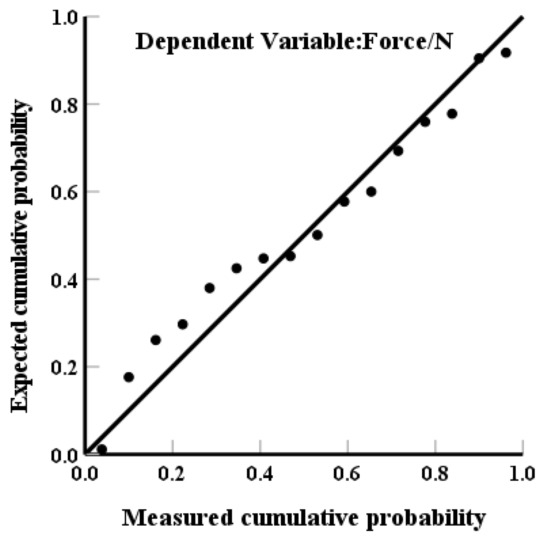
Figure 10.
Residual PP figure.
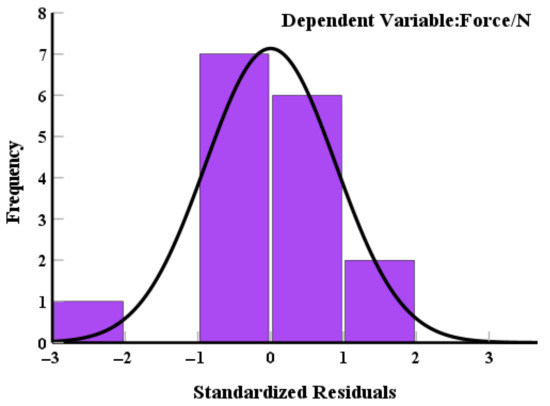
Figure 11.
Residual histogram.
The overall reliability of the model has been confirmed through rigorous validation. The fitted regression formula was subsequently applied to predict the peak hail impact forces. A goodness-of-fit plot comparing predicted and observed values is presented in Figure 12. As illustrated in Figure 12, the model exhibits strong agreement between predictions and experimental data, demonstrating its robustness. Therefore, the use of this regression model to estimate the peak structural loads induced by hail impacts is reasonably justified for engineering applications.
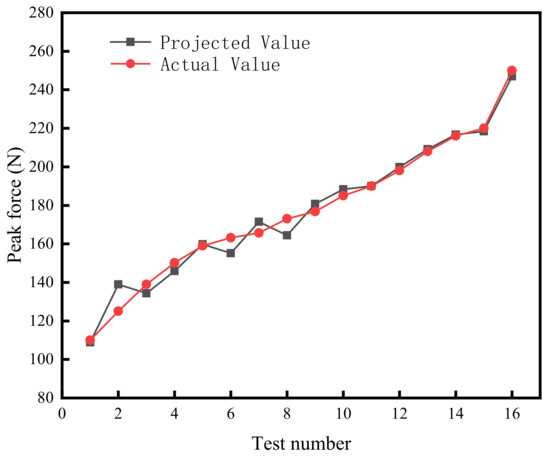
Figure 12.
Prediction effect of regression equation.
5. Conclusions
This study, based on a self-developed hail impact simulation platform, conducted hail impact experiments under varying wind speeds in a wind tunnel laboratory. The influence of wind speed, hailstone diameter, and velocity on hail impact characteristics was systematically analyzed, leading to the following key conclusions:
Wind speed exerts significant effects on hail impact dynamics: Higher wind speeds shorten impact duration, accelerate peak force attainment, and amplify peak force magnitudes, thereby enhancing the destructive potential of wind-driven hailstones. When wind speed and hailstone diameter vary simultaneously, peak impact forces increase with both parameters, though smaller hailstones exhibit reduced sensitivity to wind speed. Similarly, combined increases in wind speed and hail velocity escalate peak forces, necessitating distinct analyses of ice material behavior under impact versus high-velocity scenarios. Notably, under high wind speeds, impact forces surpass those in windless conditions due to the momentum transfer from fragmented hail clusters, which converts additional aerodynamic energy into impact forces. Building on these findings, a predictive model for peak structural loads was developed using the multivariate regression analysis of wind–hail coupled simulation data, offering actionable insights for wind–hail-resistant structural design.
While this study systematically investigated the influence of wind speed on hail impact dynamics and yielded notable insights into aerodynamic coupling mechanisms, it remained constrained by the authors’ methodological expertise and experimental resources, positioning the work as a preliminary exploratory phase within this research domain. Though actual hailstorms are often accompanied by heavy rainfall, the effect of rainfall on the impact behavior of hail was not explored in this study. Subsequent researchers can carry out experiments in this area to conduct a theoretical analysis of the impact of rain on hail and the actual mechanism of action, in order to use the findings to solve the problems of practical engineering.
Author Contributions
Conceptualization, Yimin Dai (Y.D.); methodology, Yimin Dai (Y.D.) and Yao Deng (Y.D.); Formal analysis Yimin Dai (Y.D.) and H.L.; investigation, Y.L. and H.L.; data curation, Yao Deng (Y.D.); writing—original draft, Yao Deng (Y.D.); writing—review and editing, H.L. and Y.L.; funding acquisition, Yimin Dai (Y.D.). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 52178478) and the Hunan Provincial Natural Science Foundation of China (No. 2022JJ30247). Funder: Yimin Dai.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to reasons related to data ownership.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Density of the hailstone, kg/m3 | |
| Air density, kg/m3 | |
| Gravitational acceleration, m/s2 | |
| Hail radius, m | |
| Hail diameter, m | |
| Hail mass, kg | |
| Theoretical velocity of hail, m/s | |
| Wind velocity, m/s | |
| Actual speed of hail, m/s | |
| Kinetic energy of hail, j | |
| Peak load of the hail impact on the structure, N | |
| Actual value of the peak impact force, N | |
| Predicted value of the peak impact, N | |
| Dimensionless drag coefficient | |
| Residual | |
| Regression model coefficients | |
| The circular ratio |
References
- Guan, Y.; Zheng, F.; Zhang, P.; Qin, C. Spatial and temporal changes of meteorological disasters in China during 1950–2013. Nat. Hazards 2015, 75, 2607–2623. [Google Scholar] [CrossRef]
- Dejanovic, T.; Trbić, G.; Popov, T. Hail as a natural disaster in Bosnia and Herzegovina. In Climate Change Adaptation in Eastern Europe: Managing Risks and Building Resilience to Climate Change; Springer: Cham, Switzerland, 2019; pp. 245–266. [Google Scholar] [CrossRef]
- Miao, C.; Xie, J.; Li, Y. Evaluating the risk and its acceptability of crop yield reduction in Northwest China under the impact of wind hail disasters. Nat. Hazards 2024, 120, 14027–14048. [Google Scholar] [CrossRef]
- Ha, T.; Shen, Y.; Duddu, H.; Johnson, E.; Shirtliffe, S.J. Quantifying hail damage in crops using sentinel-2 imagery. Remote Sens. 2022, 14, 951. [Google Scholar] [CrossRef]
- Gensini, V.A.; Ashley, W.S.; Michaelis, A.C.; Haberlie, A.M.; Goodin, J.; Wallace, B.C. Hailstone size dichotomy in a warming climate. NPJ Clim. Atmos. Sci. 2024, 7, 185. [Google Scholar] [CrossRef]
- Xingzhi, T.; Rong, Z.; Wenyu, W. Temporal and spatial distribution characteristics of hail disaster events in China from 2010 to 2020. Torrential Rain Disasters 2023, 42, 223–231. [Google Scholar] [CrossRef]
- Wang, X.; Ran, L.; Qi, Y.; Jiang, Z.; Yun, T.; Jiao, B. Analysis of Gravity Wave Characteristics during a Hailstone Event in the Cold Vortex of Northeast China. Atmosphere 2023, 14, 412. [Google Scholar] [CrossRef]
- Rigo, T.; Farnell, C. A Summary of Hail Events during the Summer of 2022 in Catalonia: A Comparison with the Period of 2013–2021. Remote Sens. 2023, 15, 1012. [Google Scholar] [CrossRef]
- Cui, Q.; Yang, J. Evaluation of numerical simulation methods and ice material models for intermediate-velocity hail impact simulation. Eng. Struct. 2021, 244, 112831. [Google Scholar] [CrossRef]
- Tippmann, J.D.; Kim, H.; Rhymer, J.D. Experimentally validated strain rate dependent material model for spherical ice impact simulation. Int. J. Impact Eng. 2013, 57, 43–54. [Google Scholar] [CrossRef]
- Macdonald, J.R.; Stack, M.M. Some thoughts on modelling hail impact on surfaces. J. Bio- Tribo-Corros. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Sadighi, M.; Alderliesten, R.; Fathi, A.; Soltannia, B.; Hedayati, R. Delamination link-ups in composite laminates due to multiple hail impacts. Eng. Struct. 2023, 294, 116729. [Google Scholar] [CrossRef]
- Donaldson, J.; DeLeon, M.; Savage, K.J. Hail Impact Effects on the Wind Uplift Resistance of Fully Adhered Single-Ply Roof Membranes. In Proceedings of the 8th Congress on Forensic Engineering, Austin, TX, USA, 29 November–2 December 2018; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 31–40. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H. Experimental and numerical study of composite lightweight structural insulated panel with expanded polystyrene core against windborne debris impacts. Mater. Des. 2014, 60, 409–423. [Google Scholar] [CrossRef]
- Liu, C.; Deng, X.; Liu, J.; Peng, T.; Yang, S.; Zheng, Z. Dynamic response of saddle membrane structure under hail impact. Eng. Struct. 2020, 214, 110597. [Google Scholar] [CrossRef]
- Song, Z.; Luong, S.; Whisler, D.; Kim, H. Honeycomb core failure mechanism of CFRP/Nomex sandwich panel under multi-angle impact of hail ice. Int. J. Impact Eng. 2021, 150, 103817. [Google Scholar] [CrossRef]
- Uz, M.E.; Kop, M.D.; Yildirim, E.M. Analysis of out-of-plane hail impact resistance of steel roof panels. Exp. Tech. 2022, 46, 509–527. [Google Scholar] [CrossRef]
- Kim, H.; Kedward, K.T. Modeling hail ice impacts and predicting impact damage initiation in composite structures. AIAA J. 2000, 38, 1278–1288. [Google Scholar] [CrossRef]
- Kim, H.; Welch, D.A.; Kedward, K.T. Experimental investigation of high velocity ice impacts on woven carbon/epoxy composite panels. Compos. Part A Appl. Sci. Manuf. 2003, 34, 25–41. [Google Scholar] [CrossRef]
- Tan, X.; Feng, X.; Hu, Y.; Xie, R.; Yang, S.; Bai, Y. Experimental investigation on characteristics of layered ice spheres under high-velocity impact. Explos. Shock. Waves 2020, 40, 113301. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, Y.; Li, Y.; Wang, W.; Yang, W. Research progress and prospect of hail impact resistance of engineering structures. J. Hunan Univ. 2023, 50, 228–236. [Google Scholar] [CrossRef]
- Schuster, S.S.; Blong, R.J.; McAneney, K.J. Relationship between radar-derived hail kinetic energy and damage to insured buildings for severe hailstorms in Eastern Australia. Atmos. Res. 2006, 81, 215–235. [Google Scholar] [CrossRef]
- Willmot, E.; Bussmann, S.; Homeier, N.; Kubicek, A. Examples of ground-based hail, rain, and wind sensor networks operating in real-time. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5987–5989. [Google Scholar] [CrossRef]
- Amiranashvili, A.; Chikhladze, V.; Gvasalia, G.; Loladze, D. Statistical Characteristics of the Daily Max of Wind Speed in Kakheti in the Days with and without Hail Processes in 2017–2019. J. Georgian Geophys. Soc. 2020, 7, 197–201. [Google Scholar] [CrossRef]
- Miralles, O.M.A. Wind, Hail, and Climate Extremes: Modelling and Attribution Studies for Environmental Data. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2023. [Google Scholar] [CrossRef]
- Zhu, S.; Peng, W.; Shao, Y.; Li, S. Experimental and numerical study on the high-velocity hail impact performance of carbon fiber aluminum alloy laminates. Int. J. Impact Eng. 2023, 179, 104664. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, B.; Guo, Y.; Zhang, W.; Wang, R. Mechanical responses of CFRP/PVC foam sandwich plate impacted by hailstone. Int. J. Impact Eng. 2023, 178, 104631. [Google Scholar] [CrossRef]
- Hulton, F.; Schultz, D.M. Climatology of large hail in Europe: Characteristics of the European Severe Weather Database. Nat. Hazards Earth Syst. Sci. 2024, 24, 1079–1098. [Google Scholar] [CrossRef]
- GB/T 27957-2011; Grade of Hail. Standardization Administration of the People’s Republic of China, SAC: Beijin, China, 2011.
- Coles, L.A.; Roy, A.; Voronov, L.; Semyonov, S.; Nikhamkin, M.; Silberschmidt, V.V. Dynamic fracture in carbon-fibre composites: Effect of steel and ice projectiles. Procedia Struct. Integr. 2016, 2, 366–372. [Google Scholar] [CrossRef]
- Rhymer, J.; Kim, H.; Roach, D. The damage resistance of quasi-isotropic carbon/epoxy composite tape laminates impacted by high velocity ice. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1134–1144. [Google Scholar] [CrossRef]
- Ge, X.; Zhang, L.; Liu, Z. Effect of freezing temperature on mechanical properties of hail in airworthiness test. J. Aerosp. Power 2020, 35, 1744–1751. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Ge, X.; Liu, Z. Effects of Different Materials and Structures on Mechanical Properties of Hail Used in Aviation Testing. Aerospace 2024, 11, 508. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Z.; Kim, H.; Ma, H. Pulse shaper and dynamic compressive property investigation on ice using a large-sized modified split Hopkinson pressure bar. Lat. Am. J. Solids Struct. 2016, 13, 391–406. [Google Scholar] [CrossRef]
- Sun, J.; Lam, N.; Zhang, L.; Ruan, D.; Gad, E. Contact forces generated by hailstone impact. Int. J. Impact Eng. 2015, 84, 145–158. [Google Scholar] [CrossRef]
- Heymsfield, A.; Szakáll, M.; Jost, A.; Giammanco, I.; Wright, R. A comprehensive observational study of graupel and hail terminal velocity, mass flux, and kinetic energy. J. Atmos. Sci. 2018, 75, 3861–3885. [Google Scholar] [CrossRef]
- Punge, H.J.; Kunz, M. Hail observations and hailstorm characteristics in Europe: A review. Atmos. Res. 2016, 176, 159–184. [Google Scholar] [CrossRef]
- Dieling, C.; Smith, M.; Beruvides, M. Review of impact factors of the velocity of large hailstones for laboratory hail impact testing consideration. Geosciences 2020, 10, 500. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar] [CrossRef]
- Sureiman, O.; Mangera, C.M. F-test of overall significance in regression analysis simplified. J. Pract. Cardiovasc. Sci. 2020, 6, 116–122. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).