Abstract
Thermal printing is a prevalent method due to its advantages of rapid output, cost effectiveness, and ease of use. However, the quality of thermal printing is influenced by the printing speed, the temperature, and the concentration and characteristics of the materials. This research employs a BP neural network to forecast print quality, utilizing two activation functions. The findings indicate that a dual-layer hidden configuration utilizing the GeLU activation function yields a lower root-mean-square error (RMSE). The optimal configuration identified consists of six neurons in the first hidden layer and three neurons in the second hidden layer. To enhance the predictive performance, a PSO algorithm was integrated with the PSO-BP model to refine the parameter selection, which included ambient temperature, printing speed, and printing concentration, with iterative training and validation conducted via the gradient descent algorithm. The PSO-BP network achieved an MAE of 0.1108, an RMSE of 0.145, an MSE of 0.021, and an R2 value of 0.9916 in predicting print quality. These results substantiate the stability and reliability of the neural network model developed with the PSO algorithm. Further validation with ten sets of test samples demonstrated that the model attained an average absolute error of 2.77% in print quality predictions, indicating robust generalization capabilities and precise forecasting.
1. Introduction
1.1. Traditional Printing Quality
Thermal barcode printing technology is an economical, fast, and environmentally friendly printing method that has been widely used in various fields, such as logistics, retail, and healthcare, in recent years. Its working principle involves heating thermal paper with a thermal print head, causing a chemical reaction in the thermal coating on the paper to form images or text. However, the quality of thermal printing is influenced by various factors, such as the temperature control of the print head, printing speed, and paper material [1]. Small changes in these factors can lead to fluctuations in printing quality, which, in turn, affect the readability of the barcode and the overall printing effect. In practical applications, the readability of barcodes is directly related to the accurate transmission of logistics information and the efficiency of inventory management, while fluctuations in print quality may result in barcode scanners failing to correctly identify the barcodes, which, in turn, can trigger a series of chain reactions, such as logistics delays and inventory errors. Therefore, the instability of thermal barcode print quality is an urgent issue that needs to be addressed, and how to accurately predict and control the print quality of thermal barcodes has become a current research hotspot and challenge.
Conventional quality control methods in printing predominantly depend on empirical parameter adjustments and manual inspections [2]. These approaches are characterized by inefficiency and struggle to adapt to the complexities and variability in printing environments [3]. Consequently, the integration of contemporary artificial intelligence and machine learning technologies, particularly neural network-based predictive models, presents a promising avenue for addressing these challenges [4]. Neural networks possess robust nonlinear mapping capabilities and can analyze extensive datasets to predict and optimize printing parameters, thereby enhancing the stability and precision of printing quality [5].
1.2. The Quality Prediction of Printing with BP Neural Networks and PSO
Concerning pertinent studies and predictions, a back-propagation artificial neural network (BP neural network) model has been used to predict the performance of gel printing [2,6]. Therefore, a BP neural network is a multilayer feed-forward neural network that uses error back-propagation, which has the characteristics of a simple structure and strong fault tolerance [4], and a BP neural network also has powerful generalization and nonlinear mapping capabilities [7]. The methods focus on data normalization in order to improve the maximum speed limit, the inertia constant, and the fitness function by using a BP neural network for color prediction [8], predicting the flow of ink during 3D bio-printing [9], and using the BP neural network to optimize parameters on 3D printing [10]. To optimize the selection of parameters, it is common to combine particle swarm optimization (PSO) algorithms with BP networks to improve model performance [11,12,13,14]. For 3D printing, artificial neural networks (ANNs) are also applied in potential solutions [15,16], and both multiple regression analysis (MRA) and ANNs are used to analyze the influence of machining parameters [17].
1.3. The Optimal Parameters of Printing Quality Using Machine Learning
Other related prediction methods include the application of convolutional neural networks (CNNs) to predict printing errors 17 and an AI-driven approach to identify and forecast printing errors using CNNs and the Cox proportional hazards (CPH) approach [18]. Other research used learning algorithms to successfully predict the failure mode of printed thermal resistance [19,20] and to predict the relationships between measured color and four control factors by a multilayer perceptron (MLP) neural network model [5]. Another study also employed eight distinct classification algorithms, including K-nearest neighbors, support vector machines, and Gaussian naive Bayes, to assess print quality [21]. About the quality of printing, automated algorithms were adopted to analyze and compare differences in original and printed documents [22], real-time programming methods were chosen to detect the level of prints [23], shape and color classification algorithms were used to classify printing defects [24], and image segmentation and color image analysis techniques were proposed to detect the quality of printing [3]. By introducing advanced machine learning algorithms, such as support vector machine (SVM) and Random Forest, the high-precision classification of different printing materials and technologies was achieved using printing pattern features, demonstrating more than 92% classification accuracy [25]. Another study also used machine learning with optimal input parameters [26]. In terms of printing parameter adjustment, a fast self-calibration method for laser displacement sensors was proposed to complete parameter calibration at one time [27], and, in addition, iterative function calculations were found to improve the measurement accuracy of printing [28]. Expert experience was also used to design and formulate multiple sets of parameters to analyze the rules of influence [29,30]. Regarding 3D printing, some studies applied machine learning for the determination of optimal parameters. Using metadata and video data from the 3D printing process, a unique image dataset was constructed, and a regression model was trained to accurately predict and adjust the flow of printing material [31].
1.4. The Purpose of This Research
To enhance the accuracy of models within a constrained data range, this research employs the well-established PSO-BP to leverage the distinctive benefits for the optimization of thermal parameters via gradient descent while also considering factors such as the volume of training data and the interpretability of parameters. The objective is to facilitate the effective adjustment of parameters in industrial printers, thereby ensuring their operational availability and supporting informed decision making. Therefore, this article discusses the prediction effect of the BP neural network on printing parameters and uses a simple and fast solution PSO algorithm to solve the optimal weight and threshold of the BP neural network, thus improving the convergence speed and optimization accuracy of the BP neural network.
2. The Principle of Printing and Key Parameters
Hot barcode printing is a method for generating barcodes by heating. When the print head is heated, the thermal coating reacts chemically to display the barcode information. Thermal printing primarily involves controlling the thermal print head to generate heat, thereby heating the thermally sensitive medium to enable information printing. The core of the thermal printer is the thermal print head, which is an electronic component that uses Joule heating effects to print information. As shown in Figure 1, it is mainly composed of resistors, ceramic substrates, driver chips, circuit boards, socket interfaces, radiators, and other components. The quality of barcode printing is influenced by several key parameters, including print head temperature, print speed, print density, and print quality.
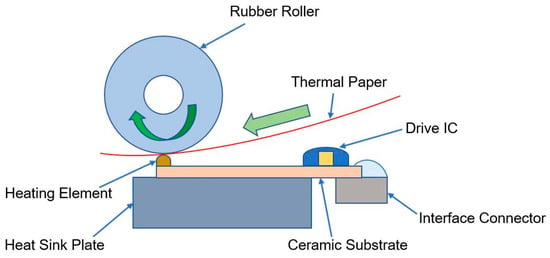
Figure 1.
The principle of thermal printing.
The printer firmware manages the printing speed by adjusting the rotational speed of the stepping motor, thereby allowing for various speed settings. Additionally, the firmware controls the printing concentration by regulating the heating duration of the printer head to achieve different levels of concentration. Temperature is modeled to reflect the ambient temperature of the natural environment.
The temperature of the print head plays a vital role in determining the quality of the thermal barcode printing, as shown in Figure 2. If the temperature is too high or too low, unsatisfactory printing results can be obtained, including unclear or damaged barcodes. Different countries and regions experience diverse climate conditions, which can notably affect printing quality, particularly in colder environments. In this study, the temperature examined variable pertains to the ambient temperature, which was simulated in a temperature-controlled chamber to mimic the actual conditions. Print density affects the darkness of barcodes; if the density is too high, the barcode may become overly dark and difficult to scan, whereas if it is too low, the barcode might be too light and prone to blurring. Furthermore, the type of thermal paper used and the conditions under which it is stored can affect the print density of thermal barcodes. This density is mainly adjusted through software that offers 15 different settings.

Figure 2.
Temperature-controlled chamber.
Printing at excessively high speeds can lead to inadequate contact time between the print head and thermal paper, which can negatively impact the print quality. However, printing too slowly may cause the print head to overheat, damaging the thermal coating. The speed variable discussed in this study was categorized into nine levels. The primary equipment used for testing barcodes is the WebScan Barcode Verifier (Barcode Detection Scanning Sensor, Model USB-DC71), and its accompanying barcode detection software is the Barcode Recognition Prediction System V1.0 (1D and 2D Barcode Recognition and Detection). The specific evaluation metrics of the scan reflectance profile offer important insights into quality control in the barcode printing process. Consequently, when assessing the quality grades of the barcode symbols, such as grades A, B, C, D, and E, we can compute the average values of the individual evaluation metrics from each scan reflectance profile and determine the arithmetic mean of the grades for each parameter across the profiles. To enhance information regarding the quality of the barcode symbol, the average values of these evaluation metrics or their grade averages can be included in the test report data, as illustrated in Table 1 and Figure 3.

Table 1.
The grades of letters (ANSI) corresponding to the level of the numeric symbol.
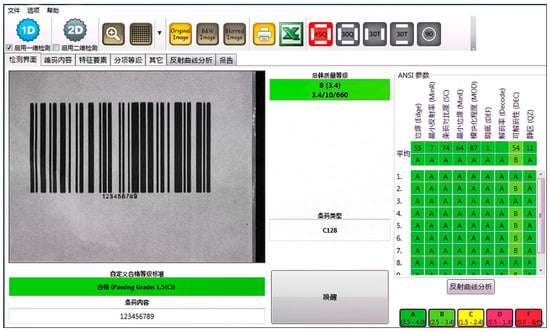
Figure 3.
The quality of printed test results.
3. Methodology
3.1. The Experimental Technique
This research employed an experimental technique known as Latin Hypercube Sampling (LHS) to train and validate the data required for the BP neural network. The primary operational features of the LHS in this study consisted of two main steps: random sampling and probability distribution reconstruction. Random sampling involves selecting samples randomly from a multivariate parameter distribution to analyze a small yet representative set of samples. Probability distribution reconstruction is the process of creating a probability distribution from a limited number of samples, thereby yielding a representative dataset. This comprehensive experimental study comprised seven phases, ranging from data preparation to evaluating the performance of the models, as illustrated in Figure 4.

Figure 4.
The experimental process of the PSO-BP model.
3.2. Experimental Samples
The prediction of thermal printing quality is a common situation involving a limited number of samples and many dimensions. Considering factors such as production costs, equipment lifespan management, and time efficiency, this study employed simplified parameters to improve sample representativeness. To ensure comprehensive feature coverage, an enhanced Latin Hypercube Sampling (LHS) method was utilized to select 30 key samples with the aim of achieving the best balance between data volume, cost, and accuracy.
Random sampling was approximated from the multivariate parameter distribution using LHS, and the probability distribution was re-established with fewer samples. A set of thirty data points was selected as the sample, including the printing speed, printing concentration, printing temperature, and printing quality. The experimental samples are listed in Table 2. Then, these data were used to train and improve the BP neural network model to verify its predictive performance.

Table 2.
The data of the samples.
3.3. Modeling of the BP Neural Network
This study focused on enhancing a BP neural network by employing suitable optimization techniques. These include modifying the network architecture (e.g., adding or removing hidden layers and changing the number of nodes), refining learning algorithms (e.g., incorporating momentum terms, adjusting the learning rate, and selecting different optimizers), and choosing or creating more effective activation and loss functions. The goal was to boost the generalization capability of the model. By evaluating and analyzing various aspects, such as prediction accuracy, stability, and computational efficiency, we aimed to demonstrate the benefits of the improved BP neural network in predicting the quality of thermal barcode printing.
In this study, a neural network model was built in PyTorch 2.7 to accurately forecast printing quality by inputting essential parameters, such as temperature, printing speed, and printing concentration. Initially, it efficiently loaded data from a CSV file and conducted thorough preprocessing to ensure the quality and consistency of the data. The data were then transformed into a PyTorch tensor, and a data loader was established to facilitate an efficient data stream for training and evaluating the model.
In the construction phase of the model, a neural network featuring two fully connected layers was created, as shown in Figure 5 and Table 3, employing the GeLU activation function to improve the model’s ability to express nonlinear relationships. The loss function was based on the Standardized Mean Absolute Error (SAME) average absolute error to maintain the sensitivity to prediction errors during training. The Adam optimizer was chosen to enhance the model convergence through its effective parameter update method. Throughout the training process, the model underwent continuous iterations, adjusting weights to minimize the loss function, outputting the training loss by 10 iterations, and tracking the learning progress.
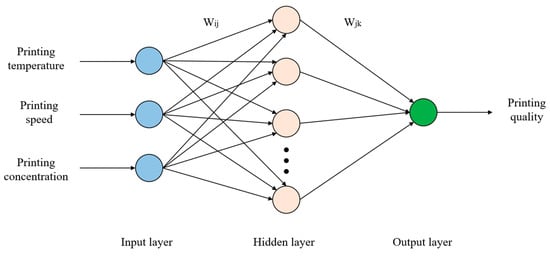
Figure 5.
Printing quality with the BP neural network.

Table 3.
Parameters of the BP neural network.
During the evaluation stage, the model’s performance was assessed using a test dataset, and the average test loss was computed to measure the generalization ability of the model. Finally, predictions were made using new data, and the root-mean-square error (RMSE) was calculated to objectively evaluate the accuracy of the model’s predictions. The entire process represents a comprehensive BP neural network workflow encompassing data processing, model construction, training, evaluation, and prediction. The main steps include the following:
- (1)
- Data reading and preprocessing.
- (2)
- Conversion of data into a PyTorch tensor and creation of a data loader.
- (3)
- Definition and initialization of neural network models.
- (4)
- Specification of the loss function and optimizer.
- (5)
- Model training.
- (6)
- Model evaluation.
- (7)
- Prediction of new data and RMSE calculation.
3.4. Optimization of the PSO-BP Model
BP neural networks are highly influenced by the choice of initial weights and biases. If initialization is not performed correctly, it can result in reduced prediction accuracy. To enhance the prediction accuracy, a particle swarm optimization (PSO) algorithm was introduced to optimize the parameter selection of the BP neural network, thereby improving the model’s predictive capabilities. Additionally, the GeLU function was utilized as the activation function in the hidden layer, whereas the loss function employed the SAME average smoothing absolute error. By optimizing the BP neural network with PSO, we explored the weight and bias search space more effectively, leading to better solutions and improved performance and generalization of the neural network. This approach helped avoid local optima and aimed to determine global or near-global optimal weight configurations.
The fitness function used in the PSO algorithm aligns with the loss function of the BP neural network, utilizing both mean square error (MSE) functions. This article outlines the process of training a BP neural network using the PSO algorithm to optimize its initial parameter settings, which includes the following steps.
- (1)
- Data preparation: Split the dataset into training and testing sets and normalize the samples.
- (2)
- Network architecture setup: Determine the number of layers and nodes in the hidden layers of the BP neural network.
- (3)
- PSO optimization of initial parameters: Use the MSE regression loss function as the fitness function for the PSO algorithm to iteratively update and obtain the initial weights and biases for the neurons in each layer of the BP neural network.
- (4)
- Training the BP neural network: Input the training set into the BP neural network for training while calculating the fitness value and historical best position for each particle.
- (5)
- Parameter updating and model output: Incorporate the parameters optimized by the PSO algorithm into the neural network, apply the gradient descent algorithm to update the network parameters, and ultimately produce the optimal network model.
4. Results
4.1. The Framework of the BP Neural Network
This study aimed to assess model performance in the context of network structure by utilizing the sigmoid activation function and examining the configurations of single-layer and double-layer hidden layers. In the case of the single-layer hidden layer, the model achieved its lowest root-mean-square error when configured with six neurons, indicating optimal prediction accuracy, as illustrated in Table 4. Conversely, the double-layer hidden-layer configuration generally resulted in a reduced root-mean-square error. For the task of predicting printing quality, the most effective configuration was identified as having 6 neurons in the first hidden layer and 10 neurons in the second hidden layer. This structural modification led to a significant enhancement in the model performance, as detailed in Table 5.

Table 4.
The printing quality of the hidden layer with a single layer (using the sigmoid activation function).

Table 5.
The printing quality of the hidden layer with a double layer (using the sigmoid activation function).
The Gaussian error linear unit (GeLU) activation function offers significant advantages over the sigmoid activation function in terms of smoothness, ability to express nonlinearity, computational efficiency, resource utilization, generalization, and applicability. These benefits have led GeLU to become a popular choice in contemporary deep learning. This study aimed to investigate more optimized activation functions by comparing them with the sigmoid function. When using GeLU as the activation function in a hidden layer with six neurons, the model achieved the lowest root-mean-square error and highest prediction accuracy. In comparison to a model with a sigmoid activation function in a two-layer hidden layer setup, the GeLU model demonstrated superior prediction accuracy, as shown in Table 6. In addition, in a two-layer hidden layer configuration utilizing GeLU, the model consistently exhibited lower root-mean-square error values, as indicated in Table 7. This research identified that the best configuration for predicting printing quality consists of six neurons in the first hidden layer and three neurons in the second hidden layer. Furthermore, this study examined three-layer configurations to analyze the arrangement of hidden layer neurons. The findings revealed that the three-layer hidden layer model suffers from overfitting and issues with gradient disappearance or explosion, leading to subpar performance. Consequently, we chose a two-layer hidden layer model architecture for the experiments. Table 4, Table 5, Table 6 and Table 7 provide detailed information regarding the number of hidden layers and activation functions. Figure 6 illustrates the accuracy across different parameters, with the hidden layer of the double layer using GeLU yielding the best results.

Table 6.
The printing quality of the hidden layer with a single layer (using the GeLU activation function).

Table 7.
The printing quality of the hidden layer with a double layer (using the GeLU activation function).
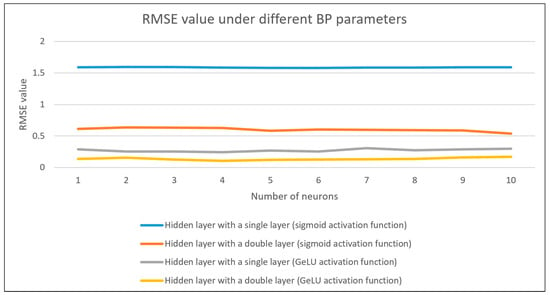
Figure 6.
The value of RMSE with different BP parameters.
The ideal fitting performance of printing quality is shown in Figure 7, where the target value perfectly matches the predicted value. The solid line represents the optimal fitting line for practical use, while the R value indicates the correlation between the output and predicted values. A value closer to 1 signifies a better fitting performance. The blue dots represent the actual and predicted values, whereas the red line denotes the ideally matched trend line. The proximity of these points to the red line suggests a strong alignment between the actual and predicted values. The notation “Test: R = 0.9477” indicates that the correlation coefficient (R value) for the test set is 0.9477, which is close to 1, signifying a stronger correlation between the predicted and the actual values and reflecting improved model performance.

Figure 7.
The fitting effect of printing quality.
This relationship is illustrated in Figure 8, which depicts the effects of various parameters on the overall printing quality. This 3D diagram highlights the intricate connections among temperature, velocity, concentration, and mass, using different colors to represent specific numerical values related to print quality. As the temperature, speed, and concentration fluctuate, the quality also demonstrates corresponding trends, providing valuable insights for parameter optimization and enhancing quality.
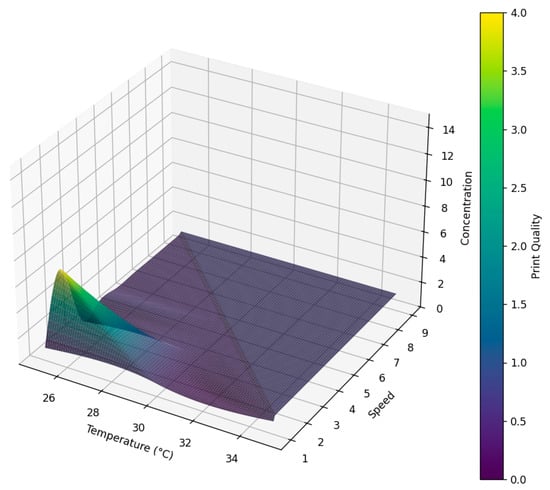
Figure 8.
Printing quality generated by different parameters.
The printing quality assessment demonstrates strong results with the optimal network structure, further validating the model’s predictive accuracy. Moreover, when the ambient temperature is held constant, the impact of printing speed on quality is minimal, while the effect of the printing concentration on printing quality exhibits considerable variability. Conversely, when the printing speed is constant, the influences of the printing concentration and ambient temperature on quality become more pronounced. Additionally, under consistent conditions of ambient temperature and printing concentration, printing quality tends to decline as the printing speed increases.
4.2. Training and Prediction of the PSO-BP Model
The quality prediction model was constructed using a PSO-BP neural network architecture. This model incorporates input variables such as ambient temperature, printing speed, and printing concentration, with printing quality serving as the output variable. The model undergoes iterative training facilitated by the gradient descent algorithm, followed by validation. The parameters for the PSO were established as follows: a population size of 50, an inertia weight (ω) of 0.8, and learning factors (c1 and c2) both set at 2.0, with a total of 100 iterations. Upon completion of parameter configuration, 60 datasets were selected from a single experimental group, with 50 sets designated as training samples and 10 sets allocated for testing the model’s generalization performance. Figure 9 and Figure 10 illustrate the comparison between the actual values of the training samples and the corresponding predicted values.
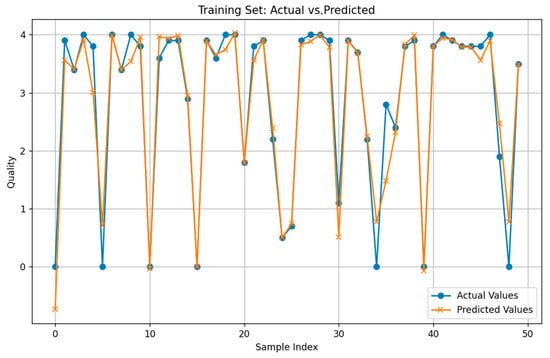
Figure 9.
The training of the PSO-BP model for printing quality.

Figure 10.
The prediction of the PSO-BP model for printing quality.
Figure 9 displays the training outcomes of the PSO-BP model for predicting quality. This research indicates that the predicted values are generally closer to the actual values at most points, demonstrating that the model’s strong predictive capability on the training dataset. Figure 10 illustrates how the PSO-BP model predicts print quality on the test dataset, with actual and predicted values closely aligning in certain samples. This alignment suggests that the model provides more accurate predictions at those points.
4.3. The Optimization of Models with Prediction
This study employed four distinct metrics to conduct a comprehensive assessment of the model’s predictive accuracy, namely, the R2 (coefficient of determination), MSE, RMSE, and Mean Absolute Error (MAE), as detailed in Table 8. Regarding the prediction of printing quality, the MAE is recorded at 0.1108, the RMSE at 0.145, the MSE at 0.021, and the R2 at 0.9916. The outcomes of the network training substantiate the stability and reliability of the neural network model developed using the PSO algorithm.

Table 8.
The result of the PSO-BP model.
To evaluate the predictive efficacy of the PSO-BP neural network model, this study selected ten sets of test samples for experimentation and validation. The experimental data, illustrated in Figure 11, indicate that the model attained an average absolute error of 2.77% in predicting printing quality. These findings substantiate the capability of the developed PSO-BP model to effectively forecast the nonlinear relationships among various influencing parameters on printing quality. The experimental results demonstrate that the model not only possesses a high degree of predictive accuracy but also exhibits robust generalization capabilities, allowing it to accurately predict printing quality.

Figure 11.
Ten sets of data for experiments and verification.
4.4. Summary
Regarding comparisons with various algorithms, considering the actual needs and feasibility of the current situation, we will expand this section in future research to gain a deeper understanding of the advantages of various algorithms. First, this study used traditional BP for analysis, followed by comparison with BP-PSO to enhance the model’s accuracy. The accuracy comparison of BP-PSO is shown in Figure 12. The findings indicate that the BP-PSO model is more suitable for predicting printing quality.

Figure 12.
A comparison of the accuracy between BP and BP-PSO.
This research indicates that the PSO-BP model for thermal barcode printing demonstrates significant advantages in parameter application within specific domains, as well as the practical viability of the algorithms in real-world scenarios. In terms of parameter application in specialized fields, the PSO-BP model exhibits the ability to adapt to dynamic thermal fluctuations in real time and is compatible with hardware suited for existing production environments. Furthermore, it shows robust convergence even with limited training data, a common characteristic in industrial settings. The model’s capabilities minimize the response time, reduce the carbon footprint of production, and facilitate interpretable parameter adjustments, such as production debugging. This will enable the rapid establishment of an optimized printing environment.
In terms of algorithmic feasibility, the PSO approach requires only an objective function (fractional values that reflect printing quality) and does not depend on precise mathematical models. This method facilitates the implementation of predictive conditions that are crucial for real-world industrial applications, especially in situations where accurately simulating thermal printing parameters is challenging. The penalty function of the model can directly incorporate maximum temperature and pressure limits, allowing for flexible constraint management without the need for reprocessing. Furthermore, the concurrent investigation of multiple parameter combinations by various particles can significantly reduce the time needed for experimental trials and lead to a faster convergence rate compared to sequential techniques, such as grid search.
Following the training of the model and its subsequent validation in thermal printing, the PSO-BP model introduced in this study demonstrates significant applicability and practical importance. Consequently, this paper presents three key findings.
- (1)
- Rapid debugging and optimization settings.
In the stage of production and commissioning for thermal printing, the PSO-BP model can efficiently determine the optimal combination of printing parameters. By inputting various factors, such as printing speed, temperature, and concentration, the model can predict the resulting printing quality. This assists operators in quickly identifying parameter configurations that meet standards of quality, reducing debugging time, and enhancing overall production efficiency.
- (2)
- Real-time observation and feedback.
While thermal printers are in operation, the PSO-BP model can be employed to monitor print quality in real time. By consistently gathering data on printing parameters and print quality, the model can make real-time adjustments to these parameters to maintain high printing quality. Additionally, the model provides immediate feedback on printing quality, assisting operators in identifying and addressing potential quality issues.
- (3)
- Quality control and assessment.
The PSO-BP model is applicable in the quality control of thermal printers for assessing the quality of printed barcodes. By inputting data on various influencing factors, it can effectively predict the printing quality of the barcode and assign an appropriate quality rating. This enables production staff to quickly identify and resolve quality issues, thereby ensuring product reliability and consistency while enhancing customer satisfaction.
- (4)
- Dynamic Parameter Optimization.
As production settings and material properties change, the parameters of thermal printers must be adjusted accordingly. The PSO-BP model can re-optimize these parameters in response to new production conditions and material characteristics, ensuring that printing quality consistently remains at an optimal level. This ability enables thermal printers to adapt to various complex and changing environments, thereby maintaining stable printing quality.
In summary, the PSO-BP model has extensive applications in thermal printing. It enhances the accuracy of predicted printing quality and production efficiency while also offering strong support for quality control and advancements within the printing industry.
5. Conclusions
Thermal-sensitive barcodes are widely used in areas such as commodity distribution and logistics management, where the quality of their printing significantly impacts information accuracy and circulation efficiency. Improving prediction accuracy and refining the printing process can help minimize errors and losses associated with barcode quality issues, thereby enhancing overall operational efficiency. As neural network technology continues to advance, research focused on predicting the printing quality of thermal barcodes through advanced PSO-BP neural networks aligns with technological trends and provides innovative solutions to the practical challenges of barcode printing quality. This study investigates the structure, algorithms, and parameter designs of BP neural networks to conduct comprehensive experiments aimed at achieving optimal results under various conditions. The model considers multiple influencing factors to accurately forecast the printing quality of thermal-sensitive barcodes, which can lead to increased production efficiency and higher customer satisfaction. Furthermore, this research can serve as a valuable reference for the thermal printing industry regarding material selection and equipment maintenance strategies.
This research demonstrates promising outcomes in predicting printing quality by using BP-PSO. However, the inclusion of data volumes and multiple parameters presents some challenges for industrial applications. In the future, we will aim to identify superior models to expand the range of data collected from manufacturers, including substrate materials and ambient humidity. The goal is not only to enhance but also to optimize energy efficiency and minimize material waste. Consequently, our research will focus on multi-objective algorithms to derive production parameters that align with low-carbon and energy-saving principles, making it more beneficial for industrial applications.
Author Contributions
Conceptualization, C.-L.H.; methodology, Z.W. and S.Q.; validation, C.-L.H. and T.-C.C.; formal analysis, Z.W.; resources, Z.W.; data curation, T.-C.C. and S.Q.; writing—original draft preparation, Z.W.; writing—review and editing, C.-L.H. and S.Q.; visualization, T.-C.C.; supervision, C.-L.H.; funding acquisition, C.-L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, J.; Ma, Y.; Han, Z.; Wang, Q.; Ma, T. Thermal design of printed circuit heat exchanger used for lead-bismuth fast reactor. Appl. Therm. Eng. 2023, 226, 120343. [Google Scholar] [CrossRef]
- Jiao, X.; Ren, G.; Law, C.L.; Li, L.; Cao, W.; Luo, Z.; Pan, L.; Duan, X.; Chen, J.; Liu, W. Novel strategy for optimizing of corn starch-based ink food 3D printing process: Printability prediction based on BP-ANN model. Int. J. Biol. Macromol. 2024, 276, 133921. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Zhong, Z.; Fu, C. Research of on-line printing quality detection based on mathematical morphology. Packag. J. 2013, 5, 35–39. [Google Scholar] [CrossRef]
- Sun, H.W.; Huang, Y.C.; Tang, T.H.; Shen, J.; Gu, L.J.; Wang, J.S. A prediction model for the replication quality of nanoimprinting patterns based on BP neural network. Microsyst. Technol. 2025. [Google Scholar] [CrossRef]
- Wei, X.J.; Zou, N.; Li, Z. PolyJet 3D printing: Predicting color by multilayer perceptron neural network. Ann. 3D Print. Med. 2022, 5, 100049. [Google Scholar] [CrossRef]
- Bao, Y.; Li, L.; Chen, J.; Weiwei Cao Liu, W.; Ren, G.; Luo, Z.; Pan, L.; Duan, X. Prediction of 3D printability and rheological properties of different pineapple gel formulations based on LF-NMR. Food Chem. X 2024, 24, 101906. [Google Scholar] [CrossRef] [PubMed]
- Jun, J. A train F-TR lock anti-lifting detection method based on improved BP neural network Journal of Measurements in Engineering. J. Meas. Eng. 2024, 12, 149–161. [Google Scholar]
- Miao, H.T.; Zhang, L.Z. The color characteristic model based on optimized BP neural network. In Advanced Graphic Communications, Packaging Technology and Materials; Springer: Singapore, 2016; Volume 369, pp. 55–63. [Google Scholar]
- Wu, X.; Wang, S. Prediction of ink flow for 3D bioprinting of tubular tissue based on a back propagation neural network. J. Comput. Methods Sci. Eng. 2023, 23, 3071–3080. [Google Scholar] [CrossRef]
- Li, Y.; Ding, F.; Tian, W. Optimization of 3D printing parameters on deformation by BP neural network algorithm. Metals 2022, 12, 1559. [Google Scholar] [CrossRef]
- Lin, Z.; Fan, Y.; Tan, J.; Li, Z.; Yang, P.; Wang, H.; Duan, W. Tool wear prediction based on XGBoost feature selection combined with PSO-BP network. Sci. Rep. 2025, 15, 3096. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, L.; Wang, L. Urban virtual environment landscape design and system based on PSO-BP neural network. Sci. Rep. 2024, 14, 13747. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yang, D.; Chen, R.J.; Li, K.; Zhou, X. Research on quality prediction of POI based on KPCA-GA-BP neural network. J. Telecommun. Sci. 2023, 39, 108–116. [Google Scholar]
- Wei, H.; Tang, L.; Qin, H.; Wang, H.; Chen, C.; Li, Y.; Wang, C. Optimizing FDM 3D printing parameters for improved tensile strength using the Takagi–Sugeno fuzzy neural network. Mater. Today Commun. 2024, 38, 108268. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Visan, A.I.; Ristoscu, C.; Mihailescu, I.N. Artificial neural network algorithms for 3D printing. Materials 2020, 14, 163. [Google Scholar] [CrossRef]
- Janmanee, P.; Ratchapakdee, P. Comparison of artificial neural network and response surface methodology in predicting the tensile strength and optimization of 3D printed objects. Eng. Appl. Sci. Res. 2024, 51, 704–715. [Google Scholar]
- Djurović, S.; Lazarević, D.; Ćirković, B.; Mišić, M.; Ivković, M.; Stojčetović, B.; Petković, M.; Ašonja, A. Modeling and prediction of surface roughness in hybrid manufacturing–milling after FDM using artificial neural networks. Appl. Sci. 2024, 14, 5980. [Google Scholar] [CrossRef]
- Bauer, M.; Augenstein, C.; Schäfer, M.; Theile, O. Artificial Intelligence in Laser Powder Bed Fusion Procedures–Neural Networks for Live-Detection and Forecasting of Printing Failures. Procedia CIRP 2022, 107, 1367–1372. [Google Scholar] [CrossRef]
- Phillip, L. Predicting the Failure of a Thermal Print-Head Resistor. Ph.D. Thesis, University of Portsmouth, Portsmouth, UK, 2019. [Google Scholar]
- Rafieyan, S.; Ansari, E.; Vasheghani-Farahani, E. A practical machine learning approach for predicting the quality of 3D (bio)printed scaffolds. Biofabrication 2024, 16, 045014. [Google Scholar] [CrossRef]
- Olowe, M.; Ogunsanya, M.; Best; Hanif, Y.; Bajaj, S.; Vakkalagadda, V.; Fatoki, O.; Desai, S. Spectral features analysis for print quality prediction in additive manufacturing: An acoustics-based approach. Sensors 2024, 24, 4864. [Google Scholar] [CrossRef]
- Liu, B.; Chen, Y.; Xie, J.; Chen, B. Industrial printing image defect detection using multi-edge feature fusion algorithm. Complexity 2021, 2021, 036466. [Google Scholar] [CrossRef]
- Bai, W.G.; Qiu, C.L.; Zhang, J. Research on evaluation and detection method of print quality based on the CCD information. Appl. Mech. Mater. 2013, 303–306, 543–549. [Google Scholar] [CrossRef]
- Karina, Z.; Hoeppener, S. Schubert, Inkjet printing and 3D printing strategies for biosensing, analytical, and diagnostic applications. Adv. Mater. 2022, 34, 2105015. [Google Scholar]
- Nguyen, Q.T.; Mai, A.; Chagas, L.; Nadège, R.B. Microscopic printing analysis and application for classification of source printer. Comput. Secur. 2021, 108, 102320. [Google Scholar] [CrossRef]
- Ratnavel, R.; Viswanath, S.; Subramanian, J.; Selvaraj, V.K.; Prahasam, V.; Siddharth, S. Predicting the optimal input parameters for the desired print quality using machine learning. Micromachines 2022, 13, 2231. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Kang, R.; Sun, J.S. A fast self-calibration method of line laser sensors for on-machine measurement of honeycomb cores. Opt. Lasers Eng. 2022, 152, 106981. [Google Scholar] [CrossRef]
- Jie, L.; Cai, Z.Q.; Yao, B. Error compensation and accuracy analysis of laser measurement system based on laser-beam calibration. Optik 2020, 200, 163272. [Google Scholar]
- Yang, L.X.; Zhou, W.M. Study on precision of PS/ABS composite powders formed parts based on selective laser sintering. China Plast. Ind. 2017, 45, 35–38. [Google Scholar]
- Bo, F.X.; He, B.; Zong, X.M. Experimental study on selective laser sintering of coated sand. Laser Optoelectron. Prog. 2017, 54, 247–253. [Google Scholar]
- Brion, D.A.J.; Pattinson, S.W. Quantitative and real-time control of 3D printing material flow through deep learning. Adv. Intell. Syst. 2022, 4, 2200153. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).