Abstract
As robots become increasingly integrated into society, a future in which humans and robots collaborate is expected. In such a cooperative society, robots must possess the ability to predict human behavior. This study investigates a human–robot cooperation system using RoboCup soccer as a testbed, where a robot observes human actions, infers their intentions, and determines its own actions accordingly. Such problems have typically been addressed within the framework of multi-agent systems, where the entity performing an action is referred to as an ‘agent’, and multiple agents cooperate to complete a task. However, a system capable of performing cooperative actions in an environment where both humans and robots coexist has yet to be fully developed. This study proposes an action decision system based on self-organizing maps (SOM), a widely used unsupervised learning model, and evaluates its effectiveness in promoting cooperative play within human teams. Specifically, we analyze futsal game data, where the agents are professional futsal players, as a test case for the multi-agent system. To this end, we employ Tensor-SOM, an extension of SOM that can handle multi-relational datasets. The system learns from this data to determine the optimal movement speeds in x and y directions for each agent’s position. The results demonstrate that the proposed system successfully determines optimal movement speeds, suggesting its potential for integrating robots into human team coordination.
1. Introduction
Robots and computer systems are well known for their ability to efficiently perform predefined and repetitive tasks. While this capability has facilitated widespread use in structured environments, these systems often struggle when confronted with dynamic or ambiguous situations [1,2]. To improve adaptability and decision-making in such contexts, many studies have focused on incorporating biologically inspired information processing methods. Among them, soft computing techniques—such as neural networks, fuzzy logic, and genetic algorithms—have shown significant potential in addressing the limitations of conventional approaches [3,4].
In addition to enhancing individual robot performance, there has been growing interest in multi-agent systems (MAS) and multi-robot systems (MRS), where multiple agents cooperate to solve complex tasks. MAS are composed of autonomous agents that interact with each other and with the environment to achieve common goals, typically based on local observations and real-time decision-making.
Although centralized control systems are often used to coordinate such agents due to their simplicity and effectiveness, they may lack scalability and robustness in dynamic environments. Enhancing the autonomy of individual agents is essential for achieving more flexible and decentralized coordination [5]. However, developing fully autonomous robots remains a challenging task, requiring capabilities such as motion control, environmental perception, and self-localization [6,7].
Despite advancements in learning-based algorithms and soft computing techniques, real-world deployment of Human–Robot Interaction (HRI) and Multi-Agent Systems (MAS) continues to face significant challenges. In HRI, issues such as reproducibility, generalizability across different contexts, and ethical considerations—including trust, privacy, and user acceptance—remain critical concerns [8,9]. Similarly, MAS implementations often grapple with problems like communication delays, partial observability, and scalability, which can hinder effective coordination and decision-making among agents [10]. Addressing these challenges is essential for the successful integration of robotic systems into dynamic and unstructured real-world environments.
The domain of soccer, especially in the context of human actions, provides a rich and dynamic testbed for developing and evaluating autonomous decision-making systems. Human soccer behavior is inherently multi-agent, strategic, and responsive to fast-changing conditions—qualities that closely mirror many real-world scenarios where autonomous robots are expected to operate, such as search and rescue, autonomous driving, and logistics. By modeling robot behavior based on human-like soccer interactions, we can simulate and study complex coordination, competition, and adaptation under uncertainty. This not only challenges the agents in a controlled, replicable environment like RoboCup but also yields transferable insights that can improve real-world robotic applications requiring teamwork, perception, and decision-making under constraints.
The RoboCup Soccer competition serves as a representative MAS testbed, providing a dynamic and interactive environment for testing cooperative decision-making strategies. In particular, the RoboCup Middle Size League (MSL) features soccer-playing robots that must interpret complex sensor data, recognize their state and surroundings, and determine appropriate actions during a match. Recent approaches have employed learning-based methods, including reinforcement learning and neural networks, to address these challenges.
This study focuses on the use of Self-Organizing Maps (SOM), an unsupervised neural network model, to develop a behavior decision-making system for MSL soccer robots. SOM is capable of dimensionality reduction and feature extraction, making it suitable for interpreting high-dimensional sensor data and recognizing relevant environmental patterns [11].
Furthermore, to analyze team dynamics and cooperative behavior, we address relational data—large-scale data characterized by interdependent elements. For this purpose, we employ the Tensor Self-Organizing Map (Tensor-SOM), an extension of SOM that enables interpolation and modeling of complex input-output relationships in multidimensional spaces. Tensor-SOM allows for intuitive visualization of team behaviors and facilitates understanding of coordinated decision-making processes [12,13].
However, one important consideration in robot soccer, which involves dynamic physical interactions and motion constraints, is whether approximation methods could serve as a viable alternative for behavior decision-making. While current methods like Self-Organizing Maps (SOM) and Tensor-SOM are powerful in analyzing relational data and team dynamics, there remains the question of whether interpolation-based or approximation-based neural network approaches might provide more interpretable and physically consistent frameworks for robot behavior modeling.
Recent studies have explored the potential of interpolation and approximation methods, which are capable of maintaining consistency with physical constraints and enhancing the interpretability of learned behaviors. For example, methods based on approximation models have been shown to offer valuable insights in scenarios where dynamic adjustments are needed, and they may also improve the overall understanding of agent interactions in constrained environments. These approaches could be particularly beneficial in environments such as robot soccer, where motion constraints and the need for real-time decision-making are central to effective coordination and behavior generation.
Several recent studies have examined these ideas. For instance, [14] have proposed an approximation-based framework for decision-making under motion constraints, while [15] explored the use of interpolation methods for improved behavior prediction and decision consistency in dynamic environments. Incorporating such methods into multi-agent systems could enhance both the efficiency and interpretability of the robots’ decision-making processes.
In this study, we primarily focus on the Tensor-SOM model for behavior decision-making, but future work will consider the integration of approximation-based methods to further improve the system’s interpretability and physical consistency in dynamic, real-world scenarios.
The main contributions of this paper are as follows:
- We propose a behavior decision system for autonomous agents using SOM.
- We introduce Tensor-SOM to analyze relational data and interpret team dynamics.
- We evaluate the system’s effectiveness in the context of RoboCup MSL through experiments.
The remainder of this paper is structured as follows: Section 2 describes the design of agent behavior decision algorithms. Section 3 introduces SOM as a behavior decision-making method. Section 4 presents the Tensor-SOM model and its properties. Section 5 evaluates performance in terms of data completion and interpolation. Section 6 outlines the learning of input-output relationships. Section 7 reports experimental results and analysis. Section 8 concludes the study and discusses future work.
2. Development of Algorithms for Agent Behavior Determination
Previous studies have analyzed the determinants and methodologies for agent behavior decision-making within multi-agent systems (MAS). It has been suggested that, for both humans and robotic agents, the relationships with other agents at a given moment serve as crucial factors influencing behavioral decisions [16].
Moreover, various algorithms for behavior determination have been investigated, with particular attention paid to the application of Tensor Self-Organizing Maps (Tensor-SOM). This approach has demonstrated potential in mapping sequences of behaviors in a structured and interpretable manner [17].
A promising method for facilitating mutual learning among agents involves the use of tensor data. Tensor data, often referred to as relational data [18], are widely utilized in big data analytics and are especially effective in handling data characterized by high diversity and complexity. By employing tensor representations, it becomes possible for individual agents to influence each other’s learning processes, even under identical environmental conditions. Such mutual influence can foster the emergence of novel behavioral strategies. The greater the number and diversity of agents and scenarios involved in training, the more extensive and diverse the learned behavior repertoire becomes. Consequently, an algorithm with robust interpolation capabilities is desirable.
This property is particularly advantageous not only for robotic agents but also when integrating human soccer behavior data, where an increased volume and density of data contribute to more effective learning outcomes. In this study, we developed a behavior determination algorithm based on the Self-Organizing Map (SOM) framework, aiming to exploit the advantages of tensor-based learning in MAS environments.
In the context of RoboCup, numerous studies have focused on the development and refinement of agent behavior models to enable effective team coordination and decision-making in dynamic, adversarial environments. For example, early RoboCup teams widely employed rule-based systems and finite state machines to encode predefined strategies and reactive behaviors [19]. Although these methods offer robustness in controlled situations, they exhibit limited adaptability to unforeseen scenarios.
In recent years, machine learning approaches—particularly those based on reinforcement learning and neural network architectures—have been adopted to enhance agents’ adaptability and decision-making abilities [20,21]. These techniques allow agents to acquire optimal actions through interactions with both their environment and teammates, thereby reducing reliance on hand-crafted rules.
Furthermore, several studies have incorporated models that account for the spatio-temporal dynamics of the game—such as opponent positioning and ball trajectories—as core inputs for behavior generation [22]. These models have significantly improved agents’ strategic awareness, resulting in more context-sensitive decision-making.
Despite these advancements, accurately capturing the relational complexity among agents under varying game contexts remains a significant challenge. This limitation underscores the potential of tensor-based approaches, such as Tensor-SOM, which are capable of modeling and leveraging multidimensional relationships among agents, actions, and temporal sequences in a scalable and interpretable manner.
3. SOM as a Behavior Decision Algorithm
Self-Organizing Maps (SOMs) are capable of representing the structural features of input vectors on a competitive layer through unsupervised learning, and support fast vector quantization using nearest neighbor learning. However, due to the absence of an explicit output mechanism, SOMs cannot directly model input-output relationships.
To address this limitation, various SOM-based approaches have been proposed to approximate input-output mappings while maintaining key characteristics such as topological preservation. Representative examples include counter-propagation networks [23], Local Linear Mapping (LLM) [24], and Vector-Quantized Temporal Associative Memory (VQAM) [25], which have been applied in fields such as system modeling [26], filter design [27], control [28], and chemical analysis [29]. These methods, however, rely on supervised learning using teacher signals, and are therefore unsuitable when such signals are unavailable.
To enable learning without explicit supervision, the Self-Organizing Relationship (SOR) network was proposed. SOR uses input-output vector pairs along with evaluation values obtained through trial-and-error to self-organize input-output mappings through competitive learning. Meanwhile, the Modular Network SOM (mnSOM) extends SOM by replacing each unit with a trainable function module, such as a neural network [30]. This modular design allows mnSOM to represent functional mappings and flexibly adapt to various data types and training objectives.
The TensorSOM framework integrates the key ideas of both mnSOM and SOR: it inherits the modular, function-oriented architecture of mnSOM, and the trial-and-error-based self-organizing learning approach of SOR. In the present study, we utilize TensorSOM to develop a behavior decision algorithm that can operate effectively under dynamic environmental conditions. By leveraging TensorSOM’s ability to flexibly handle structured input-output relationships and perform unsupervised learning based on evaluative feedback, we aim to construct a decision-making framework that is adaptive, modular, and capable of learning from experience without the need for explicit supervision.
The proposed method is designed to learn adaptive behavior selection strategies through interactions with a changing environment. The overall framework is described in the following section.
In behavior decision-making algorithms operating under dynamic environmental conditions, it is essential that decisions be made in real time. Although the learning process of SOM and TensorSOM can require substantial time depending on the number and dimensionality of the input data as well as the number of training iterations, once training is completed, the model provides immediate one-to-one mapping from input to output. This property ensures that response times during deployment are effectively instantaneous. Furthermore, the modular structure of TensorSOM allows for the quick incorporation of new input patterns, enabling rapid adaptation and continual learning even after initial training.
4. Tensor-SOM
In a standard Self-Organizing Map (SOM), a single map is generated from a single dataset. However, in many real-world applications, it is desirable to generate multiple maps simultaneously to capture more complex and structured data.
For instance, when analyzing animal-specific feature vectors, SOM can be employed to visualize and cluster animals based on their characteristics. However, if we further incorporate the temporal aspect—i.e., how these characteristics evolve with age—the amount of data per subject increases significantly. Such data, which span multiple relational dimensions (e.g., features over time), are referred to as relational data. Instead of handling the data as a simple one-dimensional array, we can model it as a two-dimensional relation tensor, with one axis representing features and the other representing time (or age). This approach not only enables the extraction of richer patterns from the data but also supports learning of complex input-output relationships.
In this context, the Tensor Self-Organizing Map (Tensor-SOM)—an extended SOM model incorporating concepts from SOR and mnSOM—proves highly effective. In this study, we utilize Tensor-SOM to develop both an action learning system and an action selection system tailored to high-dimensional relational data.
4.1. Tensor-SOM Data Structure
To clarify how Tensor-SOM works, let us consider an example dataset consisting of feature evaluations of animals at different ages. In this dataset, each animal is associated with a set of features that are measured at multiple time points. Here, “animal” is referred to as the first mode, and “age” as the second mode of the data structure. Suppose each animal is evaluated on D features at each age. Then, the feature vector for animal i at age j is a D-dimensional vector . The entire dataset can thus be represented as a third-order tensor:
where I is the number of animals, J is the number of age points, and D is the feature dimension.
4.2. Structure of Tensor-SOM
Tensor-SOM constructs two self-organizing maps, each corresponding to one mode of the tensor. The map for the first mode (animals) consists of K units, indexed by , and the map for the second mode (ages) consists of L units, indexed by .
In addition to the maps, Tensor-SOM includes a set of primary models, which can be understood as sub-SOMs responsible for modeling data in each mode. For example, for a specific animal i, we consider the series of feature vectors as a dataset representing that animal over time. This is modeled as:
which can be interpreted as a temporal model for animal i, and constitutes the primary model for the first mode.
Conversely, for a specific age j, we use the data to model the distribution of animal features at that age. This results in:
which represents the animal model restricted to age j, forming the primary model for the second mode. At the beginning of the algorithm, both and are initialized with random values to ensure non-deterministic starting conditions and to avoid biasing the learning process.
4.3. Reference Vectors in Tensor-SOM
In conventional SOM, each unit is associated with a single reference vector. In contrast, Tensor-SOM assigns one reference vector to each unit pair , corresponding to one point in the two-dimensional map space formed by the two modes. As a result, the model contains reference vectors in total, forming a third-order tensor:
The reference tensor is also randomly initialized to ensure unbiased and exploratory learning at the initial stage.
4.4. Advantages of Tensor-SOM
By structuring the model in this way, Tensor-SOM is capable of learning and visualizing complex interactions across two relational dimensions—such as “animal” and “age”—in a manner that is both computationally efficient and intuitively interpretable. This makes it an ideal approach for relational data analysis, where multi-dimensional dependencies play a crucial role in understanding the underlying patterns.
4.5. Algorithm of Tensor-SOM
The algorithm is briefly described in three steps: deciding the best matching unit, calculation of the amount of learning, and model update. Figure 1 presents an overview of the Tensor-SOM architecture along with an illustrative example. As shown in the figure, once the Best Matching Unit (BMU) is determined, the amount of weight update for each unit is computed accordingly. Subsequently, all associated models are updated based on these computed learning rates.
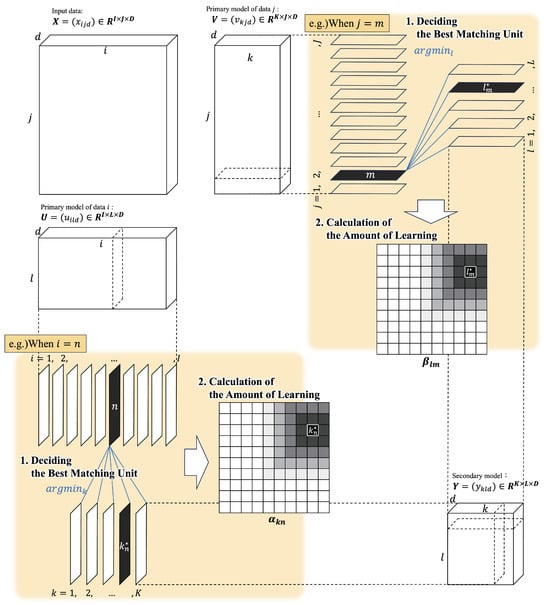
Figure 1.
Schematic Overview of the Tensor-SOM Framework (specific examples are indicated by the colored boxes).
4.5.1. Deciding the Best Matching Unit
4.5.2. Calculation of the Amount of Learning
Equations (3) and (4) are used to calculate the amount of learning. is the change in units near the BMU with respect to mode 1, and is the change with respect to mode 2.
In this context, and denote the Euclidean distances within the secondary model between the best matching units (BMUs), referred to as (for mode 1) and (for mode 2), and all other units in their respective modes, denoted as k and l.
4.5.3. Model Update
- Secondary Model Update
- Primary Model Update
These three steps are repeated while the neighborhood radius, , , are monotonically decreased according to the time constant, from to .
5. Tensor-SOM Completion and Interpolation Performance
Tensor-SOM has the same interpolation capabilities as SOM and can interpolate between training data for each mode for data related to two modes. In addition, missing values can be estimated even for data with missing values in the input data. Tensor-SOM also has interpolation performance for unlearned values, and if the input-output relationship is learned, the output can always be uniquely determined for the input. Here, Tensor-SOM trains 3D point clouds on five planes, and the results are shown. The five planes used for training are shown in the following Equations (10)–(14), and the 3D point clouds are random x and y coordinate values (, ) and the z coordinate value () calculated at that time by Equations (10)–(14).
The flow for estimating missing values using Tensor SOM is shown in Figure 2. First, as a learning process, the Tensor SOM is trained with 3D data for each point in all five planes. Then, the z coordinates are obtained by inputting the x,y coordinates into the model obtained by learning. The parameters used for learning are shown in Table 1.
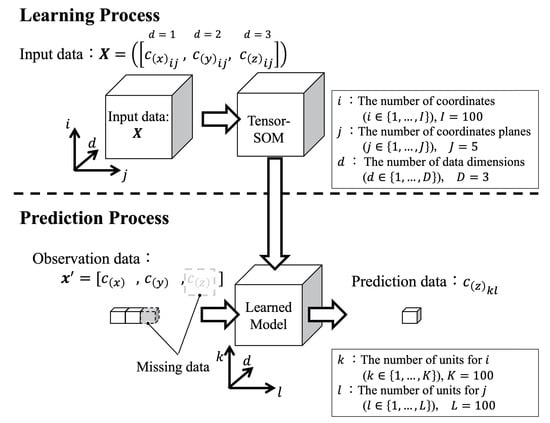
Figure 2.
Model flow for missing value completion using Tensor SOM.

Table 1.
Tensor-SOM learning parameters for complementary performance evaluation experiments.
Tensor-SOM Interpolation Performance Verification Results
To compare the results of Tensor-SOM and SOM, we also trained SOM under the same conditions. Figure 3 and Figure 4 show the point clouds and their approximate curves when Tensor-SOM and SOM were trained and was estimated for new and .
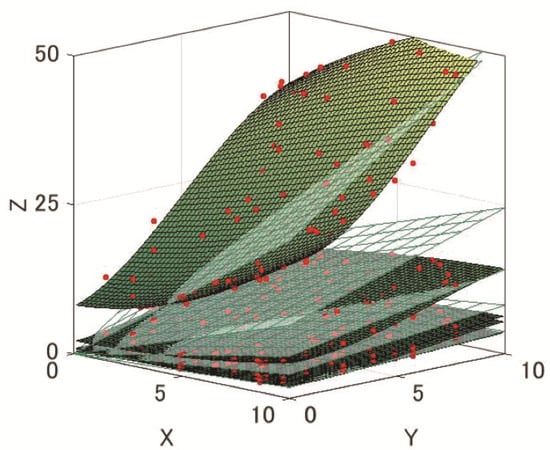
Figure 3.
Point cloud estimated by SOM and approximate curved surface.

Figure 4.
Point cloud estimated by Tensor-SOM and approximate curved surface.
Figure 4 can be compared for the estimation of the SOM and Tensor-SOM Z coordinate, and it is clear that Tensor-SOM has better accuracy of prediction. Thus, we can say that Tensor-SOM has higher completion and interpolation performance than SOM with respect to multiple related data.
6. Development of a Decision Making System by Learning Input-Output Relationships
We developed a system that can learn the input-output relationship by learning the parameters in the input-output relationship as a single vector element, and can acquire actions when environmental information is input as input information. The data acquisition method in the developed decision-making system is shown in Figure 5.
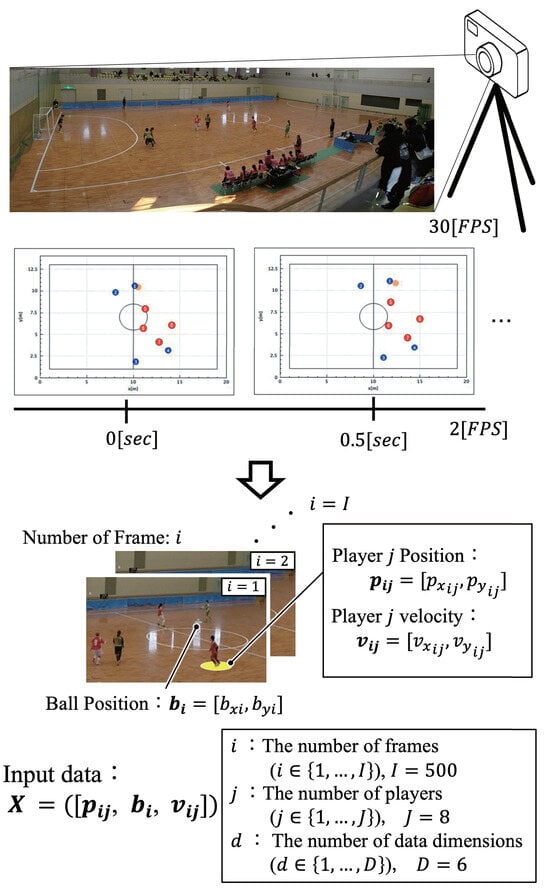
Figure 5.
Data acquisition methods in decision-making systems.
First, the learning process involves learning the position of the agent, the position of the ball, and the speed of the agent’s movement, which are directly related to the action taken from the video data. Secondly, only the agent position and ball position are input to the learned Tensor-SOM model, and the output is generated by Tensor-SOM’s complementary performance with respect to the agent’s movement speed.
System Evaluation Experiment
An evaluation experiment of the system was conducted. The target was a female futsal team, and match data was recorded using a video camera to obtain the position coordinates of each agent. Evaluation experiments were conducted on the basis of these data. The input vector is shown in the Equation (15). The video was taken at 30 fps, of which the actual analysis data used was 2 fps. In this analysis, the x-axis is the longitudinal direction of the field, and the y-axis refers to the shortitudinal direction of the field.
Note that and are the absolute coordinates of the agent and the ball on the field, respectively, and is the agent’s velocity vector of movement, as shown in Equation (16). Also, i is the ID of the time series data.
Here, we use the position coordinates of the agents and except for the goalkeepers and 10, since we are targeting agents other than the goalkeepers in this case. For simplicity, the team consisting of agents with is the blue team, and the team consisting of agents with is the red team. In addition, data were discarded on the following selection criteria:
- A sequence of play from set play to shooting
- Throughout a single try, no substitutions of agents were performed
A try is a series of plays, from a single set piece to a shot. In this experiment, we used data from a total of 10 tries, all in completely different situations. The rationale behind this condition is to exclude behaviors that occur during out-of-play situations—such as agent substitutions or instances where the ball leaves the field—in order to prevent non-goal-directed actions from being treated as noise. This ensures that the analysis focuses solely on actions relevant to the primary objective of the futsal match, namely, shooting the ball toward the opponent’s goal.
To show that all tries were in completely different situations, the ball trajectory data for all situations is shown in Figure 6. The red dot is the coordinate at which the TRY was started, and the green dot is the coordinate at which the TRY ended (the coordinate of the shooting point).
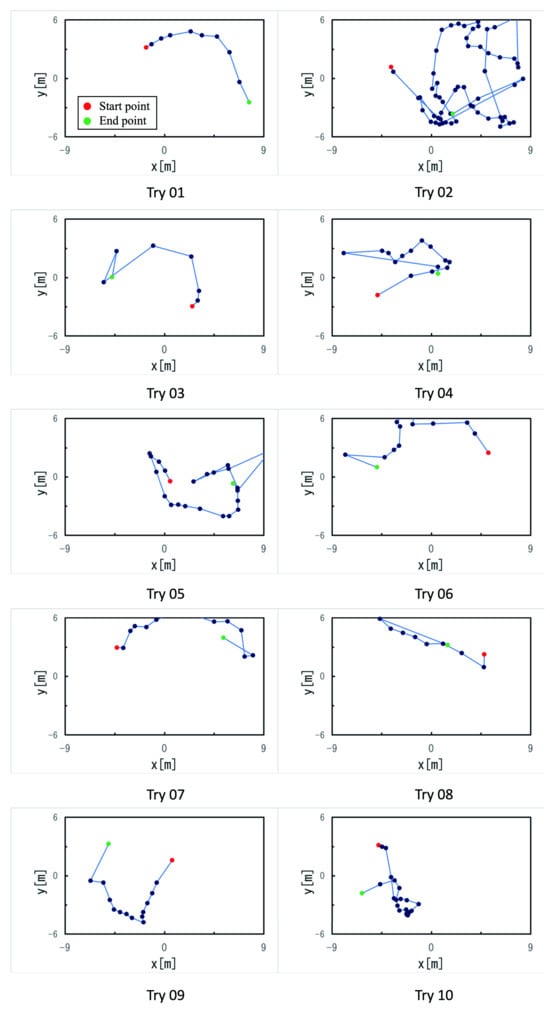
Figure 6.
Trajectory data of the ball for all 10 total tries(red dot for start, green dot for end).
Table 2 shows the parameters. Figure 7 and Figure 8 show the learning convergence status. The average error of all units converged 1500 times, indicating that the learning of the input-output relationship by Tensor-SOM was completed.

Table 2.
Tensor-SOM learning parameters for the action acquisition system.
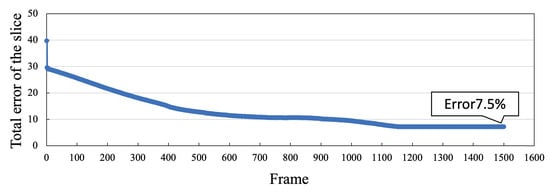
Figure 7.
Average Error per Unit (mode1 ) to Visualize Learning Convergence.
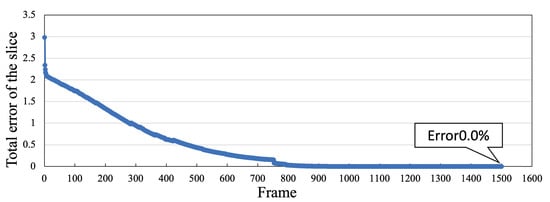
Figure 8.
Average Error per Unit (mode2 ) to Visualize Learning Convergence.
7. Experimental Results
As experimental results, we compared the moving speed of the agent actually used during training with the speed output when the system inputs environmental information after training. As a representative example, the results for the blue team with j = 1–4 are shown in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. Orange is the Agent’s movement speed during training, and blue is the result of the decision-making system using Tensor-SOM. These data are the same Frame clipped for each Agent from all data. Furthermore, the root mean square errors (RMSE) of and for each agent are presented in Table 2.
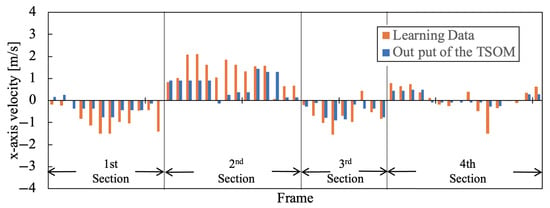
Figure 9.
according to the situation of .
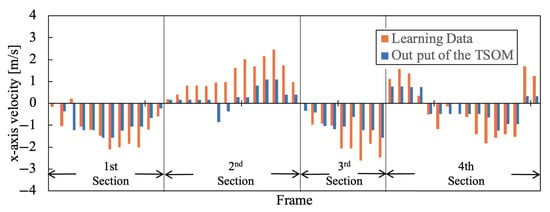
Figure 10.
according to the situation of .
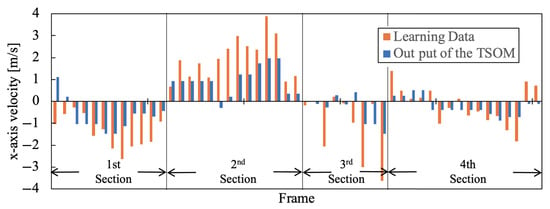
Figure 11.
according to the situation of .
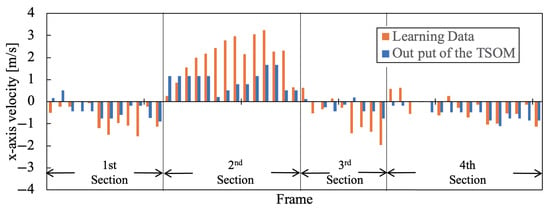
Figure 12.
according to the situation of .
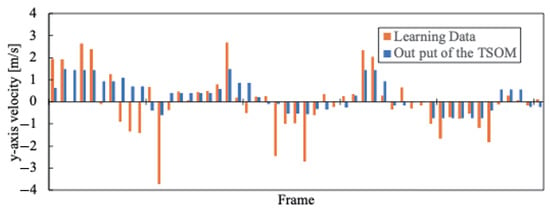
Figure 13.
according to the situation of .
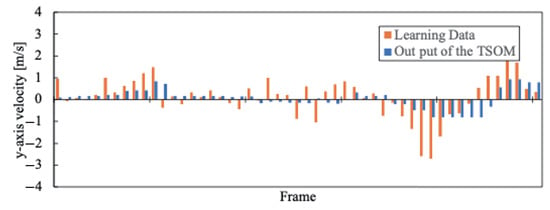
Figure 14.
according to the situation of .
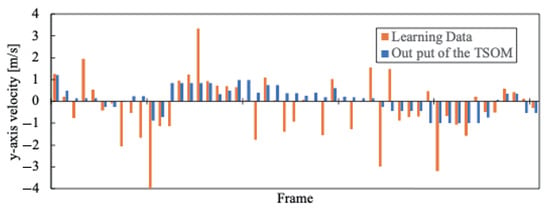
Figure 15.
according to the situation of .
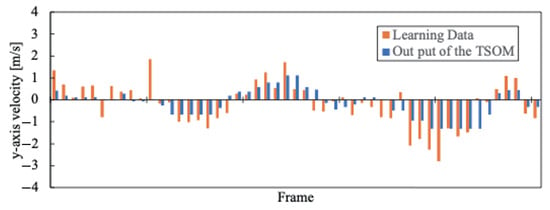
Figure 16.
according to the situation of .
First, as a decision-making system utilizing Tensor-SOM, unique output results were obtained for all inputs. This is an inherent characteristic of Tensor-SOM; however, it does not pose a problem as the system is capable of interpolating data that was not included in the training process and uniquely determining decisions.
The x-direction refers to the longitudinal direction of the field. The output results for velocity in the x-direction are characterized for each section, as shown in Figure 9, Figure 10, Figure 11 and Figure 12. The transition from the Section 1 to the Section 4 occurs where the velocity changes positively and negatively during the training of Tensor-SOM. We believe that these characteristics reflect whether the team is on offense or defense, depending on the game situation. Furthermore, the Tensor-SOM decision-making system exhibits a similar pattern, following these characteristics consistently from the Section 1 to the Section 3. However, in the Section 4, the positive and negative velocities vary among different agents. This is because each agent has a distinct role. Nevertheless, Tensor-SOM functions effectively as a decision-making system, successfully capturing and reflecting the unique characteristics of each agent.
On the other hand, the results for velocity in the y-direction are less effective in capturing the characteristics of the original data compared to those in the x-direction. We believe this is because the y-direction represents the shorter dimension of the field, and the direction in which an agent should move varies depending on their position and the specific game situation. As a result, the decision-making system deviates from the original training data in many aspects in the y-direction compared to the x-direction. This trend is quantitatively confirmed by the Root Mean Square Error (RMSE) values reported in Table 3. Although the difference is modest, the average RMSE for is consistently greater than that for , suggesting that the estimation performance for the component is comparatively superior. We believe this issue can be mitigated in the future by utilizing data that better captures these characteristics, such as representing velocity as a vector rather than decomposing it into x- and y-components.

Table 3.
Comparison of Root Mean Square Errors (RMSE) in the X and Y Velocity Components (, ) for Each Agent.
Additionally, the decision-making system, as a whole, does not reflect sudden changes in speed. This is likely due to the generalization property of Tensor-SOM, which could be improved by shortening the data acquisition period.
Several potential reasons are considered for why the decision-making system failed to predict some cases accurately. These are as follows:
- Influence of Other Agents: Since Tensor-SOM learns all agents simultaneously, the state of other agents may influence the prediction results. While this could introduce errors, it is not necessarily a problem. In fact, it reflects that the system is learning the collective behavioral tendencies of the team. By modeling the interactions between agents, the system can capture the team’s overall behavior pattern, which is useful in complex multi-agent environments for making decisions.
- Unmodeled Behavioral Factors: The prediction errors could be due to factors influencing agent behavior that are not included in the model. Specifically, individual decision-making strategies, physical characteristics, or external factors such as the agent’s condition on the day of the match may significantly influence behavior. These unmodeled factors could lead to discrepancies between predicted and actual behavior.
- Teamwork and Coordination: Improving prediction accuracy may require refining teamwork and coordination. If agents act in a more coordinated and unified manner, the predictions could become more accurate. Strengthening the team’s overall cooperation could lead to more predictable behavior and better system performance.
- Utilization of Detailed Agent Information: In this study, only information obtained from video data was used, which limits the understanding of agent behavior. Incorporating more detailed information about each agent, such as physical characteristics or condition on the day of the game, could significantly improve prediction accuracy. These additional factors could help deepen the understanding of agent behavior and reduce prediction errors.
These insights suggest that improving system performance requires the introduction of more detailed data, enhancing the learning process, and considering the interactions between multiple agents.
8. Conclusions and Future Work
Tensor-SOM effectively models team decision-making but struggles with sudden speed changes and y-direction movements.
The results presented in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 demonstrate that the system’s output (shown in blue) is largely consistent with the training data (shown in orange). However, the system’s output tends to be slightly lower on average. This discrepancy may be attributed to the simultaneous training of multiple agents, which could have led to the cancellation of individual agent characteristics. Further analysis is required to determine the extent to which this effect influences the overall performance of the model.
Additionally, the results indicate that the velocity component in the x-direction () is more accurately modeled than the velocity component in the y-direction (). This suggests that movement in the x-direction plays a more significant role in offensive and defensive strategies within the given context. The difference in modelability between these two velocity components highlights the importance of considering domain-specific movement characteristics when designing predictive models for robotic decision-making.
To improve the system’s accuracy, future work should explore methods to reduce the observed bias in the output and align it more closely with the values observed in the training data. One potential approach involves adjusting the learning process to better capture the unique characteristics of individual agents while maintaining generalization capability. Fine-tuning the training parameters or incorporating additional contextual information may further enhance the model’s predictive performance.
In this study, we developed an action acquisition system based on the Tensor Self-Organizing Map, which enables learning of input-output relationships through unsupervised training. Our findings confirm that Tensor-SOM successfully captures the underlying structure of the data, as demonstrated by the convergence of the learning process. These results suggest that Tensor-SOM is a viable approach for modeling complex human movement patterns and can be effectively applied to decision-making in autonomous robotic systems.
Moving forward, we aim to refine the proposed system by incorporating additional environmental factors and improving its adaptability to dynamic scenarios. Furthermore, extending this framework to real-time decision-making applications in robotics could pave the way for more sophisticated and responsive autonomous systems capable of interacting seamlessly with human teams.
Future work will also explore several important directions to enhance the practical applicability of the proposed system. First, we plan to incorporate and evaluate real-time learning capabilities, enabling agents to adapt their behavior dynamically in response to changing environments. Second, the system will be tested on larger-scale datasets to assess its scalability and generalization performance under more diverse and complex scenarios. Lastly, we aim to investigate the integration of Tensor-SOM with other learning frameworks, such as reinforcement learning, to examine potential synergies between unsupervised and reward-based learning paradigms. These extensions are expected to further improve the adaptability, robustness, and real-world applicability of the proposed approach.
Author Contributions
Conceptualization, K.I. and M.T.; methodology, M.T.; software, Y.T.; validation, M.T.; writing—original draft preparation, M.T.; writing—review and editing, K.I. and Y.T.; visualization, M.T.; supervision, K.I.; project administration, M.T.; funding acquisition, M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI Grant Number 24K20876.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank Fukuoka Futsal Federation for Providing match data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Swapna Rekha, H.; Nayak, J.; Naik, B.; Pelusi, D. Soft Computing in Robotics: A Decade Perspective. In Applications of Robotics in Industry Using Advanced Mechanisms; Nayak, J., Balas, V.E., Favorskaya, M.N., Choudhury, B.B., Rao, S.K.M., Naik, B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 59–78. [Google Scholar]
- Akbarzadeh-T, M.-R.; Kumbla, K.; Tunstel, E.; Jamshidi, M. Soft Computing for Autonomous Robotic Systems. Comput. Electr. Eng. 2000, 26, 5–32. [Google Scholar] [CrossRef]
- Velivela, A.; Shilpa, S.; Sagar, Y.A.; Reddy, M.S.R.L.; Rao, A.N.; Jyothi, N. Soft Computing Approaches in Robotics: State-of-the-Art and Future Directions. In Cybernetics, Human Cognition, and Machine Learning in Communicative Applications; Gunjan, V.K., Senatore, S., Kumar, A., Eds.; Springer Nature: Singapore, 2025; pp. 65–80. [Google Scholar] [CrossRef]
- Dzitac, S.; Nădăban, S. Soft Computing for Decision-Making in Fuzzy Environments: A Tribute to Professor Ioan Dzitac. Mathematics 2021, 9, 1701. [Google Scholar] [CrossRef]
- Mahanta, G.B.; Deepak, B.B.V.L.; Biswal, B.B. Application of Soft Computing Methods in Robotic Grasping: A State-of-the-Art Survey. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 236, 712–726. [Google Scholar] [CrossRef]
- Dong, L.; He, Z.; Song, C.; Sun, C. A Review of Mobile Robot Motion Planning Methods: From Classical Motion Planning Workflows to Reinforcement Learning-Based Architectures. arXiv 2021, arXiv:2108.13619. [Google Scholar] [CrossRef]
- Chen, C.; Wang, B.; Lu, C.X.; Trigoni, N.; Markham, A. A Survey on Deep Learning for Localization and Mapping: Towards the Age of Spatial Machine Intelligence. arXiv 2020, arXiv:2006.12567. [Google Scholar] [CrossRef]
- Gunes, H.; Broz, F.; Crawford, C.S.; der Pütten, A.R.V.; Strait, M.; Riek, L. Reproducibility in Human-Robot Interaction: Furthering the Science of HRI. Curr. Robot. Rep. 2022, 3, 281–292. [Google Scholar] [CrossRef]
- Etemad-Sajadi, R.; Soussan, A.; Schöpfer, T. How Ethical Issues Raised by Human–Robot Interaction Can Impact the Intention to Use the Robot? Int. J. Soc. Robot. 2022, 14, 1103–1115. [Google Scholar] [CrossRef]
- Nweye, K.; Liu, B.; Stone, P.; Nagy, Z. Real-World Challenges for Multi-Agent Reinforcement Learning in Grid-Interactive Buildings. Energy AI 2022, 10, 100202. [Google Scholar] [CrossRef]
- Berna, A.Z.; Trowell, S.; Clifford, D.; Cynkar, W.; Cozzolino, D. Pattern Recognition and Anomaly Detection by Self-Organizing Maps in a Multi Month E-nose Survey at an Industrial Site. Sensors 2020, 20, 1887. [Google Scholar] [CrossRef]
- Itonaga, K.; Yoshida, K.; Furukawa, T. Tensor Self-Organizing Map for Kansei Analysis. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 796–801. [Google Scholar] [CrossRef]
- Drakopoulos, G.; Giannoukou, I.; Mylonas, P.; Sioutas, S. On Tensor Distances for Self-Organizing Maps: Clustering Cognitive Tasks. In Database and Expert Systems Applications; Hartmann, S., Küng, J., Kotsis, G., Tjoa, A.M., Khalil, I., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 195–210. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Young, D.L.; Hon, Y.C.; Chen, C.S. Power-enhanced residual network for function approximation and physics-informed inverse problems. Appl. Math. Comput. 2024, 480, 128910. [Google Scholar] [CrossRef]
- Carriere, J.; Oliver, M.L.; Hamilton-Wright, A.; Young, C.; Gordon, K.D. Can Machine Learning Enhance Computer Vision-Predicted Wrist Kinematics Determined from a Low-Cost Motion Capture System? Appl. Sci. 2025, 15, 3552. [Google Scholar] [CrossRef]
- Tominaga, M.; Takemura, Y.; Ishii, K. Behavior Selection System for Human–Robot Cooperation using Tensor SOM. J. Robot. Netw. Artif. Life 2020, 7, 81–85. [Google Scholar] [CrossRef]
- Tominaga, M.; Takemura, Y.; Ishii, K. Behavior Learning System for Robot Soccer Using Neural Network. J. Robot. Mechatron. 2023, 35, 1385–1392. [Google Scholar] [CrossRef]
- Khosravi, H.; Bina, B. A Survey on Statistical Relational Learning. In Advances in Artificial Intelligence; Farzindar, A., Kešelj, V., Eds.; Springer: Berlin, Germany, 2010; pp. 256–268. [Google Scholar] [CrossRef]
- Riley, P.; Veloso, M. Planning for Team Behaviors in RoboCup Simulation. In Proceedings of the Fifth International Conference on Autonomous Agents, Montreal, QC, Canada, 28 May–1 June 2001; ACM: New York, NY, USA, 2001; pp. 295–296. [Google Scholar]
- Fukushima, T.; Nakashima, T.; Akiyama, H. Evaluation-Function Modeling with Multi-Layered Perceptron for RoboCup Soccer 2D Simulation. Artif. Life Robot. 2020, 25, 440–445. [Google Scholar] [CrossRef]
- Zhang, Z. Pass Strategy of Robocup Robot System Based on Deep Learning Network. In Proceedings of the 2022 4th International Conference on Robotics, Intelligent Control and Artificial Intelligence (RICAI 2022), Dongguan, China, 16–18 December 2022; pp. 80–86. [Google Scholar] [CrossRef]
- Gao, Z.; Yi, M.; Jin, Y.; Zhang, H.; Hao, Y.; Yin, M.; Cai, Z.; Shen, F. A survey of research on several problems in the RoboCup3D simulation environment. Auton. Agents Multi. Agent Syst. 2024, 38, 13. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Counterpropagation networks. Appl. Opt. 1987, 26, 4979–4984. [Google Scholar] [CrossRef]
- Walter, J.; Riter, H.; Schulten, K. Nonlinear prediction with self-organizing maps. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, Washington, DC, USA, 17–21 June 1990; pp. 589–594. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef]
- Whittaker, A.D.; Cook, D.F. Counterpropagation neural network for modelling a continuous correlated process. Int. J. Prod. Res. 1995, 33, 1901–1910. [Google Scholar] [CrossRef]
- Barreto, G.A.; Souza, L.G.M. Adaptive filtering with the self-organizing map: A performance comparison. Neural Netw. 2006, 19, 785–798. [Google Scholar] [CrossRef]
- Lan, J.; Cho, J.; Erdogmus, D.; Principe, J.C.; Motter, M.A.; Xu, J. Local linear PID controllers for nonlinear control. Control Intell. Syst. 2005, 33, 26–35. [Google Scholar] [CrossRef]
- Zupan, J.; Novič, M.; Ruisánchez, I. Kohonen and counterpropagation artificial neural networks in analytical chemistry. Chemom. Intell. Lab. Syst. 1997, 38, 1–23. [Google Scholar] [CrossRef]
- Tokunaga, K.; Furukawa, T. Modular network SOM. Neural Netw. 2009, 22, 82–90. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).