Achieving Optimal Injection Molding Parameters to Minimize Both Shrinkage and Surface Roughness Through a Multi-Objective Optimization Approach
Abstract
Featured Application
Abstract
1. Introduction
- Warpage: Deformation of the product due to uneven cooling or internal stress.
- Volumetric Shrinkage: Reduction in volume as the molten plastic cools and solidifies in the mold.
- Sink Marks: Depressions on the product’s surface caused by uneven cooling or insufficient packing pressure.
- Flash: Excess material that flows out of the mold cavity and forms thin protrusions along the parting line.
- Short Shots: Incomplete filling of the mold, resulting in parts that are not fully formed.
2. Experiments
2.1. Injection Molding Experiments
2.2. Process Parameter Testing Points
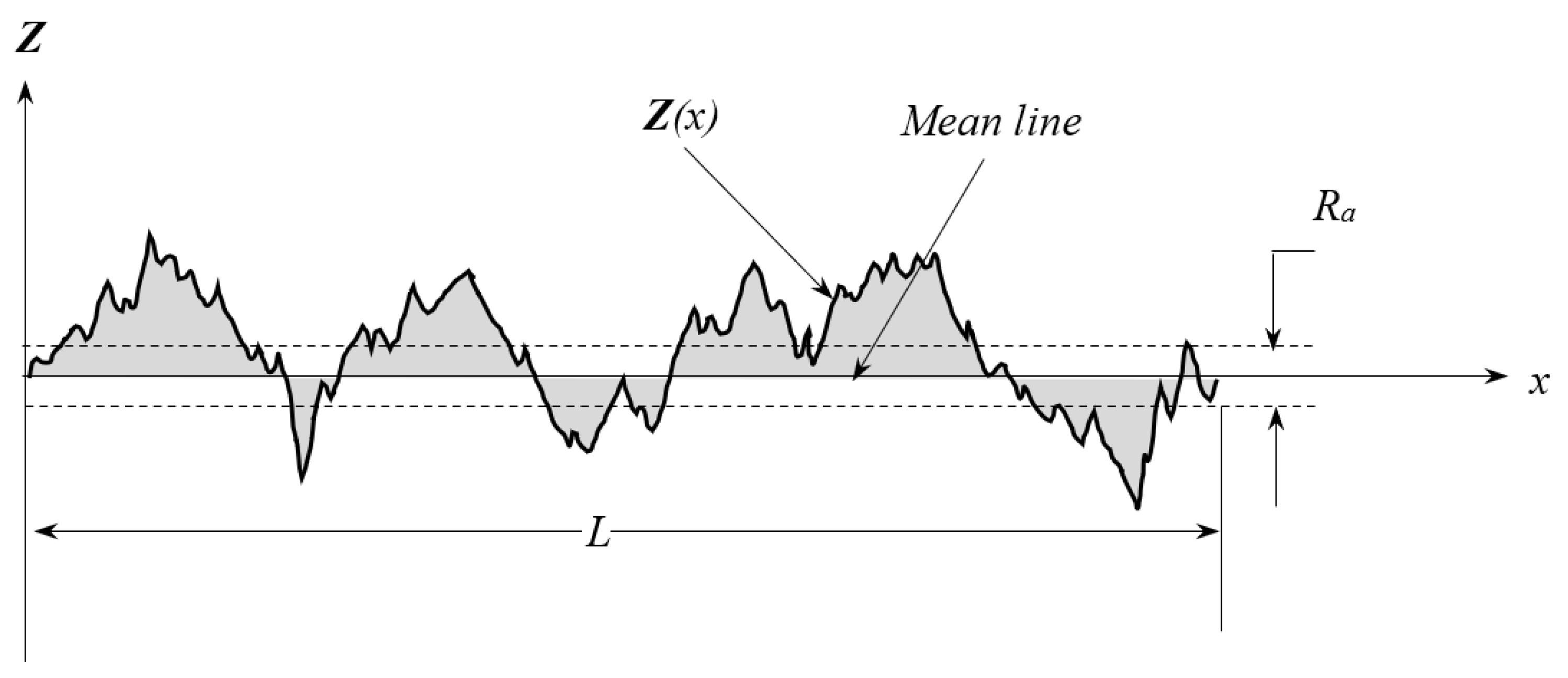
2.3. Quantification of Volumetric Shrinkage and Surface Roughness
2.3.1. Quantification of Volumetric Shrinkage
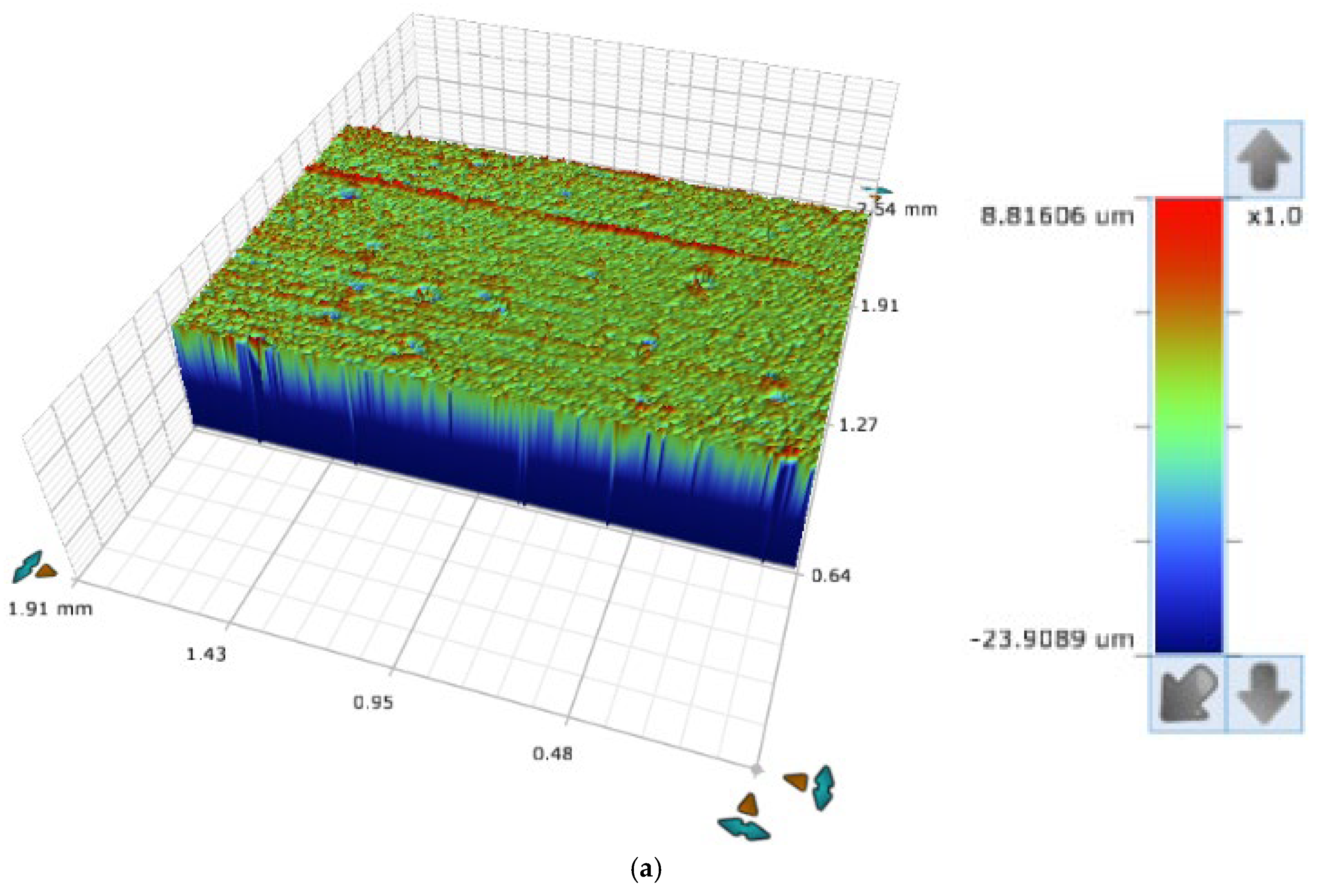
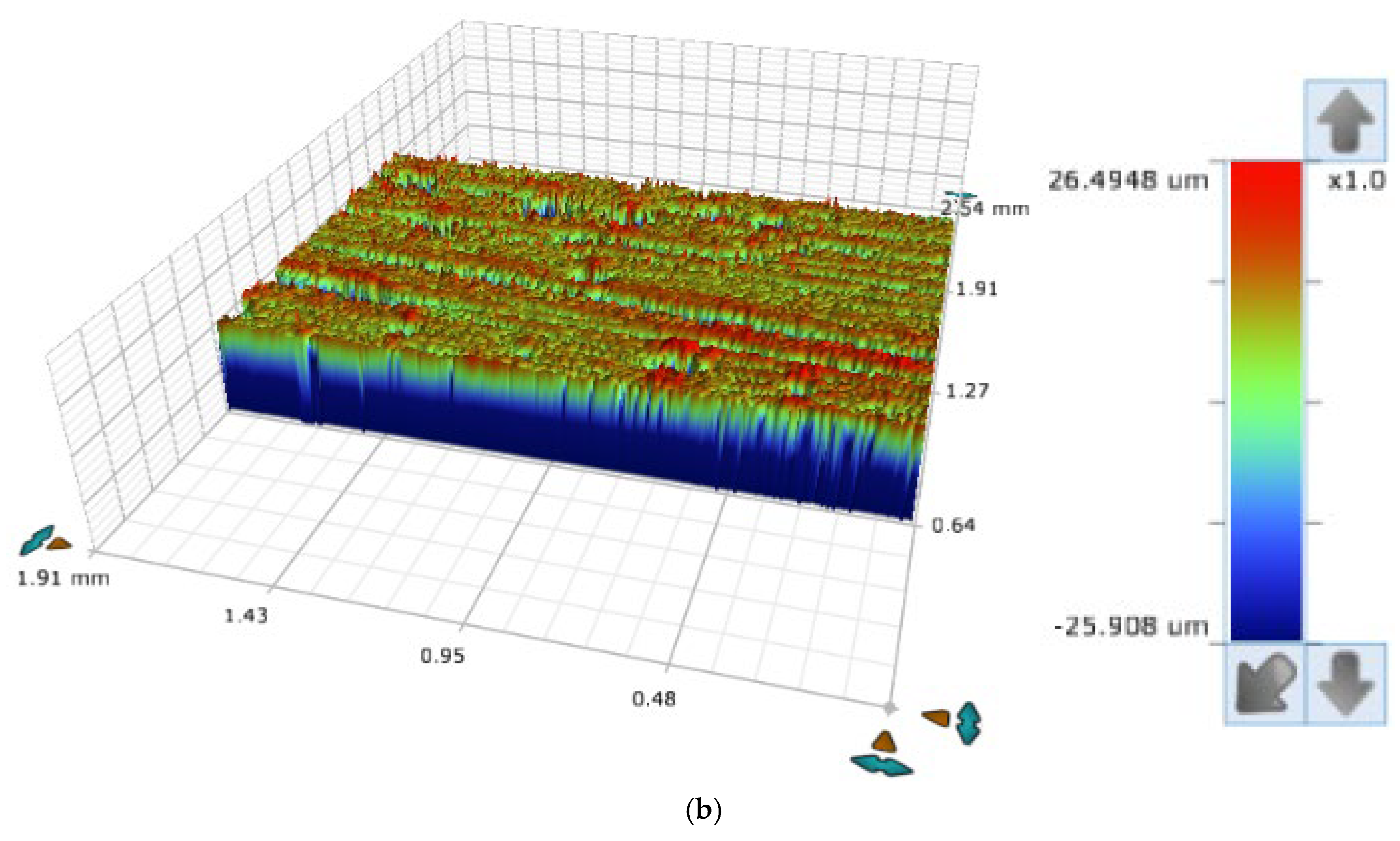
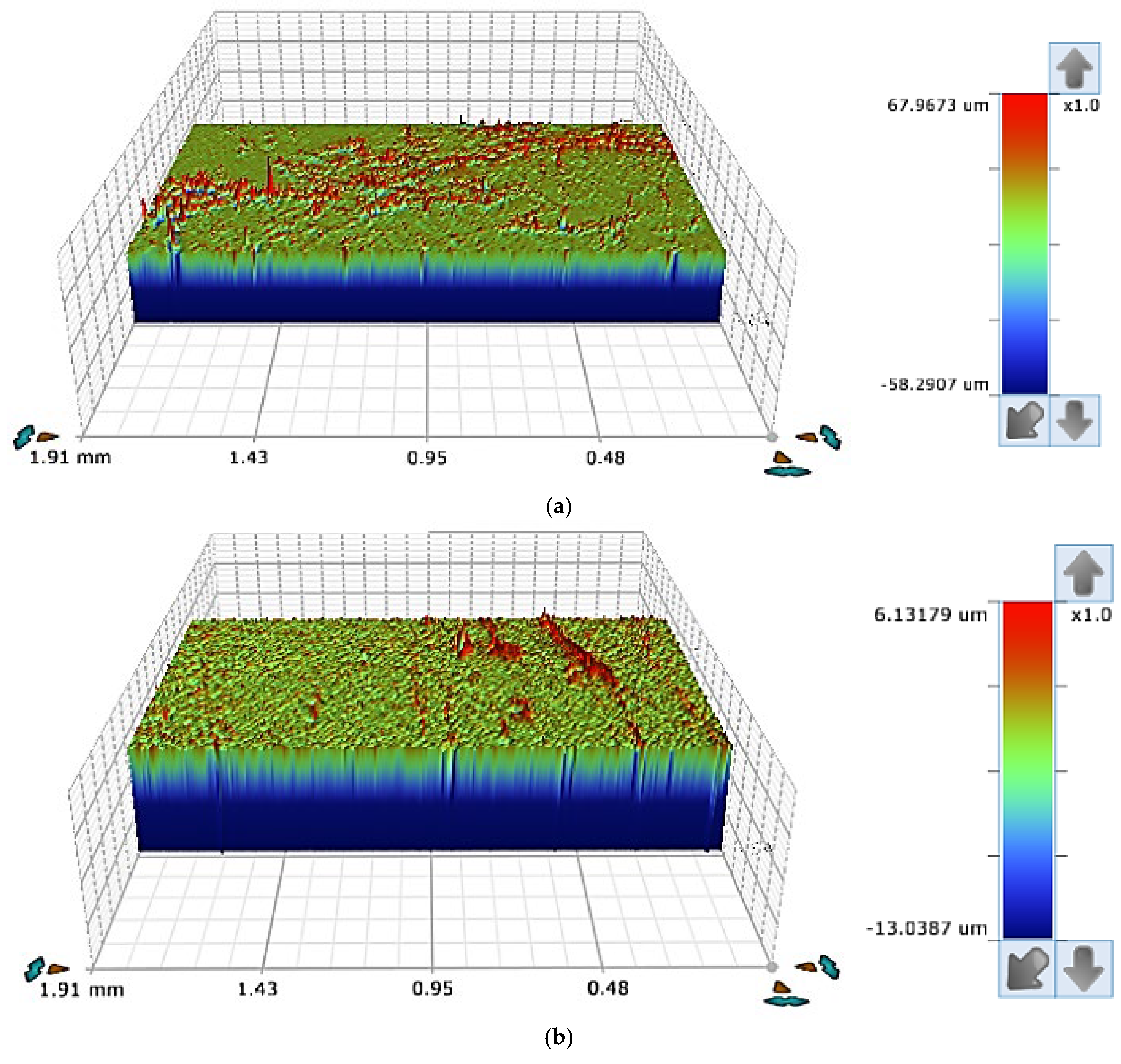
2.3.2. Surface Roughness Quantification
2.4. Experimental Results from Injection Molding Tests
3. Surrogate Modeling and Multi-Objective Optimization
3.1. Surrogate Modeling: Kriging
3.2. Multi-Objective Optimization
4. Concluding Remarks
- Volumetric shrinkage generally decreases with increasing injection pressure, packing pressure, packing time, and cooling time.
- Surface roughness generally decreases with increasing mold temperature, packing time, injection pressure, and melt temperature.
- Point 1: Minimizes volumetric shrinkage (1.9314 mm3) but results in the highest surface roughness (0.55956 µm).
- Point 2: Achieves the lowest surface roughness (0.20557 µm) but results in the highest volumetric shrinkage (3.9286 mm3).
- Point 3: Offers the best compromise with a volumetric shrinkage of 2.2348 mm3 and a surface roughness of 0.28246 µm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, R.; Roger, I.T.; Xi-Jun, F. Injection Molding: Integration of Theory and Modeling Methods; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2011; p. 188. [Google Scholar]
- Rosato, D.V.; Rosato, D.V.; Rosato, M.G. Injection Molding Handbook, 3rd ed.; Springer: New York, NY, USA, 2000; Volume 1. [Google Scholar]
- Dang, X.-P. General frameworks for optimization of plastic injection molding process parameters. Simul. Model. Pract. Theory 2014, 41, 15–27. [Google Scholar] [CrossRef]
- Choi, G.H.; Lee, K.D.; Chang, N.; Kim, S.G. Optimization of Process Parameters of Injection Molding with Neural Network Application in a Process Simulation Environment. CIRP Ann. 1994, 43, 4. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Nasiri, S. Injection molding manufacturing process: Review of case-based reasoning applications. J. Intell. Manuf. 2020, 31, 847–864. [Google Scholar] [CrossRef]
- Kurtaran, H.; Erzurumlu, T. Efficient warpage optimization of thin shell plastic parts using response surface methodology and genetic algorithm. Int. J. Adv. Manuf. Technol. 2005, 27, 468–472. [Google Scholar] [CrossRef]
- Ozcelik, B.; Erzurumlu, T. Determination of effecting dimensional parameters on warpage of thin shell plastic parts using integrated response surface method and genetic algorithm. Int. Commun. Heat Mass Transf. 2005, 32, 1085–1094. [Google Scholar] [CrossRef]
- Kurtaran, H.; Ozcelik, B.; Erzurumlu, T. Warpage optimization of a bus ceiling lamp base using neural network model and genetic algorithm. J. Mater. Process. Technology. 2005, 169, 314–319. [Google Scholar] [CrossRef]
- Ozcelik, B.; Erzurumlu, T. Comparison of the warpage optimization in the plastic injection molding using ANOVA, neural network model and genetic algorithm. J. Mater. Process. Technol. 2006, 171, 437–445. [Google Scholar] [CrossRef]
- Deng, W.-J.; Chen, C.-T.; Sun, C.-H.; Chen, W.-C.; Chen, C.-P. An Effective Approach for Process Parameter Optimization in Injection Molding of Plastic Housing Components. Polym.-Plast. Technol. Eng. 2008, 47, 910–919. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X. An effective warpage optimization method in injection molding based on the Kriging model. Int. J. Adv. Manuf. Technol. 2008, 37, 953–960. [Google Scholar] [CrossRef]
- Chen, C.-C.; Su, P.-L.; Lin, Y.-C. Analysis and modeling of effective parameters for dimension shrinkage variation of injection molded part with thin shell feature using response surface methodology. Int. J. Adv. Manuf. Technol. 2009, 45, 1087–1095. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X. Surrogate-based process optimization for reducing warpage in injection molding. J. Mater. Process. Technol. 2009, 209, 1302–1309. [Google Scholar] [CrossRef]
- Altan, M. Reducing shrinkage in injection moldings via the Taguchi, ANOVA and neural network methods. Mater. Des. 2010, 31, 599–604. [Google Scholar] [CrossRef]
- Farshi, B.; Gheshmi, S.; Miandoabchi, E. Optimization of injection molding process parameters using sequential simplex algorithm. Mater. Des. 2011, 32, 414–423. [Google Scholar] [CrossRef]
- Yin, F.; Mao, H.; Hua, L. A hybrid of back propagation neural network and genetic algorithm for optimization of injection molding process parameters. Mater. Des. 2011, 32, 3457–3464. [Google Scholar] [CrossRef]
- Yin, F.; Mao, H.; Hua, L.; Guo, W.; Shu, M. Back Propagation neural network modeling for warpage prediction and optimization of plastic products during injection molding. Mater. Des. 2011, 32, 1844–1850. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, G.; Ruan, S.; Li, Z. Multi-objective optimization design of injection molding process parameters based on the improved efficient global optimization algorithm and non-dominated sorting-based genetic algorithm. Int. J. Adv. Manuf. Technol. 2015, 78, 1813–1826. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Zhang, W.; Zhang, P. Optimization of injection molding process parameters to improve the mechanical performance of polymer product against impact. Int. J. Adv. Manuf. Technol. 2015, 76, 2199–2208. [Google Scholar] [CrossRef]
- Mohan, M.; Ansari, M.N.M.; Shanks, R.A. Review on the Effects of Process Parameters on Strength, Shrinkage, and Warpage of Injection Molding Plastic Component. Polym.-Plast. Technol. Eng. 2017, 56, 1132466. [Google Scholar] [CrossRef]
- Kitayama, S.; Miyakawa, H.; Takano, M.; Aiba, S. Multi-objective optimization of injection molding process parameters for short cycle time and warpage reduction using conformal cooling channel. Int. J. Adv. Manuf. Technol. Vol. 2017, 88, 1735–1744. [Google Scholar] [CrossRef]
- Singh, G.; Pradhan, M.K.; Verma, A. Multi Response optimization of injection moulding Process parameters to reduce cycle time and warpage. Mater. Today Proc. 2018, 5, 8398–8405. [Google Scholar] [CrossRef]
- Ramesh, S.; Nirmala, P.; Ramkumar, G.; Sahoo, S.; Anitha, G.; Gnanasekar, A.K.; Isaac JoshuaRamesh Lalvani, J. Simulation Process of Injection Molding and Optimization for Automobile Instrument Parameter in Embedded System. Adv. Mater. Sci. Eng. 2021, 2021, 9720297. [Google Scholar] [CrossRef]
- Mohd Hanid, M.H.; Abd Rahim, S.Z.; Gondro, J.; Sharif, S.; Al Bakri Abdullah, M.M.; Zain, A.M.; El-hadj Abdellah, A.; Mat Saad, M.N.; Wysłocki, J.J.; Nabiałek, M. Warpage Optimisation on the Moulded Part with Straight Drilled and Conformal Cooling Channels Using Response Surface Methodology (RSM), Glowworm Swarm Optimisation (GSO) and Genetic Algorithm (GA) Optimisation Approaches. Materials 2021, 14, 1326. [Google Scholar] [CrossRef] [PubMed]
- Kitayama, S.; Matsubayashi, A.; Takano, M.; Yamazaki, Y.; Kubo, Y.; Aiba, S. Numerical optimization of multistage packing pressure profile in plastic injection molding and experimental validation. Polym. Adv. Technol. 2022, 33, 3002–3012. [Google Scholar] [CrossRef]
- Chen, J.; Cui, Y.; Liu, Y.; Cui, J. Design and Parametric Optimization of the Injection Molding Process Using Statistical Analysis and Numerical Simulation. Processes 2023, 11, 414. [Google Scholar] [CrossRef]
- Martínez-Mateo, I.; Carrión-Vilches, F.J.; Sanes, J.; Bermúdez, M.D. Surface damage of mold steel and its influence on surface roughness of injection molded plastic parts. Wear 2011, 271, 2512–2516. [Google Scholar] [CrossRef]
- Kaneda, R.; Takahashi, T.; Takiguchi, M.; Hijikata, M.; Ito, H. Optical Properties of HDPE in Injection Molding and Injection Press Molding for IR System Lenses Part II: Mold Temperature and Surface Roughness Effects on Injection Molding. Int. Polym. Process. 2017, 32, 237–244. [Google Scholar] [CrossRef]
- Oliveira, M.J.; Brito, A.M.; Costa, M.C.; Costa, M.F. Gloss and surface topography of ABS: A study on the influence of the injection molding parameters. Polym. Eng. Sci. 2006, 46, 1394–1401. [Google Scholar] [CrossRef]
- Theilade, U.A.; Hansen, H.N. Surface microstructure replication in injection molding. Int. J. Adv. Manuf. Technol. 2007, 33, 157–166. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, G.; Wang, X. Experimental research on the effects of cavity surface temperature on surface appearance properties of the moulded part in rapid heat cycle moulding process. Int. J. Adv. Manuf. Technol. 2013, 68, 1293–1310. [Google Scholar] [CrossRef]
- Lee, J.; Turng, L.-S. Improving surface quality of microcellular injection molded parts through mold surface temperature manipulation with thin film insulation. Polym. Eng. Sci. 2010, 50, 1281–1289. [Google Scholar] [CrossRef]
- Guo, G. Investigation on surface roughness of injection molded polypropylene parts with 3D optical metrology. Int. J. Interact. Des. Manuf. 2021, 16, 17–23. [Google Scholar] [CrossRef]
- Usman Jan, Q.M.; Habib, T.; Noor, S.; Abas, M.; Azim, S.; Yaseen, Q.M. Multi response optimization of injection moulding process parameters of polystyrene and polypropylene to minimize surface roughness and shrinkage’s using integrated approach of S/N ratio and composite desirability function. Cogent Eng. 2020, 7, 1781424. [Google Scholar] [CrossRef]
- Arburg. Allrounder 420 C Golden Edition. Available online: https://www.arburg.com/media/daten/publications/technical_data/hydraulic_machines/golden_edition/ARBURG_ALLROUNDER_420C_GOLDEN_EDITION_TD_523676_de.pdf (accessed on 2 October 2022).
- SABIC. SABIC® HDPE M80064 High Density Polyethylene for Injection Moulding. Available online: http://www.b2bpolymers.com/TDS/SABIC_M80064.pdf (accessed on 10 January 2022).
- Oehlert, G.W. A First Course in Design and Analysis of Experiments; Freeman W. H.: New York, NY, USA, 2000. [Google Scholar]
- Blunt, L.; Jiang, X. Advanced Techniques for Assessment Surface Topography: Development of a Basis for 3D Surface Texture Standards “Surfstand”. Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Lonardo, P.M.; Trumpold, H.; De Chiffre, L. Progress in 3D Surface Microtopography Characterization. CIRP Ann. 1996, 45, 589–598. [Google Scholar] [CrossRef]
- Petheram, T.G.; Bone, M.; Joyce, T.J.; Serrano-Pedraza, I.; Reed, M.R.; Partington, P.F. Surface finish of the Exeter Trauma Stem: A cause for concern? Bone Jt. J. 2013, 95, 173–176. [Google Scholar] [CrossRef] [PubMed]
- Zein, H. Investigation of Surface Texture and Surface Residual Stresses in the Dry Face Turning Process of AL2024-T351. Int. J. Mech. Mechatron. Eng. 2020, 20, 123–143. [Google Scholar]
- ISO 4287; Geometrical product specifications (GPS)–Surface texture: Profile method–terms, definitions and surface texture parameters. International Organization for Standardization: Geneva, Switzerland, 1997.
- Dong, W.; Sullivan, P.; Stout, K. Comprehensive study of parameters for characterising three-dimensional surface topography: III: Parameters for characterising amplitude and some functional properties. Wear 1994, 178, 29–43. [Google Scholar] [CrossRef]
- Dong, W.P.; Sullivan, P.J.; Stout, K.J. Comprehensive study of parameters for characterising three-dimensional surface topography: IV: Parameters for characterising spatial and hybrid properties. Wear 1994, 178, 45–60. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Handbook of Surface and Nanometrology; Taylor & Francis: Oxfordshire, UK, 2002. [Google Scholar]
- Thomas, T.R. Rough Surfaces; World Scientific: Singapore, 1998. [Google Scholar]
- Pisciotti, F.; Boldizar, A.; Rigdahl, M.; Ariño, I. Effects of injection-molding conditions on the gloss and color of pigmented polypropylene. Polym. Eng. Sci. 2005, 45, 1557–1567. [Google Scholar] [CrossRef]
- Shen, C.; Wang, L.; Li, Q. Optimization of injection molding process parameters using combination of artificial neural network and genetic algorithm method. J. Mater. Process. Technol. 2007, 183, 412–418. [Google Scholar] [CrossRef]
- Shen, C.-Y.; Wang, L.-X.; Zhang, Q.-X. Process Optimization of Injection Molding by the Combining ANN/HGA Method. Polym. Mater. Sci. Eng. 2005, 21, 23–27. [Google Scholar]
- Zhou, J.; Turng, L.-S.; Kramschuster, A. Single and multi objective optimization for injection molding using numerical simulation with surrogate models and genetic algorithms. Int. Polym. Process. 2006, 21, 509–520. [Google Scholar] [CrossRef]
- Martin, J.D.; Simpson, T.W. Use of Kriging Models to Approximate Deterministic Computer Models. AIAA J. 2005, 43, 853–863. [Google Scholar] [CrossRef]
- Paramasivam, C.; Venkatramanan, S. An introduction to various spatial analysis techniques. In GIS and Geostatistical Techniques for Groundwater Science; Venkatramanan, S., Prasanna, M., Chung, S., Eds.; Elsevier: Amsterdam, Netherlands, 2019; pp. 23–30. [Google Scholar]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE—A Matlab Kriging Toolbox. In IMM Informatiocs and Mathematical Modelling, 2nd ed.; Technical University of Denmark: Copenhagen, Denmark, 2002; pp. 1–34. [Google Scholar]
- Gim, J.; Turng, L.-S. A review of current advancements in high surface quality injection molding: Measurement, influencing factors, prediction, and control. Polym. Test. 2022, 115, 107718. [Google Scholar] [CrossRef]
- Lee, J.L.; Ho, C.H.; Lin, Y.; Shen, Y.K. Fabrication and detection for the skeletons of micro aerial vehicle using precision injection molding. Key Eng. Mater. 2010, 443, 75–80. [Google Scholar] [CrossRef]
- Huang, M.-C.; Tai, C.-C. The effective factors in the warpage problem of an injection-molded part with a thin shell feature. J. Mater. Process. Technol. 2001, 110, 1–9. [Google Scholar] [CrossRef]
- Nian, S.; Yang, S. Molding of thin sheets using impact micro-injection molding. Int. Polym. Process. 2022, 20, 441–448. [Google Scholar] [CrossRef]
- Chen, C.-S.; Chen, S.-C.; Liao, W.-H.; Chien, R.-D.; Lin, S.-H. Micro injection molding of a micro-fluidic platform. Int. Commun. Heat Mass Transf. 2010, 37, 1290–1294. [Google Scholar] [CrossRef]
- An, C.-C.; Chen, R.-H. The experimental study on the defects occurrence of SL mold in injection molding. J. Mater. Process. Technology. 2008, 201, 706. [Google Scholar] [CrossRef]
- Meiabadi, M.S.; Moradi, M.; Kazerooni, A.; Demers, V. Multi-objective optimisation of plastic injection moulding process using mould flow analysis and response surface methodology. Int. J. Mater. Prod. Technol. 2022, 64, 140–155. [Google Scholar] [CrossRef]
- Raz, K.; Sedlacek, F. Effect of melt temperature on weld line strength. Key Eng. Mater. 2019, 801, 264–269. [Google Scholar] [CrossRef]
- Rizvi, S. Effect of injection molding parameters on crystallinity and mechanical properties of isotactic polypropylene. Int. J. Plast. Technol. 2017, 21, 404–426. [Google Scholar] [CrossRef]
- Farotti, E.; Natalini, M. Injection molding. Influence of process parameters on mechanical properties of polypropylene polymer. A first study. Procedia Struct. Integr. 2018, 8, 256–264. [Google Scholar]
- Sánchez, R.; Aisa, J.; Martinez, A.; Mercado, D. On the relationship between cooling setup and warpage in injection molding. Measurement 2012, 45, 1051–1056. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Xu, Y.-X. A simple method of improving warpage and cooling time of injection molded parts simultaneously. The Int. J. Adv. Manuf. Technol. 2022, 122, 619–637. [Google Scholar] [CrossRef]
- Turng, L.S.; Kharbas, H. Effect of process conditions on the weld-line strength and microstructure of microcellular injection molded parts. Polym. Eng. Sci. 2003, 43, 157–168. [Google Scholar] [CrossRef]
- Custódio, A.L.; Madeira, J.A.; Vaz, A.I.F.; Vicente, L.N. Direct multisearch for multiobjective optimization. SIAM J. Optim. 2011, 21, 1109–1140. [Google Scholar] [CrossRef]
- Madić, M.; Radovanović, M. Optimization of machining processes using pattern search algorithm. Int. J. Ind. Eng. Comput. 2014, 5, 223–234. [Google Scholar] [CrossRef]







| Ref. No. | Year | Objectives to Be Optimized | Process Parameters | Description of the Study |
|---|---|---|---|---|
| [6] | 2005 | Warpage | Cooling time, packing pressure, mold temperature, packing time, and melt temperature | The researchers investigated effective strategies for optimizing warpage in thin-shell plastic parts by employing a combination of response surface methodology (RSM) and genetic algorithms (GAs). This hybrid approach was used to minimize warpage defects in injection-molded thin-shell plastic components. |
| [7] | 2005 | Warpage | Dimensional parameters | This study aimed to determine the impact of dimensional parameters on the warpage of thin-shell plastic parts. An integrated approach combining response surface methodology (RSM) and genetic algorithms (GAs) was employed to analyze and optimize the dimensional parameters influencing warpage in injection-molded components. |
| [8] | 2005 | Warpage | Cooling time, mold temperature, melt temperature, packing pressure, and packing time | The authors conducted a study focused on optimizing warpage in a bus ceiling lamp base. They employed a neural network model in combination with a genetic algorithm to optimize injection molding process parameters. This integrated approach aimed to minimize warpage, thereby improving the manufacturing process and enhancing the quality and performance of the final product. |
| [9] | 2006 | Warpage | Mold temperature, melt temperature, packing pressure, packing time, and cooling time | The authors conducted a comparative study on warpage optimization techniques in plastic injection molding. This research evaluated the effectiveness of three approaches: analysis of variance (ANOVA), neural network modeling, and genetic algorithm (GA) optimization. The primary objective was to optimize warpage by assessing and comparing the performance of these different optimization methods within the injection molding process. |
| [10] | 2008 | Warpage | Velocity pressure switch, injection molding velocity, injection time, and packing pressure (used in an illustrative example) | The optimal process parameters for minimizing warpage were determined using a hybrid approach that combined the Taguchi method, regression analysis, and the Davidon–Fletcher–Powell (DFP) optimization technique. Initially, the Taguchi method was employed to estimate the preliminary process parameters. Subsequently, regression analysis was used to develop a surrogate model that relates the process parameters to warpage. Finally, the DFP method was applied to optimize the process parameters based on the developed model. |
| [11] | 2008 | Warpage | Mold temperature, melt temperature, injection time, and packing pressure | The authors developed an effective warpage optimization method for injection molding based on the Kriging model. The proposed method was implemented on a cellular phone. |
| [12] | 2009 | Shrinkage | Melt temperature, mold temperature, packing pressure, and injection velocity | The aim of this research was to minimize the shrinkage of thin-shell injection-molded products through the optimization of the process parameters. The response surface methodology was used to develop a relationship between the parameters and shrinkage, which was then optimized to identify the optimal process parameters. |
| [13] | 2009 | Warpage | Mold temperature, melt temperature, injection time, packing time, and packing pressure | Process parameter optimization for achieving the minimum warpage was conducted. The Kriging surrogate approach was used in combination with design of experiments to create a relationship between process parameters and warpage. An adaptive optimization procedure was then used to optimize the process parameters. The developed procedure was applied in the development of a cellular phone cover. |
| [14] | 2010 | Shrinkage | Packing time, injection pressure, melt temperature, and packing pressure | This work focused on reducing shrinkage in injection moldings using a combination of the Taguchi method, an analysis of variance (ANOVA), and neural network methods. The researchers aimed to optimize injection molding process parameters to minimize shrinkage in the final molded products. The Taguchi method helped design efficient experiments, the ANOVA provided insights into the significance of different parameters, and neural network methods facilitated predictive modeling for shrinkage reduction. |
| [15] | 2011 | Warpage and shrinkage | Mold temperature, melt temperature, holding pressure, packing time, pressure switch-over, and coolant inlet temperature | The authors optimized these process parameters to minimize warpage and shrinkage defects using a sequential simplex algorithm. |
| [16] | 2011 | Warpage | Cooling time, mold temperature, packing time, packing pressure, and melt temperature | The multi-objective optimization of process parameters was carried out to achieve optimal warpage and clamping force. The suggested optimization approach uses both a backpropagation neural network technique and a genetic algorithm. |
| [17] | 2011 | Warpage | Mold temperature, melt temperature, packing pressure, packing time, and cooling time | This research involved using backpropagation neural network (BPNN) modeling for warpage prediction and the optimization of plastic products during injection molding. By integrating neural network techniques with optimization methods, this study aimed to improve product quality, reduce defects, and enhance manufacturing efficiency in plastic injection molding processes. |
| [18] | 2015 | Sink marks, shrinkage, and warpage | Injection time, melt temperature, packing time, packing pressure, cooling temperature, and cooling time | This study involved the development of a framework for minimizing product defects though a two-stage optimization approach. In the first stage, an improved efficient global optimization algorithm was used to establish the relationship between the defect and the process parameters. In the second stage, a non-dominated sorting genetic algorithm was used to conduct multi-objective optimization. |
| [19] | 2015 | Warpage | Molt temperature, melt temperature, injection velocity, compression distance, compression force, compression velocity, and compression waiting time | In this study, a neural network and particle swarm optimization were used to optimize injection process parameters to improve mechanical performance, as it is affected by warpage. |
| [20] | 2017 | Strength, warpage, and shrinkage | Mold temperature, holding pressure, cooling time, holding time, melt temperature, injection pressure, and melt temperature | The effects of process parameters on the strength, warpage, and shrinkage of injection molding products were investigated. The mold temperature and holding pressure had the greatest effects on warpage and shrinkage. |
| [21] | 2017 | Warpage | Cooling temperature, packing time, injection time, packing pressure, cooling time, and melt temperature | The authors studied cooling performance for conformal cooling channels in the injection molding process by considering warpage and cycle time. This study was conducted both numerically and experimentally. Due to the high cost of simulating the injection molding process, sequential approximate optimization based on a radial basis network approach was used to generate a Pareto front. It is reported in this study that the conformal cooling channels perform better than conventional cooling channels. |
| [22] | 2018 | Warpage and cycle time | Packing time, packing pressure, injection pressure, and melt temperature | The authors determined the optimal warpage and cycle time through multi-response optimization. This study utilized optimization techniques and experimental design methodologies to identify the optimal combination of process parameters that would lead to improved efficiency and reduced defects in injection-molded components. |
| [23] | 2021 | Shrinkage and warpage | Packing time, mold temperature, packing pressure, melt temperature, and cooling temperature | This study concentrated on the simulation process of injection molding and optimization for automobile instrument parameters in embedded systems. |
| [24] | 2021 | Warpage | Cooling time, packing pressure, melt temperature, and coolant temperature | This study involved the warpage optimization of molded parts with straight-drilled and conformal cooling channels. This research utilized multiple optimization approaches including response surface methodology (RSM), Glowworm Swarm Optimization (GSO), and genetic algorithms (GAs). The researchers aimed to optimize the warpage of molded parts by comparing the effectiveness of different cooling channel designs, specifically straight-drilled channels versus conformal cooling channels. |
| [25] | 2022 | Warpage and cycle time | Melt temperature, packing pressure, cooling time, packing time, injection time, and cooling temperature | Kitayama et al. conducted a study on the numerical optimization of multistage packing pressure profiles in plastic injection molding and validated their findings through experimentation. The researchers aimed to optimize the packing pressure profile during plastic injection molding. Packing pressure is a critical parameter that influences the final properties and dimensions of molded parts. The authors reported that the proposed procedure can reduce warpage and cycle time, as well as the clamping force. |
| [26] | 2023 | Warpage | Melt temperature, mold temperature, injection pressure, holding time, and cooling time | The authors aimed to minimize the warpage of polyethylene terephthalate by performing process parameter optimization through experimental, statistical, and numerical approaches. Through the presented approaches, the authors reported a reduction in warpage of approximately 7.7%. |
| Material Property | Units | Magnitude |
|---|---|---|
| Flow Rate of the Melt (conducted at 2160 g and 190 °C) | g/10 min | 8 |
| Density | g/mm3 | |
| Vicat Softening Temp. (performed at 10.0 N) | °C/°F | 128/262 |
| Stress at Breaking Stress Point | Pa | |
| Stress at Yield | Pa |
| Injection Molding Parameters | Symbol | Lower Bound | Upper Bound | Units |
|---|---|---|---|---|
| Injection pressure | 450 | 800 | bar | |
| Packing pressure | 100 | 400 | bar | |
| Packing time | 3 | 9 | s | |
| Cooling time | 10 | 30 | s | |
| Injection speed | 15 | 60 | mm/s | |
| Melt temperature | 200 | 250 | °C | |
| Mold temperature | 15 | 45 | °C |
| Injection Pressure (Bar) Ip | Measured Injection Pressure (Bar) Ip | Packing Pressure (Bar) Pp | Packing Time (s) Pt | Cooling Time (s) Ct | Injection Speed (mm/s) Is | Melt Temp. (°C) MT | Mold Temp. (°C) MOT | Volumetric Shrinkage (mm3) W | Surface Roughness (µm) Ra | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Center of Sample | 10 mm from Injection Point | ||||||||||
| 1 | 450 | 457 | 100 | 9 | 10 | 15 | 200 | 15 | 3.97 | 0.791 | 0.162 |
| 2 | 450 | 457 | 100 | 3 | 30 | 15 | 200 | 15 | 5.17 | 0.871 | 1.932 |
| 3 | 450 | 457 | 400 | 3 | 10 | 15 | 200 | 15 | 4.59 | 0.624 | 0.193 |
| 4 | 450 | 457 | 400 | 9 | 30 | 15 | 200 | 15 | 2.45 | 0.823 | 0.149 |
| 5 | 800 | 462 | 100 | 3 | 10 | 15 | 200 | 15 | 5.26 | 0.691 | 0.257 |
| 6 | 800 | 461 | 100 | 9 | 30 | 15 | 200 | 15 | 3.95 | 0.729 | 0.304 |
| 7 | 800 | 460 | 400 | 9 | 10 | 15 | 200 | 15 | 2.55 | 0.743 | 0.173 |
| 8 | 800 | 461 | 400 | 3 | 30 | 15 | 200 | 15 | 4.49 | 0.756 | 1.986 |
| 9 | 450 | 452 | 100 | 3 | 10 | 60 | 200 | 15 | 5.38 | 0.788 | 0.81 |
| 10 | 450 | 452 | 100 | 9 | 30 | 60 | 200 | 15 | 4 | 0.776 | 1.869 |
| 11 | 450 | 452 | 400 | 9 | 10 | 60 | 200 | 15 | 2.63 | 0.622 | 0.796 |
| 12 | 450 | 452 | 400 | 3 | 30 | 60 | 200 | 15 | 4.62 | 0.661 | 4.619 |
| 13 | 800 | 785 | 100 | 9 | 10 | 60 | 200 | 15 | 4.34 | 0.588 | 0.425 |
| 14 | 800 | 783 | 100 | 3 | 30 | 60 | 200 | 15 | 5.21 | 0.61 | 0.619 |
| 15 | 800 | 791 | 400 | 3 | 10 | 60 | 200 | 15 | 4.1 | 0.632 | 0.544 |
| 16 | 800 | 787 | 400 | 9 | 30 | 60 | 200 | 15 | 1.97 | 0.629 | 1.346 |
| 17 | 450 | 447 | 100 | 3 | 10 | 15 | 200 | 45 | 5.33 | 0.698 | 0.65 |
| 18 | 450 | 445 | 100 | 9 | 30 | 15 | 200 | 45 | 4.05 | 0.594 | 0.508 |
| 19 | 450 | 450 | 400 | 9 | 10 | 15 | 200 | 45 | 3.24 | 0.653 | 0.445 |
| 20 | 450 | 447 | 400 | 3 | 30 | 15 | 200 | 45 | 5.09 | 0.633 | 0.788 |
| 21 | 800 | 445 | 100 | 9 | 10 | 15 | 200 | 45 | 4.1 | 0.788 | 0.481 |
| 22 | 800 | 446 | 100 | 3 | 30 | 15 | 200 | 45 | 5.55 | 0.8 | 1.656 |
| 23 | 800 | 444 | 400 | 3 | 10 | 15 | 200 | 45 | 5.17 | 0.815 | 0.351 |
| 24 | 800 | 446 | 400 | 9 | 30 | 15 | 200 | 45 | 3.15 | 0.647 | 0.283 |
| 25 | 450 | 453 | 100 | 9 | 10 | 60 | 200 | 45 | 4.19 | 0.586 | 0.368 |
| 26 | 450 | 452 | 100 | 3 | 30 | 60 | 200 | 45 | 5.68 | 0.634 | 5.675 |
| 27 | 450 | 453 | 400 | 3 | 10 | 60 | 200 | 45 | 5.31 | 0.641 | 0.404 |
| 28 | 450 | 453 | 400 | 9 | 30 | 60 | 200 | 45 | 3.25 | 0.657 | 0.313 |
| 29 | 800 | 783 | 100 | 3 | 10 | 60 | 200 | 45 | 5.53 | 0.696 | 0.432 |
| 30 | 800 | 779 | 100 | 9 | 30 | 60 | 200 | 45 | 4.14 | 0.707 | 0.701 |
| 31 | 800 | 781 | 400 | 9 | 10 | 60 | 200 | 45 | 2.28 | 0.771 | 0.503 |
| 32 | 800 | 780 | 400 | 3 | 30 | 60 | 200 | 45 | 4.27 | 0.83 | 0.504 |
| 33 | 450 | 343 | 100 | 3 | 10 | 15 | 250 | 15 | 5.92 | 0.861 | 0.418 |
| 34 | 450 | 342 | 100 | 9 | 30 | 15 | 250 | 15 | 3.85 | 0.888 | 0.263 |
| 35 | 450 | 343 | 400 | 9 | 10 | 15 | 250 | 15 | 3.12 | 0.816 | 0.59 |
| 36 | 450 | 344 | 400 | 3 | 30 | 15 | 250 | 15 | 5.35 | 0.872 | 0.179 |
| 37 | 800 | 345 | 100 | 9 | 10 | 15 | 250 | 15 | 3.95 | 0.915 | 0.297 |
| 38 | 800 | 345 | 100 | 3 | 30 | 15 | 250 | 15 | 5.85 | 0.993 | 0.28 |
| 39 | 800 | 348 | 400 | 3 | 10 | 15 | 250 | 15 | 5.48 | 0.801 | 1.243 |
| 40 | 800 | 349 | 400 | 9 | 30 | 15 | 250 | 15 | 3.02 | 0.796 | 0.44 |
| 41 | 450 | 451 | 100 | 9 | 10 | 60 | 250 | 15 | 4.15 | 0.448 | 0.559 |
| 42 | 450 | 451 | 100 | 3 | 30 | 60 | 250 | 15 | 6.06 | 0.514 | 0.553 |
| 43 | 450 | 452 | 400 | 3 | 10 | 60 | 250 | 15 | 5.83 | 0.493 | 0.425 |
| 44 | 450 | 452 | 400 | 9 | 30 | 60 | 250 | 15 | 3.2 | 0.447 | 0.465 |
| 45 | 800 | 639 | 100 | 3 | 10 | 60 | 250 | 15 | 6.16 | 0.591 | 0.389 |
| 46 | 800 | 639 | 100 | 9 | 30 | 60 | 250 | 15 | 4.07 | 0.434 | 0.526 |
| 47 | 800 | 639 | 400 | 9 | 10 | 60 | 250 | 15 | 3.29 | 0.414 | 0.468 |
| 48 | 800 | 642 | 400 | 3 | 30 | 60 | 250 | 15 | 5.48 | 0.432 | 4.228 |
| 49 | 450 | 333 | 100 | 9 | 10 | 15 | 250 | 45 | 4.54 | 0.469 | 0.294 |
| 50 | 450 | 334 | 100 | 3 | 30 | 15 | 250 | 45 | 6.21 | 0.64 | 0.3 |
| 51 | 450 | 335 | 400 | 3 | 10 | 15 | 250 | 45 | 5.95 | 0.48 | 6.331 |
| 52 | 450 | 338 | 400 | 9 | 30 | 15 | 250 | 45 | 3.84 | 0.519 | 0.8 |
| 53 | 800 | 336 | 100 | 3 | 10 | 15 | 250 | 45 | 6.25 | 0.58 | 0.769 |
| 54 | 800 | 338 | 100 | 9 | 30 | 15 | 250 | 45 | 4.43 | 0.572 | 0.321 |
| 55 | 800 | 338 | 400 | 9 | 10 | 15 | 250 | 45 | 3.94 | 0.454 | 2.779 |
| 56 | 800 | 337 | 400 | 3 | 30 | 15 | 250 | 45 | 5.87 | 0.653 | 0.962 |
| 57 | 450 | 451 | 100 | 3 | 10 | 60 | 250 | 45 | 6.49 | 0.563 | 5.59 |
| 58 | 450 | 452 | 100 | 9 | 30 | 60 | 250 | 45 | 4.63 | 0.427 | 0.916 |
| 59 | 450 | 452 | 400 | 9 | 10 | 60 | 250 | 45 | 4.13 | 0.408 | 0.734 |
| 60 | 450 | 452 | 400 | 3 | 30 | 60 | 250 | 45 | 6.11 | 0.7 | 0.473 |
| 61 | 625 | 625 | 250 | 6 | 20 | 37.5 | 200 | 30 | 4.2 | 0.537 | 0.744 |
| 62 | 625 | 511 | 250 | 6 | 20 | 37.5 | 250 | 30 | 4.84 | 0.428 | 0.323 |
| 63 | 625 | 625 | 250 | 6 | 20 | 37.5 | 225 | 15 | 4.26 | 0.462 | 1.747 |
| 64 | 625 | 625 | 250 | 6 | 20 | 37.5 | 225 | 45 | 4.87 | 0.422 | 0.442 |
| 65 | 625 | 395 | 250 | 6 | 20 | 15 | 225 | 30 | 4.31 | 0.63 | 0.163 |
| 66 | 625 | 628 | 250 | 6 | 20 | 60 | 225 | 30 | 4.51 | 0.543 | 0.27 |
| 67 | 450 | 452 | 250 | 6 | 20 | 37.5 | 225 | 30 | 4.44 | 0.457 | 1.405 |
| 68 | 800 | 580 | 250 | 6 | 20 | 37.5 | 225 | 30 | 4.45 | 0.421 | 0.573 |
| 69 | 625 | 625 | 100 | 6 | 20 | 37.5 | 225 | 30 | 4.97 | 0.42 | 0.49 |
| 70 | 625 | 625 | 400 | 6 | 20 | 37.5 | 225 | 30 | 4.27 | 0.481 | 0.587 |
| 71 | 625 | 625 | 250 | 6 | 10 | 37.5 | 225 | 30 | 4.61 | 0.439 | 1.044 |
| 72 | 625 | 625 | 250 | 6 | 30 | 37.5 | 225 | 30 | 4.5 | 0.395 | 0.371 |
| 73 | 625 | 625 | 250 | 3 | 20 | 37.5 | 225 | 30 | 5.61 | 0.435 | 0.786 |
| 74 | 625 | 625 | 250 | 9 | 20 | 37.5 | 225 | 30 | 3.63 | 0.444 | 0.386 |
| 75 | 625 | 625 | 250 | 6 | 20 | 37.5 | 225 | 30 | 4.54 | 0.455 | 0.823 |
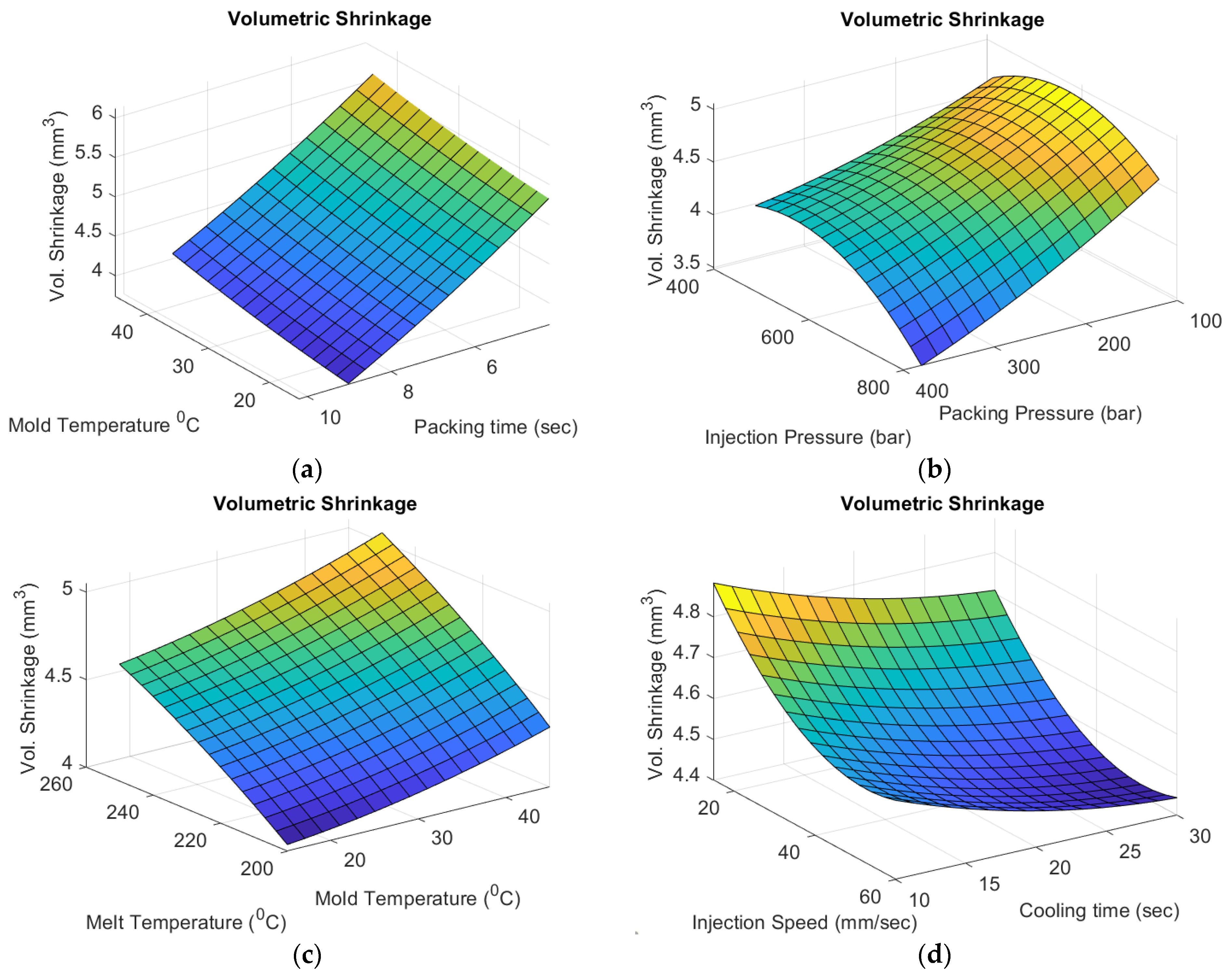
| Injection Molding Parameters | Observed Effects of Increasing the Process Parameter Value on Volumetric Shrinkage | Figure | Reference |
|---|---|---|---|
| Injection pressure | Decreases Volumetric shrinkage | Figure 9b | [55] |
| Packing pressure | Decreases Volumetric shrinkage | Figure 9b | [18,55,56] |
| Packing time | Decreases Volumetric shrinkage | Figure 9a | [18,56,57] |
| Cooling time | Decreases Volumetric shrinkage | Figure 9d | [18,58] |
| Injection speed | Increases Volumetric shrinkage | Figure 9d | - |
| Melt temperature | Increases Volumetric shrinkage | Figure 9c | [18,55] |
| Mold temperature | Increases Volumetric shrinkage | Figure 9a,c | [55,57] |
| Injection Molding Parameters | Observed Effects of Increasing the Process Parameter Value on Roughness | Figure | Previously Reported |
|---|---|---|---|
| Injection pressure | Decreased roughness | Figure 10b | [34] |
| Packing pressure | Decreased roughness (for low injection pressures) | Figure 10b | [29] |
| Packing time | Decreased roughness | Figure 10a | - |
| Cooling time | Minimal effect | Figure 10d | - |
| Injection speed | Roughness dips as injection speed increases and then increases again for higher speeds | Figure 10d | - |
| Melt temperature | Decreased roughness | Figure 10c | [29,34] |
| Mold temperature | Decreased roughness | Figure 10a | [29,59]. |
| Points | Volumetric Shrinking (mm3) | Surface Roughness Ra (µm) | Measured Injection Pressure (bar) | Packing Pressure (bar) | Packing Time (s) | Cooling Time (s) | Injection Speed (mm/s) | Melt Temp. (°C) | Mold Temp. (°C) |
|---|---|---|---|---|---|---|---|---|---|
| P1 | 1.9314 | 0.55956 | 200 | 15 | 56.531 | 800 | 400 | 30 | 9 |
| P2 | 2.2348 | 0.28246 | 250 | 15 | 45.844 | 800 | 400 | 30 | 9 |
| P3 | 3.9286 | 0.20557 | 250 | 31.062 | 35.984 | 800 | 127.03 | 30 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukras, S.M.S.; Korany, H.Z.; Omar, H.M. Achieving Optimal Injection Molding Parameters to Minimize Both Shrinkage and Surface Roughness Through a Multi-Objective Optimization Approach. Appl. Sci. 2025, 15, 5063. https://doi.org/10.3390/app15095063
Mukras SMS, Korany HZ, Omar HM. Achieving Optimal Injection Molding Parameters to Minimize Both Shrinkage and Surface Roughness Through a Multi-Objective Optimization Approach. Applied Sciences. 2025; 15(9):5063. https://doi.org/10.3390/app15095063
Chicago/Turabian StyleMukras, Saad M. S., Hussein Zein Korany, and Hanafy M. Omar. 2025. "Achieving Optimal Injection Molding Parameters to Minimize Both Shrinkage and Surface Roughness Through a Multi-Objective Optimization Approach" Applied Sciences 15, no. 9: 5063. https://doi.org/10.3390/app15095063
APA StyleMukras, S. M. S., Korany, H. Z., & Omar, H. M. (2025). Achieving Optimal Injection Molding Parameters to Minimize Both Shrinkage and Surface Roughness Through a Multi-Objective Optimization Approach. Applied Sciences, 15(9), 5063. https://doi.org/10.3390/app15095063






