Demonstration of an Advanced Rectification Strategy on a Linear Generator for Better Electricity Quality
Abstract
1. Introduction
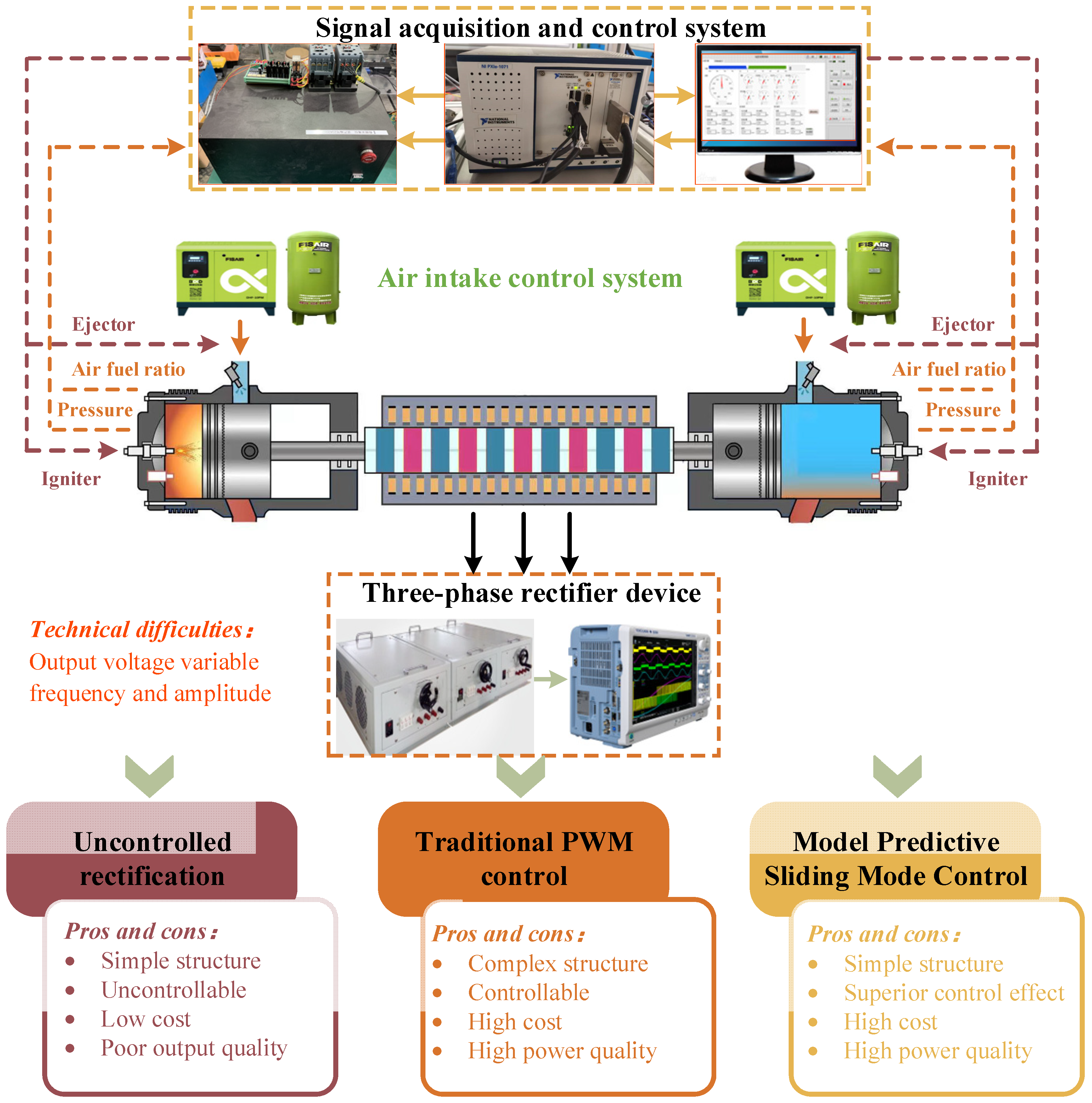
2. Analysis of the FPLG System Working Process
2.1. Working Principle of the Power Generation System
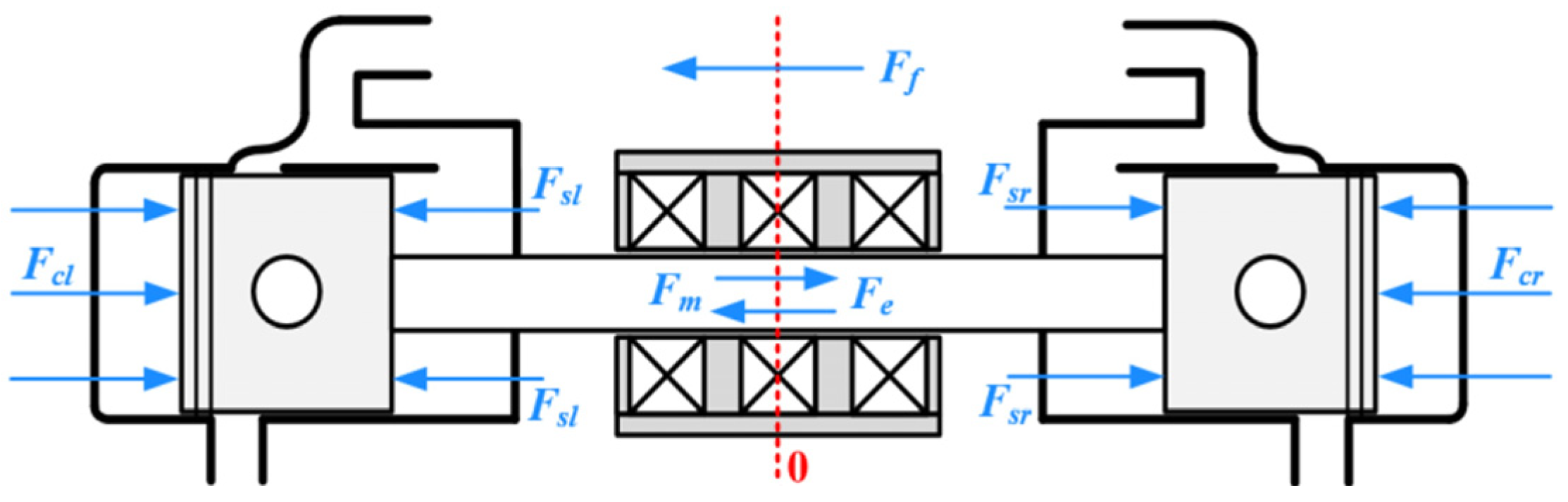
2.2. Linear Motor Modeling
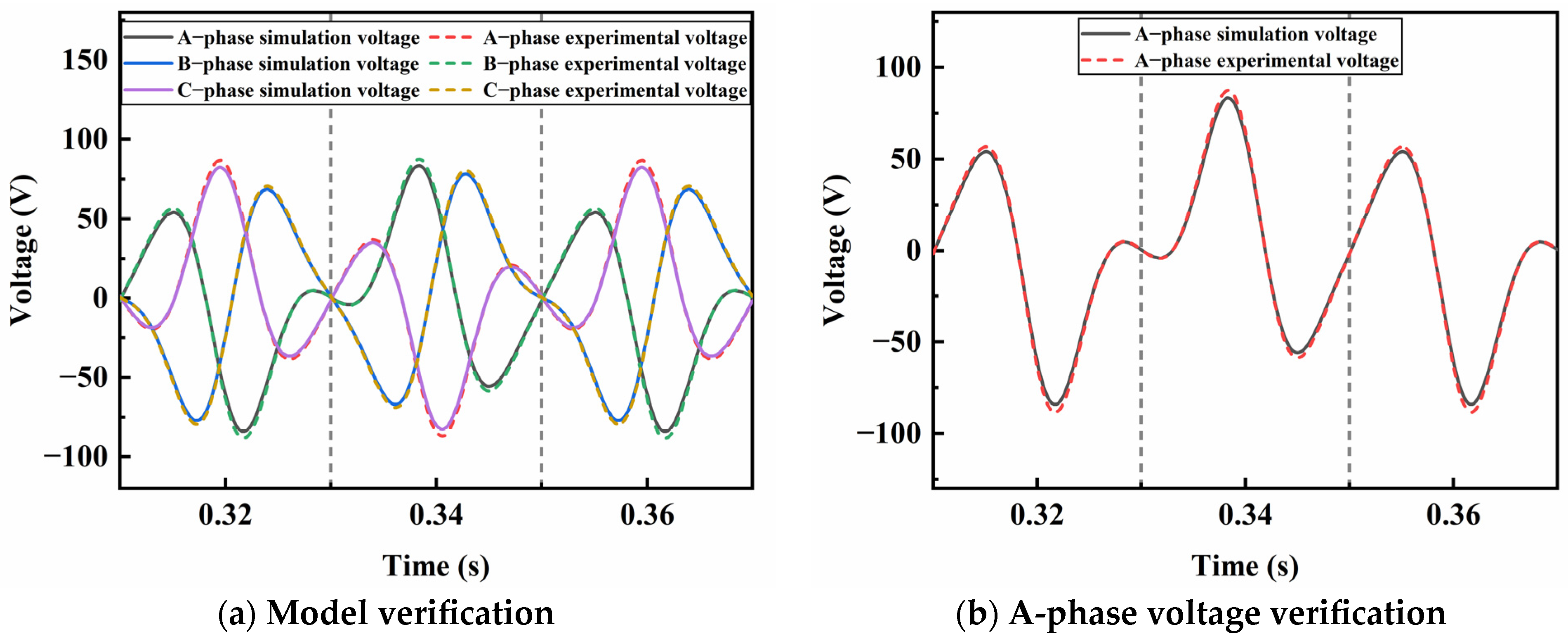
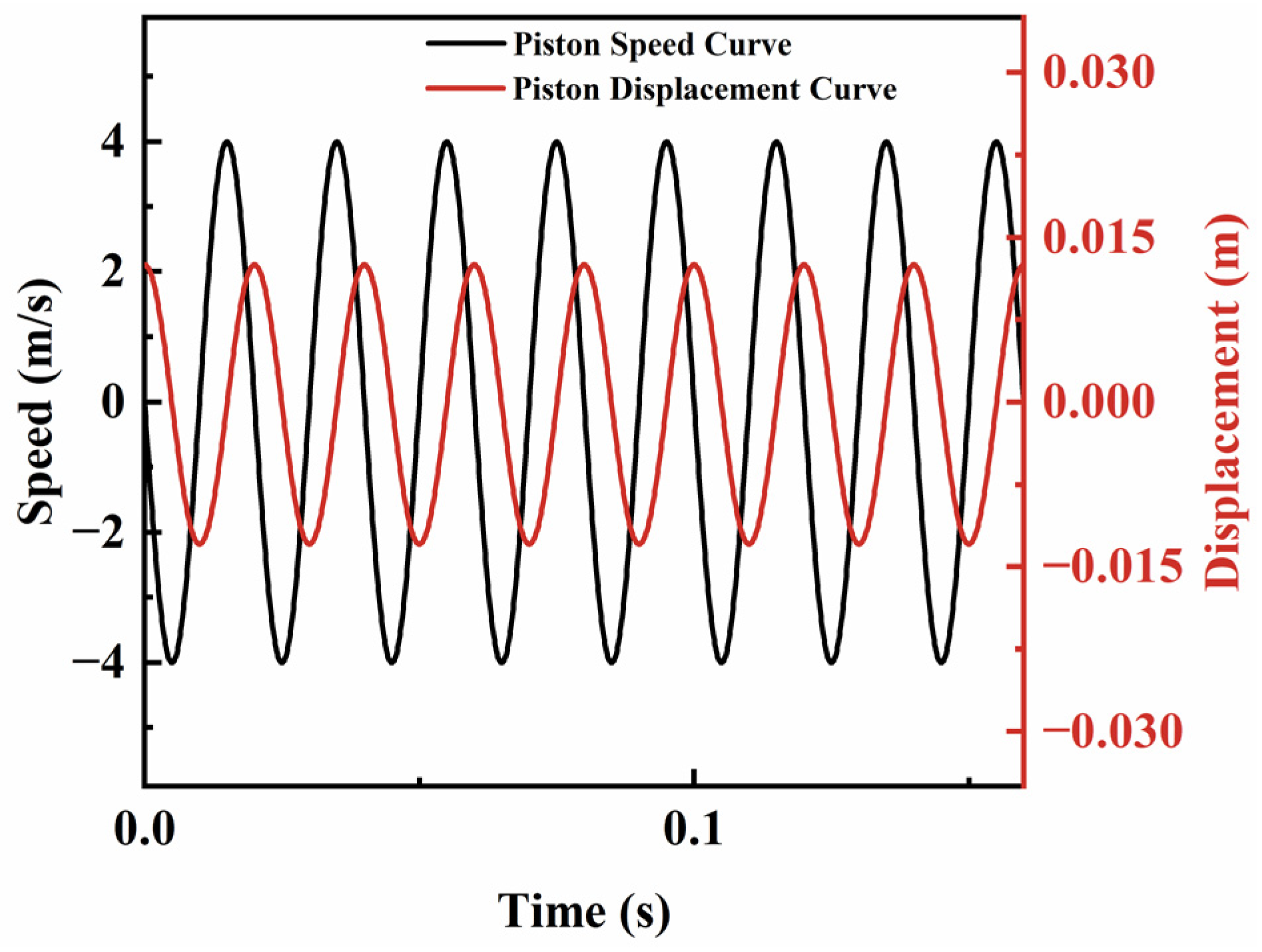
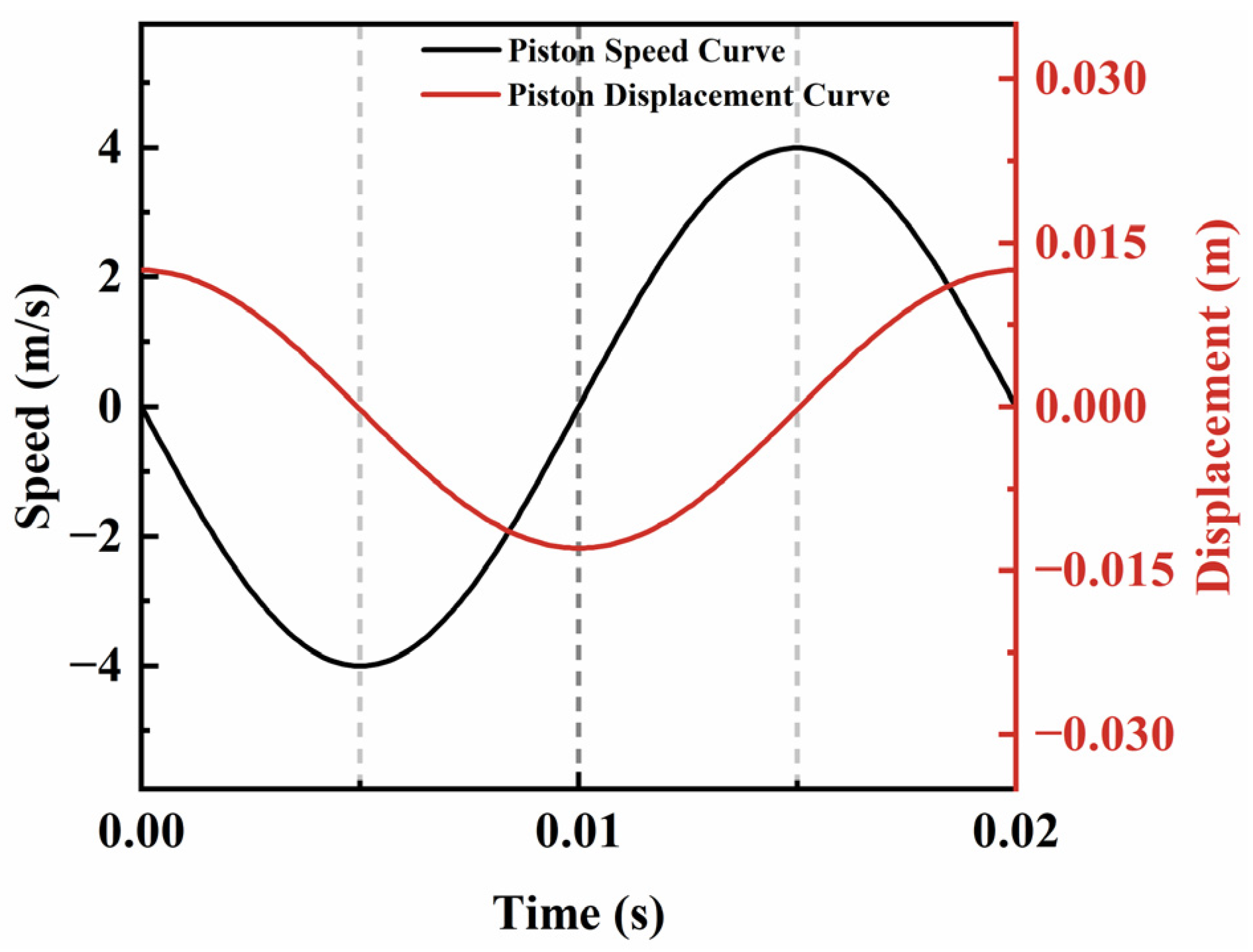
2.3. Linear Motor Model Verification
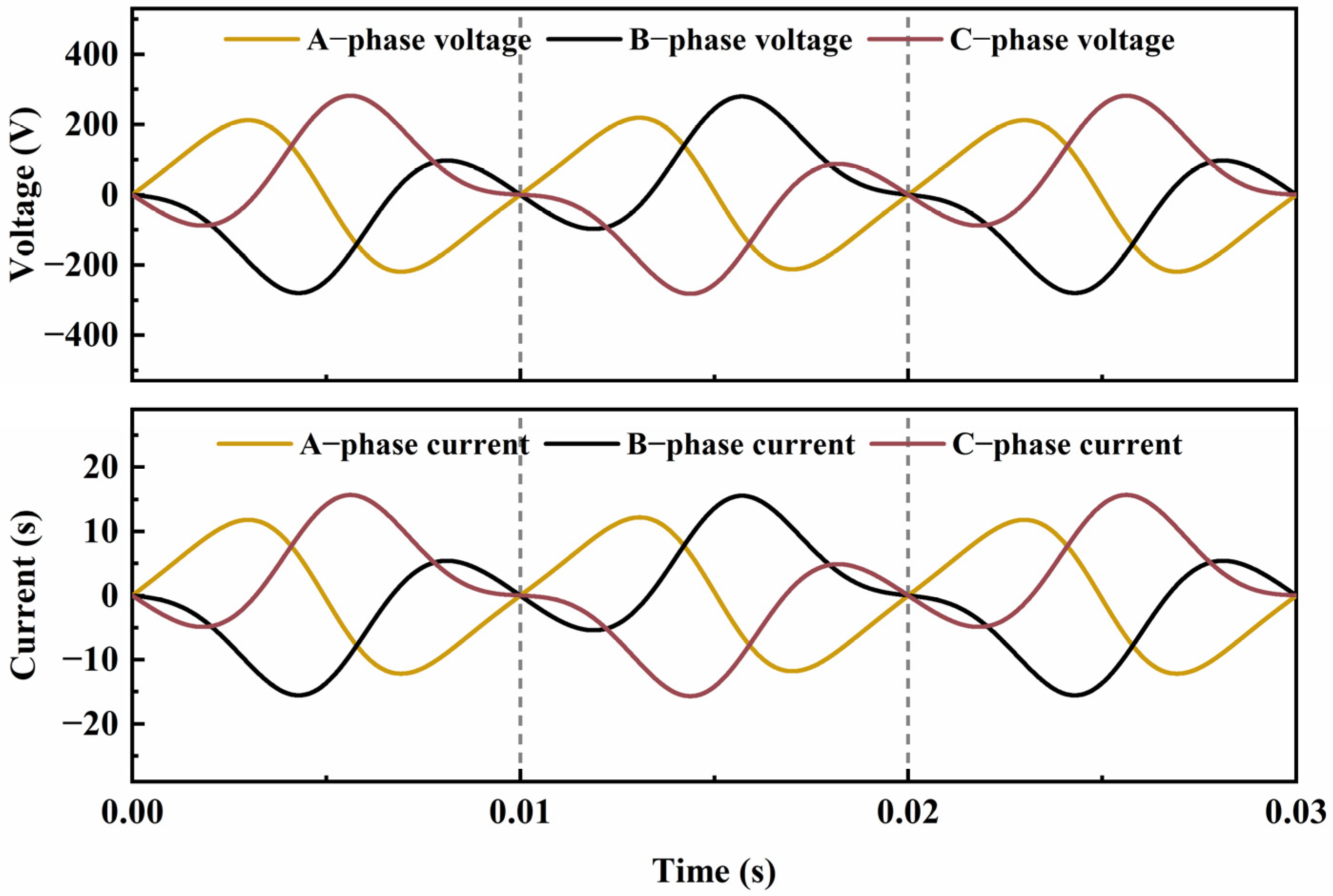
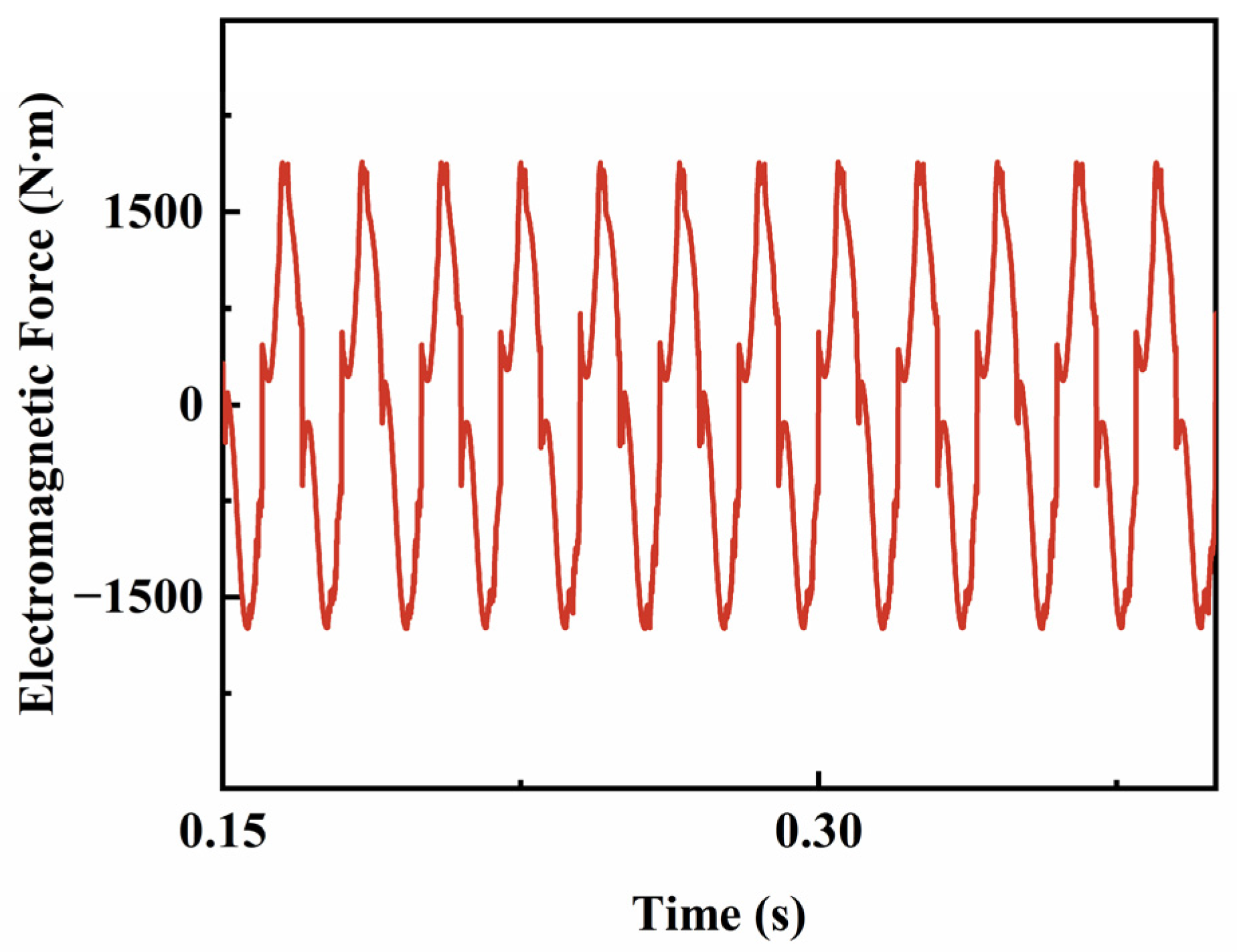
2.4. Analysis of Linear Motor Output Characteristics
3. Optimization of Controllable Rectification Based on Advanced Control Strategies
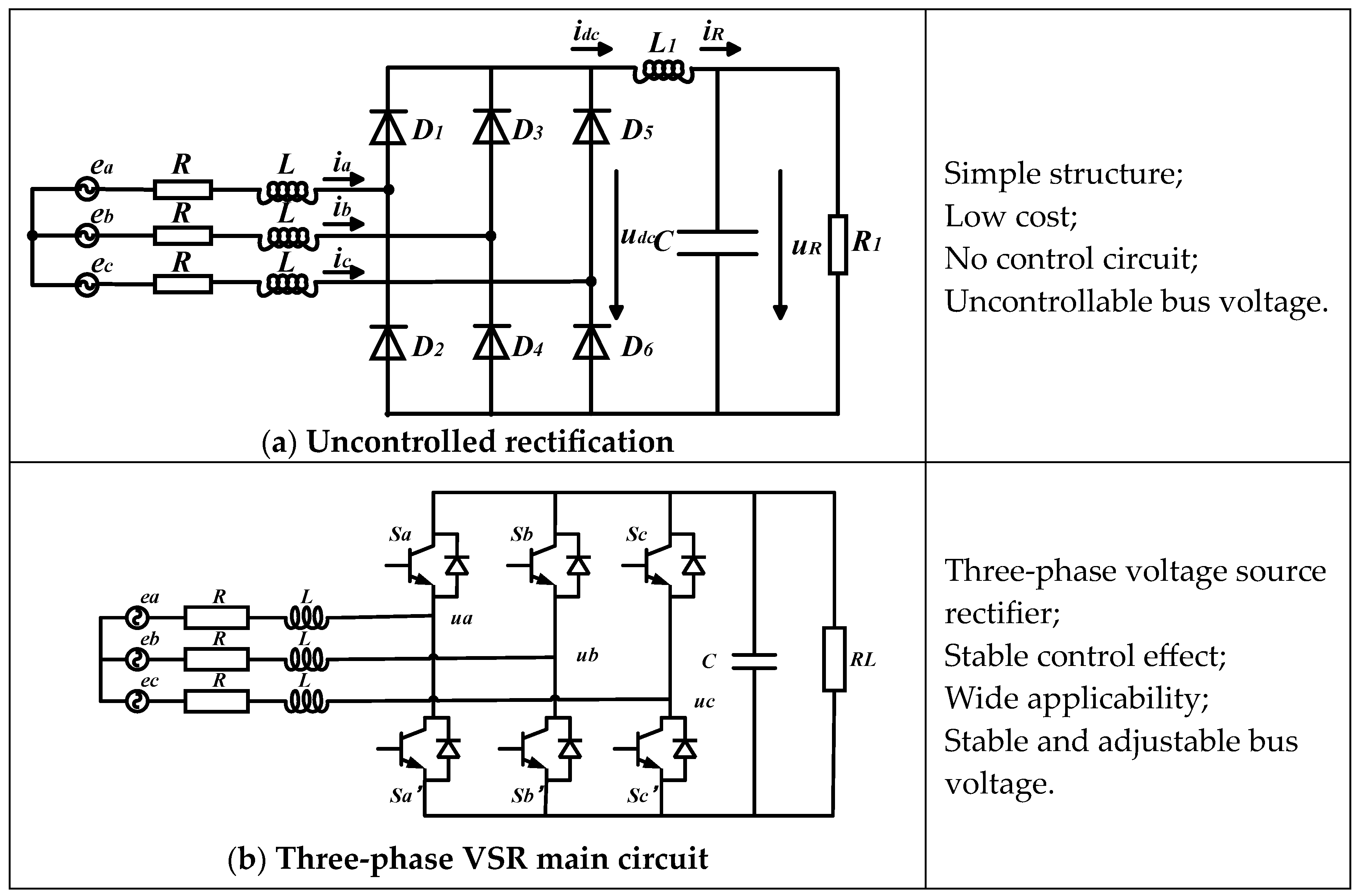
3.1. Uncontrolled Rectification
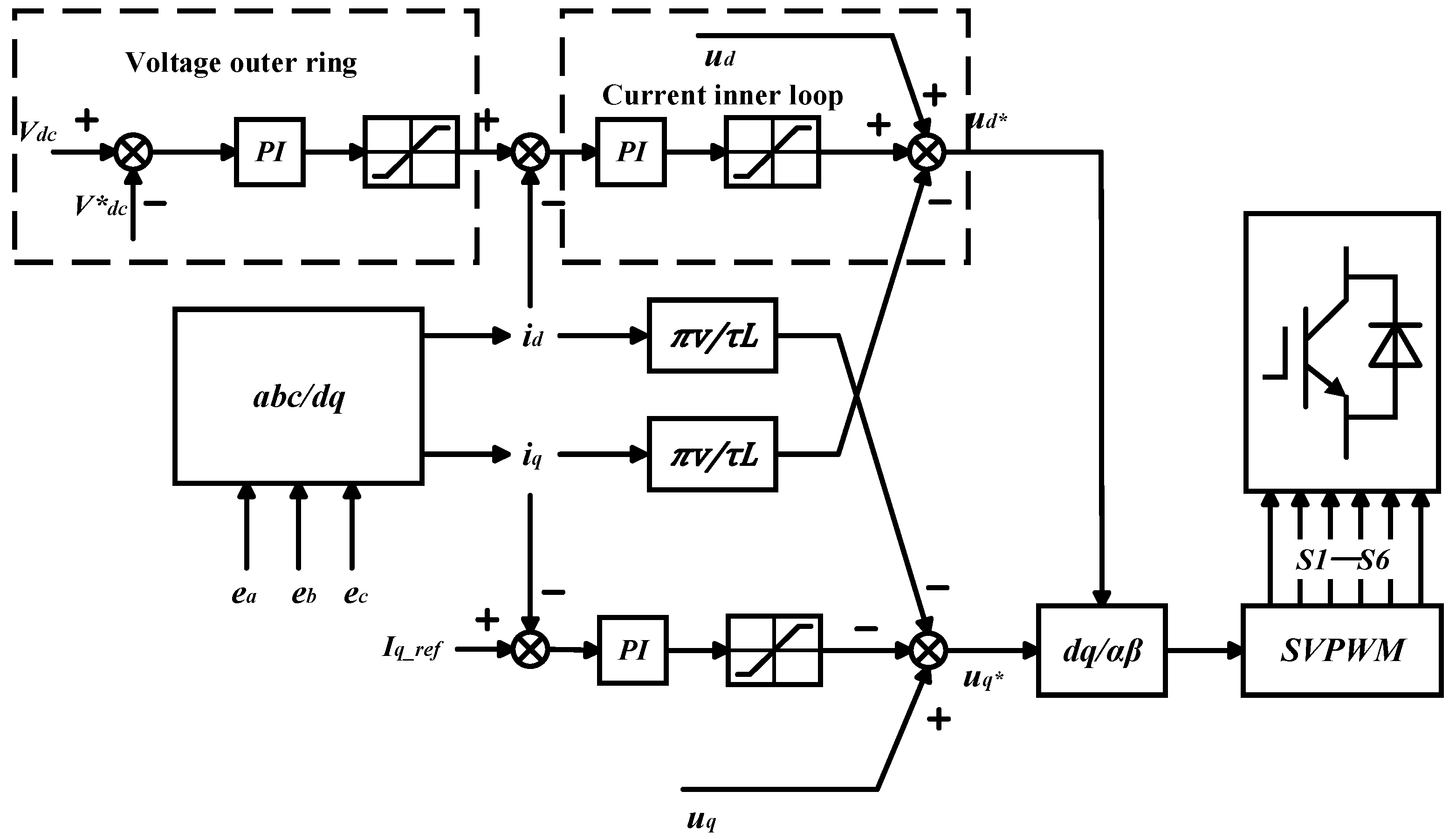
3.2. PWMC Rectification Control Strategy
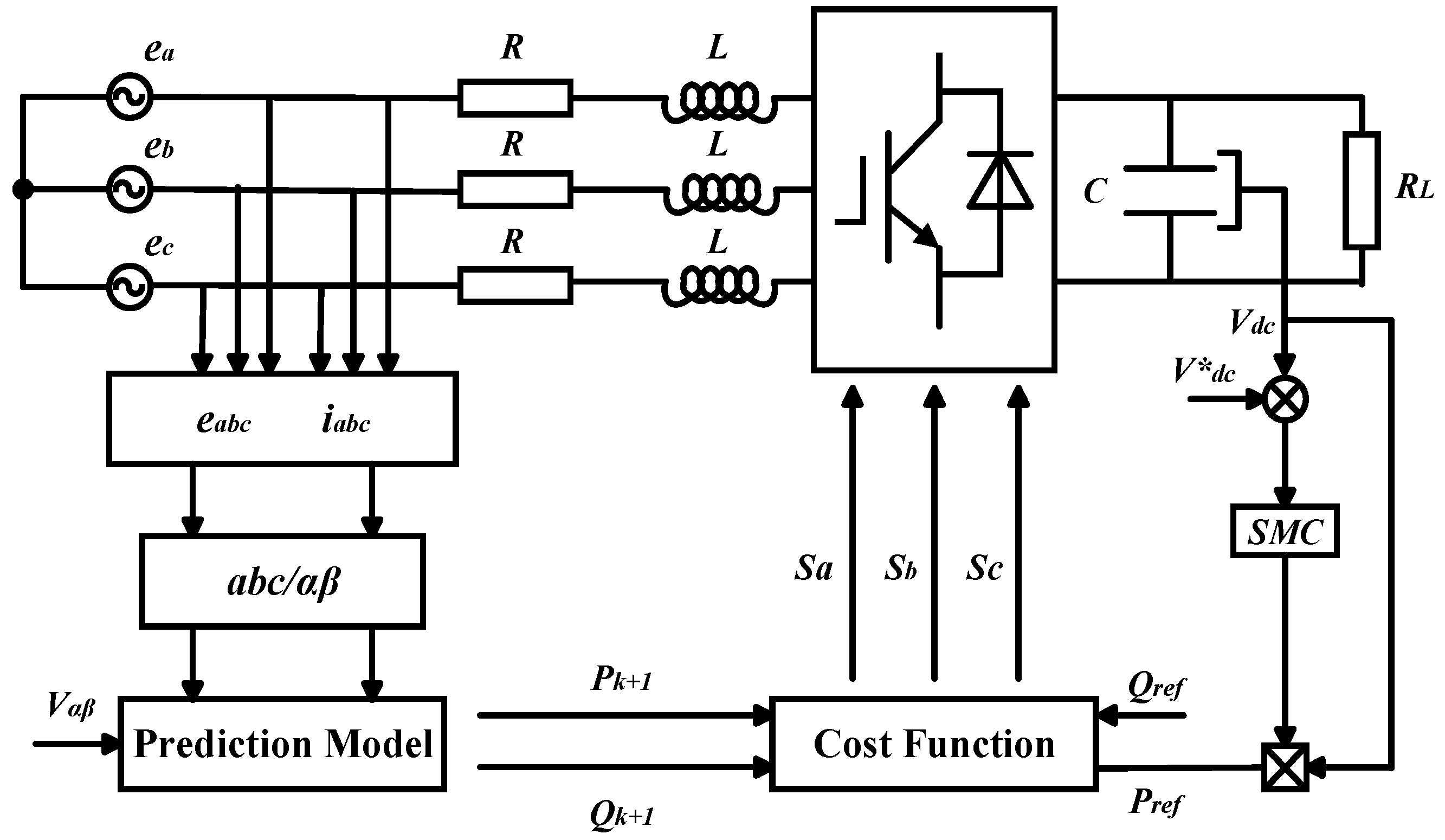
3.3. MPSMC Control Strategy
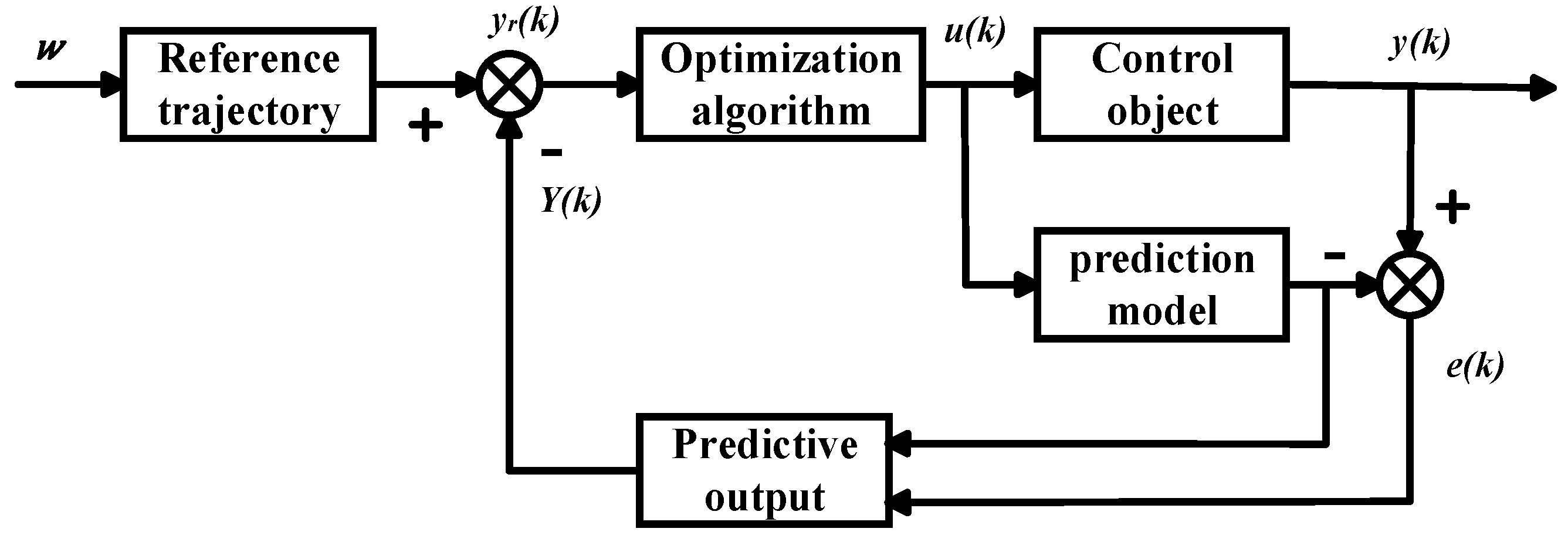
3.3.1. Design of Model Predictive Controller
- (1)
- Establish a predictive model. Establish a predictive model based on the current system model and predict the future state of the system based on its current state.
- (2)
- Perform rolling optimization. Build a suitable cost function to determine the best control quantity for upcoming systems.
- (3)
- System feedback correction. Model predictive control can provide feedback correction for errors based on the current state of system.
3.3.2. Design of Sliding Mode Controller
4. Evaluation of Electric Energy Output Quality
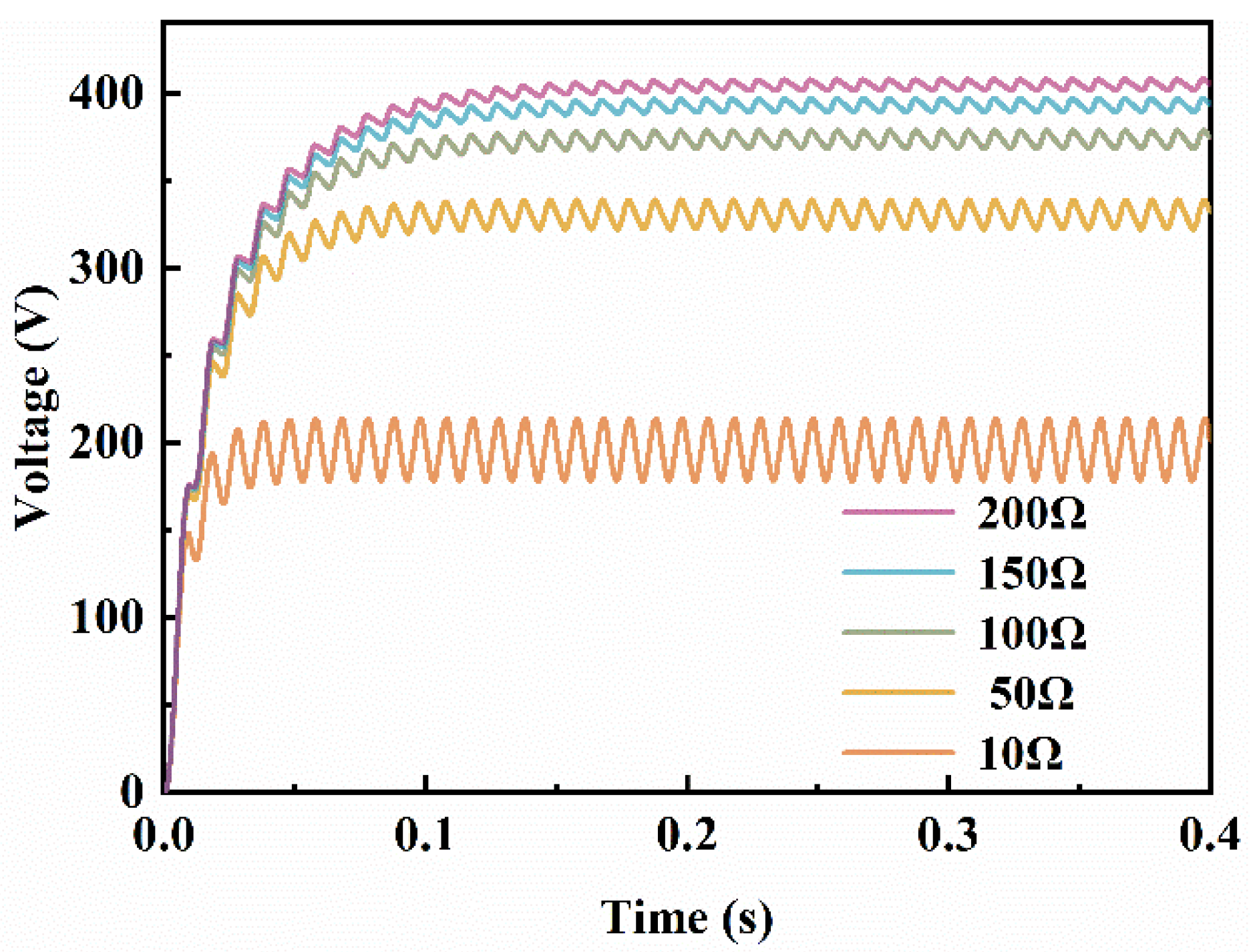
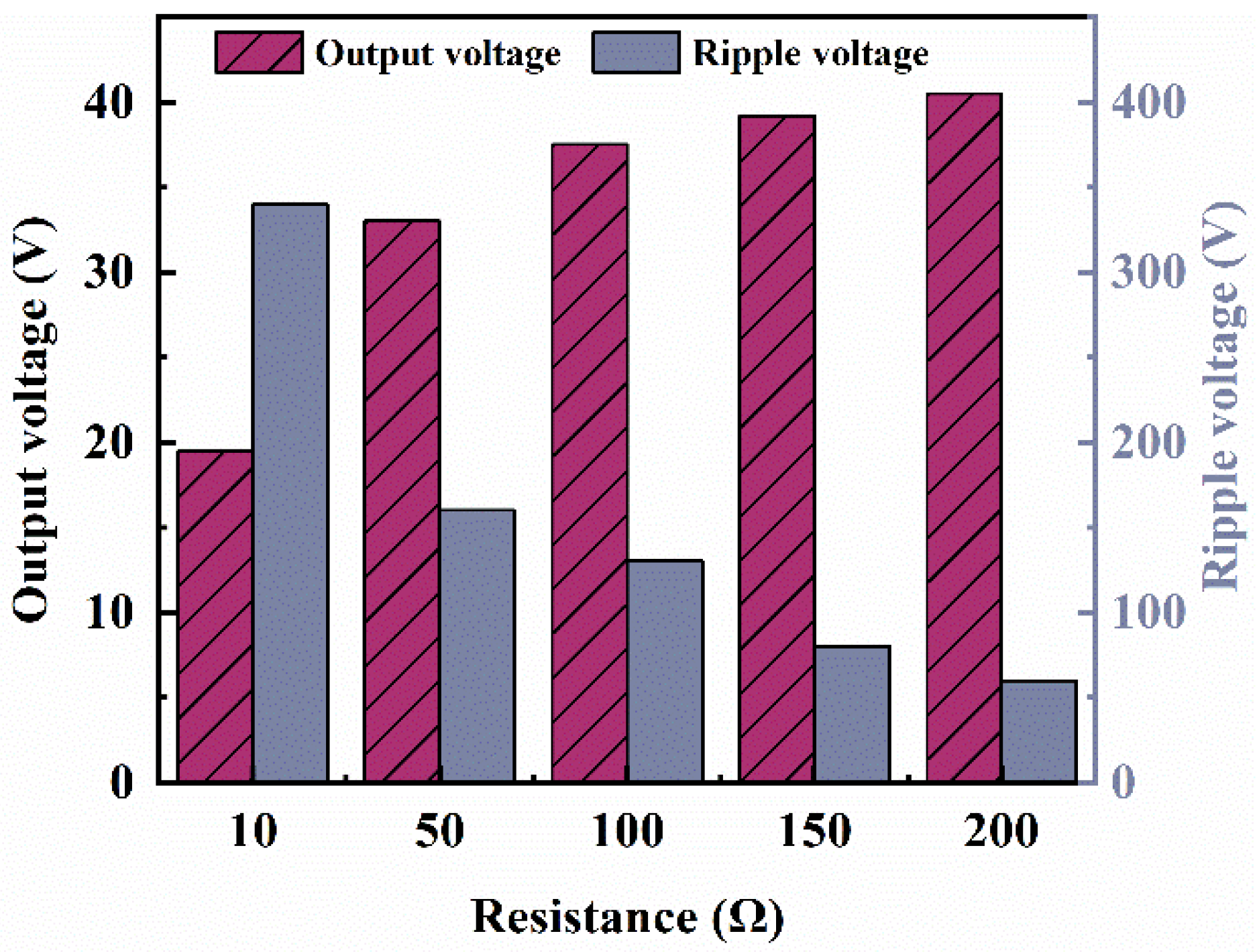
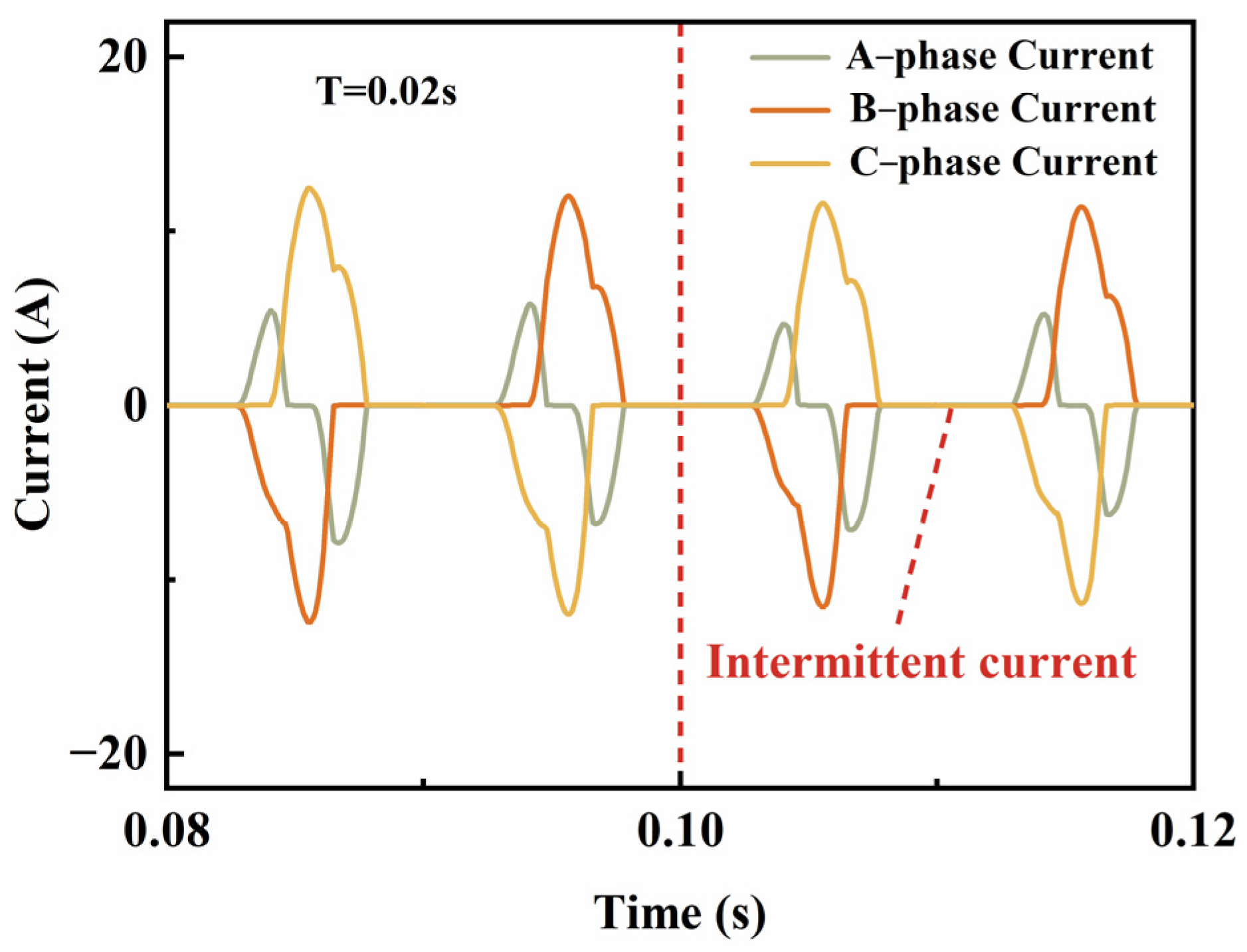
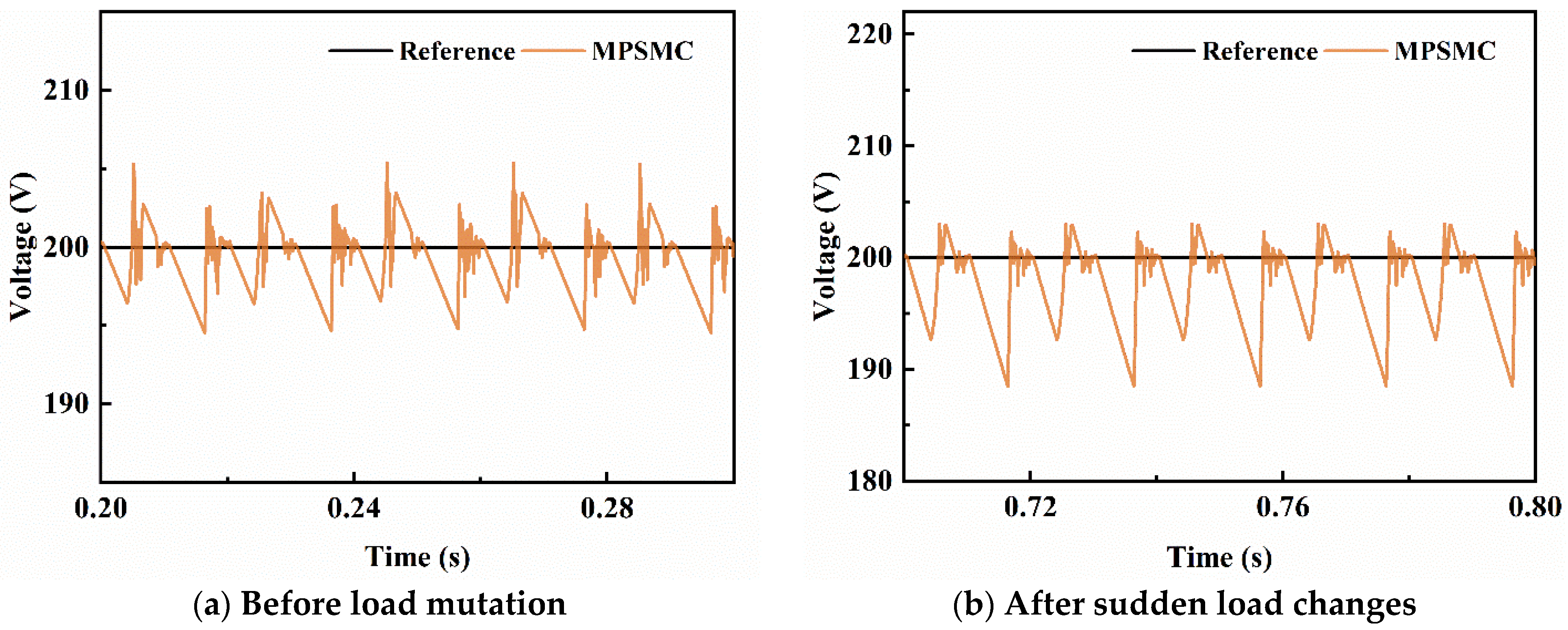
4.1. Robustness Analysis
- (1)
- Uncontrolled rectification
- (2)
- Robustness analysis of PWMC rectification and MPSMC rectification results
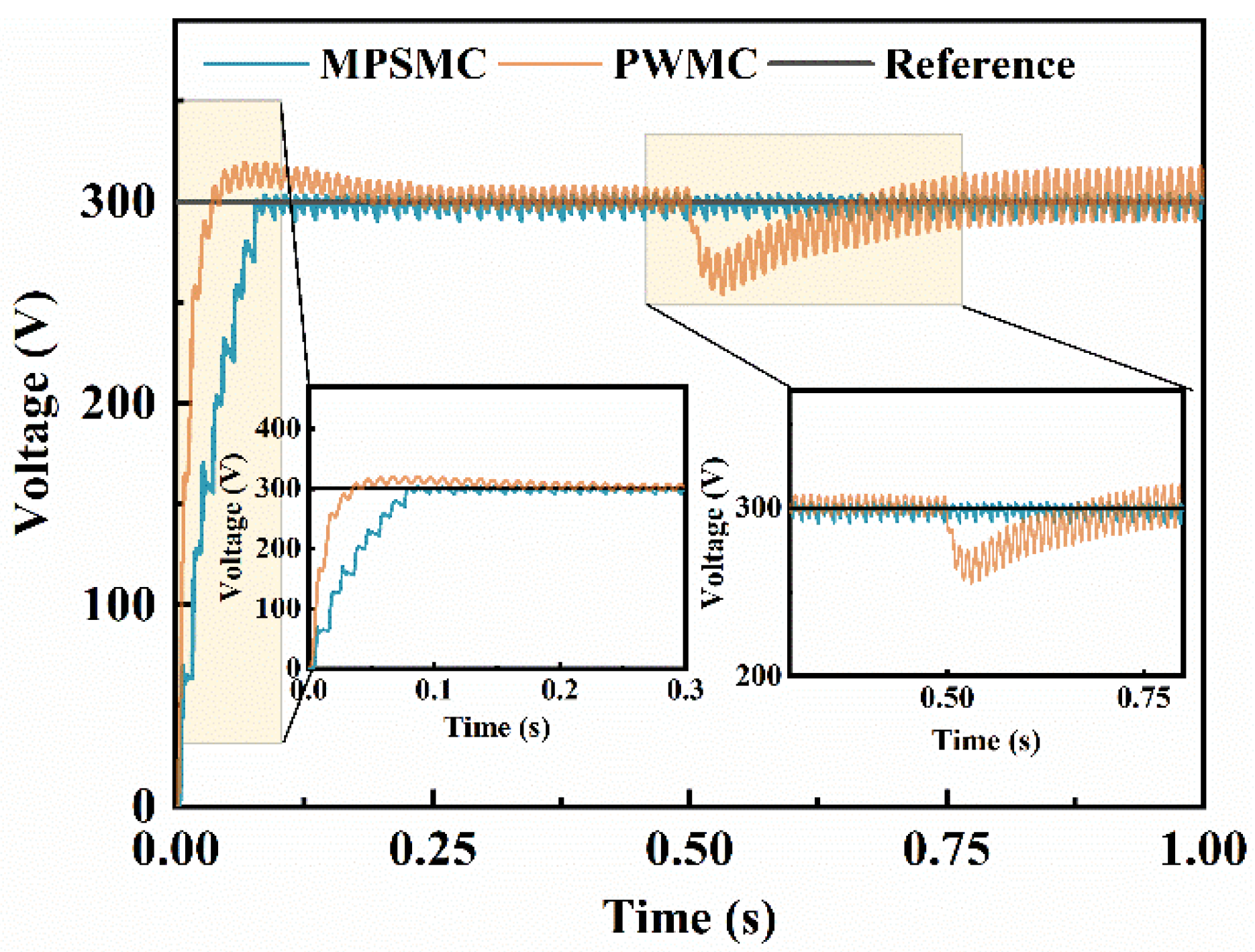
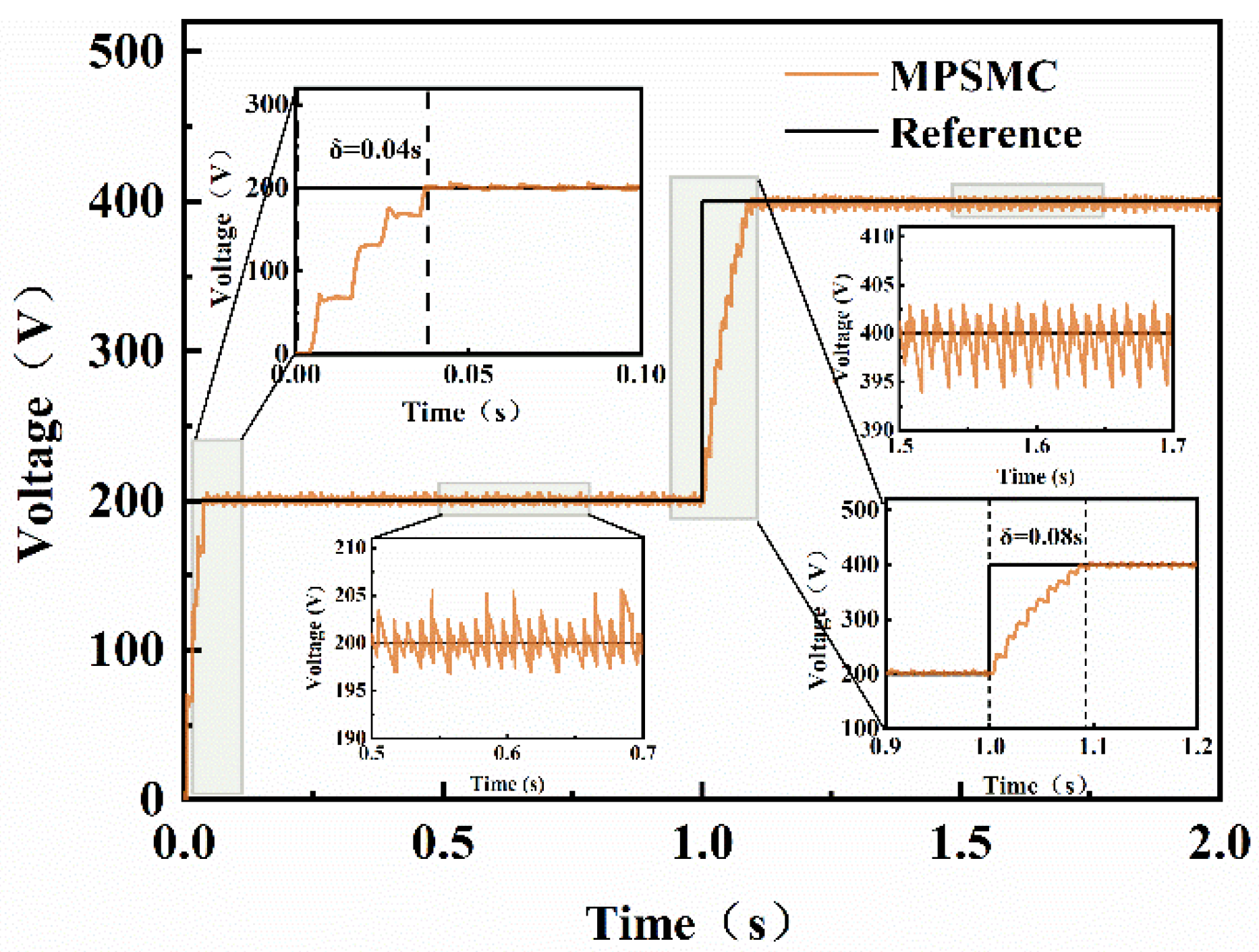
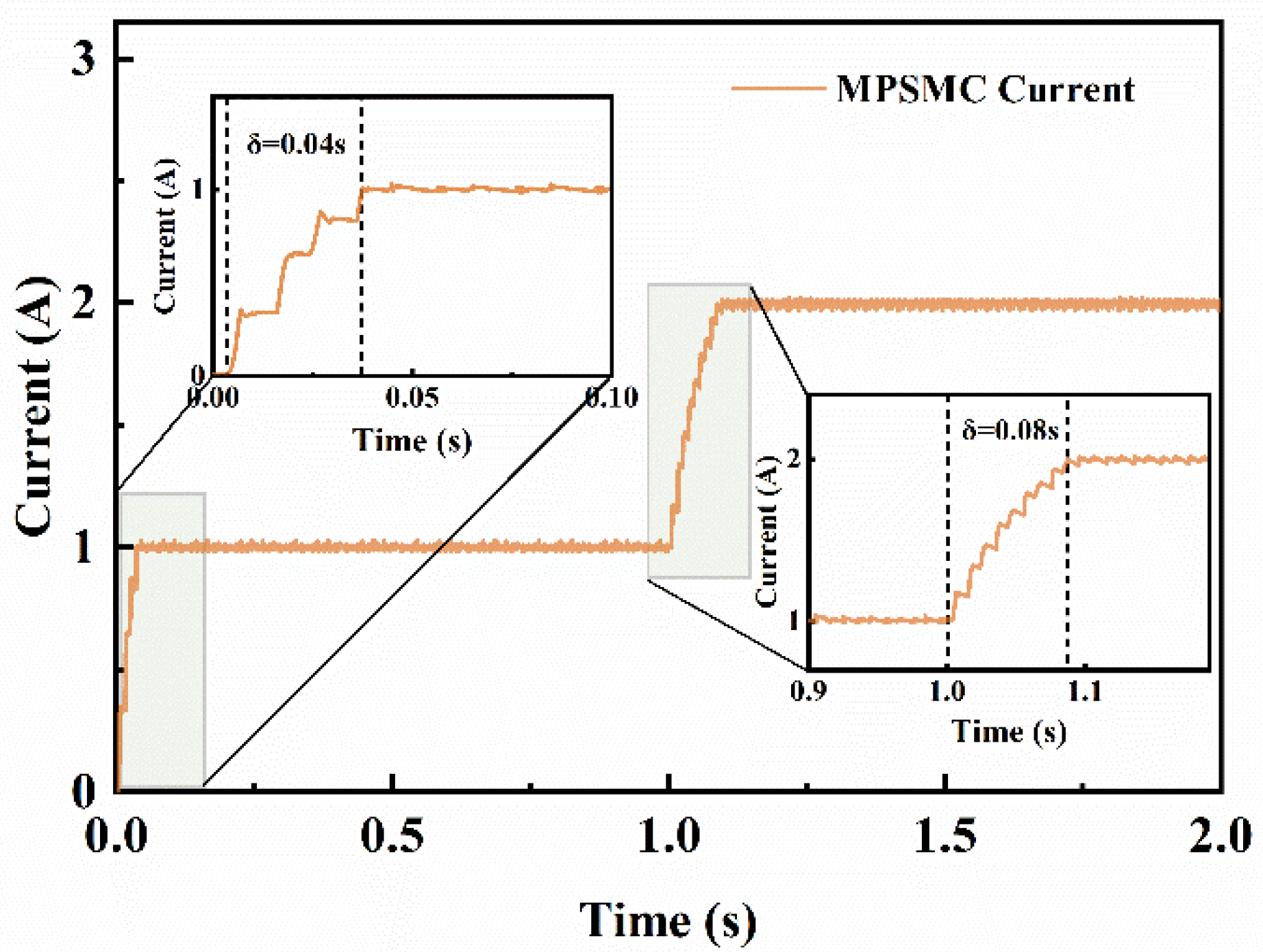
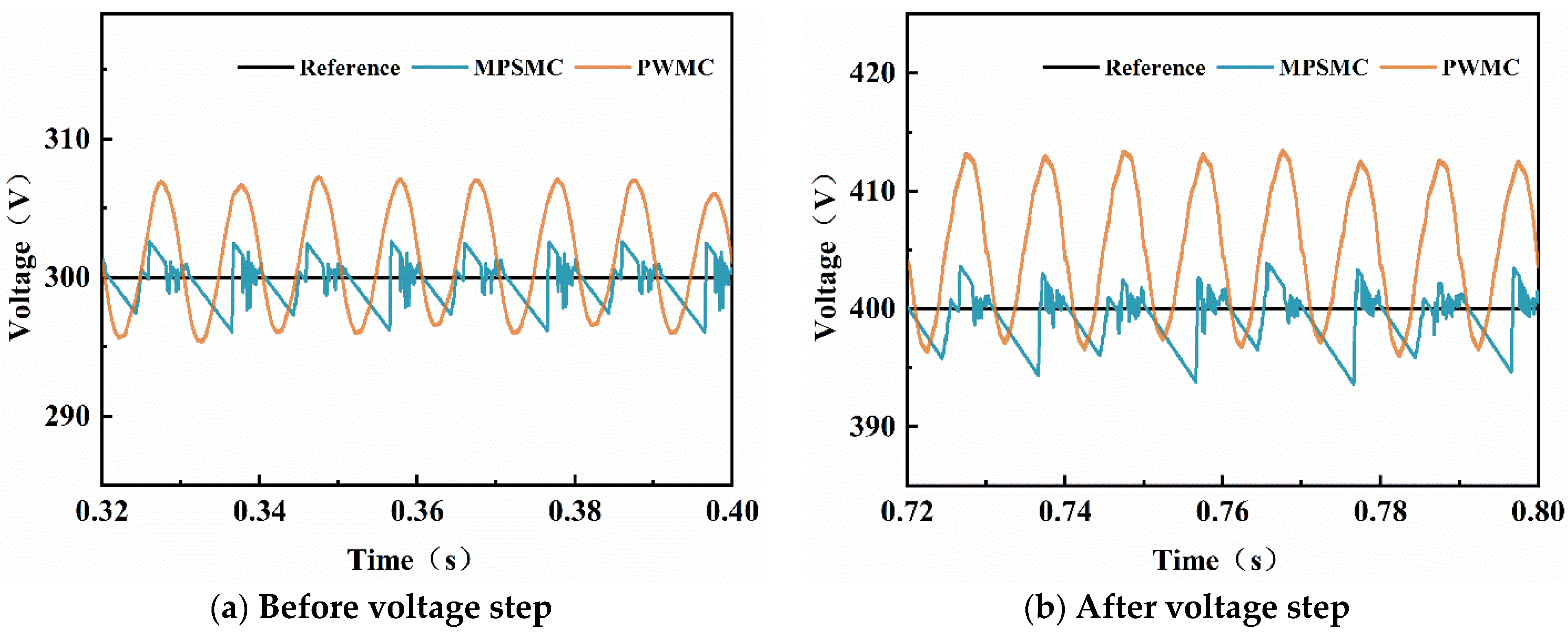
4.2. Analysis of Responsiveness and Accuracy
5. Conclusions
- (1)
- Uncontrolled rectification can convert three-phase AC to DC, but due to open-loop control, the output DC voltage is uncontrollable and fluctuates greatly, influenced by the linear motor’s characteristics.
- (2)
- Uncontrolled rectification will cause serious current disruption in the linear motor side of the system.
- (3)
- Model predictive sliding mode compound control enhances the system’s anti-interference capability. Compared to traditional PWM rectification, it offers faster response, better robustness, lower bus voltage ripple, and superior power quality.
- (4)
- Model predictive control and sliding mode control are nonlinear control methods. They adapt better in nonlinear settings like free-piston internal combustion linear power generation systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leick, M.T.; Moses, R.W. Experimental Evaluation of the Free Piston Engine-Linear Alternator (FPLA); Sandia National Lab: Albuquerque, NM, USA, 2015.
- Zheng, J.; Chen, J.; Zheng, P.; Wu, H.; Tong, C. Research on control strategy of free piston Stirling power generating system. Energies 2017, 10, 1609. [Google Scholar] [CrossRef]
- Li, J.; Zuo, Z.; Liu, W.; Jia, B.; Feng, H.; Wang, W.; Smallbone, A.; Roskilly, A.P. Generating performance of a tubular permanent magnet linear generator for application on free-piston engine generator prototype with wide-ranging operating parameters. Energy 2023, 278, 127851. [Google Scholar] [CrossRef]
- Chen, J.; Liao, Y.; Zhang, C.; Jiang, Z. Design and analysis of a permanent magnet linear generator for a free-piston energy converter. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 1719–1723. [Google Scholar]
- Gong, X.; Zaseck, K.; Kolmanovsky, I.; Chen, H. Modeling and predictive control of free piston engine generator. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4735–4740. [Google Scholar]
- Moriya, K.; Goto, S.; Akita, T.; Kosaka, H.; Hotta, Y.; Nakakita, K. Development of Free Piston Engine Linear Generator System Part3-Novel Control Method of Linear Generator for to Improve Efficiency and Stability; SAE Technical Paper; SAE: Warrendale, PA, USA, 2016. [Google Scholar]
- Lin, J.; Xu, Z.; Chang, S.; Yan, H. Finite-time thermodynamic modeling and analysis of an irreversible Miller cycle working on a four-stroke engine. Int. Commun. Heat Mass Transf. 2014, 54, 54–59. [Google Scholar] [CrossRef]
- Kock, F.; Haag, J.; Friedrich, H.E. The Free Piston Linear Generator-Development of an Innovative, Compact, Highly Efficient Range-Extender Module; SAE Technical Paper; SAE: Warrendale, PA, USA, 2013. [Google Scholar]
- Raheem, A.T.; Aziz, A.R.A.; Zulkiffi, S.A.; Rahem, A.T.; Ayandotun, W.B. A review of free piston engine control literature—Taxonomy and techniques. Alex. Eng. J. 2022, 61, 7877–7916. [Google Scholar] [CrossRef]
- Chen, C.; Tong, C.; Liu, B.; Zheng, P.; Jing, S. Trajectory-Regulation-Based Segmented Control for Dead Center Positions Tracking of Free-Piston Linear Generator. IEEE Trans. Ind. Electron. 2022, 70, 3426–3436. [Google Scholar] [CrossRef]
- Vu, D.N.; Lim, O. Piston motion control for a dual free piston linear generator: Predictive-fuzzy logic control approach. J. Mech. Sci. Technol. 2020, 34, 4785–4795. [Google Scholar] [CrossRef]
- Raheem, A.T.; Aziz, A.R.A.; Zulkiffi, S.A.; Baharom, M.B.; Rahem, A.T.; Ayandotun, W.B. Optimisation of operating parameters on the performance characteristics of a free piston engine linear generator fuelled by CNG–H2 blends using the response surface methodology (RSM). Int. J. Hydrogen Energy 2022, 47, 1996–2016. [Google Scholar] [CrossRef]
- Ayandotun, W.B.; Aziz, A.R.A.; Karim, Z.A.A.; Mohammed, S.E.; Raheem, A.T.; Ismael, M.A. Investigation on the combustion and performance characteristics of a DI free piston linear generator engine fuelled with CNG-CO2 blend. Appl. Therm. Eng. 2021, 198, 117441. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, G.; Wu, D.; Li, T.; Zhang, Z.; Wang, N. Characteristics of ammonia/ hydrogen premixed combustion in a novel Linear Engine Generator. Multidiscip. Digit. Publ. Inst. Proc. 2020, 58, 2. [Google Scholar]
- Ismael, M.A.; Aziz, A.R.A.; Mohammed, S.E.; Baharom, M.B.; Ibrahim, M.H.; Sahalan, M.; Qawiy, A. Effect of aspect ratio on frequency and power generation of a free-piston linear generator. Appl. Therm. Eng. 2021, 192, 116944. [Google Scholar]
- Sato, M.; Naganuma, K.; Nirei, M.; Yamanaka, Y.; Suzuki, T.; Goto, T.; Bu, Y.; Mizuno, T. Improving the constant-volume degree of combustion considering generatable range at low speed in a free-piston engine linear generator system. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1703–1710. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, Z.; Jia, B.; Zuo, Z.; Smallbone, A.; Roskilly, A.P. Investigation of the optimum operating condition of a dual piston type free piston engine generator during engine cold start-up process. Appl. Therm. Eng. 2021, 182, 116124. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y.; Wang, H.; Su, M.; Huang, S. A hybrid control scheme for three-phase Vienna rectifiers. IEEE Trans. Power Electron. 2017, 33, 629–640. [Google Scholar] [CrossRef]
- Tai, L.; Lin, M.; Li, H.; Li, Y. A novel three-vector-based model predictive direct power control for three-phase PWM rectifier. Electronics 2021, 10, 2579. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, C.; Zhang, G.; Song, J.; Zhang, C.; Duan, B. Disturbance observer-based finite-time control for three-phase AC–DC converter. IEEE Trans. Ind. Electron. 2021, 69, 5637–5647. [Google Scholar] [CrossRef]
- Wang, W.; Yin, H.; Guan, L. Parameter setting for double closed-loop vector control of voltage source PWM rectifier. Trans. China Electrotech. Soc. 2010, 25, 67–72. [Google Scholar]
- Kim, J.S.; Kim, D.H.; Lee, J.H.; Lee, J.S. Smooth pulse number transition strategy considering time delay in synchronized SVPWM. IEEE Trans. Power Electron. 2022, 38, 2252–2261. [Google Scholar] [CrossRef]
- He, H.; Si, T.; Sun, L.; Liu, B.; Li, Z. Linear active disturbance rejection control for three-phase voltage-source PWM rectifier. IEEE Access 2020, 8, 45050–45060. [Google Scholar] [CrossRef]
- Li, J.; Wang, M.; Wang, J.; Zhang, Y.; Yang, D.; Wang, J.; Zhao, Y. Passivity-based control with active disturbance rejection control of Vienna rectifier under unbalanced grid conditions. IEEE Access 2020, 8, 76082–76092. [Google Scholar] [CrossRef]
- Eskandari, B.; Yousefpour, A.; Ayati, M.; Kyyra, J.; Pouresmaeil, E. Finite-time disturbance-observer-based integral terminal sliding mode controller for three-phase synchronous rectifier. IEEE Access 2020, 8, 152116–152130. [Google Scholar] [CrossRef]
- Barzegar-Kalashani, M.; Tousi, B.; Mahmud, M.A.; Farhadi-Kangarlu, M. Non-linear integral higher-order sliding mode controller design for islanded operations of T-type three-phase inverter-interfaced distributed energy resources. IET Gener. Transm. Distrib. 2020, 14, 53–61. [Google Scholar] [CrossRef]
- Wenrui, J.; Zhicong, Z. Predictive Direct Power Control of Three-phase Pulse Width Modulation Rectifiers. Inf. Control. 2021, 50, 754–760. [Google Scholar]
- Ma, H.; Zhao, J.; Yang, M.; Lu, Y. Predictive Direct Power control for Three-phase Vienna Rectifier with Simplied SVM. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar]
- Yan, X.; Zhao, S.; Dong, Q.; Wang, L.; Liu, Z.; Bai, S. Comprehensive evaluation of electric vehicle charger performance. Power Syst. Prot. Control 2020, 48, 164–171. [Google Scholar]
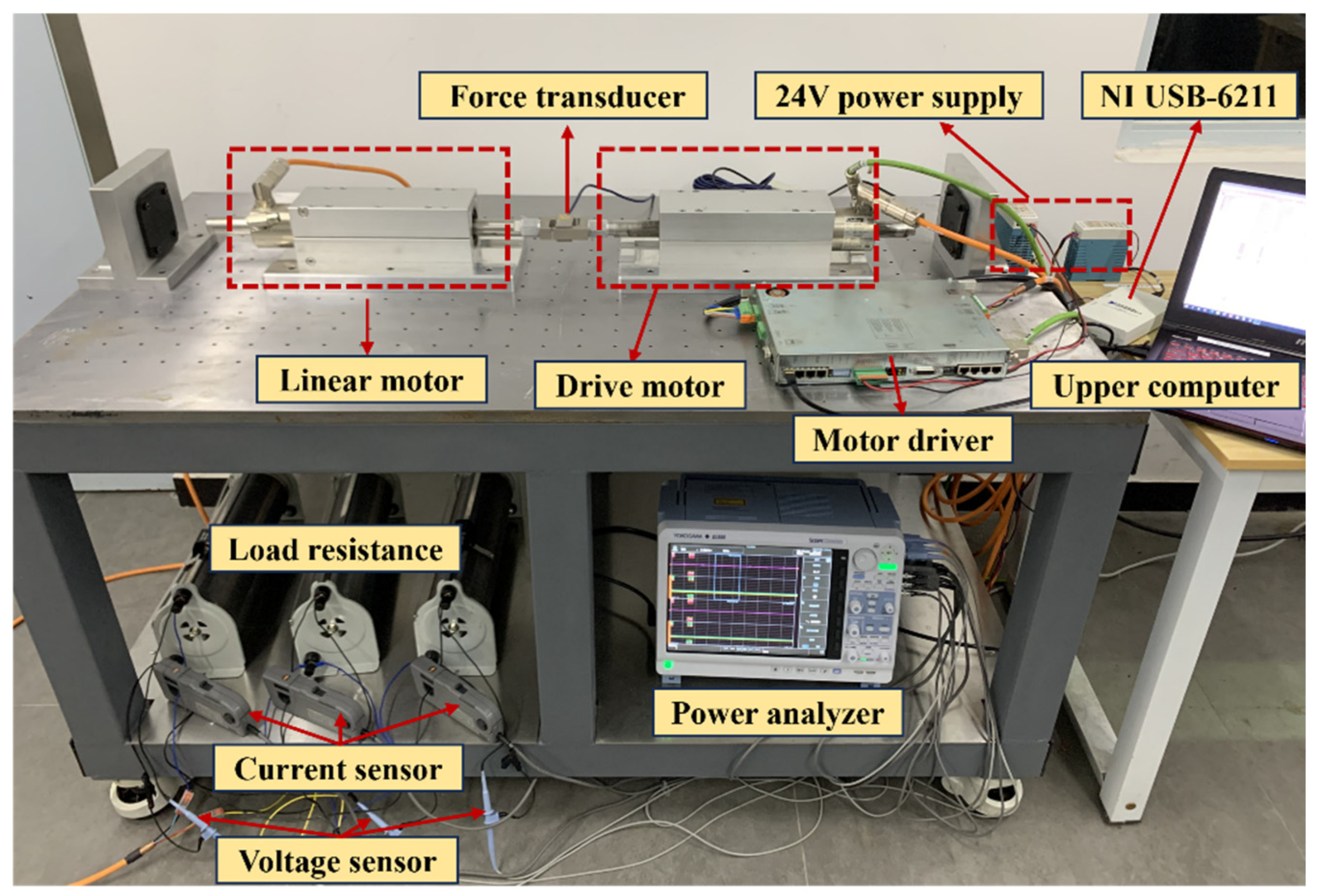






| Design Parameters | Parameter | Design Parameters | Parameter |
|---|---|---|---|
| Mass of moving sub component/kg | 3.75 | Maximum travel distance/mm | 80 |
| Cylinder diameter/m | 0.051 | Cylinder depth/m | 0.029 |
| Line resistance/Ohm | 10.16 | Line inductance/mH | 12.78 |
| Motor thrust constant/N/A | 78.9 | Permanent magnet magnetic flux | 0.24 |
| Equipment | Type | Parameter |
|---|---|---|
| Drive motor | P10 series | Peak force: 1600 N; Peak speed: 6.5 m/s; Peak current: 20 A; 20 μm |
| Motor driver | E1400 series | 32 bit; 3 400/480 VAC; Supply voltage: 24 V |
| Power analyzer | Yokogawa DL950 | 200 MS/s Sampling rate; 14 bit; 10 GE Data transmission rate; 8 G Point memory |
| Current sensor | Yokogawa probes | 150 Arms; 10 MHz; 1% Accuracy |
| Voltage sensor | Yokogawa probes | ±1000 Vpeak; 60 MHz; 10: 1 |
| Electromagnetic force sensor | HBM S9N | 1 kN; 0.02%FS; 2 MV/V |
| Data acquisition instrument | NI USB-6211 | 250 kS/s; 16 bit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, B.; Sun, L.; Wei, Y.; Feng, H.; Li, J.; Lei, Q.; Miao, J.; Zuo, Z. Demonstration of an Advanced Rectification Strategy on a Linear Generator for Better Electricity Quality. Appl. Sci. 2025, 15, 5044. https://doi.org/10.3390/app15095044
Jia B, Sun L, Wei Y, Feng H, Li J, Lei Q, Miao J, Zuo Z. Demonstration of an Advanced Rectification Strategy on a Linear Generator for Better Electricity Quality. Applied Sciences. 2025; 15(9):5044. https://doi.org/10.3390/app15095044
Chicago/Turabian StyleJia, Boru, Liutao Sun, Yidi Wei, Huihua Feng, Jian Li, Qiming Lei, Jiazheng Miao, and Zhengxing Zuo. 2025. "Demonstration of an Advanced Rectification Strategy on a Linear Generator for Better Electricity Quality" Applied Sciences 15, no. 9: 5044. https://doi.org/10.3390/app15095044
APA StyleJia, B., Sun, L., Wei, Y., Feng, H., Li, J., Lei, Q., Miao, J., & Zuo, Z. (2025). Demonstration of an Advanced Rectification Strategy on a Linear Generator for Better Electricity Quality. Applied Sciences, 15(9), 5044. https://doi.org/10.3390/app15095044







