Forging Robust Cognition Resilience in Large Language Models: The Self-Correction Reflection Paradigm Against Input Perturbations

Abstract

Large language models (LLMs) have been widely used in real-world applications due to their ability to decipher and make sense of perturbed information. However, the performance of LLMs that suffered from input perturbations has not been fully analyzed. In this paper, we propose a self-correction reflection method inspired by human cognition to improve robustness and mitigate the impact of perturbations on LLM performance. Firstly, we analyze the vulnerabilities of tokenization in LLMs through empirical demonstrations, comparative analysis with human cognition, and theoretical investigation of perturbation susceptibility. Secondly, we imitate the correction of input information in the human brain, which is enhanced by the consistency principle, aiming to enable the model to correct the perturbation and reduce the impact on the final response. Finally, we conduct experiments to validate the method’s efficacy, demonstrating improved performance across multiple models and datasets. We introduce a new evaluation metric, Model-Specific Cosine Similarity (MSCS), to quantify how well a specific model understands perturbation text, providing a more comprehensive evaluation of different LLM architectures. Particularly for different types of perturbations, after applying self-correction reflection, the average MSCS improvement across all models reaches 10.88%, while the average ACC improvement is 10.22%. The study also underscores the need for more innovative tokenization techniques and architectural design to achieve human-like cognitive robustness. This study could pave the way for more reliable, adaptable, and intelligent language models capable of thriving in practical applications.

1. Introduction

In our daily lives, the human brain demonstrates remarkable adaptability when confronted with input perturbations [1]. For instance, when faced with a sentence like “Hvae a ncie day. Hpoe you konw the infromation”, humans can typically decipher the intended meaning almost effortlessly by leveraging context and cognitive reasoning. This resilience highlights the extraordinary flexibility of human cognition and underscores the sophisticated mechanisms underlying context-based language understanding.

In stark contrast, current large language models (LLMs), despite being trained on vast amounts of natural language data, often exhibit a striking vulnerability to input perturbations [2]. Even minor perturbations in input can drastically affect the LLMs’ responses and can lead to outright misinterpretations. This fragility raises significant concerns about the reliability of LLMs, particularly in critical applications such as medicine or law, where precision is paramount.

To address the issue of LLM reliability when faced with input perturbations, our study aims to figure out the underlying reasons why LLMs are fragile and to systematically assess possible solutions. Drawing on knowledge from both neuroscience and psycholinguistics, our research reveals that the tokenization process, which breaks down inputs with a fixed vocabulary mapping, is the key source of this vulnerability. As shown in Figure 1, we demonstrate how small input changes can significantly impact the performance of various mainstream LLMs, causing semantic distortions that undermine the reliability of the models.

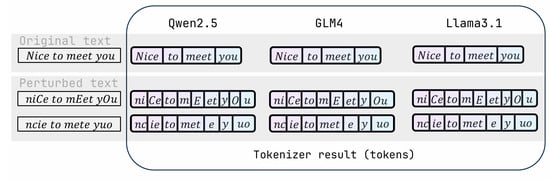
Figure 1. The significant variations in tokenization results (tokens) of the perturbed text by different LLMs.

Research [3] has shown that LLMs are capable of imitating the natural language processing abilities of the human brain, allowing us to draw an analogy between the human brain and LLMs. In this context, we further extend this analogy by comparing the working principles of LLMs with those of the human brain. Specifically, based on the work [4], we hypothesize that each LLM layer corresponds to different brain regions. Furthermore, while distinct in mechanism, the tokenization process in LLMs shares functional similarities with how the brain processes incoming linguistic information. Similarly to how neural systems transform sensory inputs into interpretable patterns [5], LLMs employ tokenization to convert raw text into vector representations suitable for computational operations. If this input information is inherently flawed and the model (or brain) fails to correct these perturbations effectively, the output will tend to be compromised [6]. Drawing on [7]’s insight that LLMs intrinsically possess perturbation-correction capabilities similar to the human brain, we develop a self-correction reflection mechanism that leverages the model’s existing capacities without additional training. Unlike approaches requiring external corrections, our method employs the consistency principle [8] to guide the model in autonomously detecting and rectifying input perturbations before response generation, thereby preserving semantic integrity while maintaining the model’s original architecture.

The main contributions of this paper are summarized as follows:

• We conduct a systematic analysis of how input perturbations influence LLM reliability from interdisciplinary perspectives (e.g., neuroscience, psychology), examining how tokenization mechanisms shape model robustness.
• We propose the Model-Specific Cosine Similarity (MSCS) framework that enables granular evaluation of perturbation sensitivity across different models, overcoming the limitation of traditional metrics (e.g., BLEU or BERTScore), which offer only coarse-grained similarity assessments and cannot diagnose model-specific perturbation sensitivity.
• We develop a self-contained reflection-based correction approach that requires neither additional training data nor external linguistic tools, distinguishing itself from conventional grammar correction systems while achieving robust performance through intrinsic consistency verification.
• We perform comprehensive architectural comparisons between Transformer, Mamba, and Hybrid models with perturbation-specific evaluation, providing practical insights for architecture selection in noise-prone scenarios.

The remainder of this paper is organized as follows. Section 2 examines the neurocognitive mechanisms for processing perturbed inputs and analyzes the limitations of existing correction methods in LLM tokenization. Section 3 details our self-correction reflection framework, presenting its formulation of variational inference and its consistency-driven enhancement mechanism. Section 4 introduces the Model-Specific Cosine Similarity (MSCS) metric to evaluate perturbation impacts across different architectures. Section 5 validates our method through systematic experiments that compare Transformer and Mamba models in various perturbation scenarios. Section 6 discusses the advantages of the proposed self-correction reflection approach, while also addressing its inherent limitations and potential challenges in practical applications. Section 7 concludes with recommendations for achieving human-level robustness through cognitive-aligned architectural innovations.

2. Related Work

2.1. Human Adaptation to Input Perturbations from Neurological and Psychological Perspectives

Human beings possess a remarkable ability to understand and make sense of various forms of input, even when it is perturbed.

From a neurological perspective, the language processing areas of the brain, including Broca’s and Wernicke’s areas, play a crucial role [9]. When presented with perturbed texts, these areas first work to decipher the intent of the text and attempt to correct it [10]. For example, studies using functional magnetic resonance imaging (fMRI) have shown that the brain initially registers irregularities and then attempts to map the chaotic elements into known language patterns [11,12]. However, such self-correction reflections remain underexplored in LLMs. When disturbed text is input, the large language model will perform autoregressive generation based on the disturbed text and will not correct the text.

Psychologically, human comprehension is dependent on context, semantic knowledge, and prior experience. The context provides valuable cues that help overcome the confusion caused by perturbations [13]. For example, in a sentence like “The cat chased the muose” with some letter swaps, the overall context of a typical predator–prey relationship allows the reader to infer the correct meaning. Furthermore, continuous exposure to a large amount of language over time allows human beings to develop heuristics and expectations [14]. We subconsciously predict what words are likely to follow based on the initial words in a sentence, which helps to compensate for perturbations. However, unlike the brain, LLMs’ word segmentation is deterministic, making them vulnerable to perturbations such as spelling errors or irregular combinations of tokens [15]. These disruptions can fragment subword units or distort semantics, where minor input deviations rarely compromise brain comprehension.

In general, the human cognitive system demonstrates remarkable resilience to input perturbations through integrated neural and psychological adaptation mechanisms. These self-adaptive processes stand in stark contrast to the current limitations of LLMs, where deterministic tokenization and rigid pattern-matching make them vulnerable to input perturbations that humans effortlessly overcome. We posit that by emulating architectures inspired by human self-correction frameworks, it may be possible to enhance the robustness of LLMs, particularly when processing perturbed inputs, whereas purely autoregressive generation approaches prove inadequate.

2.2. Limitations of External Correction Methods in Tokenization

Although LLMs have made significant advances in natural language processing, they still exhibit vulnerability when confronted with input perturbations, particularly in the tokenization stage [16]. Tokenization is the process of converting the input text into discrete units (tokens) that the model can understand [17]. However, LLMs generally rely on tokenizers that are deterministic and vulnerable to input perturbations, such as case changes. Even a small number of text perturbations can cause significant variations in input tokens, which in turn affects the model’s understanding of the text.

In recent research, the primary focus has been on improving model architectures, such as the Transformer, and newer architectures such as Mamba [18,19] and RWKV [20]. These models are designed to improve efficiency and performance in various natural language processing (NLP) tasks, but the underlying tokenization is often overlooked. Although these advances focus on improving model capacity and generalization, they do not address the issue caused by input perturbations during tokenization.

Existing solutions to mitigating errors rely predominantly on external correction methods, such as applying predefined rules or employing additional trained models to post-process perturbed inputs [21]. However, these approaches have critical drawbacks. First, external correction modifies the original input text to align with the expectations of the tokenizer, which risks altering or discarding semantically important information. For example, case normalization may erase distinctions between proper nouns and common terms. Second, such methods lack scalability: each type of perturbation often requires manual drafting rules or retraining of correction models [22]. Some recent efforts attempt to enhance robustness through runtime anomaly detection using large language models or statistical learning [23], or by embedding Covert Timing Channel (CTC) detection in system-level defenses [24]. Others improve semantic understanding with contextualized embeddings [25]. Although these methods reflect a growing emphasis on system resilience and align in part with Zero Trust principles, they still operate as external additions and do not fundamentally address the vulnerability of the tokenizers. As a result, these solutions often struggle to generalize across diverse and unpredictable perturbations in real-world inputs.

In summary, while external correction methods have achieved some success in mitigating errors during tokenization, they inherently limit the adaptability and scalability of LLM. The challenge lies in developing a more intrinsic approach that mirrors human cognitive agility and automatically adapts to noise during tokenization. Our proposed method addresses this gap by integrating self-correction capabilities through the tokenization process, ensuring semantic fidelity without external interventions. Table 1 illustrates the key differences between our approach and existing methods, emphasizing the advantages of our self-correcting mechanism in handling diverse perturbations autonomously.

Table 1. Comparison of external correction methods and the self-correction reflection.

Method	External Intervention	Scalability	Semantic Integrity
Standard External Correction	Required	Limited	Potentially Compromised
Self-Correction (ours)	Not Required	High	Preserved

3. Self-Correction Reflection

To address the limitation of the LLM’s deterministic tokenization process being vulnerable to input perturbations (e.g., spelling errors or irregular token combinations), we proposed self-correction reflection (Figure 2). It is inspired by the intrinsic ability of the human brain to correct errors during language processing [7] and leverages the consistency principle of [8], where LLMs exhibit an inherent tendency to maintain coherence across their responses. This method enables the model to detect and rectify perturbations using its existing capabilities autonomously. Unlike traditional approaches that rely on external correction tools or additional training, our method preserves semantic integrity without modifying the model architecture or requiring external resources, ensuring high practicality and scalability.

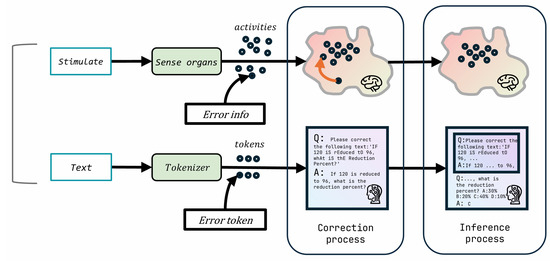
Figure 2. Illustration of the self-correction reflection for improving LLM performance by simulating the brain’s error correction ability and leveraging relevant research findings.

The design of the self-correction reflection framework comprises four key stages: Input Reception and Tokenization, Self-Correction Phase, Historical Enhancement through the Consistency Principle, and Inference with Corrected Context (Figure 3). Initially, the perturbed input undergoes tokenization and hidden-state extraction, establishing the foundation for subsequent analysis. The second stage activates the model’s self-diagnosis mechanism, where variational inference and temperature-guided sampling iteratively refine the perturbed input into a corrected version. Building on this, the third stage integrates the corrected text into the dialogue history while preserving the original perturbed context, enabling cross-attention between distorted and rectified representations to mitigate error propagation. Finally, the model performs inference using the corrected embeddings, ensuring alignment with the intended semantic space. These stages collectively mimic the brain’s error-checking loop while leveraging the LLM’s intrinsic coherence to balance correction rigor with computational efficiency.

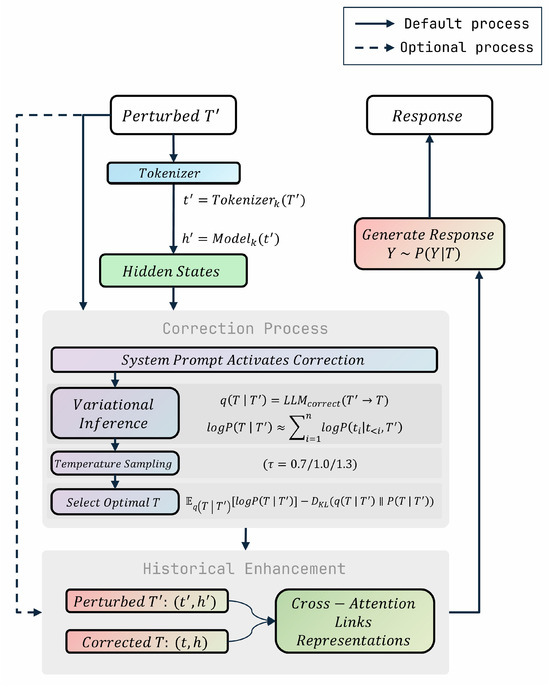
Figure 3. Flowchart of self-correction reflection process.

The self-correction reflection process operates as follows:

(1) Input Reception and Tokenization: When a user submits a perturbed input text $T^{\prime }$, the model processes it through a tokenizer to convert it into a sequence of tokens:

$$t^{\prime }={\mathrm{Tokenizer}}_k\left(T^{\prime }\right).$$

(1)

These tokens are passed through the model to extract hidden states from the final embedding layer, yielding vector representations:

$$h^{\prime }={\mathrm{Model}}_k\left(t^{\prime }\right),$$

(2)

where $h^{\prime }$ are the hidden states of the final embedding layer of ${\mathrm{Model}}_k$. Perturbations in $T^{\prime }$ may cause $h^{\prime }$ to deviate from the intended semantic representation, potentially resulting in misinterpretation.

(2) Self-Correction Phase: The model analyzes the tokenized input $t^{\prime }$ and its hidden state $h^{\prime }$ to generate a corrected text T. Using a system prompt (see Table 2), the model rectifies errors. This correction is modeled as a variational distribution:

$$q(T\mid T^{\prime })={\mathrm{LLM}}_{\mathrm{correct}}(T^{\prime }\to T),$$

(3)

which approximates the true posterior $P(T\mid T^{\prime })$. The model outputs a probability distribution over the generated tokens, and the logarithmic probability $logq(T\mid T^{\prime })$ is calculated as the sum of the logarithmic probabilities of each token in T conditioned on $T^{\prime }$. Similarly, $P(T\mid T^{\prime })$ is approximated by the model’s output probability distribution for the corrected text, computed as

$$logP(T\mid T^{\prime })\approx \sum _{i=1}^{n}logP(t_i\mid t_{<i},T^{\prime }),$$

(4)

where $t_i$ are the tokens in T, and $P(t_i\mid t_{<i},T^{\prime })$ is the model’s predicted probability for each token given the preceding tokens and the perturbed input. The model maximizes the likelihood of reconstructing the intended text by optimizing

$${\mathbb{E}}_{q(T\mid T^{\prime })}\left[logP(T\mid T^{\prime })\right]-D_{\mathrm{KL}}(q(T\mid T^{\prime })\Vert P(T\mid T^{\prime })),$$

(5)

selecting the candidate T with the highest $logq(T\mid T^{\prime })$. The reconstruction term ensures an accurate correction, while the KL divergence $D_{\mathrm{KL}}$ aligns $q(T\mid T^{\prime })$ with $P(T\mid T^{\prime })$, ensuring robust corrections.

Table 2. Example of correction process with LLM’s system prompt, input text, and response.

Correction Process Example
System Prompt	You are a professional text correction assistant. Your task is to receive a text that may have issues such as incorrect word spelling (e.g., “teh” instead of “the”), incorrect word order (e.g., “book the read” instead of “read the book”), and incorrect capitalization (e.g., “aPple” instead of “Apple”). For example, if the input text is “I likE applEs”, you should correct it to “I like apples”. Then correct the text to the correct and standard form and only output the corrected text content without adding any additional explanations or notes.
Question	Please correct the following text: “IF 120 iS rEduced tO 96, whAt iS thE Reduction Percent?”
Response	If 120 is reduced to 96, what is the reduction percent?

The overall objective is to maximize

$$logP(Y\mid T^{\prime })\ge {\mathbb{E}}_{q(T\mid T^{\prime })}\left[logP(Y\mid T)\right]-D_{\mathrm{KL}}(q(T\mid T^{\prime })\Vert P(T\mid T^{\prime })),$$

(6)

where $logP(Y\mid T)$ is computed as the log-probability of the response Y given T. Using different temperature settings ($\tau \in \{0.7,1.0,1.3\}$) during sampling, the model obtains diverse distributions $P(T\mid T^{\prime })$, allowing for systematic exploration of the correction space. This temperature-based optimization strategy selects the candidate that best achieves the objective while maintaining semantic fidelity.

The corrected text T is tokenized and embedded as $t={\mathrm{Tokenizer}}_k\left(T\right)$ and $h={\mathrm{Model}}_k\left(t\right)$, aligning h with the intended semantic representation. This approach leverages the model’s intrinsic capabilities, mimicking the brain’s error correction without requiring training.

(3) Historical Enhancement through the Consistency Principle: Following [8], the corrected text T and its embeddings h are integrated into the dialogue history as contextual augmentation. Unlike traditional methods that overwrite the original input, risking semantic loss, our approach retains both the perturbed input $T^{\prime }$ (with $t^{\prime },h^{\prime }$) and the corrected text T (with $t,h$). This historical record, processed through cross-attention mechanisms, enhances contextual awareness by linking perturbed and corrected representations, reducing error propagation. The consistency principle ensures alignment between the corrected and intended distributions, minimizing divergence in the latent space.

(4) Inference with Corrected Context: The model generates the target response Y based on the corrected text T and its hidden state h, expressed as

$$P(Y\mid T)={\mathrm{LLM}}_{\mathrm{generate}}(T\to Y).$$

(7)

The reconstruction term ensures accurate responses, and the KL divergence ensures that the correction process is robust. Using corrected embeddings h, the model produces reliable outputs under noisy conditions.

By embedding variational inference and temperature-based sampling within each step, our approach optimizes correction and inference without external models or training. The LLM’s cross-attention to link perturbed and corrected embeddings in the dialogue history mirrors human-like error mitigation, ensuring scalability and preserving the original model architecture for diverse, real-world scenarios.

The effectiveness of this method is demonstrated in Table 2 and Table 3. Table 2 illustrates the correction of a perturbed input, while Table 3 shows how the corrected text informs accurate inference, highlighting the seamless integration of correction and inference for reliable outputs.

Table 3. Example of inference process with system prompt, history, question, and response.

Inference Process Example
System Prompt	Please select and reply with only one of the options A, B, C or D. Do not provide any explanations or additional text. This is very important.
History	[(“You are a professional text correction assistant. Your task is to receive a text that may have issues such as incorrect word spelling (e.g., ‘teh’ instead of ‘the’), incorrect word order (e.g., ‘book the read’ instead of ‘read the book’), and incorrect capitalization (e.g., ‘aPple’ instead of ‘Apple’). For example, if the input text is ‘I likE applEs’, you should correct it to ‘I like apples’. Then correct the text to the correct and standard form and only output the corrected text content without adding any additional explanations or notes”, “Please correct the following text: ‘IF 120 iS rEduced tO 96, whAt iS thE Reduction Percent?”’, “If 120 is reduced to 96, what is the reduction percent?”)]
Question	If 120 is reduced to 96, what is the reduction percent? A:30% B:20% C:40% D:10%
Response	B

This cognitively inspired framework enhances LLM resilience to textual distortions, validated through experimental results demonstrating improved performance and reliability without additional training or external models.

4. Model-Specific Cosine Similarity

Traditional evaluation metrics like BERTScore and BLEU are based on single-model or rule-based calculations, where the scores are fixed once the dataset is determined and cannot effectively evaluate model performance. These metrics do not capture how different models understand perturbed input, limiting their ability to assess model-specific effects. Additionally, since both BERTScore and BLEU rely on token matching, they are unable to detect perturbations caused by word-order changes. To address this limitation, we propose Model-Specific Cosine Similarity (MSCS), a novel evaluation framework that leverages multiple LLMs to assess model performance under input perturbations comprehensively.

MSCS builds upon the well-established cosine similarity metric [26,27], which measures semantic similarity between text representations. Unlike BERTScore and BLEU, which provide static evaluations, MSCS dynamically integrates the capabilities of different models, enabling fine-grained analysis of how perturbations affect input understanding across diverse LLM architectures. This approach captures model-specific variations in processing perturbed inputs, offering insights that traditional metrics cannot provide.

The key steps of MSCS are as follows.

(1) Text Representation: First, we use different LLMs and their corresponding tokenizers to convert the two texts to be compared into vector representations. Given an input text, the model tokenizes it and converts it into tokens.

The formula for this step is the following.

$$t_i={\mathrm{Tokenizer}}_k\left(T_i\right),t_j={\mathrm{Tokenizer}}_k\left(T_j\right)$$

(8)

where $T_i$ and $T_j$ are the two input texts, and $t_i$ and $t_j$ are the corresponding tokens.

(2) Hidden States Extraction: Once the text has been tokenized, the tokens are passed through the feedforward layer of the model. In this layer, the model outputs a series of hidden states at each sublayer. To capture the semantic information, we focus on the hidden states of the final layer, as it can comprehensively integrate semantic information after being processed by previous sublayers. As shown in Figure 4, it illustrates the overall flow of the MSCS calculation process.

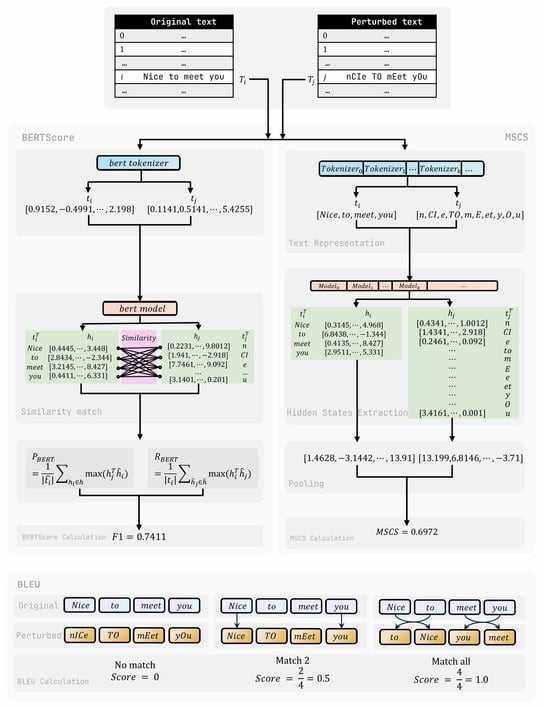
Figure 4. Flowchart of the MSCS, BERTScore, and BLEU calculation procedures.

The formula for this step is the following.

$$h_i,h_j=\{{\mathrm{Model}}_k\left(t_i\right),{\mathrm{Model}}_k\left(t_j\right)\},$$

(9)

where $h_i,h_j$ are the hidden states of the final embedding layer of ${\mathrm{Model}}_k$.

(3) Pooling: To obtain a fixed-length vector for each text, we apply mean pooling to the hidden states of the final layer. This involves averaging the hidden states across all tokens in the sequence $h_i$,$h_j$, resulting in vectors $v_i$,$v_j$ that represent the entire input text.

The formula for this step is the following.

$$v_i={\displaystyle \frac{1}{n}}\sum _{p=1}^n{h}_{ip},v_j={\displaystyle \frac{1}{n}}\sum _{p=1}^n{h}_{jp}$$

(10)

where n is the number of tokens of each text, and $v_i$ and $v_j$ are the vectors of the texts.

(4) MSCS Calculation: We compute the MSCS between the two representation vectors. MSCS is defined as the cosine of the angle between two vectors and is computed as follows:

$$\mathrm{MSCS}={\displaystyle \frac{v_i·v_j}{\parallel v_i\parallel \parallel v_j\parallel }}$$

(11)

where $v_i$ and $v_j$ are the vector representations of the two texts, and $\parallel v_i\parallel$ and $\parallel v_j\parallel$ are their Euclidean norms.

For $\forall Mode{l}_k$, MSCS ranges from $-1$ to 1. When we calculate MSCS for the perturbed text and the text before perturbation (original text), we can judge the difference between the LLM’s understanding of the text after perturbation and the understanding of the original text based on the results of MSCS. The closer the value is to 1, the more the model understands the two sentences, proving that the model basically ignores the impact of the perturbation. In contrast, the closer it is to −1, the more the model has a completely different understanding of the two sentences, proving that the perturbation has a greater effect on the model.

5. Experiments

The primary objective of our experiments is to systematically evaluate the robustness of state-of-the-art language models against various text perturbations and assess the effectiveness of self-correction reflection in mitigating performance degradation. To achieve this, we designed a comprehensive experimental framework that examines the behavior of the model in different types and intensities of perturbations. Furthermore, we conducted ablation studies to evaluate the performance of self-correction reflection using only the LLM (without leveraging consistency principles) in comparison to the complete proposed framework.

5.1. Experimental Setups

5.1.1. Models and Datasets

We selected a diverse set of models representative of state-of-the-art architectures commonly used in LLM research tasks. Specifically, we included models based on the Transformer architecture, such as Qwen2.5 (7B parameters) [28,29] (Alibaba, Hangzhou, China), GLM4 (9B parameters) [30] (Tsinghua University, Beijing, China), and Llama3.1 (8B parameters) [31] (Meta AI, Menlo Park, CA, USA), as well as models with the Mamba architecture, including Falcon3-Mamba (7B parameters) [32] (Technology Innovation Institute, Abu Dhabi, UAE). These models were chosen for their widespread adoption and proven efficacy in various tasks [33,34].

In this study, we selected two well-established benchmark datasets commonly used for evaluating LLMs: the Massive Multitask Language Understanding (MMLU) dataset [35] (the MMLU datasets can be downloaded from the following link: https://github.com/hendrycks/test, accessed on 11 November 2024) and the AGIEval dataset [36] (the AGIEval datasets can be downloaded from the following link: https://github.com/ruixiangcui/AGIEval, accessed on 15 November 2024), with a focus on the English subsets. The MMLU dataset is a widely recognized benchmark covering a broad range of tasks [37], including, but not limited to, single-choice questions in domains such as science, history, and mathematics. Similarly, the AGIEval dataset is a collection of question-answering tasks, comprising multiple sub-datasets, specifically LogiQA dataset [38], LSAT dataset [39], and SAT dataset. These datasets, consisting of single-choice questions and the corresponding answers, are designed to test the reasoning and problem-solving abilities of the models, making them ideal for assessing the generalizability of LLM [8,40].

We applied a series of controlled perturbations to the datasets, following the methodologies proposed by previous studies [7], where four different perturbation levels were used to explore the performance of the LLMs under varying degrees of input noise. The first level was No Perturbation (Baseline), where no perturbation was applied to the dataset, serving as the control condition for model evaluation. In the second level, Light Perturbation, 20% of the data points that met the specific perturbation criteria were randomly altered, introducing minor noise while preserving the original meaning. The third level, Moderate Perturbation, affected 50% of the data points that satisfied the perturbation conditions, introducing more substantial noise without completely disrupting the underlying information. The fourth level, Heavy Perturbation, applied changes to 100% of the data points, ensuring that all data underwent some form of noise introduction, simulating high levels of disturbance.

Furthermore, a case perturbation was applied based on research on human sensitivity to the letter case [41,42]. For each data point, we randomly selected 0%, 20%, 50%, or 100% of the words and swapped their case. This perturbation is regarded as real-world variations in text input with case inconsistencies, testing the model’s robustness to such a swap. Based on research on human sensitivity to letter and word order [43], we introduce additional letter and word perturbations. For letter perturbation, we randomly selected 0%, 20%, 50%, or 100% of words and swapped the order of two adjacent letters within those words, simulating typing or OCR errors. For word perturbation, we selected 0%, 20%, 50%, or 100% of adjacent words and swapped their order, mimicking sentence-level disorganization often encountered in user-generated content with non-native speakers.

With all these perturbations, three comprehensive datasets named SwapAlpha dataset, SwapWord dataset, and CaseAlpha dataset are established where each data point could be tested under varying conditions in real-world scenarios, enabling measurement of the LLMs’ resilience and ability to maintain performance across diverse, potentially unreliable perturbed inputs.

5.1.2. Evaluation Metrics

We followed established practices from previous work [8]; for the evaluation of the robustness of models to input noise, we used accuracy (ACC), which was calculated as the proportion of generated responses whose labels matched the annotated labels in the dataset. This matching was determined by an LLM. This method takes advantage of LLM evaluation, which has been shown to be as effective as human evaluation [44]. The formula for ACC is as follows:

$$ACC={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{correctly}\mathrm{predicted}\mathrm{samples}\mathrm{by}\mathrm{LLM}}{\mathrm{Total}\mathrm{number}\mathrm{of}\mathrm{samples}\mathrm{in}\mathrm{the}\mathrm{test}\mathrm{dataset}}}\times 100\%$$

(12)

Additionally, we employed MSCS (see Section 4) to evaluate the understanding of models of perturbed texts. The formula for MSCS refers to Equation (11).

To ensure consistency of the results, all the data in the subsequent experimental results were tested through at least three experiments, and the mean values were obtained.

5.1.3. Hardware and Software

Our experiments were carried out in Python 3.11 with PyTorch 2.5.1 and CUDA 11.8 on an Ubuntu 20.04 machine equipped with a Tesla V100 GPU (NVIDIA, Santa Clara, CA, USA).

5.2. Experimental Results

The experiment evaluated the performance of self-correction reflection by measuring the semantic divergence between the perturbed and original texts. We quantified this divergence using the mean semantic cosine similarity (MSCS) calculated with each model and its tokenizer, where a lower MSCS indicates stronger input perturbations from the model’s perspective. Additionally, we adopted accuracy (ACC) to assess the impact of perturbations and the improvement after self-correction.

As shown in Table 4, the mean semantic cosine similarity (Equation (11)) consistently decreases as perturbation levels increase across all evaluated language models. This demonstrates that more severe perturbations lead to greater semantic divergence between the modified text and the original version, confirming the MSCS metric’s effectiveness in quantifying semantic degradation. For unmodified texts (0% perturbation), all models maintain MSCS scores of 1.00, indicating no measurable semantic deviation from the original texts. This baseline confirms that the observed decreases in similarity scores directly result from the perturbations introduced rather than any inherent model limitations. The consistent inverse relationship between perturbation intensity and MSCS scores across all models and datasets demonstrates how textual modifications progressively degrade semantic fidelity. These findings highlight both the sensitivity of current language models to various types of perturbations and the utility of MSCS as a robust metric for quantifying these effects.

Table 4. Response MSCS among different perturbations (SwapAlpha, SwapWord, CaseAlpha) of different levels (0%, 20%, 50%, 100%) across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba).

LLMs	Dataset	MSCS	MSCS of SwapAlpha			MSCS of SwapWord			MSCS of CaseAlpha
		0%	20%	50%	100%	20%	50%	100%	20%	50%	100%
GLM4	MMLU	$1.00$	$0.9985$	$0.9960$	$0.9904$	$0.9990$	$0.9988$	$0.9985$	$0.9986$	$0.9963$	$0.9909$
	LogiQA-en	$1.00$	$0.9984$	$0.9955$	$0.9874$	$0.9984$	$0.9982$	$0.9980$	$0.9985$	$0.9958$	$0.9876$
	LSAT	$1.00$	$0.9888$	$0.9736$	$0.9466$	$0.9942$	$0.9919$	$0.9888$	$0.9908$	$0.9761$	$0.9483$
	SAT-en	$1.00$	$0.9506$	$0.8956$	$0.8243$	$0.9368$	$0.9219$	$0.9048$	$0.9625$	$0.9084$	$0.8331$
Llama3.1	MMLU	$1.00$	$0.8442$	$0.6090$	$0.3562$	$0.8051$	$0.7043$	$0.6441$	$0.8505$	$0.6924$	$0.5206$
	LogiQA-en	$1.00$	$0.7786$	$0.5475$	$0.3505$	$0.7914$	$0.7263$	$0.6884$	$0.8317$	$0.6952$	$0.5423$
	LSAT	$1.00$	$0.7067$	$0.4880$	$0.2962$	$0.7751$	$0.7104$	$0.6652$	$0.7635$	$0.6296$	$0.4781$
	SAT-en	$1.00$	$0.7260$	$0.5670$	$0.4209$	$0.6426$	$0.5967$	$0.5604$	$0.8046$	$0.7007$	$0.5787$
Qwen2.5	MMLU	$1.00$	$0.8885$	$0.7364$	$0.5597$	$0.9007$	$0.8557$	$0.8288$	$0.8917$	$0.7596$	$0.5753$
	LogiQA-en	$1.00$	$0.8284$	$0.6826$	$0.5165$	$0.8906$	$0.8565$	$0.8315$	$0.8629$	$0.7280$	$0.5369$
	LSAT	$1.00$	$0.7915$	$0.6436$	$0.4754$	$0.8770$	$0.8410$	$0.8159$	$0.8293$	$0.6914$	$0.4860$
	SAT-en	$1.00$	$0.8492$	$0.7488$	$0.6194$	$0.8435$	$0.8352$	$0.8254$	$0.8758$	$0.7803$	$0.6349$
Falcon3-Mamba	MMLU	$1.00$	$0.9168$	$0.8462$	$0.7946$	$0.9253$	$0.8940$	$0.8760$	$0.9236$	$0.8746$	$0.8382$
	LogiQA-en	$1.00$	$0.8988$	$0.8411$	$0.7981$	$0.9215$	$0.8960$	$0.8806$	$0.9209$	$0.8804$	$0.8415$
	LSAT	$1.00$	$0.8482$	$0.7869$	$0.7413$	$0.8962$	$0.8683$	$0.8489$	$0.8808$	$0.8403$	$0.8036$
	SAT-en	$1.00$	$0.8633$	$0.8060$	$0.7581$	$0.8866$	$0.8631$	$0.8471$	$0.9103$	$0.8674$	$0.8246$

In Figure 5, the radar charts of the four LLMs show the degree of impact at different levels of perturbation. Under the same perturbation type for the same LLM, the magnitude of the change in the MSCS value varies at different perturbation levels. The magnitude of MSCS’s change indicates how the specified perturbation impacts the semantic consistency of the text from the perspective of the tokenizer. A larger change in the MSCS value indicates that the perturbation causes a greater semantic difference between the original text and the perturbed text, indicating a greater impact on the LLM. This in turn may cause a larger impact on ACC, highlighting that different perturbations affect the performance of the LLM to different degrees.

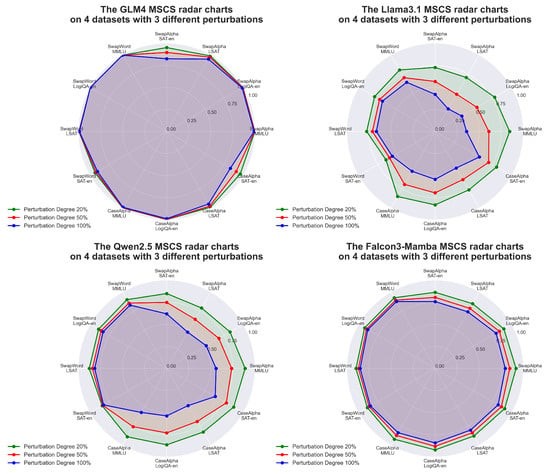
Figure 5. The MSCS variations are visualized via radar charts under 3 perturbation levels (20%, 50%, 100%) for each LLM. This demonstrates how semantic similarity changes across various perturbation types concerning 12-dimensional properties. In total, 4 datasets under 3 different perturbations are considered.

The results in Table 5 and Table 6 highlight the advantages of MSCS as a comprehensive metric to evaluate the robustness of LLMs to text perturbations, surpassing traditional metrics such as BLEU-1 and BERTScore in terms of granularity and ability to evaluate perturbations. Table 4 shows that MSCS can quantify the semantic understanding deviations of different models under different perturbations with high sensitivity. BLEU-1 (Table 5) and BERTScore (Table 6) only evaluate superficial text similarity and are powerless to understand different models. It is worth noting that BLEU-1 and BERTScore fail to effectively evaluate SwapWord perturbations, which exposes their shortcomings in handling perturbations that change word order. By explicitly detailing how perturbations affect individual model understandings, rather than just evaluating lexical correspondences, MSCS establishes a rigorous methodological framework for research that helps to accurately assess the impact of perturbations on model reasoning capabilities.

Table 5. Response BLEU-1 score among different perturbations (SwapAlpha, SwapWord, CaseAlpha) of different levels (0%, 20%, 50%, 100%) across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba).

Dataset	LLMs	BLEU-1 Score	BLEU-1 Score of SwapAlpha			BLEU-1 Score of SwapWord			BLEU-1 Score of UpperCase
		0%	20%	50%	100%	20%	50%	100%	20%	50%	100%
MMLU	GLM4	1.00	0.834	0.557	0.086	1.00	1.00	1.00	0.825	0.534	0.042
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
LogiQA-en	GLM4	1.00	0.821	0.542	0.079	1.00	1.00	1.00	0.809	0.515	0.026
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
LSAT	GLM4	1.00	0.814	0.530	0.054	1.00	1.00	1.00	0.807	0.515	0.030
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
SAT-en	GLM4	1.00	0.814	0.533	0.066	1.00	1.00	1.00	0.807	0.518	0.039
	Llama3.1
	Qwen2.5
	Falcon3-Mamba

Table 6. Response BERTScore among different perturbations (SwapAlpha, SwapWord, CaseAlpha) of different levels (0%, 20%, 50%, 100%) across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba).

Dataset	LLMs	BERTScore	BERTScore of SwapAlpha			BERTScore of SwapWord			BERTScore of UpperCase
		0%	20%	50%	100%	20%	50%	100%	20%	50%	100%
MMLU	GLM4	1.00	0.875	0.723	0.565	0.905	0.905	0.905	0.875	0.729	0.583
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
LogiQA-en	GLM4	1.00	0.858	0.698	0.522	0.885	0.885	0.885	0.855	0.696	0.525
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
LSAT	GLM4	1.00	0.827	0.665	0.510	0.879	0.879	0.879	0.822	0.660	0.515
	Llama3.1
	Qwen2.5
	Falcon3-Mamba
SAT-en	GLM4	1.00	0.794	0.681	0.607	0.911	0.911	0.911	0.789	0.674	0.610
	Llama3.1
	Qwen2.5
	Falcon3-Mamba

As presented in Table 7, different models exhibit varying performance in datasets and perturbations, due to their distinct training processes, architectures, and prior knowledge, which influence their ability to handle degraded inputs when processing perturbed text. Llama3.1 shows notable vulnerability, particularly in LogiQA-en, where ACC decreases from 39.50% to 31.81% (SwapAlpha 100%), 28.30% (SwapWord 100%), and 37.00% (CaseAlpha 100%). Across all models, Qwen2.5 consistently outperforms GLM4, Llama3.1, and Falcon3-Mamba across all datasets under three levels of perturbations, showing better performance.

Table 7. Response ACC among different perturbations (SwapAlpha, SwapWord, CaseAlpha) of different levels (0%, 20%, 50%, 100%) across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba). The subscript represents the variance in accuracy (%).

LLMs	Dataset	ACC	ACC of SwapAlpha			ACC of SwapWord			ACC of CaseAlpha
		0%	20%	50%	100%	20%	50%	100%	20%	50%	100%
GLM4	MMLU	${65.1}_{0.0}$	${62.8}_{0.0}$	${58.2}_{0.0}$	${49.3}_{0.0}$	${53.6}_{0.0}$	${50.0}_{0.0}$	${47.9}_{0.0}$	${64.0}_{0.0}$	${62.0}_{0.0}$	${59.2}_{0.0}$
	LogiQA-en	${48.8}_{0.1}$	${45.8}_{0.0}$	${42.1}_{0.0}$	${36.9}_{0.1}$	${37.1}_{0.0}$	${32.6}_{0.2}$	${31.3}_{0.0}$	${47.2}_{0.0}$	${46.7}_{0.0}$	${43.3}_{0.0}$
	LSAT	${54.5}_{0.0}$	${51.3}_{0.2}$	${48.1}_{0.0}$	${39.1}_{0.0}$	${38.9}_{0.1}$	${35.5}_{0.0}$	${31.7}_{0.1}$	${52.1}_{0.0}$	${50.8}_{0.0}$	${47.0}_{0.1}$
	SAT-en	${83.3}_{0.1}$	${78.9}_{0.1}$	${76.0}_{0.1}$	${65.8}_{0.1}$	${68.4}_{0.0}$	${60.7}_{0.0}$	${54.9}_{0.0}$	${81.3}_{0.1}$	${81.1}_{0.0}$	${80.6}_{0.0}$
Llama3.1	MMLU	${61.2}_{0.0}$	${58.8}_{0.0}$	${54.5}_{0.0}$	${47.3}_{0.3}$	${51.4}_{0.0}$	${48.9}_{0.0}$	${47.1}_{0.0}$	${59.8}_{0.0}$	${57.4}_{0.0}$	${53.8}_{0.0}$
	LogiQA-en	${39.5}_{0.0}$	${37.4}_{0.0}$	${36.8}_{0.0}$	${31.8}_{1.6}$	${33.5}_{0.2}$	${32.3}_{0.0}$	${28.3}_{0.2}$	${38.9}_{0.1}$	${37.5}_{0.2}$	${37.0}_{0.1}$
	LSAT	${49.0}_{0.0}$	${46.1}_{0.0}$	${42.7}_{0.5}$	${35.5}_{0.6}$	${36.6}_{0.2}$	${33.5}_{0.0}$	${29.7}_{1.5}$	${46.6}_{2.1}$	${42.6}_{0.2}$	${40.7}_{0.0}$
	SAT-en	${80.8}_{0.1}$	${76.9}_{0.5}$	${69.9}_{2.1}$	${52.7}_{0.5}$	${59.5}_{2.9}$	${49.5}_{0.0}$	${46.8}_{1.5}$	${76.7}_{0.2}$	${74.0}_{0.1}$	${61.2}_{0.2}$
Qwen2.5	MMLU	${69.4}_{0.0}$	${67.9}_{0.0}$	${64.7}_{0.0}$	${57.2}_{0.0}$	${57.6}_{0.0}$	${55.0}_{0.0}$	${52.7}_{0.0}$	${68.7}_{0.0}$	${67.4}_{0.0}$	${65.7}_{0.0}$
	LogiQA-en	${55.9}_{0.0}$	${53.9}_{0.0}$	${51.4}_{0.9}$	${45.2}_{0.1}$	${42.1}_{0.0}$	${40.3}_{0.1}$	${38.5}_{0.6}$	${55.1}_{0.0}$	${54.0}_{0.1}$	${51.4}_{0.0}$
	LSAT	${60.9}_{0.2}$	${60.2}_{0.0}$	${56.8}_{0.0}$	${46.3}_{0.1}$	${44.4}_{0.0}$	${38.7}_{0.0}$	${36.1}_{0.0}$	${59.7}_{0.1}$	${57.7}_{0.0}$	${54.0}_{0.0}$
	SAT-en	${85.9}_{0.9}$	${85.4}_{0.0}$	${82.3}_{0.1}$	${73.5}_{0.5}$	${69.2}_{0.1}$	${61.9}_{0.1}$	${58.7}_{0.9}$	${84.7}_{0.1}$	${83.3}_{0.1}$	${82.8}_{0.1}$
Falcon3-Mamba	MMLU	${62.6}_{0.0}$	${59.6}_{0.0}$	${55.7}_{0.0}$	${47.2}_{0.0}$	${51.9}_{0.0}$	${49.2}_{0.0}$	${47.9}_{0.0}$	${60.7}_{0.0}$	${59.0}_{0.0}$	${56.4}_{0.0}$
	LogiQA-en	${42.3}_{0.1}$	${41.6}_{0.0}$	${38.2}_{0.0}$	${33.8}_{0.0}$	${37.8}_{0.0}$	${37.1}_{0.0}$	${36.6}_{0.0}$	${41.3}_{0.0}$	${40.5}_{0.0}$	${38.5}_{0.0}$
	LSAT	${45.1}_{0.0}$	${43.8}_{0.0}$	${39.4}_{0.0}$	${35.3}_{0.0}$	${36.7}_{0.0}$	${33.9}_{0.0}$	${32.6}_{0.0}$	${44.8}_{0.0}$	${42.0}_{0.0}$	${39.0}_{0.0}$
	SAT-en	${66.5}_{0.0}$	${65.0}_{0.0}$	${64.6}_{0.0}$	${51.0}_{0.0}$	${54.4}_{0.0}$	${49.5}_{0.0}$	${48.5}_{0.0}$	${65.0}_{0.0}$	${61.7}_{0.0}$	${59.7}_{0.0}$

Table 8 indicates that Qwen2.5 consistently demonstrates the strongest robustness under SwapAlpha and CaseAlpha perturbations, where the decrease in ACC is minimal across all perturbation levels, with an average percentage decrease of 9.01% under the SwapAlpha perturbation and 4.07% under the CaseAlpha perturbation. This suggests that Qwen2.5 exhibits the least sensitivity to these perturbations. In contrast, Falcon3-Mamba shows only a 20.03% average decline in ACC under SwapWord perturbations, which is significantly smaller than the declines observed in other models, indicating that Falcon3-Mamba demonstrates exceptionally high robustness in this particular perturbation type. The consistent degradation of ACC across all models empirically validates that perturbations impair model performance by increasing the semantic divergence between input and output, making predictions increasingly error-prone without corrective mechanisms. These findings underscore the varying degrees of robustness exhibited by different models, depending on the type of perturbation, highlighting the influence of model architecture on perturbation robustness.

Table 8. Response ACC change rates (%) among different perturbations (SwapAlpha, SwapWord, CaseAlpha) of different levels (20%, 50%, 100%) across four datasets using four LLMs.

Perturbation Type	Perturbation Level	Dataset	GLM4	Llama3.1	Qwen2.5	Falcon3-Mamba
SwapAlpha	20%	MMLU	−3.62	−4.02	−2.13	−4.84
		LogiQA-en	−6.07	−5.34	−3.63	−1.66
		LSAT	−5.73	−5.96	−1.05	−2.95
		SAT-en	−5.25	−4.81	−0.56	−2.18
		Average	−5.17	−5.03	−1.84	−2.91
	50%	MMLU	−10.73	−10.97	−6.81	−11.02
		LogiQA-en	−13.72	−6.91	−8.08	−9.77
		LSAT	−11.64	−12.83	−6.67	−12.51
		SAT-en	−8.74	−13.52	−4.24	−2.92
		Average	−11.21	−11.06	−6.45	−9.06
	100%	MMLU	−24.39	−22.78	−17.62	−24.54
		LogiQA-en	−24.27	−19.52	−19.08	−20.08
		LSAT	−28.20	−27.61	−23.86	−21.76
		SAT-en	−20.98	−34.84	−14.41	−23.35
		Average	−24.46	−26.19	−18.74	−22.43
	Average		−13.61	−14.09	−9.01	−11.46
SwapWord	20%	MMLU	−17.79	−16.07	−16.98	−17.06
		LogiQA-en	−23.79	−15.19	−24.79	−10.69
		LSAT	−28.57	−25.28	−27.03	−18.67
		SAT-en	−17.78	−26.43	−19.49	−18.24
		Average	−21.98	−20.74	−22.07	−16.16
	50%	MMLU	−23.19	−20.23	−20.73	−21.36
		LogiQA-en	−33.07	−18.16	−28.00	−12.34
		LSAT	−34.85	−31.54	−36.40	−24.84
		SAT-en	−27.11	−38.75	−27.97	−25.55
		Average	−29.56	−27.17	−28.28	−21.02
	100%	MMLU	−26.43	−23.14	−24.11	−23.51
		LogiQA-en	−35.77	−28.21	−31.21	−13.45
		LSAT	−41.87	−39.44	−40.64	−27.68
		SAT-en	−34.11	−42.05	−31.63	−27.01
		Average	−34.54	−33.21	−31.90	−22.91
	Average		−28.69	−27.04	−27.42	−20.03
CaseAlpha	20%	MMLU	−1.78	−2.43	−1.09	−3.12
		LogiQA-en	−3.18	−1.60	−1.54	−2.39
		LSAT	−4.37	−4.86	−1.87	−0.64
		SAT-en	−2.33	−5.11	−1.41	−2.18
		Average	−2.92	−3.50	−1.48	−2.08
	50%	MMLU	−4.76	−6.30	−2.85	−5.77
		LogiQA-en	−4.31	−4.94	−3.34	−4.23
		LSAT	−6.65	−13.04	−5.21	−6.81
		SAT-en	−2.62	−8.41	−3.11	−7.29
		Average	−4.58	−8.17	−3.63	−6.02
	100%	MMLU	−9.21	−12.15	−5.39	−9.95
		LogiQA-en	−11.18	−6.33	−8.08	−9.03
		LSAT	−13.64	−16.89	−11.32	−13.40
		SAT-en	−3.21	−24.34	−3.67	−10.21
		Average	−9.31	−14.93	−7.12	−10.65
	Average		−5.60	−8.87	−4.07	−6.25

Figure 6 presents line charts that visualize the performance decline trends of different LLMs under varying perturbation levels. The plots demonstrate how the accuracy of the models changes across three perturbation types on four datasets. Each line in the chart represents the average performance decline of one model, with baseline performance (0% perturbation) normalized to 100%. The charts clearly show that Qwen2.5 maintains relatively stable performance with minimal decline under SwapAlpha and CaseAlpha perturbations, suggesting its robustness to these types of perturbations. Conversely, Falcon3-Mamba exhibits the smallest decrease in performance under SwapWord perturbations, indicating its higher robustness in that specific perturbation type. These visual trends emphasize how different models react to various perturbations, with each model showing varying levels of sensitivity depending on the perturbation type, thereby highlighting the impact of the model architecture on its robustness.

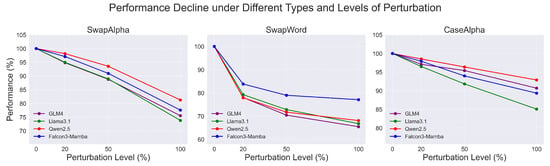
Figure 6. Line charts visualize the performance decline trends of different LLMs under 4 perturbation levels (0%, 20%, 50%, 100%). The plots demonstrate how LLMs’ ACC changes across three perturbation types (SwapAlpha, SwapWord, and CaseAlpha) on 4 datasets (MMLU, LogiQA-EN, LSAT, and SAT-EN). Each line represents one LLM’s average performance decline, with the baseline performance (0% perturbation) normalized to 100%.

Figure 7 presents radar charts that provide a detailed comparison of the ACC of each LLM under various perturbation levels across different datasets. A larger radar chart area corresponds to higher overall ACC, indicating better model performance. It can be observed that the ACC of the four evaluated models exhibits a consistent trend: the radar chart areas decrease significantly as the perturbation levels increase. Among these models, Qwen2.5 demonstrates a noticeably larger area under all perturbation levels, indicating its superior performance. The GLM model follows as the second-best performer, while the Llama model and Falcon3-Mamba show relatively poor performance, with substantially smaller radar chart areas.

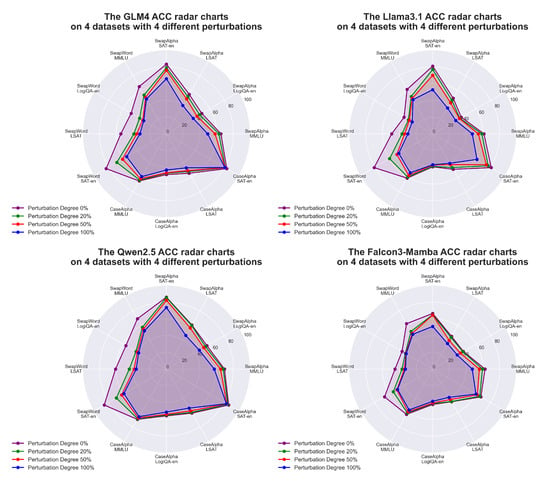
Figure 7. The ACC variations are visualized via radar charts under 4 perturbation levels (0%, 20%, 50%, 100%) for each LLM. This demonstrates how LLMs’ robustness changes across various perturbation types concerning 12-dimensional properties. In total, 4 datasets under 3 different perturbations are considered.

Figure 8 presents radar charts that provide a detailed comparison of the ACC of four LLMs across various datasets and perturbation levels. The area of each radar chart represents the ACC, with larger areas indicating a higher ACC. We observe a consistent trend across all models: lower ACC levels are achieved on the LSAT and LogiQA-en datasets, whereas higher ACC levels are observed on the SAT-en and MMLU datasets. Among the models evaluated, Qwen2.5 consistently exhibits significantly larger areas in all perturbation datasets and levels, indicating its remarkable ability to solve the perturbation task. It should be noted that although the Falcon3-Mamba model exhibits relatively poor performance under perturbations, the areas formed at different perturbation levels in the radar chart are very similar in size and shape. This suggests that the Falcon3-Mamba model is less affected by perturbations, demonstrating a high degree of robustness when faced with perturbations.

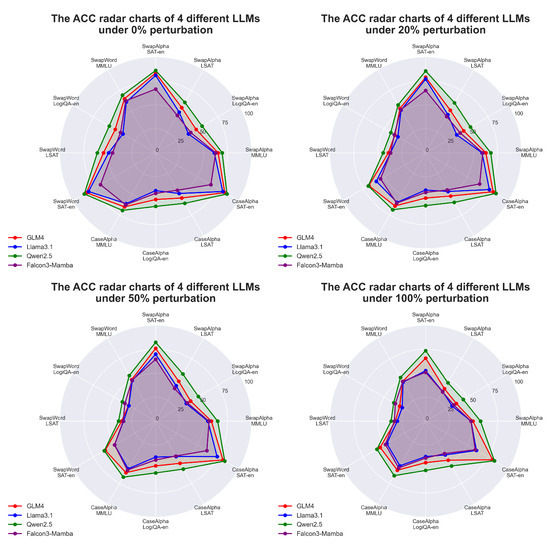
Figure 8. Illustration of ACC performance under four perturbation intensities (0%, 20%, 50%, 100%), showing how different LLMs maintain their robustness across various test scenarios.

As shown in Table 4 and Table 7, the perturbations significantly reduced both MSCS and ACC, with the degree of reduction being proportional to the strength of the perturbations. For the same model evaluated on the same perturbation type, the degree of reduction in MSCS also corresponds to the decrease in ACC. For instance, the MSCS reduction for the GLM4 model in the SAT-en dataset (from 1 to 0.9506, 0.8956, and 0.8243 under 20%, 50%, and 100% SwapAlpha perturbations, respectively) was notably greater than that on other datasets (for example, in the LogiQA-en dataset, MSCS decreased from 1 to 0.9984, 0.9955, and 0.9874 under the same perturbation levels).

We believe that comparing the correlation between MSCS and ACC for the same model under different types of perturbation is not meaningful. Generally, MSCS reductions caused by the same type of perturbation are consistent, which means that a lower MSCS for a given perturbation type within the same model typically corresponds to a lower ACC. However, in the same model, a reduction in MSCS across different perturbation types does not always lead to a corresponding reduction in ACC. Consider the following questions: “What is the last letter of the word ‘One’?” and “What is the last letter of the word ‘Apple’?” Although the semantic differences measured by MSCS are evident, the answers produced by the model, as evaluated by ACC, remain the same. This results in a significant drop in MSCS while ACC remains nearly unchanged.

To effectively mitigate input perturbations, we incorporated self-correction reflection, allowing the models to respond more accurately to the perturbed input. Through this method, we further evaluated the model performance.

The self-correction reflection demonstrates varying degrees of improvement in MSCS across different perturbation types and models as improved alignment between the model’s understanding of perturbed inputs and their original meaning, leading to more accurate semantic restoration. As shown in Table 9, for the SwapAlpha perturbation, Llama3.1 shows the most significant semantic correction, with MSCS increasing by +32.68% in MMLU and +27.35% in LSAT, reflecting the model’s improved ability to generate corrections semantically closer to the original text. For the CaseAlpha perturbation, most models demonstrate a certain degree of semantic correction, with Llama3.1 again leading to +15.92% improvement in MMLU and +15.14% in LSAT, highlighting the model’s partial success in recovering capitalization consistency. In particular, SwapAlpha consistently achieves the highest mean value in MSCS after correction (+10.88%), followed by CaseAlpha (+8.54%) and SwapWord (+1.33%).

Table 9. Response MSCS comparison before and after correction for three types of perturbations (SwapAlpha, SwapWord, CaseAlpha) at 100% intensity across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba). For each perturbation type, the table presents the MSCS values before correction (“Before”), after correction (“After”), and the improvement percentage (“Improv.”).

LLMs	Dataset	MSCS of SwapAlpha			MSCS of SwapWord			MSCS of CaseAlpha
		Before	After	Improv.	Before	After	Improv.	Before	After	Improv.
GLM4	MMLU	$0.9904$	$0.9936$	$+0.32\%$	$0.9985$	$0.9986$	$+0.01\%$	$0.9909$	$0.9939$	$+0.30\%$
	LogiQA-en	$0.9874$	$0.9922$	$+0.49\%$	$0.9980$	$0.9983$	$+0.03\%$	$0.9876$	$0.9924$	$+0.49\%$
	LSAT	$0.9466$	$0.9606$	$+1.48\%$	$0.9888$	$0.9902$	$+0.14\%$	$0.9483$	$0.9632$	$+1.57\%$
	SAT-en	$0.8243$	$0.8571$	$+3.98\%$	$0.9048$	$0.9129$	$+0.90\%$	$0.8331$	$0.8672$	$+4.09\%$
Llama3.1	MMLU	$0.3562$	$0.4726$	$+32.68\%$	$0.6441$	$0.6741$	$+4.66\%$	$0.5206$	$0.6035$	$+15.92\%$
	LogiQA-en	$0.3505$	$0.4346$	$+23.99\%$	$0.6884$	$0.7040$	$+2.27\%$	$0.5423$	$0.6148$	$+13.37\%$
	LSAT	$0.2962$	$0.3772$	$+27.35\%$	$0.6652$	$0.6828$	$+2.65\%$	$0.4781$	$0.5505$	$+15.14\%$
	SAT-en	$0.4209$	$0.4848$	$+15.18\%$	$0.5604$	$0.5753$	$+2.66\%$	$0.5787$	$0.6381$	$+10.26\%$
Qwen2.5	MMLU	$0.5597$	$0.6472$	$+15.63\%$	$0.8288$	$0.8431$	$+1.73\%$	$0.5753$	$0.6697$	$+16.41\%$
	LogiQA-en	$0.5165$	$0.5946$	$+15.12\%$	$0.8315$	$0.8420$	$+1.26\%$	$0.5369$	$0.6308$	$+17.49\%$
	LSAT	$0.4754$	$0.5561$	$+16.98\%$	$0.8159$	$0.8261$	$+1.25\%$	$0.4860$	$0.5891$	$+21.21\%$
	SAT-en	$0.6194$	$0.6833$	$+10.32\%$	$0.8254$	$0.8280$	$+0.31\%$	$0.6349$	$0.7086$	$+11.61\%$
Falcon3-Mamba	MMLU	$0.7946$	$0.8177$	$+2.91\%$	$0.8760$	$0.8847$	$+0.99\%$	$0.8382$	$0.8547$	$+1.97\%$
	LogiQA-en	$0.7981$	$0.8167$	$+2.33\%$	$0.8806$	$0.8872$	$+0.75\%$	$0.8415$	$0.8595$	$+2.14\%$
	LSAT	$0.7413$	$0.7605$	$+2.59\%$	$0.8489$	$0.8561$	$+0.85\%$	$0.8036$	$0.8214$	$+2.22\%$
	SAT-en	$0.7581$	$0.7788$	$+2.73\%$	$0.8471$	$0.8535$	$+0.76\%$	$0.8246$	$0.8441$	$+2.36\%$
Avg. Improv.		-	-	$+10.88\%$	-	-	$+1.33\%$	-	-	$+8.54\%$

As shown in Figure 9, the self-correction reflection demonstrates a significant effect in enhancing LLMs’ understanding of perturbed questions. All LLMs and datasets exhibit a consistent trend, where the radar chart area increases after applying self-correction reflection, with improvements observed in every radar chart. Notably, the radar chart area expansion is particularly pronounced for Llama3.1 and Qwen2.5, indicating their superior improvement in comprehending perturbed texts after self-correction reflection. These MSCS improvement results validate that self-correction enhances the model’s ability to process noisy inputs and produce more accurate outputs.

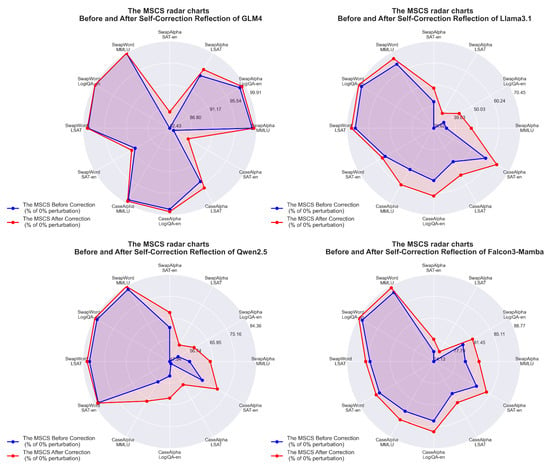
Figure 9. Illustration of MSCS improvement through self-correction reflection, comparing the semantic recovery before and after correction for each LLM. The radar chart plots normalized MSCS percentages (before/after correction relative to 0% perturbation MSCS) on axes representing distinct perturbation scenarios.

The self-correction reflection demonstrates significant improvements in ACC across different perturbation types, as shown in Table 10, which indicates improved model performance through better handling of perturbed inputs and their corrected representations. In particular, among different types of perturbation, the SwapAlpha perturbation shows the highest average improvement rate (+10.22%), significantly outperforming both CaseAlpha (+3.35%) and SwapWord (+2.89%), suggesting that self-correction reflection is particularly effective in addressing character-level swap perturbations. The ACC improvements of all of these models empirically confirm that self-correction enables better performance by processing corrected input rather than noise-degraded input.

Table 10. Response ACC comparison before and after correction for three types of perturbations (SwapAlpha, SwapWord, CaseAlpha) at 100% intensity across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba). For each perturbation type, the table presents the ACC values before correction (“Before”), after correction (“After”), and the improvement percentage (“Improv.”).

LLMs	Dataset	ACC of SwapAlpha			ACC of SwapWord			ACC of CaseAlpha
		Before	After	Improv.	Before	After	Improv.	Before	After	Improv.
GLM4	MMLU	$49.26$	$54.69$	$+11.02\%$	$47.93$	$49.27$	$+2.81\%$	$59.15$	$60.72$	$+2.64\%$
	LogiQA-en	$36.92$	$40.03$	$+8.44\%$	$31.31$	$32.40$	$+3.48\%$	$43.30$	$46.26$	$+6.83\%$
	LSAT	$39.10$	$43.81$	$+12.04\%$	$31.66$	$32.51$	$+2.66\%$	$47.03$	$48.27$	$+2.63\%$
	SAT-en	$65.78$	$73.79$	$+12.18\%$	$54.85$	$56.31$	$+2.65\%$	$80.58$	$82.04$	$+1.81\%$
Llama3.1	MMLU	$47.29$	$50.85$	$+7.51\%$	$47.07$	$48.07$	$+2.13\%$	$53.80$	$55.42$	$+3.01\%$
	LogiQA-en	$31.78$	$35.51$	$+11.76\%$	$28.35$	$29.75$	$+4.95\%$	$36.99$	$38.47$	$+4.00\%$
	LSAT	$35.48$	$39.45$	$+11.17\%$	$29.68$	$30.72$	$+3.51\%$	$40.73$	$43.11$	$+5.84\%$
	SAT-en	$52.67$	$59.71$	$+13.36\%$	$46.84$	$48.06$	$+2.59\%$	$61.16$	$64.08$	$+4.76\%$
Qwen2.5	MMLU	$57.19$	$61.80$	$+8.06\%$	$52.68$	$54.37$	$+3.22\%$	$65.68$	$66.37$	$+1.05\%$
	LogiQA-en	$45.25$	$49.22$	$+8.78\%$	$38.47$	$39.72$	$+3.24\%$	$51.40$	$52.49$	$+2.12\%$
	LSAT	$46.33$	$51.34$	$+10.80\%$	$36.12$	$37.66$	$+4.25\%$	$53.96$	$54.81$	$+1.56\%$
	SAT-en	$73.54$	$79.61$	$+8.25\%$	$58.74$	$60.19$	$+2.48\%$	$82.77$	$84.95$	$+2.64\%$
Falcon3-Mamba	MMLU	$47.24$	$52.10$	$+10.30\%$	$47.88$	$48.43$	$+1.13\%$	$56.37$	$57.56$	$+2.11\%$
	LogiQA-en	$33.80$	$37.07$	$+9.68\%$	$36.60$	$37.38$	$+2.13\%$	$38.47$	$39.56$	$+2.83\%$
	LSAT	$35.28$	$38.35$	$+8.71\%$	$32.61$	$33.60$	$+3.04\%$	$39.05$	$40.93$	$+4.82\%$
	SAT-en	$50.97$	$56.80$	$+11.43\%$	$48.54$	$49.51$	$+2.00\%$	$59.71$	$62.62$	$+4.88\%$
Avg. Improv.		-	-	$+10.22\%$	-	-	$+2.89\%$	-	-	$+3.35\%$

As shown in Figure 10, self-correction reflection increases the radar chart area across all models, with improvements observed in each individual radar chart. The radar charts also reveal that SwapAlpha perturbations consistently show larger improvements compared to SwapWord and CaseAlpha perturbations, which aligns with the average improvement rates in Table 10, respectively. This comprehensive chart suggests that self-correction reflection demonstrates varying degrees of effectiveness across different perturbation types, showing the best enhancement in SwapAlpha perturbation (+10.22%), followed by better enhancement in CaseAlpha (+3.35%), and relatively good enhancement in SwapWord perturbation (+2.89%), indicating that the method’s effectiveness varies depending on the specific type of perturbation encountered.

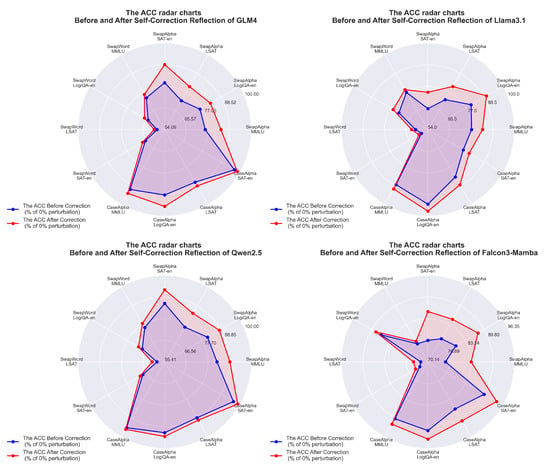
Figure 10. Illustration of ACC enhancement through self-correction reflection, displaying the performance improvement for each LLM across different perturbation types. The radar chart plots normalized ACC percentages (before/after correction relative to 0% perturbation ACC) on axes representing distinct perturbation scenarios.

Figure 11 illustrates the performance of various model architectures after applying self-correction reflection. The radar chart highlights that Qwen2.5 consistently outperformed other models, covering the largest area across all datasets and perturbation types, thus demonstrating superior robustness and accuracy. GLM4, while not as robust as Qwen2.5, achieved the second-best performance, indicating its relatively strong ability to handle perturbations after self-correction reflection. Despite the improvements brought by self-correction reflection, significant performance differences remain among the models. These differences can be attributed to variations in their underlying architectures, training objectives, and datasets, which influence each model’s ability to generalize and adapt to perturbations. This suggests that self-correction reflection, while beneficial, cannot fully eliminate the inherent limitations imposed by model design and prior knowledge.

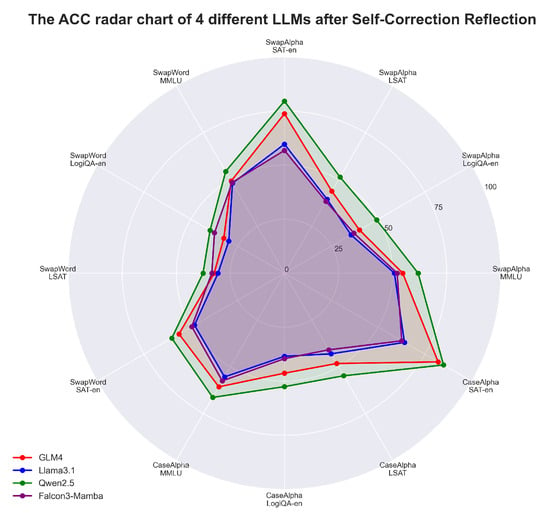
Figure 11. Illustration of ACC after self-correction reflection comparison among LLMs, revealing their relative performance strengths across different datasets and perturbation types.

To verify the novelty and effectiveness of our proposed self-correction reflection, we also used the existing advanced CTC and TextBlob correction methods mentioned in Section 2 as baselines for comparison. The data presented in Table 11 and Table 12 show that self-correction reflection consistently outperforms the baseline in terms of improvements in both MSCS and ACC. These results highlight the effectiveness of the self-correction reflection method under adversarial perturbations.

Table 11. Response MSCS comparison after correction for three types of perturbations (SwapAlpha, SwapWord, CaseAlpha) at 100% intensity across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba). For each perturbation type, the table presents the ACC values after CTC Detection (CTC), TextBlob, and the self-correction reflection (Ours).

LLMs	Dataset	MSCS of SwapAlpha			MSCS of SwapWord			MSCS of CaseAlpha
		CTC	TextBlob	Ours	CTC	TextBlob	Ours	CTC	TextBlob	Ours
GLM4	MMLU	$0.9909$	$0.9915$	$0.9936$	$0.9985$	$0.9985$	$0.9986$	$0.9914$	$0.9921$	$0.9939$
	LogiQA-en	$0.9867$	$0.9894$	$0.9922$	$0.9981$	$0.9982$	$0.9983$	$0.9877$	$0.9908$	$0.9924$
	LSAT	$0.9470$	$0.9470$	$0.9606$	$0.9891$	$0.9898$	$0.9902$	$0.9543$	$0.9561$	$0.9632$
	SAT-en	$0.8276$	$0.8278$	$0.8571$	$0.9053$	$0.9061$	$0.9129$	$0.8434$	$0.8378$	$0.8672$
Llama3.1	MMLU	$0.3895$	$0.4124$	$0.4726$	$0.6558$	$0.6563$	$0.6741$	$0.5451$	$0.5513$	$0.6035$
	LogiQA-en	$0.3663$	$0.3871$	$0.4346$	$0.6894$	$0.6890$	$0.7040$	$0.5598$	$0.5693$	$0.6148$
	LSAT	$0.3124$	$0.3280$	$0.3772$	$0.6698$	$0.6699$	$0.6828$	$0.4939$	$0.5033$	$0.5505$
	SAT-en	$0.4339$	$0.4414$	$0.4848$	$0.5619$	$0.5673$	$0.5753$	$0.5905$	$0.5959$	$0.6381$
Qwen2.5	MMLU	$0.5857$	$0.6120$	$0.6472$	$0.8346$	$0.8338$	$0.8431$	$0.6031$	$0.6221$	$0.6697$
	LogiQA-en	$0.5333$	$0.5573$	$0.5946$	$0.8330$	$0.8391$	$0.8420$	$0.5588$	$0.5645$	$0.6308$
	LSAT	$0.4931$	$0.5085$	$0.5561$	$0.8199$	$0.8167$	$0.8261$	$0.5197$	$0.5139$	$0.5891$
	SAT-en	$0.6318$	$0.6500$	$0.6833$	$0.8258$	$0.8263$	$0.8280$	$0.6495$	$0.6571$	$0.7086$
Falcon3-Mamba	MMLU	$0.8014$	$0.8089$	$0.8177$	$0.8793$	$0.8792$	$0.8847$	$0.8433$	$0.8425$	$0.8547$
	LogiQA-en	$0.8026$	$0.8055$	$0.8167$	$0.8822$	$0.8834$	$0.8872$	$0.8465$	$0.8477$	$0.8595$
	LSAT	$0.7453$	$0.7422$	$0.7605$	$0.8511$	$0.8491$	$0.8561$	$0.8077$	$0.8137$	$0.8214$
	SAT-en	$0.7630$	$0.7699$	$0.7788$	$0.8486$	$0.8502$	$0.8535$	$0.8287$	$0.8263$	$0.8441$

Table 12. Response ACC comparison after correction for three types of perturbations (SwapAlpha, SwapWord, CaseAlpha) at 100% intensity across four datasets (MMLU, LogiQA-en, LSAT, and SAT-en) using four LLMs (GLM4, Llama3.1, Qwen2.5, and Falcon3-Mamba). For each perturbation type, the table presents the ACC values after CTC Detection (CTC), TextBlob, and the self-correction reflection (Ours).

LLMs	Dataset	ACC of SwapAlpha			ACC of SwapWord			ACC of CaseAlpha
		CTC	TextBlob	Ours	CTC	TextBlob	Ours	CTC	TextBlob	Ours
GLM4	MMLU	$50.77$	$51.92$	$54.69$	$47.94$	$48.05$	$49.27$	$59.23$	$59.30$	$60.72$
	LogiQA-en	$33.80$	$34.11$	$40.03$	$28.66$	$29.75$	$32.40$	$36.76$	$36.60$	$46.26$
	LSAT	$40.21$	$41.77$	$43.81$	$31.68$	$31.94$	$32.51$	$47.17$	$47.26$	$48.27$
	SAT-en	$66.28$	$68.08$	$73.79$	$54.97$	$55.54$	$56.31$	$81.39$	$81.02$	$82.04$
Llama3.1	MMLU	$47.34$	$48.90$	$50.85$	$47.49$	$47.08$	$48.07$	$53.85$	$53.92$	$55.42$
	LogiQA-en	$33.64$	$33.18$	$35.51$	$28.84$	$29.46$	$29.75$	$37.23$	$37.50$	$38.47$
	LSAT	$36.07$	$36.66$	$39.45$	$29.70$	$29.74$	$30.72$	$41.02$	$41.72$	$43.11$
	SAT-en	$53.37$	$56.59$	$59.71$	$46.94$	$47.66$	$48.06$	$62.59$	$62.53$	$64.08$
Qwen2.5	MMLU	$58.55$	$59.46$	$61.80$	$53.32$	$53.19$	$54.37$	$66.17$	$65.79$	$66.37$
	LogiQA-en	$44.86$	$45.33$	$49.22$	$35.98$	$37.47$	$39.72$	$51.78$	$51.43$	$52.49$
	LSAT	$47.97$	$47.02$	$51.34$	$36.37$	$36.29$	$37.66$	$54.22$	$54.11$	$54.81$
	SAT-en	$74.27$	$75.24$	$79.61$	$58.77$	$58.91$	$60.19$	$83.44$	$83.16$	$84.95$
Falcon3-Mamba	MMLU	$48.50$	$51.56$	$52.10$	$47.85$	$48.00$	$48.43$	$56.52$	$56.44$	$57.56$
	LogiQA-en	$34.27$	$35.60$	$37.07$	$36.36$	$36.14$	$37.38$	$38.48$	$38.78$	$39.56$
	LSAT	$36.37$	$36.17$	$38.35$	$32.70$	$32.89$	$33.60$	$39.35$	$39.33$	$40.93$
	SAT-en	$52.91$	$53.68$	$56.80$	$48.56$	$48.66$	$49.51$	$60.62$	$59.77$	$62.62$

Using self-correction reflection, the models achieved significant improvements not only in semantics but also in stable and reliable performance in practical tasks. This indicates that the approach of self-correction reflection is an effective method for enhancing the performance of LLMs when dealing with input perturbations, offering broad application prospects and research value.

5.3. Ablation Study

To validate the importance of the consistency principle in our self-correction reflection framework, we conducted targeted ablation experiments comparing the self-correction reflection with a modified version that removes the Historical Enhancement via Consistency Principle phase (HECP). This isolates the use of the consistency principle of the large language model, so that after the correction perturbation, the historical information of the original text is not retained, which will lead to the loss of semantic information of the original text. Through this ablation experiment, we prove the comprehensiveness of our proposed method.

The ablation results in Table 13 and Table 14 show that removing HECP leads to a consistent performance drop in all evaluation scenarios, validating the necessity of preserving historical semantic information during the self-correction process. For MSCS, the full method (Ours) outperforms the ablation variant (w/o HECP) across a variety of perturbation types, suggesting that HECP mitigates the error propagation caused by semantic drift. For ACC, all models show a consistent trend that the full method (Ours) outperforms the ablated variant (w/o HECP) across perturbation types, especially in datasets with strong reasoning capabilities such as LogiQA-en and LSAT, highlighting the role of HECP in preserving task-specific knowledge during perturbation recovery. Notably, the performance gap is larger for CaseAlpha/SwapAlpha compared to SwapWord, suggesting that HECP is critical for maintaining contextual semantic consistency when corrections corrupt the lexicon itself. Together, these findings confirm that the consistency principle enforced by history augmentation is essential for robust self-correction under semantic perturbations.

Table 13. Response MSCS comparison of the self-correction reflection (Ours) with the ablated variant (w/o HECP) across three perturbation types at 100% intensity, evaluated on four datasets using four LLMs.

LLMs	Dataset	MSCS of SwapAlpha		MSCS of SwapWord		MSCS of CaseAlpha
		w/o HECP	Ours	w/o HECP	Ours	w/o HECP	Ours
GLM4	MMLU	$0.9913$	$0.9936$	$0.9985$	$0.9986$	$0.9922$	$0.9939$
	LogiQA-en	$0.9885$	$0.9922$	$0.9982$	$0.9983$	$0.9878$	$0.9924$
	LSAT	$0.9478$	$0.9606$	$0.9897$	$0.9902$	$0.9553$	$0.9632$
	SAT-en	$0.8284$	$0.8571$	$0.9059$	$0.9129$	$0.8470$	$0.8672$
Llama3.1	MMLU	$0.4068$	$0.4726$	$0.6590$	$0.6741$	$0.5589$	$0.6035$
	LogiQA-en	$0.3820$	$0.4346$	$0.6931$	$0.7040$	$0.5735$	$0.6148$
	LSAT	$0.3282$	$0.3772$	$0.6727$	$0.6828$	$0.5177$	$0.5505$
	SAT-en	$0.4452$	$0.4848$	$0.5649$	$0.5753$	$0.6019$	$0.6381$
Qwen2.5	MMLU	$0.5997$	$0.6472$	$0.8355$	$0.8431$	$0.6190$	$0.6697$
	LogiQA-en	$0.5460$	$0.5946$	$0.8364$	$0.8420$	$0.5660$	$0.6308$
	LSAT	$0.5089$	$0.5561$	$0.8212$	$0.8261$	$0.5286$	$0.5891$
	SAT-en	$0.6454$	$0.6833$	$0.8257$	$0.8280$	$0.6644$	$0.7086$
Falcon3-Mamba	MMLU	$0.8047$	$0.8177$	$0.8801$	$0.8847$	$0.8460$	$0.8547$
	LogiQA-en	$0.8056$	$0.8167$	$0.8818$	$0.8872$	$0.8494$	$0.8595$
	LSAT	$0.7487$	$0.7605$	$0.8526$	$0.8561$	$0.8109$	$0.8214$
	SAT-en	$0.7660$	$0.7788$	$0.8495$	$0.8535$	$0.8322$	$0.8441$

Table 14. Response ACC comparison of the self-correction reflection (Ours) with the ablated variant (w/o HECP) across three perturbation types at 100% intensity, evaluated on four datasets using four LLMs.

LLMs	Dataset	ACC of SwapAlpha		ACC of SwapWord		ACC of CaseAlpha
		w/o HECP	Ours	w/o HECP	Ours	w/o HECP	Ours
GLM4	MMLU	$50.86$	$54.69$	$47.98$	$49.27$	$59.85$	$60.72$
	LogiQA-en	$29.91$	$40.03$	$29.13$	$32.40$	$39.56$	$46.26$
	LSAT	$40.80$	$43.81$	$31.74$	$32.51$	$47.26$	$48.27$
	SAT-en	$67.25$	$73.79$	$55.46$	$56.31$	$81.45$	$82.04$
Llama3.1	MMLU	$47.51$	$50.85$	$47.75$	$48.07$	$54.01$	$55.42$
	LogiQA-en	$33.80$	$35.51$	$29.15$	$29.75$	$37.89$	$38.47$
	LSAT	$36.75$	$39.45$	$29.73$	$30.72$	$41.22$	$43.11$
	SAT-en	$54.94$	$59.71$	$47.49$	$48.06$	$63.68$	$64.08$
Qwen2.5	MMLU	$59.18$	$61.80$	$53.43$	$54.37$	$66.14$	$66.37$
	LogiQA-en	$46.04$	$49.22$	$36.34$	$39.72$	$51.87$	$52.49$
	LSAT	$48.27$	$51.34$	$37.26$	$37.66$	$54.41$	$54.81$
	SAT-en	$75.24$	$79.61$	$59.31$	$60.19$	$83.92$	$84.95$
Falcon3-Mamba	MMLU	$49.42$	$52.10$	$47.97$	$48.43$	$57.06$	$57.56$
	LogiQA-en	$35.38$	$37.07$	$36.60$	$37.38$	$38.56$	$39.56$
	LSAT	$36.79$	$38.35$	$32.99$	$33.60$	$39.45$	$40.93$
	SAT-en	$53.28$	$56.80$	$48.59$	$49.51$	$60.65$	$62.62$

We additionally analyze the GPU memory consumption characteristics of both versions to verify computational feasibility. Table 15 demonstrates that while the full method incurs marginally higher memory usage (average +6.18% across models) due to history retention, the absolute increase remains negligible (0.77–1.2 GB) compared to baseline model memory footprints (16.34–18.55 GB). This confirms that the primary memory burden stems from base model parameters rather than our augmentation mechanisms.

Table 15. Response GPU memory usage (in GB) of the self-correction reflection (Ours) with the ablated variant (w/o HECP) evaluated on four datasets using four LLMs.

LLMs	Dataset	GPU Usage (GB)		Extra Overhead (%)
		w/o HECP	Ours
GLM4	MMLU	18.55	19.32	4.15
	LogiQA-en
	LSAT
	SAT-en
Llama3.1	MMLU	16.34	17.37	6.30
	LogiQA-en
	LSAT
	SAT-en
Qwen2.5	MMLU	16.67	17.86	7.14
	LogiQA-en
	LSAT
	SAT-en
Falcon3-Mamba	MMLU	16.84	18.04	7.13
	LogiQA-en
	LSAT
	SAT-en

6. Discussion

The experimental results indicate that although LLMs experience performance declines when confronted with various perturbations, the introduction of the self-correction reflection method significantly enhances the models’ capabilities, demonstrating improved robustness and accuracy. In particular, for the SwapAlpha perturbation, after applying self-correction reflection, the average MSCS improvement across all models reaches 10.88%, while the average ACC improvement is 10.22%.

The self-correction reflection method proposed in this study provides a promising approach to enhance the robustness of the response. By simulating the brain’s sequential steps to correct input perturbations, this mechanism effectively mitigates the reduction in accuracy caused by input perturbations. This improvement is consistent with neurological and psychological research on input perturbations. Experimental results demonstrated that integrating self-correction reflection can significantly improve model performance under input perturbation conditions.

We did not undertake generation tasks in our evaluation of LLMs because assessing the output quality can often be challenging. Large language models are capable of generating highly creative or high-quality text, which makes evaluation difficult without reference outputs. According to [45], these challenges can impair effective assessment. Therefore, we opted for classification tasks with clear answers for our tests. Future work may include optimizing these evaluation methods.

Despite these advances, our results also highlight the limitations of current approaches. While self-correction reflection improves the model’s ability to handle input perturbations, it also increases energy consumption due to the implementation of the consistency principle, which expands the context input. The additional context grows with the size of the user’s input text, leading to extra memory or GPU memory overhead for data processing. However, these additional overheads are negligible (average +6.18% across models, or an absolute increase of 0.77–1.2 GB) compared to the substantial memory and GPU memory consumption primarily caused by the huge number of parameters of LLMs during operation (16.34–18.55 GB).

7. Conclusions

This study adopts studies of human sensitivity in neuroscience and psychology to handle input perturbations, providing a novel perspective for the development of LLM technology. By systematically analyzing the limitations of tokenization and introducing the self-correction reflection method inspired by human cognition, we provide a method to mitigate the impact of input perturbations on LLMs.

The experimental results validate the efficacy of self-correction reflection, demonstrating improved performance across multiple models and datasets. Across different models and perturbation types, the ACC demonstrates an average improvement of 5.49% through self-correction reflection. However, this study also underscores the need for more innovation in tokenization techniques and architectural design to achieve truly human-like cognitive robustness. It is the first integration of predictive coding and the noisy channel model to achieve cognitive-inspired robustness.

Future work could focus on integrating dynamic correction strategies within the tokenization process itself, as well as exploring cross-disciplinary approaches that combine advances in artificial intelligence with deeper insights from neuroscience, psychology, and other relevant disciplines. By continuing to refine the interplay between human-inspired mechanisms and machine learning architectures, we can pave the way for more reliable, adaptable, and intelligent language models capable of thriving in real-world applications.