Computational Investigation of Aerodynamic Behaviour in Rubber O-Ring: Effects of Flow Velocity and Surface Topology

Abstract

This report uses computational fluid dynamics (CFDs) to investigate the aerodynamics of a rubber O-ring, with a focus on assessing the influence of fluid velocity and surface topology whilst providing a detailed methodology that promotes correct procedures. A steady state scenario was set up, modelling laminar airflow across two O-rings with 5 μm and 100 μm surface finishes, respectively. Analysis showed that increasing the fluid velocity from 0.01 m/s to 2 m/s significantly translates the separation points downstream, consolidating wake regions behind the airfoil. The CFD simulations also infer that as the fluid velocity increases, the frictional drag coefficients decrease from 3.13 to 0.11, and the pressure drag coefficients increase from 0.55 to 0.6, implying that the recirculation of flowlines behind the O-ring becomes the most hindering factor on aerodynamics. Conversely, variations in surface roughness showed negligible effects on the flow field. This insensitivity is attributed to the low Reynolds number (Re) used in all simulations, where a roughness of 5 μm or 100 μm remains well within the laminar sublayer, therefore minimising their impact on boundary layer disruption and flow separation.

1. Introduction

Computational fluid dynamics (CFDs) utilises digital code and numerical algorithms to analyse elaborate fluid state scenarios more efficiently than theoretical or experimental techniques. Within business, CFD is commonly used to design heating, ventilation and cooling systems, or to investigate the aerodynamic performance of airfoils [1,2]. For instance, Ismail, Sharudin, Talib, Hassan and Yusoff’s [3] work involved studying a closed-wing, micro air vehicle. Whilst older studies have researched the basics of torus aerodynamics [4], and modern scholars have identified its benefits within the aerospace and closed-wing systems [3,5], no studies have analysed the downstream effects of a torus or augmented the field with CFD simulations and computational evidence.

Thus, this report utilises CFD to examine the downstream flow behind a rubber O-ring and investigate the influence of flow velocity and surface topography on aerodynamic behaviour (Figure 1), supplementing the literature field and augmenting previous work regarding O-ring paper planes [3]. This article pays special attention to the boundary layer (from separation points to turbulent flow), velocity and pressure distributions, and the wake region (specifically the subsequent impact on drag coefficients and vortex generation). A secondary criterion of this methodology is to promote a correct procedure that can be used as a benchmark for industrial applications. To achieve these aims, this article presents eight setups (Table 1 and Table 2) that simulate airflow across a rubber O-ring (Figure 1 and Figure 2) whilst providing a detailed methodology and comparing results with published data.

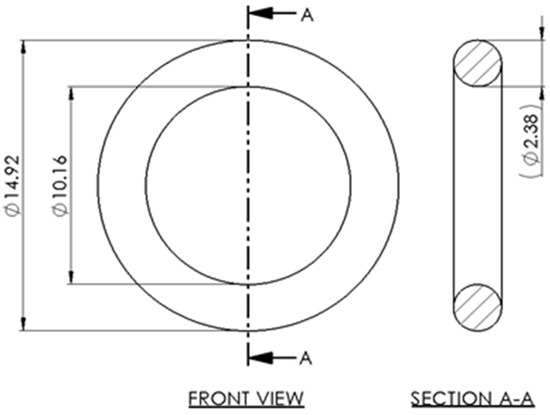
Figure 1. O-ring schematic.

Table 1. Overview of simulation setups.

Setup	Analysis Type	Fluid Composition	O-Ring Material	O-Ring Topography (μm)	Fluid Velocity (m/s)
1	External	Air	Natural Rubber	5	0.01
2				5	1.00
3				5	0.02
4				5	2.00
5				100	0.01
6				100	1.00
7				100	0.02
8				100	2.00

Table 2. Detailed conditions of simulation setups.

Settings	Setup 1	Setup 2	Setup 3	Setup 4	Setup 5	Setup 6	Setup 7	Setup 8
Analysis Type
Analysis Type	External	External	External	External	External	External	External	External
Physical Feature	Fluid Flow	Fluid Flow	Fluid Flow	Fluid Flow	Fluid Flow	Fluid Flow	Fluid Flow	Fluid Flow
Fluids
Fluids	Air	Air	Air	Air	Air	Air	Air	Air
Flow Type	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent	Laminar and Turbulent
Wall Condition
Wall Conditions	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall	Adiabatic Wall
Roughness	5 μm	5 μm	5 μm	5 μm	100 μm	100 μm	100 μm	100 μm
Initial and Ambient Conditions
Thermodynamic Parameters:
Pressure	101,325 Pa	101,325 Pa	101,325 Pa	101,325 Pa	101,325 Pa	101,325 Pa	101,325 Pa	101,325 Pa
Temperature	293.2 K	293.2 K	293.2 K	293.2 K	293.2 K	293.2 K	293.2 K	293.2 K
Velocity Parameters:
Definition	3D Vector	3D Vector	3D Vector	3D Vector	3D Vector	3D Vector	3D Vector	3D Vector
Velocity X	0	0	0	0	0	0	0	0
Velocity Y	0.01 m/s	1.00 m/s	0.02 m/s	2.00 m/s	0.01 m/s	1.00 m/s	0.02 m/s	2.00 m/s
Velocity Z	0	0	0	0	0	0	0	0
Turbulence Parameters	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A

Figure 2. Direction of fluid flow.

2. Methodology

2.1. Pre-Processing

Before conducting CFD, a Computer-Aided Design (CAD) model of the O-ring was created (Figure 1). The designed model was then exported to SolidWorks Flow Simulation version 2021 (SWFS) by Solidworks Corporation (Waltham, MA, USA), where detailed conditions were applied to define the problem for numerical computation [4,5]. Since the precision of the final results are determined largely by the pre-processing routine [4,5,6], this report separates the procedure into four key steps.

2.1.1. Detailed Conditions and Cloning

First, the detailed conditions were applied to Setup 1 using the values outlined in Table 2. This process involved defining the analysis, flow, wall, thermodynamic and velocity parameters. As shown (Table 2), the thermodynamic parameters were set to a standard environment of atmospheric pressure at 20 °C, whilst the velocity parameters were defined as a 3D vector to ensure airflow was only modelled in the Y axis. It is important to note that the results are dependent on these settings, and slight changes to pressure, temperature or flow direction will all affect the post-processing results. Low velocity (laminar flow) was utilised as the steady flow provides more repeatable and regular calculations, enabling analysis to concentrate on the impact of surface roughness and increased velocity. Once Setup 1 was fully complete (post-processing included), the clone tool was used to efficiently generate the remaining seven experiments [6]. The boundary conditions were then amended as per Table 1.

2.1.2. Computational Domain

The computational domain defines the boundaries for CFD calculation. For external flow scenarios, the dimensions are dependent on fluid behaviour. The upstream region must enable a stabilised flow, while the downstream and side regions must accommodate flow deviations and wake formations. This study established a computational domain by adapting the “Silsoe Cube” simulation by Revuz, Hargreaves and Owen [7] (Figure 3). In this study, ‘H’ was amended to the outer diameter (Equation (1)), and the domain height ‘6H’ was replaced with 5H on both sides (Figure 3).

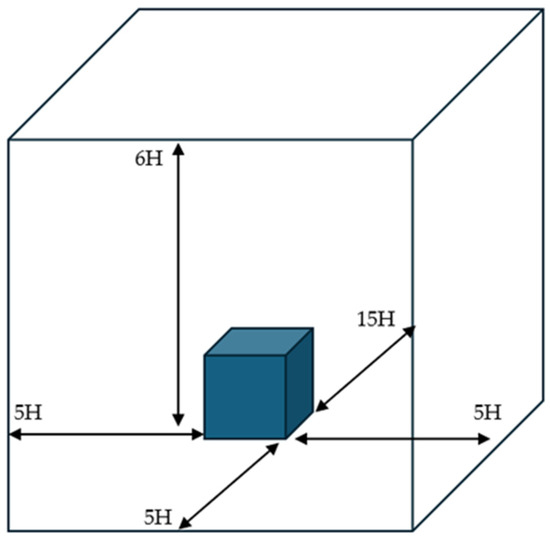
Figure 3. Computational domain used for Silsoe Cube simulations [7].

The computational domain can be further optimised through a trial-and-error approach to ascertain a better wall time-to-information ratio. However, this report had quick calculation times for all simulations, with flow deviation being accurately captured, necessitating no need for further action.

$$H=OuterDiameter=14.92\mathrm{m}\mathrm{m}$$

(1)

2.1.3. Mesh Generation

To enable accurate calculations, the computational domain was divided into a structured mesh consisting of rectangular parallelepipeds [8]. A mesh convergence analysis was then completed to find the optimum precision-to-wall time relationship [1,6,7,8,9,10,11,12] (Figure 4). In the case of this report, the global mesh was refined to increase discretisation (a refinement value of six was used on SWFS), whilst a ratio factor was introduced to improve precision and minimise the computational cost by refining the mesh in close proximity to the O-ring and coarsening it towards the periphery; a ratio factor of one was assigned using SWFS (Figure 5). As presented in Figure 4, the optimised mesh (refinement of 6 and a ratio factor of 1) combines quick processing with accurate flow trajectories, and no unnecessary eddies were generated in the wake region unlike trials (b) and (d), and a wall time of 816 s was significantly less than trials (g–i) (Figure 4).

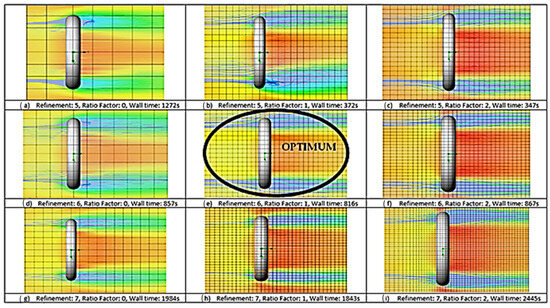
Figure 4. Mesh convergence analysis results.

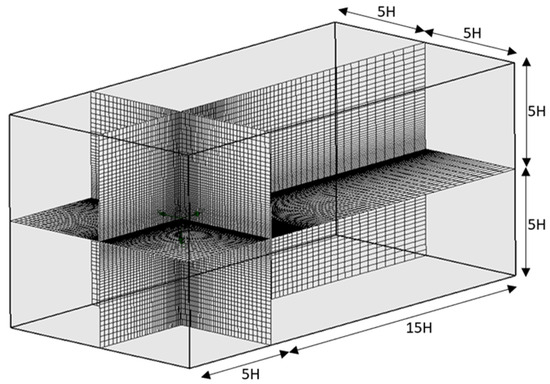
Figure 5. Discretised computational domain used for all setups.

2.1.4. Objectives

Five global goals were then created to accelerate the solution process and reduce errors in the calculated parameters [6]: (a) pressure, (b) velocity, (c) velocity in the Y-axis, (d) normal force in the Y-axis and (e) frictional force in the Y-axis. Secondary objectives were then established using the following equations (Table 3); these would help analyse the trends concerning variations in the inlet velocity/Reynolds number (Re) as well as determine frictional and pressure drag coefficients (Cd) [11,12].

$$TotalCd={\displaystyle \frac{F_N\left(Yaxis\right)}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rho V^{2}A}}$$

(2)

$$FrictionalCd={\displaystyle \frac{F_{FR}\left(Yaxis\right)}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rho V^{2}A}}$$

(3)

$$Pressure Cd=Total Cd-FrictionalCd$$

(4)

$$\mathrm{R}\mathrm{e}={\displaystyle \frac{V\rho L}{\mu }}$$

(5)

Table 3. Values for Equations (2) to (5).

Symbol	Name	Value	Units
$\rho$	Density	1.204	kg/m3
μ	Dynamic Viscosity	1.825 × 10−5	Kg/ms
L	Characteristic Linear Dimension	0.01492	m
A	Area	9.376 × 10−5	m2
V	Velocity	Dependant on trial	m/s
FN	Normal Force	Dependant on trial	N
FFR	Frictional Force	Dependant on trial	N

2.2. Post-Processing

Once the numerical calculations were completed, the following plots were created to visualise the data, helping to see relationships between flow velocity, surface roughness and aerodynamic behaviour:

• Contour Plot: uses a colour gradient to show changes in pressure and velocity distributions, up and downstream of the O-ring.
• Surface Plot: used to study the interface between the O-ring body and fluid boundary (Figure 6)
  

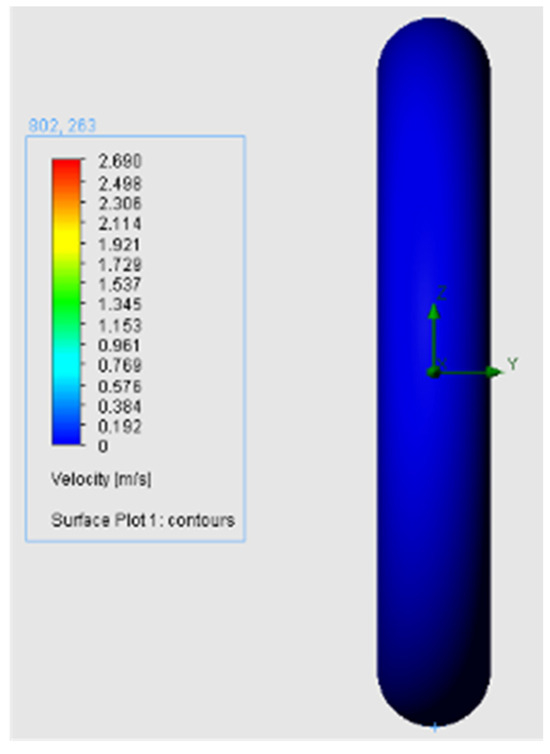  Figure 6. Evidence of non-slip conditions (Setup 8).
• Flow Trajectories: creates flowlines within the domain, providing a visual representation of the boundary layer and wake region (Figure 7, Figure 8, Figure 9 and Figure 10)
  

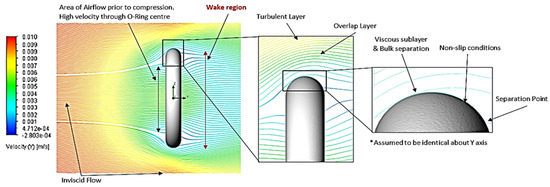  Figure 7. Boundary layer of Setup 1 (0.01 m/s, 5 μm).
  

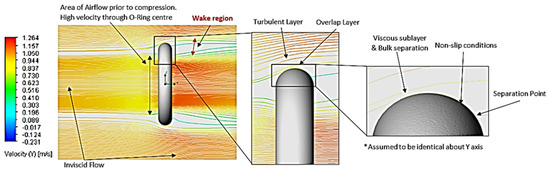  Figure 8. Boundary layer of Setup 2 (1 m/s, 5 μm).
  

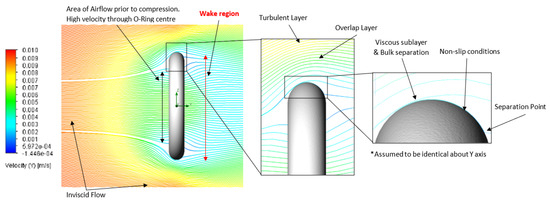  Figure 9. Boundary layer of Setup 5 (0.01 m/s, 100 μm).
  

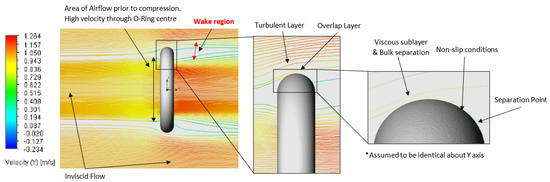  Figure 10. Boundary layer of Setup 6 (1 m/s, 100 μm).

3. Results

3.1. Boundary Layer

The first major finding is that fluid velocity equals zero at the surface boundary (Figure 6), proving the concept of non-slip conditions claimed by other authors [13,14,15]; as the flowlines then distance from the O-ring, frictional forces decrease, enabling fluid flow to return to maximum velocity [13]. This region of varying velocity is classified as the boundary layer and incorporates a viscous sublayer, buffer layer, overlap layer and turbulent layer. Within internal, turbulent flow scenarios, the proximity near the wall can be stratified into distinct sublayers: the viscous sublayer, directly adjacent to the no-slip boundary, where molecular viscosity dominates, resulting in a linear velocity profile and high viscous shear stress; the buffer layer, transitioning from the viscous sublayer, where turbulent kinetic energy increases, leading to instability and the onset of turbulent fluctuations; the overlap (log-law) layer, further from the wall, exhibiting a logarithmic velocity profile governed by the balance between diminishing viscous shear stress and increasingly dominant turbulent shear stress, as described by the logarithmic law of the wall; and the outer layer, where turbulent shear stress significantly outweighs viscous stress, resulting in an inviscid turbulent flow characterised by momentum transport driven by large-scale eddies and approaching the free-stream velocity, with accurate representation in this layer reliant on turbulent kinetic energy cascade and eddy viscosity models [15,16].

3.1.1. Relationship Between Flow Velocity and Boundary Layer

At low Re, the simulations produced a laminar boundary layer, as shown in Figure 7, indicative of a viscous-dominated flow. As Re increased, corresponding to higher fluid inertia, the laminar boundary layer extended further along the surface profile. Concurrently, the separation points were observed to shift downstream (Figure 7, Figure 8, Figure 9 and Figure 10). This downstream displacement resulted in a reduction in the wake region, consequently minimising the pressure drag inflicted on the O-ring. This behaviour aligns with the established relationship between Re, boundary layer development, separation and pressure drag in external flows [13,17,18,19,20].

3.1.2. Relationship Between Surface Roughness and Boundary Layer

Theoretically, an increased topography should induce similar effects to increase fluid velocity on boundary layer behaviour; however, the O-ring simulation setups (Figure 7, Figure 8, Figure 9 and Figure 10) demonstrated negligible variations in flow characteristics across a range of surface topographies (5 μm to 100 μm). This lack of observable difference is attributed to the roughness height remaining significantly smaller than the laminar sublayer thickness in all simulated cases, effectively rendering the O-ring surface hydraulically smooth. This interpretation is not unrealistic and is the case in Ismail, Sharudin, Talib, Hassan and Yusoff’s [3] application of O-ring planes and with Dugdale’s [15] assertion that when the roughness element diameter is smaller than the laminar sublayer thickness, the surface behaves as a smooth boundary [15,19,20,21]. However, as the surface roughness increases past this critical value, friction is increased on nearby flowlines, expediting the transition from laminar to turbulent flow within the boundary layer; subsequently, this can induce separation points in regions where flow is already unstable, thus increasing drag on the airfoil.

3.2. Velocity and Pressure Distribution

Across all setups, the streamlined visualisations (Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12) demonstrate a deflection of flow trajectories around the O-ring, indicating the presence of an adverse pressure gradient. This deflection induced increased shear stress between fluid layers, resulting in momentum loss and a corresponding decrease in velocity upstream of the O-ring, as highlighted by the velocity magnitude contours (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28). Subsequently, the streamlines show recirculation patterns within the low-pressure regions downstream of the O-ring, forming a wake characterised by reduced velocity magnitudes [13], also illustrated in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28.

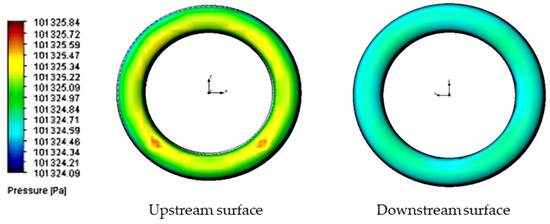
Figure 11. Surface pressure for Setup 6 (1 m/s, 100 μm).

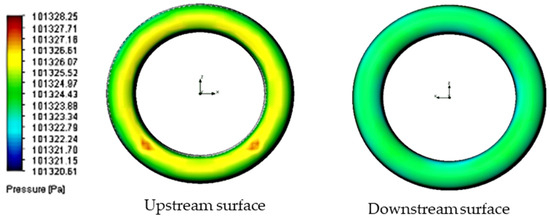
Figure 12. Surface pressure for Setup 8 (2 m/s, 100 μm).

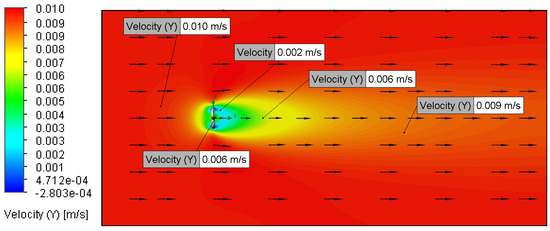
Figure 13. Velocity plot for Setup 1 (0.01 m/s, 5 μm).

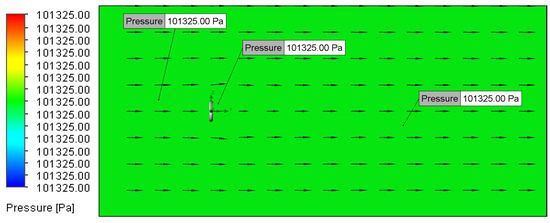
Figure 14. Pressure plot for Setup 1 (0.01 m/s, 5 μm).

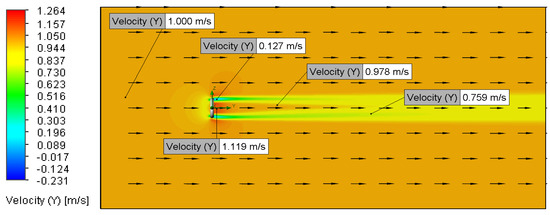
Figure 15. Velocity plot for Setup 2 (1 m/s, 5 μm).

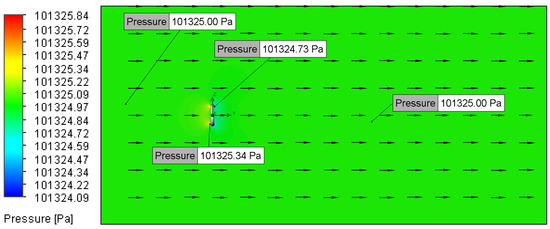
Figure 16. Pressure plot for Setup 2 (1 m/s, 5 μm).

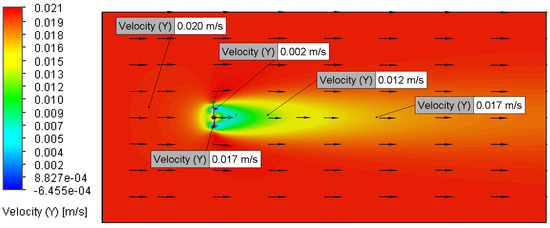
Figure 17. Velocity plot for Setup 3 (0.02 m/s, 5 μm).

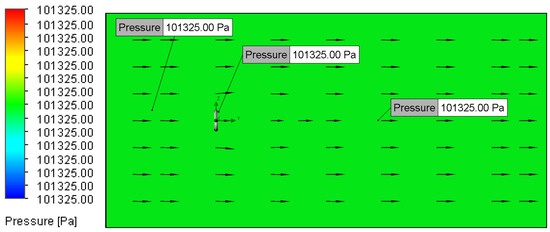
Figure 18. Pressure plot for Setup 3 (0.02 m/s, 5 μm).

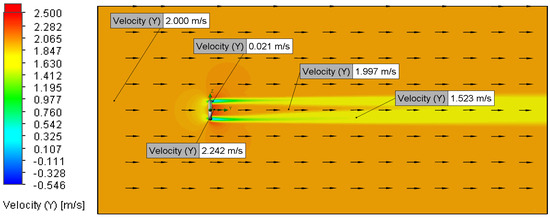
Figure 19. Velocity plot for Setup 4 (2 m/s, 5 μm).

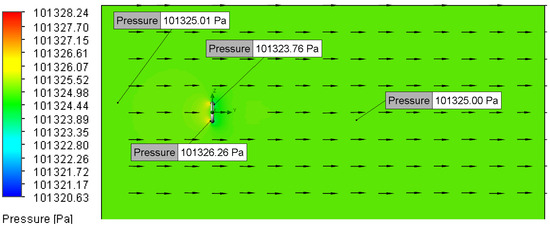
Figure 20. Pressure plot for Setup 4 (2 m/s, 5 μm).

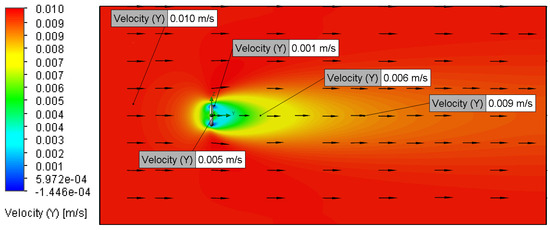
Figure 21. Velocity plot for Setup 5 (0.01 m/s, 100 μm).

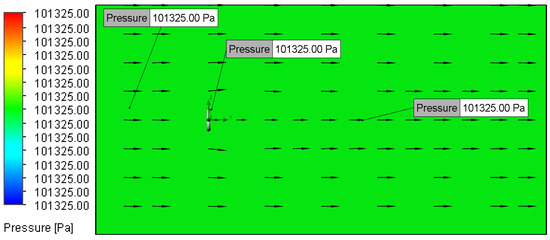
Figure 22. Pressure plot for Setup 5 (0.01 m/s, 100 μm).

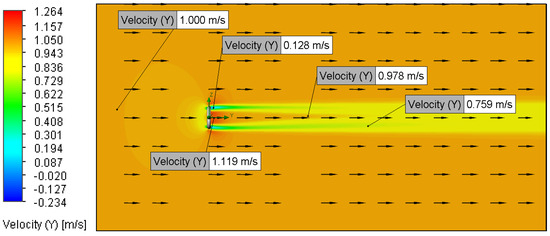
Figure 23. Velocity plot for Setup 6 (1 m/s, 100 μm).

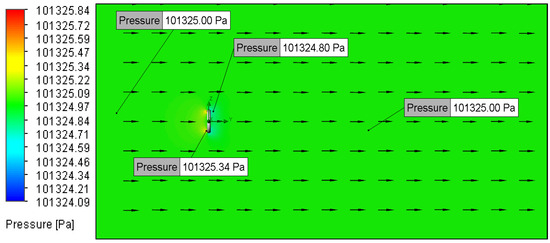
Figure 24. Pressure plot for Setup 6 (1 m/s, 100 μm).

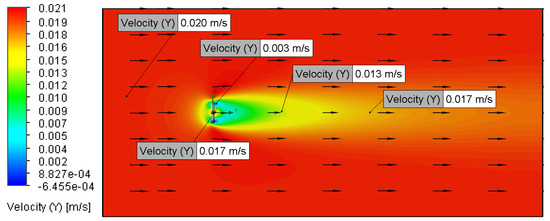
Figure 25. Velocity plot for Setup 7 (0.02 m/s, 100 μm).

Figure 26. Pressure plot for Setup 7 (0.02 m/s, 100 μm).

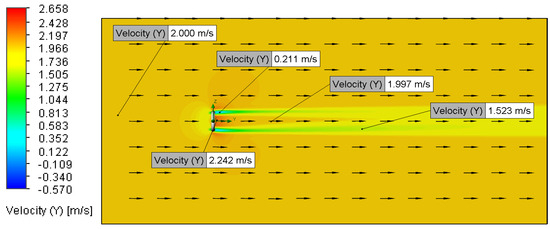
Figure 27. Velocity plot for Setup 8 (2 m/s, 100 μm).

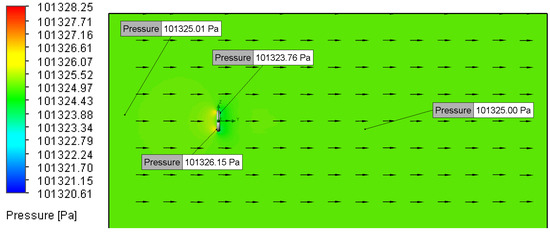
Figure 28. Pressure plot for Setup 8 (0.01 m/s, 100 μm).

3.2.1. Relationship Between Flow Velocity and Velocity Distribution

Increasing the inlet velocity from 0.01 m/s to 2 m/s resulted in a noticeable reduction in the wake region, as observed in the streamline and velocity magnitude contour plots (Figure 7, Figure 8, Figure 9, Figure 10, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28). This phenomenon aligns with established fluid dynamics principles [13,17,18], attributing the wake reduction to a downstream shift in the boundary layer separation points, consistent with prior discussion. However, no apparent variations in the wake structure were observed between inlet velocities of 0.01 m/s and 0.02 m/s (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28), likely due to the minimal difference between these low-magnitude velocities, rendering the flow behaviour effectively indistinguishable within the simulation’s resolution [13,17,18].

All Setups also showed a localised region of accelerated flow through the O-ring’s central aperture (Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25). This velocity increase is attributed to the streamline convergence necessitated by the reduced cross-sectional area, a phenomenon governed by the continuity equation for incompressible, steady flow (Equation (6) [17]). Theoretically, this acceleration can be calculated using the continuity equation, with a 2 m/s inlet velocity, predicts a higher velocity than the simulated 2.242 m/s. As depicted in velocity magnitude contours (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28), the magnitude of this acceleration was directly proportional to the inlet flow velocity. Specifically, Setups 4 and 8, employing an inlet velocity of 2 m/s, resulted in a simulated maximum flow speed of 2.242 m/s through the O-ring’s centre. The divergence between the theoretical calculation and the simulated result may be due to factors not accounted for in the simplified continuity equation, such as viscous effects or the specific geometry of the O-ring’s aperture (Table 4).

$${\rho }_1{A}_1{V}_1={\rho }_2{A}_2{V}_2$$

(6)

Table 4. Values for Equations (6) and (7).

Symbol	Name	Value	Units
ρ	Density	1.204	kg/m3
V1	Initial Velocity	Dependant on trial	m/s
V2	Velocity through O-Ring	Dependant on trial	m/s
A1	The area before compression	Approximately: 0.00579	m2
A2	Area through O-Ring	0.00508	m2

Including incompressible conditions, as follows:

$$A_1{V}_1=A_2{V}_2$$

(7)

3.2.2. Relationship Between Surface Roughness and Velocity Distribution

While theoretical expectations suggest that an increased surface roughness would cause a reduction in the wake area and diminish the downstream length of low-velocity flow, the setups demonstrated negligible variations in wake characteristics between the 5 μm and 100 μm surface roughness configurations. This lack of sensitivity is attributed to the roughness of element heights in both cases remaining significantly smaller than the calculated laminar sublayer thickness. Consequently, the CFD model effectively treated the O-ring surface as hydraulically smooth, negating the anticipated influence of roughness on boundary layer separation and wake formation [13,17,18].

3.2.3. Relationship Between Flow Velocity and Pressure Distribution

When simulating low-speed airflow (0.01 m/s and 0.02 m/s), the static pressure distribution stayed constant, approximating the ambient pressure of 101,325 Pa (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28). However, with increasing inlet velocities (1 m/s and 2 m/s), a distinct pressure gradient developed around the O-ring (Figure 11 and Figure 12). Upstream, a high-pressure region formed due to the fluid’s stagnation and the normal force exerted on the O-ring surface, particularly at the stagnation points. Conversely, downstream, the static pressure decreased as a result of flow separation and the formation of a low-pressure wake region [13].

3.2.4. Relationship Between Surface Roughness and Pressure Distribution

This report identified no noticeable changes caused by an increased surface topography (5 μm to 100 μm), as both textures were deemed irrelevant, as previously discussed. Therefore, no post-processing plots are presented.

3.3. Vortex Shedding

Due to the O-ring blocking the inlet flow, regions of low pressure are immediately created behind the body (Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28). These vacuums inevitably introduce a pressure gradient, causing nearby trajectories to separate from the main flow to fill the voids in a diffusion-like movement. This random recirculation causes flowlines to produce turbulent eddies in the wake region, increasing air resistance in a process commonly referred to as form drag [13].

Relationship Between Flow Velocity/Surface Roughness and Vorticity Concentration

The setup results concur that the pressure gradient is significantly increased with airflow velocity (Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28); this subsequently expedites the diffusion movement of flowlines into the wake region and enhances the recirculation of fluid behind the O-ring, intensifying vorticity (Figure 29, Figure 30 and Figure 31) from 3.5/s (Figure 29) to 1000/s (Figure 31). However, since the wake region is consolidated at higher airflow (Figure 7, Figure 8, Figure 9 and Figure 10), the vortex distribution is controlled into narrower regions [6,13,17,18] (Figure 29, Figure 30 and Figure 31).

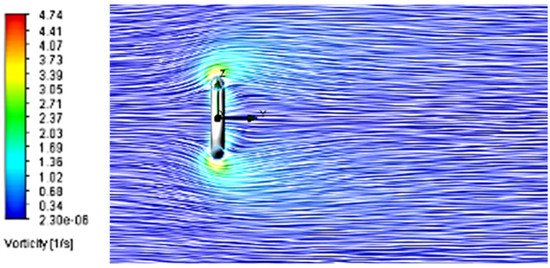
Figure 29. Vorticity plot for Setup 5 (0.01 m/s, 100 μm).

Figure 30. Vorticity plot for Setup 6 (1 m/s, 100 μm).

Figure 31. Vorticity plot for Setup 8 (2 m/s, 100 μm).

Nothing noticeable was observed when changing the flow velocities from 0.01 m/s to 0.02 m/s or between surface roughnesses of 5 μm and 100 μm. This is because both sets of values were too similar and quantitatively insignificant [13].

3.4. Drag Coefficients

By applying unique objectives (Equations (2)–(5)), this methodology calculated the total, frictional and pressure drag forces (Fds), along with their corresponding coefficients (Cd) (Table 5).

Table 5. Relationship between airflow, surface roughness and drag.

Velocity (m/s)	Re	Total Fd	Frictional Fd	Total Cd	Frictional Cd	Pressure Cd
O-Ring Roughness 5 μm
0.01	9.84	2.07 × 10−8	1.76 × 10−8	3.66	3.13	0.55
0.02	19.69	5.70 × 10−8	4.41 × 10−8	2.52	1.95	0.58
1.00	984.31	4.25 × 10−5	8.43 × 10−6	0.75	0.15	0.60
2.00	1968.62	1.59 × 10−4	2.39 × 10−5	0.71	0.11	0.60
O-Ring Roughness 100 μm
0.01	9.84	2.07 × 10−8	1.76 × 10−8	3.66	3.12	0.55
0.02	19.69	5.70 × 10−8	4.41 × 10−8	2.52	1.95	0.58
1.00	984.31	4.25 × 10−5	8.47 × 10−6	0.75	0.15	0.60
2.00	1968.62	1.59 × 10−4	2.39 × 10−5	0.71	0.11	0.60

3.4.1. Relationship Between Flow Velocity and Drag Coefficients

The results from this paper strongly concur with Matsson [6]; as fluid velocity increases, so do Re and total Fd. Mallick, Kumar, Tamboli, Kulkarni, Sati, Devi and Chandar [12] and Mott [17] attribute this to the fluid exerting a greater force on the upstream surface of the O-ring, which intensifies the pressure gradient (Figure 10 and Figure 11). This, in turn, enhances fluid recirculation in the wake region and increases the pressure Cd [6,12,13,17] (Table 5).

Table 5 also indicates that increased velocities correspond to higher frictional drag forces. As previously explained by Dugdale [13] and Mott [17], this occurs due to the expansion of the boundary layer, which enhances fluid–body interaction. Furthermore, Table 5 supports Mott’s [17] claim that as Re increases, pressure drag becomes the dominant factor, suggesting that frictional effects are most significant at low fluid velocities, as reflected in the frictional drag coefficients.

3.4.2. Impact of Surface Roughness on Drag

Most articles [11,13,20,21] suggest that increasing surface topography should reduce drag force by shifting the separation points downstream. However, this report found no significant differences between 5 μm and 100 μm, except for a slight decrease in frictional Cd at 0.01 m/s (from 3.13 to 3.12) (Table 4). This is because both surface finishes have grain dimensions smaller than the laminar sublayer [11,13,20,21].

4. Conclusions

As engineering design intensifies, the importance of mathematical computing significantly increases. By replacing manual calculations with specialist tools such as SWFS, companies can quickly solve fluid state scenarios for reduced expense.

For instance, this report was able to effectively prove that as airflow velocity increases, separation points within the boundary layer will be translated downstream. This in turn consolidates the wake region behind the body (controlling the regions of vorticity). Simulations also imply that as the velocity increases, a stronger force is inflicted on the upstream face of the airfoil; this subsequently escalates the pressure gradient around the O-ring, increasing the pressure drag coefficient whilst inevitably expediting the diffusion movement of flowlines into the wake region, enhancing the recirculation of fluid behind the O-ring and thus intensifying vorticity. Conversely, this report identified no impact regarding surface topography, but this is easily explained by the 5 μm and 10 μm grain sizes being smaller than the laminar sublayer.

This report thus incites scholars to prioritise the investigation of extreme surface finishes and their impact on aerodynamic behaviour. Future work should also compare and validate the findings with experimental and wind tunnel techniques to fully understand the precision of SWFS and the report methodology.