Task-Oriented Structural Health Monitoring of Dynamically Loaded Components by Means of SLDV-Based Full-Field Mobilities and Fatigue Spectral Methods
Abstract
1. Introduction
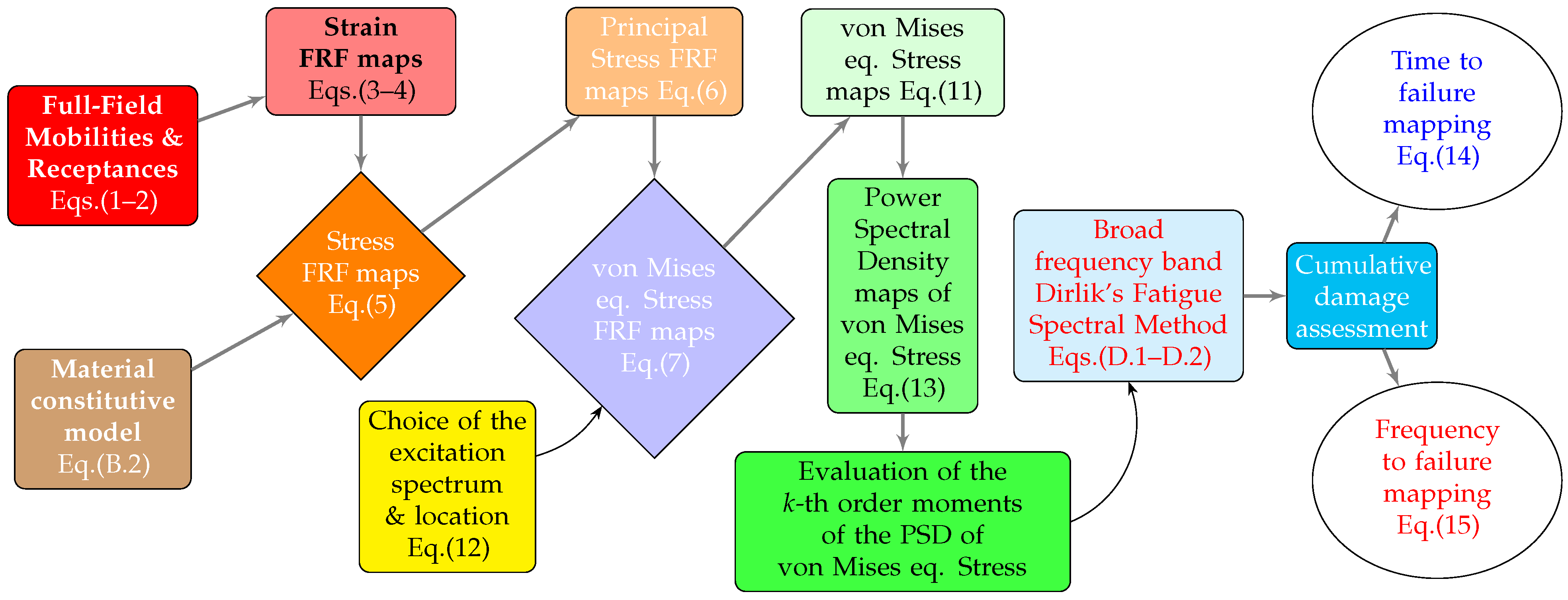
2. Materials and Methods

2.1. Full-Field SLDV-Based Mobilities and Receptances from the TEFFMA Project
2.1.1. Direct Characterisation by means of Full-Field Mobilities: a Brief Recall
2.1.2. Notes on the Plate under Test in the TEFFMA Project
2.1.3. Processing Notes about the Estimated Full-Field Mobility FRFs
2.2. Deriving New Quantities from Full-Field Receptances
2.2.1. Strain FRFs
2.2.2. Estimating the Stress FRFs




2.2.3. Estimating the Dynamic Stresses
2.3. Excitation Forces: a Simple Formulation of their Spectra
Complex-Valued Coloured Noise with Random Amplitude and Phase Variations

2.4. Spectral Methods for Cumulative Damage and Fatigue Life Assessment in Brief
3. Results
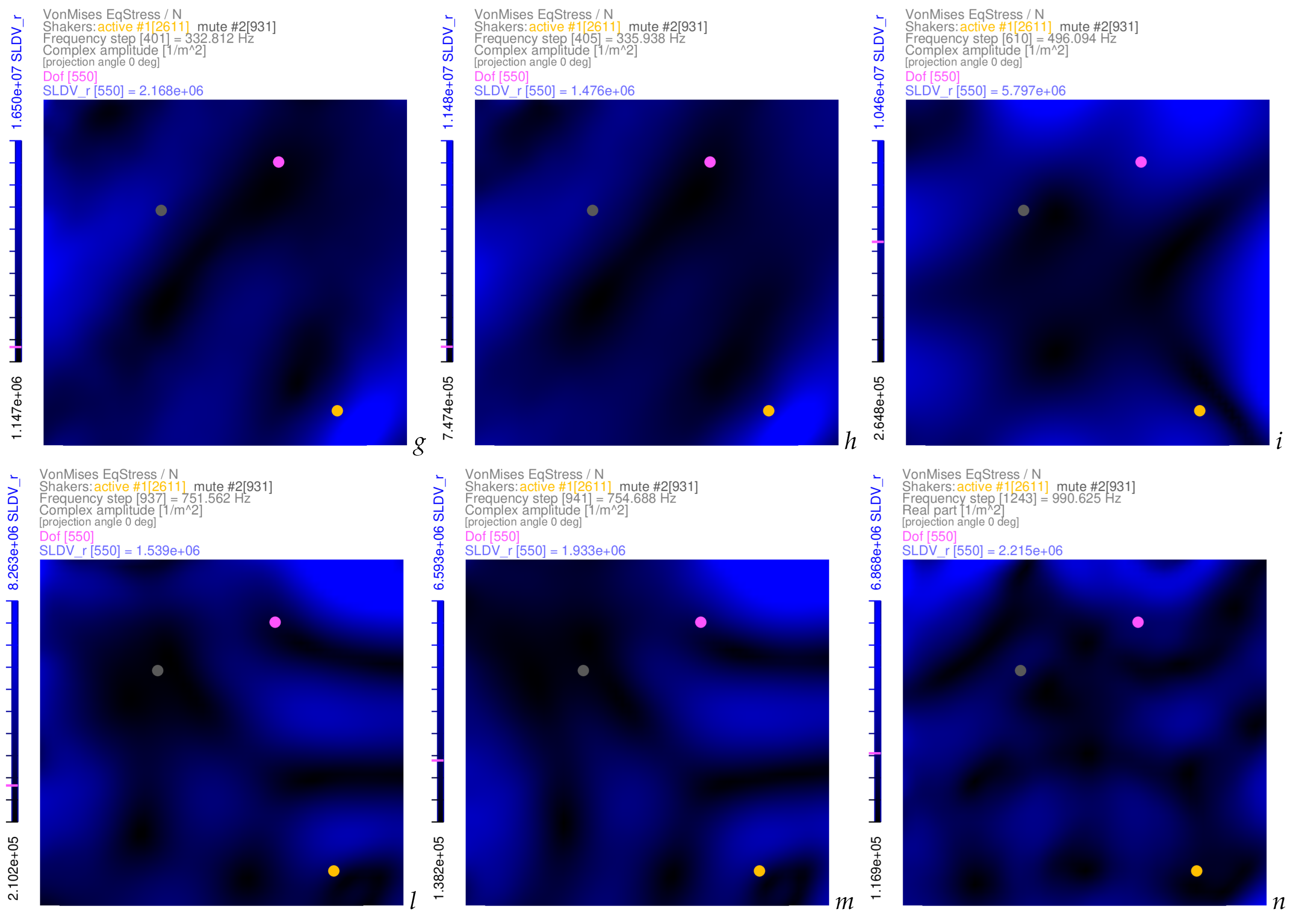
3.1. Examples of Von Mises Equivalent Stress FRFs
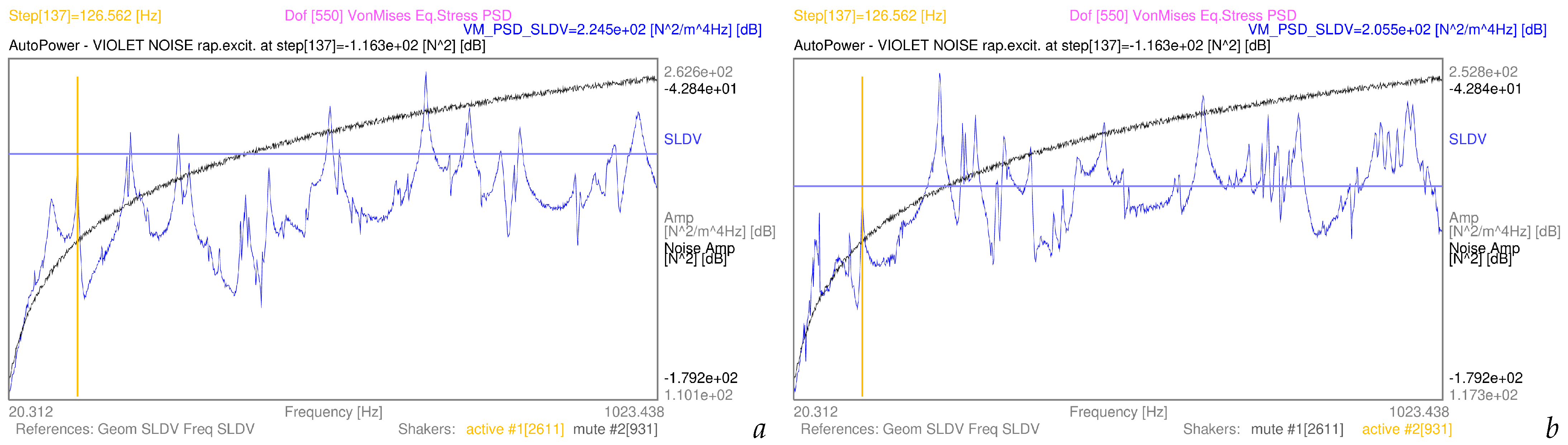
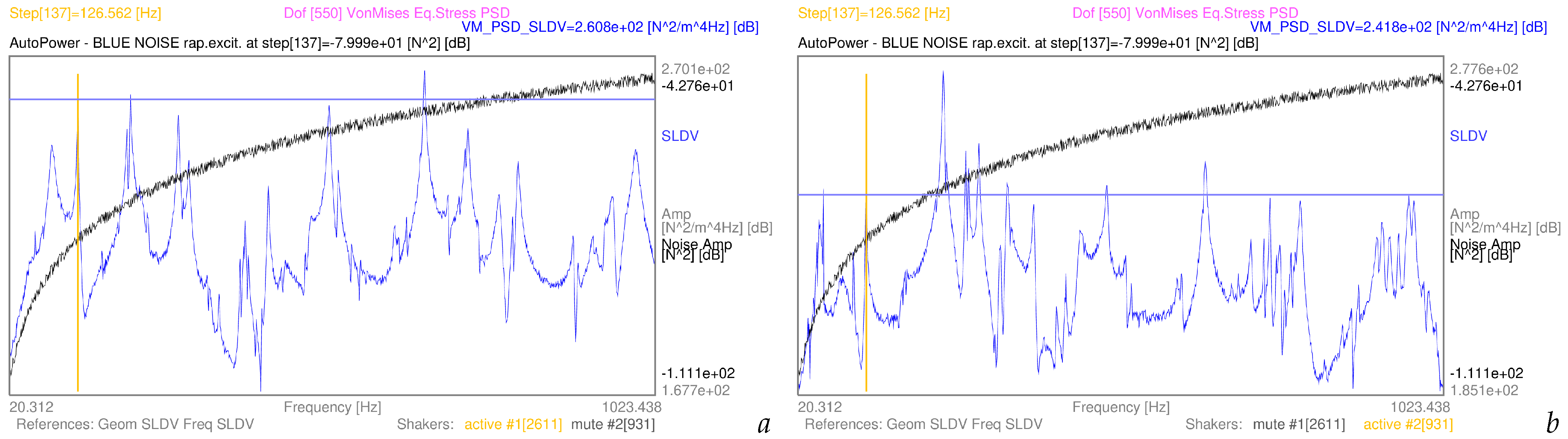
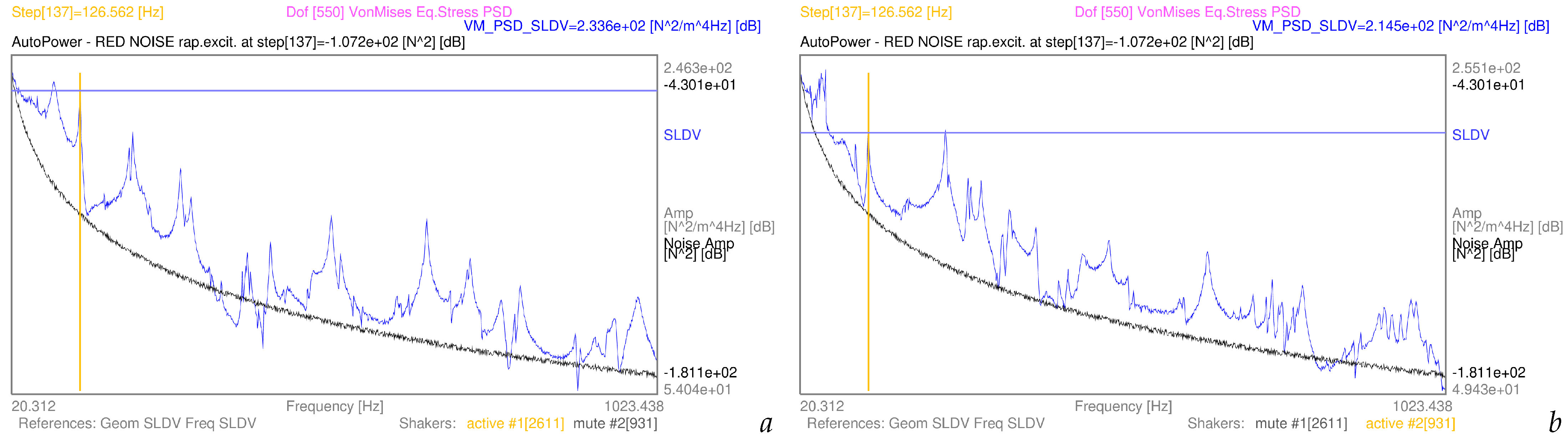
3.2. Examples of Von Mises Equivalent Stress PSDs from Complex-Valued Coloured Noise Excitations
| Noise Colour | Dof | min | Dof | max | Mean | Std.Dev. | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| + Shaker | min | [h] | max | [h] | [h] | [h] | [h2] | [/] | [/] |
| violet rap S1 | 1 | 2.462e+00 | 1107 | 3.240e+04 | 9.713e+02 | 2.719e+03 | 7.394e+06 | 6.936e+00 | 5.943e+01 |
| violet rap S2 | 1 | 2.510e-01 | 934 | 5.300e+03 | 3.790e+02 | 5.502e+02 | 3.027e+05 | 3.372e+00 | 1.568e+01 |
| blue rap S1 | 343 | 1.661e-01 | 1687 | 3.567e+02 | 3.609e+01 | 5.053e+01 | 2.554e+03 | 2.654e+00 | 8.724e+00 |
| blue rap S2 | 1 | 5.277e-02 | 2325 | 1.139e+02 | 1.554e+01 | 1.605e+01 | 2.576e+02 | 2.173e+00 | 5.555e+00 |
| white rap S1 | 1 | 5.549e-04 | 699 | 1.803e-01 | 3.121e-02 | 2.384e-02 | 5.684e-04 | 2.019e+00 | 6.452e+00 |
| white rap S2 | 1 | 2.773e-04 | 1452 | 3.239e-01 | 3.368e-02 | 3.753e-02 | 1.409e-03 | 3.170e+00 | 1.364e+01 |
| pink rap S1 | 1 | 3.942e+00 | 756 | 1.166e+03 | 1.815e+02 | 2.068e+02 | 4.279e+04 | 2.155e+00 | 4.525e+00 |
| pink rap S2 | 1 | 3.405e-01 | 1277 | 2.423e+03 | 1.062e+02 | 1.755e+02 | 3.081e+04 | 4.862e+00 | 3.297e+01 |
| red rap S1 | 2907 | 1.063e+03 | 2835 | 4.354e+05 | 4.951e+04 | 5.640e+04 | 3.180e+09 | 2.175e+00 | 6.715e+00 |
| red rap S2 | 1 | 1.728e+01 | 1277 | 4.926e+05 | 1.215e+04 | 3.486e+04 | 1.215e+09 | 6.864e+00 | 5.735e+01 |
3.3. Examples of Time-to-Failure Distributions with Complex-Valued Coloured Noise Excitations

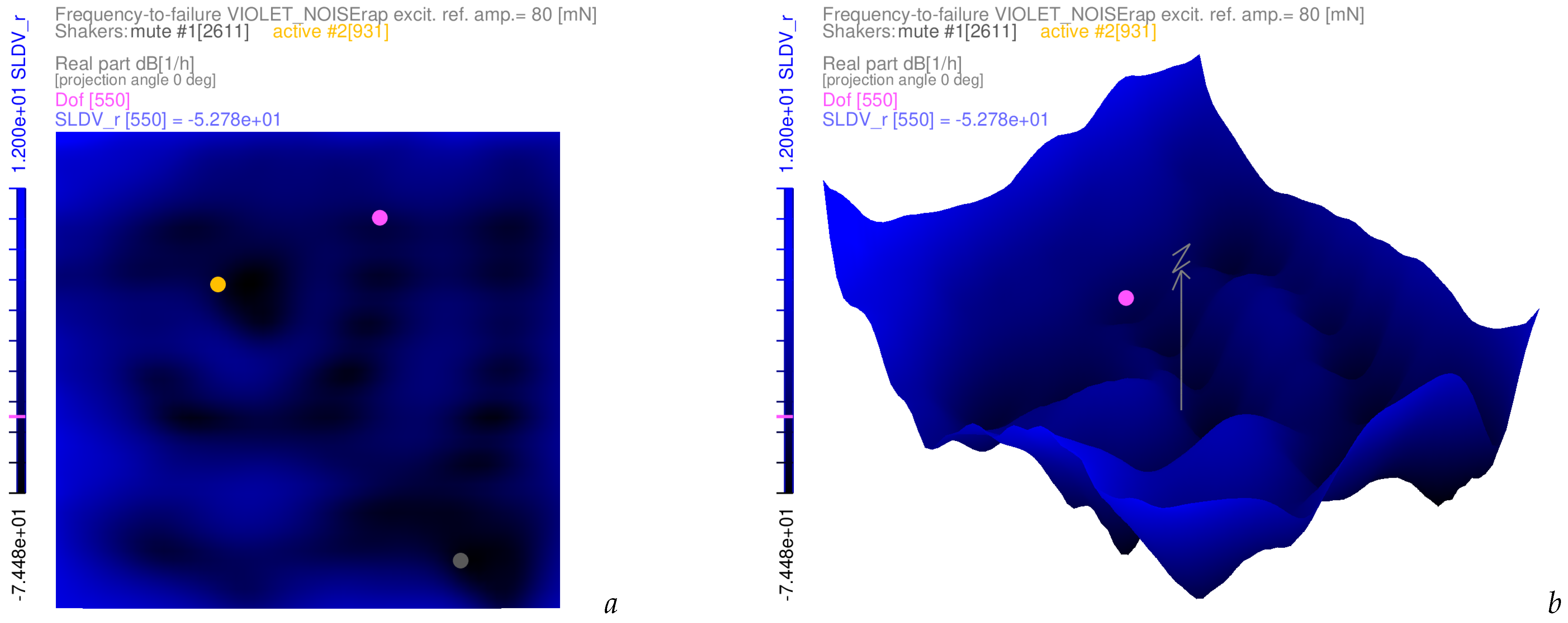
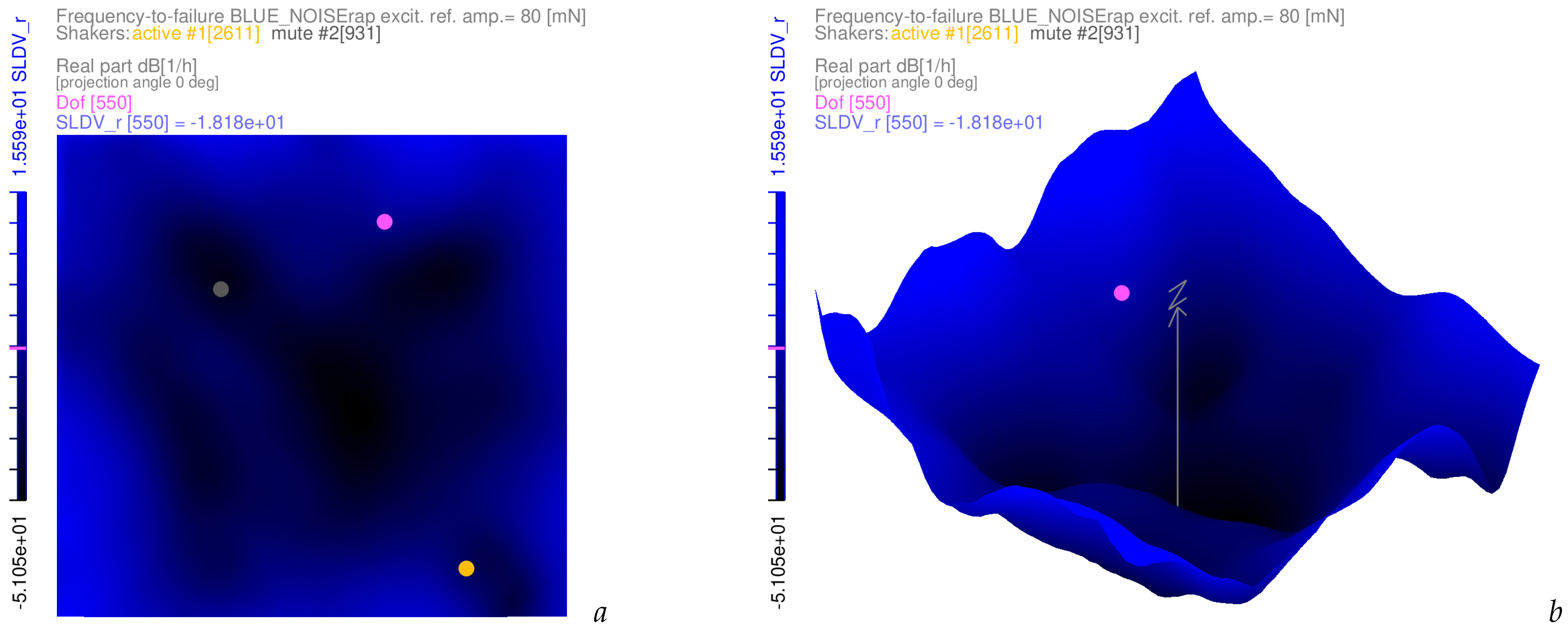
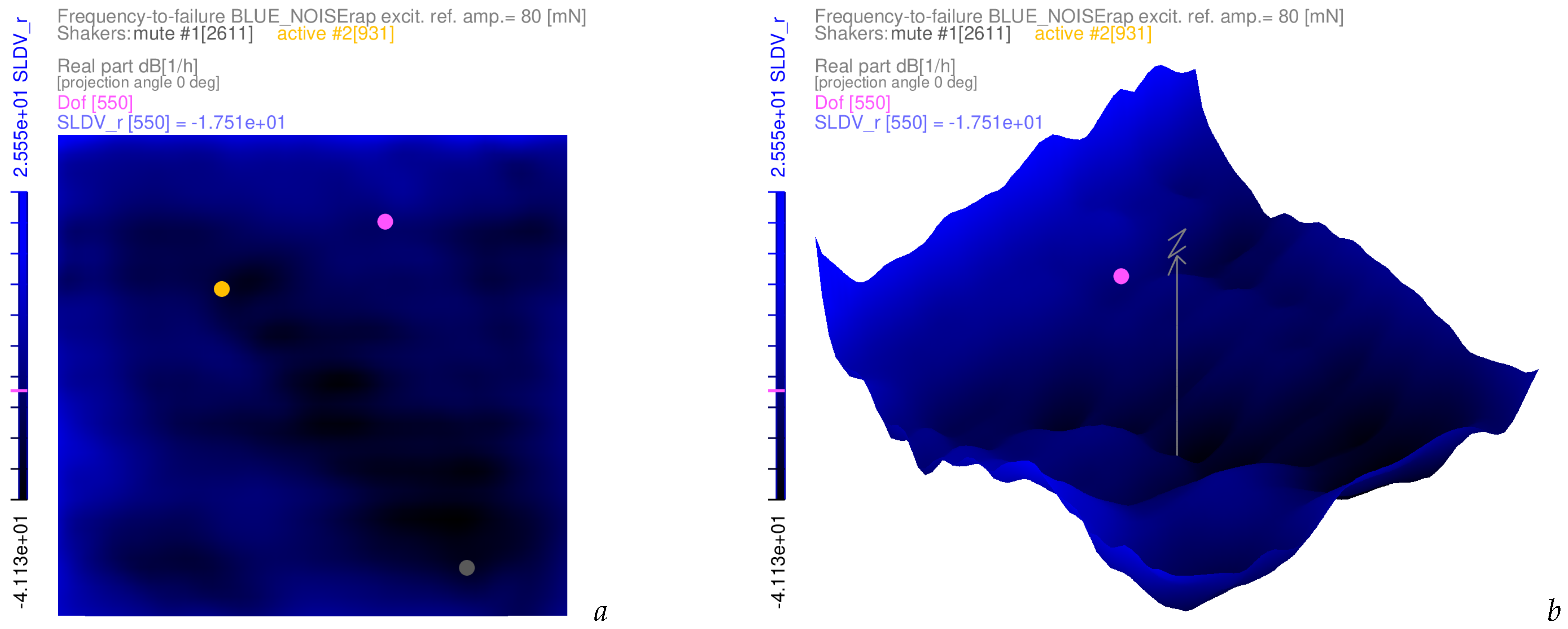
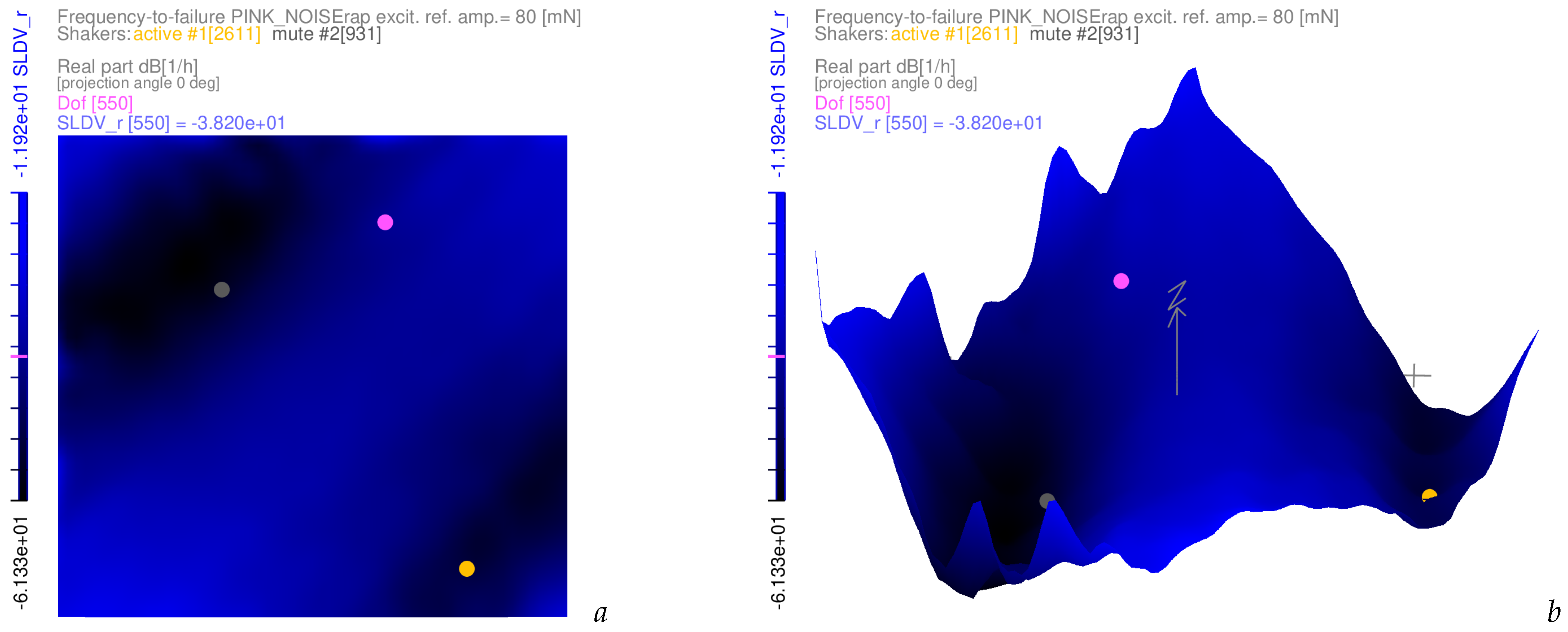
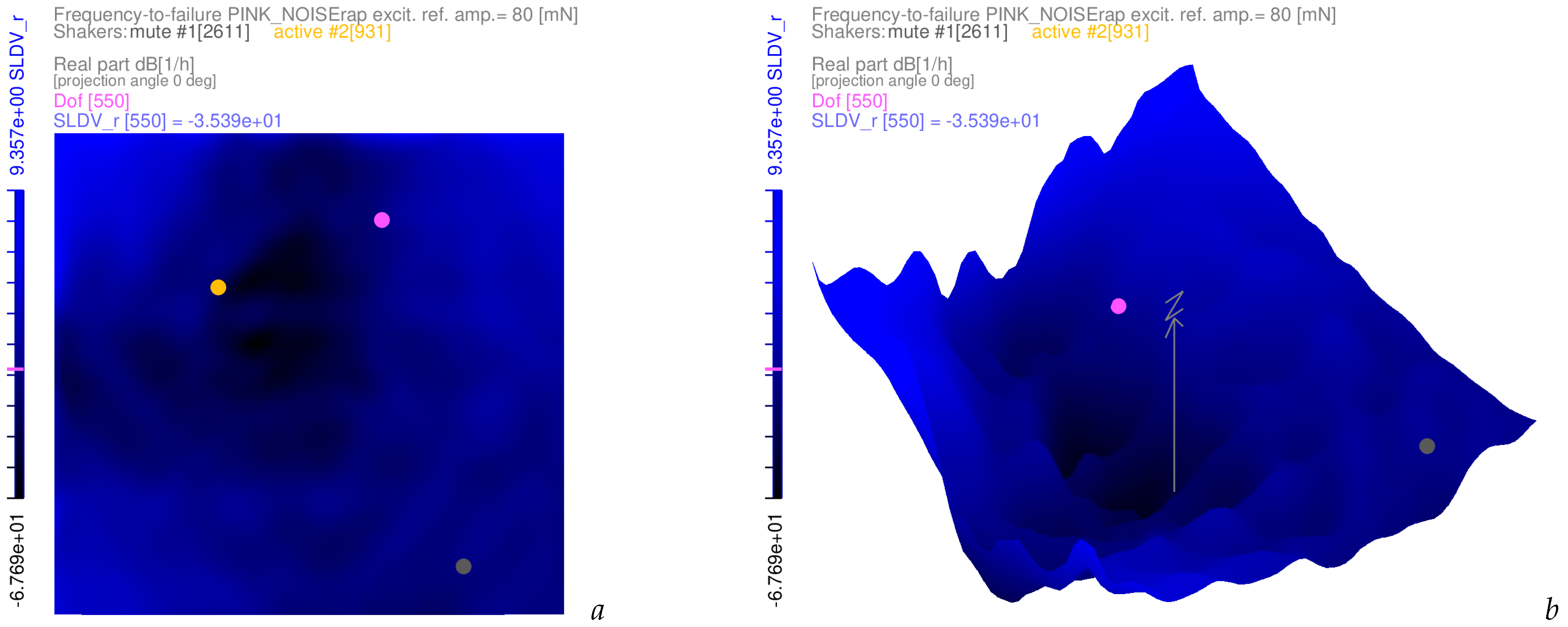
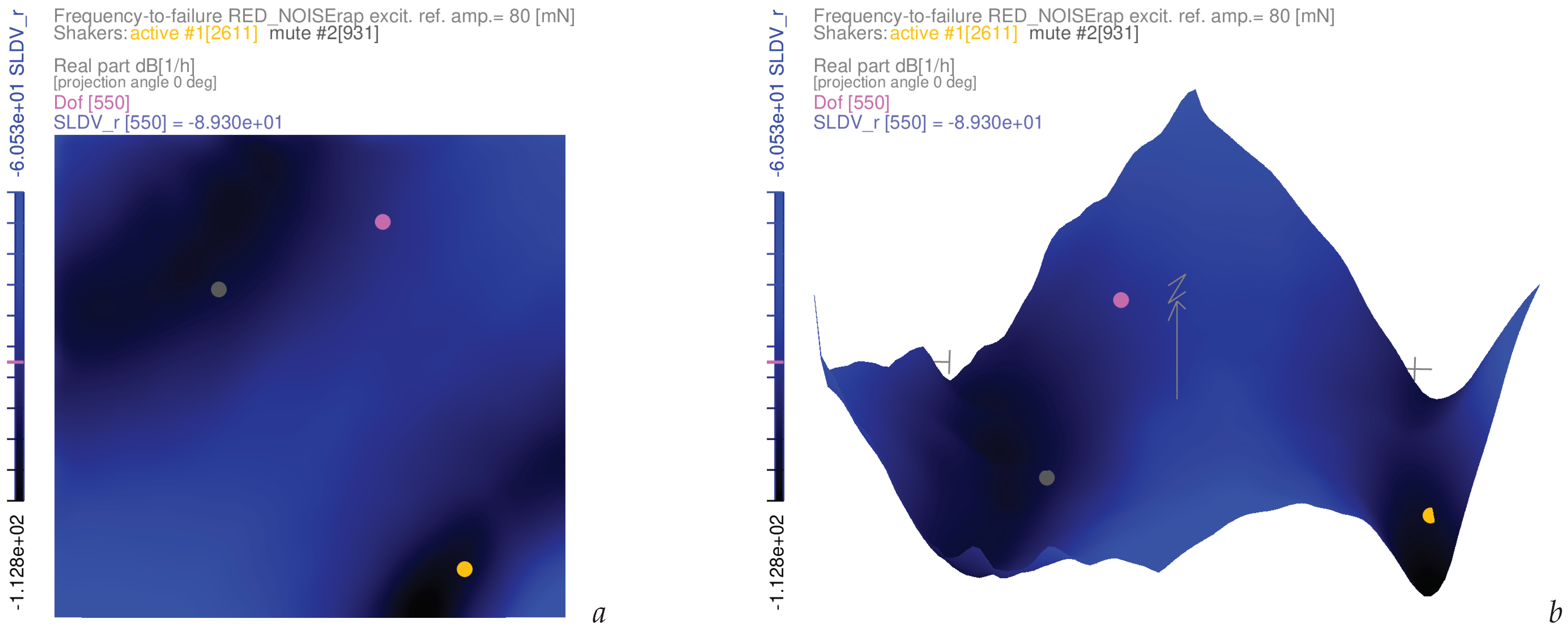
3.4. Examples of Frequency-to-Failure Maps with Complex-Valued Coloured Noise Excitations
4. Discussion
5. Conclusions
- estimation of Strain-FRF maps;
- evaluation of Stress-FRF maps by a proper constitutive model of the material;
- evaluation of von Mises Equivalent Stress-FRF maps;
- evaluation of von Mises Equivalent Stress-PSDs, as dependent on the selected complex-valued spectrum and location of the excitation;
- evaluation of high spatial resolution maps of cumulative damage and life expectations by means of fatigue spectral methods and excitation location and spectra.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Surface Strain FRFs for a Bending Plate
Appendix B. Linear Constitutive Material Model between Strain and Stress FRFs
Appendix C. von Mises Multi-Axis Equivalence
Appendix D. Parameters in the Dirlik Semi-Empirical Spectral Method
Abbreviations
| DIC | Digital image correlation |
| dof(s) | Degree(s) of freedom |
| EFFMA | Experimental full-field modal analysis |
| EMA | Experimental modal analysis |
| ESPI | Electronic speckle pattern interferometry |
| FEM | Finite-element model |
| FRF | Frequency response function |
| NDT | Non-destructive testing |
| NVH | Noise and vibration harshness |
| ODS | Operative deflection shape |
| PSD | Power spectral density |
| SHM | Structural health monitoring |
| SLDV | Scanning laser Doppler vibrometry |
| Circular frequency dependency | |
| Displacement map | |
| Excitation force | |
| Receptance map | |
| Mobility map |
References
- Friswell, M.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Solid Mechanics and Its Applications; Kuwler Academic Publishers & Springer Science+Business Media: Dordrecht, The Netherlands, 1995; p. 292. ISBN 978-0-7923-3431-6. [Google Scholar]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Zanarini, A. Full field optical measurements in experimental modal analysis and model updating. J. Sound Vib. 2019, 442, 817–842. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing – Theory, Practice and Application, 2nd ed.; Research Studies Press Ltd.: Baldock, Hertfordshire, UK, 2000; p. 400. ISBN 978-0-86380-218-8. [Google Scholar]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing, 2nd ed.; Katholieke Universiteit Leuven: Leuven, Belgium, 1998; ISBN 90-73802-61-X. [Google Scholar]
- Zanarini, A. Chasing the high-resolution mapping of rotational and strain FRFs as receptance processing from different full-field optical measuring technologies. Mech. Syst. Signal Process. 2022, 166, 108428. [Google Scholar] [CrossRef]
- Zanarini, A. On the defect tolerance by fatigue spectral methods based on full-field dynamic testing. Procedia Struct. Integr. 2022, 37, 525–532, Proceedings of The 4th International Conference on Structural Integrity, 30 August–1 September 2021. [Google Scholar] [CrossRef]
- Zanarini, A. Introducing the concept of defect tolerance by fatigue spectral methods based on full-field frequency response function testing and dynamic excitation signature. Int. J. Fatigue 2022, 165, 107184. [Google Scholar] [CrossRef]
- Zanarini, A. About the excitation dependency of risk tolerance mapping in dynamically loaded structures. In Proceedings of the ISMA2022 Including USD2022—International Conference on Noise and Vibration Engineering, Leuven, Belgium, 12–14 September 2022; pp. 3804–3818, in Vol. Structural Health Monitoring. Available online: https://past.isma-isaac.be/downloads/isma2022/proceedings/Contribution_208_proceeding_3.pdf (accessed on 22 March 2025).
- Zanarini, A. Risk Tolerance Mapping in Dynamically Loaded Structures as Excitation Dependency by Means of Full-Field Receptances. In Proceedings of the IMAC XLI—International Modal Analysis Conference—Keeping IMAC Weird: Traditional and Non-Traditional Applications of Structural Dynamics, Austin, TX, USA, 13–16 February 2023; Computer Vision & Laser Vibrometry, Volume 6, Conference Proceedings of the Society for Experimental Mechanics Series. Baqersad, J., Di Maio, D., Eds.; Springer Nature: Cham, Switzerland; SEM Society for Experimental Mechanics: Bethel, CT, USA, 2023; Chapter 9; pp. 43–56. [Google Scholar] [CrossRef]
- Zanarini, A. Exploiting DIC-based full-field receptances in mapping the defect acceptance for dynamically loaded components. Procedia Struct. Integr. 2024, 54C, 99–106, Proceedings of The 5th International Conference on Structural Integrity, 28 August–1 September, 2023. [Google Scholar] [CrossRef]
- Zanarini, A. Mapping the defect acceptance for dynamically loaded components by exploiting DIC-based full-field receptances. Eng. Fail. Anal. 2024, 163, 108385. [Google Scholar] [CrossRef]
- Van der Auweraer, H.; Dierckx, B.; Haberstok, C.; Freymann, R.; Vanlanduit, S. Structural modelling of car panels using holographic modal analysis. In Proceedings of the 1999 Noise and Vibration Conference, Traverse City, MI, USA, 17–20 May 1999; Volume 3, pp. 1495–1506, SAE P-342. [Google Scholar] [CrossRef]
- Van der Auweraer, H.; Steinbichler, H.; Haberstok, C.; Freymann, R.; Storer, D. Integration of pulsed-laser ESPI with spatial domain modal analysis: Results from the SALOME project. In Proceedings of the 4th International Conference on Vibration Measurements by Laser Techniques: Advances and Applications, Ancona, Italy, 20–23 June 2000; SPIE: Bellingham, WA, USA, 2000; Volume 4072, pp. 313–322. [Google Scholar] [CrossRef]
- Van der Auweraer, H.; Steinbichler, H.; Haberstok, C.; Freymann, R.; Storer, D.; Linet, V. Industrial Applications of Pulsed-laser ESPI vibration analysis. In Proceedings of the XIX IMAC, Kissimmee, FL, USA, 5–8 February 2001; Society for Experimental Mechanics (SEM): Bethel, CT, USA, 2001; pp. 490–496. [Google Scholar]
- Van der Auweraer, H.; Steinbichler, H.; Vanlanduit, S.; Haberstok, C.; Freymann, R.; Storer, D.; Linet, V. Application of stroboscopic and pulsed-laser electronic speckle pattern interferometry (ESPI) to modal analysis problems. Meas. Sci. Technol. 2002, 13, 451–463. [Google Scholar] [CrossRef]
- Zanarini, A. Broad frequency band full field measurements for advanced applications: Point-wise comparisons between optical technologies. Mech. Syst. Signal Process. 2018, 98, 968–999. [Google Scholar] [CrossRef]
- Zanarini, A. Competing optical instruments for the estimation of Full Field FRFs. Measurement 2019, 140, 100–119. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34, in SI: Full-field, non-contact vibration measurement methods: comparisons and applications. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.E.; Ihle, A.; Siebert, T.; Schubach, H.R. Finite element model updating from full-field vibration measurement using digital image correlation. J. Sound Vib. 2011, 330, 1599–1620. [Google Scholar] [CrossRef]
- Wang, W.; Mottershead, J.; Siebert, T.; Pipino, A. Frequency response functions of shape features from full-field vibration measurements using digital image correlation. Mech. Syst. Signal Process. 2011, 28, 333–347. [Google Scholar] [CrossRef]
- LeBlanc, B.; Niezrecki, C.; Avitabile, P.; Sherwood, J.; Chen, J. Surface Stitching of a Wind Turbine Blade Using Digital Image Correlation. In Topics in Modal Analysis II, Proceedings of the 30th IMAC, A Conference on Structural Dynamics, SEM; Allemang, R., De Clerck, J., Niezrecki, C., Blough, J., Eds.; Springer: New York, NY, USA, 2012; Volume 6, pp. 277–284. [Google Scholar] [CrossRef]
- Ehrhardt, D.A.; Allen, M.S.; Yang, S.; Beberniss, T.J. Full-field linear and nonlinear measurements using Continuous-Scan Laser Doppler Vibrometry and high speed three-dimensional Digital Image Correlation. Mech. Syst. Signal Process. 2017, 86, 82–97. [Google Scholar] [CrossRef]
- Zanarini, A. On the making of precise comparisons with optical full field technologies in NVH. In Proceedings of the ISMA2020 Including USD2020—International Conference on Noise and Vibration Engineering, Leuven, Belgium, 7–9 September 2020; pp. 2293–2308, in Vol. Optical methods and computer vision for vibration engineering. Available online: https://past.isma-isaac.be/downloads/isma2020/proceedings/Contribution_695_proceeding_3.pdf (accessed on 22 March 2025).
- Liu, W.; Ewins, D. The Importance Assessment of RDOF in FRF Coupling Analysis. In Proceedings of the IMAC 17th Conference, Kissimmee, FL, USA, 8–11 February 1999; Society for Experimental Mechanics (SEM): Bethel, CT, USA, 1999; pp. 1481–1487. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=c44ebc7b37f462e47b44aee1acb1f9de704e92d6 (accessed on 22 March 2025).
- Research Network. QUATTRO Brite-Euram Project No: BE 97-4184; Technical Report; European Commision Research Framework Programs: Brussels, Belgium, 1998. [Google Scholar]
- Haeussler, M.; Klaassen, S.; Rixen, D. Experimental twelve degree of freedom rubber isolator models for use in substructuring assemblies. J. Sound Vib. 2020, 474, 115253. [Google Scholar] [CrossRef]
- Zanarini, A. On the exploitation of multiple 3D full-field pulsed ESPI measurements in damage location assessment. Procedia Struct. Integr. 2022, 37, 517–524, Proceedings of The 4th International Conference on Structural Integrity, 30 August–1 September 2021. [Google Scholar] [CrossRef]
- Zanarini, A. On the influence of scattered errors over full-field receptances in the Rayleigh integral approximation of sound radiation from a vibrating plate. Acoustics 2023, 5, 948–986. [Google Scholar] [CrossRef]
- Zanarini, A. Assessing the retrieval procedure of complex-valued forces from airborne pressure fields by means of DIC-based full-field receptances in simplified pseudo-inverse vibro-acoustics. Aerosp. Sci. Technol. 2024, 157, 109757. [Google Scholar] [CrossRef]
- Forsyth, P. Fatigue damage and crack growth in aluminium alloys. Acta Metall. 1963, 11, 703–715, in SI: Mechanisms of fatigue in crystalline solids. [Google Scholar] [CrossRef]
- Mao, H.; Mahadevan, S. Fatigue damage modelling of composite materials. Compos. Struct. 2002, 58, 405–410. [Google Scholar] [CrossRef]
- Kyanka, G.H. Fatigue properties of wood and wood composites. Int. J. Fract. 1980, 16, 609–616. [Google Scholar] [CrossRef]
- Smith, I.; Landis, E.; Gong, M. Fracture and Fatigue in Wood; Wiley: Hoboken, NJ, USA, 2003; p. 248. ISBN 978-0-471-48708-1. [Google Scholar]
- Leyens, C.; Peters, M. (Eds.) Titanium and Titanium Alloys: Fundamentals and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003; ISBN 9783527305346. [Google Scholar] [CrossRef]
- Farahani, B.V.; Direito, F.; Sousa, P.J.; Tavares, P.J.; Infante, V.; Moreira, P.P. Crack tip monitoring by multiscale optical experimental techniques. Int. J. Fatigue 2022, 155, 106610. [Google Scholar] [CrossRef]
- Lesiuk, G.; Nykyforchyn, H.; Zvirko, O.; Mech, R.; Babiarczuk, B.; Duda, S.; Maria De Arrabida Farelo, J.; Correia, J.A. Analysis of the Deceleration Methods of Fatigue Crack Growth Rates under Mode I Loading Type in Pearlitic Rail Steel. Metals 2021, 11, 584. [Google Scholar] [CrossRef]
- Krechkovska, H.; Student, O.; Lesiuk, G.; Correia, J. Features of the microstructural and mechanical degradation of long term operated mild steel. Int. J. Struct. Integr. 2018, 9, 296–306. [Google Scholar] [CrossRef]
- Lesiuk, G.; Correia, J.A.; Krechkovska, H.V.; Pekalski, G.; Jesus, A.M.d.; Student, O. Degradation Theory of Long Term Operated Materials and Structures; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–215. [Google Scholar] [CrossRef]
- Ahmad, Z. (Ed.) Principles of Corrosion Engineering and Corrosion Control; Elsevier & Butterworth-Heinemann: Oxford, UK, 2006; pp. 1–656. [Google Scholar] [CrossRef]
- Gao, J.W.; Dai, G.Z.; Li, Q.Z.; Zhang, M.N.; Zhu, S.P.; Correia, J.A.; Lesiuk, G.; De Jesus, A.M. Fatigue assessment of EA4T railway axles under artificial surface damage. Int. J. Fatigue 2021, 146, 106157. [Google Scholar] [CrossRef]
- Gao, J.W.; Yu, M.H.; Liao, D.; Zhu, S.P.; Han, J.; Lesiuk, G.; Correia, J.A.; De Jesus, A.M. Fatigue and damage tolerance assessment of induction hardened S38C axles under different foreign objects. Int. J. Fatigue 2021, 149, 106276. [Google Scholar] [CrossRef]
- Buch, A. Prediction of the comparative fatigue performance for realistic loading distributions. Prog. Aerosp. Sci. 1997, 33, 391–430. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- George, T.J.; Seidt, J.; Shen, M.H.H.; Nicholas, T.; Cross, C.J. Development of a novel vibration-based fatigue testing methodology. Int. J. Fatigue 2004, 26, 474–486. [Google Scholar] [CrossRef]
- Dirlik, T. Application of Computers in Fatigue Analysis. Ph.D. Thesis, University of Warwick, Coventry, UK, 1985. Available online: https://wrap.warwick.ac.uk/id/eprint/2949/ (accessed on 22 March 2025).
- ESDU. Spectral methods for the estimation of fatigue life 06011. In Estimation of Fatigue Life of Structures Subjected to Random Loading; Vibration and Acoustic Fatigue Series; ESDU International Plc: London, UK, 2006; Volume 9, pp. 1–56. [Google Scholar]
- Dowling, E.N. Estimating Fatigue Life. In Fatigue and Fracture; ASM Handbook; ASM International Handbook Committee: Novelty, OH, USA, 1996; Volume 19, pp. 250–262. [Google Scholar]
- Benasciutti, D.; Tovo, R. Spectral methods for lifetime prediction under wide-band stationary random processes. Int. J. Fatigue 2005, 27, 867–877, in SI: Cumulative Fatigue Damage Conference – University of Seville 2003.. [Google Scholar] [CrossRef]
- Dirlik, T.; Benasciutti, D. Dirlik and Tovo-Benasciutti Spectral Methods in Vibration Fatigue: A Review with a Historical Perspective. Metals 2021, 11, 1333. [Google Scholar] [CrossRef]
- Shang, D.G.; Wang, D.K.; Li, M.; Yao, W.X. Local stress-strain field intensity approach to fatigue life prediction under random cyclic loading. Int. J. Fatigue 2001, 23, 903–910. [Google Scholar] [CrossRef]
- Lynn, A.K.; DuQuesnay, D.L. Computer simulation of variable amplitude fatigue crack initiation behaviour using a new strain-based cumulative damage model. Int. J. Fatigue 2003, 24, 977–986. [Google Scholar] [CrossRef]
- Koh, S.K. Fatigue damage evaluation of a high pressure tube steel using cycle strain energy density. Int. J. Press. Vessel. Pip. 2002, 79, 791–798. [Google Scholar] [CrossRef]
- Lagoda, T. Energy models for fatigue life estimation under uniaxial random loading. Part I: The model elaboration. Int. J. Fatigue 2001, 23, 467–480. [Google Scholar] [CrossRef]
- Lagoda, T. Energy models for fatigue life estimation under uniaxial random loading. Part II: Verification of the model. Int. J. Fatigue 2001, 23, 481–489. [Google Scholar] [CrossRef]
- Ling, J.; Pan, J. An engineering method for reliability analyses of mechanical structures for long fatigue lives. Reliab. Eng. Syst. Saf. 1997, 56, 135–142. [Google Scholar] [CrossRef]
- Kuroda, M. Extremely low cycle fatigue life prediction based on a new cumulative fatigue damage model. Int. J. Fatigue 2001, 24, 699–703. [Google Scholar] [CrossRef]
- ESDU. Fatigue damage and life under random loading 06009. In Estimation of Fatigue Life of Structures Subjected to Random Loading; Vibration and Acoustic Fatigue Series; ESDU International Plc: London, UK, 2006; Volume 9, pp. 1–41. [Google Scholar]
- Marines, I.; Bin, X.; Bathias, C. An understanding of very high cycle fatigue of metals. Int. J. Fatigue 2003, 25, 1101–1107. [Google Scholar] [CrossRef]
- Sherratt, F.; Bishop, N.; Dirlik, T. Predicting fatigue life from frequency domain data. J. Eng. Integr. Soc. (EIS) 2005, 18, 12–16. Available online: https://www.researchgate.net/publication/284415325_Predicting_fatigue_life_from_frequency_domain_data (accessed on 22 March 2025).
- Lee, Y.L.; Tjhung, T.; Jordan, A. A life prediction model for welded joints under multiaxial variable amplitude loading histories. Int. J. Fatigue 2007, 29, 1162–1173. [Google Scholar] [CrossRef]
- Wolfsteiner, P.; Sedlmair, S. Deriving Gaussian Fatigue Test Spectra from Measured non Gaussian Service Spectra. Procedia Eng. 2015, 101, 543–551, in SI: 3rd International Conference on Material and Component Performance under Variable Amplitude Loading, VAL 2015, Eds. J. Papuga and M. Ruzicka. [Google Scholar] [CrossRef]
- Sui, G.; Zhang, Y. Response spectrum method for fatigue damage assessment of mechanical systems. Int. J. Fatigue 2023, 166, 107278. [Google Scholar] [CrossRef]
- McDowell, D.L. Multiaxial Fatigue Strength. In Fatigue and Fracture; ASM Handbook; ASM International Handbook Committee: Novelty, OH, USA, 1996; Volume 19, pp. 263–273. [Google Scholar]
- Cameron, D.W. Fatigue Properties in Engineering. In Fatigue and Fracture; ASM Handbook; ASM International Handbook Committee: Novelty, OH, USA, 1996; Volume 19, pp. 15–26. [Google Scholar]
- ASM. Parameters for Estimating Fatigue Life. In Fatigue and Fracture; ASM Handbook; ASM International Handbook Committee: Novelty, OH, USA, 1996; Volume 19, pp. 963–979. [Google Scholar]
- Veers, P.S. Statistical considerations in Fatigue. In Fatigue and Fracture; ASM Handbook; ASM International Handbook Committee: Novelty, OH, USA, 1996; Volume 19, pp. 295–302. [Google Scholar]
- Voormeeren, S.; de Klerk, D.; Rixen, D. Uncertainty quantification in experimental frequency based substructuring. Mech. Syst. Signal Process. 2010, 24, 106–118. [Google Scholar] [CrossRef]
- Wagner, P.; Huesmann, A.P.; van der Seijs, M.V. Application of dynamic substructuring in NVH design of electric drivetrains. In Proceedings of the ISMA2020 including USD2020—International Conference on Noise and Vibration Engineering, Leuven, Belgium, 7–9 September 2020; pp. 3365–3382, in Vol. Vehicle noise and vibration (NVH). Available online: https://past.isma-isaac.be/downloads/isma2020/proceedings/Contribution_369_proceeding_3.pdf (accessed on 22 March 2025).
- Pogacar, M.; Ocepek, D.; Trainotti, F.; Cepon, G.; Boltežar, M. System equivalent model mixing: A modal domain formulation. Mech. Syst. Signal Process. 2022, 177, 109239. [Google Scholar] [CrossRef]
- Van der Auweraer, H.; Mas, P.; Peeters, P.; Janssens, K.; Vecchio, A. Modal and Path Contribution Models from In-Operation Data: Review and New Approaches. Shock Vib. 2008, 15, 403–411. [Google Scholar] [CrossRef]
- Gajdatsy, P.; Janssens, K.; Desmet, W.; Van der Auweraer, H. Application of the transmissibility concept in transfer path analysis. Mech. Syst. Signal Process. 2010, 24, 1963–1976, in Special Issue: ISMA 2010. [Google Scholar] [CrossRef]
- de Klerk, D.; Rixen, D. Component transfer path analysis method with compensation for test bench dynamics. Mech. Syst. Signal Process. 2010, 24, 1693–1710. [Google Scholar] [CrossRef]
- van der Seijs, M.V.; de Klerk, D.; Rixen, D.J. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68–69, 217–244. [Google Scholar] [CrossRef]
- Cumbo, R.; Tamarozzi, T.; Janssens, K.; Desmet, W. Kalman-based load identification and full-field estimation analysis on industrial test case. Mech. Syst. Signal Process. 2019, 117, 771–785. [Google Scholar] [CrossRef]
- Ortega Almirón, J.; Bianciardi, F.; Corbeels, P.; Pieroni, N.; Kindt, P.; Desmet, W. Vehicle road noise prediction using component-based transfer path analysis from tire test-rig measurements on a rolling tire. J. Sound Vib. 2022, 523, 116694. [Google Scholar] [CrossRef]
- Vaes, D.; Swevers, J.; Sas, P. Experimental validation of different MIMO-feedback controller design methods. Control Eng. Pract. 2005, 13, 1439–1451. [Google Scholar] [CrossRef]
- Musella, U.; D’Elia, G.; Manzato, S.; Peeters, B.; Guillaume, P.; Marulo, F. Analyses of Target Definition Processes for MIMO Random Vibration Control Tests. In Special Topics in Structural Dynamics; Dervilis, N., Ed.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2017; Volume 6, pp. 135–148. [Google Scholar] [CrossRef]
- Schumann, C.; Allen, M.; Tuman, M.; DeLima, W.; Dodgen, E. Transmission Simulator Based MIMO Response Reconstruction. Exp. Tech. 2022, 46, 287–297. [Google Scholar] [CrossRef]
- Araújo dos Santos, J.V.; Lopes, H.M.R.; Vaz, M.; Mota Soares, C.M.; Mota Soares, C.A.; de Freitas, M.J.M. Damage localization in laminated composite plates using mode shapes measured by pulsed TV holography. Compos. Struct. 2006, 76, 272–281, in SI: US Air Force Workshop Health Assessment of Composite Structures. [Google Scholar] [CrossRef]
- Lopes, H.; Araújo dos Santos, J.V.; Moreno-García, P. Evaluation of noise in measurements with speckle shearography. Mech. Syst. Signal Process. 2019, 118, 259–276. [Google Scholar] [CrossRef]
- Oliveira, T.; dos Santos, J.A.; Lopes, H. On the use of finite differences for vibration-based damage localization in laminated composite plates. Procedia Struct. Integr. 2022, 37, 698–705, Proceedings of The 4th International Conference on Structural Integrity, 30 August – 1 September, 2001. [Google Scholar] [CrossRef]
- Gu, G.; Pan, Y.; Qiu, C.; Zhu, C. Improved depth characterization of internal defect using the fusion of shearography and speckle interferometry. Opt. Laser Technol. 2021, 135, 106701. [Google Scholar] [CrossRef]
- Rogala, T.; Przystałka, P.; Katunin, A. Damage classification in composite structures based on X-ray computed tomography scans using features evaluation and deep neural networks. Procedia Struct. Integr. 2022, 37, 187–194, Proceedings of The 4th International Conference on Structural Integrity, 30 August – 1 September, 2001.. [Google Scholar] [CrossRef]
- von Mises, R. Mechanik der festen Koerper im plastisch-deformablen Zustand. Nachrichten Von Der Ges. Der Wiss. Zu Goettingen Math.-Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Benasciutti, D. Some analytical expressions to measure the accuracy of the “equivalent von Mises stress” in vibration multiaxial fatigue. J. Sound Vib. 2014, 333, 4326–4340. [Google Scholar] [CrossRef]
- Benasciutti, D. An analytical approach to measure the accuracy of various definitions of the “equivalent von Mises stress” in vibration multiaxial fatigue. In Proceedings of the ICoEV2015 International Conference on Engineering Vibration, Ljubljana, Slovenia, 7–10 September 2015; pp. 743–752, Univ. Ljubljana & IFToMM. [Google Scholar]
- Braccesi, C.; Cianetti, F.; Lori, G.; Pioli, D. An equivalent uniaxial stress process for fatigue life estimation of mechanical components under multiaxial stress conditions. Int. J. Fatigue 2008, 30, 1479–1497. [Google Scholar] [CrossRef]
- Cristofori, A.; Benasciutti, D.; Tovo, R. A stress invariant based spectral method to estimate fatigue life under multiaxial random loading. Int. J. Fatigue 2011, 33, 887–899. [Google Scholar] [CrossRef]
- Mršnik, M.; Slavič, J.; Boltežar, M. Frequency-domain methods for a vibration-fatigue-life estimation—Application to real data. Int. J. Fatigue 2013, 47, 8–17. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Lori, G.; Pioli, D. Evaluation of mechanical component fatigue behavior under random loads: Indirect frequency domain method. Int. J. Fatigue 2014, 61, 141–150. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Lori, G.; Pioli, D. Random multiaxial fatigue: A comparative analysis among selected frequency and time domain fatigue evaluation methods. Int. J. Fatigue 2015, 74, 107–118. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Tomassini, L. Random fatigue. A new frequency domain criterion for the damage evaluation of mechanical components. Int. J. Fatigue 2015, 70, 417–427. [Google Scholar] [CrossRef]
- Benasciutti, D.; Sherratt, F.; Cristofori, A. Recent developments in frequency domain multi-axial fatigue analysis. Int. J. Fatigue 2016, 91, 397–413, in SI: Variable Amplitude Loading. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Tomassini, L. An innovative modal approach for frequency domain stress recovery and fatigue damage evaluation. Int. J. Fatigue 2016, 91, 382–396, in SI: Variable Amplitude Loading. [Google Scholar] [CrossRef]
- Papuga, J.; Margetin, M.; Chmelko, V. Various parameters of the multiaxial variable amplitude loading and their effect on fatigue life and fatigue life computation. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2890–2912. [Google Scholar] [CrossRef]
- Zorman, A.; Slavič, J.; Boltežar, M. Vibration fatigue by spectral methods—A review with open-source support. Mech. Syst. Signal Process. 2023, 190, 110149. [Google Scholar] [CrossRef]
- Aimé, M.; Banvillet, A.; Khalij, L.; Pagnacco, E.; Chatelet, E.; Dufour, R. A framework proposal for new multiaxial fatigue damage and extreme response spectra in random vibrations frequency analysis. Mech. Syst. Signal Process. 2024, 213, 111338. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: England, UK, 1992; Available online: http://numerical.recipes (accessed on 22 March 2025).
- Araújo dos Santos, J.V.; Lopes, H. Savitzky-Golay Smoothing and Differentiation Filters for Damage Identification in Plates. Procedia Struct. Integr. 2024, 54, 575–584, Proceedings of The 5th International Conference on Structural Integrity, 28 August–1 September 2023. [Google Scholar] [CrossRef]
- Tisseur, F.; Meerbergen, K. The Quadratic Eigenvalue Problem. SIAM Rev. 2001, 43, 235–286. Available online: http://www.jstor.org/stable/3649752 (accessed on 22 March 2025). [CrossRef]
- Starek, L.; Inman, D. Symmetric inverse eigenvalue vibration problem and its application. Mech. Syst. Signal Process. 2001, 15, 11–29. [Google Scholar] [CrossRef]
- Hoen, C.; As, V.A. An engineering interpretation of the complex eigensolution of linear dynamic systems. In Proceedings of the International Modal Analysis Conference XXIII, Orlando, FL, USA, 31 January–5 February 2005; pp. 1–9, Society for Experimental Mechanics (SEM): Bethel, CT, USA. Available online: https://www.svibs.com/wp-content/uploads/2023/11/2005_16.pdf (accessed on 22 March 2025).
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. Reformulation in the frequency domain of a critical plane-based multiaxial fatigue criterion. Int. J. Fatigue 2014, 67, 55–61, in SI: Multiaxial Fatigue 2013. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Tomassini, L. Fast evaluation of stress state spectral moments. Int. J. Mech. Sci. 2017, 127, 4–9, in Special Issue from International Conference on Engineering Vibration – ICoEV 2015. [Google Scholar] [CrossRef]
- Papuga, J.; Nesládek, M.; Hasse, A.; Cízová, E.; Suchý, L. Benchmarking Newer Multiaxial Fatigue Strength Criteria on Data Sets of Various Sizes. Metals 2022, 12, 289. [Google Scholar] [CrossRef]
| 1 | |
| 2 | In Proceedings of the ISMA2014 including USD2014 - International Conference on Noise and Vibration Engineering, Leuven, Belgium, September 15-17, KU Leuven, 2014: see in Dynamic testing: methods and instrumentation, “On the estimation of frequency response functions, dynamic rotational degrees of freedom and strain maps from different full field optical techniques”; see in Operational modal analysis, “On the role of spatial resolution in advanced vibration measurements for operational modal analysis and model updating”. |
| 3 | In Proceedings of the ICoEV2015 International Conference on Engineering Vibration, Ljubljana, Slovenia, September 7-10, Univ. Ljubljana & IFToMM, 2015, symposium Full Field Measurements for Advanced Structural Dynamics: “Model updating from full field optical experimental datasets”; “Comparative studies on full field FRFs estimation from competing optical instruments”; “Accurate FRFs estimation of derivative quantities from different full field measuring technologies”; “Full field experimental modelling in spectral approaches to fatigue predictions”. |
| 4 | |
| 5 | See specifically [29,30], “On the approximation of sound radiation by means of experiment-based optical full-field receptances”, “Experiment-based Optical Full-field receptances in the Approximation of Sound Radiation from a Vibrating Plate”, and “On the use of full-field receptances in inverse vibro-acoustics for airborne structural dynamics”. |
| 6 | Dependent on the defect types, e.g., as in [31,32,33,34,35,37]; on the micro-structure and sizes, e.g., as in [38]; on the ageing, e.g., as in [39]; on the external damaging factors, such as corrosion, e.g., as in [40], hitting debris or impacting objects, e.g., as in [41,42]. However, this broad discussion—about the micro-scale factors—cannot be part of this paper. |
| 7 | |
| 8 | |
| 9 | The Speckle Interferometry for Industrial Needs Post-doctoral Marie Curie Industry Host Fellowship project HPMI-CT-1999-00029 was held at Dantec Ettemeyer GmbH, Ulm, Germany. In particular, for the main achievements, see: “Full field ESPI measurements on a plate: challenging experimental modal analysis”, “Fatigue life assessment by means of full field ESPI vibration measurements”, “Full field ESPI vibration measurements to predict fatigue behaviour” and “Damage location assessment in a composite panel by means of electronic speckle pattern interferometry measurements”. |
| 10 | See [58] for the relevant properties, such as the elastic modulus E = 71.7 GPa and the Poisson ratio = 0.33. |
| 11 | For further details see also Appendix C. |
| 12 | , , are the First-, the Second-, and the Third-Principal Strain FRF eigenvalue maps, in descending magnitude order. In this testing, was orders of magnitude below and , instead comparable. |
| 13 | Here the linear isotropic version in Appendix B is used. |
| 14 | , , are the First-, the Second-, and the Third-Principal Stress FRF eigenvalue maps. In this plane application, was very small compared to the others. |
| 15 | |
| 16 | , , are the First-, the Second-, and the Third-Principal Stress eigenvalue maps, in descending magnitude order. In this plane application, was very small compared to the others. |
| 17 | Suggestions can be found in [50]. |
| 18 | Here detailed in Equation (D.2) of Appendix D for the Dirlik’s semi-empirical, but widely spread, approach [46]. |
| 19 | |
| 20 | |
| 21 | The notation can be suppressed for compactness in the spatial extension of the specific spectral method parameters here discussed, which must be intended as maps. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanarini, A. Task-Oriented Structural Health Monitoring of Dynamically Loaded Components by Means of SLDV-Based Full-Field Mobilities and Fatigue Spectral Methods. Appl. Sci. 2025, 15, 4997. https://doi.org/10.3390/app15094997
Zanarini A. Task-Oriented Structural Health Monitoring of Dynamically Loaded Components by Means of SLDV-Based Full-Field Mobilities and Fatigue Spectral Methods. Applied Sciences. 2025; 15(9):4997. https://doi.org/10.3390/app15094997
Chicago/Turabian StyleZanarini, Alessandro. 2025. "Task-Oriented Structural Health Monitoring of Dynamically Loaded Components by Means of SLDV-Based Full-Field Mobilities and Fatigue Spectral Methods" Applied Sciences 15, no. 9: 4997. https://doi.org/10.3390/app15094997
APA StyleZanarini, A. (2025). Task-Oriented Structural Health Monitoring of Dynamically Loaded Components by Means of SLDV-Based Full-Field Mobilities and Fatigue Spectral Methods. Applied Sciences, 15(9), 4997. https://doi.org/10.3390/app15094997








