Algorithmic Modified Denavit–Hartenberg Modeling for Robotic Manipulators Using Line Geometry

Abstract

This paper proposes a kinematic modeling method for robotic manipulators by extracting the modified Denavit–Hartenberg (MDH) parameters using line geometry. For single-branched manipulators, various joint axes can be represented as lines using Plücker coordinates. The forward kinematics is derived by performing the product of matrices which are the exponential maps lifted from two kinds of exponential coordinates using the MDH parameters. For extracting MDH parameters, line geometry systematically analyzes the following: (1) the closest point between a point and line, (2) the closest distance and twist angle between two lines, (3) the common perpendicular line and its intersection points, and (4) classifies line relationships into collinear, distant parallel, intersected, and skewed cases. For each case, five parameters including twist angle, closest distance, common perpendicular direction vector, and both feet on a common perpendicular line are sequentially computed as results of the line geometry block. Finally, the aforementioned line geometry blocks are utilized to extract the four MDH parameters according to their definitions. The effectiveness of the proposed algorithm is verified by four examples including a typical Selective Compliance Assembly Robot Arm (SCARA) robot and three different commercial manipulators.

1. Introduction

Kinematic modeling of articulated robots is commonly categorized into two approaches according to the number of parameters required to describe the relative motion between adjacent joint axes: screw-based and line-based formulations. The screw-based formulation employs six parameters, whereas the line-based counterpart needs four. Owing to its theoretical completeness, the screw framework has been widely adopted in robotics research [1,2,3,4]. In a screw-based model, the transformation of one link with respect to its predecessor is represented by an exponential map constructed from six exponential coordinates—three rotational and three linear components. Multiplying these exponential maps sequentially produces the forward kinematics of a single-branched manipulator and extends naturally to branched or closed-loop mechanisms.

When each joint axis is regarded as an infinite line, only four independent quantities—Plücker coordinates—are sufficient to describe its pose, because a line is invariant under self-rotation and self-translation. Consequently, line-based formulations require four parameters per axis. Although screw coordinates offer superior numerical robustness for calibration, the modified Denavit–Hartenberg (MDH) notation remains the interface in industrial robot controllers. Direct identification in the MDH, however, often suffers from convergence issues caused by the coupling inherent in its parameter structure [5]. To alleviate this limitation, the present study proposes a post-processing algorithm that converts screw-identified parameters into the MDH format. A concise comparison among the standard Product-of-Exponential (PoE) form, MDH notation, and the classical DH convention—including differences in parameter count, transformation dependencies, frame consistency, and automation suitability—is provided in Table A1 in Appendix A.

Among traditional kinematic conventions, the Denavit–Hartenberg (DH) notation remains the most widely adopted. Originally introduced by Denavit and Hartenberg, it expresses the relative transformation between successive frames with four scalar parameters [6,7]. Two variants have since emerged: the distal form [8] and the proximal form—also called the Modified DH (MDH) notation—[1,9,10]. This work adopts the proximal form because every parameter is referenced to the same coordinate frame, which simplifies implementation and numerical treatment [11,12,13,14]. Deriving MDH parameters, however, requires locating the common perpendicular between consecutive joint axes; line geometry therefore becomes an essential computational tool in our framework.

The studies most closely related to this work are those of Faria et al. [15] and Liu et al. [16]. Faria et al. extract line parameters by commanding axis-specific rotations and subsequently convert them to DH parameters, but their procedure requires user-defined joint-excitation trajectories for each axis during data acquisition and manual assignment of each frame’s x-axis. Liu et al. automate the extraction of conventional DH parameters, yet their method handles only revolute joints and is incompatible with the MDH formulation. The algorithm proposed in the present study overcomes all of these limitations: it requires no constrained excitation, supports both revolute and prismatic joints, and outputs parameters directly in the MDH notation.

Recent studies [17,18,19,20] have focused on kinematic parameter identification based on screw theory, typically performed with a robot equipped with sensors attached to a TCF for calibration. Although direct identification is not performed in this study, the proposed method can be subsequently applied to convert the identified screw-based parameters into an MDH representation. This allows for seamless integration with MDH-based kinematic modeling frameworks commonly used in industrial and simulation environments.

The paper is organized as follows: Section 2 introduces the exponential map using MDH parameters, the exponential coordinates using MDH, the joint twist, and the joint matrix. Section 3 analyzes the relationships between line and point and between two lines, finds the common perpendicular line and its feet, and finally lists up the important contents into the line geometry block. Section 4 proposes how to extract the MDH parameters using two consecutive line geometry blocks. Several examples are employed to verify the proposed method in Section 5, and finally we draw conclusions.

2. Exponential Map Using MDH

Since a joint connects the adjacent links, a single branched articulated robotic manipulator having N joints has $N+1$ links and an adjacent transformation is defined between a pair of adjacent links or joints. This adjacent transformation, a homogeneous transformation matrix, is described in terms of four MDH parameters. The last frame of the robot is called the tool coordinate frame (TCF) where robotic tasks are assigned. The forward kinematics of the robotic manipulator is expressed as:

$$\begin{array}{c}\hfill {}^{0}T_{tcf}={}^{0}T_1({\theta }_1,d_1){}^{1}T_2({\theta }_2,d_2)\cdots {}^{N-1}T_N({\theta }_N,d_N){}^{N}T_{tcf},\end{array}$$

where ${\theta }_i$ and $d_i$ denote ith generalized joint variables which can be one or two degrees-of-freedom (dof) according to the joint type, the prefixed superscript and postfixed subscript of the homogeneous transformation stand for the reference frame and target frame, respectively, e.g., ${}^{N}T_{tcf}$ represents the constant adjacent transformation from frame $\left\{N\right\}$ to $\left\{tcf\right\}$.

2.1. MDH Parameters

The MDH notation describes the relationship between adjacent joint axes at zero-configuration which represents when every joint variable is zero. To define the four MDH parameters, the coordinate frames are determined according to the following procedures:

1.

Set the $\widehat{z}$-axis in the direction of the joint axis.

2.

Define the $\widehat{x}$-axis as the common perpendicular direction to the adjacent joint axes. In cases where adjacent axes are collinear, the previous $\widehat{x}$-axis is retained as the current $\widehat{x}$-axis.

3.

Determine the $\widehat{y}$-axis using the right-hand rule.

Figure 1 illustrates how to set up two coordinate frames $\{i-1\}$ and $\left\{i\right\}$ from three consecutive joint axes $i-1,i$ and $i+1$. After setting up both coordinate frames, four MDH parameters are defined as follows:

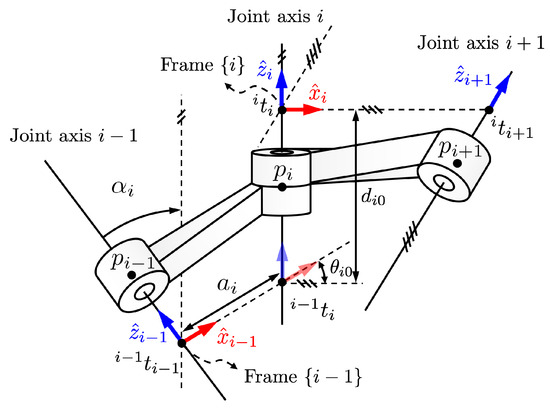
Figure 1. Modified Denavit–Hartenberg (MDH) parameters, where $p_{i-1}$ denotes the point on the $(i-1)$th joint axis, the ${\widehat{z}}_{i-1}$-axis is set along the $(i-1)$th joint axis, the ${\widehat{x}}_{i-1}$-axis is determined to be a common perpendicular direction from the ${\widehat{z}}_{i-1}$-axis to the ${\widehat{z}}_i$-axis, and the origin of the frame $\{i-1\}$ denoted by ${}^{i-1}t_{i-1}$ is an intersection point of the ${\widehat{x}}_{i-1}$-axis and the ${\widehat{z}}_{i-1}$-axis. Also, four MDH parameters are denoted as ${\alpha }_i$, $a_i$, ${\theta }_{i0}$, and $d_{i0}$.

1.

Link twist (${\alpha }_i$): this parameter represents the angle from ${\widehat{z}}_{i-1}$ to ${\widehat{z}}_i$ about the ${\widehat{x}}_{i-1}$-axis

2.

Link length ($a_i$): this denotes a distance from ${\widehat{z}}_{i-1}$ to ${\widehat{z}}_i$ along the ${\widehat{x}}_{i-1}$-axis

3.

Joint offset distance ($d_{i0}$): this is the distance from ${\widehat{x}}_{i-1}$ to ${\widehat{x}}_i$ along the ${\widehat{z}}_i$-axis

4.

Joint offset angle (${\theta }_{i0}$): this expresses the angle from ${\widehat{x}}_{i-1}$ to ${\widehat{x}}_i$ about the ${\widehat{z}}_i$-axis.

It is noted that three consecutive joint axes are required to define four MDH parameters, which are used to obtain the adjacent transformation between the frame $\{i-1\}$ and the frame $\left\{i\right\}$. Figure 1 shows a typical example of MDH parameters. Note that the terms “joint offset distance” and “joint offset angle” correspond to the standard MDH parameters $d_i$ and ${\theta }_i$, respectively. The subscript “0” is introduced to distinguish between constant geometric parameters and variable joint inputs (e.g., $q_{i,\theta }$, $q_{i,d}$) and to clarify their role in generating the transformation matrix. Using the four constant MDH parameters, the adjacent transformation can be represented by adding joint variables $q_{i,\theta }$ for the revolute joint type and $q_{i,d}$ for the prismatic joint type. For this purpose, ith generalized joint variables ${\theta }_i$ and $d_i$ are defined differently according to the joint types as follows: where h implies a pitch to denote a moving distance along the joint axis per one revolution for the helical joint. It is noted that three consecutive joint axes are required to define four MDH parameters, which are used to obtain the adjacent transformation between the frame $i-1$ and the frame i, as summarized in Table 1.

Table 1. The generalized joint variables with MDH parameters.

Joint Type	Generalized Joint Variables (${\mathit{\theta }}_{\mathit{i}},{\mathit{d}}_{\mathit{i}}$)
Revolute (R)	${\theta }_i\leftarrow {\theta }_{i0}+q_{i,\theta }$
one-dof	$d_i\leftarrow d_{i0}$
Prismatic (P)	${\theta }_i\leftarrow {\theta }_{i0}$
one-dof	$d_i\leftarrow d_{i0}+q_{i,d}$
Helical (H)	${\theta }_i\leftarrow {\theta }_{i0}+q_{i,\theta }$
one-dof	$d_i\leftarrow d_{i0}+h{q}_{i,\theta }$
Cylindrical (RP)	${\theta }_i\leftarrow {\theta }_{i0}+q_{i,\theta }$
two-dof	$d_i\leftarrow d_{i0}+q_{i,d}$

2.2. Exponential Map Using MDH

In this work, Lie group methods are employed to establish a connection between the Modified Denavit–Hartenberg (MDH) parameters and Lie algebra in the context of robot forward kinematics. For readers unfamiliar with the fundamentals of Lie groups and Lie algebras in robotic modeling, we recommend [3,4] as accessible introductions. For a more advanced treatment of Lie group integration and numerical methods, refer to [21]. In addition, screw theory, which underpins many geometric interpretations used here, is thoroughly discussed in [2]. The adjacent transformation from the coordinate frame $\{i-1\}$ to the frame $\left\{i\right\}$ in Figure 1 can be decomposed into two exponential maps because the link twist ${\alpha }_i$ and the link length $a_i$ are represented with respect to the ${\widehat{x}}_{i-1}$-axis and the generalized joint variables $d_i$ and ${\theta }_i$ with respect to the ${\widehat{z}}_i$ axis as follows:

$$\begin{array}{cc}\hfill {}^{i-1}T_i({\theta }_i,d_i)& =\mathrm{expm}\left(\lceil {\lambda }_{x_{i-1}}\rceil \right)\mathrm{expm}\left(\lceil {\lambda }_{z_i}\rceil \right),\hfill \end{array}$$

(1)

where the matrix exponential, belonging to the Lie group $SE\left(3\right)$, is defined by using the matrix $\lceil \lambda \rceil$, belonging to Lie algebra $\mathfrak{se}\left(3\right)$, as follows:

$$\begin{array}{cc}\hfill \mathrm{expm}(\lceil \lambda \rceil )& =\sum _{k=0}^{\infty }{\displaystyle \frac{{\lceil \lambda \rceil }^k}{k!}}\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill \lceil {\lambda }_{x_{i-1}}\rceil & =\left[\begin{array}{cccc}0& 0& 0& a_i\\ 0& 0& -{\alpha }_i& 0\\ 0& {\alpha }_i& 0& 0\\ 0& 0& 0& 0\end{array}\right]\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill \lceil {\lambda }_{z_i}\rceil & =\left[\begin{array}{cccc}0& -{\theta }_i& 0& 0\\ {\theta }_i& 0& 0& 0\\ 0& 0& 0& d_i\\ 0& 0& 0& 0\end{array}\right].\hfill \end{array}$$

(2c)

In other words, $\lceil \lambda \rceil$ implies Lie algebra $\mathfrak{se}\left(3\right)$ and $\mathrm{expm}(\lceil \lambda \rceil )$ is a Lie group $SE\left(3\right)$ lifted from the Lie algebra $\lceil \lambda \rceil$, where $\lambda \in {\mathbb{R}}^6$ means the exponential coordinate vector. The series expansion of $\mathrm{expm}(\lceil \lambda \rceil )$ using Equation (2a) results in:

$$\begin{array}{cc}\hfill \mathrm{expm}\left(\lceil {\lambda }_{x_{i-1}}\rceil \right)& =\left[\begin{array}{cccc}1& 0& 0& a_i\\ 0& cos{\alpha }_i& -sin{\alpha }_i& 0\\ 0& sin{\alpha }_i& cos{\alpha }_i& 0\\ 0& 0& 0& 1\end{array}\right]\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill \mathrm{expm}\left(\lceil {\lambda }_{z_i}\rceil \right)& =\left[\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_i& 0& 0\\ sin{\theta }_i& cos{\theta }_i& 0& 0\\ 0& 0& 1& d_i\\ 0& 0& 0& 1\end{array}\right].\hfill \end{array}$$

(3b)

Since Lie algebra $\mathfrak{se}\left(3\right)$ is isomorphic to a six-dimensional real vector ${\mathbb{R}}^6$, we can use it interchangeably

$$\begin{array}{c}\hfill \lambda =\left[\begin{array}{c}\eta \\ \xi \end{array}\right]\in {\mathbb{R}}^6\leftrightarrow \lceil \lambda \rceil =\left[\begin{array}{cccc}0& -{\xi }_z& {\xi }_y& {\eta }_x\\ {\xi }_z& 0& -{\xi }_x& {\eta }_y\\ -{\xi }_y& {\xi }_x& 0& {\eta }_z\\ 0& 0& 0& 0\end{array}\right]\in \mathfrak{se}\left(3\right),\end{array}$$

where $\eta ={[{\eta }_x,{\eta }_y,{\eta }_z]}^T\in {\mathbb{R}}^3$ and $\xi ={[{\xi }_x,{\xi }_y,{\xi }_z]}^T\in {\mathbb{R}}^3$ imply the linear and angular components of the exponential coordinate vector $\lambda \in {\mathbb{R}}^6$, respectively. Thus, we can find the exponential coordinates of MDH from Equations (2b) and (2c), respectively, as follows:

$$\begin{array}{cccccc}\hfill {\lambda }_{x_{i-1}}& =\left[\begin{array}{c}{a}_i\\ 0\\ 0\\ {\alpha }_i\\ 0\\ 0\end{array}\right]\hfill & \hfill \mathrm{and}& \hfill & \hfill {\lambda }_{z_i}& =\left[\begin{array}{c}0\\ 0\\ d_i\\ 0\\ 0\\ {\theta }_i\end{array}\right].\hfill \end{array}$$

(4)

2.3. Joint Twist Using MDH

Since the exponential map (or adjacent transformation) of Equation (1) using MDH is obtained by the matrix product of Equations (3a) and (3b), the joint twist is derived from the left multiplication rule [21,22] as follows:

$$\begin{array}{cc}\hfill \lceil {}^{i-1}V_i\rceil & ={}^{i-1}T_i^{-1}({\theta }_i,d_i){}^{i-1}\dot{T}_i({\theta }_i,d_i)\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill & =\lceil {\dot{\lambda }}_{z_i}\rceil \hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill \therefore {}^{i-1}V_i& ={\dot{\lambda }}_{z_i},\hfill \end{array}$$

(5c)

where ${}^{i-1}V_i={\dot{\lambda }}_{z_i}\in {\mathbb{R}}^6$ implies the ith joint twist relative to the frame $\{i-1\}$ represented in the frame $\left\{i\right\}$. It is noted that ith joint twist ${}^{i-1}V_i$ is represented in the frame $\left\{i\right\}$. Now, we can define ith joint matrix $E_i$ by separating the time-derivative of joint variable ${\dot{q}}_i$ from the joint twist as follows:

$$\begin{array}{c}\hfill {}^{i-1}V_i={\dot{\lambda }}_{z_i}:=E_i{\dot{q}}_i,\end{array}$$

(6)

where ${\dot{\lambda }}_{z_i}={[0,0,{\dot{d}}_i,0,0,{\dot{\theta }}_i]}^T={[0,0,{\dot{q}}_{i,d},0,0,{\dot{q}}_{i,\theta }]}^T$ because the joint offset distance $d_{i0}$ and the joint offset angle ${\theta }_{i0}$ as MDH parameters are constants. For given four joint types $\{R,P,H,RP\}$, each joint has its own joint matrix $E_i$ and time-derivative of joint variable ${\dot{q}}_i=\{{\dot{q}}_{i,\theta },{\dot{q}}_{i,d}\}$ as follows:

$$\begin{array}{cccccc}\hfill R& :E_i{\dot{q}}_i=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right]{\dot{q}}_{i,\theta }\hfill & \hfill & & \hfill P& :E_i{\dot{q}}_i=\left[\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right]{\dot{q}}_{i,d}\hfill \\ \hfill H& :E_i{\dot{q}}_i=\left[\begin{array}{c}0\\ 0\\ h\\ 0\\ 0\\ 1\end{array}\right]{\dot{q}}_{i,\theta }\hfill & \hfill & & \hfill RP& :E_i{\dot{q}}_i=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 1\\ 0& 0\\ 0& 0\\ 1& 0\end{array}\right]\left[\begin{array}{c}{\dot{q}}_{i,\theta }\\ {\dot{q}}_{i,d}\end{array}\right].\hfill \end{array}$$

(7)

The joint matrix $E_i$ represented in the frame $\left\{i\right\}$ can be transformed into either the base frame $\left\{0\right\}$ or the tool coordinate frame $\left\{tcf\right\}$; for this purpose, the adjoint transformation is introduced as follows:

$$\begin{array}{c}\hfill \begin{array}{cccccc}\hfill {}^{0}E_i& ={}^0\mathrm{Ad}_i{E}_i\hfill & \hfill and& \hfill & \hfill {}^{tcf}E_i& ={}^{tcf}\mathrm{Ad}_i{E}_i,\hfill \end{array}\end{array}$$

(8)

where ${}^{0}E_i$ and ${}^{tcf}E_i$ are called spatial screw and body screw in [4], respectively, and the adjoint transformation is defined by

$$\begin{array}{c}\hfill {}^a\mathrm{Ad}_b=\left[\begin{array}{cc}{}^{a}R_b& \lceil {}^{a}r_b\rceil {}^{a}R_b\\ 0_3& {}^{a}R_b\end{array}\right]\in {\mathbb{R}}^{6\times 6},\end{array}$$

(9)

using the homogeneous transformation ${}^{a}T_b({}^{a}R_b,{}^{a}r_b)$, in which ${}^{a}R_b\in SO\left(3\right)$ implies a three-dimensional rotation matrix, $\lceil {}^{a}r_b\rceil$ represents three-dimensional skew-symmetric matrix obtained from a three-dimensional displacement vector ${}^{a}r_b\in {\mathbb{R}}^3$, and $0_3$ implies three-dimensional zero matrix. Till now, we have revealed how the MDH parameters influence the exponential map, the exponential coordinate vector, the joint twist, and the joint matrix. The next section will discuss the relationships between the joint axes using the line geometry, ultimately, to find the MDH parameters.

3. Line Geometry

A line $L(\widehat{z},v)$ can be represented by a set of three-dimensional direction vector $\widehat{z}$ and three-dimensional moment vector v, where $\widehat{z}$ and v are called the Plücker coordinate after Julius Plücker [23,24]. The Plücker coordinate to express the line has four independent elements because the line has two constraints that it remains the same line when rotated about itself and translated in its direction [25]. To improve readability and reduce the complexity of the main text, detailed derivations of the equations are provided in Appendix B.

Here, $\widehat{z}\in {\mathbb{R}}^3$ is a unit vector to denote any direction in a three-dimensional space and $v\in {\mathbb{R}}^3$ is the moment of the line described from an arbitrary point p on the line represented in the frame $\left\{0\right\}$ as shown in Figure 2, which can be expressed as follows:

$$v=p\times \widehat{z}.$$

(10)

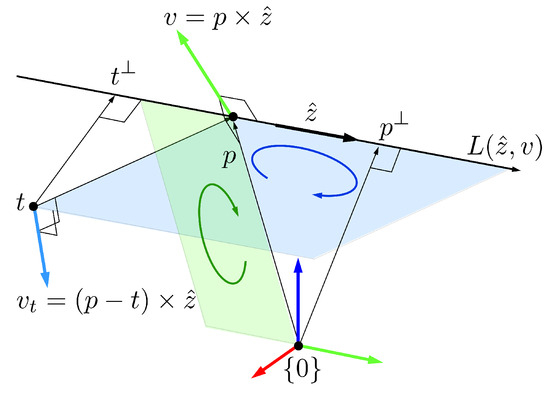
Figure 2. Relationships between a line $L(\widehat{z},v)$ and a point p on the line, and between the line and a point t out of the line in three-dimensional space.

3.1. Relationships Between Line and Points

Since the moment vector v is orthogonal to $\widehat{z}$ by Equation (10), it provides information about the closest point from the origin of frame $\left\{0\right\}$ as shown in Figure 2. Namely, the closest point $p^{\perp }$ on the line L from the origin of frame $\left\{0\right\}$ is computed by

$$\begin{array}{cc}\hfill p^{\perp }& =\widehat{z}\times v,\hfill \end{array}$$

(11)

where the closest distance from the origin of frame $\left\{0\right\}$ to the line L is $\parallel p^{\perp }\parallel =\parallel \widehat{z}\times v\parallel$. Furthermore, the moment $v_t$ of the line L about an arbitrary point t out of the line in Figure 2 is defined by

$$\begin{array}{cc}\hfill v_t& =v-t\times \widehat{z},\hfill \end{array}$$

(12)

and the closest point $t^{\perp }$ on the line L from a point t out of the line in Figure 2 is computed by

$$\begin{array}{cc}\hfill t^{\perp }& =t+\widehat{z}\times v_t,\hfill \end{array}$$

(13)

where it is represented in the frame $\left\{0\right\}$, and the closest distance from an arbitrary point t out of the line to the line L is $\parallel t-t^{\perp }\parallel =\parallel \widehat{z}\times v_t\parallel$. It is interesting that the closest point $t^{\perp }$ on the line from a point t out of the line is obtained by taking the cross-product of the direction vector $\widehat{z}$ and the moment $v_t$.

3.2. Relationships Between Two Lines

Another important property of the Plücker coordinate is the reciprocal product between two lines. When two lines are denoted as $L_1({\widehat{z}}_1,v_1=p_1\times {\widehat{z}}_1)$ and $L_2({\widehat{z}}_2,v_2=p_2\times {\widehat{z}}_2)$, as shown in Figure 3, it is defined as follows:

$$\begin{array}{c}\hfill L_1\ast L_2:={\widehat{z}}_1·v_2+{\widehat{z}}_2·v_1,\end{array}$$

(14)

where the reciprocal product implies the moment of line $L_1$ about line $L_2$ or the moment of $L_2$ about $L_1$. It is interesting that the reciprocal product is independent of the location of $p_1$ on $L_1$ or $p_2$ on $L_2$, and it is only dependent on the direction vectors ${\widehat{z}}_1$ and ${\widehat{z}}_2$. In addition, the reciprocal product is scalar, not a vector. Let us denote the moment $v_{21}$ of the line $L_2({\widehat{z}}_2,v_2)$ about the point $t_1$ using Equation (12):

$$\begin{array}{cc}\hfill v_{21}& =v_2-t_1\times {\widehat{z}}_2=(t_2-t_1)\times {\widehat{z}}_2,\hfill \end{array}$$

(15)

where $t_1$ and $t_2$ are feet of the common perpendicular line to the two lines $L_1$ and $L_2$ as shown in Figure 3.

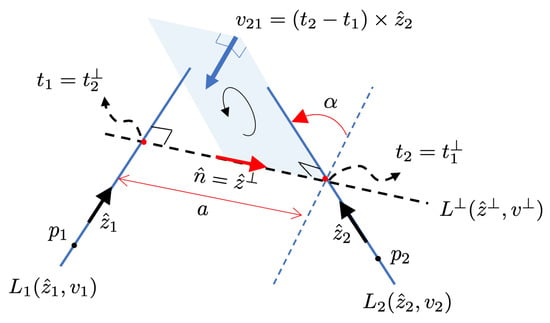
Figure 3. Relationships between two lines $L_1({\widehat{z}}_1,v_1=p_1\times {\widehat{z}}_1)$ and $L_2({\widehat{z}}_2,v_2=p_2\times {\widehat{z}}_2)$, where a is the distance between two lines, $t_1$ and $t_2$ are feet of the common perpendicular line $L^{\perp }({\widehat{z}}^{\perp },v^{\perp })$ to two lines, and $\widehat{n}={\widehat{z}}^{\perp }$ is the direction vector from $t_1$ to $t_2$.

Let us define the plane $\Pi$ containing ${\widehat{z}}_2$ and $v_{21}$ as shown in Figure 4, which is orthogonal to the common perpendicular line and parallel to ${\widehat{z}}_1$. Consequently, the plane $\Pi$ contains ${\widehat{z}}_1$ as shown in Figure 4. Using the fact that the link twist $\alpha$ is the angle of rotation from ${\widehat{z}}_1$ to ${\widehat{z}}_2$ about the common perpendicular line, the reciprocal product can be recomputed as follows:

$$\begin{array}{cc}\hfill L_1\ast L_2& =-\parallel v_{21}\parallel sin\alpha ,\hfill \end{array}$$

(16)

where $\parallel v_{21}\parallel$ implies the distance between $L_1$ and $L_2$. Thus, it provides the information on the link length a in Figure 1 as follows:

$$\begin{array}{cc}\hfill a& =\parallel v_{21}\parallel =-{\displaystyle \frac{L_1\ast L_2}{sin\alpha }}=-{\displaystyle \frac{{\widehat{z}}_1·v_2+{\widehat{z}}_2·v_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}.\hfill \end{array}$$

(17)

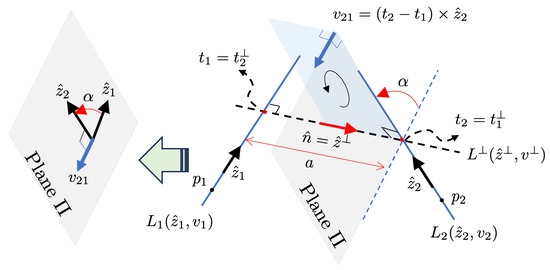
Figure 4. The plane $\Pi$ contains ${\widehat{z}}_2$ and $v_{21}$, which is orthogonal to the common perpendicular line and parallel to ${\widehat{z}}_1$; consequently, it contains ${\widehat{z}}_1$ as well, where $\alpha$ implies the twist angle of rotation from ${\widehat{z}}_1$ to ${\widehat{z}}_2$ about the common perpendicular line, and ${\widehat{z}}_2$ is perpendicular to $v_{21}$.

As a matter of fact, the reciprocal product becomes zero either when the two lines are intersected ($a=0$) or when the two lines are parallel ($\alpha =0$), where the link twist $\alpha$ in Figure 1 is defined by the angle of rotation from ${\widehat{z}}_1$ to ${\widehat{z}}_2$ about the common perpendicular line, which is calculated as follows:

$$\begin{array}{c}\hfill \alpha =\mathrm{atan}2(sin\alpha ,cos\alpha )=\mathrm{atan}2(\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,{\widehat{z}}_1·{\widehat{z}}_2),\end{array}$$

(18)

where it is effective for a positive range of $0\le \alpha \le \pi$. To cover its negative range of $-\pi \le \alpha \le 0$, the sign variable denoted by $s_x$ will be considered later.

3.3. Common Perpendicular Line

Let us find the common perpendicular line denoted by $L^{\perp }({\widehat{z}}^{\perp },v^{\perp })$ in Figure 4. Then, its direction vector ${\widehat{z}}^{\perp }$ emanating from $t_1$ is obtained as follows:

$$\begin{array}{c}\hfill {\widehat{z}}^{\perp }=\widehat{n}={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }},\end{array}$$

(19)

in fact, it is corresponding to the $\widehat{x}$-axis required to express the MDH parameters in Figure 1, and the moment vector $v^{\perp }$ is computed by:

$$\begin{array}{cc}\hfill v^{\perp }& =t_2\times {\widehat{z}}^{\perp }.\hfill \end{array}$$

(20)

Since we have obtained the common perpendicular line, we are ready to derive two intersection points $t_1$ and $t_2$ in Figure 4, which are called feet of common perpendicular line, where the former is obtained as an intersection between $L_1$ and $L^{\perp }$ and the latter between $L_2$ and $L^{\perp }$.

3.4. Feet of Common Perpendicular Line

The aforementioned intersection points (or feet) $t_1$ and $t_2$ in Figure 4 can be found through the following procedures. In fact, the related proof can be found in [25] as well. To begin with, let us set up a coordinate frame ${\widehat{z}}_1$-$\widehat{u}$-$\widehat{n}$ at the origin $\left\{0\right\}$ as shown in Figure 5, which is composed of three perpendicular unit vectors ${\widehat{z}}_1$, $\widehat{n}={\displaystyle \frac{z_1\times z_2}{\parallel z_1\times z_2\parallel }}$, and $\widehat{u}=\widehat{n}\times {\widehat{z}}_1$. The basic idea in [25] is to project the point $t_2$ onto the coordinate frames ${\widehat{z}}_1$-$\widehat{u}$-$\widehat{n}$ in Figure 5 as follows:

$$\begin{array}{cc}\hfill t_2& =(t_2·{\widehat{z}}_1){\widehat{z}}_1+(t_2·\widehat{u})\widehat{u}+(t_2·\widehat{n})\widehat{n}.\hfill \end{array}$$

(21)

Figure 5. ${\widehat{z}}_1$-$\widehat{u}$-$\widehat{n}$ coordinate frame, where ${\widehat{z}}_2$ lies in the ${\widehat{z}}_1$-$\widehat{u}$ plane, and thus $sin\alpha =\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel$ and $cos\alpha ={\widehat{z}}_1·{\widehat{z}}_2$ for $0\le \alpha \le \pi$.

For the third term ($t_2·\widehat{n}$) of the right-hand side of Equation (21), we can observe the following:

$$\begin{array}{cc}\hfill t_2·\widehat{n}& =-{\displaystyle \frac{v_2·{\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}.\hfill \end{array}$$

(22)

For the second term ($t_2·\widehat{u}$), the definitions of $\widehat{u}$ and $\widehat{n}$ are used as follows:

$$\begin{array}{cc}\hfill t_2·\widehat{u}& =-v_1·\widehat{n}.\hfill \end{array}$$

(23)

For the first term $(t_2·{\widehat{z}}_1)$, the direction vector ${\widehat{z}}_2$ lies in the plane spanned by ${\widehat{z}}_1$ and $\widehat{u}$ as shown in Figure 5, such that

$$\begin{array}{cc}\hfill {\widehat{z}}_2& =(cos\alpha ){\widehat{z}}_1+(sin\alpha )\widehat{u}\hfill \\ \hfill & =({\widehat{z}}_1·{\widehat{z}}_2){\widehat{z}}_1+\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel \widehat{u}.\hfill \end{array}$$

then, using Equation (23), we have:

$$\begin{array}{cc}\hfill t_2·{\widehat{z}}_2& =({\widehat{z}}_1·{\widehat{z}}_2)(t_2·{\widehat{z}}_1)-v_1·({\widehat{z}}_1\times {\widehat{z}}_2).\hfill \end{array}$$

(24)

Also, from the following:

$$\begin{array}{cc}\hfill {\widehat{z}}_2\times v_2& =t_2-({\widehat{z}}_2·t_2){\widehat{z}}_2,\hfill \end{array}$$

$t_2$ is obtained as:

$$\begin{array}{cc}\hfill t_2& ={\widehat{z}}_2\times v_2+({\widehat{z}}_2·t_2){\widehat{z}}_2.\hfill \end{array}$$

Then using Equation (24), $(t_2·{\widehat{z}}_1)$ is derived using $(t_2·{\widehat{z}}_2)$:

$$\begin{array}{cc}\hfill t_2·{\widehat{z}}_1& =v_2·({\widehat{z}}_1\times {\widehat{z}}_2)+{({\widehat{z}}_1·{\widehat{z}}_2)}^2(t_2·{\widehat{z}}_1)-({\widehat{z}}_1·{\widehat{z}}_2)(v_1·({\widehat{z}}_1\times {\widehat{z}}_2)),\hfill \end{array}$$

since $(t_2·{\widehat{z}}_1)$ appears in both sides of the above equation, rearranging it yields

$$\begin{array}{cc}\hfill t_2·{\widehat{z}}_1& ={\displaystyle \frac{(v_2-({\widehat{z}}_1·{\widehat{z}}_2)v_1)·\widehat{n}}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}.\hfill \end{array}$$

(25)

By inserting the three terms of Equations (22), (23), and (25) into Equation (21), finally, we have $t_2$, using $a\times (b\times c)=(a·c)b-(a·b)c$ and $\widehat{n}={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}$, as following form:

$$\begin{array}{cc}\hfill t_2& ={\displaystyle \frac{v_2\times ({\widehat{z}}_1\times ({\widehat{z}}_1\times {\widehat{z}}_2))-(v_1·({\widehat{z}}_1\times {\widehat{z}}_2)){\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}}.\hfill \end{array}$$

(26)

On the other hand, $t_1$ is obtained from Equation (26) for $t_2$ by switching subscripts 1 and 2, as follows:

$$\begin{array}{cc}\hfill \therefore t_1& ={\displaystyle \frac{v_1\times ({\widehat{z}}_2\times ({\widehat{z}}_2\times {\widehat{z}}_1))-(v_2·({\widehat{z}}_2\times {\widehat{z}}_1)){\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}}.\hfill \end{array}$$

(27)

It is noted that the derived $t_1$ and $t_2$ are computed by using the information only on two lines $L_1({\widehat{z}}_1,v_1)$ and $L_2({\widehat{z}}_2,v_2)$. The next section summarizes the five results of line geometry such as link length a (17), link twist $\alpha$ (18), $\widehat{x}$-axis $\widehat{n}$ (19), and feet of common perpendicular line $t_2$ (26) and $t_1$ (27).

3.5. Line Geometry Block, $\mathcal{LG}(L_1({\widehat{z}}_1,v_1),L_2({\widehat{z}}_2,v_2))$

The method to express how two adjacent lines (or joint axes) are located each other can be classified into four cases: collinear, distant parallel, intersected, and skewed. To begin with, criterion 1 is defined to check whether two lines are parallel or not, which is performed using the two direction vectors:

$$\begin{array}{c}\hfill \parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel =0\to \parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel <sin\left({ϵ}_{\theta }\right),\end{array}$$

(28)

where ${ϵ}_{\theta }\in {\mathbb{R}}^{+}$ denotes a small positive constant with units of radians, introduced to handle numerical issues when comparing angular values. If criterion 1 of Equation (25) is satisfied, the two lines are parallel to each other. The parallel lines can be further classified into two cases: collinear (parallel) and distant (parallel). For this purpose, criterion 2-1 is defined as the distance between the closest points from the origin of the coordinate frame to the lines using Equation (Section 3.1) as follows:

$$\begin{array}{c}\hfill \parallel p_1^{\perp }-p_2^{\perp }\parallel =0\to \parallel p_1^{\perp }-p_2^{\perp }\parallel <{ϵ}_d,\end{array}$$

(29)

where

$$\begin{array}{cc}\hfill p_1^{\perp }& ={\widehat{z}}_1\times v_1={\widehat{z}}_1\times (p_1\times {\widehat{z}}_1)\hfill \\ \hfill p_2^{\perp }& ={\widehat{z}}_2\times v_2={\widehat{z}}_2\times (p_2\times {\widehat{z}}_2).\hfill \end{array}$$

where ${ϵ}_d\in {\mathbb{R}}^{+}$ is a small positive threshold with units of meters, introduced to ensure numerical robustness when comparing distances between points. If criterion 2-1 is satisfied, the two lines are collinear (parallel); otherwise, they are distant (parallel). These parallel cases are summarized in Figure 6.

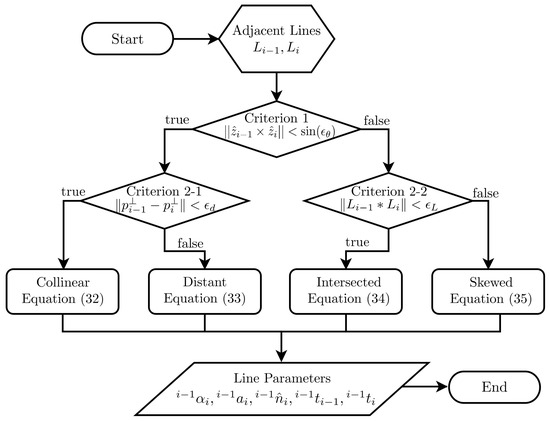
Figure 6. Flowchart of the line geometry block $\mathcal{LG}(L_{i-1},L_i)$. Given two input lines, $L_{i-1}({\widehat{z}}_{i-1},v_{i-1}=p_{i-1}\times {\widehat{z}}_{i-1})$ and $L_i({\widehat{z}}_i,v_i=p_i\times {\widehat{z}}_i)$, the block uses two criteria to classify their relationship into one of the four cases: Collinear, Distant, Intersected, or Skewed. Based on the case, it returns five parameters: ${}^{i-1}\alpha _i$, ${}^{i-1}a_i$, ${}^{i-1}\widehat{n}_i$, ${}^{i-1}t_{i-1}$, and ${}^{i-1}t_i$.

On the other hand, if criterion 1 of Equation (27) is not satisfied, the two lines are not parallel to each other. The non-parallel lines can be further classified into two cases: intersected and skewed. For this purpose, criterion 2-2 is defined as the existence of the intersection point, which is conducted using the reciprocal product (Section 3.2):

$$\begin{array}{c}\hfill |L_1\ast L_2|=0\to |L_1\ast L_2|<{ϵ}_L.\end{array}$$

(30)

where ${ϵ}_L\in {\mathbb{R}}^{+}$ is a small positive threshold used to evaluate the reciprocal product. Note that unlike ${ϵ}_{\theta }$ (in radians) and ${ϵ}_d$ (in meters), the reciprocal product is inherently dimensionless. If criterion 2-2 of Equation (30) is satisfied, two lines are intersected at one point, otherwise, they are skewed.

The line geometry block $\mathcal{LG}(L_1,L_2)$ to be designed in this section receives two lines ($L_1,L_2$) as inputs, selects one from the four cases using the criteria, and yields five parameters ($\alpha ,a,\widehat{n},t_1,t_2$) as outputs, where it is noted that two lines as the inputs consist of the direction vectors ${\widehat{z}}_1,{\widehat{z}}_2$ of joint axes and the points $p_1,p_2$ on joint axes as follows:

$$\begin{array}{cccccc}\hfill L_1({\widehat{z}}_1,v_1& =p_1\times {\widehat{z}}_1)\hfill & \hfill \mathrm{a}\mathrm{n}\mathrm{d}& \hfill & \hfill L_1({\widehat{z}}_2,v_2& =p_2\times {\widehat{z}}_2).\hfill \end{array}$$

(31)

3.5.1. Collinear

If $\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel <sin\left({ϵ}_{\theta }\right)$ and $\left|\right|p_1^{\perp }-p_2^{\perp }\left|\right|<{ϵ}_d$ are satisfied, the two lines are collinear with the following five parameter descriptions:

$$\begin{array}{cc}\hfill \alpha & =\mathrm{atan}2(\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,{\widehat{z}}_1·{\widehat{z}}_2),\hfill \end{array}$$

(32a)

$$\begin{array}{cc}\hfill a& =0,\hfill \end{array}$$

(32b)

$$\begin{array}{cc}\hfill \widehat{n}& =0_{3\times 1},\hfill \end{array}$$

(32c)

$$\begin{array}{cc}\hfill t_1& =t_2=p_1,\hfill \end{array}$$

(32d)

where link twist $\alpha$ can be either $0^{\circ }$ or ${180}^{\circ }$. In fact, the two lines are either in the same direction ($\alpha =0^{\circ }$) or in the opposite direction ($\alpha ={180}^{\circ }$) according to the link twist value. In the collinear case, the common perpendicular direction $\widehat{x}$-axis is not defined, and thus the $\widehat{x}$-axis of the previous frame is identically assigned to the new frame.

3.5.2. Distant (Parallel)

If $\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel <sin\left({ϵ}_{\theta }\right)$ and $\left|\right|p_1^{\perp }-p_2^{\perp }\left|\right|\ge {ϵ}_d$ are satisfied, the two lines are distant parallel to each other with the following five parameter descriptions:

$$\begin{array}{cc}\hfill \alpha & =\mathrm{atan}2(\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,{\widehat{z}}_1·{\widehat{z}}_2),\hfill \end{array}$$

(33a)

$$\begin{array}{cc}\hfill a& =\parallel {\widehat{z}}_1\times (v_{2}cos\alpha -v_1)\parallel ,\hfill \end{array}$$

(33b)

$$\begin{array}{cc}\hfill \widehat{n}& ={\displaystyle \frac{{\widehat{z}}_1\times (v_{2}cos\alpha -v_1)}{\parallel {\widehat{z}}_1\times (v_{2}cos\alpha -v_1)\parallel }},\hfill \end{array}$$

(33c)

$$\begin{array}{cc}\hfill t_1& =p_1,\hfill \end{array}$$

(33d)

$$\begin{array}{cc}\hfill t_2& =p_1+{\widehat{z}}_1\times (v_{2}cos\alpha -v_1),\hfill \end{array}$$

(33e)

where it is noted that $cos\alpha =1$ when the two parallel lines are in the same direction and $cos\alpha =-1$ in the opposite direction. Additionally, the closest points $p_1^{\perp }$ on line $L_1$ and $p_2^{\perp }$ on line $L_2$ yield the link length a and the common perpendicular direction $\widehat{n}$ as follows:

$$\begin{array}{cc}\hfill a\widehat{n}& =p_2^{\perp }-p_1^{\perp }=({\widehat{z}}_2\times v_2)-({\widehat{z}}_1\times v_1)\hfill \\ \hfill & =({\widehat{z}}_{1}cos\alpha \times v_2)-({\widehat{z}}_1\times v_1)={\widehat{z}}_1\times (v_{2}cos\alpha -v_1).\hfill \end{array}$$

In fact, $t_1$ is an arbitrary point on line $L_1({\widehat{z}}_1,v_1)$, but we choose $t_1$ equal to $p_1$ for practical use. Then, $t_2=p_1+{\widehat{z}}_1\times (v_{2}cos\alpha -v_1)$ since $a\widehat{n}=t_2-t_1$.

3.5.3. Intersected

If $\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel \ge sin\left({ϵ}_{\theta }\right)$ and $|L_1\ast L_2|<{ϵ}_d$ are satisfied, the two lines are intersected at one point $t_1=t_2$ with the following five parameter descriptions:

$$\begin{array}{cc}\hfill \alpha & =\mathrm{atan}2(\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,{\widehat{z}}_1·{\widehat{z}}_2),\hfill \end{array}$$

(34a)

$$\begin{array}{cc}\hfill a& =0,\hfill \end{array}$$

(34b)

$$\begin{array}{cc}\hfill \widehat{n}& ={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }},\hfill \end{array}$$

(34c)

$$\begin{array}{cc}\hfill t_1& =((v_1·{\widehat{z}}_2)I_3+{\widehat{z}}_1{v}_2^T-{\widehat{z}}_2{v}_1^T){\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}},\hfill \end{array}$$

(34d)

$$\begin{array}{cc}\hfill t_2& =t_1,\hfill \end{array}$$

(34e)

where $I_3$ is a three-dimensional identity matrix. To find the intersection point, let us rearrange the second term of $t_1$ (27) using $(a·c)b=a\times (b\times c)+(a·b)c$ as follows:

$$\begin{array}{cc}\hfill (v_2·({\widehat{z}}_2\times {\widehat{z}}_1)){\widehat{z}}_1& =v_2\times ({\widehat{z}}_1\times c)+(v_2·{\widehat{z}}_1)c,\hfill \end{array}$$

where $c:={\widehat{z}}_2\times {\widehat{z}}_1$, then $t_2$ of Equation (27) is rewritten as follows:

$$\begin{array}{cc}\hfill t_2& ={\displaystyle \frac{(v_1\times ({\widehat{z}}_2\times c))-(v_2\times ({\widehat{z}}_1\times c))-(v_2·{\widehat{z}}_1)c}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}}.\hfill \end{array}$$

Also, by using the property of cross-product operator, e.g., $a\times (b\times c)=(b{a}^T-(a·b)I_3)c$, we have

$$\begin{array}{cc}\hfill t_2& =({\widehat{z}}_2{v}_1^T-(v_1·{\widehat{z}}_2)I_3-{\widehat{z}}_1{v}_2^T){\displaystyle \frac{z_2\times z_1}{\parallel z_1\times z_2{\parallel }^2}}\hfill \\ \hfill \therefore & =((v_1·{\widehat{z}}_2)I_3+{\widehat{z}}_1{v}_2^T-{\widehat{z}}_2{v}_1^T){\displaystyle \frac{z_1\times z_2}{\parallel z_1\times z_2{\parallel }^2}},\hfill \end{array}$$

where the moments of the intersected lines are the same with each other, e.g., $v_1=v_2=v^{\perp }$ because $t_1=t_2$.

3.5.4. Skewed

If $\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel \ge sin\left({ϵ}_{\theta }\right)$ and $|L_1\ast L_2|\ge {ϵ}_d$ are satisfied, the two lines are skewed (not co-planar) with following the five parameters descriptions:

$$\begin{array}{cc}\hfill \alpha & =\mathrm{atan}2(\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,{\widehat{z}}_1·{\widehat{z}}_2),\hfill \end{array}$$

(35a)

$$\begin{array}{cc}\hfill a& =-{\displaystyle \frac{L_1\ast L_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }},\hfill \end{array}$$

(35b)

$$\begin{array}{cc}\hfill \widehat{n}& ={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }},\hfill \end{array}$$

(35c)

$$\begin{array}{cc}\hfill t_1& ={\displaystyle \frac{v_1\times ({\widehat{z}}_2\times ({\widehat{z}}_2\times {\widehat{z}}_1))+(v_2·({\widehat{z}}_1\times {\widehat{z}}_2)){\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}},\hfill \end{array}$$

(35d)

$$\begin{array}{cc}\hfill t_2& ={\displaystyle \frac{v_2\times ({\widehat{z}}_1\times ({\widehat{z}}_1\times {\widehat{z}}_2))+(v_1·({\widehat{z}}_2\times {\widehat{z}}_1)){\widehat{z}}_2}{\parallel {\widehat{z}}_2\times {\widehat{z}}_1{\parallel }^2}},\hfill \end{array}$$

(35e)

where the five results of line geometry such as link length a (17), link twist $\alpha$ (18), $\widehat{x}$-axis $\widehat{n}$ (19), and feet of common perpendicular line $t_2$ (26) and $t_1$ (27) are fully exploited for the skewed case.

The line geometry block denoted by $\mathcal{LG}$ summarizes the five parameters chosen according to criteria as shown in Figure 6, where the line geometry block is described by

$$\begin{array}{cc}\hfill \{{}^{i-1}\alpha _i,{}^{i-1}a_i,{}^{i-1}\widehat{n}_i,{}^{i-1}t_{i-1},{}^{i-1}t_i\}& =\mathcal{LG}(L_{i-1},L_i),\hfill \end{array}$$

(36)

where the inputs are two lines and the outputs are five parameters yielded from one of the four cases, which is selected using two criteria. As suggested in Figure 1, three joint axes (a set of three consecutive lines $L_{i-1},L_i$, and $L_{i+1}$) are required to extract four MDH parameters and thus two line geometry blocks are needed to describe four MDH parameters for ith joint.

4. Algorithmic MDH Parameter Extraction

This section describes how to algorithmically extract MDH parameters using the line geometry blocks suggested in the previous Section 3.5. This method can be directly applied to the single-branched articulated robotic manipulators. To extract a set of four MDH parameters for each joint, three consecutive lines (joint axes) are needed. Thus, $N+2$ line information is required with respect to the base frame $\left\{0\right\}$ including tcf denoted by $\{N+1\}$ for N-joint manipulators. Three coordinate axes of the base frame are defined by ${\widehat{x}}_0={[1,0,0]}^T$, ${\widehat{y}}_0={[0,1,0]}^T$ and ${\widehat{z}}_0={[0,0,1]}^T$, respectively. Algorithm 1 summarizes the inputs and the outputs through the computations of intermediate variables. The inputs are listed as follows:

$$\begin{array}{cc}\hfill \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e} \mathrm{f}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{\left(}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{\right)}& :\{{\widehat{z}}_0,p_0\},{\widehat{x}}_0,\hfill \\ \hfill \mathrm{1}\mathrm{s}\mathrm{t} \mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t} \mathrm{\left(}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{\right)}& :\{{\widehat{z}}_1,p_1\},\hfill \\ \hfill ⋮& \\ \hfill N\mathrm{t}\mathrm{h} \mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t} \mathrm{\left(}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{\right)}& :\{{\widehat{z}}_N,p_N\},\hfill \\ \hfill \mathrm{t}\mathrm{c}\mathrm{f} \mathrm{\left(}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{\right)}& :\{{\widehat{z}}_{N+1},p_{N+1}\},\hfill \end{array}$$

where $p_0={[0,0,0]}^T$. The adjacent two lines are applied consecutively to the line geometry blocks for ith joint as follows:

$$\begin{array}{cc}\hfill \{{}^{i-1}\alpha _i,{}^{i-1}a_i,{}^{i-1}\widehat{n}_i,{}^{i-1}t_{i-1},{}^{i-1}t_i\}& \leftarrow \mathcal{LG}(L_{i-1},L_i),\hfill \\ \hfill \{{}^i\alpha _{i+1},{}^{i}a_{i+1},{}^i\widehat{n}_{i+1},{}^{i}t_i,{}^{i}t_{i+1}\}& \leftarrow \mathcal{LG}(L_i,L_{i+1}),\hfill \end{array}$$

for $i=1,2,\cdots ,N$.

To extract four MDH parameters, we need to define ${\widehat{x}}_i$-axis to be the common perpendicular direction denoted by ${}^i\widehat{n}_{i+1}$ as shown in Figure 1. As a special case, the common perpendicular direction is not defined in the collinear case as suggested in Equations (32a)–(32d), and thus we assign the previous ${\widehat{x}}_{i-1}$-axis to ${\widehat{x}}_i$ as follows:

$$\begin{array}{c}\hfill {\widehat{x}}_i=\left\{\begin{array}{cc}{\widehat{x}}_{i-1}\hfill & \mathrm{i}\mathrm{f} L_i \mathrm{a}\mathrm{n}\mathrm{d} L_{i+1} \mathrm{i}\mathrm{s} \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{a}\mathrm{r}\hfill \\ {}^i\widehat{n}_{i+1}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.\end{array}$$

(37)

where it is noted that the origin of frame $\left\{i\right\}$ is specified as ${}^{i}t_i$. Once defining ${\widehat{x}}_i$-axis through Equation (37), the sign of link twist ${\alpha }_i$ and link length $a_i$ can be determined by using the dot-product between ${\widehat{x}}_{i-1}$ and ${}^{i-1}\widehat{n}_i$. To begin with, the sign is assigned into $+1$ when two lines are parallel. Subsequently, if ${\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i>0$, then the sign will be $+1$, and if ${\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i<0$, then the sign will be $-1$. As a summary, the sign is determined as follows:

$$\begin{array}{c}\hfill s_{ix}=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}\parallel {\widehat{z}}_{i-1}\times {\widehat{z}}_i\parallel <sin\left({ϵ}_{\theta }\right)\hfill \\ {\displaystyle \frac{{\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i}{|{\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i|}}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.\end{array}$$

(38)

The sign of the joint offset angle ${\theta }_{i0}$ can be also determined by using the dot-product between ${\widehat{z}}_i$ and $({\widehat{x}}_{i-1}\times {\widehat{x}}_i)$ as follows:

$$\begin{array}{c}\hfill s_{iz}=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}\parallel {\widehat{x}}_{i-1}\times {\widehat{x}}_i\parallel <sin\left({ϵ}_{\theta }\right)\hfill \\ {\displaystyle \frac{{\widehat{z}}_i·({\widehat{x}}_{i-1}\times {\widehat{x}}_i)}{|{\widehat{z}}_i·({\widehat{x}}_{i-1}\times {\widehat{x}}_i)|}}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.\end{array}$$

(39)

where it is noted that the sign of joint offset distance $d_{i0}$ does not have to be considered because it is obtained already by dot-product implying the projection onto the ${\widehat{z}}_i$-axis. Using the signs of $s_{ix}$ (38) and $s_{iz}$ (39), four MDH parameters are determined in the following sections.

Algorithm 1 Algorithmic MDH parameter extraction.

Require:  $\{{\widehat{z}}_0,p_0\}$, $\{{\widehat{z}}_1,p_1\}$, ⋯, $\{{\widehat{z}}_N,p_N\}$, $\{{\widehat{z}}_{N+1},p_{N+1}\}$, ${\widehat{x}}_0={[1,0,0]}^T$. Ensure:  $\{{\widehat{x}}_1,{\alpha }_1,a_1,d_{10},{\theta }_{10}\}$, ⋯, $\{{\widehat{x}}_N,{\alpha }_N,a_N,d_{N0},{\theta }_{N0}\}$ 1: for $i=1$ to N do 2:    for $j=i-1$ to $i+1$ do 3:      $v_j\leftarrow p_j\times {\widehat{z}}_j$ 4:      $L_j\leftarrow ({\widehat{z}}_j,v_j)$ 5:    end for 6:    $\{{}^{i-1}\alpha _i,{}^{i-1}a_i,{}^{i-1}\widehat{n}_i,{}^{i-1}t_{i-1},{}^{i-1}t_i\}\leftarrow \mathcal{LG}(L_{i-1},L_i)$ 7:    $\{{}^i\alpha _{i+1},{}^{i}a_{i+1},{}^i\widehat{n}_{i+1},{}^{i}t_i,{}^{i}t_{i+1}\}\leftarrow \mathcal{LG}(L_i,L_{i+1})$ 8:    if $L_i$ and $L_{i+1}$ are collinear then 9:       ${\widehat{x}}_i\leftarrow {\widehat{x}}_{i-1}$ 10:    else 11:      ${\widehat{x}}_i\leftarrow {}^i\widehat{n}_{i+1}$ 12:    end if 13:    if $\parallel {\widehat{z}}_{i-1}\times {\widehat{z}}_i\parallel <sin\left({ϵ}_{\theta }\right)$ then 14:      $s_{ix}\leftarrow 1$ 15:    else 16:      $s_{ix}\leftarrow ({\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i)/\left|({\widehat{x}}_{i-1}·{}^{i-1}\widehat{n}_i)\right|$ 17:    end if 18:    if $\parallel {\widehat{x}}_{i-1}\times {\widehat{x}}_i\parallel <sin\left({ϵ}_{\theta }\right)$ then 19:      $s_{iz}\leftarrow 1$ 20:    else 21:      $s_{iz}\leftarrow {\widehat{z}}_i·({\widehat{x}}_{i-1}\times {\widehat{x}}_i)/|{\widehat{z}}_i·({\widehat{x}}_{i-1}\times {\widehat{x}}_i)|$ 22:    end if 23:    ${\alpha }_i\leftarrow s_{ix}{}^{i-1}\alpha _i$ 24:    $a_i\leftarrow s_{ix}{}^{i-1}a_i$ 25:    $d_{i0}\leftarrow {\widehat{z}}_i·({}^{i}t_i-{}^{i-1}t_i)$ 26:    ${\theta }_{i0}\leftarrow s_{iz}\mathrm{atan}2(\parallel {\widehat{x}}_{i-1}\times {\widehat{x}}_i\parallel ,{\widehat{x}}_{i-1}·{\widehat{x}}_i)$ 27: end for

4.1. Twist Angle ${\alpha }_i$

It is defined as the angle from ${\widehat{z}}_{i-1}$ to ${\widehat{z}}_i$ about ${\widehat{x}}_{i-1}$-axis as shown in Figure 1. Since the twist angle ${}^{i-1}\alpha _i$ provided from $\mathcal{LG}(L_{i-1},L_i)$ is in the range of $0\le {}^{i-1}\alpha _i\le \pi$, the sign $s_{ix}$ should be reflected in the following form:

$$\begin{array}{cc}\hfill {\alpha }_i& =s_{ix}{}^{i-1}\alpha _i.\hfill \end{array}$$

(40)

4.2. Link Length $a_i$

It is defined as the distance from ${\widehat{z}}_{i-1}$ to ${\widehat{z}}_i$ along ${\widehat{x}}_{i-1}$-axis as shown in Figure 1. Since the distance ${}^{i-1}a_i$ is positive, the sign $s_{ix}$ is also reflected in the following form:

$$\begin{array}{cc}\hfill a_i& =s_{ix}{}^{i-1}a_i.\hfill \end{array}$$

(41)

4.3. Joint Offset Distance $d_{i0}$

It is defined as the distance from ${\widehat{x}}_{i-1}$ to ${\widehat{x}}_i$ along the ${\widehat{z}}_i$-axis as shown in Figure 1. The distance projected into ${\widehat{z}}_i$-axis is defined as follows:

$$\begin{array}{cc}\hfill d_{i0}& ={\widehat{z}}_i·({}^{i}t_i-{}^{i-1}t_i).\hfill \end{array}$$

(42)

4.4. Joint Offset Angle ${\theta }_{i0}$

It is defined as the angle from ${\widehat{x}}_{i-1}$ to ${\widehat{x}}_i$ about the ${\widehat{z}}_i$-axis as shown in Figure 1. Since the ${\widehat{x}}_i$-axis is determined by Equation (37), the sign $s_{iz}$ should be reflected as follows:

$$\begin{array}{cc}\hfill {\theta }_{i0}& =s_{iz}\mathrm{atan}2(\parallel {\widehat{x}}_{i-1}\times {\widehat{x}}_i\parallel ,{\widehat{x}}_{i-1}·{\widehat{x}}_i).\hfill \end{array}$$

(43)

The outputs of Algorithm 1 are consecutively arranged into:

$$\begin{array}{cc}\hfill 1\mathrm{s}\mathrm{t} \mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}& :\{{\widehat{x}}_1,{\alpha }_1,a_1,d_{10},{\theta }_{10}\}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}{L}_0,L_1,L_2,{\widehat{x}}_0,\hfill \\ \hfill 2\mathrm{n}\mathrm{d} \mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}& :\{{\widehat{x}}_2,{\alpha }_2,a_2,d_{20},{\theta }_{20}\}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}{L}_1,L_2,L_3,\hfill \\ \hfill ⋮& \\ \hfill N\mathrm{t}\mathrm{h} \mathrm{j}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}& :\{{\widehat{x}}_N,{\alpha }_N,a_N,d_{N0}{\theta }_{N0}\}\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m}{L}_{N-1},L_N,L_{N+1},\hfill \end{array}$$

where it is noted that the ${\widehat{x}}_0$-axis is required in advance and it is commonly chosen as ${[1,0,0]}^T$. To verify the completeness of Algorithm 1, several examples are suggested in the following section.

The algorithm does not include any iterative procedures and is composed of fixed geometric operations such as dot products and cross products. The line geometry block contains no loops, and Algorithm 1 uses a single for-loop over N joints. The overall computational complexity is $\mathcal{O}\left(N\right)$.

5. Verification

Algorithm 1 was implemented in both Python and MATLAB (The implementation for algorithmic DH parameter extraction is available at https://github.com/MinchangSung0223/AlgorithmicMDH (accessed on 27 April 2025)) and is also referenced in [26]. The algorithm was tested using PyBullet [27] and MATLAB simulations. For each joint i, the joint axis ${\widehat{z}}_i$ and a point $p_i$ on the axis were extracted from the URDF (Unified Robot Description Format) model [28]. The verification was first conducted on a simple SCARA robot, followed by testing on three commercial robotic manipulators, as described in the following sections. All verifications were conducted entirely in simulation without using the experimental hardware.

5.1. SCARA

A typical SCARA robot consists of three revolute joints and one prismatic joint, where the left side of Figure 7 shows the line information as inputs and the right side shows the extraction results of MDH parameters. For the first joint, the following three consecutive lines are applied to the Algorithm 1:

$$\begin{array}{cc}\hfill 0\mathrm{t}\mathrm{h} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}& :{\widehat{z}}_0={[0,0,1]}^T,p_0={[0,0,0]}^T,{\widehat{x}}_0={[1,0,0]}^T,\hfill \\ \hfill 1\mathrm{s}\mathrm{t} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}& :{\widehat{z}}_1={[0,0,1]}^T,p_1={[0,0,0.375]}^T,\hfill \\ \hfill 2\mathrm{n}\mathrm{d} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}& :{\widehat{z}}_2={[0,0,1]}^T,p_2={[0,0.5,0.4]}^T,\hfill \end{array}$$

where $v_i=p_i\times {\widehat{z}}_i$ for $i=0,1,2$. The zeroth line and first line have a collinear relation, and the first line and second line have a distant parallel relation by the proposed criteria in Section 3.5 regarding the line geometry block $\mathcal{LG}(L_{i-1},L_i)$. And finally, the outputs of Algorithm 1 regarding the first joint are listed as follows:

$$\begin{array}{cccccccccc}\hfill {\widehat{x}}_1& ={[0,1,0]}^T\hfill & \hfill & & \hfill & & \hfill & & \hfill & \mathrm{f}\mathrm{o}\mathrm{r} \left\{1\right\} \mathrm{f}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e},\hfill \\ \hfill {}^{0}t_1& ={[0,0,0]}^T\hfill & \hfill & & \hfill ,{}^{1}t_1& ={[0,0,0.375]}^T\hfill & \hfill & & \hfill & \mathrm{o}\mathrm{n} {\widehat{z}}_1-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s},\hfill \\ \hfill {\alpha }_1& =0\hfill & \hfill & & \hfill & & \hfill & & \hfill & \mathrm{a}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{t} {\widehat{x}}_0-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s},\hfill \\ \hfill a_1& =0\hfill & \hfill & & \hfill & & \hfill & & \hfill & \mathrm{a}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g} {\widehat{x}}_0-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s},\hfill \\ \hfill d_{10}& =0.375\hfill & \hfill & & \hfill & & \hfill & & \hfill & \mathrm{a}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g} {\widehat{z}}_1-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s},\hfill \\ \hfill {\theta }_{10}& ={90}^{\circ }\hfill & \hfill & & \hfill & & \hfill & & \hfill & \mathrm{a}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{t} {\widehat{z}}_1-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s},\hfill \end{array}$$

where these results make us to denote the frame $\left\{1\right\}$ in the right side of Figure 7. The aforementioned processes are repeated until the fourth joint. As a result, a pair of input and output data for all joints are listed in Table 2 and denoted on the right side of Figure 7. During the processes, the relations between the lines are found in Table 3.

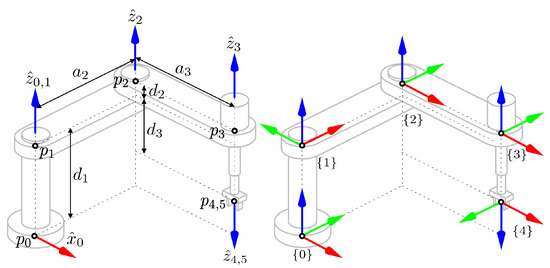
Figure 7. The SCARA robot example, where the left side shows six line information including the base and TCF and the right side illustrates the result of MDH parameters extracted using Algorithm 1, in which the red arrow denotes the ${\widehat{x}}_i$-axis, the green arrow expresses the ${\widehat{y}}_i$-axis, and the blue arrow represents the ${\widehat{z}}_i$-axis, respectively. In addition, the circle ∘ on the left side denotes the point $p_i$, and ∘ on the right side expresses the origin of the ith frame.

Table 2. MDH parameters of the Selective Compliance Assembly Robot Arm (SCARA) robot extracted when inputs are ${\widehat{z}}_i$-axis, $p_i$ on the ith joint axis, and its moments denoted by $v_i=p_i\times {\widehat{z}}_i$, where outputs of Algorithm 1 are obtained as a set of ${\widehat{x}}_i$-axis, link twist ${\alpha }_i$, link length $a_i$, joint offset distance $d_{i0}$, and joint offset angle ${\theta }_{i0}$ for the ith joint. Additionally, ${}^{i-1}t_i$ and ${}^{i}t_i$ are both feet of the common perpendicular line.

	i	0	1	2	3	4	5
input	${\widehat{z}}_i$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$
	${\overrightarrow{p}}_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.375\end{array}\right]$	$\left[\begin{array}{c}0\\ 0.5\\ 0.4\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.4\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.15\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.15\end{array}\right]$
	${\overrightarrow{v}}_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.5\\ -0.5\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.5\\ 0.5\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.5\\ 0.5\\ 0\end{array}\right]$
output	${\widehat{x}}_i$	×	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	×
	${}^{i-1}\overrightarrow{t}_i$		$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0.5\\ 0.375\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.4\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.4\end{array}\right]$
	${}^i\overrightarrow{t}_i$		$\left[\begin{array}{c}0\\ 0\\ 0.375\end{array}\right]$	$\left[\begin{array}{c}0\\ 0.5\\ 0.4\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.4\end{array}\right]$	$\left[\begin{array}{c}0.5\\ 0.5\\ 0.15\end{array}\right]$
	${\alpha }_i$		0	0	0	$\pi$
	$a_i$		0	0.5	0.5	0
	$d_{i0}$		0.375	0.025	0	0.25
	${\theta }_{i0}$		${\displaystyle \frac{\pi }{2}}$	−${\displaystyle \frac{\pi }{2}}$	0	0

Table 3. Relations between adjacent joint axes computed from the SCARA model.

	b/w 0 and 1	1 and 2	2 and 3	3 and 4	4 and 5
relation	collinear	distant	distant	collinear	collinear

Using the constant MDH parameters suggested in Table 2, the adjacent transformation can be represented by adding joint variables $q_{1,\theta },q_{2,\theta },q_{3,\theta }$ for the first, second, and third revolute joints and $q_{4,d}$ for the fourth prismatic joint. The generalized joint variables $({\theta }_i,d_i)$ for each joint are summarized in Table 4.

Table 4. The generalized joint variables with MDH parameters for the SCARA robot.

Joints	Generalized Joint Variables (${\mathit{\theta }}_{\mathit{i}},{\mathit{d}}_{\mathit{i}}$)
1st revolute	${\theta }_1\leftarrow {\theta }_{10}+q_{1,\theta }={\displaystyle \frac{\pi }{2}}+q_{1,\theta }$
	$d_1\leftarrow d_{10}=0.375$
2nd revolute	${\theta }_2\leftarrow {\theta }_{20}+q_{2,\theta }=-{\displaystyle \frac{\pi }{2}}+q_{2,\theta }$
	$d_2\leftarrow d_{20}=0.025$
3rd revolute	${\theta }_3\leftarrow {\theta }_{30}+q_{3,\theta }=q_{3,\theta }$
	$d_3\leftarrow d_{30}=0$
4th prismatic	${\theta }_4\leftarrow {\theta }_{40}=0$
	$d_4\leftarrow d_{40}+q_{4,d}=0.25+q_{4,d}$

The forward kinematics can be obtained using the MDH parameters (${\alpha }_i,a_i$) about/along the ${\widehat{x}}_{i-1}$-axis and the generalized joint variables (${\theta }_i,d_i$) about/along the ${\widehat{z}}_i$-axis as follows:

$$\begin{array}{c}\hfill {}^{0}T_{tcf}={}^{0}T_1({\theta }_1,d_1){}^{1}T_2({\theta }_2,d_2){}^{2}T_3({\theta }_3,d_3){}^{3}T_4({\theta }_4,d_4){}^{4}T_{tcf},\end{array}$$

where $tcf$ implies $\left\{5\right\}$ and ith adjacent transformation belonging to $SE\left(3\right)$ is obtained as, for $i=1,2,3,4$,

$$\begin{array}{cc}\hfill {}^{i-1}T_i({\theta }_i,d_i)& =\mathrm{expm}\left(\lceil {\lambda }_{x_{i-1}}\rceil \right)\mathrm{expm}\left(\lceil {\lambda }_{z_i}\rceil \right),\hfill \end{array}$$

in which the exponential coordinates ${\lambda }_{x_{i-1}}\in {\mathbb{R}}^6$ and ${\lambda }_{z_i}\in {\mathbb{R}}^6$ isomorphic to the Lie algebras $\lceil {\lambda }_{x_{i-1}}\rceil \in \mathfrak{se}\left(3\right)$ and $\lceil {\lambda }_{z_i}\rceil \in \mathfrak{se}\left(3\right)$ are described using Equation (4) and summarized in Table 5.

Table 5. Exponential coordinates ${\lambda }_{x_{i-1}}$, ${\lambda }_{z_i}$, and joint matrices $E_i$ for SCARA robot joints.

i	Joint Type	${\mathit{\lambda }}_{{\mathit{x}}_{\mathit{i}-1}}$	${\mathit{\lambda }}_{{\mathit{z}}_{\mathit{i}}}$	${\mathit{E}}_{\mathit{i}}$
1	R	${[0,0,0,0,0,0]}^T$	${[0,0,0.375,0,0,{\displaystyle \frac{\pi }{2}}+q_{1,\theta }]}^T$	${[0,0,0,0,0,1]}^T$
2	R	${[0.5,0,0,0,0,0]}^T$	${[0,0,0.025,0,0,-{\displaystyle \frac{\pi }{2}}+q_{2,\theta }]}^T$	${[0,0,0,0,0,1]}^T$
3	R	${[0.5,0,0,0,0,0]}^T$	${[0,0,0,0,0,q_{3,\theta }]}^T$	${[0,0,0,0,0,1]}^T$
4	P	${[0,0,0,\pi ,0,0]}^T$	${[0,0,0.25+q_{4,d},0,0,0]}^T$	${[0,0,1,0,0,1]}^T$

Additionally, we can derive the joint twist represented by ${}^{i-1}V_i={\dot{\lambda }}_{z_i}=E_i{\dot{q}}_i$ and the joint matrix $E_i$ as suggested in Section 2.3. Furthermore, the joint matrix represented in the base frame $\left\{0\right\}$ (${}^{0}E_i={}^0\mathrm{Ad}_i{E}_i$) and the joint matrix represented in the tool coordinate frame $\left\{tcf\right\}$ (${}^{tcf}E_i={}^{tcf}\mathrm{Ad}_i{E}_i$) can be obtained using the corresponding adjoint transformations ${}^0\mathrm{Ad}_i$ and ${}^{tcf}\mathrm{Ad}_i$, respectively. Two types of joint matrices denoted by ${}^{0}E_i$ and ${}^{tcf}E_i$ are called spatial screw axes and body screw axes in [4], respectively.

5.2. SCARA with Modeling Uncertainties

In practical robotic systems, modeling uncertainties often lead to deviations in the direction and displacement vectors from their ideal values. Despite such deviations, the proposed algorithm is capable of robustly computing the MDH parameters from non-ideal inputs, provided that the joint axes are correctly defined as lines, as described in Section 3. In conventional approaches to kinematic modeling using MDH or DH parameterizations, the transformations from the base frame to the first joint frame and from the last joint frame to the tool coordinate frame are typically treated as known rigid transformations. If needed, they may be modeled with additional parameters and identified separately. In our method, it is also possible to estimate the MDH parameters associated with such rigid transformations by allocating additional virtual lines to represent them. However, because these transformations are typically fixed and known with high accuracy (e.g., derived from CAD models or mechanical assembly), our algorithm assumes them to be given and instead focuses on calibrating the internal joint transformations between successive links using the line geometry-based approach (see Algorithm 1). To evaluate the robustness of the proposed method, we introduced synthetic modeling uncertainties into a simple SCARA robot. Table 6 compares the nominal and perturbed (“actual”) joint parameters encoded in the URDF. Perturbations were applied to each joint with approximately $1^{\circ }$ deviation in orientation and $0.01$ m deviation in displacement, mimicking realistic sensor or modeling noise. Based on the perturbed URDF data in Table 6, the MDH parameters extracted using the proposed algorithm are listed in Table 7. Compared to the ideal case, the modeling uncertainties caused several joint axis pairs, previously identified as “distant” in line geometry, to be reclassified as “skewed”. As a result, the joint offset distances $d_{i0}$ increased noticeably. The updated relationships between adjacent joint axes under perturbation are summarized in Table 8.

Table 6. Comparison of nominal and perturbed URDF parameters for the SCARA robot.

Joint Pair	Orientation (Roll, Pitch, Yaw) [deg]		Position (x, y, z) [m]
	Nominal	Perturbed	Nominal	Perturbed
0–1	(0, 0, 0)	(0, 0, 0)	(0, 0, 0.375)	(0, 0, 0)
1–2	(0, 0, 0)	(1, 1, −1)	(0, 0.5, 0.025)	(0.01, 0.51, −0.024)
2–3	(0, 0, 0)	(1, −1, 1)	(0.5, 0, 0)	(0.51, −0.01, 0.01)
3–4	(0, 0, 0)	(−1, −1, −1)	(0, 0, −0.25)	(−0.01, −0.01, −0.29)
4–5	(0, 0, 0)	(0, 0, 0)	(0, 0, 0)	(0, 0, 0)

Table 7. Extracted MDH parameters from the perturbed SCARA robot, using small positive threshold $sin\left({ϵ}_{\theta }\right)={ϵ}_d={ϵ}_L={10}^{-16}$.

Parameter	Joint 1	Joint 2	Joint 3	Joint 4
${\alpha }_i$ [rad]	0.0000	0.0247	0.0247	0.0247
$a_i$ [m]	0.0000	0.3614	0.3739	0.0141
$d_{i0}$ [m]	14.8930	−0.5166	−14.3041	−0.0100
${\theta }_{i0}$ [rad]	0.7678	−1.5533	−1.5883	0.0000

Table 8. Relations between adjacent joint axes computed from the perturbed URDF model.

	b/w 0 and 1	1 and 2	2 and 3	3 and 4	4 and 5
Relation	collinear	skewed	skewed	skewed	collinear

5.3. Indy7

Let us consider the MDH parameters of Indy7 manufactured by Neuromeka, which has six revolute joints based on electrical current-based control. The left side of Figure 8 shows line information denoted by $({\widehat{z}}_i,p_i)$ including the base frame and TCF, where the line information was extracted from the $\widehat{z}$-axis and the origin of the joint frame written in the URDF in [29]. The right side of Figure 8 illustrates the coordinate frames defined by MDH parameters, which were extracted from Algorithm 1. Indeed, the MDH parameters of Indy7 have been discussed in [30], but the results are different from ours. The differences between the proposed method and the reference [30] happen because the proposed method makes use of the line geometry and [30] uses the user-defined $\widehat{x}$-axis, respectively. Specifically, $d_{20}=0$ in [30] while $d_{20}=0.109$ in Table 9, and ${\widehat{x}}_5$-axis of [30], have opposite directions with the ${\widehat{x}}_5$-axis shown in Figure 8.

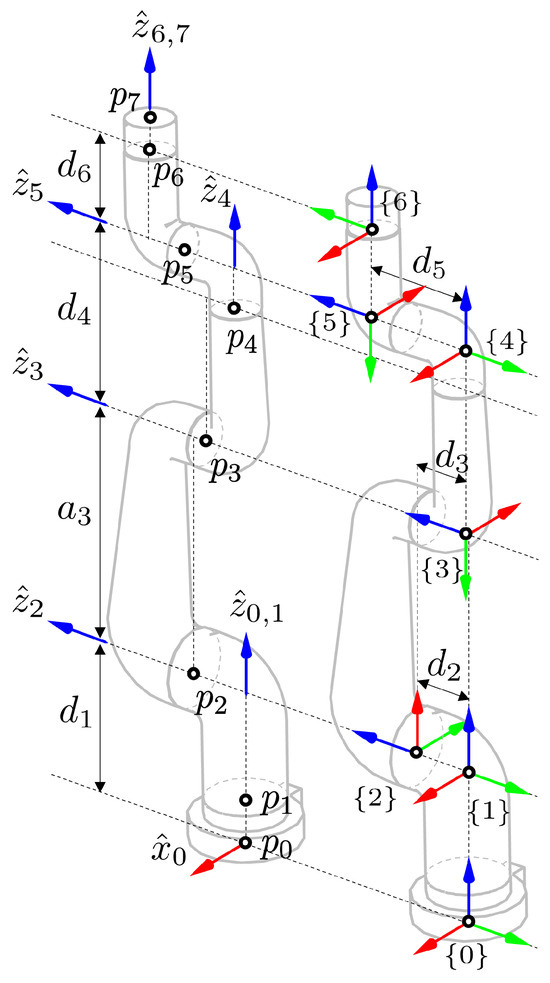
Figure 8. MDH parameters of Indy7, where the left side shows the input data regarding ${\widehat{z}}_i$ and $p_i$ denoted by the circle ∘, and the right side illustrates the frames obtained from the MDH parameters. Numerical data of input/output for Algorithm 1 are given in Table 9.

Table 9. Indy7, where upper part and lower part imply the input data to the Algorithm 1 and the output yielded from the algorithm, respectively.

	i	0	1	2	3	4	5	6	7
input	${\widehat{z}}_i$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$
	$p_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.0775\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1090\\ 0.2995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0785\\ 0.7495\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0035\\ 1.0165\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1175\\ 1.0995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1865\\ 1.2675\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1865\\ 1.3275\end{array}\right]$
	$v_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.2995\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.7495\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.0035\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1.0995\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.1865\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.1865\\ 0\\ 0\end{array}\right]$
	i	0	1	2	3	4	5	6	7
output	${\widehat{x}}_i$	×	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	×
	${}^{i-1}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.2995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1090\\ 0.7495\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0035\\ 0.7495\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0035\\ 1.0995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1865\\ 1.0995\end{array}\right]$
	${}^{i}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0.2995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1090\\ 0.2995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0035\\ 0.7495\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0035\\ 1.0995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1865\\ 1.0995\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.1865\\ 1.2675\end{array}\right]$
output	${\alpha }_i$		0	${\displaystyle \frac{\pi }{2}}$	0	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$
	$a_i$		0	0	$0.4500$	0	0	0
	$d_{i0}$		$0.2995$	$0.1090$	$-0.1055$	$0.3500$	$0.1830$	$0.1680$
	${\theta }_{i0}$		0	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	$\pi$	$\pi$	0

For Indy7, when the input data suggested in Table 9 are applied to Algorithm 1, the line geometry blocks are called by the algorithm, and the spatial relationships between the joint axes are determined as summarized in Table 10.

Table 10. Relations between adjacent joint axes computed from the Indy7 model.

	b/w 0 and 1	1 and 2	2 and 3	3 and 4
relation	collinear	intersected	distant	intersected
	4 and 5	5 and 6	6 and 7
relation	intersected	intersected	collinear

The aforementioned selections yield the MDH parameters for Indy7 in the Algorithm 1. As a result, a pair of input and output data for all joints are listed in Table 9 and denoted on the right side of Figure 8. Note that any point $p_i$ can be arbitrarily chosen along the line $L_i({\widehat{z}}_i,v_i)$ (i.e., the joint axis) since the MDH parameterization only requires that $p_i$ lies on the axis direction ${\widehat{z}}_i$. For example, if $p_2={[0,0,0.2995]}^T$ is selected as the intersection point between $L_1$ and $L_2$, then the resulting value of $d_{20}$ becomes zero.

5.4. KUKA LBR Iiwa

The KUKA LBR iiwa is one of the widely used seven-dof robotic manipulators, which has seven revolute joints. The left side of Figure 9 shows line information denoted by $({\widehat{z}}_i,p_i)$ including the base frame and TCF, where the line information was extracted from the $\widehat{z}$-axis and the origin of the joint frame written in the URDF in [31]. The right side of Figure 9 illustrates the coordinate frames defined by MDH parameters extracted from Algorithm 1. When the input data suggested in Table 11 are applied to Algorithm 1, the line geometry blocks are called by the algorithm, and the spatial relationships between the joint axes are determined as summarized in Table 12.

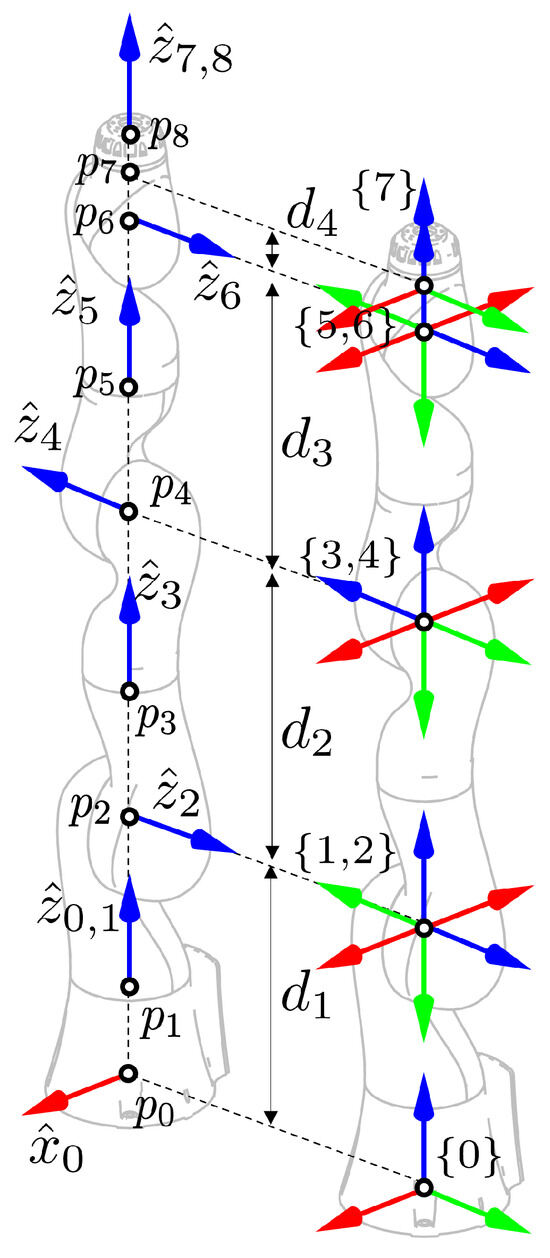
Figure 9. MDH parameters of KUKA LBR iiwa, where the left side shows the input data regarding ${\widehat{z}}_i$ and $p_i$ denoted by the circle ∘, and the right side illustrates the frames obtained from the MDH parameters. Numerical data of input/output related to Algorithm 1 are given in Table 11.

Table 11. KUKA LBR iiwa, where upper part and lower part imply the input data to the Algorithm 1 and the output yielded from the algorithm, respectively.

	i	0	1	2	3	4	5	6	7	8
input	${\widehat{z}}_i$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ -1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$
	$p_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.1575\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.3600\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.5645\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.7800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.9645\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.1800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.2610\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.3060\end{array}\right]$
	$v_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.3600\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.7800\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1.1800\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$
output	${\widehat{x}}_i$	×	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	×
	${}^{i-1}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.3600\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.3600\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.7800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.7800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.1800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.1800\end{array}\right]$
	${}^{i}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0.3600\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.3600\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.7800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.7800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.1800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.1800\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1.2610\end{array}\right]$
	${\alpha }_i$		0	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$
	$a_i$		0	0	0	0	0	0	0
	$d_{i0}$		$0.3600$	0	$0.4200$	0	$0.4000$	0	$0.0810$
	${\theta }_{i0}$		$\pi$	$\pi$	0	$\pi$	0	$\pi$	0

Table 12. Relations between adjacent joint axes computed from the KUKA LBR iiwa model.

	b/w 0 and 1	1 and 2	2 and 3	3 and 4
relation	collinear	intersected	intersected	intersected
	4 and 5	5 and 6	6 and 7	7 and 8
relation	intersected	intersected	intersected	collinear

According to the above selection, the MDH parameters for KUKA LBR iiwa are obtained by the Algorithm 1. As a result, a pair of input and output data for all joints are listed in Table 11 and denoted on the right side of Figure 9.

5.5. UR5

The UR-5 is one of the widely used six-dof robotic manipulators, which has six revolute joints. The left side of Figure 10 shows line information denoted by $({\widehat{z}}_i,p_i)$ including the base frame and TCF, where the line information was extracted from the $\widehat{z}$-axis and the origin of the joint frame written in the URDF [32]. The right side of Figure 10 illustrates the coordinate frames defined by MDH parameters extracted from Algorithm 1. When the input data suggested in Table 13 are applied to Algorithm 1, the line geometry blocks are called by the algorithm, and the spatial relationships between the joint axes are determined as shown in Table 14.

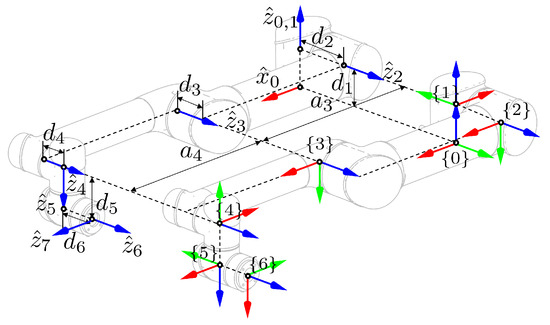
Figure 10. MDH parameters of UR5, where the left side shows the input data regarding ${\widehat{z}}_i$ and $p_i$ denoted by the circle ∘, and the right side illustrates the frames obtained from the MDH parameters. Numerical data of input/output related to Algorithm 1 are given in Table 13.

Table 13. UR5, where the upper part and lower part imply the input data to the Algorithm 1 and the output yielded from the algorithm, respectively.

	i	0	1	2	3	4	5	6	7
input	${\widehat{z}}_i$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$	$\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$
	$p_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0\\ 0.1358\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.4250\\ 0.0161\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.0161\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ -0.0055\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1915\\ -0.0055\end{array}\right]$
	$v_i$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.0892\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-0.0892\\ 0\\ 0.4250\end{array}\right]$	$\left[\begin{array}{c}-0.0892\\ 0\\ 0.8173\end{array}\right]$	$\left[\begin{array}{c}-0.1091\\ 0.8173\\ 0\end{array}\right]$	$\left[\begin{array}{c}0.0055\\ 0\\ 0.8173\end{array}\right]$	$\left[\begin{array}{c}0\\ -0.0055\\ -0.1915\end{array}\right]$
output	${\widehat{x}}_i$	×	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$	×
	${}^{i-1}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$	$\left[\begin{array}{c}0\\ 0\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.4250\\ 0.1358\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.0161\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ -0.0055\end{array}\right]$
	${}^{i}t_i$		$\left[\begin{array}{c}0\\ 0\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0\\ 0.1358\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.4250\\ 0.0161\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ 0.0892\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1091\\ -0.0055\end{array}\right]$	$\left[\begin{array}{c}0.8173\\ 0.1915\\ -0.0055\end{array}\right]$
	${\alpha }_i$		0	${\displaystyle \frac{\pi }{2}}$	0	0	${\displaystyle \frac{\pi }{2}}$	${\displaystyle \frac{\pi }{2}}$
	$a_i$		0	0	$0.4250$	$0.3923$	0	0
	$d_{i0}$		$0.0892$	$0.1358$	$-0.1197$	$0.0930$	$0.0946$	$0.0823$
	${\theta }_{i0}$		$\pi$	$\pi$	0	$\pi$	$\pi$	${\displaystyle \frac{\pi }{2}}$

Table 14. Relations between adjacent joint axes computed from the UR5 model.

	b/w 0 and 1	1 and 2	2 and 3	3 and 4
relation	collinear	intersected	distant	distant
	4 and 5	5 and 6	6 and 7
relation	intersected	intersected	intersected

According to the above selection, the MDH can be obtained. As a result, a pair of input and output data for all joints are listed in Table 13 and denoted on the right side of Figure 10.

6. Conclusions

This paper has presented how to extract the MDH parameters of single-branched robotic manipulators using the line geometry, ultimately, for kinematic modeling. The extracted MDH parameters could be used to define the adjacent transformation between the coordinate frames while finding out the exponential coordinates, joint twists, and joint matrices derived from the MDH parameters. The line geometry played core roles in extracting the MDH parameters based on the relation between line and points, the relation between two lines, a common perpendicular line, and the feet of a common perpendicular line, which are concatenated into the line geometry block. Also, it was important to classify how two adjacent lines are located relative to each other such as collinear, distant parallel, intersected, and skewed. Finally, the MDH extraction method was summarized in the algorithm to yield four parameters such as link twist, link length, joint offset distance, and joint offset angle. By combining parts of MDH parameters into the generalized joint variables, forward kinematics could be completed. The completeness of the proposed algorithm was verified through the conventional SCARA robot and three different commercial Indy7, KUKA LBR iiwa, and UR5 robots. Although the kinematic modeling using the MDH parameters was not new, the proposed algorithm was able to overcome the disadvantage that the MDH parameters are differently defined by user-defined coordinate frames, because the line geometry provides a unique and systematic method.

Appendix B.1. Deviation of Equation (11)

This derivation shows the step-by-step procedure to obtain the closest point $p^{\perp }$:

$$\begin{array}{cc}\hfill p^{\perp }& =p-(p·\widehat{z})\widehat{z}\hfill \end{array}$$

(A1a)

$$\begin{array}{cc}\hfill & =(\widehat{z}·\widehat{z})p-(\widehat{z}·p) \widehat{z} since \widehat{z} isaunitvector\hfill \\ \hfill & =\widehat{z}\times (p\times \widehat{z}) using a\times (b\times c)=(a·c)b-(a·b)c\hfill \end{array}$$

(A1b)

$$\begin{array}{cc}\hfill & =\widehat{z}\times v,\hfill \end{array}$$

(A1c)

Appendix B.2. Deviation of Equation (13)

This derivation shows the step-by-step procedure to obtain the closest point $t^{\perp }$ from an arbitrary point t:

$$\begin{array}{cc}\hfill t^{\perp }& =p-((p-t)·\widehat{z})\widehat{z}\hfill \end{array}$$

(A2a)

$$\begin{array}{cc}\hfill & =t+(\widehat{z}·\widehat{z})(p-t)-((p-t)·\widehat{z})\widehat{z}\hfill \end{array}$$

(A2b)

$$\begin{array}{cc}\hfill & =t+\widehat{z}\times ((p-t)\times \widehat{z})\hfill \end{array}$$

(A2c)

$$\begin{array}{cc}\hfill & =t+\widehat{z}\times v_t,\hfill \end{array}$$

(A2d)

Appendix B.3. Deviation of Equation (16)

This derivation shows the procedure to calculate the moment vector $v^{\perp }$ of the common perpendicular line connecting two lines $L_1$ and $L_2$:

$$\begin{array}{cc}\hfill L_1\ast L_2& ={\widehat{z}}_1·v_2+{\widehat{z}}_2·v_1\hfill \\ \hfill & ={\widehat{z}}_1·(v_{21}+t_1\times {\widehat{z}}_2)+{\widehat{z}}_2·v_1 using a·(b\times c)=(a\times b)·c\hfill \end{array}$$

(A3a)

$$\begin{array}{cc}\hfill & ={\widehat{z}}_1·v_{21}+({\widehat{z}}_1\times (t_1-p_1))·{\widehat{z}}_2\hfill \end{array}$$

(A3b)

$$\begin{array}{cc}\hfill & ={\widehat{z}}_1·v_{21}\hfill \end{array}$$

(A3c)

$$\begin{array}{cc}\hfill & =\parallel {\widehat{z}}_1\parallel \parallel v_{21}\parallel cos\left(\alpha +{\displaystyle \frac{\pi }{2}}\right)\hfill \end{array}$$

(A3d)

$$\begin{array}{cc}\hfill & =-\parallel v_{21}\parallel sin\alpha ,\hfill \end{array}$$

(A3e)

Appendix B.4. Deviation of Equation (20)

This derivation shows the procedure to calculate the moment vector $v^{\perp }$ of the common perpendicular line connecting two lines $L_1$ and $L_2$:

$$\begin{array}{cc}\hfill v^{\perp }& =t_2\times {\widehat{z}}^{\perp }\hfill \\ \hfill & ={\displaystyle \frac{t_2\times \left({\widehat{z}}_1\times {\widehat{z}}_2\right)}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}\mathrm{using} a\times (b\times c)=(a·c)b-(a·b)c\hfill \\ \hfill & ={\displaystyle \frac{\left(t_2·{\widehat{z}}_2\right){\widehat{z}}_1-\left(t_2·{\widehat{z}}_1\right){\widehat{z}}_2}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}\hfill \\ \hfill & ={\displaystyle \frac{\left(\left(t_1+t_2-t_1\right)·{\widehat{z}}_2\right){\widehat{z}}_1-\left(t_2·{\widehat{z}}_1\right){\widehat{z}}_2}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}\because \left(t_2-t_1\right)\perp {\widehat{z}}_2\hfill \\ \hfill & ={\displaystyle \frac{\left({\widehat{z}}_2·t_1\right){\widehat{z}}_1-\left({\widehat{z}}_1·t_2\right){\widehat{z}}_2}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}\mathrm{using} (a·b)c=(a·c)b-a\times (b\times c)\hfill \\ \hfill & ={\displaystyle \frac{{\widehat{z}}_1\times v_2-{\widehat{z}}_2\times v_1}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}+{\displaystyle \frac{{\widehat{z}}_1·{\widehat{z}}_2}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}\left(t_1-t_2\right)\mathrm{using} t_2-t_1=a\widehat{n}=-{\displaystyle \frac{{\widehat{z}}_1·v_2+{\widehat{z}}_2·v_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\widehat{n}\hfill \\ \hfill =& {\displaystyle \frac{{\widehat{z}}_1\times v_2-{\widehat{z}}_2\times v_1}{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}}+{\displaystyle \frac{\left({\widehat{z}}_1·{\widehat{z}}_2\right)({\widehat{z}}_1·v_2+{\widehat{z}}_2·v_1)}{{∥{\widehat{z}}_1\times {\widehat{z}}_2∥}^2}}\widehat{n}.\hfill \end{array}$$

(A4)

Appendix B.5. Deviation of Equation (22)

This derivation shows how the scalar projection $t_2·\widehat{n}$ of the intersection point $t_2$ onto the vector $\widehat{n}$ is computed:

$$\begin{array}{cc}\hfill t_2& =(t_2·{\widehat{z}}_1){\widehat{z}}_1+(t_2·\widehat{u})\widehat{u}+(t_2·\widehat{n})\widehat{n}.\hfill \end{array}$$

(A5)

For the third term ($t_2·\widehat{n}$) of the right-hand side of Equation (21), since we can observe the following

$$\begin{array}{cc}\hfill v_2·{\widehat{z}}_1& =(t_2\times {\widehat{z}}_2)·{\widehat{z}}_1 \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} (a\times b)·c=a·(b\times c)\hfill \\ \hfill & =-t_2·({\widehat{z}}_1\times {\widehat{z}}_2) \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} \widehat{n}={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\hfill \\ \hfill & =-(t_2·\widehat{n})\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel ,\hfill \end{array}$$

then we have

$$\begin{array}{cc}\hfill \therefore t_2·\widehat{n}& =-{\displaystyle \frac{v_2·{\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}.\hfill \end{array}$$

(A6)

Appendix B.6. Deviation of Equation (23)

This derivation shows the procedure to calculate the projection of the intersection point $t_2$ onto the vector $\widehat{u}$:

$$\begin{array}{cc}\hfill t_2·\widehat{u}& =t_2·(\widehat{n}\times {\widehat{z}}_1) \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} a·(b\times c)=(a\times b)·c\hfill \\ \hfill & =(t_2\times \widehat{n})·{\widehat{z}}_1 \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} \widehat{n}={\widehat{z}}^{\perp }={\displaystyle \frac{{\widehat{z}}_1\times {\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\hfill \\ \hfill & =(t_2\times {\widehat{z}}^{\perp })·{\widehat{z}}_1 \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} v^{\perp }=t_2\times {\widehat{z}}^{\perp }\hfill \\ \hfill & =v^{\perp }·{\widehat{z}}_1\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{E}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \left(20\right)\hfill \\ \hfill & =-{\displaystyle \frac{({\widehat{z}}_2\times v_1)·{\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\hfill \\ \hfill & =-{\displaystyle \frac{v_1·({\widehat{z}}_1\times {\widehat{z}}_2)}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\hfill \\ \hfill \therefore & =-v_1·\widehat{n}.\hfill \end{array}$$

(A7)

Appendix B.7. Deviation of Equation (25)

This derivation shows the procedure to calculate the scalar projection $t_2·{\widehat{z}}_1$:

$$\begin{array}{cc}\hfill t_2·{\widehat{z}}_1& ={\displaystyle \frac{(v_2·({\widehat{z}}_1\times {\widehat{z}}_2))-({\widehat{z}}_1·{\widehat{z}}_2)(v_1·({\widehat{z}}_1\times {\widehat{z}}_2))}{1-{({\widehat{z}}_1·{\widehat{z}}_2)}^2}}\hfill \\ \hfill & ={\displaystyle \frac{(v_2·({\widehat{z}}_1\times {\widehat{z}}_2))-({\widehat{z}}_1·{\widehat{z}}_2)(v_1·({\widehat{z}}_1\times {\widehat{z}}_2))}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}}\hfill \\ \hfill \therefore & ={\displaystyle \frac{(v_2-({\widehat{z}}_1·{\widehat{z}}_2)v_1)·\widehat{n}}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}.\hfill \end{array}$$

(A8)

Appendix B.8. Deviation of Equation (26)

This derivation shows the procedure to obtain the explicit expression for intersection point $t_2$:

$$\begin{array}{cc}\hfill t_2& =(t_2·{\widehat{z}}_1){\widehat{z}}_1+(t_2·\widehat{u})\widehat{u}+(t_2·\widehat{n})\widehat{n}\hfill \\ \hfill & ={\displaystyle \frac{(v_2-({\widehat{z}}_1·{\widehat{z}}_2)v_1)·\widehat{n}}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}{\widehat{z}}_1-(v_1·\widehat{n})\widehat{u}-{\displaystyle \frac{v_2·{\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\widehat{n}\hfill \\ \hfill & ={\displaystyle \frac{(v_2·\widehat{n}){\widehat{z}}_1-(v_2·{\widehat{z}}_1)\widehat{n}}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}-(v_1·\widehat{n})\left({\displaystyle \frac{({\widehat{z}}_1·{\widehat{z}}_2){\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}+(\widehat{n}\times {\widehat{z}}_1)\right)\hfill \\ \hfill & ={\displaystyle \frac{v_2\times ({\widehat{z}}_1\times \widehat{n})}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}-(v_1·\widehat{n})\left({\displaystyle \frac{({\widehat{z}}_1·{\widehat{z}}_2){\widehat{z}}_1+({\widehat{z}}_1\times {\widehat{z}}_2)\times {\widehat{z}}_1}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2\parallel }}\right)\hfill \\ \hfill \therefore & ={\displaystyle \frac{v_2\times ({\widehat{z}}_1\times ({\widehat{z}}_1\times {\widehat{z}}_2))-(v_1·({\widehat{z}}_1\times {\widehat{z}}_2)){\widehat{z}}_2}{\parallel {\widehat{z}}_1\times {\widehat{z}}_2{\parallel }^2}}.\hfill \end{array}$$

(A9)