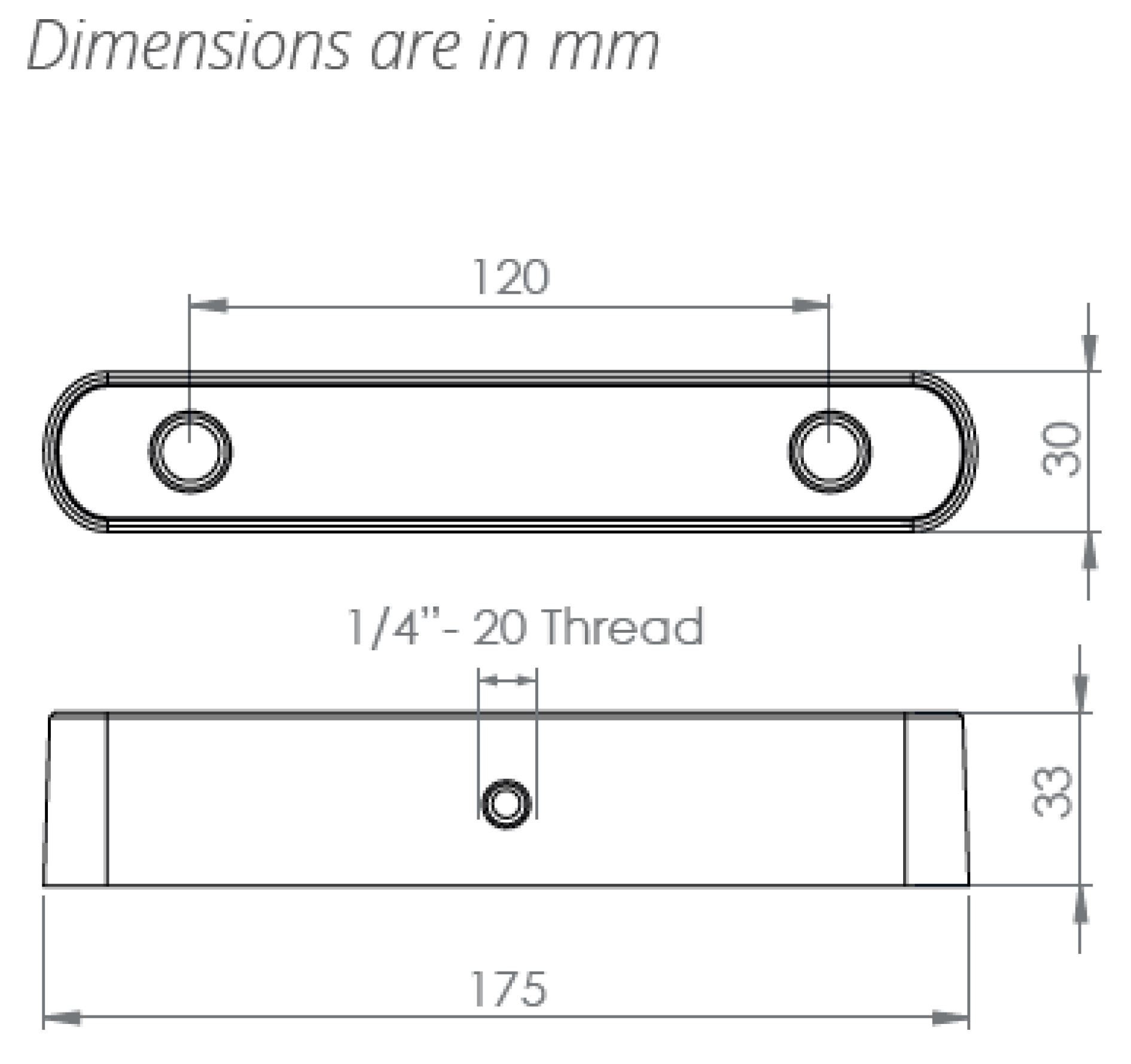
1. Introduction
Determining the accurate pose of the camera is a fundamental problem in robot manipulations, as it provides the spatial transformation needed to map 3D world points to 2D image coordinates. The task involving camera pose estimation is essential for various applications, such as augmented reality [
1], 3D reconstruction [
2], SLAM [
3], and autonomous navigation [
4]. This becomes especially critical when robots operate in unstructured, fast-changing, and dynamic environments, performing tasks such as human–robot interaction, accident recognition and avoidance, and eye-in-hand visual servoing. In such scenarios, accurate camera pose estimation ensures that visual data are readily available for effective robotic control [
5].
A classic approach to estimating the pose of a calibrated camera is solving the Perspective-n-Point (PnP) problem [
6], which establishes a mathematical relationship between a set of 3D points in the world and their corresponding 2D projections in an image. To uniquely determine the pose of a monocular camera in space, there exists the Perspective-4-Point (P4P) problem, where exactly four known 3D points and their corresponding 2D image projections are used. Bujnak et al. [
7] generalize four solutions for the P3P problem while giving a single unique solution for the P4P problem in a fully calibrated camera scenario. To increase accuracy, modern PnP approaches consider more than three 2D–3D correspondences. Among PnP solutions, the Efficient PnP method (EPnP) finds the optimal estimation of pose from a linear system that expresses each reference point as a weighted sum of four virtual control points [
8]. Another advanced approach, Sparse Quadratic PnP (SQPnP), formulates the problem as a sparse quadratic optimization, achieving enhanced accuracy by minimizing a sparse cost function [
9].
In recent years, many other methods have been developed to show improved accuracy over PnP-based methods. For instance, Alkhatib et al. [
10] utilize Structure from Motion (SfM) to estimate a camera’s pose by extracting and matching key features across various images taken from different viewpoints to establish correspondences. Moreover, Wang et al. [
11] introduce visual odometry into the camera’s pose estimations based on the movement between consecutive frames. In addition, recent advancements in deep learning have led to the development of models, such as Convolutional Neural Networks (CNNs), specifically tailored for camera pose estimation [
12,
13,
14]. However, these advanced methods often come with significant computational costs, requiring multiple images from different perspectives for accurate estimation. In contrast, PnP-based approaches offer a balance between accuracy and efficiency, as they can estimate camera pose from a single image, making them highly suitable for real-time applications such as navigation and scene understanding.
In image-based visual servoing (IBVS) [
15], the primary goal is to control a robot’s motion using visual feedback. Accurate real-time camera pose estimation is crucial for making informed control decisions, particularly in eye-in-hand (EIH) configurations [
16,
17], where a camera is mounted directly on a robot manipulator. In this setup, robot motion directly induces camera motion, making precise pose estimation essential. Due to its computational efficiency, PnP-based approaches remain widely applied in real-world IBVS tasks [
18,
19,
20]. The PnP process begins by establishing correspondences between 3D feature points and their 2D projections in the camera image. The PnP algorithm then computes the camera pose from these correspondences, translating the geometric relationship into a format that the IBVS controller can use. By detecting spatial discrepancies between the current and desired camera poses, the robot can adjust its movements accordingly.
However, PnP-based IBVS presents challenges for visual control in robotics. One key issue is that IBVS often results in an overdetermined system, where the number of visual features exceeds the number of joint variables available for adjustment. For example, at least four 2D–3D correspondences are needed for a unique pose solution [
6], but a camera’s full six-degree-of-freedom (6-DOF) pose means that a 6-DOF robot may need to align itself with eight or more observed features. In traditional IBVS [
15], the interaction matrix (or image Jacobian) defines the relationship between feature changes and joint velocities. When the system is overdetermined, this matrix contains more constraints than joint variables, leading to redundant information. Research [
15] suggests that this redundancy may cause the camera to converge to local minima, failing to reach the desired pose. Although local asymptotic stability is always ensured in IBVS, global asymptotic stability cannot be guaranteed when the system is overdetermined.
In recent research on visual servoing, various methods have been developed to address the limitations of traditional Image-Based Visual Servoing (IBVS), particularly the issue of local minima due to system overdetermination. Gans et al. [
21] proposed a hybrid switched-system control system, which alternates between IBVS and Position-Based Visual Servoing (PBVS) modes based on Lyapunov functions. This method offers formal local stability and effectively prevents loss of visual features or divergence from the goal. However, it may suffer from discontinuities near switching surfaces and is limited by local convergence guarantees. Chaumette et al. [
22] developed a 2½ D visual servoing method, which integrates both image and pose features into a block-triangular Jacobian structure, allowing for smoother and more predictable camera trajectories while avoiding singularities. Yet, it is sensitive to depth estimation errors and requires careful selection of hybrid features. Roque et al. [
23] introduced an MPC-based IBVS framework for quadrotors, which leverages model predictive control to handle under-actuation while tracking IBVS commands. It provides formal stability guarantees and supports constraint handling in real time, but its reliance on linearization around hover and the absence of direct coupling with visual dynamics limit its generality and precision in highly nonlinear settings.
While these methods achieve significant improvements in most scenarios, they also introduce computational challenges compared to traditional IBVS. The switched control method requires different control strategies tailored to specific dynamics, increasing the complexity of the overall control architecture [
24]. The 2-1/2-D visual servoing method demands real-time processing of both visual and positional data, which can impose significant computational loads and limit performance in dynamic environments [
25]. MPC approaches introduce additional computational overhead by requiring complex optimization at every time step, making real-time implementation costly [
26].
In this paper, we focus on the PnP framework for determining and controlling the pose of a stereo camera within an image-based visual servoing (IBVS) architecture. In traditional IBVS, depth information between objects and the image plane is crucial for developing the interaction matrix. However, with a monocular camera, depth can only be estimated or approximated using various algorithms [
15], and inaccurate depth estimation may lead to system instability. In contrast, a stereo camera system can directly measure depth through disparity between two image planes, enhancing system stability.
A key novelty of this paper is providing systematic proof that stereo camera pose determination in IBVS can be formulated as a Perspective-3-Point (P3P) problem, which, to the best of our knowledge, has not been explored in previous research. Since three corresponding points, totaling nine coordinates, are used to control the six DoF camera poses, the IBVS control system for a stereo camera is overdetermined, leading to the potential issue of local minima during control maneuvers. While existing approaches can effectively address local minima, they often introduce excessive computational overhead, making them impractical for high-speed real-world applications.
To address this challenge, we propose a feedforward–feedback control architecture. The feedback component follows a cascaded control loop based on the traditional IBVS framework [
15], where the inner loop handles robot joint rotation, and the outer loop generates joint angle targets based on visual data. One key improvement in this work is the incorporation of both kinematics and dynamics during the model development stage. Enhancing model fidelity in the control design improves pose estimation precision and enhances system stability, particularly for high-speed tasks. Both control loops are designed using Youla parameterization [
27], a robust control technique that enhances resistance to external disturbances. The feedforward controller takes target joint configurations, which are associated with the desired camera pose as inputs, ensuring a fast system response while avoiding local minima traps. Simulation results presented in this paper demonstrate that the proposed control system effectively moves the stereo camera to its desired pose accurately and efficiently, making it well-suited for high-speed robotic applications.
3. Proof of P3P for the Stereo Camera System
Given its intrinsic parameters and a set of n correspondences between its 3D points and 2D projections to determine the camera’s pose is known as the perspective-n-point (PnP) problem. This well-known work [
7] has proved that at least four correspondences are required to uniquely determine the pose of a monocular camera, a situation referred to as the P4P problem.
To illustrate, consider the P3P case for a monocular camera (
Figure 2). Let points A, B, and C exist in space, with
,
and
representing different perspective centers. The angles ∠AOB, ∠AOC and ∠BOC remain the same across all three perspectives. Given a fixed focal length, the image coordinates of points A, B, and C will be identical when observed from these three perspectives. In other words, it is impossible to uniquely identify the camera’s pose based solely on the image coordinates of three points.
The PnP problem with a stereo camera has not been thoroughly addressed in prior research. A stereo camera can detect three image coordinates of a 3D point in space. This paper proposes that a complete solution to the PnP problem for a stereo camera can be framed as a P3P problem. Below is the complete proof of this proposition.
Proof. For a stereo system, if all intrinsic parameters are fixed and given, we can readily compute the 3D coordinates of an object point given the image coordinates of that point. This provides a unique mapping from the image coordinates of a point to its corresponding 3D coordinates in a Cartesian frame. The orientation and position of the camera system uniquely define the origin and axis orientations of this Cartesian coordinate system in space. Consequently, PnP problem can be framed as follows: given n points with their 3D coordinates measured in an unknown Cartesian coordinate system in space, what is the minimum number n required to accurately determine the position and orientation of the 3D Cartesian coordinate frame established in that space?
- (1)
P1P problem with the stereo camera:
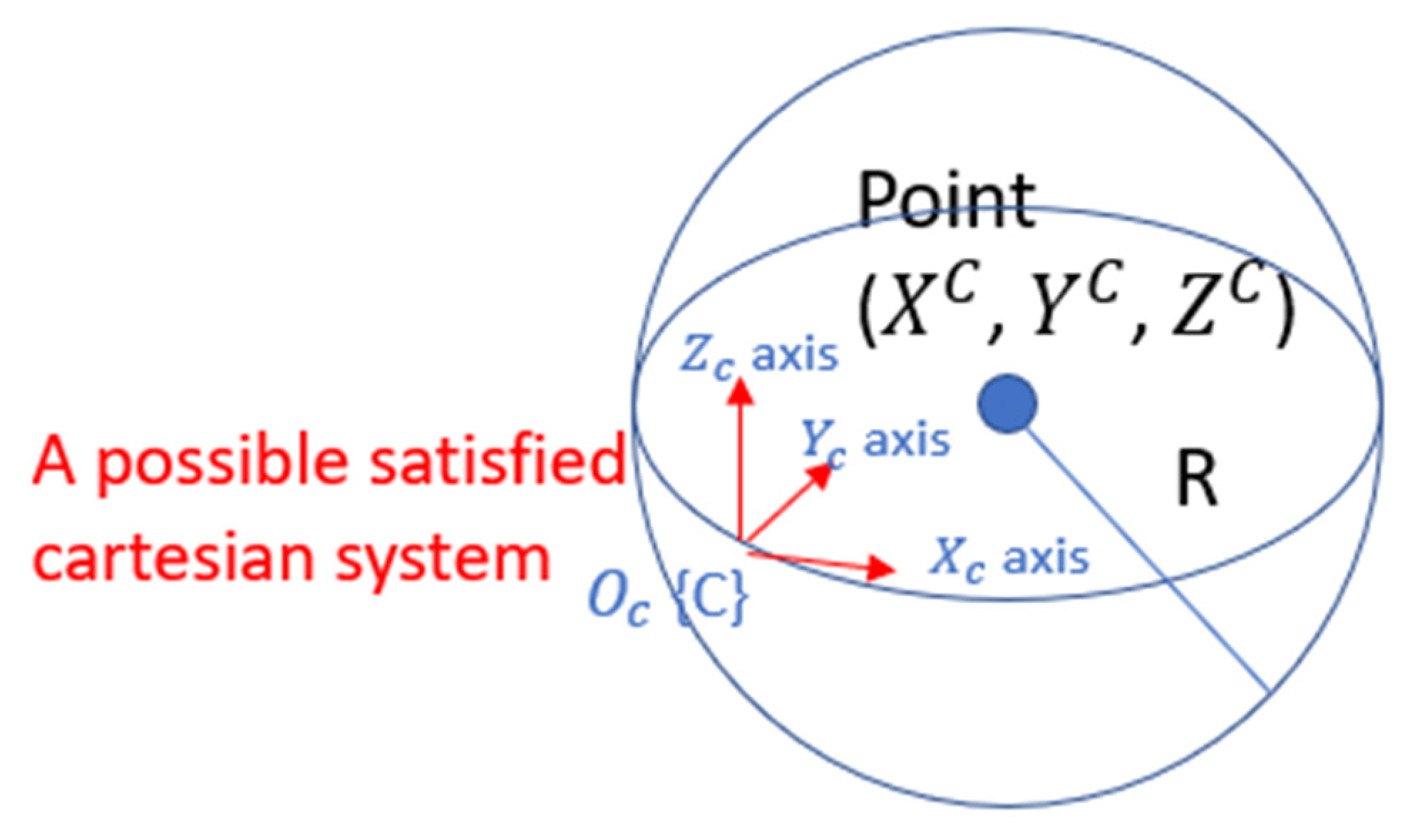
If we know the coordinates of a single point in space, defined by a 3D Cartesian coordinate system, an infinite number of corresponding coordinate systems can be established. Any such coordinate system can have its origin placed on the surface of a sphere centered at this point, with a radius
, where
are the coordinates measured by the Cartesian system (see
Figure 3).
- (2)
P2P problem with the stereo camera:
When the coordinates of two points in space are known, an infinite number of corresponding coordinate systems can be established. Any valid coordinate system can have its origin positioned on a circle centered at point
O with a radius
as illustrated in
Figure 4. This circle is constrained by the triangle formed by points
,
, and
, where the sides of the triangle are defined by the lengths
and
. Specifically,
The radius of the circle R corresponds to the height of the base D of the triangle. The center of the circle O is located at the intersection of the height and the base.
- (3)
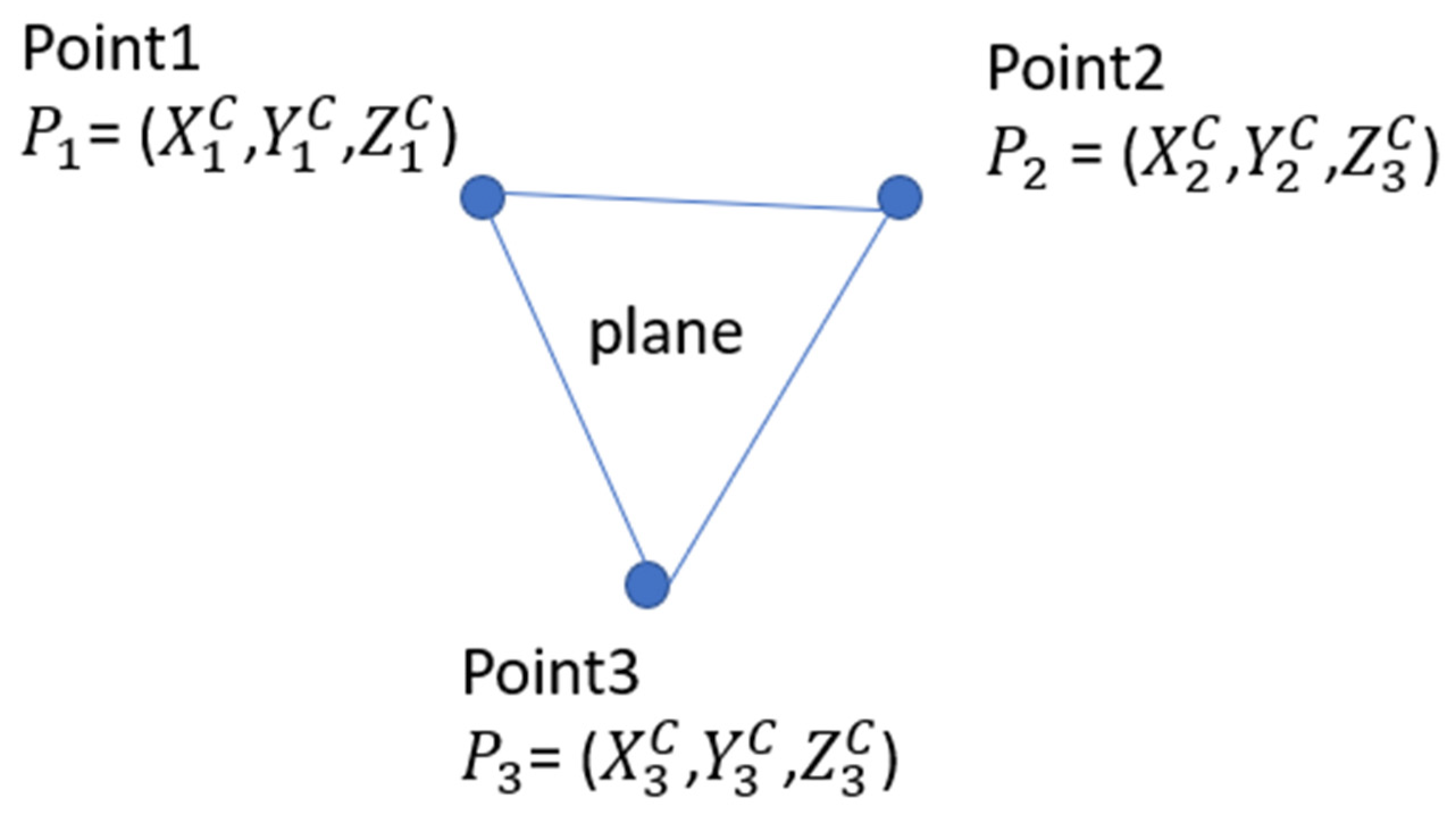
P3P problem with the stereo camera:
When three points in space are known, and the lines connecting these points are not collinear, we can uniquely establish one coordinate system. As illustrated in the
Figure 5 below, three non-collinear points define a plane in space, which has a uniquely defined normal unit vector
. Given the coordinates of the three points, we can calculate vectors as follows: the vector
= (
), and the vector
= (
). The unit vector
which is perpendicular to the plane formed by these three points, can be expressed as:
Here, × denotes the cross product.
The angles between
and XYZ axes of the coordinate system can be expressed as follows:
where
and
are the angles between
and the unit vectors in the X, Y, and Z directions, denoted as
,
and
, respectively. Therefore, with the direction
fixed in space, the orientations of each axis of the coordinate system can be computed uniquely.
According to the P1P problem, the origin of the coordinate system must lie on the surface of a sphere centered at
with radius
as depicted in
Figure 3. Each coordinate system established with a different origin point on the surface of this sphere results in a unique configuration of the axis orientations. Therefore, as the orientations of the axes are defined in space, the position of the frame (or the position of the origin) is also uniquely defined.
In conclusion, the P3P problem is sufficient to solve the PnP problem for a stereo camera system.
Proof concluded □
This proposition indicates that to uniquely determine the full six DoFs of the stereo camera, at least three points (or nine 2D features) are required to match in the image-based visual servoing control.
4. Model Development
4.1. Stereo Camera Model
Depth between the objects to the camera plane is either approximated or estimated in the IBVS for generating the interaction matrix [
15]. Using a stereo camera system in IBVS eliminates the inaccuracies associated with monocular depth estimation, as it directly measures depth by leveraging the disparity between the left and right images.
The stereo camera model is illustrated in
Figure 6. A stereo camera consists of two lenses separated by a fixed baseline
b. Each lens has a focal length
(measured in mm) which is the distance from the image plane to the focal point. Assuming the camera is calibrated, the intrinsic parameters:
b,
is accurately estimated. A scene point
is measured in the 3D coordinate frame {C} centered at the middle of the baseline with its coordinates as
. The stereo camera model maps the 3D coordinates of this point to its 2D coordinates projected on the left and right image plane as
and
, respectively. The full camera projection map, incorporating both intrinsic and extrinsic parameters, is given by:
where
are the image coordinates of the point and
are the 3D coordinates measured in the camera frame {
C}.
is the scale factor that ensures correct projection between 2D and 3D features.
is the intrinsic matrix with a size of 3 × 3, and the mathematical expression is presented as:
where
is the skew factor, which represents the angle between the image axes (
u and
v axis).
and
are coordinates offsets in image planes.
In Equation (5),
R is the rotational matrix from camera frame {C} to each image coordinate frame, and
T is the translation matrix from camera frame {C} to each camera lens center. Since there is no rotation between the camera frame {C} and image frames but only a translation along the
axis occurs, the transformation matrices for the left and right image planes are expressed as:
Assume the
and
axis are perfectly perpendicular (take
k = 0), and there are no offsets in the image coordinates (take
) for both lens. Also, set factor
accounts for perspective depth scaling. The projection equations for the left and right image planes can be rewritten in homogeneous coordinates as:
Equations (9) and (10) establish the mathematical relationship between the 3D coordinates of a point in the camera frame {C} and its 2D projections on the left and right image planes. The pixel value along the
-axis remains the same for both images. As a result, a scene point’s 3D coordinates can be mapped to a set of three image coordinates in the stereo camera system, expressed as:
The mapping function is nonlinear and depends on the stereo camera parameters , specifically b, and .
4.2. Robot Manipulator Forward Kinematic Model
A widely used method for defining and generating reference frames in robotic applications is the Denavit–Hartenberg (D-H) convention [
29]. In this approach, each robotic link is associated with a Cartesian coordinate frame
. According to the D-H convention, the homogeneous transformation matrix
, which represents the transformation from frame
to frame
, can be decomposed into a sequence of four fundamental transformations:
The parameters
,
,
and
define the link and joint characteristics of the robot. Here,
is the link length,
is the joint rotational angle,
is the twist angle, and
is the offset between consecutive links. The values for these parameters are determined following the procedure outlined in [
29].
To compute the transformation from the end-effector frame
(denoted as {E}) to the base frame
(denoted as {O}), we multiply the individual transformations along the kinematic chain:
Furthermore, the transformation matrix from the base frame {O} to the end-effector frame {E} can be derived by taking the inverse of
:
If a point
is defined in the base frame, its coordinates in the end-effector frame
can be found using:
Equation (17) describes a coordinates transformation process from the base frame to the end-effector frame.
4.3. Eye-to-Hand Transformation Model
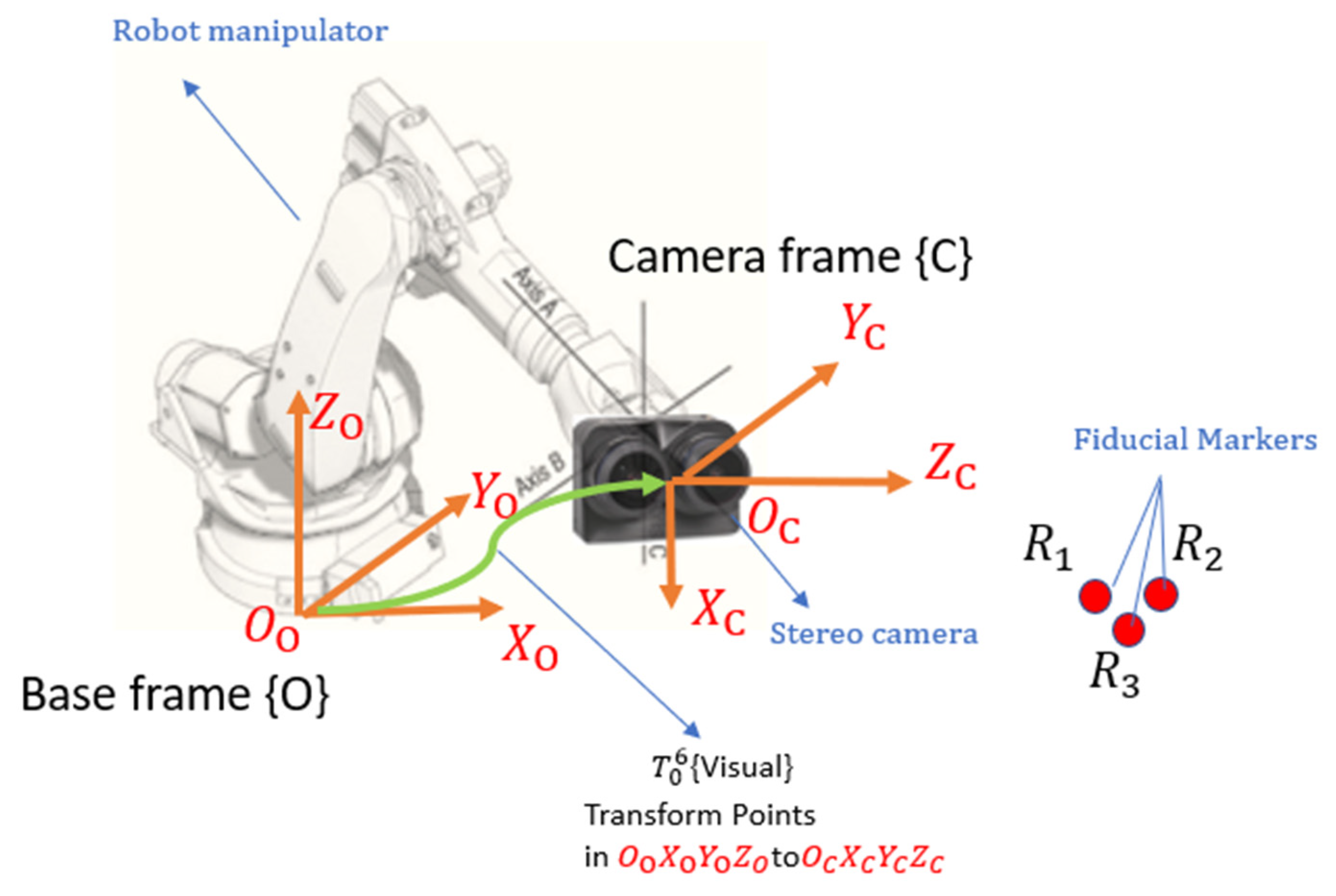
Assuming the camera remains fixed relative to the robot’s end-effector, we introduce a constant transformation matrix that maps points from the end-effector frame {E} to the camera frame {C}. The process of finding the matrix is called Eye-to-Hand Calibration.
In general, the goal is to solve for
, such that:
Here, is transformation of the end-effector between robot poses to pose , and represents the transformation of a fixed object (e.g., a marker) as observed in the camera frame during the same motion.
These transformations are computed as:
where
and
denote the poses of the end-effector at robot configurations
and
, measured in the base frame, as defined in Equation (17).
and
denote the transformations of a marker M observed in the camera frame at the same respective robot poses. Further details are provided in
Appendix C.
Various methods have been proposed to accurately estimate using multiple pairs. While calibration techniques are not the primary focus of this paper, several recent approaches are summarized for reference:
Kim et al. [
30] presented a technique for eye-on-hand configurations, deriving a closed-form solution for Equation (18) using two robot movements. Evangelista et al. [
31] introduced a unified iterative method based on reprojection error minimization, applicable to both eye-on-base and eye-in-hand setups. This approach does not require explicit camera pose estimation and demonstrates improved accuracy compared to traditional methods. Strobl and Hirzinger [
32] proposed an optimal calibration method for eye-in-hand systems, utilizing a novel metric on SE(3) and an error model for nonlinear optimization. This method adapts to system precision characteristics and performs well in Equation (18) formulation.
4.4. Robot-to-Camera Kinematic Model
For a stereo camera system, this camera frame is located at the center of the stereo baseline, as shown in
Figure 6. The coordinates of a point in space, measured in the base frame, can then be expressed in the camera frame as:
Equation (21) describes how a given 3D point in the base frame
= [
] is mapped to the camera frame
= [
] using transformation:
The mapping function is nonlinear and depends on the current joint angle of robot , robot geometric parameter = [, , |i ϵ 1,2,3,4,5,6], and constant transformation matrix
4.5. Eye-in-Hand Kinematic Model
By combining the stereo camera mapping
from Equation (11) and the robot manipulator mapping
from Equation (22), we define a nonlinear transformation
, which maps any point measured in the base frame {O} to its image coordinates as captured by the stereo camera. This transformation is expressed as:
The Mapping
is nonlinear and depends on variables current joint angles:
and parameters
, which includes stereo camera parameter
, robot geometric parameter
and transformation matrix
. In other words:
4.6. Robot-to-Camera Inverse Kinematic Model
Inverse kinematics determines the joint angles required to achieve a given camera pose relative to the inertial frame. The camera pose in the inertial frame can be expressed as a 4 × 4 matrix:
Here, the vectors , and represent the camera’s directional vectors for Yaw, Pitch, and Roll, respectively, in the base frame {C}. Additionally, the vector denotes the absolute position of the camera center in the base frame {C}.
The camera pose in the camera frame {C} is straightforward as it can be expressed as another 4 × 4 matrix:
The nonlinear inverse kinematics problem involves solving for the joint angles
that satisfy the equation:
where
is the transformation from the end-effector frame to the camera frame, and
represents the transformation from the base frame to the end-effector frame, which is a function of the joint angles
.
The formulas for computing each joint angle are derived from the geometric parameters of the robot. The results of the inverse kinematics calculations for the ABB IRB 4600 elbow manipulator [
33], used for simulations in this paper, are summarized in
Appendix A.
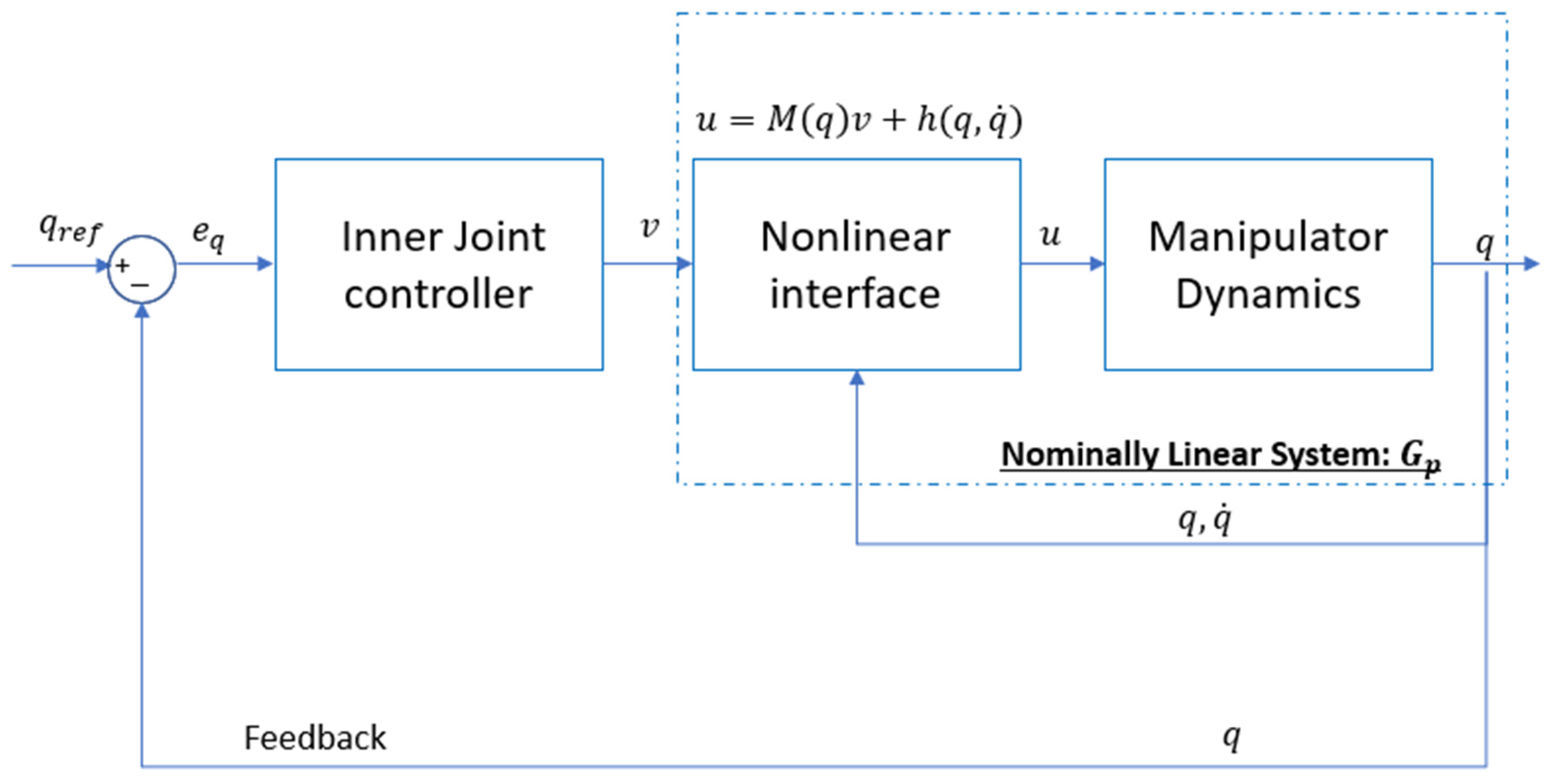
4.7. Robot Dynamic Model
Dynamic models are included in the inner joint control loop, which will be discussed in
Section 6. Without derivation, the dynamic model of a serial of 6-link rigid, non-redundant, fully actuated robot manipulator can be written as [
34]:
where
is the vector of joint positions, and
is the vector of electrical power input from DC motors inside joints,
is the symmetric positive defined matrix,
is the vector of centripetal and Coriolis effects,
is the vector of gravitational torques,
is a diagonal matrix expressing the sum of actuator and gear inertias,
is the damping factor,
is the gear ratio.
5. Control Policy Diagram
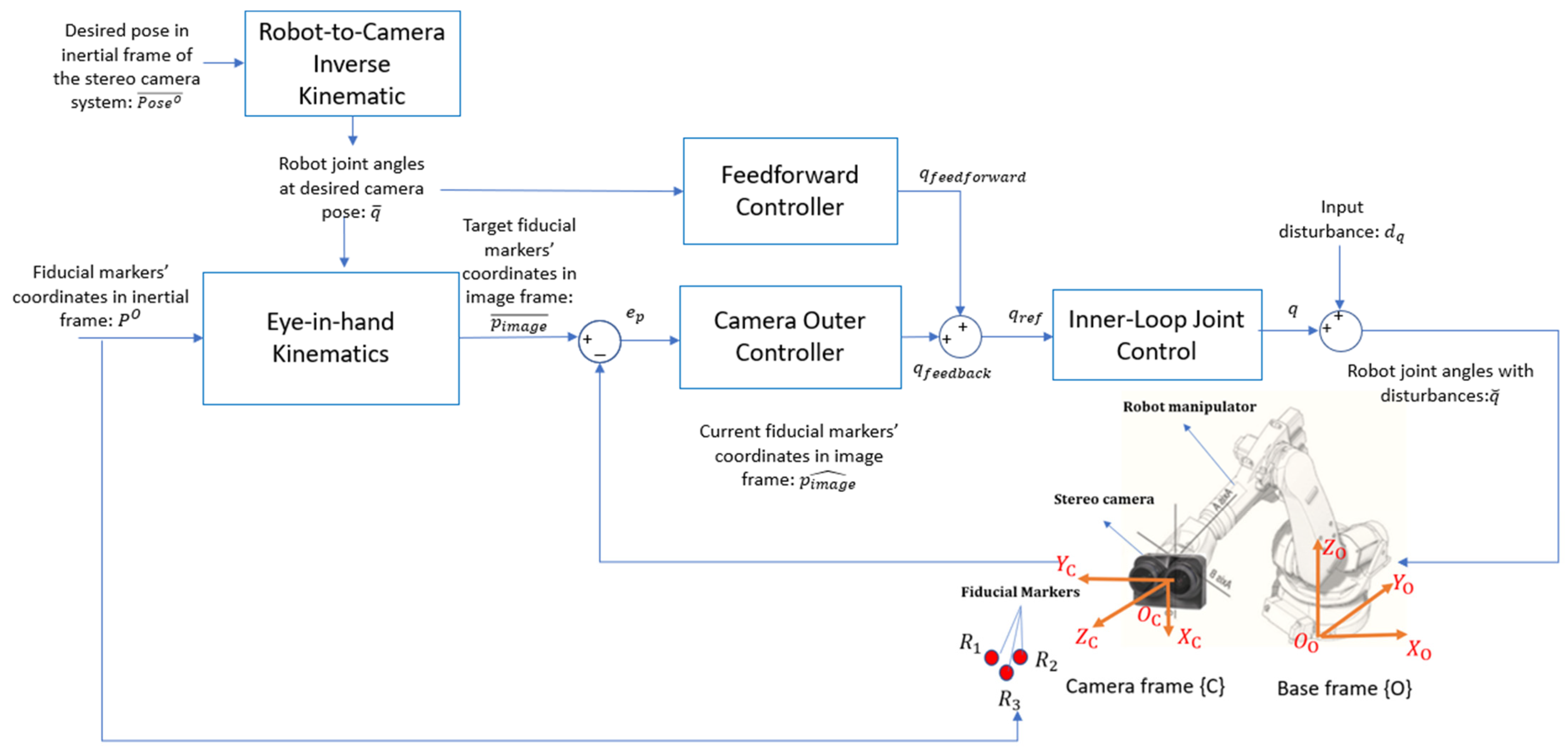
Figure 7 illustrates the overall control system architecture, designed to guide the robot manipulator so that the camera reaches its desired pose,
, in the world space. This architecture follows a similar structure to that used in prior work on tool trajectory control for robotic manipulators [
35]. To facilitate visual servoing, three fiducial markers are placed within the camera’s field of view, with their coordinates in the inertial frame pre-determined and represented as
. Using the robot’s inverse kinematics and the eye-in-hand kinematic model, the expected image coordinates of these fiducial markers, when viewed from the desired camera pose, are computed as
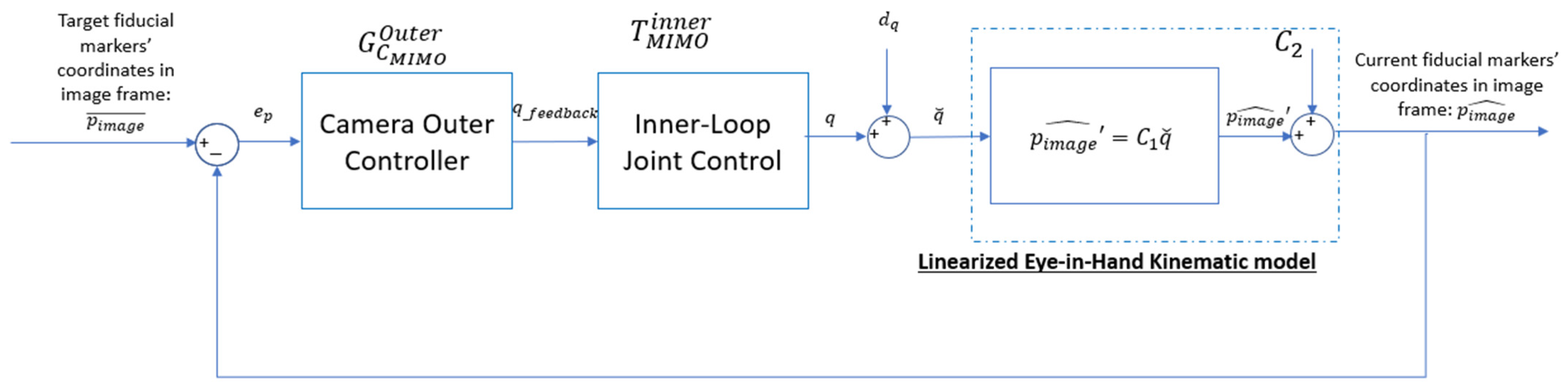
. These computed image coordinates serve as reference targets in the feedback control loop.
The IBVS framework is implemented within a cascaded feedback loop. In the outer control loop, the camera controller processes the visual feedback error, , which represents the difference between the image coordinates of the fiducial points at the current and desired camera poses. Based on this error, the outer loop generates reference joint angles, , to correct the robot’s configuration.
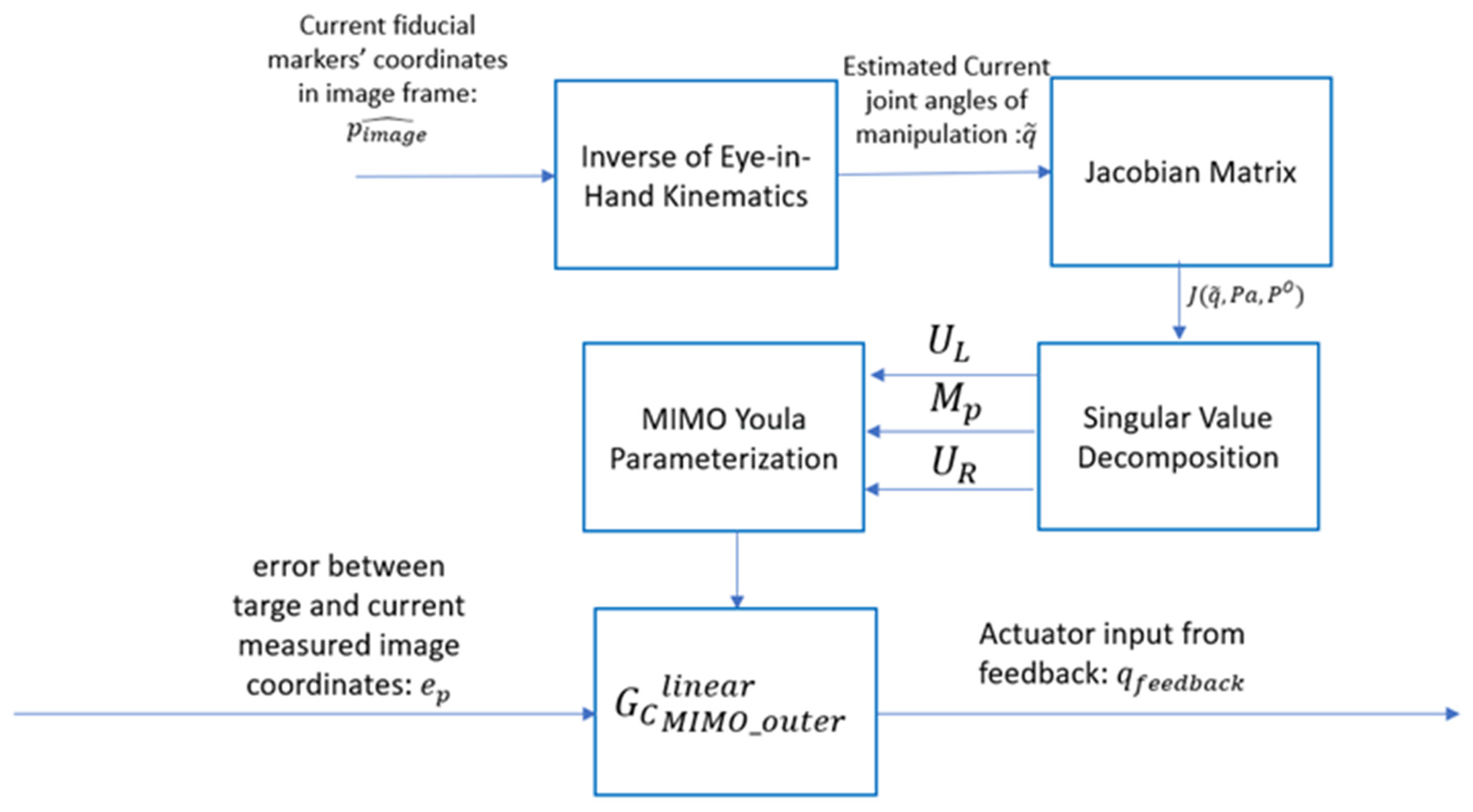
The inner control loop, shown in
Figure 8, incorporates the robot’s dynamic model to regulate the joint angles, ensuring they align with the commanded reference angles,
. However, due to the limitations of low-fidelity and inexpensive joint encoders, as well as inherent dynamic errors such as joint compliance, high-frequency noises and low-frequency model disturbances are introduced into the system. All sources of errors from the joint control loop are collectively modeled as an input disturbance,
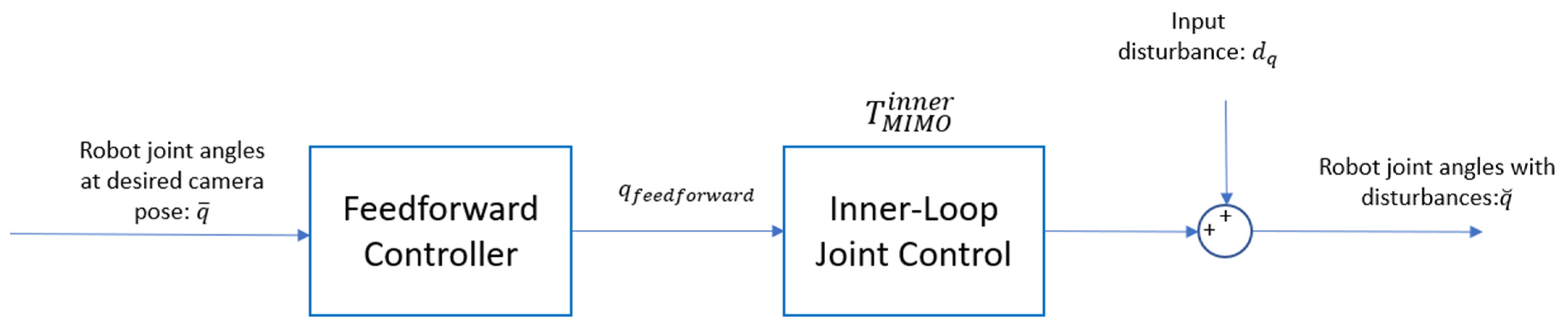
, which affects the outer control loop.
The feedforward control loop operates as an open-loop system, quickly bringing the camera as close as possible to its target pose, despite the presence of input disturbances. The feedforward controller outputs a reference joint angle command, , which is sent to the inner loop to facilitate rapid convergence to the desired configuration.
7. Simulations Results
To evaluate the performance of our controller design, we simulated two scenarios in MATLAB R2024b Simulink using a Zed 2 stereo camera system [
37] and an ABB IRB 4600 elbow robotic manipulator [
33]. All simulations are conducted entirely in Simulink, with hardware-in-the-loop components replaced by their corresponding mathematical models. The specifications for the camera system and robot manipulator are summarized in the tables in the appendix. The camera system performs 2D feature estimation of three virtual points in space, with their coordinates in the inertial frame selected as:
,
,
.
Many camera noise removal algorithms have been proposed and shown to be effective in practical applications, such as spatial filters [
38], wavelet filters [
39], and the image averaging technique [
40]. Among these denoising methods, there is always a tradeoff between computational efficiency and performance. For this paper, we assume that the images captured by the camera have been preprocessed using one of these methods, and the noise was almost perfectly attenuated. In other words, the only remaining disturbances in the system are due to unmodeled joint dynamics, such as compliance and flexibility, which are modeled as input disturbances in the controlled system.
Two scenarios were simulated:
In both scenarios, the camera system starts from an initial pose in the inertial frame, denoted as
, and maneuvers target pose, denoted as
.
Table 1 summarizes the initial and final poses for each scenario, along with the corresponding joint configurations. The results are demonstrated in
Figure 13 and
Figure 14 for scenario 1, and
Figure 15 and
Figure 16 for scenario 2.
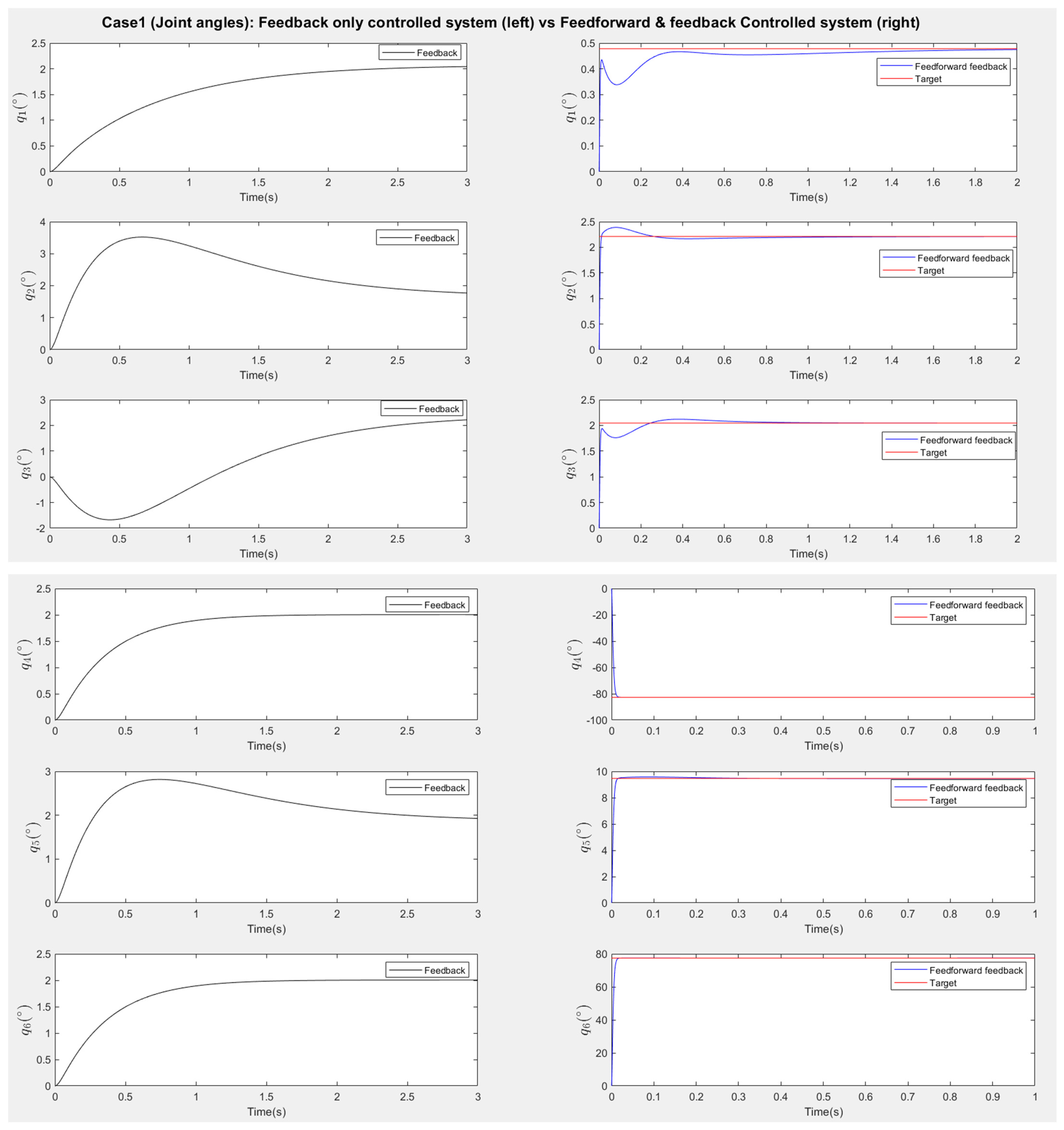
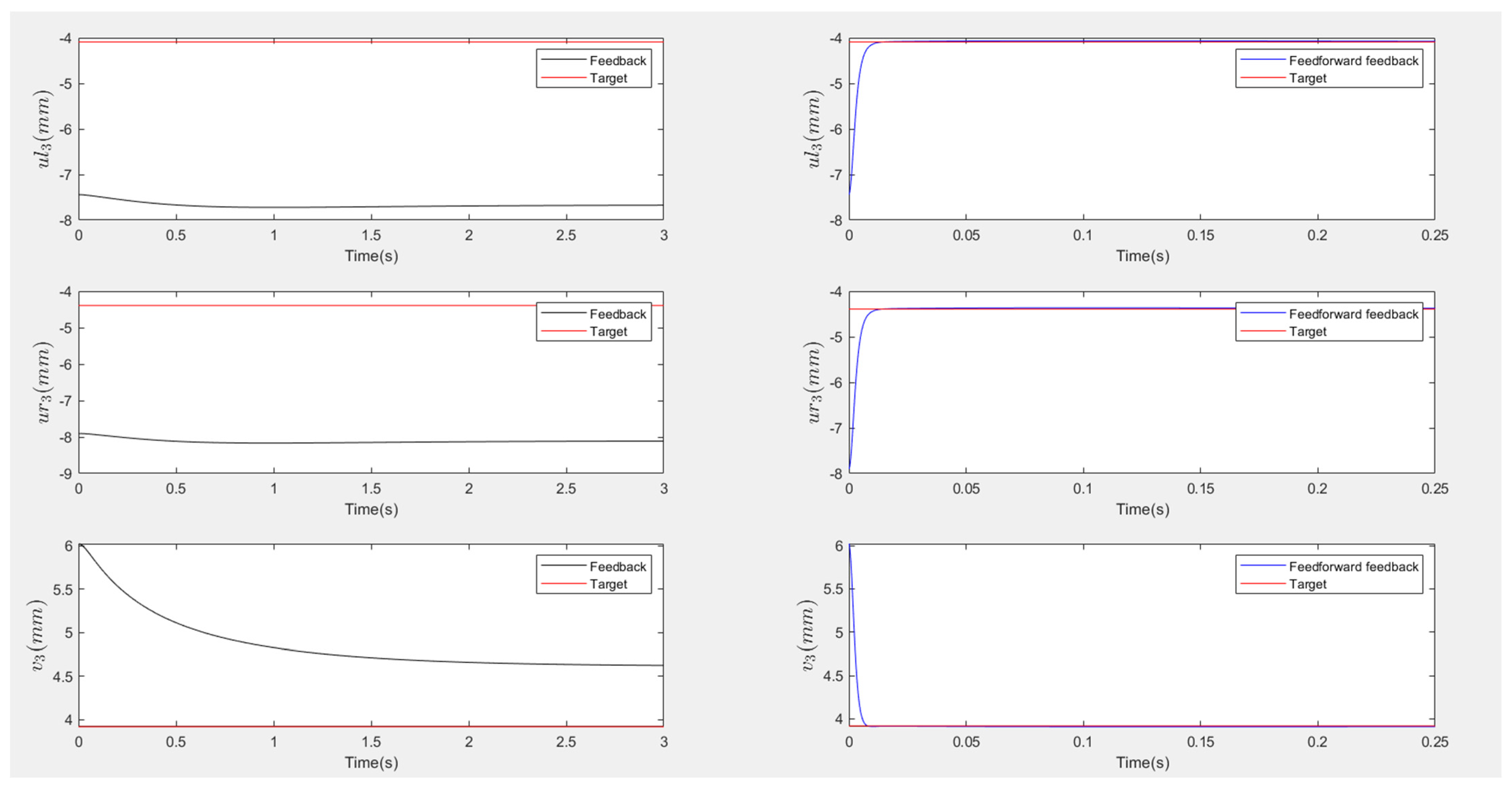
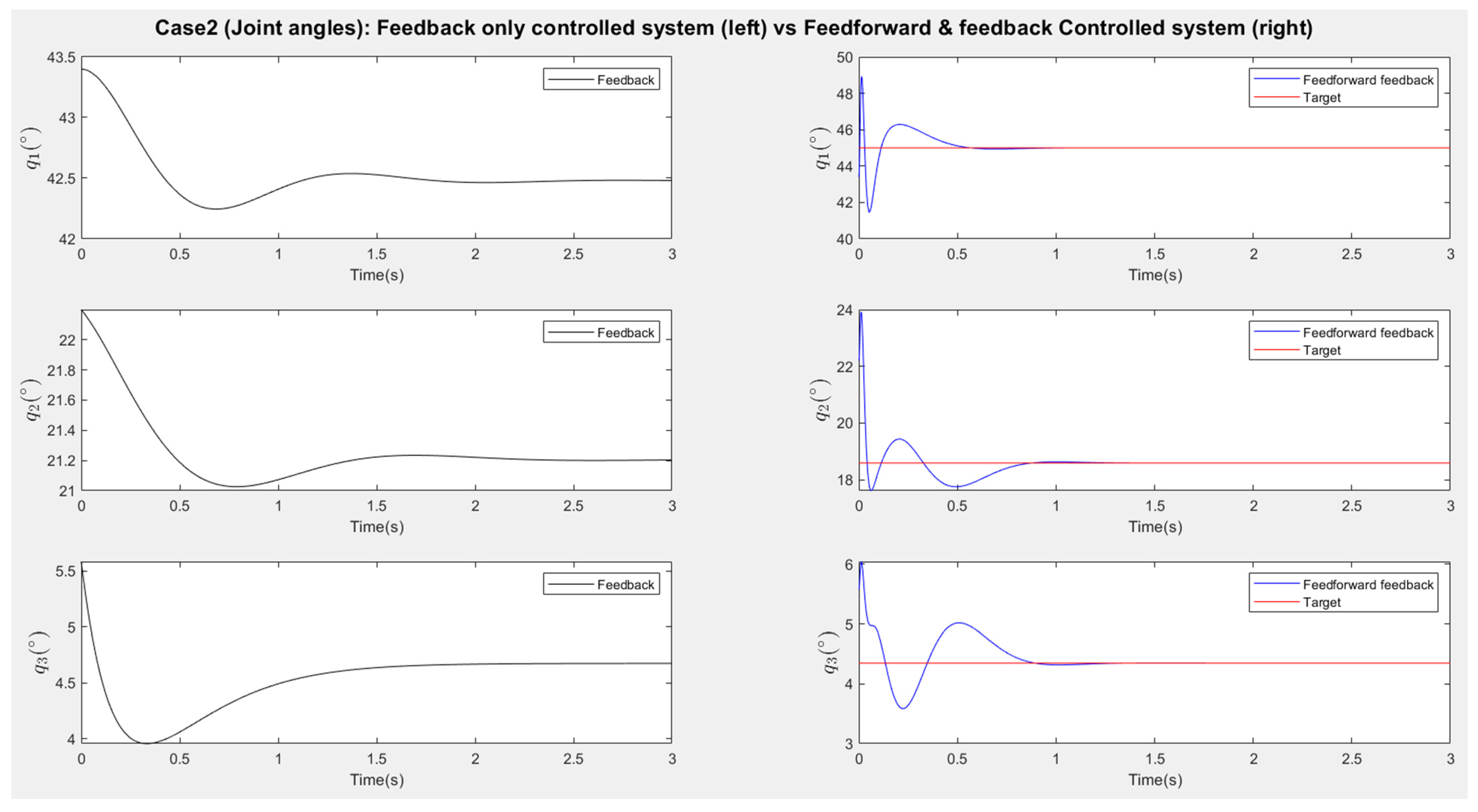
Figure 13 and
Figure 15 present the responses of the six joint angles for the two scenarios, respectively.
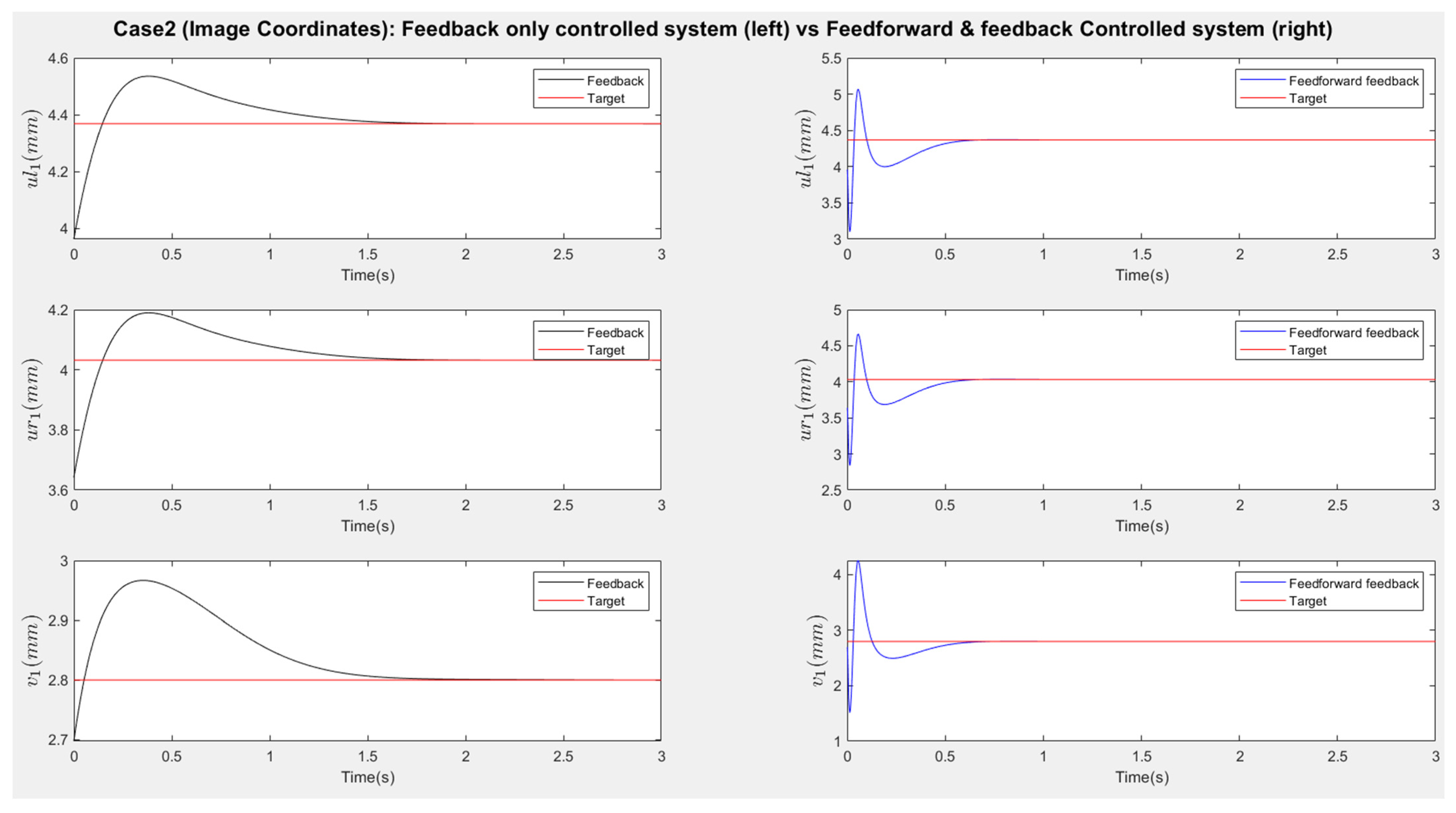
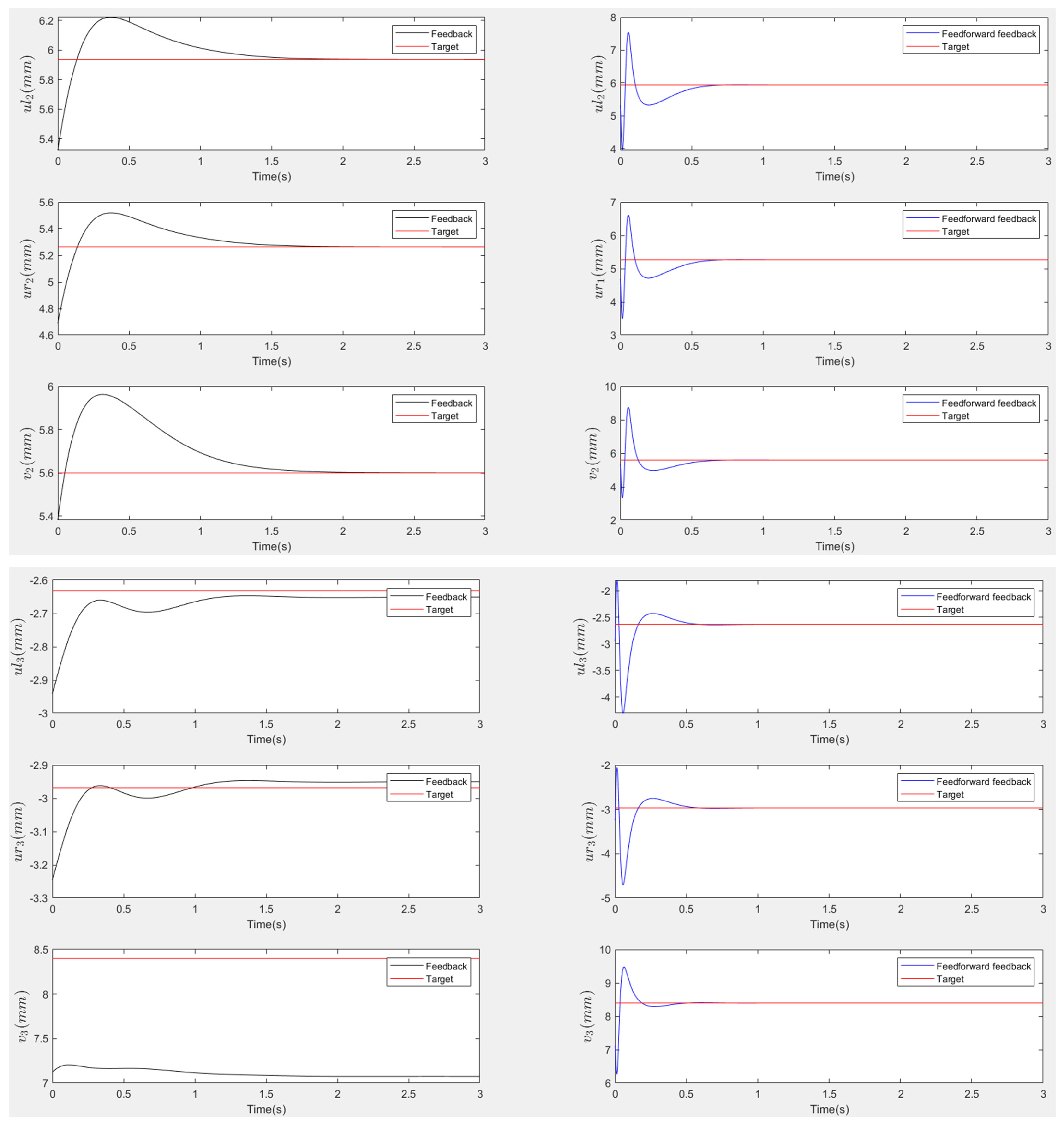
Figure 14 and
Figure 16 show the responses of the nine image coordinates over time for each scenario. In each case, the feedback-only controlled system (left plot) is compared to the feedforward-and-feedback controlled system (right plot). These comparisons focus on overshoot, response time, and target tracking performance.
The bandwidth of actuators in industrial robot manipulators typically ranges from 5 Hz to 100 Hz, corresponding approximately to 31 rad/s to 628 rad/s. For the purposes of this simulation, we assume that the inner loop—representing joint-level control—operates at a fixed bandwidth of 100 rad/s across all scenarios. This corresponds to a time constant of:
In cascaded control architectures, it is standard practice to design the inner loop to be at least 10 times faster than the outer loop to ensure proper time-scale separation and prevent interference. Accordingly, the outer-loop bandwidth is selected as one-tenth of the inner-loop bandwidth:
Additional parameters for the controller are either computed analytically or selected based on design guidelines. In the feedforward controller, the time constant
is chosen to be one-tenth of the inner-loop time constant, as described in Equation (49):
To ensure the outer-loop response is overdamped, and thus suppresses overshoot, the damping ratio ζ is selected to be relatively large:
The response plots indicate that both the feedback-only controller and the combined feedforward-and-feedback controller successfully stabilize the system and reach a steady state within three seconds, even in the presence of small input disturbances (Scenario Two). However, the feedback-only controller fails to guide the camera to its desired pose and falls into local minima, as evident from the third point’s coordinates (, ), which do not match the target at steady state. This issue arises from the overdetermined nature of the stereo-based visual servoing system, where the number of output constraints (9) exceeds the degrees of freedom (DoFs) available for control (6). As a result, the feedback controller can only match six out of nine image coordinates, leaving the rest coordinates unmatched.
In contrast, the feedforward-and-feedback controller avoids local minima and accurately moves the camera to the target pose. This is because the feedforward component directly controls the robot’s joint angles rather than image features. Since the joint angles (6 DoFs) uniquely correspond to the camera’s pose (6 DoFs), the feedforward controller helps the system reach the global minimum by using the desired joint configurations as inputs.
When comparing performance, the system with the feedforward controller exhibits a shorter transient period (less than 2 s) compared to the feedback-only system (less than 3 s). However, the feedforward controller can introduce overshoot, particularly in the presence of disturbances. This occurs because feedforward control provides an immediate control action based on desired setpoints, resulting in significant initial actuator input that causes overshoot. Additionally, a feedforward-only system is less robust against disturbances and model uncertainties. Fine-tuning the camera’s movement under these conditions requires a feedback controller.
Therefore, the combination of feedforward and feedback control ensures fast and accurate camera positioning. The feedforward controller enables rapid convergence toward the desired pose, while the feedback controller improves robustness and corrects errors due to disturbances or uncertainties. Together, they work cooperatively to achieve optimal performance.
8. Conclusions
This work addresses a fundamental challenge in stereo-based image-based visual servoing (IBVS): the presence of local minima arising from the overdetermined nature of aligning the 6-DOF camera poses with a higher number of image feature constraints. Through a formal reformulation of the stereo camera pose estimation problem as a Perspective-3-Point (P3P) case, we clarify the minimum information needed to uniquely resolve the camera pose and highlight the risk of instability when controlling more image features than available degrees of freedom. To overcome this, a cascaded control framework was introduced, combining a feedforward joint-space controller with an adaptive Youla-parameterized feedback loop. The feedforward loop accelerates convergence by directly commanding joint configurations associated with the desired pose, while the feedback loop ensures robustness and fine-tuned tracking under disturbances or modeling uncertainties.
When compared to existing solutions, the proposed method offers a number of compelling advantages. Unlike hybrid switched controllers, which require explicit mode-switching logic and may suffer from discontinuities, our approach provides a unified framework that avoids local minima without controller mode changes. In contrast to 2½ D visual servoing, which blends pose and image features into a hybrid Jacobian, our design maintains the pure IBVS structure while preserving real-time feasibility. Moreover, compared to model predictive control (MPC) approaches that require high-frequency optimization, our strategy achieves comparable performance using linear control theory and avoids excessive computational overhead.
The
Table 2 below summarizes the key differences between the four approaches:
Despite these advantages, several practical considerations must be acknowledged. The open-loop nature of the feedforward controller can introduce overshoot, particularly in systems with low damping or compliance in joints. While this is mitigated by tuning time constants and damping ratios, it underscores the importance of dynamic modeling accuracy. Additionally, the feedback controller’s reliance on linearized approximations restricts global validity, though the proposed adaptive update strategy helps maintain performance over a broad state space. Implementation in real hardware would also require precise stereo calibration and real-time computation of joint-space inverse kinematics, both of which may present engineering challenges.
Overall, this work demonstrates that combining classical control design with geometric insights and modern parameterization techniques can yield a robust, efficient, and scalable solution to a longstanding problem in visual servoing. Future research may explore multi-rate updates, gain-scheduled switching between linearized controllers, or simultaneous
feedforward–feedback design [
41] to further enhance robustness and applicability in unstructured environments.
In summary, this paper investigates the overdetermination problem in stereo-based IBVS tasks. While future improvements to the algorithm are possible, the proposed control policy has demonstrated significant potential as an accurate and fast solution for real-world eye-in-hand (EIH) visual servoing tasks.