3.1. Characterization of the Initial Powder
The powder synthesized via the precipitation route described in
Section 2.1 is shown in
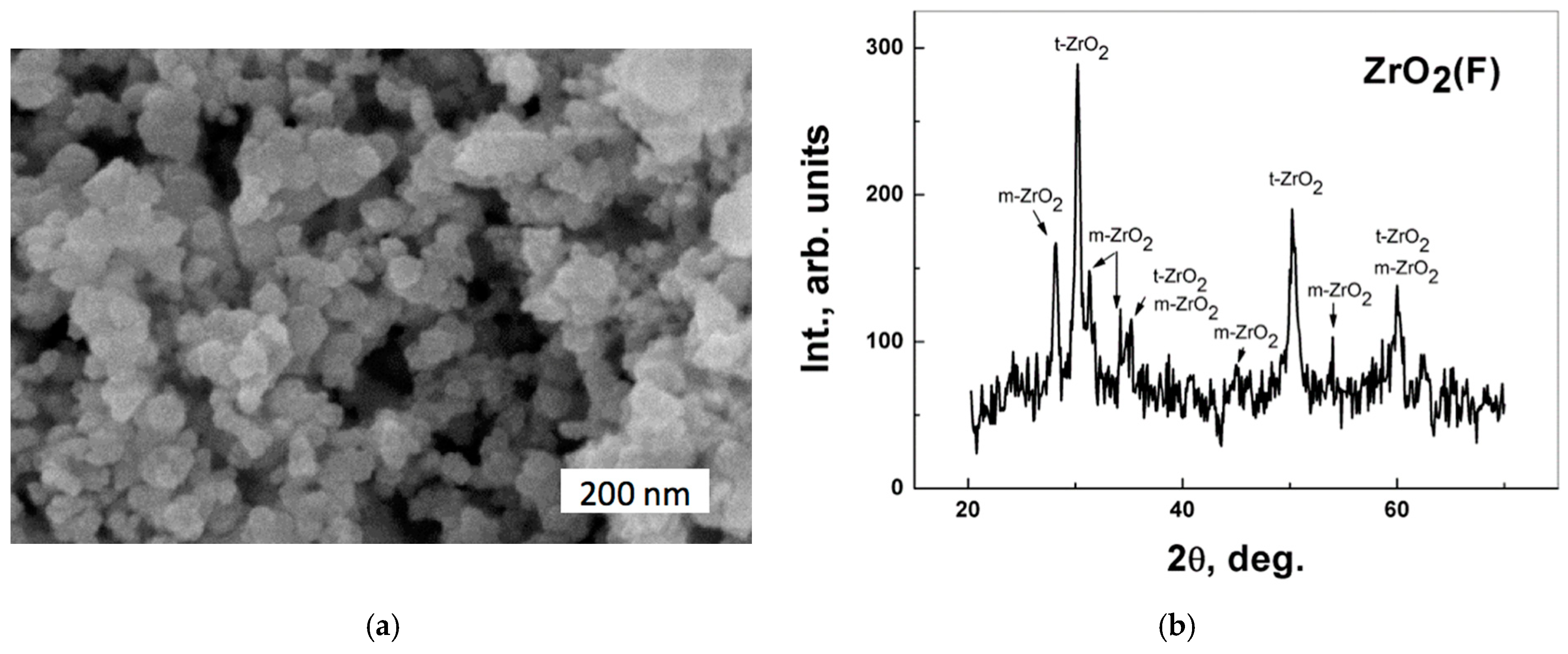
Figure 3. In particular, the SEM image is presented in
Figure 3a, and the XRD diagram is provided in
Figure 3b.
The homogeneity of powder morphology can be noted from the SEM image (
Figure 3a). It can be expected that the highly uniform particle size distribution contributed to the improved sinterability of the zirconia powder. The XRD diagram (
Figure 3b) exhibits the presence of both phases, tetragonal
t-ZrO
2 and monoclinic
m-ZrO
2. Thus, the sample under investigation exhibits a biphasic structure.
Figure 4 shows the BET (Brunauer–Emmett–Teller) isotherm of the initial powder. Its specific surface area
asBET was found to be 6.3. Compared to the powder obtained by other means, this powder was of significantly higher quality. The specific surface area for the second powdered sample was
asBET = 3.7, and this powder was of poor quality and thus excluded from further studies.
The hysteresis shown in
Figure 4a belongs to a Type IVa isotherm, according to the classification provided in [
40]. Its two branches represent adsorption and desorption associated with capillary condensation. Capillary condensation typically occurs in granular or porous media and can strongly alter the properties of the materials. Its presence suggests the van der Waals interactions between the molecules assemble crystals to create atomic-scale capillaries in the condensed state.
Although the final saturation plateau is very small, this indicates a mesoporous material. The increase in mesoporosity can be attributable to the augmented number of grain boundaries, consequent to the formation of phase-separated nanocomposites.
For nitrogen, adsorption took place in cylindrical pores at 77 K, and hysteresis started to occur for pores above 4 nm in width. The pore volume versus pore diameter shown in
Figure 4b reveals three local extremes at diameter values of about 2.5, 7.5, and 11 nm.
The observed morphology and the results of the BET analysis indicated that the initial powder exhibited good sinterability.
3.2. Microstructural Analysis of the Sintered Specimens
The microstructure of a sintered sample is shown in
Figure 5. The structure of the specimen was found to be homogeneous with several small dark inclusions of distinguishable size. The three areas selected for the elemental analysis are illustrated in
Figure 5b, and the numerical data are listed in
Table 1.
The data in
Table 1 suggest that some non-uniformity of ceria distribution in the zirconia matrix took place. However, its scale does not threaten the strength characteristics of the sintered material. From the perspective of fracture toughness, the proportion of tetragonal to monoclinic zirconia appeared more important. Overall, the
t-ZrO
2 phase constituted ca. 95%, while the content
m-ZrO
2 phase was ca. 5% in the sintered specimen. An increase in the monoclinic phase content upon cooling of zirconia sintered at temperatures higher than 1400 °C was reported in [
41], which should not be expected in the present experiments with the zirconia sintered at 1400 °C. Thus, the negative effect of the monoclinic phase could be considered negligible.
The presence of the different phases (i.e., monoclinic, tetrahedral, and cubic) is evidenced in the experimental studies. The histogram shown in
Figure 6 provides a concise overview of these data. The horizontal axis shows the mol% value, while the
Y-axis is utilized to demonstrate the number of mentions of these structures in the literature.
When the mol% of CeO2 in a given composite falls between 10% and 80%, the existence of the composite in various phases has been reported. The higher CeO2 content, the higher the symmetry (for mol% < 8% formulation, it is typically monoclinic, 8 < mol% < 75% tetrahedral, or cubic and mol% > 75% cubic). The nanopowders with mol% equal to 10, 25, 50, and 75% exhibit tetrahedral symmetry, while with mol% equal to 90% exhibits cubic symmetry. Consequently, elevated mol% is associated with higher symmetry.
The addition of CeO
2 results in a significant enhancement of the stability, high-temperature resistance, and mechanical properties of ZrO
2. In contrast, the higher amounts of CeO
2 enhance the mobility of grain boundaries and increase the grain size following sintering. Therefore, the CeO
2 addition should be minimized. As demonstrated in
Figure 6, at low molar percentage values (below 8 mol%), the m-phase has thus far been achieved. The electroconsolidation method outlined in this study facilitates the production of a t-phase composite comprising only 5 mol% of CeO
2, a distinctive feature.
3.3. Strength Analysis
In
Figure 7, there is an SEM image of a sintered sample fracture surface presented. It can be seen that after sintering, the grain size of around 1 μm was partially retained.
The destruction of grains observed in
Figure 6 is predominantly transcrystalline, which indicates the strength of inter-grain boundaries. The bending strength
σb of the specimen under three-point bending conditions was determined according to the following formula:
where
F is the force value at the moment of separation of the sample into parts, N;
l is the length of the sample, mm;
b is the width of the sample, mm;
h is the thickness of the sample in the parallel direction to the force applied to the sample, mm.
Different brittle materials experience rupture at different maximum tensile stresses. Statistically, the brittle fracture is dependent on the weakest element in the material’s volume. According to the two-parameter Weibull distribution, the probability of failure
Pf at a given the stress value,
σ, is defined as follows [
42,
43]:
where
m is the shape parameter of the Weibull distribution;
σ is the actual inner stress under the applied force, MPa; and
σ0 denotes the scale parameter, MPa. (The threshold value, below which no specimen is expected to fail, is neglected).
To estimate the the Weibull parameters, Equation (1) is twice logarithmed and reduced to a linear form, as follows:
The shape and scale parameters,
m and
σ0, respectively, are obtained from Equation (3) by the least squares method. The density of fracture probability
f dependent on the value of
σ0 is described by the equation, as follows:
To perform the calculations, the entered experimental data are ordered in ascending order, and for each
i-th value, the empirical probability function
Pexp(
i) is determined according to the following formula:
where
N is the number of tested samples.
The results of the tensile strength measurement and of related calculations are collected in
Table 2.
Using the obtained data, the Weibull graph, the so-called Weibull probability plot, was plotted and is presented in
Figure 7. The values calculated from the experimental data were fitted using a linear equation, as follows:
where the parameters
a0 and
a1 were determined using the least squares method. The Weibull modulus
m corresponds to the parameter
a0.
The scale parameter
σ0 is related to both
a0 and
a1 according to the following relation:
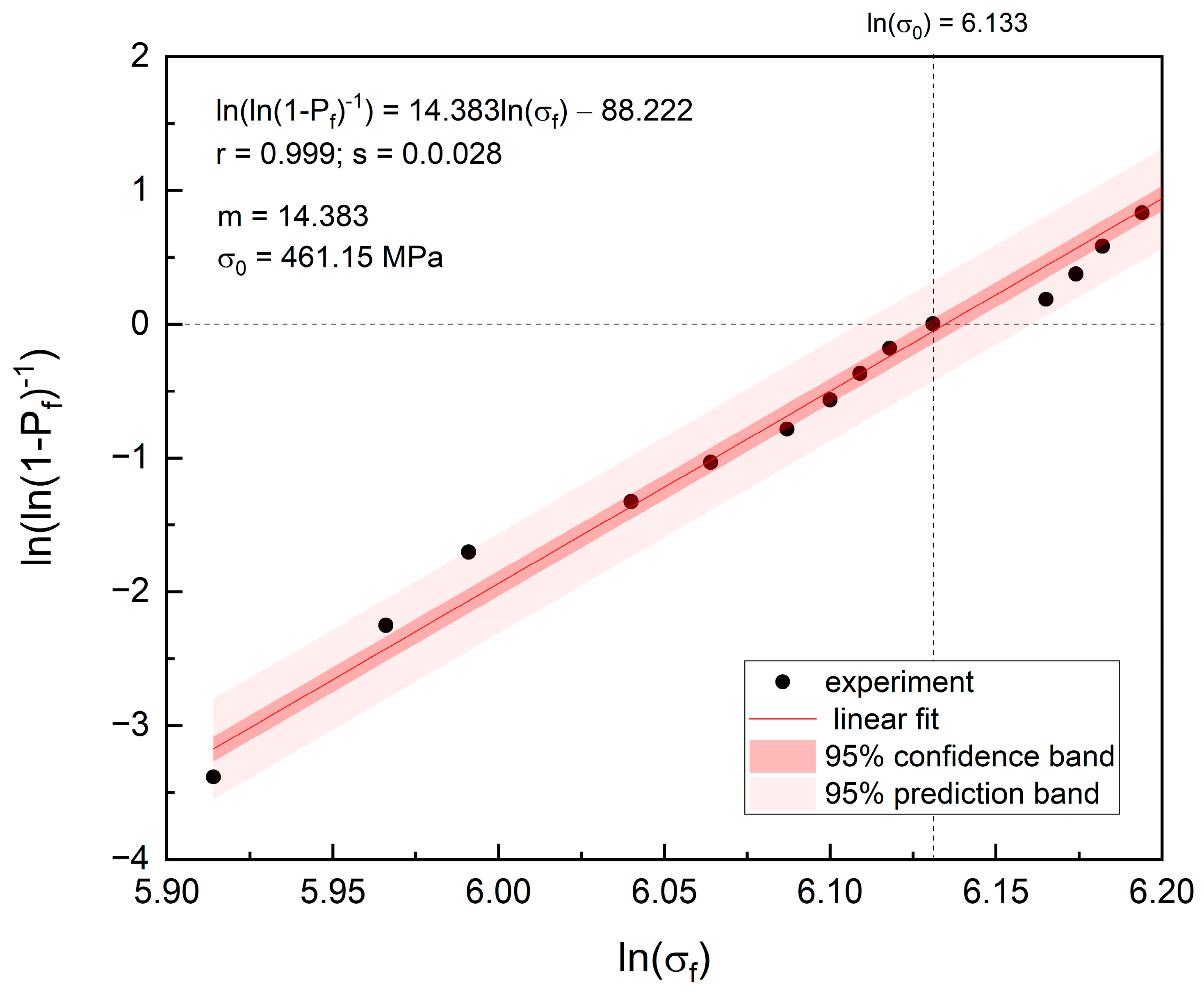
Figure 8 shows a Weibull graph, where
y = ln(ln(1 −
Pf)
−1) represents the double logarithmic transformation of the cumulative probability of failure and
x = ln(
σ) describes the natural logarithm of the failure bending stress. The black dots correspond to the experimental data points. The linear regression model, fitted to the data points, yielded parameters describing the Weibull distribution listed in
Table 3.
It is noteworthy that the high Pearson’s coefficient 0.999 and low curve fit standard deviation s = 0.28 of the experimental points from linearity suggest the high quality fit of the Weibull distribution.
The slope of the line is the shape parameter m of the Weibull distribution, the so-called modulus. Its positive value characterizes the curve as S-shaped with upward curvature followed by a turning (inflection) point. The m value of 14.383 indicates the variability of the material’s strength. A relatively high Weibull modulus suggests a narrow flaw size population and, in a consequence, a narrow range of bending strengths.
The value of the Weibull modulus of the investigated sample is consistent with previously published studies [
44,
45]. Typically, zirconia ceramics are reported to exhibit a Weibull modulus below 7, while that of alumina ceramics can reach up to 10 [
24]. However, there are reports demonstrating that the
m values of the zirconia, both ZrO
2–Al
2O
3 microparticle and nanoparticle composites, were in a range between 10.07 and 12.02 [
46]. In general, a higher Weibull modulus value represents a narrower dispersion of the fracture strength, and thus a more homogeneous distribution of flaws, providing higher reliability [
46]. Thus, a high modulus suggests that the nanopowder studied is high quality and reliable.
The scale parameter σ₀ equal to 461.15 MPa is indicative of characteristic strength, representing the stress level at which 63.2% of the population would fail.
Figure 8 reveals that the studied sample exhibits a high breakdown strength of 461.15 MPa.
The expected value to failure (mean value to failure) can be calculated based on the following equation:
where G is a gamma function. The average durability of the sample in terms of tensile strength measured by the expected value to failure is equal to 432.91 MPa. The median and mode are 449.54 and 461.08 MPa, respectively, and the standard deviation does not exceed 37.86 MPa,
Table 4.
The mean and median values differ by 17 MPa. The median is a slightly more accurate estimator than the mean when the distribution is unsymmetrical.
The reliability function, which represents the probability that the sample will keep its properties without failure, and the failure function, which represents the probability of failure, are shown in
Figure 9 (Both were plotted based on the parameters from the linear fit shown in
Figure 8).
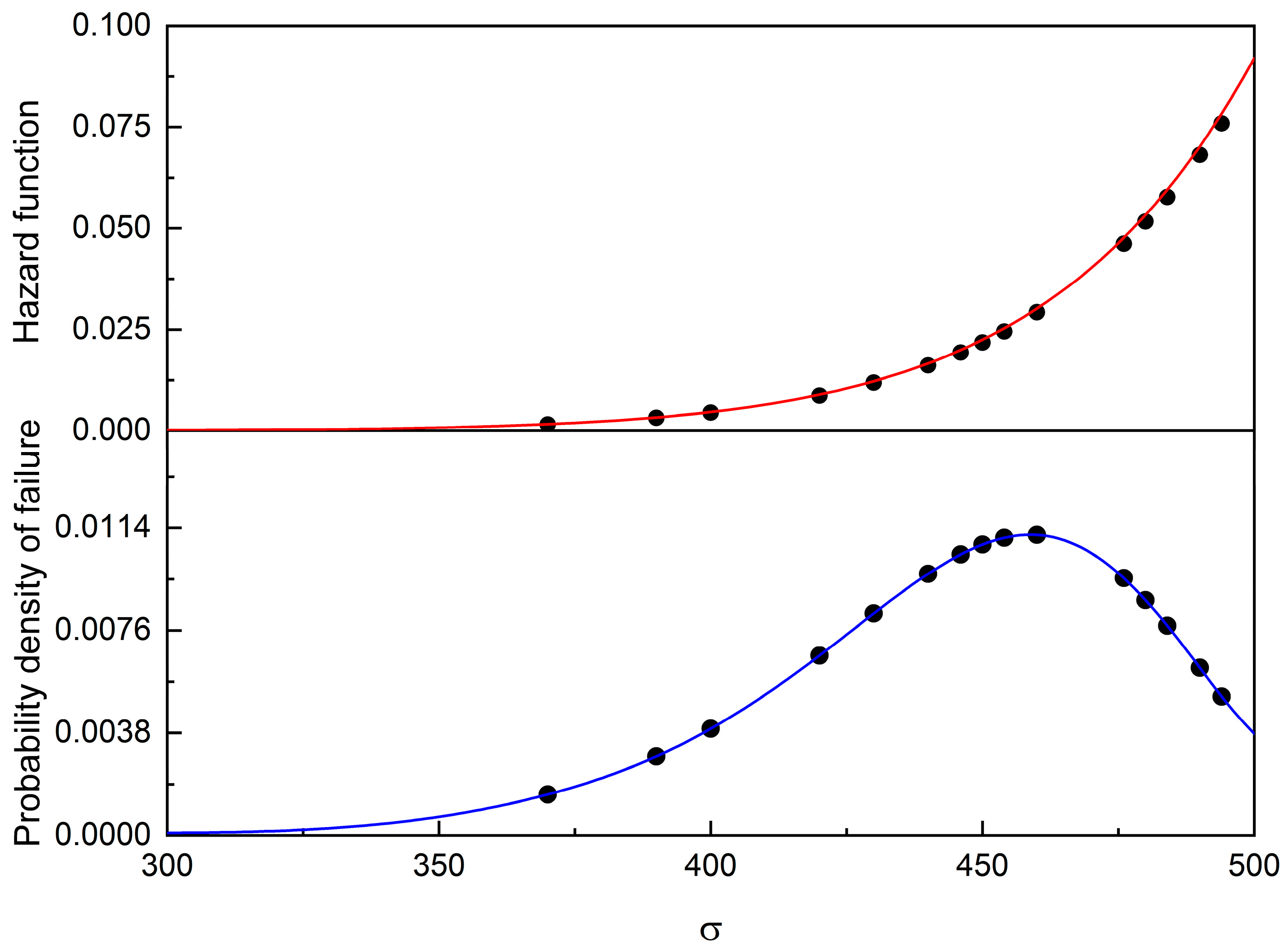
The hazard function, which describes the “conditional density”, i.e., the conditional distribution of a random variable, given that the event has not yet occurred, and the failure distribution, i.e., the probability density of failures, are shown in
Figure 10.
An examination of the graphs shown in
Figure 8 and
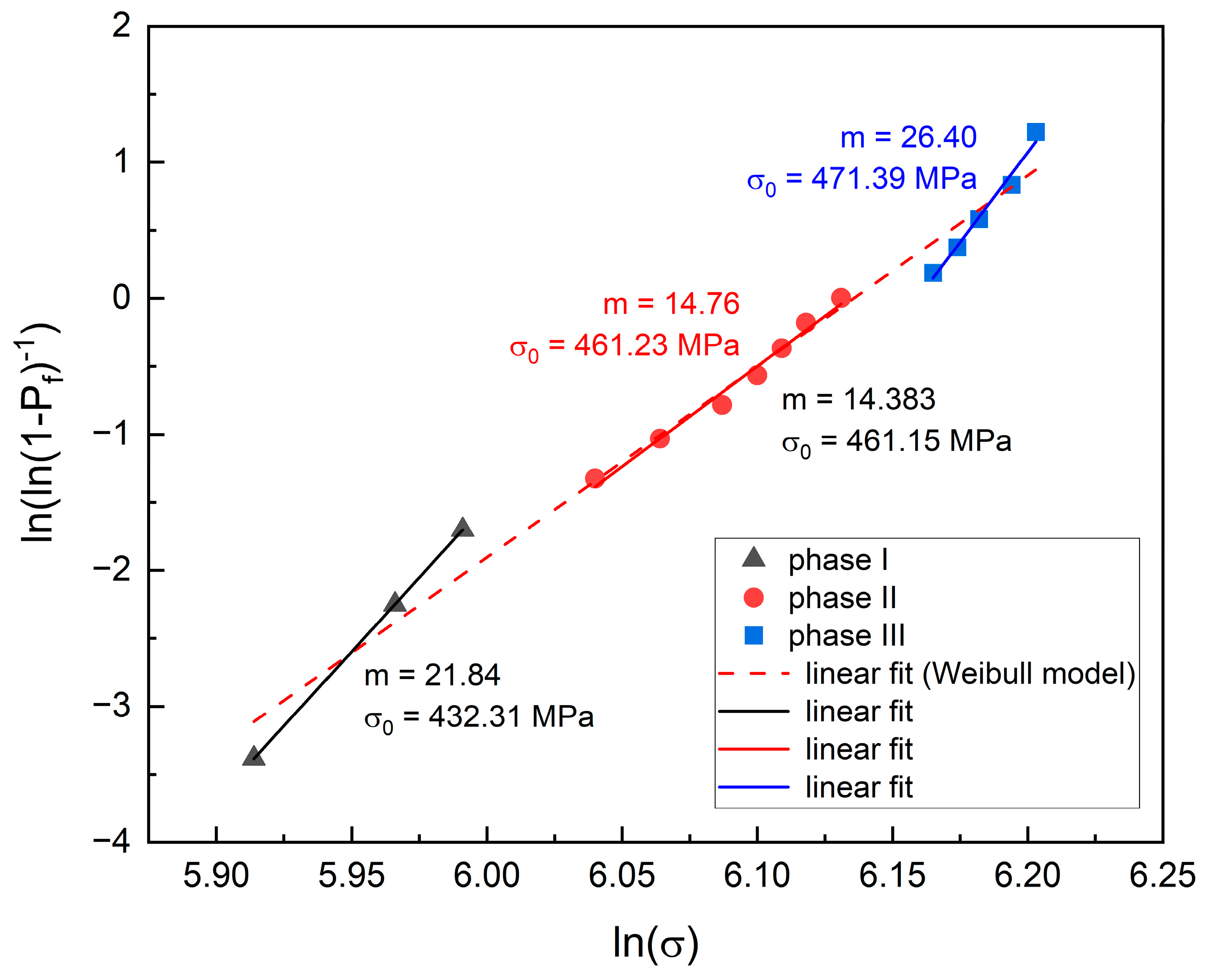
Figure 9 suggests that despite the high-quality fit, the scattering of the points from the Weibull model reveals a characteristic feature—splitting data into three groups. Well-defined groups of the points suggest that the Weibull model consists of three components as shown in
Figure 11 and listed in
Table 5.
The slope of all three lines shown in
Figure 11 is positive, but only the slope of the points in the middle part, shown in solid red, resembles those of the whole Weibull distribution (dashed line). The three lower points delineate phase I, the subsequent seven points delineate phase II, and the final five points delineate phase III. The Weibull modulus is different for each phase,
Table 5. In the lower range, m is nearly 21.84, in the middle, it does not exceed 14.76, and in the upper range, it reaches 26.4. Although the differences in the m values may seem large, a comparison of the differences between the slope of the total Weibull model and each linear fit (phase I, II, or III) converted to degrees (inclination angles in degrees), Δm, shows that they are small. The percentages of phases are listed in the table. The characteristic strength values estimated based on these data are 432.31, 461.21, and 471.39 MPa, respectively. Thus, the three lower points (370, 390, and 400) reveal a greater influence of the m-phase, seven points in the middle of the graph reveal a mixture of the m-phase and t-phase, and the upper five (476, 480, 484, 490, and 494) reveal the larger influence of the t-phase. In each of them, the Weibull modulus is slightly different, the highest for the upper and the smallest for the middle part. The variation in the Weibull distribution parameters seems to be related to the temperature gradient during sintering, which in turn is related to the grain size.
3.4. Hardness Analysis
The procedure previously described was employed once more in order to analyze the distribution of the values of hardness. The results of the Vickers hardness measurement are collected in
Table 6.
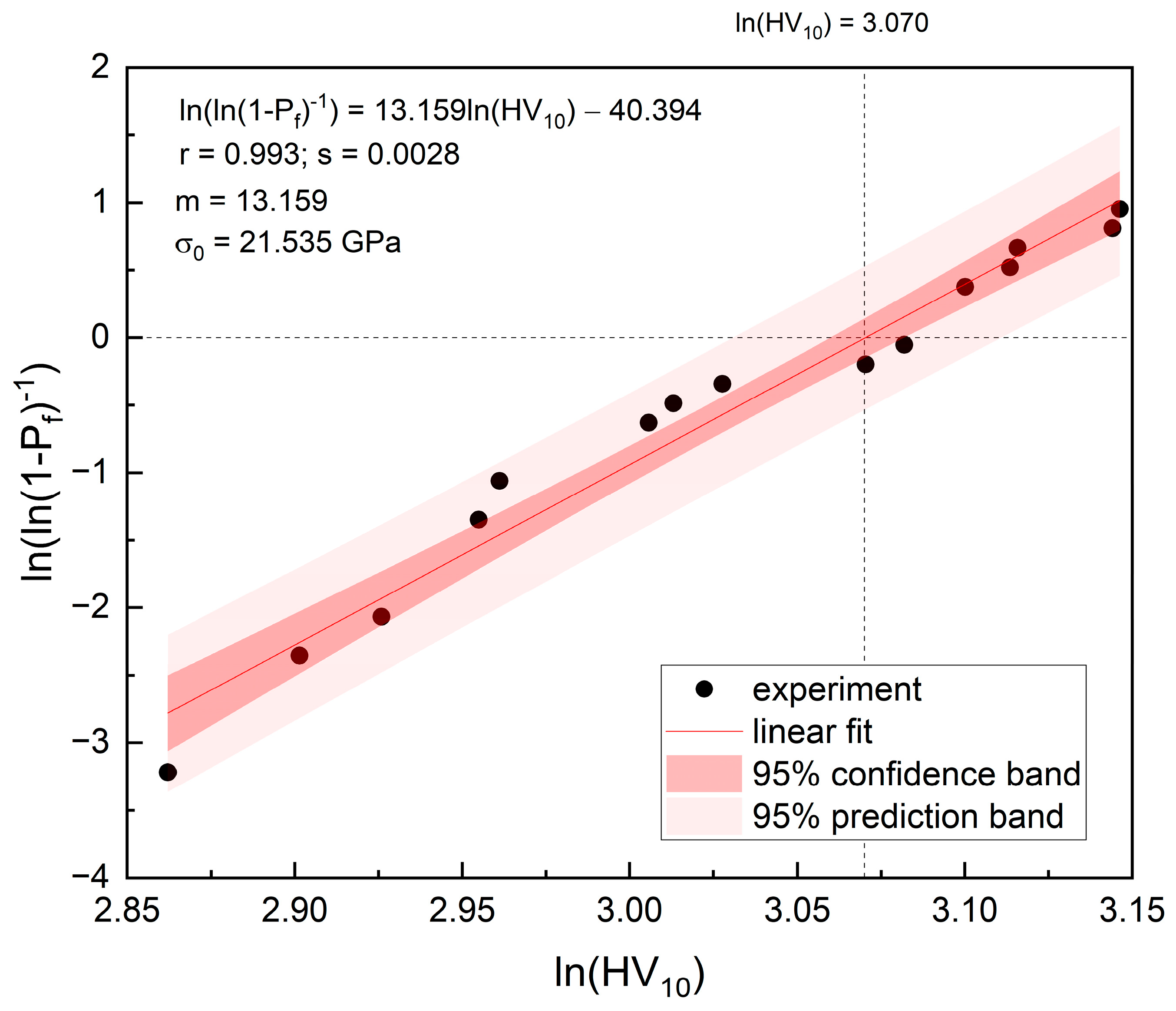
Figure 12 shows a Weibull graph, where
y = ln(ln(1 −
Pf)
−1) represents the double logarithmic transformation of the cumulative probability of failure and
x = ln(HV
10) describes the natural logarithm of the failure of Vicker hardness. The black dots correspond to the experimental data points. The linear regression model, fitted to the data points, yielded the parameters describing the Weibull distribution listed in
Table 7.
The relatively high Weibull modulus,
m, of 13.159 suggests a narrow range of the hardness values, indicating a constant material hardness. The scale parameter σ₀, that does not exceed 21.535 GPa, is the characteristic hardness value reached or exceeded by as much as 63.2% of the population. The value of the Weibull modulus of 13.159 GPa is consistent with results obtained from the bending strength analysis presented in
Section 3.3 and with those published in other reports [
44,
45,
46].
The expected value to failure (mean value to failure) was calculated based on Equation (8). The average durability of the sample in terms of hardness measured by the expected value to failure is equal to 20.079 GPa,
Table 8.
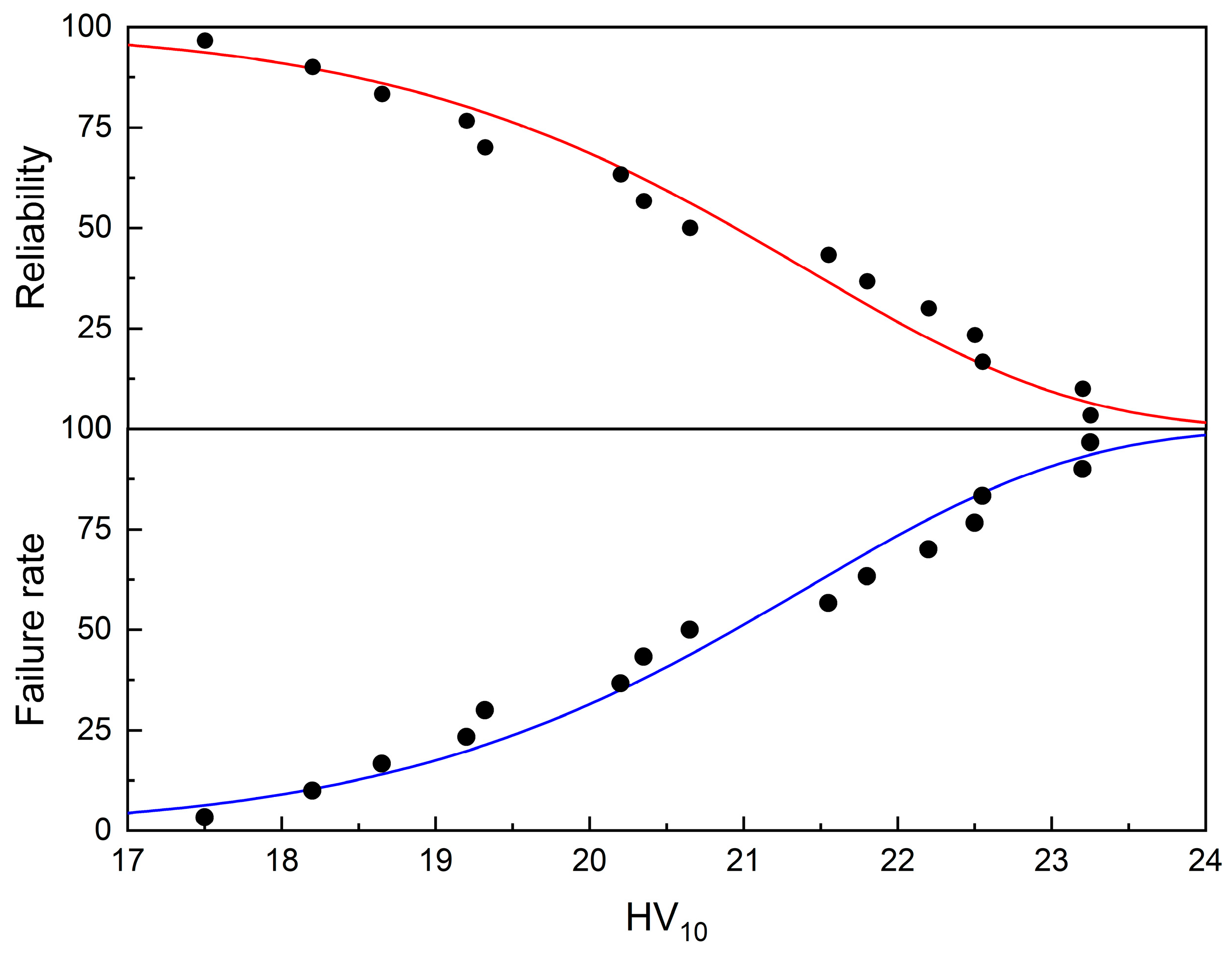
The median and the mean are almost identical, suggesting a moderately symmetrical distribution. The reliability function (the probability that the sample will keep its properties without failure) as well as failure function (the probability of failure) are shown in
Figure 13. (Both were plotted based on the parameters from the linear fit shown in
Figure 12).
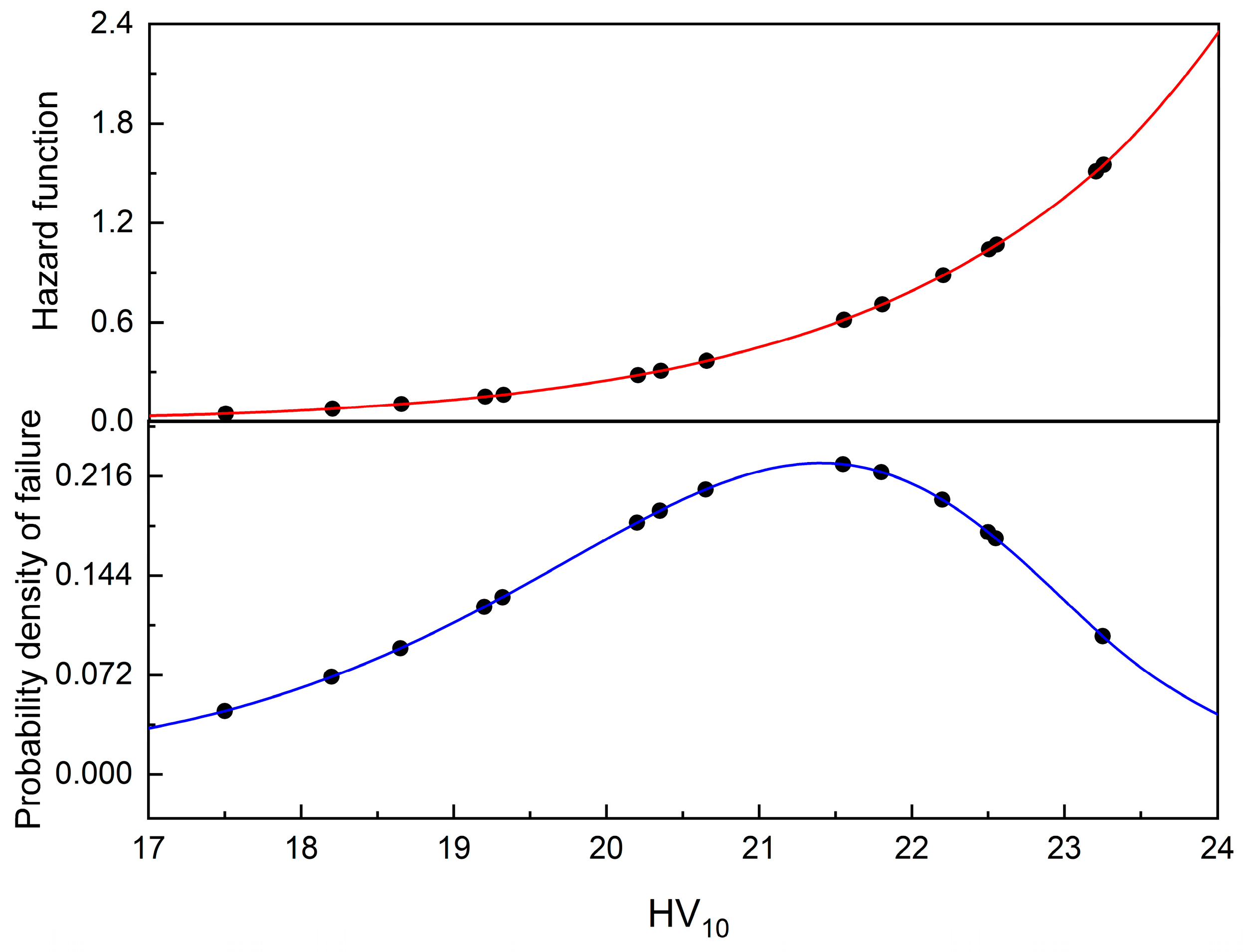
The failure function, widely known as the hazard rate, and the probability density of failure are shown in
Figure 14.
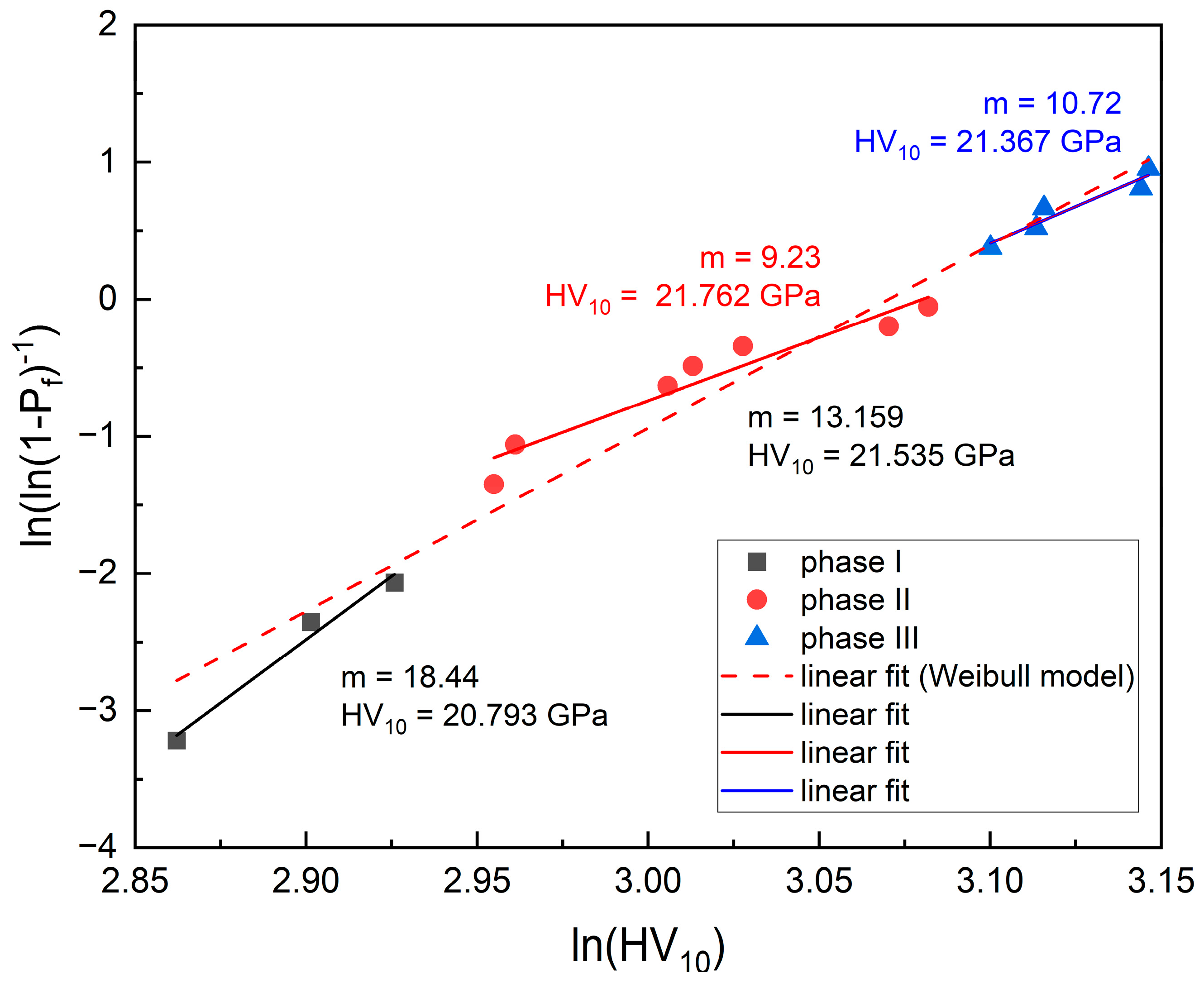
A thorough analysis of the data from the Weibull model depicted in
Figure 12 reveals the presence of three distinct groups in the distribution. This indicates the Weibull model comprises three components, as illustrated in
Figure 15 and listed in
Table 9.
Figure 15 shows that all three lines have a positive slope, but only the blue points at the top match the whole dataset slope (dashed line). Thus, the Weibull model describes in fact three different distributions. The three lower points delineate phase I, the subsequent seven points delineate phase II, and the final five points delineate phase III. The Weibull modulus is different in each phase,
Table 9. In the lower range, m is almost 18.44, in the middle, it does not exceed 9.23, and in the upper range, it reaches 10.72. Although the differences in the m values may seem large, a comparison of the differences between the slope of the total Weibull model and each linear fit (phase I, II, or III) converted to degrees (inclination angles in degrees), Δm, shows that they are small. The percentages of the phases are listed in the table. The characteristic hardnesses estimated based on these data are equal to 20.703, 21.762, and 21.367 GPa, respectively. Thus, the three lower points (370, 390, and 400; depicted in black) reveal a negligible influence of the m-phase, which has lower symmetry. The seven points in the middle of the graph (depicted in red) reveal a mixture of the m-phase and t-phase, and the top five (476, 480, 484, 490, and 494; depicted in blue) reveal a negligible influence of the t-phase. The difference between the hardness in the phases I, II, and III is negligible. Thus, the hardness is very stable.
The Weibull modulus, when greater than 4, is indicative of the inherent property limitations of materials, e.g., ceramic brittleness. However, it also is indicative of severe problems in the manufacturing process, or of minor variability in the manufacturing process or in the material itself. The results obtained indicate a high homogeneity of the material tested, not only as regards strength but also hardness. Thus, the high values of the Weibull modulus suggest that the nanopowder studied is high quality and reliable in terms of hardness and strength.