Predicting Filter Medium Performances in Chamber Filter Presses with Digital Twins Using Neural Network Technologies
Abstract
1. Introduction
2. Methodology
2.1. Experimental Setup of the Chamber Filter Press
2.2. Parameter Selection
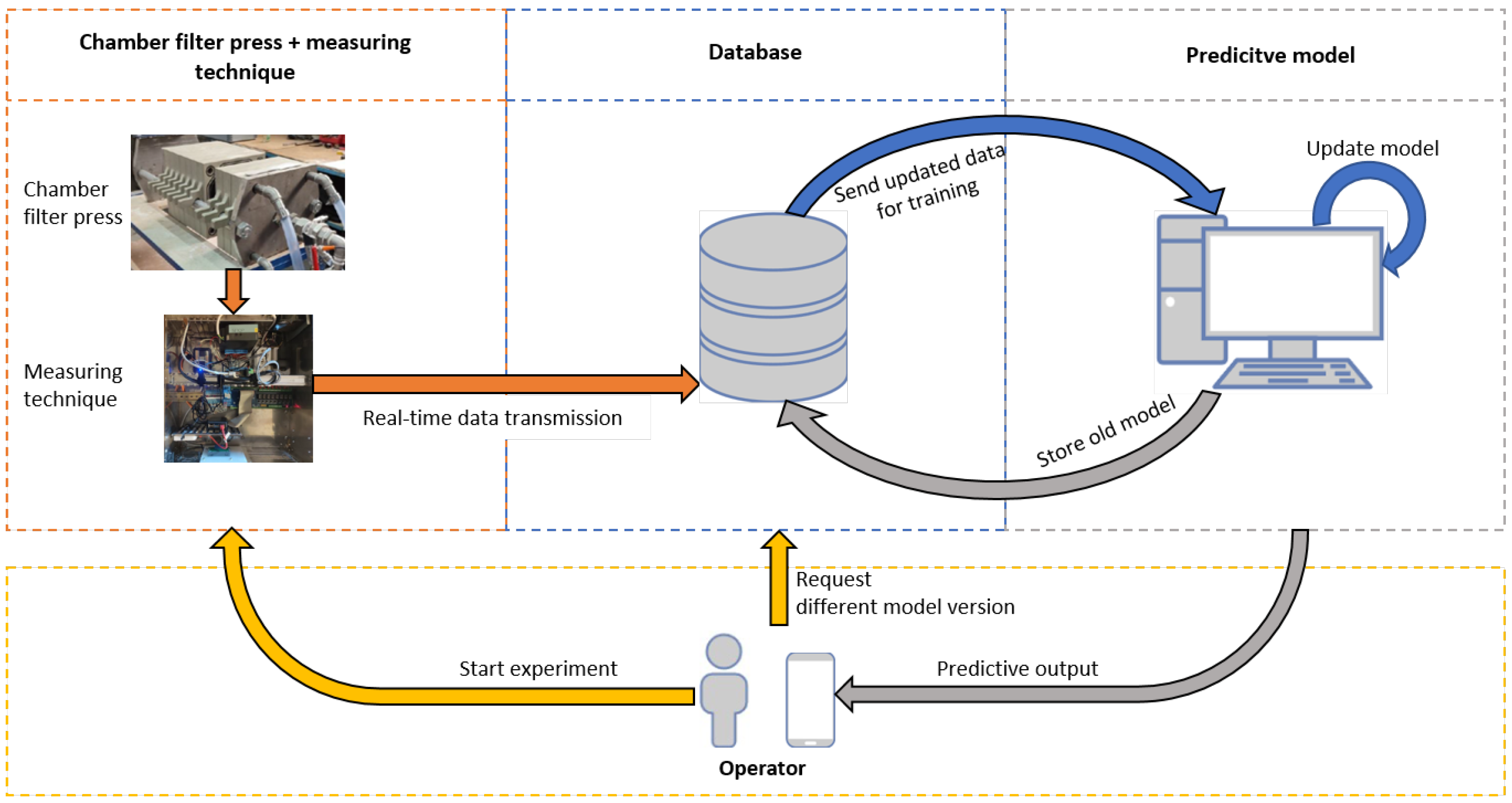
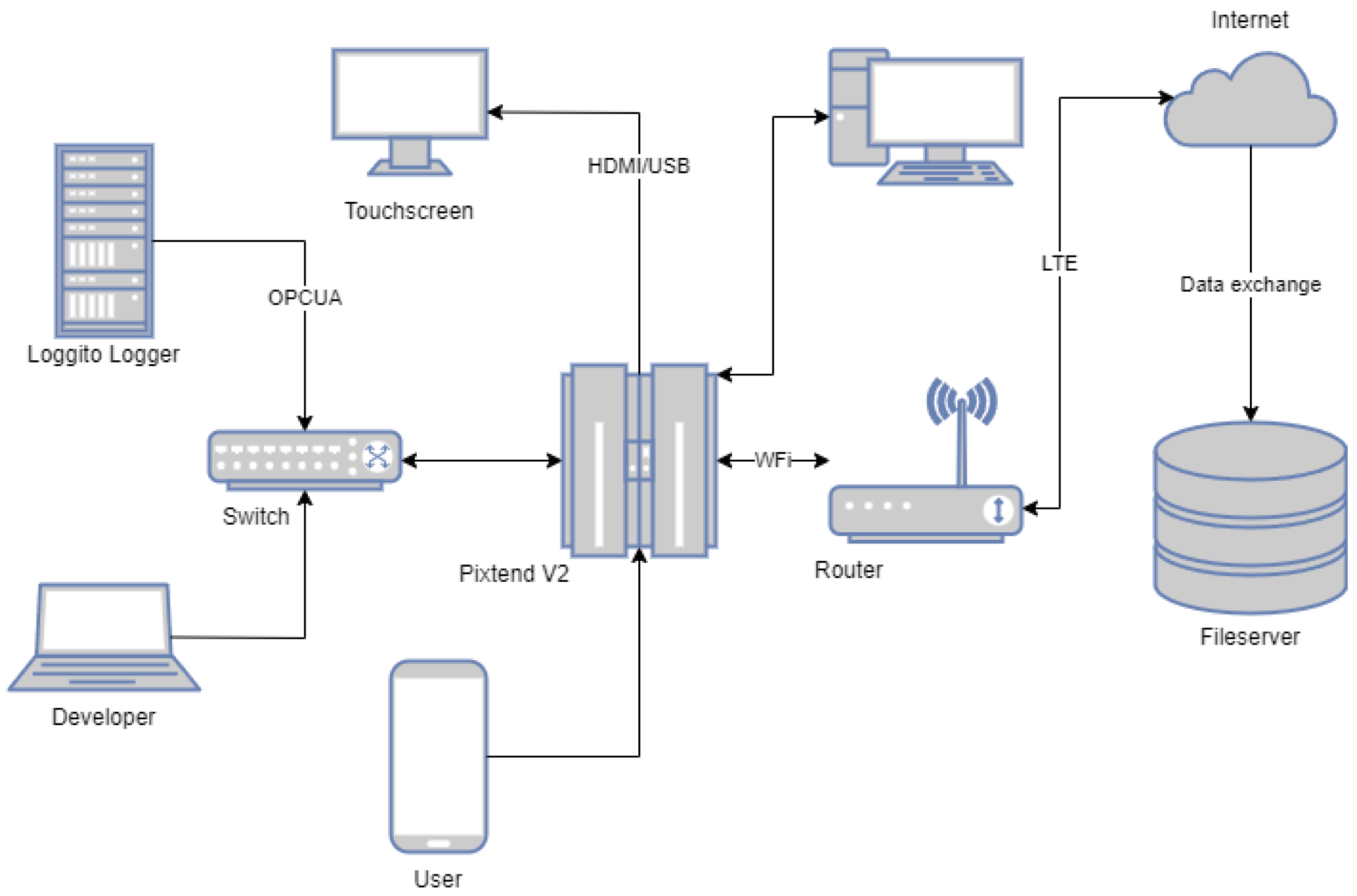
2.3. Digital Twin Architecture
2.4. Experiments
2.5. Data Logging and Database Development
2.6. Neural Network Model
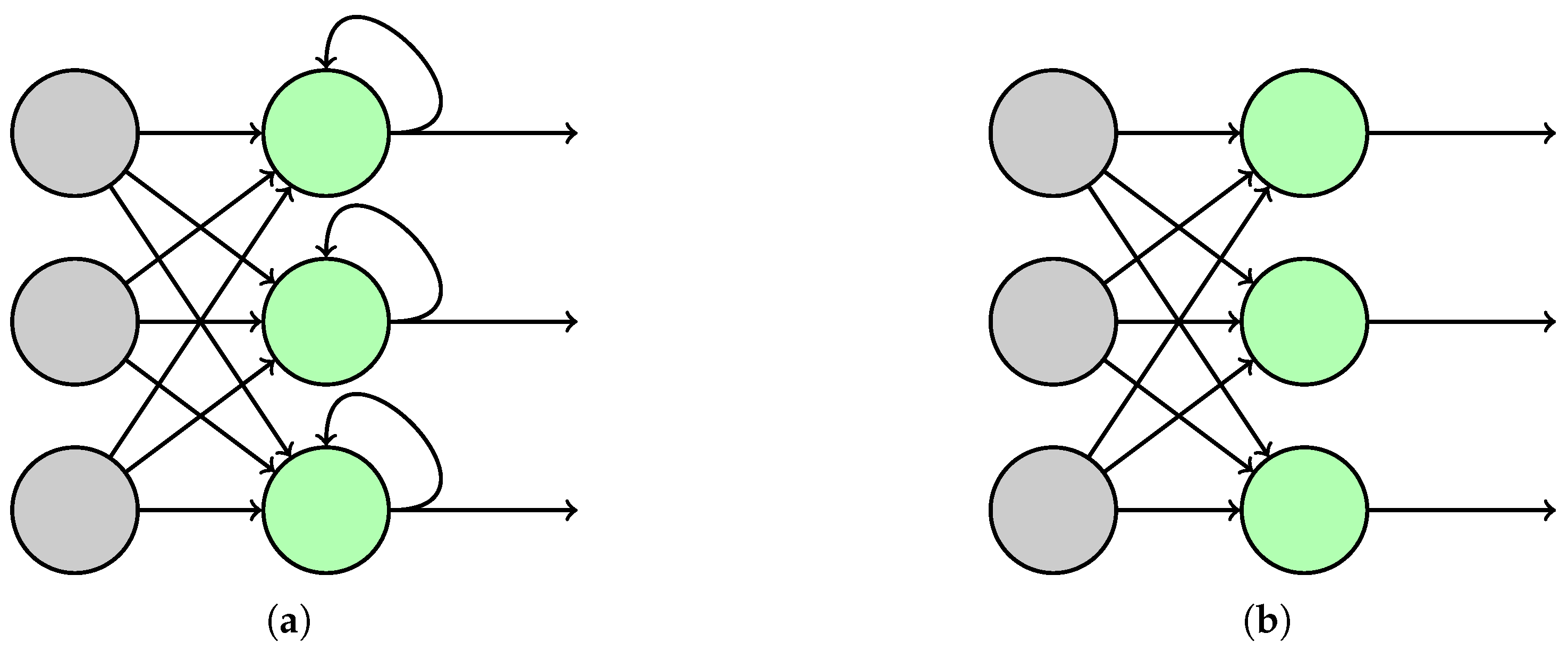
2.6.1. Selection of Neural Network Type
2.6.2. Model Architectures
2.6.3. Data Preparation
2.6.4. Model Evaluation
3. Results
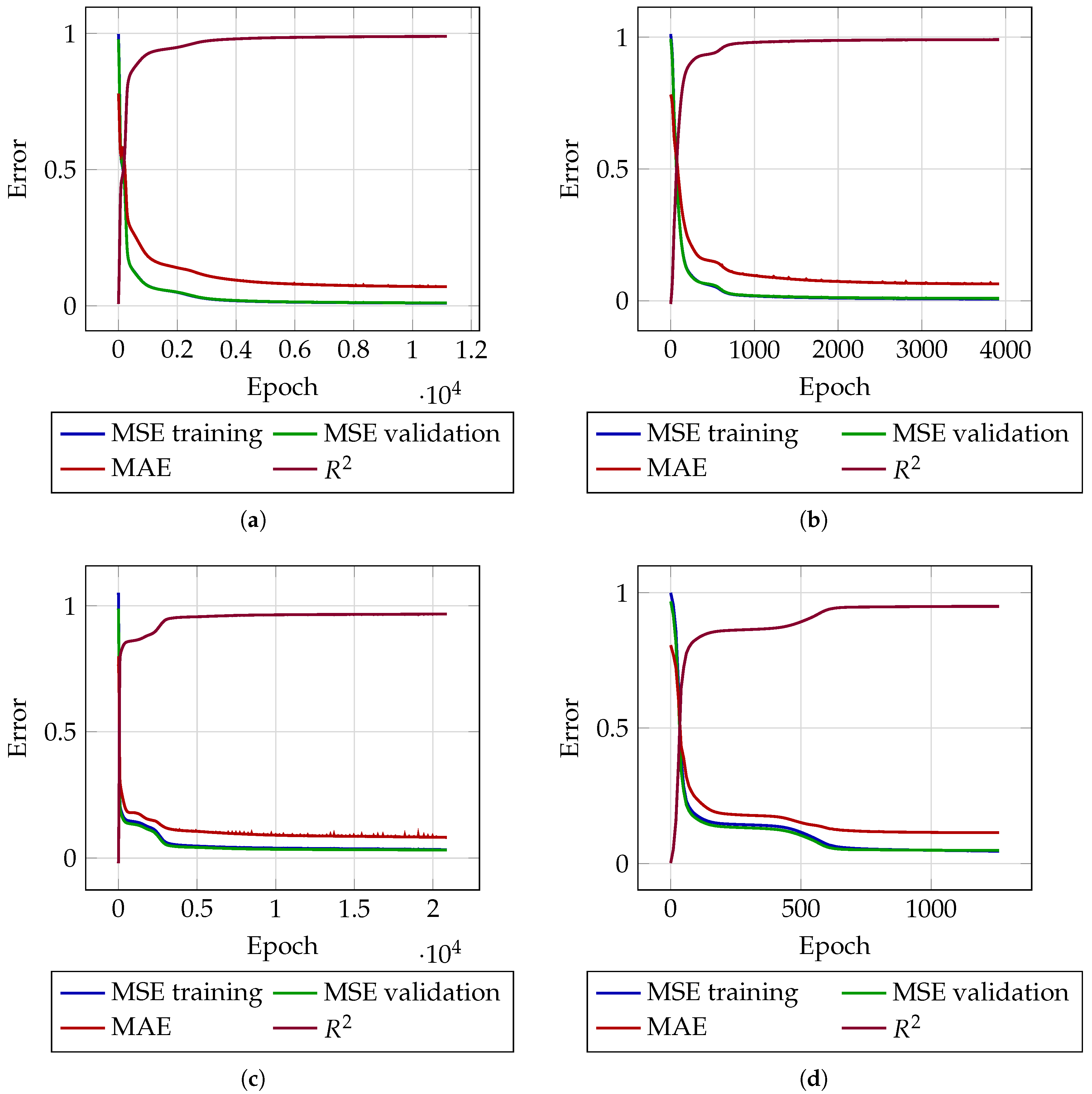
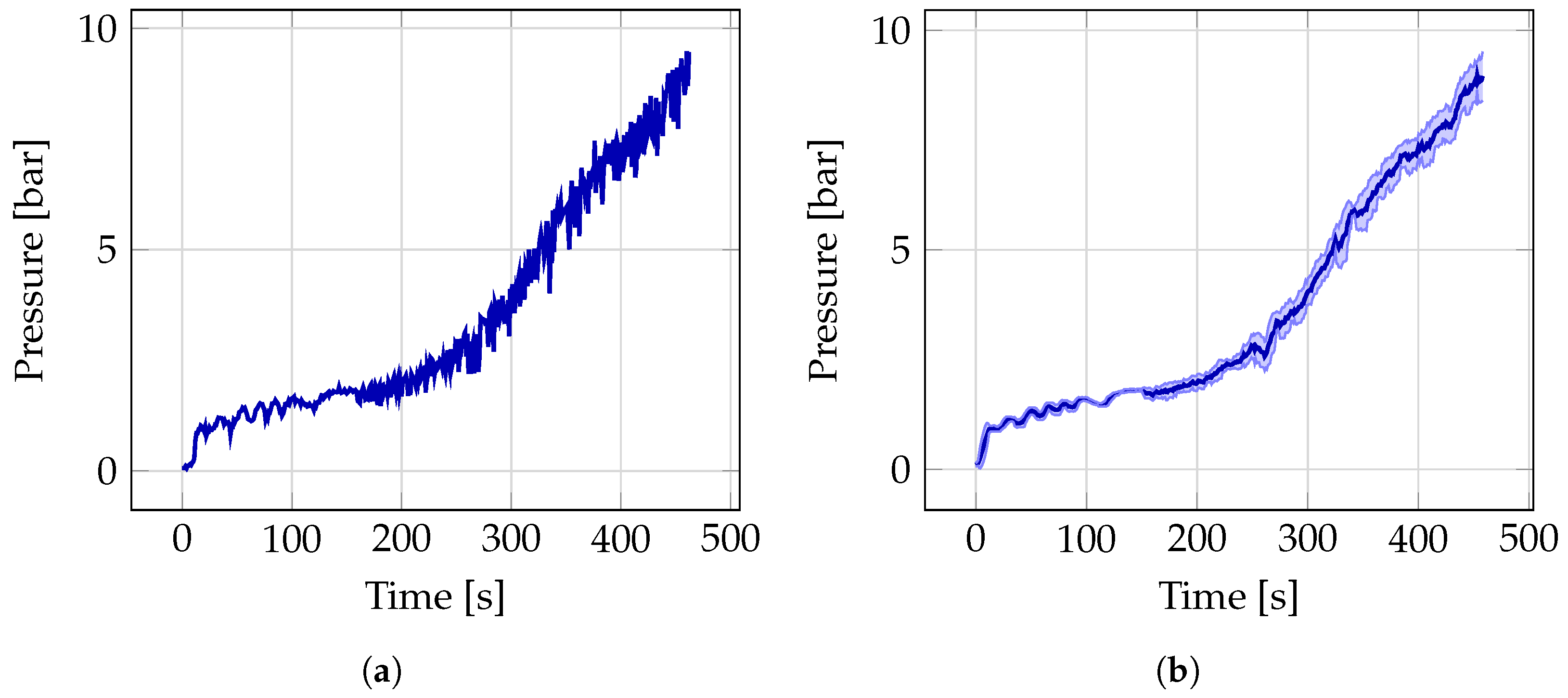
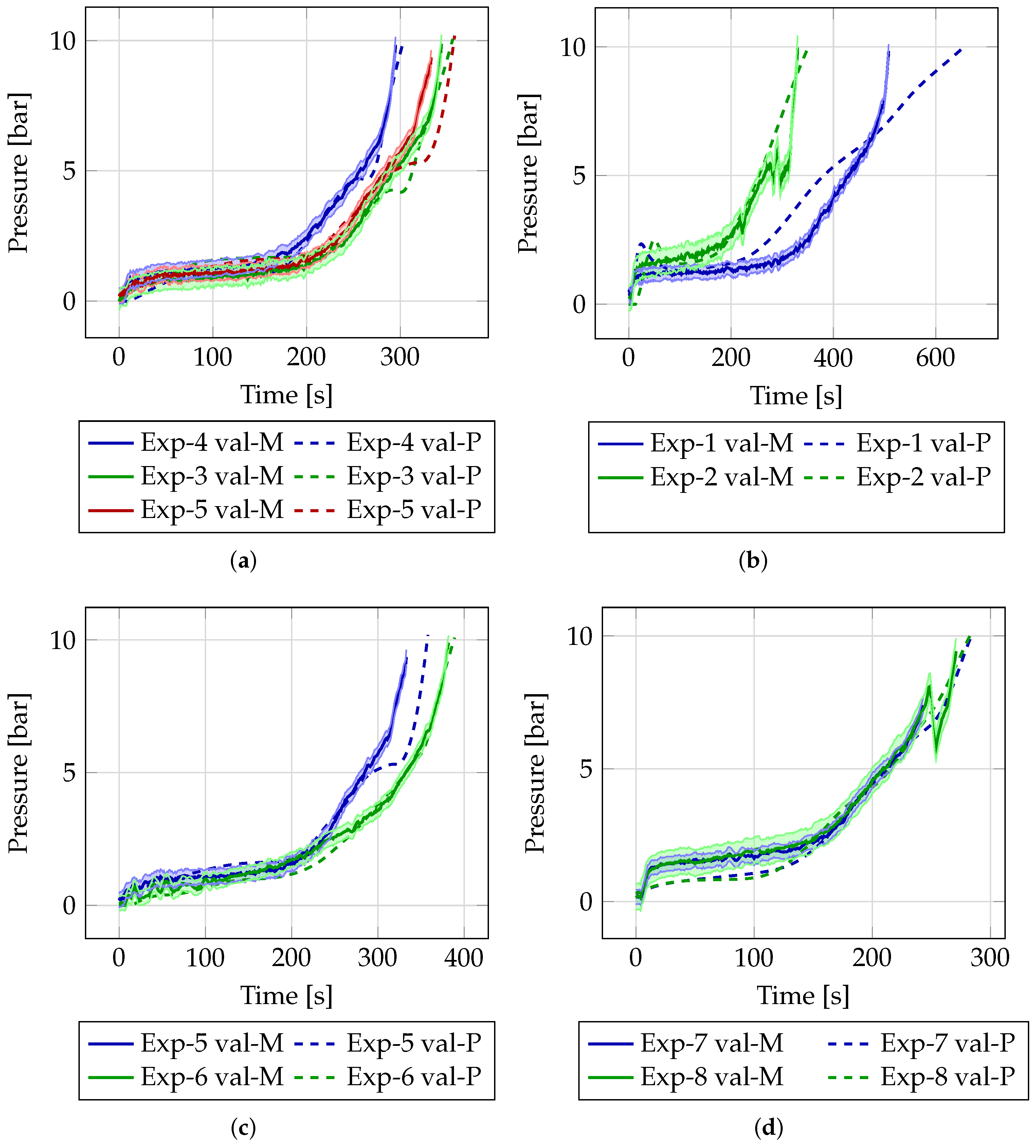
3.1. Pressure Prediction
- Partially known data
- Unknown experiments
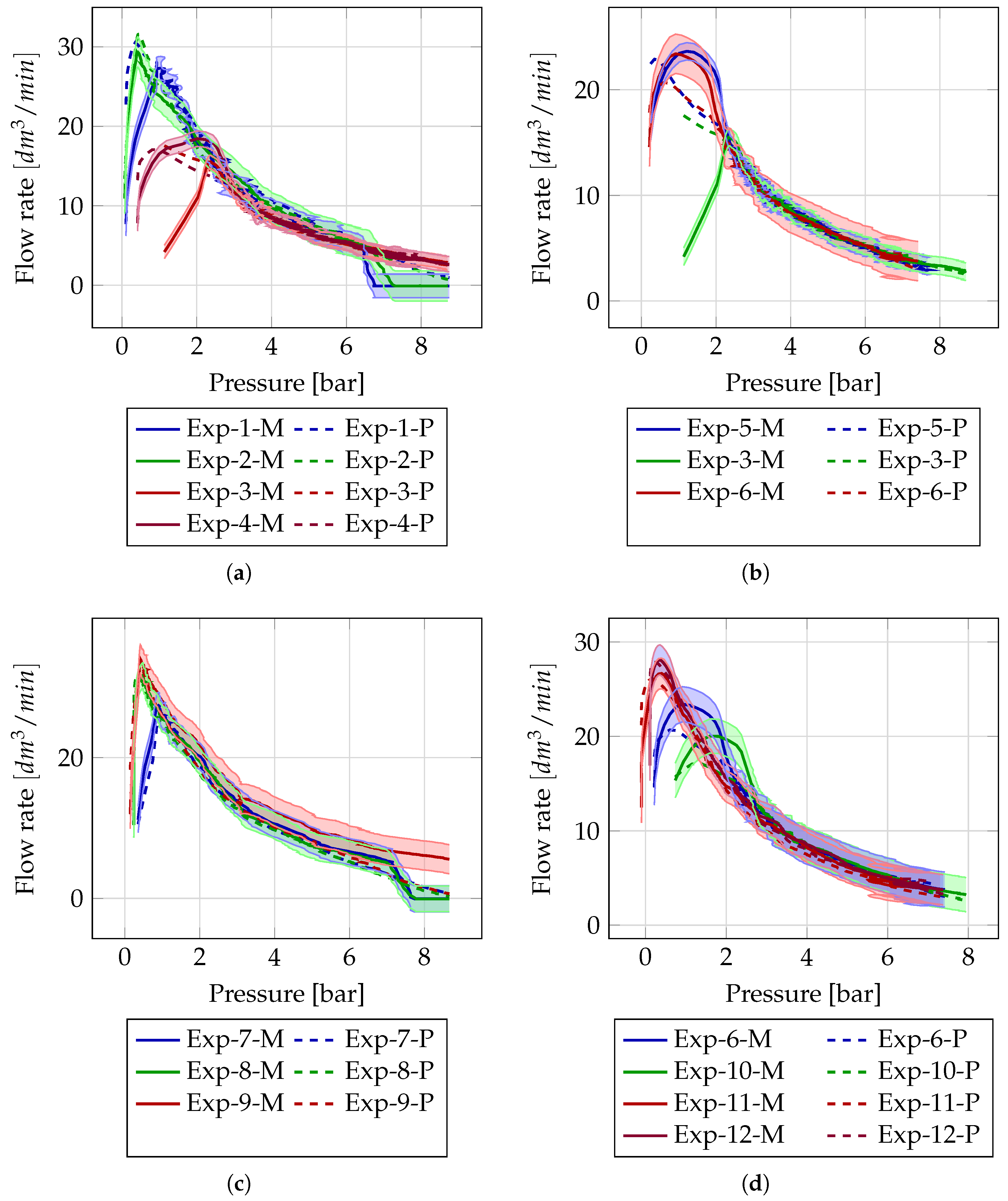
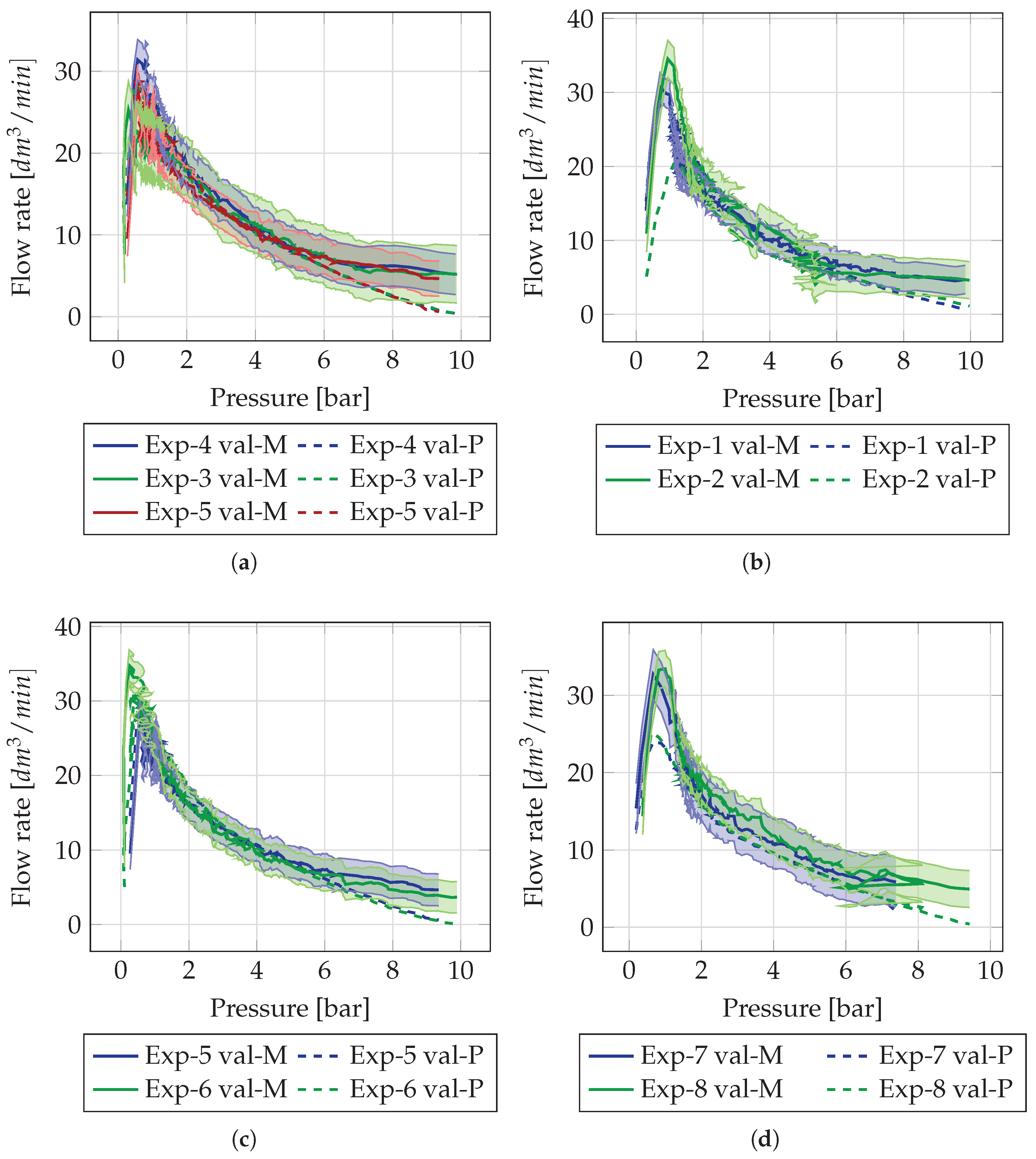
3.2. Flow Rate Prediction
- Partially known data
- Unknown experiments
| Experiment | Pressure | Flow Rate | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | RMSE | RL2N [%] |
RL2N-B [%] | PIB [%] | MSE | RMSE | RL2N [%] |
RL2N-B [%] | PIB [%] | |
| 1 | 0.041 | 0.202 | 4.6 | 0.5 | 96 | 4.955 | 2.226 | 13.4 | 5.3 | 50 |
| 2 | 0.011 | 0.103 | 2.6 | 0.1 | 98 | 3.868 | 1.967 | 9.8 | 2.3 | 64 |
| 3 | 0.041 | 0.202 | 4.1 | 1.3 | 74 | 2.150 | 1.466 | 16.7 | 10.6 | 77 |
| 4 | 0.036 | 0.190 | 3.7 | 0.9 | 75 | 0.468 | 0.684 | 8.4 | 3.4 | 69 |
| 5 | 0.006 | 0.075 | 1.7 | 0.3 | 97 | 0.339 | 0.582 | 6.2 | 2.6 | 89 |
| 6 | 0.178 | 0.421 | 9.8 | 4.7 | 64 | 1.413 | 1.189 | 10.2 | 3.6 | 62 |
| 7 | 0.013 | 0.114 | 2.7 | 0.2 | 98 | 2.905 | 1.704 | 9.2 | 3.3 | 60 |
| 8 | 0.045 | 0.211 | 5.8 | 2.4 | 76 | 3.953 | 1.988 | 9.1 | 4.9 | 91 |
| 9 | 0.008 | 0.088 | 2.2 | 0.0 | 100 | 3.934 | 1.983 | 8.5 | 1.6 | 77 |
| 10 | 0.038 | 0.196 | 4.1 | 0.5 | 86 | 0.984 | 0.992 | 9.9 | 2.7 | 66 |
| 11 | 0.066 | 0.257 | 6.7 | 2.3 | 75 | 1.082 | 1.040 | 7.0 | 3.1 | 93 |
| 12 | 0.124 | 0.352 | 9.2 | 4.8 | 71 | 0.914 | 0.956 | 6.1 | 3.1 | 98 |
| Mean | 0.048 | 0.185 | 5.0 | 1.8 | 82 | 2.579 | 1.545 | 9.3 | 3.7 | 74 |
| Experiment | Pressure | Flow Rate | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | RMSE | RL2N [%] |
RL2N-B [%] | PIB [%] | MSE | RMSE | RL2N [%] |
RL2N-B [%] | PIB [%] | |
| 1-val | 0.838 | 0.915 | 28.2 | 15.8 | 20.00 | 10.281 | 3.206 | 18.0 | 6.7 | 50.00 |
| 2-val | 0.709 | 0.842 | 24.2 | 11.9 | 46.00 | 12.593 | 3.549 | 20.9 | 7.8 | 35.00 |
| 3-val | 0.250 | 0.500 | 16.1 | 5.9 | 47.00 | 13.845 | 3.721 | 20.9 | 5.1 | 55.00 |
| 4-val | 0.171 | 0.414 | 13.3 | 4.3 | 54.00 | 1.737 | 1.318 | 6.6 | 1.3 | 84.00 |
| 5-val | 0.488 | 0.699 | 22.3 | 13.1 | 52.00 | 6.323 | 2.515 | 13.5 | 3.7 | 37.00 |
| 6-val | 0.100 | 0.317 | 9.9 | 2.9 | 64.00 | 6.531 | 2.555 | 12.6 | 5.7 | 49.00 |
| 7-val | 0.273 | 0.523 | 16.8 | 7.1 | 54.00 | 4.876 | 2.208 | 12.7 | 2.8 | 63.00 |
| 8-val | 0.397 | 0.630 | 16.4 | 4.8 | 56.00 | 9.649 | 3.106 | 17.9 | 5.4 | 45.00 |
| Mean | 0.403 | 0.605 | 18.4 | 8.2 | 49.13 | 8.229 | 2.772 | 15.4 | 4.8 | 52.25 |
3.3. Current Limitations and Future Work
- Material specificity: As described in Section 2.1, all experiments were carried out using a single suspension, perlite, to ensure consistent results. However, other suspensions such as kieselgur exhibit significantly different behaviours due to their high porosity and fluid retention characteristics. This may affect the direct applicability of the current model to a broader range of materials.
- Limited scalability: The experiments were performed using a chamber filter press with a plate size of 300 mm. While the current model has shown that it can adapt to different configurations if such setups are included during training, its ability to generalize to presses of different sizes remains dependent on the diversity of the training data. Without sufficient variation, scaling the model to untested press sizes or configurations may be less reliable.
- Hardware dependency: The predictive accuracy of the model is influenced by the mechanical state of the system. Irregularities, such as inefficiencies in the membrane pump, leaks, or hardware degradation, can affect performance and introduce noise into the training data. If such anomalies remain undetected, they could gradually influence model performance.
4. Conclusions
- Pressure prediction (training and validation): Overall, MSE was , RMSE was and RL2N was . Deviation from the CI90% bounds was .
- Flow rate prediction (training and validation): Overall, MSE was , RMSE was and RL2N was . Deviation from the CI90% bounds was .
- Pressure prediction (unknown data): Overall MSE was , RMSE was and RL2N was . Deviation from the CI90% bounds was .
- Flow rate prediction (unknown data): Overall MSE was , RMSE was , and RL2N was . Deviation outside CI90% bounds was .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| AR | augmented reality |
| CI90 | 90% confidence interval |
| CFD | computational fluid dynamics |
| CNN | convolutional neural network |
| DT | digital twin |
| FFNN | feedforward neural network |
| GRU | gated recurrent unit |
| LBM | Lattice Boltzmann method |
| LSTM | long short-term memory |
| MA | moving average |
| MAE | mean absolute error |
| M | measured |
| MSE | mean square error |
| ML | machine learning |
| NN | neural network |
| NTP | network time protocol |
| OPC UA | open platform communications unified architecture |
| P | predicted |
| PIB | point inside bounds |
| PTP | precision time protocol |
| ReLU | rectified linear unit |
| RL2N | relative -norm |
| RL2N-B | relative -norm bounds |
| RMSE | root mean square error |
| RNN | recurrent neural network |
| STD | standard deviation |
References
- Garner, R.; Naidu, T.; Saavedra, C.; Matamoros, P.; Lacroix, E. Water Management in Mining: A Selection of Case Studies; International Council on Mining & Metals: London, UK, 2012. [Google Scholar]
- Gunson, A.; Klein, B.; Veiga, M.; Dunbar, S. Reducing mine water requirements. J. Clean. Prod. 2012, 21, 71–82. [Google Scholar] [CrossRef]
- Baker, E. Mine Tailings Storage: Safety Is No Accident; GRID-Arendal: Arendal, Norway, 2017. [Google Scholar]
- Matschullat, J.; Gutzmer, J. Mining and Its Environmental Impacts. In Encyclopedia of Sustainability Science and Technology; Springer: New York, NY, USA, 2012; pp. 6633–6645. [Google Scholar] [CrossRef]
- Tran, T.; Truong, T.; Tran, T.; Hài, N.; Dao, Q. An overview of the application of machine learning in predictive maintenance. Petrovietnam J. 2021, 10, 47–61. [Google Scholar] [CrossRef]
- McCoy, J.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Anagnostopoulos, I.; Chatzilygeroudis, K.; Maragos, P. A Prototype Implementation of Factory Monitoring Using VR and AR Technologies. arXiv 2023, arXiv:2306.09692. [Google Scholar]
- Alpha Wastewater. Wastewater Treatment and Augmented Reality: Visualizing Processes and Optimizing Operations. 2023. Available online: https://www.alphawastewater.com/wastewater-treatment-and-augmented-reality-visualizing-processes-and-optimizing-operations/?utm_source=chatgpt.com (accessed on 16 April 2025).
- Alatawi, H.; Albalawi, N.; Shahata, G.; Aljohani, K.; Alhakamy, A.; Tuceryan, M. An AR-Assisted Deep Reinforcement Learning-Based Model for Industrial Training and Maintenance. Sensors 2023, 23, 6024. [Google Scholar] [CrossRef]
- Landman, K.A.; White, L.R. Predicting filtration time and maximizing throughput in a pressure filter. AIChE J. 1997, 43, 3147–3160. [Google Scholar] [CrossRef]
- Puig-Bargués, J.; Duran-Ros, M.; Arbat, G.; Barragán, J.; Ramírez de Cartagena, F. Prediction by neural networks of filtered volume and outlet parameters in micro-irrigation sand filters using effluents. Biosyst. Eng. 2012, 111, 126–132. [Google Scholar] [CrossRef]
- Hawari, A.H.; Alnahhal, W. Predicting the performance of multi-media filters using artificial neural networks. Water Sci. Technol. 2016, 74, 2225–2233. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, K.; Andrews, R. Application of artificial neural networks for filtration optimization. J. Environ. Eng. 2011, 137, 1040–1047. [Google Scholar] [CrossRef]
- Khan, W.A.; Chung, S.H.; Awan, M.U.; Wen, X. Machine learning facilitated business intelligence (Part I): Neural networks learning algorithms and applications. Ind. Manag. Data Syst. 2020, 120, 657–698. [Google Scholar] [CrossRef]
- Khan, W.A.; Chung, S.H.; Eltoukhy, A.E.; Khurshid, F. A novel parallel series data-driven model for IATA-coded flight delays prediction and features analysis. J. Air Transp. Manag. 2024, 114, 102488. [Google Scholar] [CrossRef]
- Spielman, L.; Goren, S.L. Model for predicting pressure drop and filtration efficiency in fibrous media. Environ. Sci. Technol. 1968, 2, 279–287. [Google Scholar] [CrossRef]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—Open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Krause, M.J.; Klemens, F.; Henn, T.; Trunk, R.; Nirschl, H. Particle flow simulations with homogenised lattice Boltzmann methods. Particuology 2017, 34, 1–13. [Google Scholar] [CrossRef]
- Trunk, R.; Bretl, C.; Thäter, G.; Nirschl, H.; Dorn, M.; Krause, M.J. A Study on Shape-Dependent Settling of Single Particles with Equal Volume Using Surface Resolved Simulations. Computation 2021, 9, 40. [Google Scholar] [CrossRef]
- Stipić, D.; Budinski, L.; Fabian, J. Sediment transport and morphological changes in shallow flows modelled with the lattice Boltzmann method. J. Hydrol. 2022, 606, 127472. [Google Scholar] [CrossRef]
- Hafen, N.; Dittler, A.; Krause, M.J. Simulation of particulate matter structure detachment from surfaces of wall-flow filters applying lattice Boltzmann methods. Comput. Fluids 2022, 239, 105381. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.; Zhang, Z.; Zhang, X. Lattice Boltzmann modeling and analysis of ceramic filtration with different pore structures. J. Taiwan Inst. Chem. Eng. 2022, 132, 104–113. [Google Scholar] [CrossRef]
- Haussmann, M.; Ries, F.; Jeppener-Haltenhoff, J.B.; Li, Y.; Schmidt, M.; Welch, C.; Illmann, L.; Böhm, B.; Nirschl, H.; Krause, M.J.; et al. Evaluation of a Near-Wall-Modeled Large Eddy Lattice Boltzmann Method for the Analysis of Complex Flows Relevant to IC Engines. Computation 2020, 8, 43. [Google Scholar] [CrossRef]
- Wichmann, K.R. Evaluation and Development of High Performance CFD Techniques with Focus on Practice-Oriented Metrics. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- Callé, S.; Bémer, D.; Thomas, D.; Contal, P.; Leclerc, D. Changes in the performances of filter media during clogging and cleaning cycles. Ann. Occup. Hyg. 2001, 45, 115–121. [Google Scholar] [CrossRef]
- Kandra, H.S.; McCarthy, D.; Fletcher, T.D.; Deletic, A. Assessment of clogging phenomena in granular filter media used for stormwater treatment. J. Hydrol. 2014, 512, 518–527. [Google Scholar] [CrossRef]
- Kehat, E.; Lin, A.; Kaplan, A. Clogging of filter media. Ind. Eng. Chem. Process. Des. Dev. 1967, 6, 48–55. [Google Scholar] [CrossRef]
- Fränkle, B.; Morsch, P.; Nirschl, H. Regeneration assessments of filter fabrics of filter presses in the mining sector. Miner. Eng. 2021, 168, 106922. [Google Scholar] [CrossRef]
- Callé, S.; Contal, P.; Thomas, D.; Bémer, D.; Leclerc, D. Description of the clogging and cleaning cycles of filter media. Powder Technol. 2002, 123, 40–52. [Google Scholar] [CrossRef]
- Lyu, Z. (Ed.) Handbook of Digital Twins, 1st ed.; CRC Press: Boca Raton, FL, USA; Routledge: London, UK, 2024. [Google Scholar] [CrossRef]
- Teutscher, D.; Weckerle, T.; Öz, Ö.F.; Krause, M.J. Interactive Scientific Visualization of Fluid Flow Simulation Data Using AR Technology-Open-Source Library OpenVisFlow. Multimodal Technol. Interact. 2022, 6, 81. [Google Scholar] [CrossRef]
- Sandberg, I.W.; Lo, J.T.; Fancourt, C.L.; Principe, J.C.; Katagiri, S.; Haykin, S. Nonlinear Dynamical Systems: Feedforward Neural Network Perspectives; John Wiley & Sons: Hoboken, NJ, USA, 2001; Volume 21. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Comprehensive Review of Architectures, Variants, and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- McClarren, R. Feed-Forward Neural Networks; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 119–148. [Google Scholar] [CrossRef]



| Concentration [g/L] | Filter Plate Number | End Pressure [bar] | Cycles | Frequency |
|---|---|---|---|---|
| 6.25 | 2 | 2.0 | 34 | 1 |
| 6.25 | 2 | 4.0 | 32 | 1 |
| 6.25 | 2 | 5.0 | 31 | 1 |
| 6.25 | 2 | 6.0 | 30 | 1 |
| 6.25 | 2 | 8.0 | 29 | 1 |
| 12.50 | 1 | 10 | 4 | 1 |
| 12.50 | 2 | 10.0 | 2, 4, 5, 6, 7, 14, 23, 35, 36 | 9 |
| 12.50 | 2 | 7.0 | 5 | 1 |
| 12.50 | 2 | 8.0 | 6 | 1 |
| 12.50 | 2 | 0.2 | 1 | 1 |
| 12.50 | 2 | 0.5 | 10,11 | 2 |
| 12.50 | 2 | 0.7 | 12,13 | 2 |
| 12.50 | 3 | 10 | 1,2,3 | 3 |
| 25.00 | 2 | 10.0 | 24 | 1 |
| 25.00 | 2 | 5.0 | 18 | 1 |
| 25.00 | 2 | 6.0 | 19 | 1 |
| 25.00 | 2 | 7.0 | 20 | 1 |
| 25.00 | 2 | 8.0 | 21 | 1 |
| 25.00 | 2 | 9.0 | 22 | 1 |
| 25.00 | 2 | 10.0 | 23 | 1 |
| 25.00 | 3 | 10.0 | 25 | 1 |
| 25.00 | 4 | 10.0 | 26 | 1 |
| Experiment | Concentration [g/L] | Filter Plate Number | End Pressure (bar) | Cycles |
|---|---|---|---|---|
| 1 | 12.5 | 2 | 10 | 2 |
| 2 | 12.5 | 2 | 10 | 7 |
| 3 | 12.5 | 2 | 10 | 35 |
| 4 | 12.5 | 2 | 10 | 36 |
| 5 | 6.25 | 2 | 8 | 29 |
| 6 | 25 | 2 | 10 | 23 |
| 7 | 12.5 | 1 | 10 | 4 |
| 8 | 12.5 | 3 | 10 | 2 |
| 9 | 12.5 | 2 | 10 | 5 |
| 10 | 25 | 1 | 10 | 24 |
| 11 | 25 | 3 | 10 | 25 |
| 12 | 25 | 4 | 10 | 26 |
| Experiment | Concentration [g/L] | Filter Plate Number | End Pressure (bar) | Cycles |
|---|---|---|---|---|
| 1 val | 6.25 | 2 | 10 | 24 |
| 2 val | 12.5 | 2 | 10 | 30 |
| 3 val | 12.5 | 2 | 10 | 11 |
| 4 val | 12.5 | 2 | 10 | 10 |
| 5 val | 12.5 | 2 | 10 | 9 |
| 6 val | 12.5 | 3 | 10 | 6 |
| 7 val | 15 | 2 | 10 | 7 |
| 8 val | 15 | 2 | 10 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teutscher, D.; Weber-Carstanjen, T.; Simonis, S.; Krause, M.J. Predicting Filter Medium Performances in Chamber Filter Presses with Digital Twins Using Neural Network Technologies. Appl. Sci. 2025, 15, 4933. https://doi.org/10.3390/app15094933
Teutscher D, Weber-Carstanjen T, Simonis S, Krause MJ. Predicting Filter Medium Performances in Chamber Filter Presses with Digital Twins Using Neural Network Technologies. Applied Sciences. 2025; 15(9):4933. https://doi.org/10.3390/app15094933
Chicago/Turabian StyleTeutscher, Dennis, Tyll Weber-Carstanjen, Stephan Simonis, and Mathias J. Krause. 2025. "Predicting Filter Medium Performances in Chamber Filter Presses with Digital Twins Using Neural Network Technologies" Applied Sciences 15, no. 9: 4933. https://doi.org/10.3390/app15094933
APA StyleTeutscher, D., Weber-Carstanjen, T., Simonis, S., & Krause, M. J. (2025). Predicting Filter Medium Performances in Chamber Filter Presses with Digital Twins Using Neural Network Technologies. Applied Sciences, 15(9), 4933. https://doi.org/10.3390/app15094933






