Abstract
A fundamental limitation of fMRI based on the BOLD effect is its limited spatial specificity. This is because the BOLD signal reflects neurovascular coupling, leading to macrovascular changes that are not strictly limited to areas of increased neural activity. However, neuronal activation also induces microstructural changes within the brain parenchyma by modifying the diffusion of extracellular biological water. Therefore, diffusion-weighted imaging (DWI) has been applied in fMRI to overcome BOLD limits and better explain the mechanisms of functional activation, but the results obtained so far are not clear. This is because a DWI signal depends on many experimental variables: instrumental, physiological, and microstructural. Here, we hypothesize that the γ parameter of the fractional diffusion representation could be of particular interest for DW-fMRI applications, due to its proven dependence on local magnetic susceptibility and diffusion multi-compartmentalization. BOLD fMRI and DW-fMRI experiments were performed at 3T using an exemplar application to task-based activation of the human visual cortex. The results, corroborated by simulation, highlight that γ provides complementary information to conventional diffusion fMRI and γ can quantify cellular morphology changes and neurovascular regulation during neuronal activation with higher sensitivity and specificity than conventional BOLD fMRI and DW-fMRI.
1. Introduction
Functional MRI (fMRI) is crucial for studying brain function [1]. It allows researchers to map neural activity in response to different cognitive and sensory tasks, providing valuable insights into brain connectivity and functional organization. On the other hand, diffusion MRI [2,3] is essential for investigating the brain’s microstructure by tracking the movement of biological water molecules. It enables the reconstruction of neural pathways and the assessment of structural integrity to study neurodevelopment, aging, and neurological disorders.
A key limitation of fMRI, which is based on the blood-oxygen-level-dependent (BOLD) effect, is its limited spatial specificity. This arises because the BOLD signal is related to the neurovascular coupling, which leads to macrovascular changes that are not strictly confined to the regions with increased neural activity [4,5,6,7].
The origin of the BOLD fMRI effect lies in the different magnetic properties of oxy-hemoglobin, which is approximately isomagnetic relative to tissue, and deoxy-hemoglobin, which is slightly paramagnetic relative to tissue [8]. The magnetic susceptibility difference (Δχ) decreases during activation due to changes in the relative amounts of oxy- and deoxy-hemoglobin. This, in turn, leads to an increase in T2 and T2*, resulting in an enhanced BOLD signal. The reduction in Δχ during activation [9] is associated with a reduction in internal magnetic field inhomogeneities (called internal or background gradients) Gi.
However, the brain parenchyma also contains some other microstructural changes associated with neuronal activation. For example, cell swelling and membrane expansion involving neural soma, axons, and glial cells have been observed in vitro using invasive techniques [10,11].
Considering the potential of diffusion techniques to infer microstructural changes in vivo [12,13,14], diffusion-weighted imaging (DWI) techniques have also been applied in the field of fMRI, the so-called DW-fMRI.
Early studies conducted at intermediate-to-low b-values revealed that the apparent diffusion coefficient (ADC) time course closely mirrors the vascular BOLD signal, alongside an observed increase in water ADC during activation. This phenomenon can be attributed to the inverse dependence of ADC on Gi [15,16,17]. Moreover, DWI at b-values lower than 500 s/mm2 has been used to eliminate the unwanted (mostly perfusion) signal from arteries and large vessels [18,19], which can be spatially displaced from the site of neural activity [20].
Other studies have proposed the hypothesis that DW-fMRI signals at high b-values may be coupled to neuronal activity more directly than the regional blood flow, which is exploited in conventional fMRI approaches [21,22]. Notably, instead of the usual increase in ADC values during brain activation, using b = 1400 s/mm2, Darquie and Le Bihan [22] found a synchronized decrease in ADC that was attributed to cell swelling induced by enhanced neuronal activity, together with the suppression of the intravascular signal due to high b-values. In subsequent studies using a bi-exponential diffusion model [23,24], the feeble/moderate decrease in ADC was interpreted as an effect of small dilation of the slow diffusion water compartment and a volume decrease in the fast diffusion water compartment in the extravascular space.
While Le Bihan and co-workers in subsequent high-b-value experiments using drugs to block the neurovascular effect have reinforced the hypothesis of ADC decrease being associated with cellular swelling [25,26], other groups suggested that a large component of the DW-fMRI signal at high b-values is vascular rather than neuronal [27,28]. Moreover, in simultaneous calcium fluorescence imaging and DW-fMRI, no evidence was found that diffusion signals directly correlate with normal spontaneous neuronal activity [29].
The abovementioned studies highlighting a transient decrease in water ADC during activation were conducted using bipolar diffusion gradients and suitable strategies to eliminate the contribution of the Gi, such as using a high g strength [23,30] and diffusion-sensitized double spin-echo EPI sequence [26]. Indeed, as underlined by Pampel [31], the ADC increase due to Δχ changes is in contrast to the minute effect suggested by Le Bihan. Therefore, the Gi contributions in DW-fMRI measurements may mask or even cancel out the effect of an ADC decrease [32,33]. In particular, Pampel showed that the interaction between diffusion gradients and Δχ-induced Gi around vessels has an impact on ADC measurements and fMRI experiments [31].
However, using both low–medium and high b-values, activation maps are compatible with conventional BOLD fMRI-derived maps, and the activated brain areas obtained using DW-fMRI were reported to be more “localized” and detailed compared to BOLD areas [18,23,26,34,35].
In contrast to conventional DWI approaches based on Normal Gaussian diffusion [36], non-Gaussian models provide a superior intrinsic specificity and sensitivity to detect microscopic tissue changes [37,38,39,40,41]. Indeed, a recent study showed the time dependence of the diffusional kurtosis in neural activity in rodents [42], using higher b-values () than those used in previous studies and showing a greater sensitivity of the kurtosis parameter to the neural activation.
In this brief communication, we aim to take a step forward, adopting fractional diffusion representation [43,44,45,46] with higher b-values () to provide preliminary novel insights into the ongoing DW-fMRI debate.
Fractional diffusion describes diffusion with a fractional order derivative, which allows for more flexibility in capturing non-Gaussian diffusion. Fractional derivatives differ from conventional derivatives in that they allow for differentiation in a non-integer (fractional) order. Unlike conventional derivatives, which measure the rate of change at a specific point, fractional derivatives describe processes with memory and spatial correlations, making them suitable for modeling complex diffusion in biological tissues. In neuro-MRI, these fractional orders serve as quantifiable parameters, meaning that they can be measured and interpreted to provide insights into the brain’s microstructure.
The fractional diffusion representation is based on the generalization of the diffusion equation to fractional order derivatives (e.g., as in the Continuous-time random walk—CTRW—framework [47,48]) and introduces the time fractional exponent and the spatial fractional exponent . These new parameters are specific imaging biomarkers of tissue complexity and magnetic property heterogeneities [43,44,45,46,49,50,51,52,53,54].
Here, we hypothesize that the γ parameter, the fractional exponent of the space derivative, could be of particular interest for DW-fMRI applications due to its proven dependence on both the local Δχ [43,44,46] and diffusion multi-compartmentalization [52]. Hence, we studied whether γ can quantify cellular morphology changes and neurovascular regulation during neuronal activation with higher sensitivity and specificity than conventional BOLD fMRI and DW-fMRI, with an exemplar application to task-based activation of the human visual cortex. The dependence of the ADC parameter on microstructures and other physiological variables is well recognized; however, this is not the case for the γ parameter. For this reason, to better interpret the data related to γ experiments, we performed simulations to highlight the dependence modality of γ on Δχ variations and changes in the extracellular space due to cellular swelling.
Finally, we discuss the preliminary results and future further investigation and validation directions.
2. Materials and Methods
2.1. Theoretical Background
It is known that the DW signal that is obtained using a PFG [13,17] experiment is proportional to the Fourier transform (FT) of the motion propagator (MP) that describes the probability of spin motion. When the MP is Gaussian and Brownian, the PFG signal attenuation as a function of the b-values follows a mono-exponential decay. On the other hand, when the MP is non-Brownian, it is possible to define, in general, the average MP as the solution of the fractional diffusion equation (e.g., as introduced within the framework of the CTRW model [47]). This equation introduces two parameters, the fractional exponent of the time derivative, α, and the fractional exponent of the space derivative, γ, which are the time and space derivative fractional orders. Specifically, α is measured by varying the diffusion time Δ in a PFG sequence [43,48,49,53,54,55], and it has been recently shown to be a generalization of the Kurtosis representation [50]. Conversely, γ is measured by varying the gradient strength g in a PFG sequence [46,48,52,56]. Of relevance for DW-fMRI applications, it has been reported both in vitro [44,45] and in vivo in the human brain [40,46] that γ maps show a useful image contrast to highlight tissue interfaces. The resulting image contrast of γ maps, deriving from water diffusion multi-compartmentalization, strictly reflects he local Δχ, and thus, it allows for improved discrimination of the interface between different compartments compared to T2* images.
Leaving aside here any discussion about the real anomalous diffusion of extracellular water in the human brain, in the last 10 years, through various experiments conducted in vitro [52] and in vivo on the human brain [40,46], we have highlighted that the DW signal representation of the anomalous superdiffusion may furnish a new useful image contrast in neuroimaging studies. We have recognized that, in a complex system such as the brain, the fractional diffusion representation related to the fractional exponent of the space derivative, γ, can better describe water diffusion multi-compartmentalization, also thanks to its peculiar sensibility to magnetic field inhomogeneity. The magnetic field inhomogeneities may arise from the presence of heavy metal accumulation or the difference in local magnetic susceptibility between different adjacent compartments or tissues. In the human brain, extracellular water can diffuse with Brownian diffusion, non-Gaussian diffusion, or, in the context of anomalous diffusion, with subdiffusion. We do not find superdiffusion, which is quantified by the γ parameter. Superdiffusion is not real but mimicked by the nuclear spins of biological water, which, due to local inhomogeneities of the magnetic field and due to their indistinguishability, simulate superdiffusion dynamics. Due to the inhomogeneities, magnetization disappears in a voxel to “appear” in an adjacent (or even distant) one where there are magnetic field gradient conditions that are favorable to the refocusing of the magnetization components. For this reason, we say that γ quantifies pseudo-superdiffusion, and we use the fractional diffusion formalism to extract the γ parameter.
Briefly, the fractional diffusion representation is based on the following relation [43,47]:
where is the FT of MP, are generalized diffusion constants, whose units are (ms−1), is the wave vector, and .
To measure γ, expression (1) has to be fitted to data obtained by PFG signal decay as a function of , where is the diffusion gradient duration, collected by changing the g strength at a constant value of . Since is a constant, the stretched exponential function that is used to quantify can easily be derived from expression (1) [57,58]. By replacing in Equation (1), the following relations can be derived:
where S(b) is the b-weighted signal, is the unweighted signal, D is the diffusion coefficient, ρ2(γ−1) and Δ(γ−1) are fractional-order space and time constants that preserve units, and Deff is an effective diffusion constant.
2.2. Participants
Five healthy volunteers (males, mean age: 26 ± 1 years) with no history of neurological or psychiatric illness or injury participated in this study after giving written informed consent, according to the national laws and the local ethics committee guidelines (Santa Lucia Foundation Ethical Committee). All subjects gave written informed consent under the Declaration of Helsinki.
2.3. Stimulus Paradigm
The visual stimulation, used during conventional and diffusion fMRI, was obtained from a flickering half-dartboard (frequency, 8 Hz) projected on a screen within the MRI scanner room through a video projector. Only the right half of the checkerboard was displayed against a black background. This stimulation was presented in a block design, alternating with a baseline consisting of a black screen and a gray central fixation point. Epochs lasted 16 scans each (corresponding to 22.4 s). See Figure 1 for details.
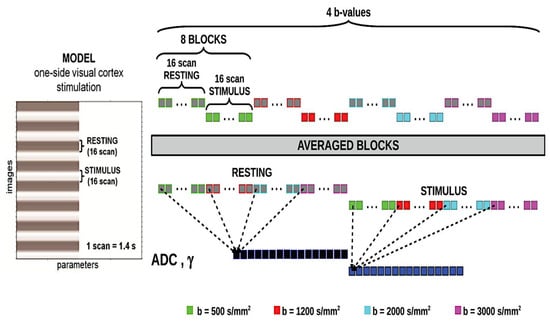
Figure 1.
The temporal scheme of the model used to produce the one-side visual cortex stimulation and schematic representation of the signal processing flow for a data set obtained from a single subject. Blocks are repeated twice to repeat acquisitions two times. The resulting block-averaged ADC and γ time courses for the rest and stimulation conditions are then averaged across subjects to give the group-averaged data.
2.4. MRI Acquisition
A 3T scanner (Siemens Magnetom Allegra, Erlangen, Germany), equipped with a circularly polarized transmit–receive coil was used. The maximum gradient strength was 40 mT m−1, with a maximum slew rate of 400 mT m−1 ms−1. Eight oblique slices centered on the calcarine fissure were selected from a rapid localization scan. A total of 256 volumes of a double spin-echo echo-planar imaging sequence (DSEDW-EPI) were acquired for ten consecutive functional runs using the following parameters: TR/TE = 1400/112 ms, slice thickness 3 mm, with 50% gap, matrix size 64 × 64, and in-plane resolution of 3 × 3 mm2. The diffusion encoding gradients were applied along readout and slice directions at 5 different b-values, 80, 500, 1500, 2000, and 3000 s/mm2, with Δ/δ = 107/45 ms by varying g strength. The acquisitions were repeated twice in a random order for each of the four b-values to increase the signal-to-noise ratio. BOLD fMRI images were acquired by using a T2*-weighted gradient-echo sequence with the same TR = 1400 ms of the DW-EPI, 24 slices of 1 mm thickness. A volumetric T1-weighted scan was acquired for anatomical reference.
2.5. Processing
Activation maps were computed for each subject. DW images were corrected for motion artifacts and eddy currents (by using the “eddy” tool within FSL [59]) and were then registered to the T1 image, followed by spatial smoothing with a Gaussian filter of 6 mm full width at half maximum, by using SPM8 (www.fil.ion.ucl.ac.uk/spm, accessed on 28 April 2025). The DW signal was averaged voxel-by-voxel over the two acquisitions and directions acquired at each b-value. The signal time course for each b-value of the data set was then folded into a single [activation–rest] epoch by averaging the eight subsequent epochs of the paradigm (Figure 1).
The time course of the conventional ADC and corresponding activation maps were obtained by using SPM8 [22,23] according to the following:
where S1 is the signal at b1 = 80 s/mm2, and S2 is the signal at b2 = 2000 s/mm2. The time course of the γ parameter and the corresponding activation maps were calculated using the full range of b-values. A nonlinear Levenberg–Marquardt algorithm was used to efficiently estimate from the signal S at each b-value, voxel-by-voxel, the γ parameter in parallel on GPU (Nvidia GeForce GT650M) according to the stretched exponential model:
where η takes into account the Rician noise variance.
BOLD fMRI maps were obtained using the conventional pipeline of SPM8. The activation maps (γ maps) were obtained using SPM8 and following the same procedure employed for calculating ADC maps. In all imaging modalities (BOLD, ADC, and γ maps) voxels were classified as significantly activated at uncorrected p-values < 0.005.
2.6. Simulations
Two-dimensional simulations were performed to study the γ behavior as a function of cell packing ϕ in extravascular tissue in the absence and presence of different degrees of Δχ. Magnetic susceptibility difference values of 0.08 ppm were used, which is a value that is generally found at the interfaces of brain tissues and equal to 0.2 ppm, which indicates a greater difference in susceptibility due to, for example, the presence of paramagnetic substances or heavy metals [46]. On the other hand, the cell packing was varied from a value of 45 up to 85.
Monte Carlo simulation of 2 × 106 spins was performed to numerically simulate the pulse gradient spin echo (PGSE) signal attenuation and the corresponding γ under different structural (different sphere-packing cells) and physiological (different Δχ) conditions by using the phase accumulation approach, as described by Palombo and co-workers [60].
3. Results
The time course of BOLD, ADC, and γ within a specific volume of interest (VOI) were compared separately for each subject. VOIs were defined by thresholding activation maps at Zscore ≥ 10 for BOLD and Zscore ≥ 3 for ADC and γ maps. The response as a function of the scan number (1 scan number = 1.4 s) for a representative subject and the average among all the subjects are displayed in Figure 2a,b, respectively. Please note that the absolute value of ADC, γ, and BOLD variation between a resting and activated state is displayed.
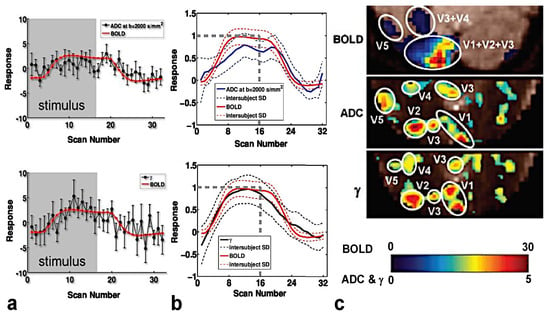
Figure 2.
Time courses of the γ parameter and BOLD fMRI signals (lower row), Normal Gaussian diffusion quantified by ADC (obtained with b = 2000 s/mm2 and b = 80 s/mm2), and BOLD fMRI signals (upper row) for a representative subject (a); time courses of the γ and BOLD fMRI signals (lower row), ADC (obtained with b = 2000 s/mm2 and b = 80 s/mm2), and BOLD fMRI signals (upper row) for the averaged signal among all the investigated subjects (b). The gray swathes/dashed lines indicate stimulation and rest blocks (time expressed in scan units; 1 scan = 1.4 s). The error bars in (a) represent the standard deviation of the response across the corresponding eight epochs. Please note that the absolute value of ADC, γ, and BOLD variation between the resting and activated state is displayed. Indeed, during activation, ADC decreases, whereas the γ and BOLD signals increase. BOLD fMRI, Normal Gaussian diffusion (ADC) fMRI, and γ activation maps for a representative subject (c). Voxels were classified as significantly activated at uncorrected p-values < 0.005. The maps displayed in (c) show that ADC and γ maps provide improved localization of activation areas (visual areas, V1, V2, V3, V4, V5) compared to BOLD localization.
In agreement with Le Bihan [23], the ADC time course showed a feeble decrease at stimulus onset, and overall, the BOLD and ADC expansion time courses were approximately similar in shape (Figure 2a,b, upper row). Conversely, the γ time course showed a feeble-medium increase at stimulus onset. In Figure 2a,b (upper row), the BOLD and γ expansion time courses were compared to each other, highlighting a better matching than that observed between ADC and BOLD. Moreover, the γ response is higher (but not significantly when the results of all the subjects are considered) than that of ADC.
In all subjects, the ADC and γ activation maps (displayed in Figure 2c), directly calculated from the raw diffusion-sensitized MRI signals, clearly showed activation of primary as well as secondary visual areas, such as the visual motion area MT/V5, which is typically activated by flickering stimuli [61]. The spatial extent of the activation was more restricted to the primary visual region for γ and DW fMRI than BOLD, in agreement with Williams et al. [62] and other authors [28,34].
The interpretation of these results is that γ could be more sensitive than ADC to the neurophysiological changes that occur during activation. Looking at the activation maps, the better localization of the activation areas expressed by the γ maps would suggest a greater dependence of γ than BOLD and ADC on the neuronal component that produces cellular swelling and/or a greater sensitivity to local Δχ changes. However, these observations are the result of experiments performed on only five subjects. These preliminary results need confirmation, which can be obtained from a large cohort of volunteers.
Finally, the activated voxels from the γ maps compared with those from the ADC maps showed a tendency towards a higher contrast-to-noise ratio (Figure 2c).
In Figure 3, the γ behavior as a function of cell packing ϕ in extravascular tissue and physiological condition highlighted by the Δχ changes is displayed. In accordance and coherently with what was observed previously [40,45,46,52], the value of the γ parameter increases with the decrease in the extracellular space where the water diffuses, and it decreases with the increase in the magnetic susceptibility difference between adjacent tissues.
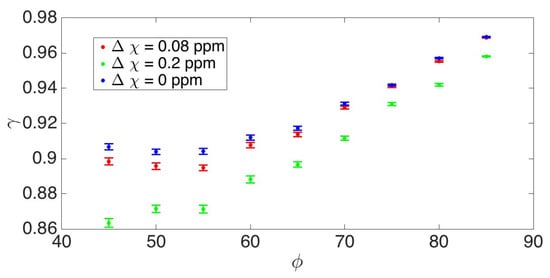
Figure 3.
γ behavior as a function of cell packing ϕ in extravascular tissue and physiological condition (different Δχ). The γ vs. ϕ graph shows that when increasing the cell packing, i.e., decreasing the extracellular space, γ increases. This feature of γ suggests it to be a potential candidate for investigating the cell swelling occurring during neuronal activation. On the other hand, the γ-value decreases as the magnetic susceptibility difference between the tissues increases.
The γ vs. cell packing plot indicates that considering the extracellular space, which in gray matter has a ϕ of about 40%, as the cell packing increases (corresponding to a decrease in extracellular space), γ also increases. This trend highlights the potential of γ as a biomarker to detect cell swelling, a key event during neuronal activation.
However, γ also increases when the magnetic susceptibility difference (Δχ) between tissues decreases, which is what happens during activation. This suggests that γ is influenced not only by microstructural properties, but also by the tissue composition and magnetic properties, correlated with changes in blood oxygenation or iron content. These results indicate that γ could serve as a valuable tool to assess changes due to the vascular component as well.
To disentangle the two γ dependencies (neuronal and vascular effect during activation) and investigate the role of the neuronal component through cell swelling, it would therefore be necessary to design animal experiments using drugs that block the vascular effect during activation combined with DW-fmri acquisition sequences that use efficient bipolar gradients that greatly decrease γ’s dependence on magnetic susceptibility differences.
4. Discussion
DW-fMRI performed in this preliminary study shows that the γ parameter (i.e., the fractional order of the space derivative in the fractional diffusion representation) response to a brain activation is opposite to that provided by ADC at high b-values and matches well to the BOLD activation, being more pronounced than that observed using conventional ADC methods (Figure 2). However, to obtain the ADC results, we used b = 2000 s/mm2 and b = 80 s/mm2 instead of the optimized b-values to eliminate any T2-BOLD and perfusion residue (i.e., b = 1800 s/mm2 and b = 1000 s/mm2) [30]. Consequently, the ADC fMRI result could be affected by residual effects of T2-BOLD, which attenuate the ADC signal decrease during activation.
The increase in γ during activation, which is opposite to the ADC decrease, can be explained by considering γ’s dependence on diffusion multi-compartmentalization and local Δχ. At first glance, the similarity of the time course shown for γ and the BOLD response would suggest that the Δχ dependence largely predominates, and therefore, γ’s response is due to the vascular contribution of capillaries and small veins. Although the changes may likely be vascular, they appear more localized than those of BOLD, probably due to minimal intravascular effects. However, it is worth noting that γ increases not only when Δχ decreases, but also when the multi-compartmentalization decreases.
In particular, the presumed cell swelling occurring during functional activation involves a decrease in the multiplicity of extracellular diffusion compartments. To better elucidate the biophysical mechanism underpinning the γ parameter and its relationship with the physiological phenomena occurring during activation, we performed a 2D simulation to obtain γ’s behavior as a function of cell packing in extravascular tissue, ϕ. In Figure 3, the graph of γ vs. ϕ shows that when increasing the cell packing (i.e., decreasing the diffusion multi-compartmentation), γ increases. In parallel, γ increases when Δχ decreases, a phenomenon that occurs during activation.
Considering that the diffusion signal that we acquire in vivo derives from extracellular water, our results confirm that ADC decreases during activation, probably due to cellular swelling, and increases a little with the decrease in DX. In fact, γ depends, as ADC, on Δχ and cellular swelling, but in a different way. As already highlighted in vitro on phantoms [43,44], in ex vivo excised tissues [45,52] and in vivo in the human brain [40,46], γ increases significantly with a decrease in Δχ, more than ADC does [44], and γ, in contrast to ADC, increases with cellular swelling. In Figure 4, we report a simple scheme to highlight the main dependencies of the T2*, ADC, and γ parameters on the main physiological and microstructural variations that occur during neuronal activation. Therefore, the greater signal intensity observed in the functional γ maps shown in Figure 2c is because the two main variations that occur during activation cause a coherent sum of γ responses. This feature of γ supports it being a potential candidate for performing innovative diffusion fMRI experiments.
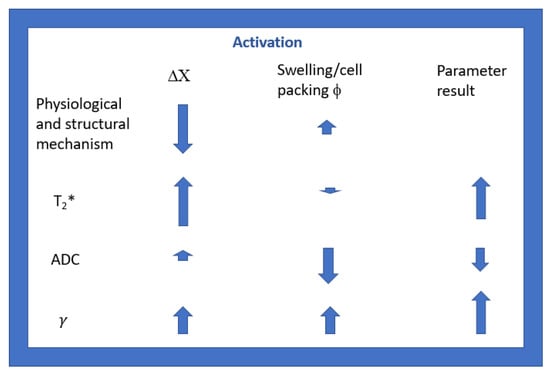
Figure 4.
Schematic representation highlighting the main dependencies of the T2*, ADC, and γ parameters on the main physiological (Δχ) and microstructural (ϕ) variations that occur during neuronal activation. The size of the arrows is proportional to the degree of variation, and the upward or downward direction indicates an increase or decrease.
To summarize, Gi induces an ADC increase during activation that may mask the ADC-decreasing effect due to extravascular cell swelling [31,32,33]. On the other hand, Gi induces an increase in γ (higher than the ADC one) [46], which sums up to its additional increase due to extravascular cell swelling. This ensures the potential sensitivity of γ to extracellular space changes due to cell swelling, independently of the Gi strength.
The main challenge of the ongoing debate about the role of diffusion fMRI is that both vascular and neuronal factors influence DW-fMRI signals, and it can be difficult to separate them. In this work, we propose to use a new contrast parameter, the γ parameter, that could better highlight the vascular and/or neuronal dependence of the DW-fMRI signal. In recent years, a study by Ding et al. [63] showed that DW-fMRI could detect activity-related changes in both gray and white matter during working memory tasks, suggesting a neuronal basis for the observed signal changes. Moreover, another study by Cagnon et al. [64] provided models and experimental data that are relevant to understanding vascular effects in DW-fMRI, while in a study by Abe et al. [65], DW-fMRI has been proposed as an alternative functional imaging method to detect brain activity without confounding hemodynamic effects in a neuropsychiatric disease mouse model.
The current consensus acknowledges that DW-fMRI signals at high b-values likely encompass both neuronal and vascular components. The challenge lies in accurately quantifying the relative contributions of each. Factors such as the choice of b-values, diffusion time, type of magnetic field gradients, and the specific brain region under investigation play critical roles in this determination.
Overall, to clarify the biophysical basis of DW-fMRI, the implementation of DW acquisition sequences in spectroscopic modality to check the behavior of specific metabolites during activation [66] may be useful. In particular, sophisticated DW sequences with high-strength diffusion gradients (of short duration) and high-performing gradient units and using bipolar gradients and double spin-echo modality are needed to clearly attenuate the effects of Gi on γ-values (see Figure 4 of reference [43]). Currently, it would be only possible to perform this kind of optimization in pre-clinical scanners or state-of-the-art human scanners, such as the Siemens Connectom [67,68,69]. However, the emergence of new commercial systems with ultra-strong ultra-performing gradients promises exciting new perspectives for further studies and validation in humans with larger cohorts.
In these conditions, we suggest performing experiments using DW-fMRI with high-performance mono- and bipolar magnetic field gradients using both ADC and γ, as they seem, to our current knowledge, to be independent and complementary parameters to investigate DW-fMRI’s properties. Using monopolar magnetic field gradients maximizes γ’s dependence on magnetic susceptibility differences, while this is minimized using efficient bipolar magnetic field gradients.
Future studies could focus on the quantification of γ’s dependence on vascular effects, for example in murine models using intravascular paramagnetic contrast agents at rest and under stimulation. The obtained information can be utilized in experiments using pharmacological challenges to modify or disrupt the neurovascular coupling. For instance, nitroprusside infusion is expected to inhibit neurovascular coupling, with no effects on the diffusion response or local field potentials [26]. In these conditions, a decrease in ADC, together with an increase in γ, evaluated by subtracting any contribution that was quantified in the first experiment, would allow one to quantify the relative weight of the two vascular and extravascular effects, contributing to the observed transient changes in water diffusion during brain activation.
5. Conclusions
This study highlights the potential of the γ parameter in DW-fMRI as a sensitive and complementary metric to traditional ADC-based approaches for investigating brain activation. Although our preliminary conclusions are based on experiments conducted on only five subjects, the γ response showed a robust and spatially specific correlation with BOLD activation, surpassing conventional ADC in its sensitivity. While the ADC measurements in this study may have been affected by residual T2-BOLD effects due to non-optimal b-values, the γ parameter showed a distinct response, likely driven by its dependence on Δχ in relation to vascular contributions and extracellular compartmentalization changes.
Future advancements in diffusion MRI technology, such as ultra-strong and bipolar gradient systems, could pave the way for more precise investigations of DW-fMRI’s properties. Studies using γ and ADC in combination, alongside vascular-modulating experiments, could help disentangle vascular and extravascular contributions to DW-fMRI signals. Such studies hold promise for refining our understanding of neurovascular coupling and the interplay of diffusion dynamics during brain activation.
Author Contributions
Conceptualization, S.C. and M.P.; methodology, A.M., E.M. and M.P.; software, M.P, G.G. and A.M.; validation, M.P., F.G., E.M., G.G. and S.C.; formal analysis, M.P. and E.M.; investigation, S.C., M.B. and M.P.; resources, M.B.; data curation, M.P. and A.M.; writing—original draft preparation, S.C. and M.P; writing—review and editing, all authors.; visualization, M.P. and S.C.; supervision, S.C. and E.M.; project administration, S.C.; funding acquisition, M.B. and E.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of Santa Lucia foundation (protocol code CE/AG4-PROG.226-33).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
In the manuscript, we report the first results of DW-fMRI. Further experiments will follow. The corresponding author, Silvia Capuani, is maintaining the data and can be contacted at the following e-mail address: silvia.capuani@cnr.it.
Acknowledgments
We thank the MRI technicians who work at the Santa Lucia Foundation for their high professionalism and availability.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADC | Apparent diffusion coefficient |
| BOLD | blood-oxygen-level-dependent |
| DW | Diffusion-weighted |
| DWI | Diffusion-weighted imaging |
| DW-fMRI | Diffusion-weighted functional Magnetic Resonance Imaging |
| Δχ | Magnetic susceptibility difference |
| fMRI | Functional Magnetic Resonance Imaging |
| Gi | Internal magnetic field gradient |
References
- Rosen, B.R.; Savoy, R.L. fMRI at 20: Has it changed the world? NeuroImage 2012, 62, 1316–1324. [Google Scholar] [CrossRef] [PubMed]
- Neil, J.; Miller, J.; Mukherjee, P.; Hüppi, P.S. Diffusion tensor imaging of normal and injured developing human brain—A technical review. NMR Biomed. 2002, 15, 543–552. [Google Scholar] [CrossRef] [PubMed]
- Le Bihan, D. Diffusion MRI: What water tells us about the brain. EMBO Mol. Med. 2014, 6, 569–573. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Tank, D.W.; Menon, R.; Ellermann, J.M.; Kim, S.G.; Merkle, H.; Ugurbil, K. Intrinsic signal changes accompanying sensory stimulation: Functional brain mapping with magnetic resonance imaging. Proc. Natl. Acad. Sci. USA 1992, 89, 5951–5955. [Google Scholar] [CrossRef]
- Ugurbil, K.; Toth, L.; Kim, D.S. How accurate is magnetic resonance imaging of brain function? Trends Neurosci. 2003, 26, 108–114. [Google Scholar] [CrossRef]
- O’Herron, P.; Chhatbar, P.Y.; Levy, M.; Shen, Z.; Schramm, A.E.; Lu, Z.; Kara, P. Neural correlates of single-vessel haemodynamic responses in vivo. Nature 2016, 534, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Sundqvist, N.; Sten, S.; Thompson, P.; Andersson, B.J.; Engström, M.; Cedersund, G. Mechanistic model for human brain metabolism and its connection to the neurovascular coupling. PLoS Comput. Biol. 2022, 18, e1010798. [Google Scholar] [CrossRef] [PubMed]
- Schenck, J.F. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med. Phys. 1996, 23, 815–850. [Google Scholar] [CrossRef]
- Spees, W.M.; Yablonskiy, D.A.; Oswood, M.C.; Ackerman, J.J. Water proton MR properties of human blood at 1.5 Tesla: Magnetic susceptibility, T1, T2, T2*, and non-Lorentzian signal behavior. Magn. Reson. Med. 2001, 45, 533–542. [Google Scholar] [CrossRef]
- Takagi, S.; Obata, T.; Tsubokawa, H. GABAergic input contributes to activity-dependent change in cell volume in the hippocampal CA1 region. Neurosci. Res. 2002, 44, 315–324. [Google Scholar] [CrossRef]
- Tasaki, I. Rapid structural changes in nerve fibers and cells associated with their excitation processes. Japan. J. Physiol. 1999, 49, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Basser, P.J. Inferring microstructural features and the physiological state of tissues from diffusion-weighted images. NMR Biomed. 1995, 8, 333–344. [Google Scholar] [CrossRef]
- Callaghan, P.T. Principles of Nuclear Magnetic Resonance Microscopy, Oxford Science Publications; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Jones, D.K. Diffusion MRI; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Zhong, J.; Kennan, R.P.; Fulbright, R.K.; Gore, J.C. Quantification of intravascular and extravascular contributions to BOLD effects induced by alteration in oxygenation or intravascular contrast agents. Magn. Reson. Med. 1998, 40, 526–536. [Google Scholar] [CrossRef] [PubMed]
- Does, M.D.; Zhong, J.; Gore, J.C. In vivo measurement of ADC change due to intravascular susceptibility variation. Magn. Reson. Med. 1999, 41, 236–240. [Google Scholar] [CrossRef]
- Price, W.S. NMR Studies of Translational Motion: Principles and Applications; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780521806961. [Google Scholar]
- Song, A.W.; Woldorff, M.G.; Gangstead, S.; Mangun, G.R.; McCarthy, G. Enhanced Spatial Localization of Neuronal Activation Using Simultaneous Apparent-Diffusion-Coefficient and Blood-Oxygenation Functional Magnetic Resonance Imaging. Neuroimage 2002, 17, 742–750. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.P.; Silva, A.C.; Kim, S.G. Comparison of diffusion-weighted high-resolution CBF and spin-echo BOLD fMRI at 9.4T. Magn. Reson. Med. 2002, 47, 736–741. [Google Scholar] [CrossRef]
- Turner, R. How much cortex can a vein drain? Downstream dilution of activation-related cerebral blood oxygenation changes. Neuroimage 2002, 16, 1062–1067. [Google Scholar] [CrossRef]
- Zhong, J.; Petroff, O.A.C.; Prichard, J.W.; Gore, J.C. Changes in water diffusion and relaxation properties of rat cerebrum during status epilepticus. Magn. Reson. Med. 1993, 30, 241–246. [Google Scholar] [CrossRef]
- Darquie, A.; Poline, J.B.; Poupon, C.; Saint-Jalmes, C.H.; Le Bihan, D. Transient decrease in water diffusion observed in human occipital cortex during visual stimulation. Proc. Natl. Acad. Sci. USA 2001, 98, 9391–9395. [Google Scholar] [CrossRef]
- Le Bihan, D.; Urayama, S.; Aso, T.; Hanakawa, T.; Fukuyama, H. Direct and fast detection of neuronal activation in the human brain with diffusion MRI. Proc. Natl. Acad. Sci. USA 2006, 103, 8263–8268. [Google Scholar] [CrossRef]
- Le Bihan, D. The ‘wet mind’: Water and functional neuroimaging. Phys. Med. Biol. 2007, 52, 57–90. [Google Scholar] [CrossRef] [PubMed]
- Abe, Y.; Tsurugizawa, T.; Le Bihan, D.I. Water diffusion closely reveals neural activity status in rat brain loci affected by anesthesia. PLoS Biol. 2017, 15, e2001494. [Google Scholar] [CrossRef]
- Tsurugizawa, T.; Ciobanu, L.; Le Bihan, D. Water diffusion in brain cortex closely tracks underlying neuronal activity. Proc. Natl. Acad. Sci. USA 2013, 110, 11636–11641. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.L.; Bulte, D.P.; Devlin, H.; Robson, M.D.; Wise, R.G.; Woolrich, M.W.; Jezzard, P.; Behrens, T.E.J. Evidence for a vascular contribution to diffusion fMRI at high b value. Proc. Natl. Acad. Sci. USA 2007, 104, 20967–20972. [Google Scholar] [CrossRef] [PubMed]
- Jin, T.; Kim, S.-G. Functional changes of apparent diffusion coefficient during visual stimulation investigated by diffusion-weighted gradient-echo fMRI. NeuroImage 2008, 41, 801–812. [Google Scholar] [CrossRef]
- Bai, R.; Stewart, C.V.; Plenz, D.; Basser, P.J. Assessing the sensitivity of diffusion MRI to detect neuronal activity directly. Proc. Natl. Acad. Sci. USA 2016, 113, E1728–E1737. [Google Scholar] [CrossRef]
- Aso, T.; Urayama, S.I.; Poupon, C.; Sawamoto, N.; Fukuyama, H.; Le Bihan, D. An intrinsic diffusion response function for analysing diffusion functional MRI time series. Neuroimage 2009, 47, 1487–1495. [Google Scholar] [CrossRef]
- Pampel, A.; Jochimsen, T.H.; Möller, H.E. BOLD background gradient contributions in diffusion-weighted fMRI—Comparison of spin-echo and twice-refocused spin-echo sequences. NMR Biomed. 2010, 23, 610–618. [Google Scholar] [CrossRef]
- Jin, T.; Zhao, F.Q.; Kim, S.G. Sources of functional apparent diffusion coefficient changes investigated by diffusion-weighted spin-echo fMRI. Magn. Reson. Med. 2006, 56, 1283–1292. [Google Scholar] [CrossRef]
- Yacoub, E.; Uludag, K.; Ugurbil, K.; Harel, N. Decreases in ADC observed in tissue areas during activation in the cat visual cortex at 9.4 T using high diffusion sensitization. Magn. Reson. Imaging 2008, 26, 889–896. [Google Scholar] [CrossRef][Green Version]
- Nicolas, R.; Gros-Dagnac, H.; Aubry, F.; Celsis, P. Comparison of BOLD, diffusion-weighted fMRI and ADC-fMRI for stimulation of the primary visual system with a block paradigm. Magn. Reson. Imaging 2017, 39, 123–131. [Google Scholar] [CrossRef] [PubMed]
- Nguyen-Duc, J.; De Riedmatten, I.; Spencer, A.P.; Perot, J.B.; Olszowy, W.; Jelescu, I. Mapping Activity and Functional Organisation of the Motor and Visual Pathways Using ADC-fMRI in the Human Brain. Hum. Brain Mapp. 2025, 46, e70110. [Google Scholar] [CrossRef]
- Costantini, G.; Capuani, S.; Farrelly, F.A.; Taloni, A. A new perspective of molecular diffusion by nuclear magnetic resonance. Sci. Rep. 2023, 13, 1703. [Google Scholar] [CrossRef]
- Jensen, J.H.; Helpern, J.A.; Ramani, A.; Lu, H.; Kaczynski, K. Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 2005, 53, 1432–1440. [Google Scholar] [CrossRef]
- Wu, E.X.; Cheung, M.M. MR diffusion kurtosis imaging for neural tissue characterization. NMR Biomed. 2010, 23, 836–848. [Google Scholar] [CrossRef] [PubMed]
- Ingo, C.; Magin, R.L.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn. Reson. Med. 2014, 71, 617–627. [Google Scholar] [CrossRef]
- Guerreri, M.; Palombo, M.; Caporale, A.; Fasano, F.; Macaluso, E.; Bozzali, M.; Capuani, S. Age-related microstructural and physiological changes in normal brain measured by MRI γ-metrics derived from anomalous diffusion signal representation. NeuroImage 2019, 188, 654–667. [Google Scholar] [CrossRef] [PubMed]
- Palombo, M.; Gentili, S.; Bozzali, M.; Macaluso, E.; Capuani, S. New insight into the contrast in diffusional kurtosis images: Does it depend on magnetic susceptibility? Magn. Reson. Med. 2015, 73, 2015–2024. [Google Scholar] [CrossRef]
- Hertanu, A.; Pavan, T.; Jelescu, I.O. Somatosensory-evoked response induces extensive diffusivity and kurtosis changes associated with neural activity in rodents. Imaging Neurosci. 2025, advance publication. [Google Scholar] [CrossRef]
- Palombo, M.; Gabrielli, A.; De Santis, S.; Cametti, C.; Ruocco, G.; Capuani, S. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. J. Chem. Phys. 2011, 135, 034504. [Google Scholar] [CrossRef]
- Palombo, M.; Gabrielli, A.; De Santis, A.; Capuani, S. The γ parameter of the stretched-exponential model is influenced by internal gradients: Validation in phantoms. J. Magn. Reson. 2012, 216, 28–36. [Google Scholar] [CrossRef]
- Capuani, S.; Palombo, M.; Gabrielli, A.; Orlandi, A.; Maraviglia, B.; Pastore, F.S. Spatio-temporal anomalous diffusion imaging: Results in controlled phantoms and in excised human meningiomas. Magn. Reson. Imaging 2013, 31, 359–365. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Caporale, A.; Palombo, M.; Macaluso, E.; Guerreri, M.; Bozzali, M.; Capuani, S. The γ-parameter of anomalous diffusion quantified in human brain by MRI depends on local magnetic susceptibility differences. Neuroimage 2017, 147, 619–631. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Capuani, S.; Palombo, M. Mini review on anomalous diffusion by MRI: Potential advantages, pitfalls, limitations, nomenclature, and correct interpretation of literature. Front. Phys. 2020, 7, 248. [Google Scholar] [CrossRef]
- Zhou, X.J.; Gao, Q.; Abdullah, O.; Magin, R.L. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn. Reson. Med. 2010, 63, 562–569. [Google Scholar] [CrossRef]
- Yang, Q.; Reutens, D.C.; Vegh, V. Generalisation of continuous time random walk to anomalous diffusion MRI models with an age-related evaluation of human corpus callosum. NeuroImage 2022, 250, 118903. [Google Scholar] [CrossRef]
- Barrick, T.R.; Spilling, C.A.; Ingo, C.; Madigan, J.; Isaacs, J.D.; Rich, P.; Jones, T.L.; Magin, R.L.; Hall, M.G.; Howe, F.A. Quasi-diffusion magnetic resonance imaging (QDI): A fast, high b-value diffusion imaging technique. Neuroimage 2020, 211, 116606. [Google Scholar] [CrossRef]
- Caporale, A.; Bonomo, G.B.; Tani Raffaelli, G.; Tata, A.M.; Avallone, B.; Wehrli, F.W.; Capuani, S. Transient anomalous diffusion MRI in excised mouse spinal cord: Comparison among different diffusion metrics and validation with histology. Front. Neurosci. 2022, 15, 797642. [Google Scholar] [CrossRef]
- Palombo, M.; Gabrielli, A.; Servedio, V.D.P.; Ruocco, G.; Capuani, S. Structural disorder and anomalous diffusion in random packing of spheres. Sci. Rep. 2013, 3, 2631. [Google Scholar] [CrossRef]
- Palombo, M.; Barbetta, A.; Cametti, C.; Favero, G.; Capuani, S. Transient anomalous diffusion MRI measurement discriminates porous polymeric matrices characterized by different sub-microstructures and fractal dimension. Gels 2022, 8, 95. [Google Scholar] [CrossRef]
- Özarslan, E.; Shepherd, T.M.; Koay, C.G.; Blackband, S.J.; Basser, P.J. Temporal scaling characteristics of diffusion as a new MRI contrast: Findings in rat hippocampus. Neuroimage 2012, 60, 1380–1393. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fan, Y.; Gao, J.H. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys. Rev. E 2015, 92, 012707. [Google Scholar] [CrossRef] [PubMed]
- Magin, R.L.; Ingo, C.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater. 2013, 178, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Magin, R.L.; Abdullah, O.; Baleanu, D.; Zhou, X.J. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J. Magn. Reson. 2008, 190, 255–270. [Google Scholar] [CrossRef]
- Andersson, J.L.; Sotiropoulos, S.N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage 2016, 125, 1063–1078. [Google Scholar] [CrossRef]
- Palombo, M.; Najac, C.; Valette, J. Potential effect of varying background B0 gradients on diffusion measurements: An in silico study. Proc. Intl. Soc. Mag. Reson. Med. 2015, 23, 4752. [Google Scholar]
- Kubova, Z.; Kuba, M.; Spekreijse, H.; Blakemore, C. Contrast dependence of motion-onset and pattern-reversal evoked potentials. Vision Res. 1995, 35, 197–205. [Google Scholar] [CrossRef]
- Williams, R.J.; Reutens, D.C.; Hocking, J. Influence of BOLD contributions to diffusion fMRI activation of the visual cortex. Front. Neurosci. 2016, 10, 279. [Google Scholar] [CrossRef]
- Ding, Z.; Huang, Y.; Bailey, S.K.; Gao, Y.; Cutting, L.E.; Rogers, B.P.; Newton, A.T.; Gore, J.C. Detection of synchronous brain activity in white matter tracts at rest and under functional loading. Proc. Acad. Sci. USA 2018, 115, 595–600. [Google Scholar] [CrossRef]
- Gagnon, L.; Sakadžić, S.; Lesage, F.; Musacchia, J.J.; Lefebvre, X.; Fang, Q.; Yücel, M.A.; Evans, K.C.; Mandeville, E.T.; Cohen-Adad, J.; et al. Quantifying the Microvascular Origin of BOLD-fMRI from First Principles with Two-Photon Microscopy and an Oxygen-Sensitive Nanoprobe. J. Neurosci. 2015, 35, 3663–3675. [Google Scholar] [CrossRef] [PubMed]
- Abe, Y.; Takata, N.; Sakai, Y.; Hamada, H.T.; Hiraoka, Y.; Aida, T.; Tanaka, K.; Le Bihan, D.; Doya, K.; Tanaka, K.F. Diffusion functional MRI reveals global brain network functional abnormalities driven by targeted local activity in a neuropsychiatric disease mouse model. NeuroImage 2020, 223, 117318. [Google Scholar] [CrossRef] [PubMed]
- Branzoli, F.; Techawiboonwong, A.; Kan, H.; Webb, A.; Ronen, I. Functional diffusion-weighted magnetic resonance spectroscopy of the human primary visual cortex at 7 T. Magn. Reson. Med. 2013, 69, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.K.; Alexander, D.C.; Bowtell, R.; Cercignani, M.; Dell’Acqua, F.; McHugh, D.J.; Miller, K.L.; Palombo, M.; Parker, G.J.M.; Rudrapatna, U.S.; et al. Microstructural imaging of the human brain with a ‘super-scanner’: 10 key advantages of ultra-strong gradients for diffusion MRI. NeuroImage 2018, 182, 8–38. [Google Scholar] [CrossRef]
- Uhl, Q.; Pavan, T.; Molendowska, M.; Jones, D.K.; Palombo, M.; Jelescu, I.O. Quantifying human gray matter microstructure using neurite exchange imaging (NEXI) and 300 mT/m gradients. Imaging Neurosci. 2024, 2, 1–19. [Google Scholar] [CrossRef]
- Huang, S.Y.; Witzel, T.; Keil, B.; Scholz, A.; Davids, M.; Dietz, P.; Rummert, E.; Ramb, R.; Kirsch, J.E.; Yendiki, A.; et al. Connectome 2.0: Developing the next-generation ultra-high gradient strength human MRI scanner for bridging studies of the micro-, meso- and macro-connectome. NeuroImage 2021, 243, 118530. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).