Review on the Recent Numerical Studies of Liquid Atomization
Abstract
Featured Application
Abstract
1. Introduction
2. General Overview of Liquid Atomization
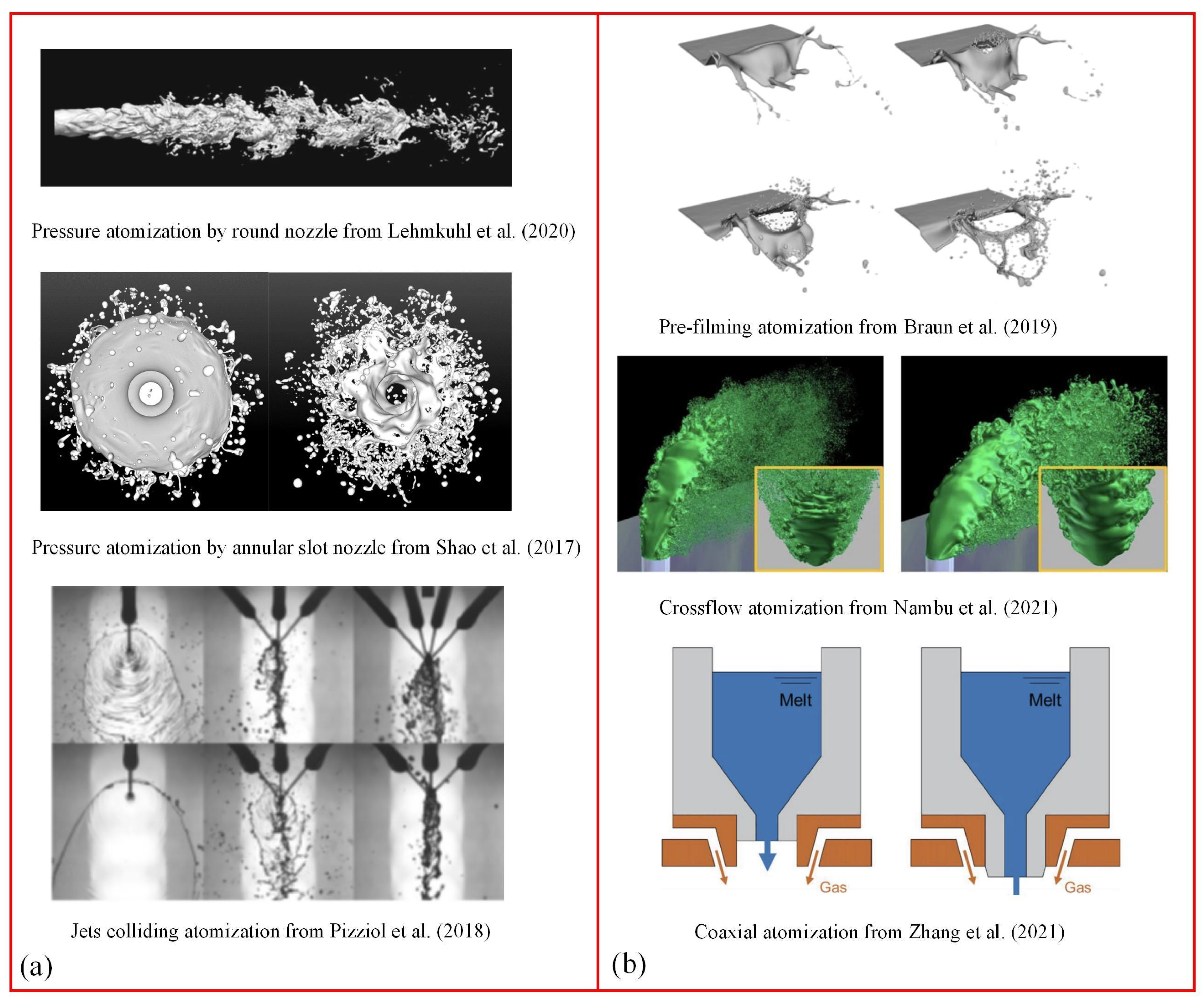
2.1. Atomization Types
2.2. Two Atomization Regions
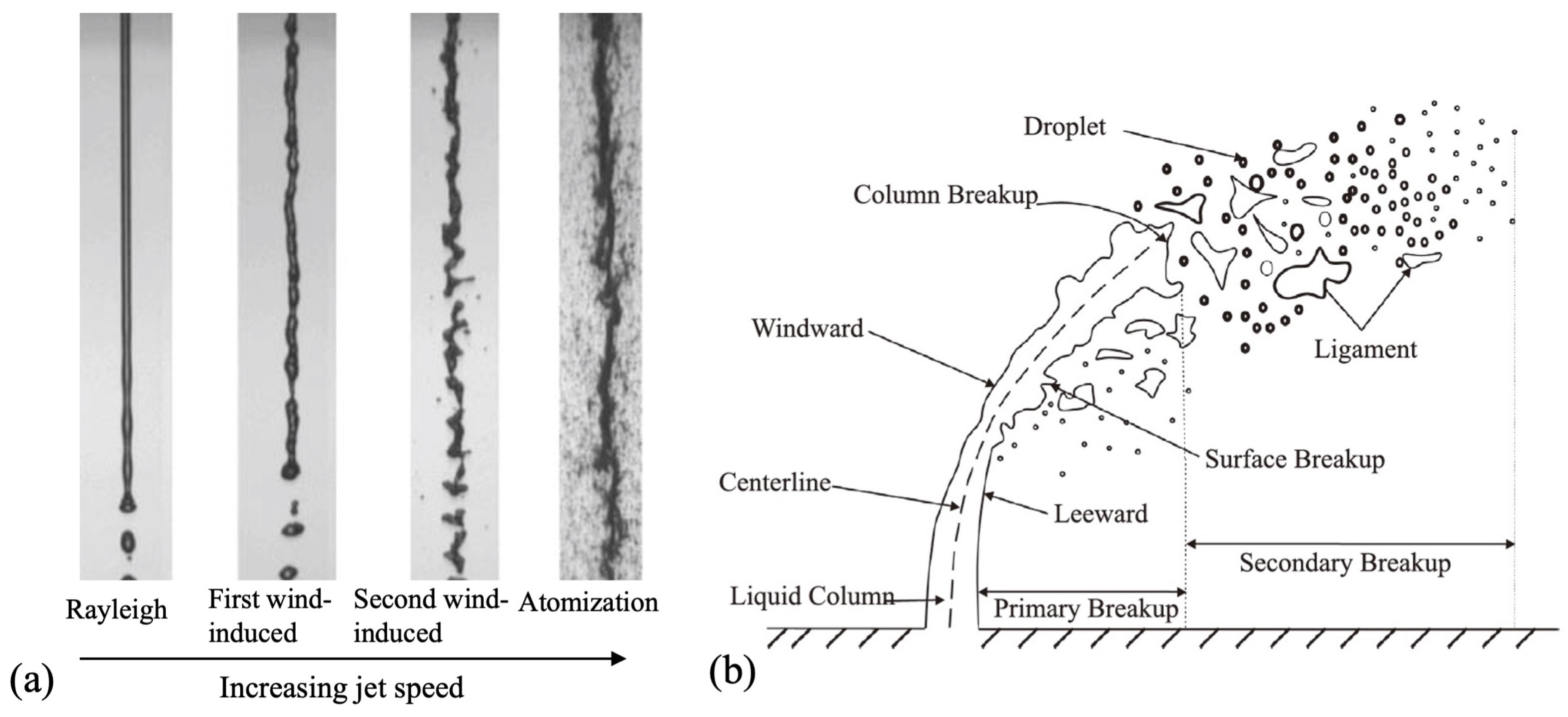
2.2.1. Primary Breakup
2.2.2. Secondary Breakup
2.3. Non-Dimensional Groups
3. Interface Capturing
3.1. Mathematical Description
3.2. Application Cases
3.3. Summary
4. Particle Tracking
4.1. Mathematical Description
4.2. Breakup Models
4.2.1. Huh-Gosman Model
4.2.2. Wu-Faeth Model
4.2.3. Taylor Analogy Breakup Model
4.2.4. Kelvin–Helmholtz Model
4.2.5. Rayleigh–Taylor Model
4.2.6. Comparison of Breakup Models
4.3. Application Cases
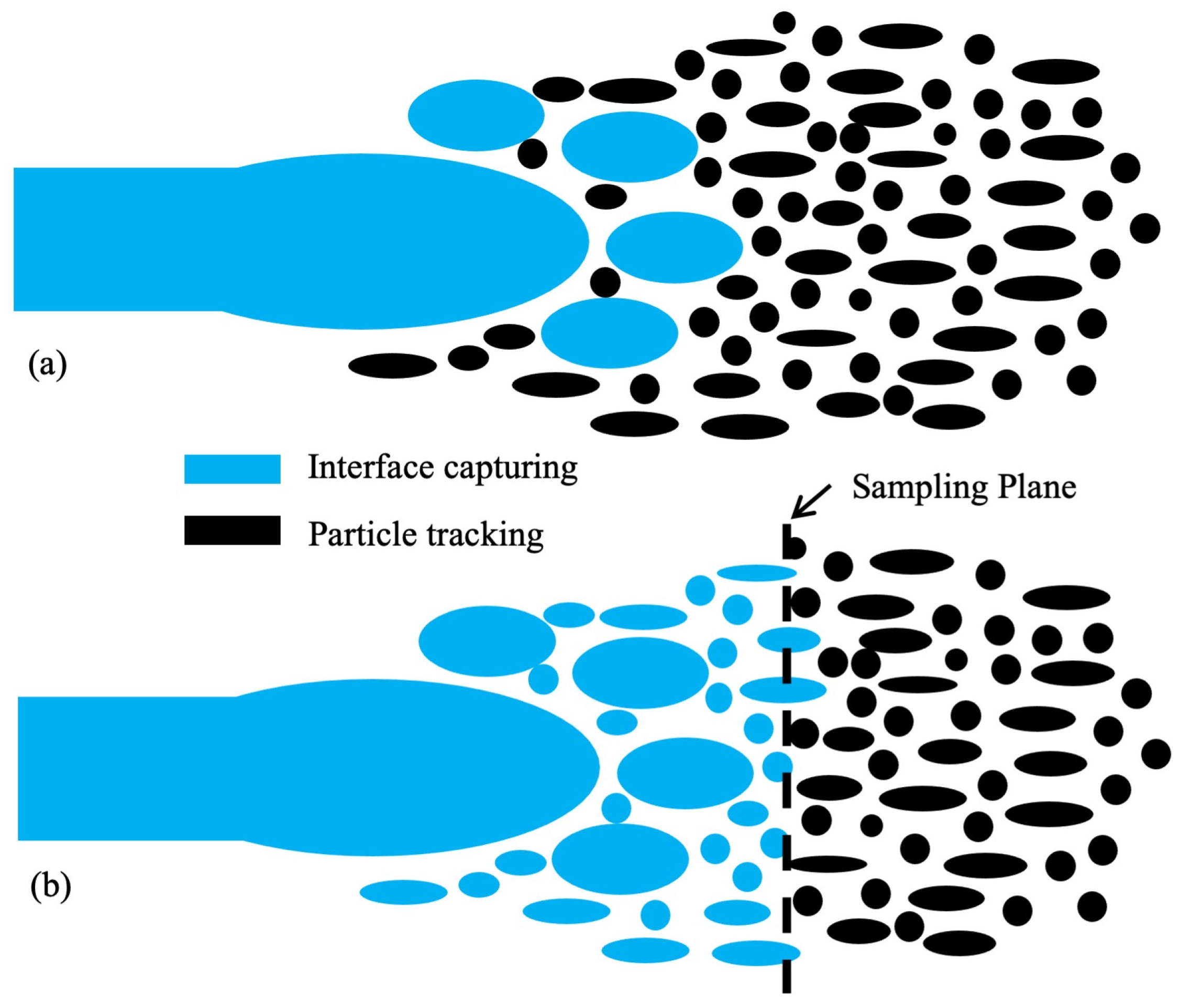
5. Hybrid of Interface Capturing and Particle Tracking
5.1. Basic Idea
5.2. Application Cases
6. Multi-Fluid and Multi-Scale Eulerian Method
6.1. Theoretical Bases
6.2. Application Cases
7. Smoothed Particle Hydrodynamics
8. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACT | aerodynamic–cavitation–turbulence |
| AIAD | algebraic interfacial area density |
| AMR | adaptive mesh refinement |
| DNS | direct numerical simulation |
| DPM | discrete particle method |
| FGVT | fine grid volume tracking |
| GFM | ghost fluid method |
| HG | Huh–Gosman |
| iMUSIG | inhomogeneous MUlti-SIze Group |
| KH | Kelvin–Helmholtz |
| LBM | lattice Boltzmann method |
| LES | large eddy simulation |
| LS | level set |
| MFMS | multi-fluid and multi-scale |
| RANS | Reynolds-averaged Navier-Stokes |
| RT | Rayleigh–Taylor |
| SGS | studied sub-grid scale |
| SPH | smoothed particle hydrodynamics |
| TAB | Taylor analogy breakup |
| VOF | volume of fluid |
| WF | Wu–Faeth |
References
- Opfer, L.; Roisman, I.V.; Tropea, C. Primary Atomization in an Airblast Gas Turbine Atomizer; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Salvador, F.; Romero, J.-V.; Roselló, M.-D.; Jaramillo, D. Numerical simulation of primary atomization in diesel spray at low injection pressure. J. Comput. Appl. Math. 2016, 291, 94–102. [Google Scholar] [CrossRef]
- Solomatin, Y.; Shlegel, N.E.; Strizhak, P.A. Atomization of promising multicomponent fuel droplets by their collisions. Fuel 2019, 255, 115751. [Google Scholar] [CrossRef]
- Zhang, S.; Alavi, S.; Kashani, A.; Ma, Y.; Zhan, Y.; Dai, W.; Li, W.; Mostaghimi, J. Simulation of Supersonic High-Pressure Gas Atomizer for Metal Powder Production. J. Therm. Spray Technol. 2021, 30, 1968–1994. [Google Scholar] [CrossRef]
- Mullis, A.M.; Kumar, A.P.A.; Borman, D.J. CFD Modelling of High Pressure Gas Atomization of Liquid Metals. In CFD Modeling and Simulation in Materials Processing 2018; Springer: Cham, Switzerland, 2018; pp. 77–84. [Google Scholar]
- Xu, Q.; Cheng, D.; Trapaga, G.; Yang, N.; Lavernia, E. Numerical analyses of fluid dynamics of an atomization configuration. J. Mater. Res. 2002, 17, 156–166. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, J.; Zhu, X.; Zhang, S. Effect of atomization gas pressure variation on gas flow field in supersonic gas atomization. Sci. China Technol. Sci. 2009, 52, 3046–3053. [Google Scholar] [CrossRef]
- Mantripragada, V.T.; Kumar, K.; Kumar, P.; Sarkar, S. Modeling of Powder Production During Centrifugal Atomization. J. Sustain. Met. 2021, 7, 620–629. [Google Scholar] [CrossRef]
- Hernandez, F.; Riedemann, T.; Tiarks, J.; Kong, B.; Regele, J.D.; Ward, T.; Anderson, I.E. Numerical Simulation and Validation of Gas and Molten Metal Flows in Close-Coupled Gas Atomization. In TMS 2019 148th Annual Meeting & Exhibition Supplemental Proceedings; Springer: Cham, Switzerland, 2019; pp. 1507–1519. [Google Scholar]
- Wang, J.; Zhou, G.; Wei, X.; Wang, S. Experimental characterization of multi-nozzle atomization interference for dust reduction between hydraulic supports at a fully mechanized coal mining face. Environ. Sci. Pollut. Res. 2019, 26, 10023–10036. [Google Scholar] [CrossRef]
- Kou, B.-F.; Liu, Q.-Z.; Cao, S.-C.; Hu, X.-H.; Li, Y.-F.; Wang, Y.-R.; Zhao, B.-H. Experimental investigation on atomization and collecting efficiency of wind-spray dust controller and its parameters optimization. J. Central South Univ. 2015, 22, 4213–4218. [Google Scholar] [CrossRef]
- Yin, W.; Zhou, G.; Gao, D. Simulation analysis and engineering application of distribution characteristics about multi-stage atomization field for cutting dust in fully mechanized mining face. Adv. Powder Technol. 2019, 30, 2600–2615. [Google Scholar] [CrossRef]
- Musiu, E.M.; Qi, L.; Wu, Y. Evaluation of droplets size distribution and velocity pattern using Computational Fluid Dynamics modelling. Comput. Electron. Agric. 2019, 164, 104886. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: New York, NY, USA, 2010. [Google Scholar]
- Liu, J.; Li, Q.; Zhen, Z.; Wu, H. Numerical simulation of flow field in pressure-swirl injector based on VOF interface tracking method. J. Aerosp. Power 2011, 26, 1986–1994. [Google Scholar]
- Wang, D.; Liu, J.; Li, Q.; Ni, G.; Wang, S. Investigation on the Influence of Pressure on Enhancing Atomization Effect of Molten Metal Stream. Trans. Indian Inst. Met. 2024, 77, 2787–2795. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, J.; Guo, X. Effects of Pressure and Nozzle Size on the Spray Characteristics of Low-Pressure Rotating Sprinklers. Water 2020, 12, 2904. [Google Scholar] [CrossRef]
- Cui, L.; Sun, Y.; Zhou, Z.; Sun, Z.; Xi, G. Numerical Study of Double Jet Impact Atomization Using Meshless MPS Method. J. Eng. Thermophys. 2024, 45, 1385–1394. [Google Scholar]
- Grosshans, H.; Szász, R.-Z.; Fuchs, L. Enhanced liquid–gas mixing due to pulsating injection. Comput. Fluids 2015, 107, 196–204. [Google Scholar] [CrossRef]
- Nygård, A.; Altimira, M.; Semlitsch, B.; Wittberg, L.P.; Fuchs, L. Analysis of vortical structures in intermittent jets. In Proceedings of the 5th International Conference on Jets, Wakes and Separated Flows (ICJWSF2015), Stockholm, Sweden, 15–18 June 2015; Springer Proceedings in Physics. Springer: Cham, Switzerland, 2016; Volume 185, pp. 3–10. [Google Scholar]
- Lehmkuhl, O.; Mira, D.; Gasparino, L.; Owen, H.; Houzeaux, G. Large-Eddy Simulation of Primary Atomization Using an Entropy Stable Conservative Level Set. In Direct and Large Eddy Simulation XII; Springer: Cham, Switzerland, 2020; pp. 207–213. [Google Scholar]
- Shao, C.; Luo, K.; Yang, Y.; Fan, J. Detailed numerical simulation of swirling primary atomization using a mass conservative level set method. Int. J. Multiph. Flow 2017, 89, 57–68. [Google Scholar] [CrossRef]
- Pizziol, B.; Costa, M.; Panão, M.O.; Silva, A. Multiple impinging jet air-assisted atomization. Exp. Therm. Fluid Sci. 2018, 96, 303–310. [Google Scholar] [CrossRef]
- Braun, S.; Wieth, L.; Holz, S.; Dauch, T.F.; Keller, M.C.; Chaussonnet, G.; Gepperth, S.; Koch, R.; Bauer, H. Numerical prediction of air-assisted primary atomization using Smoothed Particle Hydrodynamics. Int. J. Multiph. Flow 2019, 114, 303–315. [Google Scholar] [CrossRef]
- Nambu, T.; Mizobuchi, Y. Detailed numerical simulation of primary atomization by crossflow under gas turbine engine combustor conditions. Proc. Combust. Inst. 2021, 38, 3213–3221. [Google Scholar] [CrossRef]
- Liu, R.; Zhong, L.; Li, S.; Li, J.; Ji, H. Numerical investigation on the spray characteristics of biodiesel with gas-assisted atomization injection. Fuel 2023, 358, 130178. [Google Scholar] [CrossRef]
- Xu, T.; Yang, F.; Zhu, M.; Ye, T.; Zhou, J.; Song, Y. Numerical simulation of spray atomization in crossflow using an empirical primary atomization model. Int. J. Multiph. Flow 2024, 174, 104768. [Google Scholar] [CrossRef]
- Zhang, T.; Mu, X.; Ge, S.; Li, S.; Ren, S.; Zhao, S.; Tao, S. Supersonic coaxial aerodynamic atomization dust removal technolo. Powder Technol. 2024, 444, 120076. [Google Scholar]
- Wang, Y.; Zhang, P.; Li, W.; Liu, Y.; Yan, Y. Experimental investigation of the atomization characteristics of pre-filming atomizer with low-temperature fuel. Phys. Fluids 2024, 36, 125159. [Google Scholar] [CrossRef]
- Dumouchel, C. On the experimental investigation on primary atomization of liquid streams. Exp. Fluids 2008, 45, 371–422. [Google Scholar] [CrossRef]
- Olyaei, G.; Kebriaee, A. Experimental study of liquid jets injected in crossflow. Exp. Therm. Fluid Sci. 2020, 115, 110049. [Google Scholar] [CrossRef]
- Wu, P.-K.; Tseng, L.-K.; Faeth, G.M. Primary breakup in gas/liquid mixing layers for turbulent liquids. At. Sprays 1992, 2, 295–317. [Google Scholar] [CrossRef]
- Mashayek, A.; Ashgriz, N. Atomization of a Liquid Jet in a Crossflow. In Handbook of Atomization and Sprays; Springer: Boston, MA, USA, 2011; pp. 657–683. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; López-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Luo, K.; Shao, C.; Chai, M.; Fan, J. Level set method for atomization and evaporation simulations. Prog. Energy Combust. Sci. 2019, 73, 65–94. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Warncke, K.; Gepperth, S.; Sauer, B.; Sadiki, A.; Janicka, J.; Koch, R.; Bauer, H.-J. Experimental and numerical investigation of the primary breakup of an airblasted liquid sheet. Int. J. Multiph. Flow 2017, 91, 208–224. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, X. Numerical simulations of atomization and evaporation in liquid jet flows. Int. J. Multiph. Flow 2019, 119, 180–193. [Google Scholar] [CrossRef]
- Arachchilage, K.H.; Haghshenas, M.; Park, S.; Zhou, L.; Sohn, Y.; McWilliams, B.; Cho, K.; Kumar, R. Numerical simulation of high-pressure gas atomization of two-phase flow: Effect of gas pressure on droplet size distribution. Adv. Powder Technol. 2019, 30, 2726–2732. [Google Scholar] [CrossRef]
- Ketterl, S.; Reißmann, M.; Klein, M. Large eddy simulation of multiphase flows using the volume of fluid method: Part 2—A-posteriori analysis of liquid jet atomization. Exp. Comput. Multiph. Flow 2019, 1, 201–211. [Google Scholar] [CrossRef]
- Mingalev, S.; Inozemtsev, A.; Gomzikov, L.; Sipatov, A.; Abramchuk, T. Simulation of Primary Film Atomization in Prefilming Air-assisted Atomizer Using Volume-of-Fluid Method. Microgravity Sci. Technol. 2020, 32, 465–476. [Google Scholar] [CrossRef]
- Hua, D.; Zongfang, D.; Yanwei, L. Simulation and experimental research on the injection characteristics of the laser processing injection hole. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 202. [Google Scholar] [CrossRef]
- Pairetti, C.; Villiers, R.; Zaleski, S. On shear layer atomization within closed channels: Numerical simulations of a cough-replicating experiment. Comput. Fluids 2021, 231, 105125. [Google Scholar] [CrossRef]
- Mukundan, A.A.; Ménard, T.; de Motta, J.C.B.; Berlemont, A. Detailed numerical simulations of primary atomization of airblasted liquid sheet. Int. J. Multiph. Flow 2022, 147, 103848. [Google Scholar] [CrossRef]
- Gepperth, S.; Muller, A.; Koch, R.; Bauer, H.-J. Ligament and droplet characteristics in prefilming airblast atomization. In Proceedings of the 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Chang, J.; Chen, L.; He, L.; Zhou, Y. Numerical simulation of primary atomization process of liquid jet in subsonic crossflow. Energy Rep. 2022, 8, 1–15. [Google Scholar] [CrossRef]
- Chryssakis, C.A.; Assanis, D.N.; Tanner, F.X. Atomization Models. In Handbook of Atomization and Sprays; Springer: Boston, MA, USA, 2011; pp. 215–231. [Google Scholar] [CrossRef]
- Huh, K.Y.; Gosman, A.D. A phenomenological model of diesel spray atomization. Int. Conf. Multiph. Flow 1991, 2, 515–518. [Google Scholar]
- Wu, P.-K.; Faeth, G.M. Aerodynamic effects on primary breakup of turbulent liquids. At. Sprays 1993, 3, 265–289. [Google Scholar] [CrossRef]
- Taylor, G.I. The Shape and Acceleration of a Drop in a High Speed Air Stream. In Scientific Papers of G. I. Taylor; Batchelor, G.K., Ed.; Technical Report; Cambridge University Press: Cambridge, UK, 1963. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. The TAB Method for Numerical Calculation of Spray Droplet Breakup; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1987; p. 872089. [Google Scholar] [CrossRef]
- Reitz, R.D. Mechanisms of Atomization Processes in High-Pressure Vaporizing Sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: Hoboken, NJ, USA, 1962. [Google Scholar]
- Xin, J.; Ricart, L.; Reitz, R. Computer Modeling of Diesel Spray Atomization and Combustion. Combust. Sci. Technol. 1998, 137, 171–194. [Google Scholar] [CrossRef]
- Ye, X.; An, X.; Zhang, H.; Wang, S.; Guo, B.; Yu, A. Process simulation on atomization and evaporation of desulfurization wastewater and its application. Powder Technol. 2021, 389, 178–188. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, G.; Zhang, L.; Sun, B.; Wang, N.; Yang, H.; Liu, W. Numerical simulation and engineering application of multistage atomization dustfall at a fully mechanized excavation face. Tunn. Undergr. Space Technol. 2020, 104, 103540. [Google Scholar] [CrossRef]
- Shi, Y.; Lu, W.; Sun, W.; Zhang, S.; Yang, B.; Wang, J. Impact of gas pressure on particle feature in Fe-based amorphous alloy powders via gas atomization: Simulation and experiment. J. Mater. Sci. Technol. 2022, 105, 203–213. [Google Scholar] [CrossRef]
- Li, Z.-H.; He, B.-Q.; Zhao, H. Application of a hybrid breakup model for the spray simulation of a multi-hole injector used for a DISI gasoline engine. Appl. Therm. Eng. 2014, 65, 282–292. [Google Scholar] [CrossRef]
- Magnotti, G.M.; Genzale, C.L. Exploration of Turbulent Atomization Mechanisms for Diesel Spray Simulations; Georgia Institute of Technology: Atlanta, Georgia, 2017. [Google Scholar]
- Magnotti, G.M.; Genzale, C.L. Recent Progress in Primary Atomization Model Development for Diesel Engine Simulations. In Two-Phase Flow for Automotive and Power Generation Sectors; Springer: Singapore, 2019; pp. 63–107. [Google Scholar]
- Li, Y.; Huang, Y.; Luo, K.; Liang, M.; Lei, B. Development and validation of an improved atomization model for GDI spray simulations: Coupling effects of nozzle-generated turbulence and aerodynamic force. Fuel 2021, 299, 120871. [Google Scholar] [CrossRef]
- Estivalèzes, J.L.; Zuzio, D.; DiPierro, B. An Improved Multiscale Eulerian-Lagrangian Method for Simulation of Atomization Process. In Turbulence and Interactions; Springer: Cham, Switzerland, 2018; pp. 65–77. [Google Scholar]
- Duarte, B.A.d.F.; Barbi, F.; Villar, M.M.; Serfaty, R.; da Silveira Neto, A. Primary atomization of a turbulent liquid jet in crossflow: A comparison between VOF and FGVT methods. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 277. [Google Scholar] [CrossRef]
- Wei, M.; Chen, S.; Sun, M.; Liang, J.; Liu, C.; Wang, M. Atomization simulation and preparation of 24CrNiMoY alloy steel powder using VIGA technology at high gas pressure. Powder Technol. 2020, 367, 724–739. [Google Scholar] [CrossRef]
- Luo, S.; Wang, H.; Gao, Z.; Wu, Y.; Wang, H. Interaction between high-velocity gas and liquid in gas atomization revealed by a new coupled simulation model. Mater. Des. 2021, 212, 110264. [Google Scholar] [CrossRef]
- Yu, H.; Jin, Y.-C.; Cheng, W.; Yang, X.; Peng, X.; Xie, Y. Multiscale simulation of atomization process and droplet particles diffusion of pressure-swirl nozzle. Powder Technol. 2021, 379, 127–143. [Google Scholar] [CrossRef]
- Wen, J.; Hu, Y.; Nishiie, T.; Iino, J.; Masri, A.; Kurose, R. A flamelet LES of turbulent dense spray flame using a detailed high-resolution VOF simulation of liquid fuel atomization. Combust. Flame 2022, 237, 111742. [Google Scholar] [CrossRef]
- Ayad, F.; Baghdada, M.; Bouaichaoui, Y.; Höhne, T. Verification & validation of CFD predictions regarding pressurized thermal shock (PTS) situations in ROCOM installation: Comparison with IAEA benchmark. Nucl. Eng. Des. 2023, 413, 112498. [Google Scholar] [CrossRef]
- Höhne, T.; Vallée, C. Experiments and Numerical Simulations of Horizontal Two-Phase Flow Regimes Using an Interfacial Area Density Model. J. Comput. Multiph. Flows 2010, 2, 131–143. [Google Scholar] [CrossRef]
- Faeth, G.; Hsiang, L.-P.; Wu, P.-K. Structure and breakup properties of sprays. Int. J. Multiph. Flow 1995, 21, 99–127. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Saeedipour, M.; Pirker, S.; Bozorgi, S.; Schneiderbauer, S. An Eulerian–Lagrangian hybrid model for the coarse-grid simulation of turbulent liquid jet breakup. Int. J. Multiph. Flow 2016, 82, 17–26. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical Model for Drop and Bubble Breakup in Turbulent Dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Prince, M.J.; Blanch, H.W. Bubble Coalescence and Break-Up in Air-Sparged Bubble Columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Höhne, T.; Deendarlianto; Lucas, D. Numerical simulations of counter-current two-phase flow experiments in a PWR hot leg model using an interfacial area density model. Int. J. Heat Fluid Flow 2011, 32, 1047–1056. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Krepper, E.; Höhne, T. A multi-field two-fluid concept for transitions between different scales of interfacial structures. Int. J. Multiph. Flow 2012, 47, 171–182. [Google Scholar] [CrossRef]
- Höhne, T.; Mehlhoop, J.-P. Validation of closure models for interfacial drag and turbulence in numerical simulations of horizontal stratified gas–liquid flows. Int. J. Multiph. Flow 2014, 62, 1–16. [Google Scholar] [CrossRef]
- Höhne, T.; Krepper, E.; Montoya, G.; Lucas, D. CFD-simulation of boiling in a heated pipe including flow pattern transitions using the GENTOP concept. Nucl. Eng. Des. 2017, 322, 165–176. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, Y.; Qi, X.; Guo, Q. Modeling of gas jet flow into a liquid bath using the inhomogeneous poly-dispersed method. Prog. Nucl. Energy 2021, 137, 103773. [Google Scholar] [CrossRef]
- Qu, X.; Revankar, S.; Qi, X.; Guo, Q. Exploring on a three-fluid Eulerian-Eulerian-Eulerian approach for the prediction of liquid jet atomization. Appl. Therm. Eng. 2021, 195, 117160. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Szewc, K.; Pozorski, J.; Minier, J. Analysis of the incompressibility constraint in the smoothed particle hydrodynamics method. Int. J. Numer. Methods Eng. 2012, 92, 343–369. [Google Scholar] [CrossRef]
- Igari, N.; Iso, T.; Nishio, Y.; Izawa, S.; Fukunishi, Y. Numerical simulation of droplet-formation in rotary atomizer. Theor. Appl. Mech. Lett. 2019, 9, 202–205. [Google Scholar] [CrossRef]
- Braun, S.; Koch, R.; Bauer, H.-J. Smoothed Particle Hydrodynamics for Numerical Predictions of Primary Atomization. In High Performance Computing in Science and Engineering ’16; Springer: Cham, Switzerland, 2016; pp. 321–336. [Google Scholar]


| Name | Abbreviation | Expression |
|---|---|---|
| Weber number | We | |
| Ohnesorge number | Oh | |
| Density Ratio | ε | |
| Viscosity Ratio | N | |
| Reynolds number | Re | |
| Momentum Ratio | q |
| Reference | Mathematical Model | Key Parameters | Grid Size | Application Scenario |
|---|---|---|---|---|
| [28] | VOF, LES | Gas–liquid velocity ratio, turbulence intensity | ~10 million cells | Primary breakup of airblasted liquid sheets in combustion systems |
| [29] | VOF, Level Set, Ghost Fluid Method | Weber number, Reynolds number, evaporation rate | 4.23 billion cells | Atomization and evaporation in turbulent liquid jet flows |
| [30] | Two-phase CFD with Eulerian–Lagrangian coupling | Gas pressure (1–10 MPa), droplet Sauter mean diameter | ~1 million cells | High-pressure gas atomization for metal powder production |
| [31] | LES with VOF | Turbulence models, interfacial tension | ~5 million cells | Liquid jet atomization in multiphase flows |
| [32] | Entropy-stable conservative Level Set | Surface tension, viscosity, density ratio | Not reported | Primary atomization in fuel injectors |
| [33] | VOF with adaptive mesh refinement | Air–liquid momentum flux ratio, film thickness | ~3 million cells | Prefilming air-assisted atomizers in aerospace engines |
| [34] | Experimental and CFD (ANSYS Fluent) | Injection pressure, nozzle geometry | ~500,000 cells | Laser-processed fuel injection holes in automotive systems |
| [35] | VOF with shear-stress transport (SST) models | Cough-induced shear flow, droplet size distribution | ~2 million cells | Biofluid atomization in respiratory systems |
| [36] | High-resolution VOF and DNS | Turbulent kinetic energy, breakup length scales | 6 billion cells | Primary atomization of airblasted liquid sheets in industrial burners |
| [37] | Experimental/PIV and LES | Ligament formation time, droplet velocity | Not reported | Prefilming airblast atomization in gas turbines |
| [38] | CLSVOF (Coupled Level Set/VOF) | Crossflow velocity, jet-to-crossflow momentum ratio | ~100 million cells | Liquid jet atomization in subsonic crossflow (e.g., scramjet combustors) |
| Model Name | Application Scenario | Core Mechanism | Advantages | Disadvantages |
|---|---|---|---|---|
| Huh–Gosman (HG) | Primary breakup in high-pressure nozzles | Turbulent eddy-driven interface instability | 1. Directly links nozzle turbulence parameters 2. High engineering usability | 1. Relies on empirical constants (C1–C4) 2. Fails to capture secondary breakup |
| Wu–Faeth (WF) | Primary breakup in transverse jets | Turbulence-surface wave coupling | 1. Incorporates radial turbulent integral scales 2. Suitable for non-axisymmetric flows | 1. Requires precise nozzle exit measurements 2. Fails at high Weber numbers (We > 500) |
| TAB | Low-speed, low-We droplets (We < 100) | Spring-mass-damper system analogy | 1. Physically intuitive 2. Low computational cost | 1. Neglects shear-dominated breakup 2. Inapplicable to high-viscosity fluids (Oh > 0.1) |
| KH | High Weber numbers (We > 100) | Shear-induced surface wave instability | 1. Resolves rapid surface wave growth 2. Suitable for fuel injection | 1. Neglects acceleration effects 2. Overpredicts small droplets (error ~20%) |
| KH-RT | High-speed, high-pressure multiphase flows (e.g., IC engines) | Shear (KH) + acceleration (RT) instability | 1. Dual-mechanism coupling improves accuracy 2. Industrially validated | 1. High computational complexity 2. Requires manual liquid core region (L) definition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Wang, G.; Qu, X. Review on the Recent Numerical Studies of Liquid Atomization. Appl. Sci. 2025, 15, 4928. https://doi.org/10.3390/app15094928
Luo L, Wang G, Qu X. Review on the Recent Numerical Studies of Liquid Atomization. Applied Sciences. 2025; 15(9):4928. https://doi.org/10.3390/app15094928
Chicago/Turabian StyleLuo, Lincong, Gang Wang, and Xiaohang Qu. 2025. "Review on the Recent Numerical Studies of Liquid Atomization" Applied Sciences 15, no. 9: 4928. https://doi.org/10.3390/app15094928
APA StyleLuo, L., Wang, G., & Qu, X. (2025). Review on the Recent Numerical Studies of Liquid Atomization. Applied Sciences, 15(9), 4928. https://doi.org/10.3390/app15094928