Abstract
The Semi-Soft Clustered Vehicle Routing Problem (SemiSoftCluVRP) is a relaxed version of the Clustered Vehicle Routing Problem (CluVRP) and an enhanced variant of the Soft Clustered Vehicle Routing Problem (SoftCluVRP). In the SemiSoftCluVRP, all customers are partitioned into several clusters, and these clusters are further divided into two types: hard clusters and soft clusters. Within a hard cluster, customers must be served by the same vehicle without interruption, whereas within a soft cluster, customers must also be served by the same vehicle, but interruptions are permitted. To solve this problem, a mathematical model is first developed, followed by the design of a two-level genetic algorithm that integrates a variable neighborhood descent method. Computational experiments demonstrate that the proposed algorithm produces high-quality solutions and exhibits excellent performance. Compared with the results of CluVRP and SoftCluVRP, the results of SemiSoftCluVRP can reduce and increase logistics costs by up to 6.50% and 7.52%, respectively. In practical applications, by adjusting the hard and soft attributes of clusters, more flexible decision-making references can be provided for relevant decision-makers.
1. Introduction
The Vehicle Routing Problem (VRP) [1] is a classical combinatorial optimization problem. Since the problem was proposed, it has attracted extensive attention from researchers. As research has deepened, many variants of the VRP have been developed by integrating practical applications, such as the VRP with time windows [2], two-echelon VRP [3], multi-compartment VRP [4], electric VRP [5], green VRP [6], pickup and delivery VRP [7], stochastic VRP [8], multi-objective VRP [9], and so on. The Clustered VRP (CluVRP) [10] and the Soft Clustered VRP (SoftCluVRP) [11] are two other variants of the VRP. In the CluVRP, customers to be served are divided into several subsets, each of which is called a cluster. A feasible route requires that customers within each cluster must be served continuously by the same vehicle without interruption. That is, once a vehicle enters a cluster to serve customers, it must serve all customers within that cluster before entering the next cluster for service or returning to the depot. The SoftCluVRP is a relaxed version of the CluVRP, in which the service of customers within a cluster is allowed to be interrupted, as long as they are served by the same vehicle.
The CluVRP was originally developed to simulate the package delivery operations of courier companies [10]. All customers are divided into several clusters based on their geographical locations. According to the information of these clusters, the packages to be delivered are sorted into corresponding containers. During the delivery process, the packages in a cluster must be delivered completely before moving on to deliver the packages in the next cluster. The CluVRP can also be used to simulate many other practical scenarios, such as urban solid waste collection [12], medical services in emergency environments [13], services within gated communities [14], and so on. In the CluVRP, if a deliveryman can always access all containers carried by the vehicle, it then becomes a SoftCluVRP [11].
In the SoftCluVRP, when a vehicle is serving clusters assigned to it, it is assumed that any cluster can be interrupted by other clusters, which is too loose. In the CluVRP, it is assumed that all clusters are not allowed to be interrupted, which is too strict. Therefore, this paper considers a problem that falls between these two assumptions, namely the Semi-Soft CluVRP (SemiSoftCluVRP). In the SemiSoftCluVRP, all clusters are classified into two categories: hard clusters and soft clusters. Customers within hard clusters are not allowed to interrupt service, while customers within soft clusters are allowed to interrupt service. By setting the hard and soft attributes of clusters, decision-makers are provided with greater operational flexibility and richer decision-making insights, ultimately improving delivery efficiency and reducing operational costs. Specifically, the main contributions of this paper are as follows:
(1) The SemiSoftCluVRP is proposed, which is a generalization of the CluVRP and the SoftCluVRP. Therefore, the SemiSoftCluVRP can simulate a wider range of practical scenarios, and designing solution methods for it holds greater practical significance.
(2) Based on the existing mathematical models of the CluVRP and the SoftCluVRP in the literature, an integer linear programming model is established.
(3) A two-level genetic algorithm integrated with a variable neighborhood descent (VND) method is designed. The algorithm decomposes the original problem into a low-level traveling salesman problem (TSP) and a high-level capacitated VRP (CVRP), and then solves each using a specific genetic algorithm. In addition, to enhance the local search ability of the algorithm, a VND method with inter-route and intra-route neighborhood search operators is applied after each generation of genetic operations.
(4) Extensive computational experiments are conducted using a set of instances adapted from the existing literature, which includes 77 instances, thereby verifying the effectiveness of the proposed algorithm.
The remainder of the paper is organized as follows: Section 2 provides a literature review related to SemiSoftCluVRP; Section 3 introduces the SemiSoftCluVRP and its mathematical model; and Section 4 presents an improved genetic algorithm for solving the SemiSoftCluVRP. The experimental results and discussion are given in Section 5. Finally, the conclusions are drawn in Section 6.
2. Literature Review
For the CluVRP, Barthélemy et al. [15] converted the problem into a CVRP by adding a sufficiently large positive constant M to all inter-cluster edges, and then applied a simulated annealing method to solve it. Pop et al. [16] provided two mathematical models for the Generalized VRP (GVRP) and then further extended them to the CluVRP. Battarra et al. [12] proposed two exact solution approaches: a branch and cut as well as a branch and cut and price. The algorithms were tested on benchmark instances and applied to solve real-world scenarios of solid waste collection. Vidal et al. [17] introduced two iterative local search algorithms and a hybrid genetic algorithm. By decomposing the original problem into two sub-problems at high-level and low-level: the former is the route problem of determining the visiting order between clusters, and the latter is the route problem of determining the visiting order of customers within each cluster, Expósito-Izquierdo et al. [13] proposed a two-level optimization technique, in which a meta-heuristic algorithm is used to solve the high-level sub-problem and several exact and approximate methods are dedicated to solve the low-level sub-problem; Defryn and Sörensen [11] developed an efficient two-level variable neighborhood search (VNS) heuristic algorithm to solve the CluVRP; Horvat-Marc et al. [18] solved the two sub-problems using a genetic algorithm and a simulated annealing algorithm, respectively; Pop et al. [19] solved the high-level sub-problem using a genetic algorithm and transformed the low-level sub-problem into a TSP, which was then solved using the Concorde TSP solver. Hintsch and Irnich [20] presented a large multiple neighborhood search algorithm. In the proposed method, multiple cluster destroy and repair operations were employed, and then a local search improvement scheme based on VND was adopted for further optimization. Islam et al. [14] developed a particle swarm optimization (PSO) algorithm integrating a VNS. The PSO is responsible for ensuring the solution diversity, while the VNS is in charge of enhancing the local search capability of the algorithm.
For the SoftCluVRP, Defryn and Sörensen [11] proposed a two-level VNS solution method by making slight modifications to the algorithm for solving the CluVRP. Hintsch and Irnich [21] designed and analyzed different branch-and-price exact algorithms. The computational experiments demonstrated that their method is capable of optimally solving SoftCluVRP instances with over 500 customers or more than 50 clusters. Heßler and Irnich [22] introduced a branch-and-cut exact algorithm. The computational experiments showed that several previously open instances can now be solved to proven optimality. Hintsch [23] proposed a large multiple neighborhood search algorithm where multiple cluster destroy and repair operations were employed, followed by the use of two post-optimization components based on VND. Cosma et al. [24] developed a two-level based genetic algorithm that splits the original problem into two sub-problems at macro-level and micro-level. The former sub-problem aims to determine the assignment of clusters to vehicles, while the latter sub-problem focuses on determining the order in which each vehicle serves its customers. Zhou et al. [25] introduced an efficient bilevel memetic search method that integrates three modules: a group matching-based crossover, a bilevel hybrid neighborhood search, and a tabu-driven population reconstruction strategy, to explore search space at both cluster and customer levels. Xu [26] proposed a two-level VND algorithm that includes two-stage construction, intensification at cluster and customer levels, and a perturbation mechanism, to solve a split delivery clustered vehicle routing problem with soft cluster conflicts and customer-related costs arising in automotive parts of milk-run logistics with supplier cluster distribution in China.
3. Problem Description and Mathematical Modeling
3.1. Problem Description
The SemiSoftCluVRP can be described as follows: Let be a complete undirected graph, where is the set of vertices, and is the set of edges. Vertex 0 represents the depot, and vertices are customer, denoted by . Each customer is associated with a demand . The vertex set is divided into non-empty and mutually disjoint subsets , where . Each subset is called a cluster. Let . is further divided into two disjoint subsets and , where represents the set of hard clusters, and represents the set of soft clusters. Each edge is associated with a distance . There are identical vehicles available at the depot, each with a capacity of .
The requirement of the problem is to design a route for each vehicle such that each customer is visited exactly once, subject to the following constraints: (1) the total demand of customers assigned to a vehicle cannot exceed its capacity ; (2) each vehicle’s route must start and end at the depot; (3) customers within each cluster must be served by the same vehicle. Meanwhile, if is a hard cluster, the service for its customers is not allowed to be interrupted, while if is a soft cluster, there is no such restriction for its customers. The objective of the problem is to minimize the total distance traveled by all vehicles.
Figure 1 provides a schematic diagram of feasible solutions for the CluVRP, SoftCluVRP, and SemiSoftCluVRP, where the number of customers is 16, and all the customers are divided into five clusters: V1, V2, V3, V4, and V5. Furthermore, in the SemiSoftCluVRP, V1, V2, and V3 are hard clusters, while V4 and V5 are soft clusters. In the figure, to more intuitively distinguish between hard clusters and soft clusters, we use solid-line rectangular boxes to represent hard clusters and dashed-line rectangular boxes to represent soft clusters.
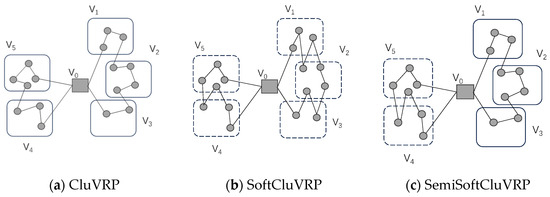
Figure 1.
Schematic diagram of feasible solutions for the CluVRP, SoftCluVRP, and SemiSoftCluVRP.
3.2. Mathematical Modeling
For convenience in modeling, the following notations are introduced: Let denote any non-empty subset of . Let denote the set of arcs . Let denote the set of arcs . Additionally, the following two decision variables are defined:
The mathematical programming model for the SemiSoftCluVRP is as follows:
In the above mathematical model, the objective function (1) minimizes the total distance traveled by all vehicles. Constraint (2) ensures that each customer is visited exactly once. Constraint (3) indicates that the number of vehicles does not exceed the number of clusters. Constraint (4) guarantees that all the vehicles used should visit the depot. Constraint (5) ensures that the same vehicle that arrives at a customer also leaves from that customer. Constraints (6) and (7) are the vehicle capacity constraint and the subtour elimination constraint, respectively. Constraints (8) and (9) impose the service restrictions for hard and soft clusters, respectively. Constraint (10) ensures that the customers in each cluster are served by the same vehicle. Finally, constraints (11) and (12) define the domain of the decision variables.
4. Solution Methodology
Genetic algorithm is a meta-heuristic method. Due to its strong global search capability and parallelism, it can effectively solve complex problems. Meanwhile, one of the encodings of chromosomes, the integer representation, can be directly mapped to the solution of the VRP, that is, the allocation of customers to vehicles and the service order of customers. Therefore, the use of genetic algorithm to solve the VRP has also been favored by researchers (Chen et al. [27], Zhang et al. [28], Palamutçuoglu et al. [29], Liu et al. [30]). This paper proposes a two-level genetic algorithm integrated with a VND method to solve the SemiSoftCluVRP. Next, we first introduce the proposed improved genetic algorithm in detail and then analyze its time complexity.
4.1. Improved Genetic Algorithm
The algorithm proposed in this paper employs a two-level strategy to solve the SemiSoftCluVRP, which is also one of the widely used methods for solving the CluVRP and the SoftCluVRP. The algorithm decomposes the original problem into two sub-problems at low-level and high-level. The former aims to determine the visiting order of customers within each cluster, while the latter aims to determine the allocation of all clusters to vehicles and the visiting order between them. For these two sub-problems, first abstract them as a TSP and a CVRP, respectively, and then use genetic algorithms tailored to solve the corresponding problems. In addition, after each generation of genetic operations, a VND method including inter-route and intra-route neighborhood search operators is used to enhance the local search capability of the algorithm. The flowchart of the proposed algorithm is shown in Figure 2 and the pseudocode of the proposed algorithm is shown in Algorithm 1.
| Algorithm 1: Pseudocode of the improved genetic algorithm |
| Input: Maximum number of iterations , population size , crossover probability , mutation probability Output: Optimal solution |
| Begin 1: Solve the low-level sub-problem and provide the initial visiting order of customers within each cluster; 2: ← Initialize population for the high-level sub-problem; 3: ← Compute the fitness values of all individuals and record the best individual; 4: While the stopping criteria is not met 5: While the population size is not satisfied 6: ← Randomly select two individuals from the current population using the binary tournament method; 7: ← Crossover (); 8: End While 9: ← Population generated by the crossover operator; 10: ← Mutation (); 11: ← Perform VND at inter-route cluster level (); 12: ← Perform VND at intra-route cluster level (); 13: ← Perform VND at intra-route customer level (); 14: ← Truncation selection (); 15: ← Compute the fitness values of all individuals and record the best individual; 16: End While 17: Return the optimal solution ; End |
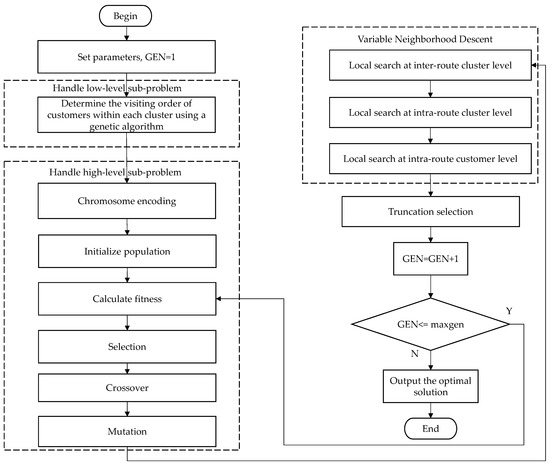
Figure 2.
Flowchart of the improved genetic algorithm.
4.1.1. Handling the Low-Level Sub-Problem
For each cluster, since the sum of the demands of all customers within it must not exceed the vehicle’s capacity, the determination of their visiting order can be achieved by solving the corresponding TSP while disregarding the customer demands. A genetic algorithm is employed to solve this TSP. Here, chromosomes are encoded using integer encoding, where each gene corresponds to a customer, and the gene sorting determines the visiting order of customers; the initial population is generated in a random manner; the fitness function is the reciprocal of the length of the TSP tour; the selection operator uses the binary tournament method; the crossover operator uses the partial matching crossover and two-point order crossover strategies with equal probability; and the mutation operator uses the swap mutation and inversion mutation strategies with equal probability.
4.1.2. Handling the High-Level Sub-Problem
Each cluster is treated as a whole, with its demand being the sum of the demands of all customers within it, thus abstracting a CVRP. A genetic algorithm is used to solve this CVRP. Here, chromosomes are encoded using integer encoding, where the total number of genes is , the non-zero genes correspond to the clusters, the zero genes are used to determine the assignment of all clusters to the vehicles, and the order of genes within each segment determines the order in which the vehicle visits the clusters; the initial population is randomly generated from the feasible solution space; the fitness function is the reciprocal of the objective function value of the SemiSoftCluVRP feasible solution; select and use selection operator, crossover operator, and mutation operator in the same way as in Section 4.1.1.
In the above genetic algorithm, the following points need to be noted:
- (1)
- The method for generating the SemiSoftCluVRP feasible solution corresponding to each chromosome is as follows: Each vehicle first departs from the depot, and then selects the nearest customer from the first cluster as the entrance to serve that cluster. From the two customers adjacent to that customer, it selects the customer closest to the second cluster as the exit, and so on, until the vehicle returns to the depot.
- (2)
- During the generation of the initial population and after the completion of the crossover and mutation operations, it is necessary to check the vehicle capacity. If the demand load exceeds the vehicle capacity, it needs to be repaired. The repair method is as follows: First, arrange the vehicle loads in descending order, then randomly select a cluster from the vehicle with the highest load, and place the cluster into the vehicle with the highest loading rate after loading it, and so on, until all vehicles meet the load requirements.
- (3)
- When the next generation is generated from the current population, the truncation selection strategy is used. Specifically, for the current population and its offspring generated, sort them in descending order according to their fitness values, and then select the best μ individuals as the next generation population.
4.1.3. Variable Neighborhood Descent
The proposed algorithm employs the VND method at three levels: inter-route cluster level, intra-route cluster level, and intra-route customer level. The neighborhood search operators at inter-route cluster level consist of Relocate, Relocate2, and Swap. The neighborhood search operators at intra-route cluster level include Relocate and Swap. In this case, each customer in the soft clusters is treated as an independent cluster and is executed together with the hard clusters using these two operators. The neighborhood search operators at intra-route customer level also include Relocate and Swap. At this time, only customers within the hard clusters are subjected to these two operators. The function of Relocate is to move a gene to a different position, the function of Relocate2 is to move two adjacent genes to a different position, and the function of Swap is to exchange two genes.
4.2. Computational Complexity of Improved Genetic Algorithm
The time complexity of the improved genetic algorithm mainly consists of processing the low-level and high-level sub-problems and executing the VND. Because the time complexities of the partial matching crossover, two-point order crossover, and inversion mutation are all of the order of the chromosome length, while the time complexity of the swap mutation is , the time complexity for processing the low-level sub-problem is
Since the time complexities for generating feasible solutions for the SemiSoftCluVRP from the chromosomes corresponding to the high-level sub-problem, repairing the vehicle capacities, and generating the next generation population through the truncation selection are , , and , respectively, the time complexity for processing the high-level sub-problem is
that is, . Because the time complexities of Relocate, Relocate2, and Swap are all of the order of the square of the chromosome length, the time complexities of the VND strategies at the inter-route cluster level, intra-route cluster level, and intra-route customer level are , , and , respectively. Here, and represent the numbers of hard clusters and soft clusters, respectively, while and represent the numbers of customers within hard clusters and soft clusters, respectively. In summary, the time complexity of the proposed improved genetic algorithm is
5. Results and Discussion
5.1. Experimental Environment
The proposed algorithm was implemented using Python 3.9.13, and the computational environment consists of an Intel(R) Core (TM) i5-8300H CPU @ 2.30 GHz with 16 GB of RAM. Based on the CluVRP instances from Defryn and Sörensen [11], 77 SemiSoftCluVRP instances of types A, B, M, and P were constructed by setting the hard–soft attributes of the clusters. The details of the test instances are shown in Appendix A. In Table A1, the first instance A-n32-C11-V2-Q100 is taken as an example, and its meaning is as follows: “A” represents the instance type, 32 indicates the number of vertices, 11 represents the number of clusters, 2 denotes the number of vehicles, and 100 is the vehicle capacity.
5.2. Determination of Algorithm Parameters
The dynamic experimental method is one of the commonly used methods for determining algorithm parameters in the literature. The basic idea of the method is to vary one selected parameter within a certain range while keeping the other parameters constant, and to determine the value of that parameter by comparing fitness values. Here, we also use this method to determine the relevant parameters of the proposed improved genetic algorithm. The parameters of the algorithm are determined as follows: the population size μ has been set at 50, the crossover probability was set at 95%, and the mutation probability was set at 5%. The algorithm terminates when the best individual in the population does not improve for 30 consecutive iterations or when the maximum iteration number of 50 is reached.
5.3. Computational Experiments
To validate the effectiveness of the algorithm proposed in this paper, and to analyze the impact of the hard–soft attributes of the clusters on the experimental results, the proposed algorithm was applied to solve the 77 test instances in Table A1, as well as their corresponding CluVRP and SoftCluVRP instances. The results are shown in Table 1. In Table 1, Column 3 shows the best results for the CluVRP instances from the literature [11]; Columns 4 and 8 present the best results obtained by running the proposed algorithm 10 times to solve the CluVRP and SoftCluVRP instances, respectively; Columns 5 and 6, respectively, present the best and average results obtained by running the proposed algorithm 10 times to solve the SemiSoftCluVRP instances; Column 7 shows the deviation between the average and best results obtained by running the proposed algorithm 10 times to solve the SemiSoftCluVRP instances; Column 9 shows the best results for the SoftCluVRP instances from the literature [23]. Here, the calculation formula for Gap is as follows: Gap = (Avg − Best)/Best × 100%.

Table 1.
The results obtained by the algorithm proposed in this paper for solving CluVRP, SoftCluVRP, and SemiSoftCluVRP instances and comparisons from the literature.
In addition, the meaning of the values in parentheses in the relevant columns in Table 1 is as follows: Column 4 (8) shows the difference between the results obtained by the proposed algorithm and the corresponding results in [11,23] when solving the CluVRP (SoftCluVRP) instances. The values in the left (right) parentheses of Column 5 represent the difference between the results obtained using the proposed algorithm to solve the SemiSoftCluVRP and CluVRP (SoftCluVRP) instances.
5.3.1. Stability Evaluation of the Proposed Algorithm
To analyze the stability of the proposed algorithm, in Table 1, we present the best and average results obtained by running the algorithm 10 times to solve the SemiSoftCluVRP instances. The experimental results show that among the 77 test instances, the average values of 63 instances are equal to the optimal values, that is, the Gap is 0%. In the remaining 14 test instances, the maximum value of Gap does not exceed 0.82%. Therefore, the algorithm proposed in this paper demonstrates excellent stability.
5.3.2. Comparisons of Results for the CluVRP Instances
In the SemiSoftCluVRP, if all clusters are set to be hard, it will degenerate into a CluVRP. Therefore, the CluVRP is a special case of the SemiSoftCluVRP. To verify the effectiveness of the algorithm proposed in this paper to a certain extent, we compared the results with those of [11] for the CluVRP instances. From Columns 3 and 4 of Table 1, it can be seen that the algorithm proposed in this paper can obtain 73 existing best results among 77 CluVRP instances; among the remaining four results, the deviation of solving the instance P-n101-C34-V2-Q400 is 2.80%, and the deviation of solving the three instances of type M is at most 6.84%, indicating the effectiveness of the algorithm proposed in this paper.
5.3.3. Comparisons of Results for the SoftCluVRP Instances
In the SemiSoftCluVRP, if all clusters are set to be soft, it will degenerate into a SoftCluVRP. Therefore, the SoftCluVRP is another special case of the SemiSoftCluVRP. To verify the effectiveness of the algorithm proposed in this paper to a certain extent, we compared the results with those of [23] for the SoftCluVRP instances. From Columns 8 and 9 of Table 1, it can be observed that the algorithm proposed in this paper can obtain 73 existing best results among 77 SoftCluVRP instances; among the remaining four results, the deviation of solving the instance P-n101-C34-V2-Q400 is 5.08%, and the deviation of solving the three instances of type M is at most 9.79%, indicating the effectiveness of the algorithm proposed in this paper.
5.3.4. Comparisons of Results for the SemiSoftCluVRP Instances
To analyze the influence of the hard–soft attributes of clusters on the experimental results, we set up two groups of comparative experiments. The first group is the comparison of the results of the SemiSoftCluVRP instances with the corresponding CluVRP instances, and the second group is the comparison of the results of the SemiSoftCluVRP instances with the corresponding SoftCluVRP instances.
For the first group of comparative experiments, the results are shown in the left parentheses in Column 5 of Table 1. From these results, it can be seen that compared to the results of the CluVRP, 55 of the results of the SemiSoftCluVRP have been improved, accounting for 71.43% of the total number of instances, with a maximum improvement of 6.50%. From the perspective of the type of instances, the number of improved results for A, B, P, and M-type instances accounted for 74.07%, 60.87%, 79.17%, and 66.67% of their respective total numbers, respectively; the maximum improvements in results were 4.93%, 2.41%, 6.50%, and 1.12%, respectively. Therefore, in the CluVRP, relaxing the hard attributes of some clusters to soft can help reduce the logistics costs of enterprises, but the specific effect is also related to the type of instance, as well as further factors such as the location of customers and depot.
For the second group of comparative experiments, the results are shown in the right parentheses in Column 5 of Table 1. From these results, it can be observed that compared to the results of the SoftCluVRP, the objective function values of 54 corresponding SemiSoftCluVRP instances increased, accounting for 70.13% of the total number of instances, with a maximum increase of 7.52%. From the perspective of the type of instances, for A, B, P, and M-type instances, the number of instances with increased objective function values accounted for 62.96%, 56.52%, 87.50%, and 100% of their respective total numbers, respectively; the maximum increments in results were 7.52%, 3.27%, 7.30%, and 3.01%, respectively. Therefore, in the SoftCluVRP, if some clusters are enhanced to be hard, it will lead to an increase in the objective function values of most instances, with the magnitude of the increase varying depending on the type of instance. However, overall, it can be shown that the hard attributes of clusters have a significant impact on the logistics costs of enterprises.
5.3.5. Sensitivity Analysis and Management Insights
To analyze the impact of the hard–soft attributes of clusters on the experimental results, we conducted a sensitivity analysis on the proportion of hard–soft clusters among all clusters. Let ρ denote the percentage of soft clusters among all clusters. The values of ρ are set to 0%, 25%, 50%, 75%, and 100%, respectively. It is noted that when ρ takes the values of 0% and 100%, the corresponding instances degenerate into CluVRP and SoftCluVRP instances, respectively. We selected one test instance of each type A and B for experimentation. The experimental results are shown in Figure 3.
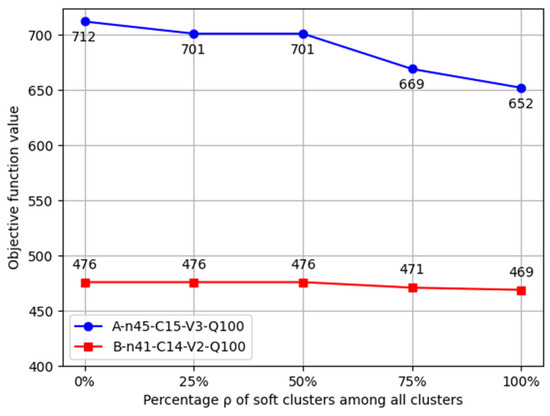
Figure 3.
The objective function values of the test instances under different values of ρ.
From the results of the above two instances, it can be seen that for the Type A instance, when ρ = 0%, the objective function value was 712. At this time, since the number of soft clusters was 0, the constraint conditions were relatively strict, resulting in a higher objective value. When ρ increased to 25%, the objective value dropped to 701. This indicates that moderately increasing the proportion of soft clusters can reduce the objective value. When ρ was further increased to 50%, the objective value remained at 701. This shows that at this stage, the further increase in the proportion of soft clusters had little effect on objective value reduction. When ρ reached 75%, the objective value was further reduced to 669, achieving a significant objective value improvement. When ρ = 100%, the objective value was 652 and continued to decrease. This indicates that when all clusters were soft, the route delivery scheme obtained was the most efficient. For the Type B instance, when ρ ranged from 0% to 50%, the objective value remained at 476 all the time. This may be due to the combined influence of factors such as customer distribution in this instance. When ρ increased to 75%, the objective value dropped to 471. This shows that at this point, the increase in the proportion of soft clusters began to have an impact on the cost. When ρ = 100%, the objective value was 469, and the objective value continued to decrease as well.
By synthesizing the experimental results of the above two instances, it can be seen that as ρ gradually increases, the objective value generally shows a downward trend, and the extent of the decrease is related to the type of the instance. In Figure 4, we present the representation of the solutions of the instance A-n45-C15-V3-Q100 when ρ = 0%, 75%, and 100%. Here, the red solid circle represents the depot, while other solid circles of the same color represent customers from the same cluster, and the solid lines of the same color constitute the route of the same vehicle. The figure more clearly illustrates the changes in vehicle routes in the corresponding solutions after the clusters are relaxed from hard to soft.
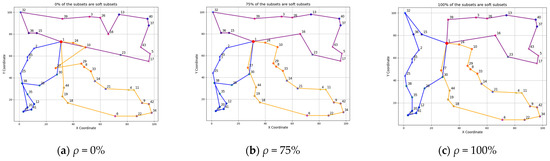
Figure 4.
Representation of the solutions of instance A-n45-C15-V3-Q100.
From the above experimental results, we can offer some managerial suggestions to provide decision-making references for managers of relevant enterprises. Since in most cases the logistics costs of enterprises can be significantly reduced when the proportion of soft clusters among all clusters is relatively high, relaxing some hard clusters into soft clusters can bring considerable economic benefits to enterprises. To relax hard clusters into soft clusters, we believe that two aspects should be considered. On the one hand, a thorough investigation of all clusters should be conducted. Based on the actual conditions of these clusters, they should initially be classified into hard clusters and soft clusters. On the other hand, through computational experiments, several key hard clusters that can significantly reduce the enterprise’s logistics costs should be identified. Subsequently, measures such as cooperation or compensation should be taken to relax these key hard clusters into soft clusters as much as possible, thereby minimizing the enterprise’s logistics costs.
6. Conclusions
There have been many studies on the CluVRP and the SoftCluVRP in the literature. In this paper, we considered a problem that falls between these two problems regarding the assumptions of customers, namely the SemiSoftCluVRP. In the SemiSoftCluVRP, all customers are divided into clusters, and all clusters are further partitioned into hard clusters and soft clusters. Customers within the hard cluster require uninterrupted service from the same vehicle, while customers within the soft cluster only need to be served by the same vehicle. For the SemiSoftCluVRP, a two-level genetic algorithm that integrates a VND method was proposed.
To verify the effectiveness of the algorithm proposed in this paper, we applied it to solve the CluVRP and SoftCluVRP instances from the literature, which are special cases of the SemiSoftCluVRP instances. From the results obtained, it can be seen that in 77 test instances, the proposed algorithm can achieve more than 94% of the literature results, while the four instances that did not achieve the literature results had differences of no more than 6.84% and 9.79%, respectively, which to some extent demonstrates the effectiveness of the algorithm proposed in this paper. To analyze the impact of the hard–soft attributes of clusters on the experimental results, we compared the results of SemiSoftCluVRP with those of CluVRP and SoftCluVRP. From the results obtained, it can be observed that compared to the results of CluVRP, the results of SemiSoftCluVRP can improve logistics costs by up to 6.50%; compared to the results of SoftCluVRP, the results of SemiSoftCluVRP can be increased by up to 7.52%. Therefore, in practical applications, decision-makers can provide more flexible operational options and richer decision-making references for enterprises by setting the hard–soft attributes of clusters, which can ultimately meet the actual needs of customers while reducing the logistics costs of enterprises.
However, from the results of CluVRP and SoftCluVRP, it can be seen that there is still room for further improvement in the performance of the proposed algorithm when solving large-scale instances. In future research, firstly, we will further design high-performance solution methods tailored for the SemiSoftCluVRP, such as exploiting novel algorithmic operators and developing new hybrid algorithms. Secondly, we will explore its related variants, such as multi-depot variants, multi-objective variants that incorporate additional objectives, etc., in order to better simulate a wider range of practical problems. Thirdly, we will conduct surveys of real enterprises and solve their real-world cases to address their genuine practical challenges.
Author Contributions
Conceptualization, X.B.; methodology, Y.M. and X.B.; software, Y.M.; validation, Y.M. and X.B.; formal analysis, Y.M. and X.B.; investigation, Y.M.; resources, X.B.; data curation, Y.M.; writing—original draft, Y.M.; writing—review and editing, Y.M. and X.B.; visualization, Y.M.; supervision, X.B.; project administration, X.B.; funding acquisition, X.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under grant number 11701363.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The hard–soft attributes of the clusters in the SemiSoftCluVRP instances.
Table A1.
The hard–soft attributes of the clusters in the SemiSoftCluVRP instances.
| Index | Instances | Hard Clusters | Soft Clusters |
|---|---|---|---|
| 1 | A-n32-C11-V2-Q100 | [5, 10, 3] | [8, 9, 1, 6, 2, 11, 4, 7] |
| 2 | A-n33-C11-V2-Q100 | [4, 5, 1] | [8, 9, 10, 3, 7, 2, 11, 6] |
| 3 | A-n33-C11-V2-Q100 | [8, 4, 2] | [11, 3, 9, 5, 1, 7, 6, 10] |
| 4 | A-n34-C12-V2-Q100 | [6, 9, 1] | [7, 8, 4, 10, 12, 3, 5, 2, 11] |
| 5 | A-n36-C12-V2-Q100 | [8, 2, 9] | [11, 3, 6, 5, 10, 12, 1, 4, 7] |
| 6 | A-n37-C13-V2-Q100 | [10, 11, 9, 5] | [4, 7, 8, 6, 2, 1, 13, 3, 12] |
| 7 | A-n37-C13-V2-Q100 | [5, 3, 4, 6] | [12, 10, 7, 2, 11, 13, 8, 9, 1] |
| 8 | A-n38-C13-V2-Q100 | [6, 4, 10, 8] | [12, 5, 2, 11, 9, 13, 1, 3, 7] |
| 9 | A-n39-C13-V2-Q100 | [4, 1, 3, 11] | [10, 5, 2, 12, 13, 9, 8, 7, 6] |
| 10 | A-n39-C13-V2-Q100 | [11, 13, 1, 5] | [8, 3, 2, 12, 4, 10, 6, 7, 9] |
| 11 | A-n44-C15-V2-Q100 | [2, 11, 13, 6] | [8, 7, 4, 10, 3, 15, 14, 12, 5, 1, 9] |
| 12 | A-n45-C15-V3-Q100 | [3, 12, 5, 13] | [15, 1, 2, 10, 8, 7, 11, 9, 4, 6, 14] |
| 13 | A-n45-C16-V3-Q100 | [8, 3, 12, 14] | [1, 11, 2, 7, 5, 15, 13, 4, 9, 6, 10] |
| 14 | A-n46-C16-V3-Q100 | [1, 8, 12, 9] | [11, 5, 7, 13, 2, 14, 10, 3, 4, 16, 6, 15] |
| 15 | A-n48-C16-V3-Q100 | [2, 11, 5, 8] | [6, 16, 4, 12, 7, 3, 15, 9, 1, 14, 10, 13] |
| 16 | A-n53-C18-V3-Q100 | [4, 8, 12, 16, 3] | [18, 2, 5, 14, 1, 7, 13, 6, 15, 17, 11, 10, 9] |
| 17 | A-n54-C18-V3-Q100 | [13, 7, 8, 11, 4] | [5, 15, 6, 18, 3, 14, 12, 10, 17, 16, 2, 9, 1] |
| 18 | A-n55-C19-V3-Q100 | [18, 19, 17, 11, 3] | [5, 9, 14, 10, 6, 16, 7, 8, 13, 15, 12, 1, 2, 4] |
| 19 | A-n60-C20-V3-Q100 | [20, 7, 11, 4, 10] | [9, 8, 6, 13, 1, 5, 19, 2, 17, 3, 16, 14, 18, 15, 12] |
| 20 | A-n61-C21-V4-Q100 | [9, 18, 13, 4, 3, 16] | [20, 15, 21, 17, 11, 1, 8, 14, 12, 2, 19, 5, 7, 6, 10] |
| 21 | A-n62-C21-V3-Q100 | [17, 6, 9, 18, 8, 3] | [11, 14, 13, 21, 16, 2, 7, 12, 19, 5, 1, 10, 20, 15, 4] |
| 22 | A-n63-C21-V4-Q100 | [12, 14, 11, 3, 18, 1] | [7, 16, 4, 6, 2, 20, 15, 19, 21, 10, 9, 13, 17, 8, 5] |
| 23 | A-n63-C21-V3-Q100 | [1, 14, 5, 16, 4, 6] | [10, 19, 8, 13, 12, 21, 7, 9, 11, 3, 18, 17, 2, 20, 15] |
| 24 | A-n64-C22-V3-Q100 | [6, 14, 21, 10, 16, 2] | [3, 7, 11, 19, 1, 9, 20, 17, 15, 18, 5, 13, 4, 8, 22, 12] |
| 25 | A-n65-C22-V3-Q100 | [4, 1, 2, 9, 14, 17] | [15, 20, 12, 10, 11, 21, 7, 18, 22, 13, 5, 16, 3, 8, 19, 6] |
| 26 | A-n69-C23-V3-Q100 | [6, 3, 5, 18, 8, 2] | [17, 10, 7, 22, 11, 9, 20, 16, 15, 19, 13, 21, 23, 1, 4, 12, 14] |
| 27 | A-n80-C27-V4-Q100 | [22, 14, 11, 8, 3, 20, 7] | [1, 19, 18, 12, 25, 27, 13, 4, 24, 5, 26, 2, 16, 15, 10, 23, 17, 21, 6, 9] |
| 28 | B-n31-C11-V2-Q100 | [3, 9, 7] | [6, 11, 5, 8, 2, 4, 10, 1] |
| 29 | B-n34-C12-V2-Q100 | [10, 7, 1] | [12, 3, 6, 2, 5, 9, 8, 11, 4] |
| 30 | B-n35-C12-V2-Q100 | [6, 3, 5] | [9, 8, 12, 7, 1, 2, 11, 4, 10] |
| 31 | B-n38-C13-V2-Q100 | [9, 13, 1, 6] | [7, 10, 5, 2, 3, 11, 4, 12, 8] |
| 32 | B-n39-C13-V2-Q100 | [12, 13, 3, 1] | [8, 4, 11, 7, 6, 5, 2, 10, 9] |
| 33 | B-n41-C14-V2-Q100 | [1, 2, 10, 3] | [12, 4, 5, 8, 7, 9, 6, 11, 14, 13] |
| 34 | B-n43-C15-V2-Q100 | [7, 9, 11, 8] | [10, 3, 6, 1, 4, 12, 15, 2, 13, 14, 5] |
| 35 | B-n44-C15-V3-Q100 | [11, 14, 9, 3] | [10, 8, 5, 12, 6, 13, 1, 15, 4, 2, 7] |
| 36 | B-n45-C15-V2-Q100 | [14, 3, 8, 9] | [5, 13, 2, 12, 15, 7, 10, 6, 1, 11, 4] |
| 37 | B-n45-C15-V2-Q100 | [14, 12, 9, 13] | [15, 4, 1, 3, 2, 8, 6, 10, 11, 7, 5] |
| 38 | B-n50-C17-V3-Q100 | [13, 2, 4, 11, 17] | [12, 3, 6, 14, 5, 10, 9, 1, 8, 16, 15, 7] |
| 39 | B-n50-C17-V3-Q100 | [6, 14, 16, 2, 11] | [8, 1, 15, 12, 13, 17, 5, 3, 4, 7, 10, 9] |
| 40 | B-n51-C17-V3-Q100 | [16, 9, 5, 6, 7] | [1, 4, 15, 10, 13, 14, 3, 2, 12, 17, 11, 8] |
| 41 | B-n52-C18-V3-Q100 | [15, 6, 12, 1, 17] | [7, 5, 4, 13, 3, 11, 14, 10, 16, 9, 2, 8, 18] |
| 42 | B-n56-C19-V3-Q100 | [6, 12, 2, 16, 10] | [17, 1, 14, 7, 8, 9, 11, 15, 18, 19, 5, 3, 13, 4] |
| 43 | B-n57-C19-V3-Q100 | [15, 19, 16, 11, 13] | [14, 8, 12, 3, 5, 18, 7, 2, 1, 9, 10, 17, 6, 4] |
| 44 | B-n57-C19-V3-Q100 | [10, 16, 5, 1, 11] | [13, 14, 6, 18, 4, 3, 12, 9, 7, 2, 15, 8, 17, 19] |
| 45 | B-n63-C21-V3-Q100 | [10, 5, 11, 2, 7, 1] | [13, 14, 15, 9, 12, 8, 6, 20, 16, 3, 21, 17, 4, 18, 19] |
| 46 | B-n64-C22-V4-Q100 | [17, 16, 3, 14, 18, 21] | [12, 4, 22, 19, 13, 20, 5, 15, 11, 2, 9, 10, 6, 7, 8, 1] |
| 47 | B-n66-C22-V3-Q100 | [6, 21, 4, 9, 15, 18] | [10, 12, 22, 5, 14, 16, 19, 20, 3, 17, 11, 7, 8, 13, 2, 1] |
| 48 | B-n67-C23-V4-Q100 | [22, 12, 15, 8, 5, 14] | [18, 20, 6, 10, 11, 2, 9, 17, 4, 16, 23, 1, 7, 3, 21, 19, 13] |
| 49 | B-n68-C23-V3-Q100 | [4, 12, 8, 10, 19, 14] | [5, 1, 16, 13, 11, 7, 23, 22, 18, 2, 17, 21, 20, 9, 3, 15, 6] |
| 50 | B-n78-C26-V4-Q100 | [9, 3, 21, 4, 5, 25, 18] | [24, 19, 14, 2, 23, 20, 6, 17, 8, 26, 13, 15, 7, 12, 1, 10, 22, 11, 16] |
| 51 | P-n16-C6-V4-Q35 | [4, 2] | [6, 3, 5, 1] |
| 52 | P-n19-C7-V1-Q160 | [4, 1] | [2, 5, 6, 3, 7] |
| 53 | P-n20-C7-V1-Q160 | [6, 2] | [5, 3, 4, 1, 7] |
| 54 | P-n21-C7-V1-Q160 | [5, 6] | [4, 3, 2, 1, 7] |
| 55 | P-n22-C8-V1-Q160 | [8, 1] | [5, 6, 7, 4, 2, 3] |
| 56 | P-n22-C8-V4-Q160 | [5, 1] | [3, 4, 8, 7, 6, 2] |
| 57 | P-n23-C8-V3-Q40 | [2, 4] | [7, 5, 6, 3, 1, 8] |
| 58 | P-n40-C14-V2-Q140 | [14, 13, 10, 6] | [4, 12, 9, 7, 2, 1, 8, 3, 11, 5] |
| 59 | P-n45-C15-V2-Q150 | [4, 2, 13, 14] | [7, 8, 12, 3, 11, 10, 6, 15, 1, 9, 5] |
| 60 | P-n50-C17-V4-Q150 | [14, 1, 5, 13, 11] | [16, 2, 8, 10, 17, 4, 15, 9, 6, 12, 3, 7] |
| 61 | P-n50-C17-V3-Q120 | [9, 12, 11, 4, 17] | [6, 1, 15, 10, 5, 14, 16, 3, 2, 7, 13, 8] |
| 62 | P-n50-C17-V3-Q100 | [14, 3, 6, 11, 15] | [9, 13, 1, 10, 5, 7, 2, 12, 17, 16, 8, 4] |
| 63 | P-n51-C17-V4-Q80 | [4, 14, 3, 1, 15] | [2, 6, 5, 12, 11, 8, 7, 16, 13, 9, 10, 17] |
| 64 | P-n55-C19-V4-Q115 | [2, 17, 15, 18, 10] | [16, 8, 3, 12, 5, 6, 7, 13, 1, 11, 19, 9, 4, 14] |
| 65 | P-n55-C19-V6-Q70 | [8, 1, 7, 13, 10] | [9, 3, 5, 16, 19, 12, 4, 11, 2, 14, 17, 18, 6, 15] |
| 66 | P-n55-C19-V3-Q170 | [10, 1, 5, 15, 17] | [8, 13, 14, 11, 19, 6, 12, 4, 18, 2, 3, 7, 9, 16] |
| 67 | P-n55-C19-V3-Q160 | [4, 8, 15, 3, 1] | [2, 6, 5, 7, 18, 19, 12, 13, 16, 17, 9, 10, 11, 14] |
| 68 | P-n60-C20-V4-Q120 | [8, 16, 11, 2, 15] | [5, 3, 20, 18, 6, 13, 12, 4, 7, 10, 14, 17, 9, 19, 1] |
| 69 | P-n60-C20-V5-Q80 | [9, 12, 2, 15, 16] | [6, 13, 8, 11, 20, 3, 19, 17, 7, 18, 14, 10, 1, 4, 5] |
| 70 | P-n65-C22-V4-Q130 | [15, 19, 7, 6, 10, 16] | [8, 14, 4, 5, 9, 2, 20, 21, 22, 18, 13, 17, 3, 12, 11, 1] |
| 71 | P-n70-C24-V4-Q135 | [1, 23, 10, 15, 11, 14] | [4, 9, 17, 20, 18, 6, 12, 21, 22, 5, 19, 13, 24, 3, 8, 2, 7, 16] |
| 72 | P-n76-C26-V2-Q350 | [18, 24, 26, 8, 16, 1, 22] | [6, 21, 14, 19, 10, 7, 17, 23, 13, 15, 4, 25, 11, 20, 2, 9, 12, 3, 5] |
| 73 | P-n76-C26-V2-Q280 | [2, 20, 17, 23, 25, 13, 12] | [1, 6, 21, 8, 19, 3, 14, 5, 10, 18, 11, 16, 26, 24, 4, 15, 7, 22, 9] |
| 74 | P-n101-C34-V2-Q400 | [27, 22, 8, 23, 14, 20, 18, 15, 29] | [34, 25, 28, 9, 13, 12, 19, 24, 31, 32, 2, 3, 5, 26, 30, 6, 16, 10, 17, 11, 33, 1, 4, 21, 7] |
| 75 | M-n101-k10-C34-V4-Q200 | [10, 25, 3, 9, 19, 1, 2, 29, 8] | [7, 23, 32, 31, 4, 16, 33, 20, 17, 28, 24, 13, 22, 15, 18, 11, 27, 21, 5, 14, 12, 30, 6, 34, 26] |
| 76 | M-n121-k7-C41-V3-Q200 | [1, 2, 30, 12, 11, 7, 35, 14, 9, 34, 22] | [19, 6, 31, 4, 37, 40, 10, 17, 13, 15, 27, 20, 32, 18, 8, 28, 26, 39, 21, 36, 23, 16, 33, 5, 3, 24, 41, 25, 29, 38] |
| 77 | M-n151-k12-C51-V4-Q200 | [19, 29, 48, 46, 39, 49, 17, 45, 38, 30, 31, 3, 1] | [18, 44, 13, 41, 33, 15, 2, 10, 20, 42, 35, 14, 6, 22, 26, 5, 8, 23, 50, 32, 21, 16, 37, 36, 51, 28, 24, 9, 25, 34, 7, 12, 40, 11, 43, 27, 4, 47] |
References
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Chen, G.; Gao, J.; Chen, D. Research on Vehicle Routing Problem with Time Windows Based on Improved Genetic Algorithm and Ant Colony Algorithm. Electronics 2025, 14, 647. [Google Scholar] [CrossRef]
- Zamal, M.A.; Schrotenboer, A.H.; Van Woensel, T. The Two-Echelon Vehicle Routing Problem with Pickups, Deliveries, and Deadlines. Comput. Oper. Res. 2025, 179, 107016. [Google Scholar] [CrossRef]
- Baptista, G.; Vieira, M.; Pinto, T. An Exact Approach to the Multi-Compartment Vehicle Routing Problem: The Case of a Fuel Distribution Company. Mathematics 2024, 12, 527. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, C.; Wei, Y.; Wei, Y.; Wang, H. Collaboration and Resource Sharing for the Multi-Depot Electric Vehicle Routing Problem with Time Windows and Dynamic Customer Demands. Sustainability 2025, 17, 2700. [Google Scholar] [CrossRef]
- Meng, W.; He, Y.; Zhou, Y. Q-Learning-Driven Butterfly Optimization Algorithm for Green Vehicle Routing Problem Considering Customer Preference. Biomimetics 2025, 10, 57. [Google Scholar] [CrossRef]
- Wang, Y.; Gou, M.; Luo, S.; Fan, J.; Wang, H. The Multi-Depot Pickup and Delivery Vehicle Routing Problem with Time Windows and Dynamic Demands. Eng. Appl. Artif. Intell. 2025, 139, 109700. [Google Scholar] [CrossRef]
- Vargas-Quintero, A.; Morillo-Torres, D.; Escobar, J.W. Two-Stage Linear Stochastic Programming Formulations for the Stochastic Vehicle Routing Problem with Backhauls and Time Windows. Int. J. Syst. Sci.-Oper. Logist. 2025, 12, 2451223. [Google Scholar] [CrossRef]
- Nourmohammadi, Z.; Hu, B.; Rey, D.; Saberi, M. A Data-Driven Preference Learning Approach for Multi-Objective Vehicle Routing Problems in Last-Mile Delivery. Transp. Res. Pt. C-Emerg. Technol. 2025, 174, 105101. [Google Scholar] [CrossRef]
- Sevaux, M.; Sörensen, K. Hamiltonian Paths in Large Clustered Routing Problems. In Proceedings of the EU/Meeting 2008 Workshop on Metaheuristics for Logistics and Vehicle Routing, Troyes, France, 23–24 October 2008. [Google Scholar]
- Defryn, C.; Sörensen, K. A Fast Two-Level Variable Neighborhood Search for the Clustered Vehicle Routing Problem. Comput. Oper. Res. 2017, 83, 78–94. [Google Scholar] [CrossRef]
- Battarra, M.; Erdoğan, G.; Vigo, D. Exact Algorithms for the Clustered Vehicle Routing Problem. Oper. Res. 2014, 62, 58–71. [Google Scholar] [CrossRef]
- Expósito-Izquierdo, C.; Rossi, A.; Sevaux, M. A Two-Level Solution Approach to Solve the Clustered Capacitated Vehicle Routing Problem. Comput. Ind. Eng. 2016, 91, 274–289. [Google Scholar] [CrossRef]
- Islam, M.A.; Gajpal, Y.; ElMekkawy, T.Y. Hybrid Particle Swarm Optimization Algorithm for Solving the Clustered Vehicle Routing Problem. Appl. Soft Comput. 2021, 110, 107655. [Google Scholar] [CrossRef]
- Barthélemy, T.; Rossi, A.; Sevaux, M.; Sörensen, K. Metaheuristic Approach for the Clustered VRP. In Proceedings of the EU/ME 2010-10th Anniversary of the Metaheuristics Community, Lorient, France, 3–4 June 2010. [Google Scholar]
- Pop, P.C.; Kara, I.; Marc, A.H. New Mathematical Models of the Generalized Vehicle Routing Problem and Extensions. Appl. Math. Modell. 2012, 36, 97–107. [Google Scholar] [CrossRef]
- Vidal, T.; Battarra, M.; Subramanian, A.; Erdogan, G. Hybrid Metaheuristics for the Clustered Vehicle Routing Problem. Comput. Oper. Res. 2015, 58, 87–99. [Google Scholar] [CrossRef]
- Horvat-Marc, A.; Fuksz, L.; Pop, P.C.; Dănciulescu, D. A Decomposition-Based Method for Solving the Clustered Vehicle Routing Problem. Log. J. IGPL 2018, 26, 83–95. [Google Scholar] [CrossRef]
- Pop, P.C.; Fuksz, L.; Marc, A.H.; Sabo, C. A Novel Two-Level Optimization Approach for Clustered Vehicle Routing Problem. Comput. Ind. Eng. 2018, 115, 304–318. [Google Scholar] [CrossRef]
- Hintsch, T.; Irnich, S. Large Multiple Neighborhood Search for the Clustered Vehicle-Routing Problem. Eur. J. Oper. Res. 2018, 270, 118–131. [Google Scholar] [CrossRef]
- Hintsch, T.; Irnich, S. Exact Solution of the Soft-Clustered Vehicle-Routing Problem. Eur. J. Oper. Res. 2020, 280, 164–178. [Google Scholar]
- Heßler, K.; Irnich, S. A Branch-and-Cut Algorithm for the Soft-Clustered Vehicle-Routing Problem. Discrete Appl. Math. 2021, 288, 218–234. [Google Scholar]
- Hintsch, T. Large Multiple Neighborhood Search for the Soft-Clustered Vehicle-Routing Problem. Comput. Oper. Res. 2021, 129, 105132. [Google Scholar] [CrossRef]
- Cosma, O.; Pop, P.C.; Sitar, C.P. A Two-Level Based Genetic Algorithm for Solving the Soft-Clustered Vehicle Routing Problem. Carpathian J. Math. 2022, 38, 117–128. [Google Scholar] [CrossRef]
- Zhou, Y.; Kou, Y.; Zhou, M. Bilevel Memetic Search Approach to the Soft-Clustered Vehicle Routing Problem. Transp. Sci. 2023, 57, 701–716. [Google Scholar] [CrossRef]
- Xu, R.; Huang, Y.; Xiao, W. A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs. Sustainability 2023, 15, 7639. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Lee, K.Y. Two-Step Genetic Algorithm for Dynamic Route Optimization of Electric Vehicles Based on Demand Analysis. Arab. J. Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Y.; Zhang, L.; Yuan, X. Application of Improved Genetic Algorithm to Vehicle Routing Problem Considering the Environmental Self-Regulation of the Freight Companies. Expert Syst. Appl. 2025, 274, 127010. [Google Scholar] [CrossRef]
- Palamutçuoğlu, B.; Çavuşoğlu, S.; Çamlı, A.; Virlanuta, F.; Bacalum, S.; Züngün, D.; Moisescu, F. Solution of the Capacity-Constrained Vehicle Routing Problem Considering Carbon Footprint within the Scope of Sustainable Logistics with Genetic Algorithm. Sustainability 2025, 17, 727. [Google Scholar] [CrossRef]
- Liu, J.; Tong, L.; Xia, X. A Genetic Algorithm for Vehicle Routing Problems with Time Windows Based on Cluster of Geographic Positions and Time Windows. Appl. Soft Comput. 2025, 169, 112593. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).