1. Introduction
Synthetic Aperture Radar (SAR), as an advanced imaging technology, has been widely used in fields such as Earth observation, environmental monitoring, and disaster assessment due to its high-resolution, all-weather, and all-weather imaging capabilities [
1,
2,
3]. Unlike optical imaging, SAR images can penetrate clouds and rain, providing high-quality images of the Earth’s surface [
4,
5]. However, due to the coherence of radar signals, the quality of SAR images is affected by various factors, among which the most significant is the interference of noise, manifested as granular texture in the image, which seriously affects the visualization effect and subsequent analysis and processing of the image [
6]. Therefore, developing efficient SAR image denoising algorithms has become an important task in remote sensing image processing research.
The challenge of SAR image denoising lies in its unique imaging mechanism. SAR imaging relies on reflection signals obtained from different angles, processed through synthetic aperture to form high-resolution images. This process inherently introduces noise, especially speckle noise, whose impact is closely related to the scattering characteristics of the target object, radar operating parameters, and imaging environment [
7]. In traditional denoising methods, filtering technology is the most commonly used one. These methods include mean filtering, median filtering, and adaptive filtering [
8,
9]. Although these methods are effective in denoising, they often cause distortion when processing edge and detail features, making it difficult to meet the high-quality requirements of SAR images [
10,
11]. In addition, model-based methods such as wavelet transform and statistical model denoising have also been widely applied in SAR image denoising [
12,
13]. However, these methods often rely on accurate modeling of the statistical characteristics of noise, and their performance is not ideal in complex scenarios. Despeckling methods, including spatial filters, transform-domain techniques, and non-local means (NLM), often struggle with over-smoothing or introducing artifacts. The aforementioned methods generally rely on predefined models and assumptions that may not effectively capture the complex, nonlinear nature of SAR data, potentially limiting their denoising performance.
In contrast, deep learning-based methods can learn intricate patterns and representations directly from data, enabling them to adapt to the unique characteristics of SAR imagery and achieve superior noise reduction. Particularly, Convolutional Neural Networks (CNNs) [
14,
15,
16], have demonstrated excellent performance by learning complex noise-to-clean mappings. However, their reliance on paired “noisy-clean” datasets for supervised training introduces a critical limitation. Real-world SAR applications often lack noise-free ground truth images, forcing models to rely on synthetic data with domain gaps in terms of scattering and noise characteristics. This mismatch results in suboptimal performance when applied to real SAR images. Self-supervised learning strategies, have recently gained attention by eliminating the need for clean references. For instance, Yuan Ye et al. [
17] proposed a segmentation-guided semantic-aware self-supervised SAR image denoising method, named SARDeSeg. This method combines a segmentation network with a denoising network, guiding it to learn and perceive the semantic information of the noisy input SAR images. The self-supervised enhanced Noise2Noise (EN2N) method is proposed in [
18], which addresses the challenges of spatial detail loss, dependence on noise-free training data, and low computational efficiency of traditional methods in removing multiplicative noise from SAR images [
19]. This is achieved by integrating pre-trained CNN features with a hybrid loss function.
In recent years, the rapid development of deep learning technology has provided new solutions for SAR image denoising. Deep learning algorithms can automatically learn features from data by constructing complex neural network models, thereby achieving better performance in denoising tasks. For example, the successful application of CNNs in image processing has inspired researchers to apply it to denoising SAR images [
20,
21]. For example, reference [
22] proposes combining residual learning and batch normalization strategies to propose the SAR-CNN denoising algorithm, which can achieve some improvements in running speed and denoising performance. In order to achieve end-to-end learning, reference [
22] proposed processing based on multi-layer wavelet networks, and further improved the denoising quality. Wang et al. [
23] first applied the principle of generative adversarial networks to SAR images. In order to improve denoising performance and image detail preservation ability, Gu et al. [
24] proposed a speckle noise suppression network based on adversarial generative networks. Zhang et al. [
25] used an Autoencoder structure for SAR image denoising. The SAR image denoising method based on deep learning has stronger adaptability and flexibility, but in specific scenarios or tasks, the annotation and acquisition of SAR image data may be very difficult, and problems such as low feature matching and large computational complexity. Meanwhile, the denoising process may lead to the loss of image details, especially in processing important features such as target information, resulting in poor performance in dealing with complex noise distributions and SAR images.
In response to the above issues, this paper proposes a convolutional neural network SAR image denoising algorithm based on self-learning strategy. Unlike traditional methods that rely on hand-crafted features or supervised training with noisy-clean pairs, our approach leverages a self-supervised training strategy that learns directly from the noisy SAR data. This allows the model to capture complex noise distributions inherent in SAR images, thereby significantly enhancing denoising performance and generalization. Considering that SAR images are affected by various types of noise, a noise recognition method based on residual statistical features was first designed. Digital image processing techniques were used to simulate the superposition state of SAR images with different noises, in order to determine the type of noise. In response to the problem of unknown noise, this paper further proposes a SAR image denoising algorithm based on Denoising Convolutional Neural Network (DnCNN). Based on the self-learning DnCNN denoising model, a twin convolutional network structure is adopted, which can specifically adapt to the characteristics of SAR images and enhance the model’s generalization ability to different noise types and complex noise distributions. By constructing a noise original image dataset sample pair for training, image features and noise distribution are automatically learned, significantly improving the denoising effect of SAR images and having stronger generalization ability. Simulation experiments have demonstrated the effectiveness of the proposed method.
The remainder of this paper is organized as follows.
Section 2 introduces the SAR image denoising algorithm based on self-learning strategy DnCNN, including the algorithm design, data augmentation, and network structure.
Section 3 presents simulation experiment results, including the evaluation of denoising effect and comparison with existing method.
Section 4 concludes this paper.
2. SAR Image Denoising Algorithm Based on Self-Learning Strategy DnCNN
2.1. Algorithm Design
Based on the idea of self-learning strategy [
26] and dual-path structure on denoising [
27], this article modifies and designs the traditional DnCNN model to fully utilize the image features of SAR images in terms of denoising effect. We add Gaussian noise to img.H to generate img.L, which involves preparing a set of noisy image datasets and corresponding noise free image datasets. These noisy datasets can be obtained by simulating the addition of noise on the corresponding noise free image datasets. Specifically, we added Gaussian noise to the clean simulation datasets to obtain corresponding noisy image datasets. During the training process, the input noisy image needs to be fed into the network for forward propagation to obtain the output denoised image. Then, compare the output denoised image with the corresponding noiseless image and calculate the value of the loss function. Next, use the backpropagation algorithm to update the network parameters to minimize the value of the loss function. This process requires multiple iterations until the model converges. The loss function used for training is the Mean Square Error (MSE) loss function. During the training process, the model parameters with the best training effect were selected and tested on the simulation dataset. It can be intuitively seen that the denoising effect has been greatly improved compared to previous methods, and the Gaussian noise added to the image itself has been basically completely removed.
2.2. Data Augmentation
To address the issue of a small number of training samples, data augmentation methods are adopted to expand the training sample set, thereby constructing a target dataset suitable for SAR imaging recognition. This article uses the following three data augmentation methods to expand the training dataset of ISAR images of large aerial targets.
(1) Target displacement: In SAR imaging results, the grayscale values of the target are concentrated in the middle position of the image. However, under ideal conditions, the target may shift in various directions, causing the target data to deviate from the central area of the image. In this situation, if the random displacement process of the image can be simulated, the generated image can be regarded as an enhancement of the original image.
(2) Image rotation: During the process of SAR image acquisition, target rotation is also possible, and there are 360 ways to enhance images by measuring rotation by 1°. Therefore, rotating the original image by multiple angles is also a way to expand the training set.
(3) Image denoising: Due to the SAR imaging mechanism and possible interference in the system, the obtained image is highly likely to have noise interference, manifested as numerous and dense white spots on the image. Therefore, adding noise with different variances to the original image is also a reasonable and effective image enhancement method. For example, noise with different means and levels of variance can be used to implement a data augmentation scheme with added noise.
2.3. Network Structure
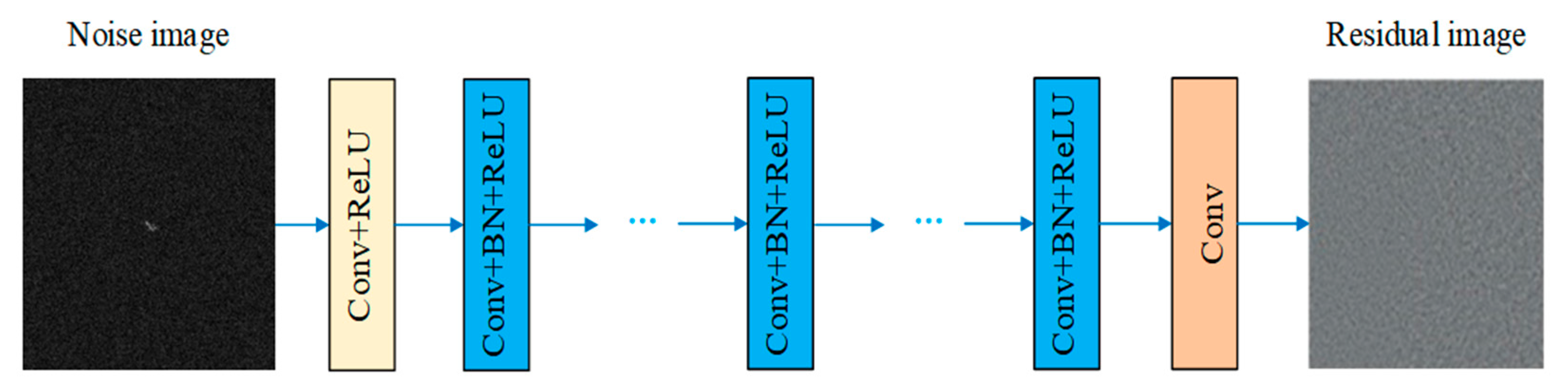
DnCNN is designed to predict the residual image (noise) from a noisy input image. The residual image is the difference between the noisy image and the clean image. The self-learning strategy in DnCNN involves training the network to learn the mapping from noisy images to their residuals, which can then be subtracted from the noisy image to recover the clean image. In the context of DnCNN, analyzing the histogram of the residual image could help understand the characteristics of the noise being learned by the network and can be used as a preprocessing step to focus on the intensity component of the image, which is often the most affected by noise. As for the self-learning strategy, it plays a crucial role in our approach by allowing the network to adapt to varying noise distributions without requiring explicitly labeled noise-free images. Specifically, our model employs a residual learning framework where the network is trained to predict the noise residual from a given noisy input. This residual is then subtracted from the noisy image to recover a clean image. The training process is guided by a mean squared error loss function that directly measures the discrepancy between the predicted and actual noise components. To be specific, transforming the image to the HSV color space and extracting the V (Value) channel is calculated as follows:
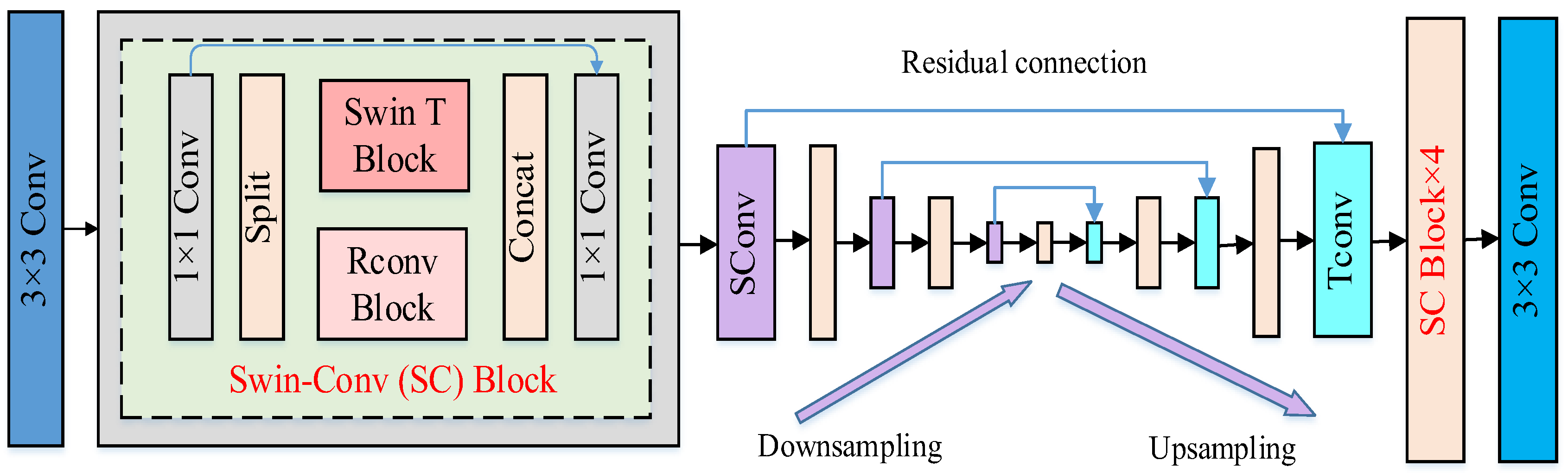
Another approach to dealing with unknown noise is to train a self-learning strategy denoising algorithm that has generalization ability for different types of noise. This paper proposes a denoising algorithm design and simulation based on image reconstruction. The network structure is shown in
Figure 1. The algorithm adopts a twin convolutional network referring to swin-conv (SC) network structure and is trained by constructing a noise original image sample pair. Regarding the twin convolutional network structure, we selected this structure because it enables simultaneous feature extraction from two complementary views of the data—one branch processing the noisy input and the other estimating the corresponding clean representation. This structure helps to enhance the robustness of feature learning by enforcing consistency between the two branches. It integrates two parallel but interdependent convolutional pathways designed to capture complementary features from SAR imagery. Unlike conventional dual-path models, which often process features independently, our SC network employs a feature fusion mechanism that dynamically aggregates spatial and textural information, making it particularly effective for SAR image denoising.
The clean noise sample pair of SAR images are shown in
Figure 2. The denoising effect can be evaluated by the background suppression factor BSF. The commonly used classic image processing methods for noise reduction include mean filtering, Gaussian filtering, median filtering, bilateral filtering, etc. These classic methods are used to denoise the noise simulation images in the noise simulation dataset, and the denoising effect is compared.
Mean filtering is a corresponding operation performed in the spatial domain. During the filtering process, a template is selected, and the pixel value of each point in the image is replaced by the mean of the pixel values of all points in this template. The mean filtering formula is:
The denoising effect of the image after applying mean filtering is shown in
Figure 3.
Gaussian filtering is a method of blurring an image and removing details and noise. In this sense, it is similar to mean filtering. However, it uses a different weight kernel that represents the shape of a Gaussian (bell shaped) bulge. This method is used for various functions such as image blurring, noise reduction, and detail smoothing. The formula for Gaussian filter kernel is
where
x and
y are the distances from the origin to the horizontal and vertical axes,
σ is the standard deviation of Gaussian distribution. The denoising effect of the image after applying Gaussian filtering is shown in
Figure 3.
Median filtering is a denoising method that processes in the spatial domain. The filtering method involves selecting a template and performing corresponding operations within it. Firstly, the pixel values in the template are sorted, and the median of the pixels in the sequence is selected as the central pixel value of the template. This can remove noise points in the image that differ significantly from the surrounding pixels, thus achieving the goal of denoising. The selection of filtering templates is diverse, which can be square or rectangular matrices, circular, or cross shaped. The denoising effect of the image after applying median filtering is shown in
Figure 3.
Bilateral filtering is also a denoising method that processes in the spatial domain. By considering the influence of distance factors and pixel value differences, it can effectively preserve the feature information of the image while denoising. The denoising effect of the image after applying bilateral filtering is shown in
Figure 3.
Non-local average denoising uses redundant information commonly found in natural images to remove noise. Unlike commonly used bilinear filtering, median filtering, and other methods that utilize local information in the image for filtering, it uses the entire image for denoising, searching for similar regions in the image on a block by block basis, and then averaging these regions to effectively remove Gaussian noise present in the image. Algorithms consume more time, but the results are better. The image denoising effect after applying non-local average denoising is shown in
Figure 3.
From the denoising results, it can be concluded that although the above five classic image denoising algorithms have a certain filtering effect on the noise of single channel noise simulation images, the effect is not good and there is still a lot of room for improvement. We train the DnCNN network based on self-learning by adding Gaussian noise to the original dataset, enabling the algorithm to fully utilize the advantages of deep neural networks in feature extraction and improve denoising performance. Specifically, as shown in
Figure 4, the main structure of the DnCNN model includes:
Layer 1 Conv + ReLU: The input is a 35 × 35 × c image, and after 64 3 × 3 × 3 convolution kernels, the output is 64 35 × 35 feature maps, which are 35 × 35 × 64 images. Layer (2~(d-1)) Conv + BN + ReLU: There are 64 3 × 3 × 64 convolution kernels, so the input and output of these layers are all 35 × 35 × 64 images. Add batch normalization between convolution and activation functions. The last layer Conv: Reconstruct a c-dimensional image using c 3 × 3 × 64 convolution kernels as output. Each layer has zero padding to ensure consistent input and output sizes. This prevents the generation of boundary artifacts.
DnCNN combines ResNet’s residual learning, also known as residual learning. The difference is that DnCNN does not add connections between neural network layers, but directly changes the output of the network learning process to residuals. Assuming the clean image is x and the noisy image is y, then y = x + n, where n is the residual, which is the noise. In the learning process of DnCNN, the optimization goal is no longer the loss between clean images and network output, but the error between residuals and network output. The effect of directly using the DnCNN model to load pre training parameters for denoising single channel noise simulation images is as follows. As shown in
Figure 3, it can be seen that the untrained and optimized DnCNN model has poor denoising performance on SAR images.
2.4. Complexity Analysis
The computational complexity of our proposed CNN-based SAR denoising algorithm is primarily determined by the convolutional layers. For each convolutional layer, the complexity is approximately
where
H and
W denote the height and width of the feature maps,
Cin and
Cout are the numbers of input and output channels, and
K is the kernel size. Since the proposed network consists of several such layers, the total computational load scales linearly with the number of layers.
4. Conclusions and Future Work
At present, traditional denoising methods based on manual feature extraction have certain drawbacks, such as the assumption that encoding relies on the original image, low matching degree of encoded features in real images, reduced performance and flexibility of the method in practical applications, and the feature extraction process of the method is cumbersome, time-consuming, and computationally intensive, which is not suitable for processing real noise with complex distributions. At the same time, the denoising effect on SAR images is poor, and so on. In this paper, we first proposed a self-learning based DnCNN denoising model to effectively solve these problems. By using noisy image datasets and corresponding noise free image datasets to train and optimize the model, it can automatically learn the features and noise distribution in the image, greatly improving the denoising effect of the model on SAR images. Compared with traditional denoising algorithms based on manual feature extraction, the self-learning based SAR image denoising algorithm can provide better denoising effect and stronger generalization ability. In future work, we plan to conduct more extensive experiments to quantify performance variations across different noise models and refine the training process to further reduce any sensitivity to the specific noise type used during training, as well as the trade-offs between denoising effectiveness and processing speed for potential optimization strategies. Alternative loss functions, such as perceptual loss and total variation loss, can better capture perceptual and structural aspects of the images. A more comprehensive evaluation of alternative loss functions will be left for our future work.