Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm
Abstract
1. Introduction
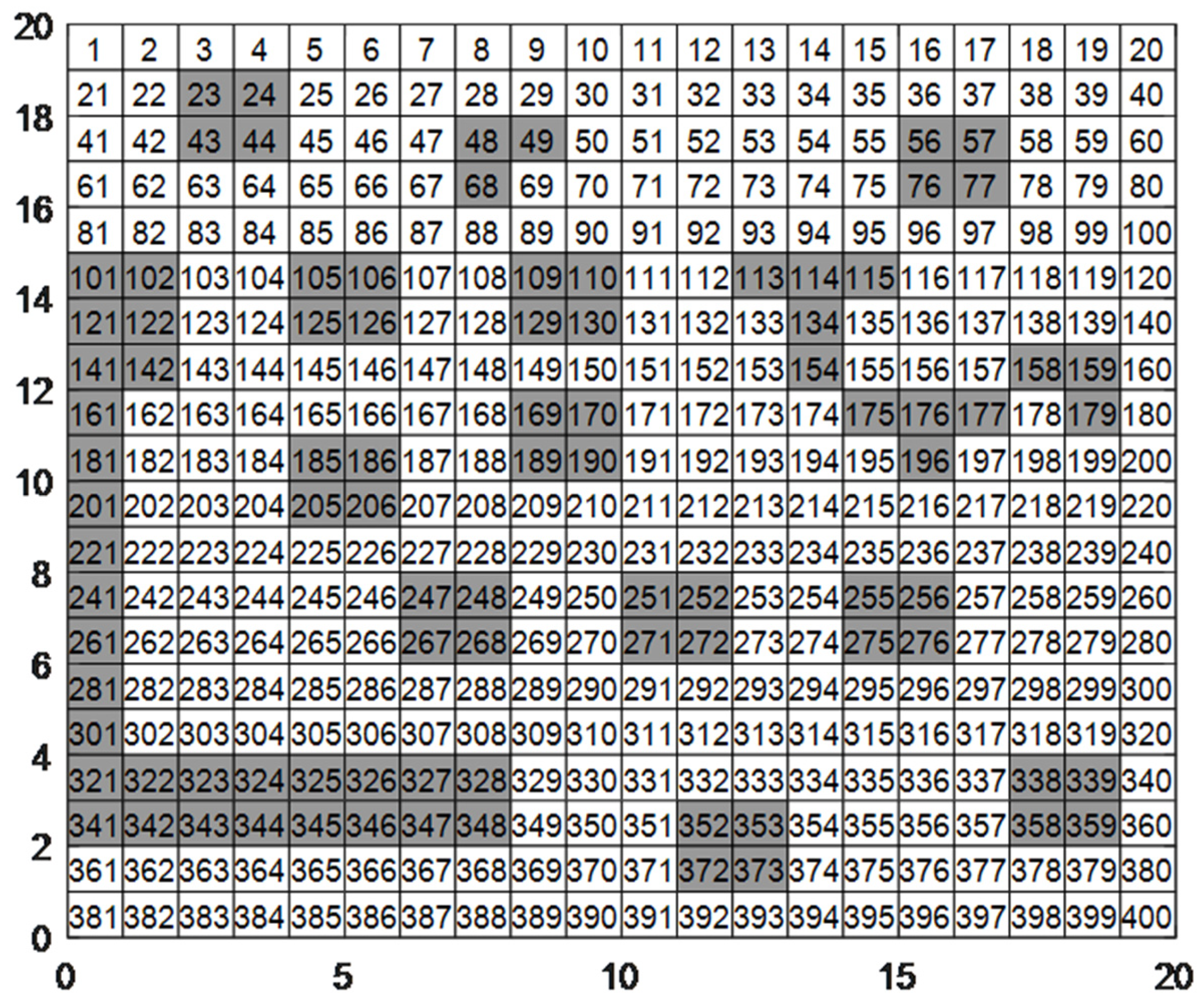
2. Environment Modeling
3. Basic Algorithms
3.1. ACA
3.1.1. Path Selection Probability
3.1.2. Update PC
3.2. APF Method
3.2.1. Gravitational Potential Field
3.2.2. Repulsive Potential Field (RPF)
3.2.3. Resultant Force and Motion
4. ACA Integrated with the APF Method
4.1. Improvement of HF Based on the Attraction of APF
4.2. Improvement of Pheromone Volatilization Factor ρ
4.3. Improvement of the Pheromone Update Mechanism
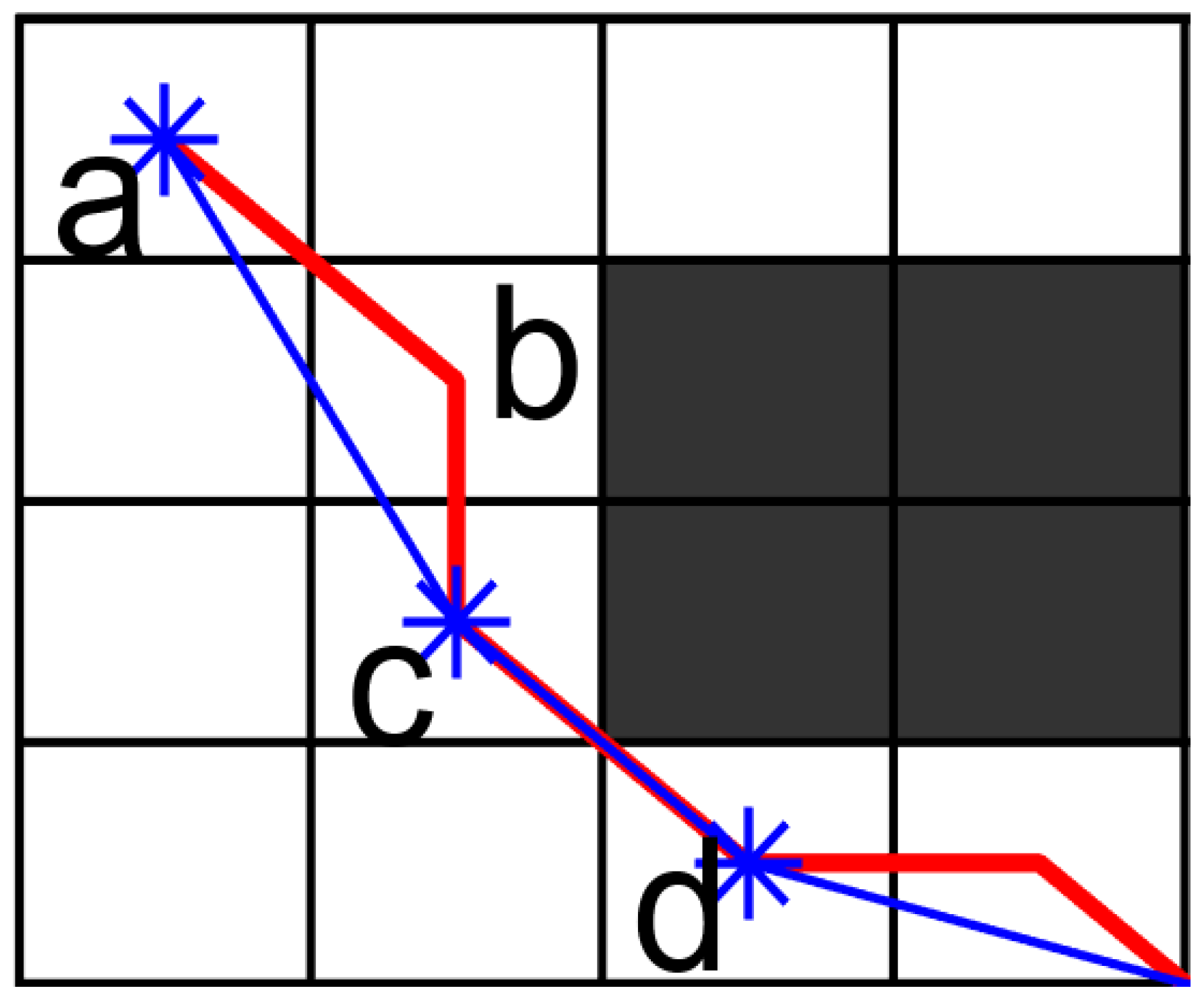
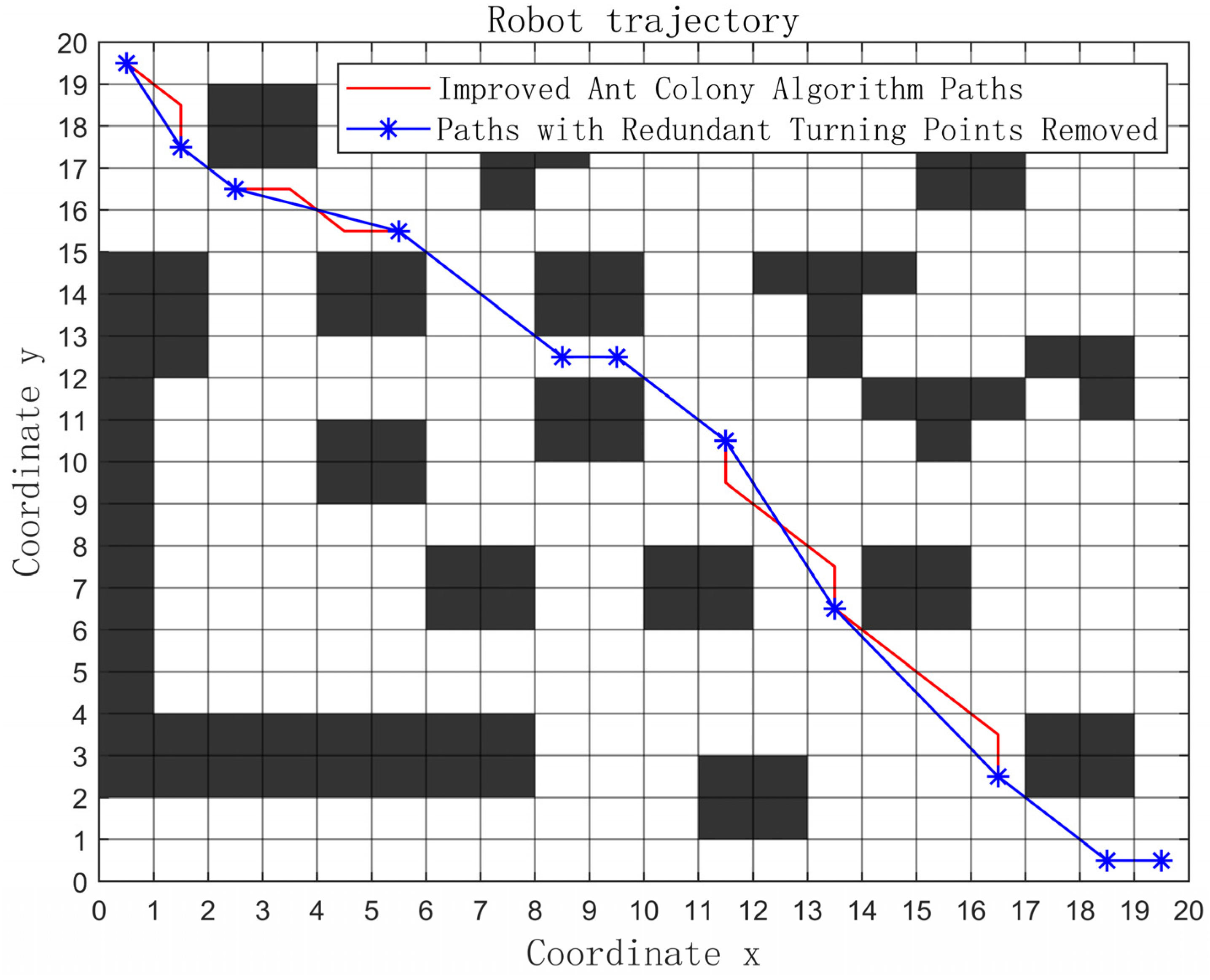
4.4. Pruning Method for Path Optimization and Update
4.5. Algorithm Execution Process
5. Algorithm Simulation and Analysis
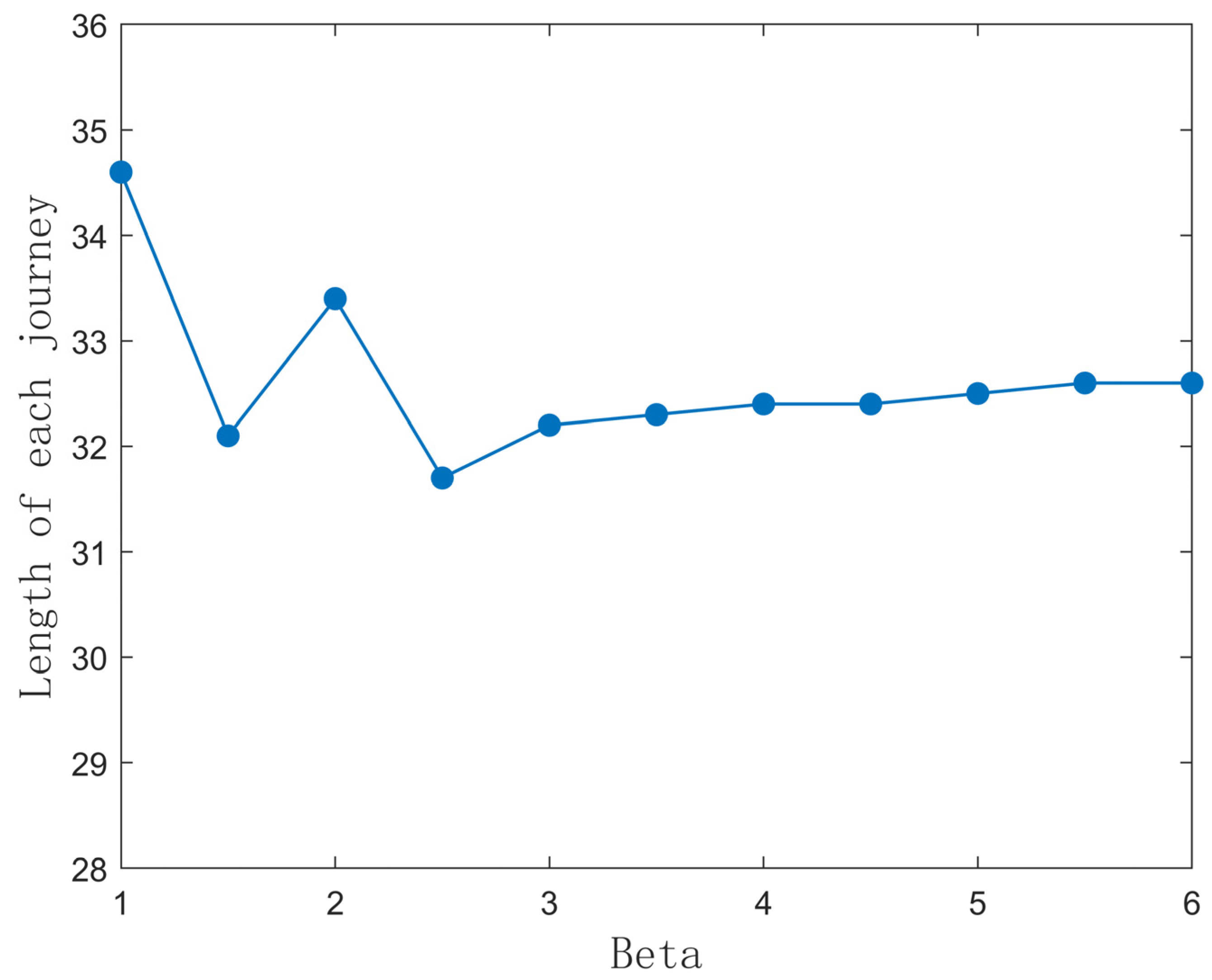
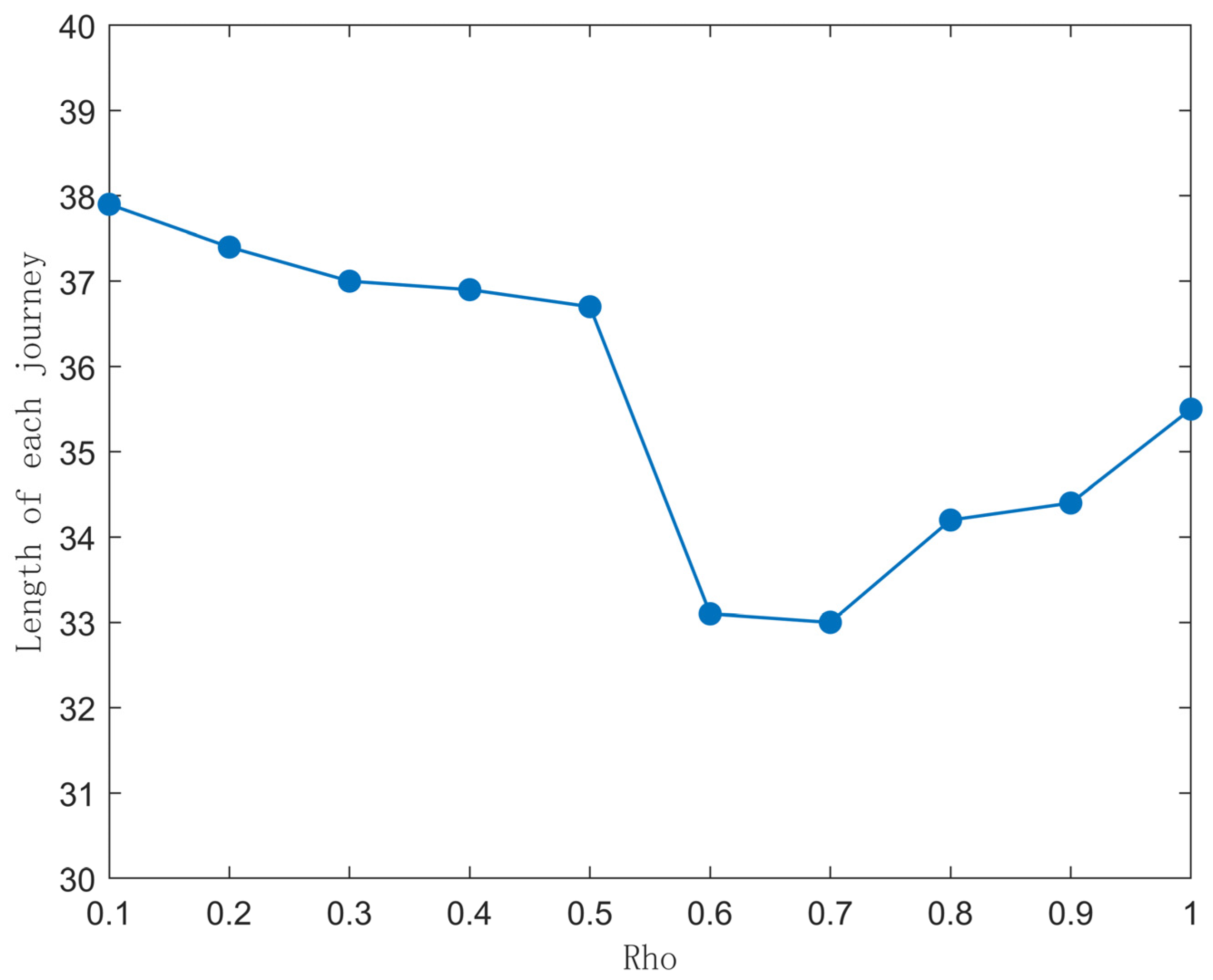
5.1. Parameter Sensitivity Analysis
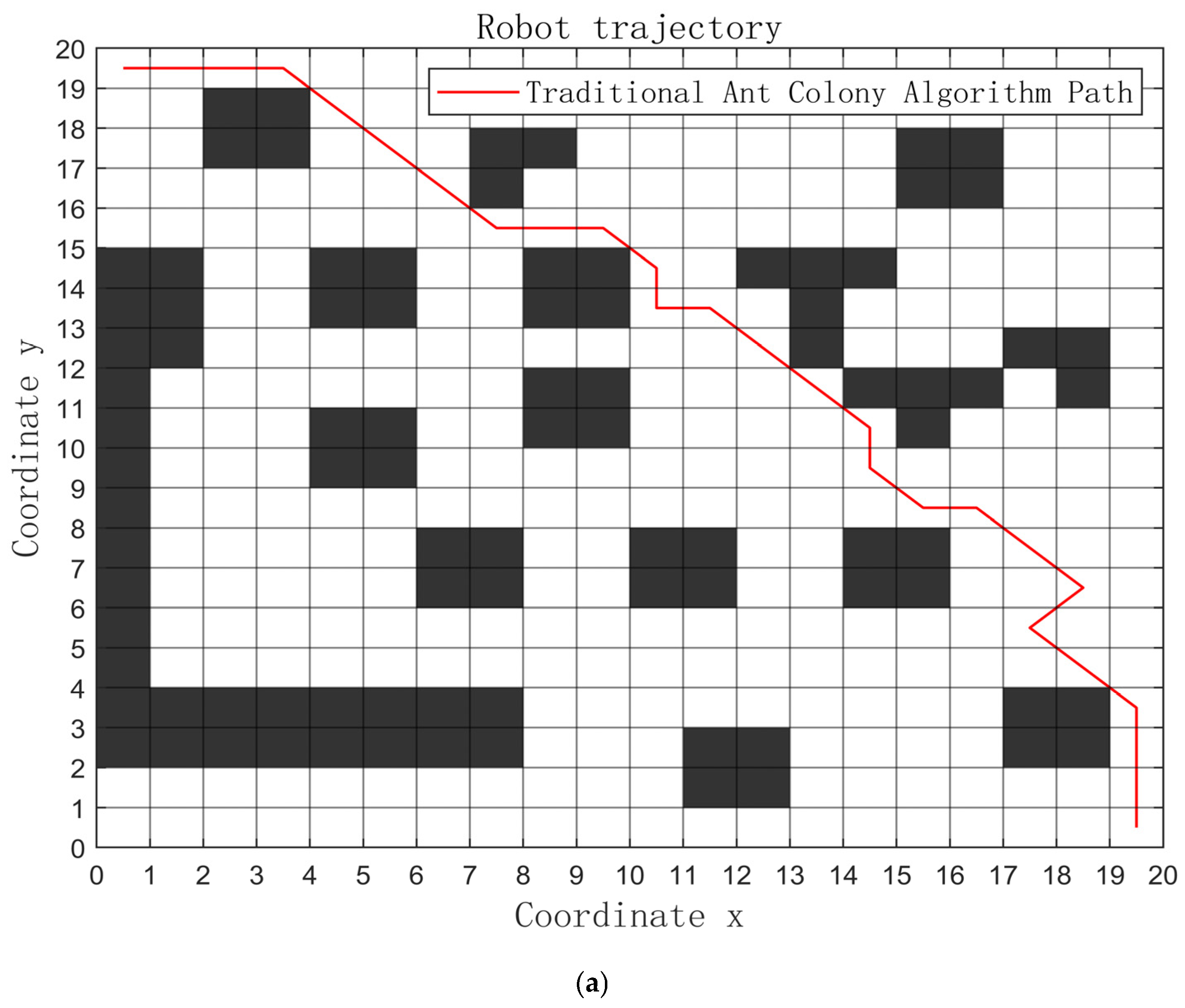
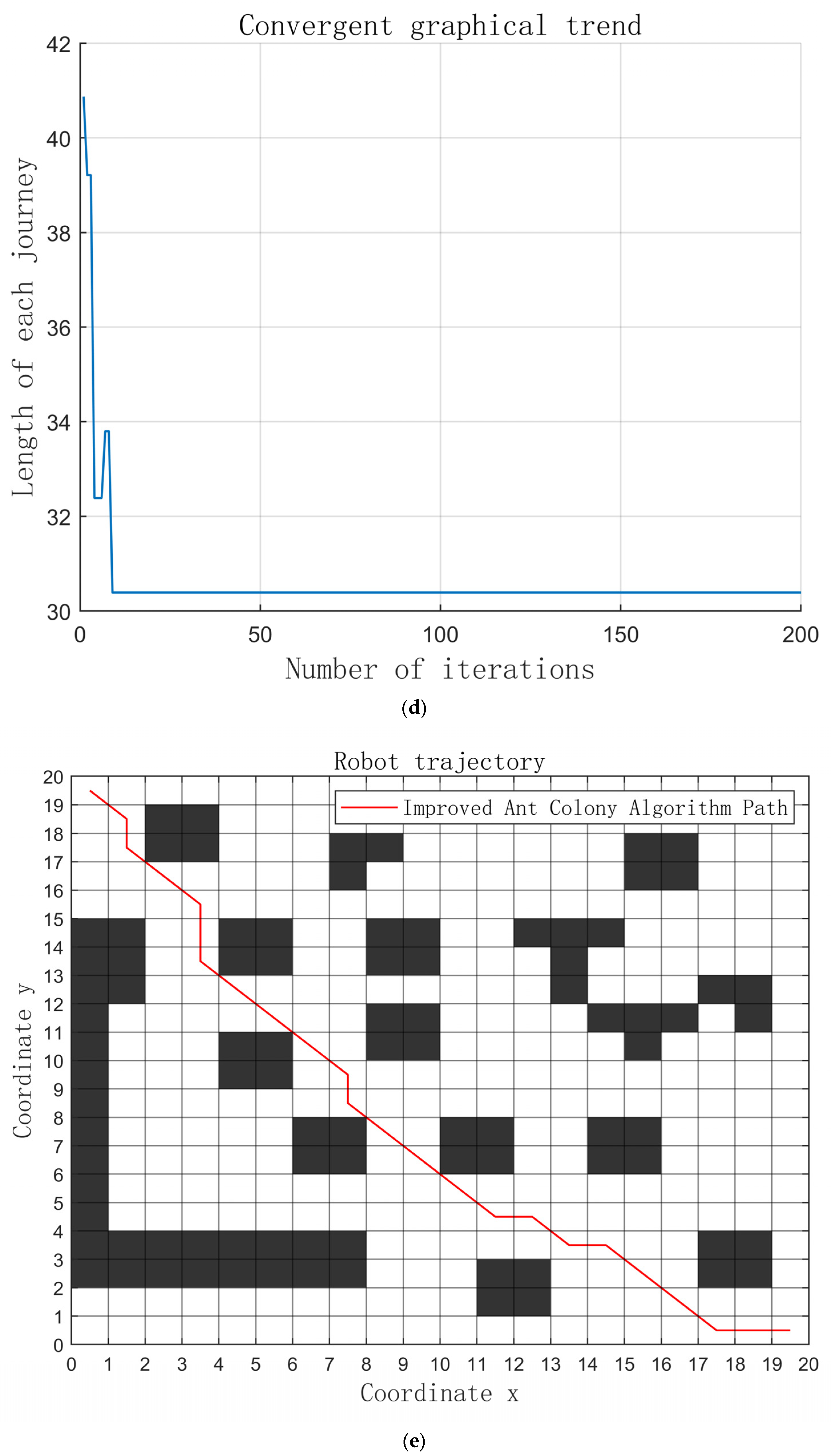
5.2. A 20 × 20 Grid Map
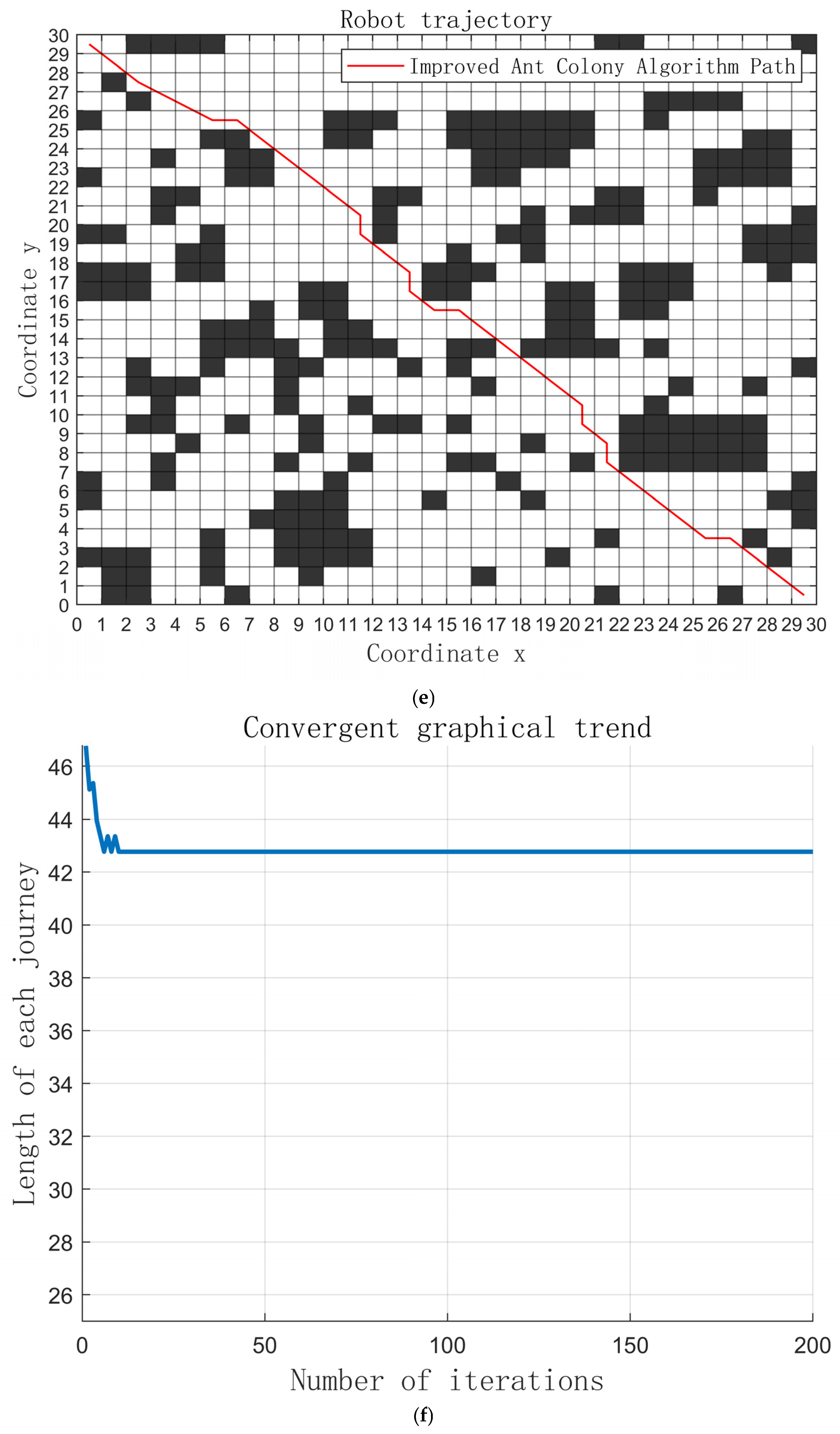
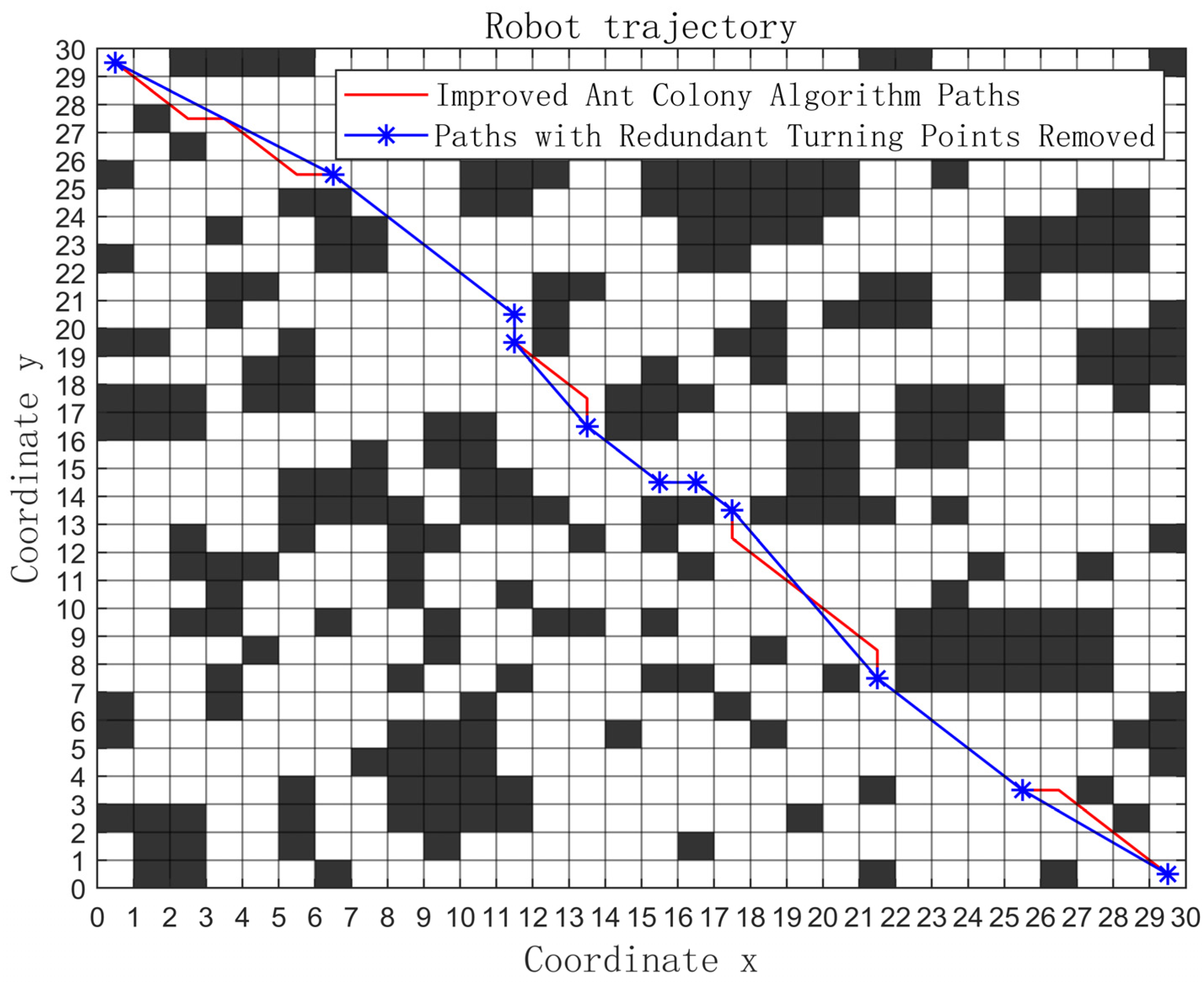
5.3. A 30 × 30 Grid Map
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Luo, J.; Zhang, L.; Yu, H.; Liu, X.; Wang, S. Research on Traversal Path Planning and Collaborative Scheduling for Corn Harvesting and Transportation in Hilly Areas Based on Dijkstra’s Algorithm and Improved Harris Hawk Optimization. Agriculture 2025, 15, 233. [Google Scholar] [CrossRef]
- Zhang, C. An Improved Dijsktra Algorithm and Its Implementation in GIS. Comput. Appl. Softw. 2011, 28, 275–277. [Google Scholar]
- Liu, L.; Wang, B.; Xu, H. Research on Path-Planning Algorithm Integrating Optimization A-Star Algorithm and Artificial Potential Field Method. Electronics 2022, 11, 3660. [Google Scholar] [CrossRef]
- Yin, X.; Cai, P.; Zhao, K.; Zhang, Y.; Zhou, Q.; Yao, D. Dynamic Path Planning of AGV Based on Kinematical Constraint A* Algorithm and Following DWA Fusion Algorithms. Sensors 2023, 23, 4102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Huang, P.; Zhang, G.; Jin, Z.; Chen, Y.; Zong, M.; Chi, J.; Qiu, Z. Research on Adaptive Path Planning Based on Improved A* Algorithm. Commun. Inf. Technol. 2025, 1, 43–45+122. [Google Scholar]
- Sun, P.; Liu, C.; Shi, X.; Zhang, H.; Zha, W. Research on Path Planning for Mobile Robots Based on Improved A* Algorithm [J/OL]. J. Heilongjiang Inst. Technol. 2025, 1–8. Available online: http://kns.cnki.net/kcms/detail/23.1498.N.20250115.1809.004.html (accessed on 1 March 2025).
- Zhang, Q. Design of Data Mining Method for Logistics Engineering Based on A* Algorithm and Cluster Analysis. J. Guiyang Univ. (Nat. Sci. Ed.) 2024, 19, 45–48+56. [Google Scholar]
- Chi, X.; Li, H.; Fei, J. Research on Random Obstacle Avoidance Method for Robots Based on Improved A* Algorithm and Dynamic Window Approach. J. Instrum. 2021, 42, 132–140. [Google Scholar]
- Kang, J.-G.; Lim, D.-W.; Choi, Y.-S.; Jang, W.-J.; Jung, J.-W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef]
- Fu, J.; Mu, L.; Di, X.; Zhang, X.; Zhang, H. Research on Complex Obstacle Avoidance Path Planning for Manipulators Based on Improved RRT Algorithm. Mod. Electron. Technol. 2025, 48, 180–186. [Google Scholar]
- Zhou, R.; Liu, H.; Peng, X. Intelligent Vehicle Path Planning Strategy Based on Optimized RRT Algorithm. Softw. Eng. 2024, 27, 49–52. [Google Scholar]
- He, X.; Zhou, Y.; Liu, H.; Shang, W. Improved RRT*-Connect Manipulator Path Planning in a Multi-Obstacle Narrow Environment. Sensors 2025, 25, 2364. [Google Scholar] [CrossRef]
- Wang, J.; Li, T.; Li, B.; Meng, M.Q.-H. GMR-RRT*: Sampling-based Path Planning Using Gaussian Mixture Regression. IEEE Trans. Intell. Veh. 2022, 7, 690–700. [Google Scholar] [CrossRef]
- Teng, Y.; Feng, T.; Song, C.; Li, J.; Yang, S.X.; Zhu, H. Path Planning of Mobile Robot Based on Dual-Layer Fuzzy Control and Improved Genetic Algorithm. Symmetry 2025, 17, 609. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Bai, X.; Zhang, S.; Xu, C. The Path Planning of Mobile Robots Based on an Improved Genetic Algorithm. Appl. Sci. 2025, 15, 3700. [Google Scholar] [CrossRef]
- Liu, C. Multi-UAV Route Planning Method Based on Improved Genetic Algorithm. Fire Control Command. Control 2019, 44, 18–22. [Google Scholar]
- Song, Y.; Gao, G.; Liang, C.; Xu, J. Path Planning of Unmanned Aerial Vehicles Based on Multi-Strategy Improved Grey Wolf Algorithm. Electron. Meas. Technol. 2025, 48, 84–91. [Google Scholar]
- Liu, G.; Jin, S.; Li, Z.; Liu, B. Path Planning of Urban Passenger Electric Vertical Takeoff and Landing Aircraft Based on Improved Artificial Electric Field Algorithm. Sci. Technol. Eng. 2025, 25, 238–244. [Google Scholar]
- Xue, M.; Xu, H.; Wang, S. Path Planning of Unmanned Surface Vessels Based on Particle Swarm Optimization Algorithm. China Sci. Technol. Inf. 2018, 24, 69–70. [Google Scholar]
- Deng, D.; Xu, J.; Meng, H.; Yang, W. Path Planning of Mobile Robots Based on the Fusion of Ant Colony Algorithm and Artificial Potential Field Method. J. Instrum. Instrumnetation 2025, 1–16. [Google Scholar] [CrossRef]
- Luo, Z.; He, G.; Zheng, X.; Huang, Y. Research on Robot Path Planning Based on Improved Ant Colony Hybrid Algorithm. J. Kunming Univ. Sci. Technol. (Nat. Sci. Ed.), 2025; 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, D.; Li, Y.; Li, J. AGV Path Planning Based on the Fusion of Jump Point Search and Bidirectional Ant Colony Algorithm. J. Xi’an Polytech. Univ. 2021, 35, 37–43. [Google Scholar]
- Jiao, Z.; Ma, K.; Rong, Y.; Wang, P.; Zhang, H.; Wang, S. A path planning method using adaptive polymorphic ant colony algorithm for smart wheelchairs. J. Comput. Sci. 2018, 25, 50–57. [Google Scholar] [CrossRef]
- Lu, D.; Wu, S. Robot Path Planning Based on Potential Field Ant Colony Algorithm. Syst. Eng. Electron. 2010, 32, 1277–1280. [Google Scholar]
- Kong, X. Research on Global Path Planning Algorithm for Mobile Robots Integrating Ant Colony Algorithm and Genetic Algorithm. Master’s Thesis, Northeastern University, Boston, MA, USA, 2018. [Google Scholar] [CrossRef]
- Stutzle, T.; Hoos, H.H. MAX-MIN Ant System. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Pan, J.; Wang, X.; Cheng, Y. Path Planning of Mobile Robots Based on Improved Ant Colony Algorithm. J. China Univ. Min. Technol. 2012, 41, 108–113. [Google Scholar]
- Yu, J.; Li, R.; Zhao, A.; Yu, Z.; Wang, J. Research on Path Planning of Warehouse AGV Based on Parallel Sorting Ant Colony Algorithm. Mech. Sci. Technol. 2021, 40, 609–618. [Google Scholar]
- Liu, L.; Yuan, G.; Dai, Y. Multi-Ant Colony Pseudo-Parallel Optimization Algorithm. Comput. Eng. 2007, 23, 199–201. [Google Scholar]
- Jin, D.; Yang, B.; Liu, J.; Liu, D.; He, D. Cluster Structure Detection in Complex Networks: An Ant Colony Algorithm Based on Random Walk. J. Softw. 2012, 23, 451–464. [Google Scholar] [CrossRef]







| Parameter | Letter Code | Value |
|---|---|---|
| Ant population | M | 50 |
| Iteration times | K | 200 |
| Importance factor of PC | α | 1 |
| Importance factor of HF | β | 4 |
| Pheromone evaporation degree factor | ρ | 0.7 |
| Total pheromone amount | Q | 10 |
| Influence factor of APF attraction | a | 0.3 |
| Gravity gain coefficient | k | 0.01 |
| Algorithm | Shortest Path Length | Convergent Iteration Times | Path Turning Points | Running Time |
|---|---|---|---|---|
| Traditional ACA | 31.80 | 81 | 13 | 25.35 |
| ACA fused with GA | 30.38 | 9 | 12 | 9.80 |
| ACA fused with APF | 29.21 | 7 | 11 | 5.16 |
| Algorithm | Shortest Path Length | Convergent Iteration Times | Path Turning Points | Running Time |
|---|---|---|---|---|
| Traditional ACA | 49.60 | 133 | 20 | 124.73 |
| ACA fused with AG | 44.80 | 86 | 17 | 24.97 |
| ACA fused with APF | 43.36 | 16 | 16 | 7.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, Y. Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm. Appl. Sci. 2025, 15, 4522. https://doi.org/10.3390/app15084522
Li Y, Liu Y. Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm. Applied Sciences. 2025; 15(8):4522. https://doi.org/10.3390/app15084522
Chicago/Turabian StyleLi, Yuhua, and Yuanhua Liu. 2025. "Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm" Applied Sciences 15, no. 8: 4522. https://doi.org/10.3390/app15084522
APA StyleLi, Y., & Liu, Y. (2025). Research on Path Planning Based on the Integrated Artificial Potential Field-Ant Colony Algorithm. Applied Sciences, 15(8), 4522. https://doi.org/10.3390/app15084522





