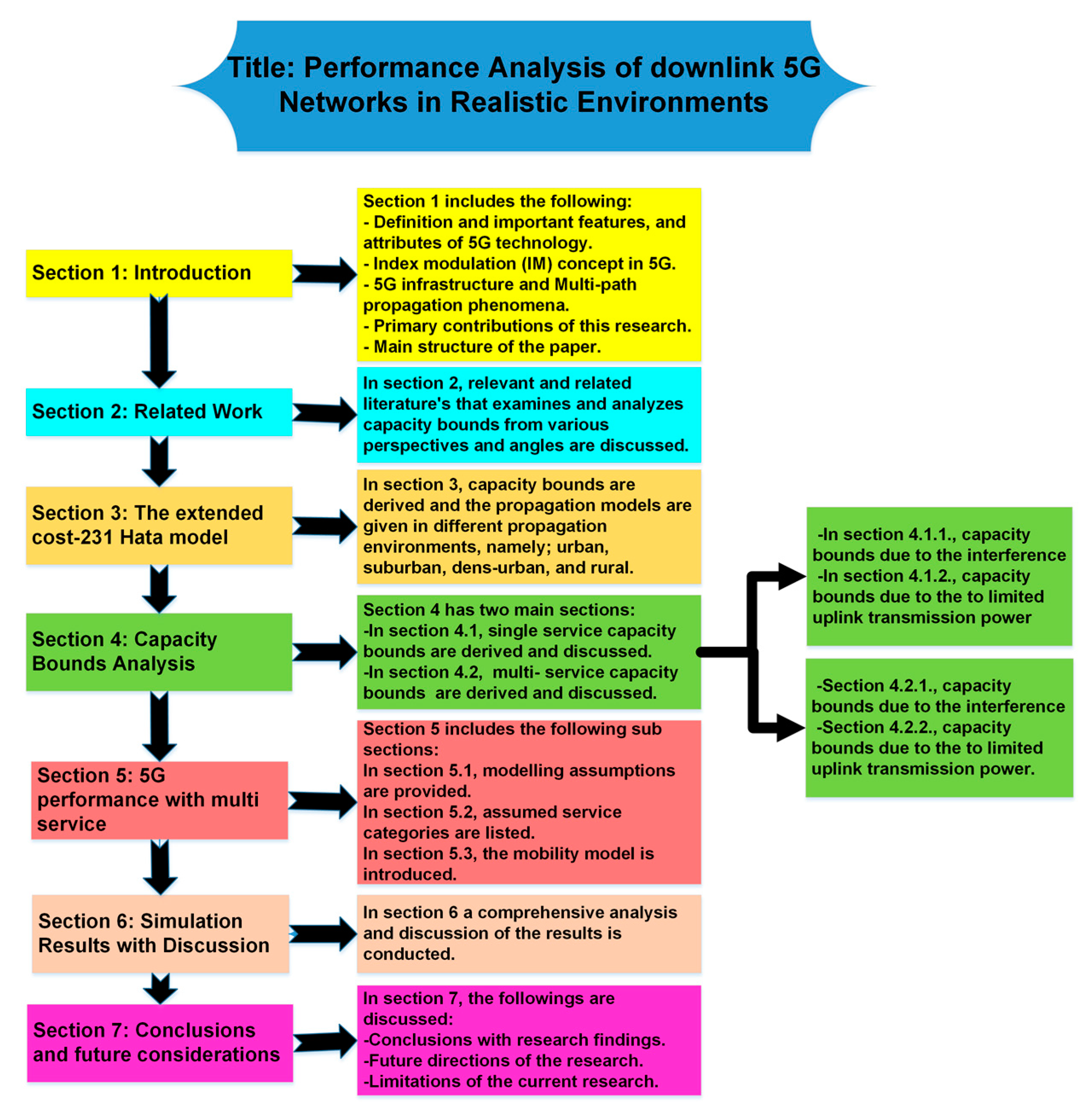
Performance Analysis of Downlink 5G Networks in Realistic Environments
Abstract
1. Introduction
- Enhanced Speed: Fifth-generation provides much faster data transfer rates compared to earlier generations, achieving peak speeds of up to 10 gigabits per second (Gbps). This allows for quicker downloads, uninterrupted streaming of high-definition material, and real-time interactions with minimal delay.
- Low Latency: Fifth-generation technology minimizes network latency to as little as 1 millisecond (ms), enabling nearly immediate communication between devices and reducing delays. This is essential for applications such as self-driving cars, telemedicine, and live gaming.
- High Capacity: Fifth-generation networks are capable of supporting a large number of connected devices at the same time. The technology employs advanced frequency bands, such as higher-frequency millimeter waves, to enhance network capacity and support the increasing number of Internet of Things (IoT) devices.
- Improved Coverage: Fifth-generation networks use a range of technologies, such as small cells, massive MIMO (multiple-input multiple-output), and beamforming, to enhance coverage and signal strength. This allows for dependable connectivity even in densely populated areas and isolated locations.
- Network Slicing: Fifth-generation brings in the idea of network slicing, enabling network operators to develop several virtual networks within one physical framework. Each network slice can be tailored to fulfill the unique needs of various applications, sectors, or user groups.
- Enhanced Energy Efficiency: Fifth-generation technologies are designed to be more energy-efficient than earlier generations. This is accomplished by the means of optimized network architecture, decreased power usage of network equipment, and smart network management.
- Fifth-generation is anticipated to play a crucial role in facilitating emerging technologies like autonomous vehicles, augmented reality (AR), virtual reality (VR), smart cities, industrial automation, and remote telemedicine. Fifth-generation networks meet the requirements of these advanced applications through their high speeds, low latency, and extensive connectivity.
- Enhanced Mobile Broadband (eMBB): IM techniques can support high data rates and improved spectral efficiency, which are essential for eMBB services [7].
- Massive Machine-Type Communications (mMTCs): The energy efficiency of IM makes it suitable for mMTCs, where numerous devices require low-power communication [7].
- Ultra-Reliable Low-Latency Communication (URLLC): IM can help achieve the low latency and high reliability required for URLLC applications by optimizing resource usage [7].
- This work is a continuation of the research presented in [18].
- The work presented at the conference focused on deriving 5G performance and capacity bounds for a single-service example. The capacity bounds are also derived in this enhanced version for multiservice applications, and the capacity of 5G networks is evaluated accordingly.
- This research study derives capacity bounds in various propagation scenarios while considering mobility scenarios and two crucial elements that affect performance: interference and restricted transmission power.
- Based on the multiservice case of the derived capacity bounds, new numerical results with a discussion and explanation of the new results are presented in this extended version, taking into consideration the cell breathing phenomenon, which affects cell coverage and capacity by considering different cell sizes.
- Because performance analysis of the new generation of mobile networks will not be realistic considering only the free-space propagation model, the capacity bounds analysis in this research work, along with a comprehensive discussion through the numerical results, will provide a key indicator for mobile operators to be well thought out in the future planning of 5G networks.
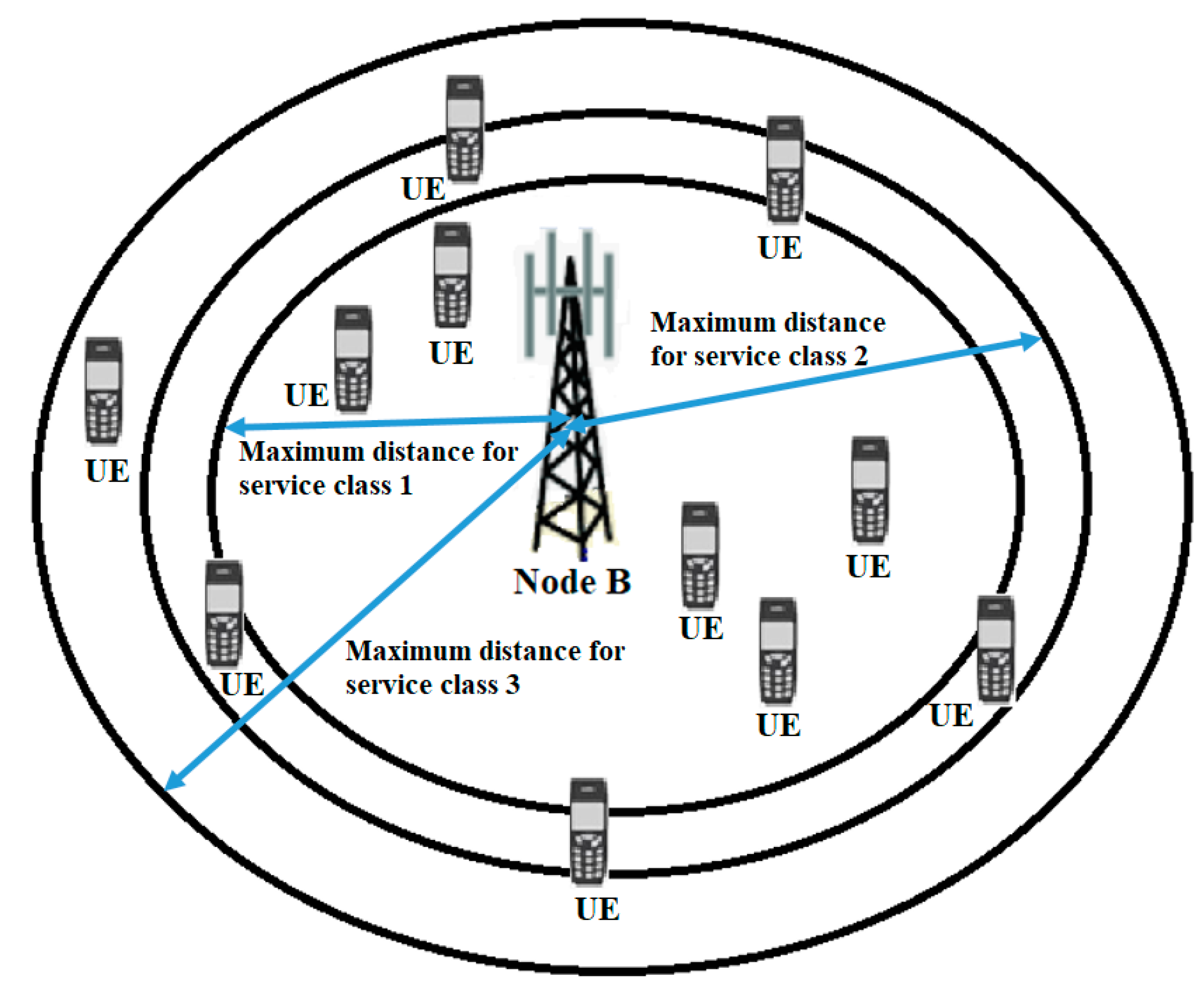
- The following new figures illustrate how the maximum distance and coverage change based on the selected service class.
- In addition, the following parts are changed, modified, or added:
- ○
- The Abstract and Conclusions have been changed.
- ○
- The Introduction and related work have been modified, and additional references have been added.
- ○
- The derivation of the capacity bounds in a multiservice case is given.
- ○
- A new group of results is added to reflect the effect of the multiservice case capacity bounds on cell coverage and capacity considering different service categories and mobility scenarios. Consequently, the “Simulation results and discussions” Section is changed to demonstrate this effect.
- The impacts of cell breathing, interference, and environment-specific path loss (via COST-231 Hata extensions) are quantified.
- Actionable insights for network planning (e.g., trade-offs between coverage and capacity) are provided.
2. Related Work
3. The Extended COST-231 Hata Model
- 1.
- The propagation model for an urban environment is as follows:
- 2.
- The propagation model for the suburban environment is as follows:
- 3.
- The propagation model for the dense urban environment is as follows:
- 4.
- The propagation model for a rural environment is as follows:
4. Capacity Bounds Analysis
4.1. Single-Service Capacity Bounds
4.1.1. Capacity Bounds Due to the Interference
4.1.2. Capacity Bounds Due to Limited Uplink Transmission Power
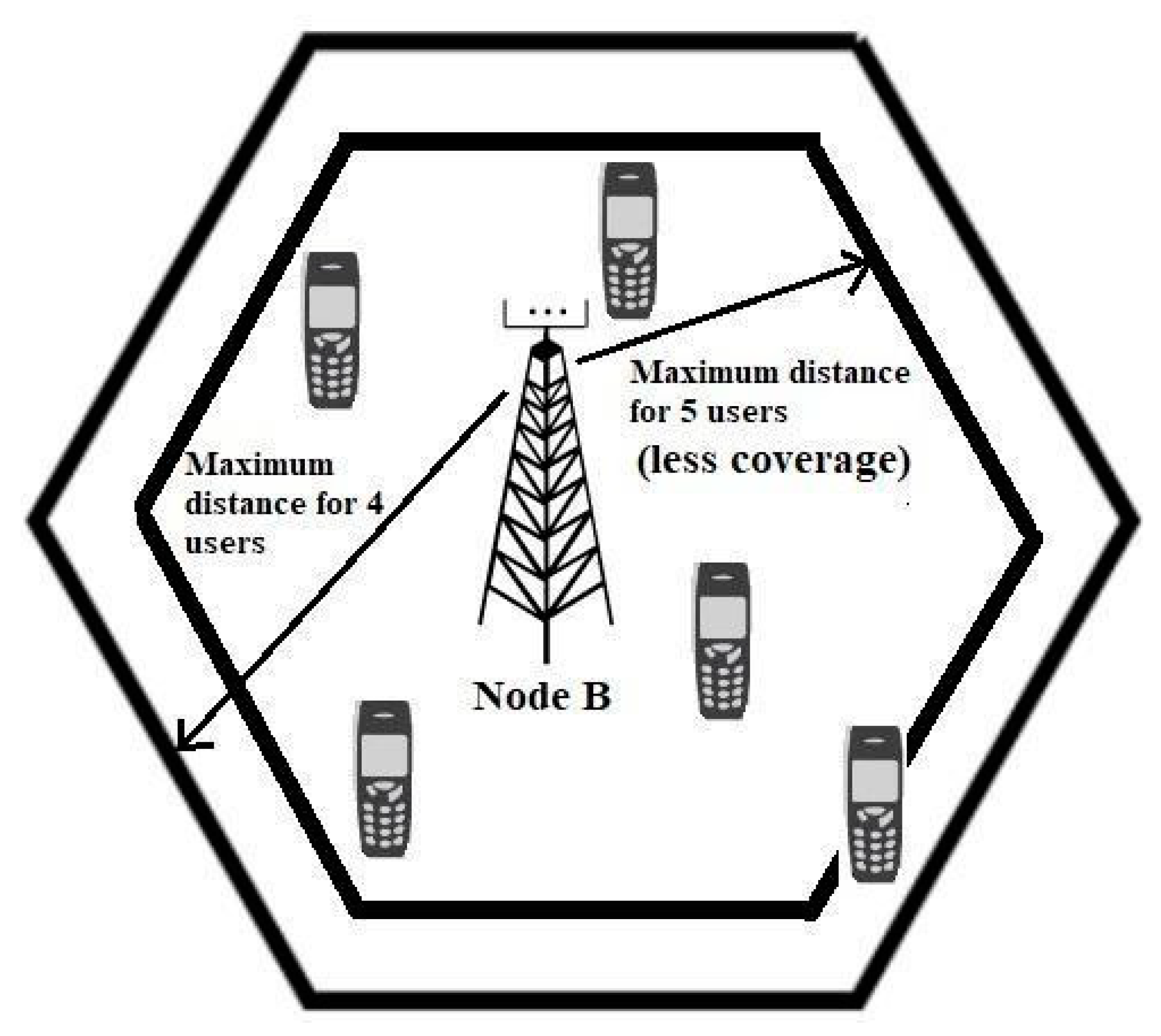
4.2. Multiservice Capacity Bounds
- is the number of active users requiring the same radio service () with identical service factor values, .
- The non-orthogonality factor, , is equal for different user signals and using the same service factor, .
- The inter-class interference between users due to the non-orthogonality of the codes for a single-service type is assumed to be . In contrast, the inter-class interference factor, , is between all users of service , and all users of service are assumed to be the same.
- The received power, , required at node B is assumed to be the same for all user signals using the same service, . In this case, the received power at node B is denoted by .
4.2.1. Capacity Bounds Due to Interference
4.2.2. Capacity Bounds Due to Limited Uplink Power
5. Fifth-Generation Performance with Multiservice
5.1. Modeling Assumptions
- We assume that a single 5G cell has the maximum capacity. The capacity is affected by the 5G modulation schemes and the maximum number of users in the cell.
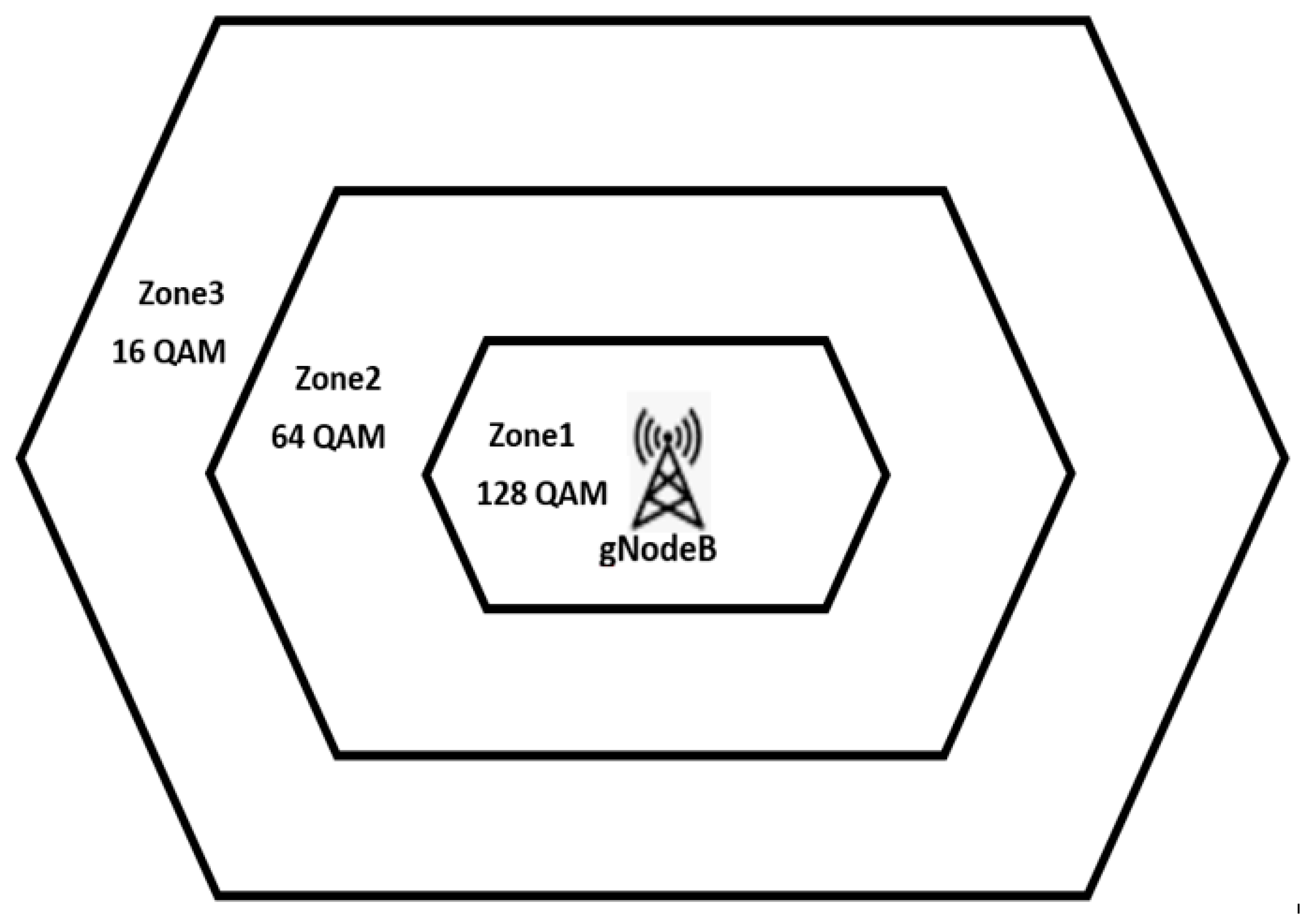
- As per the modulation scheme in 5G, which is based on OFDMA (Orthogonal Frequency Division Multiple Access), the cell is divided into three virtual zones, as shown in Figure 4. According to 3GPP Release 15 [36,37], the physical layer of 5G downlinks uses different modulation schemes. Three modulation methods were assumed in this analysis, namely 128 Quadrature Amplitude Modulation (QAM) for zone 1 with 7 bits of transmitted information per symbol, 64 Quadrature Amplitude Modulation (QAM) for zone 2 with 6 bits of transmitted information per symbol, and 16 QAM for zone 3 with 4 bits.
- We assume a Poisson inter-arrival time within the cell. The traffic load is determined based on the zone areas (, zone ) and user density in the cell.
- The call admission control algorithm (CACA) relies on a minimum bit rate threshold that users must meet to be admitted to the system.
- The call admission control algorithm proposed in [12] was used in the proposed analysis.
5.2. Assumed Service Categories
- (1)
- Web browsing via a new radio (WBo5G): This service allows users to browse, find, and download web content from the internet at speeds exceeding one gigabyte. Because most internet activities involve web browsing, 60% of the available services are for this type of service.
- (2)
- Video Streaming-over-5G (STRo5G): This service provides real-time video streaming, video on demand (VoD), and virtual and augmented reality video experiences. To ensure minimal latency for multimedia services, 30% of all multimedia services are designated for this type of service.
- (3)
- Voice-over-5G (Vo5G): Also known as voice over new radio, this provides high-definition (HD) voice communication for smartphones. It is infrequently used and is mainly reserved for emergency calls; thus, it constitutes the remaining 10% of all available services.
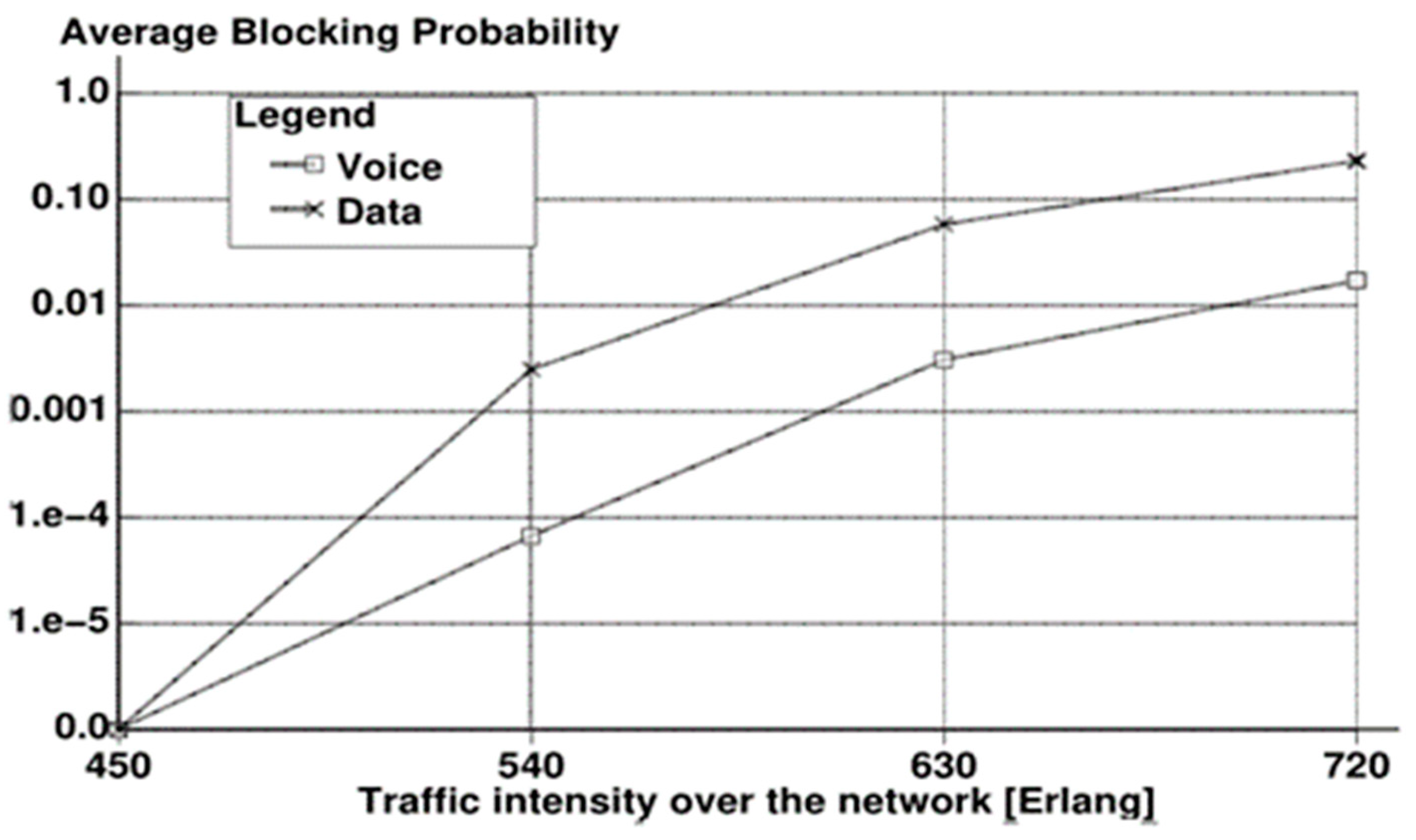
- Blocking Probability: The likelihood of call rejection if the call’s bit rate falls below the minimum threshold bit rate assumed in the cell.
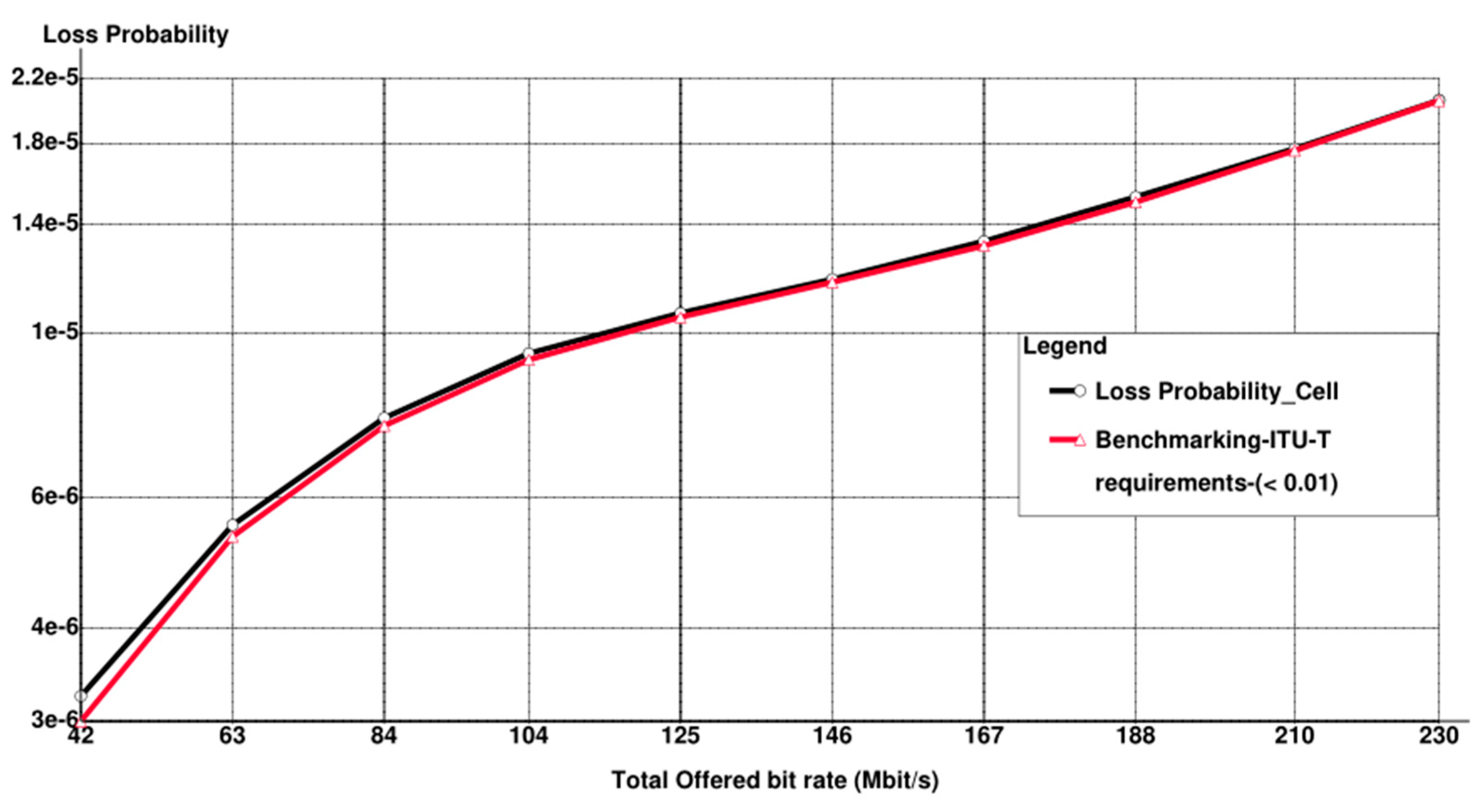
- Loss Probability: The likelihood of a call drop after admission when the user’s bit rate falls below the threshold value due to interference or channel quality degradation.
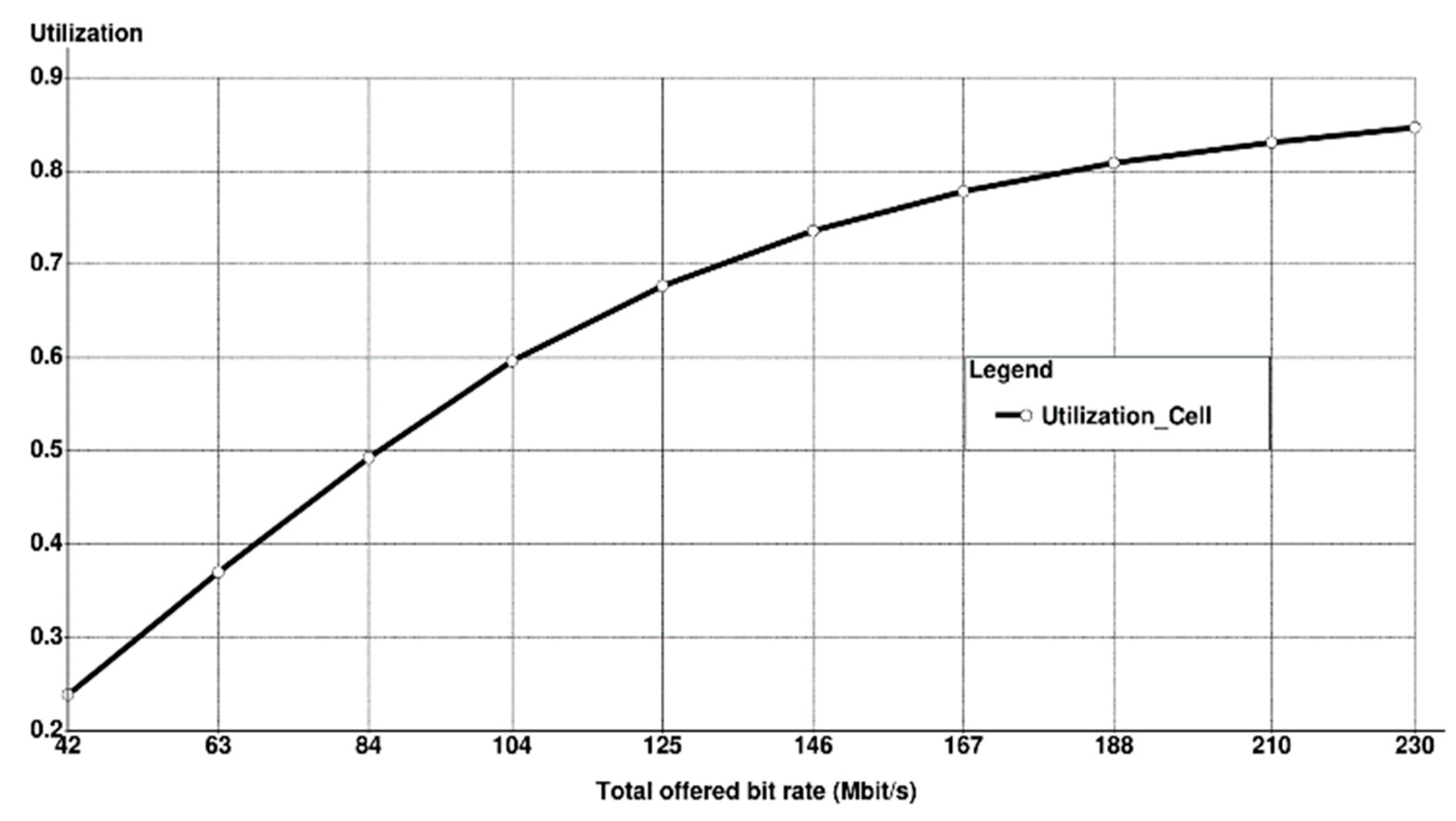
- Utilization: Average total bit rate relative to maximum cell capacity.
- Cell Delay: The time taken for a message to successfully reach its destination compared to the time the first bit is sent from the source.
- Average Bitrate of the Cell: The mean total nitrate in the cell relative to the average session duration.
- Aggregate Bit Rate of the Cell: The average total bit rate across all services in the cell.
- Aggregate Bit Rate per Service: The aggregate bit rate is calculated as the average number of jobs in each service multiplied by the average bit rate required for that service’s area.
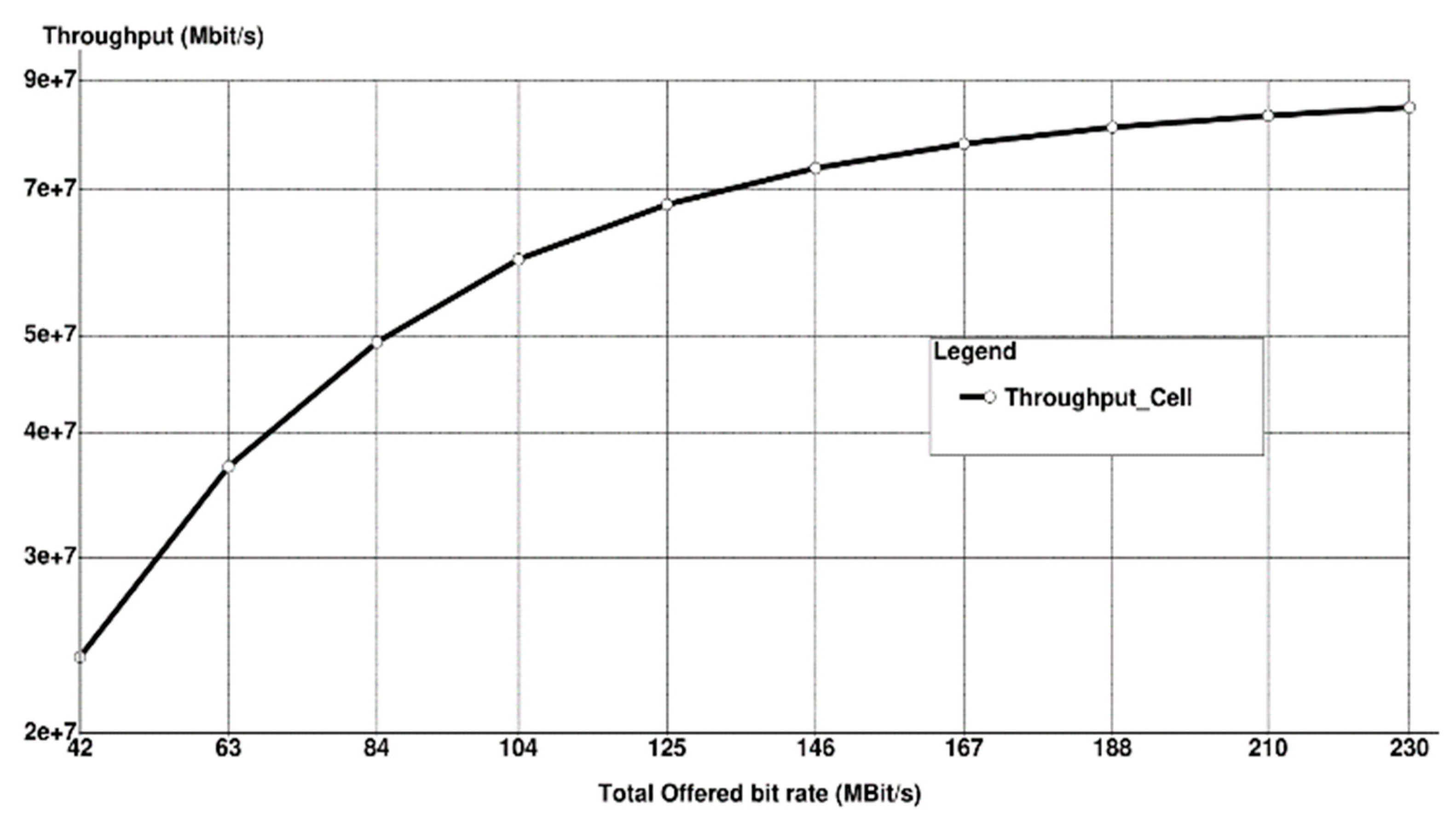
- Throughput: Calculated as the mean total bit rate in all zones for all services of the cell.
5.3. Mobility Model
6. Simulation Results with Discussion

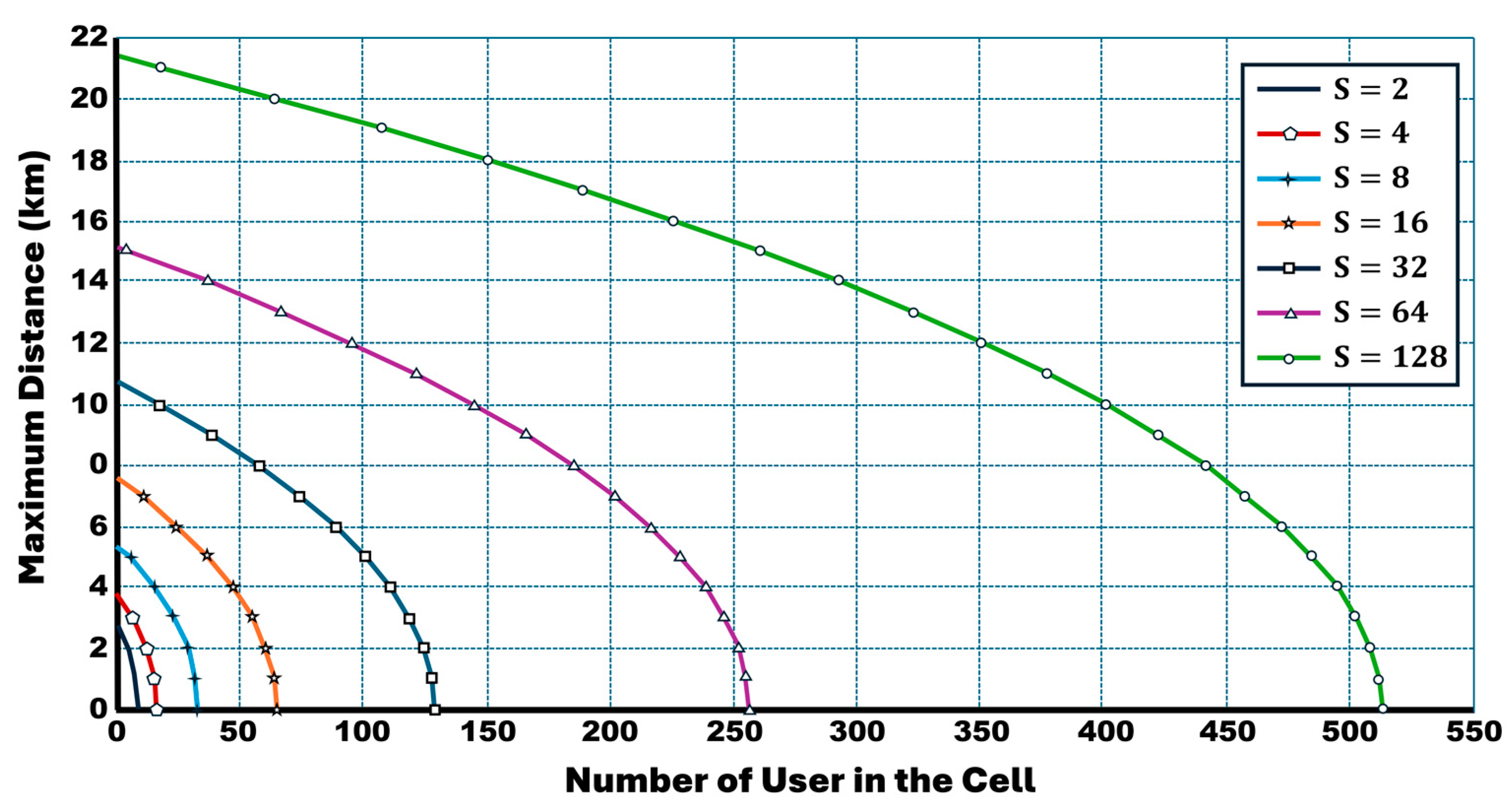

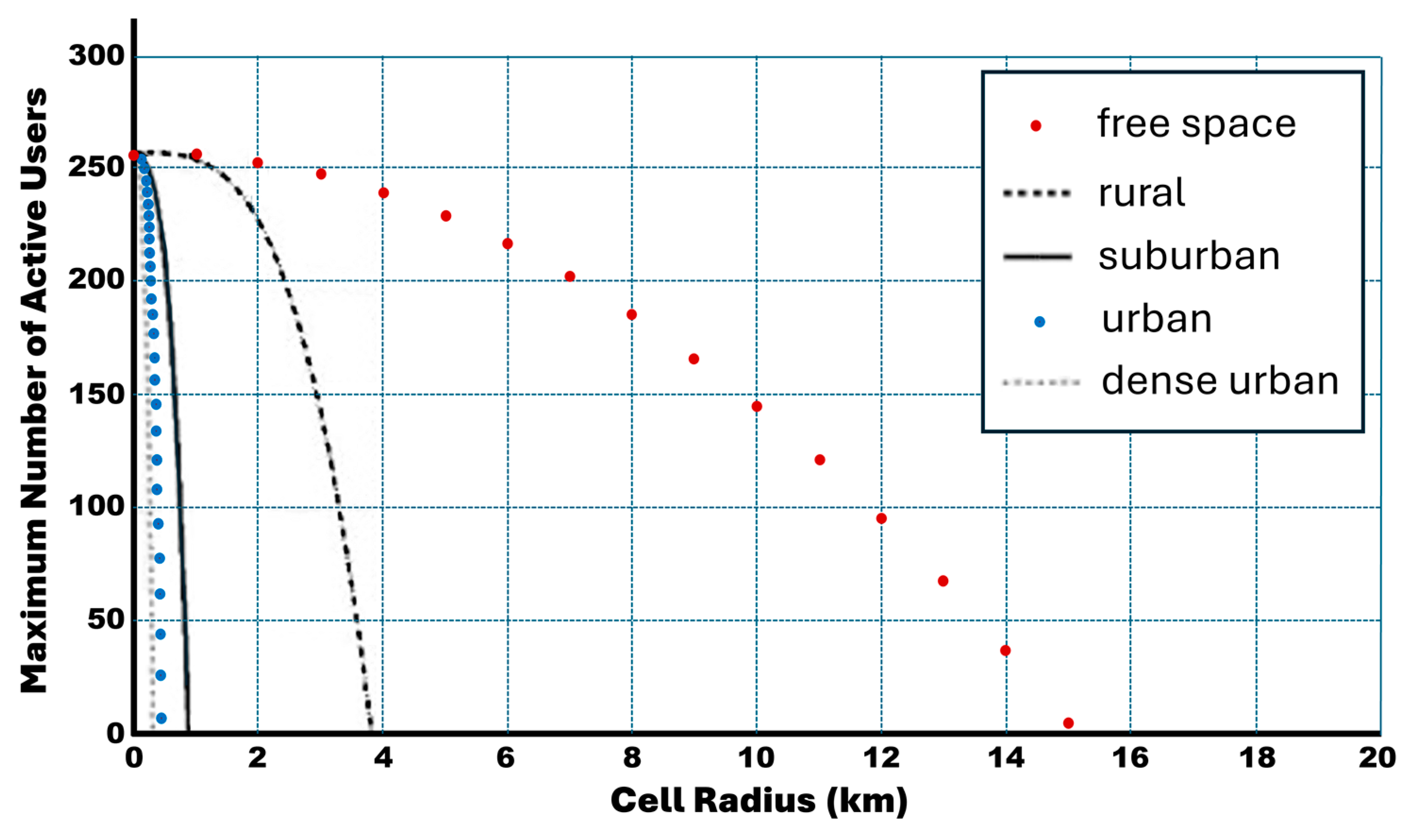
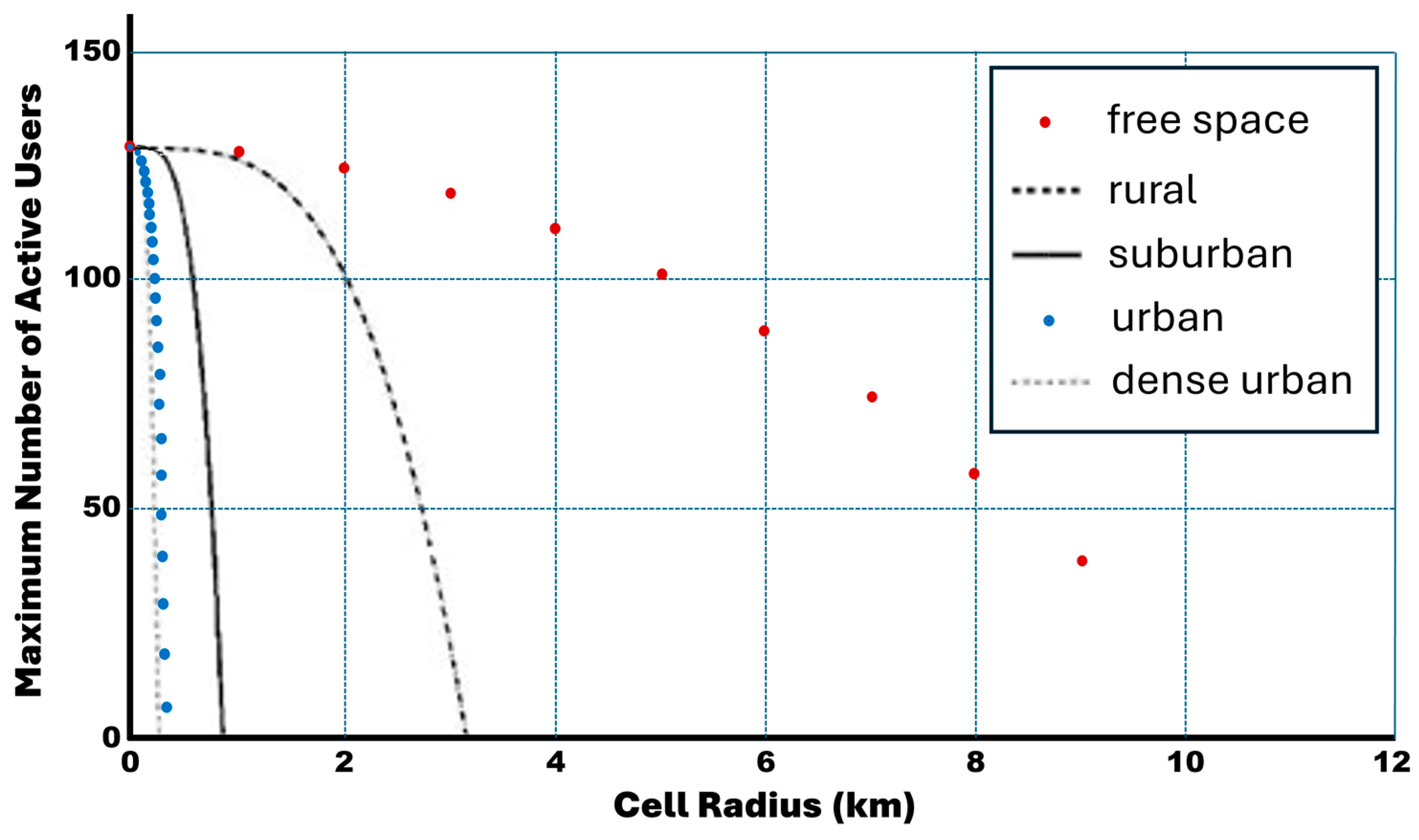
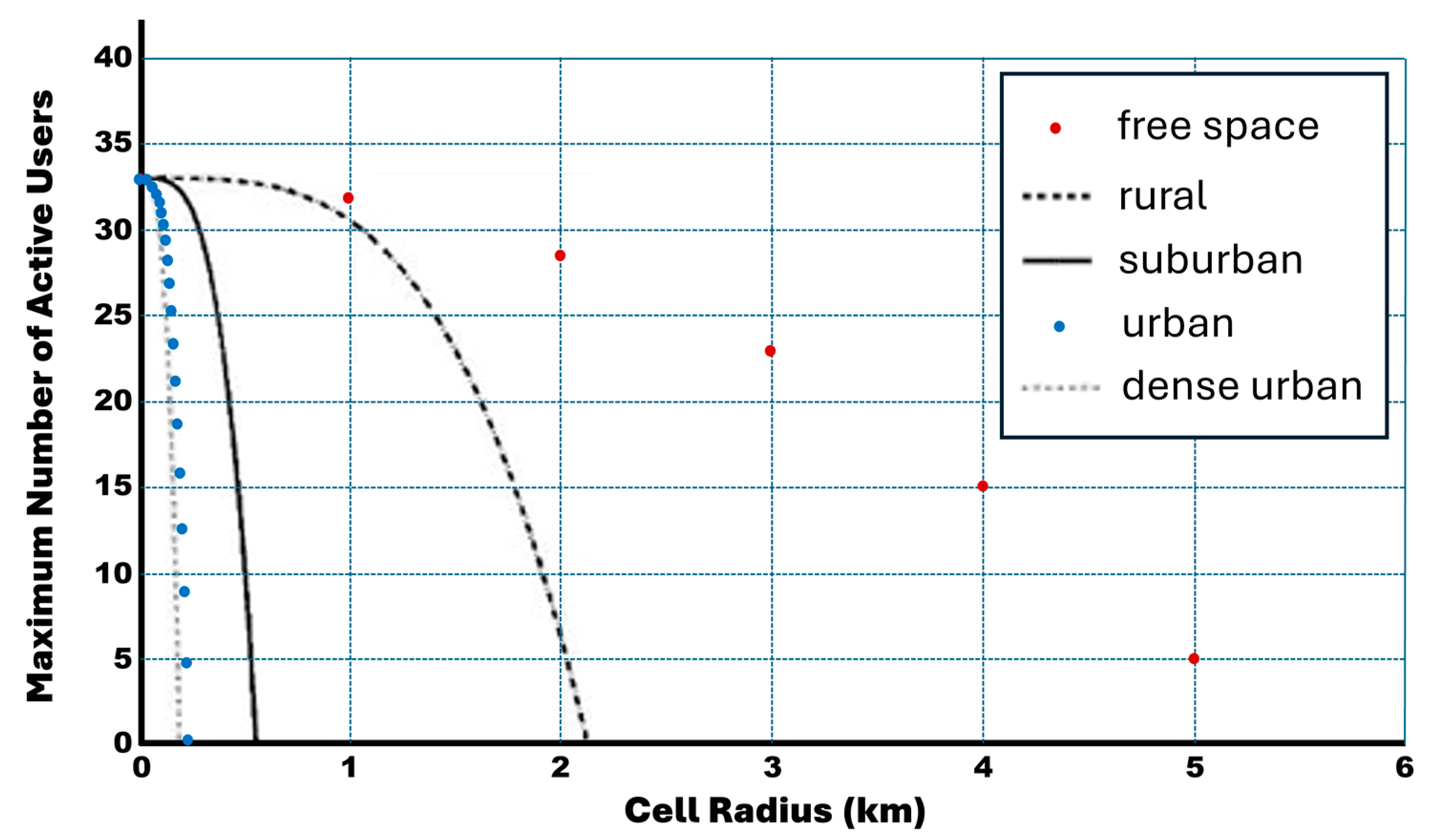
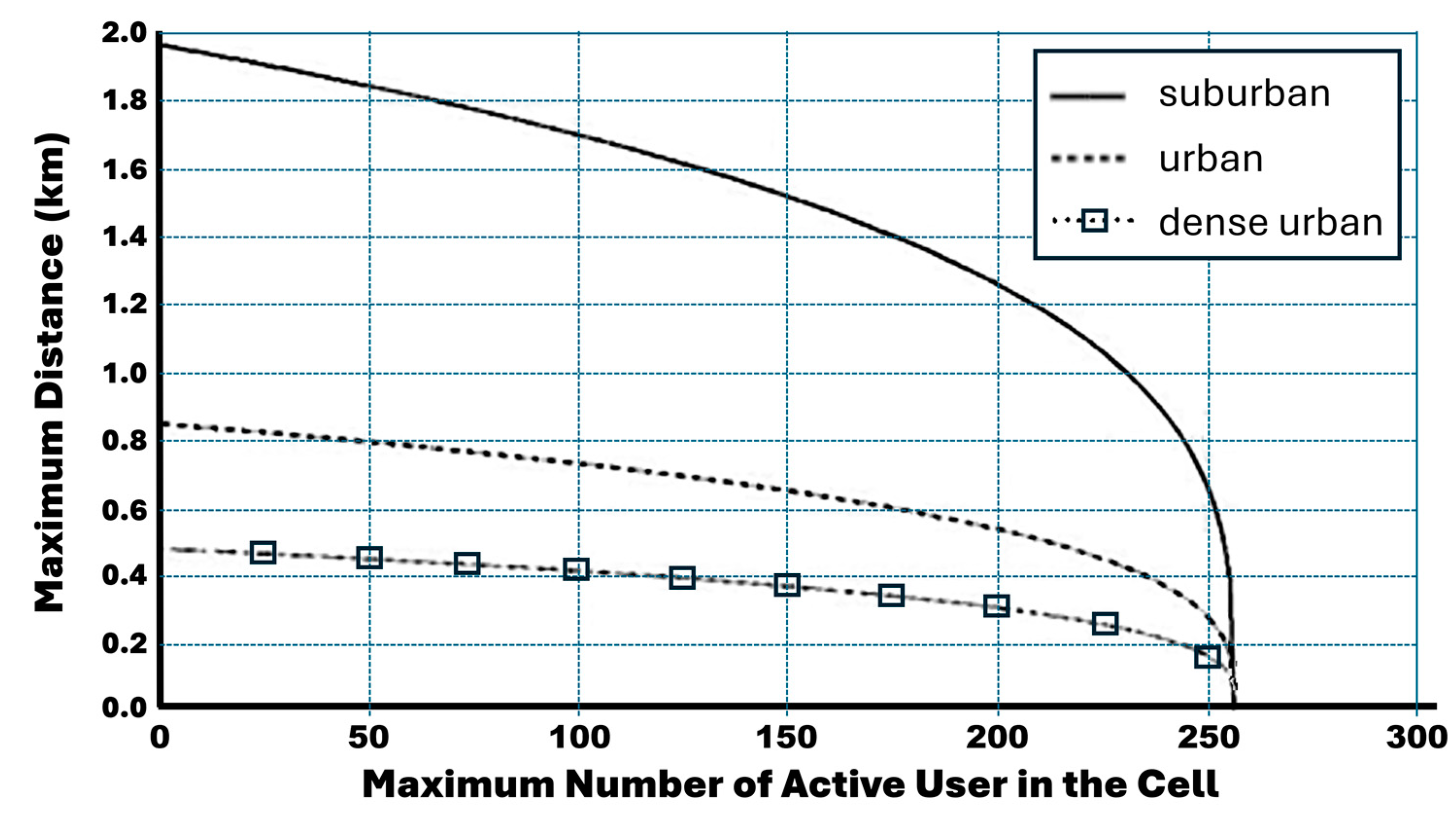
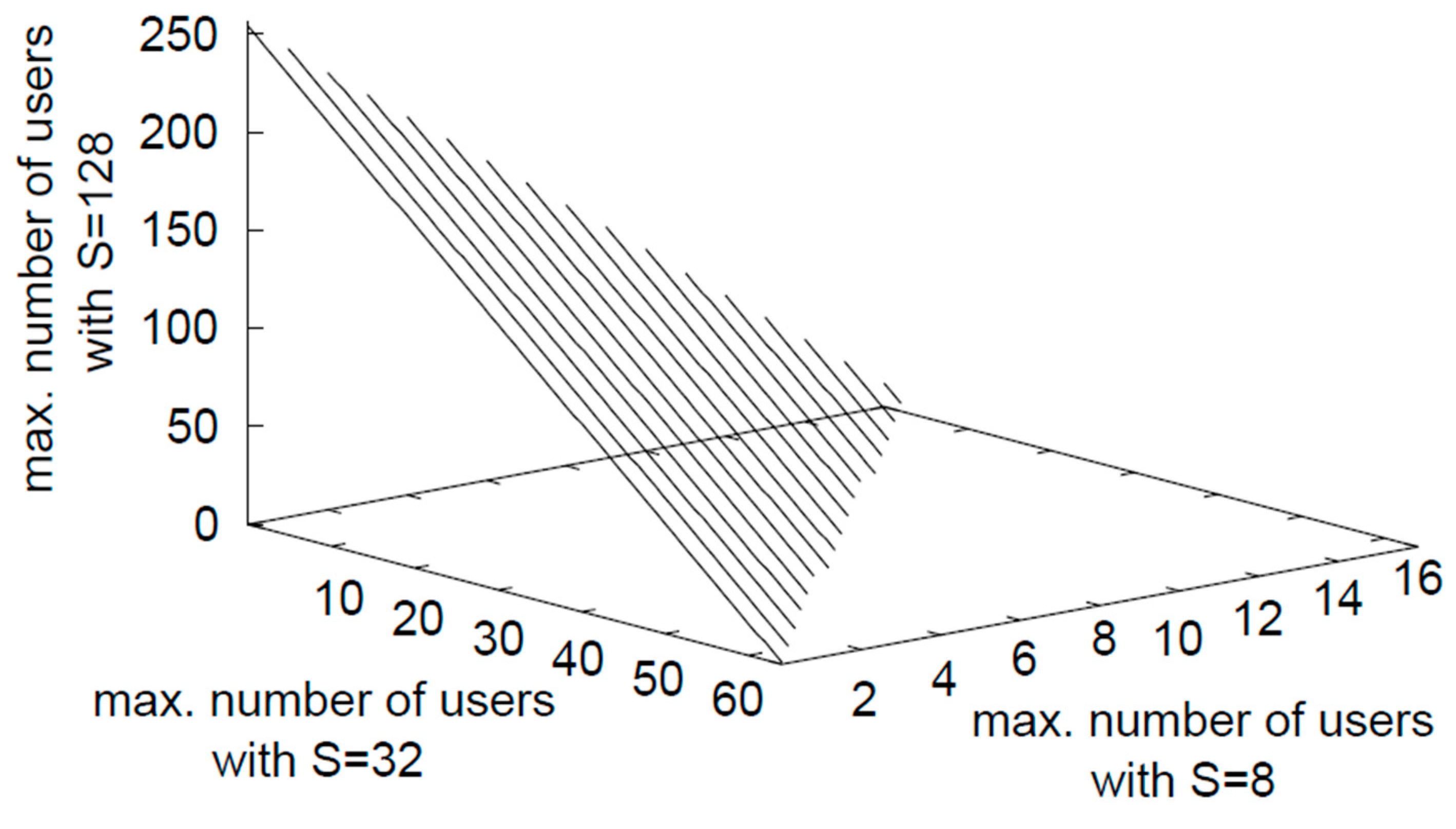
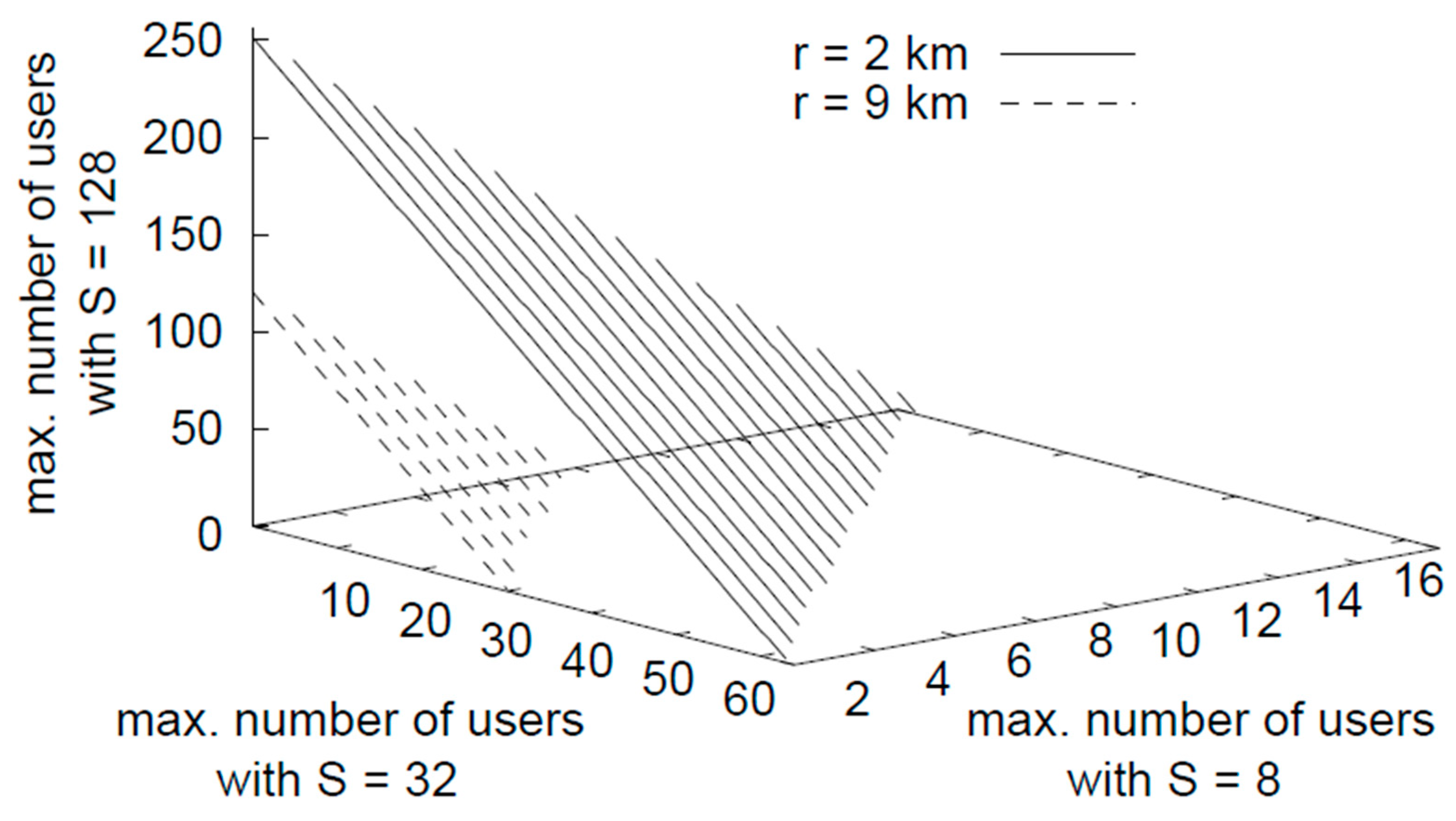
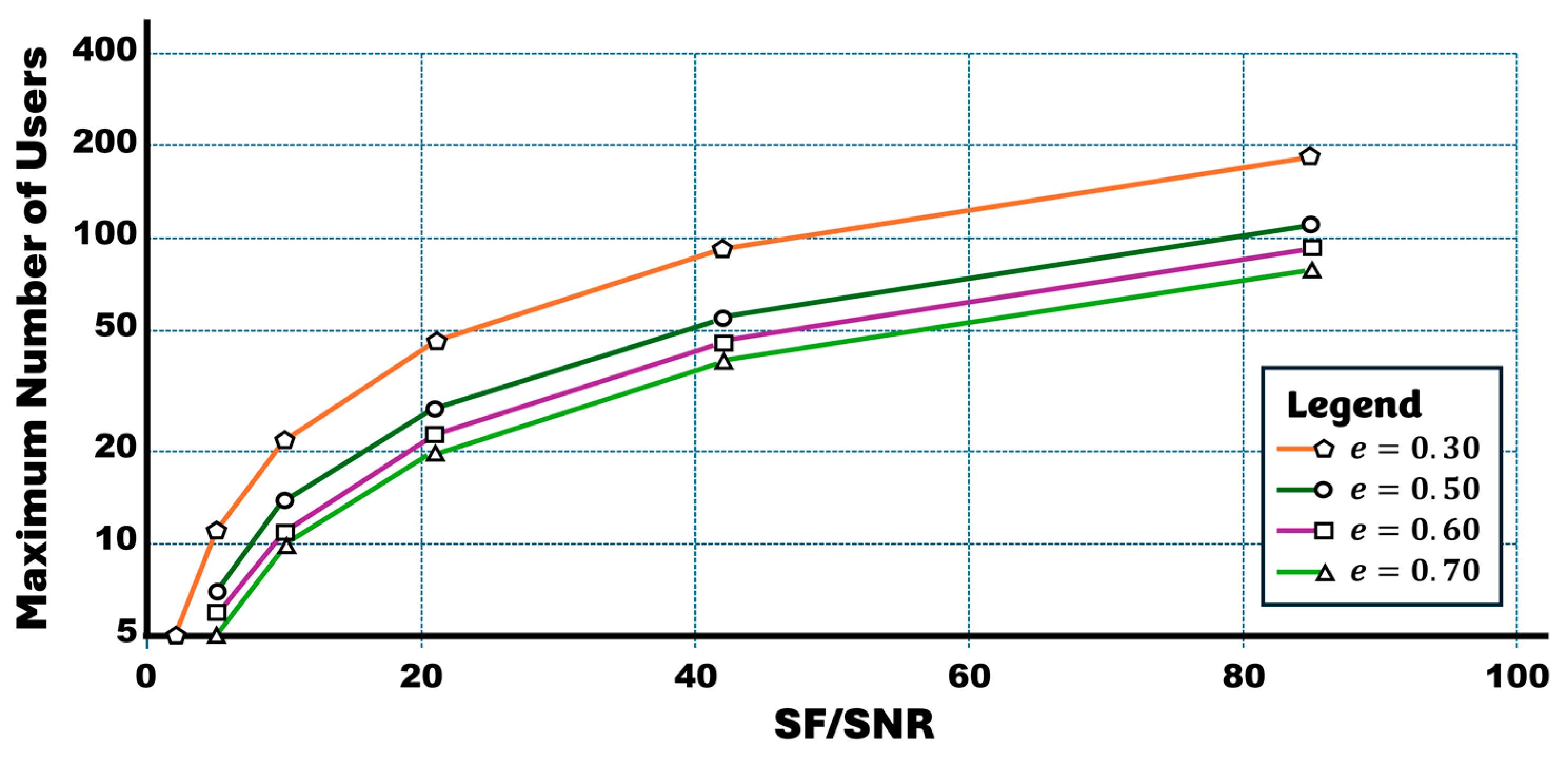
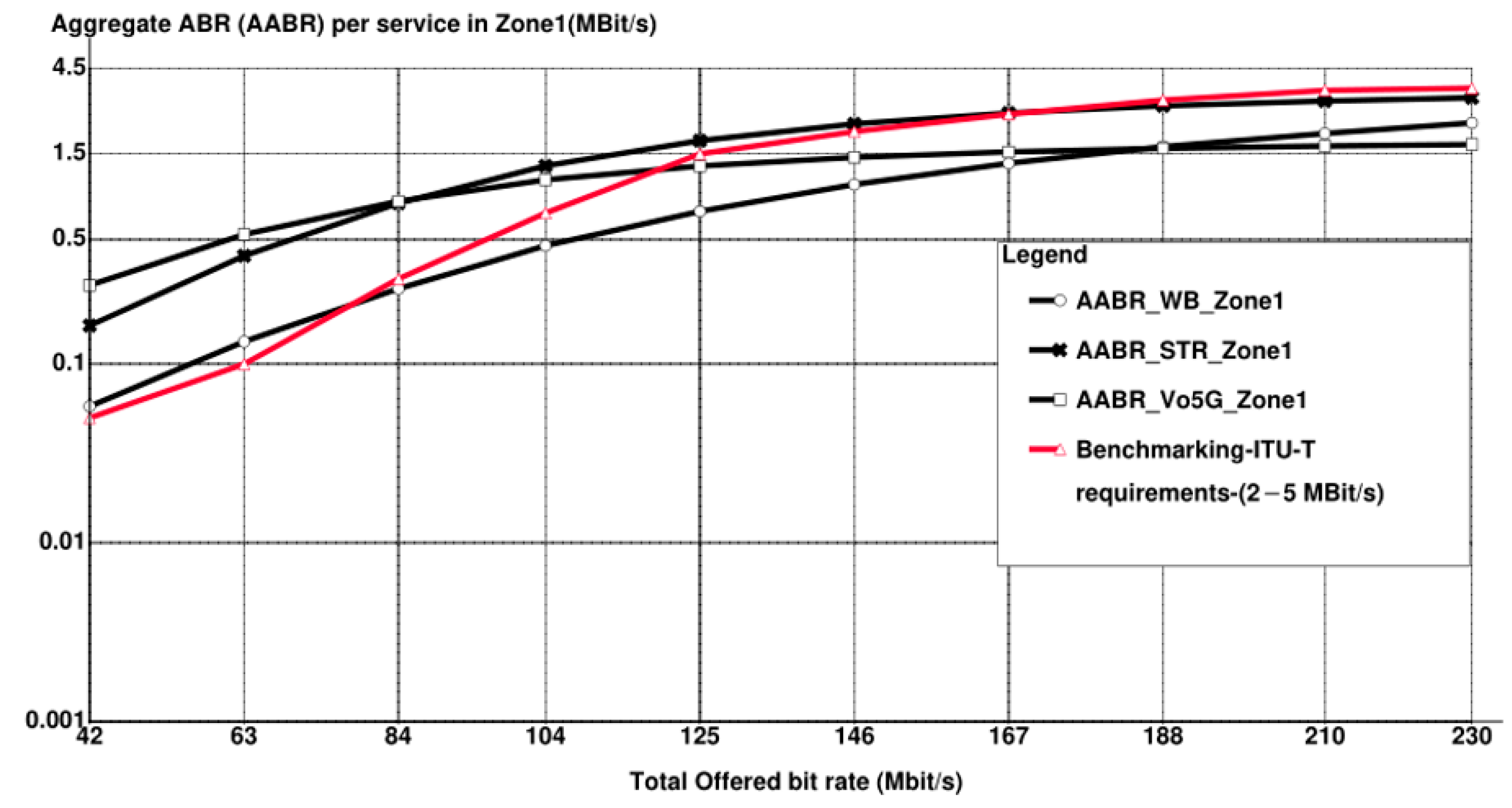

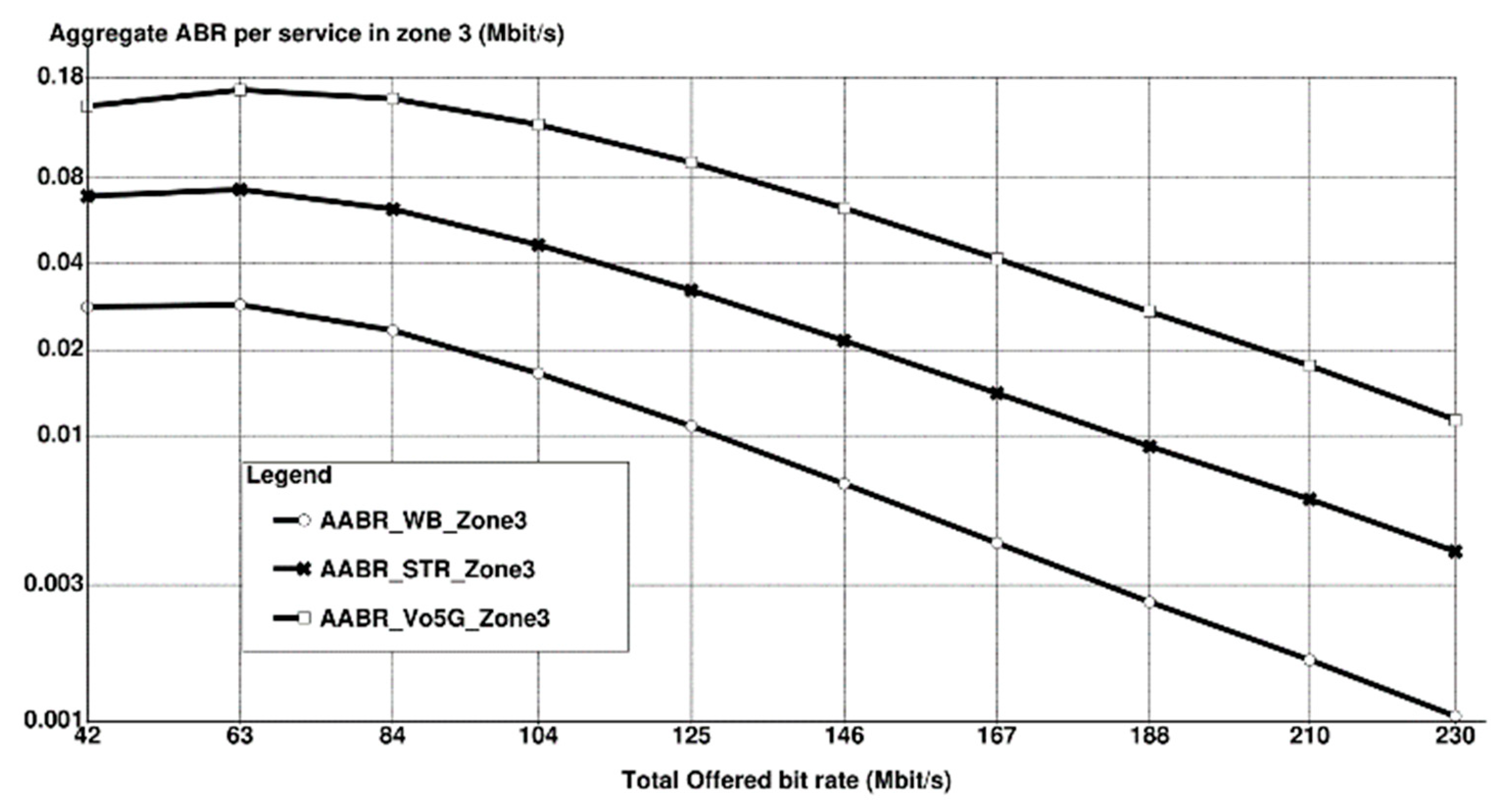
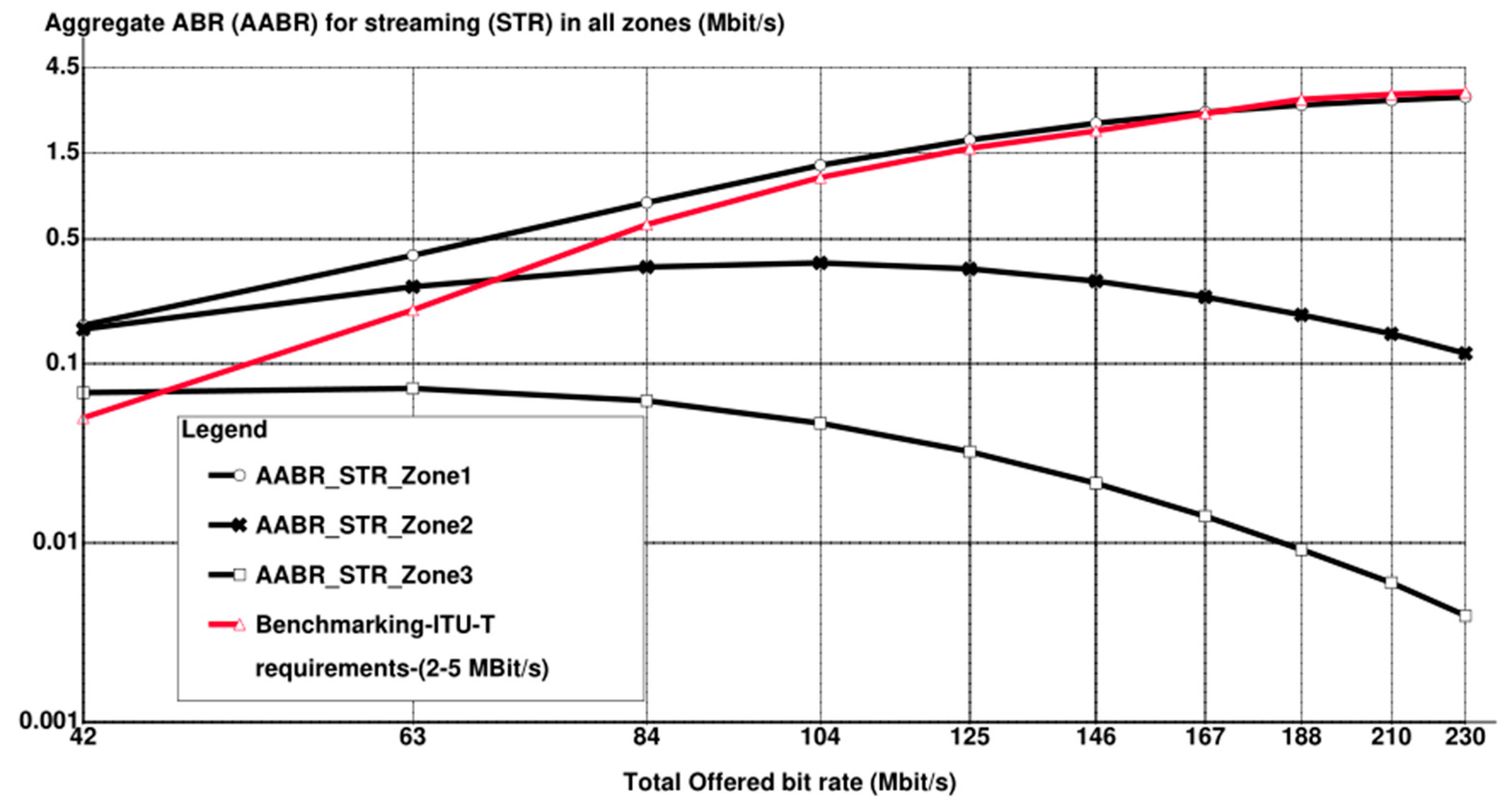
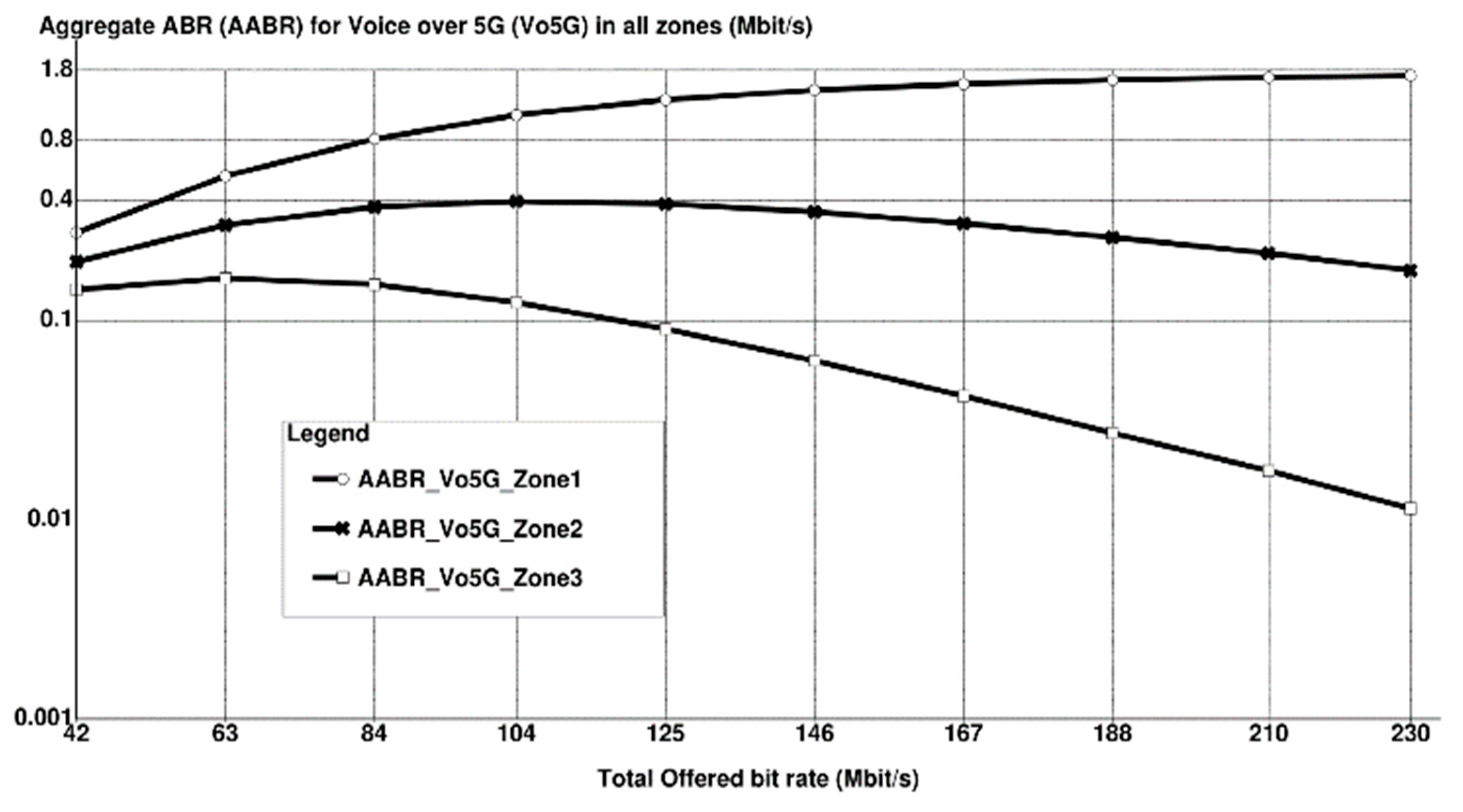

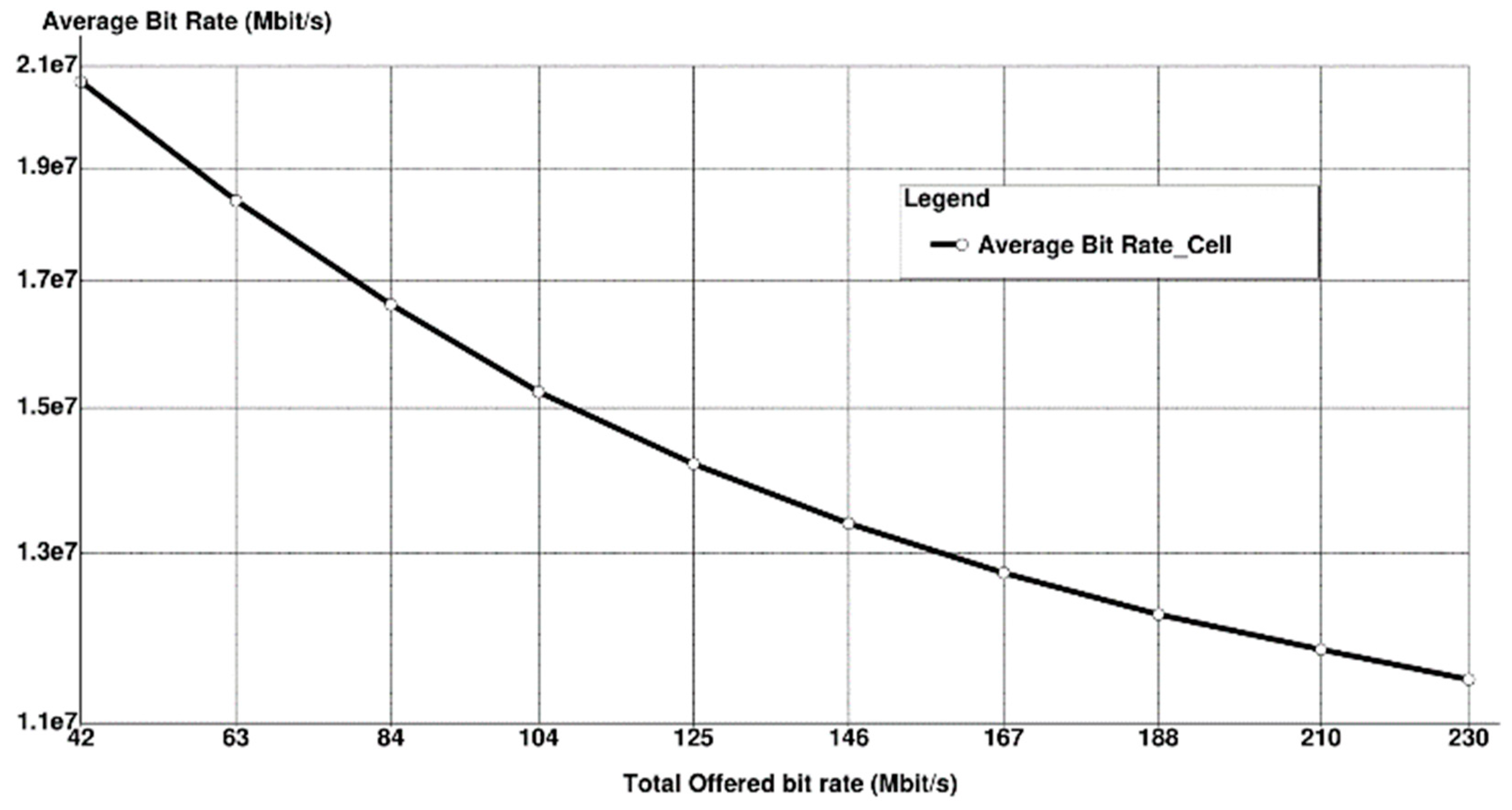
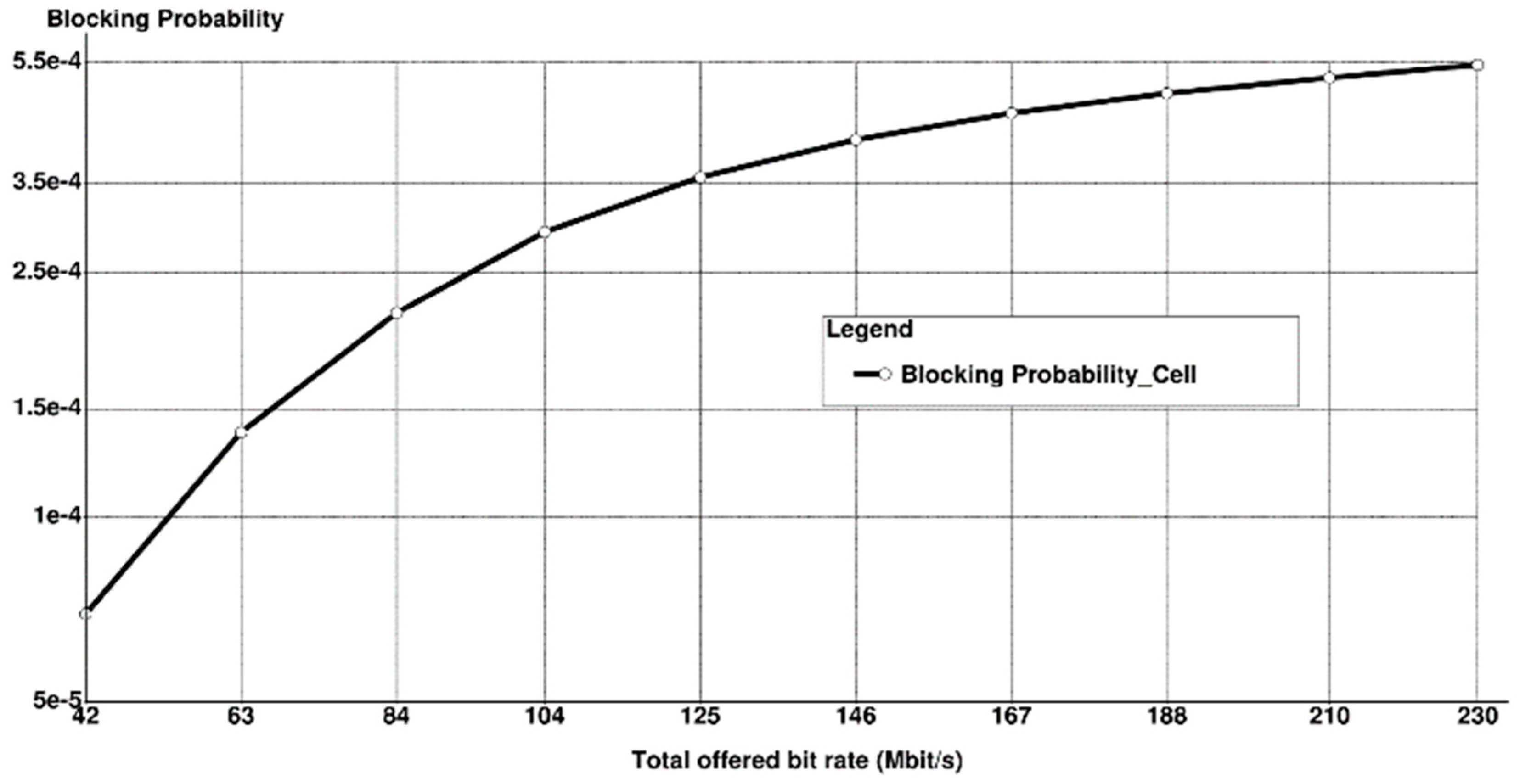
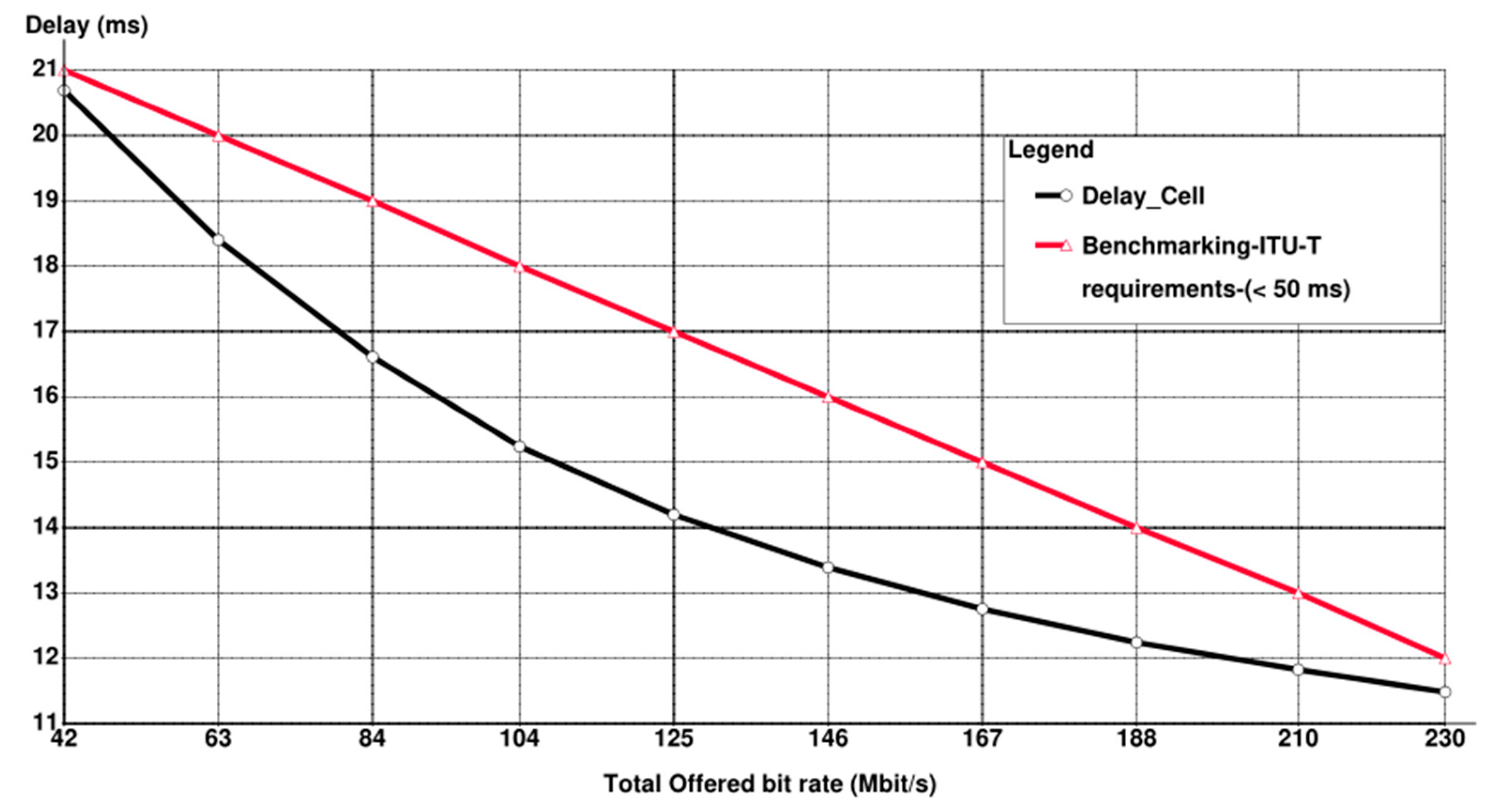

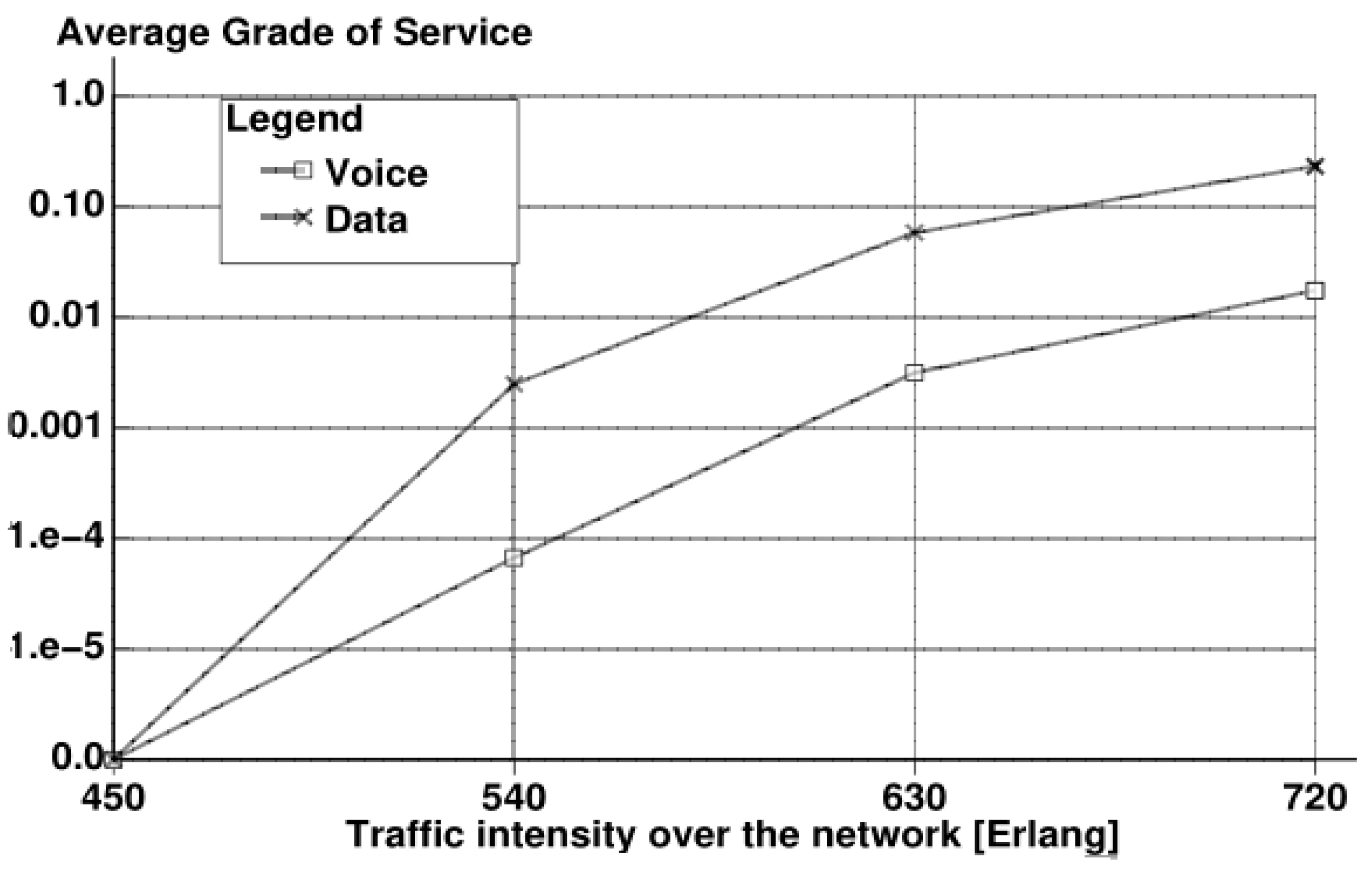


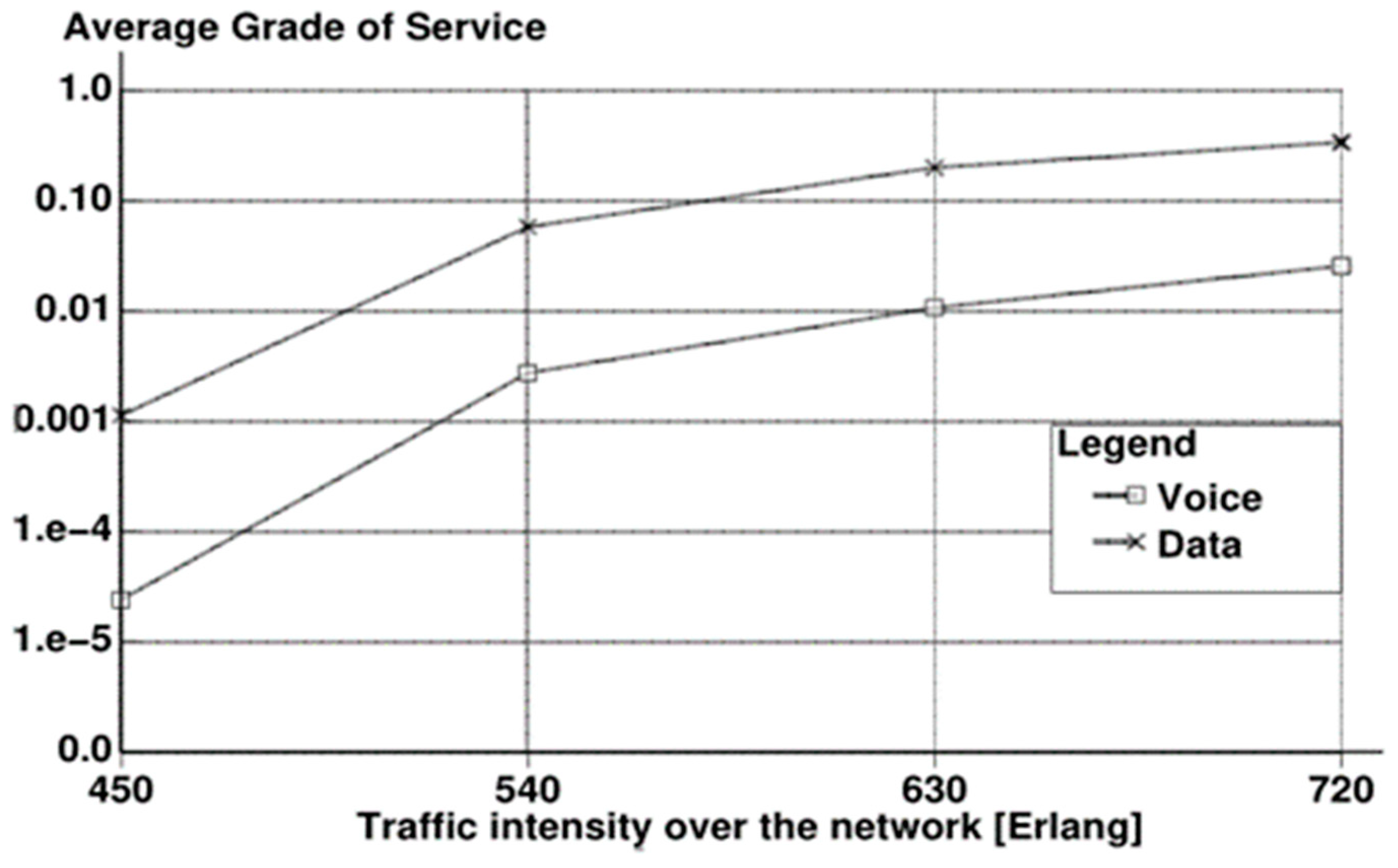

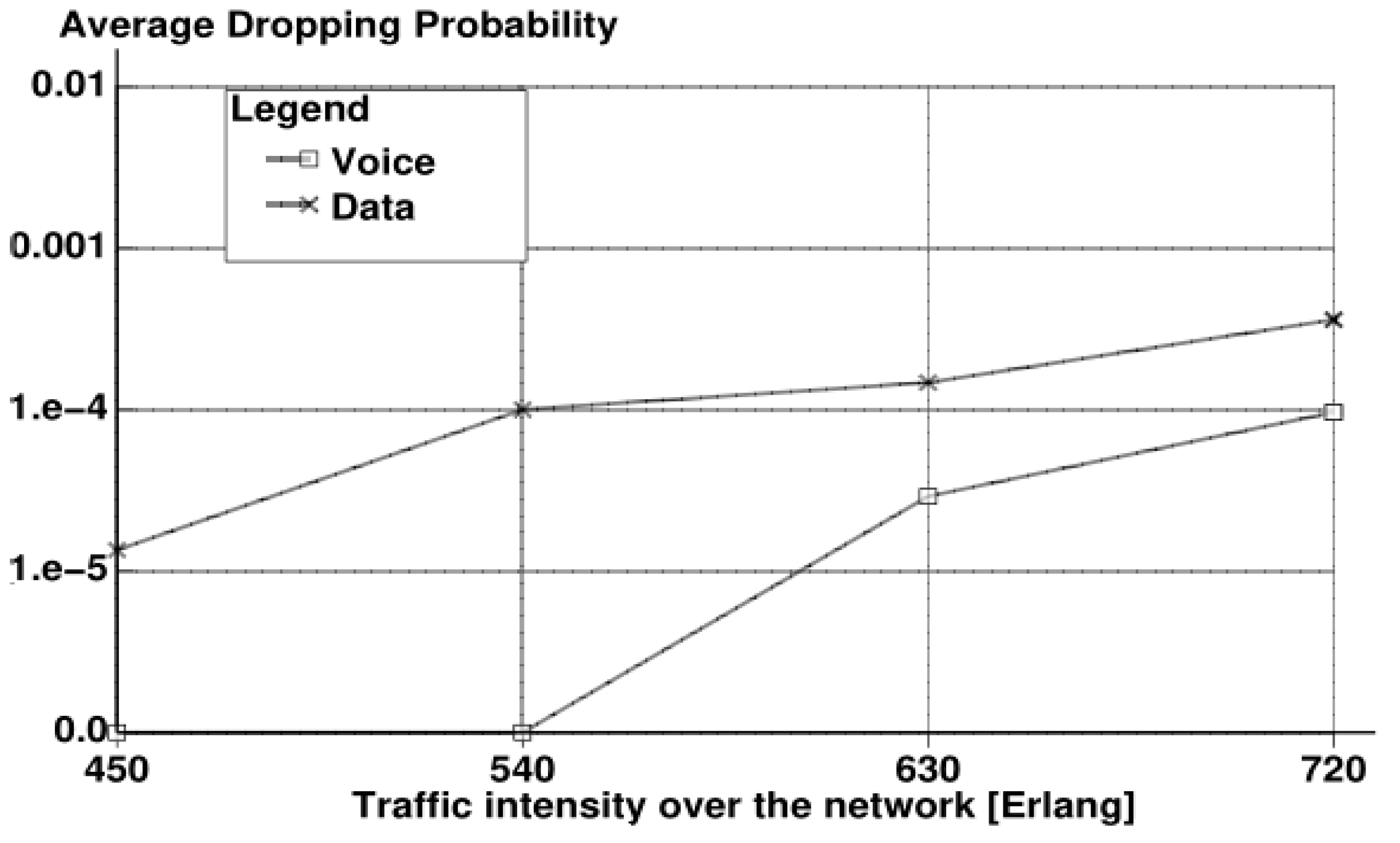


7. Conclusions and Future Considerations
- ○
- Although the proposed CACA works on a network level of this system, only one cell was considered in the analysis and discussion. This work should be extended to a network-level scenario considering 5G seamless handover between the original and neighboring cells.
- ○
- Due to the scarcity of resources in the literature with similar scenarios in this research and not deviating from the main objective of this research, it was not possible to conduct a comparison with other works in the literature. However, for the sake of validation, a benchmarking of ITU-T QoS requirements for 5G is added to some results.
- ○
- In future research directions, the above limitations will be considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Kaushik, A.; Masouros, C. Pre-scaling and codebook design for joint radar and communication based on index modulation. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1–5. [Google Scholar]
- Huang, T.; Shlezinger, N.; Xu, X.; Liu, Y.; Eldar, Y.C. MAJoRCom: A dual-function radar communication system using index modulation. IEEE Trans. Signal Process 2020, 68, 3423–3438. [Google Scholar] [CrossRef]
- Ma, H.; Fang, Y.; Chen, P.; Mumtaz, S.; Li, Y.A. Novel Differential Chaos Shift Keying Scheme With Multidimensional Index Modulation. IEEE Trans. Wirel. Commun. 2023, 22, 237–256. [Google Scholar] [CrossRef]
- Lee, H.; Shin, S. A novel index modulation scheme with impedance matching. Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 1203–1209. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Wen, M.; Yang, L. Index Modulation for 5G: Striving to Do More with Less. IEEE Wirel. Commun. 2018, 25, 126–132. [Google Scholar] [CrossRef]
- Mgobhozi, B.; Nleya, B. Efficient Index Modulation Techniques for 5G and Beyond. In Proceedings of the 2023 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 16–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Doğan Tusha, S.; Tusha, A.; Basar, E.; Arslan, H. Multidimensional Index Modulation for 5G and Beyond Wireless Networks. Proc. IEEE 2021, 109, 170–199. [Google Scholar] [CrossRef]
- Deng, T.; Ding, J.; Liang, P. Investigating and Applying Orthogonal Frequency Division Multiplexing with Index Modulation. In Proceedings of the 2024 4th Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 24–26 February 2024; pp. 791–794. [Google Scholar] [CrossRef]
- Bouhlel, A.; Sakly, A.; Ikki, S. Performance analysis of DWT based OFDM with index modulation under channel estimation error. In Proceedings of the 2017 International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 11 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Öztürk, E.; Basar, E.; Çırpan, H.A. Generalized Frequency Division Multiplexing With Flexible Index Modulation Numerology. IEEE Signal Process. Lett. 2018, 25, 1480–1484. [Google Scholar] [CrossRef]
- Kadir, M.I. Generalized Space–Time–Frequency Index Modulation. IEEE Commun. Lett. 2019, 23, 250–253. [Google Scholar] [CrossRef]
- Zreikat, A.I. Load balancing call admission control algorithm (CACA) based on soft-handover in 5G Networks. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC2022), Las Vegas, NV, USA, 26–29 January 2022; pp. 863–869. [Google Scholar]
- Zreikat, A.I.; Al-abed, S. Performance Modeling and Analysis of LTE/Wi-Fi Coexistence. Electronics 2022, 11, 1035. [Google Scholar] [CrossRef]
- Chen, J.; Lin, W.; Yan, P.; Xu, J.; Hou, D.; Hong, W. Design of mm-Wave transmitter and receiver for 5G. In Proceedings of the 2017 10th Global Symposium on Millimeter-Waves, Hong Kong, China, 24–26 May 2017; pp. 92–93. [Google Scholar] [CrossRef]
- Banaseka, F.K.; Dotse, S. New deployments and Research challenges for 5G wireless systems and networks. Int. J. Curr. Res. 2017, 9, 46626–46631. [Google Scholar]
- Hata, M. Empirical formula for propagation loss in land mobile radio services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- Nkordeh, N.S.; Atayero, A.A.A.; Idachaba, F.E.; Oni, O.O. LTE Network Planning using the Hata-Okumura and the COST-231 Hata Path loss Models. In Proceedings of the World Congress on Engineering 2014 (Vol I, WCE 2014), London, UK, 2–4 July 2014. [Google Scholar]
- Zreikat, A.I. Capacity Bounds Analysis of 5G networks in different propagation environments. In Proceedings of the 2023 IEEE 13th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–11 March 2023; pp. 988–993. [Google Scholar] [CrossRef]
- Preben, M.; Wei, N.; Istvan, Z.K.; Frank, F.; Akhilesh, P.; Klaus, I.P.; Troels, K.; Klaus, H.; Markku, K. LTE Capacity Compared to the Shannon Bound. In Proceedings of the 2007 IEEE 65th Vehicular Technology Conference (VTC2007-Spring), Dublin, Ireland, 22–25 April 2007; pp. 1234–1238. [Google Scholar] [CrossRef]
- Dutta, S.; Khalili, A.; Erkip, E.; Rangan, S. Capacity Bounds for Communication Systems with Quantization and Spectral Constraints. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 2038–2043. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Poor, H.V. Statistical Delay-Bounded QoS Provisioning Over 5G Multimedia Mobile Wireless Networks in the Finite Blocklength Regime. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Xiao, L.; Xiao, P.; Liu, Z.; Yu, W.; Haas, H.; Hanzo, L. A Compressive Sensing Assisted Massive SM-VBLAST System: Error Probability and Capacity Analysis. IEEE Trans. Wirel. Commun. 2020, 19, 1990–2005. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, G.; Ai, B.; Li, J.; Tellambura, C. Backscatter Aided Wireless Communications on High-Speed Rails: Capacity Analysis and Transceiver Design. IEEE J. Sel. Areas Commun. 2020, 38, 2864–2874. [Google Scholar] [CrossRef]
- Tlebaldiyeva, L.; Maham, B.; Tsiftsis, T.A. Capacity Analysis of Device-to-Device mmWave Networks Under Transceiver Distortion Noise and Imperfect CSI. IEEE Trans. Veh. Technol. 2020, 69, 5707–5712. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.K.; Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Ergodic Capacity Analysis of AF DH MIMO Relay Systems With Residual Transceiver Hardware Impairments: Conventional and Large System Limits. IEEE Trans. Veh. Technol. 2017, 66, 7010–7025. [Google Scholar] [CrossRef]
- Cao, F.; Han, Y.; Liu, Q.; Wen, C.-K.; . Jin, S. Capacity Analysis and Scheduling for Distributed LIS-aided Large-Scale Antenna Systems. In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 659–664. [Google Scholar] [CrossRef]
- Nossire, Z.; Gupta, N.; Almazaydeh, L.; Xiong, X. New Empirical Path Loss Model for 28 GHz and 38 GHz Millimeter Wave in Indoor Urban under Various Conditions. Appl. Sci. 2018, 8, 2122. [Google Scholar] [CrossRef]
- Parsons, J.D. The Mobile Radio Propagation Channel, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2000; pp. 16–17, 75–77, 116–118. [Google Scholar]
- Wang, C.; Deng, D.; Xu, L.; Wang, W.; Gao, F. Joint Interference Alignment and Power Control for Dense Networks via Deep Reinforcement Learning. IEEE Wirel. Commun. Lett. 2021, 10, 966–970. [Google Scholar] [CrossRef]
- Chen, X.; Wu, C.; Liu, Z.; Zhang, N.; Ji, Y. Computation Offloading in Beyond 5G Networks: A Distributed Learning Framework and Applications. IEEE Wirel. Commun. 2021, 28, 56–62. [Google Scholar] [CrossRef]
- Mogensen, P.E.; Wigard, J. COST Action 231: Digital Mobile Radio—Towards Future Generation Systems; Final Report, EUR 18957, Chapter 4; European Commission: Brussels, Belgium, 1999. [Google Scholar]
- Zreikat, A.I. Radio Resource Management and Modeling for Wireless Mobile Networks: Enhancement of Call Admission Control Algorithms (CACAs) and Capacity Bounds in UMTS/GSM Networks; LAMBERT Academic Publishing: Saarbrücken, Germany, 2011; 216p, ISBN 3846534994/978-3846534991. [Google Scholar]
- Benni, N.S.; Manvi, S.S. Clustering Algorithm To Mitigate Intra And Inter-Cell Interference In 5G Backhaul Wireless Mesh Networks. In Proceedings of the 2022 IEEE 19th India Council International Conference (INDICON), Kochi, India, 24–26 November 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Holma, H.; Toskala, A. WCDMA for UMTS: Radio Access for Third Generation Mobile Communications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2002; pp. 167–248. [Google Scholar]
- Holma, H.; Laakso, J. Uplink admission control and soft capacity with MUD in CDMA. In Proceedings of the Gateway to 21st Century Communications Village. VTC 1999-Fall. IEEE VTS 50th Vehicular Technology Conference (Cat. No.99CH36324), Amsterdam, The Netherlands, 19–22 September 1999; pp. 431–435. [Google Scholar] [CrossRef]
- ITU: 5G networks and 3GPP Release 15. Available online: https://www.itu.int/en/ITU-D/Regional-Presence/AsiaPacific/SiteAssets/Pages/ITU-ASP-CoE-Training-on-/session7_5G%20networks%20and%203GPP%20release%2015.pdf (accessed on 18 July 2024).
- 3GPP-TS 138.214. Release 16.2.0 5G NR. Available online: https://www.etsi.org/deliver/etsi_ts/138200_138299/138214/16.02.00_60/ts_138214v160200p.pdf (accessed on 14 July 2024).
- Tong, W.; Ma, J.; Zhu Huawei, P. Enabling technologies for 5G air interface with emphasis on spectral efficiency in the presence of very large number of links. In Proceedings of the 2015 21st Asia-Pacific Conference on Communications (APCC), Kyoto, Japan, 14–16 October 2015; pp. 184–187. [Google Scholar] [CrossRef]
- Zreikat, A.I.; Mathew, S. Performance Evaluation and analysis of Urban-Suburban 5G Cellular Networks. Computers 2024, 13, 108. [Google Scholar] [CrossRef]
- Zreikat, A.I.; Mercan, S. Performance Study of 5G Downlink Cell. In Internet of Things, Smart Spaces, and Next Generation Networks and Systems, Proceedings of the 6th International Conference, NEW2AN 2006, St. Petersburg, Russia, 29 May–2 June 2006; Lecture Notes in Computer Science; Galinina, O., Andreev, S., Balandin, S., Koucheryavy, Y., Eds.; Springer: Cham, Switzerland, 2019; p. 11660. [Google Scholar] [CrossRef]
- MOSEL Home Page. Available online: https://www4.cs.fau.de/Projects/MOSEL/ (accessed on 15 July 2024).
- Badia, L.; Zorzi, M.; Gazzini, A. On the impact of user mobility on call admission control in WCDMA systems. In Proceedings of the IEEE 56th Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002; Volume 1, pp. 121–126. [Google Scholar] [CrossRef]
- Candan, I.; Salamah, M. Dynamic Time-Threshold Based Scheme for Voice Calls in Cellular Networks. In Next Generation Teletraffic and Wired/Wireless Advanced Networking, Proceedings of the 6th International Conference, NEW2AN 2006, St. Petersburg, Russia, 29 May–2 June 2006; Lecture Notes in Computer Science; Koucheryavy, Y., Harju, J., Iversen, V.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4003. [Google Scholar] [CrossRef]
- TSG-RAN Working Group 1 Meeting #6. Available online: https://www.3gpp.org/ftp/tsg_ran/wg1_rl1/TSGR1_06/Docs/Pdfs/r1-99818.pdf (accessed on 8 January 2025).
- Radio Access Network (RAN) Delay Budget Reporting in the Multimedia Telephony Service for Internet Protocol (IP) Multimedia Subsystem (IMS) (MTSI). Available online: https://www.etsi.org/deliver/etsi_tr/126900_126999/126910/16.00.00_60/tr_126910v160000p.pdf (accessed on 25 July 2024).
- Tarafder, P.; Chun, C.; Ullah, A.; Kim, Y.; Choi, W. Channel Estimation in 5G-and-Beyond Wireless Communication: A Comprehensive Survey. Electronics 2025, 14, 750. [Google Scholar] [CrossRef]

| Code | |
|---|---|
| Free Space | |
| Urban | |
| Suburban | |
| Dense Urban | |
| Rural |
| Parameter | Value |
|---|---|
| Average packet size-(Pareto distribution) | 480 bytes |
| Average requested file size (25 × 480 bytes)-(Pareto distribution) | 12 Kbytes |
| Average number of packet calls within a session-)-(Pareto distribution) | 5 |
| Average reading time between packet calls)-(Pareto distribution) | 412 s |
| Average amount of packets within a packet call)-(Pareto distribution) | 25 |
| Average inter-arrival time between packets)-(Pareto distribution) | 0.0625 |
| Number of codes (N) | 64 |
| Frequency, f | 20 GHz |
| Height of the mobile, hm | 1.5 m |
| Base station height, hb | 50 m |
| Service Factor, S(SF/SINR) | 2–128 |
| The cell radius r | 0–20 Km |
| Spreading factor (SF) | 32, 64, 128, 256 chips/symbol |
| Maximum transmission power (Psmax) | 120 W |
| Thermal Noise, N0 | −103 dBm |
| Signal-to-interference noise ratio (SNR) | 2 dB |
| Interference factor, ε | 0.30–0.70 |
| Wavelength, λ | 0.15 m |
| Number of zones | 3 |
| Ratio of web browsing | 0.60 |
| Ratio of streaming | 0.30 |
| Ratio of voice over 5G | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zreikat, A.I.; Kang, H. Performance Analysis of Downlink 5G Networks in Realistic Environments. Appl. Sci. 2025, 15, 4526. https://doi.org/10.3390/app15084526
Zreikat AI, Kang H. Performance Analysis of Downlink 5G Networks in Realistic Environments. Applied Sciences. 2025; 15(8):4526. https://doi.org/10.3390/app15084526
Chicago/Turabian StyleZreikat, Aymen I., and Hunseok Kang. 2025. "Performance Analysis of Downlink 5G Networks in Realistic Environments" Applied Sciences 15, no. 8: 4526. https://doi.org/10.3390/app15084526
APA StyleZreikat, A. I., & Kang, H. (2025). Performance Analysis of Downlink 5G Networks in Realistic Environments. Applied Sciences, 15(8), 4526. https://doi.org/10.3390/app15084526






