Abstract
To address the challenges of robotic arm path-planning in dynamic environments, this study proposes a reinforcement learning-based dynamic obstacle avoidance method. The study concerns a robot with six rotational degrees of freedom when moving outside of singular configurations, enabling more flexible and precise motion-planning. First, a dynamic exploration guidance mechanism is designed to enhance learning efficiency and reduce ineffective exploration. Second, an adaptive reward function is developed to enable real-time path-planning while avoiding obstacles. A simulation environment is constructed using CoppeliaSim software, and the experiment is performed with two cylindrical obstacles that move randomly within the workspace. The experimental results demonstrate that the improved method significantly outperforms traditional algorithms in terms of convergence speed, reward value, and success rate.
1. Introduction
With the advancement of high-performance computing, the Internet of Things, and artificial intelligence technologies, robotic arms have been widely applied in areas such as automated production, urban security and services, and space exploration, continuously progressing toward the intelligent objectives of self-learning and self-regulation [1]. In most cases, robots can effectively avoid the static obstacles present in various environments. Nevertheless, the utilized algorithms exhibit insufficient adaptability to dynamically changing obstacles, making it challenging to quickly and accurately avoid them [2]. Probability sampling-based motion planning algorithms such as Rapid Random Tree (RRT) can swiftly search high-dimensional spaces; however, their limited environmental exploration ability leads to poor performance in handling dynamic obstacles and complex tasks. Therefore, in this context, finding the right training algorithm is important [3,4]. A combination of the Artificial Potential Field (APF) algorithm with numerical methods based on the Jacobian matrix has been employed to address obstacle avoidance-based path-planning in unknown environments [5].
However, due to the aforementioned limitations of traditional algorithms in dynamic environments, academic circles are paying more and more attention to the development of reinforcement learning-based approaches [6].
The rapid advancements in deep learning and computational capabilities have made deep reinforcement learning a reality, which is progressively being employed in domains such as gaming, robot navigation, and industrial production [7]. DeepMind has developed models such as AlphaZero based on Deep Reinforcement Learning (DRL) [8], which defeated world-class chess players in competitions, demonstrating that this technology can achieve a superhuman performance in complex environments. To address the challenges of non-Markovian tasks in multi-agent systems, one study proposed a synchronized decentralized training paradigm based on GR(1) specifications [9]. By decomposing the synthesized GR(1) strategies into individual reward structures, this approach guides the multi-agent reinforcement learning (MARL) process, thereby effectively preserving the safety and liveness properties of the system. DRL has made significant strides not only in academia, but also in industry. For instance, IBM’s artificial intelligence system Watson employs deep reinforcement learning techniques to assist doctors in diagnosing cancer. Furthermore, in areas such as inverted pendulum control and unmanned surface vehicle control [10], DRL is considered one of the most promising cutting-edge artificial intelligence technologies.
Reinforcement learning has similarly garnered the interest of experts and scholars in the field of robotics, demonstrating exceptional performance in path-planning within complex environments in scenarios characterized by a lack of prior knowledge. For example, Liu et al. [11] innovatively integrated digital twin technology with DRL and proposed a multitasking training approach based on the twin synchro-control (TSC) scheme to enhance the control performance of humanoid robot arms. A data acquisition system was developed to collect human joint angle data, which served as a prior knowledge input for DRL, thereby optimizing the reward function of the deep deterministic policy gradient (DDPG) algorithm and improving the learning stability and convergence speed. This approach was successfully applied in the humanoid robot BHR-6, enabling it to perform tasks that are challenging to train using existing methods. Sun et al. [12] proposed an end-to-end navigation strategy based on causal reinforcement learning, which is learned directly from the data, bypassing the traditional mapping and planning steps, thereby improving the responsiveness of drones in obstacle avoidance and navigation tasks. To address the issue of local minima in robotic arm collision avoidance using Artificial Potential Field (APF), a study proposed a method that integrates APF with deep reinforcement learning (DRL) and improves Hindsight Experience Replay (HER) into HER-CA to enhance training efficiency [13]. Wang et al. [14] proposes a decision reconstruction network integrated into the SAC algorithm. This network dynamically reconfigures network layers to enable cross-layer information exchange, effectively mitigating gradient conflicts and addressing the optimization challenges caused by parameter-sharing in robotic multi-task reinforcement learning. Yadav et al. [15] examined regularization-based methods like synaptic intelligence for sequential learning in offline RL, finding they reduce learning time and mitigate forgetting but offer limited knowledge transfer. The study proposed a deep reinforcement learning-based coverage path planning approach, using actor–critic methods to train mobile robots for exploration and full coverage [16]. Zhao et al. [17] introduced the Efficient Progressive Policy Enhancement (EPPE) framework, which integrates sparse and process rewards to improve DRL training efficiency and global optimality in path-planning.
Zhong et al. [18] have used a welding robot path-planning method based on the DDPG algorithm to solve the path-planning problem in a high-dimensional continuous state and action space. Cao et al. [19] proposed a multi-agent reinforcement learning approach for square shaft-hole assembly. The method designs a reward function based on the Decoupled Multi-Agent Deep Deterministic Policy Gradient (DMDDPG) algorithm and models the first three and last three joints of the robotic arm as a multi-agent system. Liu et al. [20] proposed DRL-based path planning method incorporates a safety verification mechanism to achieve collision-free trajectories. However, it still has limitations such as fixed end-effector orientation and the requirement for a smaller threshold in trajectory merging. Wang Y. et al. [21] introduced a method to control a mobile robotic arm to perform door-opening operations based on an improved Proximal Policy Optimization (PPO) algorithm. Wu et al. [22] achieved the requirements of online trajectory-planning by training a strategy consisting of a feedforward neural network in the simulation environment. Lindner et al. [23] employed the DDPG algorithm to optimize the static obstacle-avoidance performance of robotic arms; however, they did not extend their approach to dynamic obstacle environments. To address high-dimensional path-planning challenges, Prianto et al. [24] proposed a path-planning algorithm based on the Soft Actor–Critic (SAC) framework, utilizing configuration space augmentation to manage the complex configuration spaces associated with multi-arm systems. They also incorporated the Hindsight Experience Replay (HER) technique to enhance the sampling efficiency, enabling the real-time and rapid generation of any end-to-end shortest path. Singla et al. [25] combined recurrent neural networks with temporal attention processes and deep reinforcement learning, allowing agents to remember important contextual data in order to prevent collisions. However, the extensive operational space of robotic arms makes it challenging to quickly obtain successful samples, causing DRL algorithms to expend significant time on ineffective exploration and resulting in slow convergence rates. To mitigate this issue, researchers have proposed leveraging “expert guidance” to accelerate the convergence of DRL algorithms. Xu et al. [26] developed a strategy for axis–hole assembly problems guided by impedance control algorithms assisted by the DDPG for the correction of trajectories. Rahmatizadeh et al. [27] used a deep neural network controller based on a Long Short-Term Memory (LSTM) network to generate trajectories. At the same time, a mixture density network (MDN) was used to calculate the error signal to adapt to multimodal demonstration data. Through imitation learning, the robotic arms were able to reasonably plan paths to complete the picking and placing of objects. Chen et al. [28] designed a comprehensive reward function that combines dynamic obstacle avoidance and target proximity, which was integrated with the priority experience replay (PER) approach to improve the utilization of samples, finally allowing for the realization of real-time path-planning. Li et al. [29] integrated the APF and DDPG algorithms, using approximate poses derived from the APF algorithm as expert guidance. They implemented a phased approach to obstacle-avoidance trajectory planning, where the DDPG algorithm dominated training during the obstacle-avoidance phase and the approximate poses from APF guided DDPG training during the target-planning phase. Additionally, they proposed a guiding mechanism to connect the control outputs of the two phases, thereby efficiently training a policy model tailored to address the research problem at hand.
However, trajectory-planning approaches for robotic arms based on DRL methods still encounter challenges in achieving convergence and conducting efficient explorations, particularly within unstructured work environments that feature both dynamic and static obstacles. The core issue lies in managing a substantial amount of failed explorations and sparse rewards, which result in training failure and make it difficult to learn effective strategies.
In order to solve the problem in which robot arms face difficulties in avoiding obstacles and reaching the target point in environments characterized by dynamic obstacles, we propose a new path-planning method based on reinforcement learning. Through designing a dynamic exploration guidance mechanism and an adaptive obstacle avoidance reward function, we optimize the robotic arm’s performance in terms of path-planning. The overall environmental structure is illustrated in Figure 1. During the training process, the policy network receives the state vector as input and outputs the selected action; the critic network receives the state vector and action as input and outputs a value function that evaluates the expected reward or value of selecting the action in the state. During the testing process, the state vector obtained from the simulation environment is input into the policy network to obtain the selected action. This study implements a path planning strategy that ensures that the robotic arm remains stable during learning, and evaluates the effectiveness of this strategy in environments featuring dynamic obstacles.
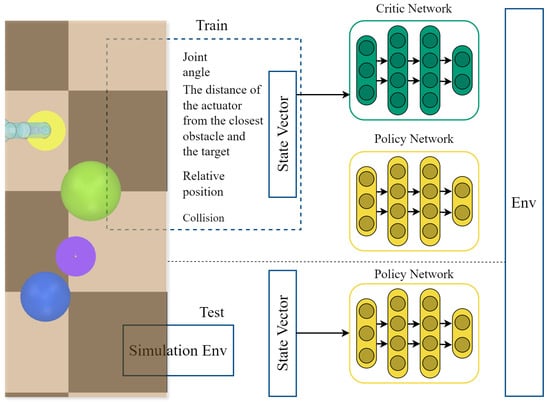
Figure 1.
Overall environment architecture.
2. Preliminaries
2.1. Markov Decision Process
Broadly speaking, Reinforcement Learning (RL) addresses sequential decision-making issues by seeking decision sequences that maximize the expected cumulative reward. The Markov decision process (MDP) provides a mathematical framework to model the motion control problem of the robot arm as a reinforcement learning problem. The reinforcement learning algorithm learns the optimal strategy through continuous interaction (trial and error), allowing the robot arm to make autonomous decisions. In RL tasks, MDPs are typically chosen as the mathematical models to describe decision problems, which are represented as tuples , where S and A denote finite continuous state and action spaces, respectively; the reward function specifies the reward received from the environment upon transitioning between states; the transition probability defines the probability distribution of moving to state after taking action a in state S; and the discount factor adjusts the significance of future rewards. The agent’s behavior is defined by the policy , which maps states to probability distributions across actions.
2.2. Kinematic Modeling
The kinematics of robotic arms primarily reflect the relationships among displacements, velocities, and accelerations between joints. In this study, a six-degrees-of-freedom welding robotic arm is modeled using the Denavit–Hartenberg (D-H) parameter method [30]. As a standard approach for serial robotic arm kinematic modeling, the D-H parameter method is both rigorous and widely applicable. Based on this method, the geometric relationships of the robotic arm’s joints are systematically described, and the standard D-H parameters are presented in Table 1. A picture of the robotic arm with some of the DH parameters marked is shown in Figure 2.

Table 1.
D-H parameters of the robotic arm.
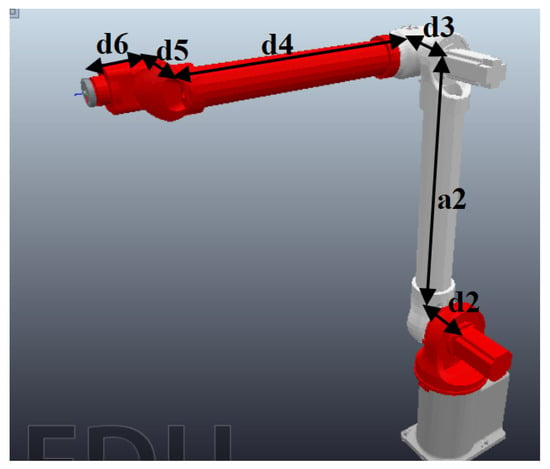
Figure 2.
Robotic arm 3D model.
The robotic arm possesses six degrees of freedom, allowing the end-effector’s pose and position to be represented by . Vectors n, o, and a form a 3 × 3 matrix that describes the end effector’s pose, while the vector p denotes its positional information. Utilizing the D-H parameters presented in Table 1, the link transformation matrices of the robotic arm can be determined.The following is the expression for the transformation matrix between the base coordinate frame and the end effector coordinate frame:
Here, the superscript of the coordinate T denotes the coordinate system being transformed, while the subscript indicates the target coordinate system; represents the normal vector of the robotic arm’s end effector; indicates the sliding vector; is the approach vector; and represents the position vector of the end effector. The homogeneous transformation matrix describes the pose of link i’s coordinate system relative to that of link , as shown by the following formula:
The final link is typically referred to as the end effector, to which an effector with a reference frame (e.g., a welding torch) is attached. The homogeneous transformation matrix of the end effector relative to the base link, denoted as , can be defined as:
where represents the pose, in which is the three-dimensional position and denotes the orientation in Cartesian space.
As most motions are defined directly in Cartesian space, the robot arm needs to convert Cartesian motion into joint motion in joint space. If the Cartesian velocity of the end effector is given, the corresponding joint velocity is expressed as follows:
where represents the 6 × 6 Jacobian matrix of the six-degree-of-freedom robotic arm.
3. Method
The state space and action space for the dynamic obstacle-avoidance path-planning of robotic arms are explained in detail in this section. We also list the adaptive reward function and the dynamic exploration guidance mechanism. As illustrated in Figure 3, in order to use the MDP to solve the robotic arm path-planning problem discussed in this research, we must specify the interaction process between the algorithm and the simulation environment.
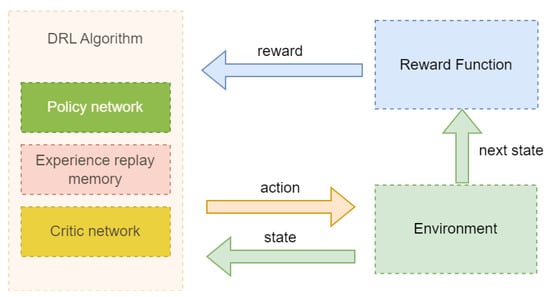
Figure 3.
Framework for the DRL algorithm to interact with the environment.
3.1. State Space
In a real working environment, the state information can be vast (and even infinite), making it impractical to enumerate all possible states. Therefore, in practical applications, key features are usually extracted for representation, in order to reduce the computational complexity and improve learning efficiency. In DRL, state information is not only important for the agent to perceive the environment, but also directly affects its decision-making process and the evaluation of long-term rewards. As such, reasonable state design can significantly improve the convergence, convergence speed, and final performance of the algorithm.
This study aims to train an agent to autonomously control the joint motion of a six-axis robot arm, while avoiding collisions and getting as close as possible to a specified target. The state space can be represented by Equation (5):
where denotes the joint angles of the end effector; represents the Cartesian position of the end effector’s reference coordinate system relative to the target coordinate system; the scalar indicates the Euclidean distance between the end effector and the origin of the target coordinate system; and is the shortest Euclidean distance between the end effector and the two types of obstacles. The final component—collision, which can be obtained via the CoppeliaSim API function—is a Boolean value that indicates whether the manipulator has collided with any environmental obstacles.
3.2. Action Space
The agent in the environment is a 6-DOF welding robot arm. For the motion control of the robot arm, the control strategy of the agent adopts the velocity control method, using the joint velocity as the control input, in order to achieve the real-time adjustment and trajectory optimization of the robot arm in the continuous action space. This method can dynamically adjust the angular velocity of each joint according to the current state, such that the robot arm moves along the optimal trajectory to minimize the distance between the end effector and the target position. Therefore, the action space is defined as follows:
In this context, denotes the target angular velocity of each servo motor–driven rotational joint within its allowable range. The dimension of the action space is 6.
3.3. Reward Signal
To address the issue of sparse rewards in DRL-based trajectory-planning for robotic arms within dynamic environments, this study introduces an adaptive reward function that seamlessly integrates existing reward mechanisms with energy function constraints, drawing on the principles of artificial potential field methods and energy functions. This adaptive function facilitates a smooth transition between the two reward mechanisms and carries out dynamic adjustments according to the distance between the end effector and the obstacle to ensure that the path-planning result is both safe and efficient:
Specifically, is designed such that, when the end effector is sufficiently distant from obstacles, serves as the dominant factor; when the distance between the end effector and an obstacle falls below the critical distance , the energy function takes precedence. can be expressed as follows:
where
It is evident that the function yields a smooth transition from 0 to 1: when is large, approaches 1; meanwhile, when is small, it approaches 0. Here, serves as a tuning parameter that adjusts the smoothness of the reward mechanism. is designed to prompt the robotic arm to accomplish the task, which mainly includes the following aspects:
The first term on the right-hand side of Equation (11) is designed to guide the end effector toward a specific target position. It is defined based on the difference in the end effector–-target distance between the current step and the previous step:
In robotic arm path-planning tasks, we do not necessarily expect the end-effector to reach the designated location in a single step every time; instead, a gradual approach strategy is adopted. Specifically, the end effector is controlled to move incrementally at each step, gradually closing in on the target position. In designing the reward feedback, the distance between the end effector’s current position and the target point is introduced as a key parameter. Compared with relying solely on a one-step Euclidean distance, this reward function may slow down the movement process, yet it effectively reduces control complexity and meets the path-planning objective under higher-precision requirements.
Furthermore, in path-planning, precision and efficiency often impose mutual constraints. To enhance the reward mechanism’s effectiveness, when the current state nears boundary conditions (e.g., when the distance to the target point is relatively small), each slight movement in the correct direction should receive a stronger positive reward. This approach guides the robotic arm to gradually refine its path, ultimately achieving high-precision control of the target position.
The second term, , is the obstacle avoidance reward function designed to guide the robotic arm in evading obstacles:
Here, represents the smallest gap between the robotic arm and obstacles, and denotes the decay rate of the reward function.
The third term, , is the termination reward function, primarily designed to reward the achievement of the target and collisions with obstacles:
Considering the complexity of dynamic environments, the likelihood of collisions during the initial phases of training is substantially higher than that of reaching the target. Consequently, the reward for successfully attaining the target should be several times greater than the penalty imposed for collisions, and the reward is set to zero when the target is not achieved.
3.4. Dynamic Exploration Guidance Mechanism
There are two main challenges regarding path-planning in dynamic obstacle avoidance tasks: one is the need to avoid collisions with obstacles, and the other is the need to successfully reach the specified target point. However, it is very complicated to deduce the relationship between the state space and the action space from the perspective of the agent. This is because the state space is usually large and continuous, especially in a dynamic environment, and the agent must not only deal with the current state, but also predict and react to possible changes. In order to learn how to choose the appropriate action from the current state, the agent usually requires a large number of training iterations and calculations. This process may involve billions of training rounds and calculations, which is very time-consuming and computationally intensive for real-world applications. Therefore, in order to solve this problem, a better approach is to transform the infinite state space into a finite state space. Specifically, by limiting the range of states, the originally very large or continuous state space can be simplified into a finite set.
Consequently, it is difficult to directly start training the robot path-planning model using reinforcement learning algorithms. By restricting the state space, the agent can focus on exploring only those states that are relevant to the path-planning task, which is crucial for ensuring efficient convergence and learning. This approach excludes irrelevant and extraneous states, thereby simplifying the agent’s decision-making process. Rather than being overwhelmed by an unlimited and irrelevant state space, the agent concentrates on pertinent states, resulting in more effective decision making and faster learning. Therefore, implementing dynamic policy selection enables quicker convergence during training. Through the combination of a guiding term with stochastically sampled actions that include exploration noise from deep reinforcement learning algorithms, the selected action is dynamically integrated. Due to the presence of obstacles in the working environment, relying solely on the velocity output generated by the inverse kinematics (IK) module is insufficient to achieve effective obstacle avoidance. To address this limitation, this paper incorporates an additional action term at produced by a deep reinforcement learning (DRL) policy network. This action serves as a compensatory component to the IK output, guiding the manipulator to avoid obstacles while maintaining goal-directed motion. The resulting hybrid action formulation is given by
where denotes the time step duration. This formulation enables the manipulator to adaptively adjust its trajectory in response to environmental constraints while efficiently progressing toward the target. We introduced the dynamic scale factor to adjust the proportion of dynamic exploration guidance mechanism:
In addition, when operating a robotic arm manually, the speed of operation slows down as the arm approaches the target point to maintain accuracy. Similarly, in robotic arm control, the movement step size should gradually decrease to ensure a certain level of precision. Therefore, the agent’s joint angles are controlled as follows:
In this context, rate is a dynamic scaling factor that increases rapidly during the initial phase and slows its growth in the later stages; Current_episode and Max_episode denote the current and maximum number of training episodes, respectively, and refers to a randomly sampled action augmented with exploration noise. The training workflow incorporating the dynamic exploration guidance strategy is illustrated in Figure 4.
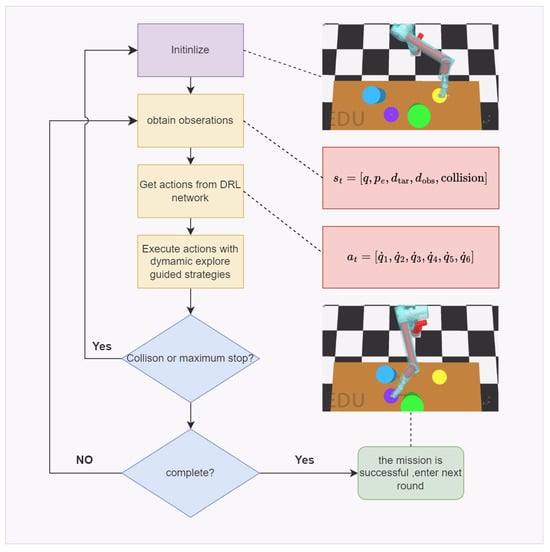
Figure 4.
Training flowchart after applying the dynamic exploration guidance mechanism.
By dynamically adjusting the scaling factor, the initial phase of training significantly increases the probability of the robotic arm obtaining positive samples, effectively preventing the waste of training resources caused by ineffective exploration and alleviating the issue of sparse rewards in the early stages. As the number of training iterations increases, the scaling factor gradually grows, diminishing the influence of inverse kinematics, while the proportion of randomly sampled actions markedly rises, resulting in greater randomness in the robotic arm’s action selection. Building on the sufficient number of positive samples obtained from the preliminary training, the model achieves efficient convergence optimization, progressively mastering the ability to realize path-planning in dynamic obstacle-avoidance environments.
4. Experiments And Analysis
4.1. Experimental Setup
The simulation platform employed for the experiments was CoppeliaSim Edu version 4.2. For the implementation of the algorithm, the reinforcement learning frameworks PyTorch and OpenAI’s Gym were utilized with the code developed in Python. The inverse kinematics module was provided by MATLAB. With the support of CoppeliaSim’s Remote API, network communication between Python and the CoppeliaSim platform was achieved, as illustrated in Figure 5. The state information of the robotic arm was obtained by parsing the feedback data from the CoppeliaSim Edu simulation platform. Regarding the hardware, a PC (CPU i7-12600H @2.70 GHz, RAM 32 GB, GPU RTX 3070 8 GB) was used to support the training of the algorithms.
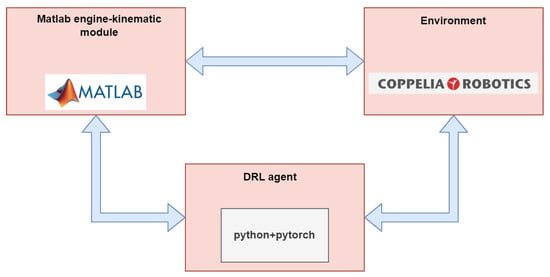
Figure 5.
Network connections in the simulation framework.
As shown in Figure 6, each environment included two cylindrical obstacles with a base diameter of 0.15 m and a height of 0.3 m. In environment 1, the two obstacles remained stationary while the state of the obstacles in environment 2 changed; namely, the obstacles moved randomly at every step. Their maximum linear velocity was set to 150 mm/s to simulate real-time environmental changes. The initial positions of the two obstacles relative to the robot base were set as [900, −400, 300] mm for Obstacle 1 and [1050, −300, 300] mm for Obstacle 2. Similarly, the target point was located at [100, −350, 300] mm relative to the robot base.In both cases, the robot arm had to bypass the obstacles and reach the target point to be considered successful. The location of the target point was randomly generated after the robot arm reached it. To ensure numerical stability and generalizability, all robot configurations during training and testing were selected to be sufficiently far from singularities and joint limits. Training in the first environment was conducted for 5000 episodes.
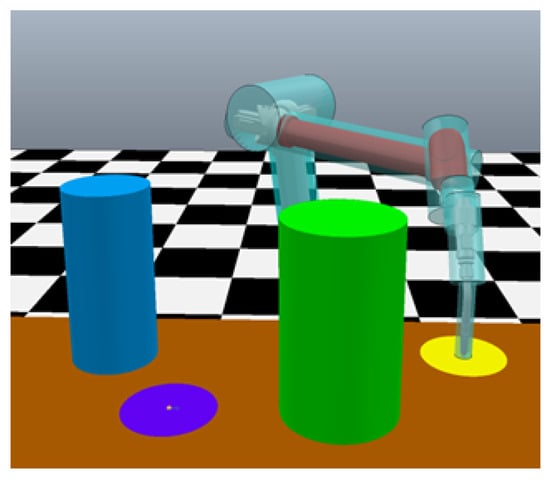
Figure 6.
Diagram of the experimental scene.
4.2. Algorithm Performance Evaluation
The reward function parameters employed in the experiments are presented in Table 2.

Table 2.
Parameters of the reward function.
The experiments involved comparing the traditional DDPG and SAC algorithms with two improved versions of these training algorithms, incorporating a dynamic policy selection mechanism and adaptive rewards. Figure 7 illustrates the growth curve of reward values over 5000 episodes for the traditional algorithms, as well as the corresponding performance of the improved algorithms in Environment 1. The improved algorithms typically converged at around 3000 episodes, whereas the traditional algorithms generally took approximately 4000 episodes to converge. In Environment 2, the introduction of randomly moving obstacles complicated the training environment. To ensure that the trained policy models could handle nearly all situations, the number of training episodes was increased to 10,000. The resulting reward curves, as shown in the figure, indicate that the improved SAC algorithm began to converge around 6000 episodes, while the traditional algorithms generally converged at around 7000 episodes. Evidently, the improved algorithms exhibited significant advancements over the traditional algorithms. The results presented in the figure demonstrate that the dynamic exploration guidance mechanism and adaptive rewards contribute positively to the convergence speed and stability of the algorithms.
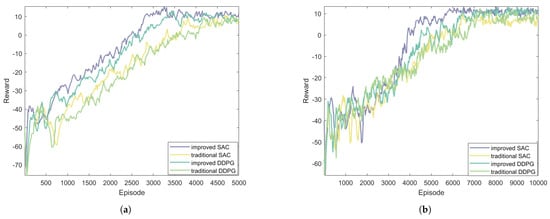
Figure 7.
Comparison of four algorithms in (a) Environment 1 and (b) Environment 2.
To evaluate the model’s adaptability to complex environments, we conducted tests within a simulated setting, specifically utilizing the more intricate Environment 2. Figure 8 illustrates the complete process of dynamic obstacle avoidance while reaching the target within a single episode.
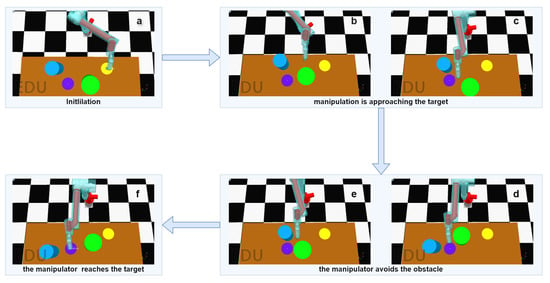
Figure 8.
The entire path-planning and dynamic obstacle-avoidance process of the manipulator. (a–f) illustrate key stages of the task: (a) Initialization of the manipulator; (b,c) The manipulator moves toward the target while detecting the surrounding environment; (d,e) The manipulator encounters the dynamic obstacle and adjusts its path to avoid it; (f) The manipulator successfully reaches the target.
In environment 2, although the obstacles were designed to move randomly during the training phase to introduce dynamic complexity, they were configured to move along predefined straight-line trajectories during the testing phase (as shown in Figure 9). This setup was intentionally chosen to control variables and ensure consistent environmental conditions across different algorithms, thereby enabling a fair and direct performance comparison. Since both the initial point and the target point were located on the tabletop surface, and the reward function encourages the robot to complete the task in as few steps as possible, the motion of the robot’s end-effector showed only minor variation along the z-axis and was primarily confined to the x-y plane.
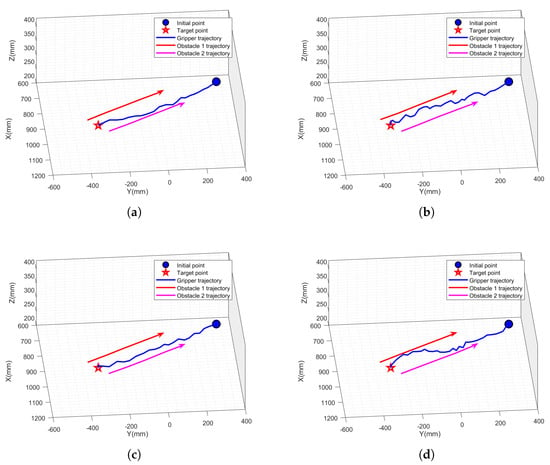
Figure 9.
The robot manipulator and obstacle trajectories: (a) improved SAC algorithm; (b) traditional SAC algorithm; (c) improved DDPG algorithm; and (d) traditional DDPG algorithm.
We used the four algorithms to perform multiple simulations in the same dynamic simulation environment. The trajectory diagrams obtained from the experiment are shown in Figure 9. In this figure, a blue sphere is used to denote the starting point, while the red five-pointed star represents the end point. The robot’s motion trajectory is depicted in blue, and the motion trajectories of the obstacles are shown in red and pink. It is evident that the robot avoided collision with obstacles throughout its movement. Figure 9a,c shows the trajectory diagrams for the improved algorithm, from which it is obvious that the trajectories of the improved algorithms were shorter and smoother than those of the traditional algorithms.
A total of 500 test trials were performed. The final results are presented in Table 3, which includes the average success rate, average reward, and average number of steps, as well as the reward variance and step variance for both the traditional algorithms and their improved versions under the condition of two randomly moving obstacles. The results indicate that the SAC algorithm is more suitable than the DDPG algorithm for the obstacle-avoidance path-planning of robotic arms in high-dimensional spaces. However, the method proposed in this paper enhanced the performance metrics of both algorithms, thereby validating the stability and robustness of the proposed approach.

Table 3.
Test results.
In particular, the reward variance and step variance further confirm the improvements in algorithm stability and efficiency. For SAC, the reward variance decreased from 8.47 to 4.13, a reduction of approximately 51.3%, and the step variance dropped from 20.55 to 8.27, a reduction of about 59.8%. For DDPG, the reward variance decreased from 11.87 to 6.63 (a 44.2% reduction), and the step variance was reduced from 27.57 to 11.90 (a 56.8% reduction). These significant decreases in variance clearly demonstrate that the improved methods produce a more stable, consistent performance across multiple trials. In our experiments, the obstacle speed was reasonably set to within a realistic range. The robot joint velocity during obstacle avoidance remained smooth and complied with both the joint position and velocity constraints, making the entire motion process feasible for future real-world implementations.
These findings demonstrate that the newly proposed reinforcement learning-based obstacle-avoidance path-planning method is not only practical but also more robust and reliable. By significantly improving both the average performance and its stability, the method proves effective in accomplishing real-time obstacle avoidance tasks for robotic arms operating in dynamic, high-dimensional environments.
5. Discussion
In this study, we proposed a reinforcement learning (RL)-based path-planning approach for a robotic manipulator in dynamic obstacle-avoidance tasks, integrating inverse kinematics (IK) with a dynamic exploration guidance mechanism. Path-planning under dynamic conditions involves two fundamental challenges: collision-free navigation around obstacles and successful arrival at designated targets. Due to the large and continuous nature of the state space in dynamic environments, traditional reinforcement learning approaches often require significant computational resources and extensive training iterations to deduce the state-action relationships effectively.
To overcome these challenges, we introduced a novel hybrid action formulation that combines the deterministic velocity output from an IK module with an adaptive compensatory action generated by a deep reinforcement learning (DRL) policy network. Specifically, this compensatory action dynamically guides the manipulator to effectively avoid obstacles while maintaining goal-directed motion. Furthermore, our method incorporates a dynamic scaling factor to adaptively modulate exploration intensity. This scaling factor rapidly increases at the early training stages, promoting effective exploration and preventing inefficient exploration, and gradually slows down in later stages to refine the manipulator’s movements and decision-making precision. Additionally, the designed adaptive reward mechanism derived from an energy function further supports effective policy training by improving the exploration–exploitation balance.
The effectiveness of our proposed method was clearly demonstrated through rigorous comparisons with traditional DRL algorithms. The experimental results indicate that our improved SAC algorithm achieved an average success rate of 86.65%, significantly higher than the 75.25% success rate of traditional SAC. Likewise, our improved DDPG method reached a success rate of 80.56%, markedly surpassing the traditional DDPG’s 71.33%. Moreover, the improved algorithms exhibited considerably lower reward and step variances, implying more stable and robust performance. Specifically, the improved SAC and DDPG recorded reward variances of 4.1266 and 6.6281, respectively, compared to their traditional counterparts (8.4654 and 11.8709). Step variances also decreased significantly from 20.55 to 8.27 (SAC) and from 27.57 to 11.90 (DDPG).
The superior performance of the proposed approach compared to traditional methods can be attributed primarily to the underlying strategy of transforming an infinite or extensive state space into a manageable finite subset. Traditional reinforcement learning methods often suffer from inefficient convergence due to their exhaustive exploration of irrelevant states, which contributes to higher variance and reduced success rates. In contrast, our dynamic exploration guidance, combined with adaptive reward-shaping and IK-based policy refinement, significantly narrows the exploration scope. This targeted approach not only accelerates convergence but also ensures more informed and precise decision-making, substantially enhancing the robot’s real-time path-planning capabilities.
6. Conclusions
In this study, we addressed the problem of obstacle-avoidance trajectory-planning for robotic arms in dynamic environments by proposing a planning method that integrates a dynamic exploration guidance strategy with adaptive rewards. The algorithm leverages the principles of deep reinforcement learning, modeling the research problem as an MDP. Taking into account the interactive training between the robot and its environment, we introduced and designed the state space, action space, and reward function. To enhance the training convergence efficiency and control performance of the algorithm, the planning process undergoes dynamic adjustments, allowing a dynamic exploration guidance mechanism to be developed. This mechanism is guided by inverse kinematics during the initial phase of training and shifts to random exploration in the later stages. Additionally, an adaptive reward function is incorporated, enabling the robotic arm to focus not only on obstacle avoidance but also on task execution. Ultimately, a policy model that is capable of addressing the research problem can be trained. The effectiveness of the proposed algorithm was validated through simulation experiments. The experimental results demonstrated that, compared to traditional approaches, the proposed method facilitates faster convergence, achieves higher success rates, and produces robotic arm control strategies with a superior performance.
Author Contributions
Conceptualization, S.Y.; methodology, S.Y. and Y.Z.; validation, S.Y., Y.Z. and C.Z.; investigation, S.Y., Y.Z., C.Z. and Q.C.; writing, S.Y., Y.Z., W.C. and J.Z.; supervision, Y.Z. and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Jiangsu Graduate Research Fund Innovation Project (grant number KYCX23_3059), and the APC was funded by Changzhou University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to considerations of privacy protection and ethical principles.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Niloy, M.A.K.; Shama, A.; Chakrabortty, R.K.; Ryan, M.J.; Badal, F.R.; Tasneem, Z.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; et al. Critical Design and Control Issues of Indoor Autonomous Mobile Robots: A Review. IEEE Access 2021, 9, 35338–35370. [Google Scholar] [CrossRef]
- Ekrem, Ö.; Aksoy, B. Trajectory planning for a 6-axis robotic arm with particle swarm optimization algorithm. Eng. Appl. Artif. Intell. 2023, 122, 106099. [Google Scholar] [CrossRef]
- Azizi, M.R.; Rastegarpanah, A.; Stolkin, R. Motion planning and control of an omnidirectional mobile robot in dynamic environments. Robotics 2021, 10, 48. [Google Scholar] [CrossRef]
- Shi, W.; Wang, K.; Zhao, C.; Tian, M. Obstacle avoidance path planning for the dual-arm robot based on an improved RRT algorithm. Appl. Sci. 2022, 12, 4087. [Google Scholar] [CrossRef]
- Park, S.O.; Lee, M.C.; Kim, J. Trajectory planning with collision avoidance for redundant robots using jacobian and artificial potential field-based real-time inverse kinematics. Int. J. Control Autom. Syst. 2020, 18, 2095–2107. [Google Scholar] [CrossRef]
- Semnani, S.H.; Liu, H.; Everett, M.; De Ruiter, A.; How, J.P. Multi-agent motion planning for dense and dynamic environments via deep reinforcement learning. IEEE Robot. Autom. Lett. 2020, 5, 3221–3226. [Google Scholar] [CrossRef]
- Finean, M.N.; Petrović, L.; Merkt, W.; Marković, I.; Havoutis, I. Motion planning in dynamic environments using context-aware human trajectory prediction. Robot. Auton. Syst. 2023, 166, 104450. [Google Scholar] [CrossRef]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, J.; Si, W.; Wang, X.; Wang, F. Multi-agent reinforcement learning with synchronized and decomposed reward automaton synthesized from reactive temporal logic. Knowl.-Based Syst. 2024, 306, 112703. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Wei, X.; Wang, H. Sim-real joint experimental verification for an unmanned surface vehicle formation strategy based on multi-agent deterministic policy gradient and line of sight guidance. Ocean Eng. 2023, 270, 113661. [Google Scholar] [CrossRef]
- Liu, C.; Gao, J.; Bi, Y.; Shi, X.; Tian, D. A multitasking-oriented robot arm motion planning scheme based on deep reinforcement learning and twin synchro-control. Sensors 2020, 20, 3515. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Gu, J.; Mou, J. UAV autonomous obstacle avoidance via causal reinforcement learning. Displays 2025, 87, 102966. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, T.; Zhou, K.; Lin, Y.; Ju, W. Active Collision Avoidance for Robotic Arm Based on Artificial Potential Field and Deep Reinforcement Learning. Appl. Sci. 2024, 14, 4936. [Google Scholar] [CrossRef]
- Wang, T.; Ruan, Z.; Wang, Y.; Chen, C. Control strategy of robotic manipulator based on multi-task reinforcement learning. Complex Intell. Syst. 2025, 11, 175. [Google Scholar] [CrossRef]
- Yadav, S.P.; Nagar, R.; Shah, S.V. Learning vision-based robotic manipulation tasks sequentially in offline reinforcement learning settings. Robotica 2024, 42, 1715–1730. [Google Scholar] [CrossRef]
- Garrido-Castañeda, S.I.; Vasquez, J.I.; Antonio-Cruz, M. Coverage Path Planning Using Actor–Critic Deep Reinforcement Learning. Sensors 2025, 25, 1592. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y.; Xie, Z. EPPE: An Efficient Progressive Policy Enhancement framework of deep reinforcement learning in path planning. Neurocomputing 2024, 596, 127958. [Google Scholar] [CrossRef]
- Zhong, J.; Wang, T.; Cheng, L. Collision-free path planning for welding manipulator via hybrid algorithm of deep reinforcement learning and inverse kinematics. Complex Intell. Syst. 2022, 8, 1899–1912. [Google Scholar] [CrossRef]
- Cao, G.; Bai, J. Multi-agent deep reinforcement learning-based robotic arm assembly research. PLoS ONE 2025, 20, e0311550. [Google Scholar] [CrossRef]
- Liu, J.; Yap, H.J.; Khairuddin, A.S.M. Path Planning for the Robotic Manipulator in Dynamic Environments Based on a Deep Reinforcement Learning Method. J. Intell. Robot. Syst. 2025, 111, 3. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Zhao, Y. Research on door opening operation of mobile robotic arm based on reinforcement learning. Appl. Sci. 2022, 12, 5204. [Google Scholar] [CrossRef]
- Wu, Y.H.; Yu, Z.C.; Li, C.Y.; He, M.J.; Hua, B.; Chen, Z.M. Reinforcement learning in dual-arm trajectory planning for a free-floating space robot. Aerosp. Sci. Technol. 2020, 98, 105657. [Google Scholar] [CrossRef]
- Lindner, T.; Milecki, A. Reinforcement learning-based algorithm to avoid obstacles by the anthropomorphic robotic arm. Appl. Sci. 2022, 12, 6629. [Google Scholar] [CrossRef]
- Prianto, E.; Kim, M.; Park, J.H.; Bae, J.H.; Kim, J.S. Path planning for multi-arm manipulators using deep reinforcement learning: Soft actor–critic with hindsight experience replay. Sensors 2020, 20, 5911. [Google Scholar] [CrossRef] [PubMed]
- Singla, A.; Padakandla, S.; Bhatnagar, S. Memory-based deep reinforcement learning for obstacle avoidance in UAV with limited environment knowledge. IEEE Trans. Intell. Transp. Syst. 2019, 22, 107–118. [Google Scholar] [CrossRef]
- Xu, J.; Hou, Z.; Wang, W.; Xu, B.; Zhang, K.; Chen, K. Feedback deep deterministic policy gradient with fuzzy reward for robotic multiple peg-in-hole assembly tasks. IEEE Trans. Ind. Inform. 2018, 15, 1658–1667. [Google Scholar] [CrossRef]
- Rahmatizadeh, R.; Abolghasemi, P.; Behal, A.; Bölöni, L. From virtual demonstration to real-world manipulation using LSTM and MDN. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Chen, P.; Pei, J.; Lu, W.; Li, M. A deep reinforcement learning based method for real-time path planning and dynamic obstacle avoidance. Neurocomputing 2022, 497, 64–75. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Chai, L. Collaborative obstacle avoidance trajectory planning for mobile robotic arms based on artificial potential field DDPG algorithm. Comput. Integr. Manuf. Syst. 2023, 30, 4282. [Google Scholar]
- Paredis, C.J.; Khosla, P.K. Kinematic design of serial link manipulators from task specifications. Int. J. Robot. Res. 1993, 12, 274–287. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).