Research on Pressure Exertion Prediction in Coal Mine Working Faces Based on Data-Driven Approaches
Abstract
1. Introduction
2. Materials and Methods
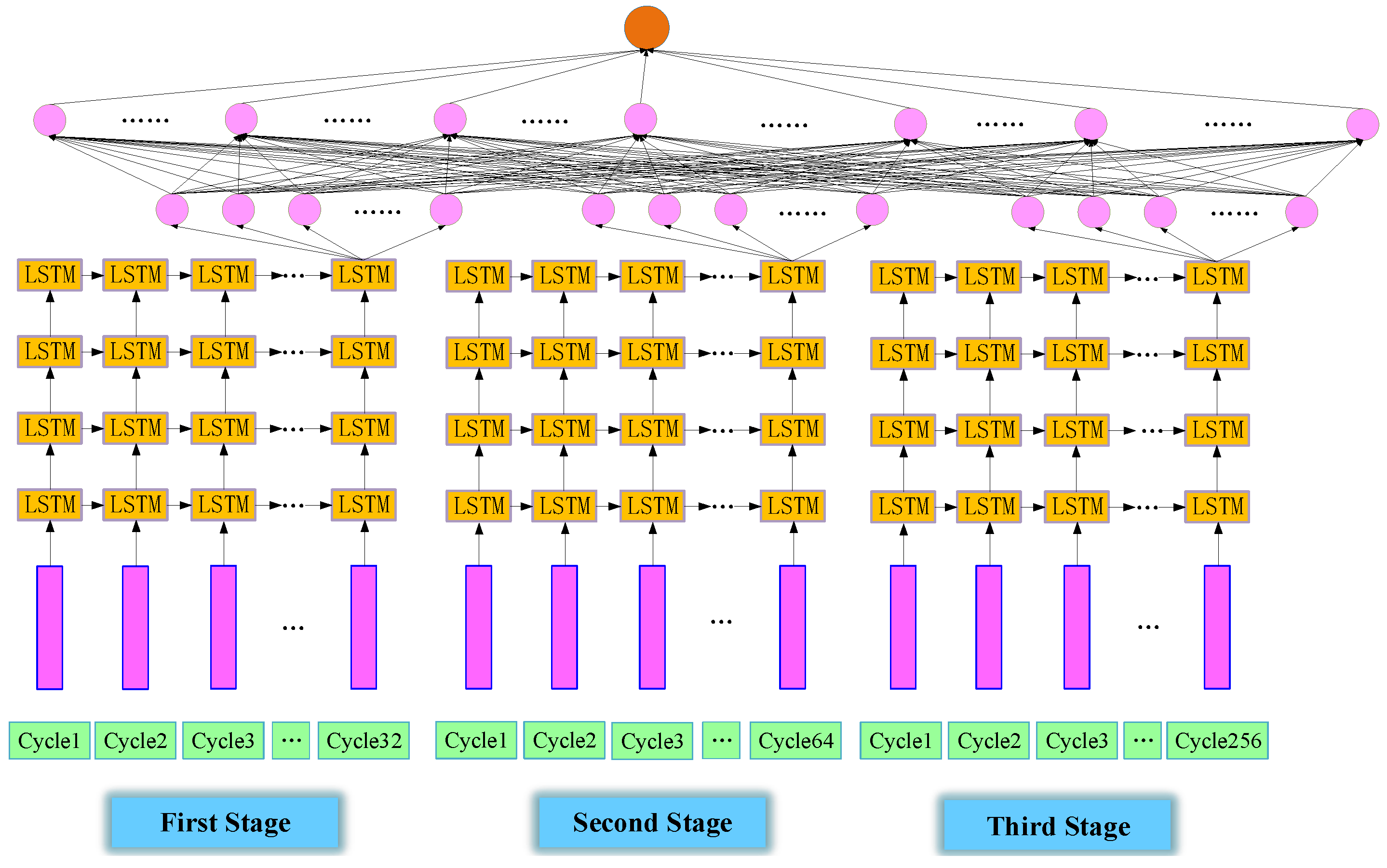
2.1. Modeling of Pressure Exertion Prediction in Working Faces Driven by Data
2.2. Method for Solving Pressure Exertion Characteristics Based on Historical Data
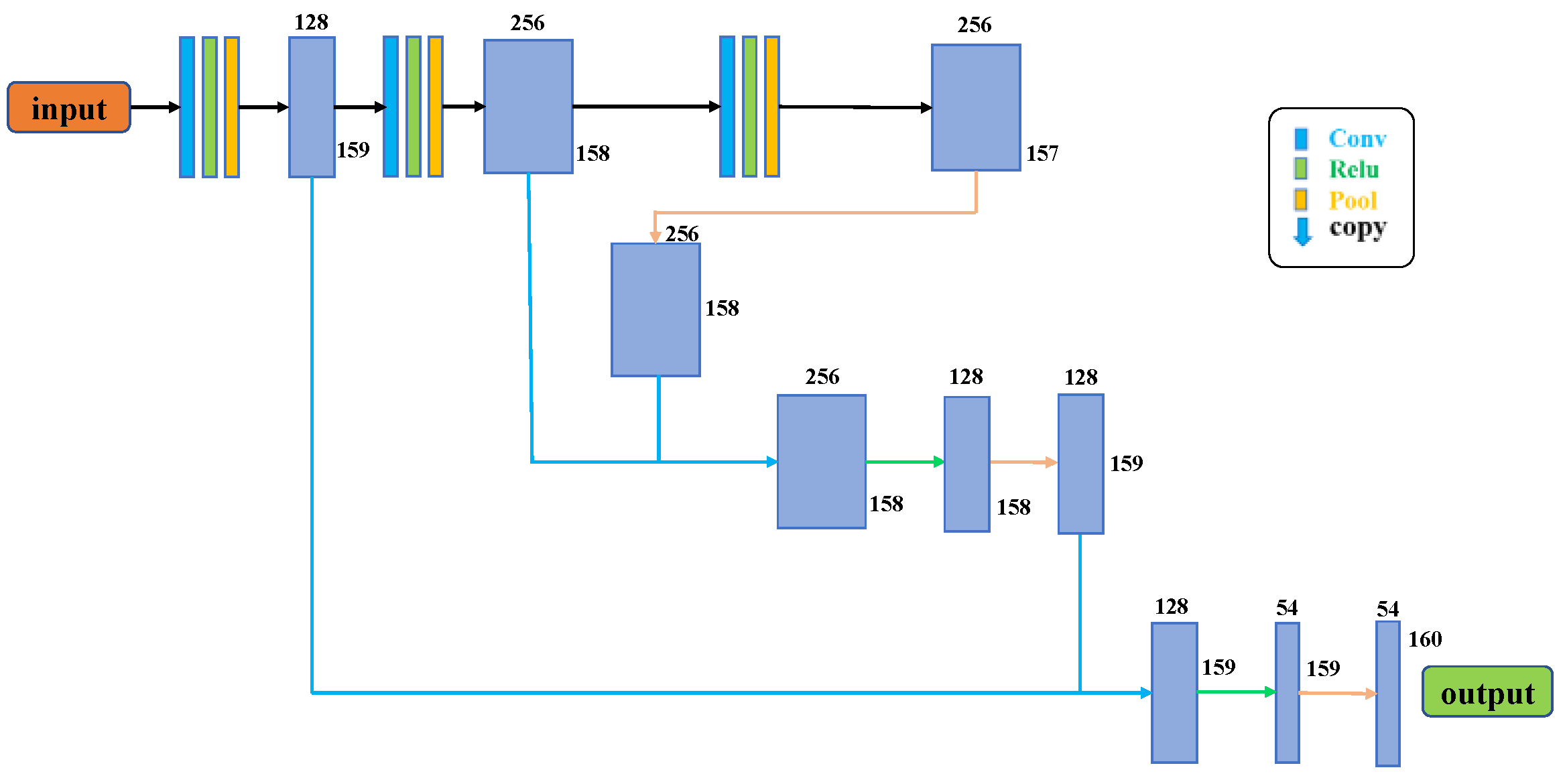
2.3. Method for Predicting Support Resistance Data
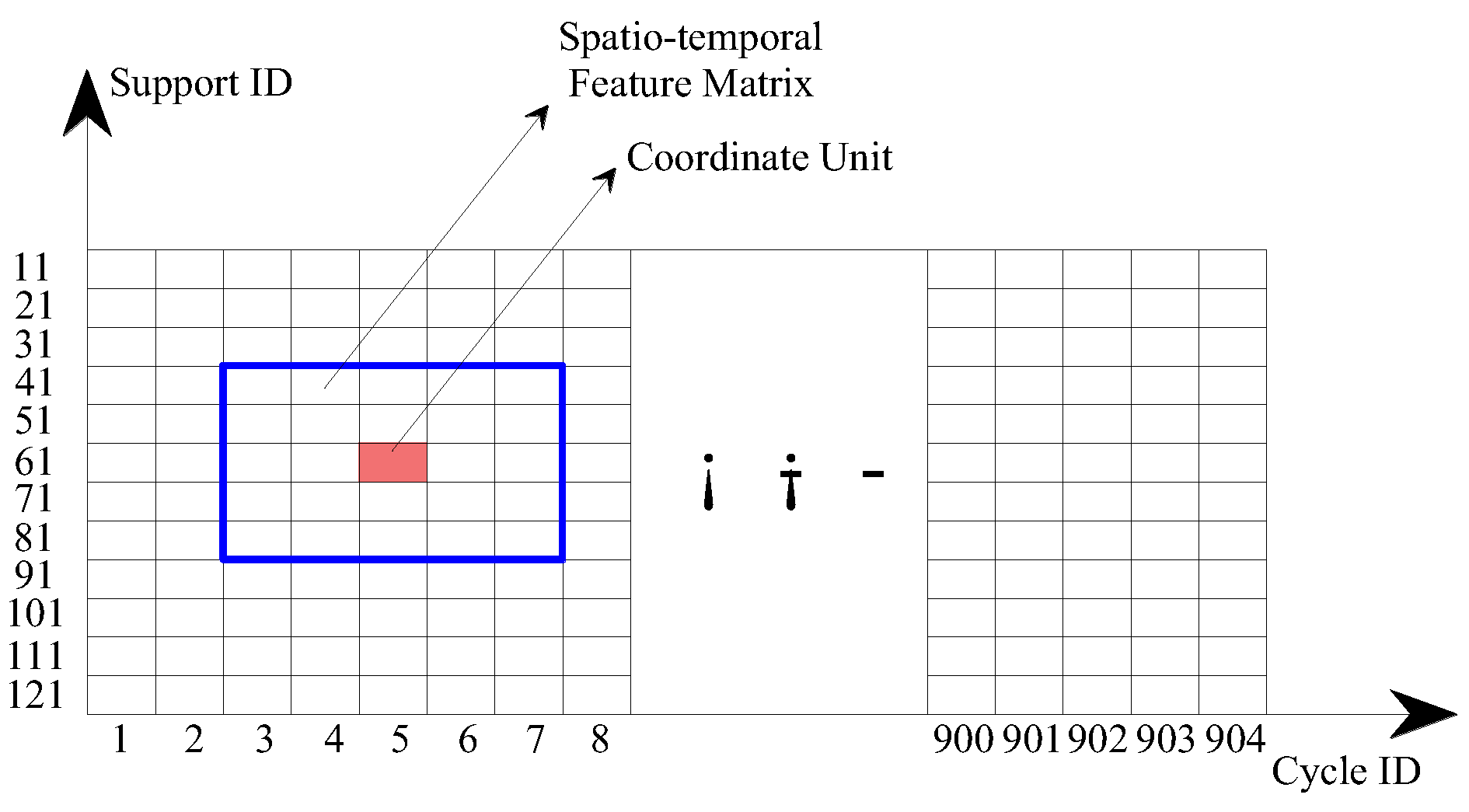
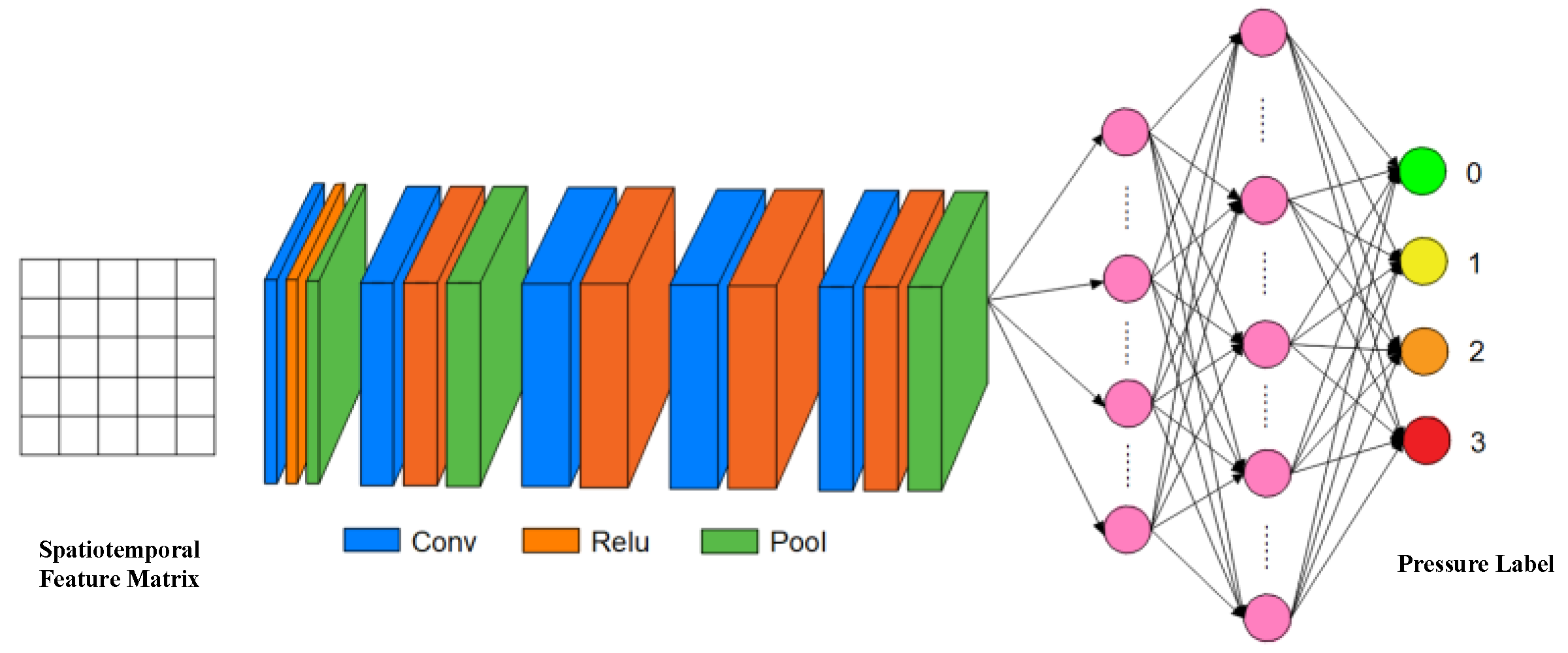
2.4. Real-Time Classification Method for Pressure Labels of Coordinate Units
2.5. Method for Predicting Pressure Exertion Characteristic Parameters
3. Results and Discussion
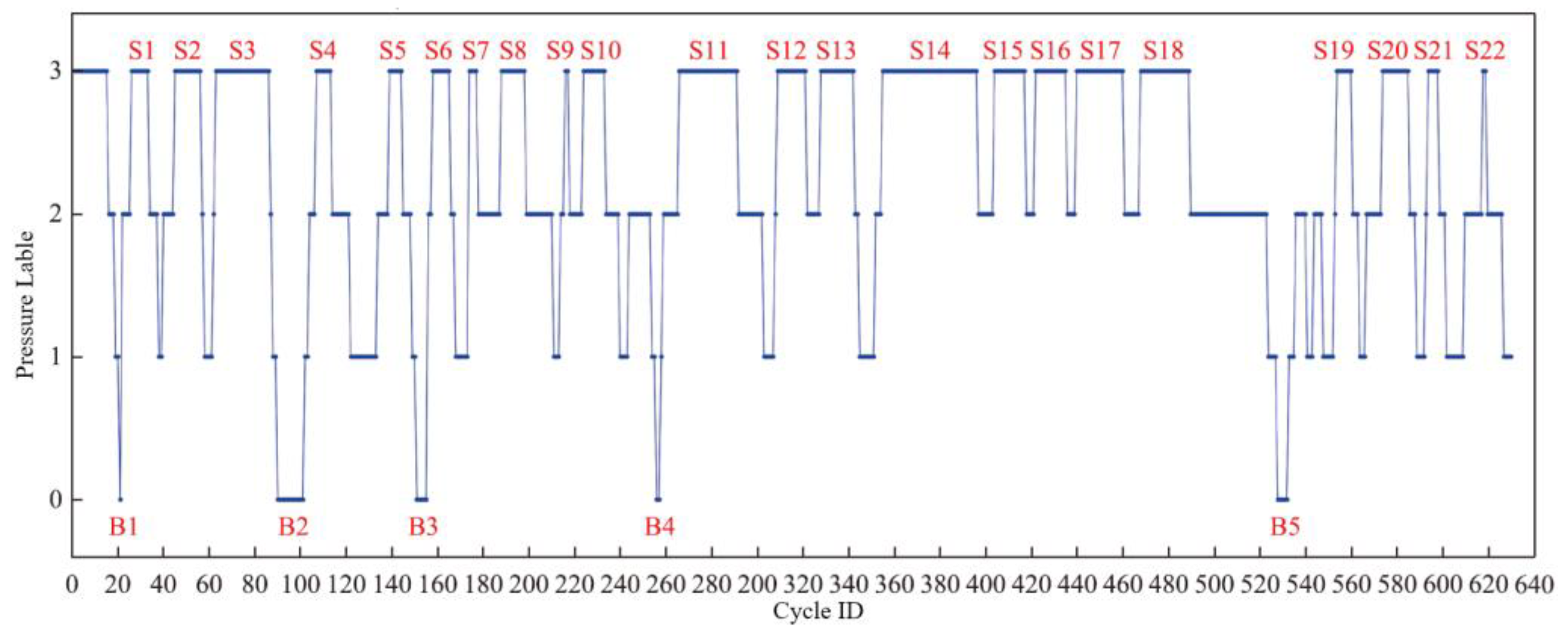
3.1. On-Site Data Acquisition and Preprocessing
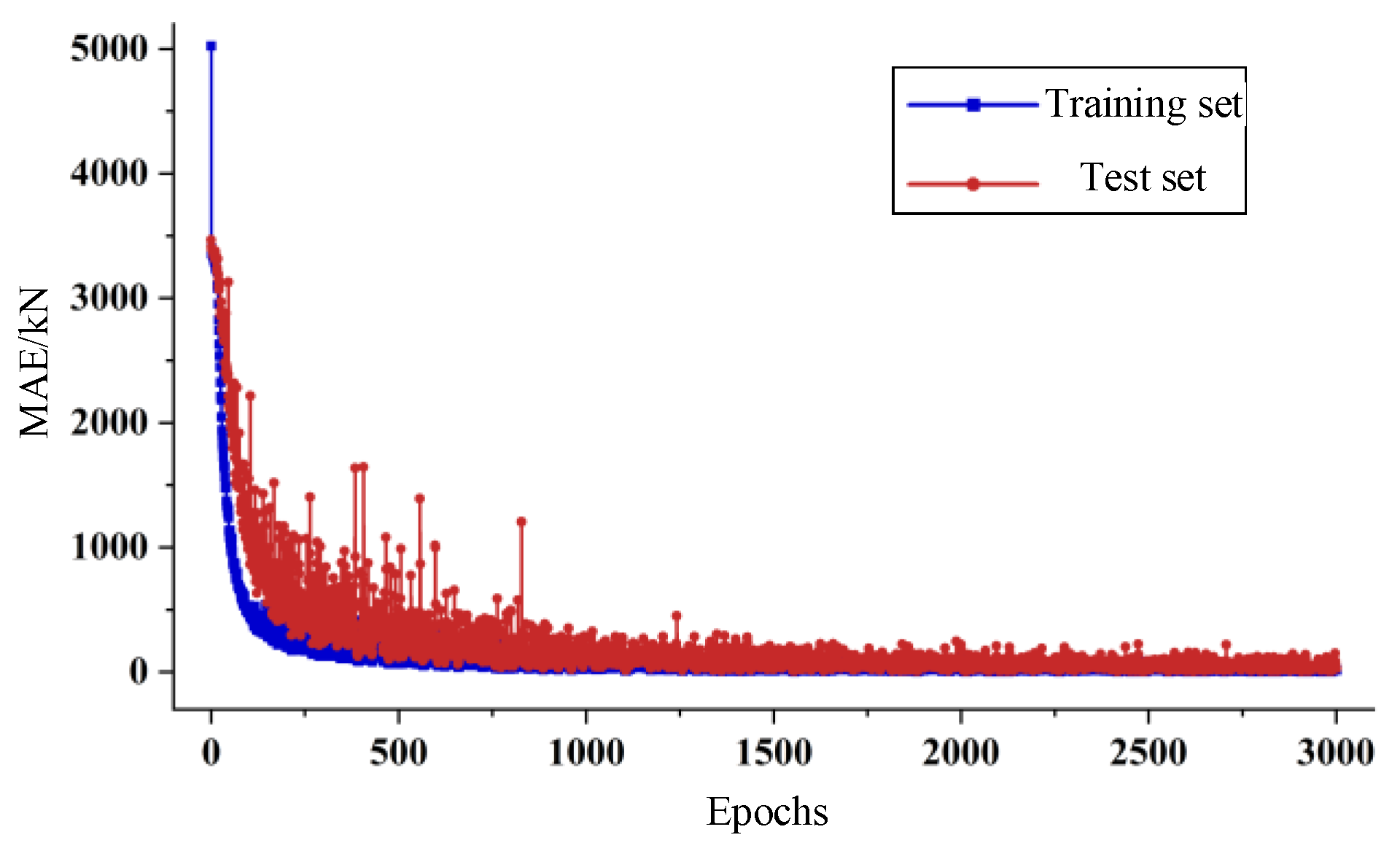
3.2. Training of Support Resistance Prediction Model
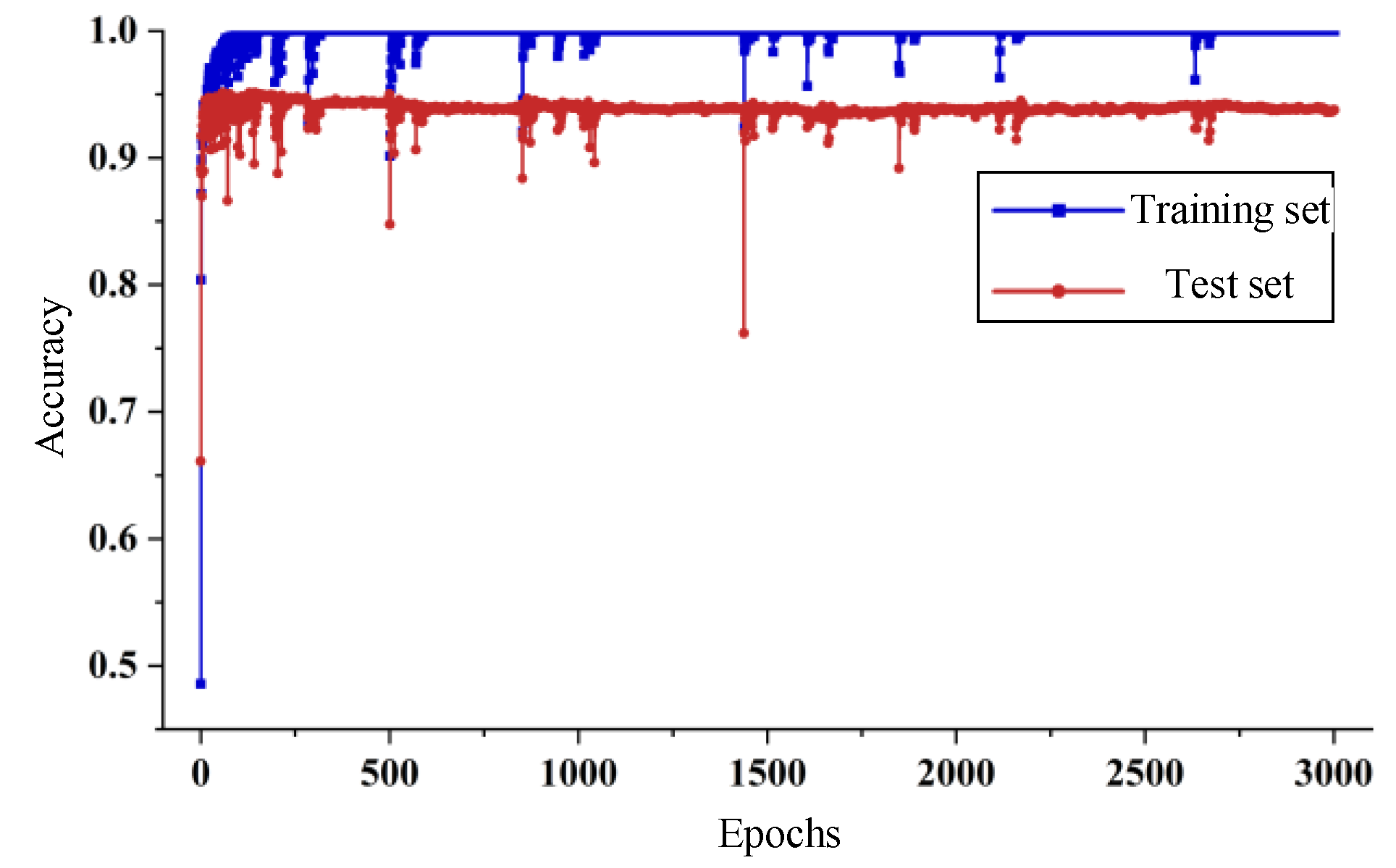
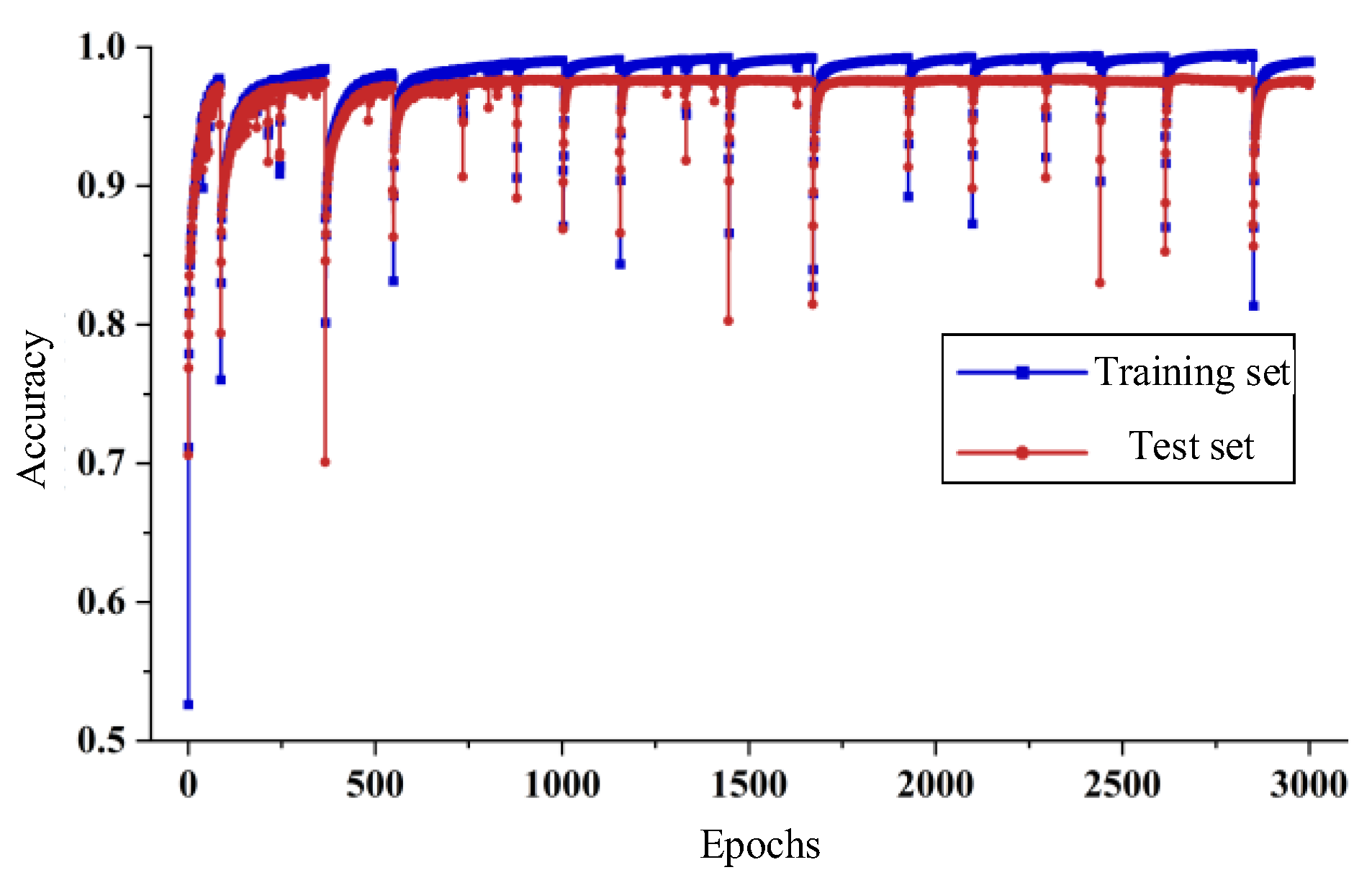
3.3. Training of Coordinate Unit Pressure Label Classification Model
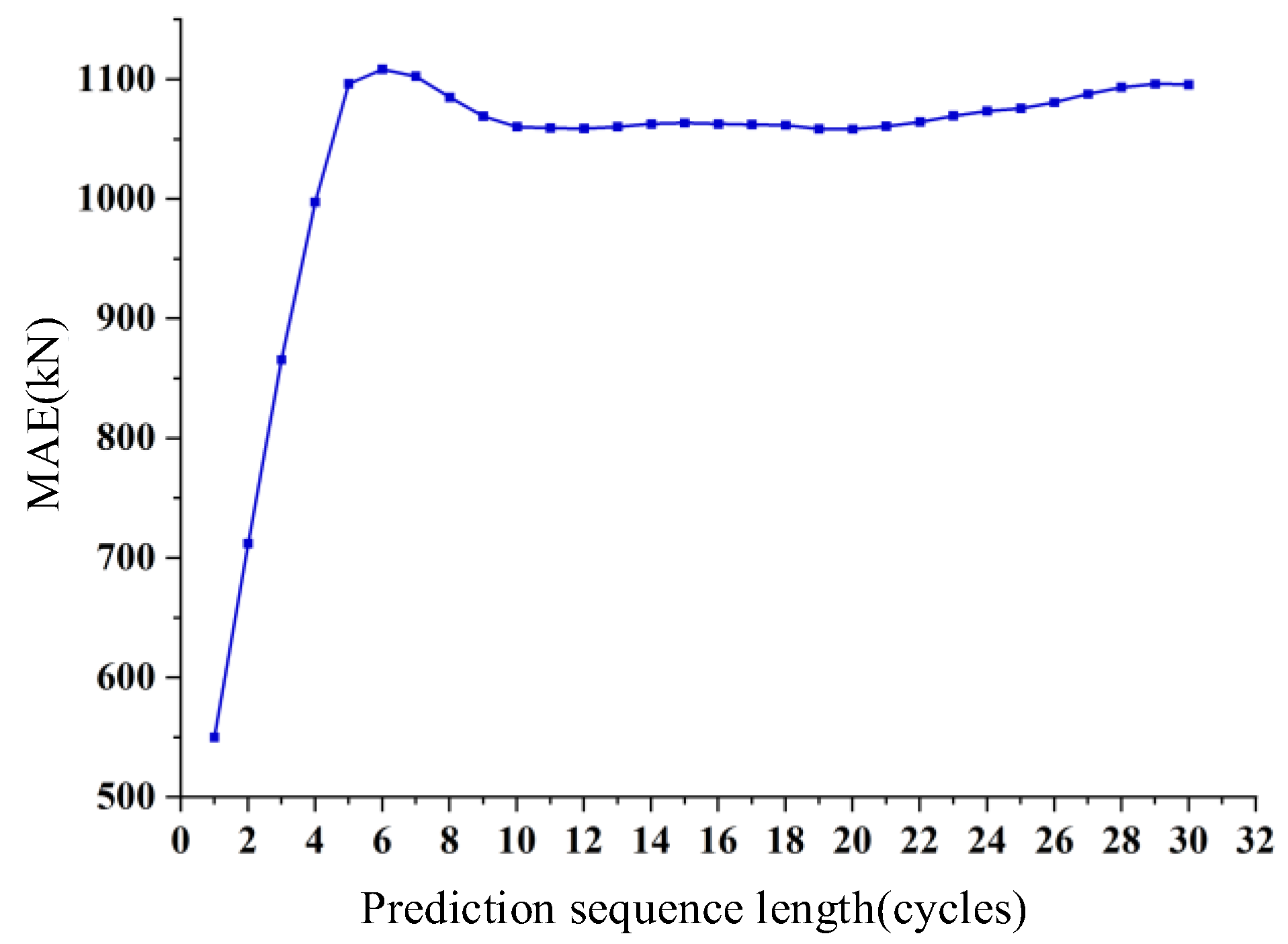
3.4. Training of the Predictive Model for Pressure Exertion Characteristic Parameters
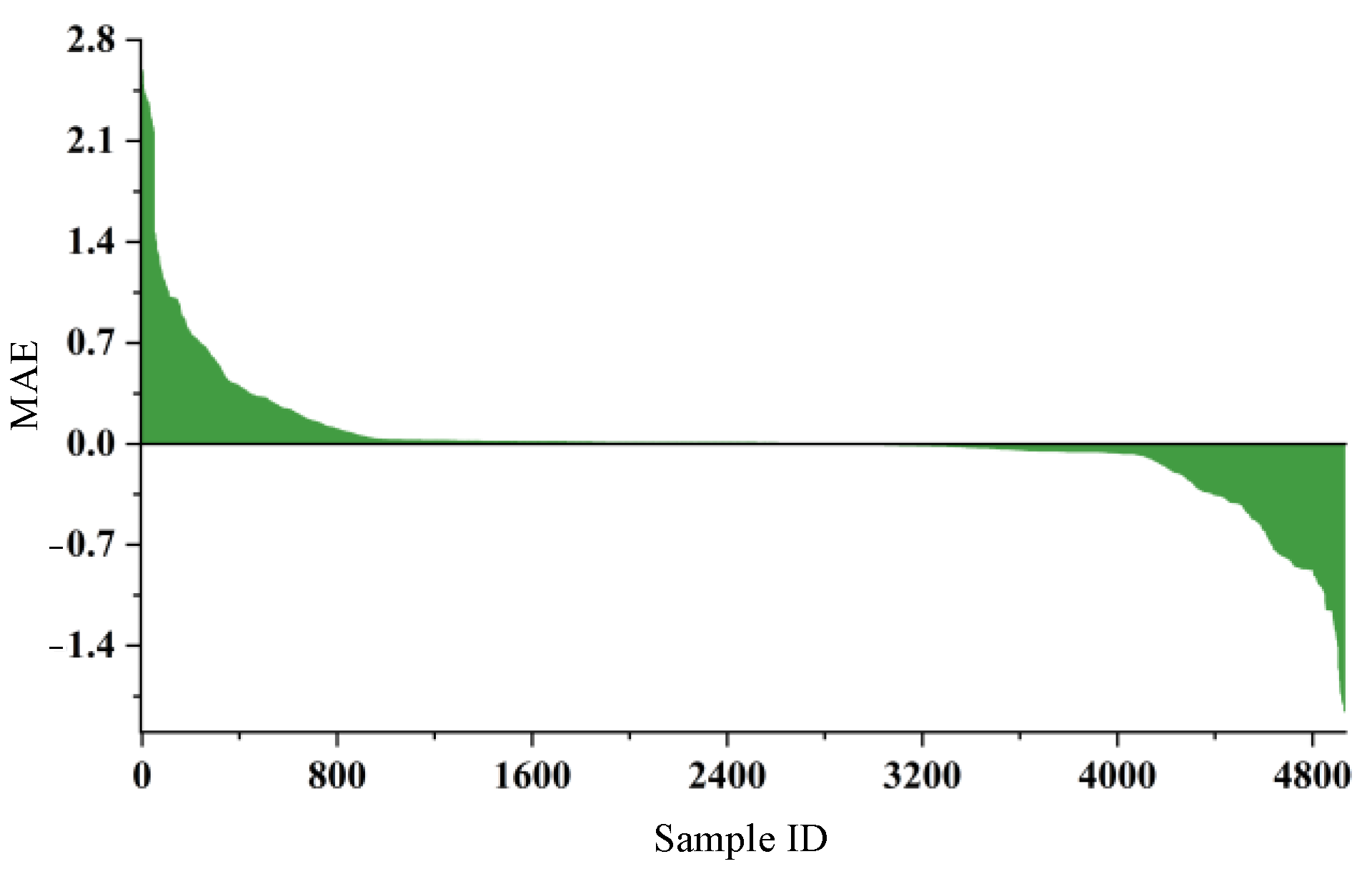
3.5. Pressure Exertion Prediction Based on Pre-Trained Models
- (1)
- Support resistance
- (2)
- Pressure label
- (3)
- count of pressure occurrences
- (4)
- Characteristic parameters of pressure exertion
4. Conclusions
- (1)
- A data-driven method for predicting pressure exertion in coal mine working faces has been proposed, which defines the content of such predictions. The prediction process is divided into three steps: the first step is to predict the support resistance data ahead of the working face; the second step is to classify the pressure labels of the coordinate units; and the third step is to predict the characteristic parameters of pressure exertion.
- (2)
- A method for solving the characteristics of pressure exertion based on historical data is proposed, and a three-step prediction model for pressure exertion is designed and discussed. In the first step, a deep spatiotemporal sequence model is selected for support resistance prediction. In the second step, an image segmentation-based classification model is chosen for pressure label classification. In the third step, a fusion model consisting of three LSTM networks is designed.
- (3)
- The model was trained using data from 10 working faces in the Datong mining area. The training set error for the first step was 1.83 kN, and the test set error was 4.65 kN. The training set accuracy for the second step was 99.38%, and the test set accuracy was 97.77%. For the third step, the dynamic pressure coefficient error was 0.17, the maximum resistance error during pressure exertion was 810.93 kN, the error in the number of cycles during pressure exertion was 9.96 cycles, and the accuracy for pressure exertion type classification was 92.35%.
- (4)
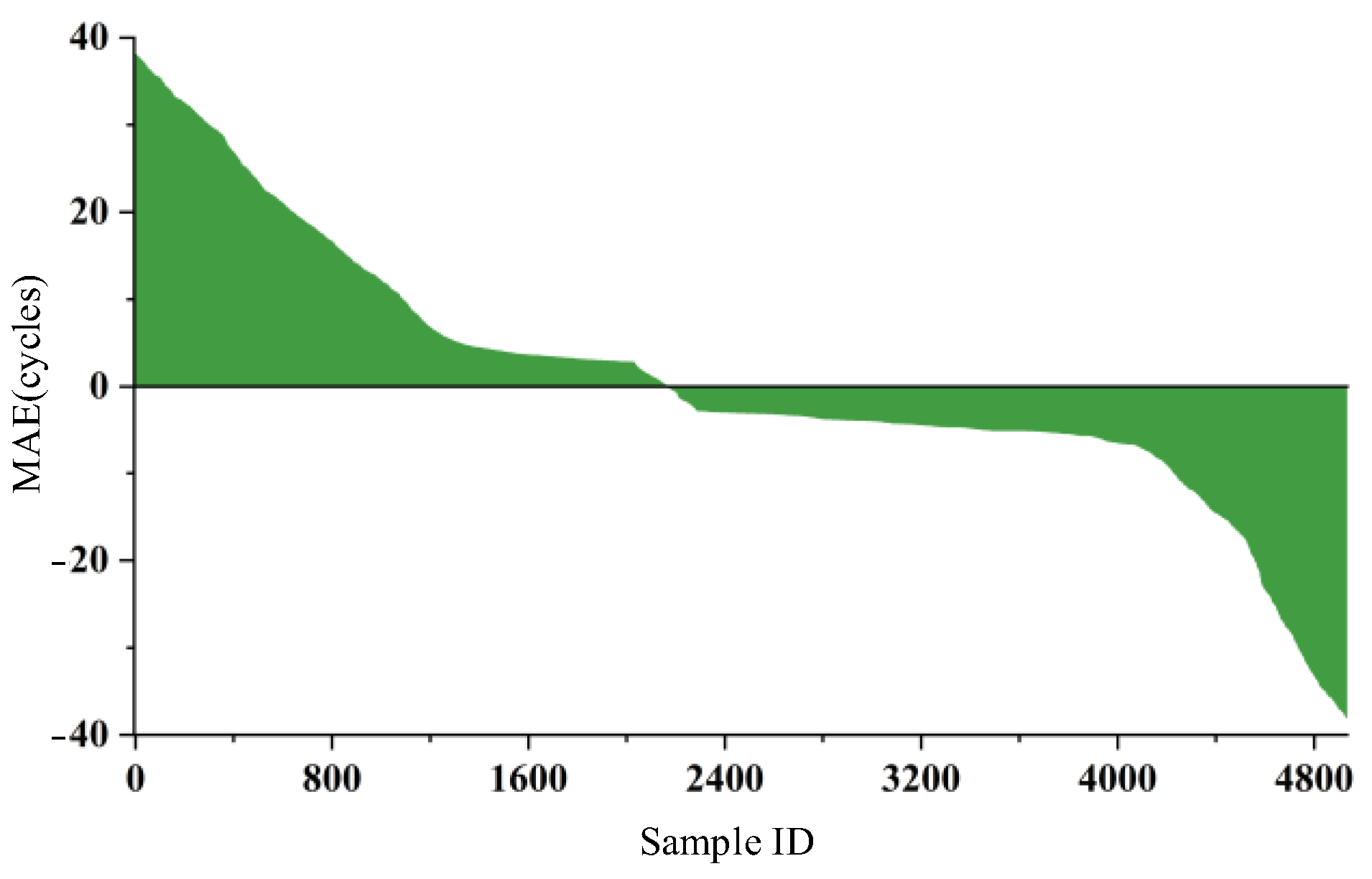
- To simulate the actual conditions of application scenarios, the input data for the second and third steps were set as the output data from the previous step, and the model was evaluated. The model’s mean absolute error for support resistance prediction was 1035.21 kN, and its classification accuracy for coordinate unit pressure labels was 82.90%, with a cycle pressure label accuracy of 90.93%. In the simulated scenario, there were 9922 actual instances of pressure exertion, and the model predicted 10336 instances, with 9046 of these predictions corresponding to actual instances of pressure exertion. An evaluation was conducted of the feature parameter predictions for 4946 instances of pressure exertion that included three complete pressure exertion phases. The mean absolute error for the dynamic pressure coefficient was 0.21, the maximum resistance during pressure exertion was 1218.31 kN, the number of cycles during pressure exertion was 11.03 cycles, and the classification accuracy for pressure exertion types was 91.75%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Shen, Y.; Song, S.; Liu, L.; Gu, L.; Wei, J. Change of coal energy status and green and low-carbon development under the “dual carbon” goal. J. China Coal Soc. 2023, 48, 2599–2612. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Q.; Tu, K.; Zeng, Y.F.; Liu, S.Q. Discussion on the main problems and countermeasures for building an upgrade version of main energy (coal) industry in China. J. China Coal Soc. 2019, 44, 1625–1636. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.; Xu, L.; Gao, Q.; Liu, N.; Wang, C.; Li, K. Effect of consumer subsidies on coal mine efficiency and its transmission mechanism. Energy Policy 2024, 196, 114412. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Z.; Jia, T. Analysis of Coal Mine Safety Accidents and Research on Safety Countermeasures in China from 2010 to 2021. Coal Technol. 2023, 42, 128–131. (In Chinese) [Google Scholar] [CrossRef]
- Fan, C.; Wang, Y.; Yang, L.; Xu, S.; Qiu, F. Statistics and Regularity Analysis of Coal Mine Safety Accidents from 2012 to 2021. Min. Res. Dev. 2023, 43, 182–188. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Su, M. Study on Law of Coal Mine Accidents in Shanxi Province from 2016 to 2022. Coal Technol. 2023, 42, 187–190. (In Chinese) [Google Scholar] [CrossRef]
- Cai, G.S.; An, L.Q.; Zhu, X.X.; An, J.L.; Mao, L.T. Study on Close Coal Seam Pressure Behavior Law of Zhong Xing Mine by Physical Model. Appl. Mech. Mater. 2012, 204, 1439–1444. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Ren, X.; Wu, X.; Zhou, C. Roof breaking characteristics and mining pressure appearance laws in close distance coal seams. Energy Explor. Exploit. 2023, 41, 728–744. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Zhang, J.; Yin, W.; Wang, Y.; Zhang, Q. Technical system and mining pressure law of full mining and local filling in a deep mine. Int. J. Oil Gas Coal Technol. 2023, 33, 369–387. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, Y.; Zhao, C. Distribution Law of Mine Ground Pressure via a Microseismic Sensor System. Minerals 2023, 13, 649. [Google Scholar] [CrossRef]
- Lan, T.; Liu, Y.; Yuan, Y.; Liu, H.; Liu, H.; Zhang, S.; Wang, S. Mine pressure behavior law of isolated island working face under extremely close goaf in shallow coal seam. Sci. Rep. 2023, 13, 20576. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, Y.; Xue, B.; Li, J.; Han, L.; Yu, H. Research on mine pressure law of isolated working face in close-distance thin coal seam under the influence of remaining coal pillar. Int. J. Oil Gas Coal Technol. 2024, 35, 299–320. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, Q.; Wang, Y. Evolution Laws of Water-Flowing Fracture Zone and Mine Pressure in Mining Shallow-Buried, Hard, and Extra-Thick Coal Seams. Appl. Sci. 2024, 14, 2915. [Google Scholar] [CrossRef]
- Jia, C.; Lai, X.; Cui, F.; Xu, H.; Zhang, S.; Li, Y.; Zong, C.; Luo, Z. Mining Pressure Distribution Law and Disaster Prevention of Isolated Island Working Face Under the Condition of Hard “Umbrella Arch”. Rock Mech. Rock Eng. 2024, 57, 8323–8341. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, L.; Xiong, H.; Chen, X.; Lu, A.; Zeng, Y.; Wang, B. Data-driven real-time prediction for attitude and position of super-large diameter shield using a hybrid deep learning approach. Undergr. Space 2024, 15, 275–297. [Google Scholar] [CrossRef]
- Jing, Y.; Bian, Y.; Hu, Z.; Wang, L.; Xie, X.Q.S. Deep Learning for Drug Design: An Artificial Intelligence Paradigm for Drug Discovery in the Big Data Era. AAPS J. 2018, 20, 58. [Google Scholar] [CrossRef]
- Guo, S.; Agarwal, M.; Cooper, C.; Tian, Q.; Gao, R.X.; Grace, W.G.; Guo, Y.B. Machine learning for metal additive manufacturing: Towards a physics-informed data-driven paradigm. J. Manuf. Syst. 2022, 62, 145–163. [Google Scholar] [CrossRef]
- Cai, S.; Fang, F.; Tang, X.; Zhu, J.; Wang, Y. A Hybrid Data-Driven and Data Assimilation Method for Spatiotemporal Forecasting: PM2.5 Forecasting in China. J. Adv. Model. Earth Syst. 2024, 16, e2023MS003789. [Google Scholar] [CrossRef]
- Dariane, A.B.; Behbahani, M.R.M. Maximum energy entropy: A novel signal preprocessing approach for data-driven monthly streamflow forecasting. Ecol. Inform. 2024, 79, 102452. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Gong, J.; Xuan, F.Z. Machine learning-based fatigue life prediction of metal materials: Perspectives of physics-informed and data-driven hybrid methods. Eng. Fract. Mech. 2023, 284, 109242. [Google Scholar] [CrossRef]
- Xiao, T.; Zhang, L.M. Data-driven landslide forecasting: Methods, data completeness, and real-time warning. Eng. Geol. 2023, 317, 107068. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Liu, C.Y.; Liu, J.R.; Yang, P.J.; Lu, S.; Wei, J.K. Study on support pressure continuity classification and mine pressure characteristics by unifying spatiotemporal characteristics modelling. J. Min. Saf. Eng. 2021, 38, 1–11. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, Y.X.; Yang, Z.L.; Ma, B.J.; Song, H.H.; Yang, D.H. Deep learning prediction and model generalization of ground pressure for deep longwall face with large mining height. J. China Coal Soc. 2020, 45, 54–65. (In Chinese) [Google Scholar] [CrossRef]
- Yang, Z. Separation and Extraction of Measured Time Series Data and Advanced Prediction of Mineral Pressure. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2022. (In Chinese). [Google Scholar]
- Liu, Y. Mineral Pressure Manifestation Prediction Method Based on Machine Learning. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2021. (In Chinese). [Google Scholar]
- Miao, Y. Research on Prediction of Working Face Periodic Pressure Based on Recurrent Neural Network. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2021. (In Chinese). [Google Scholar]
- Li, Z. Research on Prediction Method of Mining Pressure in Coal Face Based on LSTM. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2020. (In Chinese). [Google Scholar]
- Gao, X.; Hu, Y.; Liu, S.; Yin, J.; Fan, K.; Yi, L. An AGCRN Algorithm for Pressure Prediction in an Ultra-Long Mining Face in a Medium-Thick Coal Seam in the Northern Shaanxi Area, China. Appl. Sci. 2023, 13, 11369. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv 2014. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, C.; Liu, J.; Yang, P.; Wu, F.; Liu, S.; Liu, H.; Yu, X. Intelligent prediction for support resistance in working faces of coal mine: A research based on deep spatiotemporal sequence models. Expert Syst. Appl. 2024, 238, 122020. [Google Scholar] [CrossRef]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent Neural Networks for Predictive Learning using Spatiotemporal LSTMs. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Hariharan, B.; Arbeláez, P.; Girshick, R.; Malik, J. Simultaneous Detection and Segmentation. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Volume 8695, pp. 297–312. [Google Scholar] [CrossRef]
- Gupta, S.; Girshick, R.; Arbeláez, P.; Malik, J. Learning Rich Features from RGB-D Images for Object Detection and Segmentation. In Proceedings of the 13th European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; Volume 8695, pp. 345–360. [Google Scholar] [CrossRef]
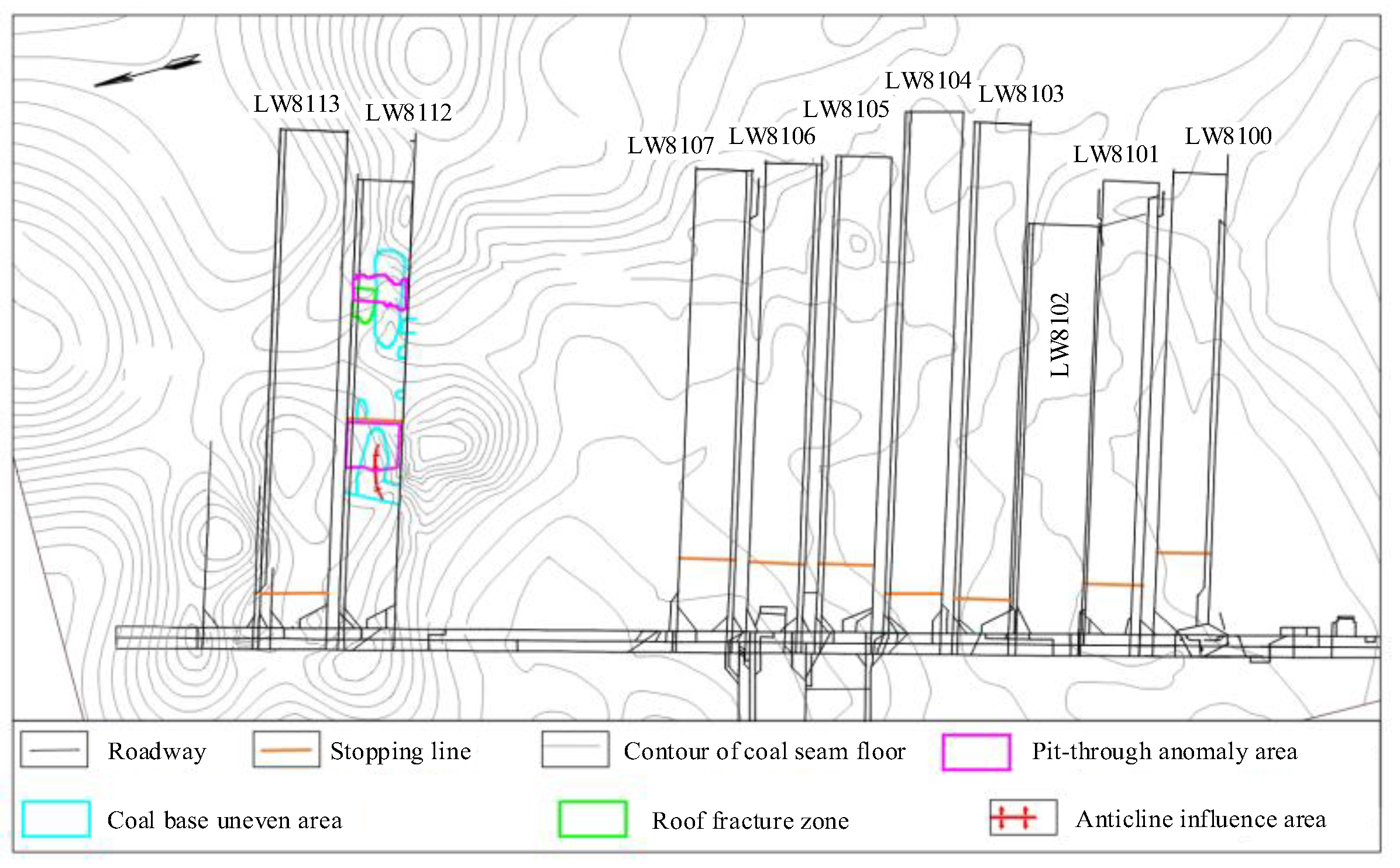

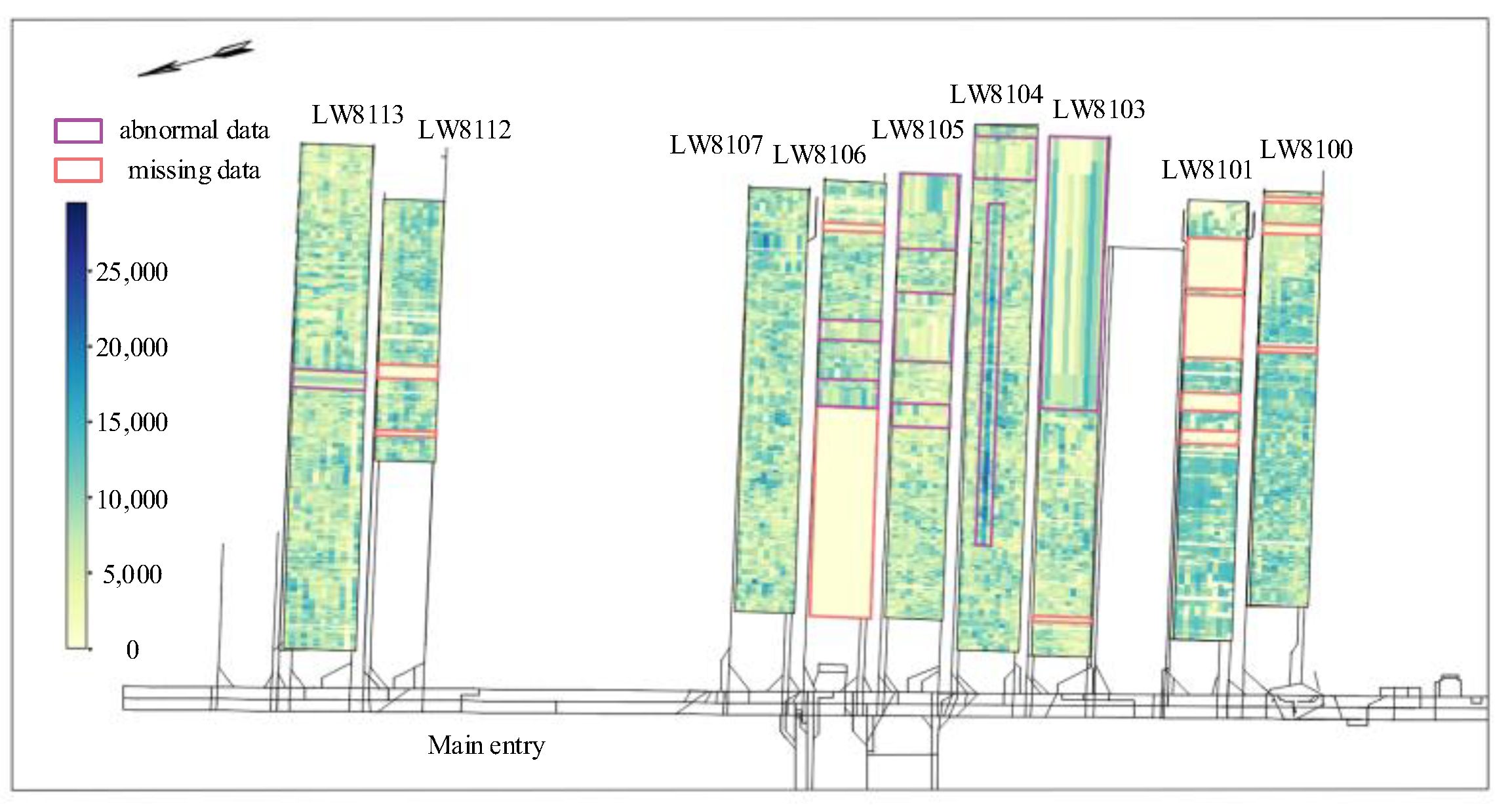

| Workface Name | Extraction Sequence | Start Time | End Time | Strike Length/m | Mining Situation of Adjacent Workface in the Same Level |
|---|---|---|---|---|---|
| LW8100 | ② | 2010.10 | 2011.07 | 1413.26 | one side gob |
| LW8101 | ① | 2009.10 | 2010.10 | 1500.93 | first mining face |
| LW8102 | ⑩ | 2020.03 | 2021.08 | 1516.55 | bilateral coal |
| LW8103 | ⑦ | 2014.02 | 2015.03 | 1773.49 | one side gob |
| LW8104 | ⑥ | 2013.07 | 2014.05 | 1793.30 | one side gob |
| LW8105 | ⑤ | 2012.11 | 2013.07 | 1521.77 | one side gob |
| LW8106 | ③ | 2011.07 | 2012.03 | 1448.79 | bilateral coal |
| LW8107 | ④ | 2012.03 | 2012.11 | 1449.52 | one side gob |
| LW8112 | ⑨ | 2017.03 | 2018.05 | 891.86 | one side gob |
| LW8113 | ⑧ | 2015.03 | 2016.06 | 1724.93 | bilateral coal |
| Workface ID | Pressure Exertion Location (Cycle ID) | Number of Pressure Exertions |
|---|---|---|
| 8100 | 300, 319, 358, 409, 473 | 5 |
| 8103 | 1902, 1962 | 2 |
| 8104 | 224, 245, 259, 329, 341, 406, 472, 489, 521, 597, 648, 687, 695, 763, 801, 810, 930, 952, 1283, 1361, 1402, 1415, 1557, 1588, 1608, 1700, 1742, 1761, 1797, 1823, 1972, 2043, 2082, 2119 | 34 |
| 8105 | 899 | 1 |
| 8106 | 234, 292, 340, 434, 471, 515, 539 | 7 |
| 8107 | 1426, 1459, 1537, 1600, 1621, 1625, 1662, 1737 | 8 |
| 8113 | 43, 90, 124, 171, 188, 194, 283, 297, 371, 412, 451, 512, 549, 588, 653, 673, 686, 746, 854, 989, 1035, 1054, 1097, 1107, 1115, 1128, 1166, 1232, 1497, 1538, 1608, 1636, 1642, 1661, 1705 | 35 |
| Input | Dynamic Pressure Coefficient | Error of Maximum Resistance | Error of Duration | Accuracy for Pressure Exertion Type | ||||
|---|---|---|---|---|---|---|---|---|
| Epochs | MAE | Epochs | MAE/kN | Epochs | MAE/Cycles | Epochs | Acc/% | |
| “Third stage” | 513 | 0.23 | 221 | 1137.51 | 144 | 10.45 | 204 | 76.14 |
| “Second stage” +“Third stage” | 12 | 0.24 | 34 | 977.93 | 963 | 11.58 | 813 | 78.32 |
| “First stage” +“Second stage” +“Third stage” | 927 | 0.17 | 48 | 810.93 | 32 | 9.96 | 73 | 92.35 |
| “Second stage” | 324 | 0.23 | 37 | 947.05 | 61 | 23.92 | 608 | 58.65 |
| Predicted Labels | 0 | 1 | 2 | 3 | Recall | Precision | F1-Score | |
|---|---|---|---|---|---|---|---|---|
| True Labels | ||||||||
| 0 | 749,300 | 44,293 | 3188 | 70 | 0.94 | 0.84 | 0.89 | |
| 1 | 88,219 | 652,313 | 33,005 | 701 | 0.84 | 0.69 | 0.76 | |
| 2 | 42,606 | 125,541 | 49,4781 | 1008 | 0.75 | 0.87 | 0.80 | |
| 3 | 6895 | 121,124 | 34,926 | 535,670 | 0.77 | 1.00 | 0.87 | |
| Predicted Labels | 0 | 1 | 2 | 3 | Recall | Precision | F1-Score | |
|---|---|---|---|---|---|---|---|---|
| True Labels | ||||||||
| 0 | 4048 | 441 | 92 | 0 | 0.88 | 0.63 | 0.73 | |
| 1 | 595 | 5620 | 670 | 3 | 0.82 | 0.41 | 0.54 | |
| 2 | 1733 | 6803 | 50,462 | 283 | 0.85 | 0.82 | 0.83 | |
| 3 | 62 | 985 | 10,515 | 162,158 | 0.93 | 1.00 | 0.96 | |
| Predicted Labels | 0 | 1 | 2 | 3 | Recall | Precision | F1-Score | |
|---|---|---|---|---|---|---|---|---|
| True Labels | ||||||||
| 0 | 417 | 5 | 0 | 0 | 0.99 | 0.72 | 0.84 | |
| 1 | 151 | 4927 | 522 | 52 | 0.87 | 0.97 | 0.92 | |
| 2 | 8 | 169 | 1614 | 164 | 0.83 | 0.74 | 0.78 | |
| 3 | 0 | 4 | 37 | 79 | 0.66 | 0.27 | 0.38 | |
| Predicted Type | Small Pressure | Large Pressure | Strong Pressure | Recall | Precision | F1-Score | |
|---|---|---|---|---|---|---|---|
| True Type | |||||||
| Small Pressure | 2509 | 112 | 27 | 0.95 | 0.93 | 0.94 | |
| Large Pressure | 146 | 938 | 54 | 0.82 | 0.88 | 0.85 | |
| Strong Pressure | 53 | 16 | 1091 | 0.94 | 0.93 | 0.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, C.; Zhang, N.; Liu, H.; Yu, X.; Liu, S.; Hu, J. Research on Pressure Exertion Prediction in Coal Mine Working Faces Based on Data-Driven Approaches. Appl. Sci. 2025, 15, 4192. https://doi.org/10.3390/app15084192
Chen Y, Liu C, Zhang N, Liu H, Yu X, Liu S, Hu J. Research on Pressure Exertion Prediction in Coal Mine Working Faces Based on Data-Driven Approaches. Applied Sciences. 2025; 15(8):4192. https://doi.org/10.3390/app15084192
Chicago/Turabian StyleChen, Yiqi, Changyou Liu, Ningbo Zhang, Huaidong Liu, Xin Yu, Shibao Liu, and Jianning Hu. 2025. "Research on Pressure Exertion Prediction in Coal Mine Working Faces Based on Data-Driven Approaches" Applied Sciences 15, no. 8: 4192. https://doi.org/10.3390/app15084192
APA StyleChen, Y., Liu, C., Zhang, N., Liu, H., Yu, X., Liu, S., & Hu, J. (2025). Research on Pressure Exertion Prediction in Coal Mine Working Faces Based on Data-Driven Approaches. Applied Sciences, 15(8), 4192. https://doi.org/10.3390/app15084192







