Mathematical Study of a Product-Gripping Mechanism for Industrial Transportation

Abstract

In this paper, a study that describes the mathematical analysis of a mechanical gripping system with a lifting-tong-type mechanism is presented. The study involves the geometrical analysis of the investigated mechanism. What distinguishes this work from other studies in the specialized literature is the way the analysis of the mechanism under study is carried out. Specifically, the working methodology proposes the analysis of the entire mechanism and not its decomposition into structural groups, thus obtaining complex mathematical equations. By using values, the mathematically obtained results were able to describe the movement of the mechanism’s components, as well as the variations in their velocities. To verify the correctness of the results, a simulation was carried out using the Linkage simulation software.

1. Introduction

Different material handling systems are used to carry out the transport process in industrial activities, such as individual, bulk, palletized, or containerized items. These systems have been adapted considering the dimensional characteristics of the material/product (i.e., the size, shape, density, and surface condition of the product being transported), as well as the operator’s requirements and local resources [1,2,3,4,5,6,7].

The systems for handling the transportation of products involve carrying out three main operations: loading, moving, and unloading the product [8]. The equipment used to carry out these operations, in addition to the source generating the movement and the load-bearing elements, also has systems for clamping the material so that it can be handled as easily as possible.

A number of different devices are used in order to safely grip and handle the product, such as textile lifting slings; lifting-and-lashing rings; lifting rings; lifting clamps; lifting beams; chain grabs; overhead crane grabs; general hoists and electric hoists; electric and manual winches; hydraulic lifting platforms; lifting magnets; general clamps and clamps for curbs and pipelines; vacuum grabs; forklift grabs; gripping systems for forklifts; gripping systems for slewing cranes; and gripping systems for hydraulic cranes [9,10,11].

These product clamping systems are based on a series of mechanisms (mechanical components) and hydraulic or electrical components, which makes it possible to carry out simple or complex movements, i.e., clamping or unclamping [12,13,14,15,16,17,18].

Referring only to the mechanical systems used for explanations from a mathematical point of view and to optimize the movements performed by these elements, different methods of analysis have been used, starting from mathematical, vectorial, or computerized analysis (using a series of programs to simulate the movement of the elements and to identify the stresses occurring in the active elements of the mechanism) [13,15,16,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46].

In this article, we will study, from a mathematical point of view, the movement of a simple mechanism for gripping materials, which is a mechanism used mainly in transportation installations. Crane tongs (Figure 1) are used to lift different types of loads. These types of mechanisms are characterized by the fact that the clamping force of the product is minimal (which is why it cannot generate deformations on the product’s surface), which is realized by means of gravitational forces, the clamping force directly proportional to the weight of the supported product [38,47]. From a constructional point of view, these devices are designed to hold the product via clamping or supporting operations [48,49].

Due to the simplicity of their construction, the mechanical crane tong lifting systems found in transport installations have not been studied, which is why this article focuses on such mechanisms. The specialized literature is rich in studies presenting theoretical analyses and simulations aimed at identifying the deformations that occur in different clamping systems encountered in different fields [21,25,26,27,30,35,41,42,43,51].

Standard analyses of a mechanism involve decomposing it into small structural groups (of at least two elements) and identifying the mathematical relationships in them [24,32,33,34,35,36,39,44,45,46]. In this article, we did not use this method. The whole mechanism, which contains three elements, was taken into consideration, and its motion was studied.

The aim of the article is to present a mathematical analysis of the behavior of the mechanical elements that make up such gripping and transport systems used in various industrial fields (handling of railway rails, blocks of material, sheet metal rolls, pipes, battened products, boxes, etc.) and beyond.

In this article, we propose determining, from a geometric point of view, the movements exerted by the main kinematic couplings of the mechanism under study. For this, the classical analysis method (where the mechanism is structured into simple components) was not adopted; instead, the entire dimensional structure (all dimensions of the elements that make up the mechanism) was considered. This new type of approach represents a major difference from the studies carried out so far in this field. As a result of this study, we aim to identify new calculation relations corresponding to the main elements of the mechanism (position coordinates). In addition to these new calculation relations, it was also possible to obtain new calculation formulas corresponding to the parameters of linear velocity and acceleration relative to the components studied.

2. Materials and Methods

In this study, a crane tong lifting system consisting of binary elements clamped together by means of coupling was investigated (Figure 1). This crane tong lifting system is found in the literature in various forms and is used for clamping and transporting various types of materials.

The working steps used in the study of the gripping and lifting mechanism are as follows:

-

Identify the mathematical calculation relationships required to determine the value of various components of the mechanism. Only their final forms are presented in this paper.

-

Realization of the mechanism operation by means of a simulation program. For this purpose, the use of the Linkage program (free program) was chosen.

-

A comparison was made between the values obtained using the two work methods: mathematical and simulation.

The following programs were used to study the motion of this mechanism:

-

Mathcad v.15 (PTC Mathcad) [52] was used to perform mathematical calculations using the computational relations corresponding to the coordinates of the analyzed points.

-

Linkage v. 3.11.3 (developed by David M. Rector) [53] was used to simulate the movement of the studied mechanism and to verify the correctness of the results obtained from the mathematical calculation.

Figure 2 shows the schematic of the clamping and lifting mechanism. It should be noted that this representation (Figure 2) does not correspond to reality (the mode of operation and use is that of Figure 1). The mechanism is rotated 90° in order to occupy less space in this article.

The geometrical components of the mechanism under study are as follows:

-

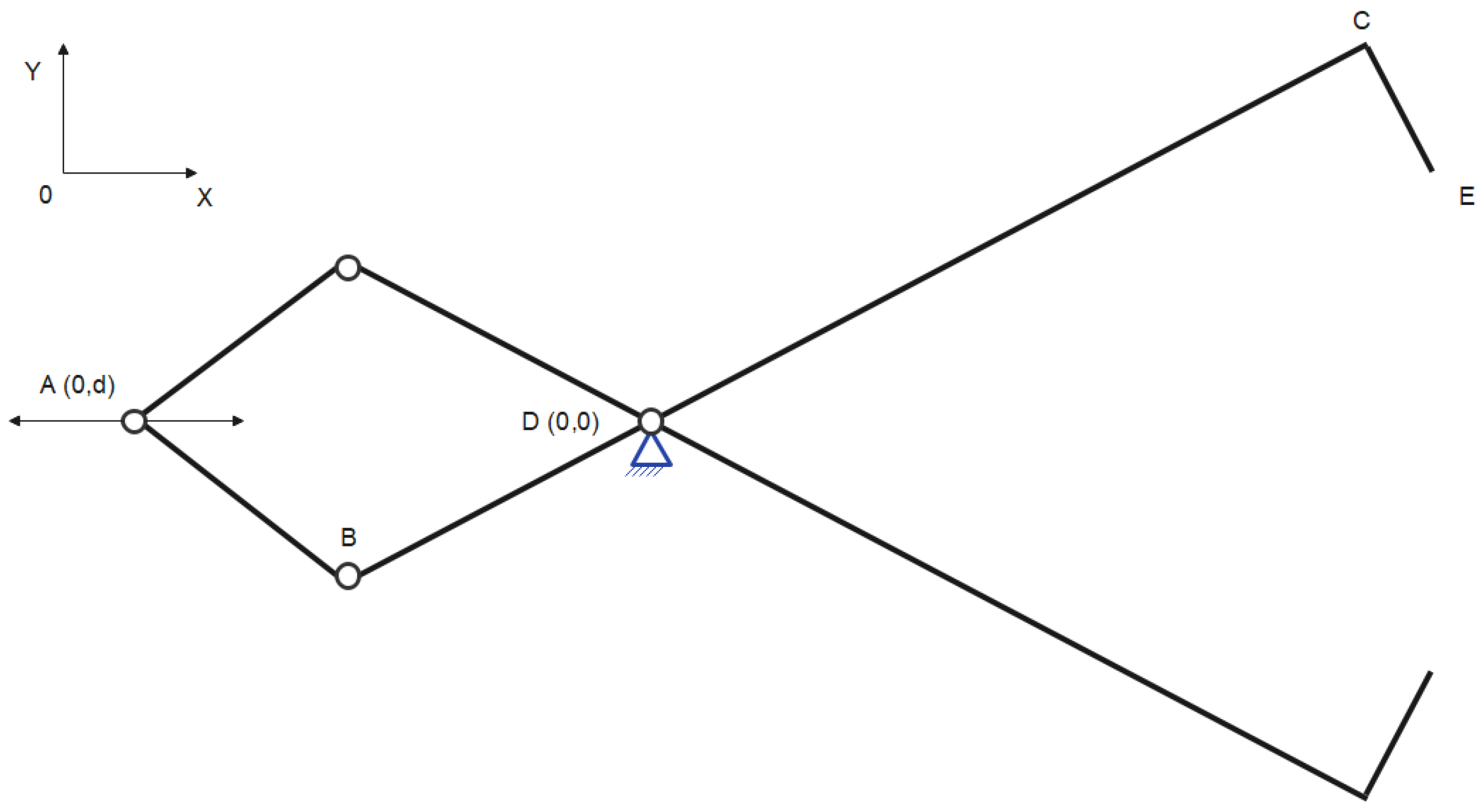
Coupling (Figure 2):

• The fixed position of coupling A with coordinates (0, d), where the coordinate is 0 on the OX axis, and for the OY axis, it is d (distance from the origin of the OY axis to coupling A).
• Coupling B—mechanism articulation.
• Coupling D—fixed and positioned at the origin of the coordinate system.
• Coupling C—rigid, to which the CE element is connected.
• Coupling E—the end of the CE element, representing the zone of contact between the lifting mechanism and the moved product.

-

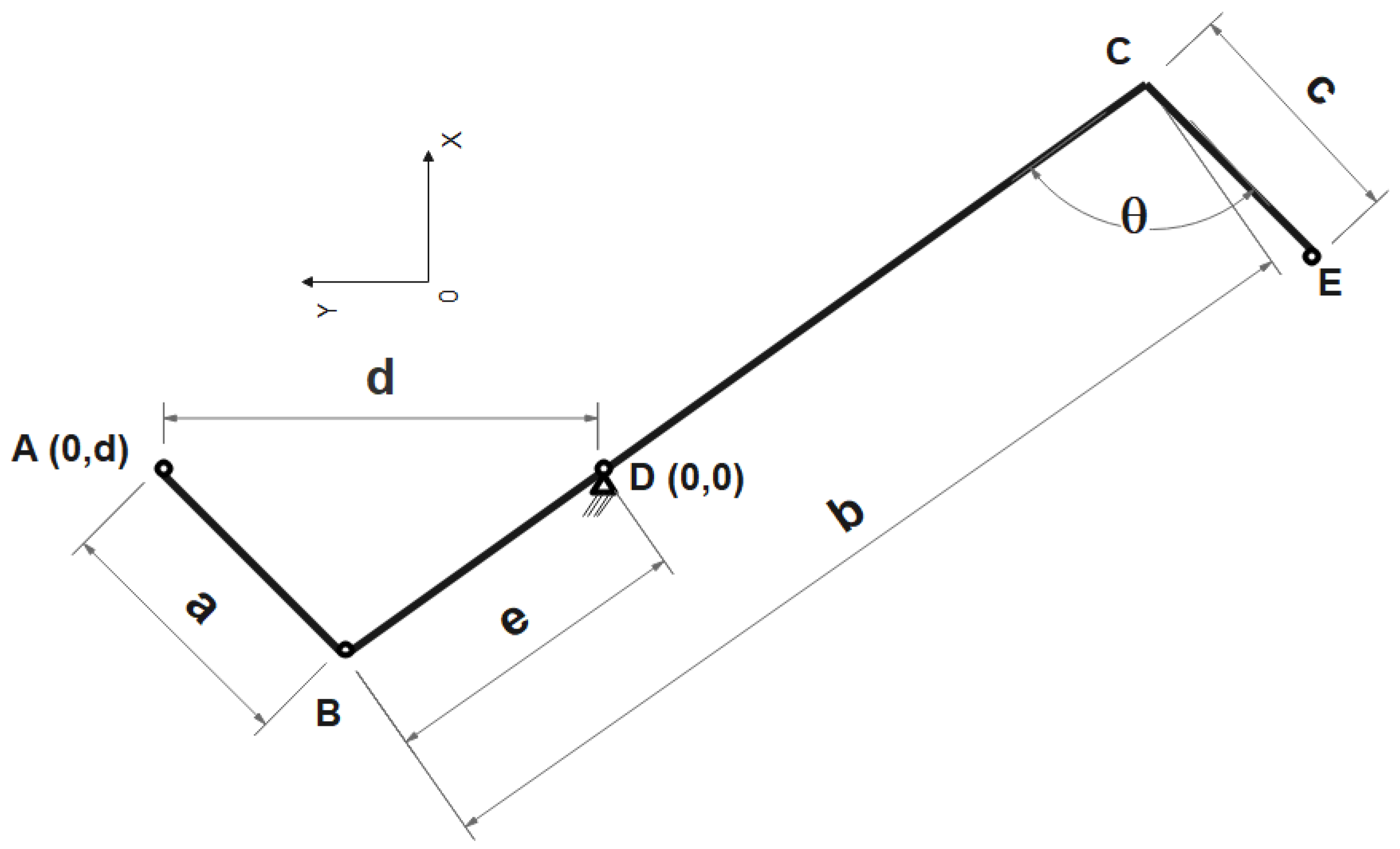
Binary elements (Figure 3):

• Element AB, for which its dimensions are a.
• Element BC, for which its dimensions are b.
• Element CE, for which its dimensions are c.
• Element BD, for which its dimensions are e.

-

Angle θ is the angle generated by elements BC and CE (Figure 3). The value of the angle is given by the device and can be modified according to the type and nature of the material used. The CE element is rigidly attached to the BC element.

Because the analyzed mechanism is composed of two symmetric structural groups, it was chosen to analyze the mechanism presented in Figure 3. As in the case of Figure 2, the mechanism shown in Figure 3 is flipped (rotated 90°) to occupy less space within the article.

The geometrical analysis of the mechanism under study is based on the following premises:

-

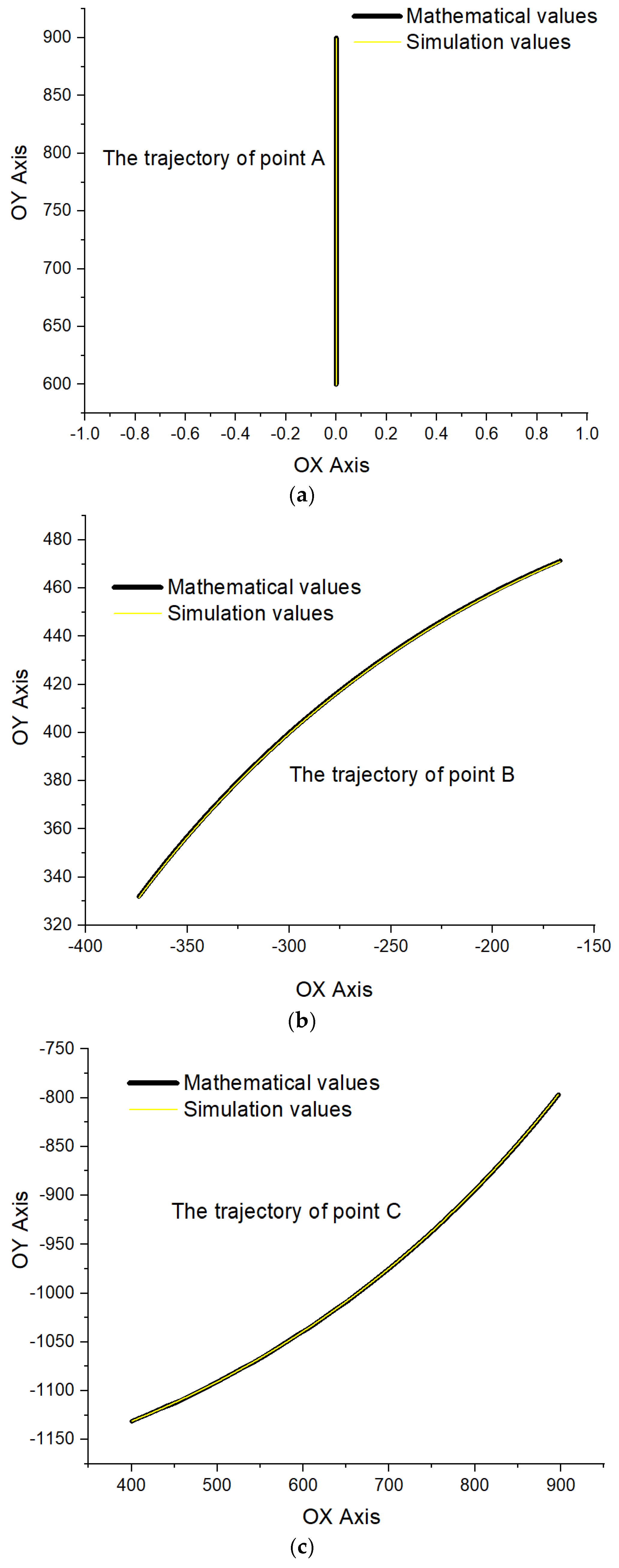
The mechanism is analyzed in relation to a coordinate system with an origin corresponding to point D.

-

Points A and D are on the same axis OY.

-

The distance between points A and D varies. The movement of point A allows the closing or opening of the gripping claws (EC element) by decreasing or increasing the distance between point E and the vertical OY axis, thus allowing the operation of gripping or detaching the load.

The calculation relations obtained for determining the movement executed by the various components of the mechanism are given below:

-

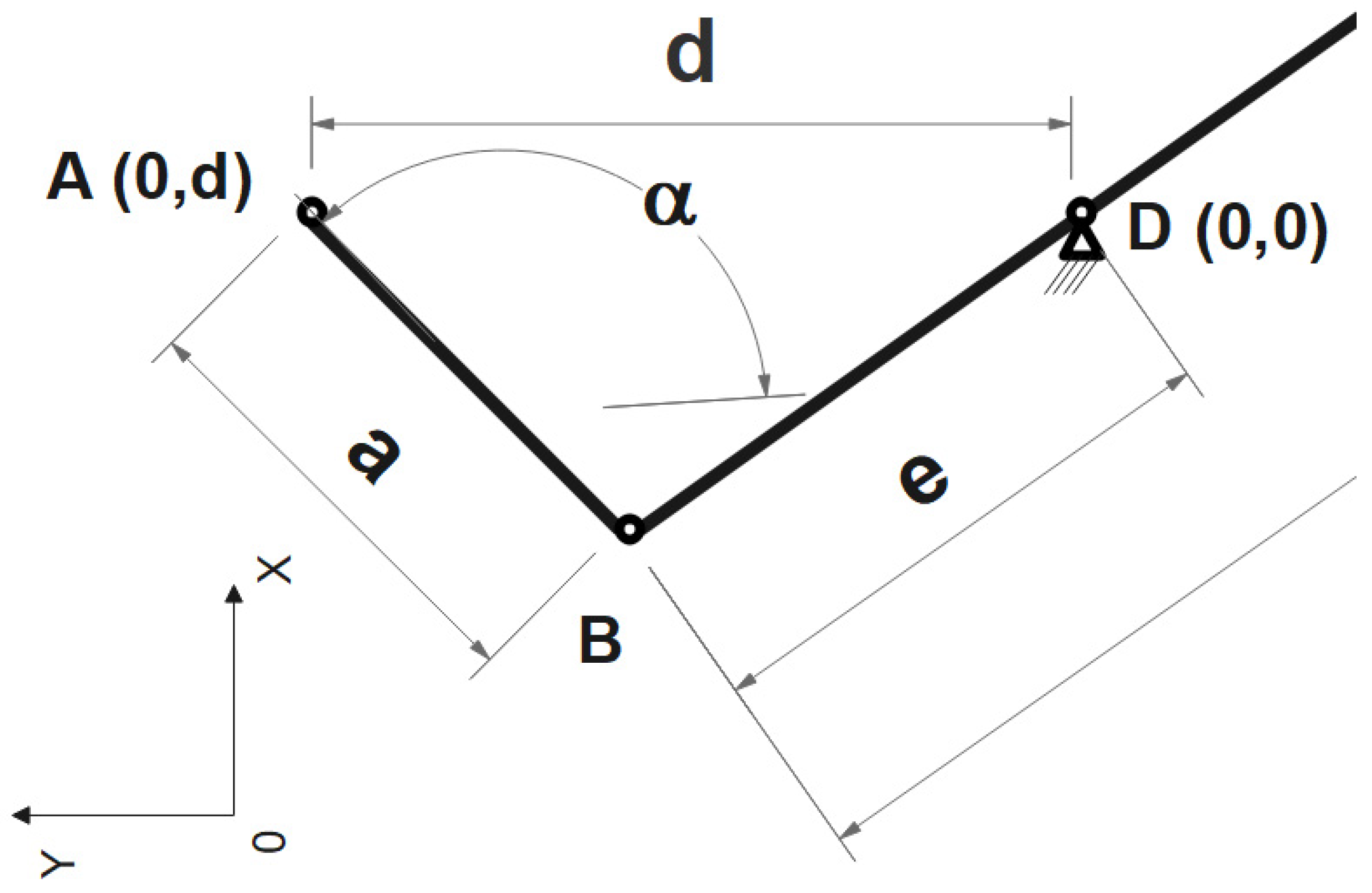
As a result of the movement of point A, several elements of the mechanism change their position. Also, the angles that these form in relation to the OX axis will vary in value. Thus, the angle described by element AB in relation to the OX axis is given via the following calculation relation (Figure 4):

$$\alpha =180+arctan\left({\displaystyle \frac{a^2{-e^2+d}^2}{\sqrt{a+d+e}·\sqrt{a+d-e}·\sqrt{a-d+e}·\sqrt{-a+d+e}}}\right),$$

(1)

-

The coordinates of point B are given in Equations (2) and (3):

$$x_B={\displaystyle \frac{-\sqrt{a+d+e}·\sqrt{a+d-e}·\sqrt{a-d+e}·\sqrt{-a+d+e}}{2d}},$$

(2)

$$y_B={\displaystyle \frac{-a^2+d^2+e^2}{2d}},$$

(3)

-

Because element BC is rigid but the fixed coupling at point D is attached to it, the coordinates of coupling C constantly change (with the movement of point A). The coordinates of coupling C can be determined using Equations (4) and (5):

$$x_C={\displaystyle \frac{-b ·u_1}{e}}-{\displaystyle \frac{\sqrt{a+d+e}·\sqrt{a+d-e}·\sqrt{a-d+e}·\sqrt{-a+d+e}}{2d}},$$

(4)

$$y_C={\displaystyle \frac{d}{2}}-{\displaystyle \frac{a^2}{2d}}+{\displaystyle \frac{e^2}{2d}}-{\displaystyle \frac{b·v_1}{e}},$$

(5)

where elements u₁ and v₁ can be determined by means of calculating Equations (6) and (7):

$$u_1={\displaystyle \frac{-\sqrt{a+d+e}·\sqrt{a+d-e}·\sqrt{a-d+e}·\sqrt{-a+d+e}}{2d}}=x_B,$$

(6)

$$v_1={\displaystyle \frac{-a^2+d^2+e^2}{2d}}=y_B,$$

(7)

By analyzing the computational relations corresponding to coupling C and coupling B, relations (3) and (4) give equations of the following form:

$$x_C={\displaystyle \frac{-b ·u_1}{e}}+x_B=x_B\left(1-{\displaystyle \frac{b }{e}}\right),$$

(8)

$$y_C=y_B-{\displaystyle \frac{b·v_1}{e}}=y_B\left(1-{\displaystyle \frac{b}{e}}\right),$$

(9)

-

The coordinates of point E are given by the following equations:

$$x_E=u_2-{\displaystyle \frac{b·u_2}{e}}-{\displaystyle \frac{c·\left(2·d^2-w_1·sin\theta \right)}{2·d·e}}+{\displaystyle \frac{c·u_2·cos\theta }{e}},$$

(10)

$$y_E=v_2-{\displaystyle \frac{b·v_2}{e}}+{\displaystyle \frac{c·u_1·sin\theta }{e}}+{\displaystyle \frac{c·v_2·cos\theta }{e}},$$

(11)

where

$$u_2={\displaystyle \frac{-w_2}{2d}},$$

(12)

$$v_2={\displaystyle \frac{w_1}{2d}},$$

(13)

and

$$w_2=\sqrt{a+d+e}·\sqrt{a+d-e}·\sqrt{a-d+e}·\sqrt{-a+d+e}={-x}_B·2·d,$$

(14)

$$w_1=-a^2+d^2+e^2=y_B·2·d,$$

(15)

By replacing the components of relations (12) ÷ (15) in Equations (10) and (11), we obtain the following:

$$x_E=x_B-{\displaystyle \frac{b·x_B}{e}}-{\displaystyle \frac{c·\left(2·d^2-y_B·2·d·sin\theta \right)}{2·d·e}}+{\displaystyle \frac{c·x_B·cos\theta }{e}},$$

(16)

$$y_E=y_B-{\displaystyle \frac{b·y_B}{e}}-{\displaystyle \frac{c·\left({-x}_B·2·d\right)·sin\theta }{2·d·e}}+{\displaystyle \frac{c·y_B·cos\theta }{e}},$$

(17)

By reduction,

$$x_E=x_B-{\displaystyle \frac{b·x_B}{e}}-{\displaystyle \frac{c·\left(d-y_B·sin\theta \right)}{e}}+{\displaystyle \frac{c·x_B·cos\theta }{e}},$$

At the end, the following is obtained:

$$x_E={\displaystyle \frac{x_B\left(e-b\right)+c·(d-x_B·cos\theta -y_B·sin\theta )}{e}},$$

(18)

For coordination from the OY axis, it follows that

$$y_E=y_B-{\displaystyle \frac{b·y_B}{e}}+{\displaystyle \frac{c·\left(x_B·2\right)·sin\theta }{2·e}}+{\displaystyle \frac{c·y_B·cos\theta }{e}},$$

$$y_E={\displaystyle \frac{y_B(e-b)+c·(x_{B·}sin\theta +y_B·cos\theta )}{e}},$$

(19)

At the same time, in addition to the coordinates of the components of the studied mechanism, it was also possible to determine the distance variation described by point E in relation to the OY axis:

$$d_E=\left|-\left(u_2-{\displaystyle \frac{b·u_2}{e}}-c·\left(\left({\displaystyle \frac{\left(-a^2+d^2+e^2\right)·sin\theta }{2d}}\right)\right)-\left({\displaystyle \frac{u_2·cos\theta }{e}}\right)\right)\right|,$$

(20)

where u₂ is presented in Equation (12):

Then,

$$d_E=\left|-\left(x_B-{\displaystyle \frac{b·x_B}{e}}-c·y_B·sin\theta -\left({\displaystyle \frac{x_B·cos\theta }{e}}\right)\right)\right|,$$

(21)

$$d_E=\left|-\left({\displaystyle \frac{{e·x}_B-b·x_B-2·c·y_B·sin\theta -x_B·cos\theta }{e}}\right)\right|,$$

(22)

At the end, we obtain the following:

$$d_E=\left|{\displaystyle \frac{x_B(e-b-cos\theta )-2·c·y_B·sin\theta }{e}}\right|,$$

(23)

In addition to these equations, which helped us determine the motion of the components of the mechanism studied, it was also possible to mathematically determine the following relations:

-

Variation in the velocity of point B:

$$v_{Bx}={\displaystyle \frac{v_A·\left({-a}^4+2·a^2·e^2-e^4+d^4\right)}{2·d^2·\sqrt{a+e+d}·\sqrt{a+e-d}·\sqrt{a-e+d}·\sqrt{-a+e+d}}},$$

(24)

$$v_{By}={\displaystyle \frac{v_A·\left(a^2-e^2+d^2\right)}{2·d^2}},$$

(25)

-

The variation in the speed of point C:

$$v_{Cx}={\displaystyle \frac{v_A·\left(a^4-2·a^2·c^2+c^4-d^4\right)·\left(b-c\right)}{2·c·d^2·\sqrt{a+c+d}·\sqrt{a+c-d}·\sqrt{a-c+d}·\sqrt{-a+c+d}}},$$

(26)

$$v_{Cy}={\displaystyle \frac{v_A·\left(-a^2+c^2-d^2\right)·\left(b-c\right)}{2·c·d^2}},$$

(27)

-

Variation in the acceleration of point B:

$$a_{Bx}={\displaystyle \frac{{v_A}^2·\left[\left(-a^8+3·a^6·d^2-3·a^4·d+a^2·d^6-e^8+e^6·\left(4·a^2+3·d^2\right)+e^4·\left(-6·a^4-3·a^2·d^2-3·d^4\right)+e^2·\left(4·a^6-3·a^4·d^2+6·a^2·d^4+d^6\right)\right)\right]}{d^3·{\left(a+d+e\right)}^{\frac{3}{2}}·{\left(a+d-e\right)}^{\frac{3}{2}}·{\left(a-d+e\right)}^{\frac{3}{2}}·{\left(-a+d+e\right)}^{\frac{3}{2}}}},$$

(28)

$$a_{By}={\displaystyle \frac{{v_A}^2·\left({-a}^2+e^2\right)}{d^3}},$$

(29)

-

Variations in the acceleration of point C:

$$a_{Cx}={\displaystyle \frac{{v_A}^2·\left[\left(\begin{array}{c}(a^{8}b-3a^{6}b{d}^2+3a^{4}b{d}^4-a^{2}b{d}^6+\left(-a^8+3a^6{d}^2-3a^4{d}^4+a^2{d}^6\right)e+\left(-4a^{6}b+3a^{4}b{d}^2-6a^{2}b{d}^4-b{d}^6\right)e^2+\\ +\left(4a^6-3a^4{d}^2+6a^2{d}^4+d^6\right)e^3+\left(6a^{4}b+3a^{2}b{d}^2+3b{d}^4\right)e^4+\left(-6a^4-3a^2{d}^2-3d^4\right)e^5+\\ +(-4a^{2}b-3b{d}^2)e^6+(4a^2+3d^2)e^7+b{e}^8-e^9\left)v^2\right)\end{array}\right)\right]}{{e·d}^3·{\left(a+e+d\right)}^{\frac{3}{2}}·{\left(a+e-d\right)}^{\frac{3}{2}}·{\left(a-e+d\right)}^{\frac{3}{2}}·{\left(-a+e+d\right)}^{\frac{3}{2}}}},$$

(30)

$$a_{Cy}={\displaystyle \frac{{v_A}^2·\left(a^2·b-a^2·e-b·e^2+e^3\right)}{e·d^3}}$$

(31)

where v_A is the velocity corresponding to point A.

The analysis of the calculation relations shows that both the velocity and acceleration of the two points under analysis depend directly on the velocity at which point A moves. The equations corresponding to the two parameters (velocity and acceleration) were determined via the classical method used in the analysis of mechanisms, namely by vector analysis.

3. Results

The following values were chosen to verify the calculation relations shown previously:

-

The distance is d = 900 mm, although the displacement of coupling A moved in the range of 600–900 mm over a distance of 300 mm;

-

The coordinates of coupling D are (0,0);

-

Value of element AB = 460 mm (noted by a in Figure 3);

-

Value of element BC = 1700 mm (noted by b in Figure 3);

-

Value of element BD = 500 mm (noted by e in Figure 3);

-

Value of element CE = 200 mm (noted by c in Figure 3);

-

Value of angle θ = 77° (the angle generated by elements BC and CE, as shown in Figure 3).

The values of the parameters used to check the correctness of the mathematical results (presented above) are not taken based on a real model. This was not possible because the manufacturers made the equipment to order. Due to the constructive simplicity of the equipment, they are not made in large production series; instead, they are made according to the operator’s requirements.

First, the movements made by the couplings of the studied mechanism are determined using the mathematical relationships and values presented previously. For the calculations, program Mathcad 15 was used (as mentioned in Section 2). Using the calculation relationships presented previously, the trajectories of the moving couplings corresponding to the mechanism studied were obtained, which are presented in Figure 5. During the verification of the calculation (for the movement of the components of the mechanism), the real working position of the mechanism was considered (positioning and movement were carried out according to the representation in Figure 1).

Figure 6 shows variations in the linear velocity obtained by substituting the values in Equations (24)–(27). For this calculation, a constant displacement velocity of 0.075 m/s for point A was chosen and represents a random value. Due to the construction of this mechanism, it is observed that the movement speeds of couplings B and C are closely dependent on the variations in the linear speed corresponding to coupling A.

From the graphical representation, Figure 6 details the following:

-

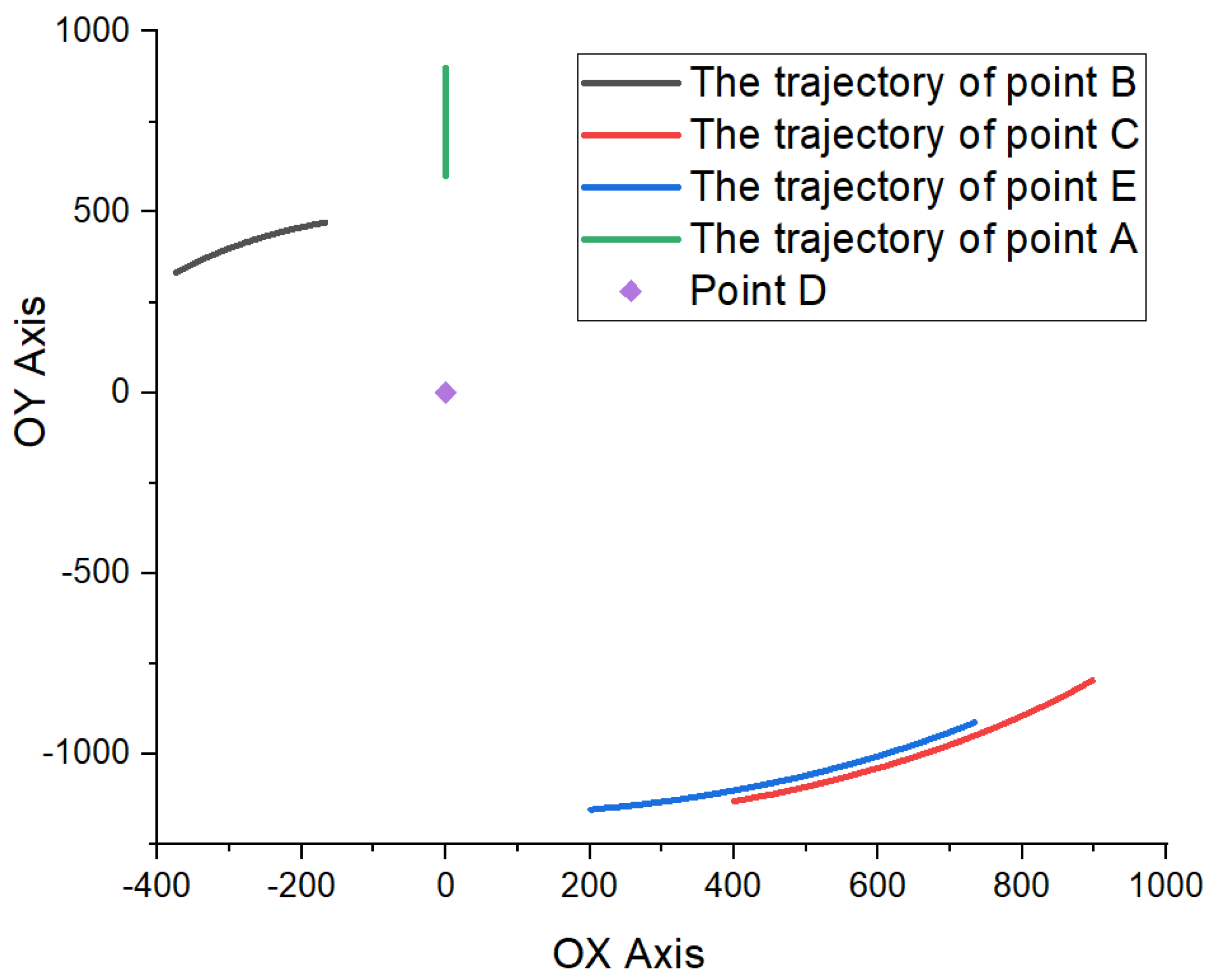
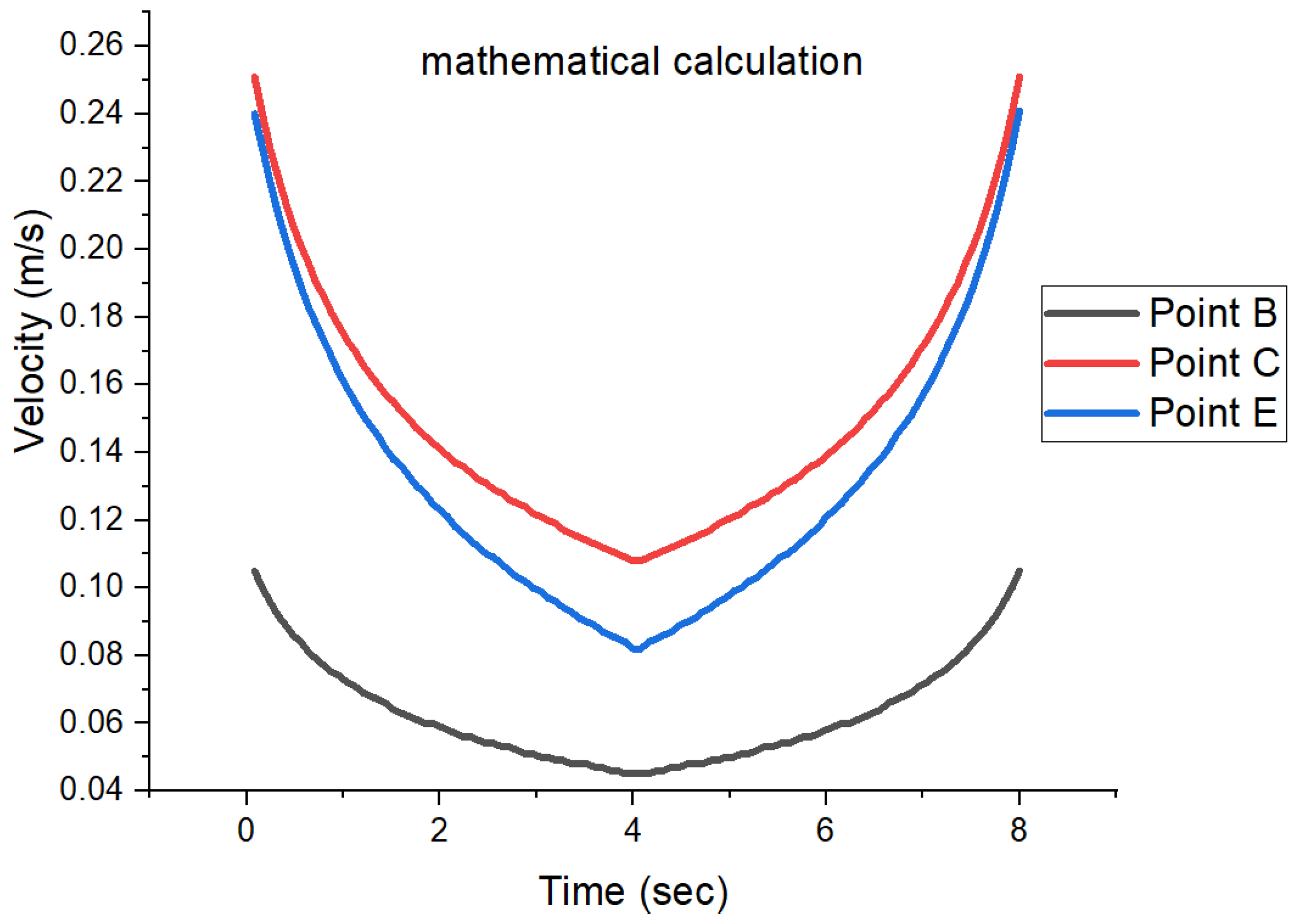
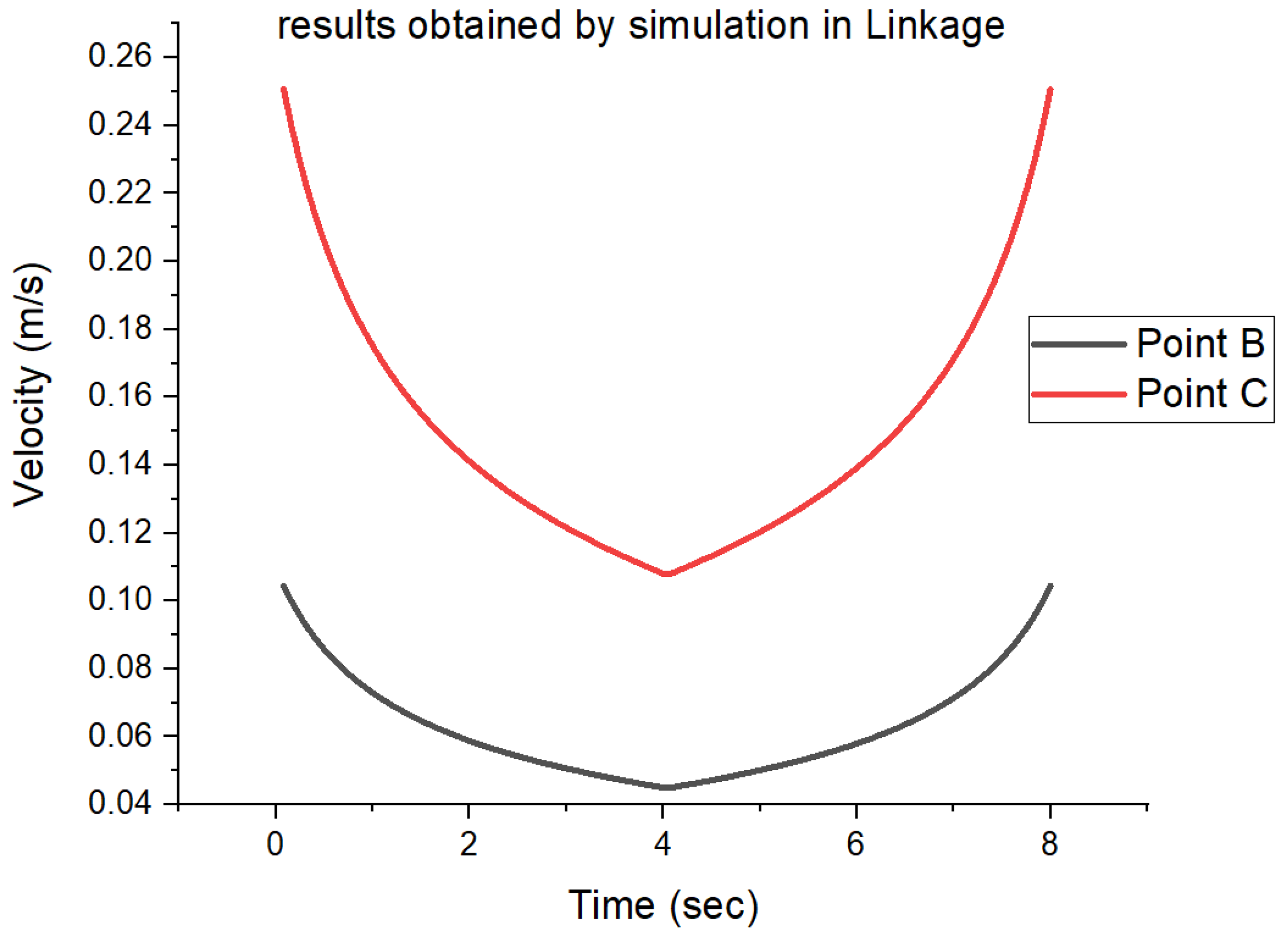
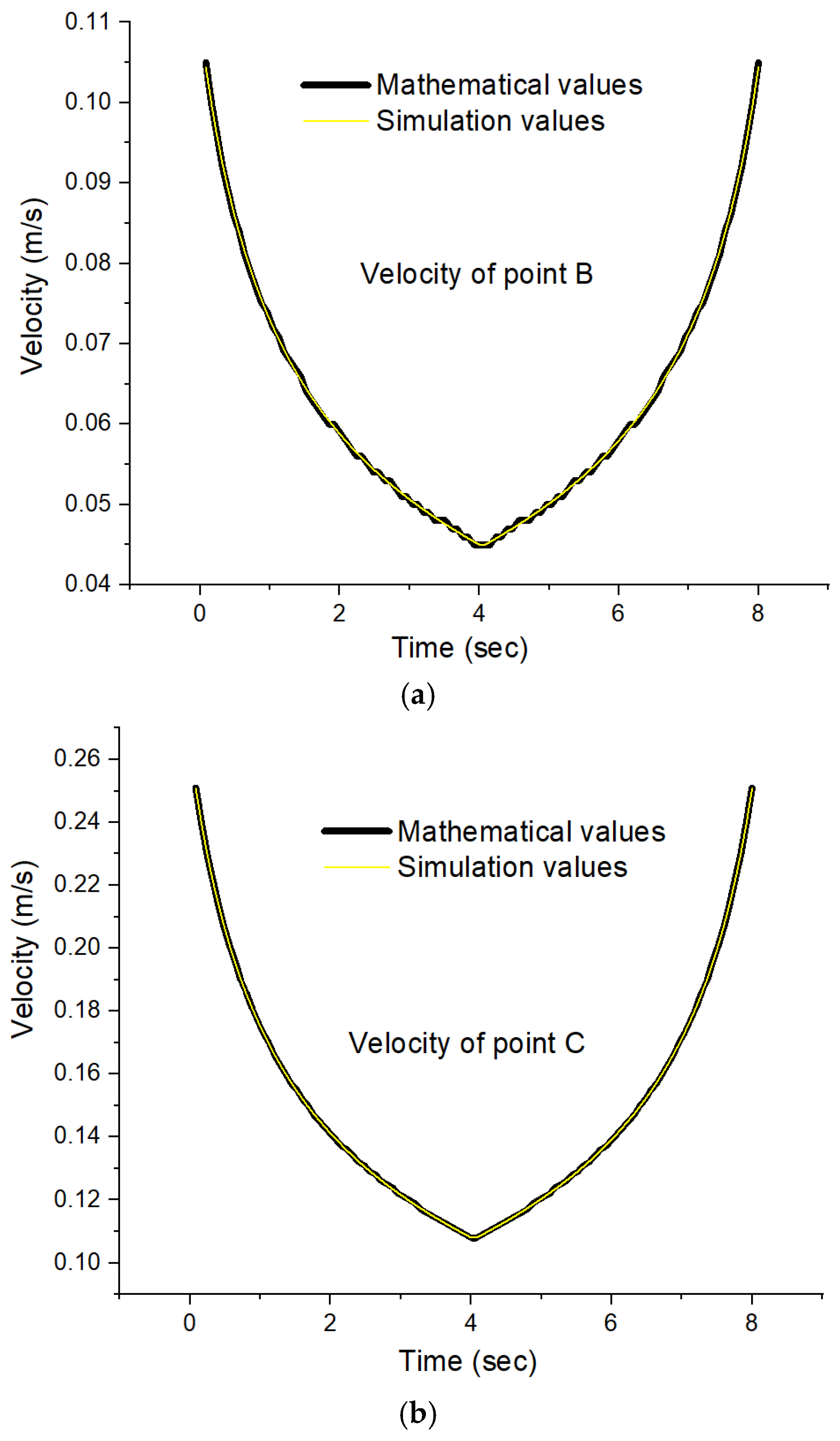
Regardless of which point is subject to the analysis (B, C, or E), variations in linear velocity have the shape of a parabola, with its depth closely related to the position of the point in relation to the vertical axis (at the maximum tightening position of the mechanism).

-

The highest value of the linear velocity was obtained for coupling C and is 0.25 m/s while the lowest value was obtained for coupling B and is 0.04 m/s.

-

By analyzing each coupling, the following observations were found:

○

For coupling B, the difference between the minimum and maximum value of the studied parameter is 0.07 m/s.

○

The maximum speed of 0.25 m/s corresponding to the displacement of coupling C is obtained when the distance between points A and D is at the maximum, and the lowest value of 0.11 m/s is obtained when the distance between points A and D is at the minimum.

○

As for the variation in the linear velocity of point E, it shows the same variation as for coupling C, but the minimum value is 0.08 m/s and the maximum value is 0.24 m/s.

To verify the correctness of the calculation relations presented above, the simulation program Linkage was used (in Figure 7, the mechanism is rotated at 90°). The studied mechanism was realized according to the specified dimensional values using a sliding system (piston type). The simulation of the movement of point A was performed at a constant speed. For the realization of the movement of point A in the Linkage program, the following has been done:

-

point A is positioned on the fixed element GD, thus being transported in the translation coupling;

-

the fixed element GD is parallel to the axis OY. Thus, the movement that point A must realize is respected;

-

a hydraulic piston was used to move point A at constant speed (it connects points A and G).

After simulating the motion of the studied mechanism, it was possible to determine the trajectories obtained by the couplings of the mechanism (Figure 8). The coordinates of points B and C were exported (using the function “Export Motion Paths…” in Linkage). After processing these coordinates, it was possible to plot the linear velocity variation for the two analyzed points (Figure 9).

By analyzing the values obtained using the calculation relations and those obtained via the simulation program, it was found that there are no differences between them. This is shown in Figure 10 in which individual movements executed by points A, B, and C are plotted. In the graphs from Figure 10a–c, the values obtained from mathematical calculations and those resulting from the simulation are placed together with the Linkage program.

The same was carried out for the speed parameter (for which its values are shown in Figure 6 and Figure 9). The comparison of the values obtained via the two methods (mathematical and simulation) is presented in Figure 11.

From the analysis of the graphs in Figure 10 and Figure 11, there are no significant differences between the two working methods (mathematical calculation and simulation). This means that the calculation relations, which describe the movement of the product-gripping mechanism, are correct, and the obtained values accurately describe the functioning of the mechanism.

4. Conclusions

Industrial conveyor plants use various methods and systems to safely hold different types of products. This equipment was analyzed both theoretically and experimentally to identify the best constructive solutions. Systems that include mechanical components were studied to understand their behavior during transport operations.

In the specialized literature, numerous studies present determinations of the motion mode of components within a mechanism. These studies are aimed at identifying the geometrical coordinates of a mechanism that performs the motion and not for specific imposed situations.

The mathematical analysis of the lifting pincer mechanism, as presented in this paper, aimed to identify mathematical relations corresponding to the coordinates of the hinge elements (coupling), which have a general deterministic character (not obtained for specific cases).

The equations obtained and presented in this article are complex and highly original.

To identify the mode of motion of the studied mechanism, a series of chosen values were used so that they comply with the motion requirements of the mechanism. These values were not taken from the manufacturers (in general, they were not presented) in order to emphasize the generalizability of the calculation relations used in this study.

The values used not only allowed us to analyze the motion of the mechanism but also to visualize the variations in linear velocity corresponding to its components.

Strictly speaking, the variation in the linear velocity displacement of points B and C (no matter which method of determination is used) is closely related to the way in which the displacement of point A is realized. More precisely, the following can be said:

-

Both linear velocity variations were parabolic.

-

Both linear speed variations had a minimum point that occurred at the time of 4 sec (this time corresponds to moving point A from 900 mm to 600 mm).

By superimposing the results obtained using the two working methods, it was found that there are no significant differences between them (the maximum difference between the values is 0.1 mm). What can be said is that there is a high degree of correctness with respect to the computational relations used.

The implementation of the theoretical results, as presented in this study, in the design of such mechanisms substantially helps by simplifying the number of equations used in determining the motion of the components of the mechanism, but this method has a great disadvantage in that it increases the complexity of the equations used.