Evaluation of Deflection Errors in Traffic Speed Deflectometer Measurements on Inverted Asphalt Pavement Structures

Abstract

This study developed a dynamic model for the Traffic Speed Deflectometer (TSD) on inverted asphalt pavement structures. It is aimed at evaluating the deflection slope and quantifying measurement errors. First, the reliability of the ABAQUS model in simulating the dynamic response of asphalt pavements was validated by comparing with previous studies. The deflection slope curves of inverted and semi-rigid base pavements with varying thicknesses were compared, revealing that the inverted pavement exhibited complex deflection slope trends in TSD measurements. A significant decrease in peak deflection was observed at 0.15 m from the load gap center with increasing surface thickness. The deflection velocity measurement value of the TSD calibration sensor (S3500) on the inverted asphalt pavement is not zero, which causes the road surface deflection to be lower than the actual deflection, with an error as high as 80.1%, which overestimated the pavement’s structural capacity. These findings suggest that the sensor configuration and measurement strategy of TSD should be reconsidered when applied to inverted asphalt pavement structures. The results provide useful insights that may support the refinement of TSD application strategies.

1. Introduction

The accurate assessment of pavement deflection is a critical factor in ensuring road safety and extending the lifespan of roads. The Falling Weight Deflectometer (FWD), currently the most widely used device for pavement deflection measurement, applies a fixed pulse load to simulate the actual loading of moving vehicles, enabling a precise deflection measurement of the pavement [1]. It has also been widely studied for evaluating pavement modulus and deformation behavior [2]. However, FWD operation is limited to static measurements and requires temporary road closures, which hinders its efficiency and convenience [3].

In contrast, the Traffic Speed Deflectometer (TSD), based on the laser Doppler effect, was jointly developed by the Danish Road Directorate and Greenwood Engineering in the 1990s. Due to its operational safety, high efficiency, and ability to continuously collect data, TSD has been widely adopted globally [4]. TSD not only significantly improves the safety and efficiency of measurement operations, but its continuous data acquisition also offers excellent accuracy and resolution, making it particularly suitable for large-scale network evaluations [5,6,7,8,9].

In recent years, numerous scholars have conducted in-depth studies on the precise assessment of traditional asphalt pavements using TSD. Nasimifar et al. [10] evaluated various deflection algorithms and dynamic analysis models based on TSD deflection slope data. The results indicated that the deflection indices generated by all the algorithms were similar, making them applicable for estimating the residual structural capacity of traditional pavement structures at the network level. Shen et al. [11], using the Semi-Analytical Finite Element Method (SAFEM), simulated the dynamic load on flexible pavements with viscoelastic asphalt layers. They studied the effect of pavement roughness on TSD measurements and highlighted the need to develop correction methods for TSD deflection measurements on rough pavements. Kazemi et al. [12] used the finite element method, considering the nonlinear stress dependence of unbonded granular materials and fine-grained soils with transverse isotropy, to study the impact on TSD deflection slope results and pavement performance predictions. Despite the global application and research on TSD technology, its applicability and measurement accuracy on specific pavement structures have not been fully validated. Wu et al. [13] found that the 7 m deflection basin assumption proposed during TSD development does not apply to commonly used semi-rigid base asphalt pavements in China. Their calculations revealed that the deflection error caused by the TSD calibration sensor can reach 87.3%. Further analysis [14] revealed that these pavements exhibit a “three-peak” deflection slope curve, which shifts to a “single-peak” profile under subgrade-induced longitudinal cracking, with deflection slope peaks increasing by an order of magnitude.

However, investigations into the current pavement conditions in China reveal that semi-rigid base pavements exhibit structural failure within their design lifespan [15,16]. This is due to the combined effect of load and environmental factors, which causes cement-stabilized materials to crack easily, and the cracks will propagate to the road surface, ultimately leading to reflection cracks across the entire surface [17,18]. To prevent the occurrence of reflective cracks on the pavement, researchers have designed an inverted asphalt pavement structure [19]. Similar designs have been reported in countries such as South Africa, Australia, Brazil, and parts of the United States. Unlike conventional asphalt pavement structures, inverted asphalt pavements feature a relatively soft transition layer (graded crushed stone) between the asphalt surface and a stiff cement-stabilized base [20,21]. The reversed structural arrangement of inverted asphalt pavements alters mechanical responses under moving loads, notably in stress distribution and deflection propagation. Similarly to semi-rigid asphalt pavements, inverted structures exhibit a deflection basin range exceeding the 7 m assumption used in early TSD design, largely due to the high stiffness of the base layer. This results in a flatter and wider deflection basin, with non-zero deflection velocities occurring at reference points traditionally assumed to be zero in standard TSD configurations. Although inverted pavements are increasingly used in China, there is limited evidence that TSD systems have been calibrated for their unique structural behavior. Most applications continue to rely on sensor configurations designed for conventional pavements, suggesting that similar measurement inaccuracies may exist globally. This highlights the urgent need for adaptable TSD calibration strategies across diverse pavement types.

In light of the above, this study aims to address the existing gap in understanding the behavior of TSD measurements on inverted asphalt pavement structures. The specific objectives are as follows: (1) to develop and validate a dynamic finite element model of the TSD using ABAQUS, incorporating viscoelastic material behavior and realistic loading conditions; (2) to analyze the deflection slope characteristics of inverted asphalt pavements with varying surface layer thicknesses and compare them with conventional semi-rigid base structures; (3) to quantify the measurement errors introduced by the standard TSD calibration sensor (S3500) when applied to inverted structures; and (4) to propose sensor layout adjustments or calibration strategies that could enhance the measurement accuracy of TSD in these contexts. These objectives are intended to support the more accurate application of TSD technology and offer insight into its adaptation for non-traditional pavement systems.

2. Laser Doppler Principle and TSD Testing Theory

The Traffic Speed Deflectometer (TSD) has been widely adopted worldwide due to its high detection efficiency. This device utilizes the Doppler effect principle to measure the instantaneous deflection velocity of asphalt pavements under high-speed loading, effectively evaluating the pavement’s bearing capacity.

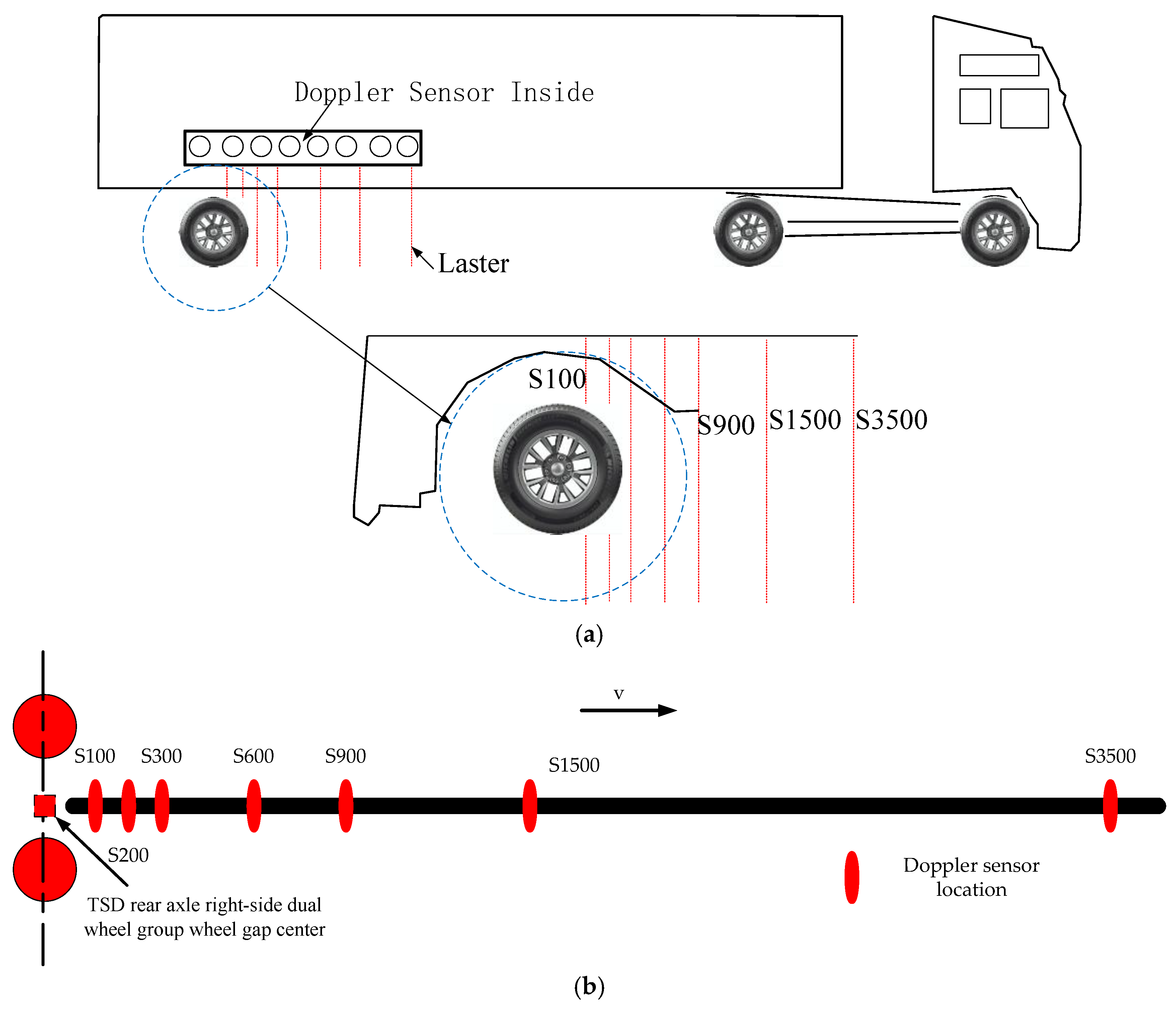
TSD is considered the most advanced pavement deflection measurement device currently available. Its primary components include the carrying vehicle, Doppler laser sensors, and a temperature control system. As shown in Figure 1a, the measurement vehicle of TSD is equipped with several Doppler laser sensors mounted between the two rear wheels of the trailer. These sensors are responsible for capturing the instantaneous deformation velocity of the pavement surface.

To ensure measurement accuracy, one of the Doppler sensors, located at a distance of 3.5 m, is set as a reference point for calibrating the readings of the other sensors, as shown in Figure 1b. This setup allows TSD to perform rapid and continuous data acquisition without interrupting traffic flow, thereby improving the efficiency and accuracy of road inspection and maintenance work [22].

During the measurement process, the vehicle moves at a high speed of V, emitting a laser with a frequency of f₁. After reflection, the frequency changes to f₂. The deflection velocity of the pavement at this point can be calculated using Equation (1).

$$V_V={\displaystyle \frac{(f_2-f_1)\lambda }{2}}$$

(1)

After measuring the deflection velocity with TSD, it is converted into the deflection slope using Equation (2). In the equation, f₁ (Hz) represents the emission frequency, f₂ (Hz) is the received frequency, λ (m) is the emitted laser wavelength, V_v (mm/s) is the deflection velocity, and S (mm/m) represents the deflection slope.

$$S={\displaystyle \frac{V_v}{V}}$$

(2)

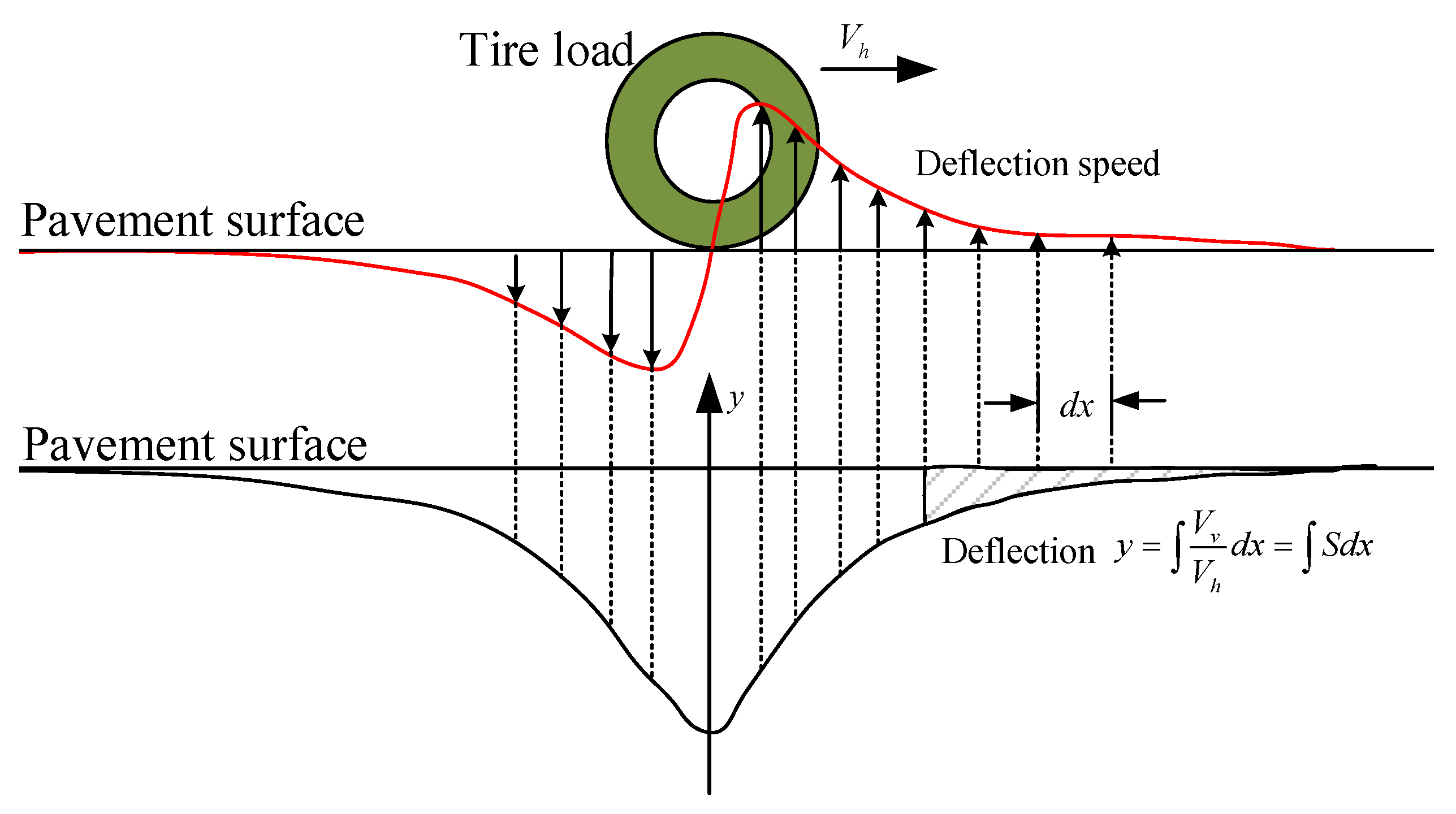
Figure 2 illustrates the process by which deflection velocity is converted into pavement deflection. This is achieved through the integration of the deflection slope along the longitudinal direction.

3. Pavement Dynamics Theory and Finite Element Model Verification

3.1. Pavement Dynamics Theory

According to the layered dynamic theory of asphalt pavements, the finite element dynamic equation for the layered pavement structure is given by:

$$M\left\{\ddot{u}\right\}+C\left\{\dot{u}\right\}+K\left\{u\right\}=P(t)$$

(3)

In the equation, $\stackrel{..}{u}$, $\stackrel{.}{u}$, and u represent the acceleration, velocity, and displacement vectors, respectively. P (t) is the vehicle load matrix, and M, C, and K are the mass, damping, and stiffness matrices, respectively.

The mass matrix M, damping matrix C, and stiffness matrix K are defined as follows:

$$M_{ij}={\displaystyle \underset{V}{\int }\rho N_i{N}_{j}dV}$$

(4)

$$C=\alpha M+\beta K$$

(5)

$$K_{ij}={\displaystyle \underset{V}{\int }{B}_i^T\rho D{B}_{j}dV}$$

(6)

In the equation, ρ represents the material density, N_i and N_j are the shape functions used to describe the relationship between the displacement at any point within the element and the nodal displacements, and V is the element volume. α and β are the damping coefficients, while B_i and B_j are the strain-displacement matrices that describe the relationship between the element strain and nodal displacements. D is the elastic matrix.

3.2. Finite Element Model Verification

In the field of road engineering research, ABAQUS software (version 6.10) has become an essential tool for analyzing the dynamic response of asphalt pavement structures under moving loads. As a widely used large-scale finite element analysis software, ABAQUS has been proven in numerous studies to provide high reliability and accuracy in pavement structure dynamic response analysis [23,24,25,26,27].

To validate the developed model, its results were compared with those from the literature [28]. This reference used a semi-analytical numerical procedure to compute the dynamic response of a three-layer pavement system under elastic and viscoelastic conditions, subjected to non-uniform contact pressure and irregular tire impressions. The results were then compared in detail with finite element simulations.

In this study, ABAQUS was used to establish a finite element model considering the viscoelastic properties of the surface layer and non-uniform tire load distribution, simulating the tire’s interaction with the pavement. The surface asphalt layer was modeled as a linear viscoelastic material using the Prony series representation available in ABAQUS. The viscoelastic behavior was defined by inputting time-dependent shear relaxation modulus values, which describe how the material response evolves under loading. The pavement structure and material parameters are detailed in

Table 1. Pavement material parameters.

Structural Layer	Elastic Modulus (MPa)	Poisson’s Ratio	Density (kg/m3)	Thickness (m)
Surface layer	4000	0.35	2400	0.2
Base layer	1000	0.3	2000	0.4
Subgrade	200	0.4	1500	---

and

Table 2. Surface-layer asphalt mixture Prony series parameters.

τi	gi	Instant Modulus (MPa)
1000	0.000541	10,000
100	0.000902
10	0.002705
1	0.007663
0.1	0.025243
0.01	0.071131
0.001	0.148753
0.0001	0.185896
0.00001	0.457167

, and the non-uniform load distribution is shown in Figure 3. The DLOAD subroutine was employed to simulate the dynamic application of non-uniform tire loads over time on the pavement. Figure 4 presents a comparison between the finite element results, considering the viscoelastic characteristics of the surface layer, and the semi-analytical solution from the literature [28]. The comparison shows that the simulated and reference vertical strain values at a depth of 0.2 m exhibit consistent trends, with closely matching peak values. The relative error in peak strain is approximately 2.4%. This result effectively validates the model and provides reliable theoretical support for the subsequent analysis of the deflection slope characteristics of inverted asphalt pavement structures.

4. Analysis of the Deflection Slope Characteristics of Inverted Asphalt Pavement Structures

4.1. Finite Element Model Construction

Based on the above model, this study used ABAQUS software (version 6.10) to construct a finite element model for the inverted asphalt pavement under TSD high-speed moving load. To simplify the calculations and focus on key factors, the following assumptions were made during the model construction: (1) All pavement layers are considered isotropic to unify the material behavior description and reduce model complexity; (2) Inter-layer contact issues and pavement roughness effects are ignored, with a focus on simulating load transfer and material response.

This study examined three inverted asphalt pavement structures with varying surface layer thicknesses, along with a commonly used semi-rigid base layer pavement structure. These structures represent different design standards and application scenarios, aiming to cover performance under various road conditions. The structural parameters and material properties of the models are detailed in

Table 3. Pavement structure parameters.

Structural Layer	Material	Thickness (cm)
		Structure 1	Structure 2	Structure 3	Structure 4 (Semi-Rigid)
Surface Layer	Asphalt Concrete	12	16	20	12
Transition Layer	Graded Crushed Stone	15	15	15	---
Base Layer	Cement-Stabilized Crushed Stone	30	30	30	30
Subbase Layer	Cement-Stabilized Crushed Stone	20	20	20	20
Subgrade	Fine-grained Soil	---	---	---	---

and

Table 4. Material properties.

Material	Elastic Modulus (MPa)	Poisson’s Ratio	Density (kg/m3)
Asphalt Concrete (25 °C)	7000	0.25	2450
Graded Crushed Stone	400	0.35	2250
Cement-Stabilized Crushed Stone-Base Layer	6000	0.25	2400
Cement-Stabilized Crushed Stone-Subbase Layer	5600	0.25	2350
Fine-grained Soil	80	0.4	1750

[29].

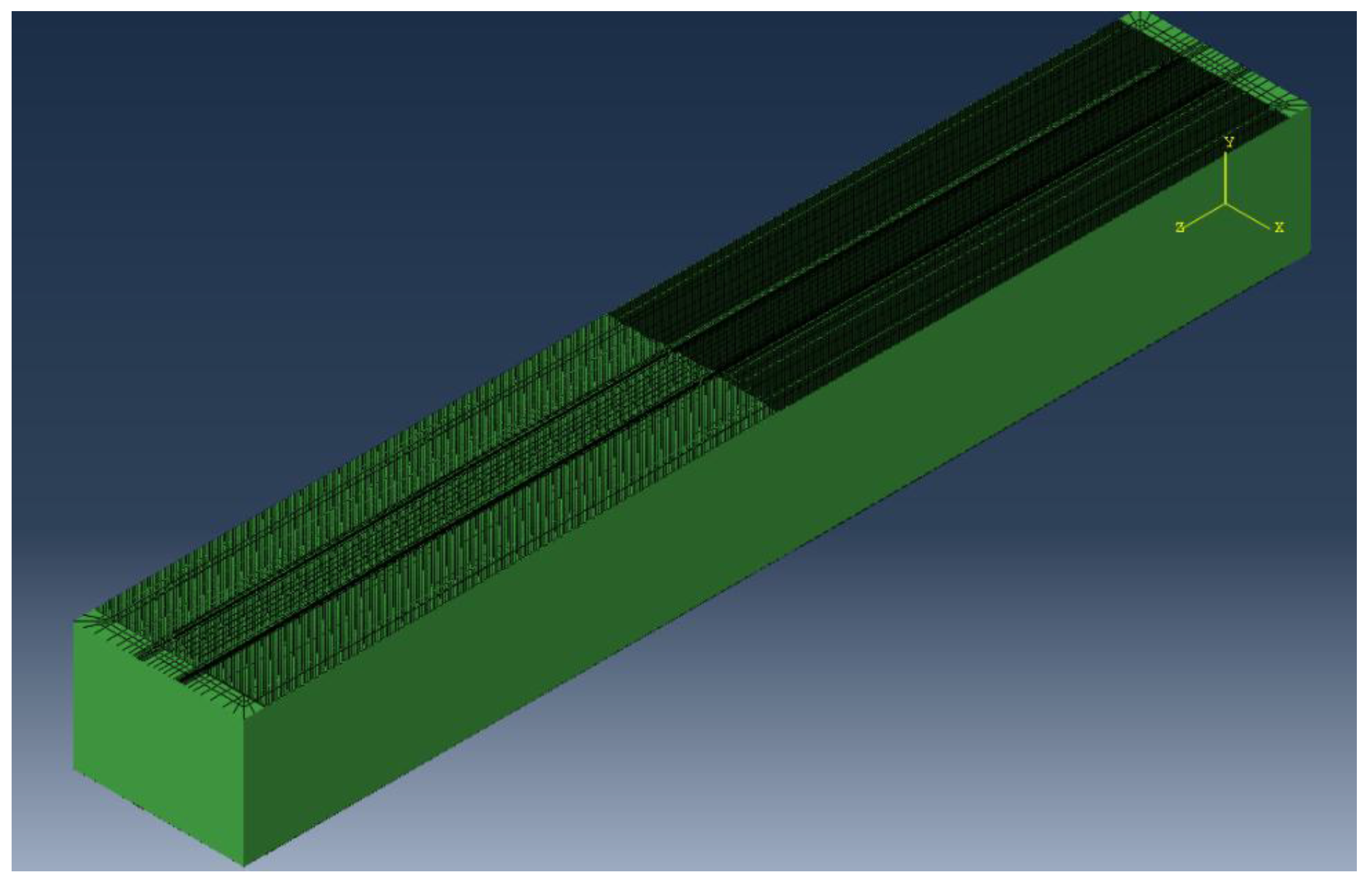
As shown in Figure 5, to ensure the accuracy of the simulation and simulate real working conditions, the dimensions of the model were set to 50 m in the longitudinal direction, 8 m in the lateral direction, and 6 m in the vertical direction. These dimensions cover the load action area and the surrounding large influence zone. In the dynamic analysis, to prevent stress reflection phenomena caused by boundary conditions, infinite elements were added around the model. This helps simulate the propagation of waves in an infinite medium and avoids boundary reflections interfering with the simulation results.

Furthermore, to optimize computational resources, the model used refined meshing in the load action area, and relatively coarse meshing in regions away from the load. Boundary conditions were set with fixed normal displacement on all sides and complete fixation at the bottom, ensuring the model’s stability and reliability under load. The TSD load model used a rear axle single-wheel load with dual wheels, where the center distance between the wheels was 34.3 cm, and the distance between the outer edges of the two tires was 61.7 cm. The total axle load was set to 100 kN, and the contact pressure between the tire surface and the pavement was 0.8 MPa [30].

The vehicle load speed was set to 72 km/h, reflecting common conditions in actual TSD operations. This detailed model setup and parameter configuration aim to provide a comprehensive performance evaluation of the inverted asphalt pavement under real operational conditions, offering a scientific basis for future pavement design and maintenance.

4.2. TSD Deflection Slope Curve Characteristics for Inverted Pavement Structure

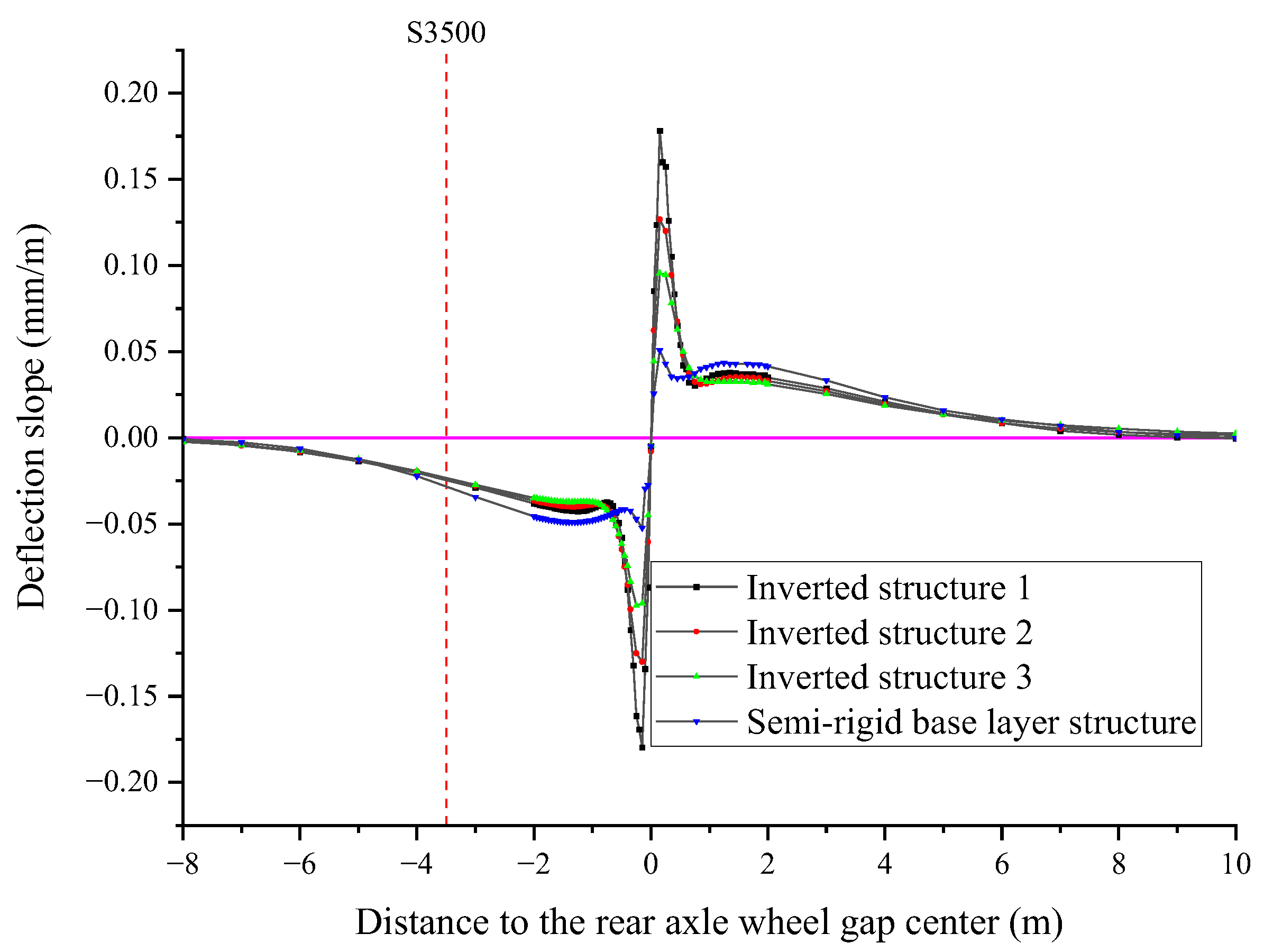
In this study, due to the symmetric distribution of both the pavement structure and vehicle load, the analysis was simplified to consider only the wheel gap center of the left wheel group. Figure 6 presents a comparison of the deflection slope curves between the inverted asphalt pavement and the semi-rigid base asphalt pavement. The results show that the deflection slope curve trends of both pavement structures are generally similar. Both structures initially rise, then fall, followed by a slow rise and a gradual decrease to zero at a distance of 10 m from the wheel gap center. Additionally, both structures exhibit extreme points at multiple locations, which is consistent with the results in reference [14].

However, it is noteworthy that at a distance of 0.15 m from the wheel gap center, the extreme point for the inverted pavement structure is significantly higher than that for the semi-rigid base pavement structure. This is attributed to the graded crushed stone layer, which causes a redistribution of stress within the pavement structure.

Upon further analysis of Figure 6, it can be observed that the deflection slope variation trend for the inverted asphalt pavement remains relatively consistent for different surface layer thicknesses. However, the extreme point at 0.15 m decreases significantly as the surface layer thickness increases. This phenomenon indicates that the modulus of the graded crushed stone layer in the inverted pavement structure is relatively small, while the base layer modulus is large. This combination of material properties leads to increased complexity in the deflection slope curve.

Although Inverted Structure 1 includes an additional graded crushed stone transition layer, the measurement errors associated with TSD are not significantly different between the two structures. Both rely on a stiff base layer, resulting in a wide deflection basin and non-zero deflection velocity at the reference sensor position (S3500). While the crushed stone layer slightly alters stress distribution, it does not substantially increase the magnitude of error.

5. Deflection Slope Test Error Analysis for Inverted Asphalt Pavement Structure

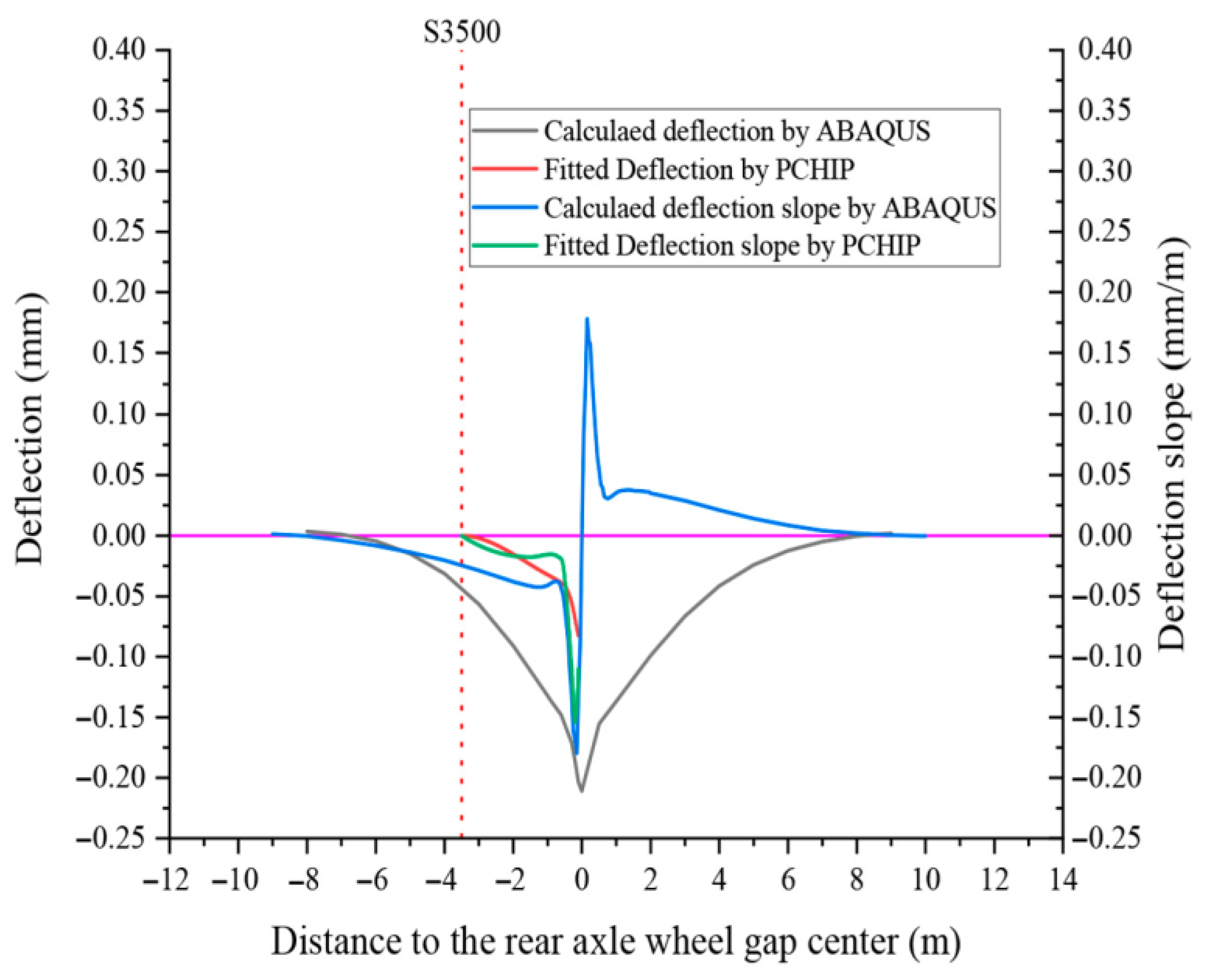
In the design of the TSD equipment, the S3500 sensor was set as the reference sensor based on the assumption that the deflection response at this location for traditional asphalt pavement structures tends to zero. However, as shown in the previous analysis, for the inverted pavement structure, the actual measurement value from the Doppler sensor at the S3500 position is not zero. The complex structural response characteristics at this location invalidate this assumption. As a result, the accuracy of the entire measurement system is affected. This limitation in the design assumption leads to deviations in the measurement data from other sensor locations, which in turn impacts the overall deflection measurement results for the inverted asphalt pavement.

This phenomenon reveals a key issue within the TSD system: when the Doppler sensor at the S3500 position is used to calibrate the readings from other sensors, significant measurement errors may be introduced. To accurately assess this error, this study used the TSD calibration principles and fitting by the Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) method to calculate the deflection error when applying TSD to Inverted Pavement Structure 1. As shown in Figure 7, the calculation results show that for the inverted pavement application, the deflection errors at the S100 to S1500 Doppler sensor positions relative to the deflection values obtained from the finite element simulation are 59.3%, 70.4%, 67.7%, 73.8%, 75.2%, and 80.1%, with the maximum error reaching 80.1%.

The substantial deflection errors observed when applying TSD to inverted asphalt pavement structures have important practical implications. Since the TSD system underestimates actual deflection due to incorrect sensor calibration, it may significantly overestimate the structural bearing capacity of the pavement. This misjudgment can lead to under-designed maintenance interventions or deferred rehabilitation schedules, increasing the risk of unexpected pavement failures and long-term maintenance costs. Furthermore, inaccurate TSD data, when used in network-level pavement management systems, may compromise the reliability of condition assessments and disrupt optimal resource allocation strategies.

6. Conclusions

This study investigated the limitations of Traffic Speed Deflectometer (TSD) measurements when applied to inverted asphalt pavement structures, which are characterized by a reversed stiffness hierarchy—placing a soft graded crushed stone transition layer above a stiff cement-stabilized base. This non-traditional arrangement alters the pavement’s mechanical response under moving loads, particularly in terms of stress transmission and deflection propagation. As a result, conventional TSD calibration assumptions, such as the zero-deflection velocity at the reference sensor (S3500), are no longer valid, leading to substantial measurement errors.

To address this issue, a dynamic finite-element model incorporating viscoelastic asphalt behavior and realistic moving loads was developed in ABAQUS and validated against published data. The model was used to analyze deflection slope characteristics and quantify sensor-related measurement errors across multiple structural configurations.

The key findings are as follows:

Deflection Characteristics: Inverted asphalt pavements exhibit multi-peak deflection slope curves, similar to those of semi-rigid base structures. However, the peak near 0.15 m from the load center is significantly higher in inverted pavements.

Measurement Errors: The assumption of zero velocity at the reference sensor location (S3500) is invalid in inverted structures. Consequently, TSD measurements systematically underestimate deflection slope, with simulated errors reaching up to 80.1%.

Impact on Pavement Management: Such errors can result in overestimated structural capacity, potentially leading to under-designed maintenance or deferred rehabilitation. When used in network-level pavement management systems, these inaccuracies may compromise condition assessments and resource allocation.

Recommendations: To improve TSD applicability in inverted pavement systems, we recommend relocating the reference sensor to a position located further downstream where the deflection slope is closer to true zero [13,31], and conducting parametric simulations to optimize sensor layouts for different pavement types.