Abstract
The increasing adoption of blockchain technology has presented significant challenges in maintaining the security and reliability of smart contracts. This study addresses the problem of identifying security flaws in smart contracts, which may result in monetary damages and diminished confidence in blockchain systems. A Hybrid Quantum–Classical Deep Neural Network (HQCDNN) approach was proposed, combining quantum computing principles with classical deep learning methods to identify various vulnerability types, including access control, arithmetic, front-running, reentrancy, time manipulation, denial of service, and unchecked low calls. The SmartBugs Wild Dataset was used for training, with TF-IDF employed as a preprocessing technique optimized for hybrid architectures. Experiments were conducted using hybrid architectures with 2-qubit and 4-qubit quantum layers, alongside a classical deep neural network (DNN) model for comparative analysis. The HQCDNN model attained accuracy levels ranging from 96.4% to 78.2% and F1-scores between 96.6% and 80.2%, showcasing enhanced performance compared to the classical and deep learning models referenced in the literature. These results highlight the capability of HQCDNNs to improve the identification of security flaws in smart contracts. Future work could focus on evaluating the model on actual quantum devices and expanding its application to larger datasets for further validation.
1. Introduction
Blockchain technology has established itself as a revolutionary development in recent years, bringing about new paradigms in transaction processing and data management [1]. Among its most impactful innovations is the Ethereum blockchain network—a decentralized platform that extends blockchain capabilities beyond mere transactional operations by assisting in the creation of smart contracts and decentralized apps (DApps) [2]. Recognized as Blockchain 2.0, Ethereum pioneered support for smart contracts with Turing-complete capabilities, establishing itself as the earliest and most extensively adopted platform for this feature [3]. Its design, which enables complex computations and programmable agreements, has solidified Ethereum as a cornerstone in the evolution of blockchain technologies [4]. While Bitcoin focuses on secure and decentralized value transfers, the Ethereum Virtual Machine (EVM) allows developers to create DApps and automated, reliable digital contracts [5]. Additionally, Ethereum’s gas mechanism determines the computational costs of smart contracts, ensuring the network operates securely and efficiently [6]. As a result, Ethereum has evolved beyond a simple payment system into a foundational infrastructure for large-scale applications across various industries.
The Ethereum Virtual Machine (EVM) serves as the execution environment that enables smart contract processing within the Ethereum blockchain, ensuring deterministic and decentralized computation [5]. While the blockchain functions as a secure and immutable ledger that records transactions, the EVM facilitates the execution of complex programmable logic, allowing for trustless automation through smart contracts [7]. Smart contracts, typically written in Solidity, are compiled into bytecode and executed on the EVM, with each Ethereum node replicating the computations to maintain network consensus [8]. The EVM allows developers to launch applications that execute precisely as intended, ensuring they operate without downtime, censorship, fraud, or interference from third parties [5]. It compiles code into bytecode executable on the blockchain, guaranteeing that every node across the network arrives at the same outcome for computation results [6]. This virtual machine serves as a cornerstone for preserving the Ethereum network’s integrity and functionality, offering a robust platform for smart contract execution [7,8].
Smart contracts function as self-enforcing digital agreements, with their conditions seamlessly woven into the code, running on decentralized blockchain networks like Ethereum [9]. These contracts automatically enforce agreements without intermediaries, promising enhanced efficiency and reduced costs across various industries [6]. Because blockchain technology is unchangeable, after a smart contract is put into place, it remains unchangeable and transactions are final, ensuring transparency and trustworthiness. That is, once smart contracts are placed on the blockchain, they are immutable, meaning that their code cannot be changed or removed [10]. However, this immutability also implies that any vulnerabilities in the smart contract code remain permanent, posing significant security risks [10,11].
The rise of smart contracts has been accompanied by considerable security challenges, especially throughout the Ethereum ecosystem. Flaws in smart contract code have facilitated high-profile exploits, causing significant monetary losses and eroding trust in blockchain systems. The complexity of the EVM and the novelty of smart contract programming introduce risks that traditional software development practices may not fully address. For instance, the notorious Decentralized Autonomous Organization (DAO) breach in 2016 leveraged a reentrancy vulnerability, culminating in the theft of around 3.6 million Ether [11,12]. Similarly, the Parity Wallet vulnerability in 2017 exposed a multi-signature wallet flaw, leading to over $150 million worth of Ether being permanently frozen [10]. Another significant exploit occurred in 2022 when the Wormhole Bridge was hacked, resulting in the loss of approximately $320 million due to a flaw in its smart contract validation mechanism [13]. More recently, the Ronin Bridge hack in 2022 exploited validator weaknesses, allowing attackers to drain over $600 million from Axie Infinity’s network [14].
Traditional methods for detecting these vulnerabilities often involve formal verification and static analysis tools tailored for the EVM and Solidity [10]. While these methods are effective to some extent, they may struggle with scalability and the complexity of detecting sophisticated or novel attack vectors inherent in the Ethereum network. Machine learning (ML) has been proposed as a solution to enhance vulnerability detection by learning patterns associated with insecure code within the EVM context [15]. Classical machine learning approaches can sift through extensive datasets to pinpoint possible security weaknesses more effectively than manual techniques. However, they are limited by computational constraints and may not fully capture the intricacies inherent in smart contract vulnerabilities, especially as the Ethereum blockchain grows in size and complexity [16]. Moreover, classical machine learning models struggle with feature engineering limitations, often failing to extract complex vulnerability patterns due to reliance on predefined features [17]. They also exhibit poor generalization to novel attack vectors, making them ineffective against previously unseen exploits [18].
Quantum machine learning (QML) represents an innovative avenue for overcoming these constraints by harnessing quantum computing fundamentals—such as superposition and entanglement. Quantum computing itself, fueled by quantum bits (qubits), unlocks groundbreaking possibilities for tackling challenges that lie beyond the scope of classical systems, enabling QML to tackle computationally intensive tasks with unprecedented efficiency and scalability [19]. QML algorithms have the potential to process and analyze data at unprecedented speeds [20]. The application of QML to vulnerability detection could significantly enhance the ability to identify and mitigate security risks in smart contracts executed on the EVM, offering a new layer of protection in blockchain ecosystems [21].
Quantum Neural Networks (QNNs) offer a great advantage over classical methods by combining the power of quantum computing with ML [22]. QNNs can provide higher processing speed and accuracy, especially when processing large and complex datasets. However, the physical limitations of current quantum computers and the difficulties encountered in training QNNs are the biggest obstacles to this technology reaching its full potential.
The sensitivity to noise in current quantum devices and the constraints imposed by having a small qubit count pose significant challenges, making it difficult for QNNs to implement deep, intricate architectures [17]. Additionally, QNNs face the “barren plateau” problem, where gradients rapidly approach zero during training. This phenomenon undermines the efficiency of optimizing model parameters and negatively impacts the training process [23]. During the transitional quantum stage often termed the Noisy Intermediate-Scale Quantum (NISQ) era, these issues are compounded by two more hurdles to creating QML models that outdo classical approaches: (1) the scarcity of locally accessible quantum data and (2) the absence of specialized quantum memory (QRAM) and sufficiently advanced quantum hardware to manage large-scale information. These barriers collectively impede the advancement of independent and robust QNNs, thereby slowing overall progress in the field [22].
HQCDNNs aim to unify the strongest features of classical methodologies with quantum frameworks, leading to more efficient and optimized models [22]. In this approach, some of the computations are performed on classical deep neural networks, while critical computations are performed on quantum circuits. In this way, the potential of quantum computing is exploited, despite the limitations of existing QNNs [23]. HQCDNNs are particularly advantageous in handling large and complex datasets where classical methods face limitations such as reduced generalization capacity and prolonged processing times [20,24]. By leveraging quantum computing’s parallel processing capabilities, superposition, and entanglement, HQCDNNs can model intricate relationships within data more efficiently [20,23]. For instance, in the security analysis of smart contracts, the complexity of EVM opcode structures and the need for applicability on resource-constrained devices highlight the significant advantages of the hybrid design of HQCDNNs. This approach provides enhanced performance and efficiency in such scenarios [18].
This paper examines the incorporation of HQCDNN methods for identifying security weaknesses in smart contracts deployed on the Ethereum blockchain network. Our objective is to unite recent quantum computing breakthroughs with real-world security solutions in blockchain technology. By adapting hybrid quantum algorithms to analyze smart contract code within the EVM environment, we seek to improve detection accuracy and processing efficiency compared to classical approaches.
Our contributions are threefold. First, we conduct an in-depth survey of current techniques for uncovering security flaws in Ethereum smart contracts, highlighting their shortcomings. Second, we introduce a framework for applying hybrid classical–QNN algorithms to this problem domain, incorporating advanced feature extraction techniques suitable for the EVM’s opcode structure. Third, we share experimental findings that highlight the potential benefits of our hybrid approach, accompanied by an examination of the obstacles and future research paths in this domain.
2. Literature Review
In recent years, researchers have proposed diverse strategies to bolster the reliability and security of on-chain agreements. These strategies primarily involve symbolic execution, fuzz testing, formal verification, programmatic analysis, and ML-based approaches [3,25,26].
Symbolic execution facilitates precise and comprehensive program analysis by simulating program execution using symbolic inputs rather than concrete values. Oyente is among the first tools created for analyzing the security of Ethereum smart contracts. It leverages symbolic execution to simulate the behavior of contracts and identify vulnerabilities such as reentrancy, mishandled exceptions, and transaction-ordering issues. By modeling the EVM, Oyente explores different execution paths to uncover potential weaknesses. Symbolic inputs are formulated by aggregating constraints that must be satisfied for execution to traverse a specific program path, facilitating the analysis of smart contract behavior. A path is considered infeasible if its condition cannot be met; on the other hand, a path is called feasible if the condition can be met [3,10,27,28]. Mythril is a sophisticated, open-source security analysis tool developed to identify vulnerabilities within the EVM bytecode. Leveraging advanced methodologies such as symbolic execution, Satisfiability Modulo Theories (SMT) solving, and taint analysis, Mythril is highly effective in pinpointing critical security issues in smart contracts, such as reentrancy vulnerabilities, integer underflows/overflows, and access control misconfigurations [29]. MAIAN focuses on identifying weaknesses that may lead to significant security threats. These threats are classified into three primary categories: suicidal (contracts that can be arbitrarily destroyed), prodigal (contracts that may unintentionally transfer assets), and greedy (contracts that indefinitely lock funds). MAIAN integrates symbolic execution with heuristic evaluation to precisely detect these vulnerabilities [30]. Osiris expands on symbolic execution by incorporating taint analysis, enabling it to detect arithmetic issues like integer overflow, underflow, and division by zero. This makes it particularly valuable for analyzing contracts with complex numerical operations [12]. Securify serves as a verification platform, leveraging static analysis to ensure conformity with established security guidelines. It leverages compliance and violation patterns to determine if smart contracts fulfill designated security criteria or demonstrate potentially exploitable behaviors. This structured approach makes Securify scalable and efficient for analyzing large contracts [31]. Slither functions as a specialized analysis tool for Solidity code, enabling rapid and comprehensive identification of numerous security flaws. It makes use of taint tracking and data flow analysis, among other methods, to detect vulnerabilities such as reentrancy, uninitialized variables, and inefficient gas usage. Its speed and flexibility make it suitable for use in continuous development workflows [32].
Fuzzing, also known as fuzzy testing, is a dynamic approach to software security analysis aimed at detecting vulnerabilities by subjecting a program to unexpected or randomly generated inputs. Unlike static analysis, which inspects code without execution, fuzzing actively executes the software under test, systematically injecting malformed or anomalous data to observe its response. This method is particularly effective for uncovering flaws such as buffer overflows, null pointer dereferences, memory leaks, and unhandled exceptions, which may not be apparent through conventional testing techniques [3,33]. ContractFuzzer is a specialized fuzzing framework developed for identifying security vulnerabilities within Ethereum smart contracts. It operates by generating test inputs derived from the Application Binary Interface (ABI) specifications of the targeted contracts. The framework uses predefined test oracles to identify possible security issues and integrates an instrumented EVM to track and record runtime behaviors during execution. These recorded logs are subsequently analyzed to identify and report security vulnerabilities [34]. ILF leverages imitation learning to develop a fuzzing policy modeled as an ensemble of neural networks. This policy is trained using a dataset of high-quality transaction sequences generated through symbolic execution. By utilizing this approach, ILF is capable of generating effective test cases that maximize code coverage and enhance the detection of vulnerabilities [35]. In addition, fuzzing tools such as EtherFuzz [36], which uses a mutation fuzzy test method, and sFuzz [37], which is based on AFL and adopts a feedback adaptive fuzzification strategy, have been developed.
Formal verification is the process of using mathematical methods to prove or disprove the correctness of a system with respect to a certain formal specification. Unlike testing, which examines software behavior under specific inputs, formal verification ensures correctness across all possible inputs and states. Because of this characteristic, it is well aligned with the stringent reliability standards required by on-chain agreements [38]. A variety of solutions and frameworks now support the formal validation of on-chain contracts. For instance, KEVM provides a detailed representation of the EVM, enabling comprehensive analysis of EVM bytecode [39]. FSolidM is a solution that conceptualizes contracts using Finite-State Machines [40]. Isabelle/HOL: A general-purpose theorem prover that can model smart contract behaviors [41].
Program analysis and taint analysis have become fundamental techniques for detecting vulnerabilities in smart contracts, particularly in blockchain ecosystems. These approaches facilitate the systematic examination of code behavior and the tracking of data flows to identify potential security risks, such as unauthorized data access or unintended state changes [3,10]. Slither integrates techniques like data flow analysis, taint tracking, and custom rule detection to identify issues such as reentrancy, uninitialized variables, and inefficient gas usage [32]. SmartCheck translates the contract’s code into an intermediate representation to apply pattern-matching rules, identifying issues like reentrancy, integer overflows, and insecure function visibility. SmartCheck provides detailed reports with categorized findings for ease of remediation [42].
Researchers have investigated ML techniques for vulnerability detection to address the shortcomings of traditional methods. ML algorithms can analyze large datasets to learn patterns associated with insecure code, enhancing detection capabilities more efficiently than manual methods. Recent studies have introduced novel approaches to smart contract vulnerability detection, leveraging advancements in neural networks and graph-based models. Liu et al. [43] proposed a method combining pure neural networks with interpretable graph features and expert pattern fusion, providing a more robust mechanism for identifying security weaknesses in smart contracts. Sendner et al. [44] introduced G-Scan, a graph neural network designed for line-level vulnerability identification. This model focuses on precise detection, making it a valuable tool for developers to pinpoint vulnerabilities within specific lines of code. Chen [45] developed Vulnerability-Hunter, which employs an adaptive feature perception attention network to enhance vulnerability detection. By focusing on dynamic feature extraction and attention mechanisms, the model improves accuracy for complex vulnerability patterns. This approach highlights the increasing sophistication of ML techniques in addressing smart contract security. Qian et al. [46] conducted an extensive review of methods for identifying vulnerabilities in smart contracts, highlighting developments in both conventional and ML-driven approaches. Their work emphasizes the need for multimodal fusion strategies, integrating diverse data sources to enhance detection precision. Li et al. [47] applied deep learning combined with multimodal decision fusion to improve the identification of vulnerabilities, setting a benchmark for integrated approaches. In addition, in recent years, the frequent use of deep learning algorithms in vulnerability detection has been seen in the literature [3,45,48,49,50,51].
The field of quantum computing has gained significant attention for leveraging quantum mechanics to execute computations at speeds beyond the reach of classical computers [52]. QML combines quantum computing with ML algorithms, potentially offering exponential speedups for certain computational tasks [20]. Schuld and Petruccione [24] discussed how QML could revolutionize data processing by handling large datasets more efficiently.
In the context of blockchain security, Leng et al. [53] examined quantum computing’s potential to both threaten and enhance blockchain systems. While quantum attacks could compromise cryptographic algorithms used in blockchain, quantum solutions could also fortify security measures. Although specific studies applying QML directly to smart contract vulnerability detection are sparse, the potential to leverage quantum-enhanced feature extraction and classification aligns with the increasing complexity of blockchain systems. Future research may build on these foundational works to develop QML-enabled tools.
HQCDNNs have emerged to utilize the advantages of quantum computing in ML tasks. By incorporating quantum computing elements into classical neural network architectures, these approaches seek to leverage quantum computational capabilities while ensuring compatibility with existing classical systems. Kashif and Al-Kuwari [22] proposed a systematic methodology for the design of quantum layers in HQCDNNs, achieving significant computational advantages over pure classical architectures. In financial time series forecasting, Kea et al. [23] designed a mixed quantum–classical framework utilizing quantum-assisted LSTM networks and showcased enhanced effectiveness over traditional models. In cybersecurity, Suryotrisongko and Musashi [54] evaluated an HQCDNN model for botnet detection and achieved high performance in certain situations. Katı et al. [19] introduced an integrated quantum-based approach for identifying deepfake content. They obtained remarkable results in the study. When these studies are evaluated, they emphasize the potential of HQCDNNs in vulnerability detection by combining quantum computing capabilities with classical neural network models.
3. Materials and Methods
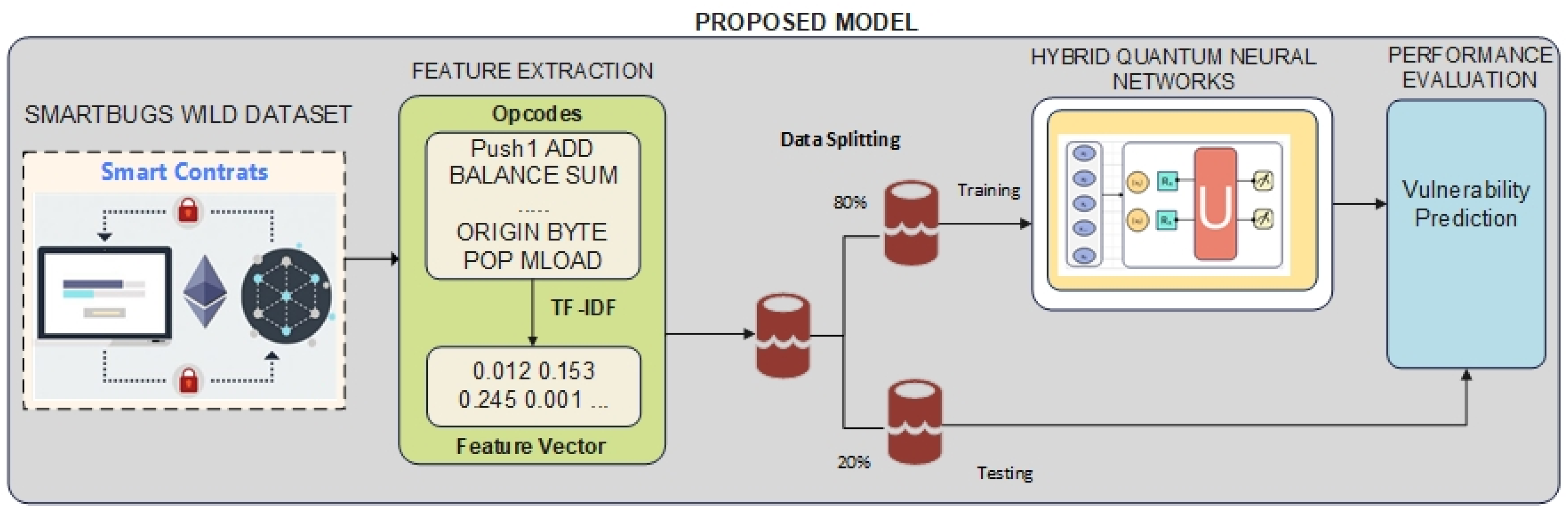
This part of the study provides a detailed overview of the dataset, hardware, and software tools used, emphasizing their importance in the implementation and evaluation of the proposed model. It also describes the classification methods employed, detailing their design, implementation, and relevance to the objectives of this research. To aid in understanding the model’s structure and functionality, Figure 1 presents a visual depiction of the proposed architecture.
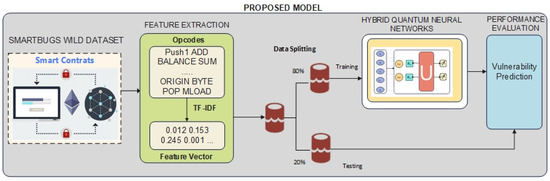
Figure 1.
Proposed model.
3.1. Dataset
The dataset used in the study is the SmartBugs Wild Dataset, created by Durieux et al., extracted from the Ethereum network and consisting of real-world data. This publicly available dataset was designed to examine potential security risks in smart contracts built on the Ethereum platform [18]. This dataset contains common types of vulnerabilities in smart contracts and was analyzed with 9 open-source tools. The dataset includes an analysis of 47,518 smart contracts. At the same time, 9 different vulnerabilities were categorized in the dataset. Table 1 shows the average time it takes open-source tools to analyze one smart contract and the time it takes to analyze the total number of smart contracts.

Table 1.
Tool execution times.
The vulnerability types examined are reentrancy, access control, arithmetic issues, unchecked return values for low-level calls, denial of service, front-running, and time manipulation. Reentry vulnerability can lead to the uncontrolled transfer of funds if the same function is called again, while access control vulnerability allows unauthorized users to access sensitive data. Arithmetic errors can lead to unexpected results such as overflows or underflows. Unsupervised return values can lead to transaction failures if failures of low-level operations go unnoticed. Denial of service leads to the contract or service becoming unavailable. Priority processing can lead to attacks due to the predictability of the transaction order. Time manipulation allows for changing the direction of transactions by abusing block timestamps. Such vulnerabilities pose serious risks in terms of financial losses for users and platform reliability.
3.2. Data Preprocessing and Feature Extraction
In our study, feature extraction was performed using the Term Frequency-Inverse Document Frequency (TF-IDF) method, and a 2-g (bigram) analysis was applied. This choice was made because the experiments showed that the performance metrics—recall, precision, accuracy, and F1-score—were low in the 1-g analysis. In particular, it was observed that the lack of contextual information hindered the proper representation of word relationships. On the other hand, the 3-g analysis could not be conducted due to insufficient resources.
Additionally, an ANOVA test and effect size analysis were performed to examine the impact of TF-IDF parameters on model performance. The ANOVA results indicated a statistically significant difference between TF-IDF parameters (F = 12.81, p = 3.74 × 10−6). According to the effect size (η2) calculations, these parameters accounted for approximately 4.9% of the variance in model performance. The tests showed that the “default” TF-IDF settings achieved the highest recall (0.992) and F1-score (0.966), making them the most successful in terms of overall model performance.
Furthermore, the “Sublinear=True” parameter improved some model results; however, it was insufficient compared to the “default” setting. The “Sublinear=True & Norm=L1” option had the lowest average metrics, with a notable drop in precision. In conclusion, the results indicate that TF-IDF parameters directly impact model performance, with the best overall accuracy and balance achieved using the “default” parameter settings. Although alternative configurations may enhance specific aspects of the model, the “default” settings are considered the most suitable option for optimal performance.
TF-IDF is a statistical approach used to determine the significance of a term (word or phrase) within a given text [55]. This method allows for distinguishing between frequently occurring but generally insignificant words and rarely occurring but important ones. By assessing the occurrence rate of a term within a text (TF) and its distribution across multiple texts (IDF), the significance of the term in the given context is determined [56].
The 2-g analysis allows us to examine the frequency of groups of two words in the text. This approach allows a deeper understanding of important word combinations by analyzing consecutive word pairs. In this way, the distribution and importance of word pairs in the text are analyzed instead of single words [57].
Operational codes (opcodes) are instructions that determine the logic of the software. When analyzing the vulnerabilities of software, the sequential use of certain opcode pairs can be essential in identifying the types of vulnerabilities present in that software. Analyzing opcodes in pairs is thought to provide a better understanding of how these instructions interact with each other and how certain combinations are associated with certain types of vulnerabilities. For example, the consecutive use of two specific opcodes may indicate a limit overflow or a specific type of vulnerability. While individual opcodes may fail to reveal such relationships, binary combinations provide a clearer picture of such relationships. Therefore, examining opcodes in pairs using TF-IDF and 2-g analysis enables more accurate and faster detection of software vulnerabilities. This method makes the vulnerability detection process more effective by analyzing the importance and distribution of opcodes in the text in more detail.
3.3. Quantum Artificial Neural Networks
In classical neural networks, input data are usually processed in numerical form and with a given distribution. As these data pass through the neural network layers, each neuron is multiplied by weights and subjected to a non-linear activation function. However, in QNNs, this process follows a different structure. QNNs work with quantum gates and qubits [58].
While in classical neural networks, data are processed with neurons and weights, in QNNs, these operations are performed through quantum gates. Qubits are processed within quantum gates, which serve as the fundamental building blocks of quantum circuits. These gates are mathematically represented by matrices and play a crucial role in quantum computing operations. In particular, superposition and entanglement allow for much more complex computations compared to the limitations of classical neural networks [59].
The superposition property of qubits allows QNNs to process multiple possibilities simultaneously. This replaces the sequential computation processes in classical networks with parallel computation processes. This enables faster processing of more complex datasets and problems [60].
Mathematically, a qubit state is expressed as in Formula (1). α and β are complex number amplitudes and satisfy the condition . Since the information that is represented as 0 or 1 in a classical system is represented by probability amplitudes at the quantum level, quantum computers can have the advantage of “parallel computing” for certain problems [61].
The entanglement property of qubits provides a great advantage for QNNs. While in classical neural networks, data are processed between independent neurons, in QNNs, entanglement creates a strong dependency between qubits. A change made in one qubit can affect other qubits. This helps to more deeply understand and process the relationships between data [62].
QNNs combine the basic principles of quantum mechanics with artificial neural network models to target high performance in specific problem classes [52]. The effectiveness of this approach relies on the premise that the high-dimensional and complex structures of classical data (e.g., images, text, or sensor data) can be represented more efficiently in quantum circuits [63]. Unfortunately, the data encoding process called “feature mapping” or “data embedding” becomes a significant cost factor as the data size increases, limiting the scalability of applications [64]. Moreover, repeating the readout process for each data sample in QNN models increases the training cost by requiring the system to be re-prepared due to the “collapse” of the quantum state after the readout [65].
These problems are particularly pronounced in the so-called NISQ era, where current quantum computers are limited to noisy processors at the 50- to several-hundred-qubit level [66]. Due to their limited qubit capacity and high noise ratios, NISQ devices face serious limitations in both data encoding and error correction approaches [67]. Moreover, handling extensive datasets during QNN training increases the risk of encountering low-gradient regions, known as “barren plateaus”, which further complicates the learning process [68]. On the other hand, the interface between classical computers and quantum processors (e.g., data preprocessing, output conversion to classical format) also increases the time and resource cost, limiting the large-scale use of QNN models.
3.4. Hybrid Quantum–Classical Deep Neural Networks
HQCDNN is a neural network architecture designed for binary classification problems, combining the advantages of both quantum and classical computing [67,69]. In this architecture, the hidden layer consists of parameterized quantum circuits and Variational Quantum Circuits (VQCs), and these circuits act as “quantum neurons” [70]. Classical data are transformed into quantum states via amplitude coding, resulting in a unique quantum state for each input [71].
Compared to standalone VQC models, HQCDNNs offer higher accuracy and lower cost on simulated quantum hardware [67]. While qubit errors and noise from quantum gates in current quantum hardware pose significant constraints for purely quantum-based models, keeping the quantum circuits in the hidden layer relatively small in the HQCDNN architecture reduces the impact of this noise [20]. As a result, the quantum layer enables a more complex and compact representation of the data in the quantum domain [64]. On the other hand, the adoption of well-established learning methods such as extensive parameter optimization and backpropagation within the classical neural network (DNN) ensures a stable and efficient training process [70]. Thus, HQCDNNs combine the advantage of rich data representation obtained in the quantum layer with the scalability and computational power of the classical layer [69].
This hybrid approach allows for higher accuracy and lower computational cost, especially on low-dimensional datasets, compared to models that use only quantum circuits or purely classical methods [67]. However, as the data dimension increases, the growing number of qubits and quantum gates required for amplitude coding can make the model more susceptible to noise and optimization challenges [64]. Nonetheless, HQCDNNs mitigate some of these high-dimensional issues commonly faced by fully quantum-based models by leveraging classical layers [70]. The ability to use classical backpropagation algorithms for parameter updates also supports this process [69].
HQCDNNs make it possible to benefit from the unique advantages of quantum computing despite the limitations of current quantum hardware and to take advantage of the scalability and efficient learning approaches of deep neural networks DNNs [20]. By processing data interactively between quantum and classical layers, this architecture provides a high-performance learning process that is more resilient to hardware constraints [67]. Current research suggests that HQCDNNs could be adapted to more complex problems as quantum technology advances and that hybrid models may become a significant part of future quantum machine learning applications [71].
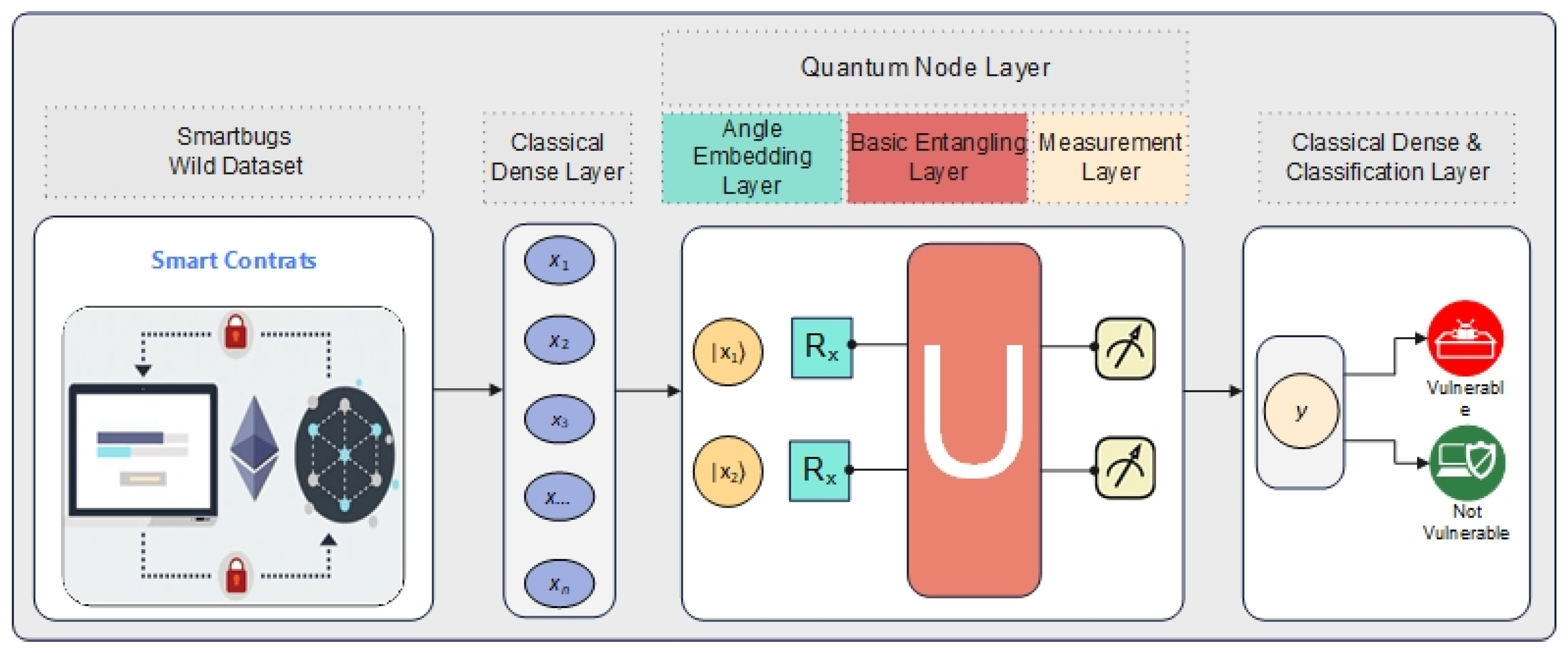
The HQCDNN model we propose in this study is shown in Figure 2. The transition between classical dense layers and quantum circuits is one of the most critical stages of hybrid classical–quantum models. This process involves the conversion of classical data into a form suitable for processing in quantum computing. The classical dense layer provides the preprocessing of classical data before it is input to the quantum circuit. In this layer, usually multidimensional classical data are reduced to dimensions that the quantum circuit can accept. For example, data consisting of n-dimensional features in a dataset are reduced to m dimensions in accordance with the number of qubits in the quantum circuit. Since 2 qubits are used in this study, the feature vectors are reduced to 2 dimensions. In order for a classical feature vector to be used in quantum computing, it must be represented in a Hilbert space, the Hilbert space in which quantum systems operate. Hilbert space is a high-dimensional space of complex vectors in which quantum states are mathematically described. Hilbert space is a vector space of complex numbers used to represent the states of quantum mechanical systems. Quantum states are represented by state vectors , which are elements of this space:
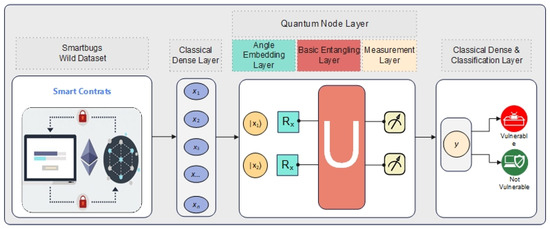
Figure 2.
HQCDNN architecture.
H: Hilbert space
ket vector
The classical feature vector , is translated into a quantum state for processing in quantum systems. This process is called embedding in Hilbert space.
Angle Encoding provides the link between classical data and quantum computing. In quantum computing systems, classical data cannot be processed directly. Instead, these data are encoded into quantum states [72].
The Angle Embedding Layer is tasked with mapping the classical input data into a quantum state, as described in Equation (2), projected onto the Bloch sphere, a quantum state vector in positional space in Equation (3), and into Hilbert space, as shown in Equation (4) [22,72].
The Angle Embedding Layer is represented using the unit matrix and is designed to link multiple single-qubit return X gates, with every qubit set to the initial state . The return gates are mathematically expressed in Equations (5) and (6) [19,22,72].
where is the rotation angle in radians and is the virtual unit. The Angle Embedding Layer is denoted by for the unit matrix representation. This is a 2-qubit quantum circuit represented in Equation (7), initially initialized as the state . This layer is designed to encode the classical feature vector , 2 with different rotation angles , based on the values corresponding to the quantum states of each qubit. The resulting state of the two-qubit Angle Embedding quantum system after Angle Embedding is expressed as a unified state at the output (Equation (8)), which is the tensor product of the rotated states of each qubit [19,22,71].
The quantum node’s second layer is referred to as the Basic Entangling Layer, which is designed to create entanglement between multiple qubits. Entanglement creates a correlation between quantum systems, which is advantageous for quantum computing. The Basic Entangling Layer used in this work is a simple and efficient structure that creates entanglement with only CNOT gates.
To construct a quantum circuit based on a 2-qubit Basic Entangling Layer (Equation (9)), the circuit generating an entangled vector is connected with a CNOT gate to create entanglement between both qubits. In this layer, entanglement is applied to only one pair of qubits and the quantum states of the system are correlated [19,22,71].
4. Experiment
In this study, an HQCDNN classification model for smart contract vulnerability detection is used. The hardware and software tools we used in the study are a computer with Intel I9-13900K CPU, 24 cores, 64 GB main memory, 6 TB SSD, Proxmox operation system, Anaconda platform (open access), Python 3.12 programming language, Pandas 2.2.3 library, NumPy 2.2.4 library, Keras 2.14.0 library, Solcx 2.0.3 library, TensorFlow 2.14.0 library, Scikit-learn (Sklearn) 1.6.1 library, PennyLane 0.40.0 library, and MongoDB 8.0 database, respectively. In the proposed model, firstly, opcode data of smart contracts are extracted and feature vectors are created using the TF-IDF method.
The SmartBugs Wild dataset initially consisted of 47,587 smart contracts. However, since the solcx library does not support Solidity versions 0.4.11 and earlier, contracts using those versions were excluded, reducing the database to 45,877 contracts. Thus, Solidity 0.4.11 and earlier make up approximately 3.5% of the entire dataset. In a 2017 announcement [73], the Solidity team addressed several security vulnerabilities found in earlier versions. Today, versions prior to 0.4.11 are no longer officially supported. Consequently, the analysis tools developed focus on Solidity 0.4.11 and later versions.
Furthermore, Wu et al. [3] used the same dataset and reported having filtered out contracts featuring what they refer to as “premature” compiler versions, ultimately experimenting on 24,957 contracts. This approach aligns with the aim of excluding outdated versions to more accurately represent the current smart contract ecosystem. In line with these considerations, our study also concentrates its analyses on Solidity ≥ 0.4.11.
Smart contract data are based on vulnerability types such as access control, arithmetic, front-running, reentrancy, time manipulation, denial of service, and unchecked low-level calls, which were flagged by dynamic and static analysis tools such as Mythril, Osiris, Oyente, Securify, Slither, and SmartCheck. Table 2 presents only the vulnerabilities and tools for which more than 1000 instances were identified. For the model to be effectively trained, a dataset containing at least 1000 vulnerable smart contracts is required for each tool and vulnerability type. This threshold plays a crucial role in enabling the model to distinguish security vulnerabilities while enhancing its ability to learn different types of weaknesses and generalize effectively.

Table 2.
Tools with over 1000 vulnerabilities.
There are 3665 smart contracts for which none of the analysis tools identified any vulnerabilities. These contracts are considered non-vulnerable and are included in the dataset as such to ensure balanced training for the models.
There are instances where multiple tools have detected the same type of vulnerability in the same smart contract. In such cases, a vulnerability is considered for evaluation only if it has been marked by multiple tools at least 1000 times within the same contract. Table 3 presents the number of vulnerabilities commonly identified by multiple tools.

Table 3.
The number of vulnerabilities marked in common by the same tools.
For each tool, tool combination, and vulnerability type, a total of 25 different models were trained. To prevent data imbalance, the number of vulnerable and non-vulnerable instances was equalized. When constructing the training dataset, if the number of vulnerable contracts exceeded 3665, a random subset of 3665 vulnerable contracts was selected for inclusion. Conversely, if the number of vulnerable contracts was less than 3665, an equal number of non-vulnerable contracts was chosen to maintain data balance. This approach helps prevent learning errors caused by data imbalance during training, ensuring that the models produce more generalizable results.
TF-IDF-based feature vectors were created using contract texts and vulnerability reports, and a model was trained.
The dataset was divided into 80% training and 20% testing. In the training phase, TF-IDF features were provided to the proposed HQCDNN architecture, and the results were compared. In the ML algorithm, we relied on “default” parameters. Our proposed HQCDNN architecture consists of three basic layers:
The classical dense layer, where the features in the dataset are initially larger than the size of the quantum circuits. The number of qubits used in a quantum circuit is 2 due to current hardware and simulation constraints. Therefore, a dense layer is used to reduce the size of the data to make it a suitable input to the quantum layer. At this stage, a non-linear transformation of the data is achieved by applying the ReLU activation function. The Quantum Circuit (Quantum Node) Layer is located at the center of the hybrid structure, where a quantum circuit with learnable parameters is run. In the study, the PennyLane library is used and the simulation device default.qubit is preferred with 2 qubits. This device simulates the quantum circuit in software without access to the actual hardware. The general flow of the quantum circuit is as follows:
- -
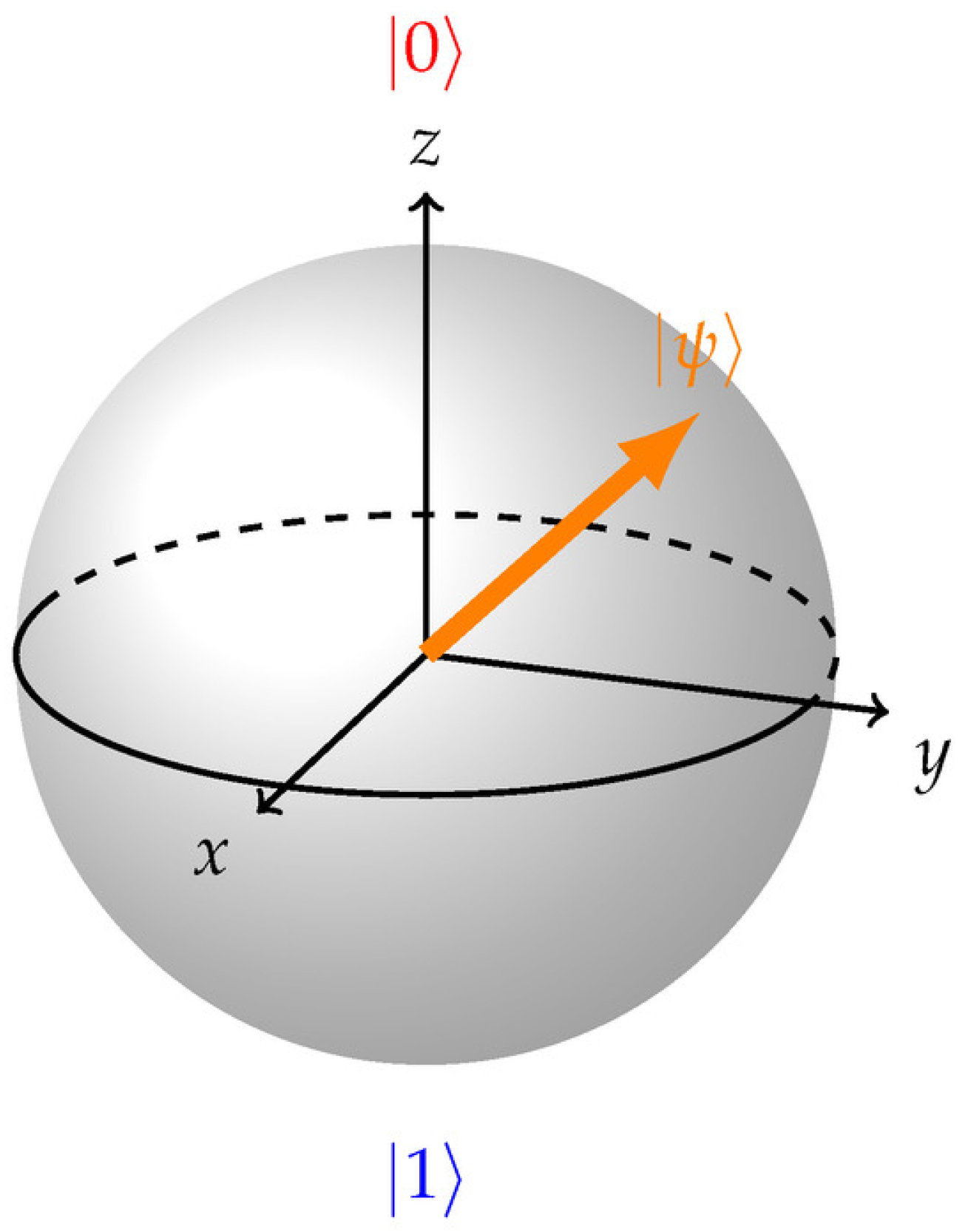
- Angle Embedding: Low-dimensional features of classical data are encoded into qubits as rotation angles with Rx, Ry, or Rz gates. Angle Encoding transforms classical data into quantum states by applying rotations on the Bloch Sphere, as shown in Figure 3, with each data feature represented as a rotation on the quantum state vector [22]. This approach enables classical data to be processed by quantum systems, leveraging quantum properties like superposition and entanglement to enhance model performance [23].
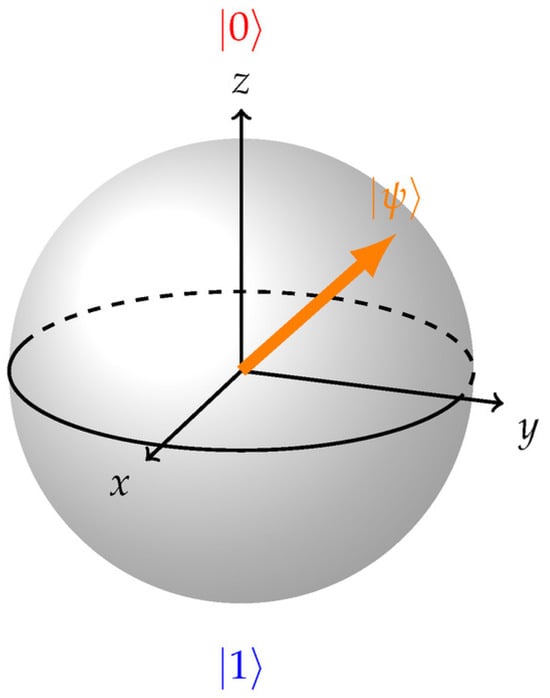 Figure 3. Bloch sphere [74].
Figure 3. Bloch sphere [74].
- -
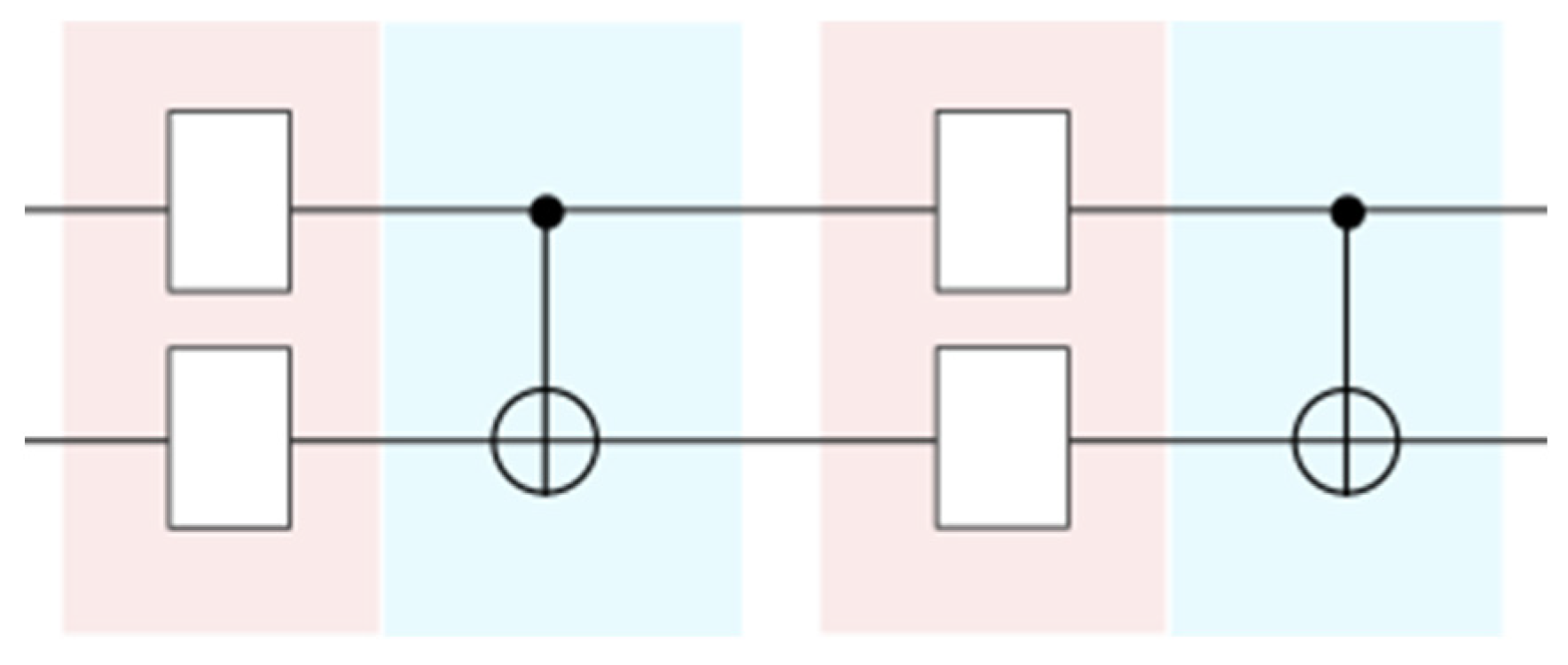
- Entangling Layer: By creating entanglement between qubits (e.g., gates such as CNOT), as shown in Figure 4, hidden correlations in the data are blended with the superposition properties of quantum mechanics.
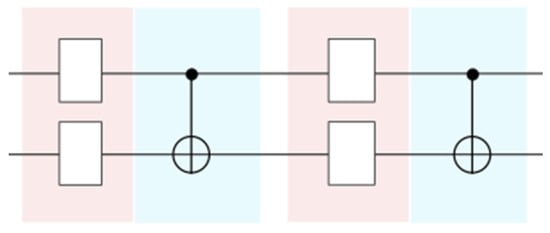 Figure 4. Basic Entangling Layer quantum circuit [74].
Figure 4. Basic Entangling Layer quantum circuit [74].
- -
- Measurement: Classical output vectors are obtained by taking the Pauli-Z expectation value for each qubit. The learnable parameters are updated with the classical backpropagation framework.
Final Classification Layer: The resulting vectors from the quantum layer are transferred back to a classical neural network layer. Here, a single-neuron dense layer performs binary classification using sigmoid activation. This produces a final prediction of “vulnerable” or “not vulnerable”.
5. Results
In this study, we analyzed the results of six vulnerability detection tools (Mythril, Osiris, Oyente, Securify, Slither, Smartcheck) that examine seven vulnerability types (access control, arithmetic, front-running, reentrancy, denial of service, time manipulation, unchecked low calls). The results obtained in the study are presented as follows.
The classification metrics for access control vulnerability are presented in Table 4. The classification results indicate that Slither consistently outperforms Mythril across all models. The 2-qubit and 4-qubit models achieve higher accuracy and recall than the DNN model, suggesting that quantum-assisted architectures improve vulnerability detection. While the 4-qubit model provides slight performance gains over the 2-qubit model, the difference is minimal.

Table 4.
Classification metrics for access control vulnerability.
For Mythril, both quantum models (2-qubit and 4-qubit) perform similarly, but the DNN model shows lower accuracy and recall, reinforcing the effectiveness of quantum-enhanced methods.
Overall, quantum models exhibit stronger precision–recall balance, making them more effective in detecting access control vulnerabilities. The DNN model, while competitive, lags behind, particularly in recall, suggesting a potential trade-off between classical and quantum approaches.
Table 5 presents classification results for reentrancy vulnerabilities, where Slither again shows the highest detection performance with an F1-score of 0.944 and an accuracy of 0.918. Mythril and Securify also perform well, achieving F1-scores of 0.927 and 0.910, respectively.

Table 5.
Classification metrics for reentrancy vulnerability.
When comparing model architectures, the 2-qubit and 4-qubit models outperform the DNN model in nearly all cases. The 4-qubit model slightly improves recall values, particularly for Mythril–Slither (0.963 recall, 0.943 accuracy), showing that increasing qubits enhances detection.
The DNN model performs the weakest, especially in recall, which is crucial for identifying reentrancy attacks. This suggests that quantum-enhanced architectures may provide a more robust approach to detecting critical security threats like reentrancy.
Table 6 presents the classification results for arithmetic vulnerabilities, where tool combinations outperform individual tools. The Osiris + Oyente + Smartcheck combination achieved the highest detection performance with 0.956 accuracy and 0.957 F1-score, confirming that using multiple tools enhances vulnerability detection.

Table 6.
Classification metrics for arithmetic vulnerability.
Among individual tools, Oyente performed the best (0.938 accuracy, 0.966 F1-score), followed by Smartcheck (0.926 accuracy, 0.944 F1-score). Mythril had the lowest performance (0.782 accuracy, 0.802 F1-score), showing that it struggles with arithmetic vulnerabilities.
When comparing model architectures, the 4-qubit model generally outperformed the 2-qubit and DNN models, especially in precision and recall. Quantum-enhanced models performed significantly better than the DNN model, which had the lowest recall across all tool configurations.
The results indicate that combining tools improves detection reliability, and quantum-enhanced models provide superior classification performance compared to classical deep learning approaches. This pattern suggests that hybrid quantum–classical models may offer a strong advantage for detecting arithmetic vulnerabilities.
Table 7 presents the classification results for time manipulation vulnerabilities, where Oyente achieved the highest performance with 0.943 accuracy and 0.944 F1-score, closely followed by Osiris (0.937 accuracy, 0.938 F1-score). Slither showed slightly lower performance (0.908 accuracy, 0.911 F1-score) but still maintained strong detection capabilities.

Table 7.
Classification metrics for time manipulation vulnerability.
Comparing model architectures, the 4-qubit model slightly outperformed the 2-qubit model, showing small but consistent gains in accuracy and F1-score. The DNN model, while competitive, had the lowest precision and recall, indicating that classical deep learning struggles more with time-based exploits.
These results suggest that quantum-enhanced models (especially with 4 qubits) provide more reliable detection of time manipulation vulnerabilities, and Oyente remains the most effective tool for identifying such exploits.
Table 8 shows that Securify achieved the highest performance in detecting front-running vulnerabilities (0.923 accuracy, 0.943 F1-score), making it the most effective tool for identifying transaction order manipulation in DeFi applications. Among model architectures, the 2-qubit model performed best, slightly outperforming the 4-qubit model, while the DNN model showed the weakest precision and F1-score, indicating higher false positives. These results highlight the advantage of quantum-enhanced models, particularly the 2-qubit approach, in detecting front-running vulnerabilities more accurately than classical deep learning.

Table 8.
Classification metrics for front-running vulnerability.
Table 9 shows that Slither achieved the highest performance in detecting denial of service vulnerabilities (0.930 accuracy, 0.932 F1-score), demonstrating its effectiveness in identifying potential attack vectors. Among model architectures, the 4-qubit model slightly outperformed the 2-qubit model, achieving 0.937 accuracy, while the DNN model had the lowest performance, particularly in F1-score (0.888). These results reinforce the advantage of quantum-enhanced models, with 4-qubit configurations providing the most reliable detection for denial of service vulnerabilities.

Table 9.
Classification metrics for denial of service vulnerability.
Table 10 shows that Slither achieved the highest performance in detecting unchecked low call vulnerabilities (0.928 accuracy, 0.954 F1-score), outperforming Smartcheck (0.876 accuracy, 0.880 F1-score). Among model architectures, the 2-qubit model performed best, while the 4-qubit model showed slightly lower accuracy (0.915) but maintained stable recall. The DNN model had the weakest performance, particularly in recall, indicating a higher risk of missed detections. These results highlight the effectiveness of quantum-enhanced models, with Slither proving to be the most reliable tool for detecting unchecked external call vulnerabilities.

Table 10.
Classification metrics for unchecked low call vulnerability.
To statistically validate the observed performance improvement of HQCDNNs, we focused on the arithmetic vulnerability detection task using the best-performing model configuration: a 2-qubit HQCDNN model trained on the combined output of the Osiris, Oyente, and Smartcheck tools. This specific setup outperformed all other 2-qubit configurations, and the same data were also used to train a classical DNN for comparison. Both models were evaluated using 10-fold cross-validation. Normality was tested via the Shapiro–Wilk test, which indicated a non-normal distribution for the DNN accuracy scores (p = 0.0266) and a normal distribution for the HQCDNN results (p = 0.7830). Given the non-normality of DNN results, we applied the non-parametric Wilcoxon Signed-Rank test to compare the models. The resulting p-value (p = 0.0020) confirms that the observed accuracy gain in HQCDNN is statistically significant and unlikely to be due to random variation. These results demonstrate that the performance improvement achieved through quantum integration is both substantial and statistically meaningful.
6. Discussion
The results of this study demonstrate the potential of HQCDNNs in the detection of vulnerabilities in smart contracts. Compared to classical machine learning models and deep learning models, HQCDNNs offer notable improvements in accuracy and efficiency, particularly in the classification of various vulnerability types such as access control, arithmetic, front-running, reentrancy, time manipulation, denial of service, and unchecked low calls. The integration of quantum computing principles into traditional deep learning methods allows for better pattern recognition within EVM opcode structures.
The comparative performance of the 2-qubit and 4-qubit HQCDNN models provides insight into the contribution of quantum layers in our framework. In our experiments, both quantum-enhanced models consistently outperformed the conventional DNN baseline across multiple vulnerability types, underlining the efficacy of integrating quantum circuits with deep learning. The 4-qubit HQCDNN variant achieved slightly higher recall and F1-scores than the 2-qubit HQCDNNs (particularly for critical vulnerabilities like reentrancy and time manipulation), suggesting that increasing the number of qubits can enhance the model’s ability to capture complex patterns in smart contract code.
This improvement is attributed to the richer expressiveness afforded by additional qubits: more qubits allow the quantum layer to encode and entangle more features simultaneously, leading to better pattern recognition within the EVM opcode sequences. Notably, the performance gap between 4-qubit and 2-qubit models was relatively small for most metrics (e.g., only a minor increase in recall), indicating that even a modest 2-qubit quantum circuit is sufficient to confer a significant performance boost over classical methods. This finding is encouraging, as it shows that useful quantum advantages can be obtained without a large quantum system, which is practical given current hardware limitations.
However, one key drawback observed in our experiments was the increased computational cost associated with the 4-qubit HQCDNN model. The training and inference times for the 4-qubit model were approximately 2 to 3 times longer than those for the 2-qubit variant. This is primarily due to the increased complexity of simulating larger quantum circuits, where the computational overhead grows exponentially with the number of qubits. While this longer runtime is expected in quantum-enhanced models, it raises practical concerns regarding scalability, especially when running on quantum simulators or near-term hardware with limited processing capabilities. Given that the performance gains from 4 qubits were only incremental compared to the 2-qubit model, the trade-off between accuracy and efficiency must be carefully considered in real-world applications.
This hybrid synergy explains the superior accuracy and balanced precision–recall of our HQCDNN models, highlighting that even a small quantum component can substantially contribute to vulnerability detection performance. At the same time, the slight edge of the 4-qubit model underscores a trend that further quantum capacity can yield incremental gains, a consideration that points toward future research with higher qubit counts once technical challenges (like noise and circuit depth limitations) are mitigated.
Other studies have used the smart wild dataset and different datasets. However, due to the differences in the tools they use, the number of samples they use in their studies may vary. Similarly, the types of vulnerabilities they study may have similarities and differences. Considering these findings, comparative results are presented in Table 11. According to these results, our HQCDNN model achieved an accuracy range of 96.4–78.2% and an F1-score range of 96.6–80.2%. This performance is superior to several classical models and deep learning models, such as those proposed by Wu et al. (2022) with a maximum accuracy of 93.36% and Zhang et al. (2022) at 93.30%. Notably, our model outperformed deep learning-based solutions such as that by Deng et al. (2023), which had a lower F1-score range of 82–42%. Additionally, our method demonstrated comparable or better performance than many studies; however, it did not exceed Sendner et al. (2023), whose Graph Neural Network model achieved an accuracy of 98.33% and an F1-score of 90.74%. This is because Sendner et al. did not consider only the reentrancy vulnerability in their study. They focused on the detection of call, send, and transfer vulnerabilities, which are subtypes of the reentrancy vulnerability.

Table 11.
Comparative analysis with other studies.
Overall, these results reinforce the notion that quantum–classical hybrid models can offer notable improvements in analysis tasks, with our study specifically demonstrating how a carefully designed 2-qubit or 4-qubit quantum layer can enhance smart contract vulnerability detection beyond what is achievable with classical deep learning alone. By comparing these variants, we also identify a trade-off: classical DNN models are easier to implement on today’s hardware but may miss subtle vulnerability patterns (reflected in lower recall), whereas quantum-augmented models capture those patterns more effectively at the cost of additional computational complexity and the need for quantum resources. This insight is crucial for guiding the development of next-generation security analysis tools that balance performance gains against practical feasibility.
The results presented in this study indicate that HQCDNNs can bridge this gap by leveraging quantum properties such as superposition and entanglement to improve model generalization and training efficiency. Specifically, our model achieved high accuracy and F1-scores, surpassing many classical approaches, particularly in reentrancy and arithmetic vulnerabilities.
7. Conclusions
This study introduces an innovative method for identifying smart contract vulnerabilities through the integration of HQCDNNs. The proposed model leverages the principles of quantum computing, specifically superposition and entanglement, to enhance feature extraction and classification efficiency. Unlike traditional deep learning and ML models, the HQCDNN framework combines classical neural networks with quantum circuits to improve detection accuracy across various vulnerability types, including access control, arithmetic, front-running, reentrancy, time manipulation, denial of service, and unchecked low calls.
The research utilizes the SmartBugs Wild Dataset, a comprehensive dataset containing real-world Ethereum smart contracts analyzed for security vulnerabilities. The feature extraction process is based on TF-IDF and 2-g analysis, allowing the model to capture significant opcode patterns.
The findings from the experiments indicate that the HQCDNN model attains higher accuracy compared to various classical and deep learning-based models. The integration of quantum computing principles, such as superposition and entanglement, enabled better pattern recognition in opcode structures, leading to improved accuracy and recall across various vulnerability types. Even with only 2 qubits, the HQCDNN model achieved superior results compared to classical deep learning, proving that a small quantum component can provide tangible benefits. The 4-qubit model offered additional improvements, particularly in complex vulnerability scenarios, though the gains were incremental rather than dramatic. One of the most notable challenges was the increased computational cost of the 4-qubit model, which took approximately 2 to 3 times longer to train and infer results compared to the 2-qubit version. This raises concerns about scalability, particularly in real-time or resource-constrained applications. While quantum hardware advancements may mitigate these issues in the future, current limitations in quantum processing power and noise sensitivity remain obstacles to large-scale implementation. The model’s performance is particularly notable in detecting reentrancy and arithmetic vulnerabilities, which are among the most exploited security risks in blockchain applications. The comparative analysis against existing approaches highlights the potential of hybrid quantum–classical models in enhancing security analysis within the Ethereum ecosystem.
Beyond smart contract vulnerability detection, HQCDNNs hold significant potential in various fields requiring high computational efficiency. In healthcare, they can enhance medical imaging analysis and genomic data processing, leading to more accurate diagnostics and personalized treatments. In cybersecurity, HQCDNNs can be leveraged for advanced threat detection and anomaly identification, improving real-time response to cyberattacks. Additionally, in finance, they can optimize risk assessment models and fraud detection systems by analyzing complex transaction patterns more efficiently than classical models. These applications highlight the versatility of hybrid quantum–classical approaches, demonstrating their value in solving complex problems across multiple industries.
Future studies may explore evaluating the model on actual quantum hardware and training it with larger and more diverse datasets. Moreover, enhancing the model for real-time analysis, ensuring its compatibility with low-resource devices, and incorporating multimodal analyses (e.g., opcode patterns, transaction behaviors) could broaden its applicability. Furthermore, evaluating the model’s robustness against adversarial attacks and refining its security capabilities could be key steps for future advancements in blockchain security.
Author Contributions
Conceptualization, E.U.K. and S.D.; methodology, E.U.K. and S.D.; formal analysis, E.U.K., S.D. and M.T.; original draft preparation, E.U.K., S.D. and M.T.; writing—review and editing, E.U.K., S.D. and M.T.; administration, E.U.K.; supervision, E.U.K. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://www.klausnordby.com/bitcoin/Bitcoin_Whitepaper_Document_HD.pdf (accessed on 13 November 2024).
- Buterin, V. A Next-Generation Smart Contract and Decentralized Application Platform. White Pap. 2014, 3, 1–36. [Google Scholar]
- Wu, H.; Dong, H.; He, Y.; Duan, Q. Smart Contract Vulnerability Detection Based on Hybrid Attention Mechanism Model. Appl. Sci. 2023, 13, 770. [Google Scholar] [CrossRef]
- Kushwaha, S.S.; Joshi, S.; Singh, D.; Kaur, M.; Lee, H.-N. Ethereum Smart Contract Analysis Tools: A Systematic Review. IEEE Access 2022, 10, 57037–57062. [Google Scholar] [CrossRef]
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 557–564. [Google Scholar]
- Antonopoulos, A.M.; Wood, G. Mastering Ethereum: Building Smart Contracts and Dapps; O’reilly Media: Sebastopol, CA, USA, 2018. [Google Scholar]
- Hirai, Y. Defining the Ethereum Virtual Machine for Interactive Theorem Provers. In Proceedings of the Financial Cryptography and Data Security, Sliema, Malta, 3–7 April 2017; Brenner, M., Rohloff, K., Bonneau, J., Miller, A., Ryan, P.Y.A., Teague, V., Bracciali, A., Sala, M., Pintore, F., Jakobsson, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 520–535. [Google Scholar]
- Szabo, N. Formalizing and Securing Relationships on Public Networks. First Monday 1997. Available online: https://firstmonday.org/ojs/index.php/fm/article/view/548 (accessed on 13 November 2024). [CrossRef]
- Luu, L.; Chu, D.-H.; Olickel, H.; Saxena, P.; Hobor, A. Making Smart Contracts Smarter. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 254–269. [Google Scholar]
- Atzei, N.; Bartoletti, M.; Cimoli, T. A Survey of Attacks on Ethereum Smart Contracts (SoK). In Principles of Security and Trust; Maffei, M., Ryan, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10204, pp. 164–186. ISBN 978-3-662-54454-9. [Google Scholar]
- Kalra, S.; Goel, S.; Dhawan, M.; Sharma, S. Zeus: Analyzing Safety of Smart Contracts. In Proceedings of the Ndss, San Diego, CA, USA, 18–21 February 2018; pp. 1–12. [Google Scholar]
- Team, C. Wormhole Hack: Lessons From The Wormhole Exploit. 2022. Available online: https://www.chainalysis.com/blog/wormhole-hack-february-2022/ (accessed on 13 March 2025).
- Hackers Steal More than $600 Million from Maker of Axie Infinity. Available online: https://www.nbcnews.com/tech/tech-news/hackers-steal-600-million-maker-axie-infinity-rcna22031 (accessed on 13 March 2025).
- Wu, Z.; Li, S.; Wang, B.; Liu, T.; Zhu, Y.; Zhu, C.; Hu, M. Detecting Vulnerabilities in Ethereum Smart Contracts with Deep Learning. In Proceedings of the 2022 4th International Conference on Data Intelligence and Security (ICDIS), Shenzhen, China, 24–26 August 2022; pp. 55–60. [Google Scholar]
- Feng, Q.; He, D.; Zeadally, S.; Khan, M.K.; Kumar, N. A Survey on Privacy Protection in Blockchain System. J. Netw. Comput. Appl. 2019, 126, 45–58. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, Z.; Qian, P.; Liu, Q.; Wang, X.; He, Q. Smart Contract Vulnerability Detection Using Graph Neural Networks. In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 3283–3290. [Google Scholar]
- Durieux, T.; Ferreira, J.F.; Abreu, R.; Cruz, P. Empirical Review of Automated Analysis Tools on 47,587 Ethereum Smart Contracts. In Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering, Seoul, Republic of Korea, 27 June–19 July 2020; pp. 530–541. [Google Scholar]
- Katı, B.E.; Küçüksille, E.U.; Sarıman, G. Enhancing Deepfake Detection Through Quantum Transfer Learning and Class-Attention Vision Transformer Architecture. Appl. Sci. 2025, 15, 525. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Dunjko, V.; Briegel, H.J. Machine Learning & Artificial Intelligence in the Quantum Domain: A Review of Recent Progress. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar]
- Kashif, M.; Al-Kuwari, S. Design Space Exploration of Hybrid Quantum–Classical Neural Networks. Electronics 2021, 10, 2980. [Google Scholar] [CrossRef]
- Kea, K.; Kim, D.; Huot, C.; Kim, T.-K.; Han, Y. A Hybrid Quantum-Classical Model for Stock Price Prediction Using Quantum-Enhanced Long Short-Term Memory. Entropy 2024, 26, 954. [Google Scholar] [CrossRef] [PubMed]
- Schuld, M.; Petruccione, F. Quantum Information. In Supervised Learning with Quantum Computers; Schuld, M., Petruccione, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 75–125. ISBN 978-3-319-96424-9. [Google Scholar]
- He, D.; Wu, R.; Li, X.; Chan, S.; Guizani, M. Detection of Vulnerabilities of Blockchain Smart Contracts. IEEE Internet Things J. 2023, 10, 12178–12185. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Z.; Wang, S.; Lei, Y.; Lin, B.; Qin, Y.; Zhang, H.; Mao, X. Peculiar: Smart Contract Vulnerability Detection Based on Crucial Data Flow Graph and Pre-Training Techniques. In Proceedings of the 2021 IEEE 32nd International Symposium on Software Reliability Engineering (ISSRE), Wuhan, China, 25–28 October 2021; pp. 378–389. [Google Scholar]
- JJ, L.; Singh, K. Enhancing Oyente: Four New Vulnerability Detections for Improved Smart Contract Security Analysis. Int. J. Inf. Tecnol. 2024, 16, 3389–3399. [Google Scholar] [CrossRef]
- Steinhöfel, D. Symbolic Execution: Foundations, Techniques, Applications, and Future Perspectives. In The Logic of Software. A Tasting Menu of Formal Methods: Essays Dedicated to Reiner Hähnle on the Occasion of His 60th Birthday; Ahrendt, W., Beckert, B., Bubel, R., Johnsen, E.B., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 446–480. ISBN 978-3-031-08166-8. [Google Scholar]
- Consensys Mythril. Available online: https://github.com/ConsenSys/mythril (accessed on 12 August 2023).
- Nikolić, I.; Kolluri, A.; Sergey, I.; Saxena, P.; Hobor, A. Finding The Greedy, Prodigal, and Suicidal Contracts at Scale. In Proceedings of the 34th Annual Computer Security Applications Conference, San Juan, PR, USA, 3–7 December 2018; ACM: New York, NY, USA, 2018; pp. 653–663. [Google Scholar]
- Tsankov, P.; Dan, A.; Drachsler-Cohen, D.; Gervais, A.; Bünzli, F.; Vechev, M. Securify: Practical Security Analysis of Smart Contracts. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; ACM: New York, NY, USA, 2018; pp. 67–82. [Google Scholar]
- Feist, J.; Grieco, G.; Groce, A. Slither: A Static Analysis Framework For Smart Contracts. In Proceedings of the 2019 IEEE/ACM 2nd International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB), Montreal, QC, Canada, 27 May 2019; pp. 8–15. [Google Scholar]
- Pani, S.; Nallagonda, H.V.; Prakash, S.; Vigneswaran, R.; Medicherla, R.K.; Rajan, M.A. Smart Contract Fuzzing for Enterprises: The Language Agnostic Way. In Proceedings of the 2022 14th International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 4–8 January 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Jiang, B.; Liu, Y.; Chan, W.K. ContractFuzzer: Fuzzing Smart Contracts for Vulnerability Detection. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Montpellier, France, 3–7 September 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 259–269. [Google Scholar]
- He, J.; Balunović, M.; Ambroladze, N.; Tsankov, P.; Vechev, M. Learning to Fuzz from Symbolic Execution with Application to Smart Contracts. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; ACM: New York, NY, USA, 2019; pp. 531–548. [Google Scholar]
- Wang, X.; Sun, J.; Hu, C.; Yu, P.; Zhang, B.; Hou, D. EtherFuzz: Mutation Fuzzing Smart Contracts for TOD Vulnerability Detection. Wirel. Commun. Mob. Comput. 2022, 2022, 1565007. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Pham, L.H.; Sun, J.; Lin, Y.; Minh, Q.T. sFuzz: An Efficient Adaptive Fuzzer for Solidity Smart Contracts. In Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering, Seoul, Republic of Korea, 27 June–19 July 2020; ACM: New York, NY, USA, 2020; pp. 778–788. [Google Scholar]
- Murray, Y.; Anisi, D.A. Survey of Formal Verification Methods for Smart Contracts on Blockchain. In Proceedings of the 2019 10th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Canary Islands, Spain, 24–26 June 2019; pp. 1–6. [Google Scholar]
- Hildenbrandt, E.; Saxena, M.; Rodrigues, N.; Zhu, X.; Daian, P.; Guth, D.; Moore, B.; Park, D.; Zhang, Y.; Stefanescu, A. Kevm: A Complete Formal Semantics of the Ethereum Virtual Machine. In Proceedings of the 2018 IEEE 31st Computer Security Foundations Symposium (CSF), Oxford, UK, 9–12 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 204–217. [Google Scholar]
- Mavridou, A.; Laszka, A. Designing Secure Ethereum Smart Contracts: A Finite State Machine Based Approach. In Financial Cryptography and Data Security; Meiklejohn, S., Sako, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 523–540. [Google Scholar]
- Amani, S.; Bégel, M.; Bortin, M.; Staples, M. Towards Verifying Ethereum Smart Contract Bytecode in Isabelle/HOL. In Proceedings of the 7th ACM SIGPLAN International Conference on Certified Programs and Proofs, Los Angeles, CA, USA, 8–9 January 2018; ACM: New York, NY, USA, 2018; pp. 66–77. [Google Scholar]
- Tikhomirov, S.; Voskresenskaya, E.; Ivanitskiy, I.; Takhaviev, R.; Marchenko, E.; Alexandrov, Y. SmartCheck: Static Analysis of Ethereum Smart Contracts. In Proceedings of the 1st International Workshop on Emerging Trends in Software Engineering for Blockchain, Gothenburg, Sweden, 27 May–3 June 2018; ACM: New York, NY, USA, 2018; pp. 9–16. [Google Scholar]
- Liu, Z.; Qian, P.; Wang, X.; Zhu, L.; He, Q.; Ji, S. Smart Contract Vulnerability Detection: From Pure Neural Network to Interpretable Graph Feature and Expert Pattern Fusion. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–27 August 2021; pp. 2751–2759. [Google Scholar]
- Sendner, C.; Zhang, R.; Hefter, A.; Dmitrienko, A.; Koushanfar, F. G-Scan: Graph Neural Networks for Line-Level Vulnerability Identification in Smart Contracts. arXiv 2023, arXiv:2307.08549. [Google Scholar]
- Chen, Y. Vulnerability-Hunter: An Adaptive Feature Perception Attention Network for Smart Contract Vulnerabilities. arXiv 2024, arXiv:2407.05318. [Google Scholar]
- Qian, P.; Liu, Z.; He, Q.; Huang, B.; Tian, D.; Wang, X. Smart Contract Vulnerability Detection Technique: A Survey. arXiv 2022, arXiv:2209.05872. [Google Scholar]
- Li, J.; Lu, G.; Gao, Y.; Gao, F. A Smart Contract Vulnerability Detection Method Based on Multimodal Feature Fusion and Deep Learning. Mathematics 2023, 11, 4823. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. Cbgru: A Detection Method of Smart Contract Vulnerability Based on a Hybrid Model. Sensors 2022, 22, 3577. [Google Scholar] [CrossRef]
- Wang, M.; Xie, Z.; Wen, X.; Li, J.; Zhou, K. Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM. Electronics 2023, 12, 2327. [Google Scholar] [CrossRef]
- Deng, W.; Wei, H.; Huang, T.; Cao, C.; Peng, Y.; Hu, X. Smart Contract Vulnerability Detection Based on Deep Learning and Multimodal Decision Fusion. Sensors 2023, 23, 7246. [Google Scholar] [CrossRef] [PubMed]
- Bani-Hani, R.M.; Shatnawi, A.S.; Al-Yahya, L. Vulnerability Detection and Classification of Ethereum Smart Contracts Using Deep Learning. Future Internet 2024, 16, 321. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Leng, J.; Zhou, M.; Zhao, J.L.; Huang, Y.; Bian, Y. Blockchain Security: A Survey of Techniques and Research Directions. IEEE Trans. Serv. Comput. 2022, 15, 2490–2510. [Google Scholar] [CrossRef]
- Suryotrisongko, H.; Musashi, Y. Evaluating Hybrid Quantum-Classical Deep Learning for Cybersecurity Botnet DGA Detection. Procedia Comput. Sci. 2022, 197, 223–229. [Google Scholar] [CrossRef]
- Qaiser, S.; Ali, R. Text Mining: Use of TF-IDF to Examine the Relevance of Words to Documents. Int. J. Comput. Appl. 2018, 181, 25–29. [Google Scholar] [CrossRef]
- Trstenjak, B.; Mikac, S.; Donko, D. KNN with TF-IDF Based Framework for Text Categorization. Procedia Eng. 2014, 69, 1356–1364. [Google Scholar] [CrossRef]
- Ou, J.; Chen, Y.; Tian, W. Lossless Acceleration of Large Language Model via Adaptive N-Gram Parallel Decoding. arXiv 2024, arXiv:2404.08698. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An Introduction to Quantum Machine Learning. Contemp. Phys. 2015, 56, 172–185. [Google Scholar] [CrossRef]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC ’96, Philadelphia, PA, USA, 22–24 May 1996; ACM Press: New York, NY, USA, 1996; pp. 212–219. [Google Scholar]
- Hidary, J.D. Quantum Computing: An Applied Approach; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-83273-5. [Google Scholar]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Theis, T.N.; Wong, H.-S.P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 2017, 19, 41–50. [Google Scholar] [CrossRef]
- Montanaro, A. Quantum Algorithms: An Overview. NPJ Quantum Inf. 2016, 2, 1–8. [Google Scholar] [CrossRef]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Quantum Science and Technology; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-96423-2. [Google Scholar]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised Learning with Quantum-Enhanced Feature Spaces. Nature 2019, 567, 209–212. [Google Scholar]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A. Quantum Supremacy Using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized Quantum Circuits as Machine Learning Models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren Plateaus in Quantum Neural Network Training Landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum Circuit Learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L. Variational Quantum Algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Qml.BasicEntanglerLayers. Available online: https://docs.pennylane.ai/en/stable/code/api/pennylane.BasicEntanglerLayers.html (accessed on 20 March 2025).
- Paayas, P.; Sridevi, S.; Kanimozhi, T.; Valliammai, M.; Mohanraj, J.; Kumar, V.; Bakiya, A.; Rithani, M. Hybrid Classical Quantum Neural Network Based Classification of Photonic Band Gap Crystal Structure Defects. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Solidity 0.4.11 Release Announcement. Available online: https://soliditylang.org/blog/2017/05/03/solidity-0.4.11-release-announcement/ (accessed on 20 March 2025).
- Filatov, S.; Auzinsh, M. Towards Two Bloch Sphere Representation of Pure Two-Qubit States and Unitaries. Entropy 2024, 26, 280. [Google Scholar] [CrossRef]
- Guo, J.; Lu, L.; Li, J. Smart Contract Vulnerability Detection Based on Multi-Scale Encoders. Electronics 2024, 13, 489. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).