Active Gait Retraining with Lower Limb Exoskeleton Based on Robust Force Control
Abstract
1. Introduction
2. Materials and Methods
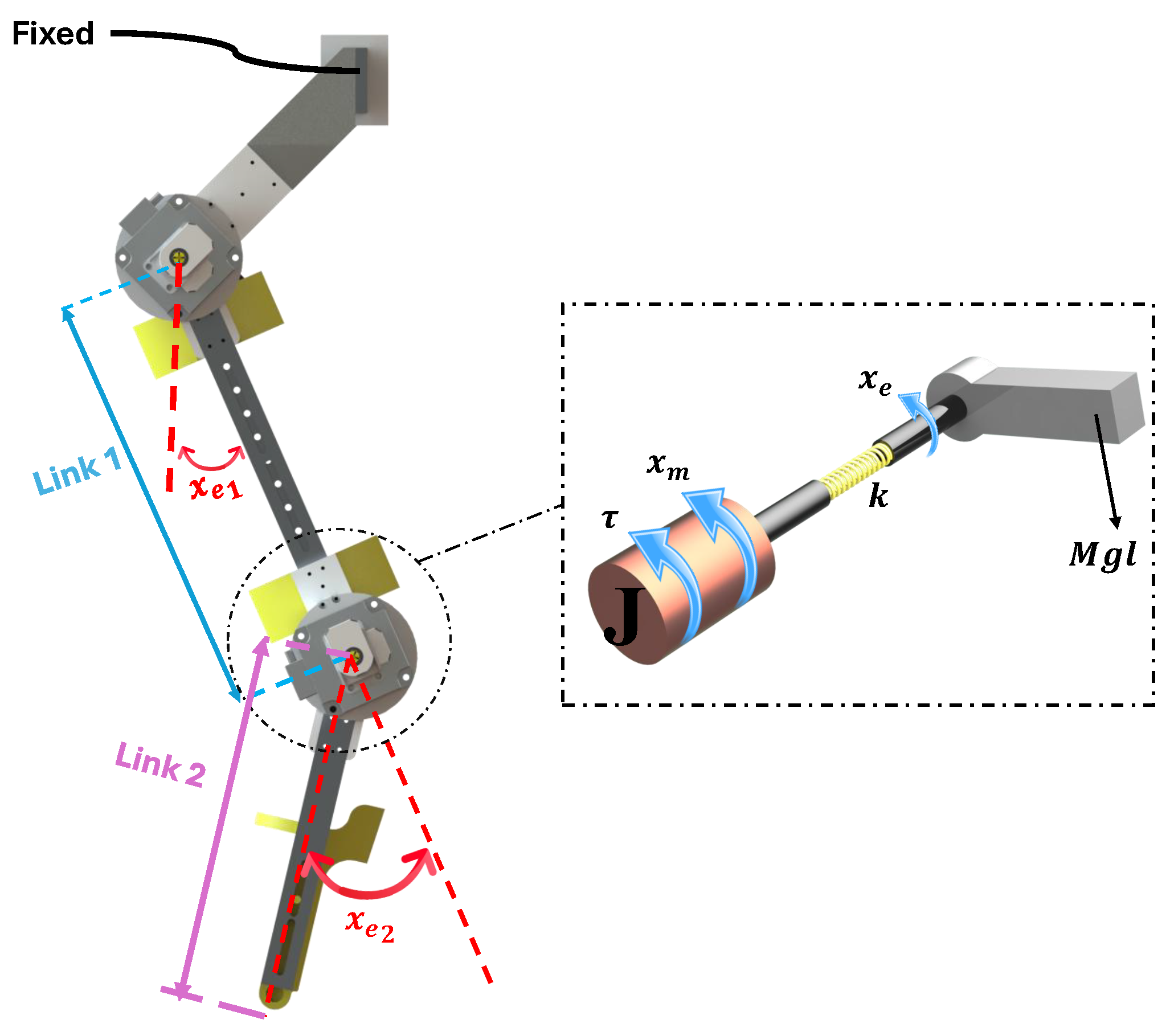
2.1. Exoskeleton Description
2.2. Exoskeleton Dynamic Model
3. Force Control of an Exoskeleton with Elastic Joints
Stability Proof
4. Tracking Control of the Exoskeleton
Stability Proof
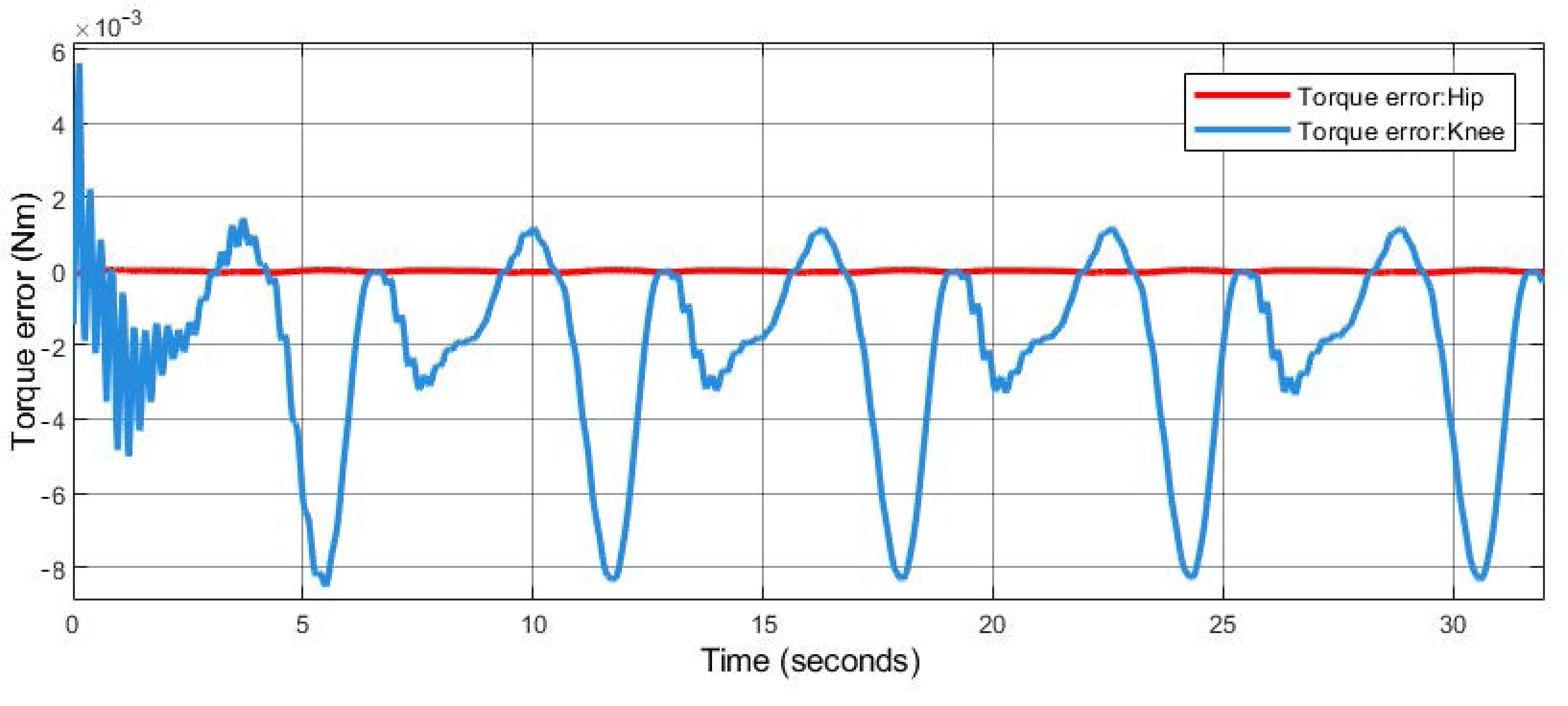
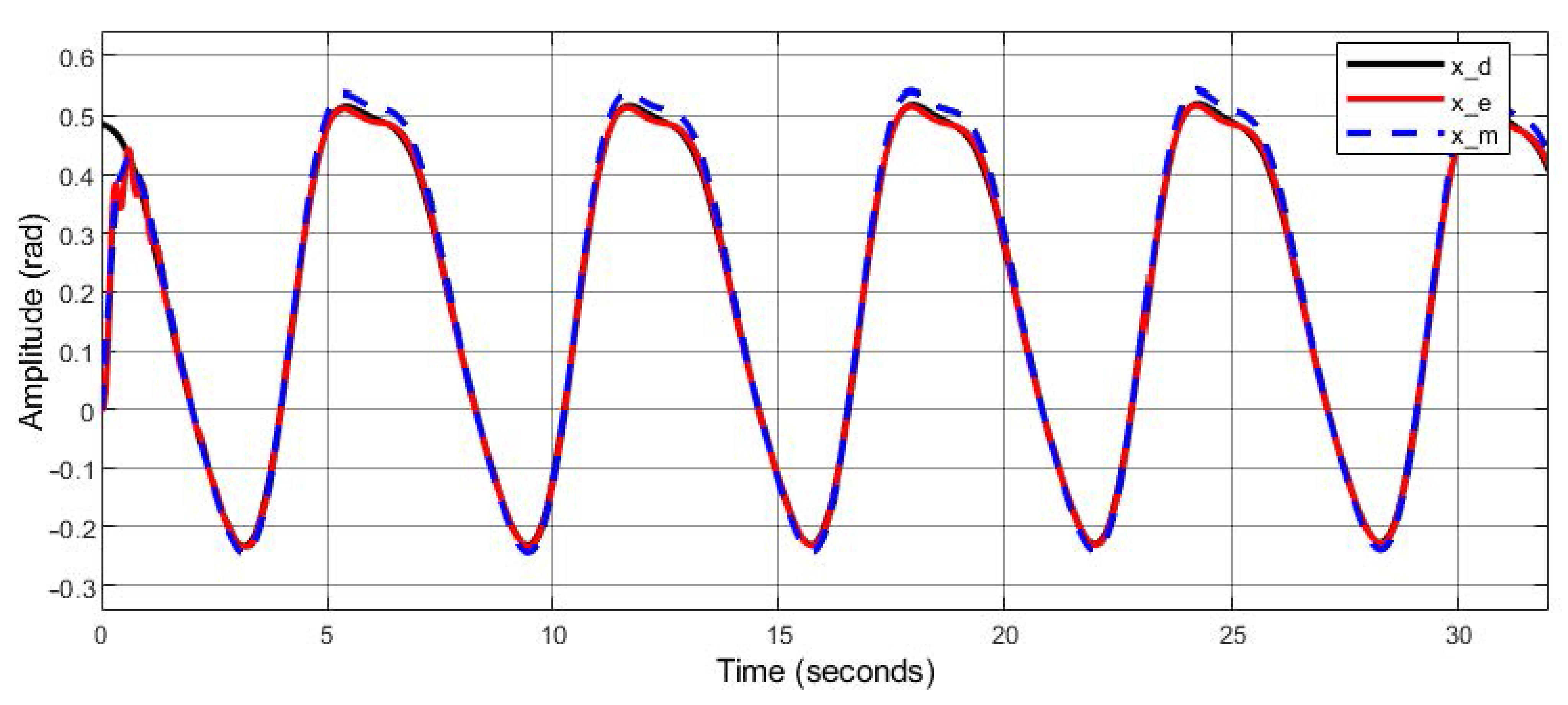
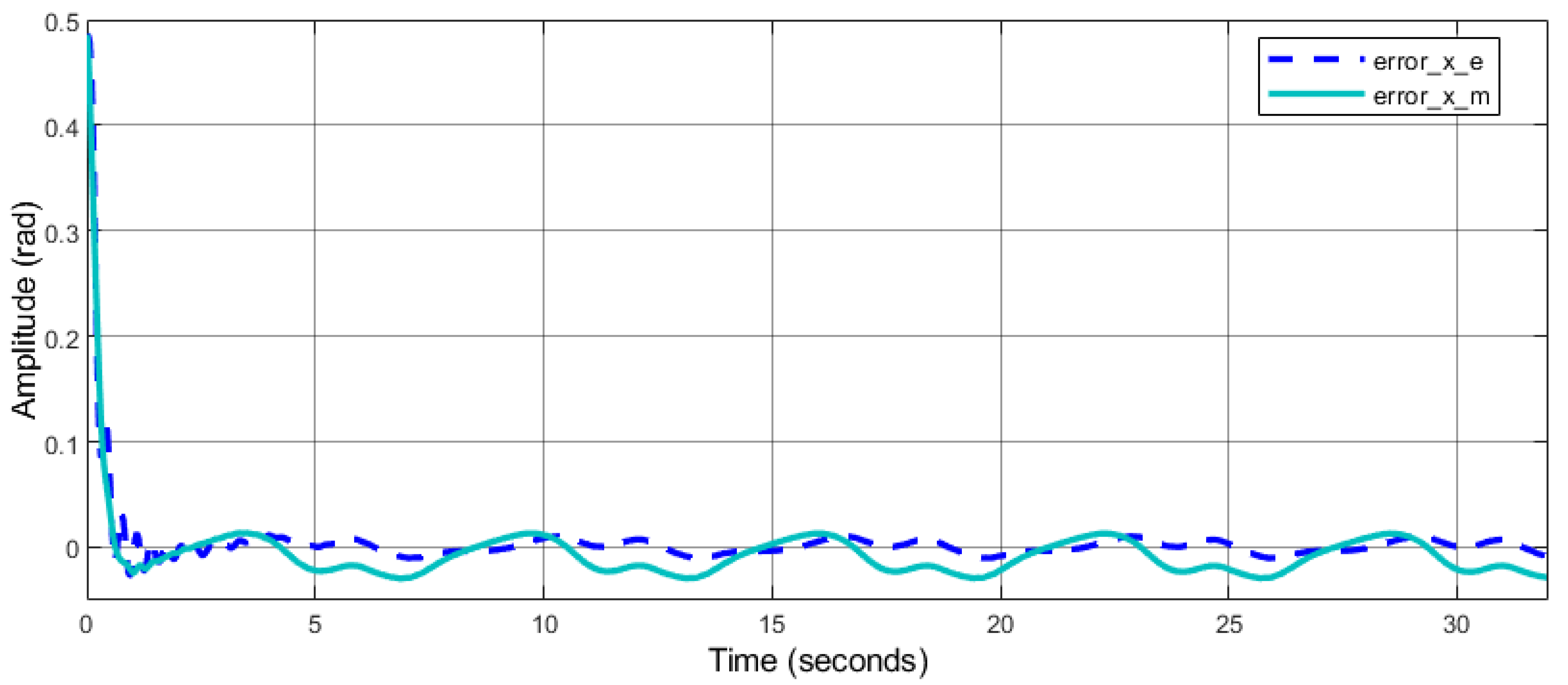
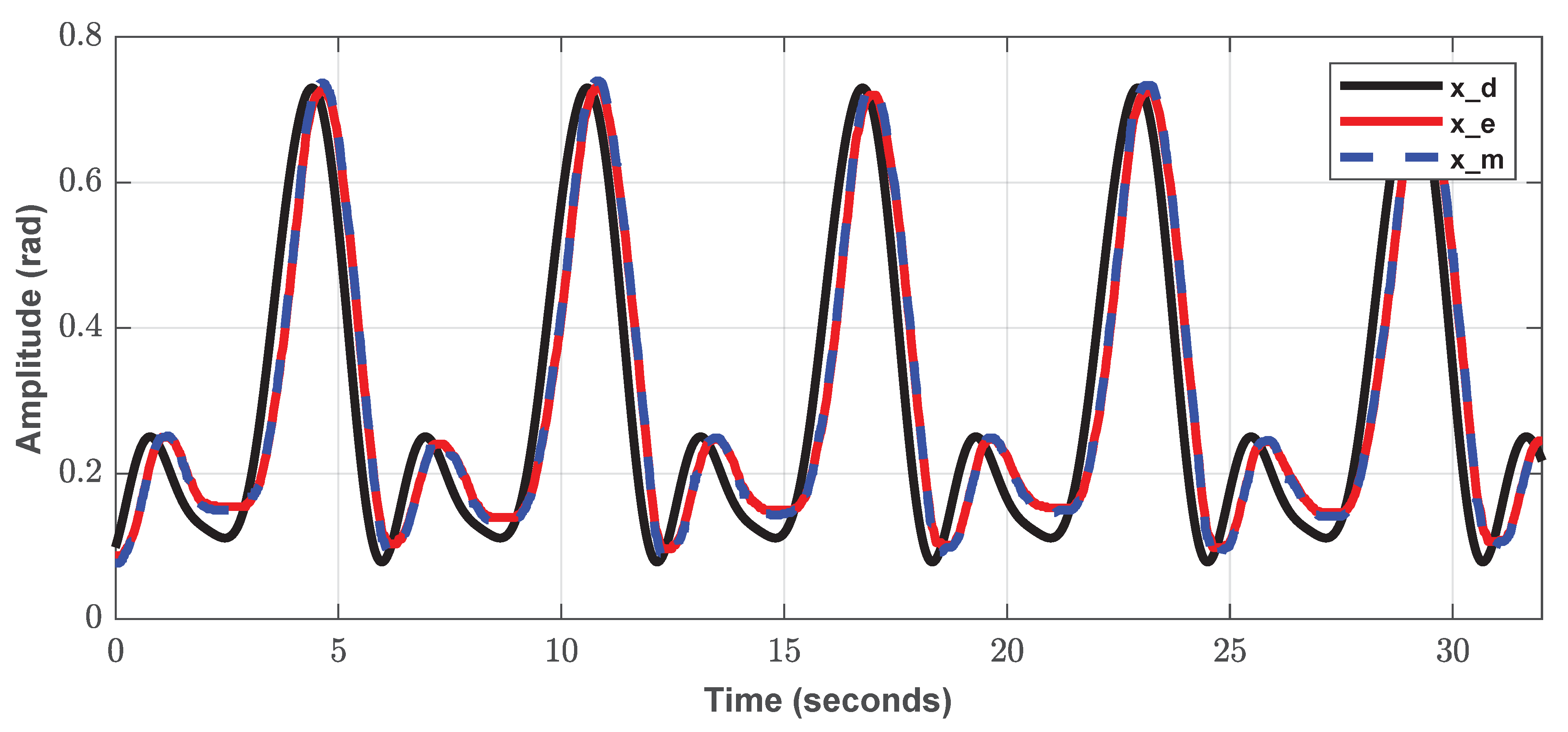
5. Experimental and Simulation Results
5.1. Simulation Results
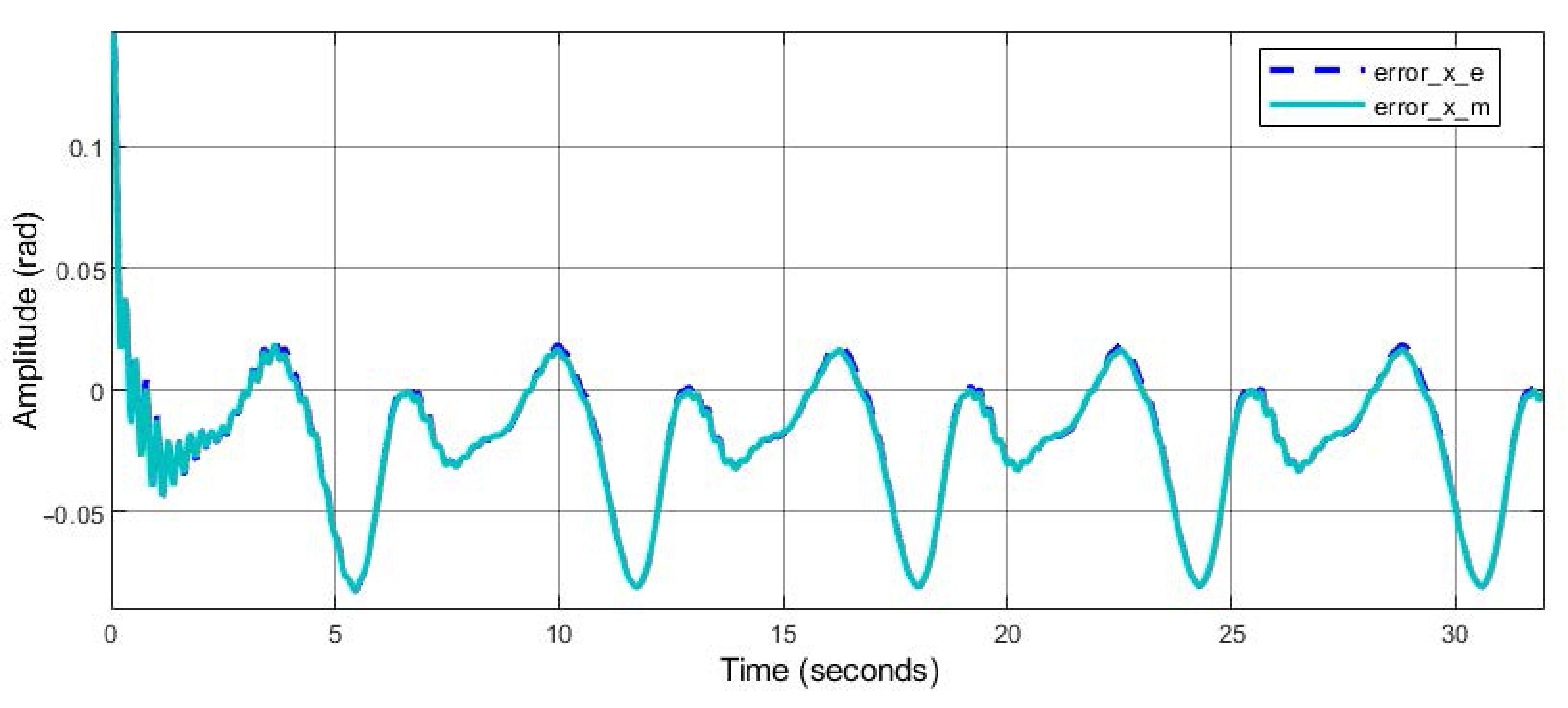
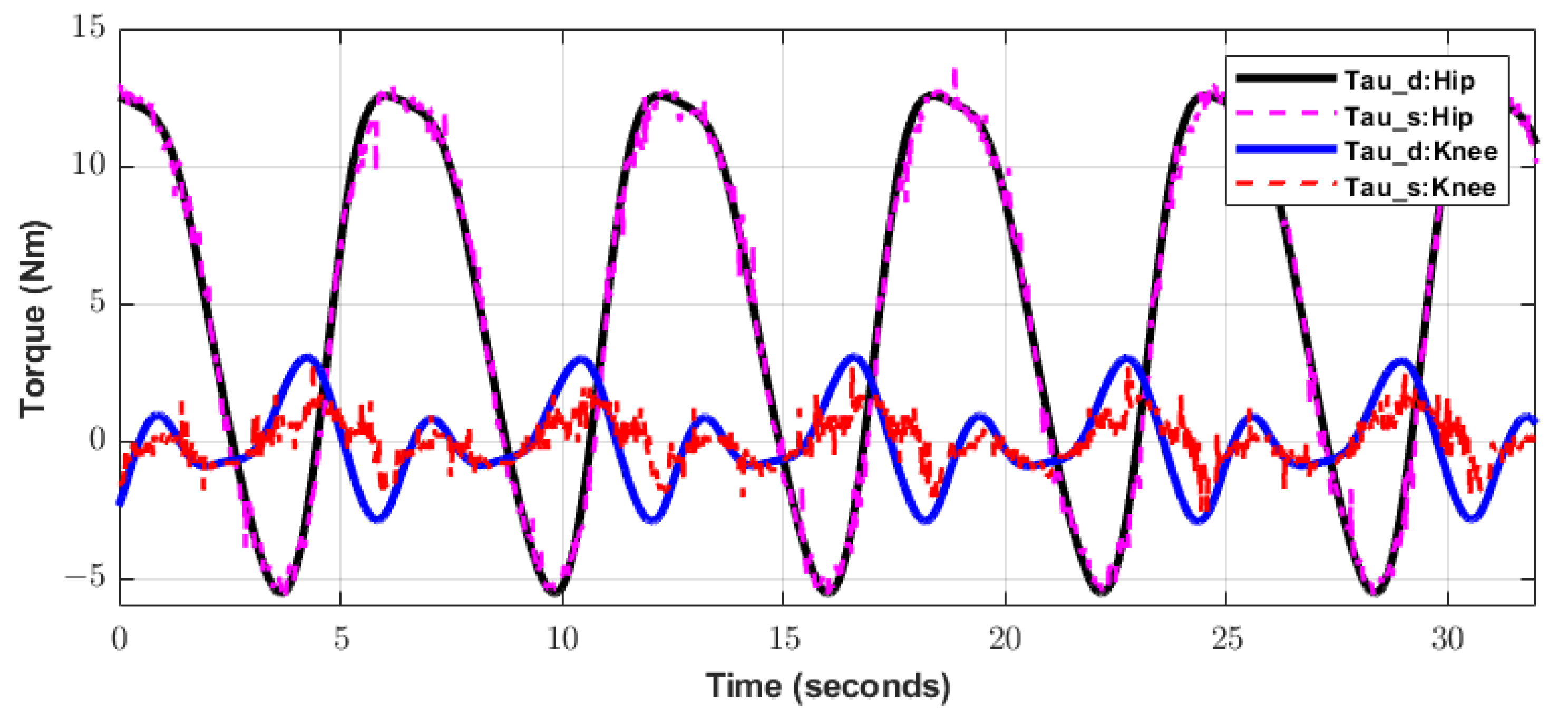
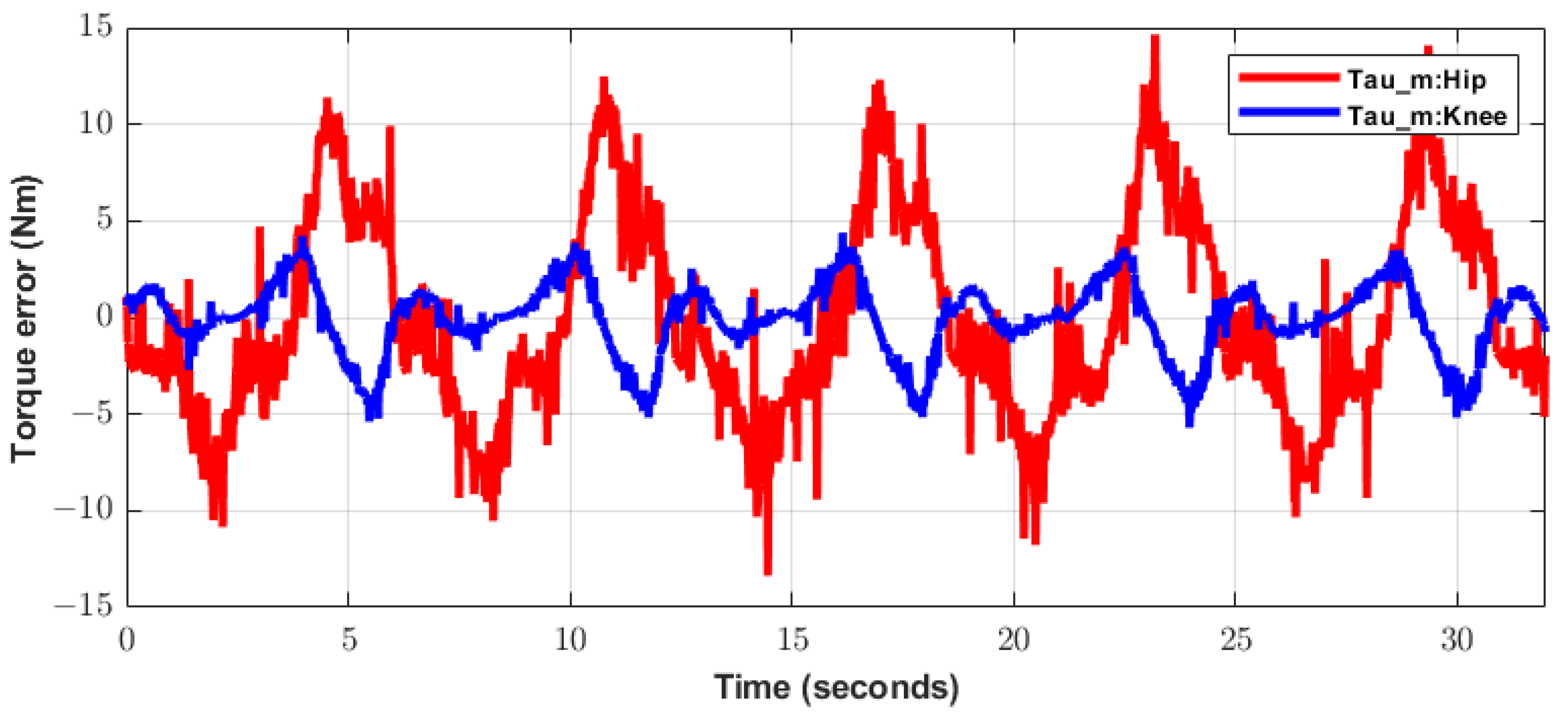
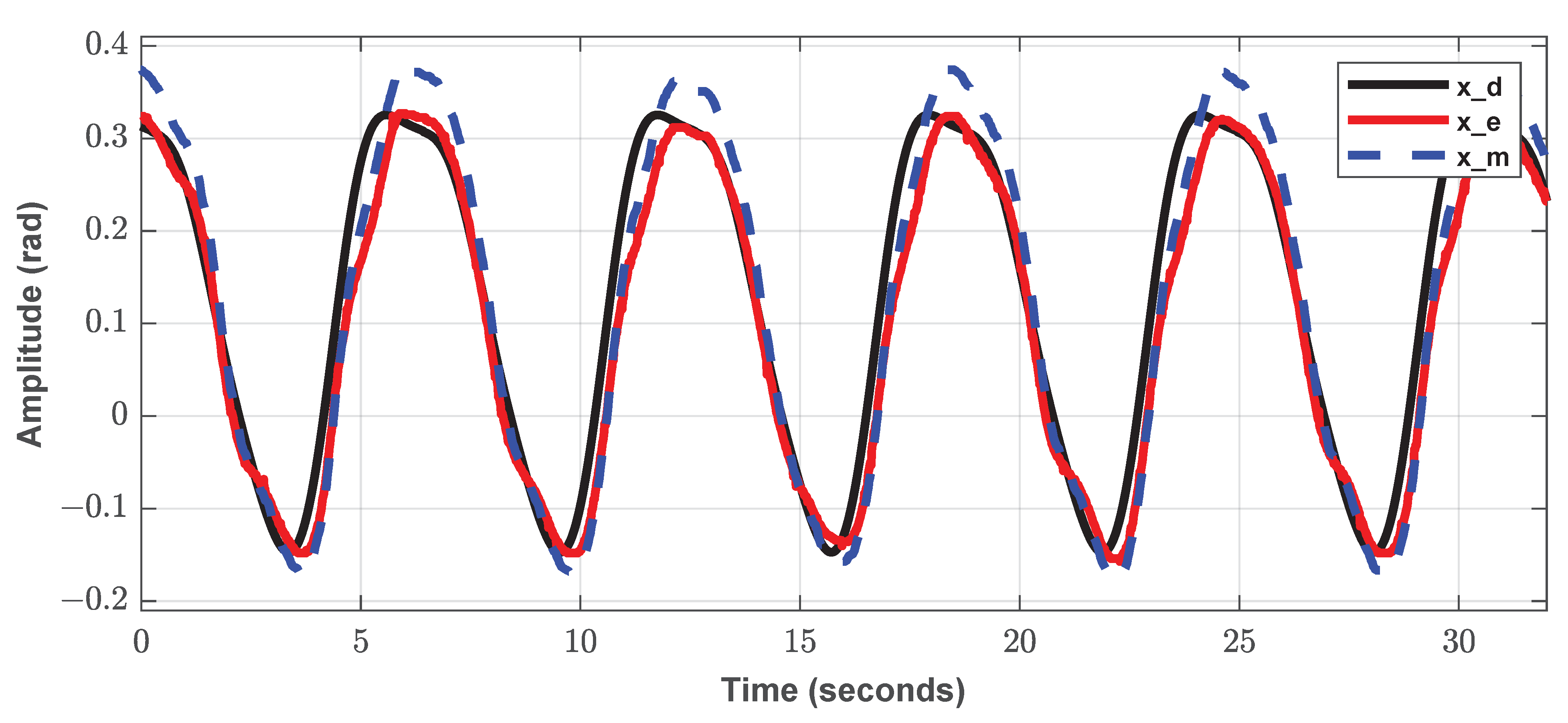
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Instituto de Salud para el Bienestar. Día Mundial de la Rehabilitación Motriz—23 de Marzo. Available online: https://www.gob.mx/insabi/articulos/dia-mundial-de-la-rehabilitacion-motriz-23-de-marzo (accessed on 31 January 2025).
- OMS and Banco Mundial. Informe Mundial sobre la Discapacidad 2011; Organización Mundial de la Salud & Banco Mundial: Geneva, Switzerland, 2011. [Google Scholar]
- Wang, Y.; Tian, Y.; Guo, Y.; Wang, H. Active torque-based gait adjustment multi-level control strategy for lower limb patient–exoskeleton coupling system in rehabilitation training. Math. Comput. Simul. 2024, 215, 357–381. [Google Scholar] [CrossRef]
- Gorgey, A.S. Robotic exoskeletons: The current pros and cons. World J. Orthop. 2018, 9, 112. [Google Scholar] [PubMed]
- Ramos, J.; Espuela, E.M.; Lora Millán, J.S.; Castano, J.A.; Borromeo, S.; Nieto, R.; Fernández, P.; Carballeira, J.; del Ama, A.J. Estrategia de control de un robot de rehabilitación de la marcha pseudoestacionario. J. Autom. 2023, 44, 95–98. [Google Scholar] [CrossRef]
- Zhu, F.; Kern, M.; Fowkes, E.; Afzal, T.; Contreras-Vidal, J.L.; Francisco, G.E.; Chang, S.H. Effects of an exoskeleton-assisted gait training on post-stroke lower-limb muscle coordination. J. Neural Eng. 2021, 18, 046039. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, A.; Lobo-Prat, J.; Font-Llagunes, J.M. Systematic review on wearable lower-limb exoskeletons for gait training in neuromuscular impairments. J. Neuroeng. Rehabil. 2021, 18, 22. [Google Scholar] [CrossRef]
- Rodriguez Tapia, G.; Doumas, I.; Lejeune, T.; Previnaire, J.G. Wearable powered exoskeletons for gait training in tetraplegia: A systematic review on feasibility, safety and potential health benefits. Acta Neurol. Belg. 2022, 122, 1149–1162. [Google Scholar]
- Nepomuceno, P.; Souza, W.H.; Pakosh, M.; Musselman, K.E.; Craven, B.C. Exoskeleton-based exercises for overground gait and balance rehabilitation in spinal cord injury: A systematic review of dose and dosage parameters. J. Neuroeng. Rehabil. 2024, 21, 73. [Google Scholar] [CrossRef]
- Edwards, D.J.; Forrest, G.; Cortes, M.; Weightman, M.M.; Sadowsky, C.; Chang, S.H.; Furman, K.; Bialek, A.; Prokup, S.; Carlow, J.; et al. Walking improvement in chronic incomplete spinal cord injury with exoskeleton robotic training (WISE): A randomized controlled trial. Spinal Cord 2020, 60, 522–532. [Google Scholar] [CrossRef]
- Tu, Y.; Zhu, A.; Song, J.; Shen, H.; Shen, Z.; Zhang, X.; Cao, G. An Adaptive Sliding Mode Variable Admittance Control Method for Lower Limb Rehabilitation Exoskeleton Robot. Appl. Sci. 2020, 10, 2536. [Google Scholar] [CrossRef]
- Narayan, J.; Abbas, M.; Dwivedy, S.K. Adaptive backstepping sliding mode subject-cooperative control for a pediatric lower-limb exoskeleton robot. Trans. Inst. Meas. Control 2025, 47, 352–368. [Google Scholar] [CrossRef]
- Pérez-San Lázaro, R.; Salgado, I.; Chairez, I. Adaptive sliding-mode controller of a lower limb mobile exoskeleton for active rehabilitation. ISA Trans. 2021, 109, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Jia, S.; Shan, J. Velocity-Free Trajectory Tracking and Active Vibration Control of Flexible Space Manipulator. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 435–450. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Shan, J. Iterative learning control of a flexible manipulator considering uncertain parameters and unknown repetitive disturbance. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 2209–2214. [Google Scholar] [CrossRef]
- Chen, W.; Lyu, M.; Ding, X.; Wang, J.; Zhang, J. Electromyography-controlled lower extremity exoskeleton to provide wearers flexibility in walking. Biomed. Signal Process. Control 2023, 79, 104096. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, K.; Zhang, L.; Wu, X.; Zhang, T.; Li, Q.; Li, X.; Su, C.Y. Human-in-the-Loop Control of a Wearable Lower Limb Exoskeleton for Stable Dynamic Walking. IEEE/ASME Trans. Mechatron. 2020, 26, 2700–2711. [Google Scholar] [CrossRef]
- Mayag, L.J.A.; Múnera, M.; Cifuentes, C.A. Human-in-the-Loop Control for AGoRA Unilateral Lower-Limb Exoskeleton. J. Intell. Robot. Syst. 2021, 104, 3. [Google Scholar] [CrossRef]
- Xie, L.; Huang, L. Wirerope-driven exoskeleton to assist lower-limb rehabilitation of hemiplegic patients by using motion capture. Assem. Autom. 2019, 40, 48–54. [Google Scholar] [CrossRef]
- Karunakaran, K.K.; Abbruzzese, K.; Androwis, G.; Foulds, R.A. A Novel User Control for Lower Extremity Rehabilitation Exoskeletons. Front. Robot. AI 2020, 7, 108. [Google Scholar] [CrossRef]
- Gui, K.; Tan, U.X.; Liu, H.; Zhang, D. Electromyography-Driven Progressive Assist-as-Needed Control for Lower Limb Exoskeleton. IEEE Trans. Med. Robot. Bionics 2020, 2, 50–58. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, J.; Chen, D.; Chen, S.; Wang, X. Adaptive Gait Trajectory and Event Prediction of Lower Limb Exoskeletons for Various Terrains Using Reinforcement Learning. J. Intell. Robot. Syst. 2023, 109, 23. [Google Scholar]
- Kolaghassi, R.; Marcelli, G.; Sirlantzis, K. Effect of Gait Speed on Trajectory Prediction Using Deep Learning Models for Exoskeleton Applications. Sensors 2023, 23, 5687. [Google Scholar] [CrossRef]
- Luo, S.; Androwis, G.; Adamovich, S.; Nunez, E.; Su, H.; Zhou, X. Robust walking control of a lower limb rehabilitation exoskeleton coupled with a musculoskeletal model via deep reinforcement learning. J. Neuroeng. Rehabil. 2023, 20, 34. [Google Scholar] [CrossRef] [PubMed]
- Ibrayev, S.; Omarov, B.; Amanov, B.; Momynkulov, Z. Development of a Deep Learning-Enhanced Lower-Limb Exoskeleton Using Electromyography Data for Post-Neurovascular Rehabilitation. Eng. Sci. 2024, 31, 1269. [Google Scholar] [CrossRef]
- Cardona, M.; García Cena, C.E.; Serrano, F.; Saltaren, R. ALICE: Conceptual Development of a Lower Limb Exoskeleton Robot Driven by an On-Board Musculoskeletal Simulator. Sensors 2020, 20, 789. [Google Scholar] [CrossRef]
- Aole, S.; Elamvazuthi, I.; Waghmare, L.; Patre, B.; Meriaudeau, F. Improved Active Disturbance Rejection Control for Trajectory Tracking Control of Lower Limb Robotic Rehabilitation Exoskeleton. Sensors 2020, 20, 3681. [Google Scholar] [CrossRef]
- Gao, M.; Wang, Z.; Pang, Z.; Sun, J.; Li, J.; Li, S.; Zhang, H. Electrically Driven Lower Limb Exoskeleton Rehabilitation Robot Based on Anthropomorphic Design. Machines 2022, 10, 266. [Google Scholar] [CrossRef]
- Ren, B.; Zhang, Z.; Zhang, C.; Chen, S. Motion trajectories prediction of lower limb exoskeleton based on long short-term memory (LSTM) networks. Actuators 2022, 11, 73. [Google Scholar] [CrossRef]
- Limcharoen, P.; Khamsemanan, N.; Nattee, C. Gait recognition and re-identification based on regional lstm for 2-second walks. IEEE Access 2021, 9, 112057–112068. [Google Scholar] [CrossRef]
- Zaroug, A.; Garofolini, A.; Lai, D.T.; Mudie, K.; Begg, R. Prediction of gait trajectories based on the Long Short Term Memory neural networks. PLoS ONE 2021, 16, e0255597. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, P.; Peng, X.; Zhao, J.; Liu, K.; Miao, M.; Zhao, P.; Luo, D.; Li, Y. Autonomous motion and control of lower limb exoskeleton rehabilitation robot. Front. Bioeng. Biotechnol. 2023, 11, 1223831. [Google Scholar] [CrossRef]
- Sharma, R.; Gaur, P.; Bhatt, S.; Joshi, D. Optimal fuzzy logic-based control strategy for lower limb rehabilitation exoskeleton. Appl. Soft Comput. 2021, 105, 107226. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, J.; Elsabbagh, A. Fuzzy radial-based impedance controller design for lower limb exoskeleton robot. Robotica 2023, 41, 326–345. [Google Scholar] [CrossRef]
- Yu, S.; Liu, C.; Ye, C.; Fu, R. Passive and Active Training Control of an Omnidirectional Mobile Exoskeleton Robot for Lower Limb Rehabilitation. Actuators 2024, 13, 202. [Google Scholar] [CrossRef]
- Sanz-Pena, I.; Blanco, J.; Kim, J.H. Computer Interface for Real-Time Gait Biofeedback Using a Wearable Integrated Sensor System for Data Acquisition. IEEE Trans. -Hum.-Mach. Syst. 2021, 51, 484–493. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Shkolnikov, I.A.; Brown, M.D. An asymptotic second-order smooth sliding mode control. Asian J. Control 2003, 5, 498–504. [Google Scholar]
- Calanca, A.; Fiorini, P. Impedance control of series elastic actuators based on well-defined force dynamics. Robot. Auton. Syst. 2017, 96, 81–92. [Google Scholar] [CrossRef]
- Rosales-Luengas, Y.; Espinosa-Espejel, K.I.; Lopéz-Gutiérrez, R.; Salazar, S.; Lozano, R. Lower Limb Exoskeleton for Rehabilitation with Flexible Joints and Movement Routines Commanded by Electromyography and Baropodometry Sensors. Sensors 2023, 23, 5252. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1.509 [kg] | 0.1213 [kg·m2] | ||
| 1.500 [kg] | 0.0116 [kg·m2] | ||
| 0.0983 [m] | J | diag (0.01, 0.01) | |
| 0.0229 [m] | B | diag (0.015, 0.015) | |
| 0.364 [m] | K | diag (138.65, 138.65) | |
| 0.26 [m] |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| diag (1000, 500) | diag (8, 15) | ||
| diag (0.085, 0.061) | diag (0.19, 0.1) |
| Resulting Error | Hip | Knee |
|---|---|---|
| Mean Squared Error (MSE) | 0.0022 rad2 | 0.0065 rad2 |
| Mean Absolute Error (MAE) | 0.0328 rad | 0.0661 rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosales-Luengas, Y.; Salazar, S.; Rangel-Popoca, S.J.; Cortés-García, Y.; Flores, J.; Lozano, R. Active Gait Retraining with Lower Limb Exoskeleton Based on Robust Force Control. Appl. Sci. 2025, 15, 4032. https://doi.org/10.3390/app15074032
Rosales-Luengas Y, Salazar S, Rangel-Popoca SJ, Cortés-García Y, Flores J, Lozano R. Active Gait Retraining with Lower Limb Exoskeleton Based on Robust Force Control. Applied Sciences. 2025; 15(7):4032. https://doi.org/10.3390/app15074032
Chicago/Turabian StyleRosales-Luengas, Yukio, Sergio Salazar, Saúl J. Rangel-Popoca, Yahel Cortés-García, Jonathan Flores, and Rogelio Lozano. 2025. "Active Gait Retraining with Lower Limb Exoskeleton Based on Robust Force Control" Applied Sciences 15, no. 7: 4032. https://doi.org/10.3390/app15074032
APA StyleRosales-Luengas, Y., Salazar, S., Rangel-Popoca, S. J., Cortés-García, Y., Flores, J., & Lozano, R. (2025). Active Gait Retraining with Lower Limb Exoskeleton Based on Robust Force Control. Applied Sciences, 15(7), 4032. https://doi.org/10.3390/app15074032







