Collaborative Optimization on Both Weight and Fatigue Life of Fifth Wheel Based on Hybrid Random Forest with Improved BP Algorithm

Abstract

The fifth wheel of the semi-trailer tractor is a key component connecting the tractor and the semi-trailer. During operation, the fifth wheel experiences frequent irregular and repetitive loading conditions. This leads to a decline in its durability and fatigue life, which can significantly impact the efficiency of cargo transport. The lightweight design enhances both the transport efficiency and fuel economy of the semi-trailer tractor. In this research, to achieve weight reduction while maintaining the wear-resistant failure protection performance in semi-trailer tractors, we selected a new material—special steel for saddles (SD600). Its stress-strain and fatigue life were analyzed under static compression, uphill lifting, and steering rollover conditions. These findings confirm the necessity of implementing lightweighting measures. Using a multi-objective genetic algorithm, we established an optimization model aimed at balancing weight reduction and fatigue life enhancement. As a result, the optimized fifth wheel achieved a 24.11% reduction in mass, while its fatigue life increased by 15 times, thus realizing the synergistic optimization of weight and fatigue life. We proposed a prediction model combining a random forest algorithm with an optimized back propagation (BP) neural network. Compared to the traditional BP approach, this model improved the mean absolute percentage error (MAPE) by 47.62%. Quadratic optimization was conducted based on the optimal design option set, using data analysis to determine the range of values of each variable under specific constraints and to verify the stress-strain and fatigue life for very small values in the range.

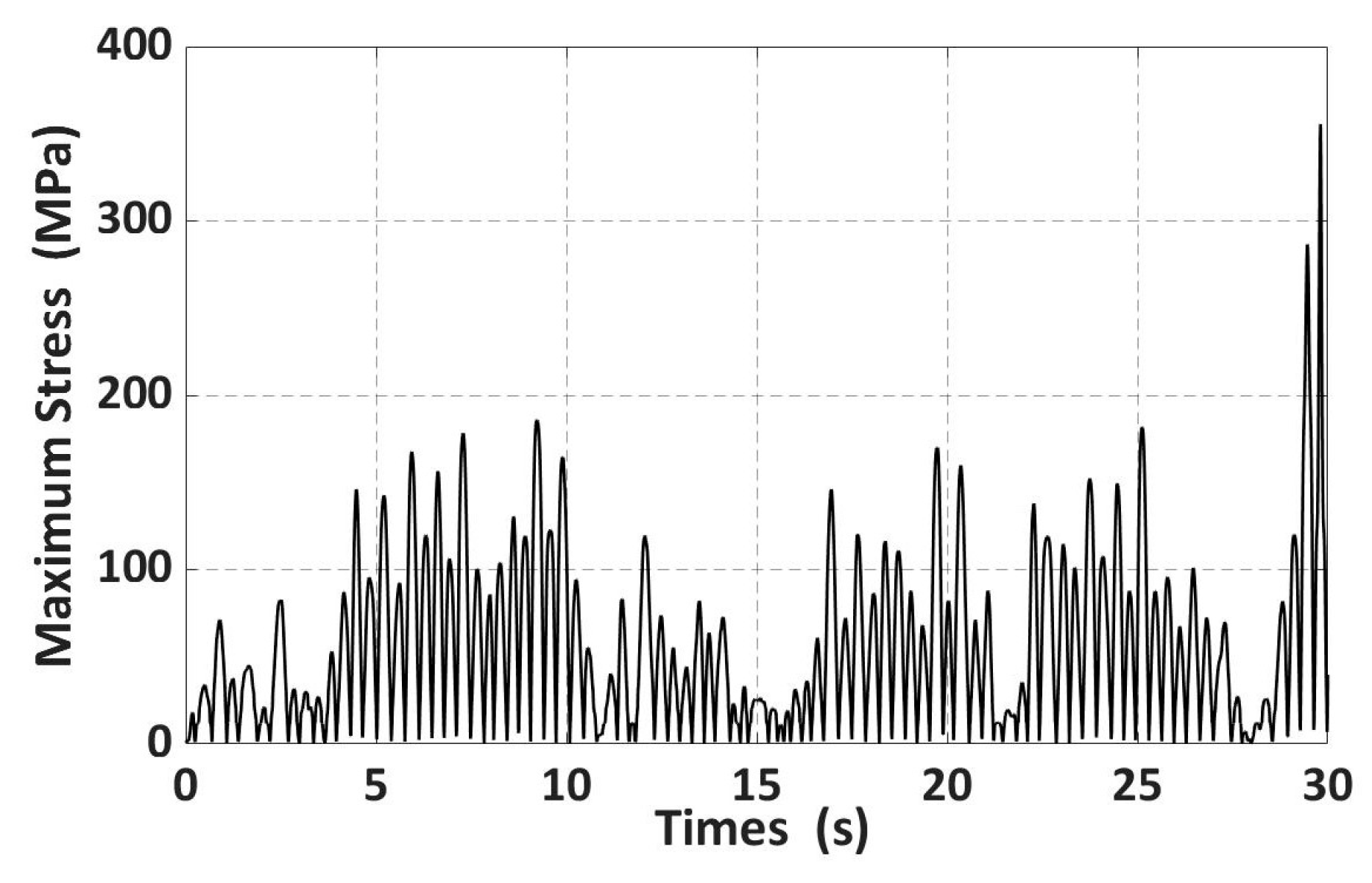
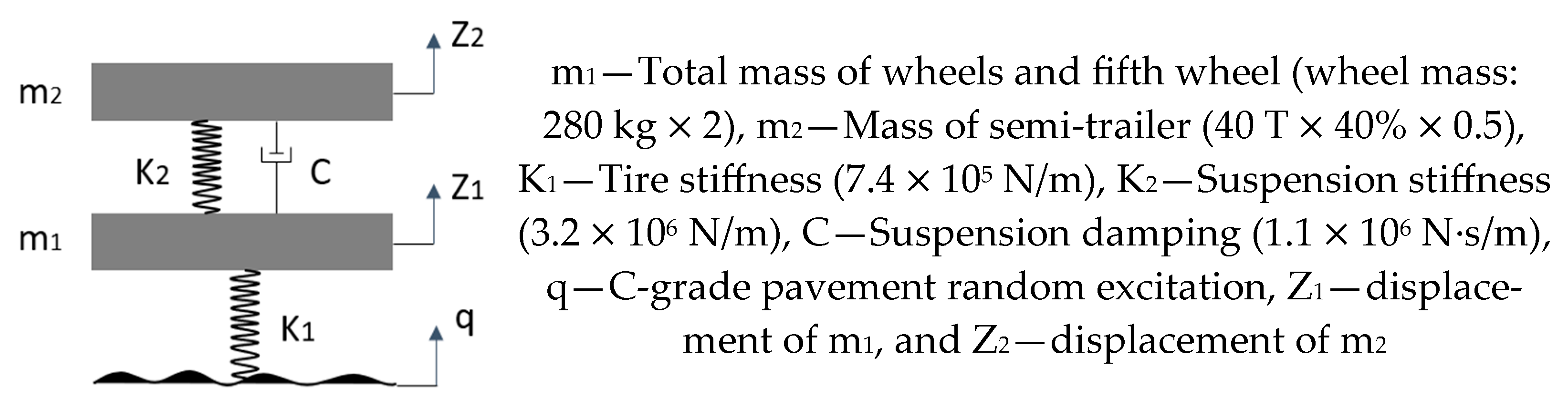1. Introduction

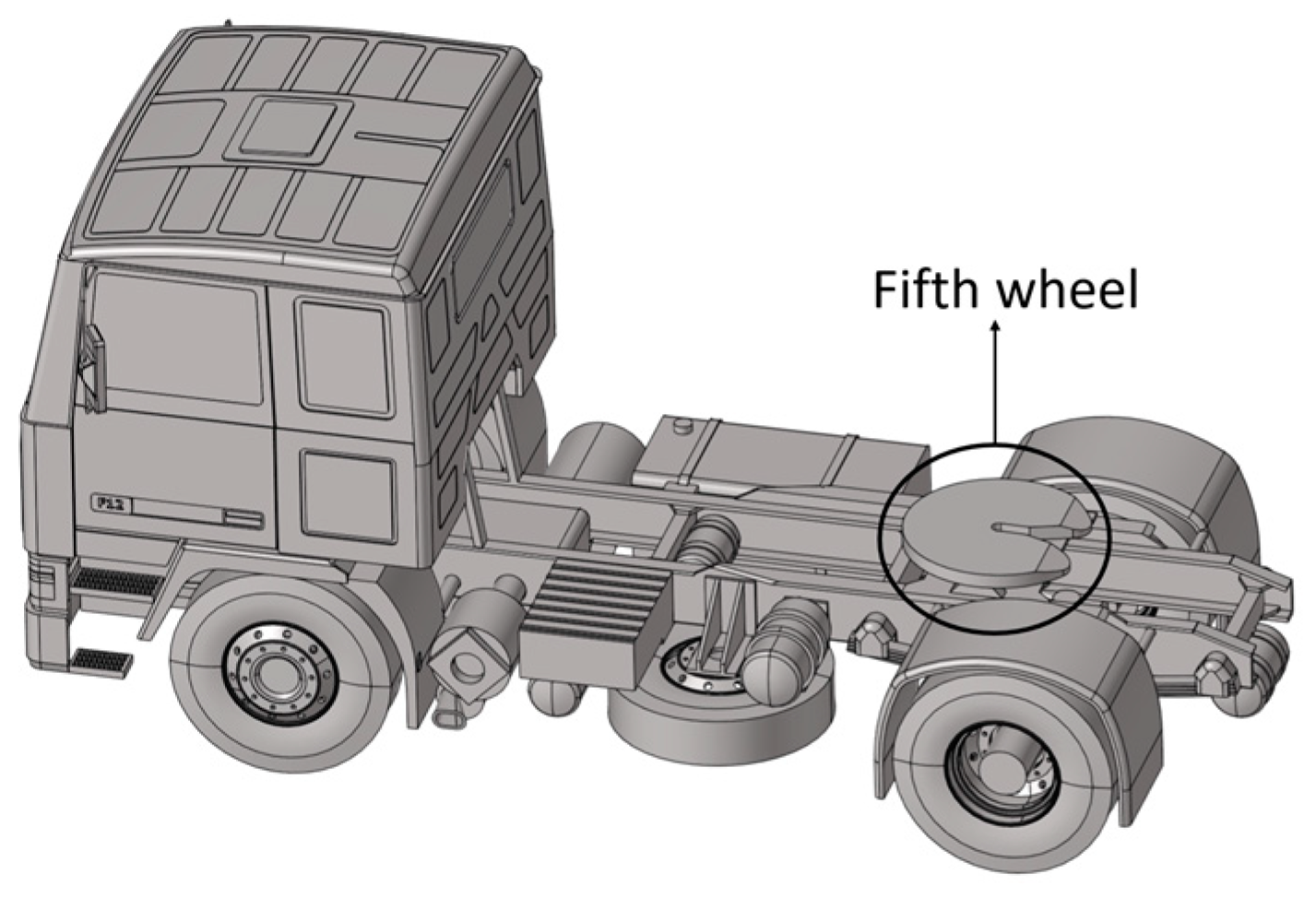
With the continuous development of commercial vehicles and the ongoing expansion of the transport market, semi-trailers (as shown in Figure 1) have become increasingly dominant in transporting goods. Compared to ordinary trucks, semi-trailers offer a significant improvement: Their transport efficiency can be increased by up to 30–50%, while reducing both transportation costs (by 30–40%) and fuel consumption (by 20–30%). The results of relevant experiments indicate that for every 100 kg reduction in overall vehicle weight, the fuel consumption per 100 km decreases by approximately 0.3 to 0.6 liters [1]. As a critical component of semi-trailers, the fifth wheel plays an essential role in connecting the tractor and the trailer, which is vital for ensuring the vehicle’s safety, stability, and reliability. To enhance these aspects further, optimizing the lightweight design of the fifth wheel represents an important area of research [2].

The fatigue performances of the fifth wheels of tractors have been studied. The mounting position of the fifth wheel on a semi-trailer largely determines the dynamics of the cab and durability of the components [3]. As the forward offset of the fifth wheel increases, the axle loads on the first, fourth, fifth, and sixth wheels increase, whereas the axle loads on the second and third wheels decrease [4]. The tractor–semi-trailer with the Split fifth wheel coupling (SFWC) model has less deviation tracking and better wear resistance than the conventional tractor–semi-trailer [5]. By building a finite element model of the semi-trailer’s fifth wheel, suspension, mechanical spring, pneumatic spring, and press components and performing fatigue analysis, it was determined that the location of the saddle where the fatigue damage occurred was in the connection area of the second beam and the force-transferring components [6,7]. According to the corresponding fatigue damage areas, combined with the layout characteristics of the semi-trailer traction seat, it is possible to perform reasonable maintenance of the fifth wheel to ensure its service life [8].

For the lightweight design and structural optimization of the fifth wheel, it is necessary to determine the corresponding conditions to verify its strength and safety performance. According to the actual condition of the fifth wheel, the stress–strain distribution is obtained, in which the maximum equivalent stress of the fifth wheel is located in the contact area of the rear reinforcement, and the maximum deformation is located at the rear top of the saddle body, which provides a basis and reference for the structural improvement and optimization of the fifth wheel [9,10]. 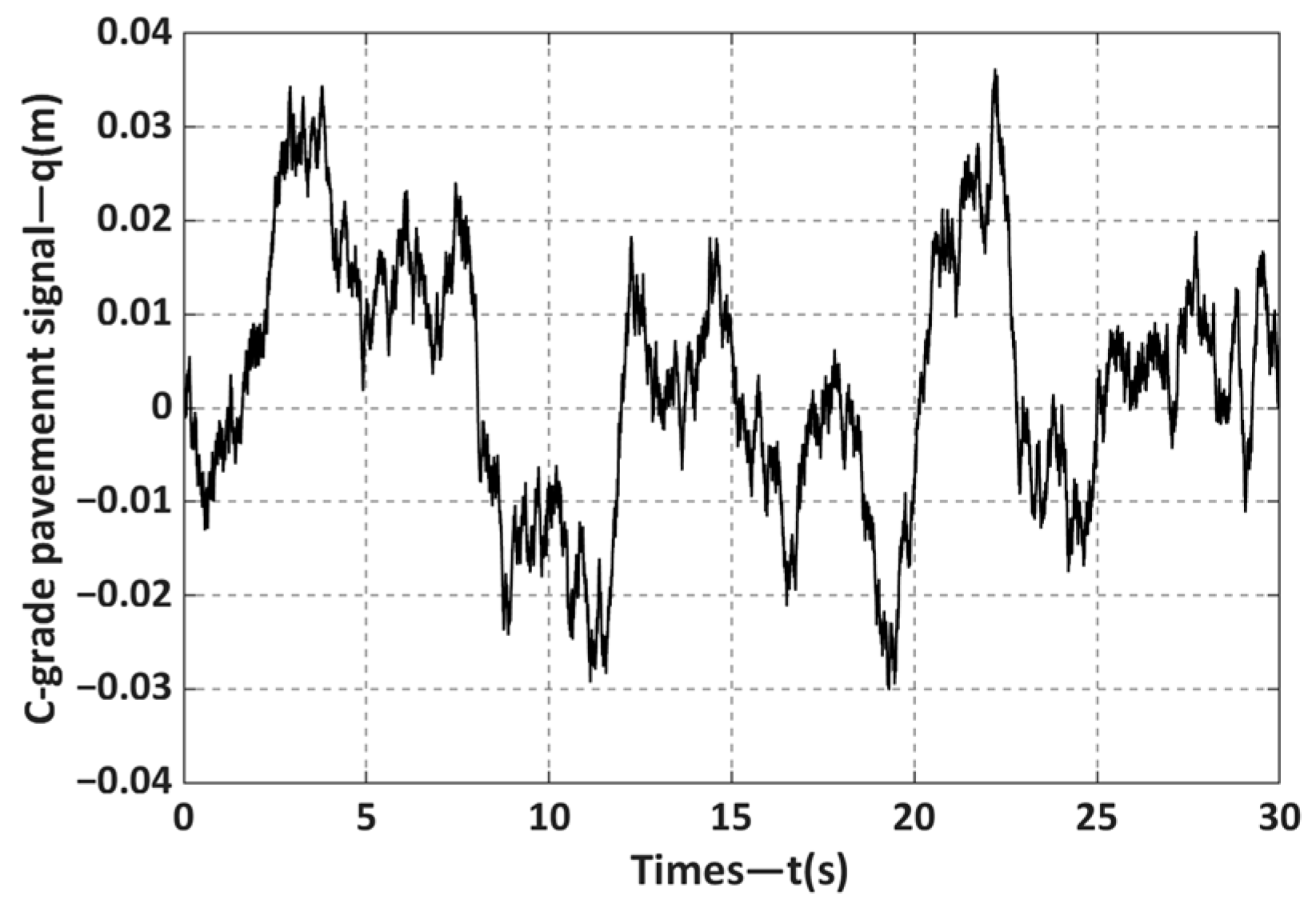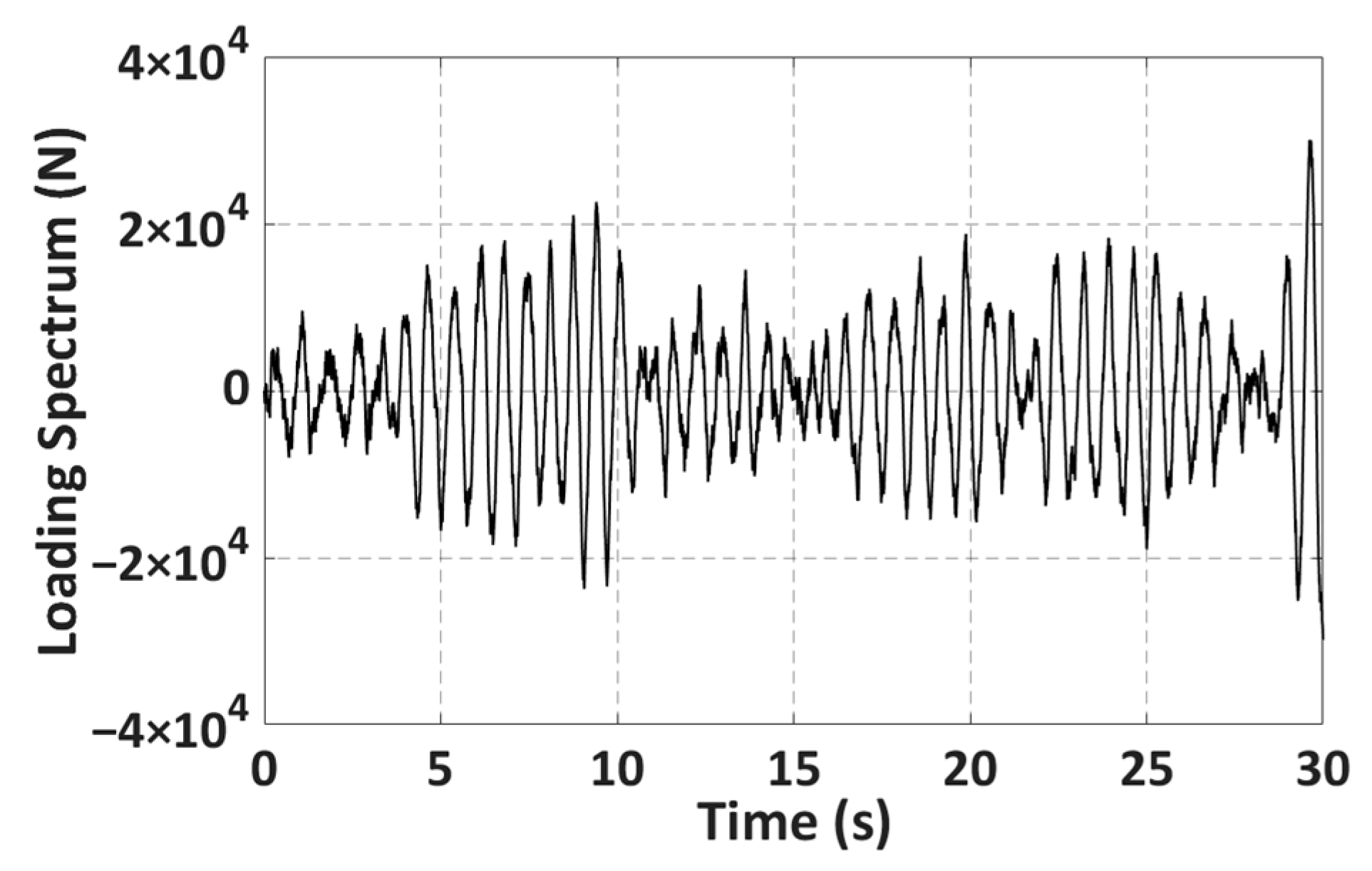According to the dynamic test methods specified in the relevant standards, a fatigue life simulation test of the fifth wheel was conducted, and the validity of the simulation test results was verified through a bench test to ensure that the fatigue life of the model’s fifth wheel was higher than the standard requirements [11]. The load spectrum of the upper surface of the fifth wheel was obtained by simulating the time-domain excitation signal of the C-grade road, and the limit fatigue life was estimated with the help of finite element software, according to the load change of the fifth wheel in the actual vehicle transport process, and the fatigue-prone key parts were identified [12]. For the lightweight design of the fifth wheel, in the optimization with mass as a single objective, a model is established by constraining the first-order modal frequency and equivalent stress of the structure, and the lightweight design of the traction seat is investigated using the optimization method of the dimensional parameters to achieve the effect of lightweight design [13,14]. For multi-objective optimization, the mass and first-order intrinsic frequency are usually taken as the objective functions for model building, and the static–dynamic performance and fatigue reliability are verified by the optimal solution to achieve the unity of lightweight and safety [15].

To achieve better lighting in vehicles, reduce costs, and improve fuel economy at the same time, some scholars have conducted considerable research related to automotive lightweighting. Zhou et al. [16] proposed a collaborative design method for the key load-bearing parts of automobiles, including the framework of the entire lightweight design process such as structural optimization, material lightweighting, and manufacturing process optimization. The steering knuckle, a load-bearing part of the automobile chassis, was designed and analyzed in detail, and a lightweight target was achieved after the optimized design of the structural topology. Zhang et al. [17] proposed a structure, design, and optimization method for a magnesium–aluminum alloy combination wheel hub through the establishment of the combination wheel bending and radial fatigue test finite element model, simulation and analysis of the fatigue performance of the combination wheels under the two conditions and their influencing factors, and multi-objective optimization of the assembled wheels, which achieves the purpose of reducing the weight; at the same time, the bending fatigue life and radial fatigue factor of safety are reduced. Li et al. [18] proposed a comprehensive lightweight design method for automobiles that analyzed the stress, strain, and safety coefficient of automotive components according to their stress, strain, and safety coefficients, determined the applicable location for lightweight design, and reapplied the finite element method to the weight-reduced parts.

Numerous researchers have explored the application of the Multi-Objective Genetic Algorithm (MOGA) to vehicle optimization design. Wang et al. [19] combined the Non-dominated Sorting Genetic Algorithm (NSGA-II) with an artificial neural network to establish a multi-objective optimization model for self-weight, stiffness, and frequency, which reduces the self-weight of the frame structure and improves the torsional stiffness and torsional frequency of the frame structure by optimizing the CSS of the thin-walled beam. Diba et al. [20] used a multi-objective genetic algorithm (MOAG) to optimize the driveline components with acceleration time, fuel consumption, and driveline price as the objective function. The overall efficiency of the optimized hybrid driveline was evaluated using a computer model simulation, which improved the overall fuel efficiency of the driveline. Aly et al. [21] developed a multi-degree-of-freedom automotive model of an improved semi-active suspension system subjected to stochastic road excitations, validated the proposed genetic operator through numerical examples, and investigated automotive suspensions with active damping, and found that the reconciliation behaviors in the objectives or constraints of the suspension problem will lead to disjoint Pareto boundaries.

To verify that the performance of a vehicle under pavement excitation meets the requirements of use, many scholars have studied the strength, stability, energy consumption, and durability of vehicles under pavement excitation. Li et al. [22] compensated for the shortcomings of the frequency domain method to a certain extent based on spectral decomposition and regularization of the stochastic dynamic load identification time domain method. Zhang et al. [23] used Gaussian–Legendre integrals to obtain non-smooth stochastic road excitations in the time domain, using applied evolutionary spectrum theory to evaluate the response in the time-frequency domain. They found that non-smooth road excitations have a great role to play in the design and optimization of the ride comfort suspension system. Vaidas et al. [24] developed a fine dynamic model and suspension for assessing vehicle stability influenced by tire treads, which enables a more accurate assessment of the road’s influence on unevenness with respect to vehicle suspension and body motion on vehicle stability. Jiang et al. [25] simplified the dynamical model by neglecting the inverse calculation method of monorail road excitation and verified the model by comparing the experimental data with the simulation results. They found that the simulation results of acceleration under the effect of inverse calculation of the road unevenness were consistent with the experimental data, which confirms the validity of the model only at low frequencies. Chin et al. [26] proposed a more accurate energy characterization method for the energy-based durability prediction of suspension coil springs under random loading conditions and found that the Morrow-based model provided the highest accuracy in fatigue life prediction. Mechanical et al. [27] developed a time-domain coupled system by modeling a two-degree-of-freedom quarter-vehicle using Galerkin’s method, which was solved using the Newmark-β direct numerical integration method based on the linear mean acceleration method by evaluating the response of the coupled system, effects of the vehicle speed, roughness of the road surface, stiffness of the soil, and effect of parameters such as suspension damping on the response. Guo et al. [28] established a longitudinal–vertical coupled dynamics model for DCT vehicles considering powertrain mounts and compared the simulation results of the longitudinal–vertical coupled dynamic DCT vehicle model, considering road excitation, with the vehicle test results. They found that the model could accurately reflect the effect of road excitation on the dynamic performance of the DCT vehicle under the conditions of starting and gear shifting.

For the lightweight and multi-objective optimal design of the fifth wheel, most scholars consider the mass, frequency, and material as the optimization objectives. Owing to the existence of a certain link between mass and fatigue performance, the smaller the mass, the lower the fatigue life, and it is not possible to ensure that the fatigue life meets the lightweight requirements simultaneously. In practical applications, the weight of the fifth wheel and its fatigue performance should be taken into account; therefore, this study establishes an optimization model with weight and fatigue life as the objectives so that the two can achieve synergistic optimization and validation.

2. Model Establishment and Analysis

2.1. Finite Element Model Building

Before performing the finite element analysis, a finite element model that contains solid and shell elements is required.

The first step is to establish a geometric model using computer-aided design (CAD) software to establish a geometric model of the semi-trailer fifth wheel, including the geometry and dimensions of the saddle body and other components, and the use of rigid body elements (RBE2) to connect the various components. The geometric model was then imported into HyperMesh (2020) for subsequent meshing and modeling operations; the material of all components was High Strength Low Alloy Structural Steels Q345.

Because the force transforming element is located in the center of the fifth wheel (as shown in part 11 of Figure 2), connecting the saddle body and other components that play a vital role, it is set as property of solid element (PSOLID) and meshed using hexahedral elements. The other ten components are set as property of shell elements (PSHELL), so that the thickness of the components can be set as a variable by using shell cells, which is convenient for the subsequent lightweight design, and meshing is conducted by using a mixture of hexahedral elements and tetrahedral elements. Finally, the initial thickness of each component was defined, as shown in

Table 1. Thickness of each part in the fifth wheel.

Fifth Wheel Components	Thickness (mm)
Saddle body (Figure 2, pos. 1)	10
Upper transverse plate (Figure 2, pos. 2)	12
Lower transverse plate (Figure 2, pos. 3)	16
Reinforcing ribs (Figure 2, pos. 4)	7
Lower reinforcing plate (Figure 2, pos. 5)	10
Swing rod support seat (Figure 2, pos. 6)	7
Guide plate (Figure 2, pos. 7)	10
Carriages (Figure 2, pos. 8)	6
Inner baffles (Figure 2, pos. 9)	16
Outer baffles (Figure 2, pos. 10)	16

, for the corresponding thickness of each component, and the obtained solid model of the fifth wheel is shown in Figure 2.

2.2. Selection of Materials

2.2.1. Material Property

The original material of all components of the fifth wheel is Q345 because the main stress areas in composite conditions 2 and 3 are the saddle body and lower transverse plate. Therefore, the material modification in this study was to upgrade the material of the saddle body and lower transverse plate in the fifth wheel to SD600, and the material of the rest of the components was still Q345. The material parameters for SD600 and Q345 [29] are listed in

Table 2. Two material parameters.

Material Parameters	Q345	SD600
Yield limit (MPa)	345	600
Tensile strength (MPa)	470	720
Elasticity modulus (GPa)	206	210
Poisson ratio	0.28	0.30
Density (g/cm3)	7.85	7.85

.

In the wear test comparing SD600 and Q345, the test standards refer to the GB/T 10124-88 [30] “laboratory uniform corrosion of metal materials full immersion test method,” a specimen size of 3.0 $\times$ 10 $\times$ 50 mm is the standard sample, and the test is conducted in the medium of tap water plus quartz sand. The test conditions are shown in

Table 3. Wear test conditions.

Test Condition	Incipient pH Value	Concentration	Particle Size of Quartz Sand (Mesh)	Linear Velocity (m/s)	Testing Temperature (°C)	Test Cycle (h)
Value	7.5	50%	20~40	2	$20 \pm$ 2	72

.

Table 4. Results of wear loss of two materials.

Category	Thickness Loss Rate (mm/a)	Weight Loss Rate (%)	Relative Erosion Rate (%)
Q345	5.1882	1.297	100
SD600	2.6630	0.665	61.5

The thickness loss rate (mm/a)$={\displaystyle \frac{1.123\times {10}^4\times \left(W_1-W_2\right)}{S·t}}$. The weight loss rate (%)$={\displaystyle \frac{W_1-W_2}{W_1}}$. W₁ is the weight before the test (g), W₂ is the weight after the test (g), S is the surface area of the sample (cm²), and t is the test time (h).

summarizes the experimental results for determining the thickness loss rate, weight loss rate, and relative wear performance of SD600 compared to Q345. Notably, SD600 exhibited a wear volume reduction of 37.5% relative to Q345, demonstrating a significant enhancement in wear resistance.

2.2.2. S–N Curve of Material

In the simulation computation of the fatigue life of the fifth wheel, the fitted Stress–Number of cycles to failure curves (S–N curves) are required to be imported into the software for fatigue calculation. Therefore, the S–N curves of two materials are necessary.

The S–N curve of the material delineates the correlation between the applied stress and the actual number of cycles to failure. Herein, S signifies the magnitude of stress experienced under an external load, while N denotes the fatigue life of the workpiece. Typically, the S–N curve of the material is derived from experimental data, specifically through a full inversion rotation bending experiment.

This paper assesses the approximate fatigue characteristics of materials in accordance with a methodology for estimating the S–N curve proposed by Fu [31]. The formula is as follows:

$$S_a={10}^C{\mathrm{N}}^b$$

(1)

The relation between parameters C and b in Equation (1) is as follows:

$$\left\{\begin{array}{l}C=\mathrm{l}\mathrm{g}{\displaystyle \frac{{\sigma }_{1000}^2}{{\sigma }_{-1}}}\\ b=-{\displaystyle \frac{1}{3}}\mathrm{l}\mathrm{g}{\displaystyle \frac{{\sigma }_{1000}}{{\sigma }_{-1}}}\end{array}\right.$$

(2)

In Equation (2), ${{\sigma }_{1000}=0.9\sigma }_b$, ${\sigma }_b$ is the tensile limit, when ${\sigma }_b$ ≤ 1379.2 MPa, ${{\sigma }_{-1}=0.5·\sigma }_b$.

The S–N curve parameters of Q345 and SD600 calculated according to the above formula are shown in

Table 5. S–N curve parameters of two materials.

Material	Q345	SD600
${\sigma }_b$ (MPa)	470	720
${\sigma }_{1000}$ (MPa)	423	648
${\sigma }_{-1}$ (MPa)	235	360
$C$	2.8816	3.0668
$b$	−0.0851	−0.0851

.

2.3. Three Working Conditions of Tractor

When a semi-trailer tractor travels on a highway, the primary load it carries originates from the cargo weight within the trailer compartment. Based on the installation configuration of the fifth wheel on the semi-trailer, it can be concluded that the fifth wheel is primarily subjected to pressure and tension during operation, with the trailer’s head pulling the carriages forward while driving. According to the specified vehicle outlines, axle loads, and allowable load limits outlined in the express provisions, the maximum allowable total mass for a three-axle semi-trailer under Class 1 conditions is 40 tons, while the maximum permissible total mass for a six-axle auto train under similar conditions is 49 tons.

2.3.1. Condition 1—Static Compression

When the tractor in the semi-trailer compartment has a fully loaded static situation, a three-axle semi-trailer maximum permissible heavy mass of 40 tons, condition 1 is subject to a loaded weight of approximately 30 tons. In this study, the unit node of the compression contact surface on the saddle was connected to the saddle proper center by creating an RBE2 rigid connection, and a 30 ton load was applied to this point so that the force was uniformly applied to the compression contact surface. According to the way the fifth wheel is installed in the tractor and the actual conditions, the center circular holes of the four inner and outer stops are constrained to limit the other five degrees of freedom except for the rotation around the X-axis.

2.3.2. Condition 2—Uphill Lifting

The tractor works with the tractor driving the semi-trailer compartment, in which the fifth wheel plays a connecting role. According to the installation of the fifth wheel, during the uphill driving process, the fifth wheel is mainly subjected to the load is the lower cross plate is subjected to the semi-trailer compartment tension. In condition 2, the lower cross plate to withstand the pulling force is set to the three-axle semi-trailer maximum permissible load of 60%, which is 24 tons. The same constraints were imposed on the center holes of the four internal and external baffles, in addition to the limit value of rotation around the X-axis and the other five degrees of freedom.

However, during the actual slope driving process of the tractor, the upper surface of the fifth wheel also experiences a certain pressure. The actual lifting condition should include the addition of a compressive force. Therefore, this study sets the second condition as a composite condition of 24 tons of lifting force and 30 tons of pressure.

2.3.3. Condition 3—Steering Rollover

For tractor trailers, steering driving on the road is essential. During steering, the fifth wheel is subjected to the center of gravity migration, thus generating from the outside to the inside of the overturning force; the lower surface of the force transforming element is subjected to force from the bottom to the top of the thrust. In this study, the RBE2 rigid connection method was used to connect the element nodes in the lower surface to the positive center of the lower surface of the force transforming element. A 50 ton rollover force was applied to this point, constraining the center circular holes of the four inner and outer baffles and limiting the other five degrees of freedom except for rotation around the X-axis.

In the actual steering process of the tractor, the upper surface of the saddle body is also subjected to a certain pressure; therefore, the third condition was set as a composite condition of 50 tons of rollover force and 30 tons of pressure.

2.4. Finite Element Analysis of the Original Fifth Wheel

2.4.1. Static Analysis

During the actual stressing process, materials often experience a complex stress state. Equivalent stress and strain analysis synthesizes multiple stress and strain components under such conditions into an equivalent value, enabling a more intuitive and comprehensive description of material behavior under complex stress situations and serving as a foundation for accurate performance assessment. In structural design, equivalent stress–strain analysis aids in identifying stress and strain distribution within the structure, revealing stress concentrations and high strain areas, thereby allowing targeted optimization to enhance structural strength and stability [32].

Under the load conditions from the above three scenarios, a static analysis of the original fifth wheel was conducted using Hyperworks (2020) simulation software. The displacement distribution diagrams under each condition are presented in Figure 3.

Among them, Figure 3a is the stress distribution diagram of condition 1, Figure 3b is the displacement distribution diagram of condition 1, Figure 3c is the stress distribution diagram of condition 2, Figure 3d is the displacement distribution diagram of condition 2, Figure 3e is the stress distribution diagram of condition 3, and Figure 3f is the displacement distribution diagram of condition 3.

The maximum stress and maximum displacement of the original fifth wheel under three working conditions are shown in

Table 6. Maximum stress displacement of the original fifth wheel.

	Maximum Stress (MPa)	Maximum Displacement (mm)
Static Compression	77.28	0.0211
Uphill Lifting	252.00	0.3369
Steering Rollover	376.00	0.1045

. The total mass is 104.20 kg.

According to the above table, the maximum stress in the case of steering rollover is 376 MPa, which exceeds the yield limit of Q345. However, the load set in this condition is 50 tons, and in the relevant standards for the maximum allowable total mass limit of the semi-trailer, the largest among the three-axle semi-tractor trailers is 40 tons.

The highest stresses in condition 1 are located in the inner baffles, and the maximum displacement is located in the two ears at the bottom of the saddle body. The maximum stresses of conditions 2 and 3 are located in the lower transverse plate. The maximum displacement of condition 2 is located in the lower transverse plate, and the maximum displacement of condition 3 is located in the force transforming element.

2.4.2. Modal Analysis

Due to the operating conditions of the tractor trailer in high-speed and heavy-duty environments, various components of the vehicle will produce different mechanical vibrations depending on the road conditions. When a large mechanical resonance occurs, it will reduce the mechanical properties of the entire tractor trailer, thereby shortening its service life. Therefore, resonance caused by external factors needs to be avoided.

The center holes of the four inner and outer baffles of the fifth wheel are constrained, limiting all six degrees of freedom. The first to tenth-order intrinsic frequency and vibration mode values of the original fifth wheel are calculated, and the results are shown in

Table 7. Modal analysis.

Order	First	Second	Third	Fourth	Fifth	Sixth	Seventh	Eighth	Ninth	Tenth
Frequency (Hz)	486	624	835	862	930	1087	1167	1185	1201	1210
Maximum vibration mode	8.86	7.97	73.13	73.18	44.22	28.37	83.63	65.86	40.97	30.98

. Among them, the distribution diagrams of the first to third modes are shown in Figure 4.

It can be seen in Figure 4 above that in the first-order vibration mode, the maximum deformation is located in the two ears at the lower end of the fifth wheel. The second-order vibration mode is relatively small, and most of the deformation is located at the edges of the carriages. The third-order deformation gradually increases, and the deformation of the left carriages bulging to the right is relatively large.

Semi-trailers are subject to various external excitations in real-world operating conditions, primarily originating from the road surface, tires, driveshafts, and the engine during vehicle motion. According to relevant research [33], the excitation frequency of the road surface is lower than 5 Hz; the excitation frequency of tires and driveshafts ranges between 30 Hz and 40 Hz; and the engine’s excitation frequency typically falls within 30 and 100 Hz. Typically, the speed of a semi-trailer ranges from 40 to 100 km/h.

The first-order intrinsic frequency of the original fifth wheel is 486 Hz, which is more than four times higher than the working range of external excitations. Therefore, the fifth wheel does not resonate with external excitations in the constrained state.

2.4.3. Multiaxial Fatigue Analysis

A multiaxial stress-life analysis of the lightweight fifth wheel was conducted using HyperLife (2020). Since the semi-trailer fifth wheel is a welded part, the FKM average stress correction method [34] was applied in the fatigue simulation analysis of the fifth wheel in this study. The survival rate was 95%, the loading method was time series, and the loading curve was sinusoidal.

In the case of condition 2, the maximum equivalent stress is lower, and the fatigue life exceeds 1.0 × 10⁷ cycles. Therefore, fatigue analysis was performed only for condition 3. The fatigue life of the original fifth wheel under condition 3 was calculated, and the minimum fatigue life was 2.826 × 10⁵ cycles. As shown in Figure 5, in the upper right corner is the fatigue life-unit node diagram. The positive direction of the X-axis represents the unit nodes of the raised side edge on the shell in the diagram, following the order indicated by the arrow. The element node number corresponding to the minimum life is 218,253.

2.5. Strength Analysis of the Fifth Wheel Under Pavement Excitation

2.5.1. Establishment of Time Domain Model Based on White Noise Pavement Roughness

Pavement roughness refers to the displacement of the actual pavement surface relative to the reference plane, and it is also known as random excitation of the pavement surface. Due to the unevenness of the pavement, the tractor tires experience vertical oscillations during driving. The resulting impact forces are transmitted from the tires to the suspension, fifth wheel, and semi-trailer compartment, causing stress and deformation in these components.

According to the “Mechanical vibration-pavement pavement spectrum measurement data report” issued in 2005, the pavement power spectral density can be expressed as:

$$G_q\left(n\right)=G_q\left(n_0\right){\left({\displaystyle \frac{n}{n_0}}\right)}^{-\omega }$$

(3)

In Equation (3), $n$ is the spatial frequency, which is the reciprocal of the wavelength, where the units are m⁻¹; $n_0$ is the reference spatial frequency, usually set to 0.1 m⁻¹; $G_q\left(n_0\right)$ is the power spectral density of the pavement surface under the reference spatial frequency, also known as the pavement roughness coefficient, which is m³; and$\omega$ is the frequency index, which determines the frequency structure of the pavement power spectral density, usually set to 2.

According to the relevant standards, the pavement surface can be divided into eight grades, A–H, according to the pavement roughness coefficient $G_q\left(n_0\right)$, as shown in

Table 8. Grading standard of pavement roughness.

Pavement Grade	${\mathit{G}}_{\mathit{q}}\left({\mathit{n}}_0\right)$$({10}^{-6} {\mathbf{m}}^3) ({\mathit{n}}_0$ = 0.1 m−1)
	Geometric Mean	Lower Limit	Upper Limit
A	16	8	32
B	64	32	128
C	256	128	512
D	1024	512	2048
E	4096	2048	8192
F	16,384	8192	32,768
G	65,526	32,768	131,072
H	262,144	131,072	524,288

.

According to statistics on relevant pavement conditions, the power spectrum range of expressway pavement falls between grades A and C, with grades B and C accounting for a significant proportion. Among these, the C-grade pavement spectrum is larger than that of B-grade pavement. Therefore, this study focuses on establishing and simulating the pavement roughness model for C-grade pavements.

In this study, the first-order band-limited white noise filtering method was used to establish a random pavement excitation model. The time pavement excitation signal is expressed as:

$$\dot{q}\left(t\right)=2\pi n_0·\sqrt{G_q\left(n_0\right)v}·\omega \left(t\right)-2\pi f_0·q\left(t\right)$$

(4)

In Equation (4), $q\left(t\right)$ is the pavement random excitation signal; $G_q\left(n_0\right)$ is the pavement roughness coefficient, with a C-grade pavement surface value range of 1.28 $\times$ 10⁻⁴ m³~5.12 $\times$ 10⁻⁴ m³ and a geometric mean of 2.56 $\times$ 10⁻⁴ m³; v is semi-trailer velocity, set to 60 km/h, which is 16.7 m/s; $\omega \left(t\right)$ is the Gaussian white noise signal with a mean value of 0; and $f_0$ is the lower cutoff frequency, set to 0.0628 Hz.

The simulation analysis was performed using Simulink (R2020a) with a sampling time of 0.001 s. The time-domain simulation model of pavement unevenness is shown in Figure 6, and the random pavement excitation signals obtained from a 30 s simulation are shown in Figure 7. The height range of the C-grade pavement fluctuations was within ±0.04 m.

2.5.2. Establishment of Dynamic Model of Semi-Trailer Tractor Wheel Suspension System

The three-dimensional model of the semi-trailer tractor is illustrated in Figure 8. As shown in the figure, the fifth wheel is installed directly above the rear wheel of the tractor, and the connection between the vehicle and the semi-trailer carriages relies on the suspension system support. Based on the corresponding positional relationship, a theoretical analysis model of the tractor tire suspension system in the vertical direction relative to the fifth wheel was established. As shown in Figure 9, the model represents a 1/4 simulation of the semi-trailer tractor, featuring two wheels, with the main load carried by the rear four wheels of the tractor. The suspension system was loaded at 40% of the 40 ton capacity when the semi-trailer was fully loaded. A 1/4 simulation model of the tractor was established; thus, the mass m² in the model was calculated as 40 tons × 40% × 0.5, resulting in 8 tons.

A kinematic differential equation for the 1/4 tractor model was established. The load of the fifth wheel is K1·(Z1-q), and the 30 s load spectrum is obtained, as shown in Figure 10.

2.5.3. Fifth Wheel Strength Analysis

As shown in Table 6, under a vertical static load of 30 tons, the maximum stress of the original fifth wheel is 77.28 MPa, which is within the yield strength range of the material. As illustrated in Figure 10, the maximum dynamic load on the fifth wheel in the tire suspension system of the semi-trailer tractor is 30,044.5 N. Typically, the maximum stress under dynamic loading is 1.5 to 3 times the maximum stress under static loading. Similarly, the calculated stress of 240 MPa falls within the allowable range of the material’s yield strength.

3. Fatigue Life Prediction Based on a Hybrid Model of Random Forest Algorithm and Improved BP Neural Network

3.1. Multi-Objective Optimization

Lightweight design plays a crucial role in vehicle manufacturing. By reducing the weight of the fifth wheel, the overall vehicle weight can be reduced, fuel efficiency can be improved, and vehicle performance and safety can be enhanced.

The fifth wheel is a key component connecting the tractor and semi-trailer. The semi-trailer operates under intense and complex working conditions, leading to significant fatigue performance challenges. If a lightweight design of the fifth wheel is implemented, the fatigue performance of the fifth wheel can be improved without compromising its weight reduction, and the overall vehicle performance will also be enhanced.

In multi-objective optimization problems, conflicting objective functions must be optimized simultaneously and cannot be simplified into a single objective function. In this study, multi-objective optimization adopted the method of a multi-objective genetic algorithm (Yongmin et al. [35]) and solved the multi-objective optimization problem through fitness sharing, Pareto frontier sorting, and crowding distance.

The basic idea of MOGA is to search for the optimal solution set of multiple objective functions by simulating the genetic mechanism of nature, obtaining a series of equilibrium solutions that achieve a good balance between multiple objective functions.

Most researchers use constrained fatigue life to minimize mass. For the fifth wheel, both lightweight design and improved fatigue life are important. Therefore, this study aims to achieve lightweight design and improve fatigue life simultaneously, rather than focusing solely on a single maximum value calculation. The multi-objective optimization in this study targets the minimum mass and maximum number of minimum lifetimes of the fifth wheel. The maximum stress under the three conditions was constrained to be less than 600 MPa. The multi-objective optimization mathematical model of the fifth wheel was formulated using Equation (5).

$$\left\{\begin{array}{c}\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d} X=\left[x_1,x_2···x_{10}\right] \\ \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} f_1\left(A\right)=M\left(\mathrm{X}\right) \\ \mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} f_2\left(A\right)=\min \left({\mathrm{N}}_{\mathrm{i}}\left(\mathrm{X}\right)\right) \\ x_1\in \left(6 \mathrm{m}\mathrm{m},7.5 \mathrm{m}\mathrm{m}\right) \\ \left[x_2,x_3···x_{10}\right]\in \left(6 \mathrm{m}\mathrm{m},20 \mathrm{m}\mathrm{m}\right) \\ \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}:\mathrm{M}\mathrm{a}\mathrm{x}\left({\mathrm{S}}_{\mathrm{i}}\left(\mathrm{X}\right)\right)\le 600 \mathrm{M}\mathrm{P}\mathrm{a} \end{array}\right.$$

(5)

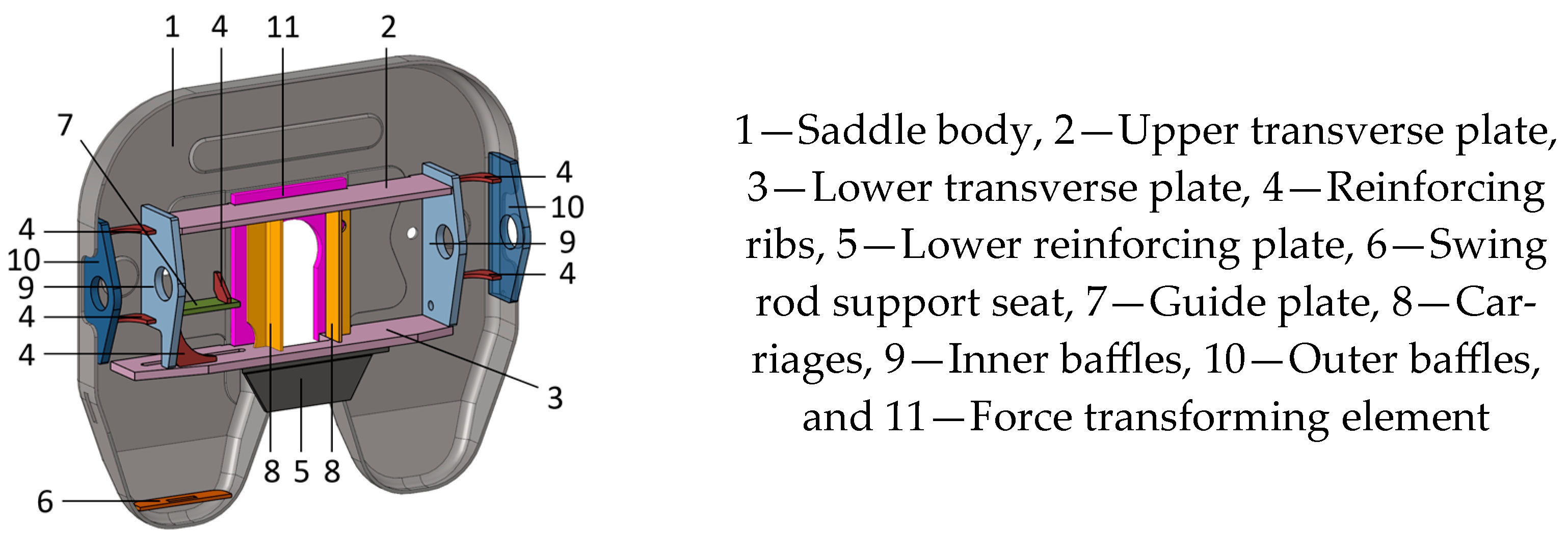
In the shell unit diagram of the fifth wheel, the force-transforming element is located at the center as a solid unit. As shown in Figure 11a, the thickness of the saddle body is in the range of 6 mm to 7.5 mm. The corresponding function is $x_1$ in X. As shown in Figure 11b–j, the thicknesses of the upper transverse plate, lower transverse plate, reinforcing ribs, lower reinforcing plate, swing rod support seat, guide plate, carriages, inner baffles, and outer baffles, respectively, range from 6 mm to 20 mm. The corresponding function is [$x_2$,$x_3$,$x_4\cdots x_{10}$] in X. 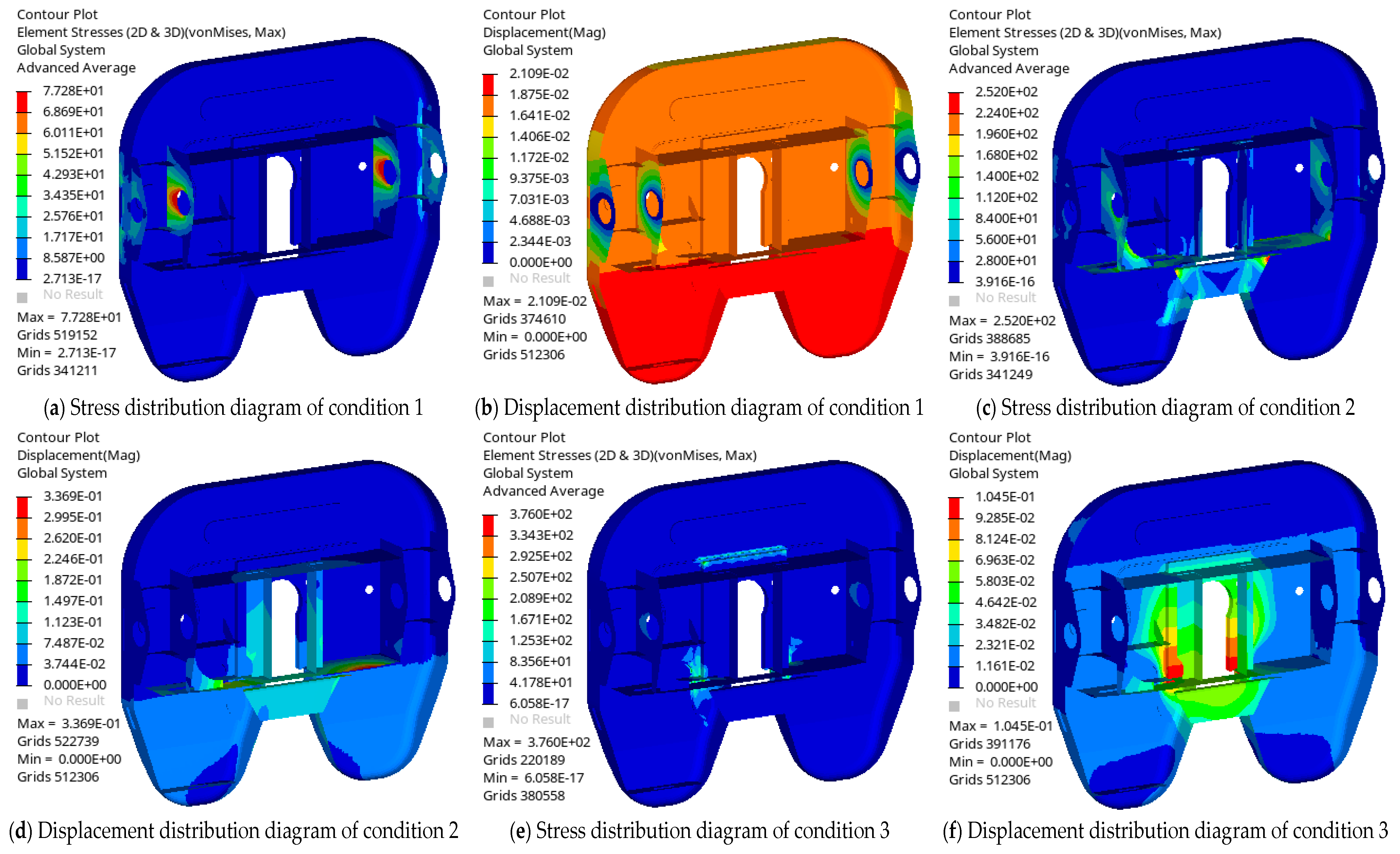Figure 11k shows the force-transforming element. M(X) represents the total mass of the fifth wheel, corresponding to the thickness of each component. Ni(X) represents the fatigue life of each unit point of the fifth wheel, corresponding to the thickness of each component under the three conditions. Si(X) represents the equivalent stress of the fifth wheel under corresponding conditions. Because the first condition is static, the stress is very small; therefore, it is not constrained. Because the maximum stresses in conditions 2 and 3 are located at the lower transverse plate, the objective function is the minimum mass f₁ and the maximum life f₂ simultaneously. It is only necessary to constrain the maximum stress of conditions 2 and 3 to less than 600 MPa of the yield strength of SD600.

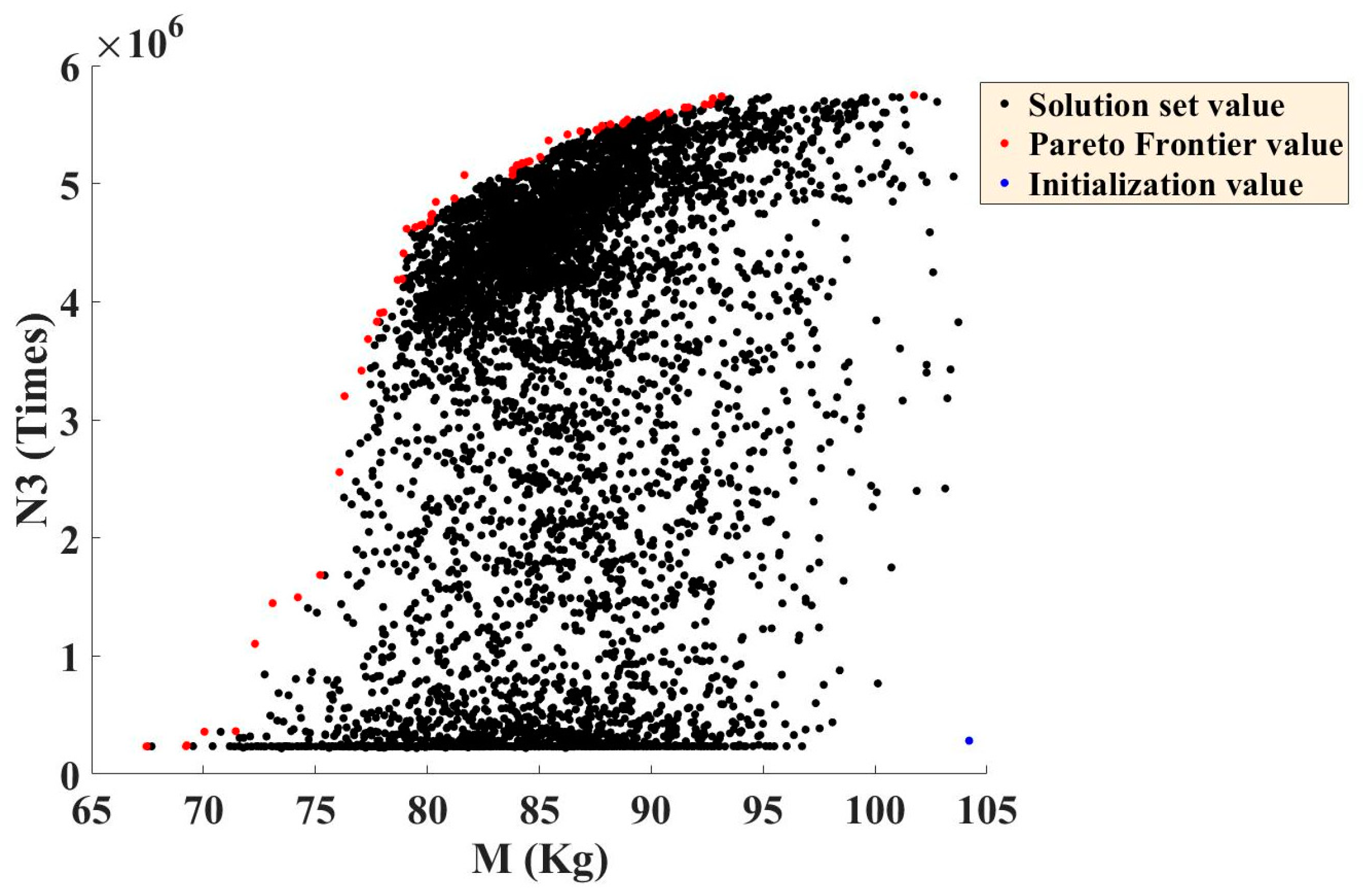
HyperStudy was utilized for multi-objective optimization. In the multi-objective optimization results, the fatigue life under condition 2 mostly exceeds 1.0 × 10⁷ cycles. Therefore, only the weight-life optimization results for condition 3 were analyzed. As shown in Figure 12, the scatter plot illustrates the relationship between weight and minimum fatigue life under condition 3. The black points represent the solution set values, the blue point in the lower right corner indicates the initial value, and the red points denote the Pareto frontier values.

From the trend of the Pareto frontier values in the scatter plot above, it is evident that the trend of the points aligns with the actual situation. Specifically, the greater the mass, the greater the fatigue life.

Next, the multi-objective optimization results were processed. First, outliers were removed. The total mass (M) of the fifth wheel fluctuates within a certain range due to the constrained thickness ranges of its components. The fatigue life data fall within the range of 1.0 × 10⁴ to 1.0 × 10⁷ cycles.

In the calculated life results, the majority of the fatigue life values under condition 2 exceeded 1.0 × 10⁷ cycles, and the fatigue performance under condition 2 was consistently stronger than that under condition 3 across all data groups. Therefore, this study focused on analyzing the fatigue life under condition 3 as the primary indicator. After removing outliers, 6000 data points remained from the optimized dataset.

3.2. Fatigue Life Prediction Based on a Hybrid Model of BP Neural Network and Improved Random Forest Algorithm

To obtain the relationship between each component of the traction seat and the total mass and fatigue life of the traction seat, this study used 6000 sets of data calculated by the multi-objective genetic algorithm for training tests, with the thickness of the ten components as the input and the total mass and fatigue life as the output.

Because there is a linear relationship between the thickness of the ten components and the total mass of the traction seat, the relationship equation between the mass and the thickness of each component was calculated as:

$$\begin{array}{c}\mathrm{M}=6.07·x_1+0.499·x_2+0.496·x_3+0.207·x_4+0.231·x_5+0.0688·\\ x_6+0.0726·x_7+0.394·x_8+0.488·x_9+0.404·x_{10}+7.70972\end{array}$$

(6)

In Equation (6), where M denotes the total mass of the fifth wheel, the [$x_1$,$x_2$,$x_3$,$x_4\cdots x_{10}$] represent, respectively, the thickness of the saddle body, upper transverse plate, lower transverse plate, reinforcing ribs, lower reinforcing plate, swing rod support seat, guide plate, carriages, inner baffles, and outer baffles.

The dataset generated by multi-objective optimization was imported after singular value processing. It was then divided into training and test sets and normalized for easier analysis. The normalized data were individually trained and predicted using the random forest model. The Mean Absolute Percentage Error (MAPE) of the predictions was calculated by adjusting the parameters of the random forest. The parameter set with the smallest MAPE was selected, and its predictions were fused with the original ten features to create a new dataset. This fused dataset was then used for training and prediction using a BP neural network, and the MAPE of the hybrid model was calculated. The model analysis processing flow is illustrated in Figure 13.

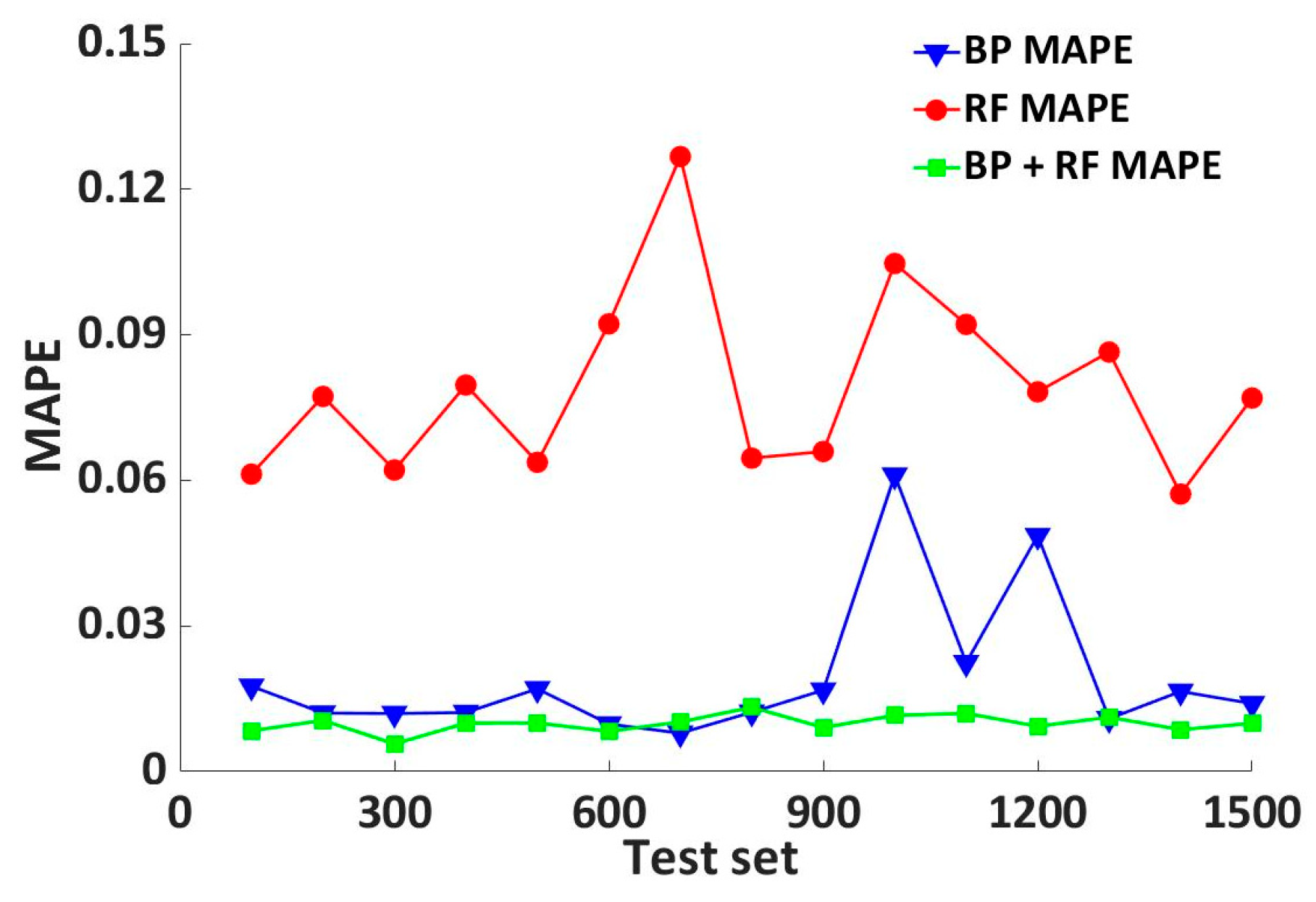
The MAPE for fatigue life prediction by the BP neural network was calculated to be 1.89%, the average absolute percentage error for fatigue life prediction by random forest algorithm was 7.73%, and the MAPE for hybrid model prediction was 0.99%.

Table 9. MAPE predicted by the three models.

Models	BP Neural Network	Random Forest Algorithm	Hybrid Model
MAPE of test set (%)	1.89	7.73	0.99

presents the results.

The MAPE comparison of the three models is shown in Figure 14, where the blue bar represents the BP neural network prediction model, the red bar represents the random forest algorithm prediction model, and the green bar represents the hybrid model prediction model. It can be observed that the hybrid model has the smallest MAPE among the three models, and its MAPE is significantly smaller than that of the other two models. In this work, which predicts the fatigue life under condition 3 based on the known thicknesses of the ten components of the fifth wheel, the hybrid model’s accuracy is 47.62% higher than that of the BP neural network.

This approach enables more accurate prediction of the fatigue life based on the thickness of individual components, eliminating the need for complex parameter settings and extensive model calculations.

3.3. Secondary Optimization and Inverse Prediction of Part Thickness

In multi-objective optimization, the objectives are to minimize the total mass of the fifth wheel and maximize the minimum fatigue life. There was a positive correlation between the two variables: The smaller the mass, the smaller the corresponding minimum fatigue life. To achieve coordinated optimization between the two, it is necessary to obtain the minimum value of f in Equation (7).

$$f=M+{\displaystyle \frac{1}{N3}}$$

(7)

In Equation (7), M is the total mass of the fifth wheel, and N3 is the minimum fatigue life of condition 3 at this mass.

Next, the mass (M) and minimum fatigue life under condition 3 (N3) from the 6000 datasets of the multi-objective optimization results were sorted. The mass (M) was sorted in ascending order. Data points from the 6(i − 1) + 1th to the 6ith positions were assigned a value of i. For example, data points from the 1st to the 6th positions were assigned a value of 1, and so on. Data points from the 6031st to the 6000th positions were assigned a value of 1000. Similarly, the minimum fatigue life under condition 3 (N3) was sorted in descending order, and data points from the 6(j − 1) + 1th to the 6jth positions were assigned a value of j.

In practical applications, the fifth wheel must consider the fatigue performance while pursuing lightweight design. If an increase of 2–3 kg in weight can enhance the fatigue life by hundreds of thousands or even millions of cycles, it is definitely a better option. Therefore, the establishment of the evaluation index in this study is more inclined to the improvement of failure protection performance, with the lightweight being controlled within a 20% reduction. After comprehensive consideration, the evaluation index was set to 0.65i + 0.35j.

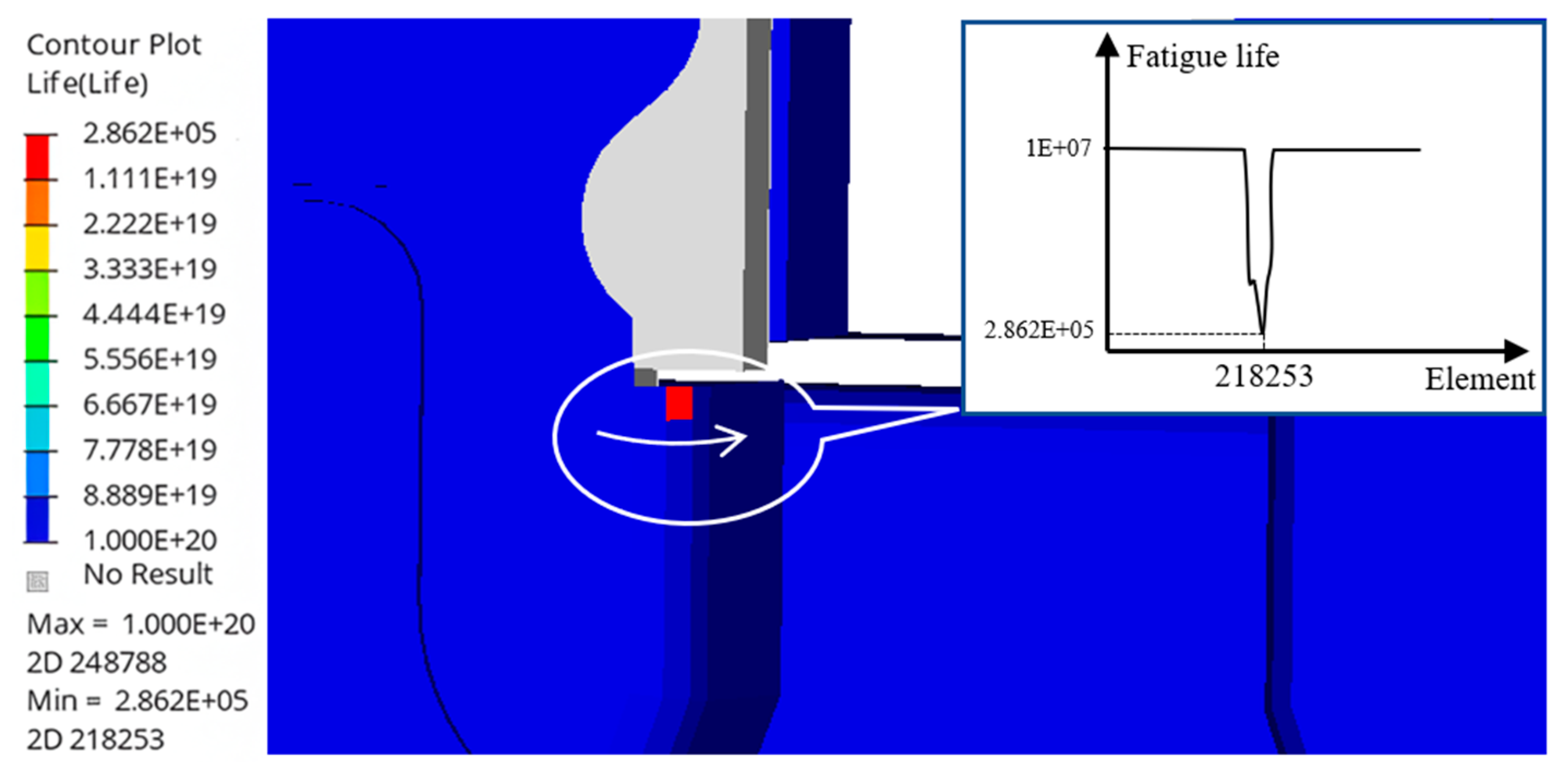
Based on the established multi-objective optimization evaluation index, the minimum value among the 6000 datasets was identified, representing the optimal balance between lightweight design and fatigue performance. This set is the optimal solution. The thickness of each component in the optimal solution is listed in

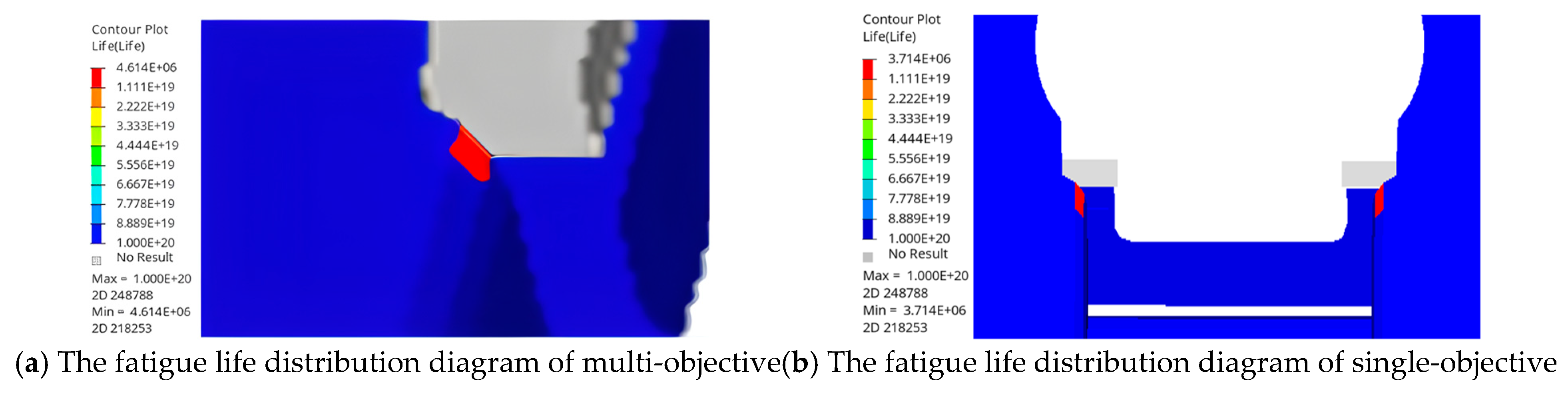
Table 10. Thickness optimizations of each component.

Fifth Wheel Components	Thickness (mm)
Saddle body	7.5
Upper transverse plate	6.0
Lower transverse plate	20.0
Reinforcing ribs	6.4
Lower reinforcing plate	10.4
Swing rod support seat	5.2
Guide plate	7.7
Carriages	6.2
Inner baffles	7.0
Outer baffles	6.0

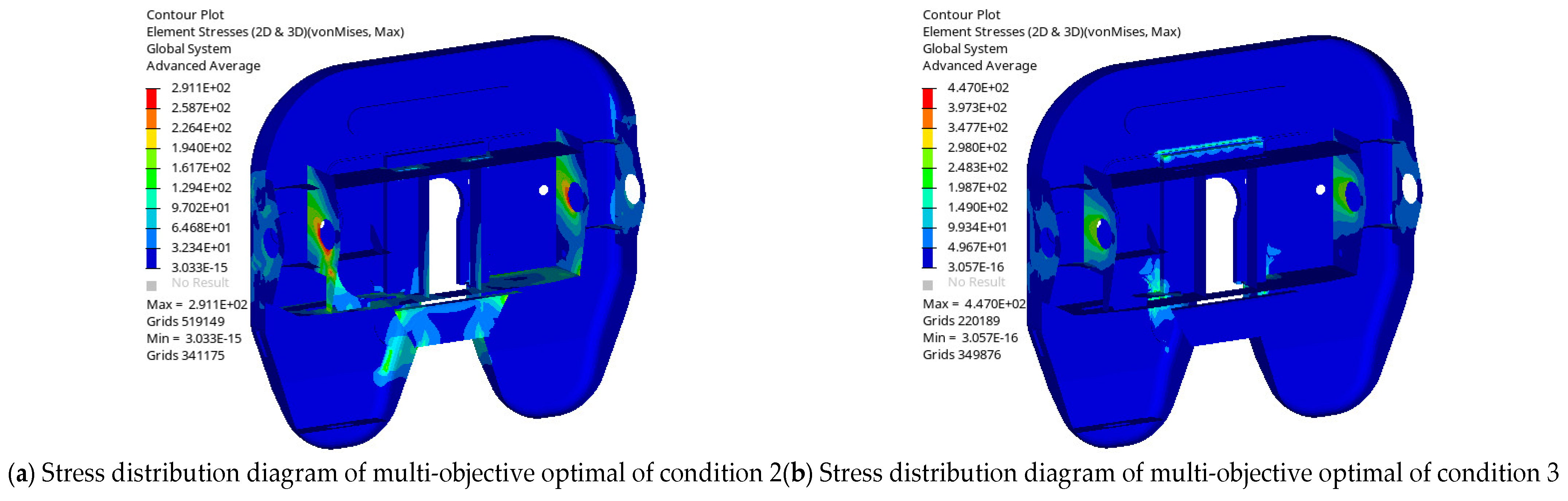
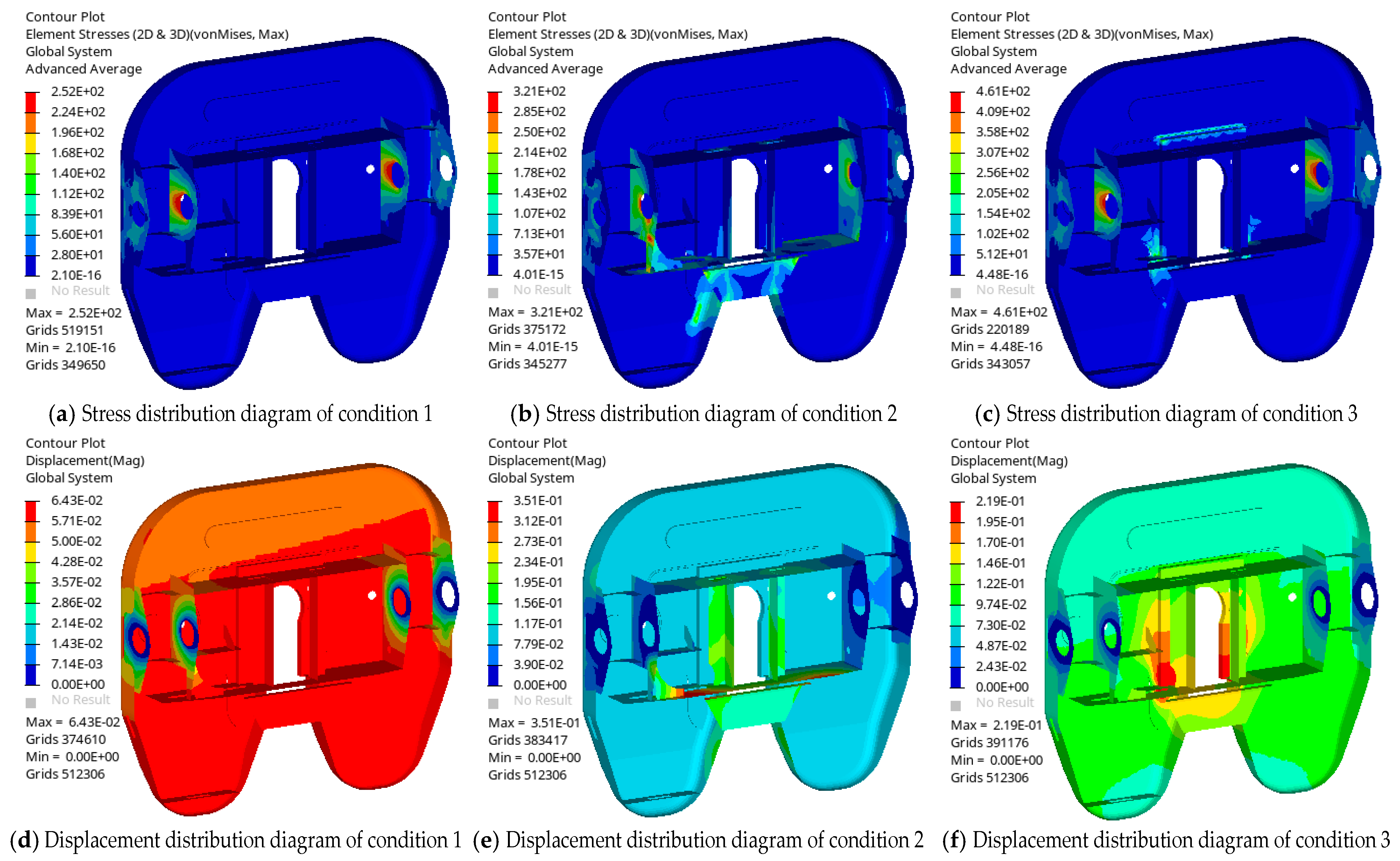
. The mass of the fifth wheel was 79.07 kg, and the minimum fatigue life reached 4.614 × 10⁶ cycles. Moreover, the maximum stress was 291.1 MPa under condition 2 and 447.0 MPa under condition 3, which is below the 600 MPa yield strength of SD600, meeting the strength requirements. The fatigue life distribution diagram is shown in Figure 15a, and the corresponding stress distribution diagrams are shown in Figure 16a,b.

Single-objective optimization was conducted based on the optimal solution. In accordance with relevant fatigue test standards, N3 was constrained to exceed 2.0 × 10⁶ cycles, and the maximum stress under both conditions 2 and 3 was limited to less than 600 MPa. The range of each variable was bounded based on the data in Table 10, with the saddle body constrained to ±1 mm and the other components constrained to ±4 mm. Optimization was then performed to minimize the mass.

The thickness of each component for the optimal design option from the single-objective optimization results is listed in

Table 11. Single-objective optimal design option for each component thickness.

Fifth Wheel Components	Thickness (mm)
Saddle body	7.2
Upper transverse plate	4.0
Lower transverse plate	20.5
Reinforcing ribs	4.3
Lower reinforcing plate	8
Swing rod support seat	6.1
Guide plate	6.8
Carriages	4.4
Inner baffles	5.0
Outer baffles	4.0

. The mass of this group of results is 72.99 kg, while the fatigue life under condition 3, as shown in Figure 15b, reaches 3.714 × 10⁶ cycles. The position of the minimum life under condition 3 is also the element node-218,253. The maximum stress is 410.1 MPa under condition 2 and 458.9 MPa under condition 3, both of which are below the 600 MPa yield strength of SD600, satisfying the strength requirements. The corresponding stress distributions are shown in Figure 17a,b.

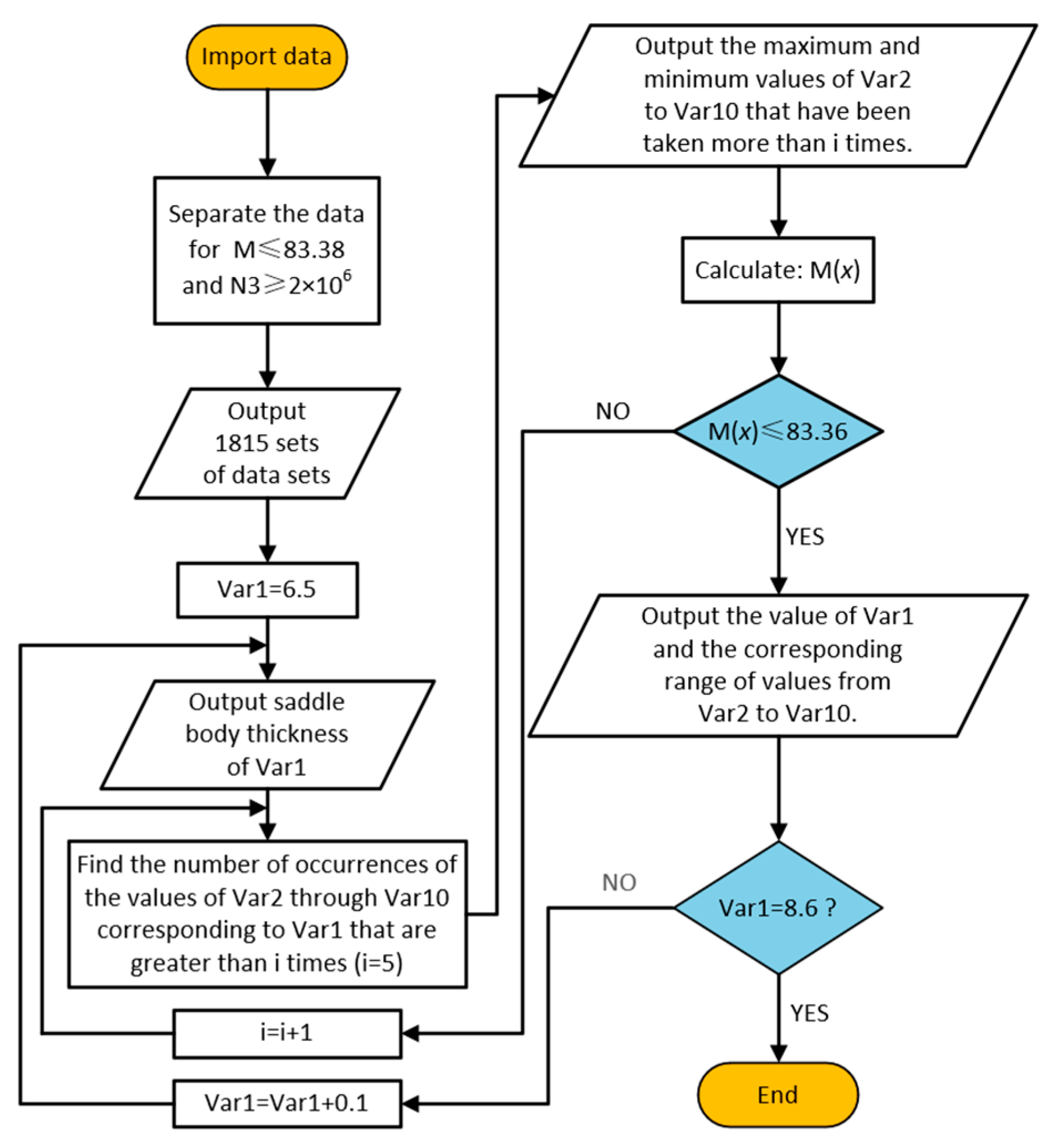
The data obtained from the single-objective optimization calculations were input and solved following the process illustrated in Figure 18. In this process, M(x) denotes the maximum mass within the range of each independent variable. The calculation method is described in Equation (6), where $x_1$ is replaced by Var1, and the maximum values within the statistical range of $x_2$ to $x_{10}$ are replaced by Var2 to Var10. The thicknesses of each component and their occurrence frequencies followed a normal distribution trend. Specifically, there is an intermediate value with the highest occurrence frequency, and the frequencies decrease symmetrically on both sides of this value. It was determined that M(x) was less than 83.36 kg, which is 80% of the original mass of the fifth wheel (104.2 kg), indicating a 20% weight reduction. The calculation results are listed in

Table 12. Range of values for each component for 20% lightweighting.

Var1	Var2	Var3	Var4	Var5	Var6	Var7	Var8	Var9	Var10
2	4.0, 7.9	20.4, 22.0	4.0, 7.9	8.0, 11.8	4.1, 7.0	5.1, 9.0	4.0, 8.0	5.0, 8.9	4.0, 7.9
7.3	4.0, 7.9	20.0, 22.0	4.0, 8.0	8.0, 11.9	4.1, 7.0	5.0, 9.0	4.0, 7.9	5.0, 9.0	4.0, 7.9
7.4	4.0, 7.9	19.6, 22.0	4.0, 8.0	8.0, 11.6	4.0, 7.0	5.2, 9.0	4.0, 7.6	5.0, 8.8	4.0, 7.6
7.5	4.0, 7.6	19.2, 21.8	4.0, 7.1	8.0, 11.7	4.2, 7.0	5.0, 8.8	4.0, 7.5	5.0, 7.5	4.0, 8.0
7.6	4.0, 6.0	18.9, 20.7	4.0, 5.9	8.0, 10.1	4.3, 7.0	5.2, 8.8	4.0, 7.9	5.0, 7.5	4.0, 6.5
7.7	4.0, 6.5	18.6, 21.5	4.0, 7.1	8.0, 11.3	5.0, 7.0	5.3, 8.2	4.0, 6.9	5.0, 8.5	4.0, 5.1
7.8	4.0, 7.3	18.2, 20.9	4.0, 7.8	8.0, 11.2	4.0, 6.9	5.0, 8.9	4.0, 7.2	5.0, 7.8	4.0, 5.3
7.9	4.0, 4.3	18.0, 20.1	4.0, 6.9	8.0, 8.5	4.9, 6.9	5.5, 7.8	4.1, 5.4	5.0, 7.8	4.0, 7.2
8.0	4.0, 4.5	18.0, 18.7	4.0, 5.6	8.0, 11.8	4.1, 7.0	5.0, 6.7	4.2, 7.7	5.0, 5.3	4.0, 6.5

. To further evaluate a 25% weight reduction, the value of 83.36 in the flowchart was adjusted to 78.15 kg, and the resulting value ranges are presented in

Table 13. Range of values for each component for 25% lightweighting.

Var1	Var2	Var3	Var4	Var5	Var6	Var7	Var8	Var9	Var10
7.2	4.0, 4.8	20.4, 21.9	4.0, 5.8	8.0, 9.4	4.7, 7.0	5.6, 8.8	4.0, 7.7	5.0, 7.3	4.0, 5.6
7.3	4.0, 4.8	20.1, 21.3	4.0, 4.9	8.0, 9.6	5.1, 6.8	6.2, 8.6	4.1, 7.3	5.0, 7.1	4.0, 5.6
7.4	4.0, 5.0	19.8, 21.6	4.0, 5.4	8.0, 9.0	4.9, 7.0	6.0, 7.5	4.1, 5.8	5.0, 7.0	4.0, 5.1
7.5	4.0, 4.5	19.4, 20.7	4.0, 4.6	8.0, 9.0	5.6, 6.9	6.0, 7.1	4.3, 5.1	5.0, 6.5	4.0, 5.1
7.6	4.0, 5.1	18.9, 20.7	4.0, 5.6	8.0, 8.8	4.3, 6.6	6.0, 7.1	4.2, 5.1	5.0, 6.1	4.0, 5.2
7.7	4.0, 4.7	18.8, 20.6	4.0, 4.8	8.0, 8.7	5.3, 6.4	5.9, 6.9	4.0, 4.6	5.0, 6.2	4.0, 5.1
7.8	4.0, 4.3	18.4, 20.4	4.0, 4.6	8.0, 8.2	4.5, 6.7	6.7, 7.0	4.1, 4.6	5.0, 5.8	4.0, 4.5
7.9	4.0, 4.3	18.1, 20.6	4.0, 4.4	8.0, 8.3	4.6, 6.7	6.9, 7.0	4.0, 4.7	5.0, 5.3	4.0, 4.4

. Var1 to Var10 represent the thicknesses of the saddle body, upper transverse plate, lower transverse plate, reinforcing ribs, lower reinforcing plate, swing rod support seat, guide plate, carriages, inner baffles, and outer baffles, respectively.

Consequently, according to the requirements of different degrees of lightweight, the thickness range of the remaining components can be obtained when the saddle body thickness is provided and the fatigue life meets the corresponding standards. Values within the range of components with different wear levels can be modified according to the different application scenarios. Correspondingly, the service life will also be improved to a certain extent by providing the product with optional design requirements.

4. Simulation and Experimental Verification

4.1. Multi-Objective Optimal Design Option Strength Verification

The optimal design option from the multi-objective optimization was verified through modal vibration analysis, dynamic test simulation, bench testing, and road excitation. The corresponding parameters of each component are listed in Table 10.

4.1.1. Modal and Vibration Verification

The center holes of the four inner and outer baffles in the fifth wheel are fixed to limit all six degrees of freedom, and the intrinsic frequency and vibration pattern values are obtained, as shown in

Table 14. Modal analysis results.

Order	First	Second	Third	Fourth	Fifth	Sixth	Seventh	Eighth	Ninth	Tenth
Frequency (Hz)	253	359	788	796	844	870	965	1042	1180	1210
Maximum vibration mode	4.74	9.29	62.27	63.17	71.16	72.00	43.22	25.32	25.56	42.23

. The mode distributions shown in Figure 19a–c are the first- to third-order mode distributions in turn. One of the first-order intrinsic frequencies is 253 Hz, which is much higher than the external excitation frequency. Therefore, the fifth wheel does not resonate with the outside world in the constrained state.

Among the first ten orders of vibration, the first, second, ninth, and tenth orders are integral modes, and the third to eighth orders are local modes.

Among the overall modes, deformation of the first-order vibration mode occurred relatively uniformly on the saddle body. The deformation of the second-order vibration mode transitions from top to bottom, and the maximum deformation occurs on the bobtail at the lower end of the saddle. The deformation of the ninth- and tenth-order vibration modes transitions from the outside to the inside, and the maximum deformation occurs at the edge of the side of the saddle body.

In the local modes, the maximum deformations of the third- and fourth-order vibration shapes are located in the upper transverse plate, where all the third-order deformations are downward concave, and the fourth-order deformations occur in the upper transverse plate with left-side convex and right-side concave shapes. The maximum deformation of the fifth-order vibration pattern occurred on the left side of the carriages and bulges to the right, and the maximum deformation of the sixth-order vibration pattern occurred on the right side of the carriages and bulges to the right. Severe deformation in the seventh-order vibration mode occurs on the right side of the saddle body, where the largest deformation is located at the lower end tail of the right side, while larger deformation in the eighth-order vibration mode occurs on the left side of the saddle body, where the largest deformation is located at the lower end tail of the left side.

4.1.2. Dynamic Simulation and Bench Test Verification

Bench testing is a widely used method for evaluating engineering structures and mechanical equipment. It can simulate load changes under real-world road surface conditions. During the test, random mechanical loads were applied to the samples, and the stress–strain values and fatigue lifetimes at corresponding points were measured to assess reliability.

According to the ‘Pavement vehicles-fifth wheel strength test’ related dynamic test standards, as shown in Figure 20, F_v,t is applied to the rigid plate, F_h,t is applied to the radial of the inner and outer baffle connecting shaft of the fifth wheel, and the load in the dynamic test is circulated sinusoidally. The loading frequency is 2 Hz. The simulation showed that the maximum stress at a certain moment was 250 MPa, and the corresponding stress distribution diagram is shown in Figure 21. The calculated dynamic test fatigue life was greater than 1.0 × 10⁷ without dynamic failure. The strength and fatigue properties of the dynamic tests were within the permissible limits of the relevant standards.

The method of applying a load in the biaxial bench test is the same as that in Figure 20. F_v,t acts vertically downwards on the rigid plate, and F_h,t is applied to the radial of the inner and outer baffle connecting shaft of the fifth wheel. The magnitude of F_v,t is 117.72 KN to 353.16 KN, and the magnitude of F_h,t is −120 KN to 120 KN. The load in the dynamic test is circulated sinusoidally. The loading frequency is 2 Hz.

According to the above finite element simulation results, it can be found the maximum stress point is located at the inner baffles restraining the circular hole. Therefore, eight strain collection points were arranged at the key positions of the outer and inner baffle connections of the fifth wheel in this test, and eight-channel dynamic strain gauges were used to synchronously collect the bench test data.

In Figure 22a, the left side shows the fifth wheel installed on the line, and in Figure 22b, the right side shows the biaxial bench test conducted after the fifth wheel was installed. The strain results of eight test points on the fifth wheel were collected, and the strain data of eight groups of periods were obtained. According to Hooke’s law, the maximum stress of the biaxial dynamic bench test is less than 250 MPa (the maximum stress value of the dynamic simulation test in Figure 21). And the final fatigue life of the fifth wheel bench test is more than 2 million cycles.

4.1.3. C-Grade Pavement Surface Excitation Verification

The mass of the fifth wheel is negligible compared to the tens of tons of the wagons, so changes in its mass before and after optimization can be disregarded. The strength analysis of the fifth wheel’s optimal design, based on the component thicknesses, was conducted using the load spectrum of a C-grade pavement at a speed of 60 km/h, as shown in Figure 10. The analyzed stress spectrum of the saddle body is shown in Figure 23, indicating that the maximum equivalent stress is below 400 MPa.

The fatigue life of the fifth wheel was estimated using the rain flow counting method. The stress spectra under 30 s of pavement excitation were counted for the frequency of stress amplitude and stress mean, and three-dimensional bar charts of stress amplitude, stress mean, and operating frequency were obtained using the three-point cyclic rainfall counting method, as shown in Figure 24.

The transformation was performed using Goodman’s empirical fatigue formula, based on the corresponding stress amplitudes and stress averages.

$$S_{ij}={\displaystyle \frac{{\sigma }_b·S_{ia}}{{\sigma }_b-S_{mj}}}$$

(8)

In Equation (8), $S_{ij}$ is the equivalent zero mean stress, $S_{ia}$ is the ith stress amplitude, $S_{mj}$ is the jth stress mean value, and ${\sigma }_b$ is the strength limit of SD600, taking 1200 MPa.

Subsequently, according to Miner’s linear cumulative fatigue damage theory, the damage amount of the fifth wheel at a certain time was obtained as follows:

$$D_{ij}={\displaystyle \frac{n_{ij}}{N_{ij}}}$$

(9)

In Equation (9), $n_{ij}$ is the working frequency of the corresponding stress amplitude and mean stress value, and $N_{ij}$ is the theoretical fatigue number obtained by $S_{ij}$ corresponding to the S–N curve of SD600.

The total damage corresponding to the rainfall matrix can be obtained by accumulating the damage values as:

$$D={\sum }_{i=1}^m{\sum }_{j=1}^n{D}_{ij}$$

(10)

The inverse of the total damage D was calculated to be 30,291 h. The fifth wheel can continue to work for 1262 days without rest, and the total distance traveled can reach 1,187,000 km.

4.2. Quadratic Optimization Best Value Verification

The stress–strain and fatigue life were verified for parts parameterized to the smallest values within the ranges shown in Table 11 and Table 12.

The minimum values of the thickness of the components were taken at a time (7.2, 4.0, 20.4, 4.0, 8.0, 4.1, 5.1, 4.0, 5.0, and 4.0), resulting in a mass of 72.46 kg, which is a reduction of 30.46% compared to the original fifth wheel of 104.2 kg.

4.2.1. Stress–Strain Verification

By analyzing the stresses and displacements under the three conditions, the maximum stress and displacement values are listed in

Table 15. Equivalent stress, displacement, and fatigue properties under three conditions.

Working Condition	Static Compression	Uphill Lifting	Steering Rollover
Maximum stress (MPa)	252	321	461
Maximum displacement (mm)	0.0643	0.351	0.219
Minimum fatigue life (cycles)	1.0 × 107	1.0 × 107	5.142 × 106

. The corresponding stress and displacement diagrams for the three conditions are shown in Figure 25. Figure 25a–c show the equivalent stress distributions for conditions 1 to 3, while Figure 25d–f show the displacement distributions for conditions 1 to 3.

According to the finite element analysis results, the maximum equivalent stress among the three conditions is 460.5 MPa, occurring in the third condition at the lower transverse plate. The material used was SD600, which has a yield strength of 600 MPa, and the stress values met the requirements. According to the relevant standard, the maximum strain in the component should be less than 0.2%. The maximum displacement in condition 1 is significantly smaller than in the other two conditions, occurring in the saddle body, which is also the widest part, and its strain ratio is much lower than in the other two conditions. The maximum displacement in condition 2 is 0.3506 mm at the lower transverse plate, corresponding to a strain of 0.15%, which is below the 0.2% limit. The maximum displacement in condition 3 is 0.2191 mm, located in the force-transforming element, corresponding to a strain of 0.08%, which is below the 0.2% limit, meeting all requirements.

4.2.2. Fatigue Performance Verification

The fatigue life under the three conditions was analyzed, and the calculated life distribution diagrams for conditions 1 and 2 are shown in Figure 26, with a fatigue life of more than 1.0 × 10⁷, which tends to an infinite life. The life distribution diagram of condition 3 is shown in Figure 27, which reaches 5.142 × 10⁶ and satisfies the corresponding standard requirements. The position of the minimum life under condition 3 is also the element node-218,253.

5. Conclusions

The purpose of this study is to achieve a lightweight design for the fifth wheel while improving its fatigue life performance, achieving coordination optimization between the two to improve the fuel economy of the semi-trailer tractor.

Through finite element analysis, the locations of maximum stress and strain in the fifth wheel under three conditions were identified, ensuring that the fifth wheel does not resonate with external excitations in the constrained state. Strength verification under road excitation ensures that the semi-trailer will not experience failure during road operation.

A multi-objective optimization model was established, and a set of solutions that best fit practical applications was identified. The feasibility of the optimal design was verified through finite element analysis. A hybrid model combining the random forest algorithm and an optimized BP neural network was developed for fatigue life prediction, eliminating the need for complex parameter settings and finite element calculations. Based on data analysis, the range of values for each variable under the corresponding constraints was determined, and the stress–strain and fatigue life were validated for the smallest values within the range.

The results of the study show the following.

(1)

The optimal design option was obtained through multi-objective optimization. The thicknesses of the corresponding components were 7.5 mm, 6.0 mm, 20.0 mm, 6.4 mm, 10.4 mm, 5.2 mm, 7.7 mm, 6.2 mm, 7.0 mm, and 6.0 mm, with a total mass of 79.07 kg. The mass of this design was reduced by 24.11% compared to the original fifth wheel, with the fatigue life exceeding 10 million cycles for conditions 1 and 2, and the minimum fatigue life for condition 3 increased to 4,614,000 cycles, achieving coordination optimization of mass and fatigue life.

(2)

The hybrid model improved the accuracy of the fatigue life prediction by 47.62% compared to the original BP neural network, enabling more accurate fatigue life predictions based on the thickness of each component.

(3)

The data from the secondary optimization were analyzed to determine the thickness ranges for each component corresponding to 20% and 25% weight reduction. These ranges can be adjusted based on different application scenarios, forces, and contact types, further enhancing the product’s performance and durability.

(4)

Validation of the optimal design option of multi-objective optimization was found to have a first-order intrinsic frequency greater than 100 Hz, which does not resonate with other components or the outside world during operation. The fatigue life is still more than 2 million cycles under the higher-intensity bench test than the standard requirement, which meets the corresponding failure protection performance. Using the rain flow counting method and Miner’s linear cumulative fatigue damage theory, the optimized fifth wheel normal operating hours reached 30,291 h, and the normal operating journey of the tractor was 1,817,000 km when facing a C-grade road surface with a greater degree of unevenness than that of the bench test.

(5)

Validation of the maximum value in the secondary optimization results reveals that the mass of this design option set is reduced by 30.46% from the original fifth wheel, and the maximum stress–strain meets the corresponding requirements. The fatigue life exceeds 1.0 × 10⁷ for conditions 1 and condition 2, and the fatigue life for condition 3 reaches 5.142 × 10⁶, which meets the corresponding criteria.