A Novel Voltage–Current Characteristic Model for Understanding of Electric Arc Furnace Behavior Using Experimental Data and Grey Wolf Optimization Algorithm
Abstract
1. Introduction
2. Material and Methods
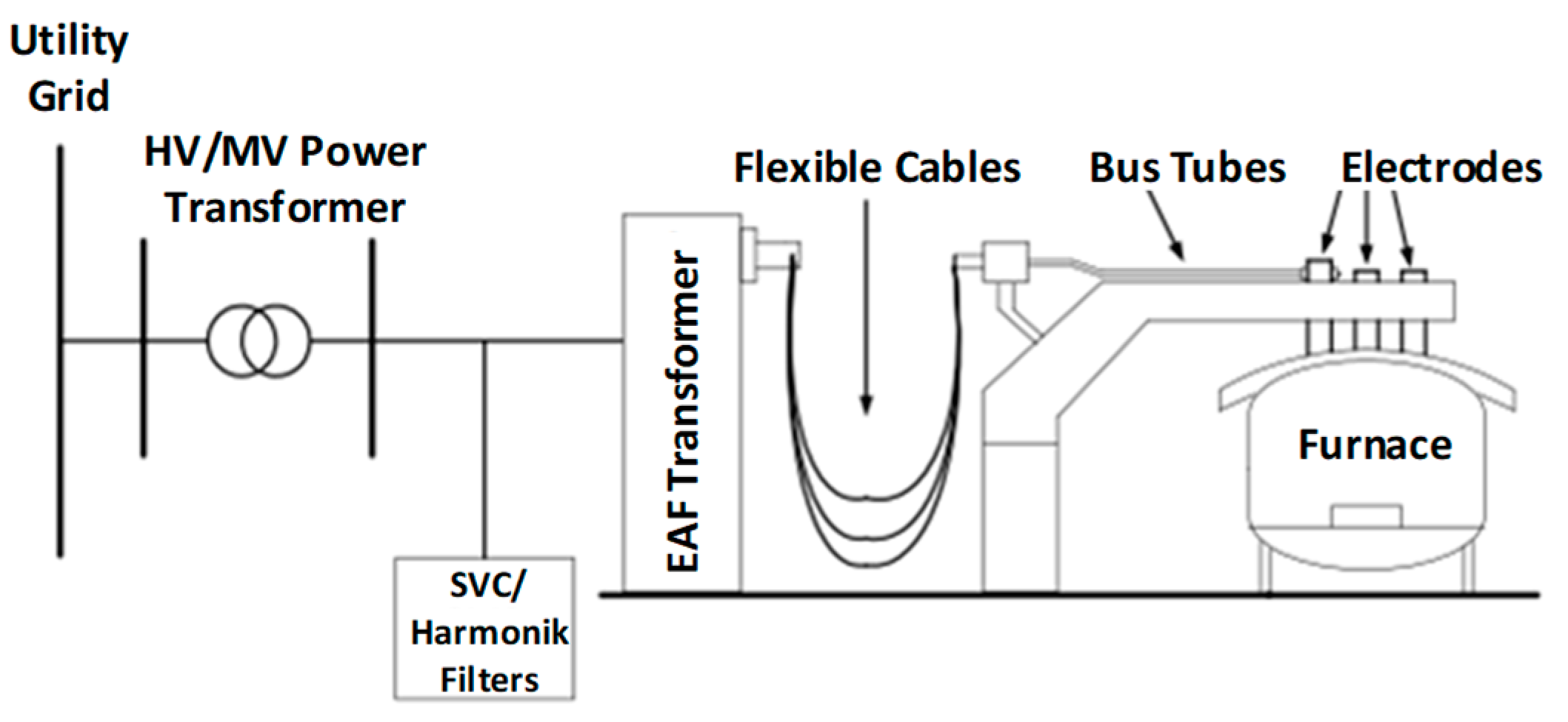
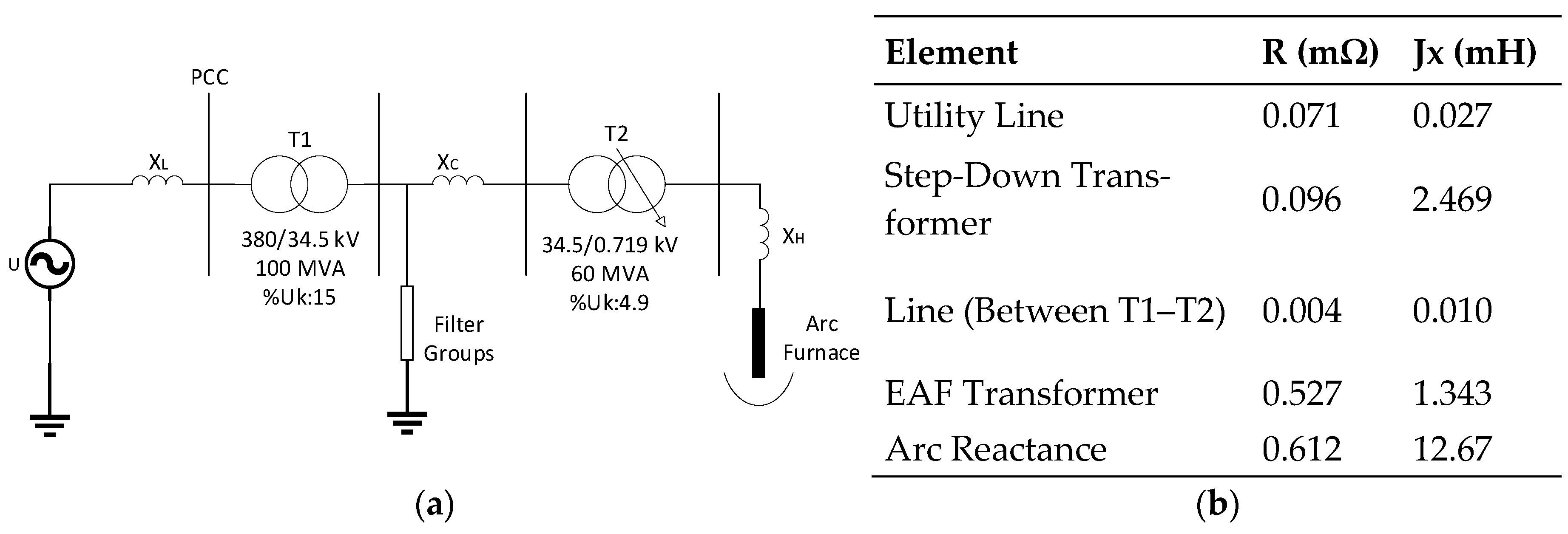
2.1. Electrical Circuit of Arc Furnaces
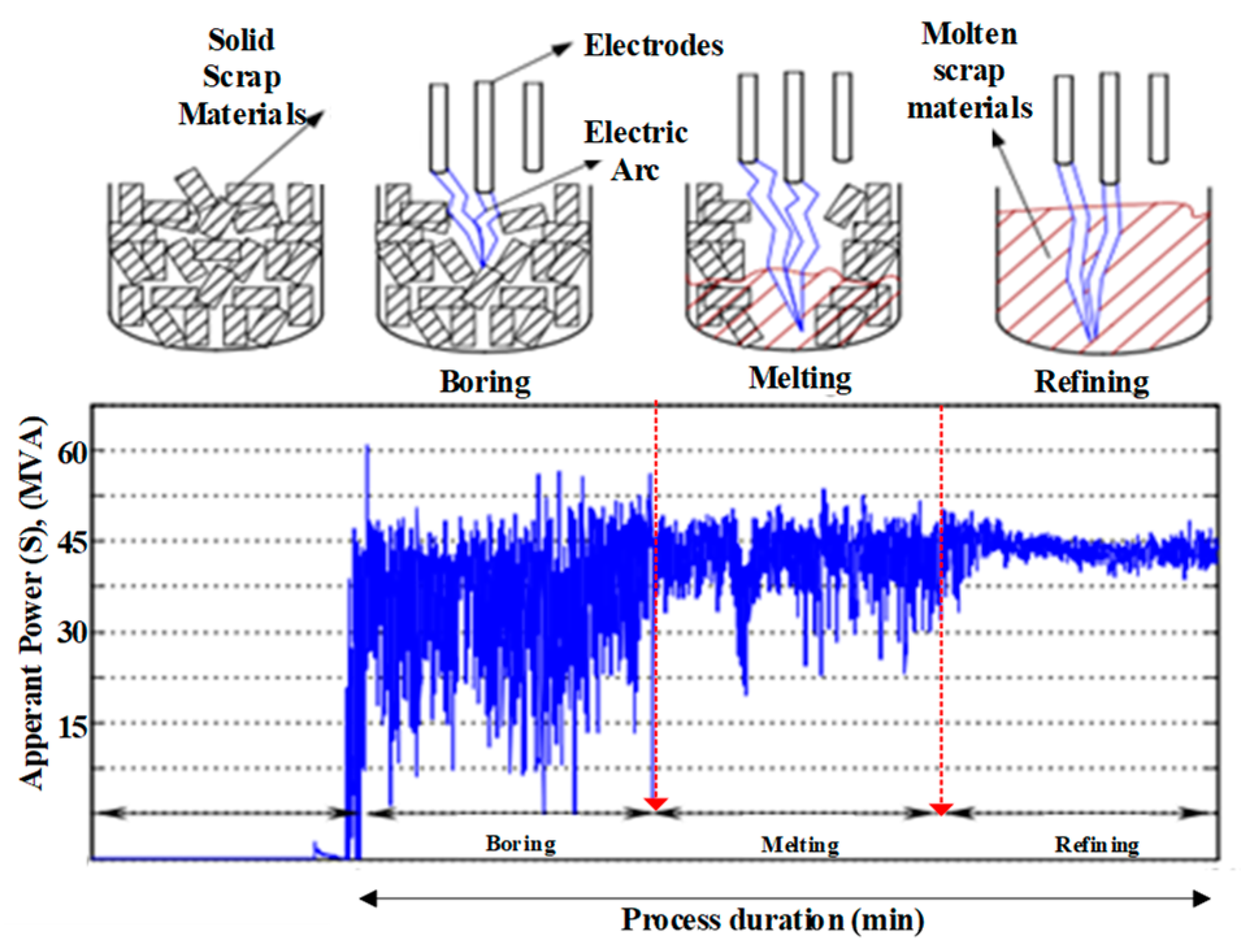
2.2. Experimental Measurement of Electrical Arc
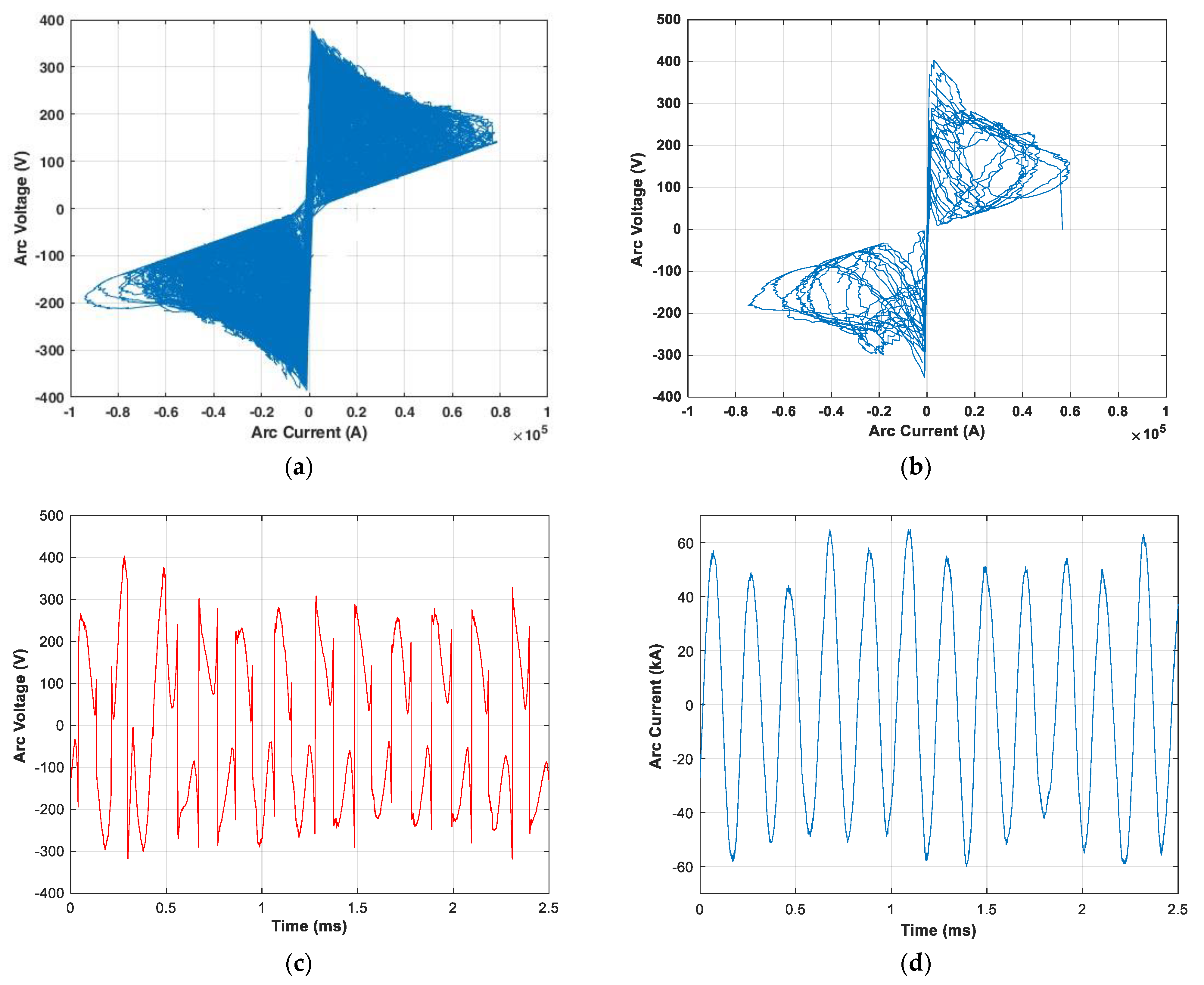
2.3. Time-Domain Methods for V–I Characteristics of EAF Arcs
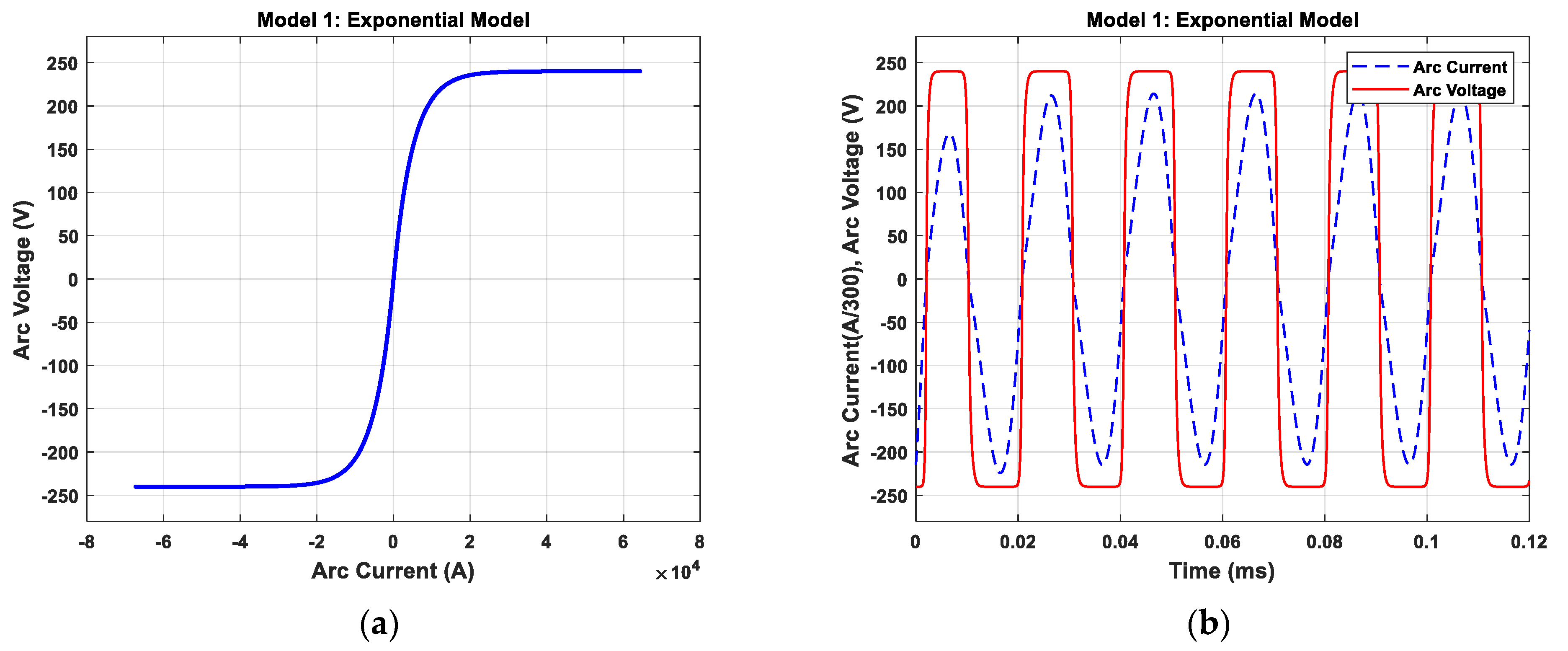
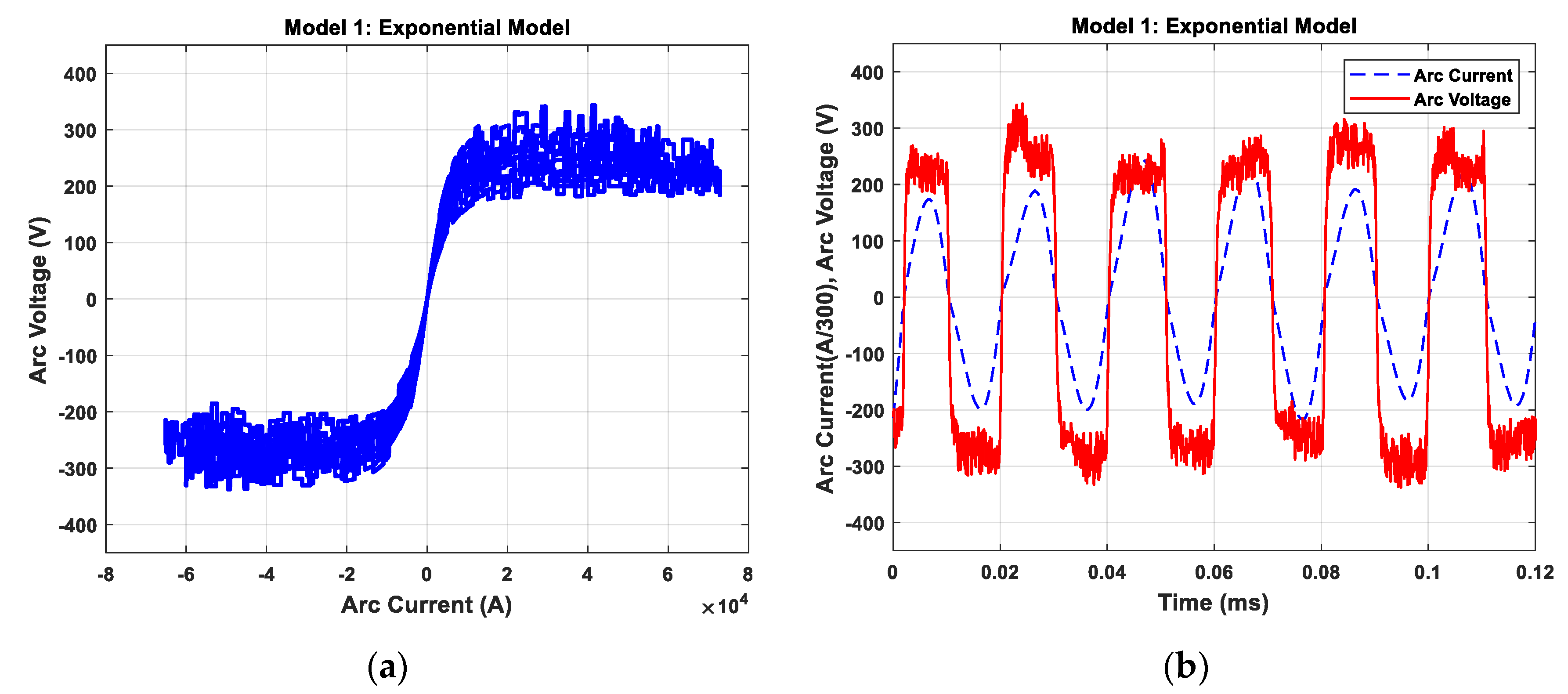
2.3.1. Exponential Model (Model 1)
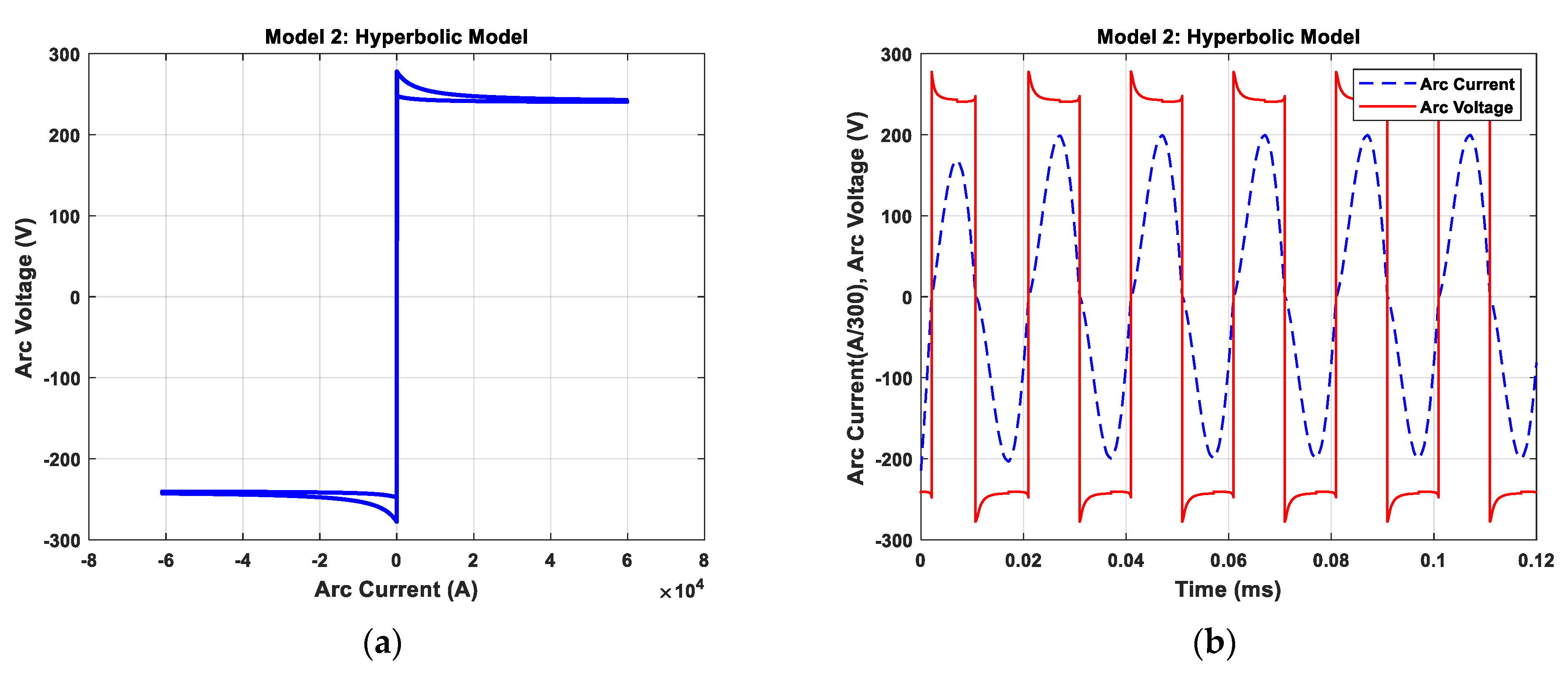
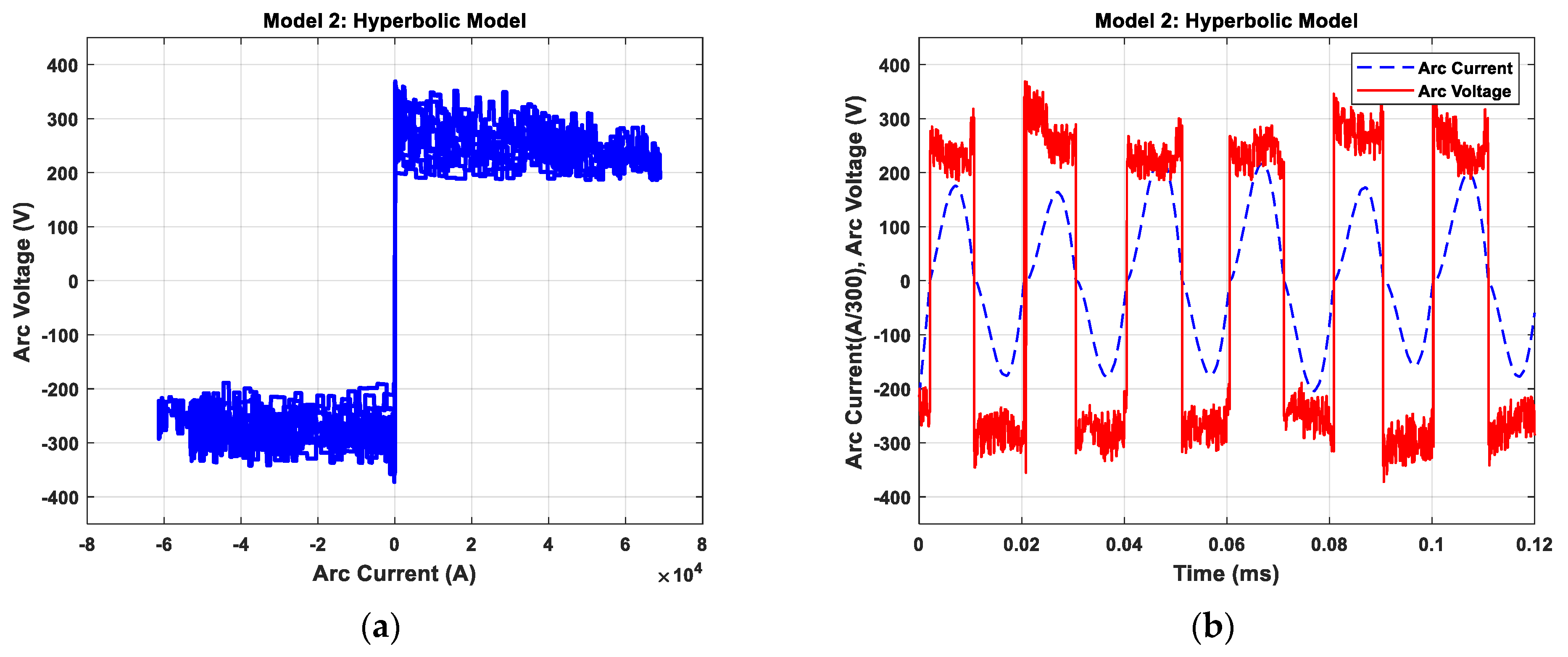
2.3.2. Hyperbolic Model (Model 2)
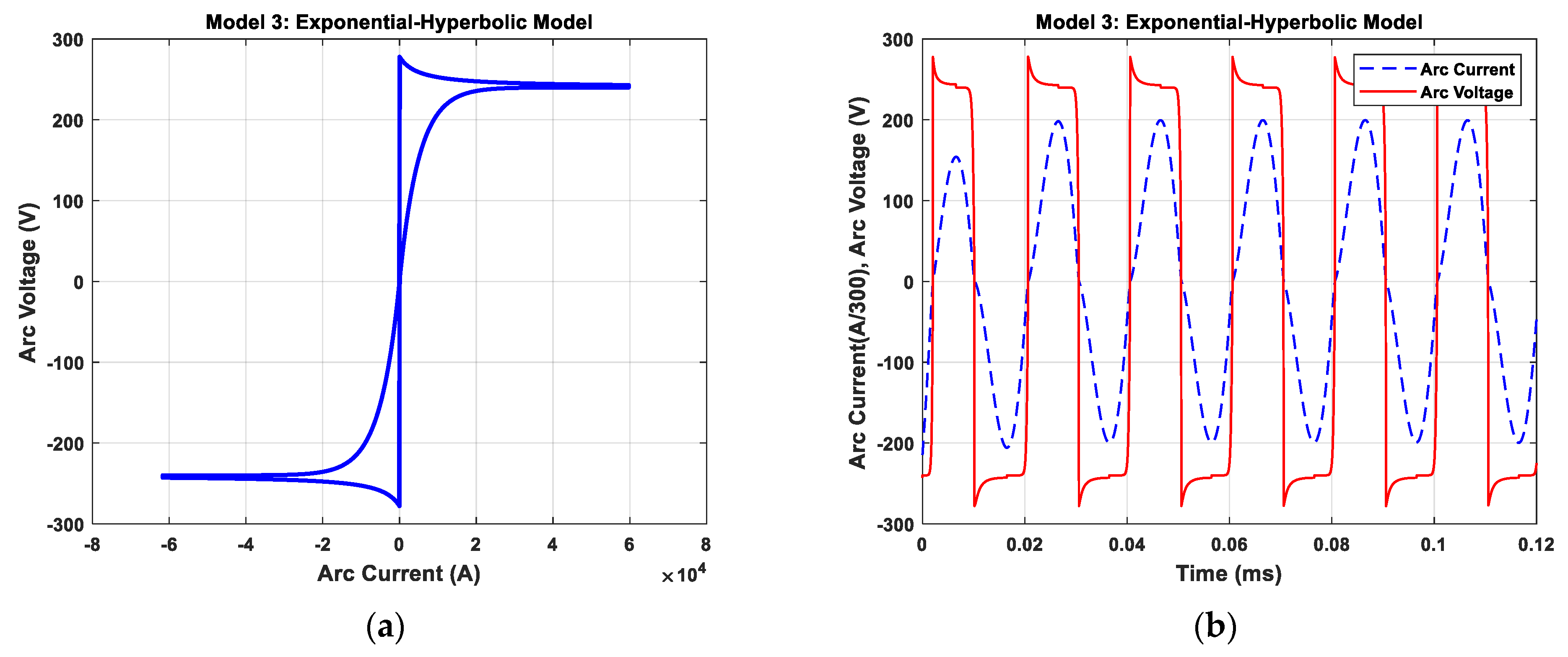
2.3.3. Exponential–Hyperbolic Model (Model 3)
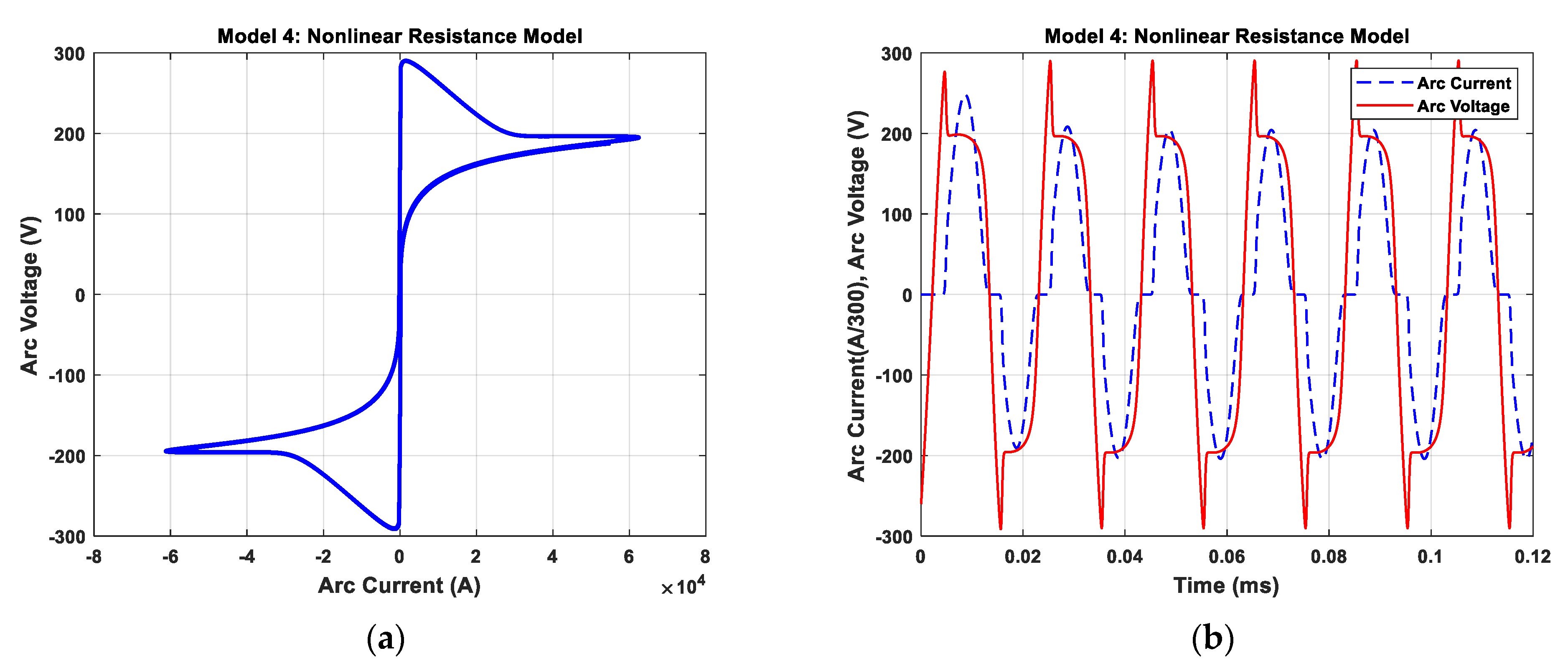
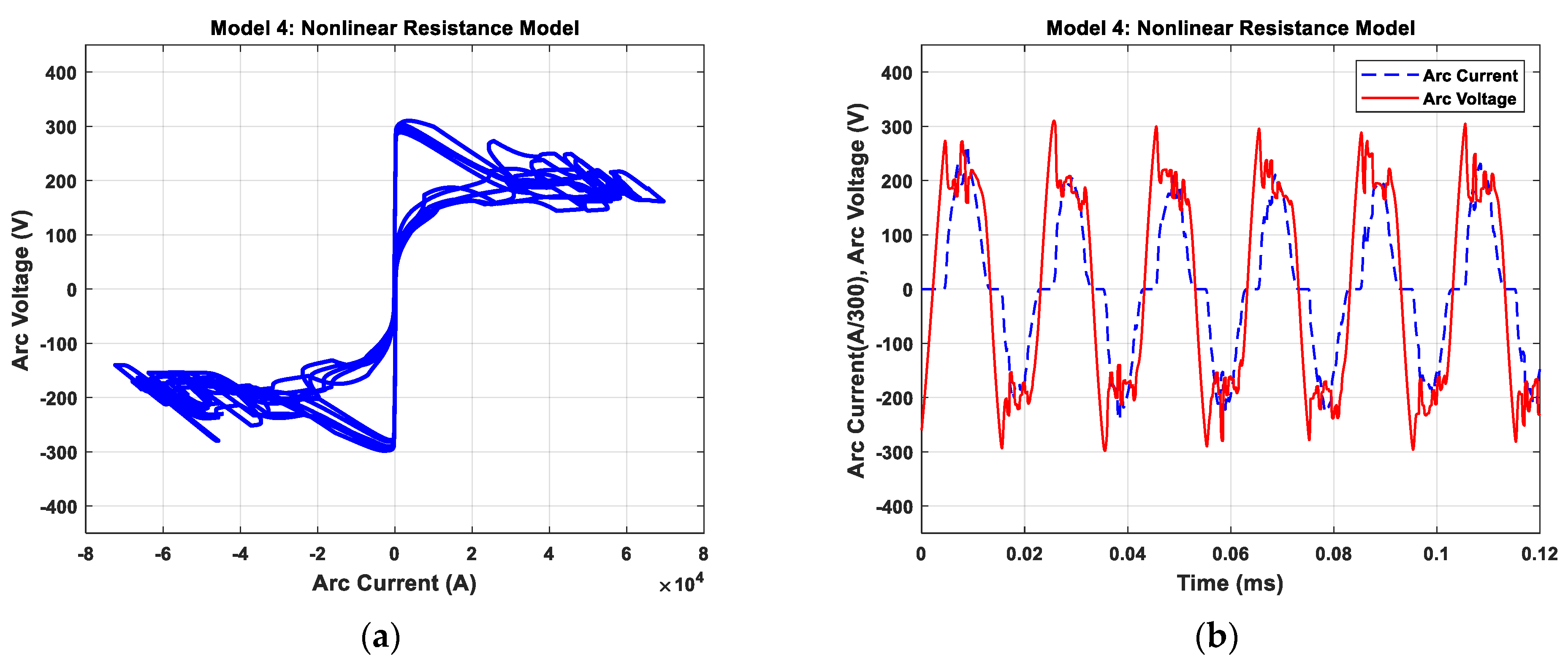
2.3.4. Nonlinear Resistance Model (Model 4)
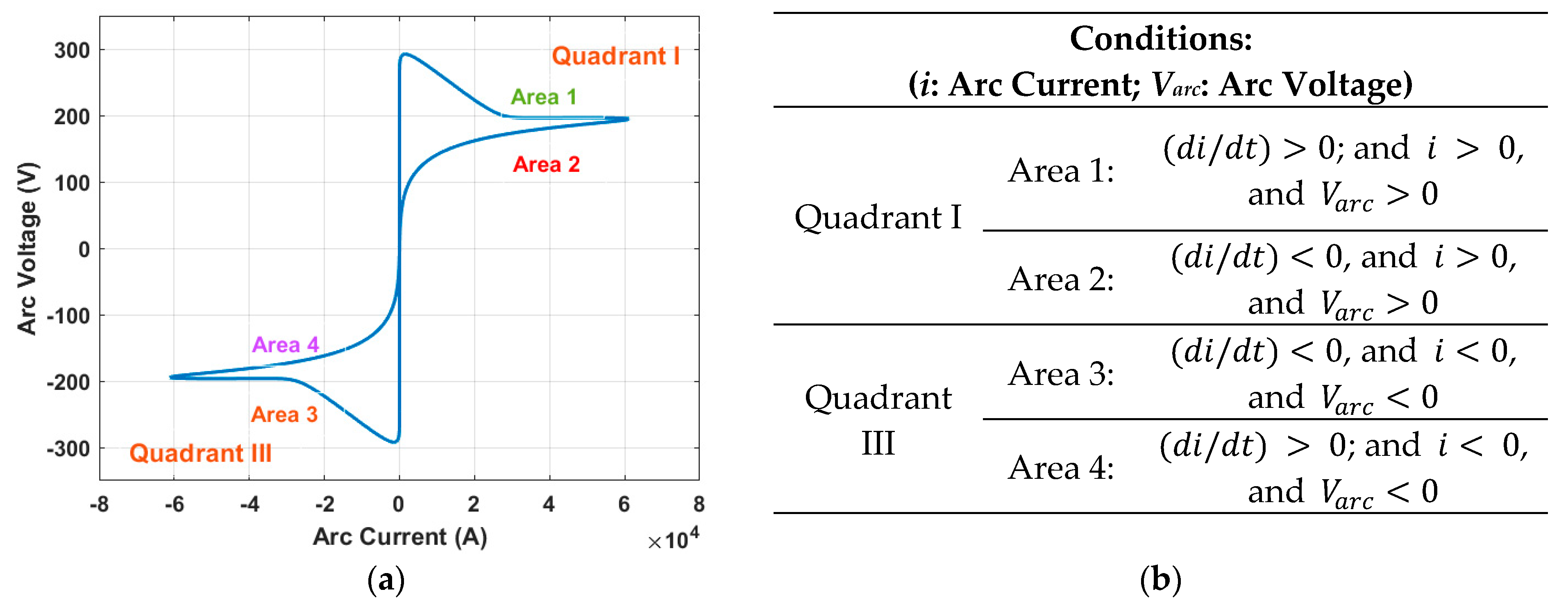
3. Proposed V–I Characteristic Model of Electrical Arc
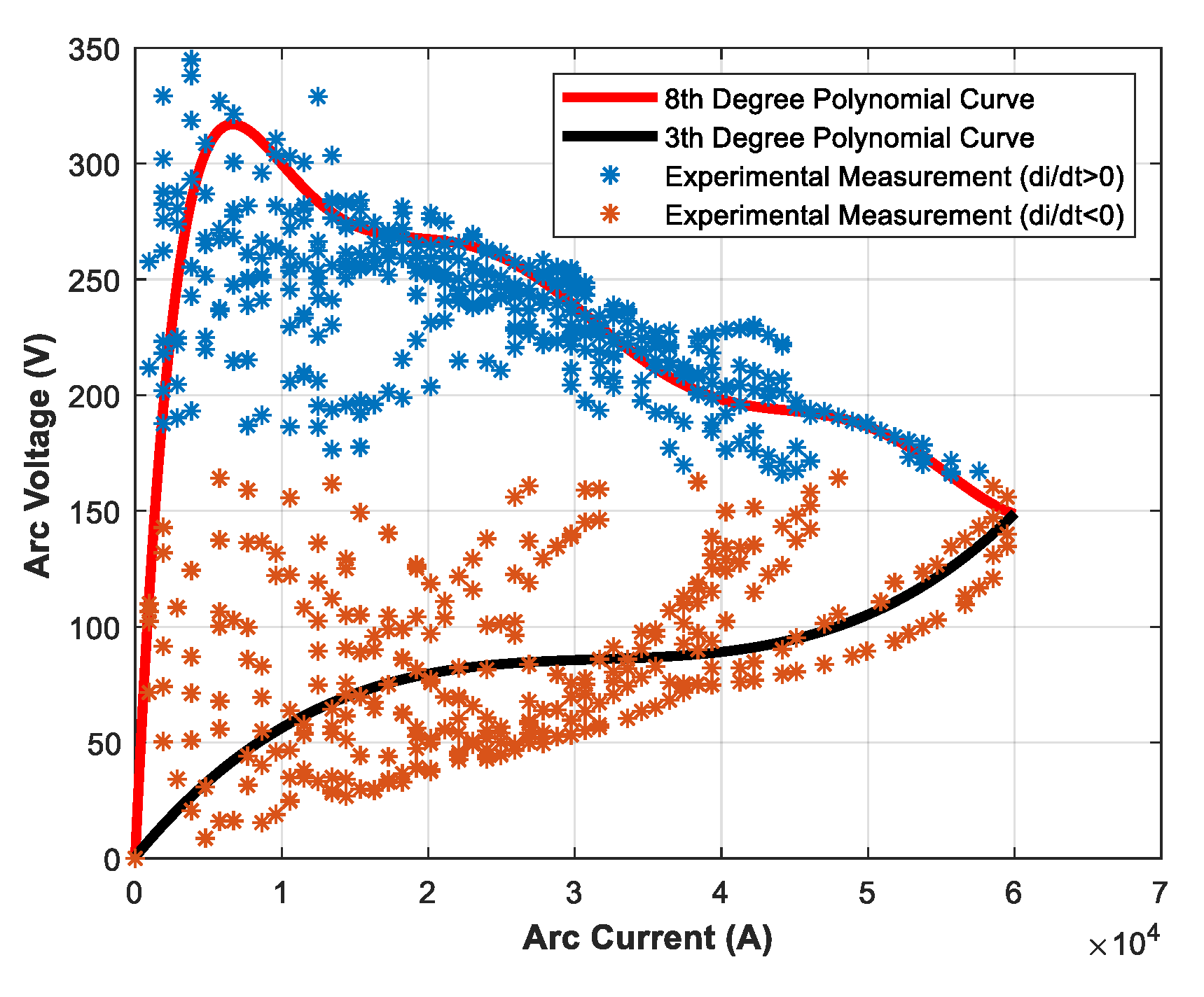
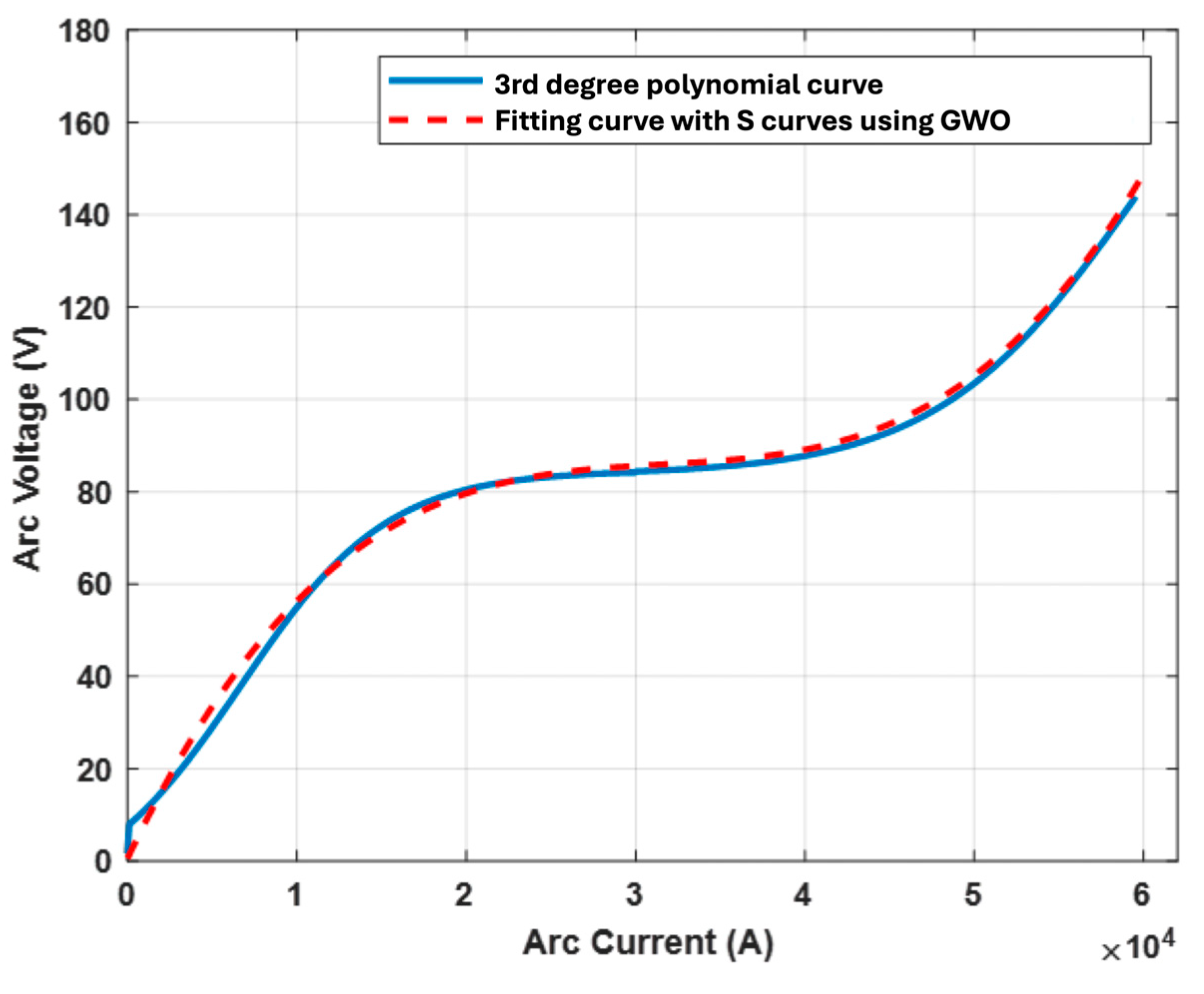
3.1. Curve-Fitting Method for Defining Polynomial V–I Characteristics of Electric Arc
- For the case where , , and , the V–I characteristic is represented by an eighth-degree polynomial expression, as formulated in Equation (6):
- For the case where , , and , the V–I characteristic is represented by a third-degree expression, as formulated in Equation (7):
- The eighth-degree polynomial expression coefficients (with 95% confidence bounds) are calculated as follows: , , , , , , , , and .
- third-degree expression coefficients (with 95% confidence bounds) are calculated as follows: , , , and .
3.2. Grey Wolf Optimization (GWO) Algorithm
| Algorithm 1. Pseudo Code of the GWO Algorithm |
| Initialize grey wolf population: Xi = [C1_i, C2_i, I1_i, I2_i, I3_i, I4_i, η_i, n_i] for i = 1 to n // C1, C2: Heidler function coefficients // I1–I4: current threshold points for Double S-curve // η, n: slope and shape parameters Set control parameters: a = 2 A and C will be computed during updates For each search agent Xi: Compute estimated voltage V_est using: - Modified Heidler Function (for rising arc regions) - Double S-curves (for falling arc regions) Calculate objective functions: f1 = RMSE(V_measured, V_test) f2 = MAE(V_measured, V_test) Identify non-dominated solutions and initialize the archive with them // Leader selection Xα = SelectLeader(archive) Temporarily remove Xα from the archive Xβ = SelectLeader(archive) Temporarily remove Xβ from the archive Xδ = SelectLeader(archive) Add Xα and Xβ back to the archive // Optimization Loop t = 1 while t < MaxIter: for each search agent Xi: Compute vectors A and C: A = 2 * a * rand() – a C = 2 * rand() Update Xi position using Equations (12a)–(12g) Enforce physical bounds on Xi parameters (e.g., C1 > 0, I1 < I2, etc.) Update control parameter a: a = 2 – (2 * t/MaxIter) For each updated Xi: Recalculate V_est from new parameters Recalculate f1 and f2 Identify non-dominated solutions Update the archive with new non-dominated solutions If archive is full: Apply grid mechanism to remove one archive member Add the new solution to the archive If any new solution lies outside current hypercubes: Update the grid structure to include the new solution(s) // Update leaders Xα = SelectLeader(archive) Temporarily remove Xα Xβ = SelectLeader(archive) Temporarily remove Xβ Xδ = SelectLeader(archive) Add back Xα and Xβ to the archive t = t + 1 // Return result Return final parameter sets for EAF V–I modeling |
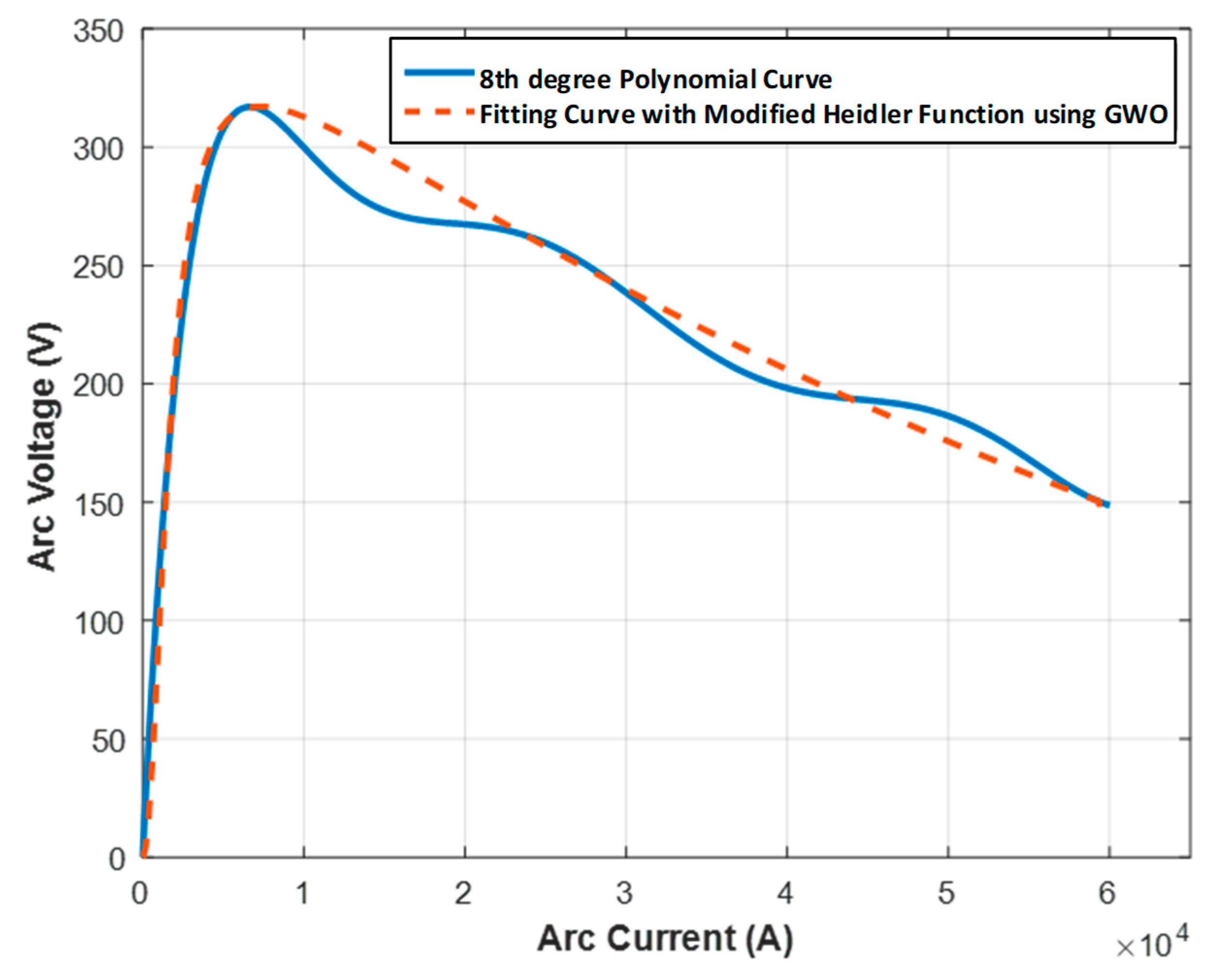
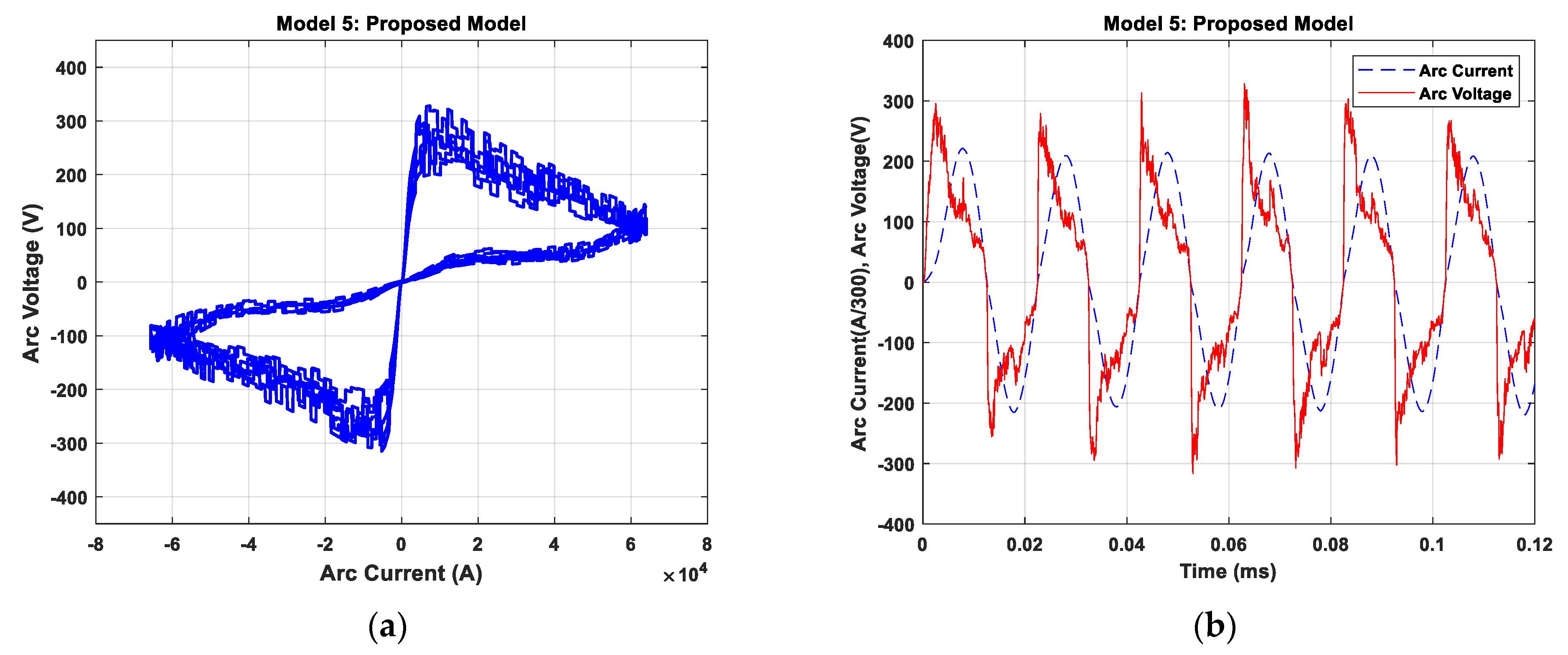
3.3. Proposed Model
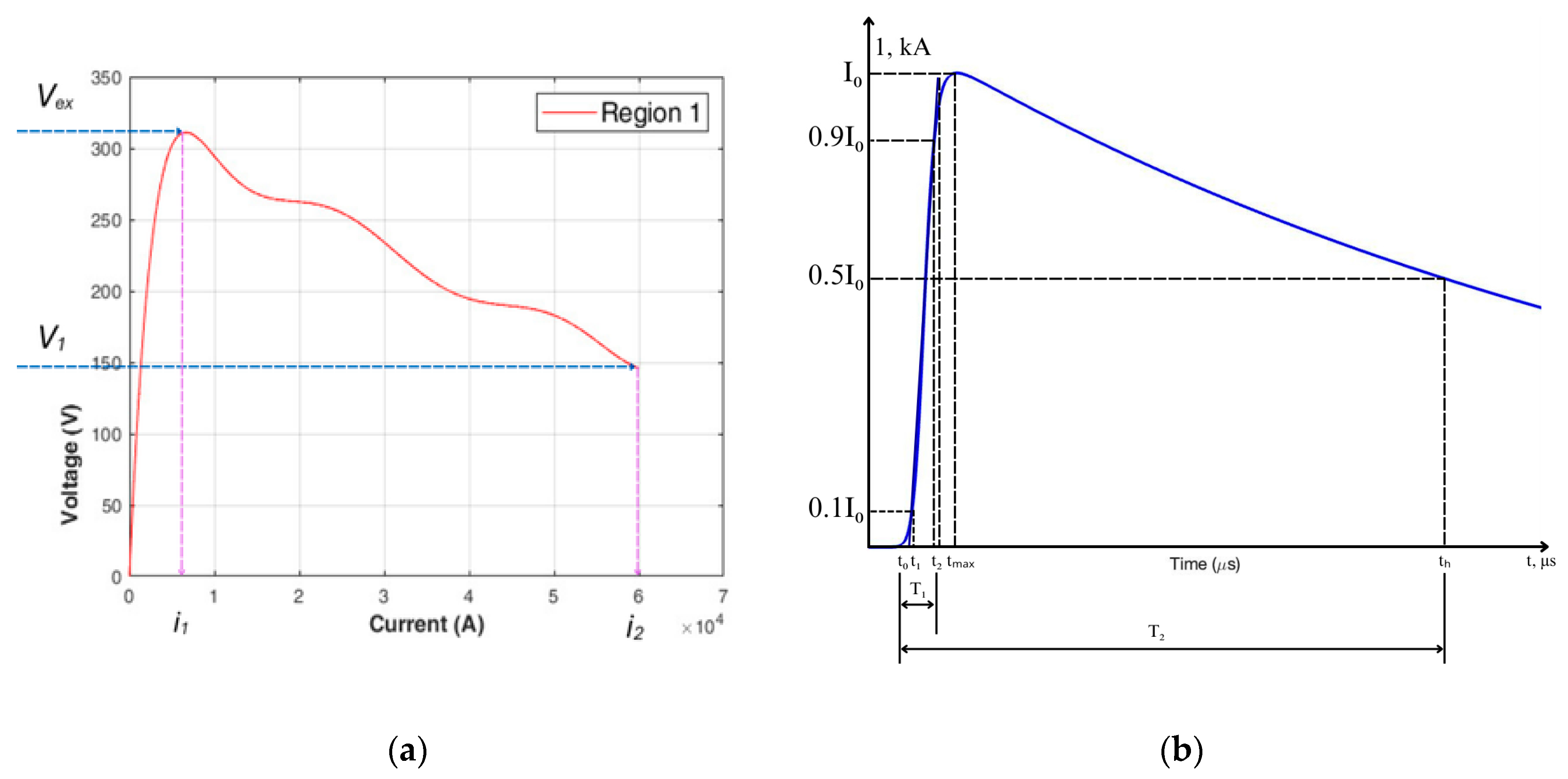
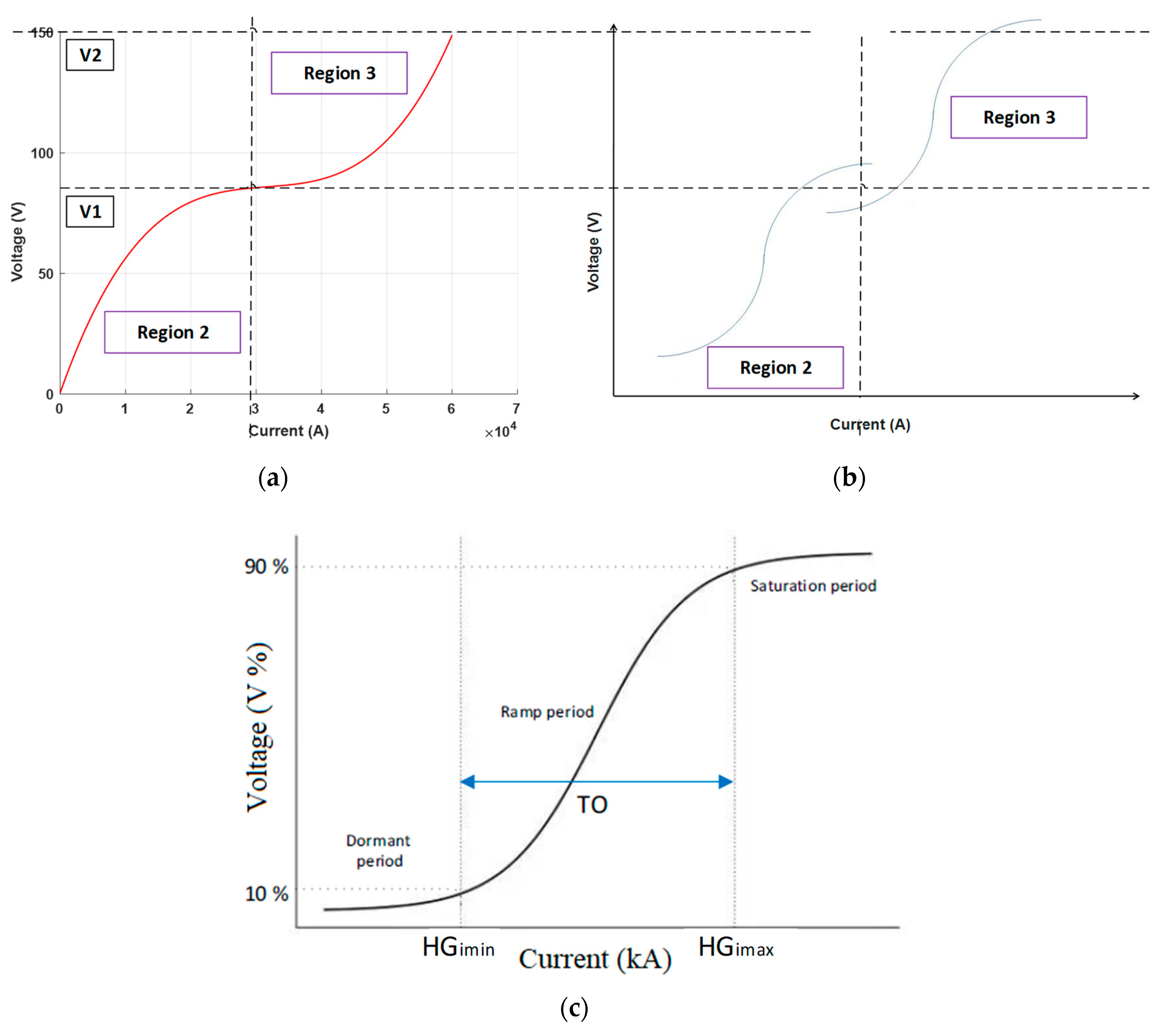
3.3.1. Region 1 and Region 4: Rising Current Phase
- (the min and max values of the arc voltage obtained in the experimental results)
- (the min and max values of the arc current obtained in the experimental results)
3.3.2. Region 2 and Region 3
| is the maximum saturation voltage on the S-curve. | |
| is the present value in the minimum hyper growth state, | |
| is the present value in the maximum hyper growth state, | |
| is the arc current. |
- In Region 2, where 0 kA, and , the mathematical correlation between arc voltage and arc current is expressed by Equation (17):
- For Region 3, under the constraints , and , the mathematical relationship between arc voltage and arc current is articulated by Equation (18):
| is the maximum voltage value of the S-curve for Region 2. | |
| is the maximum voltage value of the S-curve for Region 3. | |
| is the maximum value of the polynomial expressions obtained through curve fitting. (corresponding to the maximum value of the eighth-degree polynomial defined in Region 1) | |
| , | is the arc current value of S-curves in the minimum hyper grow state. |
| , | is the arc current values of S-curves at the highest hypergrowth condition. |
| is the coefficient values used to define the optimal solution of the polynomial expression. |
- (range of arc voltage values derived from experimental data for Region 2)
- kA (range of arc current values derived from experimental results for Region 2)
- (range of arc voltage values derived from experimental data for Region 3)
- (range of arc current values derived from experimental results for Region 3)
4. Results and Discussion
4.1. Investigation of Static V–I Characteristics of Arc Models
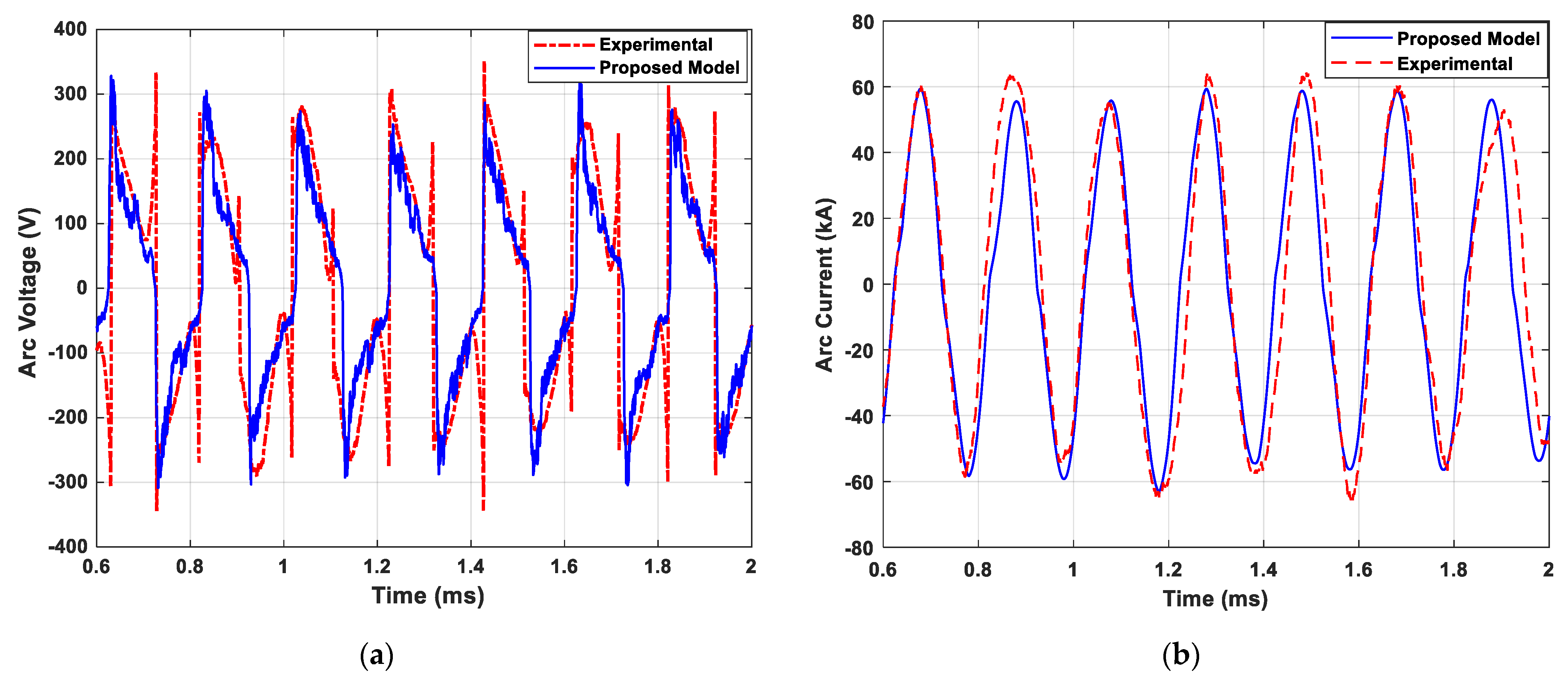
4.2. Dynamic Characteristic of Electric Arc for Melting Process
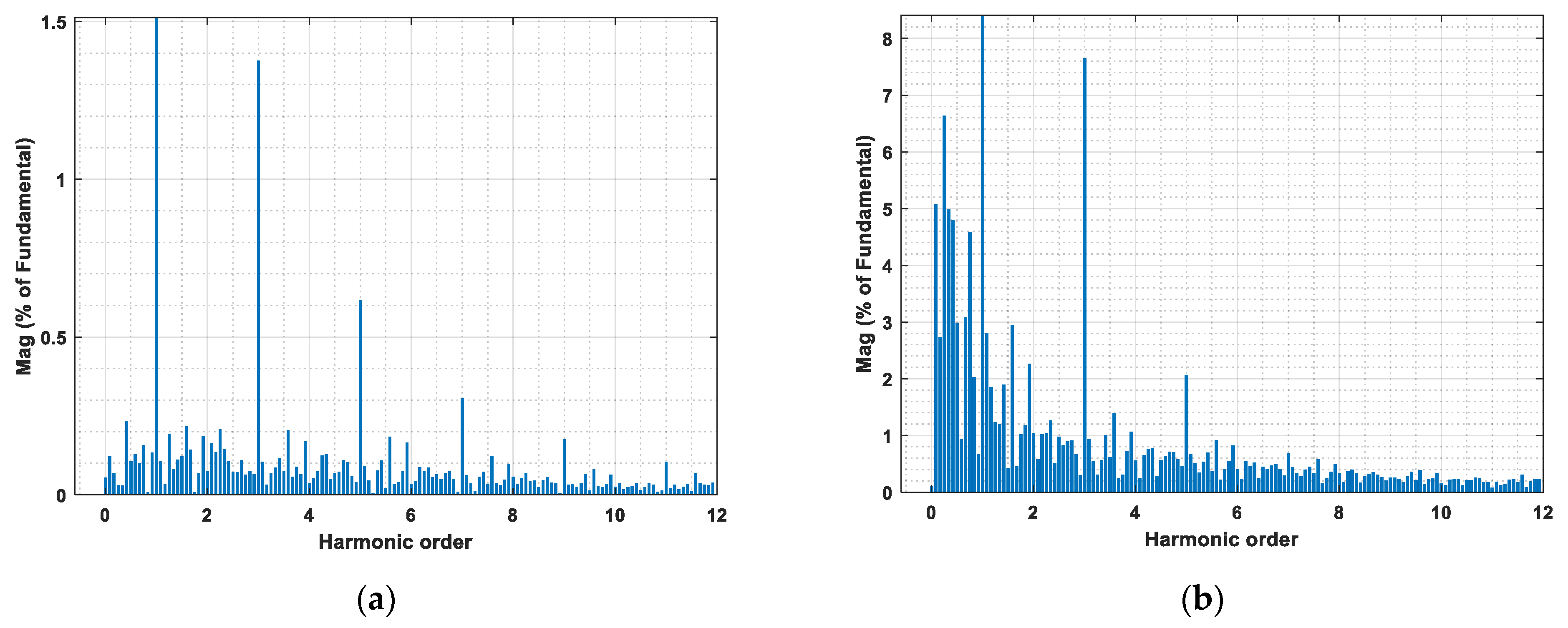
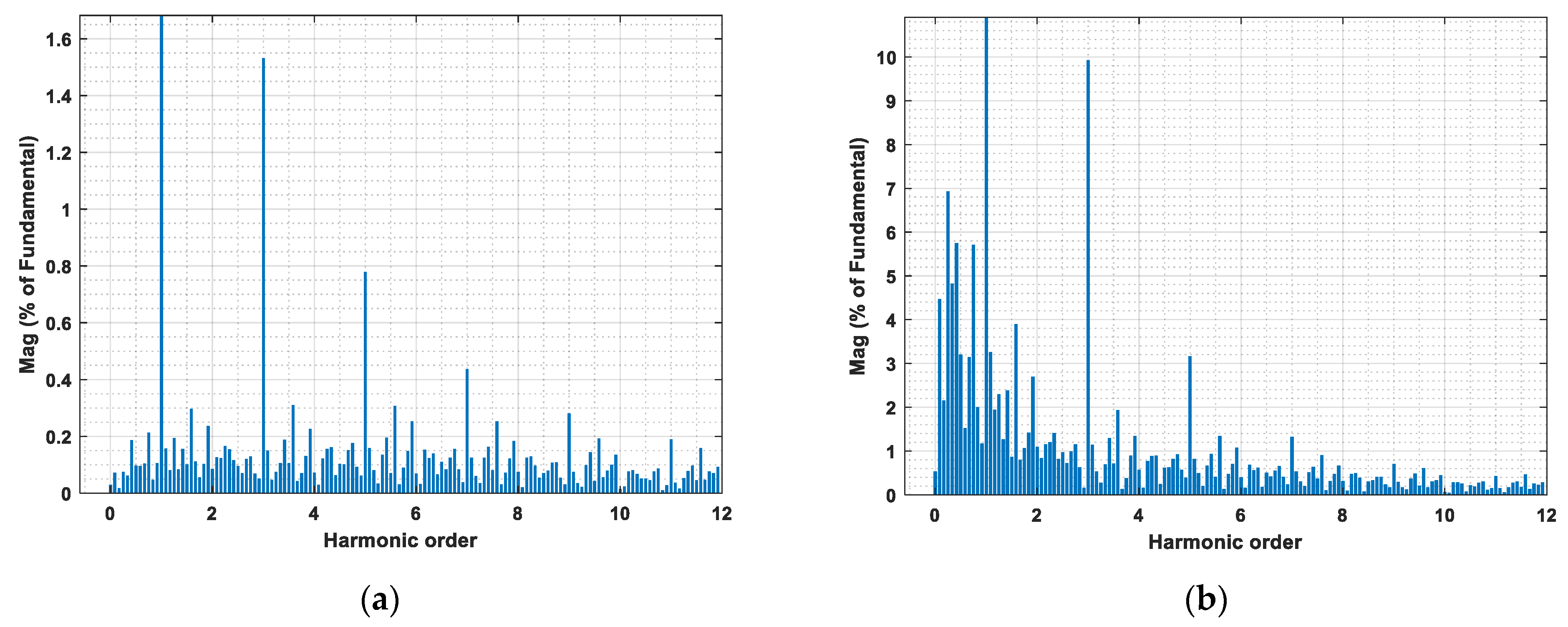
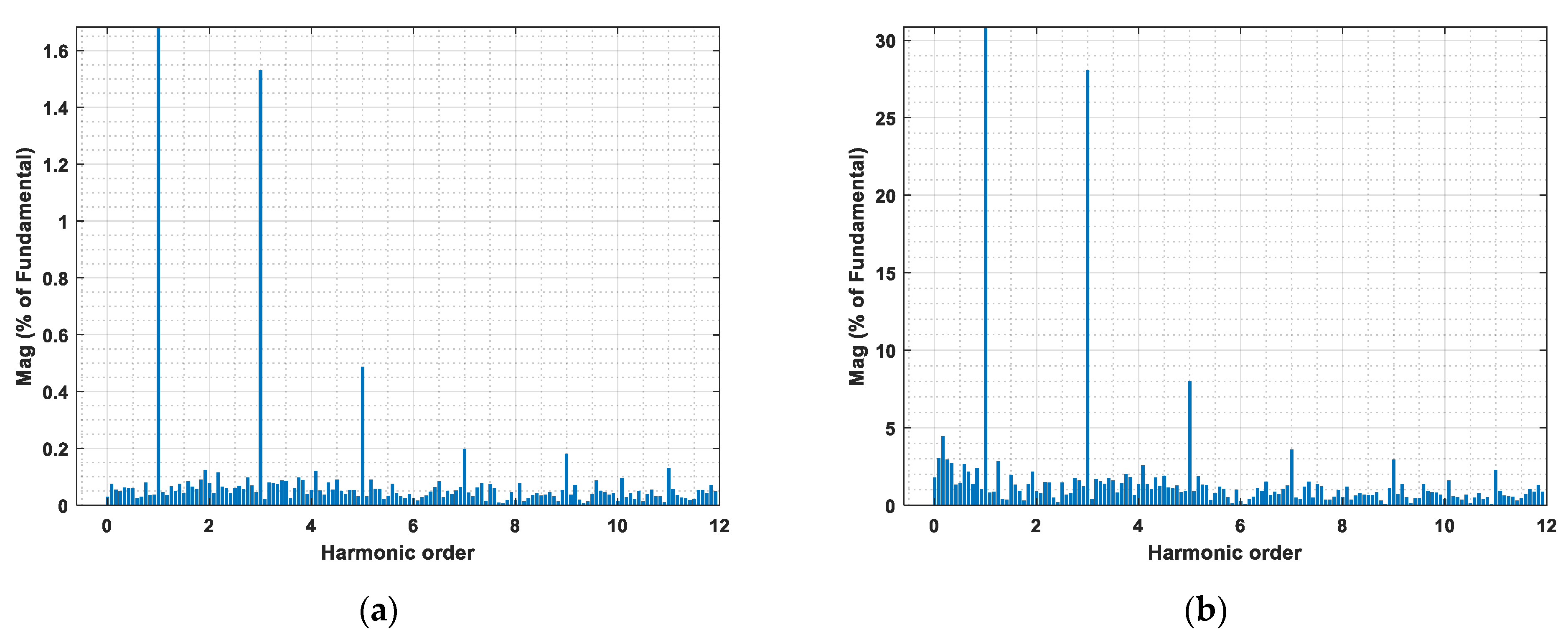
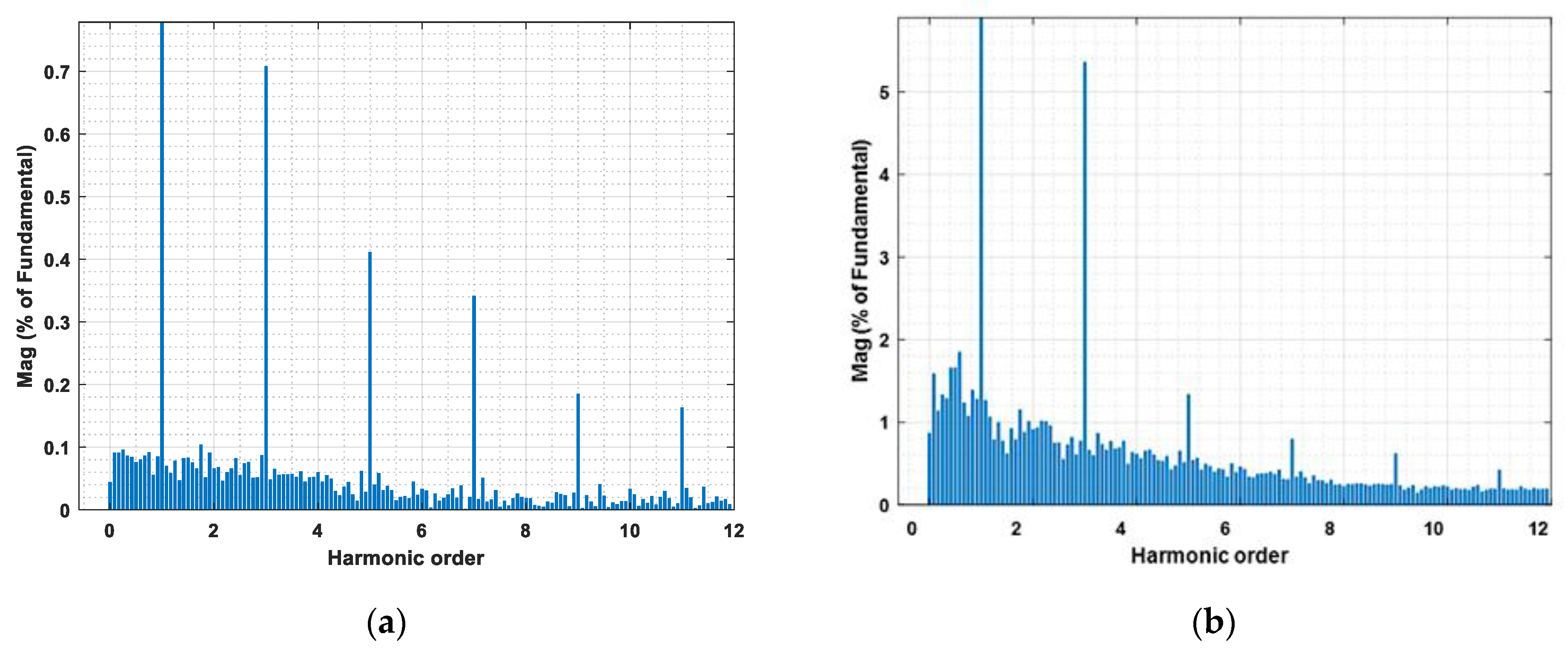
4.3. Harmonic Contents of Arc Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EAF | Electric arc furnace |
| FFT | Fast Fourier transform |
| GWO | Grey wolf optimization algorithm |
| IF | Induction furnaces |
| PPC | Point of common coupling |
| SVC | Static VAR compensator |
| THD | Total harmonic distortion |
References
- Zhao, C.; Jiang, Q.; Liu, D. Flexible Power Supply System of AC Electric Arc Furnace. J. Mod. Power Syst. Clean Energy 2023, 11, 622–633. [Google Scholar] [CrossRef]
- Torquato, M.F.; Martinez-Ayuso, G.; Fahmy, A.A.; Sienz, J. Multi-objective optimization of electric arc furnace using the non-dominated sorting genetic algorithm II. IEEE Access 2021, 9, 149715–149731. [Google Scholar] [CrossRef]
- Seker, M.; Memmedov, A.; Huseyinov, R.; Kockanat, S. Power Quality Measurementand Analysis in Electric Arc Furnace for Turkish Electricity Transmission System. Elektron. ir Elektrotechnika 2017, 23, 25–33. [Google Scholar] [CrossRef][Green Version]
- Rao, K.R.; Karsiti, M.N. Optimal Design of a Arc Furnace Transformer by Intelligent Evolutionary Methods. Electr. Power Energy Syst. 2012, 43, 1056–1062. [Google Scholar] [CrossRef]
- AMakarov, A.N.; Rybakova, V.V.; Galicheva, M.K. Electromagnetism and the Arc Eficiency of Electric Arc Steel Melting Furnace. J. Electromagn. Anal. Appl. 2014, 06, 184–192. [Google Scholar] [CrossRef]
- Marulanda-Durango, J.; Zuluaga-Ríos, C. A meta-heuristic optimization-based method for parameter estimation of an electric arc furnace model. Results Eng. 2022, 17, 100850. [Google Scholar]
- Klimas, M.; Grabowski, D. Application of the Deterministic Chaos in AC Electric Arc Furnace Modeling. IEEE Trans. Ind. Appl. 2024, 60, 4978–4986. [Google Scholar] [CrossRef]
- Klimas, M.; Grabowski, D. Application of long short-term memory neural networks for electric arc furnace modeling. Appl. Soft Comput. 2023, 145, 110574. [Google Scholar]
- Seker, M.; Memmedov, A. Investigation of Voltage Quality in Electric Arc Furnace with Matlab/Simulink. International J. Eng. Tech. Res. (IJERT) 2014, 2, 274–284. [Google Scholar]
- Babaei, Z.; Samet, H.; Jalil, M. Enhanced models with time-series coefficients used for electric arc furnace. IET Gener. Transm. Distrib. 2023, 17, 2301–2316. [Google Scholar]
- Gol, M.; Salor, O.; Alboyaci, B.; Mutluer, B.; Cadirci, I.; Ermis, M. A New Field-Data-Based EAF Model for Power Quality Studies. IEEE Trans. Ind. Appl. 2010, 46, 1230–1242. [Google Scholar] [CrossRef]
- Gök, G.; Salor, Ö.; Taplamacıoğlu, M.C. A New Electric Arc Furnace Model Based on Current Waveform Synthesis from Distributions of DFT Amplitudes and Power System Frequency. IEEE Trans. Ind. Appl. 2024, 60, 5872–5881. [Google Scholar] [CrossRef]
- Olczykowski, Z. Modeling of voltage fluctuations generated by arc furnaces. Appl. Sci. 2021, 11, 3056. [Google Scholar] [CrossRef]
- Seker, M. Experimental Study of Electrical Arc Furnace on Electric Network and Computer Aided Modelling. Ph.D. Thesis, Graduate School of Natural and Applied Science, Department of Electrical and Electronics Engineering, İnönü University, Malatya, Turkey, 2017. [Google Scholar]
- Hani, H.; Abdel-Rahman, M.A.; Ezzat, M.; Kamh, M.Z. Novel Time-Domain Modeling Approaches of Electric Arc Furnace Using Enhanced Cassie-Mayr and ARMAX Models. In Proceedings of the 2023 24th International Middle East Power System Conference (MEPCON), Mansoura, Egypt, 19–21 December 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Hani, H.; Abdel-Rahman, M.A.; Ezzat, M.; Kamh, M.Z. Estimation and Analysis of the Electric Arc Furnace Model Coefficients. IEEE Trans. Power Deliv. 2022, 37, 4956–4967. [Google Scholar] [CrossRef]
- Gomez, A.A.; Durango, J.J.M.; Mejia, A.E. Electric Arc Furnace Modelling for Power Quality Analysis. In Proceedings of the IEEE ANDESCON Conference, Bogota, Colombia, 15–17 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Babaei, Z.; Samet, H.; Jalil, M. An innovative approach considering active power and harmonics for modeling the electric arc furnace along with analyzing time-varying coefficients based on ARMA models. Int. J. Electr. Power Energy Syst. 2023, 153, 109377. [Google Scholar] [CrossRef]
- Chittora, P.; Singh, A.; Singh, M. Modelling and Analysis of Power Quality Problems in Electric Arc Furnace. In Proceedings of the Annual IEEE India Conference (INDICON), New Delphi, India, 17–20 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Bhonsle, D.C.; Kelkar, R.B. Analyzing Power Quality Issue in Electric Arc Furnace by Modelling. Energy 2016, 115, 830–839. [Google Scholar] [CrossRef]
- Balouji, E.; Salor, O.; McKelvey, T. Deep Learning Based Predictive Compensation of Flicker, Voltage Dips, Harmonics and Interharmonics in Electric Arc Furnaces. IEEE Trans. Ind. Appl. 2022, 58, 4214–4224. [Google Scholar] [CrossRef]
- Balouji, E.; Bäckström, K.; McKelvey, T.; Salor, Ö. Deep-Learning-Based Harmonics and Interharmonics Predetection Designed for Compensating Significantly Time-Varying EAF Currents. IEEE Trans. Ind. Appl. 2020, 56, 3250–3260. [Google Scholar] [CrossRef]
- Golestani, S.; Samet, H. Generalised cassie-mary electric arc furnace models. IET Gener. Transm. Distrib. 2016, 10, 3364–3373. [Google Scholar] [CrossRef]
- Choi, S.-W.; Seo, B.-G.; Lee, E.-B. Machine learning-based tap temperature prediction and control for optimized power consumption in stainless electric arc furnaces (EAF) of steel plants. Sustainability 2023, 15, 6393. [Google Scholar] [CrossRef]
- Issouribehere, P.E.; Barbero, J.C.; Barbera, G.; Issouribehere, F. Compability Between Disturbance Emission and Argentinian Power Quality Regulations in Iron and Steel Industry. In Proceedings of the IEEE/PES, Transmission, & Disturbution Conference and Exhibition (TDC 2006), Caracas, Venazuela, 15–18 August 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Mayordomo, J.; Prieto, E.; Hernandez, A.; Beites, L. Arc Furnace Characterization from an off-line Analysis of Measurement. In Proceedings of the IEEE 9th International Conference Harmonics Quality Power, Orlando, FL, USA, 1–4 October 2000; pp. 1073–1078. [Google Scholar] [CrossRef]
- Deaconu, S.I.; Popa, G.N.; Toma, A.I.; Topor, M. Modelling and Experimental Analysis for Modernization of 100-T EAF. IEEE Trans. Ind. Appl. 2010, 46, 2259–2266. [Google Scholar] [CrossRef]
- Boulet, B.; Wikston, J.; Kadar, L. The Effect of Measuring System Accuracy on Power Quality Measurements in Electric Arc Furnace. In Proceedings of the IEEE Industry Applications Society Annual Meeting, New Orleans, LA, USA, 5–9 October 1997. [Google Scholar] [CrossRef]
- Ozdemirci, E.; Akkaya, Y.; Boyrazoglu, B.; Buhan, S.; Terciyanli, A.; Unsar, O.; Altintas, E.; Haliloglu, B.; Acik, A.; Atalik, T.; et al. Mobile Monitoring System to take PQ Snapshots of Turkish Electricity Transmission System. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Warsaw, Poland, 1–3 May 2007; IMTC 20079. pp. 1–6. [Google Scholar] [CrossRef]
- Collantes-Bellido, R.; Gomez, T. Identification and Modelling of a Three Phase Arc Furnace for Voltage Disturbance Simulation. IEEE Trans. Power Deliv. 1997, 12, 1812–1817. [Google Scholar] [CrossRef]
- Mokhtari, H.; Hejri, M. A New Three Phase Time-Domain Model for Electric Arc Furnace using Matlab. In Proceedings of the IEEE/PES Transmission and Disturbution Conference and Exhibition, Yokohoma, Japan, 6–10 October 2002; pp. 2078–2083. [Google Scholar] [CrossRef]
- Alonso, M.; Donsion, M.P. An Improved Time Domain Arc Furnace Model for Harmonic Analysis. IEEE Trans. Power Deliv. 2004, 19, 367–373. [Google Scholar] [CrossRef]
- Petersen, H.; Koch, R.; Swart, P.; Van Heerden, R. Modelling Arc Furnace Flicker Investigation Compansation Techniques. In Proceedings of the Thirtieth IAS Annual Meeting International Conference Industrial Application, (IAS, 1995), Orlando, FL, USA, 8–12 October 1995; pp. 1733–1740. [Google Scholar] [CrossRef]
- Schau, H.; Stade, D. Mathematical Modelling of Three Phase Arc Furnace. In Proceedings of the IEEE International Conference Harmonics in Power System, Bologna, Italy, 1994; pp. 422–428. [Google Scholar]
- Zheng, T.; Makram, E.; Girgis, A. Effect of Different Arc Furnace Model on Voltage Distortion. In Proceedings of the IEEE Conference Harmonics and Power Quality of Power, Athens, Greece, 14–16 October 1998; pp. 1079–1085. [Google Scholar] [CrossRef]
- Montanari, G.; Loggini, M.; Cavallini, A.; Pitti, L.; Zaninelli, D. Arc Furnace Model fort he Study of Flicker Compensation in Electric Network. IEEE Trans. Power Deliv. 1994, 9, 2026–2036. [Google Scholar] [CrossRef]
- Fenghua, W.; Zhijian, J. Application of Extended Kalman Filter to the Modelling of Electric Arc Furnace for Power Quality Issues. IEEE Trans. Ower Deliv. 2005, 10, 991–996. [Google Scholar]
- Pak, L.F.; Dinavachi, V. Real Time Digital Time-Varying Harmonic Modelling and Simulation Techniques. IEEE Trans. Power Deliv. 2007, 22, 1218–1227. [Google Scholar] [CrossRef]
- Acha, E.; Semlyen, A.; Rajakovic, N. A Harmonic Domain Computation Package for Nonlinear Problems and Its Application to Electric Arc. IEEE Trans. Power Deliv. 1990, 5, 1390–1397. [Google Scholar] [CrossRef]
- Emanuel, A.E.; Orr, J.A. An Improved Method of Simulation of the Arc Voltage-Current Characteristic and Quality of Power. In Proceedings of the Ninth International Conference on Harmonics and Quality of Power. Proceedings (Cat. No.00EX441), Orlando, FL, USA, 1–4 October 2000; pp. 148–150. [Google Scholar]
- Cano, P.E.A.; Tacca, H.E. Arc Furnace Modelling in ATP-EMTP. In Proceedings of the International Conference on Power System Transient (IPST’05), Montreal, QC, Canada, 19–23 June 2005. [Google Scholar]
- Seker, M.; Memmedov, A. An Experimental Approach for Understanding V–I Characteristic of Electric Arc Furnace Load. Elektron. ir Elektrotechnika 2017, 23, 30–35. [Google Scholar] [CrossRef]
- Seker, M.; Memmedov, A.; Huseyinov, R. The Modelling of Three Phases Electric Arc Furnace System using Matlab/SIMULINK and Examining the Harmonic Effects with FFT Analysis. In Proceedings of the International Artificial Intelligence and Data Processing Symposium (IDAP 2016), Malatya, Turkey, 17–18 September 2016. [Google Scholar]
- Bello, J.R. Fundamental of the Electric Arc Furnace. In Electrical Furnace Proceedings; AIME: San Ramon, CA, USA, 1971; Volume 29, pp. 219–231. [Google Scholar]
- Borrebach, E.J. Maximum Power Operation of Electric Arc Furnace. In Iron and Steel Engineering; AIME: San Ramon, CA, USA, 1969; Volume 46, p. 74. [Google Scholar]
- Pelfrey, D.L. Specşfying Arc Furnace Transformer. In Proceedings of the Electric Furnace Conference, Pittsburg, PA, USA, 9 December 1980. [Google Scholar]
- Kurecki, M.; Meena, N.; Shyrokykh, T.; Korobeinikov, Y.; Jarnerud Örell, T.; Voss, Z.; Sridhar, S. Recycling Perspectives of Electric Arc Furnace Slag in the United States: A Review. Steel Res. Int. 2024, 2300854. [Google Scholar] [CrossRef]
- Abadi, M.M.; Tang, H.; Rashidi, M.M. A Review of Simulation and Numerical Modeling of Electric Arc Furnace (EAF) and its Processes. Heliyon 2024, 10, e32157. [Google Scholar] [CrossRef]
- IEC-61000-4-30; Electromagnetic Compatibility (EMC)—Part 4–30: Testing and Measurement Techniques—Power Quality Measurement Methods. IEC: Geneva, Switzerland, 2015.
- DiGiovanni, C.; Echterhof, T. Progress Toward Biocarbon Utilization in Electric Arc Furnace Steelmaking: Current Status and Future Prospects. J. Sustain. Metall. 2024, 10, 2047–2067. [Google Scholar]
- Mohanty, S.; Subudhi, B.; Kumar Ray, P. A new MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar]
- Mirjalili, S.; Saremia, S.; Mirjalilic, B.S.M.; Coelho, L.D.S. Multi-objective Grey Wolf Optimizer: A Novel Algorithm for Multi-Criterion Optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar]
- Şeker, M.; Çikan, M. Examining the Influence of Tower Grounding Resistance on Lightning Overvoltages for 154 kV Overhead Transmission Line with Fork Pylon Tower using ATP-EMTP. J. Inst. Sci. Technol. Iğdır Univ. 2019, 9, 1989–2001. [Google Scholar] [CrossRef][Green Version]
- Şeker, M. Long term electricity load forecasting based on regional load model using optimization techniques: A case study. Energy Sources, Part A Recover. Util. Environ. Eff. 2021, 44, 21–43. [Google Scholar] [CrossRef]
- Niyayesh, M.; Uygun, Y. Predicting endpoint parameters of electric arc furnace—Based steelmaking using artificial neural network. Int. J. Adv. Manuf. Technol. 2024. [Google Scholar] [CrossRef]





| V–I Characteristic Model | Model Parameters |
|---|---|
| Exponential Model | Vat = 240 Volt I0 = 5 kA |
| Hyperbolic Model | Vat = 240 Vol, Ci = 190 kW, Cd = 39 kW, d = 5 kA |
| Exponential–Hyperbolic Model | Vat = 240 Vol, i0 = 5 kA, Ci = 190 kW, Cd = 39 kW, d = 5 kA |
| Nonlinear Resistance Model | Active Power = 14 MW, i0 = 50 kA, α = 15, U = 120 V |
| Proposed Model | Vex = Vat = 240 V, i1 = 220 kA, i2 = 1850 A, i3 = 0 kA, i4 = 18 kA i5 = 27 kA, i6 = 92 kA, η = 12 × 1010, n = 2 |
| Harmonics | Actual | Model 1 | Model 2 | Model 3 | Model 4 | Proposed | |
|---|---|---|---|---|---|---|---|
| Arc Voltage | 2nd | 0.093% | 0.07% | 0.08% | 0.08% | 0.08% | 0.079% |
| 3rd | 0.801% | 1.37% | 1.53% | 1.51% | 1.53% | 0.660% | |
| 4th | 0.056% | 0.03% | 0.07% | 0.04% | 0.05% | 0.060% | |
| 5th | 0.531% | 0.62% | 0.78% | 0.78% | 0.49% | 0.435% | |
| 7th | 0.332% | 0.30% | 0.43% | 0.45% | 0.20% | 0.32% | |
| THD | 2.300% | 1.80% | 4.19% | 2.13% | 2.97% | 2.34% |
| Harmonics | Actual | Model 1 | Model 2 | Model 3 | Model 4 | Proposed | |
|---|---|---|---|---|---|---|---|
| Arc Current | 2nd | 1.20% | 1.04% | 1.09% | 1.16% | 0.87% | 0.92% |
| 3rd | 3.12% | 7.65% | 9.91% | 9.76% | 28.04% | 5.36% | |
| 4th | 0.79% | 0.55% | 0.56% | 0.65% | 1.33% | 0.62% | |
| 5th | 0.89% | 2.05% | 3.16% | 3.21% | 7.96% | 1.34% | |
| 7th | 0.31% | 0.68% | 1.31% | 1.42% | 3.57% | 0.81% | |
| THD | 13.76% | 11.47% | 14.55% | 14.50% | 32.54% | 11.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şeker, M.; Ünsal, E.; Aksoz, A.; Dursun, M. A Novel Voltage–Current Characteristic Model for Understanding of Electric Arc Furnace Behavior Using Experimental Data and Grey Wolf Optimization Algorithm. Appl. Sci. 2025, 15, 4005. https://doi.org/10.3390/app15074005
Şeker M, Ünsal E, Aksoz A, Dursun M. A Novel Voltage–Current Characteristic Model for Understanding of Electric Arc Furnace Behavior Using Experimental Data and Grey Wolf Optimization Algorithm. Applied Sciences. 2025; 15(7):4005. https://doi.org/10.3390/app15074005
Chicago/Turabian StyleŞeker, Mustafa, Emre Ünsal, Ahmet Aksoz, and Mahir Dursun. 2025. "A Novel Voltage–Current Characteristic Model for Understanding of Electric Arc Furnace Behavior Using Experimental Data and Grey Wolf Optimization Algorithm" Applied Sciences 15, no. 7: 4005. https://doi.org/10.3390/app15074005
APA StyleŞeker, M., Ünsal, E., Aksoz, A., & Dursun, M. (2025). A Novel Voltage–Current Characteristic Model for Understanding of Electric Arc Furnace Behavior Using Experimental Data and Grey Wolf Optimization Algorithm. Applied Sciences, 15(7), 4005. https://doi.org/10.3390/app15074005








