Abstract
In renewable and sustainable hydrogen production energy systems (RSHPES), the presence of harmonics gives rise to fluctuations in the voltage and current of the electrolysis cell (EC). This, in turn, results in an unstable electrolysis process, a reduction in hydrogen production efficiency, and an escalation in electrode corrosion. This paper puts forward a novel harmonic suppression control method (HSCM), which is devised for the single phase PWM rectifier in hydrogen production rectifiers (HPR) with the aim of alleviating the adverse impacts caused by harmonics. Initially, a highly meticulous harmonic model is constructed, which lays solid groundwork for understanding the existing problems. Subsequently, a comprehensive and detailed explanation of the HSCM is provided, accentuating its novel and inventive strategy for harmonic suppression. Thereafter, a comparison is drawn between the HSCM and traditional methods, thereby manifesting its enhanced suitability and superiority within the context of RSHPES. In conclusion, the simulation and experimental results vividly demonstrate the advantages, effectiveness, and practicality of HSCM under four conditions of power grids containing integer multiples of harmonics, interharmonics, ultraharmonics, and voltage disturbances.
1. Introduction
Electrolysis of water is an environmentally friendly and efficient method for hydrogen production, which uses renewable energy to decompose water into hydrogen and oxygen. This process not only achieves zero carbon emissions during production but also contributes to energy transition and reduces dependence on fossil fuels. Therefore, hydrogen is also considered a carrier for energy transition [1,2,3]. The renewable energy sources (RES) in RSHPES are wind power and photovoltaic (PV) [4,5,6]. Wind turbine generators connect to the AC bus via an AC-AC converter, and solar panels do the same via a DC-AC converter. The AC bus supplies electrical energy to the EC through the HPR [7,8,9]. A schematic diagram of the RSHPES is depicted in Figure 1.
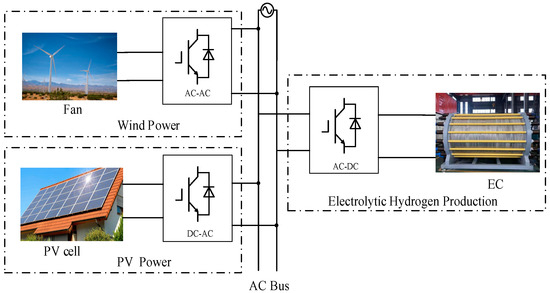
Figure 1.
The schematic diagram of the RSHPES.
With the increasing power generated by renewable energy sources, the power electronic devices of water’s electrolysis to hydrogen system have also increased accordingly. However, power electronic devices within RSEHPE are primarily responsible for generating harmonics [10,11]. These harmonics are very deleterious for the EC. They will accelerate the corrosion of the electrodes, decrease the efficiency of hydrogen production, and disrupt the balance of the electrolysis process [12]. With this threat in mind, numerous researchers have begun to investigate strategies for harmonic suppression through the control methods of the HPR. The topology of the HPR is shown in Figure 2.
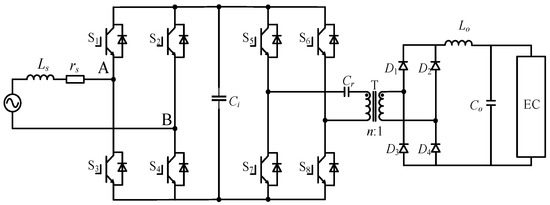
Figure 2.
The topology of the HPR.
The HPR is composed of a PWM full-bridge rectifier and a phase-shift full-bridge converter. The HSCM is adopted in the PWM full-bridge rectifier. Because the HSCM aims to reduce the harmonic content in the input current, the phase-shift full-bridge converter can be ignored in this paper.
Passive and active power filters are usually used for harmonic suppression. However, extra hardware will increase the system cost and the difficulty of operation and maintenance [13]. Therefore, digital filters have become the mainstream. A low pass filter is processed in Ref. [14] to solve the impact of the twice-frequency power pulsation of DC voltage; however, the bandwidth will be diminished. Ref. [15] introduces an additional resonant element to eliminate the third harmonic. However, control mechanisms that rely on small-signal linearized models may not guarantee stability across the entire operating range. The one-sampling-ahead-preview (OSAP) control scheme is used to suppress the harmonic in Ref. [16], although the harmonics of the AC bus will distort the reference current. Ref. [17] reduces the modulation level by reducing the output power. Therefore, the operating region is the linear modulation region. The distortion of the input current is avoided, but the efficiency decreases. A control strategy based on reactive power compensation is proposed. The power factor will be changed in this way [18,19].
As solar panels and wind turbines become more prevalent, the harmonic content will also increase, causing greater damage to EC. The amplitude and phase of the harmonics will both increase. This could potentially lead to system instability. Therefore, suppressing harmonics is an urgent priority [20,21]. At present, there is a plethora of research papers on harmonic suppression. However, few methods are capable of dealing with the ever-increasing harmonic content in RSHPES.
In this paper, the author proposes a harmonic suppression strategy for the single-phase PWM rectifier (SPR) in HPR. The proposed method solves the influence of harmonics by eliminating the harmonics of AC bus current. In addition, the challenge of increasingly growing harmonic amplitude and phase can be addressed.
The paper is organized as follows. Section 2 details the topology and control of SPR. Section 3 discusses two reasons for AC current distortion caused by grid voltage harmonics. Section 4 shows the proposed harmonic current suppression strategy. Finally, the simulation and experimental results are displayed and analyzed in Section 5 and Section 6, respectively. Section 7 concludes this paper.
2. Topology and Control
2.1. Topology
The topology of the SPR is shown in Figure 3. us is the AC bus voltage, Ls is a filter inductance, Rs is the line equivalent resistance, S1~S4 is switches on the rectifier bridge, C is a side filter capacitor, Ro is the equivalent impedance of the subsequent circuit., is is the current at AC side, idc is the output current, ic is the capacitance current, io is the load current, udc is the output voltage, and uAB is the AC side voltage of rectifier bridge.
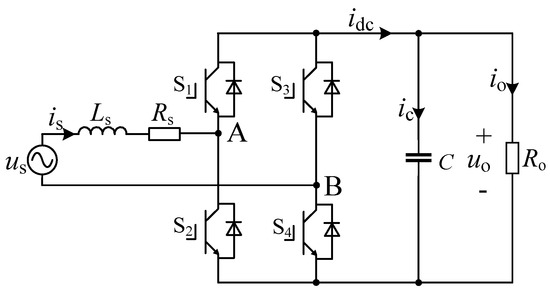
Figure 3.
The topology of the SPR.
The working modes of the SPR under the unipolar modulation are illustrated in Figure 4.
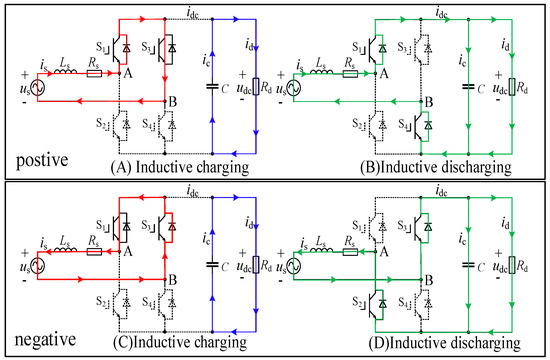
Figure 4.
The working modes of the SPR under the unipolar modulation.
The equivalent circuit of the SPR is described in Figure 5.
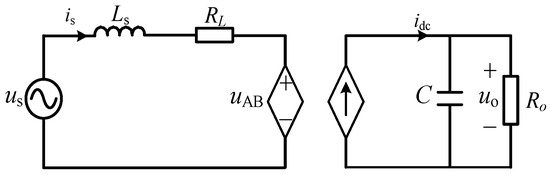
Figure 5.
The equivalent circuit of the SPR.
2.2. Control
The control block diagram of the SPR is shown in Figure 6. The common control is voltage and current double closed-loop based on the average current control mode. In Figure 6, uor is the reference of uo, isr is the reference of is, GV(s) is the controller of the outer voltage loop, GI(s) is the controller of the inner current loop, and kpwm is the modulation coefficient. 1/(sL + r) is the model of Ls and Rs. m is modulating voltage. 1/sC is the model of C.
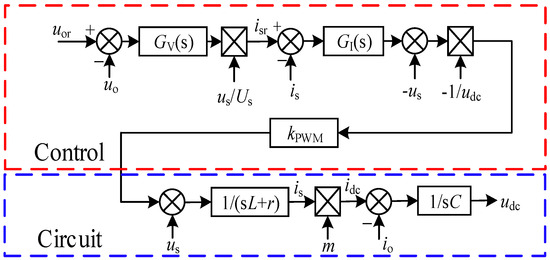
Figure 6.
The control block diagram of the SPR.
The voltage outer loop is responsible for maintaining the stability of the DC voltage, while the current inner loop is responsible for precisely controlling the input current to track the given current command. GV(s) is the proportional-integral (PI) controller. GI(s) is the quasi proportional resonant (QPR) controller.
3. Harmonic Model in RSHPES
This section analyzes the mechanism of harmonic current generated in the AC bus, The expression of us is shown in (1).
where, uso is the fundamental frequency AC bus voltage, and Uso is the root mean square (RMS) of the fundamental frequency AC bus voltage. ush is the AC bus harmonic voltage. Usk is the RMS of the AC bus harmonic voltage. AC bus voltage harmonics can generate AC bus current harmonics from both topological and control aspects.
3.1. The Topology Aspect
According to the superposition theorem, it is known the expression of uAB in the topology aspect is presented in
where UAB is the RMS, φ is the phase of the uAB. According to (2), ist is expressed as
From Equation (4), the AC bus current harmonics of the topology aspect is isht and it is as indicated in (5)
3.2. The Control Aspect
Figure 6 indicates that harmonics is introduced into the controller because uo and us/Us is sampled.
Pin is the input instantaneous power, and the expression of Pin is shown in (6).
Pout is output instantaneous power, which is expressed as (7)
where Uo and Io are the DC components, and uore represents the ripple component. When the line loss is ignored, Pin = Pout, the expression of uore can be obtained as (8).
As can be seen from Figure 6, isr can be obtained as (9).
where m = Usk/Uso. When Udc reaches the reference, Udcr − Udc = 0. The simplification results of (9) is
From (10), we can deduce that the input current will contain the 3th, (k − 2)th and (k + 2) th harmonic. When stability is achieved in the system, the expression of is is presented in (11)
This implies that the harmonic voltages on the AC bus not only generate harmonic currents but also cause a phase shift in the fundamental current.
4. Harmonic Suppression Method
4.1. The Traditional Harmonic Suppression Method
The main methods to counteract the impact of harmonic voltages in the AC bus on rectifiers include the use of the PI controllers, resonant elements, and quasi-PR(QPR) controllers [22,23,24,25,26,27,28,29]. According to Figure 6, their transform function of the inner current loop controllers GPI(s), GRE(s) and GQPR(s) are, respectively, presented in (12), (13) and (14).
where ωn is the resonant frequency, ωk is kth harmonic, kp kpRE and kpQPR are proportional coefficients, ki is an integral coefficients, and krREl and krQPR are resonance coefficients. ωc is the cut-off frequency of the QPR controller. When using the inner current loop with the aforementioned three types of controllers, their diagrams of the inner current loop are shown in Figure 7, Figure 8 and Figure 9, respectively.

Figure 7.
The control diagram of a current loop with the PI controller.
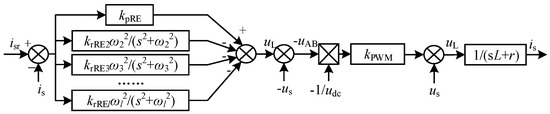
Figure 8.
The control diagram of a current loop with the resonant elements.

Figure 9.
The control diagram of a current loop with the QPR controller.
As shown in (11) and Figure 7, as long as there are harmonics present, m will not be zero. No matter how the kp and ki are adjusted, the harmonic components cannot be eliminated. Therefore, the PI controller is not suitable for suppressing the impact of harmonic voltages in the AC bus on the HPR.
Based on Figure 8, the open-loop transfer function of the inner current loop with the resonance coefficients is
The performance of the resonant elements controller is affected by kpRE and krREl. Therefore, it is necessary to plot the Bode diagrams for three different values of kpRE and krREl to analyze. Set the filter order n = 8, the first value set kpRE = 1, krRE2 = krRE3 = krRE4 = krRE5 = krRE6 = krRE7 = krRE8 = 1, the second value set kpRE = 0.35, krRE2 = 1, krRE3 = 0.1, krRE4 = 0.5, krRE5 = 0.7, krRE6 = 2, krRE7 = 1.3, krRE8 = 1.9, the third value set kpRE = 10, krRE2 = 10, krRE3 = 3.1, krRE4 = 3.2, krRE5 = 1.3, krRE6 = 2.6, krRE7 = 1.8, krRE8 = 0.3. The bode diagram is presented in Figure 10.
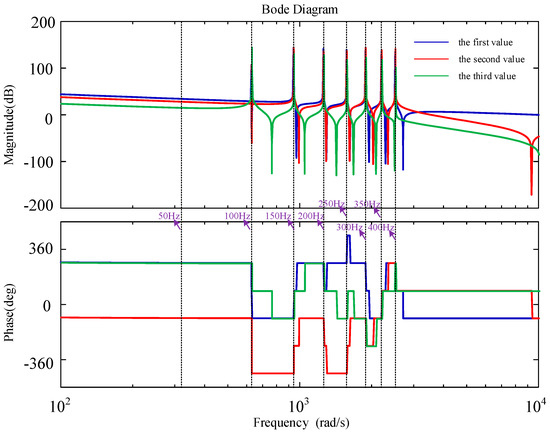
Figure 10.
The Bode diagrams of the resonant elements controller for three different values.
From Figure 10, it can be seen that the high gain at the harmonic frequencies indicates that the resonant elements have a good suppression effect on harmonics. However, in the case of the first and third values, the fundamental frequency will experience a leading phase shift, which is detrimental to the stability of the system. Therefore, the selection of coefficients has become a rather critical issue. Small deviations can cause the system to become unstable. The harmonic spectrum in RSHPES is very rich [30,31,32], including integer multiple harmonics, interharmonics, and ultraharmonics. Figure 10 only illustrates the suppression capability of the resonant elements on integer multiple harmonics, and cannot eliminate the impact brought by interharmonics and ultraharmonics.
According to Figure 9, the open-loop transfer function of the inner current loop with the QPR is
The performance of the resonant elements controller is affected by kpQPR and krQPR. Taking the kpQPR and krQPR in three different scenarios allows for the analysis of the QPR controller’s characteristics. The first value is set as kpQPR = 1, krQPR = 100, the second value is set as kpQPR = 100, krQPR = 1, and the third value is set as kpQPR = 100, krQPR = 100. The bode diagram is described in Figure 11.
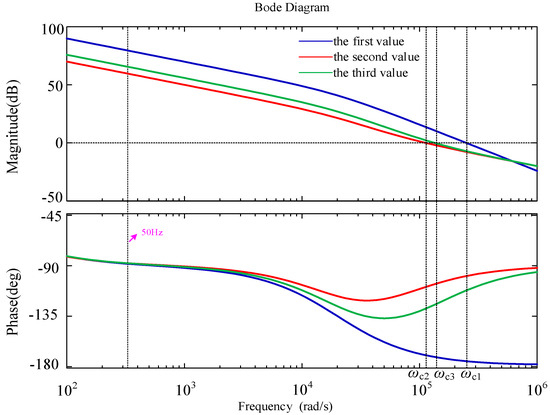
Figure 11.
The Bode diagrams of the QPR controller for three different values.
In Figure 11, ωc1 ωc2 and ωc3 are the cut-off frequencies of the HQPR(s) under the three different values. A conclusion can be drawn by ωc1 > ωc3 that reducing kpQPR will increase the system’s bandwidth and response speed, but it will also decrease the phase margin, increasing the probability of system instability. It can be obtained through ωc2 < ωc3 that diminishing krQPR will enhance the system’s phase margin, but it will cut down the system’s bandwidth, resulting in slower system response.
The fundamental gain and phase margin do not differ significantly under the three scenarios, therefore, employing a QPR controller will enhance the system’s stability. However, the QPR controller only has a suppressive effect on high-frequency harmonics and cannot eliminate the impact of low-frequency harmonics.
4.2. HSCM
The HSCM takes harmonics as the control object. The harmonic amplitude of the AC bus current is controlled to be 0, so as to eliminate the influence of harmonics.
The method for extracting harmonic components from input current is to use a 50 Hz notch filter to eliminate the fundamental component, and the rest is the harmonic component. The expression of the notch filter is shown in (17).
where Qn is the quality factor.
When ω0n = 100π, the fundamental component of the current will be filtered out and the harmonic component will be retained. The harmonic suppression control loop is shown in Figure 12.
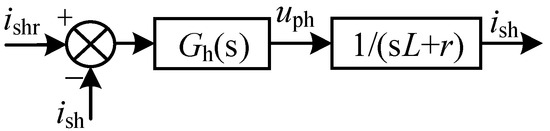
Figure 12.
The harmonic suppression control loop.
Where ish is the AC bus current harmonics. ishr is the reference value of ish, uph is the voltage harmonic of the inductor, and Gh(s) is the controller of the harmonic suppression. When ishr = 0, the controller will reduce the harmonic amplitude to 0 by adjusting the duty cycle.
The harmonic suppression loop is added to the inner current loop [29,30]. The proposed harmonic suppression method is presented in Figure 13.
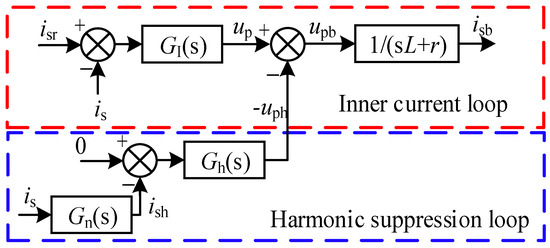
Figure 13.
The control block diagram of the harmonic suppression method.
In Figure 13, isr is the reference value of is. The current loop should have a high gain for 50 Hz current. The output of GI(s) is
where up is the voltage of the inductor, and upb is the fundamental component of up. When the output of Gh(s) is -uph, the harmonic component of up will be offset. Thus, HSCM is more suitable for application in HPR connected to the RSHPES with a rich frequency spectrum. It can effectively suppress the impact of integer multiple harmonics, interharmonics, and ultraharmonics. Gh(s) and GI(s) can use exactly the same controller, and a PI controller will suffice.
To highlight the superiority and reliability of the HSCM, the methods mentioned above are listed in Table 1 for comparison, with performance indicators including (a) low-frequency filtering performance, (b) high-frequency filtering performance, (c) stability, and (d) whether they can be applied to the HPR in the RSHPES.

Table 1.
Comparison of four methods.
The control structure diagram of the SPR in this paper is shown in Figure 14.
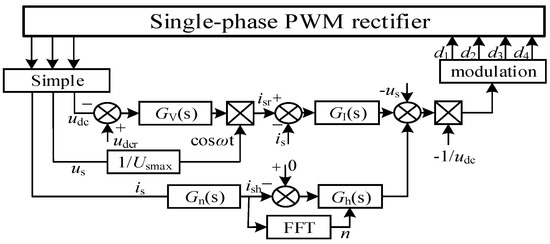
Figure 14.
The control structure diagram of the SPR.
5. Simulation
In this section, it is proved by simulation with MATLAB/Simulink that the proposed harmonic suppression strategy can effectively suppress the harmonic current. The simulation model of HPR is shown in Figure 15. S5~S8 form thee inverter bridge of the PSFB. Cr is the blocking capacitor, and T is the high frequency transformer. D1~D4 are high frequency diode rectifier bridges. Lo and Co constitute the output filtering circuit.
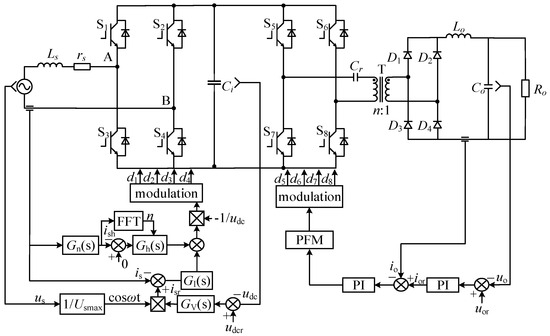
Figure 15.
The simulation model of the HPR.
The simulation parameters are displayed in Table 2.

Table 2.
Simulation parameters of the HPR.
In Table 2, fs is the switching frequency. Pout is the output power. To verify the correctness and effectiveness of the proposed method, analysis will be conducted from two aspects: the presence of harmonics in the grid voltage and the disturbance injection into the grid voltage.
Injecting harmonics into the power grid can be done in two ways: injecting harmonics of a single frequency and injecting a mixture of harmonics at multiple frequencies. The kinds of harmonic injection are shown in Table 3.

Table 3.
The kinds of harmonic in us.
When the power grid contains only the fundamental frequency, the simulation results of us and is are shown in Figure 16.
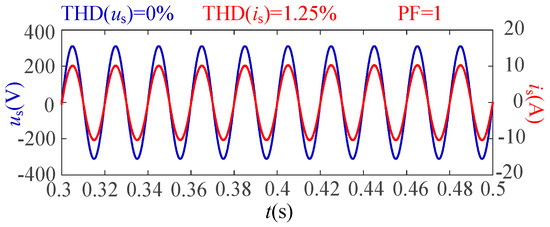
Figure 16.
us and is without harmonic distortion.
Figure 16 only shows the results of the steady state and does not display the transient process. THD(us) is THD (total harmonic distortion) of us, THD(is) is THD of is and PF is the power factor. These notations are the same for the subsequent simulation results and experimental results.
From Figure 16, it can be seen that, when there is no harmonic voltage in the power grid, both us and is are sine waves. THD(us) = 0%, THD(is) = 1.25% and PF = 1. The FFT of Figure 16 is presented in Figure 17.
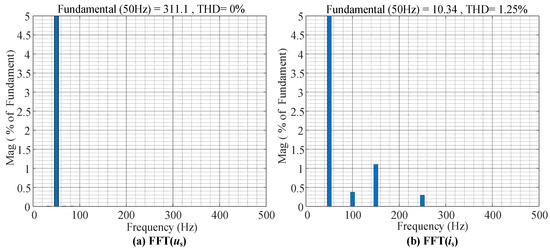
In Figure 17, FFT of us is free of harmonic components. is contains only a small amount of 2nd, 3rd, and 5th harmonics. The conclusion that can be drawn is that, when the power grid voltage is a standard sine wave, the AC-side current is harmonics-free. At the same time, the simulation results in Figure 16 and Figure 17 serve as a control experiment.
When the integer multiple harmonics are injected, the simulation results of us and is are displayed in the time period of 0.3–0.4 s in Figure 18a. Under the influence of the 3rd harmonic voltage, the current exhibits significant distortion, with THD(us) = 2.43%, and THD(is) = 32.74%. FFT(us) is demonstrated in Figure 18b. FFT(is) before 0.4 s is depicted in Figure 18c. At t = 0.4, the HSCM is applied. In Figure 18a, during the time period of 0.4–0.5 s, the current waveform is significantly improved, with the THD(is) = 1.35%, and the value of PF has changed from 0.963 to 0.998. FFT(is) after 0.4 s is shown in Figure 18d. From this, it can be seen that the harmonic content is significantly reduced.
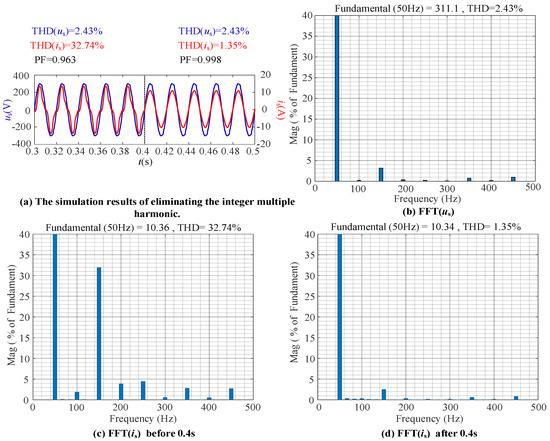
Figure 18.
The simulation results of injecting the integer multiple harmonics.
From Figure 19a and Figure 16, it can be seen that, when the interharmonics are present, the sinusoidal quality of is is very low. Figure 17 and Figure 19c illustrate that the harmonic content of is is relatively high with THD(is) = 35.03%. After the action of HSCM, the current waveform becomes a sine wave, with THD(is) = 1.43%. PF has improved from 0.947 to 0.998. The harmonic components in Figure 19d are minimal.
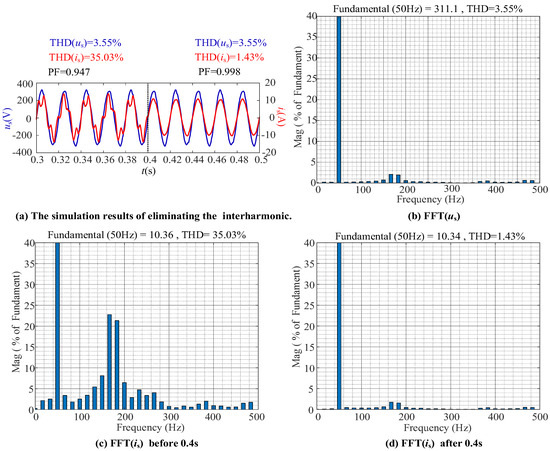
Figure 19.
The simulation results of injecting the interharmonics.
From Figure 16 and Figure 20a, it can be seen that, when supraharmonics are added to us, they do not cause distortion in is. Regardless of whether HSCM is in action or not, is always presents as a sine wave. In Figure 20b, us contains only high-frequency harmonics. Comparing Figure 17 with Figure 20c,d, it is evident that before the action of HSCM, THD(is) = 1.53%, and after the action of HSCM, THD(is) = 0.24%. Therefore, supraharmonics exert a minor influence on is, and HSCM has improved the situation of low-frequency harmonics in is.
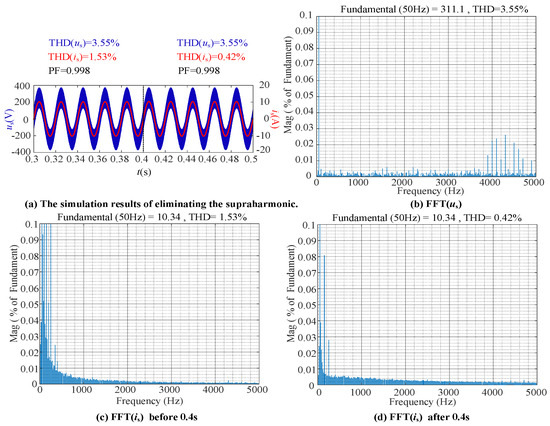
Figure 20.
The simulation results of injecting the supraharmonics.
When the circuit is in a steady state, a voltage disturbance of us1 = 50cos(100πt) is introduced at t = 0.3 s, followed by another voltage disturbance of us2 = −100cos(100πt) at t = 0.5 s. The simulated waveform is shown in Figure 21.
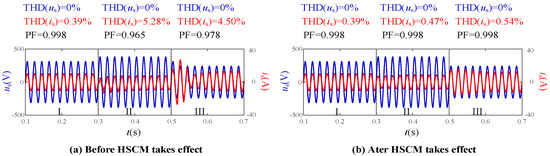
Figure 21.
The simulation results after the introduction of voltage disturbances.
In Figure 21, the intervals are set as follows. Interval I: from t = 0.1 s to t = 0.3 s, Interval II: from t = 0.3 s to t = 0.5 s, Interval III: from t = 0.5 s to t = 0.7 s. In Figure 21a, before the effect of HSCM, when us1 is superimposed on us, is drops and distortion occurs. The addition of us2 causes is to overshoot. Figure 21b shows the waveform of us and is after the disturbance is added with HSCM in effect. Whether influenced by us1 or us2, the transition of is is smoother compared to that in Figure 21a, without overshoot or distortion. Not only that, but the PF and Total THD in Figure 21b are both better than those in Figure 21a. FFT(is) with us1 and us2 are shown in Figure 22.
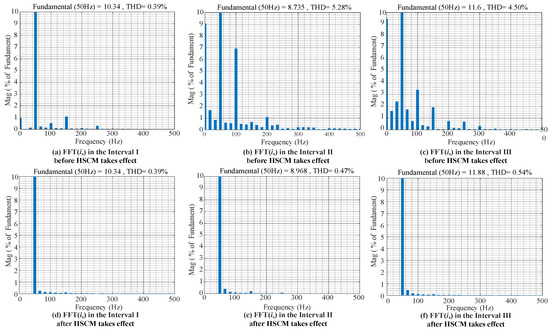
Figure 22.
FFT(is) with us1 and us2.
By comparing Figure 22b with Figure 22e, it can be seen that HSCM can prevent us1 from causing DC components and second-harmonic distortion in is. Similarly, HSCM can also prevent the damage caused by us.
From the above simulation results, we can conclude that HSCM can effectively suppress the impact of harmonic currents in the power grid on the AC-side current, including the effects of integer multiple harmonics, interharmonics, and also improve THD(is) in the case where us contains superharmonics. Additionally, HSCM can eliminate the effects of grid voltage disturbances. This ensures the integration of HPR into RSHPES.
6. Experiment
Figure 23 is a photograph of the experimental prototype. A 1500 W experimental platform was built for verifying the simulation results. The BOM (bill of materials) used in the experiment is shown in Table 4

Figure 23.
The experimental prototype.

Table 4.
The BOM of the HPR.
The input source selected in Table 4 is Chroma’s 61815-TC. This power supply can provide integer multiple harmonics, interharmonics, supraharmonics, and voltage disturbances, which is very useful for verifying the correctness and effectiveness of HSCM.
The experimental results when injecting integer multiple harmonics are shown in Figure 24, where Figure 24a is before the action of HSCM, and Figure 24b is after the action of HSCM.
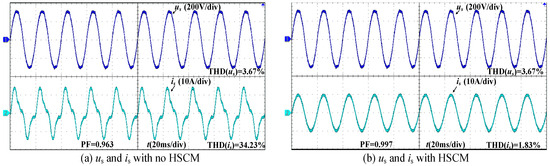
Figure 24.
The experimental results of injecting integer multiple harmonics.
In Figure 24a, THD(us) = 3.67%, THD(us) = 34.23% and PF = 0.963, and the distortion of is is quite severe. THD(us) = 3.67%, THD(us) = 1.83% and PF = 0.997 in Figure 24b, and is is a sine wave.
The experimental results when injecting interharmonics are shown in Figure 25, where Figure 25a is before the HSCM takes effect and Figure 25b is after the HSCM takes effect.
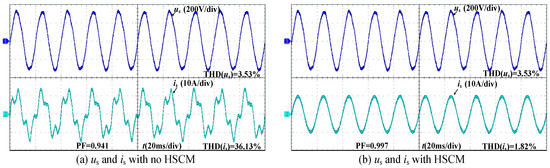
Figure 25.
The experimental results of injecting interharmonics.
From Figure 25a, THD(us) = 3.53%, THD(is) = 36.13% and PF = 0.941, and is is not a sine wave. Under the influence of an interharmonic wave, the period of it is doubled. As shown in Figure 25b, THD(us) = 3.53%, THD(is) = 1.82% and PF = 0.997. The harmonics of is are eliminated.
Under the influence of ultraharmonics, the experimental waveform of us is shown in Figure 26.
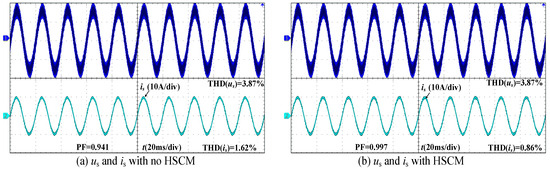
Figure 26.
The experimental results of injecting ultraharmonics. Arrow indicates where the waveform exceeds the oscilloscope’s maximum measurement point.
As shown in Figure 26, the ultraharmonics have a relatively small impact on is. However, THD improved under the influence of HSCM, changing from 1.62% to 0.86%.
Figure 26 displays the experimental waveform with voltage disturbances applied to us. Disturbance us1 was introduced at time t1, and disturbance us2 was introduced at time t2.
When us1 is applied, the amplitude of us increases. When HSCM is not in effect, is drops and distortion occurs, after t = t1 in Figure 27a. THD(is) = 5.13% and PF = 0.963. From Figure 27b, it can be seen that HSCM can cause us to change slowly under the influence of us1, without distortion. THD(is) = 1.24% and PF = 0.996. When us2 is applied, the amplitude of us decreases, is exhibits overshoot, and distortion occurs, as shown in Figure 27c. THD(is) = 4.43% and PF = 0.973. From Figure 27d, it is observed that the amplitude of us gradually increases under the influence of us2, without overshoot or distortion. THD(is) = 1.34% and PF = 0.997. Therefore, HSCM is also capable of mitigating the effects brought about by us2.
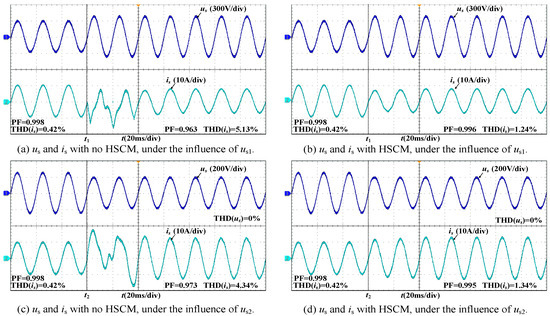
Figure 27.
The experimental results of voltage disturbances. Orange dot indicates the initial phase point.
When HSCM is in effect, the change in is is more gradual, after t = t1 in Figure 27b. us2 caused a reduction in the amplitude of us. Under the action of HSCM, is increased slowly, after t = t2 in Figure 27b. However, without the action of HSCM, is exhibited overshoot, after t = t2 in Figure 27a.
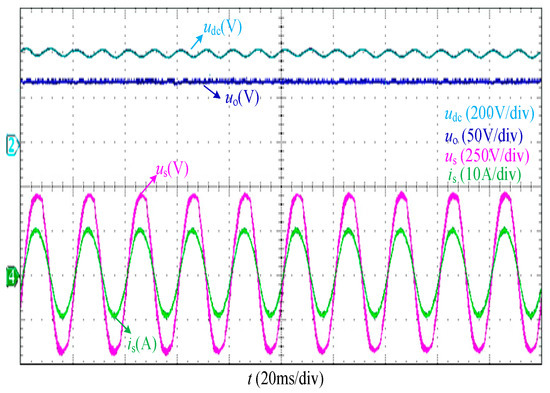
Figure 28.
The experimental results of udc and uo.
From Figure 28, it can be observed that the average value of udc is 400 V, and uo is 62 V. Combined with the parameters provided in Table 2, it is evident that the HPR has achieved the rated power output and is operating stably. The waveform of u is a straight line, which is crucial for enhancing the performance of the electrolyzer.
The aforementioned experiment further demonstrates that HSCM can eliminate the effects of integer harmonics, interharmonics, and voltage disturbances, and can improve the THD(is) in the presence of superharmonics.
7. Conclusions
The spectrum in RSHPES is very rich, not only including integer multiples of harmonics but also interharmonics and ultraharmonics. There are also various disturbances present. Traditional harmonic suppression methods cannot guarantee that HPR will be immune to the harm caused by these harmonics and disturbances. Simulation and experimental results show that HSCM can effectively eliminate the damage caused by rich harmonics and disturbances. HSCM has made a contribution to the integration of HPR into RSHPES and has also prevented the harm of harmonics to EC.
Author Contributions
Conceptualization, L.L.; validation, S.C. and Y.Z.; formal analysis, H.Y. and J.Z.; investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by Key Projects of Jiangxi Natural Science Foundation (20212ACB204004) and Jiangxi Provincial Leading Academic and Technical Talents Training Program (Grant No. 20232BCJ22004).
Data Availability Statement
The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meng, M.; Chen, M.; He, X.; Wang, J.; Liu, J. A Novel High Power Hybrid Rectifier with Low Cost and High Grid Current Quality for Improved Efficiency of Electrolytic Hydrogen Production. IEEE Trans. Power Electron. 2021, 37, 3763–3768. [Google Scholar]
- Kumar, K.; Samuel, P. Green Hydrogen Generation from the PEM Electrolyzer Powered by Solar Panel. In Proceedings of the Fifth International Conference on Electrical, Computer and Communication Technologies (ICECCT), Erode, India, 22–24 February 2023; pp. 1–6. [Google Scholar]
- Mabrak, H.; Elmazouzi, S.; Takky, D.; Naimi, Y.; Colak, I. Hydrogen Production by Water Electrolysis: Review. In Proceedings of the 12th International Conference on Renewable Energy Research and Applications (ICRERA), Oshawa, ON, Canada, 29 August–1 September 2023; pp. 372–380. [Google Scholar]
- Zeng, J.; Huang, Z.; Ling, Y.; Yang, L.; Li, Z.; Qiu, G.; Yang, B.; Yu, T. Analysis and hardware implementation of virtual resistance based PV inverters for harmonics suppression. IET Gener. Transm. Distrib. 2019, 13, 4592–4603. [Google Scholar]
- Liu, Q.; Li, Y.; Luo, L.; Peng, Y.; Cao, Y. Power Quality Management of PV Power Plant with Transformer Integrated Filtering Method. IEEE Trans. Power Deliv. 2019, 34, 941–949. [Google Scholar]
- Hari Prabhu, M.; Sundararaju, K. Power quality improvement of solar power plants in grid connected system using novel Resilient Direct Unbalanced Control (RDUC) technique. Microprocess. Microsyst. 2020, 75, 103016. [Google Scholar]
- Zhao, J.; Yang, H.; Pan, A.; Xu, F. An improved complex ICA based method for wind farm harmonic emission levels evaluation. Electr. Power Syst. Res. 2020, 179, 106105. [Google Scholar]
- Sowa, I.; Domínguez-García, J.; Gomis-Bellmunt, O. Impedance-based analysis of harmonic resonances in HVDC connected off shore wind power plants. Electr. Power Syst. Res. 2019, 166, 61–72. [Google Scholar]
- Ravikumar, S.; Vennila, H.; Deeepak, R. Hybrid power system with Total Harmonic Distortion minimization using improved Rider Optimization Algorithm: Analysis on converters. J. Power Sources 2020, 459, 228025. [Google Scholar]
- Blaabjerg, F.; Chen, Z.; Kjaer, S. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar]
- Wang, L.; Han, Z.; Ning, C.; Dong, H.; Yao, X.; Ge, Y. Research on Photovoltaic Hydrogen Generation Microgrid Harmonic Suppression Method Based on Improved Virtual Synchronous Generator Control. In Proceedings of the 4th International Conference on Electrical Engineering and Control Technologies (CEECT), Virtual Conference, 17 December 2022; pp. 1020–1026. [Google Scholar]
- Tavakoli, S.D.; Dozein, M.G.; Lacerda, V.A.; Mañe, M.C.; Prieto-Araujo, E.; Mancarella, P.; Gomis-Bellmunt, O. Grid-Forming Services from Hydrogen Electrolyzers. IEEE Trans. Sustain. Energy 2023, 14, 2205–2219. [Google Scholar]
- Agbossou, K.; Kolhe, M.; Hamelin, J.; Bose, T.K. Performance of a stand-alone renewable energy system based on energy storage as hydrogen. IEEE Trans. Energy Convers. 2004, 19, 633–640. [Google Scholar]
- Najdi, R.A.; Shaban, T.G.; Mourad, M.J.; Karaki, S.H. Hydrogen Production and Filling of Fuel Cell Cars. In Proceedings of the 3rd International Conference on Advances in Computational Tools for Engineering Applications (ACTEA), Zouk Mosbeh, Lebanon, 13–15 July 2016; pp. 43–48. [Google Scholar]
- Hedayati, M.H.; John, V. Filter Configuration and PWM Method for Single-Phase Inverters with Reduced Conducted EMI Noise. IEEE Trans. Ind. 2014, 51, 3236–3243. [Google Scholar] [CrossRef]
- Qian, Q.; Xie, S.; Huang, L.; Xu, J.; Zhang, Z.; Zhang, B. Harmonic Suppression and Stability Enhancement for Parallel Multiple Grid-Connected Inverters Based on Passive Inverter Output Impedance. IEEE Trans. Ind. Electron. 2017, 64, 7587–7598. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, S.; Li, B.; He, M.; Liu, G. A digital control strategy for three-phase PWM converter to suppress output voltage ripple under unbalanced input voltages. IEICE Electron. Express 2023, 20, 20230280. [Google Scholar]
- Cao, X.; Liu, X.; He, M.; Meng, X.; Zhou, Q. Active-Clamp Resonant Power Factor Correction Converter with Output Ripple Suppression. IEEE Access 2021, 9, 5260–5272. [Google Scholar]
- Liu, Y.; Wan, M.; He, Q.; Zhou, Q.; Meng, X. Buck-Type Single-Switch Integrated PFC Converter with Low Total Harmonic Distortion. IEEE Trans. Ind. Electron. 2020, 68, 6859–6870. [Google Scholar] [CrossRef]
- Javadi, A.; Al-Haddad, K. A Single-Phase Active Device for Power Quality Improvement of Electrified Transportation. IEEE Trans. Ind. Electron. 2015, 62, 3033–3041. [Google Scholar]
- Eroglu, H.; Cuce, E.; Mert Cuce, P.; Gul, F.; Iskenderoglu, A. Harmonic problems in renewable and sustainable energy systems: A comprehensive review. Sustain. Energy Technol. Assess. 2021, 49, 101566. [Google Scholar]
- Yang, Y.; Cao, W.; Su, Z. Harmonic Stability Analysis and Harmonic Suppression Strategy for Grid-Forming Converter with Dual-Loop Control. Sustain. Energy Technol. Assess. 2023, 49, 101566. [Google Scholar]
- Zeng, L.; He, X.; Han, P.; Wang, Y.; Wang, D.; Lin, J.; Zhao, H. Input and Output Harmonic Suppression Strategy of Single-Phase AC–DC–AC Converter. IEEE Trans. Ind. Electron. 2024, 71, 13042–13052. [Google Scholar]
- Yu, D.; Yi, H.; Zhang, H.; Jiang, X.; Zhang, Z.; Xie, Y. Suppression Method of Modulation Switching for the Inverter Oscillation caused by Harmonic Control. In Proceedings of the IEEE 4th China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 12 August 2023; pp. 1–78. [Google Scholar]
- Sun, L.; Ding, J.; Han, Z. Suppression of Input Second Harmonic Current in Three-Stage Single-Phase Inverter based on PR Control. In Proceedings of the IEEE PELS Students and Young Professionals Symposium (SYPS), Shanghai, China, 27–29 August 2023; Volume 49, p. 101566. [Google Scholar]
- Chen, Y.; Chen, M.; Cai, H.; Hu, C. A Charging Current Ripple Suppression Strategy for Three-phase Power Conversion System Based on DC-side Harmonic Current Compensation. In Proceedings of the 25th European Conference on Power Electronics and Applications (EPE 23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; Volume 49, p. 101566. [Google Scholar]
- Zhao, M.; Ge, Q. Grid-Side Harmonic Current Suppression Based on Carrier Phase-Shifted PWM and Extended State Observer for High-Power Multiple Parallel 3L-ANPC Rectifier. IEEE Trans. Ind. Electron. 2024, 71, 5399–5410. [Google Scholar] [CrossRef]
- Li, G.; Shao, Y.; Liu, X. A Voltage Harmonic Self-Suppression Strategy of Single-Phase UPS. IEEE Trans. Ind. Electron. 2024, 71, 15685–15693. [Google Scholar] [CrossRef]
- Rong, S.; Xu, M.; Chen, X.; Liu, Z.; Su, H.; Li, H. Research on Optimal Virtual Impedance Harmonic Suppression Method for Grid-Connected Inverter. In Proceedings of the 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 585–591. [Google Scholar]
- Liu, S.; Sun, Y.; Kang, Y. A Novel E-Exponential Stochastic Resonance Model and Weak Signal Detection Method for Steel Wire Rope. IEEE Trans. Ind. Electron. 2022, 69, 7428–7439. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Wang, H.; Blaabjerg, F. Artificial Intelligence-Aided Thermal Model Considering Cross-Coupling Effects. IEEE Trans. Power Electron. 2020, 35, 9998–10002. [Google Scholar] [CrossRef]
- Li, Y.; Song, H.; Jiang, J. Vertical Ion-Coupling Ga2O3 TFT with Spatiotemporal Logic Encryption. IEEE Trans. Electron. Devices 2023, 70, 3122–3125. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).