Study on the Design of the Gear Pair and Flow Characteristics of Circular-Arc Gear Pumps
Abstract
1. Introduction
2. Material and Methods
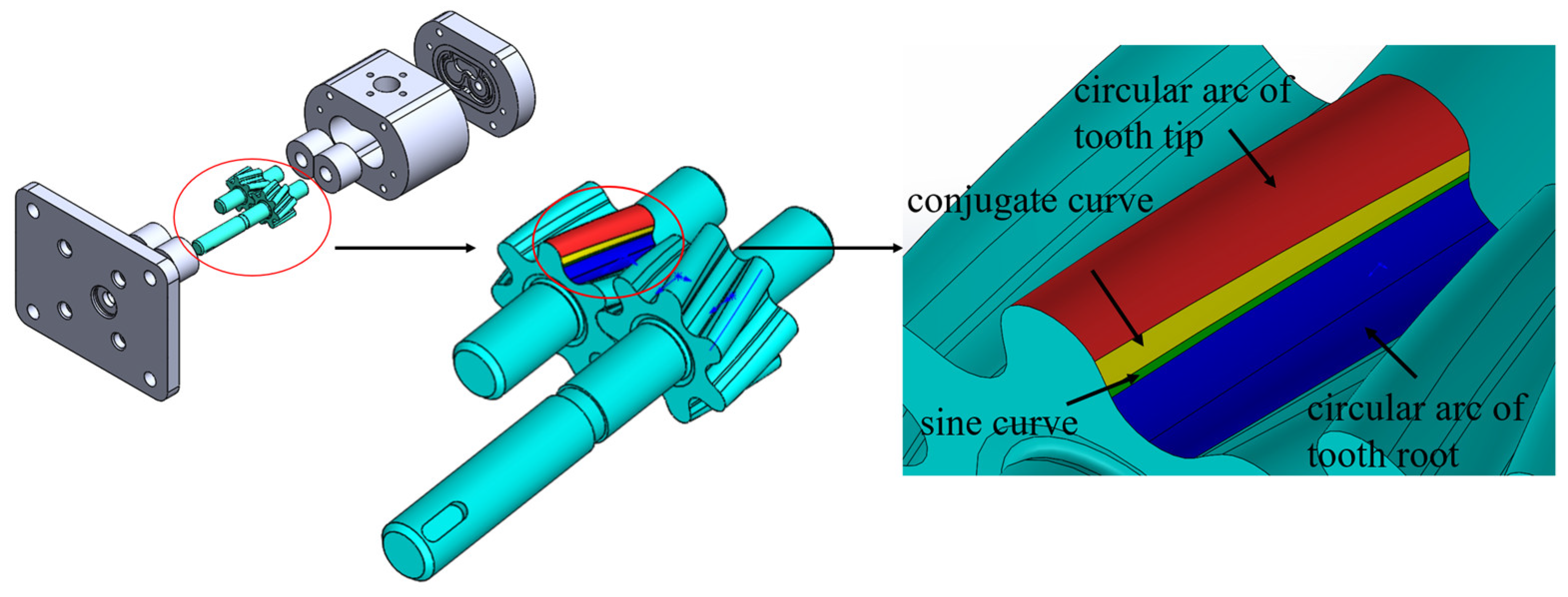
2.1. Structure of a Circular-Arc Helical Gear Pump
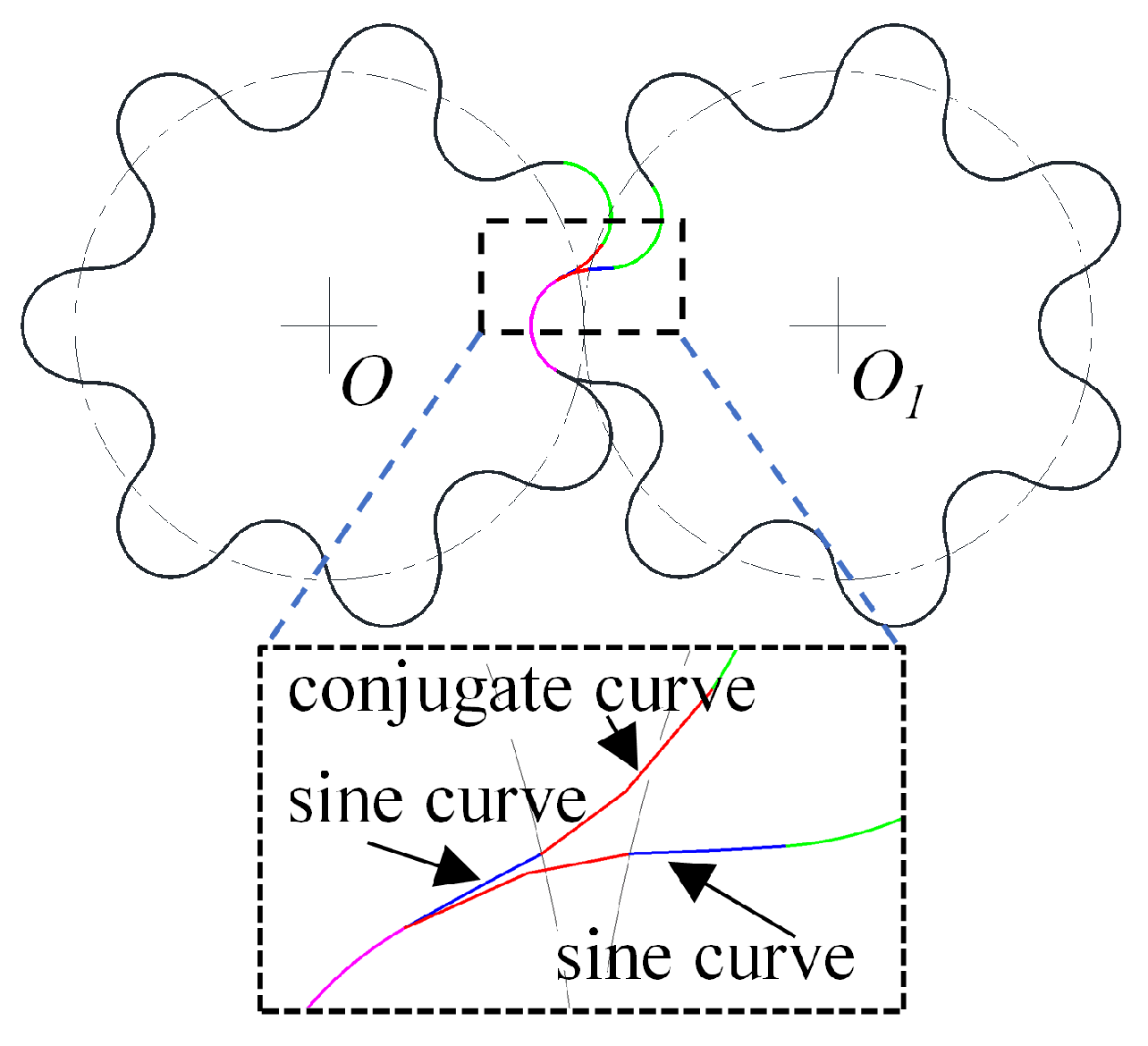
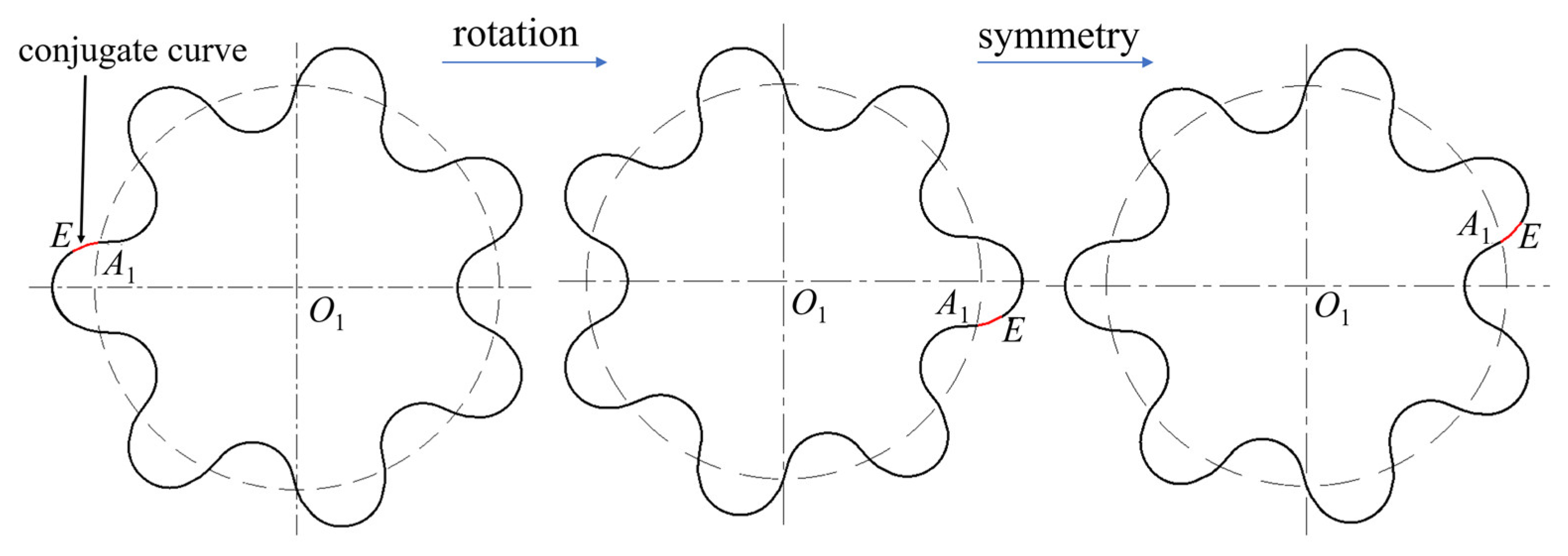
2.2. Mathematical Model of the Tooth Profile
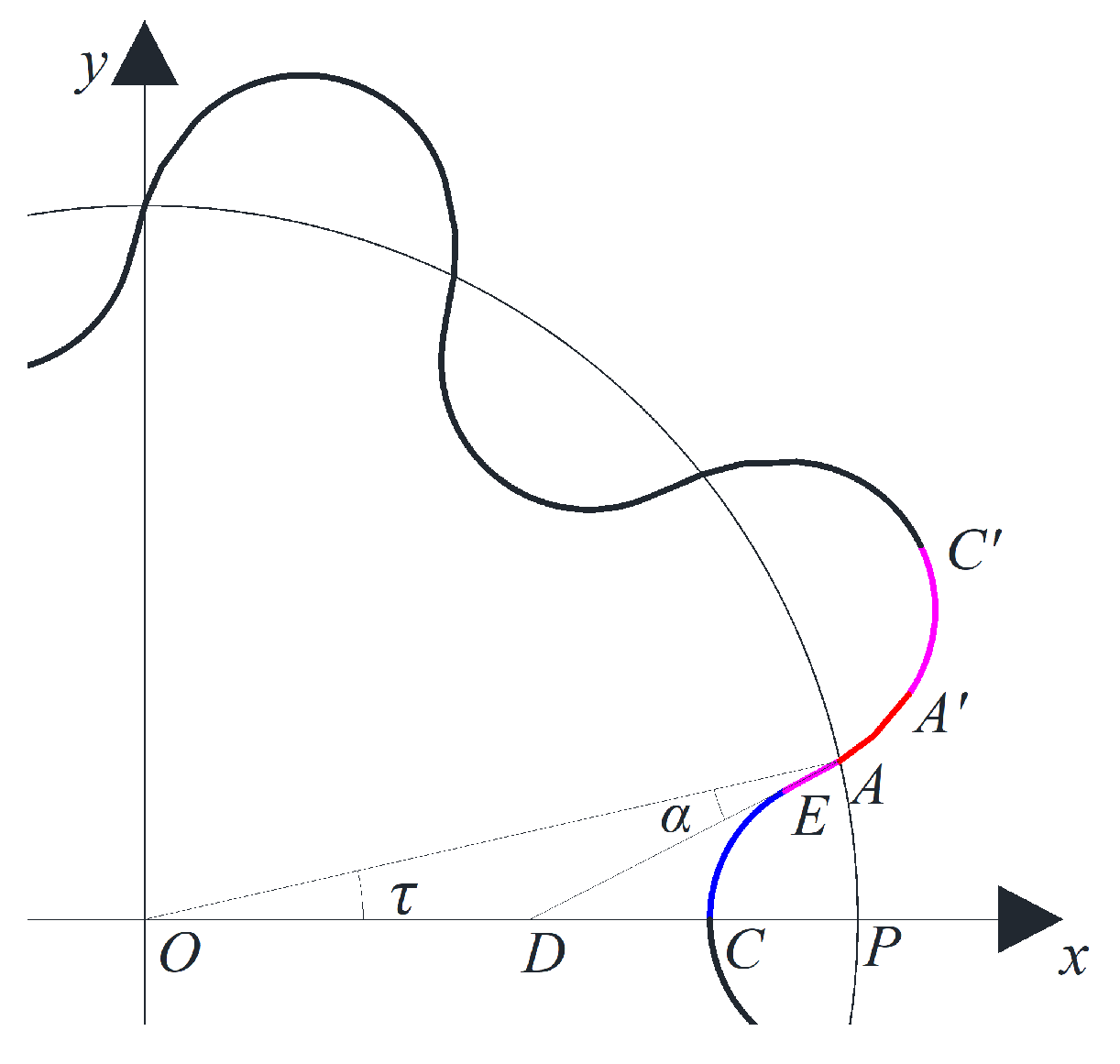
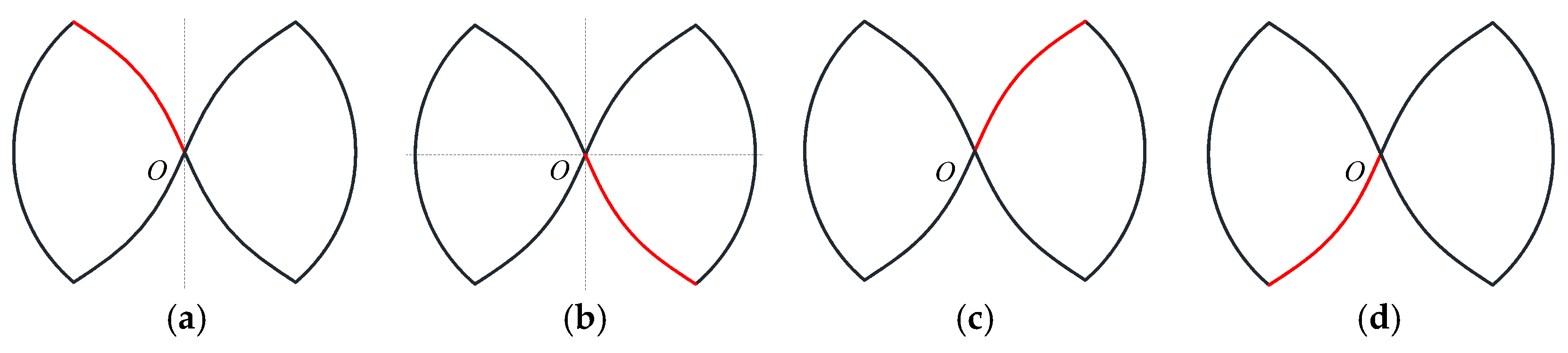
2.2.1. The Equation of the Sine Curve
2.2.2. The Equation of the Conjugate Curve
2.2.3. Equation of the Tooth Root and Tooth Tip
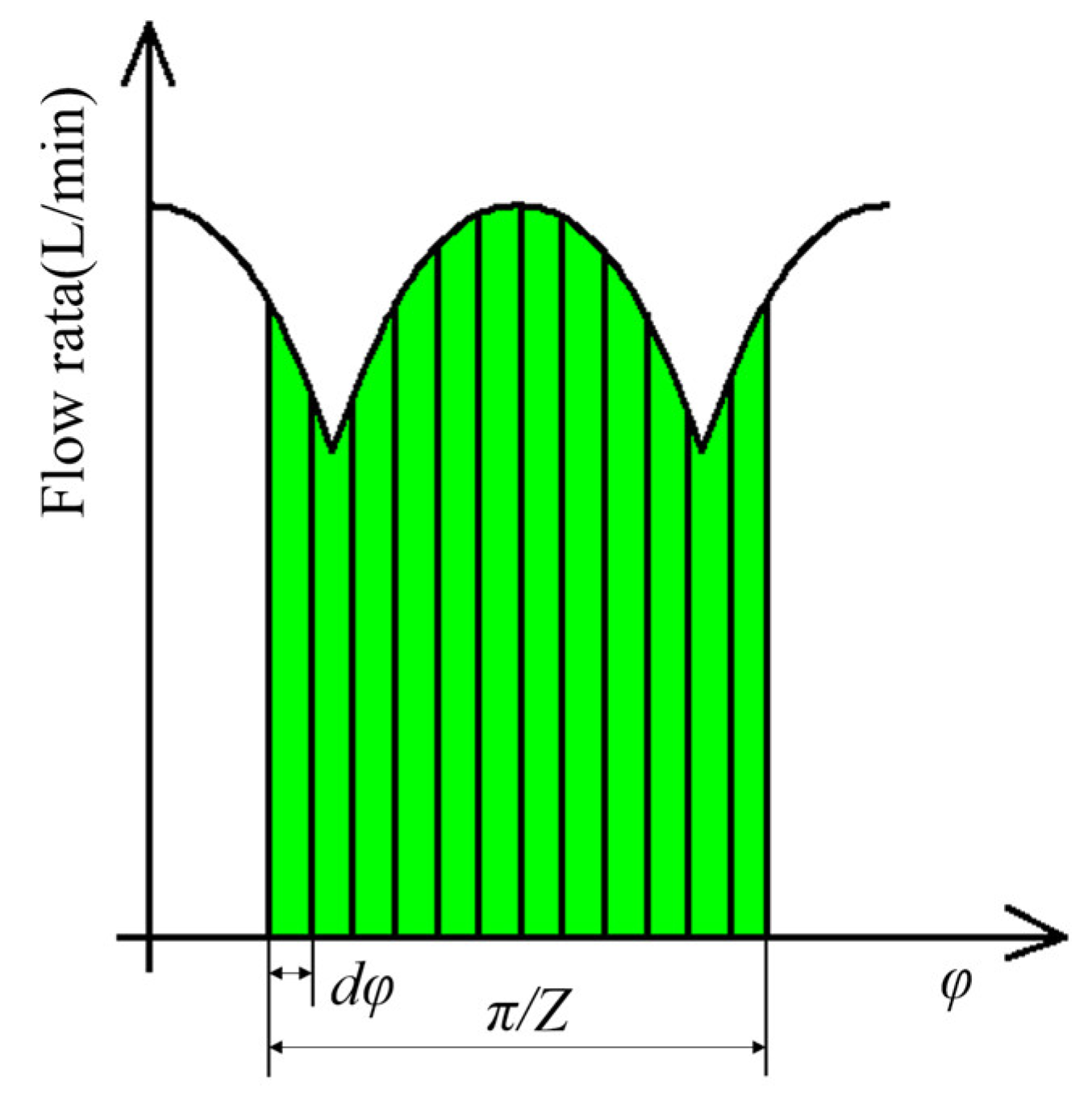
2.3. Analysis of the Flow Characteristics Mechanism
2.4. Simulation Analysis
2.4.1. Simulation Model
2.4.2. Simulation Scheme
- (1)
- Flow pulsation simulation
- (2)
- Simulation analysis of parameter influence
2.5. Pulsatility Evaluation and Spearman Rank Correlation Coefficient
3. Results
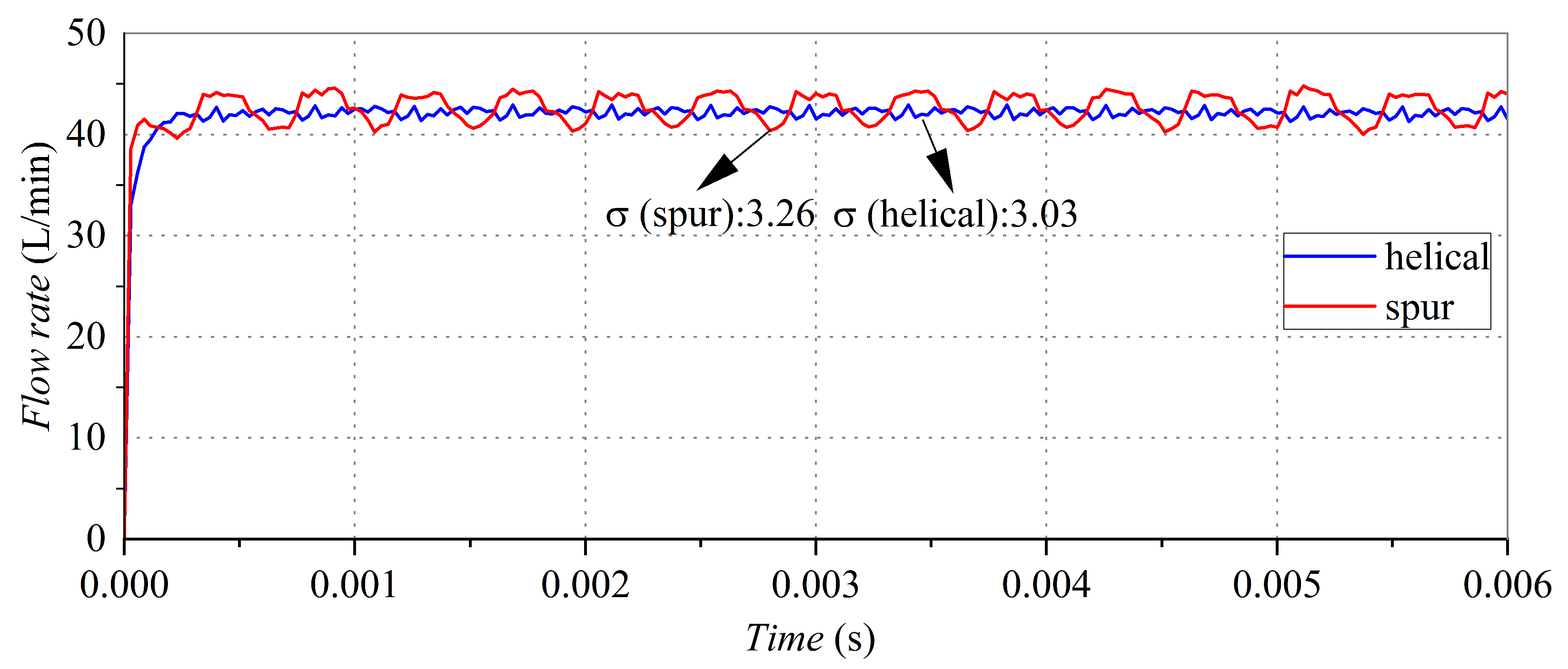
3.1. Flow Pulsation Simulation
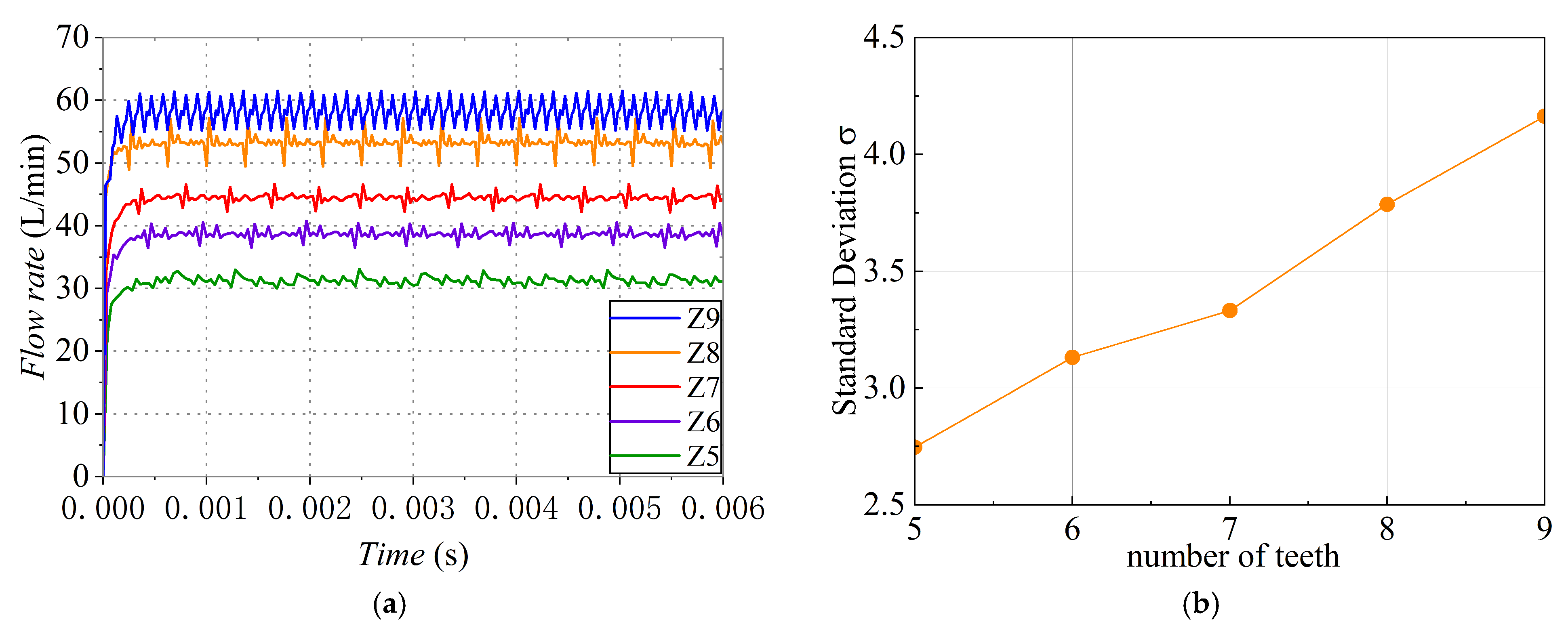
3.2. Effect of the Number of Teeth on the Flow Characteristics
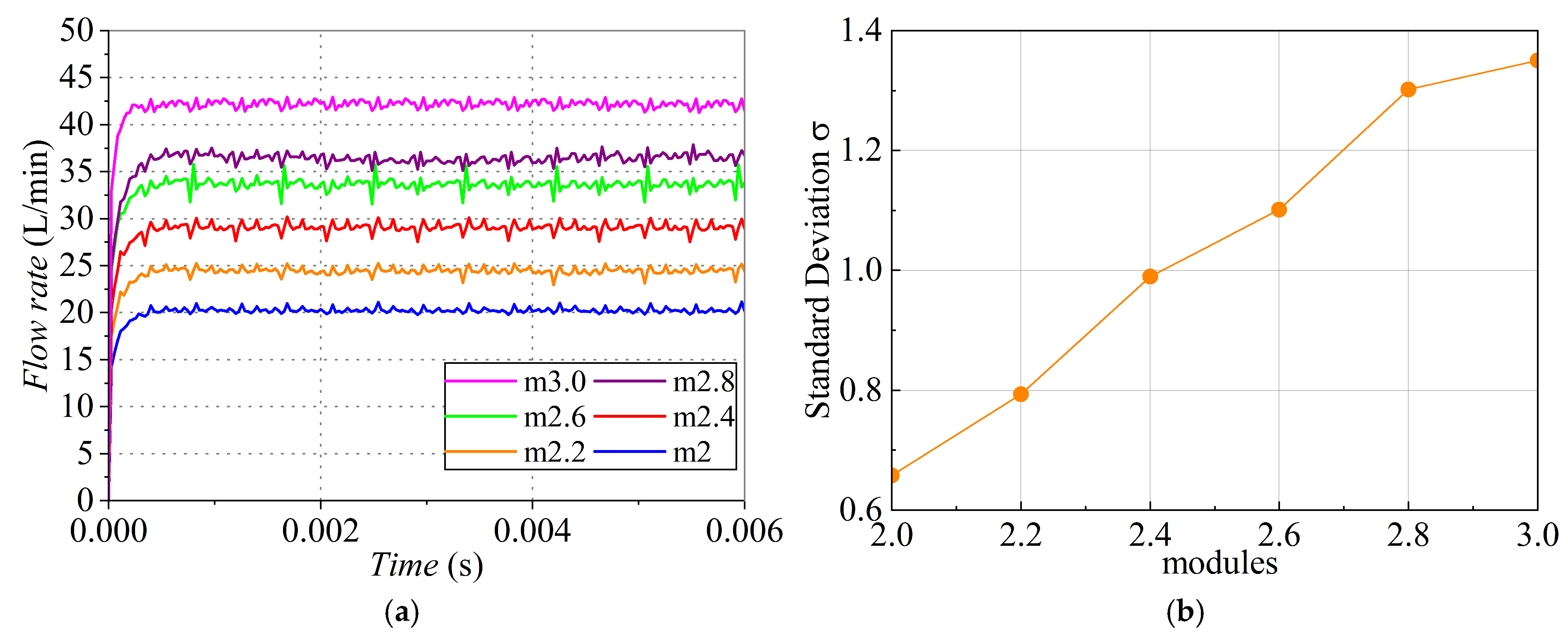
3.3. Effect of the Module on the Flow Characteristics
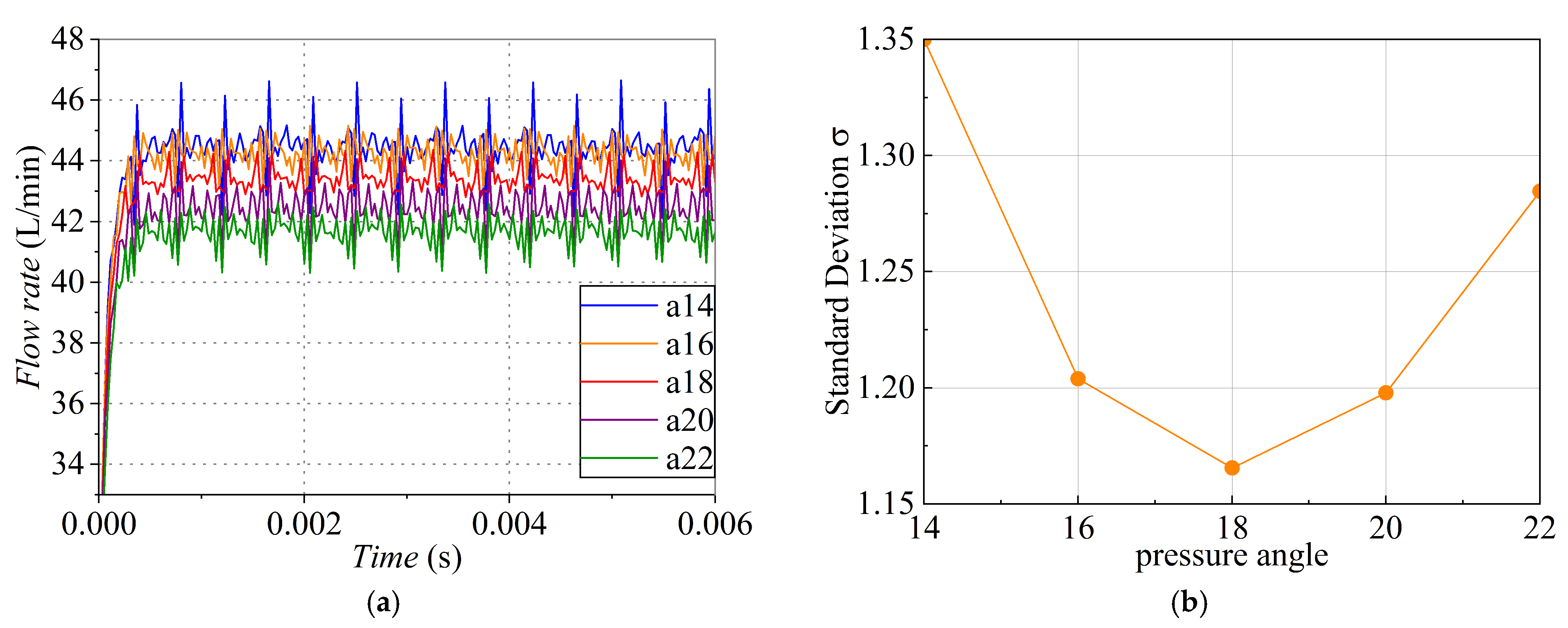
3.4. Effect of Pressure Angle on Flow Characteristics
3.5. Correlation Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: Challenges and solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar]
- Hao, Y.; Hao, J. Review of the Hydraulic and Structural Design of High-Speed Centrifugal Pumps Front. Energy Res. 2022, 10, 899093. [Google Scholar]
- Xu, B.; Liu, Q.; Zhu, Z. Influence of the Rotation Speed on the Internal Flow Characteristics of an Aircraft Fuel Gear Pump. Processes 2024, 12, 576. [Google Scholar] [CrossRef]
- Nagamura, K.; Ikejo, K.; Tutulan, F.G. Design and performance of gear pumps with a non-involute tooth profile. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 699–711. [Google Scholar]
- Zhou, Y.; Che, B.; Yuan, C. The design and analysis of a high-speed circular arc gear pump journal bearing. Adv. Mech. Eng. 2018, 10, 1687814018819288. [Google Scholar]
- Huang, K. Design and fluid analysis of the microsegment gear tooth profile for pump operating at high speed and high pressure. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 09544089231190181. [Google Scholar] [CrossRef]
- Zhang, H. Report about Hannover Messe 2011. Hydraul. Pneum. Seals 2011, 31, 5–9. [Google Scholar]
- Ransegnola, T.; Zhao, X.; Vacca, A. A comparison of helical and spur external gear machines for fluid power applications: Design and optimization. Mech. Mach. Theory 2019, 142, 103604. [Google Scholar]
- Williams, L.T. Design and Performance of a Curvilinear Circular-Arc Tooth Gear for Gear Pump Applications. In Fluid Power Systems Technology; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 83754, p. V001T01A029. [Google Scholar]
- Xu, H.; Huang, J. Research on Control Algorithm of Solvent-Free Compound Mixing Ratio Based on Feedforward Control. In China Academic Conference on Printing and Packaging; Springer Nature Singapore: Singapore, 2022; pp. 345–352. [Google Scholar]
- Liang, Y. Double Circular Arc Gear Pump Design; Zhengzhou Research Institute of Mechanical Engineering: Zhengzhou, China, 2015. [Google Scholar]
- Zhou, Y.; Hao, S.; Hao, M. Design and performance analysis of a circular-arc gear pump operating at high pressure and high speed. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 189–205. [Google Scholar]
- Zhao, X.; Vacca, A. Numerical analysis of theoretical flow in external gear machines. Mech. Mach. Theory 2017, 108, 41–56. [Google Scholar]
- Wei, X.; Han, Y. Simulation of Flow-Induced Vibration and Dynamic Performance of Circular-Arc Helical Gear Pump under Background of Machine Learning. Int. Trans. Electr. Energy Syst. 2022, 2022, 9513357. [Google Scholar]
- Wu, Y.; Ge, P.; Bi, W. Analysis of axial force of double circular arc helical gear hydraulic pump and design of its balancing device. J. Cent. South Univ. 2021, 28, 418–428. [Google Scholar]
- Gregov, G. Modeling and predictive analysis of the hydraulic GEROLER motor based on artificial neural network. Eng. Rev. 2022, 42, 91–100. [Google Scholar]
- Rundo, M. Models for flow rate simulation in gear pumps: A review. Energies 2017, 10, 1261. [Google Scholar] [CrossRef]
- Antoniak, P.; Stryczek, J. Visualization study of the flow processes and phenomena in the external gear pump. Arch. Civ. Mech. Eng. 2018, 18, 1103–1115. [Google Scholar]
- Pan, J. Tooth Profile Curve of Modern Oil Transmission Pump. Mach. Tool Hydraul. 1979, 2, 1–12. [Google Scholar]
- Li, G.; Zhang, L.; Han, W. Profile design and displacement analysis of the low pulsating gear pump. Adv. Mech. Eng. 2018, 10, 1–11. [Google Scholar]
- Zhang, X.; Liang, Z. Geometric Modeling and CFD Simulation of Curvilinear Cylindrical Gear Pumps. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1–17. [Google Scholar]
- Jang, H.; Ji, S. Numerical Study on the Instantaneous Theoretical Flow Rate of the Continuous Contact Gear Pump with a New Geometrical Approach. J. Mar. Sci. Eng. 2024, 12, 2332. [Google Scholar] [CrossRef]
- Hrcek, S.; Brumercik, F. Global Sensitivity Analysis of Chosen Harmonic Drive Parameters Affecting Its Lost Motion. Materials 2021, 14, 5057. [Google Scholar] [CrossRef]
- Zhao, X.; Andrea, V. Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation. Mech. Syst. Signal Process 2018, 109, 352–378. [Google Scholar]
- Manring, N.D. The theoretical flow ripple of an external gear pump. J. Dyn. Sys. Meas. Control 2003, 125, 396–404. [Google Scholar]
- Ali Abd Al-Hameed, K. Spearman’s correlation coefficient in statistical analysis. Int. J. Nonlinear Anal. Appl. 2022, 13, 3249–3255. [Google Scholar]

| Parameter | Value |
|---|---|
| Number of teeth Z | 7 |
| Modules m | 3 |
| Pressure angle | 18 |
| Tooth width B | 15.5 |
| Helical angle β | 17.99 |
| Tip diameter R | 25.24 |
| Displacement V | 5 |
| Variable Number of Teeth | Variable Modules | Variable Pressure Angle | |
|---|---|---|---|
| number of teeth Z | 5, 6, 7, 8, 9 | 7 | 7 |
| modules m | 3 | 2, 2.2, 2.4, 2.6, 2.8, 3 | 3 |
| pressure angle α | 14.5 | 14.5 | 14, 16, 18, 20, 22 |
| tooth width B | 15.5 | 15.5 | 15.5 |
| Number of Teeth | Module | Pressure Angle | ||
|---|---|---|---|---|
| Flow rate | correlation coefficient | 0.550 * | 0.778 ** | −0.007 |
| significance | 0.027 | 3.840 × 10−4 | 0.979 | |
| Standard deviation | correlation coefficient | 0.166 | 0.737 ** | −0.251 |
| significance | 0.538 | 0.001 | 0.349 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Liu, Y.; Han, W.; Li, D.; Wang, S.; Hao, Z. Study on the Design of the Gear Pair and Flow Characteristics of Circular-Arc Gear Pumps. Appl. Sci. 2025, 15, 3911. https://doi.org/10.3390/app15073911
Li G, Liu Y, Han W, Li D, Wang S, Hao Z. Study on the Design of the Gear Pair and Flow Characteristics of Circular-Arc Gear Pumps. Applied Sciences. 2025; 15(7):3911. https://doi.org/10.3390/app15073911
Chicago/Turabian StyleLi, Geqiang, Yunda Liu, Weifeng Han, Donglin Li, Shuai Wang, and Zhenchao Hao. 2025. "Study on the Design of the Gear Pair and Flow Characteristics of Circular-Arc Gear Pumps" Applied Sciences 15, no. 7: 3911. https://doi.org/10.3390/app15073911
APA StyleLi, G., Liu, Y., Han, W., Li, D., Wang, S., & Hao, Z. (2025). Study on the Design of the Gear Pair and Flow Characteristics of Circular-Arc Gear Pumps. Applied Sciences, 15(7), 3911. https://doi.org/10.3390/app15073911






