Ultrasonic Evaluation Method for Mechanical Performance Degradation of Fluororubber Used in Nuclear Power Facility
Abstract
1. Introduction
2. Methods
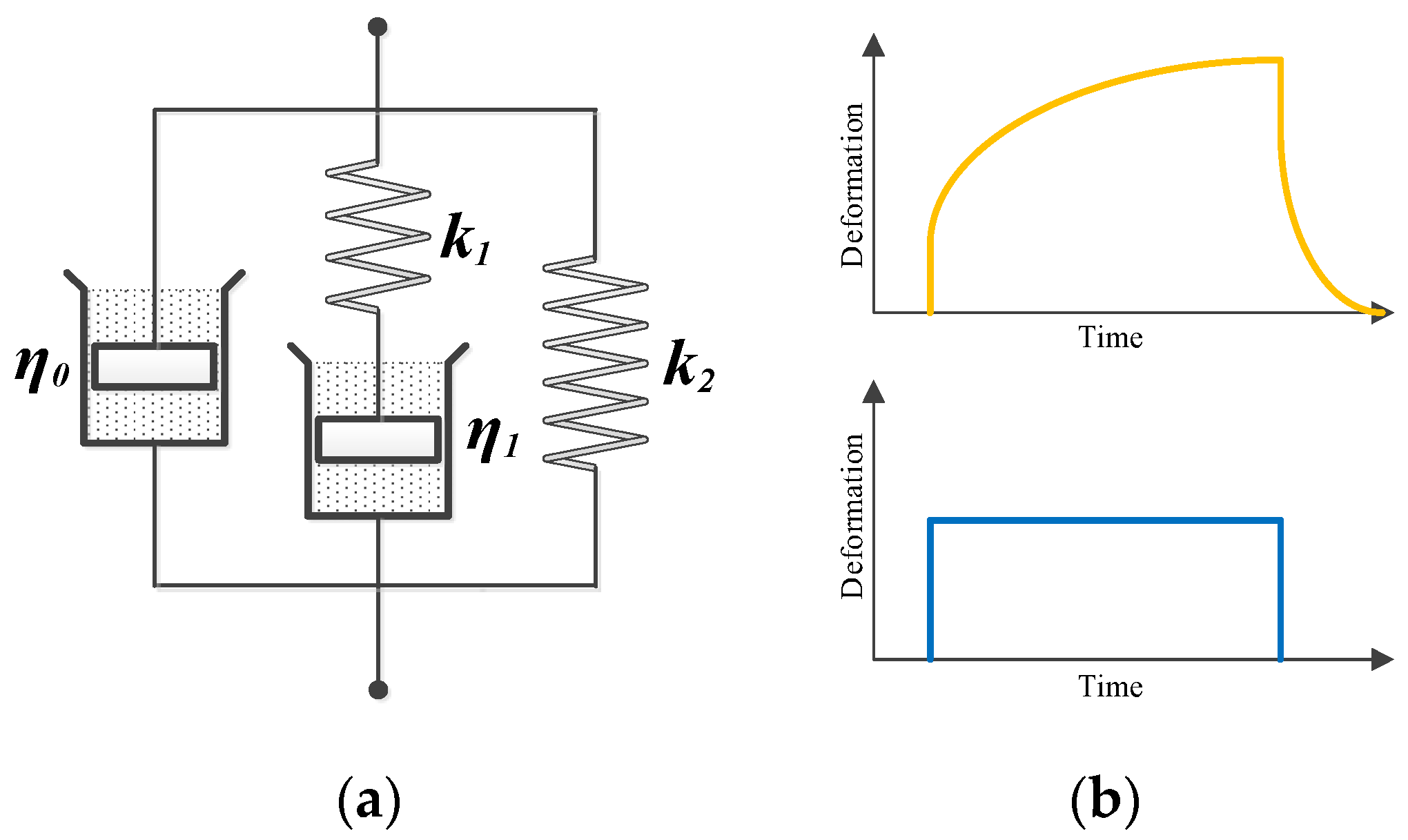
2.1. Viscoelastic Model for Acoustic Wave Propagation
2.1.1. Viscoelastic Model Construction of Fluororubber
2.1.2. Physical Interpretation of the Model
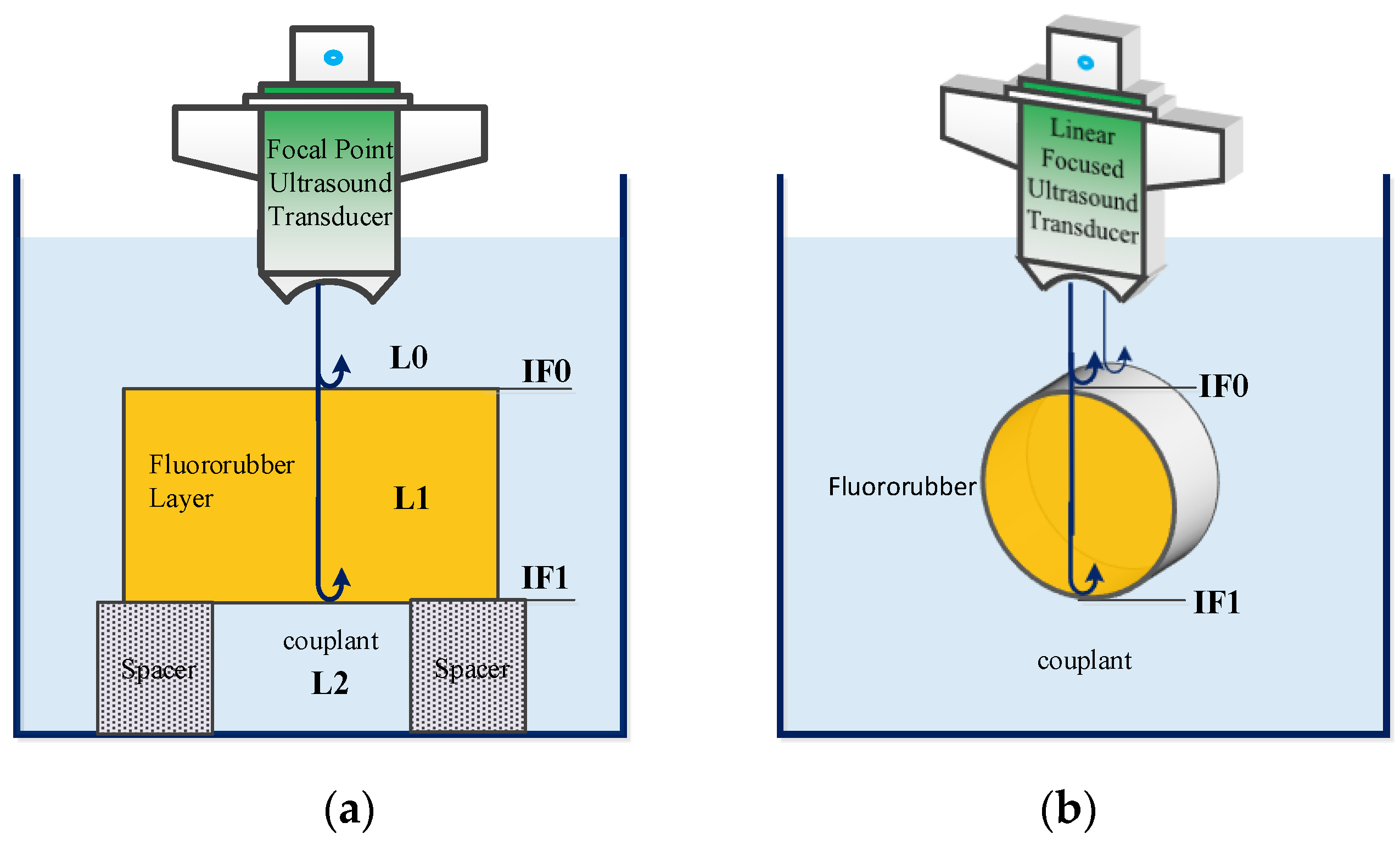
2.2. Measuring Principle
2.2.1. Acoustic Evaluation Model
2.2.2. Measurement of Ultrasonic Reflection Coefficient
2.2.3. Data Analysis Methods
3. Experiments
3.1. Ultrasound Measurement Setup
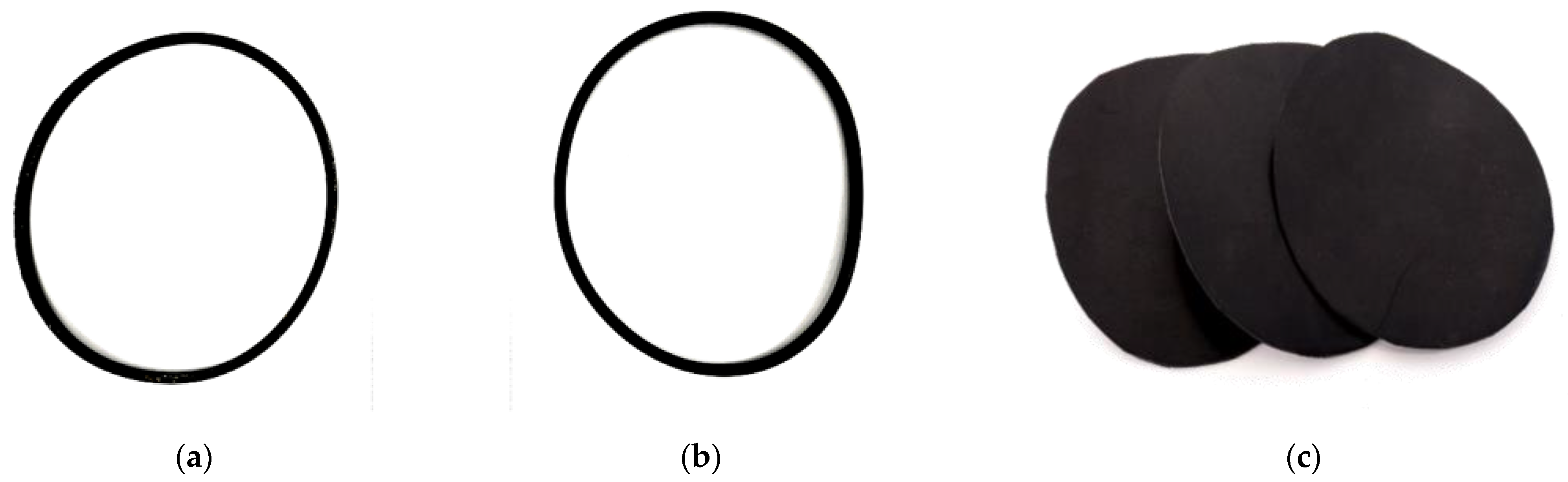
3.2. Preparation of Experimental and Reference Specimens
3.3. Experimental Design for Detection
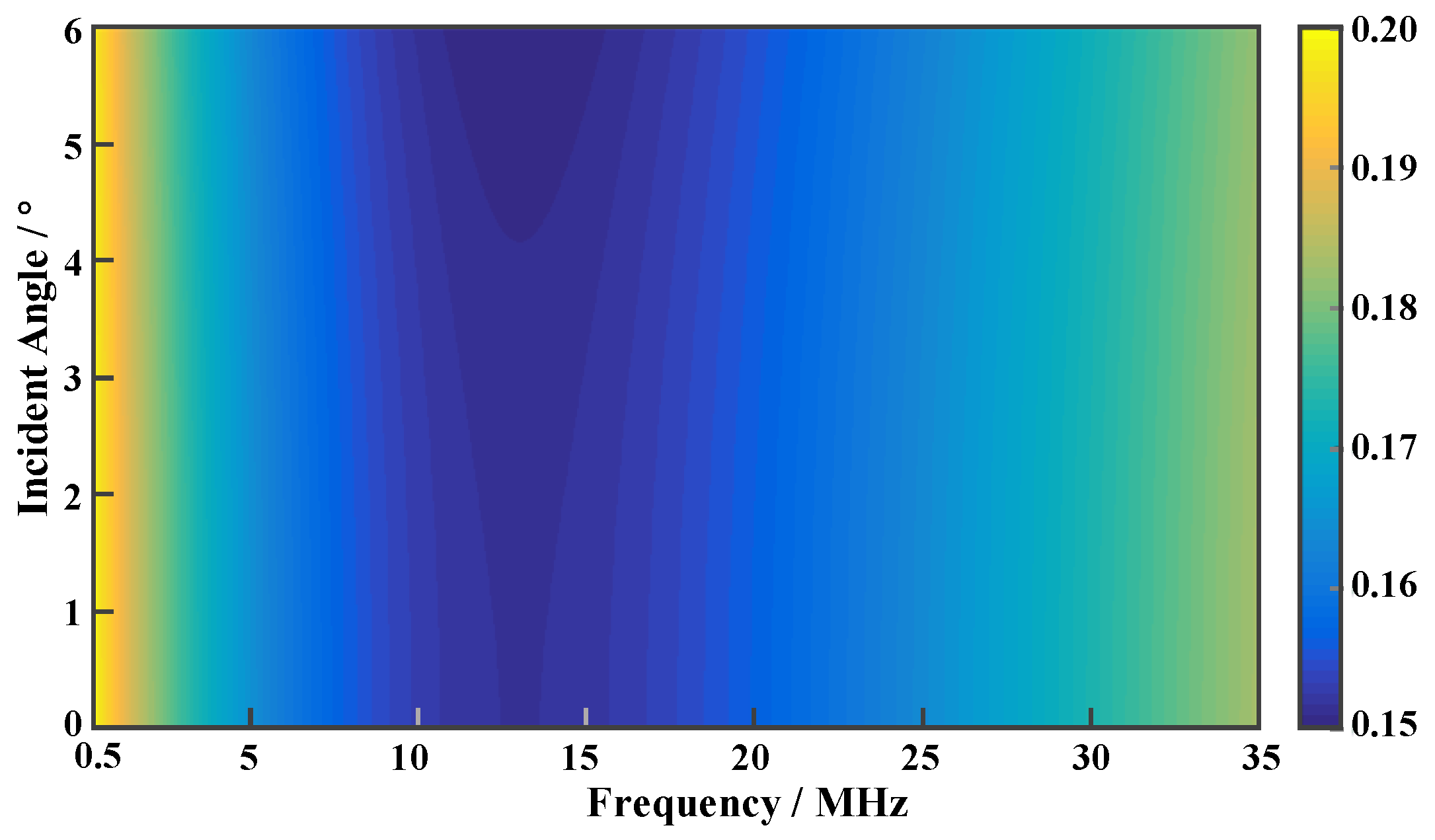
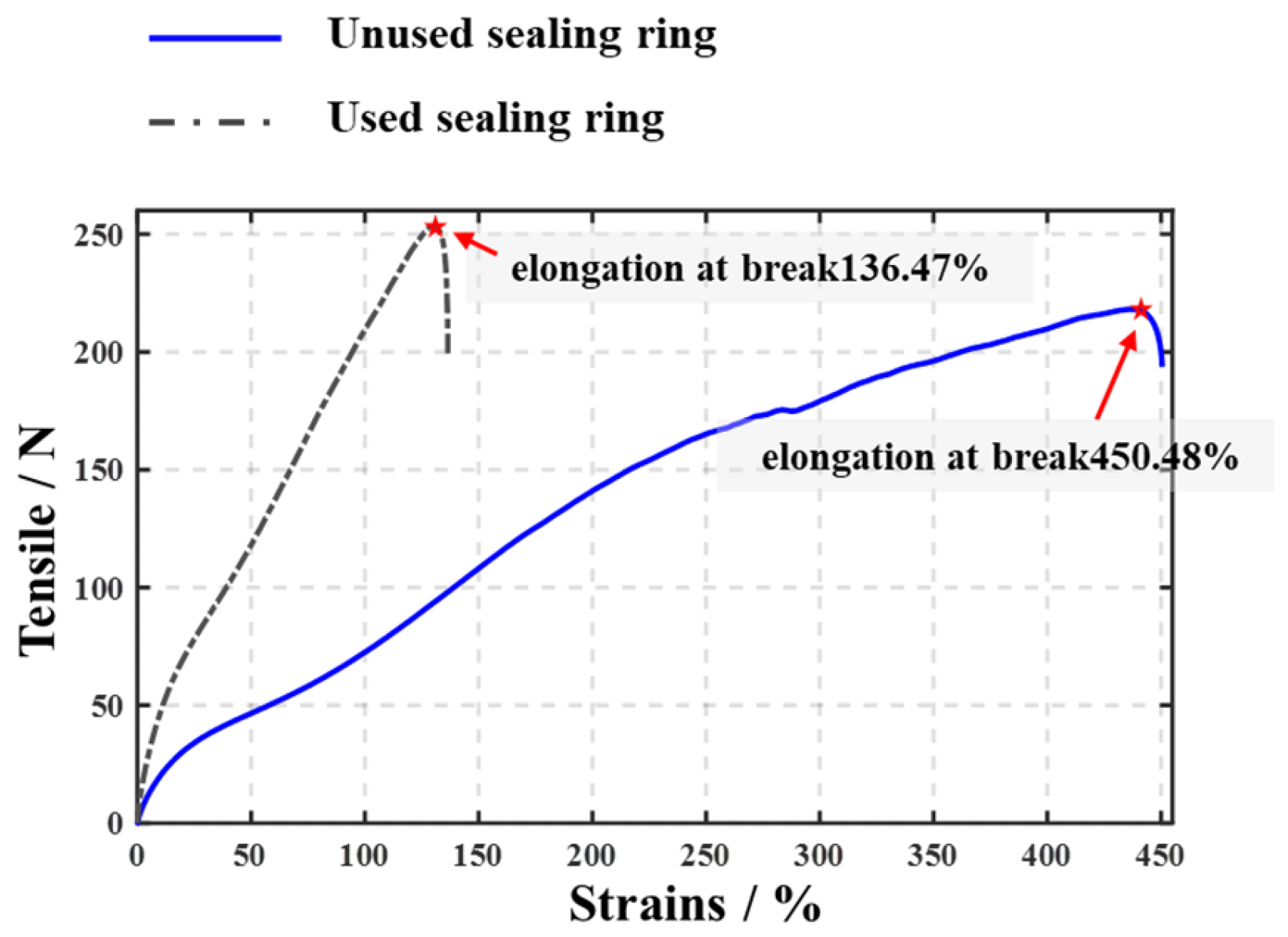
4. Results
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mello, C.C.; Costa, M.F. Fluororubber Aged Under Continuous Compression Set at Elevated Temperatures. In Volume 4: Materials Technology, Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engi-neering, St. John’s, NL, Canada, 31 May–5 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; p. V004T03A026. [Google Scholar] [CrossRef]
- Zhang, X.; Chang, X.; Chen, S.; Hua, M. Thermal Oxidation Aging Test and Life Assessment of Fluorine Rubber Sealing Materials. Equip. Environ. Eng. 2012, 9, 35–38. [Google Scholar]
- Zhang, L. Accelerated Aging Test and Life Prediction of Fluorine Rubber Under Long-Term Loading Conditions. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 2024. [Google Scholar] [CrossRef]
- Korba, A.G.; Kumar, A.; Barkey, M. A hyper-elastic thermal aging constitutive model for rubber-like materials. J. Elastomers Plast. 2020, 52, 677–700. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Z.; Tang, T.; Song, L. Thermal damage detection of fluororubber material based on terahertz wave. Laser Optoelectron. Prog. 2020, 57, 297–302. [Google Scholar]
- Shaw, M.T.; MacKnight, W.J. Introduction to Polymer Viscoelasticity, 4th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Shui, G.; Wang, Y.; Qu, J. Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound. Adv. Mech. 2005, 35, 52–68. [Google Scholar]
- Sun, A.; Bai, X.; Ju, B.-F. A new method for evaluating the degeneration of articular cartilage using pulse-echo ultrasound. Rev. Sci. Instrum. 2015, 86, 034301. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, C.; Lu, J.; Sun, A. Application of the Reciprocity Theorem to Scattering of Surface Waves by a Surface Crack in Viscoelastic Material. Appl. Sci. 2022, 12, 10785. [Google Scholar] [CrossRef]
- Panwar, R.; Lee, J.R. Performance and Non-Destructive Evaluation Methods of Airborne Radome and Stealth Structures. Meas. Sci. Technol. 2018, 29, 062001. [Google Scholar]
- Castellano, A.; Foti, P.; Fraddosio, A.; Galietti, U.; Marzano, S.; Piccioni, M.D. Characterization of Material Damage by Ultrasonic Immersion Test. Procedia Eng. 2015, 109, 395–402. [Google Scholar]
- Castellano, A.; Mazzarisi, M.; Campanelli, S.L.; Angelastro, A.; Fraddosio, A.; Piccioni, M.D. Ultrasonic Characterization of Components Manufactured by Direct Laser Metal Deposition. Materials 2020, 13, 2658. [Google Scholar] [CrossRef]
- Jhang, K. Nonlinear Ultrasonic Techniques for Nondestructive Assessment of Micro Damage in Material: A Review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar]
- Chen, H.; Zhang, G.; Fan, D.; Fang, L.; Huang, L. Nonlinear Lamb Wave Analysis for Microdefect Identification in Mechanical Structural Health Assessment. Measurement 2020, 164, 108026. [Google Scholar] [CrossRef]
- Buck, O. Harmonic Generation for Measurement of Internal Stresses as Produced by Dislocations. IEEE Trans. Sonics Ultrason. 1976, 23, 346–350. [Google Scholar] [CrossRef]
- Koissin, V.; Demcenko, A.; Korneev, V.A. Isothermal Epoxy-Cure Monitoring Using Nonlinear Ultrasonics. Int. J. Adhes. Adhes. 2014, 52, 11–18. [Google Scholar] [CrossRef]
- Demcenko, A.; Koissin, V.; Korneev, V.A. Noncollinear Wave Mixing for Measurement of Dynamic Processes in Polymers: Physical Ageing in Thermoplastics and Epoxy Cure. Ultrasonics 2014, 54, 684–693. [Google Scholar] [CrossRef]
- Lai, Q.; Xu, C.; Wang, G.; Deng, M. Assessment of Aging Degradation in Rubber Using Quasi-Static Components of Ultrasonic Longitudinal Waves. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2024, 8, 021007. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, H.; Cheng, L.; Yang, L.; Liao, R. Non-destructive method by nonlinear ultrasonic measurements for aging characterization of silicone rubber. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 3040–3044. [Google Scholar] [CrossRef]
- Zhang, S.; Zhuang, Z. Composite Materials and Viscoelastic Mechanics, 2nd ed.; China Machinal Press: Beijing, China, 2011. [Google Scholar]
- Rose, J.L.; Nagy, P.B. Ultrasonic Waves in Solid Media. J. Acoust. Soc. Am. 2000, 107, 1807–1808. [Google Scholar] [CrossRef]
- Du, G.; Zhu, Z.; Gong, X. Fundamentals of Acoustics, 3rd ed.; Nanjing University Press: Nanjing, China, 2012. [Google Scholar]
- Ding, H. Computational Ultrasound: Sound Field Analysis and Applications; Science Press: Beijing, China, 2010. [Google Scholar]
- Song, G.; Lu, D.; Lu, Y.; Liu, H.; Gao, Z.; Wu, B.; He, C. Velocity measurements of cylindrical surface waves with a large aperture line-focus acoustic transducer. Measurement 2016, 90, 103–109. [Google Scholar] [CrossRef]
- Chen, J.; Bai, X.; Yang, K.; Ju, B.-F. Angular measurement of acoustic reflection coefficients by the inversion of V(z, t) data with high frequency time-resolved acoustic microscopy. Rev. Sci. Instrum. 2012, 83, 014901. [Google Scholar] [CrossRef]
- Bai, X.; Sun, Z.; Sun, A.; Chen, J.; Ju, B.-F. Determination of the multiple local properties of thin layer with high lateral resolution by scanning acoustic microscopy. Rev. Sci. Instrum. 2014, 85, 094901. [Google Scholar] [CrossRef]
- GB/T 3512—2014; Test Methods for Accelerated Aging and Heat Resistance of Thermoplastic Rubber in Hot Air. China Standards Press: Beijing, China, 2014.
- Kader, M.A.; Bhowmick, A.K. Thermal ageing, degradation and swelling of acrylate rubber, fluororubber and their blends containing polyfunctional acrylates. Polym. Degrad. Stab. 2003, 79, 283–295. [Google Scholar] [CrossRef]
- Yang, X.; Verboven, E.; Ju, B.; Kersemans, M. Comparative study of ultrasonic techniques for reconstructing the multilayer structure of composites. NDT E Int. 2021, 121, 102460. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M. Waves in Layered Media, 2nd ed.; Academic Press: New York, NY, USA, 2021. [Google Scholar]






| Parameters | Value |
|---|---|
| 2.6 GPa | |
| 0.2 GPa | |
| 5 Pa·s | |
| 80 Pa·s | |
| Density of water | 1000 kg/m3 |
| Speed of sound in water | 1480 m/s |
| Specimen Type | Mechanical Model | Acoustic Model | ||
|---|---|---|---|---|
| Parameter Name | Fitted Value | Parameter Name | Fitted Value | |
| Used sealing ring | 2.20 ± 0.15 GPa | 2.97 ± 0.15 GPa | ||
| 1.42 ± 0.23 GPa | (2.22 ± 0.2) × 10−9 | |||
| 6.14 ± 0.35 Pa·s | 1380 ± 21 kg/m3 | |||
| 32.55 ± 1.26 Pa·s | (1.19 ± 0.57) × 10−5 s/rad·m | |||
| Unused sealing ring | 1.99 ± 0.08 GPa | 2.75 ± 0.22 GPa | ||
| 1.51 ± 0.15 GPa | (2.15 ± 0.18) × 10−9 | |||
| 6.63 ± 0.27 Pa·s | 1357 ± 16 kg/m3 | |||
| 25.23 ± 0.26 Pa·s | (2.37 ± 0.63) × 10−5 s/rad·m | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhu, L.; Wu, T.; Zhang, C.; Sun, A.; Ju, B. Ultrasonic Evaluation Method for Mechanical Performance Degradation of Fluororubber Used in Nuclear Power Facility. Appl. Sci. 2025, 15, 3903. https://doi.org/10.3390/app15073903
Wu L, Zhu L, Wu T, Zhang C, Sun A, Ju B. Ultrasonic Evaluation Method for Mechanical Performance Degradation of Fluororubber Used in Nuclear Power Facility. Applied Sciences. 2025; 15(7):3903. https://doi.org/10.3390/app15073903
Chicago/Turabian StyleWu, Lu, Liwen Zhu, Tong Wu, Chengliang Zhang, Anyu Sun, and Bingfeng Ju. 2025. "Ultrasonic Evaluation Method for Mechanical Performance Degradation of Fluororubber Used in Nuclear Power Facility" Applied Sciences 15, no. 7: 3903. https://doi.org/10.3390/app15073903
APA StyleWu, L., Zhu, L., Wu, T., Zhang, C., Sun, A., & Ju, B. (2025). Ultrasonic Evaluation Method for Mechanical Performance Degradation of Fluororubber Used in Nuclear Power Facility. Applied Sciences, 15(7), 3903. https://doi.org/10.3390/app15073903







