Abstract
In recent years, PV power plants have been widely used on the roofs of commercial buildings with grid connections, primarily to enhance self-consumption in distributed energy systems. In addition, installing PV plants on commercial buildings’ roofs is becoming increasingly important, especially in crowded cities where land is limited. Since the Sun is an intermittent energy source, PV power plants cause frequency and voltage fluctuations in the grid. The way to avoid this problem is to install PV plants together with battery storage systems. Battery storage systems prevent frequency and voltage fluctuations in the grid and provide economic benefits. This article presents the sizing and techno-economic analysis of a factory building’s rooftop PV system with a battery. The amount of energy produced by the PV plant, PV temperature, and irradiation were recorded in a data logger obtained by various sensors. These real-time measurements were continuously collected and analyzed to evaluate system performance and assess seasonal variations.Load demand data were collected through an automatic meter reading system. The installed capacity of the PV power plant is 645 kW. The optimum battery capacity determined for this factory is 130 kW for 5 h. Techno-economic analysis was carried out using metrics such as the payback period, net present value, and levelized cost of energy. As a result of the analysis using various input variables, LCOE, NPV, and PBP were determined as 0.1467 $/kWh, 4918.3 $, and 7.03 years, respectively.
1. Introduction
As CO2 emissions increasingly contribute to environmental pollution and the climate crisis, renewable energy sources (RES) are being rapidly adopted, particularly in developed and developing countries. In particular, the rate of use of wind and solar energy for electricity generation is increasing faster than other renewable energy sources [,]. However, wind and solar energy availability fluctuate throughout the day due to varying atmospheric conditions []. In addition, due to unforeseen meteorological conditions, the continuity of energy production in power generation facilities based on these resources cannot be ensured []. Therefore, to ensure the continuity of energy in electricity networks, either fossil-based power plants or energy storage systems are required [,]. Due to the negative environmental effects of fossil-based resources, energy storage systems (ESS) are becoming more prominent today. ESS used with RES not only ensures the continuity of electrical energy but also prevents voltage and frequency fluctuations caused by power plants based on RES. Since ESS has become competitive in terms of cost, both academic studies and industrial studies are carrying out studies to integrate ESS into power plants [,]. In many studies, it has been shown that ESSs eliminate the instability problems caused by the integration of RESs into the electrical grid to a large extent []. The ability of ESSs to inject and absorb active or reactive power makes RES very useful for integrating into a power system network [,]. Samantaray and Kayal (2023) [], the authors presented a strategy to optimally determine the size and discharge time of BSSs in a distribution system (DS) to improve the performance and reliability of ESSs. For this purpose, the weight-aggregated particle swarm optimization (WAPSO) technique was used. Sepúlveda et al. analyzed the effect of operating at different voltage levels on the system in battery PV systems based on the self-consumption model []. Thus, they determined the effect of operating voltage level and demanded electrical power on the energy efficiency of the system. Grajales et al. created a method and economic model based on actual regulation to evaluate the use of ESS in a power grid for different scenarios. The proposed method reveals potential barriers, challenges, and the feasibility of incorporating energy storage into RES []. Optimum sizing of ESS is necessary to meet load demand, reduce energy costs, and increase system security []. While facilitating the optimum sizing of the ESS, it is necessary to pay attention to many factors such as the optimum charge/discharge cycle, sudden load changes, power oscillations, the amount of carbon emission prevention, and interruption of transmission/distribution systems []. Therefore, many researchers have developed different optimization algorithms to find the best possible result from the traditional EES system considering low cost, high lifetime, reliability, and lower environmental impact.
Energy storage technologies are classified into five categories: mechanical, electromechanical, electrical, chemical, and thermal energy storage technologies. In this study, batteries, which are chemical storage technology, are discussed []. The oldest chemical energy storage technology is lead-acid battery technology. The lifespan and efficiency of lead-acid batteries are moderate compared to other batteries. It also has a low energy-to-weight ratio and energy-to-volume ratio. The most important advantage is that it has a high power-to-weight ratio, so it can provide a high ripple current []. The most widely used chemical energy storage technology is lithium-ion battery technology. There are many different types of lithium-ion batteries, such as lithium cobalt oxide (LiCoO2), lithium iron phosphate (LiFePO4), lithium-ion manganese oxide batteries (Li2MnO4, Li2MnO3, LMO), and lithium nickel manganese cobalt oxide (LiNiMnCoO2). Lithium-ion batteries have advantages such as portability, high energy density, and fast response time, as well as disadvantages such as capacity degradation over time and high cost [].
Wen et al. (2013), a hybrid multi-objective particle swarm optimization (HMOPSO) approach was developed to minimize power system costs and improve voltage profiles by investigating the sizing of storage units in wind turbines, considering the uncertainties in energy generation []. However, in the study, only the power system cost is considered, without considering the effect of battery energy storage systems’ (BESS’) integration on network power losses. Zhang et al. (2018), a multi-stage hybrid energy storage (ESS) system is proposed without analyzing the effect of the ESS on network power losses and voltage fluctuations and considering only the market profit and stabilizing effect of the ESS without considering the SOC model of the ESS []. Shi et al. (2020), a hierarchical optimization algorithm is proposed to simultaneously optimize the capacity of the equipment in a distributed power generation (DG) plant consisting of a wind turbine, PV system, and an ESS []. A golden section Fibonacci tree optimization (GSFTO) is used to increase efficiency and solution accuracy in the model, which aims to maximize the generation of DGs. Yan et al. (2020), the energy management and control methods of a large-scale ESS were analyzed []. The operating cost model of the ESS was developed by considering its life-cycle operating characteristics. Lu at al. (2009), an approach using ESSs is proposed to make wind power generation systems more reliable, both in terms of energy and capacity []. In the study, no optimization method was used to configure the ESS. Çakmak et al. (2024), which analyses the relationship between ESS allocation capacity and load fluctuations mitigation, an optimal capacity allocation method is proposed to minimize the overhead regulation problem of large-scale ESSs []. However, SOC for ESSs was not considered in this study. Schimpe et al. (2018), the energy performance of a lithium-ion battery system was determined during the process of storing surplus energy in a photovoltaic power plant []. Xu et al. (2018), proposed an optimal control and bidding policy for battery participation in frequency regulation markets, considering the cost of battery aging in operating strategies to increase market profits []. Sorourifar et al. (2024), a multi-scale linear programming formulation is proposed to evaluate storage system degradation for both energy and ancillary services in the day-ahead and real-time market []. Since the energy efficiency of a PV plant with an ESS is directly related to the income earned, the operating period of the plant needs to be optimized. This optimization will both increase the economic gain and positively affect the lifetime of the battery because the lifetime of batteries is determined by the number of charges and discharges. However, apart from these, the lifetime of the battery also depends on the ambient temperature, depth of charge, duration of shifting cycles, and power level []. For this reason, it should be ensured that batteries are not deeply charged.
The economic analysis results of a power plant are affected by material costs, labor costs, maintenance costs, the load profile of the power plant, electricity price tariffs, loan interest, inflation, and local support policies. Therefore, there are different economic results for PV + ESS in the literature. In addition, since PV and battery prices generally tend to decrease, projects that were not attractive in previous years may become attractive today. For example, in studies conducted in England and Australia in 2017, it was stated that PV + ESS systems were not attractive [,]. On the other hand, in studies published between 2016 and 2020, where battery costs were between EUR 138–400/kWh, it is stated that the use of a PV + ESS system in commercial buildings in Belgium and Germany may be attractive [,,,,]. A detailed financial feasibility analysis is of critical importance in long-term PV + ESS generation facility investments, as in all investment decisions. The most common and reliable method for making an investment decision is cost–benefit analysis []. Various metrics such as the levelized cost of energy (LCOE) [], net present value (NPV) [], and payback period are used to determine the economic benefits of an investment plan. These metrics can help investors decide whether an investment plan for a PV + ESS plant is worthwhile. The intermittency of PV systems can lead to imbalances in the electricity grid. To mitigate this issue, integrating energy storage systems has become increasingly important []. Peak shaving, load shifting, and valley filling strategies enhance the economic feasibility of PV-ESS systems while improving grid stability []. Large-scale BESS play a crucial role in balancing the electricity demand curve and increasing energy supply security. Studies have shown that grid losses can be reduced by 10%, and total operating costs can decrease by up to 12% through peak load reduction strategies []. In a study conducted in China, integrating demand response (DR) mechanisms with battery energy storage systems was found to increase household self-consumption rates (SCR) to 30.6% and self-sufficiency rates (SSR) to 48.9% []. BESS systems also offer significant potential for energy arbitrage and frequency regulation services (FCR). A study in Germany found that optimizing a PV-BESS system for energy arbitrage and FCR services over a 25-year period provided an economically sustainable model by increasing the NPV []. Similarly, a 100 MW capacity BESS system was shown to stabilize grid frequency deviations to 0.1 Hz and reduce energy losses by 5% []. The implementation of ESS systems has the potential to lower electricity consumption costs for commercial and industrial consumers. Rocha et al. (2023), demonstrated that active battery modules could increase the system’s lifespan and stored energy capacity by more than 50% []. The same study also found that daily energy release increased by 7%, and battery usage time was extended by 51.3%. Other commercial-scale studies have shown that BESS applications, when integrated with demand-side management, significantly lower electricity bills and enhance grid reliability []. A study conducted in a residential area in South Africa revealed that a 10 kWh lead-acid battery system could reduce peak loads by 50% []. However, the economic viability of BESS largely depends on tariff structures, energy price fluctuations, and investment costs. Research has shown that the economic profitability of BESS is influenced not only by energy storage capacity but also by demand-side management strategies and local tariff policies []. In the United Kingdom, as incentives for PV systems declined, the NPV of PV systems dropped from GBP 28,650 in 2011 to GBP 1200 in 2017, but this value could be increased by 46% through ESS integration []. Furthermore, economic modeling indicates that BESS implementation can reduce energy costs in the long term, optimizing the investment payback period (PBP) between 5 and 8 years [,].
1.1. Limitation of Previous Studies
It has been seen from the detailed literature review that there are still limitations or gaps in the techno-economic analysis of the PV + ESS systems. These gaps in the literature are listed below.
- 1
- Some of the studies in the literature analyze system performance based on static meteorological data, fixed load profiles, and energy production values derived from various databases. However, static meteorological data and fixed load profiles fail to capture the dynamic variations in PV system performance, while reliance on generalized database values reduces modeling accuracy by neglecting regional differences. In addition, neglecting sudden production and load changes causes deviations in technical and economic analyses, while studies based on historical data instead of measured field data reduce the reliability of system design.
- 2
- Some studies overlook the annual degradation of PV system performance and battery storage losses, leading to incomplete or inaccurate assessments of system efficiency. This omission results in misleading conclusions in both economic feasibility analyses and system optimization efforts.
- 3
- Some studies focus only on the simple payback period in the economic analysis of PV + ESS systems and ignore critical economic parameters such as interest rate, inflation rate and discount rate. The exclusion of these time-dependent cost and revenue factors prevents an accurate evaluation of long-term financial sustainability.
- 4
- Many studies in the literature are based on fixed rules and traditional optimization methods in the energy management of PV + ESS systems. However, these approaches cannot adequately adapt to the time-varying conditions of the system and ignore dynamic decision-making processes. In particular, ignoring fluctuations in electricity prices, demand variations, and real-time operational conditions prevents a comprehensive assessment of the system’s economic and technical efficiency.
1.2. Aims and Main Contributions
The main purpose of this article is to determine the optimum ESS capacity by analyzing the electrical performance of a PV power plant and the demand energy of the load and to make an economic analysis of the system in line with the measured data. For this purpose, meteorological data such as radiation and temperature were acquired every 5 min for a year. Electrical performance analysis was performed using these real data for each hour. The hourly demand energy of the load was provided through the automatic meter reading system. To determine the optimum ESS capacity, the amounts of energy transferred from the grid to the load, from PV to the load, and from PV to the grid were analyzed on an hourly basis. In addition, grid-to-load and PV-to-load energy price tariffs were taken into consideration when determining the optimum capacity of the ESS. The innovative aspect of this study is not only the separate consideration of gaps in literature but also the comprehensive and dynamic approach to techno-economic analysis. Many studies in the literature perform analyses using static load profiles and general meteorological data. However, in this study, real-time measurement data for PV production, load demand, and meteorological conditions were used. In addition, economic parameters such as real-time electricity price tariffs and self-sufficiency rates were integrated into the optimization process and evaluated. It is very rare to see these parameters considered together in similar studies in the literature. In existing studies, energy management for photovoltaic and storage systems is typically handled using predefined static rules, fixed threshold values, or conventional optimization methods. However, these approaches often struggle to adapt to fluctuations in grid conditions, varying load profiles, and dynamic electricity prices. The algorithm proposed in this study introduces an innovative framework that optimizes energy flow and decision-making dynamically.
The battery capacity that is most suitable for PV capacity was determined under electricity price tariffs, time of use, and feed-in tariffs using technical indicators such as the self-sufficiency rate, self-consumption rate, and economic indicators such as LCOE, NPV, and PBP. The structure of the article is as follows: first, a detailed literature review was conducted, and related papers were presented in the introduction by the subject compliance and the date of presentation. We organized the rest of this paper in the following way. The experimental setup and method are described in Section 2. The results are provided in Section 3, and the conclusion is in Section 4.
2. Experimental Setup and Proposed Method
In this study, sizing and techno-economic analysis of utility-size PV systems with battery energy storage in commercial buildings according to Gerede/Bolu meteorological conditions were used. Gerede is located at a longitude of 32.70 E, a latitude of 40.8 N, and an altitude of 1350 m. A total of 1418 panels with a power of 455 Wp and 5 inverters with a power of 110 kW were used in the PV system. The PV system was connected to the electricity grid on 1 January 2023. The PV panels were placed on both the south and north facades following the building roof slope. The tilt angle of the panels was approximately 8 degrees, and the azimuth angle was roughly 25 degrees. In Figure 1, the photograph of the PV system installed on the roof of the commercial building is provided.

Figure 1.
Experimental setup and installed 645 kWp PV system in Gerede/Bolu, Türkiye.
Each inverter used in the power plant was connected to 16 PV arrays. Each PV array had 18 PV panels connected in series. However, some arrays had 17 PV panels. Solar cables of 290 m from the farthest string to the inverter and 130 m from the nearest string to the inverter were used. The design was developed so that the voltage drop in the cables would be a maximum of 1.5%. The voltage drop on the line with the longest distance was calculated as 1.45%. The single-line diagram of the PV plant with an Energy Storage System is shown in Figure 2.
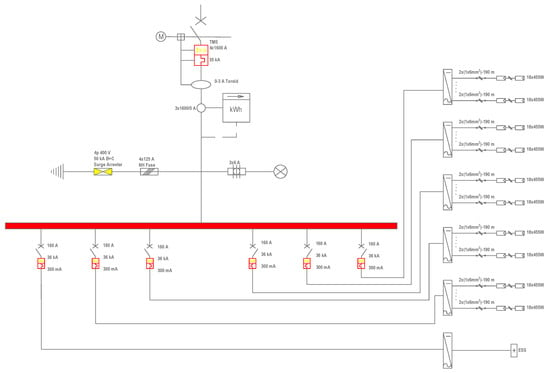
Figure 2.
Single-line diagram of the power plant.
The power of the PV panel is especially affected by irradiation and temperature. The output power of a panel is directly proportional to radiation and inversely proportional to temperature. Therefore, the panel inclination angle, which affects the amount of radiation falling on the panel surface, and the distance of the panel to the roof, which affects the panel cell temperature, are two important factors. Seraphim SRP-455-BMA-HV panels were used in this study. The specifications of the panels are shown in Table 1.

Table 1.
Specification of the PV panel.
The total energy demand of the factory where this study was carried out in 2023 was 1,163,456 kWh. The PV power plant started producing energy on 1 January 2023. Electrical quantities such as produced energy, current, voltage, and power, as well as meteorological data such as radiation and temperature, were continuously recorded. Monthly demand and produced energy are shown in Figure 3.
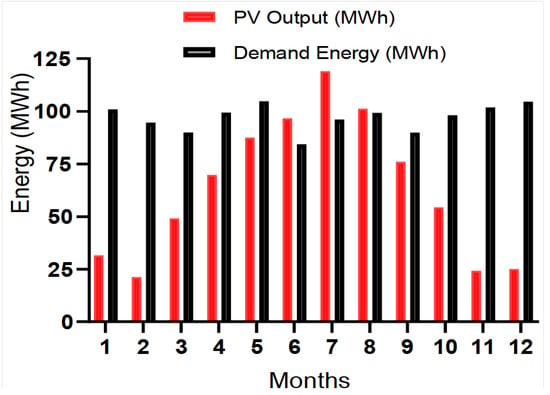
Figure 3.
Demand and generated energy.
The PV power plant produced a total of 755,518 kWh of energy between 1 January 2023 and 1 January 2024. Accordingly, approximately 64.9% of the annual energy demand was produced by the PV plant. In particular, in the winter months, the rate of meeting the demand for energy from the produced energy was very low. However, the energy produced during the summer months was higher than the energy demanded. Therefore, there is a need for an energy storage system in both winter and summer months.
The meteorological data were collected from the real-time remote reading system. The amount of energy that the PV system will produce largely depends on solar irradiation and PV cell temperature. Therefore, irradiation, cell temperature, and ambient temperature data are measured in the PV system. In this study, irradiation measurements were performed using a monocrystalline silicon (mono-Si) reference cell made of the same material as the PV modules used in the power plant. In order to ensure the accuracy of the measurements, the reference cell was calibrated in accordance with IEC 60904-2 standards []. The reference cell was placed at the same inclination angle and orientation as the PV panels. This arrangement minimizes measurement deviations that may arise from angular differences, ensuring reliable irradiation data are collected. In the PV system, meteorological and electrical data were measured at 5-min intervals. The reference cell was used for irradiation measurement, and the PT1000 (resistance) temperature sensor was used for panel cell temperature measurement. Since the roof of the commercial building is inclined in two different directions, a reference cell and a temperature sensor were used for each inclined surface. Electrical quantities of PV panels, such as current, voltage, power, and energy, were measured with the data logger with a remote monitoring feature that communicated with the inverter.
2.1. Battery Sizing and Modeling
Many different optimization algorithms have been developed for sizing ESSs, taking into account various factors such as aging, cost, propulsion strategies, durability, and carbon emissions. The main goal in business enterprises is to optimize financial return in the form of bill savings, revenue generation, or a combination of the two. There are periods during which the energy demand of the building is higher than the maximum average daily demand of the building at certain times during the day. The battery that can best meet this peak demand and the maximum demand difference can be determined as the most appropriate EES size []. The capacity of ESSs is determined following the regulations published by the Republic of Türkiye Energy Market Regulatory Authority. However, to optimize the capacity of the ESS, an objective function for the ESS capacity selection has been established for minimum network power losses and voltage fluctuations. Also, the period in which the ESS will be charged is determined by the optimization technique depending on the amount of energy produced by the PV system. Since ESSs are not currently established in this commercial enterprise, an ESS model was created to analyze the effect of ESS in this study.In this study, MATLAB [] was utilized for the mathematical optimization of the ESS. The optimization algorithm considered factors such as load demand, energy costs, and the state of charge (SOC) of the battery system. The constraints and objective functions were formulated and solved within the MATLAB environment (this study utilized MATLAB software under the academic campus license provided by Manisa Celal Bayar University). The capacity and charge/discharge efficiency of the ESS are important technical parameters. The SOC, defined as the ratio of current energy level to rated full capacity, is commonly used to model batteries []. The SOC is obtained by Equation (1).
where and are the charging and discharging power of the ESS (kW), and are the charging and discharging efficiency of the ESS, is the battery capacity (kWh), and is the time step and was set to 1 h. The reason for selecting a 1-hour time step is that the irradiance, temperature, and PV power data used in the analysis were collected on an hourly basis. Using a time step consistent with the resolution of the input data ensures the accuracy of the simulation and prevents unnecessary interpolation, which could introduce errors. Additionally, an hourly resolution is commonly employed in energy management studies to balance computational efficiency and data availability.
Energy flow during battery charging and discharging is obtained by Equations (2) and (3), respectively [].
where is the battery energy level, is the energy generated by PV, is the load demand during a time interval t, and is the inverter efficiency. Since overcharging and deep charging of the battery affects the battery life negatively, the maximum energy level of the battery is determined as small and equal to the maximum battery energy level, and the minimum energy level is determined as 20% of the maximum battery level.
Lithium-ion phosphate batteries (LIPB) batteries are preferred in this study because they have features such as a high energy density, high nominal power, long cycle life, long discharge time, and high conversion efficiency []. The characteristic parameters of the battery used in this study are listed in Table 2.

Table 2.
The characteristic parameters of lithium-ion batteries [].
Integration of ESS into the PV system consists of the stages of data input, parameter processing, and optimization of the ESS. In the first stage, the energy generation values of the PV power plant and the demand energy values are processed. In the second stage, the operating situation of the power plant is simulated, and the operating strategy of the ESS is created, taking into account the technical characteristics of the batteries and the electricity price tariff. The ESS planning and solving process is illustrated in Figure 4.
Figure 4.
The ESS planning flow chart.
The primary purpose of integrating an ESS is to enhance self-consumption within the PV-battery system while ensuring energy continuity and maximizing economic benefits. Four strategies were used throughout the analyzed period to manage energy flows between PV, ESS, grid, and loads.
- Strategy 1: Transferring the energy from the PV to loads and batteries and transferring the remaining energy to the grid.
- Strategy 2: It is an economical operating mode in which batteries are charged at low grid electricity costs and discharged when higher electricity prices occur.
- Strategy 3: This is the operating mode that aims to reduce peak demand and thus prevent voltage and frequency fluctuations in the electrical network.
- Strategy 4: This is the operating mode in which a fixed charge/discharge rate is used based on the current state of charge of the batteries and historical PV generation and load consumption values.
In line with the explanations above, the optimum ESS capacity was determined to be 130 kW with a 5-hour duration. This selection was based on a balance between energy demand, the PV production profile, and economic viability. The capacity was determined through an optimization process aimed at maximizing the own consumption of PV-generated energy while minimizing the dependency on grid electricity.
Achieving energy balance is the main goal in planning any energy generation–consumption system. In addition, economic benefits must be kept at an optimum level while ensuring energy balance. Therefore, the cost function is also used in the objective function when managing the energy flow. The purpose of a cost function is to keep the energy unit cost of the energy generation system at a minimum level when it is costly to use energy from the grid. Grid energy is used to ensure energy continuity of loads when the energy of the PV + ESS system is insufficient or when the cost of drawing energy from the grid is cheap. The objective function is to ensure energy balance by considering the power transfer to the grid, SOC, and the constraints on the capacity of the PV plant and the ESS. Objective functions and constraints are provided in Equations (4)–(6).
where is the PV energy generation (kWh), is the battery discharge energy (kWh), is the energy transferred to the grid from PV + ESS (kWh), is the load demand energy (kWh), is the battery charge energy (kWh), is the energy transferred to the load from the grid (kWh), is the maximum discharge power of the ESS, is the minimum charge stage of the ESS, and is the maximum charge stage of the ESS. The proposed method’s flow chart is shown in Figure 5. The proposed algorithm evaluates the SOC, energy consumption, energy generation, irradiance, etc., and operates the rooftop PV system with ESS support considering the introduced scenarios in this study.
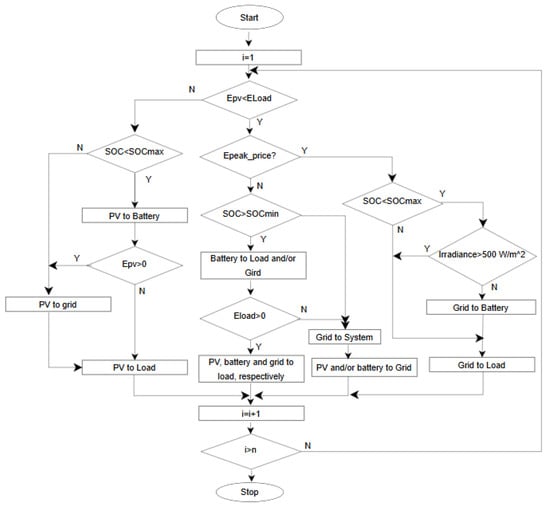
Figure 5.
The proposed algorithm for ESS support for a rooftop PV system.
Energy management begins with the evaluation of environmental and electrical inputs. The power generated by the PV system is calculated using real-time irradiance and temperature data and is evaluated together with the electricity consumption profile of the factory. At this point, one of the basic decision variables determining the energy management strategy is the radiation level, as the power output of PV panels is directly related to it. Although panels can produce power at low irradiance, the amount of power produced increases rapidly as irradiance increases. In this study, the threshold irradiance value was selected as 500 W/m2. When irradiance exceeds this level, The power generated by PV panels can be transferred to the grid. At lower irradiance levels, it is more appropriate to store the energy produced by panels in batteries or use it for internal consumption. In other words, since PV production below this threshold value is generally insufficient to meet the load demand, the missing energy is provided by the battery or the grid. If the irradiance level exceeds this threshold value, PV production not only fulfills load consumption but also begins charging the battery. When the battery is full, and the instantaneous production still exceeds the demand, and the excess energy is transferred to the grid. In this process, the energy flow is managed dynamically depending on the battery’s state of charge (SOC). When the maximum SOC limit is reached to prevent the battery from being overcharged, the battery stops charging and the excess energy is directly transmitted to the grid. Similarly, a minimum SOC limit is determined to prevent overcharging, and when this level is below, the battery is restricted from supplying power to the load. The model also incorporates economic optimization by considering time-dependent fluctuations in electricity prices. At certain times of the day, when the cost of electricity purchased from the grid is low, the battery can be charged from the grid to minimize the high-priced grid use in the following hours. On the other hand, during hours when electricity prices are high, the battery can be discharged to feed the load and reduce the electricity drawn from the grid. This approach is integrated with demand-side management strategies.
2.2. Technical Indicators
The self-consumption rate (SCR) and energy self-sufficiency rate (SSR) are widely used technical indicators that form the basis of an energy community. The SSR shows the proportion of electricity demand met by self-generated electricity. The SSR indicates the proportion of self-generated electricity used to meet electricity demands. SCR and SSR are calculated using Equations (7) and (8) [].
where is the amount of energy produced in PV transferred to the loads (kWh), is the energy which is injected into the battery from PV (kWh), is the total PV generation (kWh), is the load covered by battery discharge (kWh), and is the total load demand (kWh).
2.3. Economic Indicators
2.3.1. Levelized Cost of Energy
LCOE is a metric used to measure the lifetime cost of energy generation by a given system. The LCOE considers system-related costs, including installation, operation, maintenance, and fuel. Therefore, it is used to quickly compare the economic value and viability of systems before investing. The LCOE is calculated by dividing the present value of all costs associated with producing 1 kWh of electricity by a given system by the total number of kilowatt hours produced over the life of the system. One of the important considerations when calculating the LCOE is the determination of the discount rate. The discount rate depends on the cost of capital and the assessment of financial risk, including the balance between debt financing and equity financing. Generally, LCOEs are calculated over 20-to-40-year lifetimes and are provided in currency units per kilowatt hour. It is important to note that the LCOE, used for investment planning and consistent comparison of different electricity generation methods, as a single figure does not provide a complete picture of everything that influences the investment decision []. The LCOE is calculated by Equation (9).
where is the investment expenditures in year t (including financing), is the operations and maintenance expenditures in year t, is the fuel expenditures in year t, is the electricity generation in year t, r is the discount rate, and n is the life of the system.
2.3.2. Net Present Value
NPV is an important metric used to determine whether a project is profitable. NPV is the discounted value of all future cash flows (positive and negative) over the entire life of an investment. NPV usually considers the interest rate equal to the inflation rate; therefore, the true value of money is considered in each operating year. Also, factors such as opportunity cost, inflation, and risk are all factored into the NPV to determine the overall present value of the project. Thus, the NPV method converts future payments to present values and makes them comparable. The most important advantage of NPV is that it considers the time value of money and converts future cash flows to present value. Cash flows need to be discounted because of the concept of the time value of money. To calculate the NPV correctly, the discount rate must be determined correctly. In most cases, the discount rate can be expressed as the company’s weighted average cost of capital and includes the company’s interest rate, loan payments, and dividend payments. A positive NPV indicates that projected earnings exceed expected costs, and the investment will likely be profitable []. On the other hand, a negative NPV indicates that the investment is likely to result in a loss. NPV can be expressed mathematically by Equation (10).
where is the net cash inflow-outflow during a single period t, t is the number of periods, and r is the discount rate.
2.4. System Cost
The total cost of the 645 kWp PV plant installed in December 2022 was USD 410,000, as directly documented by the Engineering Procurement Construction (EPC) company responsible for the installation.In the literature, the general capital cost of a battery system is expressed as approximately USD 1200/kWh []. Unit electricity prices in Türkiye are determined by the Energy Market Regulatory Authority (EMRA). In September 2023, the electricity unit price tariff for industrial subscribers was determined as TRY 2.925/kWh from grid to load (USD 0.108/kWh, USD 1 = TRY 26.95 (Turkish Lira)) and TRY 2.507/kWh from PV to grid (USD 0.093/kWh, USD 1 = TRY 26.95). The invoiced net energy price is calculated by adding the distribution cost, energy fund price, and energy consumption tax to the unit energy price. Therefore, the electricity unit price for industrial subscribers has been determined as USD 0.12/kWh and USD 0.139/kWh from PV to grid and from grid to load, respectively []. The renewable energy loan interest rate in Türkiye is approximately 10%. According to the data of the Turkish Statistical Institute, when the annual percentage change in the price index between the years 2005–2023 is considered, the annual average interest rate is 14.9% []. The O&M cost of the PV system may vary depending on agreements and country to country. It has been stated in the literature that the operation and maintenance cost of these systems is around 1% of the total cost of the project []. When calculating the electrical energy produced by the PV system, annual efficiency loss should also be considered. Due to the aging of materials, PV panels lose their efficiency every year compared to the previous year. This value is stated as 0.07% per year in the manufacturer’s catalogs. In this study, the determined key input parameters are provided in Table 3.

Table 3.
Key parameters for the economic analysis.
3. Results and Discussions
The PV system generated the lowest energy in November, 24,242 kWh, the highest in July, 119,047 kWh, and a total of 755,518 kWh in 2024. Figure 6 shows the monthly output energy and irradiation in the panel plane.
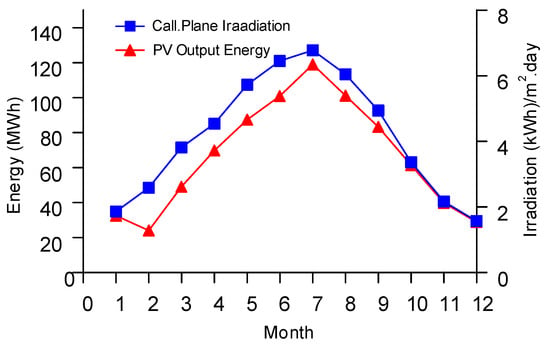
Figure 6.
PV output energy and in-plane irradiation.
The output energy of a PV plant is directly related to irradiation and temperature. The relationship between irradiation, temperature, and the energy produced is used to determine the performance ratio of the PV plant. The performance ratio is desired to be 80% and above. Figure 7 shows the irradiance, temperature, and PV energy for a typical sunny day on 10 July 2024. In the months of measurement, the irradiation was measured to be a maximum of 1128 W/m2, and the PV cell temperature was measured to be a maximum of 67 °C. Between 1 January 2023 and 1 January 2024 the amount of energy transferred from the grid to the load, from PV to the grid, from PV to the load, and the PV output power were recorded and analyzed hourly. Figure 8 shows the monthly energy transfer between the grid, PV, and load.
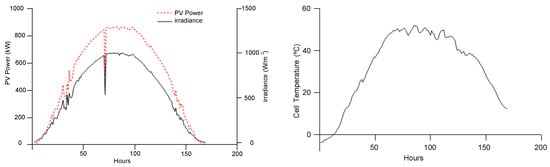
Figure 7.
In-plane irradiation, ambient temperature, and panel temperature.
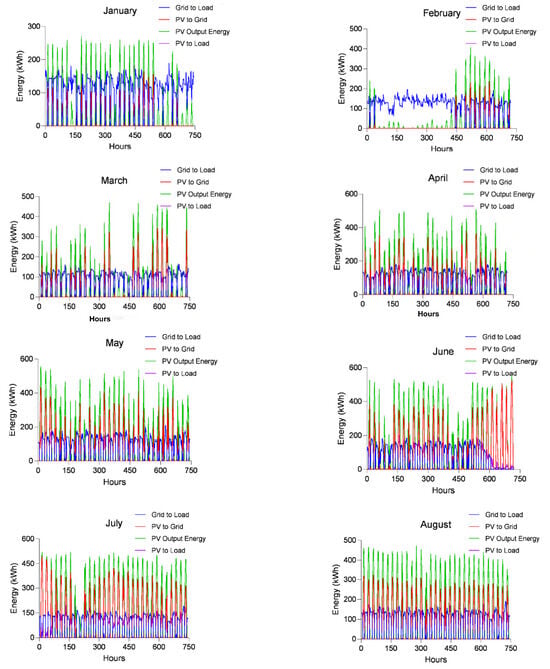
Figure 8.
The energy transfer between grid, PV, and load.
Due to the snow falling on the 3rd of February, the PV panels remained under the snow for approximately 14 days. Therefore, there was no energy transfer from PV to the grid in this process. Despite this, 6832 kWh of energy was transferred from PV to the grid in February. Table 4 shows the monthly amounts of energy transferred to the grid.

Table 4.
Transferred energy from the PV to the grid.
Figure 9 shows the analysis of daily energy transfer on the 2nd of August and 2nd of February. On the 2nd of February, 2964 kWh energy were transferred from the grid to the load, 165 kWh from the PV to the grid, and 718 kWh from the PV to the load. The total consumption of the load was 3682 kWh, and the generation of PV was 884 kWh. Even if the energy produced by PV during the day met approximately 24% of the load’s needs, if the 165-kWh energy transferred to the grid between 11:00 and 15:00 was stored in batteries, both technical and economic benefits would have been provided. On this example day, when the PV output power is at a minimum level during the year, the batteries can be fully charged instead of transferring energy from PV to the loads. Moreover, after the batteries are fully charged, the remaining energy can be transferred to the loads.
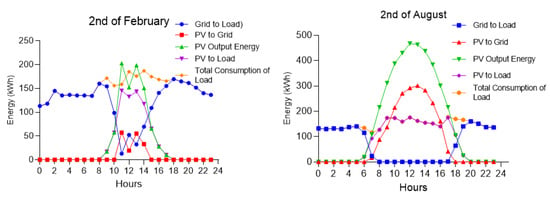
Figure 9.
The analysis of daily energy transfer on the 2nd of August and 2nd of February.
On the 2nd of August, 1734 kWh of energy were transferred from the grid to the load, 2038 kWh from the PV to the grid, and 1837 kWh from the PV to the load. The total consumption of the load was 3571 kWh, and the generation of PV was 3875 kWh. The energy produced by PV during this day met the entire need of the load. There was no energy transfer from the grid to the load between 08:00 and 17:00. During the year, on this example day, when the PV output power is at its maximum level, the batteries could be charged and discharged five times. Therefore, the technical and economic benefits of the battery PV system are much more evident in the summer months.
SOC is a measurement of the amount of energy available in a battery at a given time, expressed as a percentage. Batteries are charged when PV power exceeds load demand during the day. While energy is transferred from PV to batteries, the SOC value of the batteries increases. When the demand for the load is higher than the PV power, the SOC value decreases as the batteries must provide the difference between demand and generation. The SOC value is low, especially at night and on days when radiation is low. To maximize the economic benefit, batteries meet the energy needs of the load not only at night but also during the day. The SOC of batteries can constantly change during the day depending on meteorological conditions and load demand. The monthly SOC values of the batteries are shown in Figure 10.
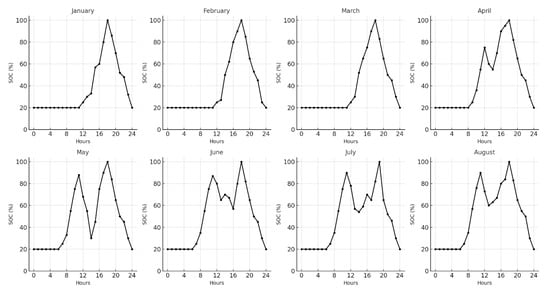
Figure 10.
Hourly average SOC (%).
In this study, the minimum SOC value of the batteries was determined to be 20%. To prevent deep discharge of batteries and to ensure longer battery life, the battery is prevented from discharging when the SCO reaches 20%. During the winter months, due to the short day length and the high number of cloudy days, the number of charge–discharge cycles of the batteries is much lower than in the summer months. While batteries can be charged only once a day in winter, they can be charged and discharged 3–4 times in summer. The annual average SOC value of batteries was determined as 63.4%. The amount of energy entering the battery in the first year was determined as 461,357 kWh/year, and the amount of energy used from the battery was 403,568 kWh/year.
The energy need of the load is met by the grid, PV, or ESS. The monthly average energy amounts transferred to the load from different sources are shown in Figure 11. The highest energy transfer from PV to load was approximately 80,000 kWh in July and August, and the lowest energy transfer was approximately 7500 kWh in January, February, and December. In proportional terms, the PV supply is lower than the battery supply. The reason for this is that energy is transferred from PV to both the load, the batteries, and the grid during the day. The monthly average efficiency of the ESS system was calculated as 83.6%.
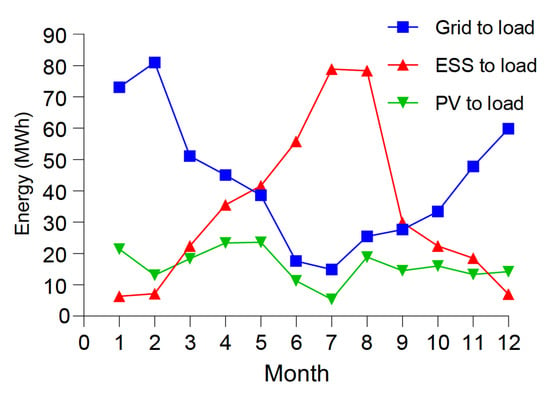
Figure 11.
Monthly energy is transferred to the load from sources.
The energy generated by the PV power plant is distributed as follows: 24.25% to the load, 50.6% to the energy storage system (ESS), and 25.14% to the grid.
The first-year operating earnings of the PV + ESS system are shown in Table 5. Taking into account that the energy produced in PV panels will decrease by 0.07% every year and that the batteries will experience a storage loss of 0.01% each year compared to the previous year due to aging, it is predicted that PV + ESS will operate for 25 years, and the batteries will be replaced after 15 years.

Table 5.
Annual benefits.
According to the price tariffs applied in Türkiye, the benefit obtained from energy transferred from PV to the grid accounts for 24.22% of the annual total revenue, the benefit obtained from energy transferred from PV to the load represents 27.05% of the annual revenue, and the benefit obtained from energy transferred from the ESS to the grid constitutes 48.73% of the annual total revenue. Since the income from transferring energy from PV to the grid is lower than the income from transferring energy from PV to the load, the aim is to transfer the energy produced in PV to the loads and ESS as much as possible. For similar reasons, it aims to transfer the energy stored in the ESS to the grid during hours when energy prices are as high as possible during the year. It is seen that the economic performance is acceptable for the market, where LCOE is calculated at USD 0.1467/kWh while NPV and PP are, respectively, estimated at USD 4918.3 and 7.03 years.
Figure 12 shows the cumulative NPV curve over time in order to evaluate the economic performance of the project. The curve starts with a negative value due to the initial capital investment and increases due to the revenues obtained from energy production as the system becomes operational. In year 7.3, the NPV becomes zero. Therefore, this point represents the payback period (PBP) of the investment. In year 15, a significant decrease is observed in the curve. This decrease can be attributed to additional costs arising from planned maintenance or equipment replacements, such as the replacement of the BESS. Then, the NPV curve enters an upward trend again, revealing the long-term profitability and sustainability of the project. This situation shows that the project has been economically advantageous throughout its life and has provided a positive return for investors.
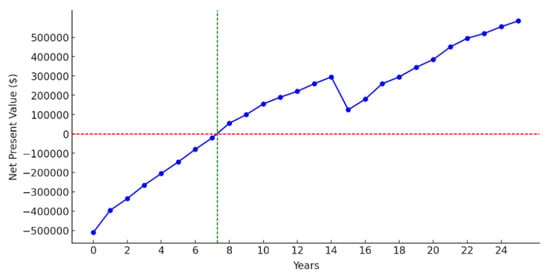
Figure 12.
Cumulative NPV trend over the project’s lifetime.
Our proposed method was developed to optimize the economic and operational performance of PV + ESS systems. Various studies have been conducted in the literature on PV + ESS integration, some of which are based on static energy management strategies, fixed pricing models, and traditional battery usage policies. Most of these studies do not adequately address real-time price fluctuations and dynamic load management. The model developed in this study aims to increase economic and operational sustainability using dynamic decision mechanisms and optimization techniques. The main differences and advantages of the proposed method compared to similar studies in the literature are summarized in Table 6.

Table 6.
Comparison of this study with existing studies.
4. Conclusions
Renewable energy plays a crucial role in mitigating environmental issues associated with energy production. In recent years, the number of PV systems has been rapidly increasing. However, the biggest disadvantage of PV systems is that they are intermittent energy sources. For this reason, various problems are encountered in energy transmission lines and power systems. Depending on these problems, various capacity restrictions are applied for the connections of PV plants to transmission/distribution line transformers. The most effective way to overcome the capacity problems caused by grid-connected PV plants and to reduce the effects of these problems is to use battery systems. In this study, PV + ESS system sizing was carried out for a commercial building located in the Bolu province of Turkey. Data such as the hourly electricity consumption of the building, grid-to-load energy price tariff, system-to-grid energy tariff, solar radiation, and ambient temperature were analyzed in detail. In line with various target functions, the system was optimized under load consumption, ESS, and PV cost scenarios. Evaluation indicators were considered from various aspects, such as SCR, SSR, LCOE, NPV, and PBP. The objectives, methods, tariffs, and effects of time analysis for optimizing PV + ESS system capacity were summarized. The proposed model provides a sustainable, economical, and environmentally friendly solution to reduce the negative impacts of PV systems on the grid. The results show that a significant amount of clean energy can be produced and stored with an LCOE of USD 0.1467/kWh and an NPV of USD 4918.3 in the first year of operation. In addition, the annual efficiency of the ESS was calculated as 83.6%, the total energy input to the battery was determined as 461,357 kWh/year, and the energy used from the battery was determined as 403,568 kWh/year. The distribution of the energy generated from the PV system was as follows: 24.25% was used to feed the load, 50.6% was directed to the ESS, and 25.14% was used to be sold to the grid. These results show that the optimized ESS sizing is effective in increasing self-consumption and minimizing grid dependency. This study provides significant contributions to the literature on the optimization of PV + ESS systems. While battery capacity was generally determined over fixed load profiles in previous studies, system performance was improved in this study using real-time measurement data and dynamic optimization methods. The results obtained reveal that the battery optimization method used provides advantages in terms of economic gain and increases energy independence. The developed methodology can be applied to energy systems with different climate conditions and grid structures. In the future, a more comprehensive analysis can be made by considering different load profiles, battery technologies, and energy price variables.
Author Contributions
Conceptualization, M.T.Ö. and G.B.; Methodology, K.B., M.T.Ö. and G.B.; Software, K.B., M.T.Ö. and G.B.; Validation, K.B., M.T.Ö. and G.B.; Formal analysis, K.B., M.T.Ö. and G.B.; Investigation, K.B., M.T.Ö. and G.B.; Resources, K.B., M.T.Ö. and G.B.; Data curation, K.B., M.T.Ö. and G.B.; Writing—original draft, K.B., M.T.Ö. and G.B.; Writing—review & editing, K.B., M.T.Ö. and G.B.; Visualization, K.B., M.T.Ö. and G.B.; Supervision, K.B.; Project administration, K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by Fırat University with FUBAP-MF.24.125. And this study was supported by the Scientific Research Projects Coordination Unit of Fırat University. Project number MF.24.125.
Data Availability Statement
Data is contained within the article. Additional data supporting the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
Authors thank to the support by Fırat University with FUBAP-MF.24.125.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bayrak, G.; Cebeci, M. Grid connected fuel cell and PV hybrid power generating system design with Matlab Simulink. Int. J. Hydrogen Energy 2014, 39, 8803–8812. [Google Scholar]
- Doğan, S.; Haydaroğlu, C.; Gümüş, B.; Mohammadzadeh, A. Innovative fuzzy logic type 3 controller for transient and maximum power point tracking in hydrogen fuel cells. Int. J. Hydrogen Energy 2024, in press. [Google Scholar]
- Haydaroğlu, C.; Yıldırım, B.; Kılıç, H.; Özdemir, M.T. The Effect of Local and Interarea Oscillations of Wind Turbine Generators Based on Permanent Magnet Synchronous Generators Connected to a Power System. Turk. J. Electr. Power Energy Syst. 2025, 5, 41–53. [Google Scholar] [CrossRef]
- Haydaroğlu, C.; Kılıç, H.; Gümüş, B. Performance analysis and comparison of performance ratio of solar power plant. Turk. J. Electr. Power Energy Syst. 2024, 4, 190–199. [Google Scholar] [CrossRef]
- Gümüs, B.; Kılıç, H.; Haydaroglu, C.; Butakın, U.Y. Fault type and fault location detection in transmission lines with 6-convolutional layered CNN. Bull. Pol. Acad. Sci. Tech. Sci. 2024, 72, e151047. [Google Scholar] [CrossRef]
- Haydaroğlu, C.; Gümüş, B. Fault Detection in Distribution Network with the Cauchy-M Estimate—RVFLN Method. Energies 2022, 16, 252. [Google Scholar] [CrossRef]
- Rouholamini, M.; Wang, C.; Nehrir, H.; Hu, X.; Hu, Z.; Aki, H.; Zhao, B.; Miao, Z.; Strunz, K. A review of modeling, management, and applications of grid-connected Li-ion battery storage systems. IEEE Trans. Smart Grid 2022, 13, 4505–4524. [Google Scholar]
- Yılmaz, A.; Bayrak, G. A new signal processing-based islanding detection method using pyramidal algorithm with undecimated wavelet transform for distributed generators of hydrogen energy. Int. J. Hydrogen Energy 2022, 47, 19821–19836. [Google Scholar] [CrossRef]
- Das, C.K.; Mahmoud, T.S.; Bass, O.; Muyeen, S.; Kothapalli, G.; Baniasadi, A.; Mousavi, N. Optimal sizing of a utility-scale energy storage system in transmission networks to improve frequency response. J. Energy Storage 2020, 29, 101315. [Google Scholar]
- Rauf, H.; Khalid, M.; Arshad, N. Machine learning in state of health and remaining useful life estimation: Theoretical and technological development in battery degradation modelling. Renew. Sustain. Energy Rev. 2022, 156, 111903. [Google Scholar]
- Bayrak, Z.U.; Bayrak, G.; Ozdemir, M.T.; Gencoglu, M.T.; Cebeci, M. A low-cost power management system design for residential hydrogen & solar energy based power plants. Int. J. Hydrogen Energy 2016, 41, 12569–12581. [Google Scholar]
- Samantaray, S.; Kayal, P. Capacity assessment and scheduling of battery storage systems for performance and reliability improvement of solar energy enhanced distribution systems. J. Energy Storage 2023, 66, 107479. [Google Scholar]
- Sepúlveda, F.; Montero, I.; Barrena, F.; Domínguez, M.; Miranda, M. Efficiency evaluation of photovoltaic systems with batteries considering different voltage levels. J. Energy Storage 2023, 63, 106971. [Google Scholar]
- López-Grajales, A.M.; González-Sanchez, J.W.; Cardona-Restrepo, H.A.; Isaac-Millan, I.A.; López-Jiménez, G.J.; Vasco-Echeverri, O.H. Economy, financial, and regulatory method for the integration of electrical energy storage in a power network. J. Energy Storage 2023, 58, 106433. [Google Scholar]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar]
- Al Busaidi, A.S.; Kazem, H.A.; Al-Badi, A.H.; Khan, M.F. A review of optimum sizing of hybrid PV–Wind renewable energy systems in oman. Renew. Sustain. Energy Rev. 2016, 53, 185–193. [Google Scholar]
- Gallo, A.; Simões-Moreira, J.R.; Costa, H.; Santos, M.M.; Dos Santos, E.M. Energy storage in the energy transition context: A technology review. Renew. Sustain. Energy Rev. 2016, 65, 800–822. [Google Scholar]
- May, G.J.; Davidson, A.; Monahov, B. Lead batteries for utility energy storage: A review. J. Energy Storage 2018, 15, 145–157. [Google Scholar]
- Hannan, M.A.; Wali, S.; Ker, P.J.; Abd Rahman, M.S.; Mansor, M.; Ramachandaramurthy, V.; Muttaqi, K.; Mahlia, T.M.I.; Dong, Z.Y. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar]
- Wen, S.; Lan, H.; Fu, Q.; David, C.Y.; Zhang, L. Economic allocation for energy storage system considering wind power distribution. IEEE Trans. Power Syst. 2014, 30, 644–652. [Google Scholar]
- Zhang, Z.; Zhang, Y.; Huang, Q.; Lee, W.J. Market-oriented optimal dispatching strategy for a wind farm with a multiple stage hybrid energy storage system. CSEE J. Power Energy Syst. 2018, 4, 417–424. [Google Scholar]
- Shi, Z.; Wang, W.; Huang, Y.; Li, P.; Dong, L. Simultaneous optimization of renewable energy and energy storage capacity with the hierarchical control. CSEE J. Power Energy Syst. 2020, 8, 95–104. [Google Scholar]
- Yan, N.; Li, S.; Yan, T.; hua Ma, S. Study on the whole life cycle energy management method of energy storage system with risk correction control. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2450–2454. [Google Scholar]
- Lu, M.S.; Chang, C.L.; Lee, W.J.; Wang, L. Combining the wind power generation system with energy storage equipment. IEEE Trans. Ind. Appl. 2009, 45, 2109–2115. [Google Scholar]
- Çakmak, R.; Meral, H.; Bayrak, G. A new intelligent charging strategy in a stationary hydrogen energy-based power plant for optimal demand side management of plug-in EVs. Int. J. Hydrogen Energy 2024, 75, 400–414. [Google Scholar] [CrossRef]
- Schimpe, M.; Naumann, M.; Truong, N.; Hesse, H.C.; Santhanagopalan, S.; Saxon, A.; Jossen, A. Energy efficiency evaluation of a stationary lithium-ion battery container storage system via electro-thermal modeling and detailed component analysis. Appl. Energy 2018, 210, 211–229. [Google Scholar] [CrossRef]
- Xu, B.; Shi, Y.; Kirschen, D.S.; Zhang, B. Optimal battery participation in frequency regulation markets. IEEE Trans. Power Syst. 2018, 33, 6715–6725. [Google Scholar] [CrossRef]
- Sorourifar, F.; Zavala, V.M.; Dowling, A.W. Integrated multiscale design, market participation, and replacement strategies for battery energy storage systems. IEEE Trans. Sustain. Energy 2018, 11, 84–92. [Google Scholar]
- Rudolf, V.; Papastergiou, K.D. Financial analysis of utility scale photovoltaic plants with battery energy storage. Energy Policy 2013, 63, 139–146. [Google Scholar] [CrossRef]
- Uddin, K.; Gough, R.; Radcliffe, J.; Marco, J.; Jennings, P. Techno-economic analysis of the viability of residential photovoltaic systems using lithium-ion batteries for energy storage in the United Kingdom. Appl. Energy 2017, 206, 12–21. [Google Scholar]
- Akter, M.; Mahmud, M.; Oo, A.M. Comprehensive economic evaluations of a residential building with solar photovoltaic and battery energy storage systems: An Australian case study. Energy Build. 2017, 138, 332–346. [Google Scholar] [CrossRef]
- Merei, G.; Moshövel, J.; Magnor, D.; Sauer, D.U. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar]
- Kaschub, T.; Jochem, P.; Fichtner, W. Solar energy storage in German households: Profitability, load changes and flexibility. Energy Policy 2016, 98, 520–532. [Google Scholar] [CrossRef]
- Hassan, A.S.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Schopfer, S.; Tiefenbeck, V.; Staake, T. Economic assessment of photovoltaic battery systems based on household load profiles. Appl. Energy 2018, 223, 229–248. [Google Scholar]
- Chaianong, A.; Bangviwat, A.; Menke, C.; Breitschopf, B.; Eichhammer, W. Customer economics of residential PV–battery systems in Thailand. Renew. Energy 2020, 146, 297–308. [Google Scholar]
- Yılmaz, A.; Ateşci, T.; Meral, H.; Bayrak, G. A Real-Time Improved ML Method for PQD Classification of a PV-Powered EV Charging Station. IEEE Trans. Ind. Electron. 2024, 72, 2622–2632. [Google Scholar] [CrossRef]
- Bayrak, G.; Yılmaz, A.; Demirci, E. Fault ride-through capability enhancement of hydrogen energy-based distributed generators by using STATCOM with an intelligent control strategy. Int. J. Hydrogen Energy 2023, 48, 39442–39462. [Google Scholar] [CrossRef]
- Andreolli, F.; D’Alpaos, C.; Moretto, M. Valuing investments in domestic PV-Battery Systems under uncertainty. Energy Econ. 2022, 106, 105721. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, Y.; He, W.; Liang, Z.; Zhang, Z.; Zhang, N. The Generation Load Aggregator Participates in the Electricity Purchase and Sale Strategy of the Electric Energy–Peak Shaving Market. Energies 2025, 18, 370. [Google Scholar] [CrossRef]
- Lazzeroni, P.; Mariuzzo, I.; Quercio, M.; Repetto, M. Economic, Energy, and Environmental Analysis of PV with Battery Storage for Italian Households. Electronics 2021, 10, 146. [Google Scholar] [CrossRef]
- Rana, M.; Atef, M.; Sarkar, M.; Uddin, M.; Shafiullah, G. A Review on Peak Load Shaving in Microgrid—Potential Benefits, Challenges, and Future Trend. Energies 2022, 15, 2278. [Google Scholar] [CrossRef]
- Cai, Q.; Qing, J.; Xu, Q.; Shi, G.; Liang, Q.M. Techno-economic impact of electricity price mechanism and demand response on residential rooftop photovoltaic integration. Renew. Sustain. Energy Rev. 2024, 189, 113964. [Google Scholar] [CrossRef]
- Dufo-López, R.; Lujano-Rojas, J.; Artal-Sevil, J.; Bernal-Agustín, J. Optimising Grid-Connected PV-Battery Systems for Energy Arbitrage and Frequency Containment Reserve. Batteries 2024, 10, 427. [Google Scholar] [CrossRef]
- Ratshitanga, M.; Ayeleso, A.; Krishnamurthy, S.; Rose, G.; Aminou Moussavou, A.; Adonis, M. Battery Storage Use in the Value Chain of Power Systems. Energies 2024, 17, 921. [Google Scholar] [CrossRef]
- Rocha, A.V.; Maia, T.A.C.; Filho, B.J.C. Improving the Battery Energy Storage System Performance in Peak Load Shaving Applications. Energies 2023, 16, 382. [Google Scholar] [CrossRef]
- Elio, J.; Milcarek, R.J. A comparison of optimal peak clipping and load shifting energy storage dispatch control strategies for event-based demand response. Energy Convers. Manag. X 2023, 19, 100392. [Google Scholar]
- Setlhaolo, D.; Xia, X. Optimal scheduling of household appliances with a battery storage system and coordination. Energy Build. 2015, 94, 61–70. [Google Scholar]
- Leadbetter, J.; Swan, L. Battery storage system for residential electricity peak demand shaving. Energy Build. 2012, 55, 685–692. [Google Scholar]
- Wang, Y.; Das, R.; Putrus, G.; Kotter, R. Economic evaluation of photovoltaic and energy storage technologies for future domestic energy systems—A case study of the UK. Energy 2020, 203, 117826. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 60904-2:2015 Photovoltaic Devices—Part 2: Requirements for Reference Solar Devices. Available online: https://webstore.iec.ch/publication/22863 (accessed on 26 March 2025).
- Bayrak, G.; Yılmaz, A.; Çalışır, A. A new intelligent decision-maker method determining the optimal connection point and operating conditions of hydrogen energy-based DGs to the main grid. Int. J. Hydrogen Energy 2023, 48, 23168–23184. [Google Scholar]
- The MathWorks, Inc. MATLAB (R2024a) [Computer software]. (Campus License). Available online: https://www.mathworks.com/products/matlab.html (accessed on 24 March 2025).
- Ashtiani, M.N.; Toopshekan, A.; Astaraei, F.R.; Yousefi, H.; Maleki, A. Techno-economic analysis of a grid-connected PV/battery system using the teaching-learning-based optimization algorithm. Sol. Energy 2020, 203, 69–82. [Google Scholar]
- Hassan, A.; Al-Abdeli, Y.M.; Masek, M.; Bass, O. Optimal sizing and energy scheduling of grid-supplemented solar PV systems with battery storage: Sensitivity of reliability and financial constraints. Energy 2022, 238, 121780. [Google Scholar] [CrossRef]
- Yang, P.; Yu, L.; Wang, X.; Zheng, P.; Lv, X.; Yue, J. Multi-objective planning and optimization of microgrid lithium iron phosphate battery energy storage system consider power supply status and CCER transactions. Int. J. Hydrogen Energy 2022, 47, 29925–29944. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Z.; Liu, J.; Xiao, H.; Liu, R.; Zhang, L. Optimal battery capacity of grid-connected PV-battery systems considering battery degradation. Renew. Energy 2022, 181, 10–23. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, Y.; Gu, W.; Xiao, G.; Yang, H.; Wang, S. Strategy comparison and techno-economic evaluation of a grid-connected photovoltaic-battery system. Renew. Energy 2022, 197, 1049–1060. [Google Scholar] [CrossRef]
- Gul, E.; Baldinelli, G.; Bartocci, P.; Bianchi, F.; Piergiovanni, D.; Cotana, F.; Wang, J. A techno-economic analysis of a solar PV and DC battery storage system for a community energy sharing. Energy 2022, 244, 123191. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, T.; Elia Campana, P.; Yamaguchi, Y.; Dai, Y. A techno-economic sizing method for grid-connected household photovoltaic battery systems. Appl. Energy 2020, 269, 115106. [Google Scholar] [CrossRef]
- Cole, W.; Frazier, A.W.; Augustine, C. Cost Projections for Utility-Scale Battery Storage: 2021 Update; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2021. [Google Scholar] [CrossRef]
- EPDK. Energy Market Regulatory Authority 2019 Activity Report; EPDK: Ankara, Türkiye, 2020. [Google Scholar]
- TCMB. Available online: http://www.tcmb.gov.tr/wps/wcm/connect/TR/TCMB+TR/Main+Menu/Istatistikler/Enflasyon+Verileri/Tuketici+Fiyatlari (accessed on 8 September 2023).
- Gu, Y.; Zhang, X.; Are Myhren, J.; Han, M.; Chen, X.; Yuan, Y. Techno-economic analysis of a solar photovoltaic/thermal (PV/T) concentrator for building application in Sweden using Monte Carlo method. Energy Convers. Manag. 2018, 165, 8–24. [Google Scholar] [CrossRef]
- Barzegkar-Ntovom, G.A.; Chatzigeorgiou, N.G.; Nousdilis, A.I.; Vomva, S.A.; Kryonidis, G.C.; Kontis, E.O.; Georghiou, G.E.; Christoforidis, G.C.; Papagiannis, G.K. Assessing the viability of Battery Energy Storage Systems coupled with Photovoltaics under a pure self-consumption scheme. arXiv 2019, arXiv:1910.07576. [Google Scholar]
- Parra, D.; Walker, G.S.; Gillott, M. Economic optimization of photovoltaic-battery systems using V2G facilities in the UK. Appl. Energy 2015, 164, 416–426. [Google Scholar]
- Babacan, O.; Ratnam, E.; Disfani, V.R.; Kleissl, J. Distributed energy storage system scheduling considering tariff structure, energy arbitrage and solar PV penetration. Appl. Energy 2017, 205, 1384–1393. [Google Scholar] [CrossRef]
- Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems—A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Mulder, G.; Six, D.; Claessens, B.; Broes, T.; Omar, N.; Mierlo, J.V. The dimensioning of PV-battery systems depending on the incentive and selling price conditions. Appl. Energy 2013, 111, 1126–1135. [Google Scholar]
- Zakeri, B.; Syri, S. Electrical energy storage systems: A comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 2015, 42, 569–596. [Google Scholar]
- Weniger, J.; Tjaden, T.; Quaschning, V. Sizing of residential PV battery systems. Energy Procedia 2014, 46, 78–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).