A Review of Traffic Flow Prediction Methods in Intelligent Transportation System Construction
Abstract
1. Introduction
1.1. Theme Background and Significance
1.2. Research Status
1.3. The Purpose of This Study
1.4. Brief Layout of the Paper
2. Prediction Method Based on Statistical Analysis Theory
2.1. Introduction to Traditional Statistical Methods
2.2. Specific Methods Listed
- (1)
- Historical average model (HA)
- (2)
- Autoregressive Integrated Moving Average model (ARIMA)
- (3)
- Kalman filter model
2.3. Disadvantages
3. Traditional Machine Learning Models
3.1. Introduction to Machine Learning Methods
3.2. Specific Methods
- (1)
- Feature extraction-based methods are primarily employed to train regression models to solve practical traffic prediction problems. Their main advantage lies in their simplicity and ease of implementation. However, these methods also suffer from limitations, such as focusing only on time series data and neglecting the complexities of spatiotemporal relationships. Cheng et al. [14] proposed an adaptive K-Nearest Neighbors (KNN) algorithm that treats spatial features of the road network as adaptive spatial neighbor nodes, time intervals, and spatiotemporal iso-value functions. The algorithm was evaluated using speed data collected from highways in California and urban roads in Beijing.
- (2)
- Gaussian process methods utilize multiple kernel functions to capture the internal features of traffic data, while considering both spatial and temporal correlations. These methods are useful and practical for traffic forecasting but come with higher computational complexity and greater data storage demands when compared to feature extraction-based methods.
- (3)
- State space modeling methods assume that the observations are derived from a hidden Markov model, which is adept in capturing hidden data structures and can naturally model uncertainty within the system. This is an ideal characteristic for traffic flow prediction applications. However, these models can be challenging when it comes to establishing nonlinear relationships. Therefore, they are not always the best choice when modeling complex dynamic traffic data, particularly in long-term forecasting scenarios. Tu et al. [15] introduced a congestion pattern prediction model, SG-CNN, based on a hidden Markov model and compared it with the well-known ARIMA baseline model for traffic prediction. Experimental results demonstrated that the SG-CNN model exhibited strong performance.
4. Deep Learning Models
4.1. Introduction to Deep Learning Technology
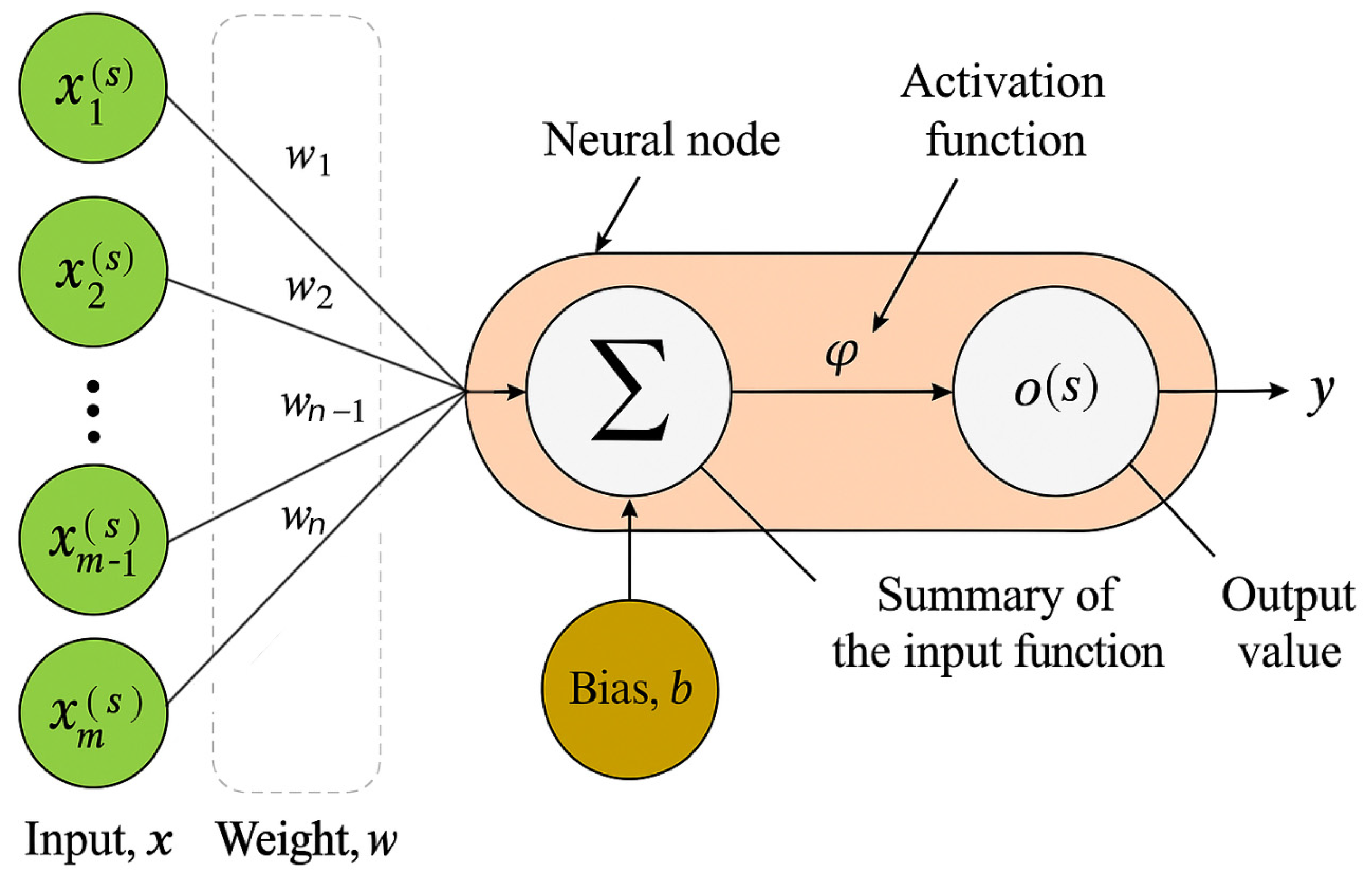
4.2. Multilayer Perceptron Network (MLP)
4.3. Convolutional Neural Networks (CNNs)
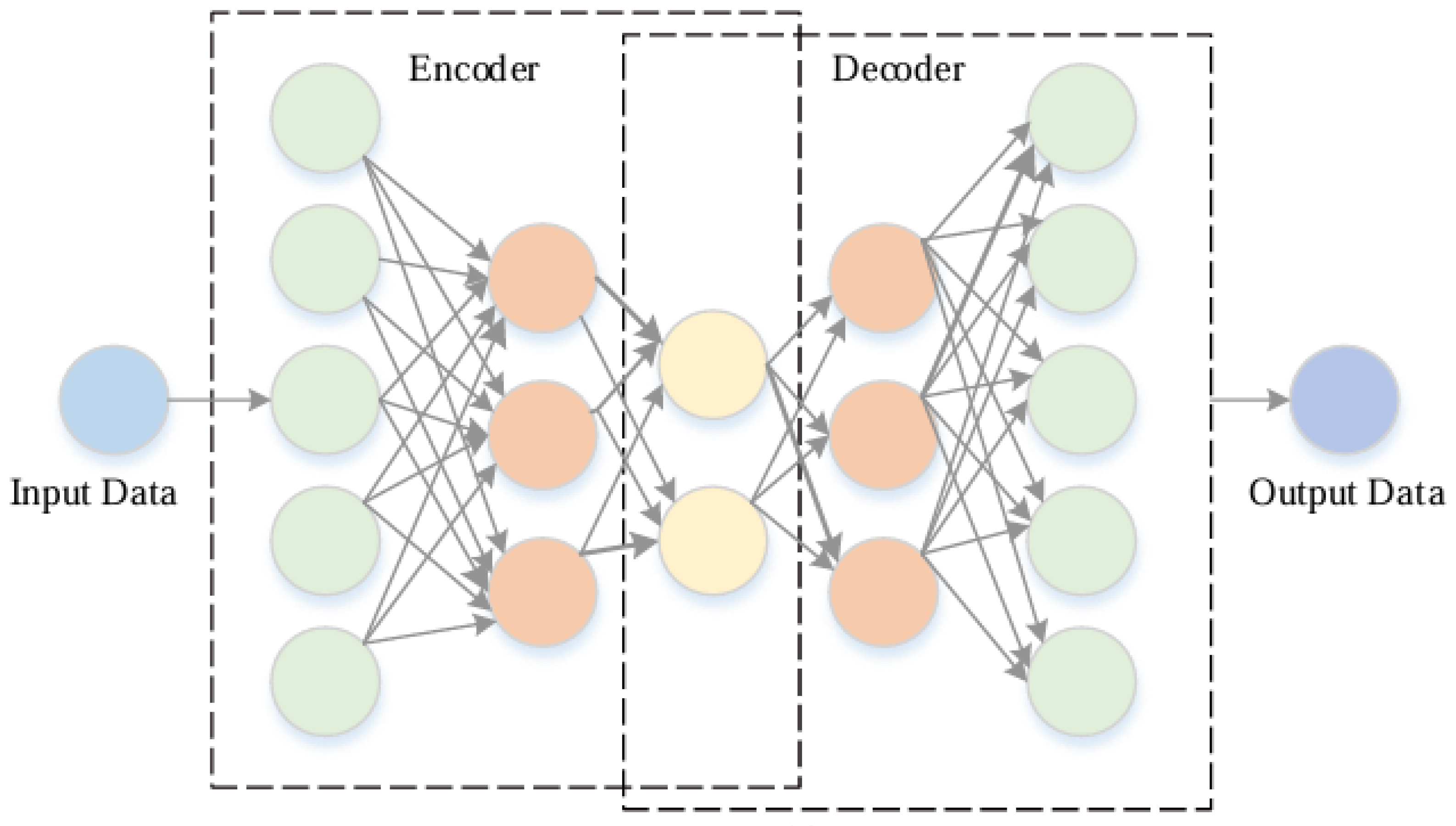
4.4. Autoencoder (AE)
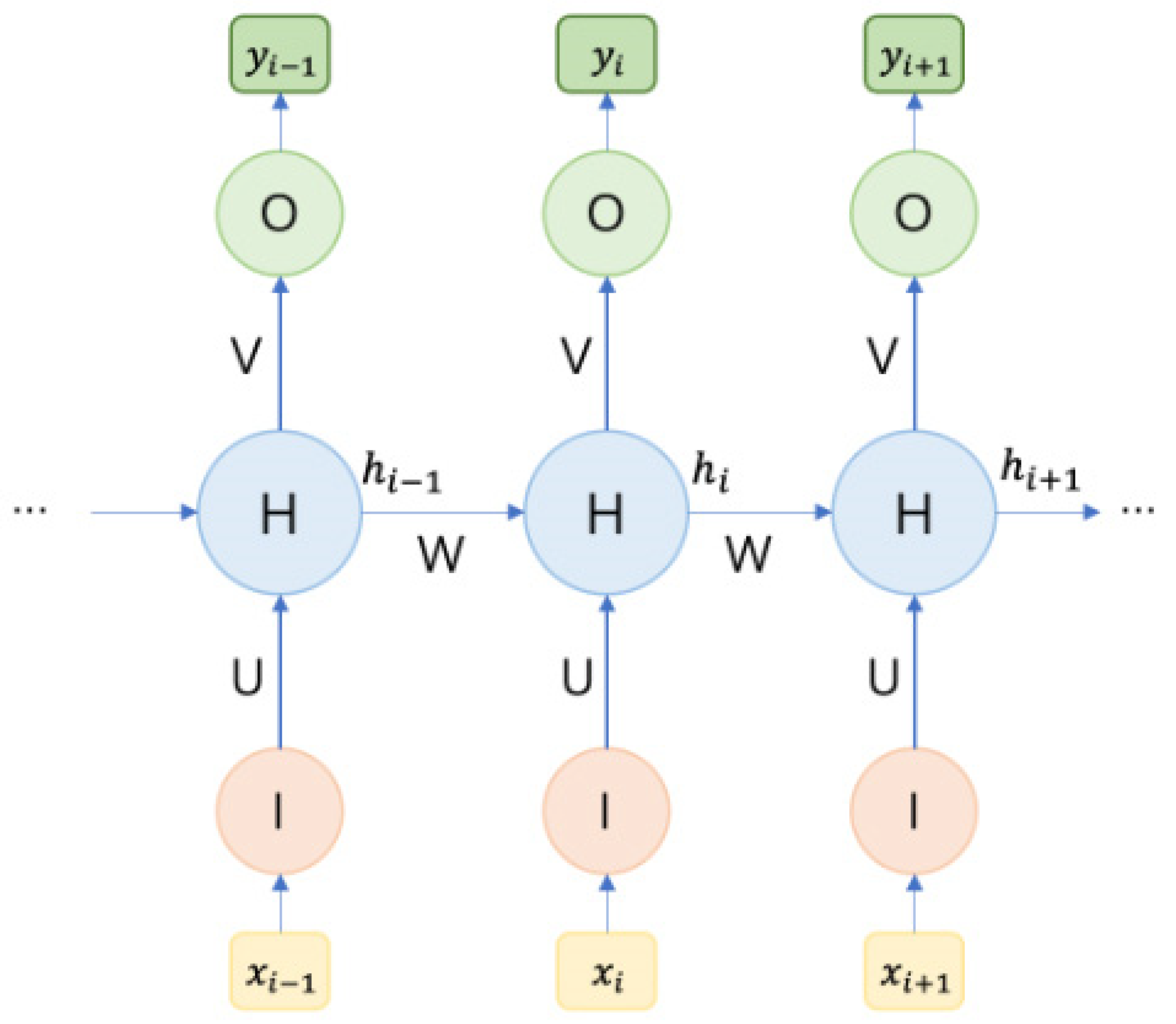
4.5. Recurrent Neural Networks (RNNs)
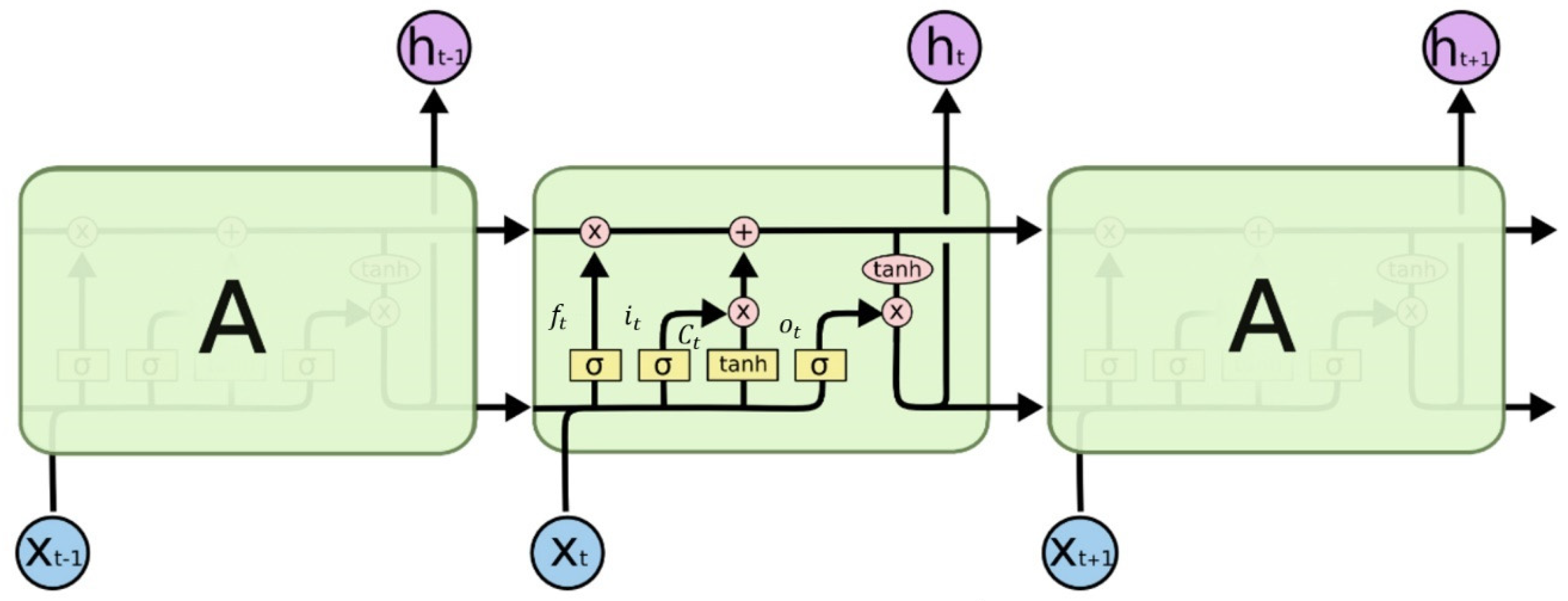
4.6. Long Short-Term Memory (LSTM) Recurrent Neural Networks
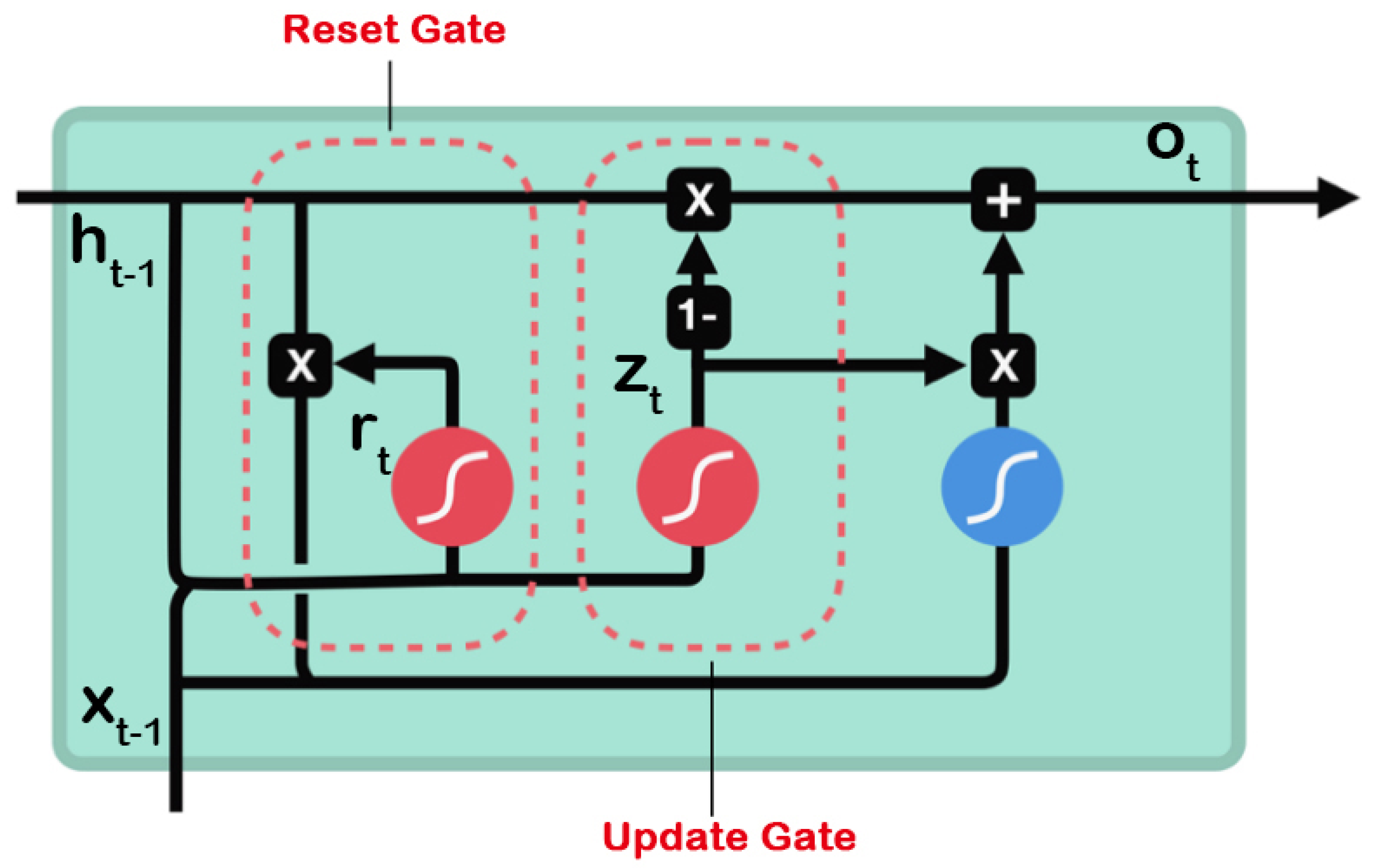
4.7. Gated Recurrent Unit (GRU)
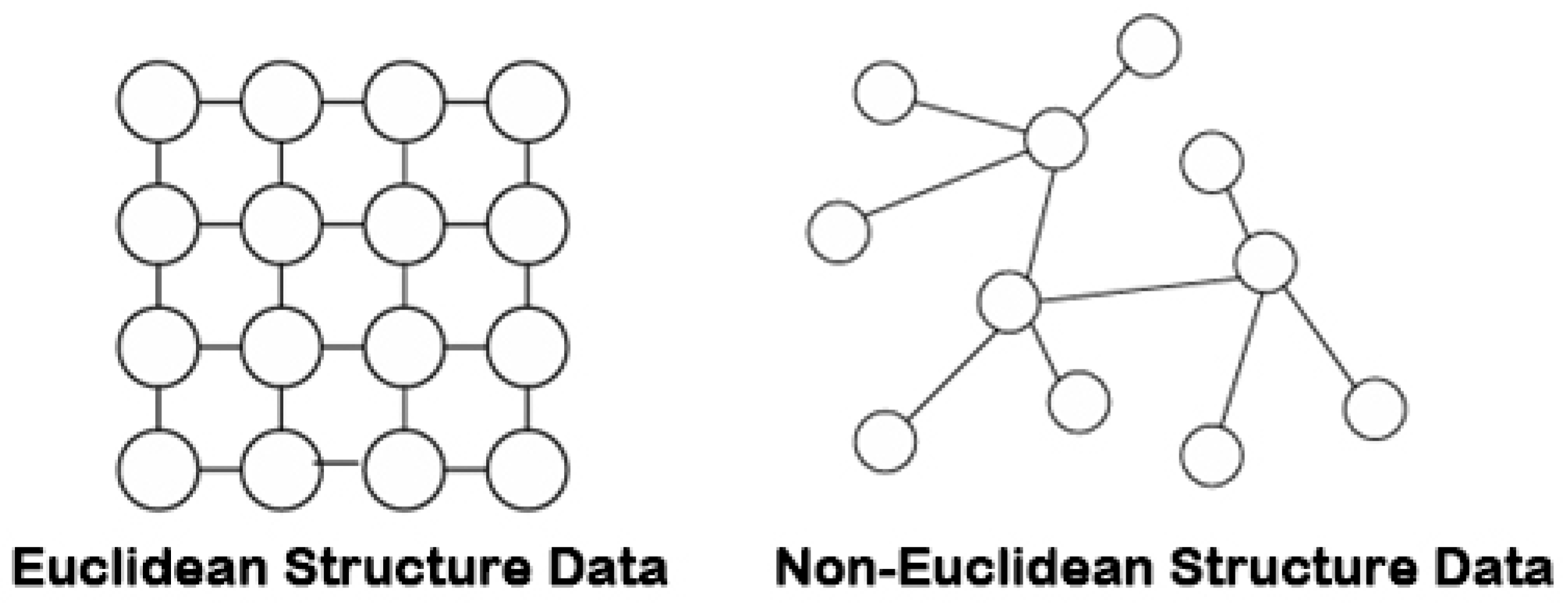
4.8. Graph Convolutional Neural Networks (GCNs)
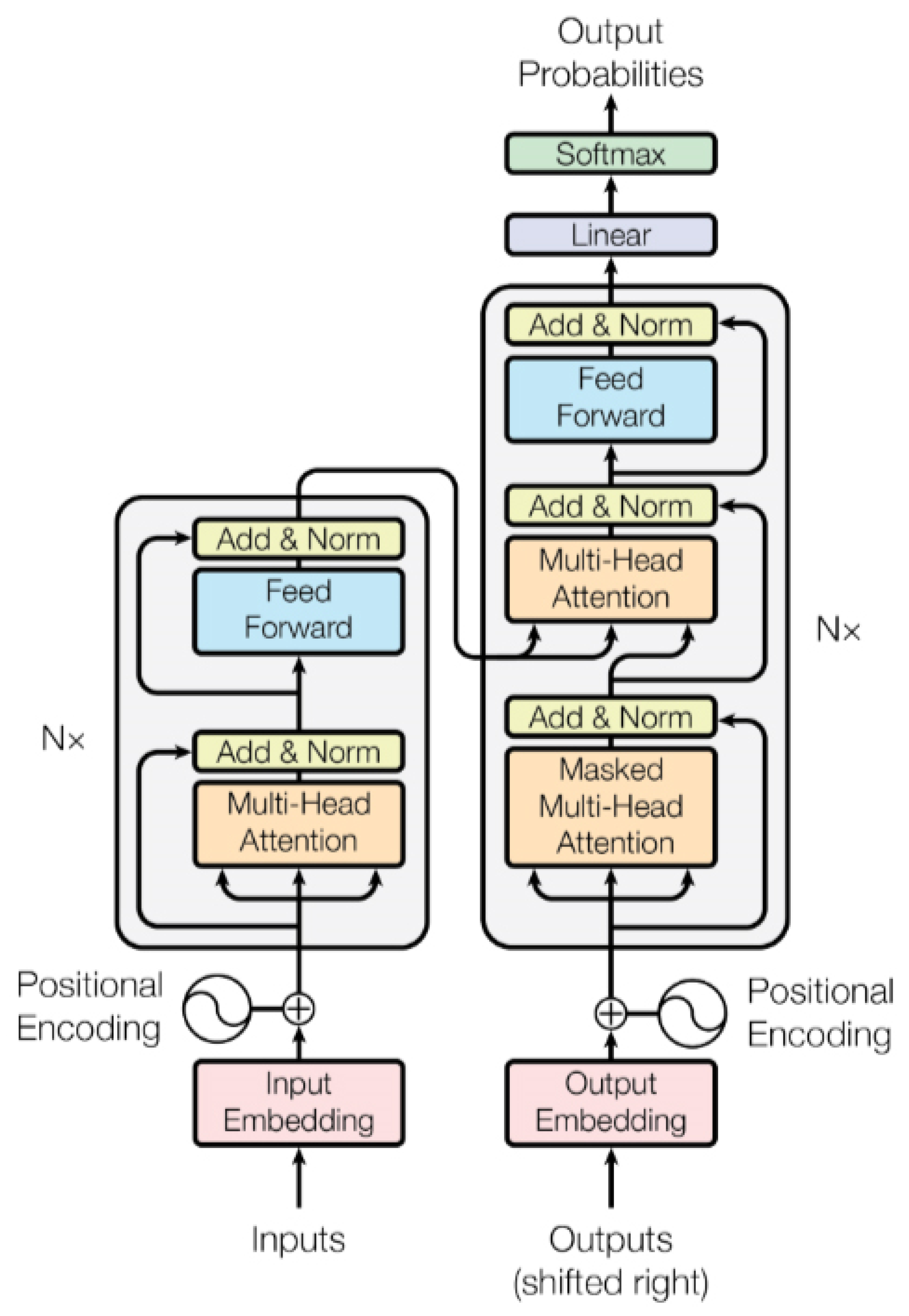
4.9. Attention Mechanism and Transformer
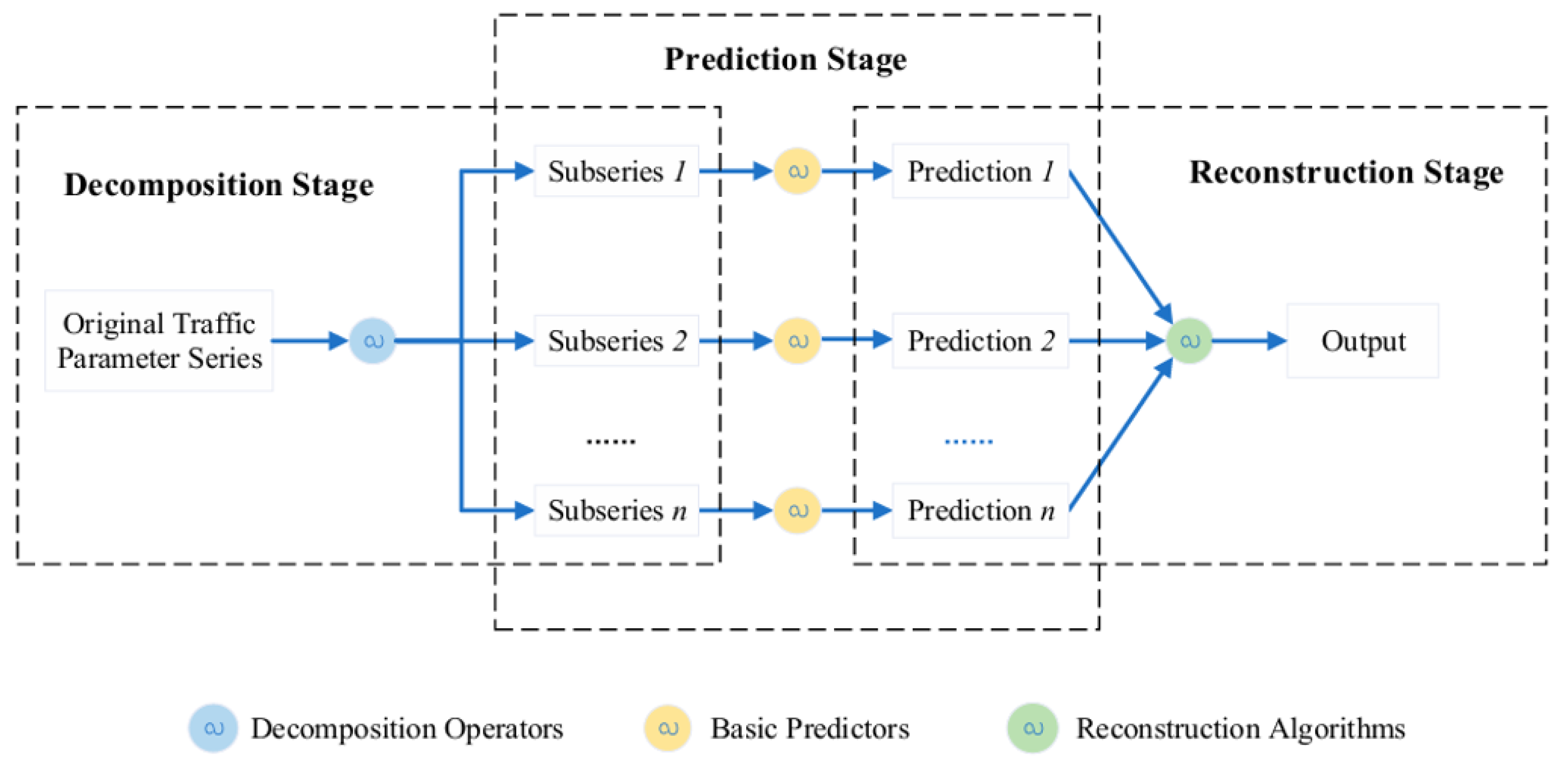
4.10. Hybrid Neural Networks
5. Traffic Prediction-Related Datasets
5.1. Stationary Traffic Data
- (1)
- PeMS: PeMS is a traffic flow database for California, containing real-time data from more than 39,000 independent detectors on California highways. Among them, the detector data are mainly from highways and metropolitan areas. These data include information such as vehicle speeds, flows, congestion, etc., which provide an important basis for traffic management, planning, and research. The minimum time interval of the data is 5 min, making them highly suitable for short-term prediction. The historical average method can be used to automatically fill in missing data. In the task of traffic flow prediction, the most commonly used sub-datasets are PeMS03, PeMS04, PeMS07, PeMS08, PeMS-BAY, etc.
- (2)
- The METR-LA traffic dataset contains traffic information collected from detectors on freeway loops in Los Angeles County. The Los Angeles Freeway Dataset contains traffic data detected by 207 detectors from 1 March to 30 June 2012, with a sampling interval of 5 min.
- (3)
- The Loop dataset contains mainly loop data from the Seattle area, covering data from four highways: I-5, I-405, I-90, and SR-520. The Loop dataset contains traffic status data from 323 sensor stations, with a sampling interval of 5 min [39].
- (4)
- The Korean urban area dataset (UVDS) contains data on major urban roads collected by 104 VDS sensors, with traffic characteristics such as traffic flows, vehicle types, traffic speeds, and occupancy rates [40].
5.2. Mobile Traffic Data
- (1)
- TaxiBJ Dataset: TaxiBJ is a dataset of Beijing taxi data that includes trajectory and meteorological data from over 34,000 taxis in the Beijing area over a period of 3 years. The data are converted into inflow and outflow traffic for various regions. The sampling interval for the dataset is 30 min, and it is primarily used for traffic demand prediction.
- (2)
- Shanghai Taxi Dataset: This dataset, proposed by the Smart City Research Group at the Hong Kong University of Science and Technology, contains GPS reports from 4000 taxis in Shanghai on 20 February 2007. The vehicle data are sampled at 1 min intervals and include information such as the vehicle ID, timestamp, longitude and latitude, and speed.
- (3)
- SZ-taxi Dataset: The SZ-taxi dataset consists of taxi trajectory data from Shenzhen, covering the period from 1 January to 31 January 2015. The dataset focuses on the Luohu District of Shenzhen and includes data from 156 main roads. Traffic speeds for each road are calculated every 15 min in this dataset.
- (4)
- NYC Bike Dataset: The NYC Bike dataset records bicycle trajectories collected from the New York City Bike Share system. The dataset includes data from 13,000 bicycles and 800 docking stations, providing detailed information about bike usage and movement across the city.
5.3. Common Evaluation Indicators
6. Method Comparison and Analysis
6.1. Model Training and Validation
6.2. Experimental Results and Method Comparison
6.3. Method Comparison
7. Conclusions and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qingcai, C.; Wei, Z.; Rong, Z. Smart city construction practices in BFSP. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2714–2717. [Google Scholar]
- Shen, X.; Zhang, Q. Thought on Smart City Construction Planning Based on System Engineering. In Proceedings of the International Conference on Education, Management and Computing Technology (ICEMCT-16), Hangzhou, China, 9–10 April 2016; Atlantis Press: Dordrecht, The Netherlands, 2016; pp. 1156–1162. [Google Scholar]
- Lana, I.; Del Ser, J.; Velez, M.; Vlahogianni, E.I. Road traffic forecasting: Recent advances and new challenges. IEEE Intell. Transp. Syst. Mag. 2018, 10, 93–109. [Google Scholar]
- Daeho, K. Cooperative Traffic Signal Control with Traffic Flow Prediction in Multi-Intersection. Sensors 2020, 20, 137. [Google Scholar]
- Ahn, J.; Ko, E.; Kim, E.Y. Highway traffic flow prediction using support vector regression and Bayesian classifier. In Proceedings of the 2016 International Conference on Big Data and Smart Computing (BigComp), Hong Kong, China, 18–20 January 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Dai, G.; Ma, C.; Xu, X. Short-term traffic flow prediction method for urban road sections based on space–time analysis and GRU. IEEE Access 2019, 7, 143025–143035. [Google Scholar]
- Smith, B.L.; Demetsky, M.J. Traffic flow forecasting: Comparison of modeling approaches. J. Transp. Eng. 1997, 123, 261–266. [Google Scholar]
- Chen, C.; Hu, J.; Meng, Q.; Zhang, Y. Short-time traffic flow prediction with ARIMA-GARCH model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Makridakis, S.; Hibon, M. ARMA models and the Box–Jenkins methodology. J. Forecast. 1997, 16, 147–163. [Google Scholar]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman filter and its application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 74–77. [Google Scholar]
- Min, X.; Hu, J.; Chen, Q.; Zhang, T.; Zhang, Y. Short-term traffic flow forecasting of urban network based on dynamic STARIMA model. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part C Emerg. Technol. 2011, 19, 606–616. [Google Scholar]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep learning on traffic prediction: Methods, analysis, and future directions. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4927–4943. [Google Scholar]
- Cheng, S.; Lu, F.; Peng, P.; Wu, S. Short-term traffic forecasting: An adaptive ST-KNN model that considers spatial heterogeneity. Comput. Environ. Urban Syst. 2018, 71, 186–198. [Google Scholar]
- Tu, Y.; Lin, S.; Qiao, J.; Liu, B. Deep traffic congestion prediction model based on road segment grouping. Appl. Intell. 2021, 51, 8519–8541. [Google Scholar]
- Ke, K.C.; Huang, M.S. Quality prediction for injection molding by using a multilayer perceptron neural network. Polymers 2020, 12, 1812. [Google Scholar] [CrossRef]
- Slimani, N.; Slimani, I.; Sbiti, N.; Amghar, M. Machine Learning and statistic predictive modeling for road traffic flow. Int. J. Traffic Transp. Manag. 2021, 3, 17–24. [Google Scholar]
- Aljuaydi, F.; Wiwatanapataphee, B.; Wu, Y.H. Multivariate machine learning-based prediction models of freeway traffic flow under non-recurrent events. Alex. Eng. J. 2023, 65, 151–162. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Bogaerts, T.; Masegosa, A.D.; Angarita-Zapata, J.S.; Onieva, E.; Hellinckx, P. A graph CNN-LSTM neural network for short and long-term traffic forecasting based on trajectory data. Transp. Res. Part C Emerg. Technol. 2020, 112, 62–77. [Google Scholar]
- Palm, R.B. Prediction as a Candidate for Learning Deep Hierarchical Models of Data; Technical University of Denmark: Lyngby, Denmark, 2012; Volume 5, pp. 19–22. [Google Scholar]
- Kashyap, A.A.; Raviraj, S.; Devarakonda, A.; Nayak, K.S.R.; KV, S.; Bhat, S.J. Traffic flow prediction models–A review of deep learning techniques. Cogent Eng. 2022, 9, 2010510. [Google Scholar]
- Zheng, H.; Lin, F.; Feng, X.; Chen, Y. A hybrid deep learning model with attention-based conv-LSTM networks for short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6910–6920. [Google Scholar]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 324–328. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1597–1600. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: Westminster, UK, 2015; pp. 2067–2075. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Han, X.; Gong, S. LST-GCN: Long Short-Term Memory embedded graph convolution network for traffic flow forecasting. Electronics 2022, 11, 2230. [Google Scholar] [CrossRef]
- Hu, N.; Zhang, D.; Xie, K.; Liang, W.; Hsieh, M.Y. Graph learning-based spatial-temporal graph convolutional neural networks for traffic forecasting. Connect. Sci. 2022, 34, 429–448. [Google Scholar]
- Zuo, D.; Li, M.; Zeng, L.; Wang, M.; Zhao, P. A Cross-Attention Based Diffusion Convolutional Recurrent Neural Network for Air Traffic Forecasting. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 2120. [Google Scholar]
- Yao, Z.; Xia, S.; Li, Y.; Wu, G.; Zuo, L. Transfer learning with spatial–temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8592–8605. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Ashish, V. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, I. [Google Scholar]
- Yan, H.; Ma, X.; Pu, Z. Learning dynamic and hierarchical traffic spatiotemporal features with transformer. IEEE Trans. Intell. Transp. Syst. 2021, 23, 22386–22399. [Google Scholar]
- Fan, Y.; Yeh, C.C.; Chen, H.; Wang, L.; Zhuang, Z.; Wang, J.; Dai, X.; Zheng, Y.; Zhang, W. Spatial-Temporal Graph Sandwich Transformer for Traffic Flow Forecasting. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Turin, Italy, 18–22 September 2023; Springer Nature: Cham, Switzerland, 2023; pp. 210–225. [Google Scholar]
- Chen, Y.; Wang, W.; Hua, X.; Zhao, D. Survey of decomposition-reconstruction-based hybrid approaches for short-term traffic state forecasting. Sensors 2022, 22, 5263. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Deep bidirectional and unidirectional LSTM recurrent neural network for network-wide traffic speed prediction. arXiv 2018, arXiv:1801.02143. [Google Scholar]
- Bui, K.H.N.; Yi, H.; Cho, J. Uvds: A new dataset for traffic forecasting with spatial-temporal correlation. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Phuket, Thailand, 7–10 April 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 66–77. [Google Scholar]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar]
- Wei, Y.; Zheng, Y.; Yang, Q. Transfer knowledge between cities. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1905–1914. [Google Scholar]
- Bui, K.H.N.; Cho, J.; Yi, H. Spatial-temporal graph neural network for traffic forecasting: An overview and open research issues. Appl. Intell. 2022, 52, 2763–2774. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar]


| Type | Dataset | Features | Time Interval | Traffic Data | Source |
|---|---|---|---|---|---|
| Stationary traffic data | PeMS | Flow, speed | 5 min | 39,000 | https://github.com//Davidham3/ASTGCN (accessed on 1 February 2025) |
| METR-LA | Speed | 5 min | 207 | https://github.com//liyaguang/DCRNN (accessed on 1 February 2025) | |
| Loop | Speed | 5 min | 323 | https://github.com/zhiyongc/Seattle-Loop-Data (accessed on 1 February 2025) | |
| UVDS | Flow, speed | 5 min | 104 | [17] | |
| Mobile traffic data | TaxiBJ | Flow | 30 min | 34,000 vehicles | https://github.com/TolicWang/DeepST/tree/master/data/TaxiBJ (accessed on 1 February 2025) |
| SZ-taxi | Flow, speed | 15 min | 156 roads | https://paperswithcode.com/dataset/sz-taxi (accessed on 1 February 2025) | |
| NYC Bike | Flow | 60 min | 13,000 bicycles | https://paperswithcode.com/dataset/nycbike1 (accessed on 1 February 2025) | |
| Shanghai Taxi Dataset | Speed | 1 min | 4000 vehicles | https://gitcode.com/open-source-toolkit/659ba (accessed on 1 February 2025) |
| Model | PEMS08 | METR-LA | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
| ARIMA | 33.04 | 50.41 | 2.04 | 5.89 |
| MLP | 26.73 | 35.81 | 1.84 | 4.62 |
| LSTM | 27.34 | 37.43 | 1.86 | 4.66 |
| GRU | 26.95 | 36.61 | 1.86 | 4.71 |
| ASTGCN | 19.63 | 27.50 | 1.31 | 3.54 |
| Category | Model | Advantages | Disadvantages | |
|---|---|---|---|---|
| Traditional statistical models | HA | The model algorithm is simple, runs quickly, and has a small execution time overhead. | The model predicts future data based on the mean of historical data. Simple linear operations cannot represent the deep nonlinear relationships of spatiotemporal series. It is not ideal for the prediction of data with strong disturbances. | |
| ARIMA | The model algorithm is simple and based on a large amount of uninterrupted data; this model has high prediction accuracy and is particularly suitable for stable traffic flows. | Its modeling capabilities for nonlinear trends or very complex time series data are relatively weak. When encountering non-stationary data, it must first be stabilized; otherwise, its applicability will be limited. | ||
| Kalman filter model | The algorithm is efficient, can quickly process large amounts of data, is adaptive, and can automatically adjust the prediction results based on historical data. It is suitable for situations where the sensor data have large noise. It can smooth data during real-time prediction and is suitable for traffic flow prediction in short time intervals. | Because of its iterative nature, it requires continuous matrix operations; the algorithm has a large time overhead and cannot adapt to nonlinear changes in traffic flows. | ||
| Machine learning models | KNN | High portability, simple principles, easy to implement. High model accuracy and good adaptability to nonlinear and non-homogeneous data. Since KNN does not require a complex training process, it is suitable for application scenarios with smaller data scales. | The processing efficiency of large-scale datasets is low, the model converges slowly, and the running time is long; thus, it may not meet the requirements for the real-time prediction of road traffic flows. | |
| Deep learning models | MLP | The training process of the MLP is relatively simple, and there are many optimization methods. It is suitable for regression tasks, such as traffic flow prediction based on static features. | The training process of the MLP may take a long time and require considerable computing resources. When the number of data or features is small, the MLP may face overfitting problems. Performance is usually limited when processing non-stationary data. | |
| CNN | CNNs can effectively extract the spatial characteristics and temporal dependencies of traffic flow data and have strong generalization abilities and high prediction accuracy. Therefore, they perform well in traffic prediction tasks based on road network topologies. | Due to the complex structure of the model, the training process requires a large amount of computing resources and time. At the same time, the structure of the CNN cannot capture time dependencies well and it has a limited ability to process sequence data. | ||
| AE | The AE can learn the laws and patterns of historical traffic data to predict future traffic flows and improve the efficiency and accuracy of traffic management. The AE is not used directly for prediction but is usually used as an auxiliary tool for feature extraction in combination with other deep learning models. | For complex data distributions, training autoencoders can be difficult and requires the careful tuning of the network structure and hyperparameters. | ||
| RNN-based models | RNN | The RNN can capture the dynamic change characteristics of time series data and effectively use historical traffic flow information to predict future trends and is suitable for processing time-dependent traffic data. It performs well in short-term traffic flow prediction. | It can easily encounter gradient vanishing or gradient exploding problems during training, making it difficult to effectively learn long-term dependencies. | |
| LSTM | LSTM’s unique gating mechanism can effectively alleviate the long-term dependency problem of traditional RNNs, enabling the model to better capture the long-term trends and periodic changes in time series and improve the prediction accuracy. It is suitable for short-term and long-term traffic flow prediction, especially when the data are highly periodic. | The LSTM model is relatively complex, takes a long time to train, and requires a large amount of historical data for training to achieve better results. | ||
| GRU | The GRU is simpler than LSTM, but it can also solve problems such as long-term dependency and gradient disappearance. It is suitable for short-term and medium-term traffic flow prediction tasks, especially when computing resources are limited. | Its prediction performance is affected by the data quality and feature selection. In complex scenarios, its prediction ability may be slightly inferior to that of LSTM. | ||
| GCN | It is suitable for processing non-Euclidean structured data, can capture the relationships between nodes, and has good generalization abilities. It is suitable for traffic flow prediction tasks with strong spatial correlation, especially traffic flow modeling based on urban road networks. | The computational resource requirements are high and overfitting may occur when processing large graphs. | ||
| Transformer | The parallel computing capabilities of the Transformer greatly improve the computing efficiency, and its self-attention mechanism enables the model to consider all positions in the sequence at the same time, thereby better capturing long-distance dependencies. It is suitable for long-term traffic flow prediction tasks. | Requires a large amount of historical data for training, and the computational cost is high. | ||
| Hybrid neural network | By integrating the strengths of multiple neural network models, hybrid neural networks enable the comprehensive learning and precise prediction of traffic flow data. This approach is particularly well suited for complex traffic forecasting tasks, including large-scale urban traffic flow modeling and intelligent transportation management systems, where capturing both spatial and temporal dependencies is essential for accurate and robust predictions. | The model is highly complex, and the training and optimization process is relatively difficult, requiring longer computing times and larger amounts of computing resources. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Shin, S.-Y. A Review of Traffic Flow Prediction Methods in Intelligent Transportation System Construction. Appl. Sci. 2025, 15, 3866. https://doi.org/10.3390/app15073866
Liu R, Shin S-Y. A Review of Traffic Flow Prediction Methods in Intelligent Transportation System Construction. Applied Sciences. 2025; 15(7):3866. https://doi.org/10.3390/app15073866
Chicago/Turabian StyleLiu, Runpeng, and Seong-Yoon Shin. 2025. "A Review of Traffic Flow Prediction Methods in Intelligent Transportation System Construction" Applied Sciences 15, no. 7: 3866. https://doi.org/10.3390/app15073866
APA StyleLiu, R., & Shin, S.-Y. (2025). A Review of Traffic Flow Prediction Methods in Intelligent Transportation System Construction. Applied Sciences, 15(7), 3866. https://doi.org/10.3390/app15073866






