Abstract
Traditional object detection methods for meat duck counting suffer from high manual costs, low image quality, and varying object sizes. To address these issues, this paper proposes FE-P Net, an image enhancement-based parallel density estimation network that integrates CNNs with Transformer models. FE-P Net employs a Laplacian pyramid to extract multi-scale features, effectively reducing the impact of low-resolution images on detection accuracy. Its parallel architecture combines convolutional operations with attention mechanisms, enabling the model to capture both global semantics and local details, thus enhancing its adaptability across diverse density scenarios. The Reconstructed Convolution Module is a crucial component that helps distinguish targets from backgrounds, significantly improving feature extraction accuracy. Validated on a meat duck counting dataset in breeding environments, FE-P Net achieved 96.46% accuracy in large-scale settings, demonstrating state-of-the-art performance. The model shows robustness across various densities, providing valuable insights for poultry counting methods in agricultural contexts.
1. Introduction
Recent advancements have boosted demand for poultry products like meat and eggs. Meat ducks, valued for their high-quality proteins and fats [1], grow faster than other poultry, quickly reaching market weight. Proper breeding density is critical for maximizing survival rates and barn space efficiency [2], which are essential for large-scale production and animal welfare. Enhancing breeding efficiency requires real-time monitoring of density and effective management of duck populations. As large-scale breeding emerges as the predominant operational model within the industry, challenges arise when relying exclusively on manual labor for the management of duck houses and the control of breeding density. The need for human observation of extensive surveillance footage not only results in inefficiencies and a heavy reliance on the subjective judgment of personnel, lacking a standardized approach [3]. This not only increases labor intensity and expenses but also poses a barrier to the advancement of the farming sector. By leveraging intelligent farming technologies grounded in deep learning algorithms, it is possible to elevate production efficiency through automation and smart decision-making support systems. These advancements facilitate precise calculation of optimal breeding densities and streamline farming processes. Consequently, while lowering labor costs, they contribute to an overall enhancement in productivity and economic returns [4].
Girshick et al. [5] introduced the R-CNN algorithm, marking a significant advancement in object detection. However, R-CNN was constrained by its requirement for fixed-size candidate regions, leading to slower detection speeds and substantial storage needs for region proposals. To address these limitations, Fast R-CNN [6] and Faster R-CNN [7] were subsequently developed. Fast R-CNN incorporated Spatial Pyramid Pooling (SPP) to accelerate processing, while Faster R-CNN introduced Region Proposal Networks (RPNs) to significantly boost both speed and detection accuracy.
In large-scale breeding, high poultry density often leads to occlusion and crowding. Traditional machine learning methods struggle to perform effectively under such conditions. Zhang et al. [8] pioneered the use of deep learning for crowd counting with a multi-column convolutional neural network, marking the first application of this technique to counting tasks. Although object detection-based counting methods have demonstrated effectiveness, they require significant manual effort for bounding box annotation, which is both costly and time-consuming. In densely occluded real-world settings, these methods often produce inaccurate counts. To overcome these challenges, Cao et al. [9] enhanced the point-supervised localization and counting method proposed by Laradji et al. [10], aiming to enable real-time processing of camera-captured images. By using DenseNet, introduced by Huang et al. [11], as the backbone network and employing point annotation instead of bounding boxes, their approach significantly reduces annotation time and boosts data processing efficiency compared to traditional methods.
Since then, research has advanced these methods, particularly in breeding scenarios. Tian et al. [12] developed a 13-layer convolutional network combining Count CNN [13] and ResNeXt [14] for pig counting, achieving low error rates on sparse datasets. Wu et al. [15] addressed fish counting on dense datasets using dilated convolutions to increase the receptive field without reducing resolution and channel attention modules to enhance feature selection, achieving a mean absolute error (MAE) of 7.07 and a mean squared error (MSE) of 19.16. Li et al. [16] used a multi-column neural network with convolutions replacing fully connected layers, resulting in an MAE of 3.33 and MSE of 4.58 on a dataset of 3200 seedling images. Sun et al. [17] introduced a comprehensive dataset of 5637 fish images and proposed an innovative two-branch network that merges convolutional layers with Transformer architectures. By integrating density maps from the convolution branch into the Transformer encoder for regression purposes, their model attained state-of-the-art performance, achieving an MAE of 15.91 and an MSE of 34.08.
Despite these advancements, significant challenges remain in large-scale breeding counting methods. Low-quality images can negatively impact model detection accuracy, while dense scenes further exacerbate the cost and complexity of bounding box annotations. Traditional labeling approaches also face difficulties in achieving precise identification, particularly in areas with severe occlusion and indistinct features.
To address the specified challenges, this study investigates a point-based detection method that reduces data annotation costs and minimizes computational demands by focusing on the approximate positioning of target points rather than bounding box regression. Leveraging PENet [18] and IOCFormer [17], we propose the Feature Enhancement Module with Parallel Network Architecture (FE-P Net), tailored for the current application. FE-P Net comprises two branches: the primary branch employs a Transformer framework with a regression head for final detection outputs, while the auxiliary convolutional branch generates density maps to enhance feature extraction in the primary branch’s encoder. Additionally, to handle low-resolution images common in industrial settings, a Gaussian pyramid module is integrated into the feature extraction process, improving feature representation and mitigating uneven illumination effects. To address feature redundancy caused by low-quality images, spatial and channel reconstruction units are incorporated into the convolutional branch, filtering out irrelevant information and emphasizing crucial features. Our method enhances annotation efficiency and detection accuracy, particularly for livestock farming data, ensuring robust performance under challenging conditions.
2. Materials and Methods
2.1. Image Acquisition for Meat Duck Counting in Large-Scale Farm
The dataset used in this experiment was collected from a poultry house located in Lishui District, Nanjing City. Spanning approximately 500 square meters, the poultry house uses net-bed breeding methods. Data were collected over June and July 2023 using Hikvision Ezviz CS-CB2 (2WF-BK) cameras, which have a resolution of 1920 × 1080 and a viewing angle of about 45°. Over 136 min of video footage were recorded, with frames sampled every 30 s. After filtering out insect-obscured images, 242 usable images were obtained, containing 20,550 meat duck instances, averaging 84.92 instances per image.
As shown in Figure 1a, the collected images exhibit low resolution, significant occlusion between targets, considerable variations in individual sizes, and varying densities across different regions. These factors present substantial challenges for detection tasks.

Figure 1.
(a) Data were collected with a visual fluorite camera. (b) Original images and labeled images.
2.2. Dataset Construction for Meat Duck Counting in Large-Scale Farm
The 242 collected images were randomly split into training and testing sets at a ratio of 7:3, yielding 171 images for the training set and 71 images for the testing set. The images were then annotated using Labelme 4.5.9, with the annotation results shown in Figure 1b.
2.3. Detail-Enhanced Parallel Density Estimation Model Architecture
As shown in Figure 2, our proposed network model combines density-based [19] and regression-based [20] approaches through three key components: the Detail Enhancement Module (DEM), a density branch utilizing convolutional networks, and a regression branch leveraging Transformers.
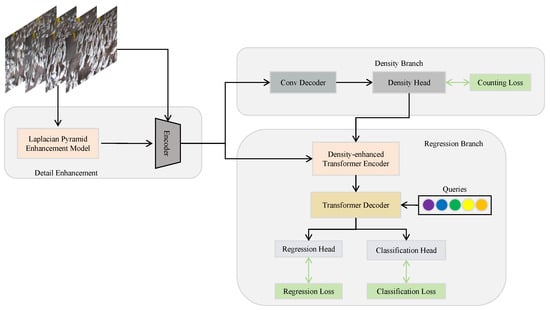
Figure 2.
FE-P Net network architecture.
The DEM enhances edge details using the Laplacian operator and captures multi-scale features via a pyramid module. It highlights duck-specific features while reducing high-frequency background noise through convolutional and pooling operations, thereby mitigating ambiguities caused by low-resolution images. The density branch generates location-sensitive density maps through a convolutional encoder. These maps are shared between the density head and the regression branch, enhancing duck position extraction and preserving spatial context. The regression branch integrates positional information from the density branch with global semantics extracted by the Transformer. This fusion of local details and global context enables highly accurate quantity prediction.
Composed of these components, the architecture ensures synergistic performance, effectively addressing the complexities of large-scale poultry breeding. This enables FE-P Net to achieve accurate meat duck counts even under challenging conditions.
2.3.1. Detail Enhancement Module (DEM)
The overall structure of the DEM is illustrated in Figure 3. It first uses the Laplacian Pyramid Enhancement Model (LPEM) [21], which is based on a pyramid structure, to extract multi-level features from input images. These feature maps are then refined by the Edge Enhancement and Background Noise Reduction Model (EBM), significantly improving their quality and providing a robust foundation for both the density and regression branches. The enhanced high-level features are subsequently upsampled, combined with low-level features, fused with the original image, and finally passed to the encoder.
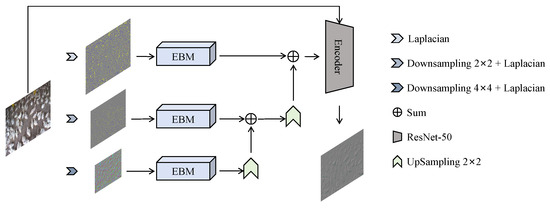
Figure 3.
Detail enhancement model.
The Laplacian pyramid employs a Gaussian kernel to capture multi-scale information. Each Gaussian pyramid operation halves the image dimensions, reducing the resolution to one-fourth of the original. For an input image , involving downsampling and Gaussian filtering , the Gaussian pyramid operation is
Since Gaussian pyramid downsampling is irreversible and leads to information loss, the Laplacian pyramid is employed to enable the reconstruction of the original image:
where and represent the Laplacian pyramid and the Gaussian pyramid at the i-th level, respectively, and is the upsampling function. During image reconstruction, the original image resolution can be restored by performing inverse operations. Ultimately, the Laplacian pyramid generates multi-scale features .
The EBM was designed to enhance local detail extraction and suppress high-frequency noise. It processes multi-scale information through two components: the Edge Enhancement module (illustrated in Figure 4 and the Low-Frequency Filter module.
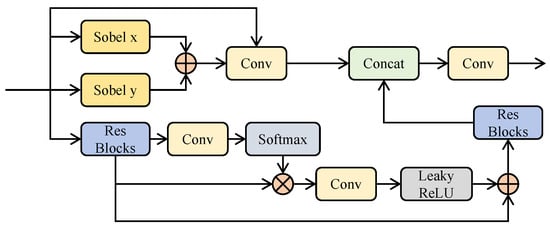
Figure 4.
Structure diagram of the Edge Enhancement module (with context and edge branches).
The context branch captures global context by modeling remote dependencies and processes them with residual blocks to extract semantic features. For a given feature , with as a linear activation function, F as a convolution operation, as a residual block, and as the Softmax function, the processed feature is defined as:
The edge branch utilizes the and operators to process input features, enhancing texture information through gradient extraction. The processed feature is
The concatenated outputs are fused via convolution to generate the final feature .
The Low-Frequency Filter module captures multi-scale low-frequency semantic information, as detailed in Figure 5, enriching the semantic content of images.
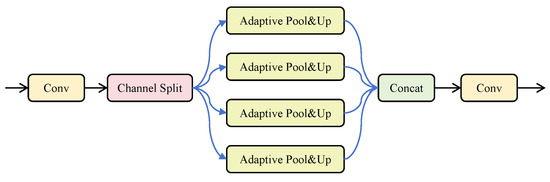
Figure 5.
Low-frequency semantic filter of the Low-Frequency Filter module.
For input features , a convolution adjusts the channel count to 32, yielding features . These features are then separated into channel-wise and filtered components [22] with adaptive average pooling using kernel sizes of , , , and , followed by upsampling. The pooling operation is defined is:
Here, represents the feature component after channel separation, denotes bilinear interpolation upsampling, and refers to adaptive average pooling with varying kernel sizes. The resulting feature tensor is concatenated and processed with a convolution operation to recover .
2.3.2. Density Branch Based on Convolutional Networks
CNNs employ fixed-size kernels to capture local semantic information [22], excelling in extracting detailed local features. However, the similarity in color and texture between the background and objects in our dataset necessitates the EBM to differentiate their features. Convolution operations can introduce redundancy by indiscriminately extracting features across both spatial and channel dimensions [23], potentially impacting final predictions. To address this redundancy, this section integrates a Spatial Reconstruction Unit (SRU) and Channel Reconstruction Unit (CRU) into the convolution branch [24]. The structure of the density branch, based on convolutions, is illustrated in Figure 6.
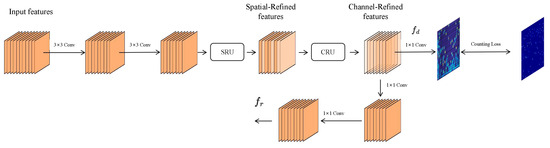
Figure 6.
The structure of the density branch based on convolutions.
The input features first undergo two sequential convolutions to compress the channel dimensions. These features are then refined by SRU and CRU modules to reduce redundancy. Finally, the processed features are used for counting loss calculation and feature fusion in the regression branch. The final expression is
Notably, the convolutional branch incorporates both an SRU and CRU in addition to convolution operations to address information redundancy. The SRU primarily comprises separation and reconstruction stages. The separation stage identifies feature maps rich in spatial information from those with less spatial detail. This is achieved using weight factors from group normalization (GN) layers [25] to evaluate the richness of the feature maps. The GN formula is
where and are the mean and variance of the features in the group, is a trainable factor that evaluates the richness of the feature mapping, is a bias parameter, and is a small positive number to avoid division by zero. To unify the sample distribution and accelerate network convergence, normalization layers process the trainable parameter , yielding the normalized weights . The expression is as follows:
After obtaining the normalized weights, the function processes the weight vector to amplify differences between rich features and coefficient features. The gating unit then inputs the processed weight vectors into two directions. Based on a set threshold , elements greater than are set to 1 (), and those less than or equal to are set to 0 (). The expression for is as follows:
The threshold operation generates two weight vectors, which are then multiplied by the input features to generate and . contains richer feature information, while contains less semantic information. To eliminate redundancy while preserving features, a spatial reconstruction module is designed to restructure the features.
Traditional convolution operations, which use fixed-size kernels for feature extraction along each channel, can introduce channel redundancy. To address this, the CRU module employs a separation and fusion strategy. Specifically, the input features are grouped, and convolutions are applied to compress the channels of these groups, thereby reducing computational costs. The key components GWC [26] and PWC [27] minimize channel redundancy: GWC applies convolutions to the grouped feature maps, while PWC uses convolutions to enhance inter-channel communication. The final output is refined to reduce redundancy and improve efficiency:
where is the trainable weight parameter of the GWC module, and is the learnable parameter of the PWC module in the upper branch. Additionally, is the input to the upper branch.
The lower branch concatenates the PWC-processed image with the original input to obtain the output :
where is the trainable parameter of the PWC module in the lower branch, and is the input to the lower branch.
The features from both branches are then fused. First, the features are concatenated and undergo adaptive pooling to obtain the pooled feature weight vector S:
The obtained weight vector is then used as a weighting coefficient to scale the original features. Finally, with and representing the sums of vectors derived from adaptive average pooling operations, the weighted features are aggregated to produce final output:
2.3.3. Regression Branch Based on Transformer
The regression branch comprises three main components: a density-enhanced encoder based on the Transformer (DETE), a Transformer decoder [28], and a regression head. Unlike traditional Transformer encoders, the DETE module enhances feature extraction by integrating outputs from a convolutional branch. This integration enables more precise capture of both global semantic information and local detail features, improving the precision of duck localization and quantity estimation. The detailed architecture of the DETE module is illustrated in Figure 7.
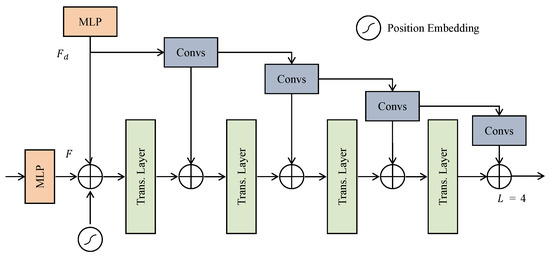
Figure 7.
The density-enhanced encoder based on the Transformer.
The module maps the information extracted by the detail enhancement module to while simultaneously mapping the features extracted by the density branch to . These features are then combined with positional embeddings and fed into a Transformer layer. The expressions for this process are as follows:
Here, represents the flattening of feature maps for subsequent Transformer processing, and represents the Transformer layer. The module consists of four layers, with each layer processing features as follows:
where represents convolution operations. The DETE module merges the output of the previous layer with the convolved density features before each Transformer layer. This process gradually combines global and local information, enabling the extraction of richer and more accurate features. After processing by the DETE module, the resulting feature maps contain precise information. The Transformer decoder then takes the obtained features and trainable query vectors as inputs, and outputs the decoded embedding vectors .
2.3.4. Loss Function
After forward propagation, the classification head maps the output to a confidence score vector, and the regression head maps it to point coordinates [20]. Assuming the query results are , where is the predicted confidence score for the pixel corresponding to the target, and are the network-predicted coordinates. These predictions are compared with ground truth points . By setting , each ground truth point can be matched with one prediction using the Hungarian algorithm [29]. To compute the average distance difference, first the average distances from the prediction to other points and from the corresponding ground truth to other points are calculated. For the i-th ground truth point and its corresponding prediction point , first the average distances and are computed:
With being the confidence score of the i-th prediction point, the cost function is
After determining the matching relationships between prediction points and ground truth points, the classification loss evaluates the confidence loss for each point. A higher loss function value indicates that the features around the point are more distinct from the target object. This loss is calculated using binary cross-entropy:
During loss calculation, the predicted confidence values are first mapped to the range [0, 1]. To make the predicted coordinates closer to the true values, the classification loss is used to express the difference between predictions and labels:
With being the weight for the density branch loss, and denoting the density branch loss. The overall loss function is
2.4. Implementation Details
The experiment used Linux Ubuntu 20.04 with 32 GB RAM and a 2080Ti GPU, using Python 3.7.13 and PyTorch 1.13.0. The parameters were initialized using the Kaiming uniform distribution initialization method. The Adam optimizer was used with a weight decay of 0.0005. Training ran for 3500 iters with an initial learning rate of 0.00001, which was reduced to 0.1 times its value at the 1200th epoch using MultiStepLR.
2.5. Evaluation Metrics
The evaluation metrics used for flow counting were MAE and MSE. MAE measures the difference between predicted individual counts and ground truth counts:
where N is the quantity of prediction images, and are the predicted and true values for the i-th image, respectively, and denotes the absolute value. In counting tasks, MAE represents the average error in estimating individual counts; a smaller MAE indicates more accurate predictions. However, MAE does not highlight outliers. MSE, which uses squared differences to emphasize larger errors and highlight outliers, is defined by the formula:
3. Results
3.1. Count Result Analysis
Figure 8 shows the prediction results of our method. Specifically, (a) represents the original images in the dataset, (b) shows the visualized label values generated from the annotation files, (c) displays the density map predicted by the convolution branch, and (d) shows the coordinate results regressed by the regression branch.

Figure 8.
The prediction results of our method: (a) is the original image in the dataset, (b) is the visual label value generated based on the annotation file, (c) is the density map predicted by the convolution branch, (d) is the coordinate result of the regression branch regression.
Table 1 compares the segmentation accuracy of various models on the broiler counting dataset. Compared to the classical convolutional networks MFF [30] and P2PNet [31], our method improves MAE by 2.92 and 1.63, and improves MSE by 2.95 and 0.90, achieving accuracy improvements of 3.45% and 1.68%, respectively. Compared to Transformer-based models MAN [32] and CCST [33], our method improves the MAE by 1.14 and 0.87, and MSE by 1.11 and 0.48, achieving improvements of 1.38% and 1.01%, respectively. Overall, Transformer-based detectors show higher accuracy than convolutional network-based detectors. This is because convolution operations are sensitive to fine-grained local semantic information but can fail to some extent when extracting features from low-resolution images. Our method achieved a mean absolute error of 3.02 and an accuracy of 96.46% on the meat duck dataset, showing improvements over other models, which means that our method can better detect individual broilers in poultry house environments.

Table 1.
Comparison of counting accuracy among models.
Figure 9 shows that Transformer-based networks excel in high-density scenarios, while convolution-based networks perform better in low-density areas. Transformers use an attention mechanism to capture long-range dependencies, improving detection of closely spaced objects without misidentifying the background. In contrast, convolutional networks effectively capture local features and edges due to their receptive fields, aiding precise object localization. Our method integrates density features from convolution branches with Transformer-extracted features using a density-fused Transformer encoder. This approach balances global semantics and local details, enhancing overall detection performance.

Figure 9.
Results of different segmentation models.
3.2. Ablation Experiments
Ablation experiments were conducted to evaluate the impact of the various substructures on model performance. Our method includes two branches and a detail enhancement module. Several ablation studies were designed to validate their effectiveness, with the results shown in Table 2.

Table 2.
Ablation experiments for the different modules.
Without the convolution branch, the model’s MAE increased to 8.44 and the MSE to 10.29. This increase is attributed to the failure of the density-enhanced Transformer encoder and the counting loss strategy used by the convolution branch, rendering the loss strategy ineffective. Adding the convolution branch significantly improved performance, reducing MAE to 4.15 and MSE to 4.95. Incorporating the LPEM module further enhanced feature representation, mitigating low-resolution image issues and improving object localization and edge detection, which lowered the MSE to 3.56. Finally, adding the SCCONV module to the convolution branch eliminated feature redundancy, allowing the Transformer encoder to integrate more precise features and reduce noise, ultimately lowering the error to 3.01. These experiments demonstrate the positive contributions of each module and validate the superiority of the dual-branch structure.
The encoder plays a crucial role in feature extraction, generating feature maps from input images to support subsequent detection tasks. Selecting an appropriate feature extraction network can significantly enhance model performance. This section evaluates the use of different feature extraction networks as the backbone encoder through a series of experiments, with the results shown in Table 3.

Table 3.
Ablation experiments for the different feature extraction networks.
The experimental results indicate that using ResNet-50 [34] as the backbone encoder achieves the best performance. Shallower networks such as ResNet-18 and ResNet-34 offer faster inference but provide less comprehensive feature extraction, leading to reduced accuracy. In contrast, using ResNet-101 as the encoder results in over-extraction due to its deeper layers, which also decreases accuracy.
4. Conclusions
In practical production environments, image quality is often low, and traditional bounding box annotation methods are labor-intensive. Our study introduces the FE-P Net architecture, which uses point annotations combined with a feature enhancement module to refine image features and improve detection accuracy. This approach offers a novel solution for enhancing poultry counting accuracy in farming scenarios.
Unlike existing methods that struggle with low-resolution images, FE-P Net employs a dual-branch architecture to integrate local detail extraction and global semantic understanding. By refining edge details and enhancing feature representations while reducing redundancy in both the spatial and channel dimensions, FE-P Net effectively mitigates issues related to low resolution, blurred edges, and uneven lighting. This results in significant performance improvements, achieving 96.46% accuracy on the meat duck dataset. Comparative experiments confirm that FE-P Net outperforms other models on this dataset, successfully completing the counting task. Ablation studies further validate the contributions of each module to overall network performance.
The findings have profound practical implications for poultry breeding. Deploying FE-P Net in real-time monitoring systems enables automated and accurate population counts, crucial for optimizing space utilization, improving animal welfare, and enhancing farm management efficiency. The use of point annotations significantly reduces the labor required for labeling, facilitating scalable deployment across large farming operations. However, there are areas for improvement. Eye-based point annotations require precise calibration, especially in highly crowded scenes with frequent occlusions. Further research should explore the model’s robustness under varying lighting and environmental conditions. Combining FE-P Net with larger models could enhance performance and adaptability.
In conclusion, this study advances the application of deep learning techniques in poultry breeding management. By addressing key challenges in image quality and object density, FE-P Net provides a promising solution for automating meat duck counting. As agriculture continues its digital transformation, innovations like ours will be essential in driving productivity and sustainability.
Author Contributions
Conceptualization, W.T. and H.Q.; methodology, W.T. and M.L.; software, W.T.; validation, H.Q., X.C. and T.W.; formal analysis, Y.E.X.; investigation, X.C. and S.S.; resources, X.C. and S.S.; data curation, W.T.; writing—original draft preparation, W.T.; writing—review and editing, H.Q., M.L. and X.C.; visualization, H.Q.; supervision, X.C.; project administration, X.C. and M.L.; funding acquisition, Y.E.X. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key R&D Program of Xinjiang Uygur Autonomous Region (Grant No. 2022B02027-1 and 2023B02013-2), the Xinjiang Uygur Autonomous Region “Tianchi Talent” Introduction Program (Grant No. 20221100619) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20210408).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to they were collected in privately-owned poultry facilities.
Acknowledgments
The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pereira, P.M.D.C.C.; Vicente, A.F.D.R.B. Meat nutritional composition and nutritive role in the human diet. Meat Sci. 2013, 93, 586–592. [Google Scholar] [CrossRef] [PubMed]
- Pettit-Riley, R.; Estevez, I. Effects of density on perching behavior of broiler chickens. Appl. Anim. Behav. Sci. 2001, 71, 127–140. [Google Scholar] [PubMed]
- Jiang, K.; Xie, T.; Yan, R.; Wen, X.; Li, D.; Jiang, H.; Jiang, N.; Feng, L.; Duan, X.; Wang, J. An Attention Mechanism-Improved YOLOv7 Object Detection Algorithm for Hemp Duck Count Estimation. Agriculture 2022, 12, 1659. [Google Scholar] [CrossRef]
- Fan, P.; Yan, B. Research on the Application of New Technologies and Products in Intelligent Breeding. Livest. Poult. Ind. 2023, 34, 36–38. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation; IEEE Computer Society: Washington, DC, USA, 2014. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, D.; Chen, S.; Gao, S.; Ma, Y. Single-Image Crowd Counting via Multi-Column Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Cao, L.; Xiao, Z.; Liao, X.; Yao, Y.; Wu, K.; Mu, J.; Li, J.; Pu, H. Automated Chicken Counting in Surveillance Camera Environments Based on the Point Supervision Algorithm: LC-DenseFCN. Agriculture 2021, 11, 493. [Google Scholar] [CrossRef]
- Laradji, I.H.; Rostamzadeh, N.; Pinheiro, P.O.; Vazquez, D.; Schmidt, M. Where Are the Blobs: Counting by Localization with Point Supervision; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Huang, G.; Liu, Z.; Laurens, V.D.M.; Weinberger, K.Q. Densely Connected Convolutional Networks; IEEE Computer Society: Washington, DC, USA, 2016. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. FCOS: Fully Convolutional One-Stage Object Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 27–2 November 2020. [Google Scholar]
- Ooro-Rubio, D.; López-Sastre, R.J. Towards Perspective-Free Object Counting with Deep Learning. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Wu, J.; Zhou, Y.; Yu, H.; Zhang, Y.; Li, J. A Novel Fish Counting Method with Adaptive Weighted Multi-Dilated Convolutional Neural Network; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Li, W.; Zhu, Q.; Zhang, H.; Xu, Z.; Li, Z. A lightweight network for portable fry counting devices. Appl. Soft Comput. 2023, 136, 110140. [Google Scholar]
- Sun, G.; An, Z.; Liu, Y.; Liu, C.; Sakaridis, C.; Fan, D.; Gool, L.V. Indiscernible Object Counting in Underwater Scenes. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 13791–13801. [Google Scholar]
- Hu, M.; Wang, S.; Li, B.; Ning, S.; Fan, L.; Gong, X. PENet: Towards Precise and Efficient Image Guided Depth Completion. arXiv 2021, arXiv:2103.00783. [Google Scholar]
- Wang, B.; Liu, H.; Samaras, D.; Hoai, M. Distribution Matching for Crowd Counting. arXiv 2020, arXiv:2009.13077. [Google Scholar]
- Liang, D.; Xu, W.; Bai, X. An End-to-End Transformer Model for Crowd Localization. arXiv 2022, arXiv:2202.13065. [Google Scholar]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Li, J.; Wen, Y.; He, L. SCConv: Spatial and Channel Reconstruction Convolution for Feature Redundancy. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 6153–6162. [Google Scholar]
- Wu, Y.; He, K. Group Normalization; Springer: New York, NY, USA, 2018. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks; NIPS: Grenada, Spain, 2012. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. arXiv 2020, arXiv:2005.12872. [Google Scholar]
- Zhang, X. Deep Learning-based Multi-focus Image Fusion: A Survey and A Comparative Study. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4819–4838. [Google Scholar]
- Yin, K.; Huang, H.; Cohen-Or, D.; Zhang, H. P2P-NET: Bidirectional Point Displacement Net for Shape Transform. ACM Trans. Graph. 2018, 37, 152.1–152.13. [Google Scholar] [CrossRef]
- Lin, H.; Ma, Z.; Ji, R.; Wang, Y.; Hong, X. Boosting Crowd Counting via Multifaceted Attention. arXiv 2022, arXiv:2203.02636. [Google Scholar]
- Li, B.; Zhang, Y.; Xu, H.; Yin, B. CCST: Crowd counting with swin transformer. Vis. Comput. 2022, 39, 2671–2682. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).