Performance Investigation of Coated Carbide Tools in Milling Procedures
Abstract
1. Introduction
2. Materials and Methods
2.1. Coated Cutting Tools and Workpiece
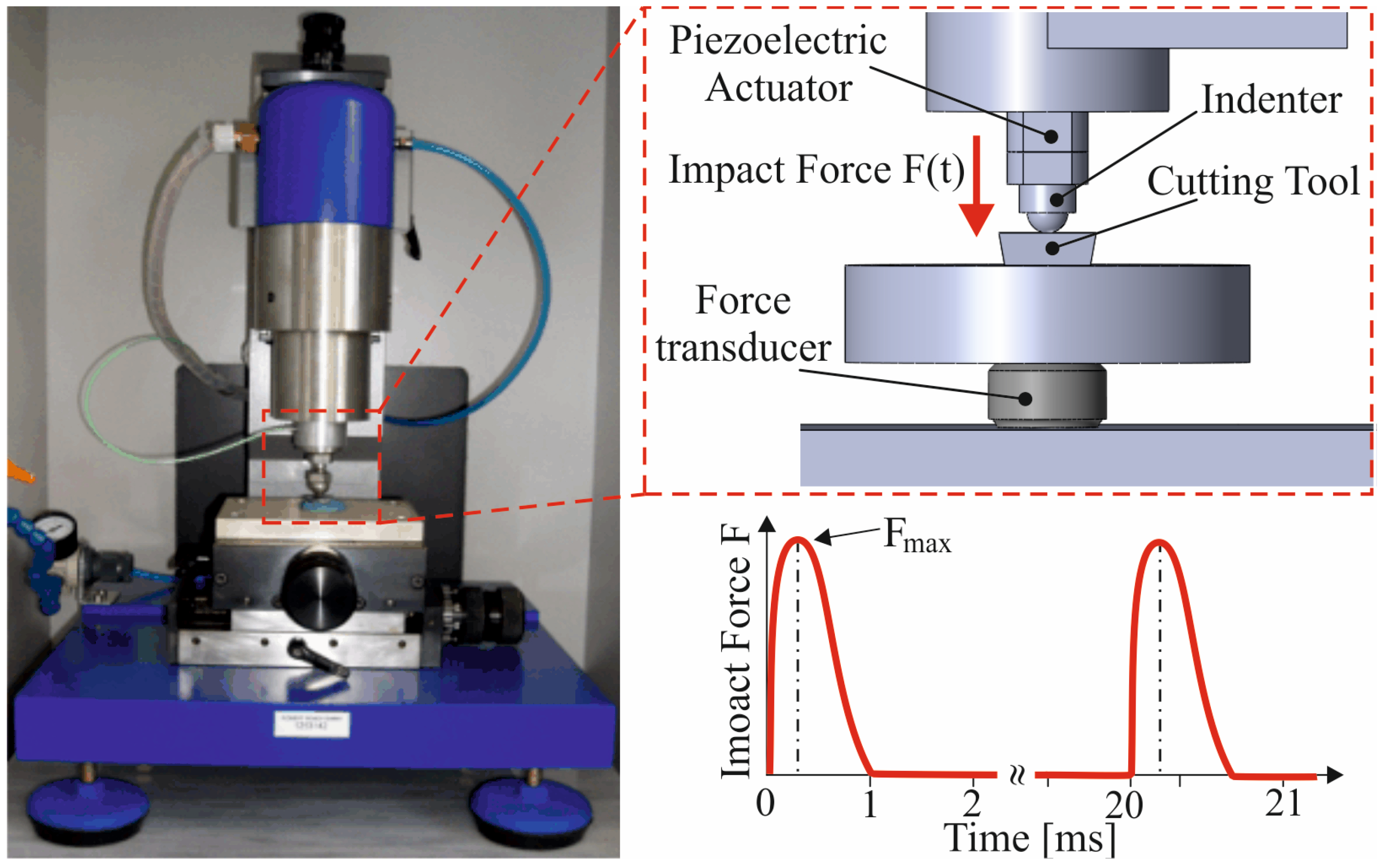
2.2. Perpendicular Impact Test
2.3. Milling Investigations
3. Results
3.1. Machine Learning Models
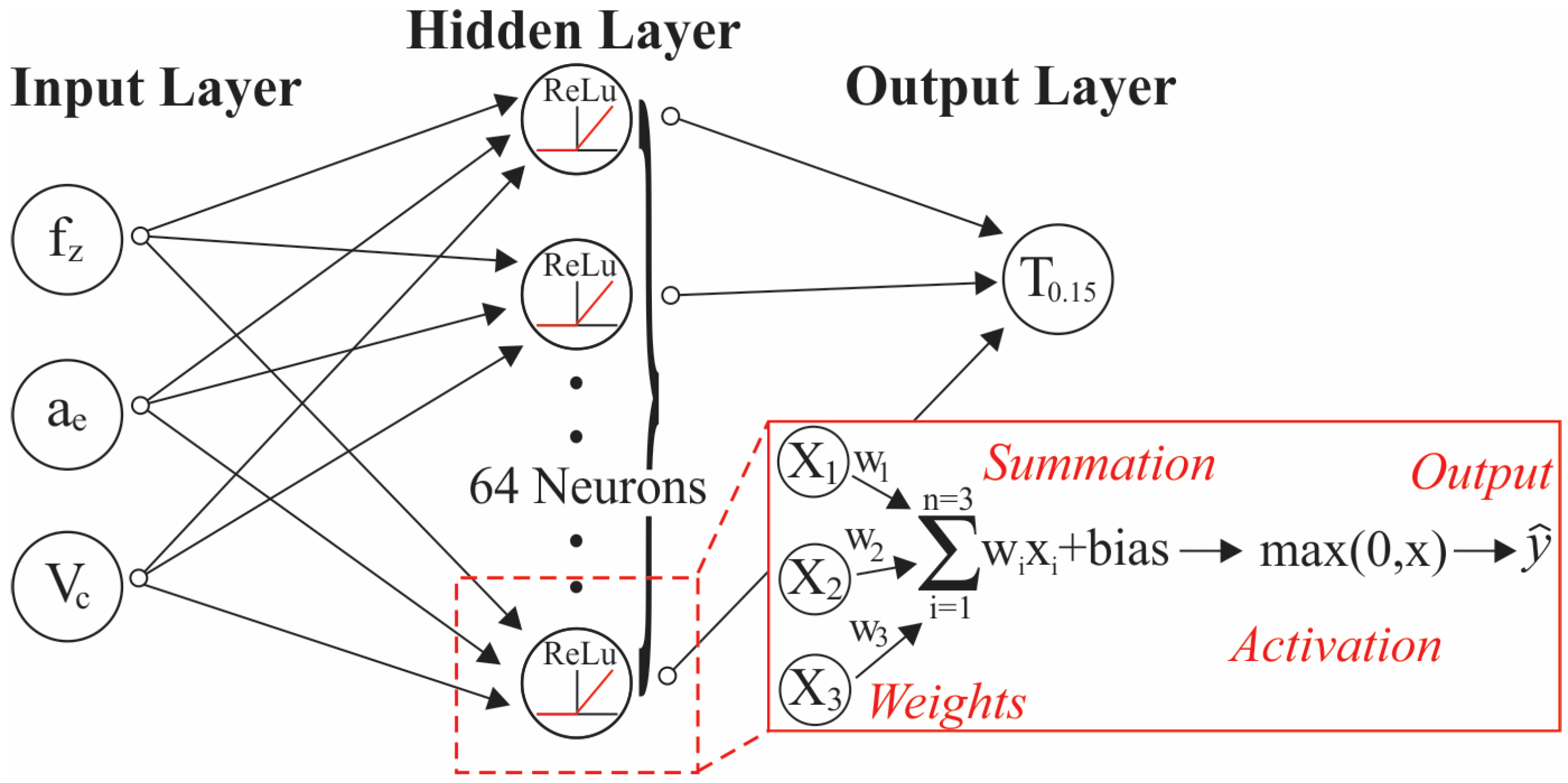
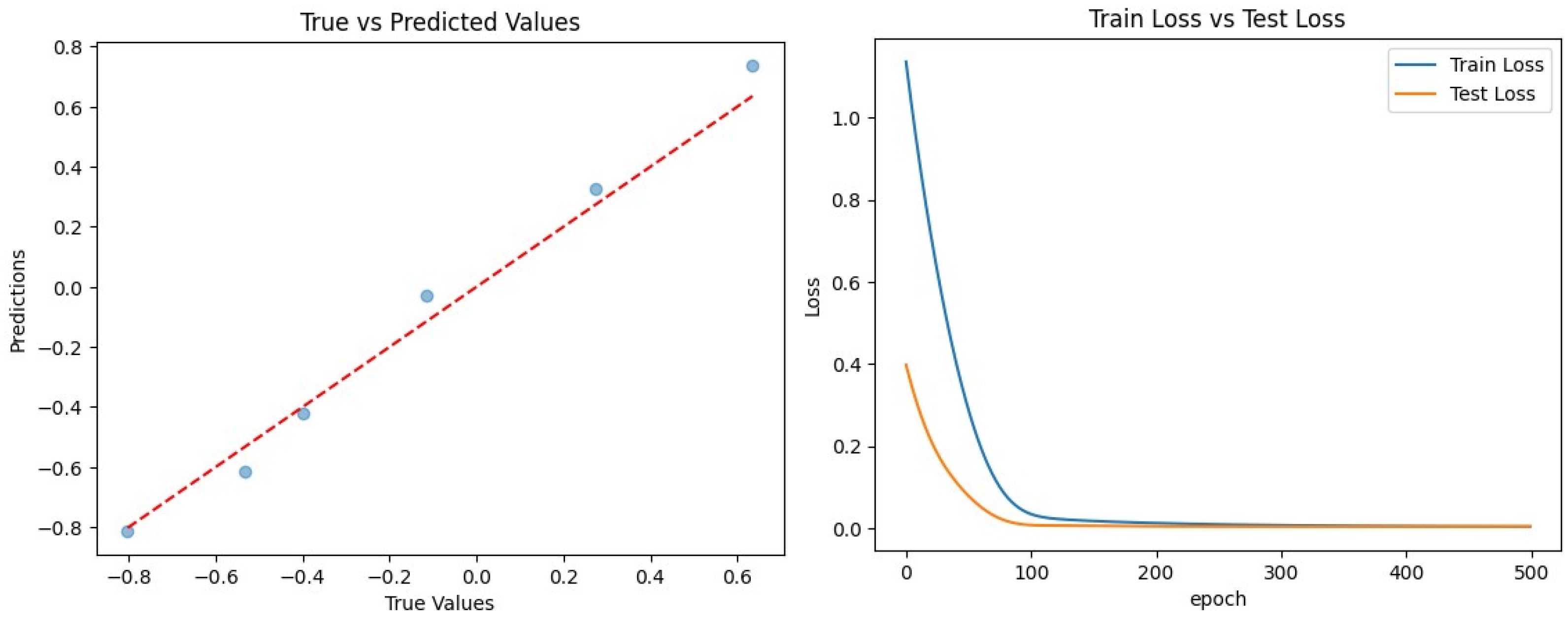
3.1.1. Artificial Neural Network
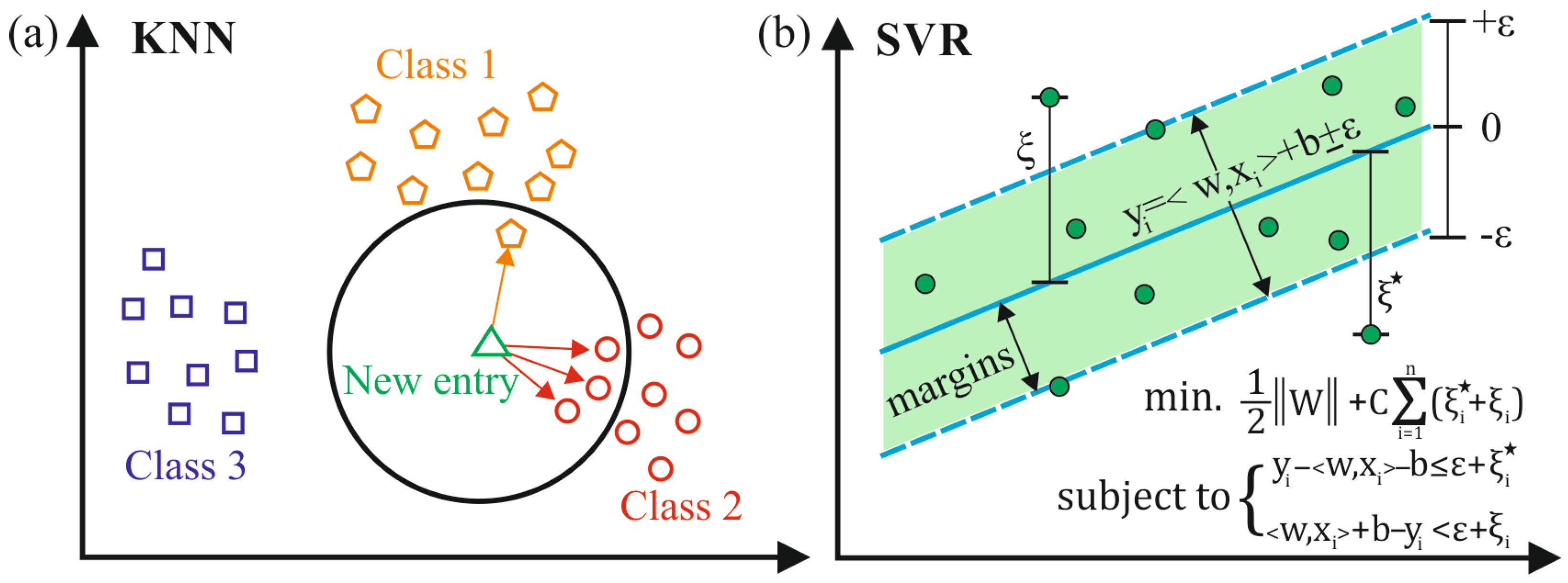
3.1.2. Regression with KNN and SVR
3.2. Tool Performance Estimation Using FEA
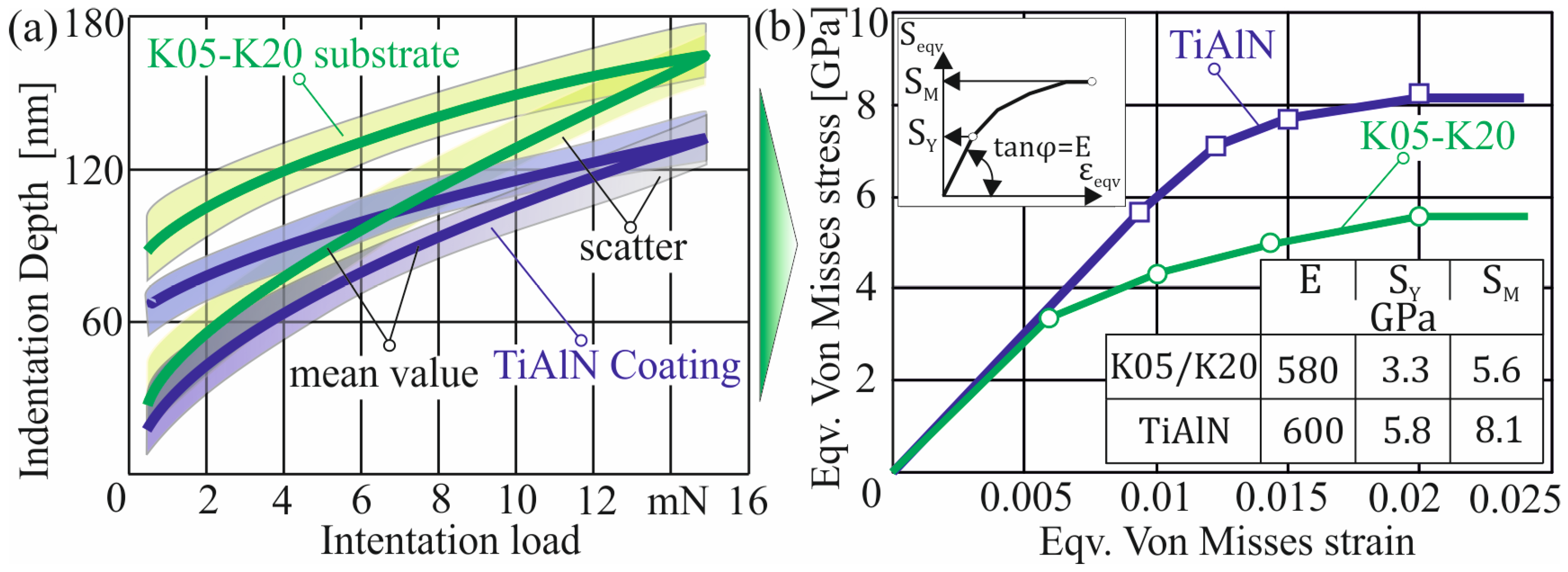
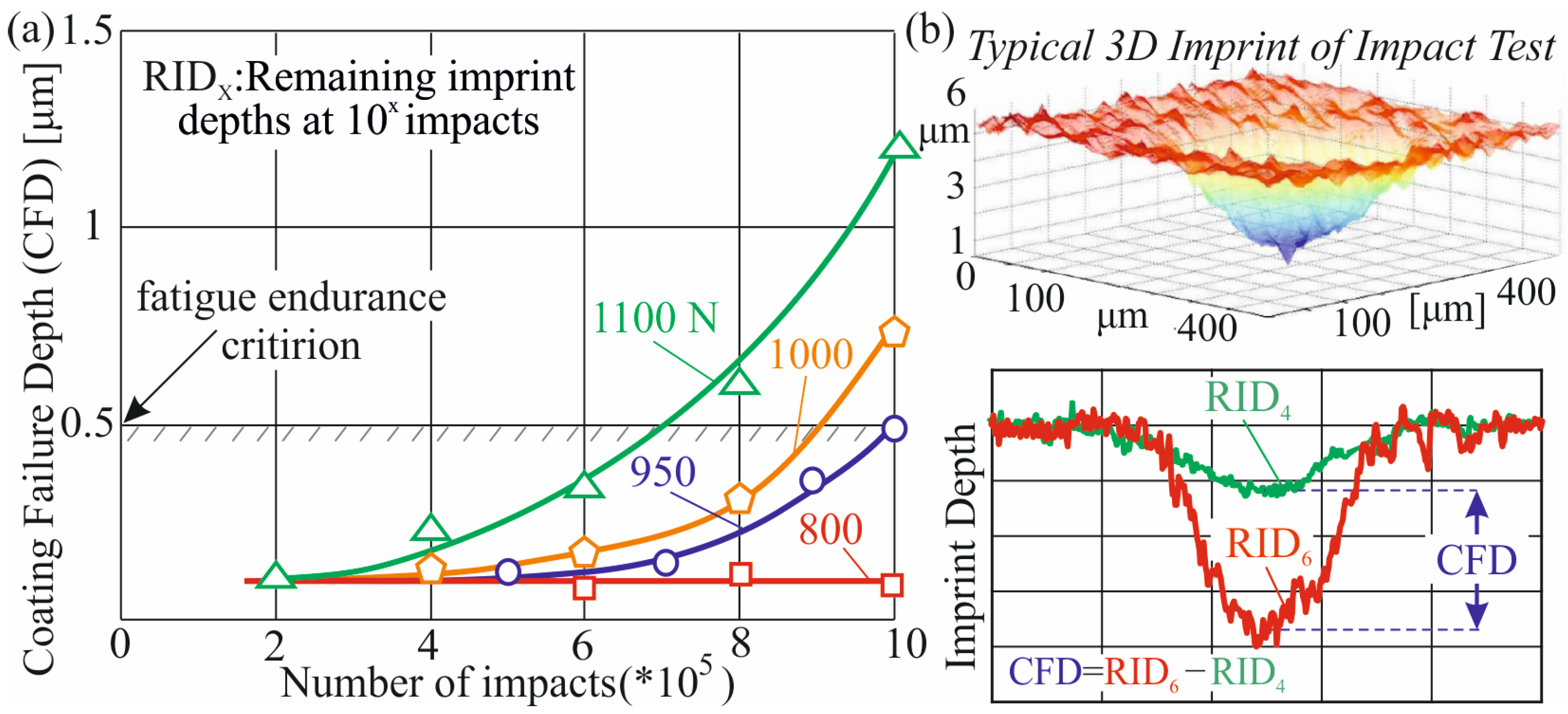
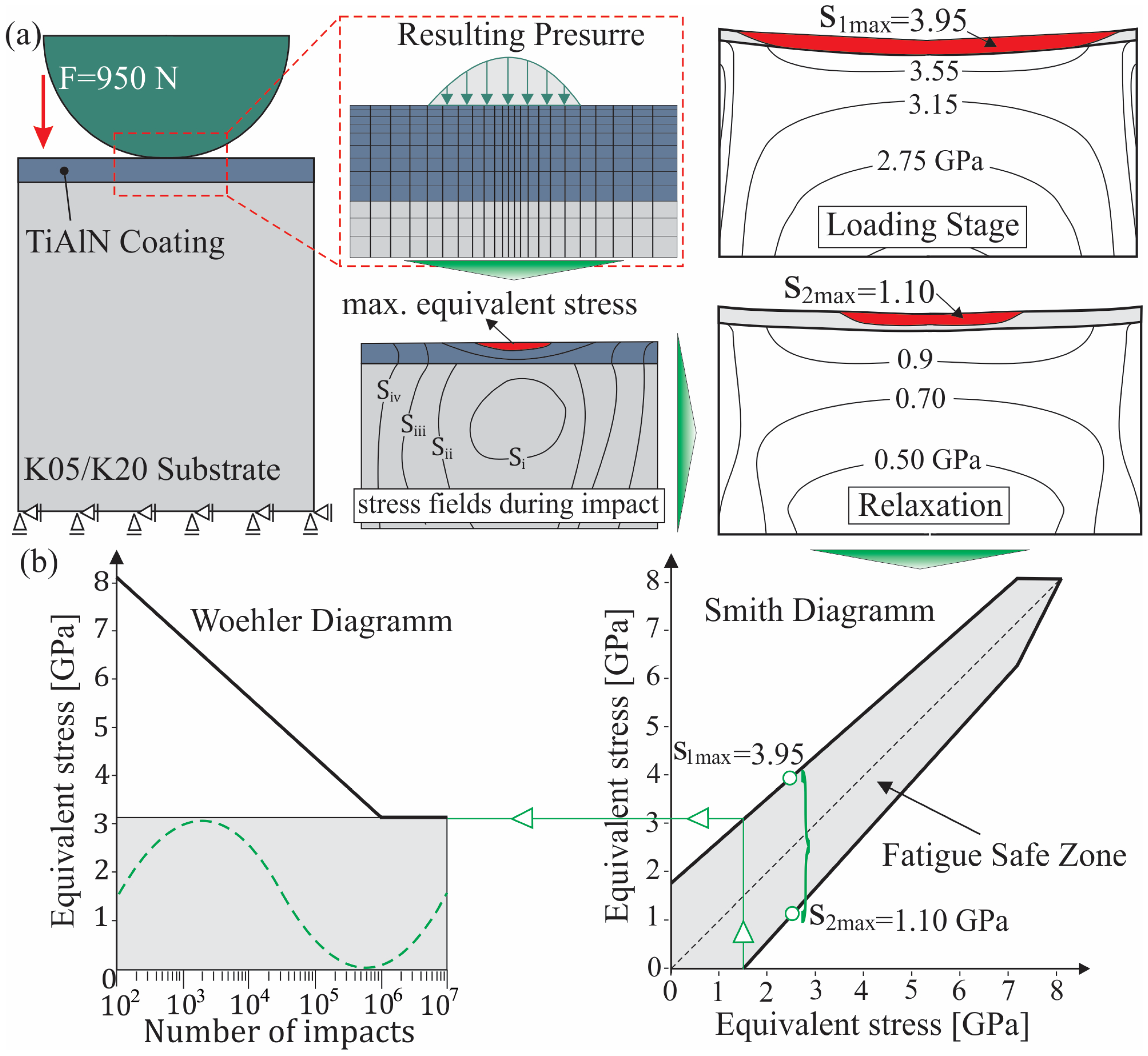
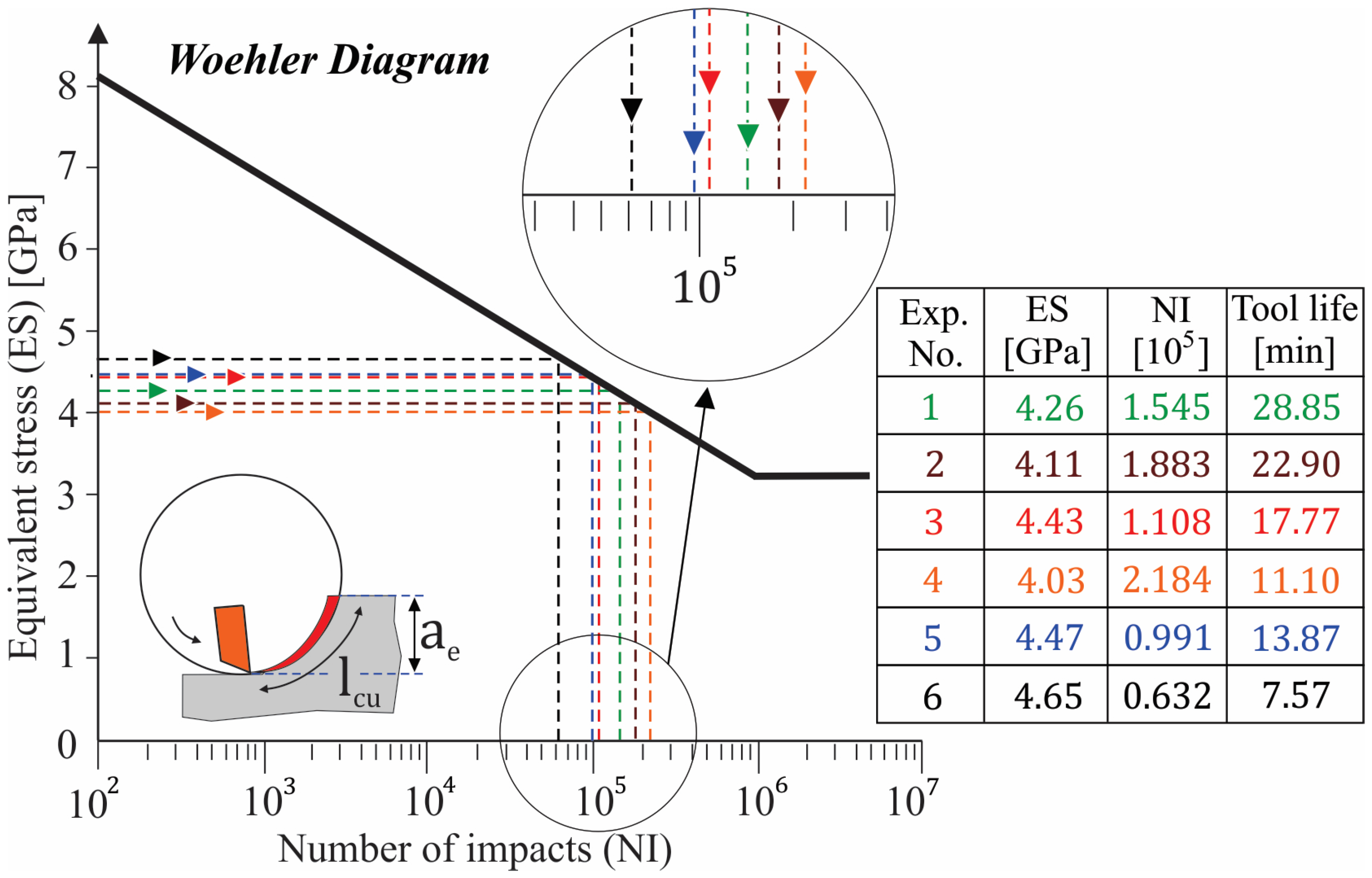
3.2.1. Fatigue Endurance Strength Determination
3.2.2. Stress Distribution During the Milling Process
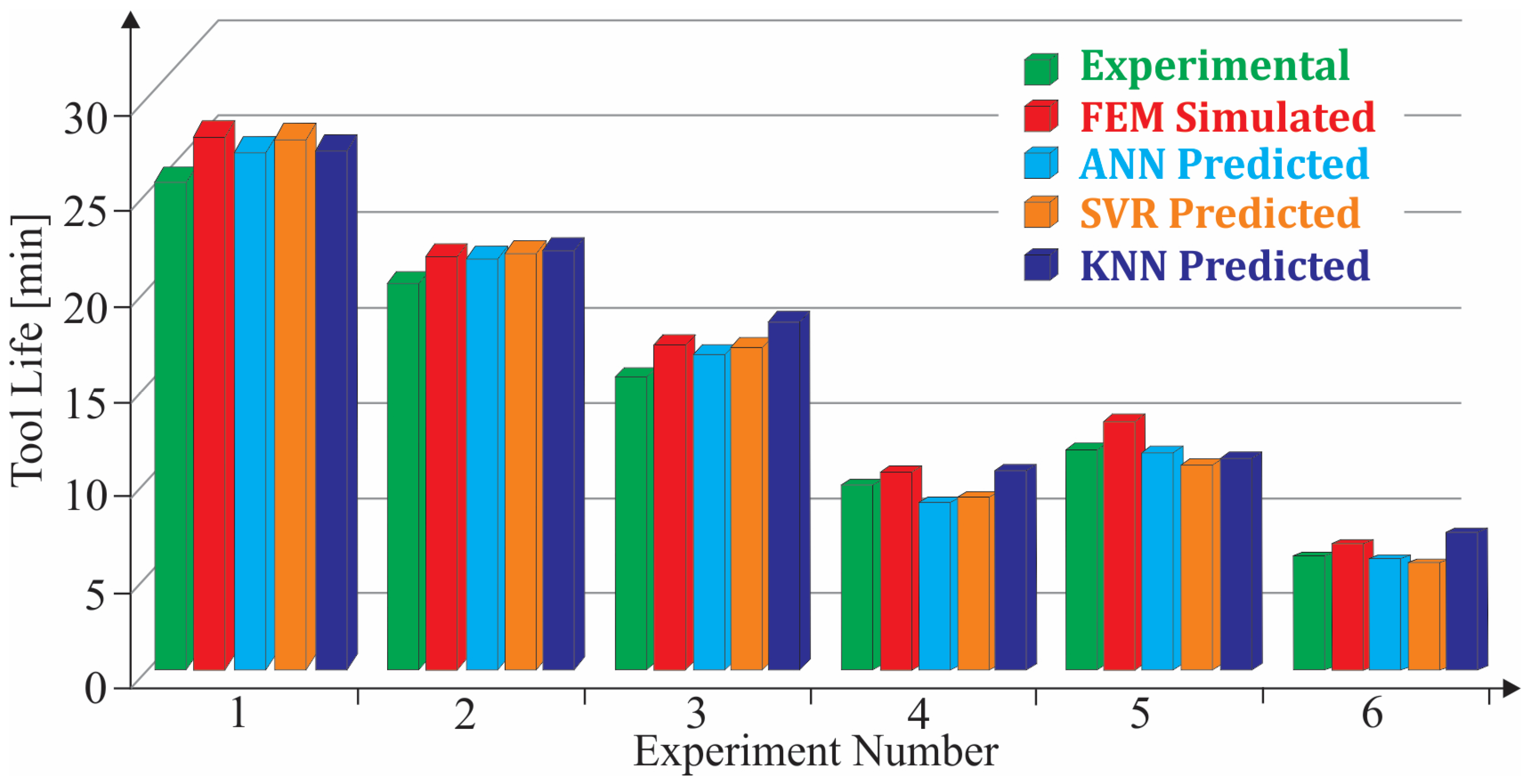
3.3. Comparison of Learning-Based Models and FEM-Supported Simulations
3.4. Cutting Tool Performance Optimization
| Algorithm 1: Pseudocode for the parameter’s optimization pipeline |
| Input: Vcmin, Vcmax: min., max. Cutting speed aemin, aemax: min., max. Radial depth fzmin, fzmax: min., max. Feed rate Vstep, astep, fstep: Step increments 1: initialize: Vc = Vcmin, ae = aemin, fz = fzmin 2: global_max = 0 3: for Vc = Vcmin && Vc ≤ Vcmax 4: for ae = Vcmin && ae ≤ aemax 5: for fz = fzmin && fz ≤ fzmax 6: tensor_data = X (Vc, ae, fz) 7: Tool_Life_Prediction = Model(tensor_data) 8: if Tool_Life_Prediction > global_max then 9: Vcopt = Vc, aeopt = ae, fzopt = fz 10: global_ max = Tool_Life_Prediction 11: end if 12: fz = fz + fstep 13: end for 14: ae = ae + astep 15: end for 16: Vc = Vc + Vstep 17: end for 18: return global_ max, Vcopt, aeopt, fzopt Output: Optimized Manufacturing Conditions (Vc = 100, ae = 20, fz = 0.2) |
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W. Advanced Manufacturing and Precision Machining. Appl. Sci. 2024, 14, 11642. [Google Scholar] [CrossRef]
- Silva, F.J.G.; Martinho, R.P.; Magalhães, L.L.; Fernandes, F.; Sales-Contini, R.C.M.; Durão, L.M.; Casais, R.C.B.; Sousa, V.F.C. A Comparative Study of Different Milling Strategies on Productivity, Tool Wear, Surface Roughness, and Vibration. J. Manuf. Mater. Process. 2024, 8, 115. [Google Scholar] [CrossRef]
- Abellán-Nebot, J.V.; Vila Pastor, C.; Siller, H.R. A Review of the Factors Influencing Surface Roughness in Machining and Their Impact on Sustainability. Sustainability 2024, 16, 1917. [Google Scholar] [CrossRef]
- Sambo, A.M.; Younas, M.; Njuguna, J. Insights into Machining Techniques for Additively Manufactured Ti6Al4V Alloy: A Comprehensive Review. Appl. Sci. 2024, 14, 10340. [Google Scholar] [CrossRef]
- Sousa, V.F.C.; Castanheira, J.; Silva, F.J.G.; Fecheira, J.S.; Pinto, G.; Baptista, A. Wear Behavior of Uncoated and Coated Tools in Milling Operations of AMPCO (Cu-Be) Alloy. Appl. Sci. 2021, 11, 7762. [Google Scholar] [CrossRef]
- Sousa, V.F.C.; Silva, F.J.G. Recent Advances on Coated Milling Tool Technology—A Comprehensive Review. Coatings 2020, 10, 235. [Google Scholar] [CrossRef]
- Muhamad, S.S.; Ghani, J.A.; Che Haron, C.H.; Yazid, H. Wear Mechanism of Multilayer Coated Carbide Cutting Tool in the Milling Process of AISI 4340 under Cryogenic Environment. Materials 2022, 15, 524. [Google Scholar] [CrossRef]
- Chowdhury, M.S.I.; Bose, B.; Rawal, S.; Fox-Rabinovich, G.S.; Veldhuis, S.C. Investigation of the Wear Behavior of PVD Coated Carbide Tools during Ti6Al4V Machining with Intensive Built Up Edge Formation. Coatings 2021, 11, 266. [Google Scholar] [CrossRef]
- Bazaz, S.M.; Ratava, J.; Lohtander, M.; Varis, J. An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis. Machines 2023, 11, 393. [Google Scholar] [CrossRef]
- Paszkiewicz, A.; Piecuch, G.; Żabiński, T.; Bolanowski, M.; Salach, M.; Rączka, D. Estimation of Tool Life in the Milling Process—Testing Regression Models. Sensors 2023, 23, 9346. [Google Scholar] [CrossRef]
- Charalampous, P. Prediction of cutting forces in milling using machine learning algorithms and finite element analysis. J. Mater. Eng. Perform. 2021, 30, 2002–2013. [Google Scholar] [CrossRef]
- Reeber, T.; Wolf, J.; Möhring, H.-C. A Data-Driven Approach for Cutting Force Prediction in FEM Machining Simulations Using Gradient Boosted Machines. J. Manuf. Mater. Process. 2024, 8, 107. [Google Scholar] [CrossRef]
- Rodríguez, J.M.; Carbonell, J.M.; Jonsén, P. Numerical Methods for the Modelling of Chip Formation. Arch. Comput. Methods Eng. 2020, 27, 387–412. [Google Scholar] [CrossRef]
- Vishwakarma, P.; Sharma, A. 3D Finite Element Analysis of milling process for non-ferrous metal using deform-3D. Mater. Today Proc. 2020, 26, 525–528. [Google Scholar] [CrossRef]
- Munaro, R.; Attanasio, A.; Del Prete, A. Tool Wear Monitoring with Artificial Intelligence Methods: A Review. J. Manuf. Mater. Process. 2023, 7, 129. [Google Scholar] [CrossRef]
- Val, S.; Lambán, M.P.; Lucia, J.; Royo, J. Analysis and Prediction of Wear in Interchangeable Milling Insert Tools Using Artificial Intelligence Techniques. Appl. Sci. 2024, 14, 11840. [Google Scholar] [CrossRef]
- Kaliyannan, D.; Thangamuthu, M.; Pradeep, P.; Gnansekaran, S.; Rakkiyannan, J.; Pramanik, A. Tool Condition Monitoring in the Milling Process Using Deep Learning and Reinforcement Learning. J. Sens. Actuator Netw. 2024, 13, 42. [Google Scholar] [CrossRef]
- Gao, P.; Liang, Z.; Wang, X.; Li, S.; Zhou, T. Effects of different chamfered cutting edges of micro end mill on cutting performance. Int. J. Adv. Manuf. Technol. 2018, 96, 1215–1224. [Google Scholar] [CrossRef]
- Skordaris, G.; Bouzakis, K.-D.; Charalampous, P.; Kotsanis, T.; Bouzakis, E.; Bejjani, R. Bias Voltage Effect on the Mechanical Properties, Adhesion and Milling Performance of PVD Films on Cemented Carbide Inserts. Wear 2018, 404–405, 50–61. [Google Scholar] [CrossRef]
- Uddeholm. Available online: http://www.uddeholm.gr/Storage/Media/Shared/SteelBrochures/Impax%20Supreme/PB_impax_supreme_english.pdf (accessed on 1 March 2025).
- Abbas, A.T.; Abdelnasser, E.; Naeim, N.; Alqosaibi, K.F.; Al-Bahkali, E.A.; Elkaseer, A. Effect of Milling Strategy on the Surface Quality of AISI P20 Mold Steel. Metals 2024, 14, 48. [Google Scholar] [CrossRef]
- Wang, T.; Zha, X.; Chen, F.; Wang, J.; Lin, L.; Xie, H.; Lin, F.; Jiang, F. Research on cutting performance of coated cutting tools by a new impact test method considering contact stress condition caused by segmented chips. J. Manuf. Process. 2021, 68, 1569–1584. [Google Scholar] [CrossRef]
- Bouzakis, E.; Bouzakis, K.-D.; Skordaris, G.; Charalampous, P.; Kombogiannis, S.; Lemmer, O. Fatigue strength of diamond coating-substrate interface assessed by inclined impact tests at ambient and elevated temperatures. Diam. Relat. Mater. 2014, 50, 77–85. [Google Scholar] [CrossRef]
- Sevgin, F. Machine Learning-Based Temperature Forecasting for Sustainable Climate Change Adaptation and Mitigation. Sustainability 2025, 17, 1812. [Google Scholar] [CrossRef]
- Shobayo, O.; Adeyemi-Longe, S.; Popoola, O.; Okoyeigbo, O. A Comparative Analysis of Machine Learning and Deep Learning Techniques for Accurate Market Price Forecasting. Analytics 2025, 4, 5. [Google Scholar] [CrossRef]
- Bouzakis, K.-D.; Asimakopoulos, A.; Michailidis, N.; Kompogiannis, S.; Maliaris, G.; Giannopoulos, G.; Pavlidou, E.; Erkens, G. The inclined impact test, an efficient method to characterize coatings’ cohesion and adhesion properties. Thin Solid Film. 2004, 469–470, 254–262. [Google Scholar] [CrossRef]


| AISI P20 Steel | |||||
|---|---|---|---|---|---|
| Composition In weight % | C | Si | Cr | Mn | Ni |
| 0.37 | 0.3 | 2.0 | 1.4 | 2.0 | |
| Mechanical Properties | Tensile Strength (MPa) | Yield Strength (MPa) | Hardness (HRΒ) | Elastic Modulus (GPa) | Fracture Elongation A [%] |
| 900 | 1020 | 310 | 205 | 20 | |
| fz = 0.1 [mm/rev] | fz = 0.3 | fz = 0.5 | fz = 1 | |
|---|---|---|---|---|
| ae [mm] | V = 100 [m/min] | |||
| ae = 1 | 31.08 [min] | 32.25 | 28.88 | 25.72 |
| ae = 3 | 32.59 | 34.56 | 30.41 | 27.02 |
| ae = 13 | 38.71 | 40.88 | 36.37 | 31.64 |
| ae = 20 | 43.49 | 45.3 | 41.64 | 35.85 |
| V = 200 | ||||
| ae = 1 | 11.44 | 12.56 | 10.18 | 9.22 |
| ae = 3 | 12.15 | 13.42 | 10.85 | 9.98 |
| ae = 13 | 17.32 | 18.78 | 15.51 | 13.92 |
| ae = 20 | 23.09 | 24.56 | 21.75 | 18.09 |
| V = 300 | ||||
| ae = 1 | 2.72 | 3.01 | 2.35 | 2 |
| ae = 3 | 3.11 | 3.42 | 2.56 | 2.14 |
| ae = 13 | 4.34 | 4.88 | 3.32 | 2.91 |
| ae = 20 | 4.91 | 5.57 | 3.78 | 3.21 |
| Algorithm | Exper. No. | Vc [m/min] | ae [mm] | fz [mm] | MSE/ MAE | Prediction | Measured | Error % |
|---|---|---|---|---|---|---|---|---|
| SVR | 1 | 125 | 8 | 0.40 | 1.502/ 1.070 | 28.62 | 26.53 | 7.89 |
| 2 | 150 | 5 | 0.25 | 22.67 | 21.58 | 5.07 | ||
| 3 | 175 | 11 | 0.90 | 17.78 | 16.25 | 9.45 | ||
| 4 | 225 | 2 | 0.15 | 9.92 | 10.54 | 5.92 | ||
| 5 | 250 | 17 | 0.60 | 11.63 | 12.40 | 6.18 | ||
| 6 | 275 | 15 | 0.80 | 6.56 | 6.87 | 4.49 | ||
| KNN | 1 | 125 | 8 | 0.40 | 2.499/ 1.371 | 28.02 | 26.53 | 5.62 |
| 2 | 150 | 5 | 0.25 | 22.88 | 21.58 | 6.01 | ||
| 3 | 175 | 11 | 0.90 | 19.18 | 16.25 | 18.01 | ||
| 4 | 225 | 2 | 0.15 | 11.40 | 10.54 | 8.19 | ||
| 5 | 250 | 17 | 0.60 | 12.03 | 12.40 | 2.98 | ||
| 6 | 275 | 15 | 0.80 | 8.15 | 6.87 | 18.59 | ||
| ANN | 1 | 125 | 8 | 0.40 | 0.865/ 0.810 | 27.93 | 26.53 | 5.28 |
| 2 | 150 | 5 | 0.25 | 22.30 | 21.58 | 3.35 | ||
| 3 | 175 | 11 | 0.90 | 17.43 | 16.25 | 7.28 | ||
| 4 | 225 | 2 | 0.15 | 9.44 | 10.54 | 10.36 | ||
| 5 | 250 | 17 | 0.60 | 12.07 | 12.40 | 2.63 | ||
| 6 | 275 | 15 | 0.80 | 6.72 | 6.87 | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charalampous, P. Performance Investigation of Coated Carbide Tools in Milling Procedures. Appl. Sci. 2025, 15, 3765. https://doi.org/10.3390/app15073765
Charalampous P. Performance Investigation of Coated Carbide Tools in Milling Procedures. Applied Sciences. 2025; 15(7):3765. https://doi.org/10.3390/app15073765
Chicago/Turabian StyleCharalampous, Paschalis. 2025. "Performance Investigation of Coated Carbide Tools in Milling Procedures" Applied Sciences 15, no. 7: 3765. https://doi.org/10.3390/app15073765
APA StyleCharalampous, P. (2025). Performance Investigation of Coated Carbide Tools in Milling Procedures. Applied Sciences, 15(7), 3765. https://doi.org/10.3390/app15073765







