Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers
Abstract
1. Introduction
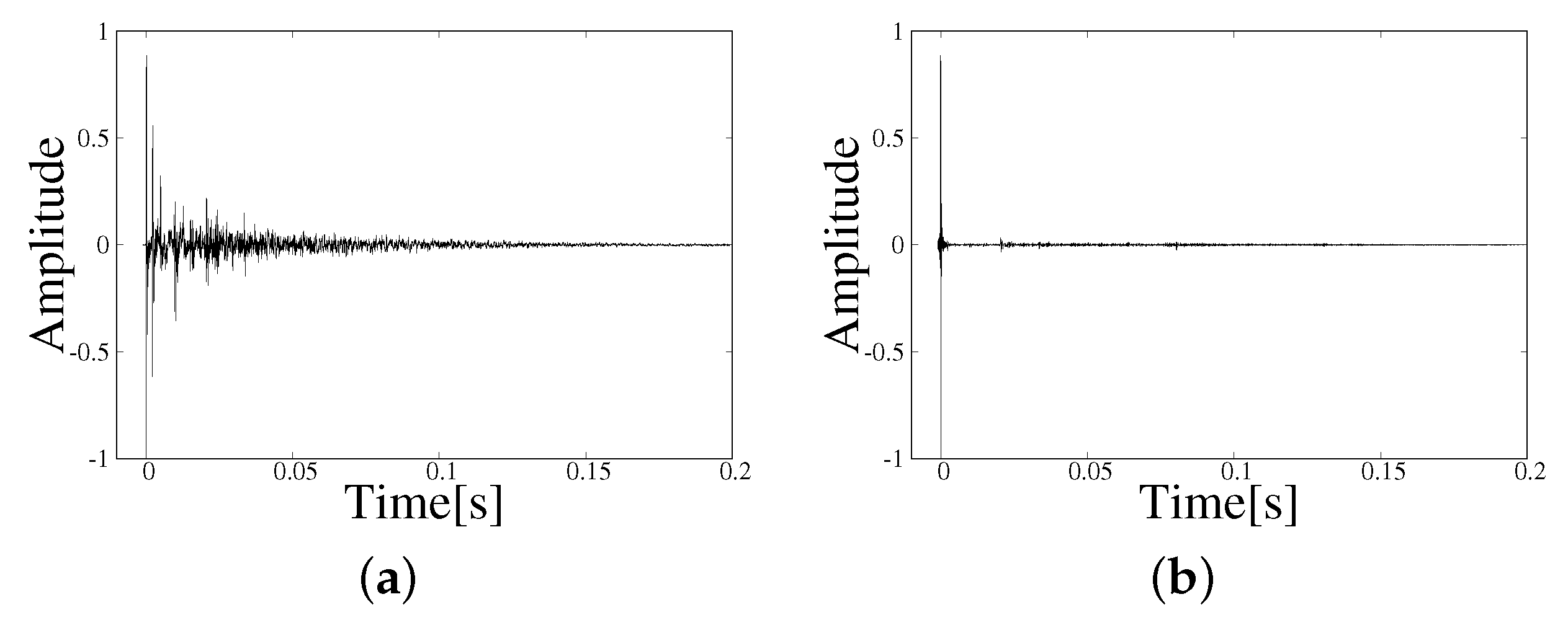
2. Analysis of Room Impulse Responses Using Parametric-Array Loudspeakers and Conventional Loudspeakers
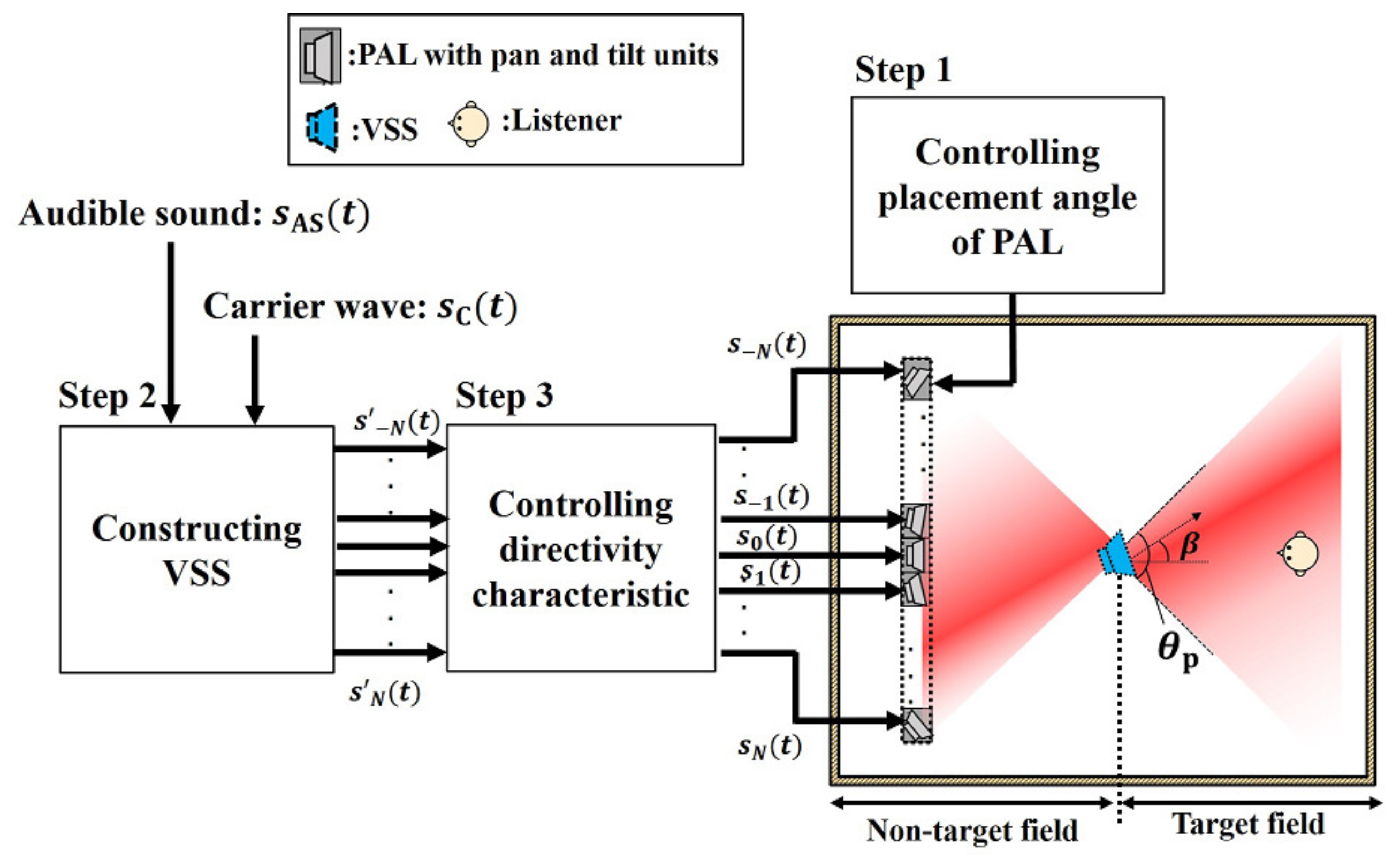
3. Conventional Construction of a VSS Based on Radiation Direction Control Using Parametric-Array Loudspeakers
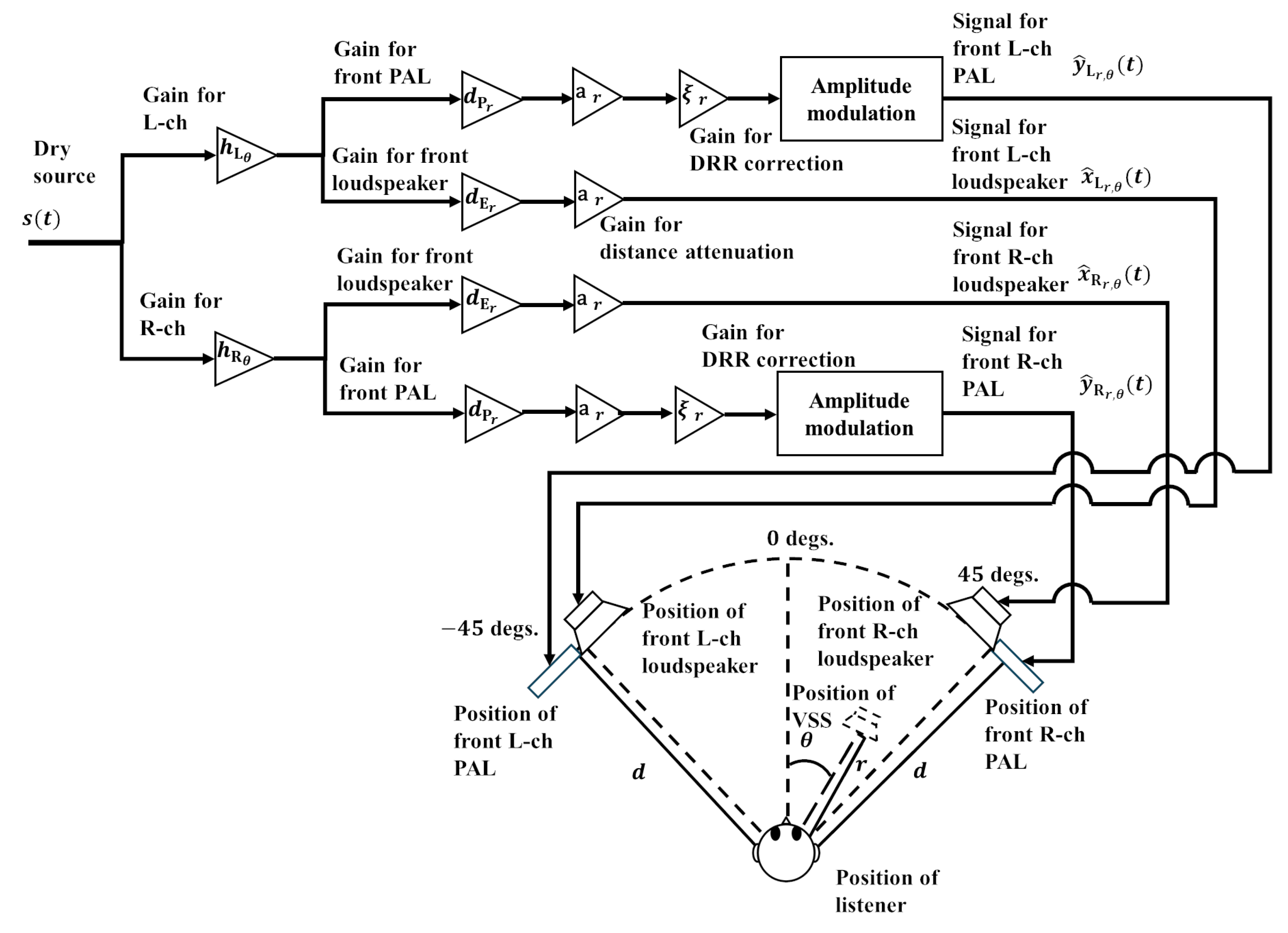
4. Proposed Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers
- The VSS in the front area (−45∘ to 45∘): The front L-ch PAL, the front L-ch loudspeaker, the front R-ch PAL, and the front R-ch loudspeaker in Figure 3 are driven;
- The VSS in the right area (45∘ to 135∘): The front R-ch PAL, the front R-ch loudspeaker, the rear R-ch PAL, and the rear R-ch loudspeaker in Figure 3 are driven;
- The VSS in the rear area (135∘ to −135∘): The rear R-ch PAL, the rear R-ch loudspeaker, the rear L-ch PAL, and the rear L-ch loudspeaker in Figure 3 are driven;
- The VSS in the left area (−135∘ to −45∘): The front L-ch PAL, the front L-ch loudspeaker, the rear L-ch PAL, and the rear L-ch loudspeaker in Figure 3 are driven.
- The output signal for the front R-ch loudspeaker: ;
- The output signal for the front R-ch PAL: ;
- The output signal for the rear R-ch loudspeaker: ;
- The output signal for the rear R-ch PAL: .
- The output signal for the rear R-ch loudspeaker: ;
- The output signal for the rear R-ch PAL: ;
- The output signal for the rear L-ch loudspeaker: ;
- The output signal for the rear L-ch PAL: .
- The output signal for the rear L-ch loudspeaker: ;
- The output signal for the rear L-ch PAL: ;
- The output signal for the front L-ch loudspeaker: ;
- The output signal for the front L-ch PAL: .
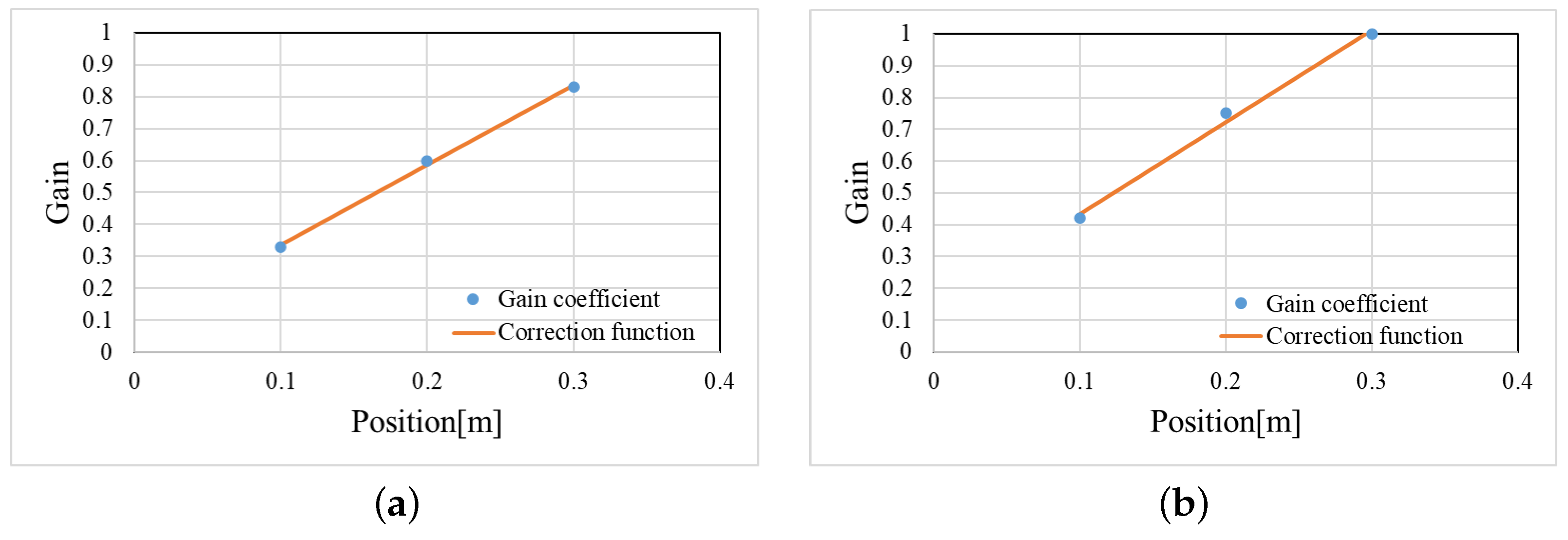
5. DRR Correction Based on a Regression Analysis
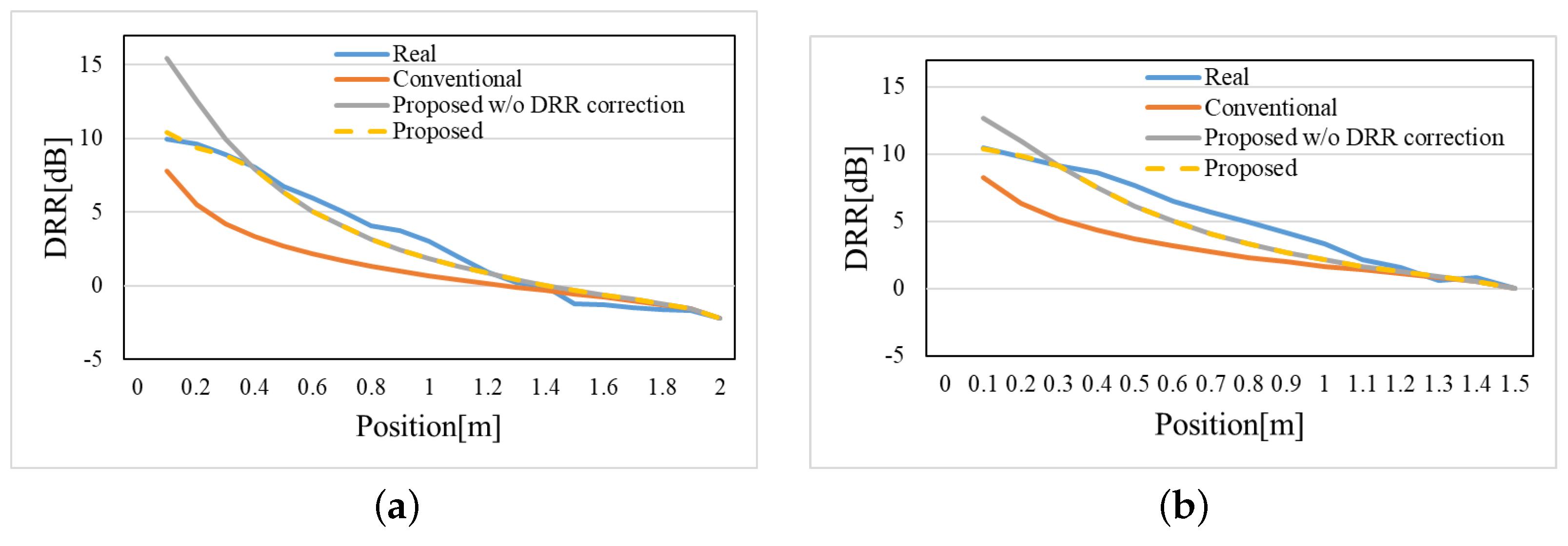
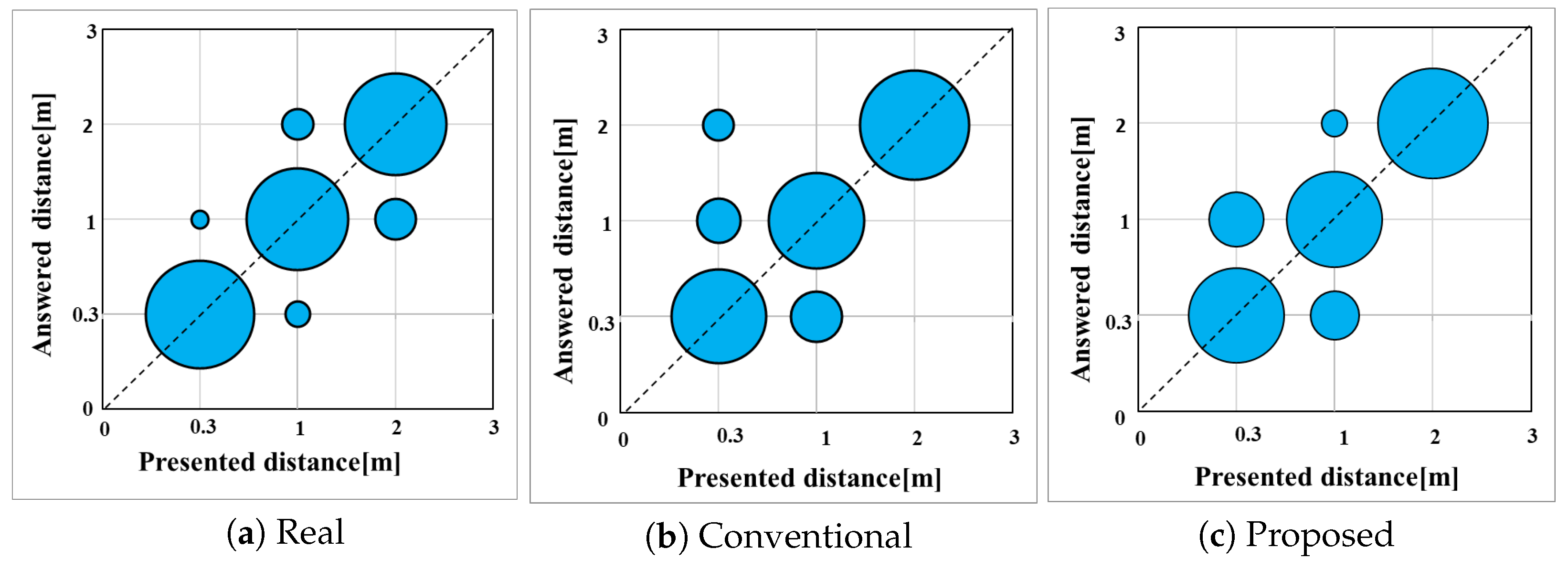
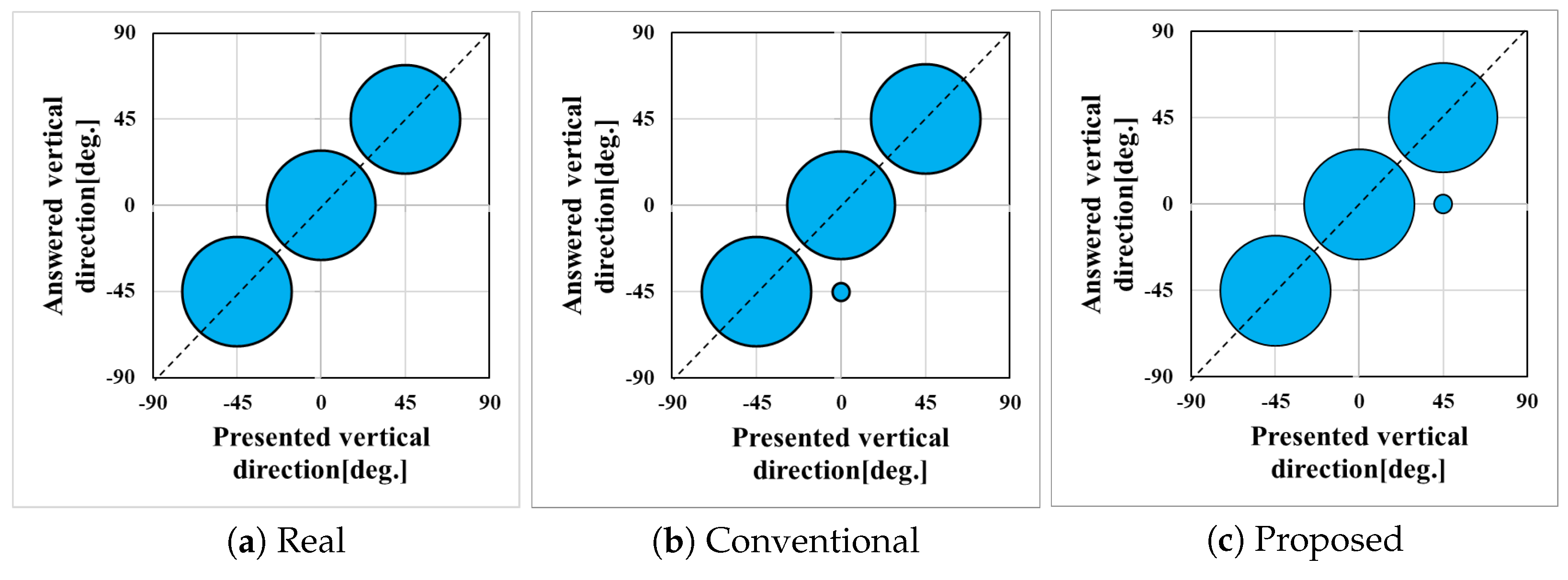
6. The Objective Evaluation Experiment
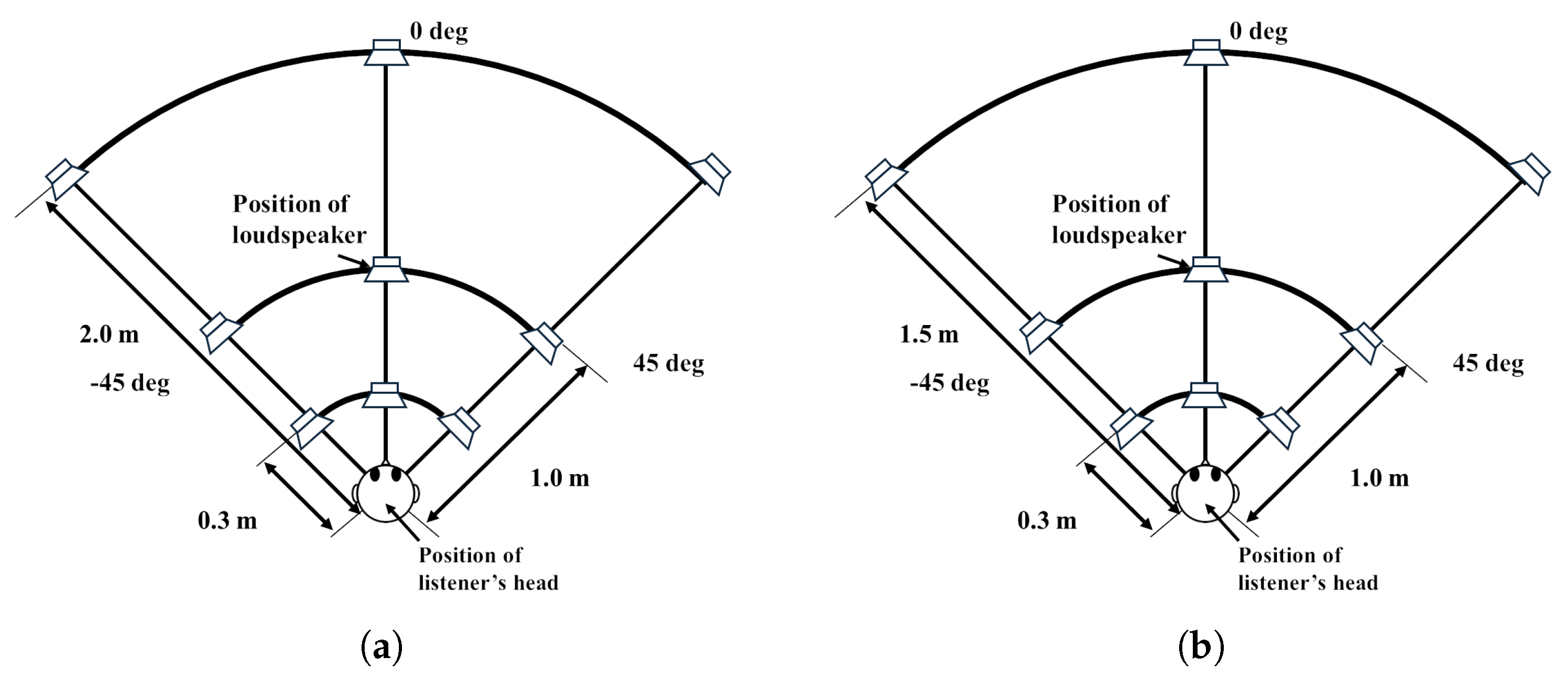
6.1. The Experimental Conditions with Objective Evaluation
- Real: The real sound source using a loudspeaker;
- Conventional: The conventional method [45];
- Proposed w/o DRR correction: The proposed method without DRR correction;
- Proposed: The proposed method.
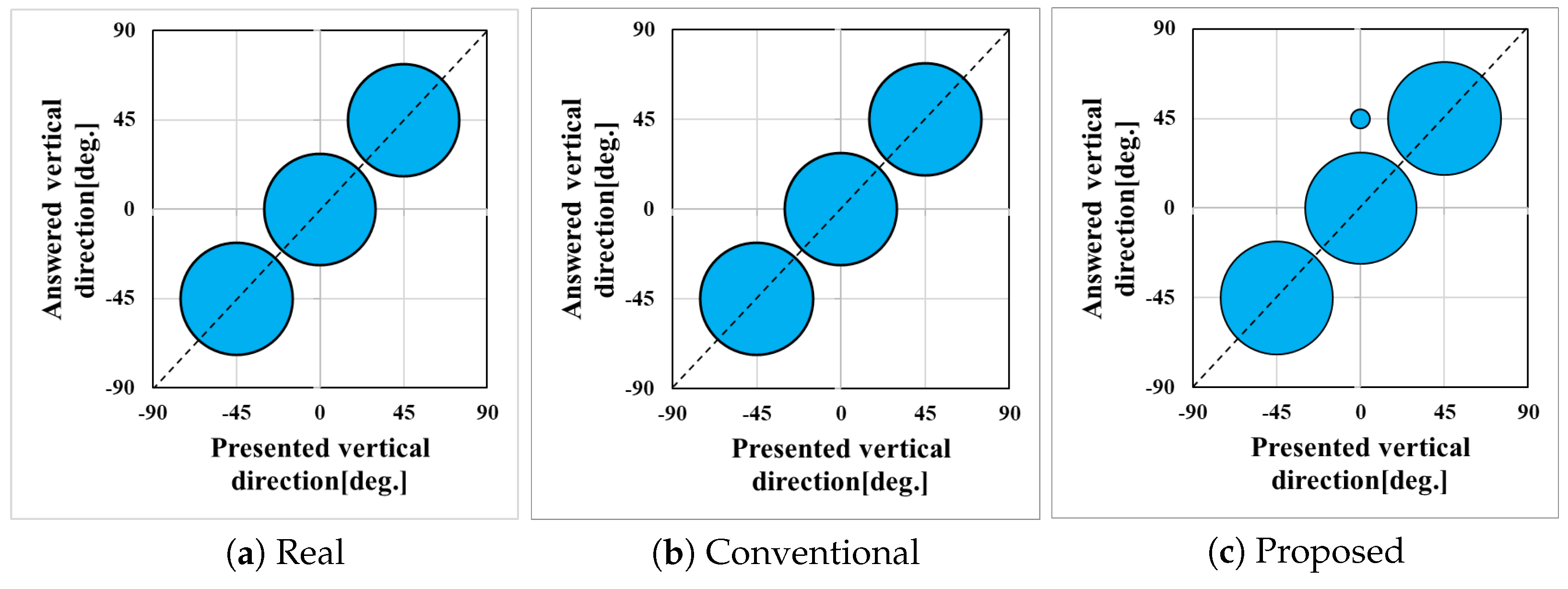
6.2. The Experimental Results Obtained Through the Objective Evaluation
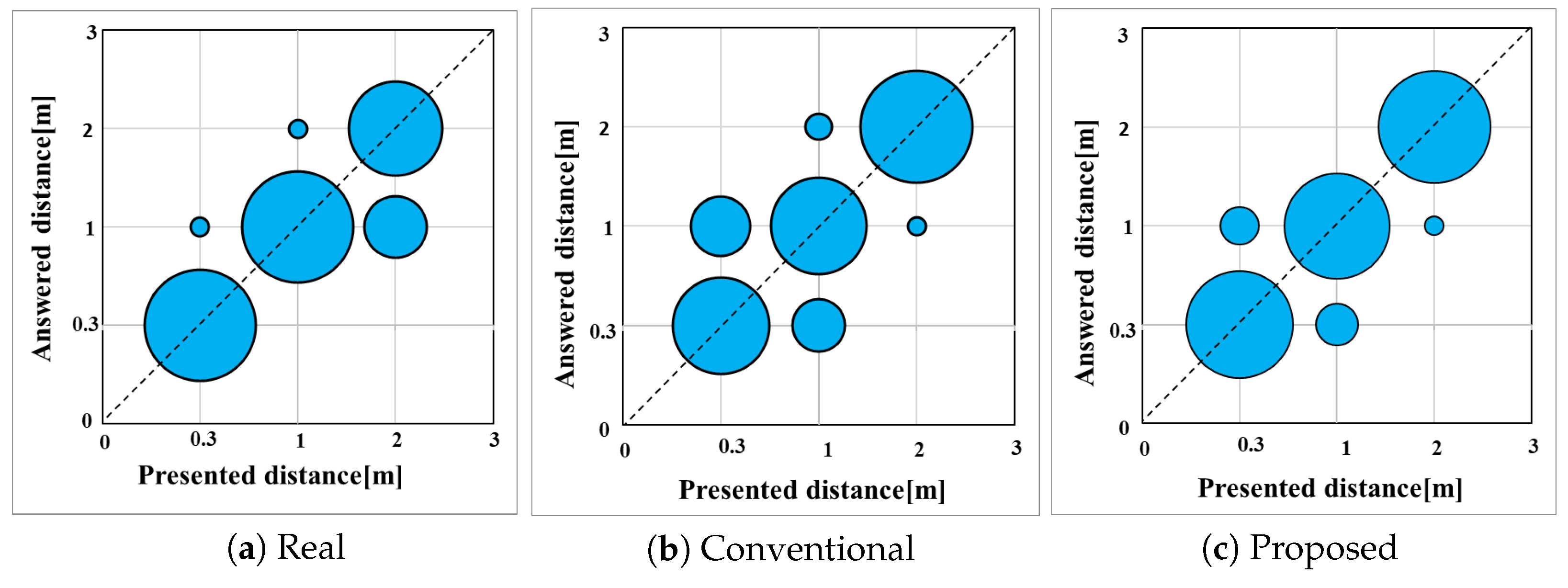
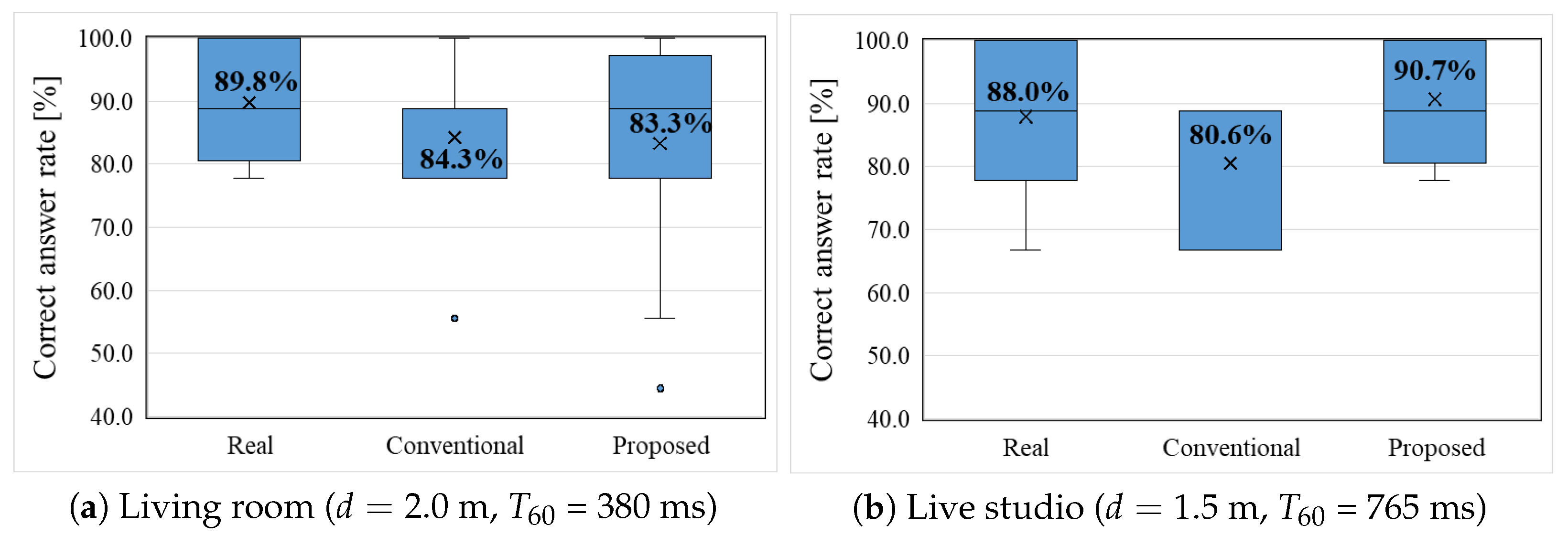
7. The Subjective Evaluation Experiment
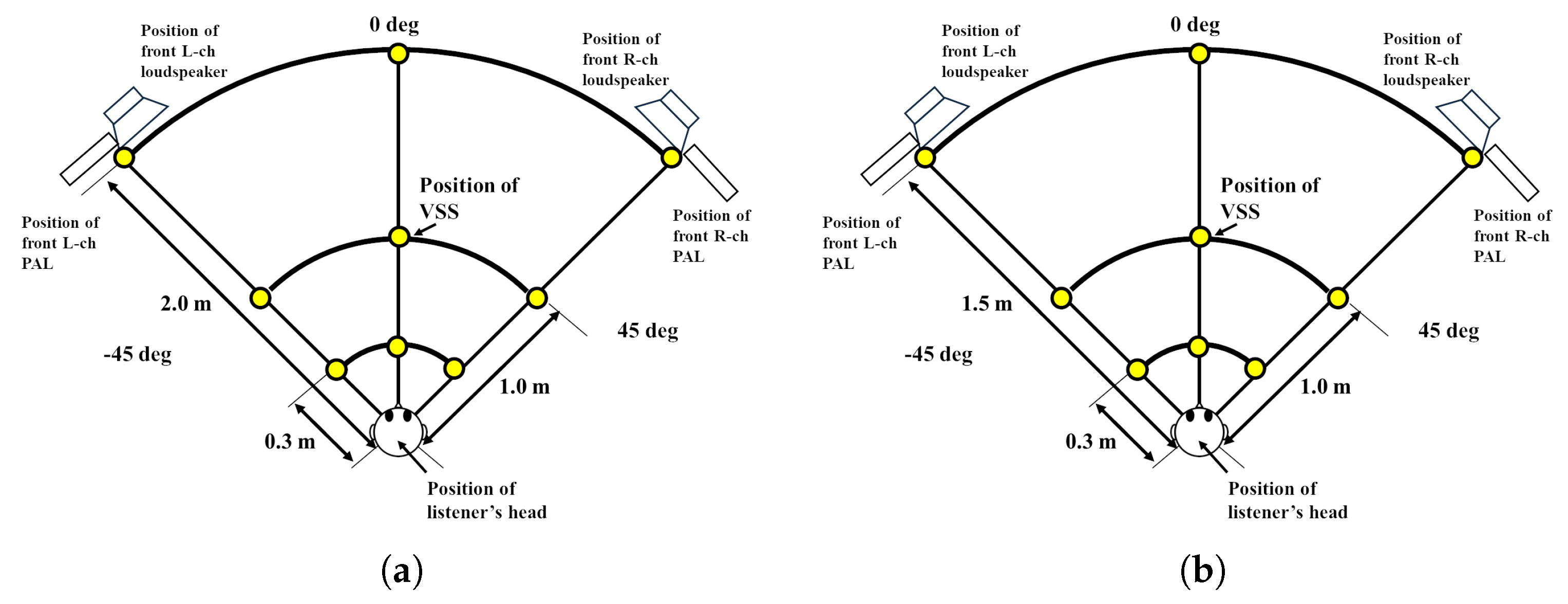
7.1. Experimental Conditions for the Subjective Evaluation
- Real: The real sound source using the loudspeaker;
- Conventional: The conventional method [45];
- Proposed: The proposed method.
7.2. Experimental Results of the Subjective Evaluation
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berkout, A.; de Vries, D.; Vogel, P. Acoustic control by wave field synthesis. J. Acoust. Soc. Am. 1993, 93, 2764–2778. [Google Scholar]
- Bauck, J.; Cooper, D. Generalized transaural stereo and applications. J. Acoust. Soc. Am. 1996, 44, 683–705. [Google Scholar]
- Zhang, G.; Huang, Q.; Liu, K. Three-dimensional sound field reproduction based on multi-resolution sparse representation. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015; pp. 1–5. [Google Scholar]
- Zhou, L.; Bao, C.; Jia, M.; Bu, B. Range extrapolation of Head-Related Transfer Function using improved Higher Order Ambisonics. In Proceedings of the Signal and Information Processing Association Annual Summit and Conference (APSIPA), 2014 Asia-Pacific, Siem Reap, Cambodia, 9–12 December 2014; pp. 1–4. [Google Scholar]
- Tomasetti, M.; Turchet, L. Playing With Others Using Headphones: Musicians Prefer Binaural Audio With Head Tracking Over Stereo. IEEE Trans.-Hum.-Mach. Syst. 2023, 53, 501–511. [Google Scholar]
- Gao, R.; Grauman, K. 2.5D Visual Sound. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 324–333. [Google Scholar]
- Zaunschirm, M.; Schorkhuber, C.; Holdrich, R. Binaural rendering of Ambisonic signals by head-related impulse response time alignment and a diffuseness constraint. J. Acoust. Soc. Am. 2018, 143, 3616–3627. [Google Scholar] [CrossRef]
- Alotaibi, S.S.; Wickert, M. Modeling of Individual Head-Related Transfer Functions (HRTFs) Based on Spatiotemporal and Anthropometric Features Using Deep Neural Networks. IEEE Access 2024, 12, 14620–14635. [Google Scholar]
- Romigh, G.D.; Brungart, D.S.; Stern, R.M.; Simpson, B.D. Efficient Real Spherical Harmonic Representation of Head-Related Transfer Functions. IEEE J. Sel. Top. Signal Process. 2015, 9, 921–930. [Google Scholar]
- Wang, Y.; Yu, G. Typicality analysis on statistical shape model-based average head and its head-related transfer functions. J. Acoust. Soc. Am. 2025, 157, 57–69. [Google Scholar]
- Kurabayashi, H.; Otani, M.; Itoh, K.; Hashimoto, M.; Kayama, M. Development of dynamic transaural reproduction system using non-contact head tracking. In Proceedings of the 2013 IEEE 2nd Global Conference on Consumer Electronics (GCCE), Tokyo, Japan, 1–4 October 2013; pp. 12–16. [Google Scholar]
- Samejima, T.; Kobayashi, K.; Sekiguchi, S. Transaural system using acoustic contrast as its objective function. Acoust. Sci. Technol. 2021, 42, 206–209. [Google Scholar]
- Shore, A.; Tropiano, A.J.; Hartmann, W.M. Matched transaural synthesis with probe microphones for psychoacoustical experiments. J. Acoust. Soc. Am. 2019, 145, 1313–1330. [Google Scholar]
- Shore, A.; Hartmann, W.M. Improvements in transaural synthesis with the Moore-Penrose pseudoinverse matrix. J. Acoust. Soc. Am. 2018, 143, 1938. [Google Scholar]
- Omoto, A.; Ise, S.; Ikeda, Y.; Ueno, K.; Enomoto, S.; Kobayashiy, M. Sound field reproduction and sharing system based on the boundary surface control principle. Acoust. Sci. Technol. 2015, 36, 1–11. [Google Scholar] [CrossRef][Green Version]
- Zheng, J.; Tu, W.; Zhang, X.; Yang, W.; Zhai, S.; Shen, C. A Sound Image Reproduction Model Based on Personalized Weight Vectors. In Advances in Multimedia Information Processing–PCM 2018: 19th Pacific-Rim Conference on Multimedia, Hefei, China, 21–22 September 2018; Proceedings, Part II 19; Springer International Publishing: Cham, Switzerland, 2018; pp. 607–617. [Google Scholar]
- Hirohashi, M.; Haneda, Y. Subjective Evaluation of a Focused Sound Source Reproducing at the positions of a Listenerfs Moving Hand. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Taipei, Taiwan, 31 October–3 November 2023; pp. 2395–2401. [Google Scholar]
- Jeon, I.; Lee, S. Driving function in wave field synthesis with integral approximation considering uneven contribution of loudspeaker units. J. Acoust. Soc. Am. 2024, 156, 3877–3892. [Google Scholar] [CrossRef] [PubMed]
- Lund, T. Enhanced Localization in 5.1 Production. J. Audio Eng. Soc. 2000, 109, 5243. [Google Scholar]
- Hamasaki, K.; Nishiguchi, T.; Okumura, R.; Nakayama, Y.; Ando, A. A 22.2 multichannel sound system for ultrahigh-definition TV. SMPTE Motion Imaging J. 2008, 117, 40–49. [Google Scholar] [CrossRef]
- Rumsey, F. Immersive Audio, Objects, and Coding. J. Audio Eng. Soc. 2015, 63, 394–398. [Google Scholar]
- Rumsey, F. Immersive Audio: Objects, Mixing, and Rendering. J. Audio Eng. Soc. 2016, 64, 584–588. [Google Scholar]
- Pulkki, V. Virtual Sound Source Positioning Using Vector Base Amplitude Panning. J. Audio Eng. Soc. 1997, 45, 456–466. [Google Scholar]
- Daniel, J.; Nicol, R.; Moreau, S. Further investigations of High Order Ambisonics and wavefield synthesis for holophonic sound imaging. In Proceedings of the Audio Engineering Society 114th International Convention, Amsterdam, The Netherlands, 22–25 March 2003; p. 5788. [Google Scholar]
- Lopez, J.; Gutierrez, P.; Cobos, M.; Aguilera, E. Sound distance perception comparison between Wave Field Synthesis and Vector Base Amplitude Panning. In Proceedings of the 2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014; pp. 165–168. [Google Scholar]
- Yang, L.; Yang, L.; Ho, K. Moving target localization in multistatic sonar using time delays, Doppler shifts and arrival angles. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3399–3403. [Google Scholar]
- Roman, N.; Wang, D.; Brow, G. Speech segregation based on sound localization. J. Acoust. Soc. Am. 2003, 114, 2236–2252. [Google Scholar] [CrossRef]
- Kuttruff, H. Room Acousticsn; Elsevier Science Publishers Ltd.: Cambridge, UK, 1973. [Google Scholar]
- Lu, Y.C.; Cooke, M. Binaural Estimation of Sound Source Distance via the Direct-to-Reverberant Energy Ratio for Static and Moving Sources. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1793–1805. [Google Scholar]
- Madmoni, L.; Tibor, S.; Nelken, I.; Rafaely, B. The Effect of Partial Time-Frequency Masking of the Direct Sound on the Perception of Reverberant Speech. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 2037–2047. [Google Scholar] [CrossRef]
- Prodi, N.; Pellegatti, M.; Visentin, C. Effects of type of early reflection, clarity of speech, reverberation and diffuse noise on the spatial perception of a speech source and its intelligibility. J. Acoust. Soc. Am. 2022, 151, 3522–3534. [Google Scholar] [PubMed]
- Ogami, Y.; Nakayama, M.; Nishiura, T. Virtual sound source construction based on radiation direction control using multiple parametric array loudspeakers. J. Acoust. Soc. Am. 2019, 146, 1314–1325. [Google Scholar] [PubMed]
- Geng, Y.; Sayama, S.; Nakayama, M.; Nishiura, T. Movable Virtual Sound Source Construction Based on Wave Field Synthesis using a Linear Parametric Loudspeaker Array. APSIPA Trans. Signal Inf. Process. 2023, 12, 1–21. [Google Scholar] [CrossRef]
- Zhu, Y.; Qin, L.; Ma, W.; Fan, F.; Wu, M.; Kuang, Z.; Yang, J. A nonlinear sound field control method for a multi-channel parametric array loudspeaker array. J. Acoust. Soc. Am. 2025, 157, 962–975. [Google Scholar]
- Ma, W.; Zhu, Y.; Ji, P.; Kuang, Z.; Wu, M.; Yang, J. Differential Volterra filter: A two-stage decoupling method for audible sounds generated by parametric array loudspeakers based on Westervelt equation. J. Acoust. Soc. Am. 2025, 157, 1057–1071. [Google Scholar]
- Westervelt, P. Parametric acoustic array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Aoki, K.; Kamakura, T.; Kumamoto, Y. Parametric loudspeaker-characteristics of acoustic field and suitable modulation of carrier ultrasound. Electron. Commun. Jpn. 1991, 74, 76–82. [Google Scholar] [CrossRef]
- Sugibayashi, Y.; Kurimoto, S.; Ikefuji, D.; Morise, M.; Nishiura, T. Three-dimensional acoustic sound field reproduction based on hybrid combination of multiple parametric loudspeakers and electrodynamic subwoofer. Appl. Acoust. 2012, 73, 1282–1288. [Google Scholar]
- Shi, C.; Nomura, H.; Kamakura, T.; Gan, W. Development of a steerable stereophonic parametric loudspeaker. In Proceedings of the Signal and Information Processing Association Annual Summit and Conference (APSIPA), 2014 Asia-Pacific, Siem Reap, Cambodia, 9–12 December 2014; pp. 1–5. [Google Scholar]
- Ikefuji, D.; Tsujii, H.; Masunaga, S.; Nakayama, M.; Nishiura, T.; Yamashita, Y. Reverberation Steering and Listening Area Expansion on 3-D Sound Field Reproduction with Parametric Array Loudspeaker. In Proceedings of the Signal and Information Processing Association Annual Summit and Conference (APSIPA), 2014 Asia-Pacific, Siem Reap, Cambodia, 9–12 December 2014; pp. 1–5. [Google Scholar]
- Geng, Y.; Shimokata, M.; Nakayama, M.; Nishiura, T. Visualization of Demodulated Sound Based on Sequential Acoustic Ray Tracing with Self-Demodulation in Parametric Array Loudspeakers. Appl. Sci. 2024, 14, 5241. [Google Scholar] [CrossRef]
- Geng, Y.; Hirose, A.; Iwagami, M.; Nakayama, M.; Nishiura, T. Enhanced Virtual Sound Source Construction Based on Wave Field Synthesis Using Crossfade Processing with Electro-Dynamic and Parametric Loudspeaker Arrays. Appl. Sci. 2024, 14, 11911. [Google Scholar] [CrossRef]
- Nakayama, M.; Nishiura, T. Distance Control of Virtual Sound Source Using Parametric and Dynamic Loudspeakers. In Proceedings of the 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, 12–15 November 2018; pp. 1262–1267. [Google Scholar]
- Ekawa, T.; Nakayama, M.; Takahashi, T. Virtual Sound Source Rendering Based on Distance Control to Penetrate Listeners Using Surround Parametric-array and Electrodynamic Loudspeakers. In Proceedings of the 2021 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Tokyo, Japan, 14–17 December 2021; pp. 1008–1015. [Google Scholar]
- Ekawa, T.; Geng, Y.; Nishiura, T.; Nakayama, M. Mid-air Acoustic Hologram Using Distance Attenuation and Phase Correction with Parametric-array and Electrodynamic Loudspeakers. In Proceedings of the 2021 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Tokyo, Japan, 14–17 December 2021; pp. 1–4. [Google Scholar]
- Berkhout, A.; de Vries, D.; Boone, M. A new method to acquir impulse responses in concert halls. J. Acoust. Soc. Am. 1980, 68, 179–183. [Google Scholar]
- Aoshima, N. Computer-generated pulse signal applied for sound measurement. J. Acoust. Soc. Am. 1981, 69, 1484–1488. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 6th ed.; Wiley Series in Probability and Mathematical Statistics; Wiley: New York, NY, USA, 2021. [Google Scholar]
- Roland. Zenbeats. 2019. Available online: https://www.roland.com/global/products/rc_zenbeats/ (accessed on 16 March 2025).



| PAL | MITSUBISHI ELECTRIC ENGINEERING in Tokyo, Japan, MSP-50E |
| Conventional loudspeaker | ELAC in Kiel, Germany, BS302 |
| Power amplifier | YAMAHA in Shizuoka, Japan, XM4180 |
| Microphone | SENNHEISER in Wedemark, Germany, MKH8020 |
| A/D, D/A converter | RME in Haimhausen, Germany, Fireface UFX II |
| Living room | 15,808, Building 15, Osaka Sangyo University in Osaka, Japan |
| Live studio | 17,104, Building 17, Osaka Sangyo University in Osaka, Japan |
| Reverberation time | Living room: = 380 ms Live studio: = 765 ms |
| Sampling frequency | 96 kHz |
| Quantization | 16 bits |
| Carrier frequency | 40 kHz |
| Modulation method | AM-DSB |
| Living Room | Live Studio | |
|---|---|---|
| 2.70 | 2.75 | |
| 0.12 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakayama, M.; Ekawa, T.; Takahashi, T.; Nishiura, T. Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers. Appl. Sci. 2025, 15, 3744. https://doi.org/10.3390/app15073744
Nakayama M, Ekawa T, Takahashi T, Nishiura T. Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers. Applied Sciences. 2025; 15(7):3744. https://doi.org/10.3390/app15073744
Chicago/Turabian StyleNakayama, Masato, Takuma Ekawa, Toru Takahashi, and Takanobu Nishiura. 2025. "Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers" Applied Sciences 15, no. 7: 3744. https://doi.org/10.3390/app15073744
APA StyleNakayama, M., Ekawa, T., Takahashi, T., & Nishiura, T. (2025). Virtual Sound Source Construction Based on Direct-to-Reverberant Ratio Control Using Multiple Pairs of Parametric-Array Loudspeakers and Conventional Loudspeakers. Applied Sciences, 15(7), 3744. https://doi.org/10.3390/app15073744








